1. Introduction
Floods are the most common and destructive natural disaster around the world. The dam-breaking and waterlogging events caused by floods have caused great losses of human lives and property throughout history [
1]. When the water level measured in large parts of a river becomes too high and exceeds its maximum capacity, flooding could occur. A recent study ranked floods as the greatest threat to 616 cities around the world over earthquakes and storms [
2]. There are many types of floods such as river floods, flash floods, urban floods, sewer flooding and coastal flooding in China. Affected by the monsoon climate and geographical conditions, China is seriously impacted by flood disasters, especially flash floods and river floods [
3]. Floods in the region has a wide range of impacts and can be sudden and strong, occur for long periods, frequent or seasonal. These obvious characteristics make floods one of the most important factors restricting China’s economic and social development. Hence, management and mitigation before and after a flood disaster are necessary and significant. The evaluation of risks in flood-prone areas and the construction of hydrological stations are effective means of prevention and monitoring before floods. Areas susceptible to flood must be detected in advance so that urbanization and industrialization can be prevented in these areas. In addition, some watersheds prone to flooding should be monitored with hydrological stations in the case of dangerous water levels.
Floods in different regions at different times are often caused directly by different factors [
4] while climate and human activities are common factors [
5]. Against the background of climate change in recent years, extreme rainy weather brings concentrated, intense and consecutive rainfall that quickly transforms into sediment and runoff [
6,
7]. Many cities were recently reported to encounter the highest recorded rainfall in history because massive urbanization and unwise city planning have replaced many forests and rivers with industrialized areas [
8]. Vegetation is able to contain soil and some rainfall [
9]. Conversely, large scale urban expansion reduces city permeability, However, the drainage functions developed in cities cannot reach the level required to swiftly discharge runoff in time [
10].
Two categories of flood models have been researched and developed which is either physically based or statistically based [
11]. The Storm Water Management Model, a good representative of many hydrological models, has been widely employed to simulate the flow and flood processes [
12]. Apart from detailed data and complicated calculations [
13], these models can only simulate the extent and velocity of flood inundation over small-scale areas through one dimensional or two-dimensional hydraulic models and require much time and hardware to compute [
14]. Both of two categories have been conducted in the many previous study based on the Yangtze River [
15].
Regarding statistical models that only consider correlation and cause-and-effect relationships, qualitative or semiquantitative methods such as multicriteria analytic hierarchy process (AHP) are frequently used to model the risks of disasters such as floods or landslides [
16,
17]. A previous study combined the AHP with a Bayesian Network to research the flooding risk in Guangzhou [
18]. These models are used widely because they have good calculation performance with simpler statistical theory. Other studies also use machine learning methods such as decision tree, SVM (support vector machine) and artificial neural network (ANN) to predict the spatial distribution of flood risk over large-scale regions with accuracies higher than 80% [
19,
20]. Expert weighting of the AHP is relatively subjective and the different factors in different regions at different times that result in disasters tend to show distinct relative importance, hence, experiences about the weights of factors in certain areas cannot be transfer directly to others [
21]. Machine learning algorithms such as ensembled decision tree model and ANN is more complicated and just like a black box so that its network structure and weight parameters are not interpretable [
22]. Moreover, these models ignore the spatial autocorrelation that exists flood disasters. Considering spatial effects in these models will probably further increase their performance.
Multivariate regression usually involves several spatial factors and non-spatial attribute data. Geographic Information System (GIS) is a powerful tool to collect, process, manage and analyze spatially referenced layers in table, vector or raster format [
23], and quantization calculation can mostly be easily integrated into it. Moreover, the visualization of GIS can make risk assessment accessible and easy to understand. Risk analysis of natural disasters integrated with GIS has been applied widely in the recent decades [
24].
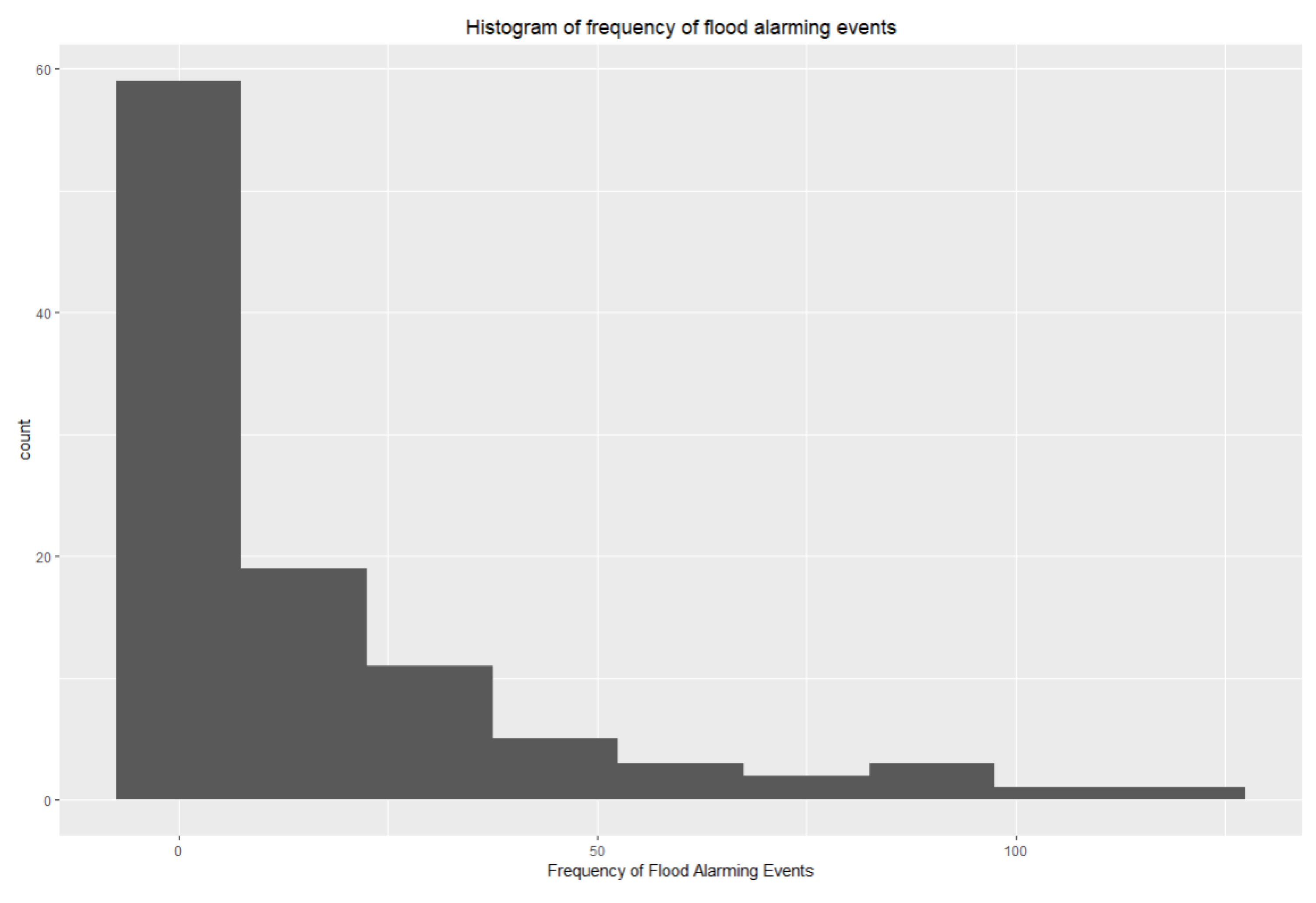
Poisson regression has been commonly applied to estimate disasters or disease risks and perform factor analysis [
25,
26]. The method is very suitable for modeling the data on the accumulated count of events that take place with low probability, such as diseases rate and death rates, especially when the observations approximately follow the Poisson distribution. Moreover, simple models such as generalized linear regression including Poisson regression are more suitable for small dataset and have more interpretability than complex machine learning algorithms. Aforementioned statistical models consider a weighted score or a probability as the metric of flood risk while the study considers the count of flood alarming events in history as the metric of flood risk because the frequency is also representative of occurrence rate when different hydrological stations have the same number of observations. The new data from hydrological stations currently available, allow a much better spatial pattern analysis. Moreover, some count observations often exhibit spatial autocorrelation which exists in most geospatial processes [
27], according to the First Law of Geography [
28]. Failure to consider spatial effects of flood alarming events based on the nature of the basin’s connectivity in the regression model will lead to model uncertainty, thus, spatial autocorrelation must be included in the regression model [
29,
30]. Whether spatial autocorrelation exists in the observations of geographical units can be tested using Moran’s I.
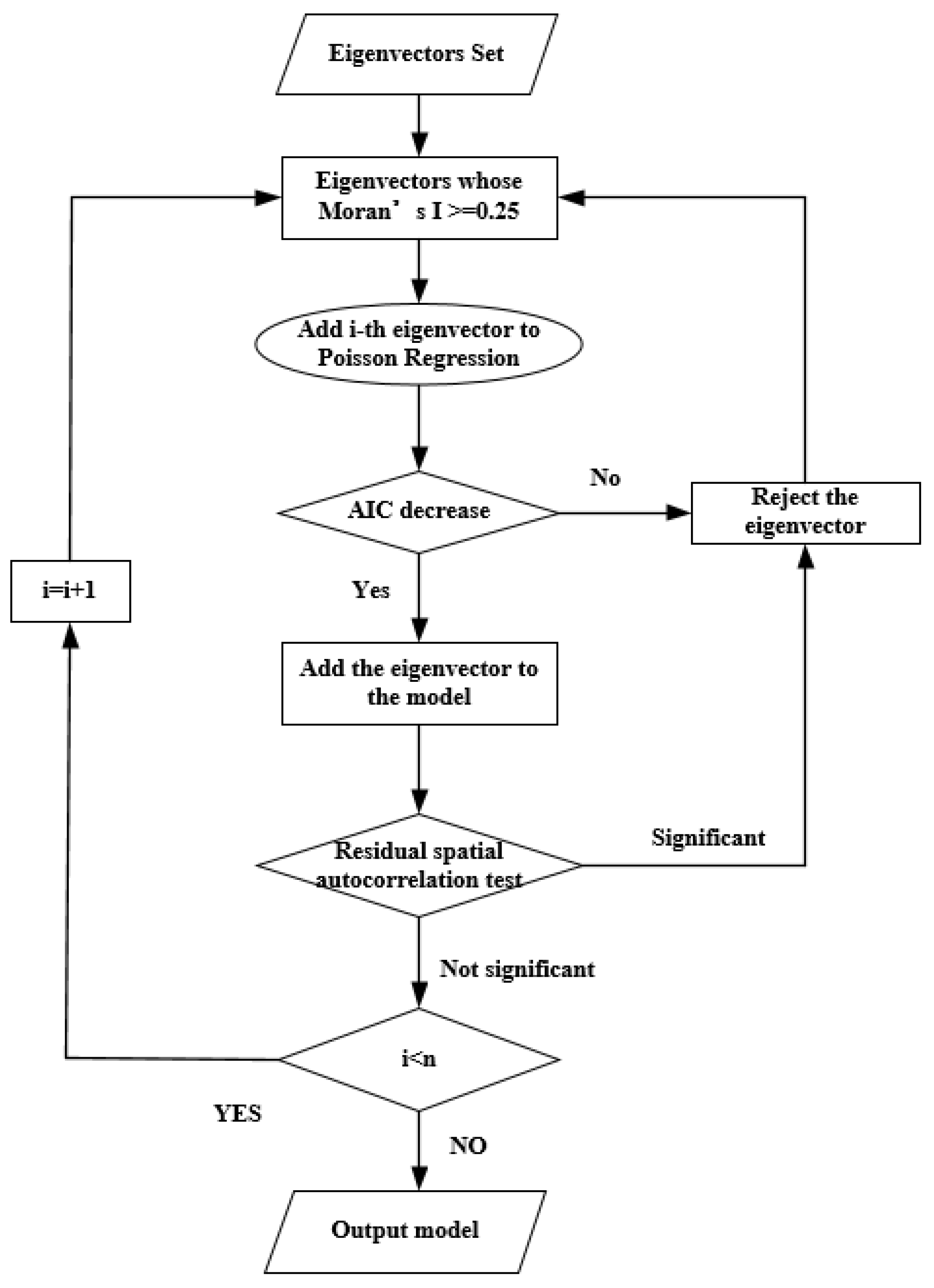
Eigenvector spatial filtering method is proposed to account for spatial effects [
31]. This method selects a subset of eigenvectors from the spatial weight matrix that represent the spatial distribution pattern and then adds them to the ordinary Poisson regression model as independent proxy variables [
32]. The linear combination of these eigenvectors filters the spatial autocorrelation out of the observations, which enables the observations in different geographical units to be independent [
33,
34].
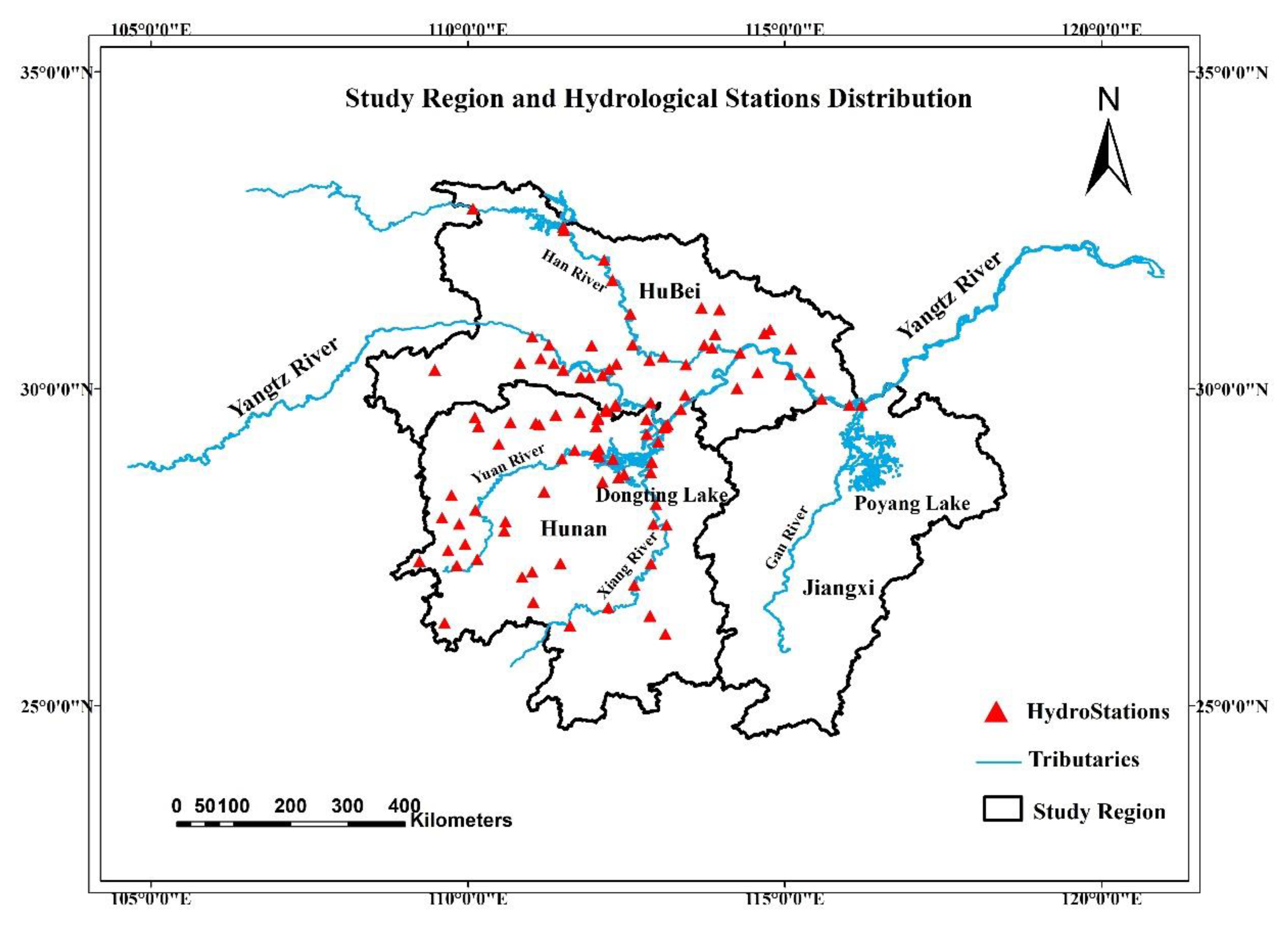
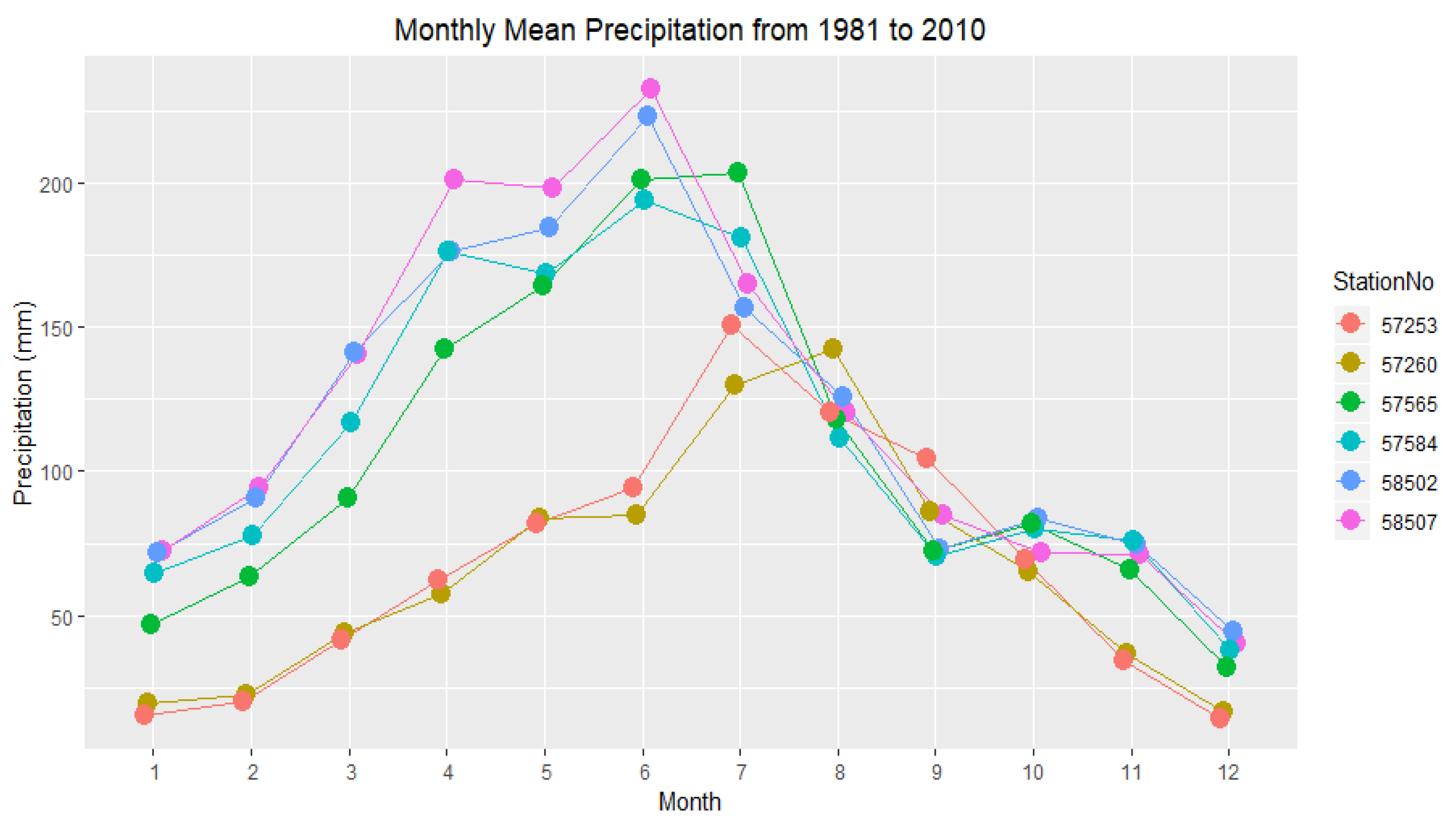
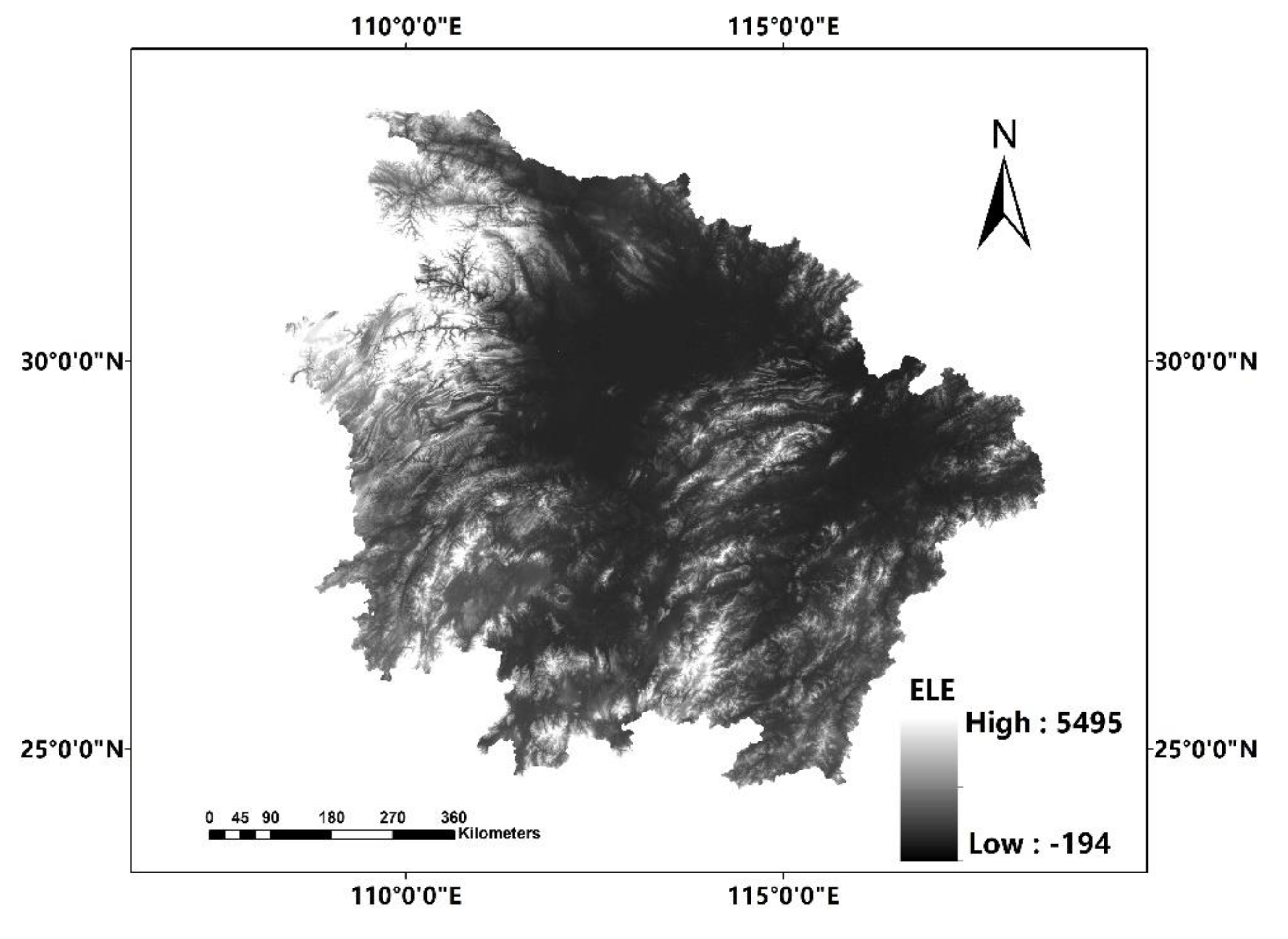
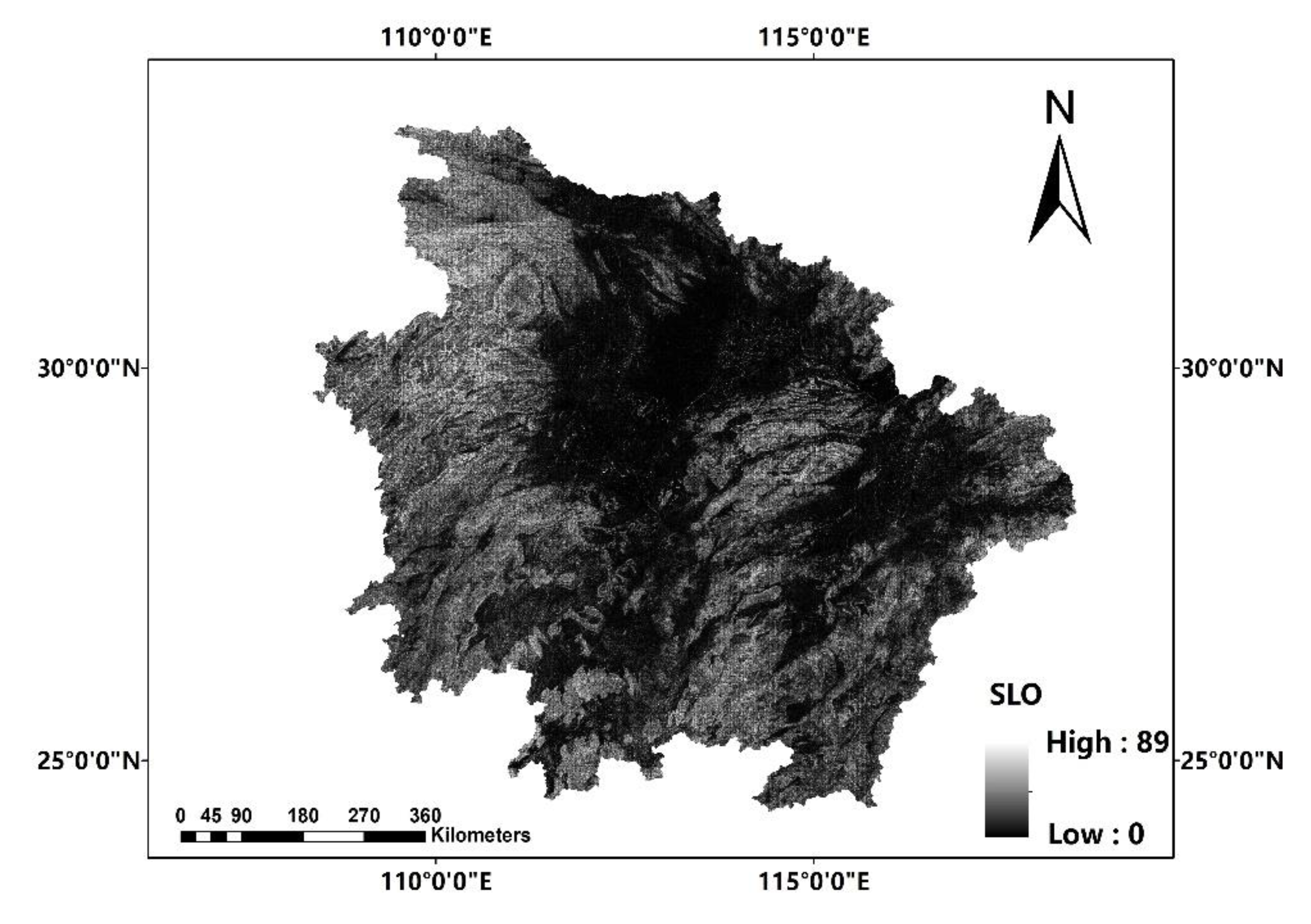
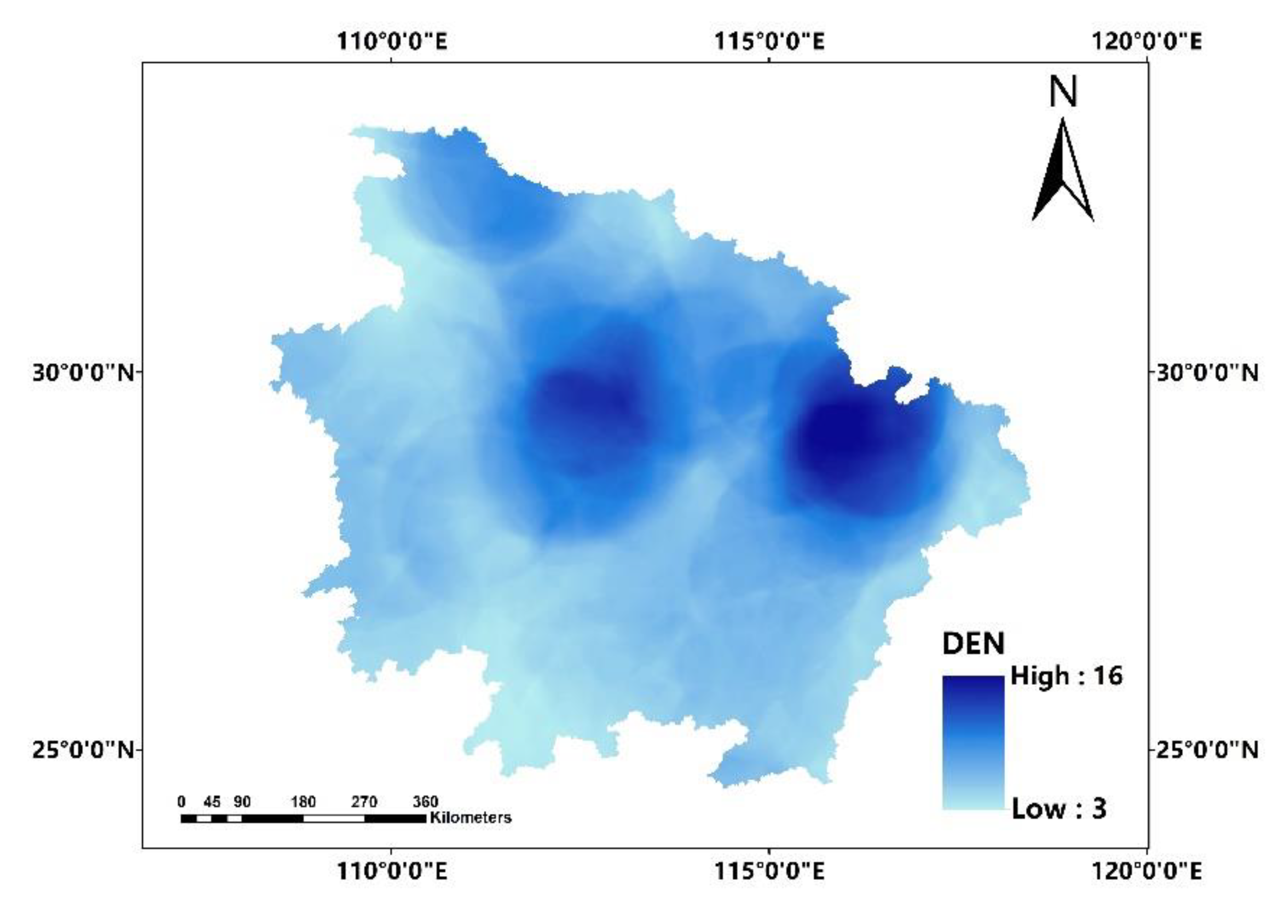
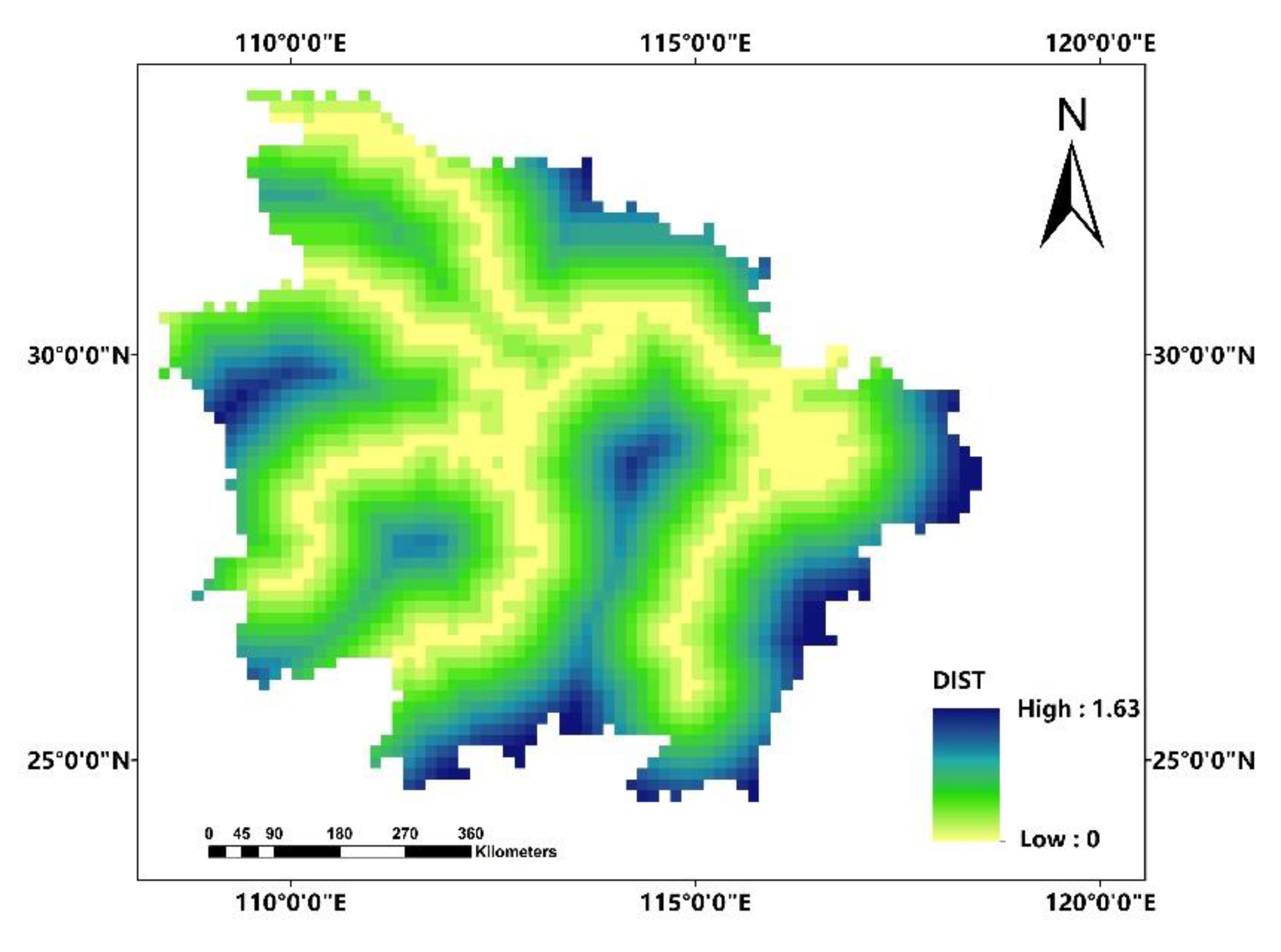
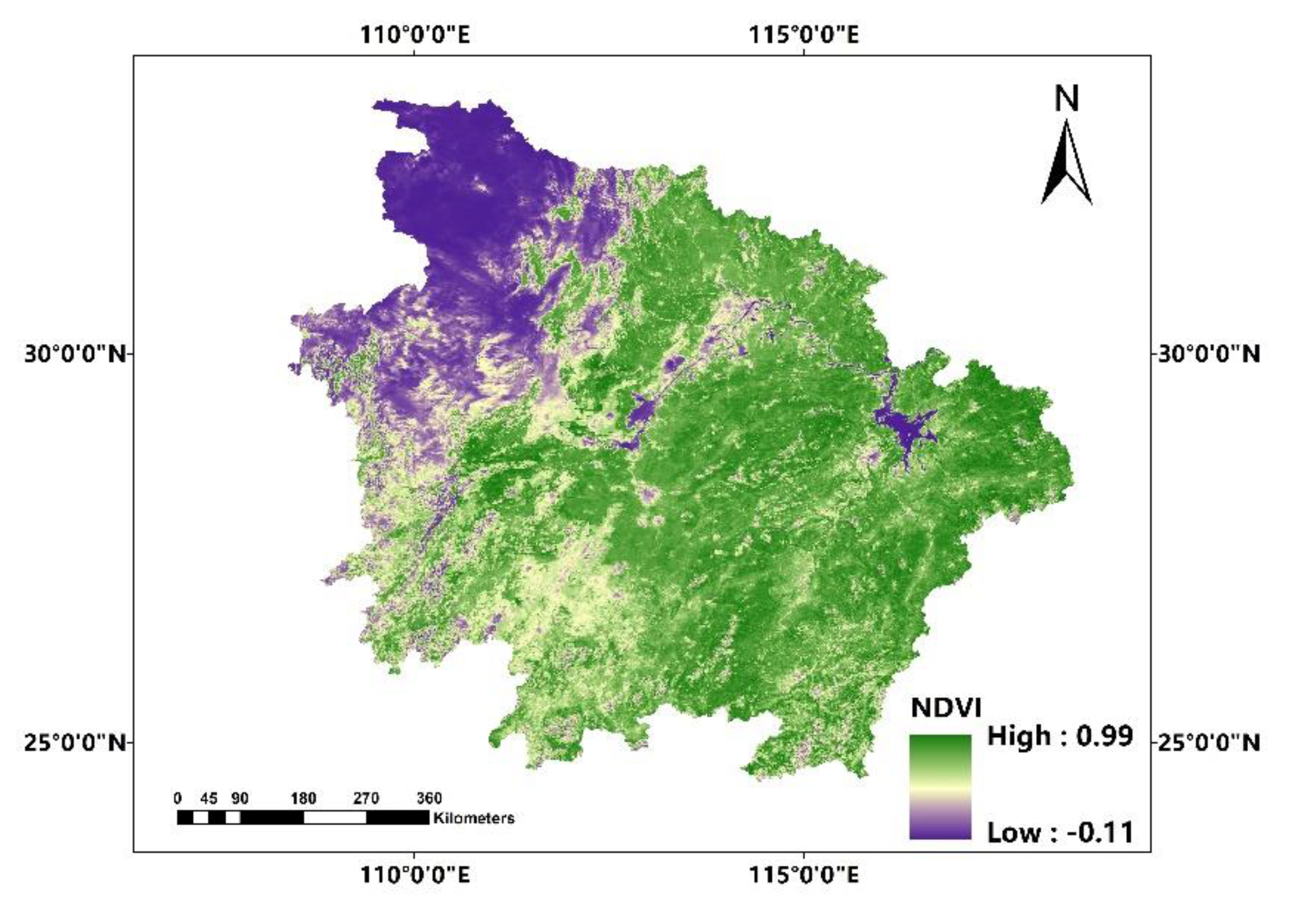
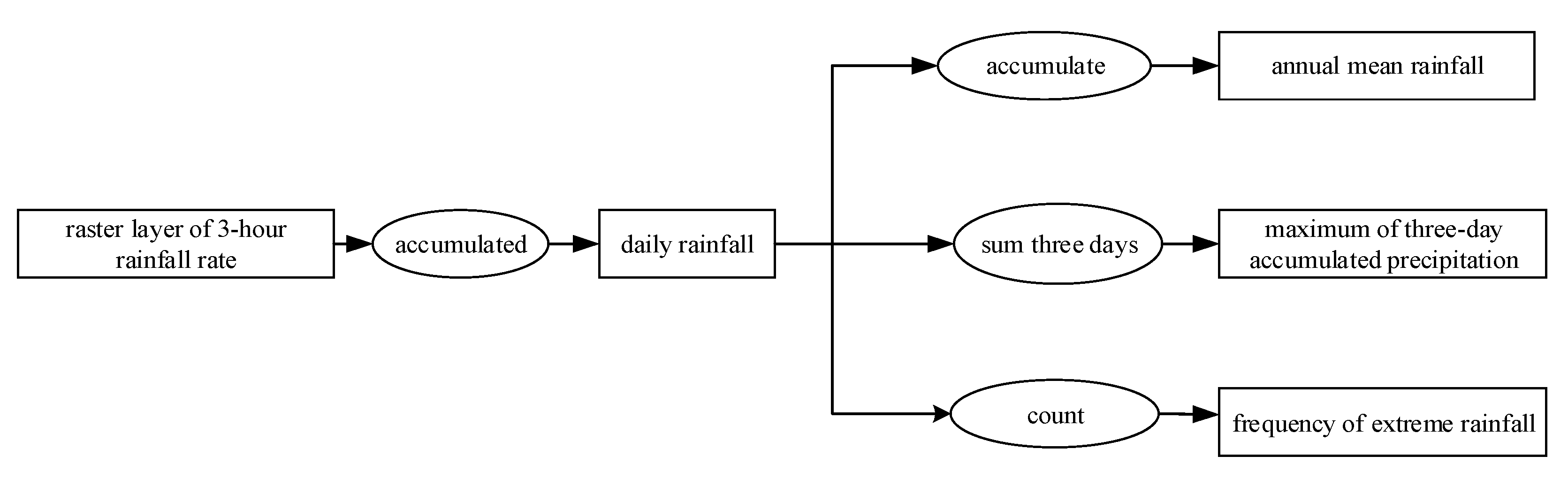
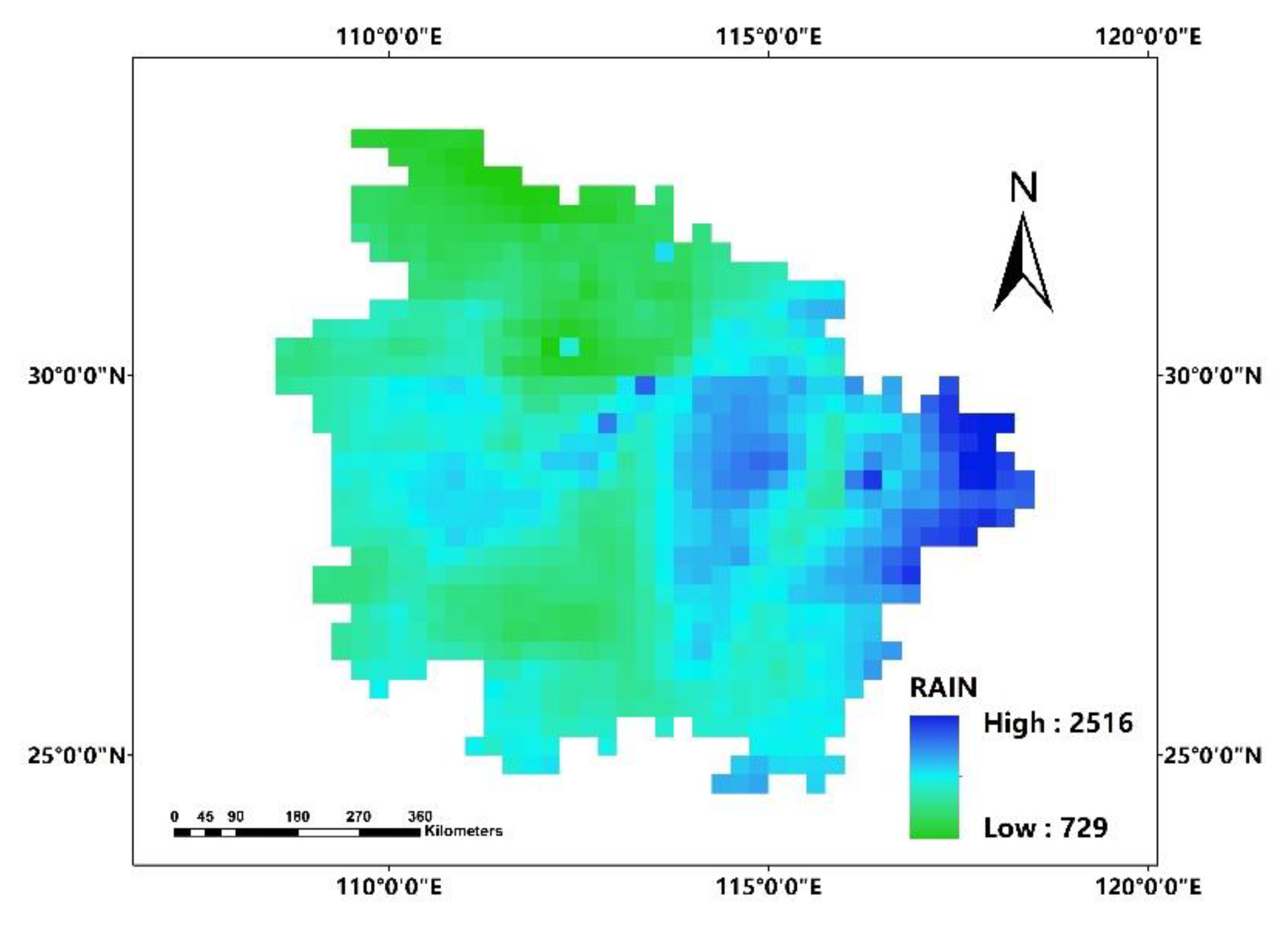
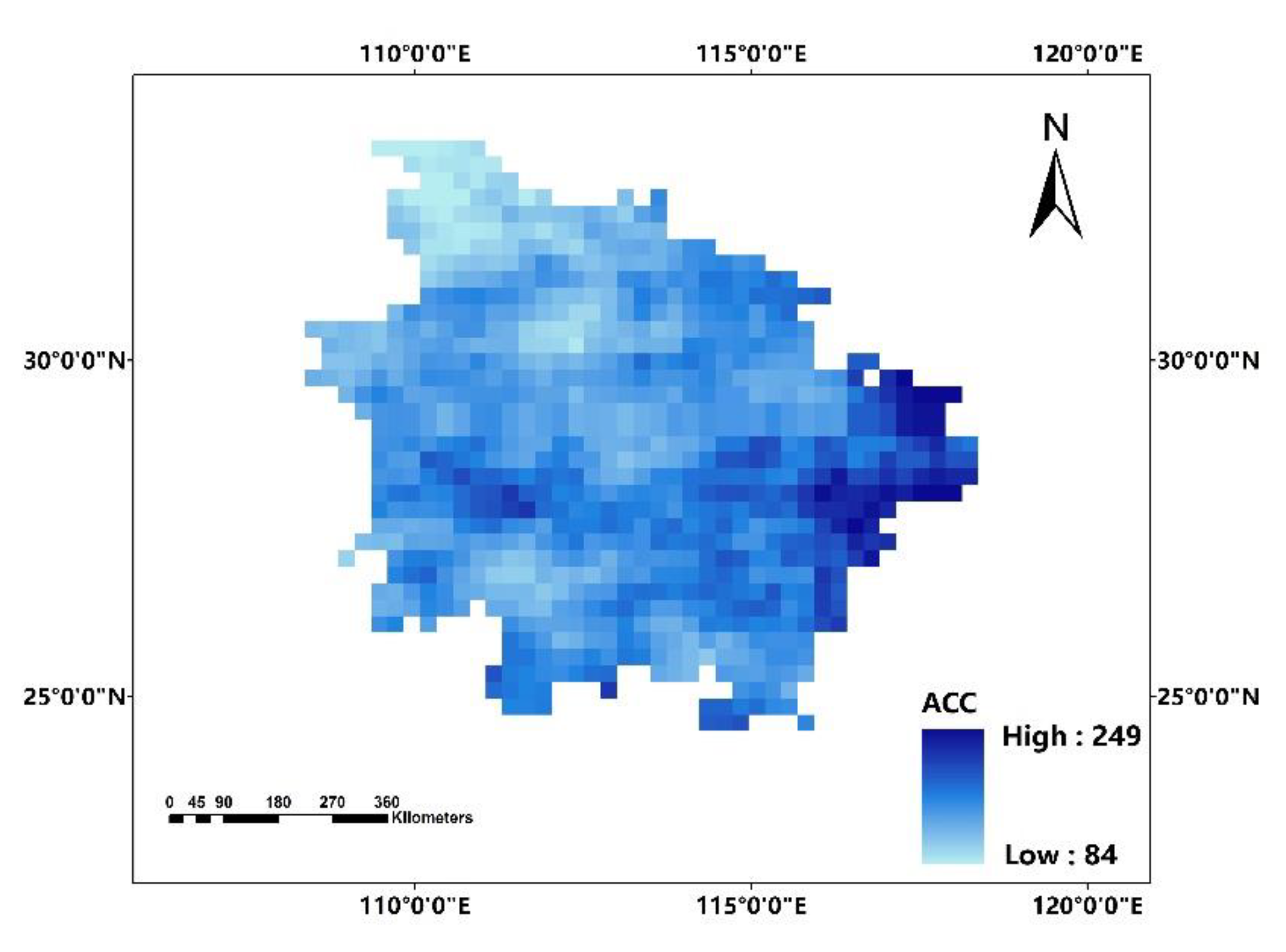
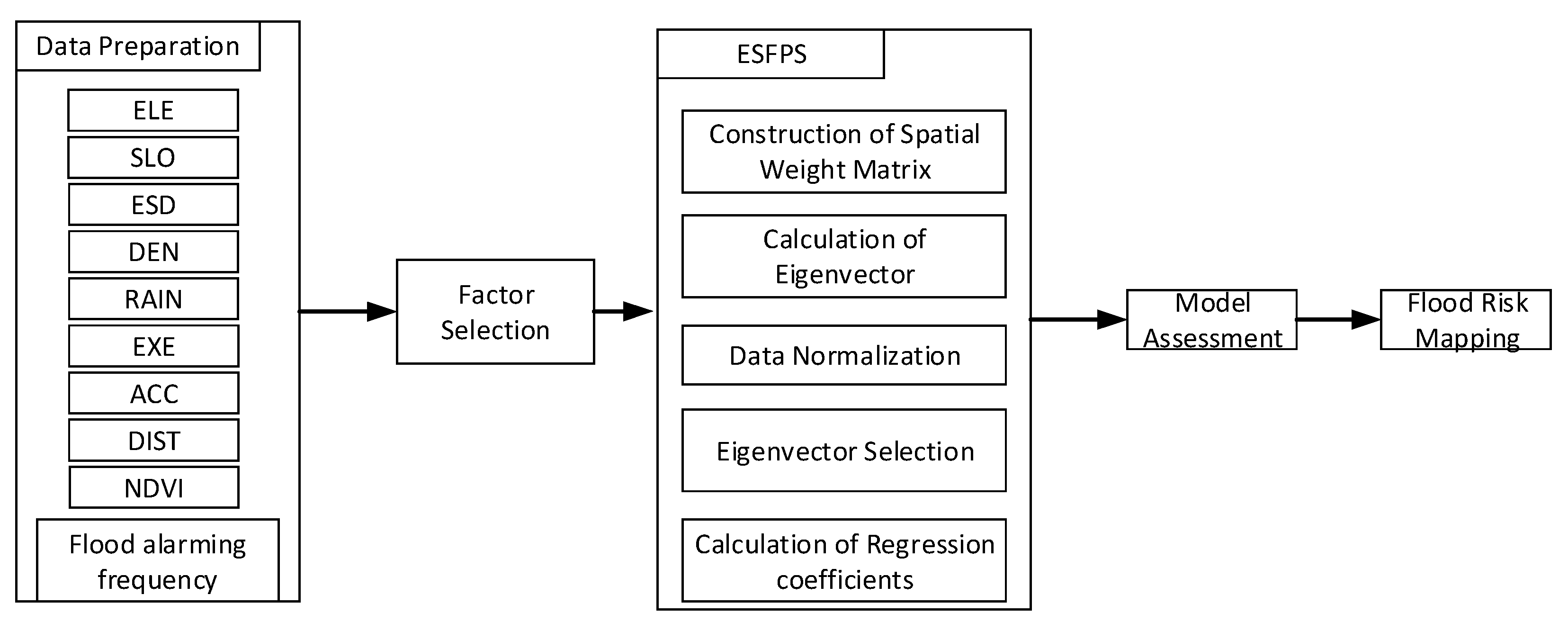
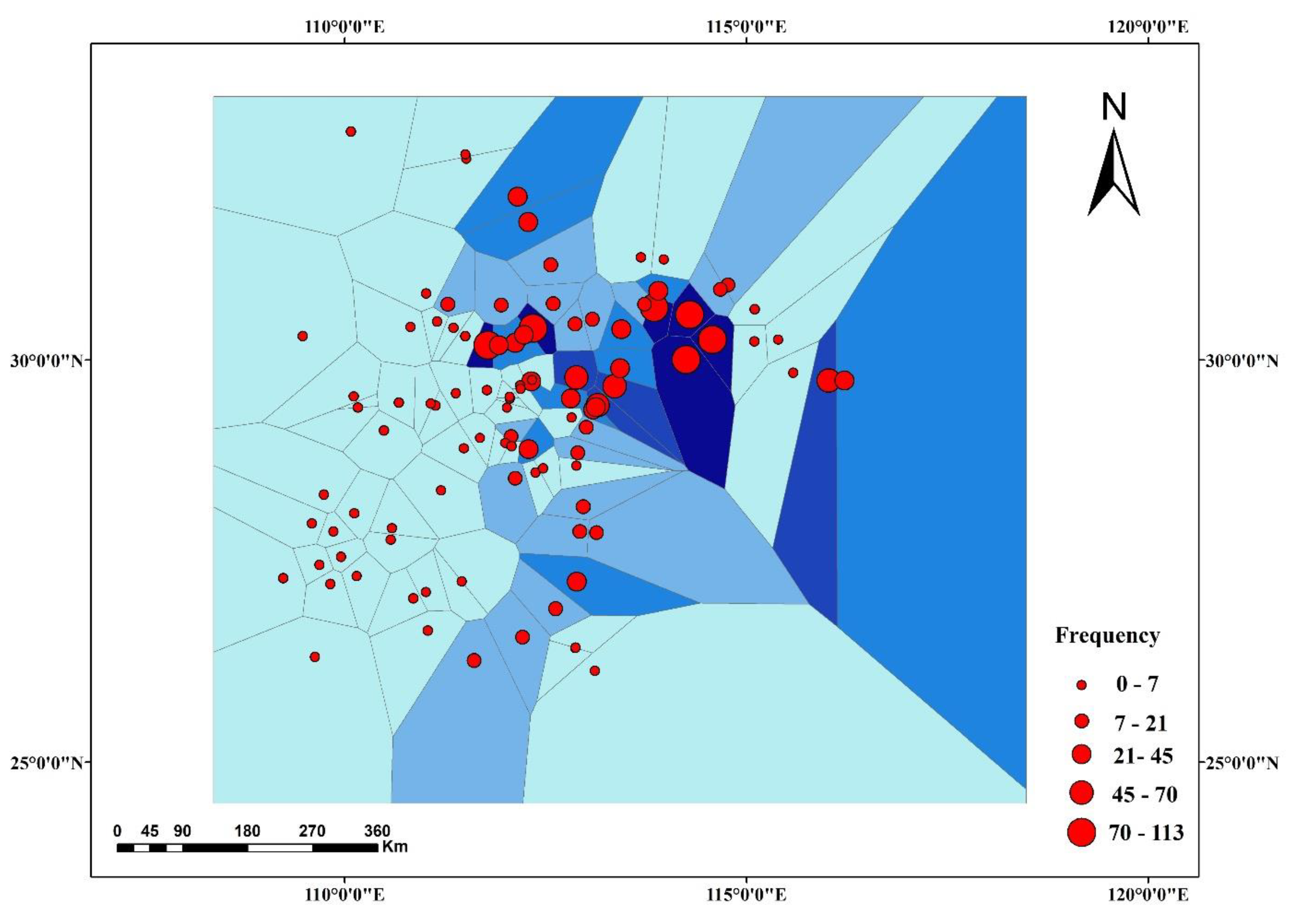
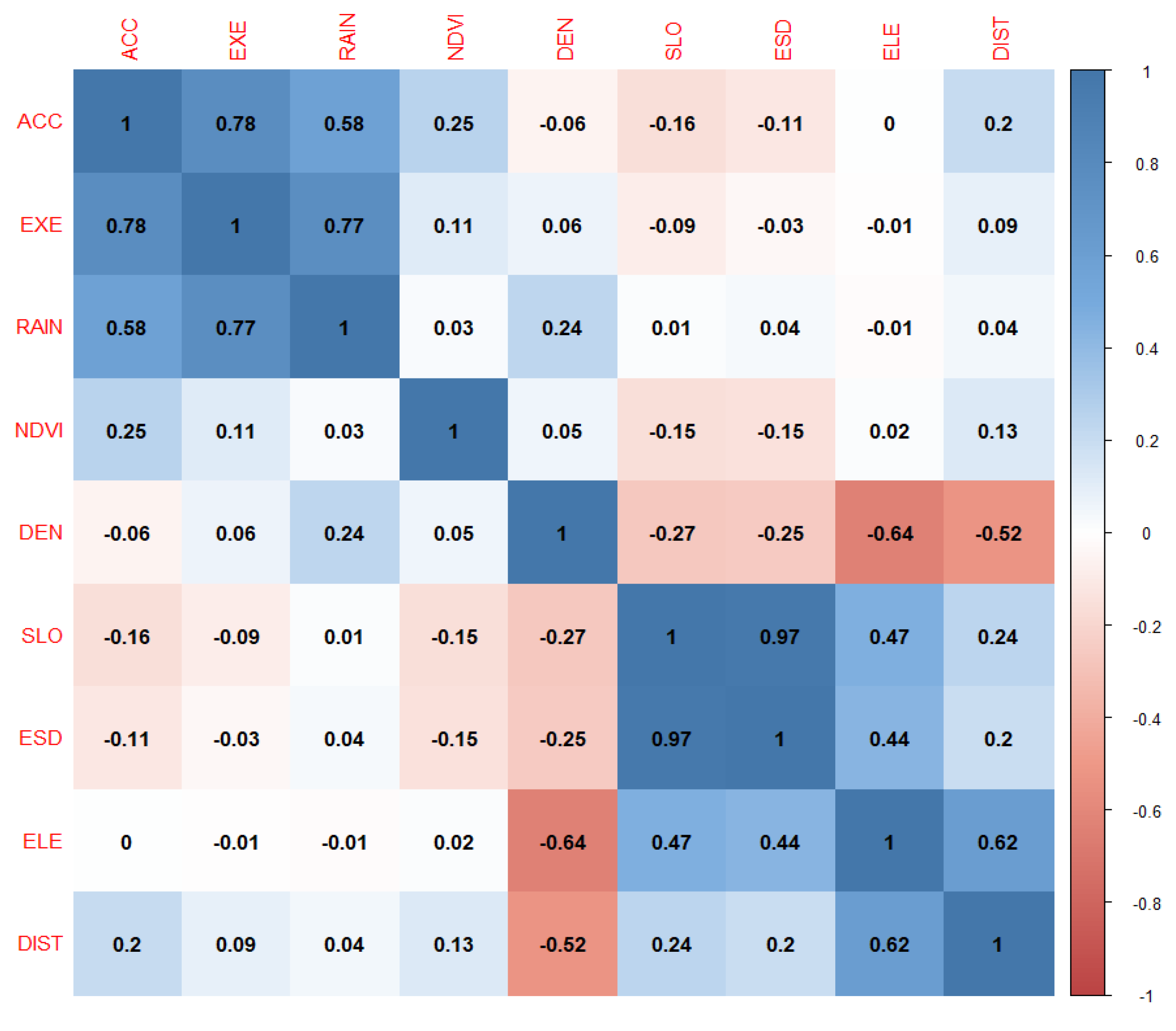
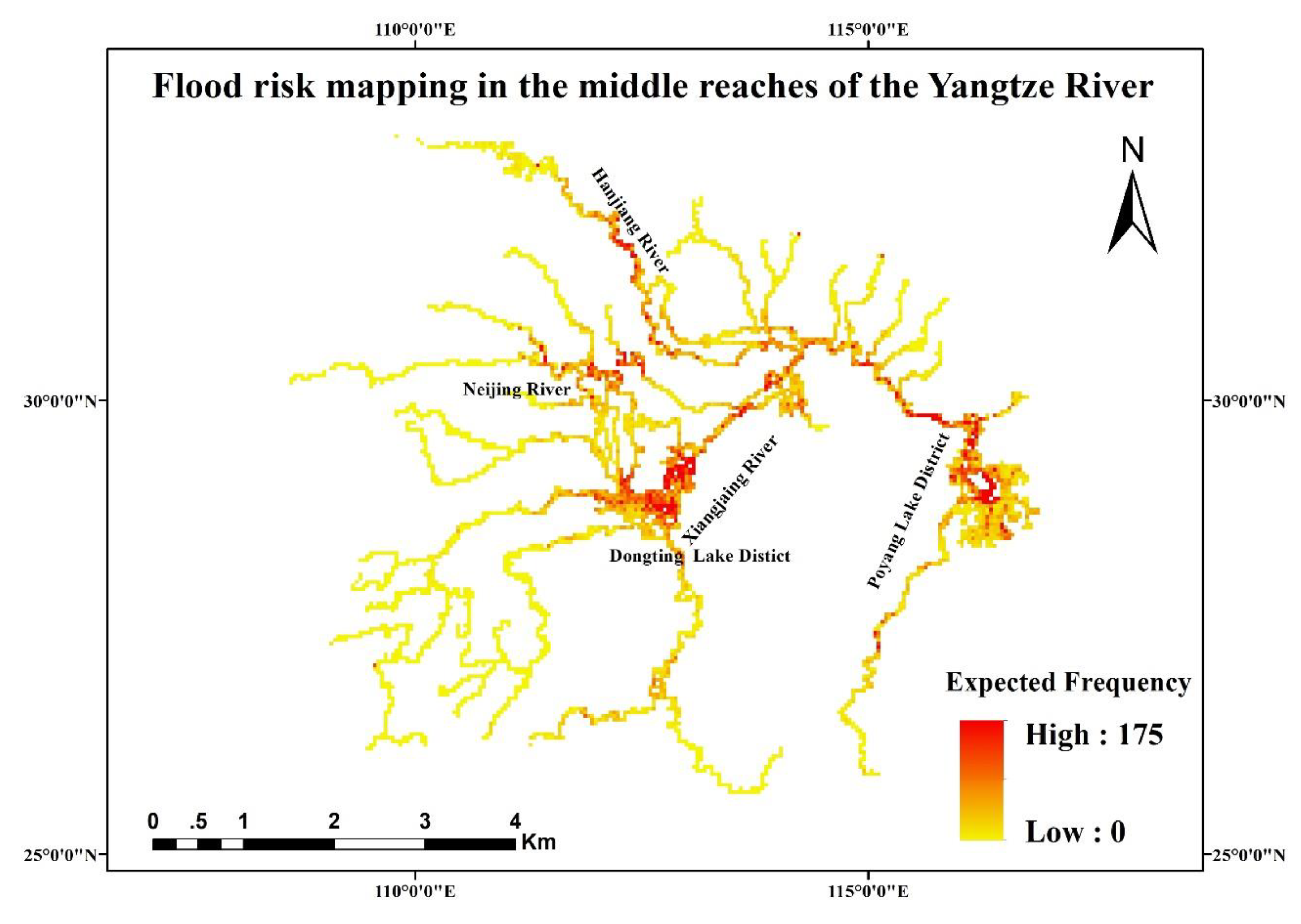
In this paper, we propose the eigenvector spatial filtering Poisson regression (ESFPS) model for the estimation of flood risk, using the frequency of flood alarming events observed by hydrological stations in the middle reaches of the Yangtze River in China. Independent hazard-causing variables include elevation (ELE), slope (SLO), elevation standard deviation (ESD), river density (DEN), distance to mainstream (DIST), normalized difference vegetation index (NDVI), annual mean rainfall, mean annual maximum of three-day accumulated precipitation (ACC) and frequency of extreme rainfall (EXE), because these factors are considered to aggravate or trigger flooding or are closely associated with flood risk in the study area. The model results will be compared with the results of Poisson regression and negative binomial regression, and the best model will be used to predict the flood risk throughout the basin and analyze the spatial distribution pattern of flood risk.