Can the Quality of the Potential Flood Risk Maps be Evaluated? A Case Study of the Social Risks of Floods in Central Spain
Abstract
1. Introduction and Objectives: The Assessment of Quality of Maps and the Peculiarities of Flood Risk Maps
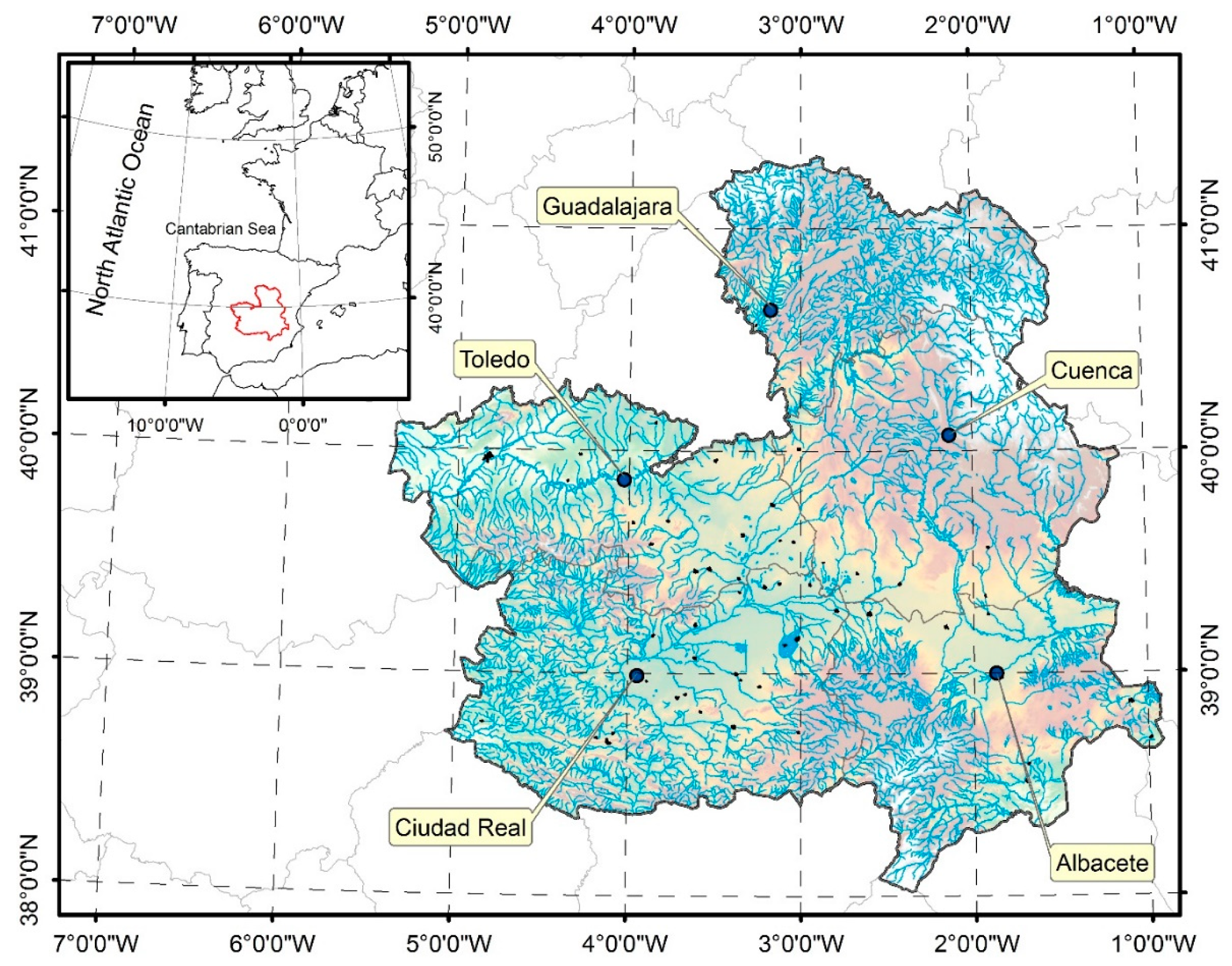
2. Study Site
2.1. Environmental Description
2.2. Social Description
3. Data Sources and Methodologies
3.1. The Flood Risk Maps of the PRICAM Project (MCA and GIS)
- River flooding,
- In situ rainfall flooding,
- Dam failure flooding.
- The so-called “La Mancha” area,
- Southeast area of the province of Albacete,
- East Zone of the province of Guadalajara,
- Axis of the Tagus River in the province of Toledo,
- Areas surrounding the city of Cuenca.
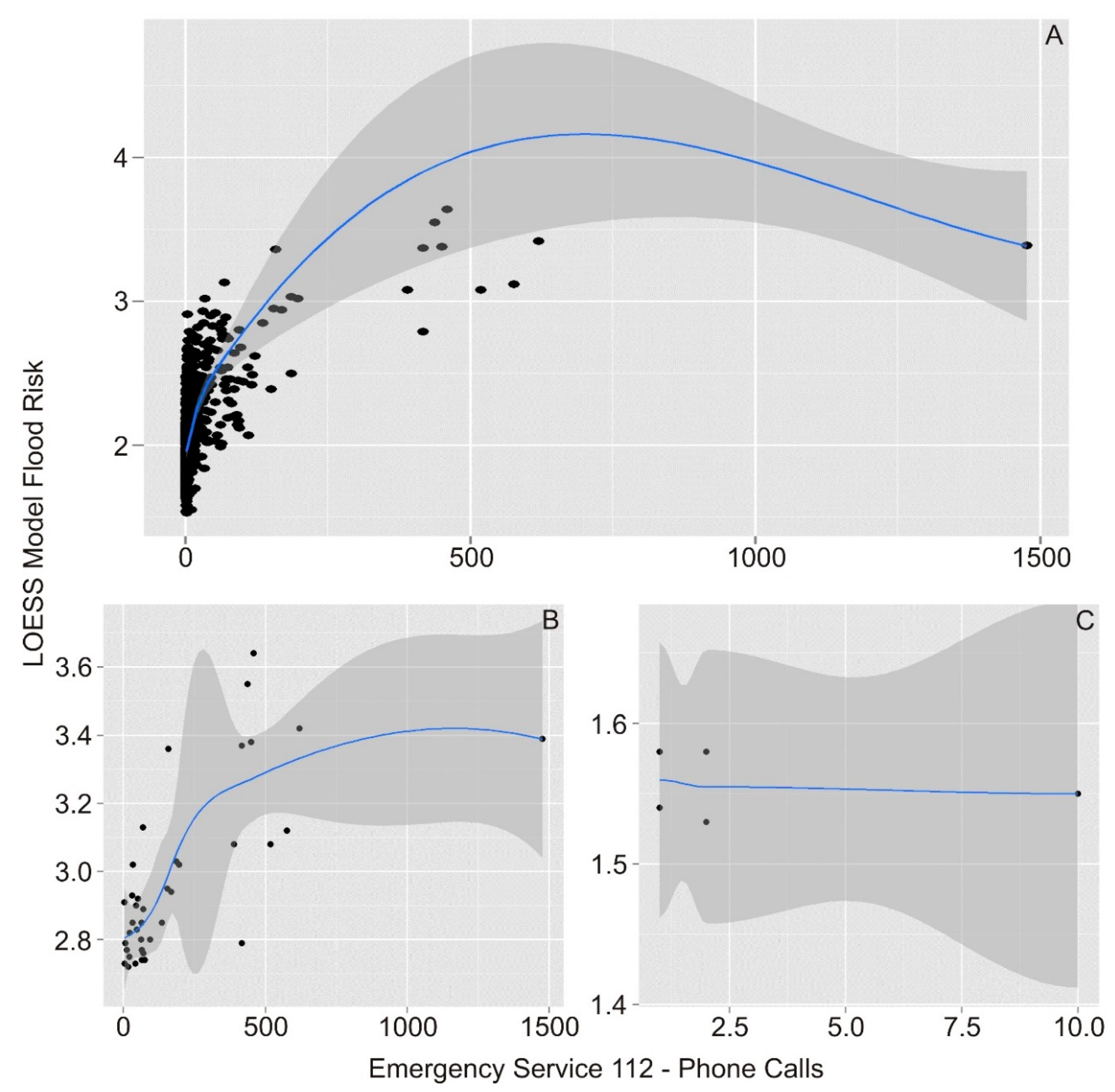
3.2. The Quality Assessment of Flood Risk Analysis (Phone Calls and LOESS)
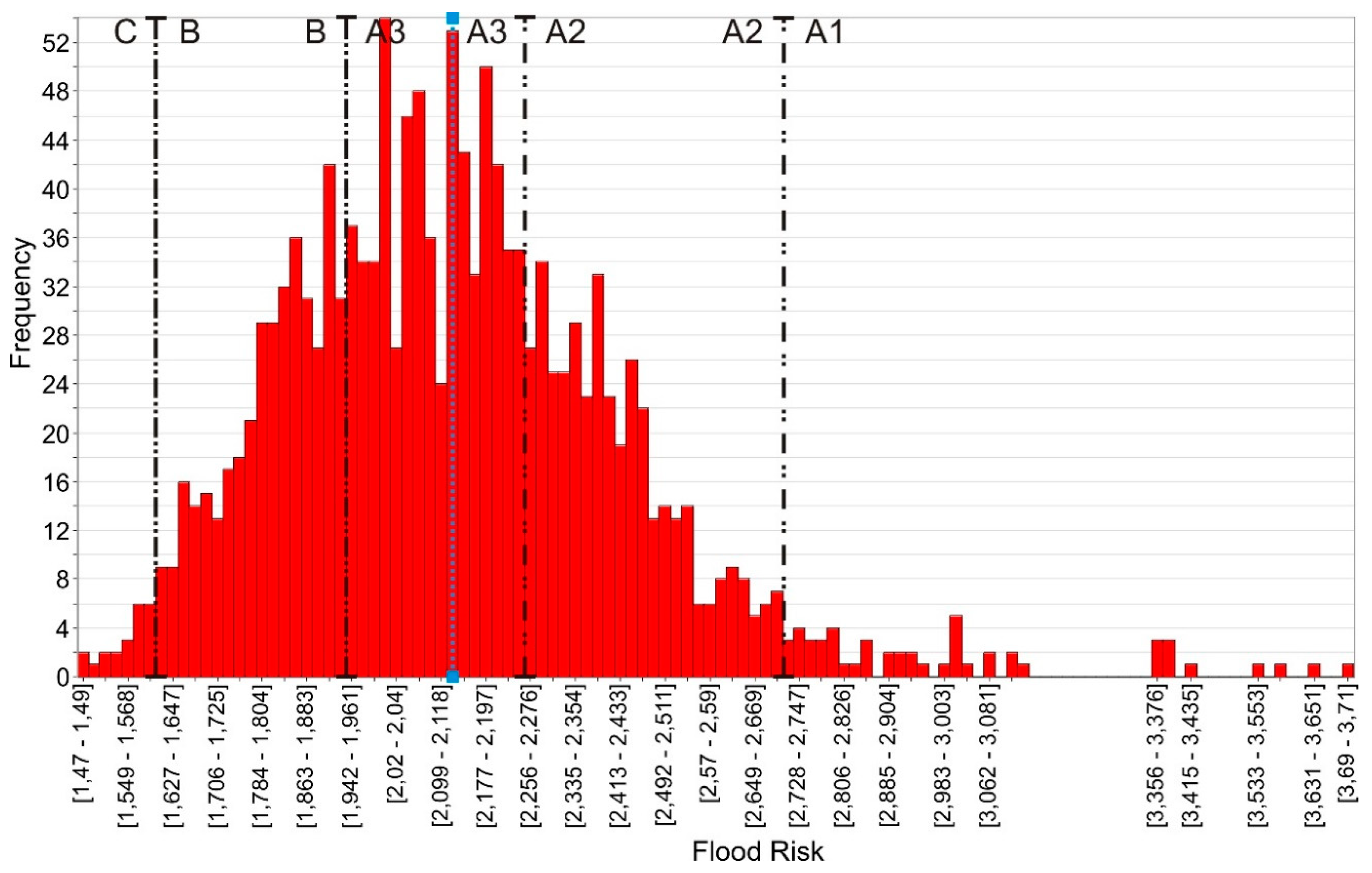
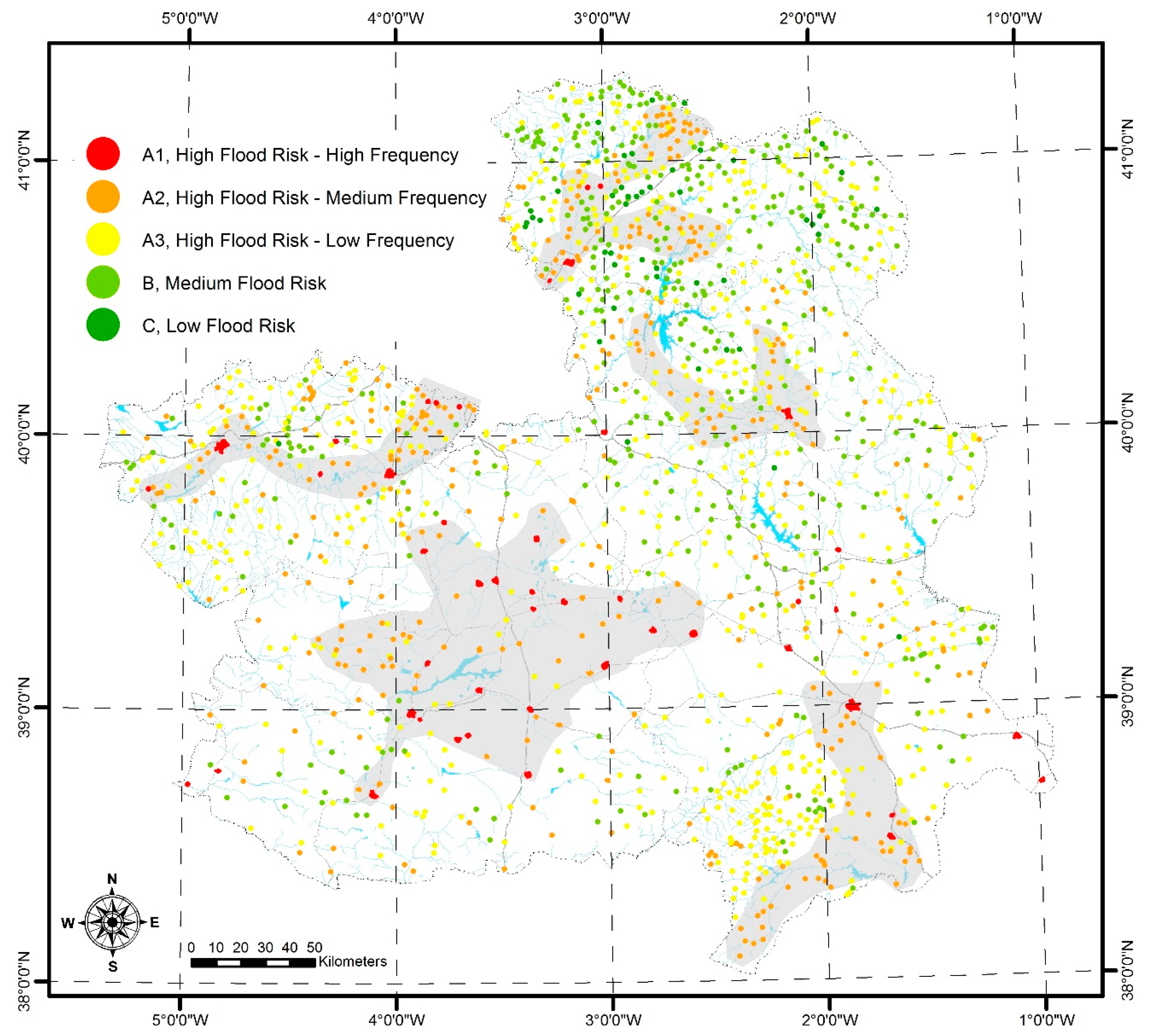
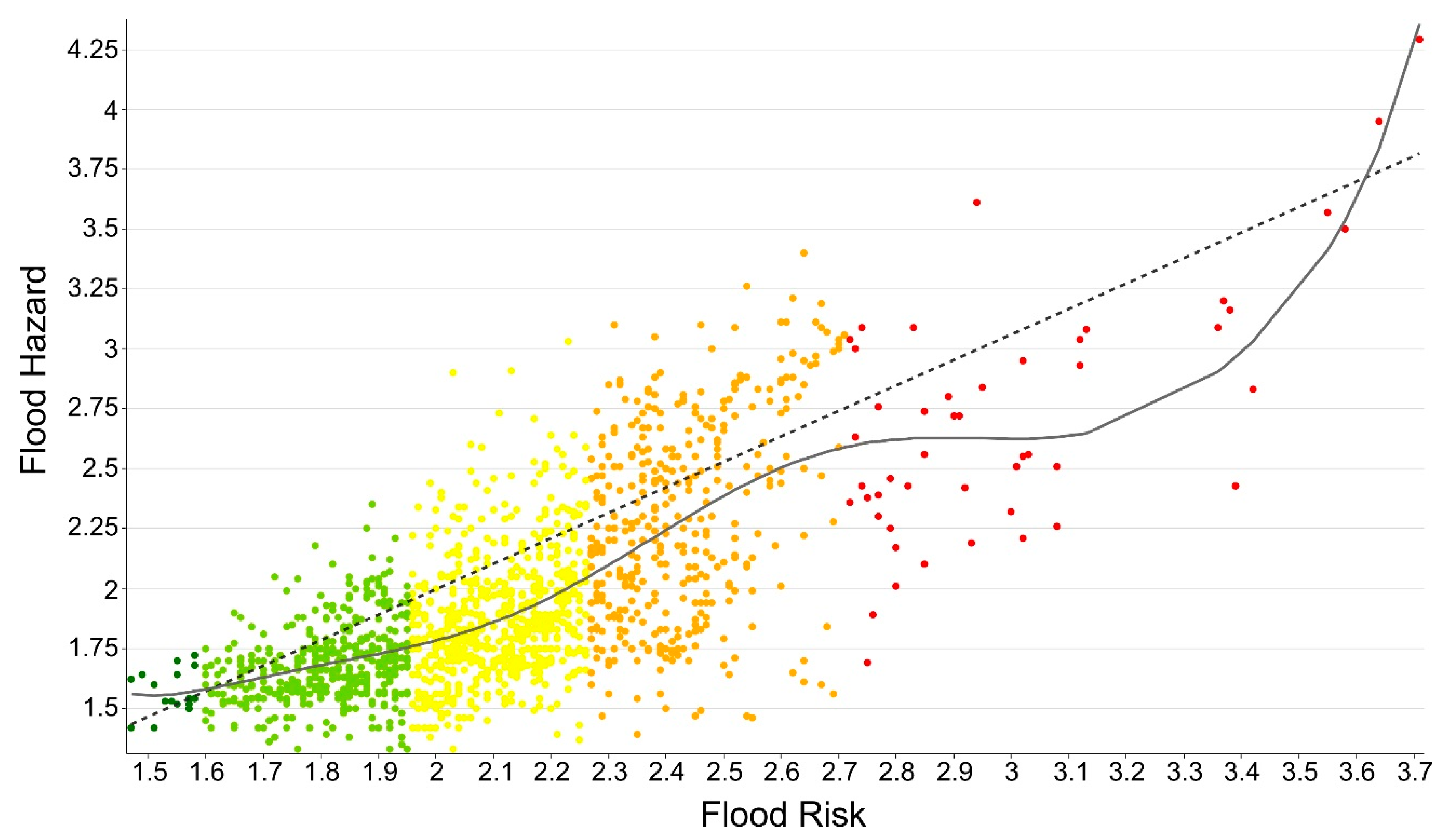
4. Results: Correlation Risk Categories vs. Number of Phone Calls
5. Discussion
5.1. Data Sources and Methodological Limitations
- High exposure linked to the total number of people in the urban center,
- High exposure linked to population density,
- High exposure linked to the presence of educational institutions, tourist camps, nursing homes, hospitals, or industrial estates,
- High vulnerability linked to the presence of children,
- High vulnerability linked to the presence of patients or convalescents (hospitals),
- Most of these major urban areas are historically developed close to rivers, thus the hazard factor (according to the characteristics of the model used) will also show a high value.
- Urban centers for which the value of the inferred flood risk (LOESS regression trend) is greater than that of the categorized risk (PRICAM model); in these urban centers, flooding events have registered consequences on people and/or assets that result in a high number of phone calls to the Emergency Service 112.
- Urban centers with a value of inferred flood risk lower than the categorized risk; in these situations, there have not been enough flooding events to justify flood risk classifications greater than those inferred by LOESS.
5.2. Future Applications
5.3. Map Update
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Centre for Research on the Epidemiology of Disasters. The International Disaster Database. Available online: http://emdat.be/emdat_db/ (accessed on 10 October 2018).
- De Moel, H.; Jongman, B.; Kreibich, H.; Merz, B.; Penning-Rowsell, E.; Ward, P.J. Flood risk assessments at different spatial scales. Mitig. Adapt. Strateg. Glob. Chang. 2015, 20, 865–890. [Google Scholar] [CrossRef] [PubMed]
- Sayers, P.; Lamb, R.; Panzeri, M.; Bowman, H.; Hall, J.; Horritt, M.; Penning-Rowsell, E. Believe it or not? The challenge of validating large scale probabilistic risk models. In Proceedings of the FLOODrisk 2016, Lyon, France, 17–21 October 2016. [Google Scholar]
- Evans, E.P.; Johnson, P.J.; Green, C.H.; Varsa, E. Risk assessment and programme prioritisation: The Hungary flood study. In Proceedings of the 35th Annual MAFF Conference of River and Coastal Engineers, London, UK, July 2000. [Google Scholar]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Penning-Rowsell, E.C. A realistic assessment of fluvial and coastal flood risk in England and Wales. Trans. Inst. Br. Geogr. 2015, 40, 44–61. [Google Scholar] [CrossRef]
- Penning-Rowsell, E.C. A ‘realist’ approach to the extent of flood risk in England and Wales. In Comprehensive Flood Risk Management: Research for Policy and Practice; Klijn, F., Schweckendiek, T., Eds.; Taylor and Francis: London, UK, 2013. [Google Scholar]
- Dottori, F.; Salamon, P.; Bianchi, A.; Alfieri, L.; Hirpa, F.A.; Feyen, L. Development and evaluation of a framework for global flood hazard mapping. Adv. Water Resour. 2016, 94, 87–102. [Google Scholar] [CrossRef]
- McCallum, I.; Liu, W.; See, L.; Mechler, R.; Keating, A.; Hochrainer-Stigler, S.; Mochizuki, J.; Fritz, S.; Dugar, S.; Arestegui, M.; et al. Technologies to support community flood disaster risk reduction. Int. J. Disaster Risk Sci. 2016, 7, 198–204. [Google Scholar] [CrossRef]
- Pappenberger, F.; Beven, K.; Frodsham, K.; Romanowicz, R.; Matgen, P. Grasping the unavoidable subjectivity in calibration of flood inundation models. A vulnerability weighted approach. J. Hydrol. 2007, 333, 275–287. [Google Scholar] [CrossRef]
- Zischg, A.P.; Mosimann, M.; Bernet, D.B.; Röthlisberger, V. Validation of 2D flood models with insurance claims. J. Hydrol. 2018, 557, 350–361. [Google Scholar] [CrossRef]
- Alfonso, L.; Lobbrecht, A.; Price, R. Using mobile phones to validate models of extreme events. In Proceedings of the 9th International Conference on Hydroinformatics, Tianjin, China, 7–11 September 2010; pp. 1447–1454. [Google Scholar]
- Poser, K.; Dransch, D. Volunteered geographic information for disaster management with application to rapid flood damage estimation. Geomatica 2010, 64, 89–98. [Google Scholar]
- Hung, K.C.; Kalantari, M.; Rajabifard, A. Methods for assessing the credibility of volunteered geographic information in flood response: A case study in Brisbane, Australia. Appl. Geogr. 2016, 68, 37–47. [Google Scholar] [CrossRef]
- Le Coz, J.; Patalano, A.; Collins, D.; Guillén, N.F.; García, C.M.; Smart, G.M.; Bind, J.; Chiaverini, A.; Le Boursicaud, R.; Dramais, G.; et al. Crowd-sourced data for flood hydrology: Feedback from recent citizen science projects in Argentina, France and New Zealand. J. Hydrol. 2016, 541, 766–777. [Google Scholar] [CrossRef]
- Rollason, E.; Bracken, L.J.; Hardy, R.J.; Large, A.R.G. The importance of volunteered geographic information for the validation of flood inundation models. J. Hydrol. 2018, 562, 267–280. [Google Scholar] [CrossRef]
- Montargil, F.; Santos, V. Citizen observatories: Concept, opportunities and communication with citizens in the first EU experiences. In Beyond Bureaucracy: Towards Sustainable Governance Informatisation; Paulin, A.A., Anthopoulos, L.G., Reddick, C.G., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 167–184. [Google Scholar]
- Assumpção, T.H.; Popescu, I.; Jonoski, A.; Solomatine, D.P. Citizen observations contributing to flood modelling: Opportunities and challenges. Hydrol. Earth Syst. Sci. 2018, 22, 1473–1489. [Google Scholar] [CrossRef]
- Schnebele, E.; Cervone, G. Improving remote sensing flood assessment using volunteered geographical data. Nat. Hazards Earth Syst. Sci. 2013, 13, 669–677. [Google Scholar] [CrossRef]
- Triglav-Čekada, M.; Radovan, D. Using volunteered geographical information to map the November 2012 floods in Slovenia. Nat. Hazards Earth Syst. Sci. 2013, 13, 2753–2762. [Google Scholar] [CrossRef]
- Smith, L.; Liang, Q.; James, P.; Lin, W. Assessing the utility of social media as a data source for flood risk management using a real-time modelling framework. J. Flood Risk Manag. 2015, 10, 370–380. [Google Scholar] [CrossRef]
- Cervone, G.; Sava, E.; Huang, Q.; Schnebele, E.; Harrison, J.; Waters, N. Using Twitter for tasking remote-sensing data collection and damage assessment: 2013 Boulder flood case study. Int. J. Remote Sens. 2016, 37, 100–124. [Google Scholar] [CrossRef]
- Li, Z.; Wang, C.; Emrich, C.T.; Guo, D. A novel approach to leveraging social media for rapid flood mapping: A case study of the 2015 South Carolina floods. Cartogr. Geogr. Inf. Sci. 2017, 45, 97–110. [Google Scholar] [CrossRef]
- Starkey, E.; Parkin, G.; Birkinshaw, S.; Large, A.; Quinn, P.; Gibson, C. Demonstrating the value of community based (“citizen science”) observations for catchment modelling and characterization. J. Hydrol. 2017, 548, 801–817. [Google Scholar] [CrossRef]
- Kusumo, A.N.L.; Reckien, D.; Verplanke, J. Utilising volunteered geographic information to assess resident’s flood evacuation shelters. Case study: Jakarta. Appl. Geogr. 2017, 88, 174–185. [Google Scholar] [CrossRef]
- Kryvasheyeu, Y.; Chen, H.; Obradovich, N.; Moro, E.; Van Hentenryck, P.; Fowler, J.; Cebrian, M. Rapid assessment of disaster damage using social media activity. Sci. Adv. 2016, 2, e1500779. [Google Scholar] [CrossRef] [PubMed]
- Goodchild, M.F.; Glennon, J.A. Crowdsourcing geographic information for disaster response: A research frontier. Int. J. Digit. Earth 2010, 3, 231–241. [Google Scholar] [CrossRef]
- Rosser, J.F.; Leibovici, D.G.; Jackson, M.J. Rapid flood inundation mapping using social media, remote sensing and topographic data. Nat. Hazards 2017, 87, 103–120. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Li, L. Assuring the quality of volunteered geographic information. Spat. Stat. 2012, 1, 110–120. [Google Scholar] [CrossRef]
- Xiao, Y.; Huang, Q.; Wu, K. Understanding social media data for disaster management. Nat. Hazards 2015, 79, 1663–1679. [Google Scholar] [CrossRef]
- Fernández-García, F. El Clima de la Meseta Meridional. Los Tipos de Tiempo; Universidad Autónoma de Madrid: Madrid, Spain, 1985; 215p. [Google Scholar]
- Instituto Nacional de Meteorología. Guía Resumida del Clima en España 1971—2000; INM: Madrid, Spain, 2001. [Google Scholar]
- Díez-Herrero, A.; Garrote, J.; Baillo, R.; Laín, L.; Mancebo, M.J.; Pérez-Cerdán, F. Análisis del riesgo de inundación para planes autonómicos de protección civil: RICAM. In El Estudio y la Gestión de Los Riesgos Geológicos; Jiménez, I.G., Huerta, L.L., Isidro, M.L., Eds.; Instituto Geológico y Minero de España: Madrid, Spain, 2008; pp. 53–70. [Google Scholar]
- Ministerio de Justicia e Interior del Gobierno de España. Directriz básica de planificación de protección civil ante el riesgo de inundaciones. Boletín Oficial del Estado 1995, 38, 4846–4858. [Google Scholar]
- Meyer, V.; Scheuer, S.; Haase, D. A multicriteria approach for flood risk mapping exemplified at the Mulde river, Germany. Nat. Hazards 2009, 48, 17–39. [Google Scholar] [CrossRef]
- Brouwer, R.; van Ek, R. Integrated ecological, economic and social impact assessment of alternative flood control policies in the Netherlands. Ecol. Econ. 2004, 50, 1–21. [Google Scholar] [CrossRef]
- Akter, T.; Simonovic, S.P. Aggregation of fuzzy views of a large number of stakeholders for multiobjective flood management decision-making. J. Environ. Manag. 2005, 77, 133–143. [Google Scholar] [CrossRef]
- Raaijmakers, R.; Krywkow, J.; van der Veen, A. Flood risk perceptions and spatial multi-criteria analysis: An exploratory research for hazard mitigation. Nat. Hazards 2008, 46, 307–322. [Google Scholar] [CrossRef]
- Huang, D.; Zhang, R.; Huo, Z.; Mao, F.; Youhao, E.; Zheng, W. An assessment of multidimensional flood vulnerability at the provincial scale in China based on the DEA method. Nat. Hazards 2012, 64, 1575–1586. [Google Scholar] [CrossRef]
- Li, C.H.; Li, N.; Wu, L.D.; Hu, A.J. A relative vulnerability estimation of flood disaster using data envelopment analysis in the Dongting Lake region of Hunan. Nat. Hazards Earth Syst. Sci. 2013, 13, 1723–1734. [Google Scholar] [CrossRef]
- Balica, S.F.; Popescu, I.; Beevers, L.; Wright, N.G. Parametric and physically based modelling techniques for flood risk and vulnerability assessment: A comparison. Environ. Model. Softw. 2013, 41, 84–92. [Google Scholar] [CrossRef]
- Linstone, H.A.; Turrof, M. The Delphi Method. Techniques and Applications; Addison-Wesley Educational Publishers Inc.: Boston, MA, USA, 1975; 621p. [Google Scholar]
- Landeta, J. El Método Delphi. Una Técnica de Previsión Para la Incertidumbre; Ariel: Barcelona, Spain, 1999; 223p. [Google Scholar]
- Nasiri, H.; Yusof, M.J.M.; Ali, T.A.M.; Hussein, M.K.B. District flood vulnerability index: Urban decision-making tool. Int. J. Environ. Sci. Technol. 2018, 16, 2249–2258. [Google Scholar] [CrossRef]
- Ministerio de Fomento. Máximas Lluvias Diarias en la España Peninsular; Ministerio de Fomento de España: Madrid, Spain, 1999; 54p, (include software program MaxPluWin).
- Instituto Geológico y Minero de España. Geological and Geomorphological Map of Spain. Available online: http://info.igme.es/cartografiadigital/portada/default.aspx?mensaje=true (accessed on 20 September 2018).
- Cleveland, W.S. Robust locally weighted regression and smoothing scatterplots. J. Am. Stat. Assoc. 1979, 74, 829–836. [Google Scholar] [CrossRef]
- Cleveland, W.S.; Devlin, S.J. Locally weighted regression: An approach to regression analysis by local fitting. J. Am. Stat. Assoc. 1988, 83, 596–610. [Google Scholar] [CrossRef]
- Calle, M.; Alho, P.; Benito, G. Channel dynamics and geomorphic resilience in an ephemeral Mediterranean river affected by gravel mining. Geomorphology 2017, 285, 333–346. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008. [Google Scholar]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Review article “Assessment of economic flood damage”. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Garrote, J.; Alvarenga, F.M.; Díez-Herrero, A. Quantification of flash flood economic risk using ultra-detailed stage—Damage functions and 2-D hydraulic models. J. Hydrol. 2016, 541, 611–625. [Google Scholar] [CrossRef]
- Malczewski, J. GIS-based multicriteria decision analysis: A survey of the literature. Int. J. Geogr. Inf. Sci. 2006, 20, 703–726. [Google Scholar] [CrossRef]
- Lee, G.; Jun, K.S.; Chung, E.S. Integrated multi-criteria flood vulnerability approach using fuzzy TOPSIS and Delphi technique. Nat. Hazards Earth Syst. Sci. 2013, 13, 1293–1312. [Google Scholar] [CrossRef]
- Thaler, T.; Hartmann, T. Justice and flood risk management: Reflecting on different approaches to distribute and allocate flood risk management in Europe. Nat. Hazards 2016, 83, 129–147. [Google Scholar] [CrossRef]
- Lowry, C.S.; Fienen, M.N.; Hall, D.M.; Stepenuck, K.F. Growing pains of crowdsourced stream stage monitoring using mobile phones: The development of crowdhydrology. Front. Earth Sci. 2019, 7, 128. [Google Scholar] [CrossRef]
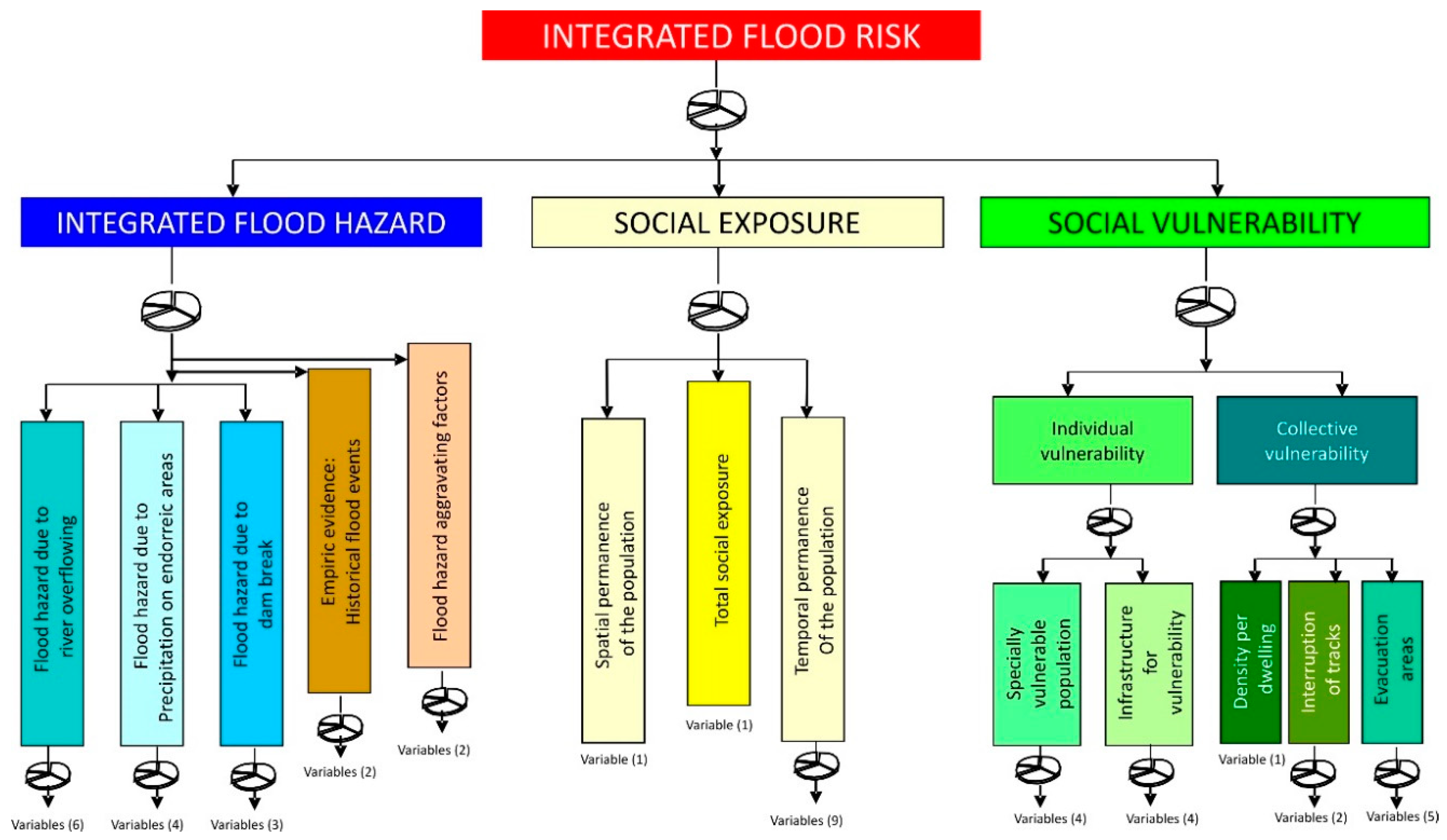

| Variable | Mean Value | Skewness | Kurtosis |
|---|---|---|---|
| Flooding probability: Qt to Qb ratio | 3.5;4.2;4.9 | −1.30 | 0.72 |
| Time of concentration (Tc) | 3.9;4.5;5.0 | −0.48 | −1.65 |
| Distance to river reach | 2.9;3.6;4.3 | −0.25 | −0.90 |
| Urban center–river reach elevation difference | 3.1;3.9;4.7 | −1.29 | 2.10 |
| Lithology and geomorphology sediments | 3.4;4.0;4.6 | −0.48 | −1.65 |
| Terrain slope | 3.6;4.1;4.6 | −0.26 | −1.12 |
| Terrain morphology (concave or convexity) | 3.7;4.2;4.7 | −0.44 | −1.23 |
| 24 h rainfall | 3.9;4.4;4.8 | −0.69 | −0.25 |
| Dam or reservoir class (volume) | 2.5;3.2;3.9 | −0.73 | 1.03 |
| Downstream distance from reservoir | 3.2;4.0;4.8 | −1.85 | 4.13 |
| N° of historical flood events | 4.0;4.5;4.9 | −0.69 | −0.25 |
| Historical vs actual reservoirs scenario | 3.2;3.8;4.4 | −0.67 | −0.10 |
| Toxic of danger materials industries | 3.4;4.1;4.8 | −1.07 | 0.37 |
| Industrial estate | 2.6;3.5;4.3 | −0.04 | −1.65 |
| Total population (number) | 3.8;4.5;5.1 | −2.05 | 4.83 |
| Population clustering by age | 2.8;3.4;3.9 | −0.85 | −0.76 |
| Unemployment index | 1.2;1.8;2.4 | 0.57 | −0.86 |
| Presence of educational institutions | 2.5;3.1;3.7 | 0.71 | 0.53 |
| Presence of hospital centers | 3.4;3.9;4.5 | −1.06 | 1.93 |
| Housing type | 3.0;3.9;4.8 | −1.25 | 1.26 |
| Under 6 year population ratio | 3.6;4.2;4.8 | −1.24 | 1.75 |
| Up 65 year population ratio | 3.8;4.4;4.9 | −1.58 | 2.78 |
| Presence of people with disabilities | 3.7;4.3;4.8 | −1.54 | 2.90 |
| Knowledge of the local language ratio | 2.0;2.8;3.6 | 0.20 | −0.81 |
| Presence of sick or convalescent people | 3.5;4.1;4.7 | −0.98 | 0.93 |
| Degree of buildings accessibility | 2.6;3.2;3.8 | −0.35 | −1.45 |
| State of buildings preservation | 2.9;3.6;4.3 | −0.27 | −0.65 |
| N° of stores above ground surface | 3.5;4.1;4.7 | −0.76 | 0.16 |
| N° of stores below ground surface | 4.3;4.7;5.2 | −1.64 | 1.13 |
| Distance to roads or evacuation paths | 2.8;3.5;4.3 | −0.51 | −0.92 |
| Distance to urban centers | 3.5;4.0;4.5 | −1.62 | 5.50 |
| Existence of defined evacuation paths | 4.4;4.7;5.0 | −0.81 | −1.65 |
| Risk Level | Description |
|---|---|
| A1 | High Frequency—High Flood Risk; 50-year flood produces significant damage to urban center |
| A2 | Medium Frequency—High Flood Risk; 100-year flood produces significant damage to urban center |
| A3 | Low Frequency—High Flood Risk; 500-year flood produces significant damage to urban center |
| B | Medium Flood Risk; 100-year flood produces significant damage outside the urban center |
| C | Low Flood Risk; 500-year flood produces significant damage outside the urban center |
| Year | Semester | N° Phone Calls |
|---|---|---|
| 2007 | 1 | 1943 |
| 2007 | 2 | 1101 |
| 2008 | 1 | 1062 |
| 2008 | 2 | 1730 |
| 2009 | 1 | 817 |
| 2009 | 2 | 2190 |
| 2010 | 1 | 1448 |
| 2010 | 2 | 1500 |
| 2011 | 1 | 1239 |
| 2011 | 2 | 584 |
| 2012 | 1 | 586 |
| 2012 | 2 | 951 |
| 2013 | 1 | 740 |
| 2013 | 2 | 825 |
| Total: | 16,828 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garrote, J.; Gutiérrez-Pérez, I.; Díez-Herrero, A. Can the Quality of the Potential Flood Risk Maps be Evaluated? A Case Study of the Social Risks of Floods in Central Spain. Water 2019, 11, 1284. https://doi.org/10.3390/w11061284
Garrote J, Gutiérrez-Pérez I, Díez-Herrero A. Can the Quality of the Potential Flood Risk Maps be Evaluated? A Case Study of the Social Risks of Floods in Central Spain. Water. 2019; 11(6):1284. https://doi.org/10.3390/w11061284
Chicago/Turabian StyleGarrote, Julio, Ignacio Gutiérrez-Pérez, and Andrés Díez-Herrero. 2019. "Can the Quality of the Potential Flood Risk Maps be Evaluated? A Case Study of the Social Risks of Floods in Central Spain" Water 11, no. 6: 1284. https://doi.org/10.3390/w11061284
APA StyleGarrote, J., Gutiérrez-Pérez, I., & Díez-Herrero, A. (2019). Can the Quality of the Potential Flood Risk Maps be Evaluated? A Case Study of the Social Risks of Floods in Central Spain. Water, 11(6), 1284. https://doi.org/10.3390/w11061284







