Numerical Simulation of Air–Water Two-Phase Flow on Stepped Spillways behind X-Shaped Flaring Gate Piers under Very High Unit Discharge
Abstract
1. Introduction
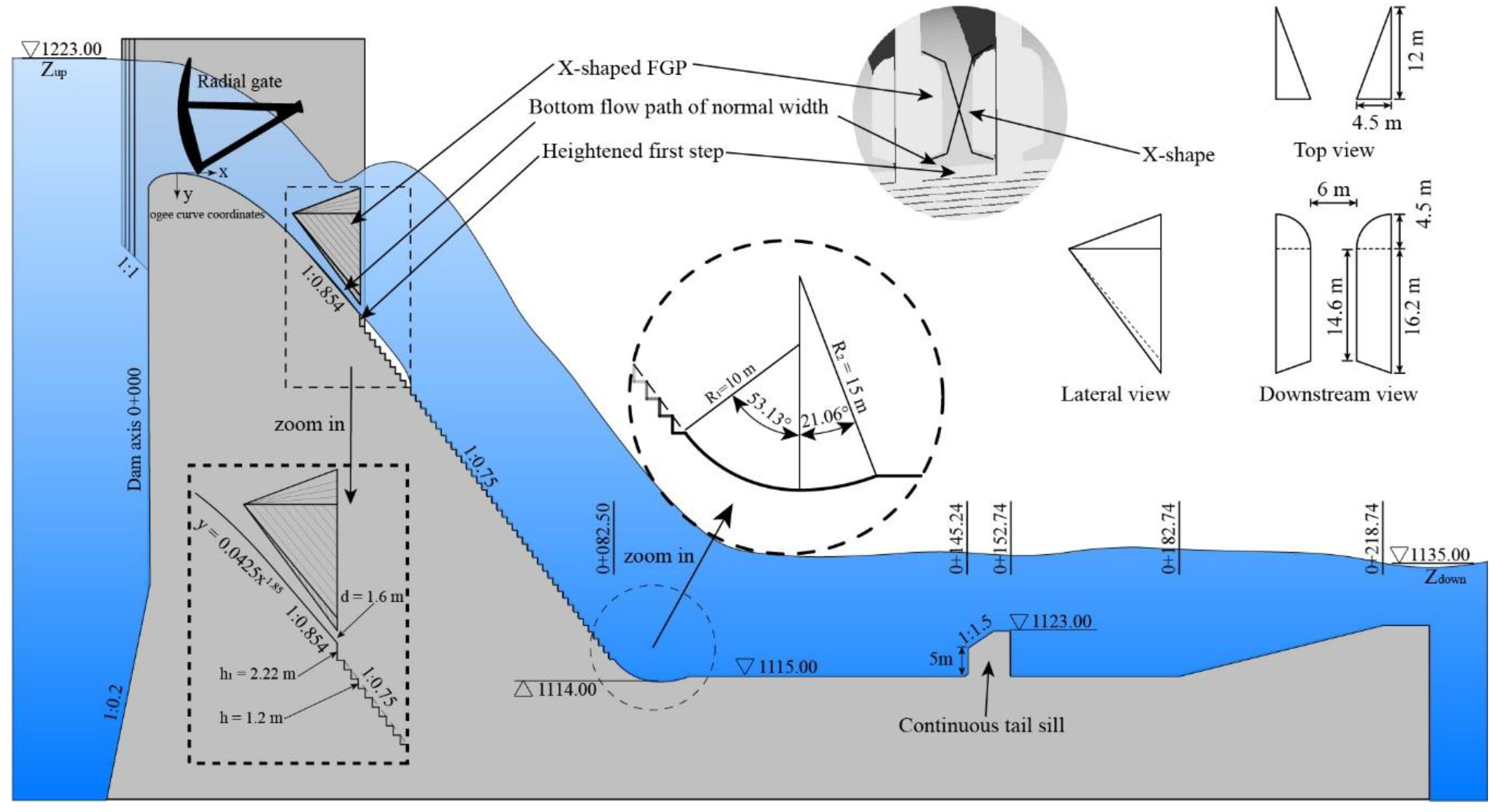
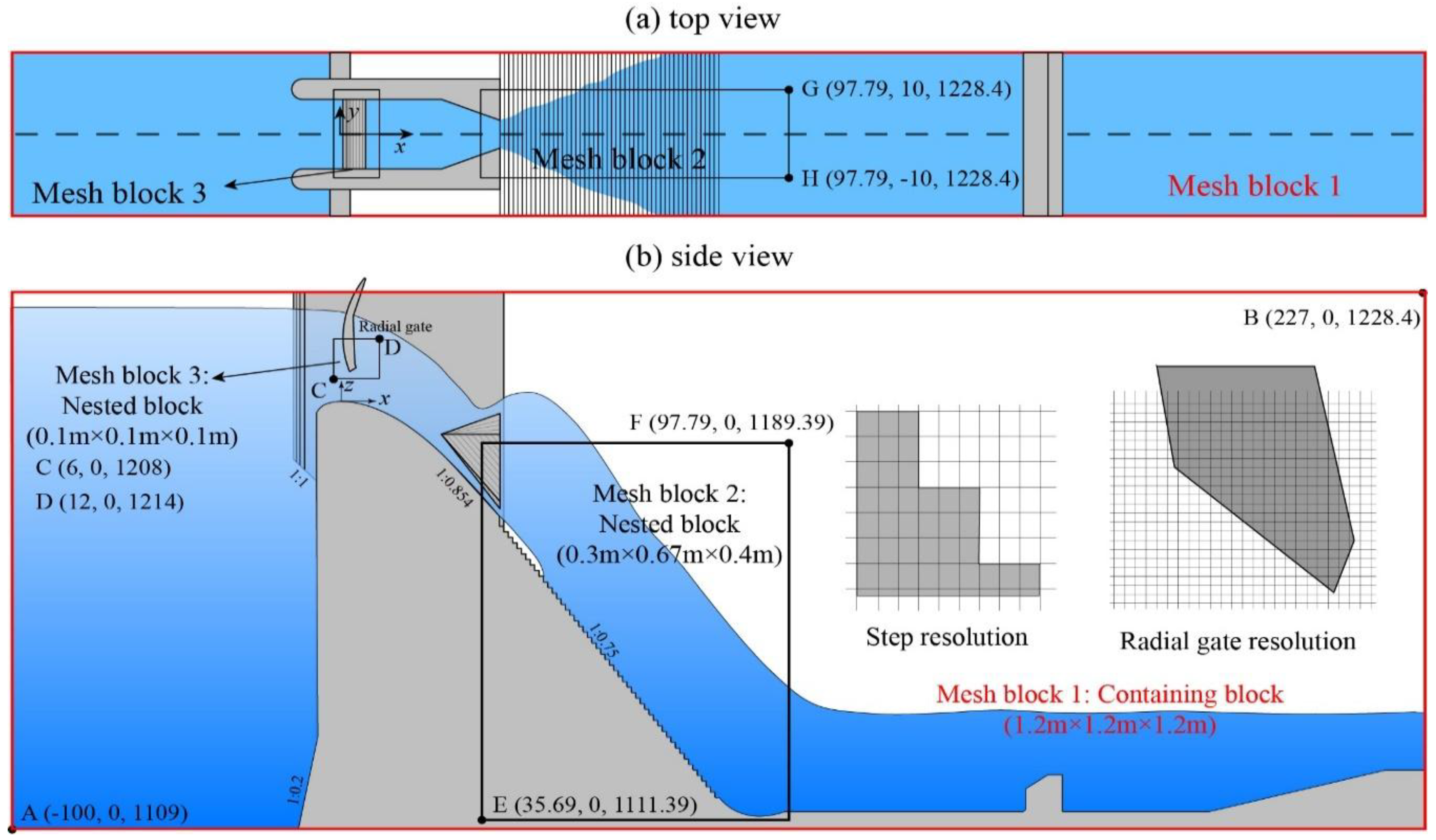
2. Prototype Site and Investigated Sub-Model
3. Mathematical Models and Simulation Setup
3.1. Mass Continuity Equation
3.2. Momentum Equation
3.3. RNG k-ε Turbulence Model
3.4. VOF Model
3.5. Air Entrainment Model
3.6. Density Evaluation Model
3.7. Drift-Flux Model
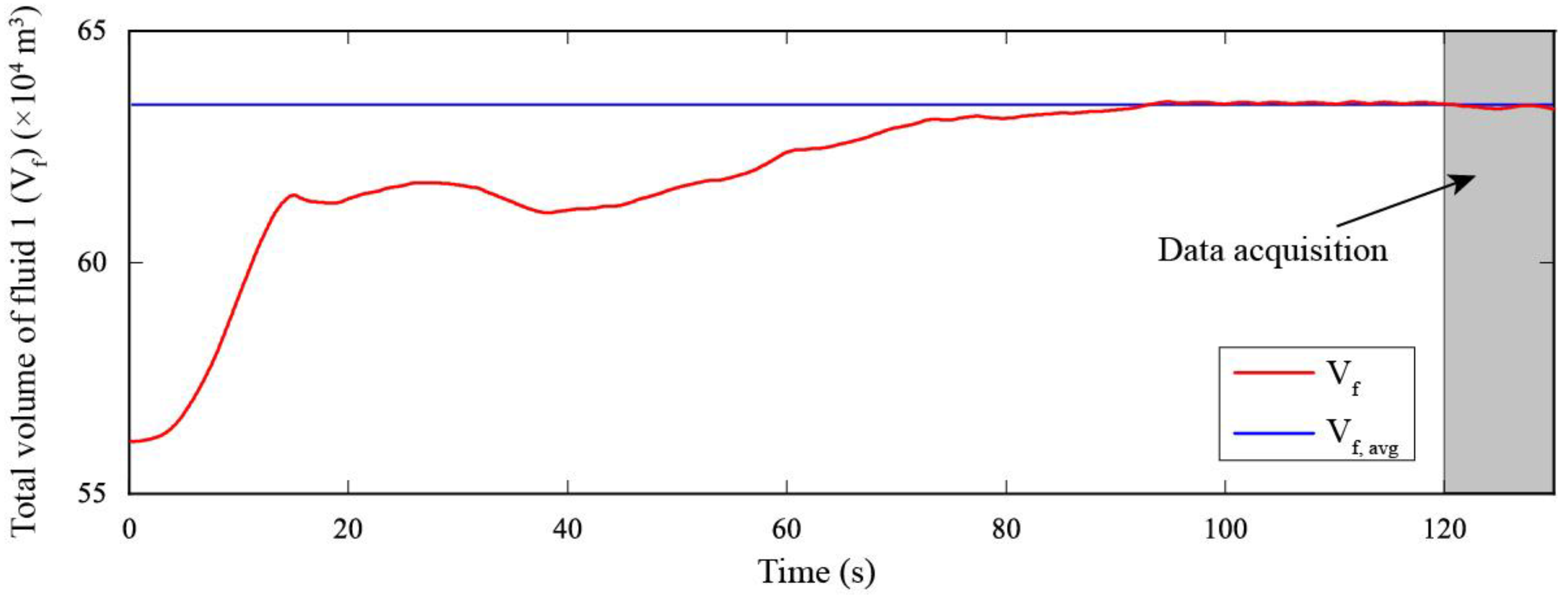
3.8. Simulation Setup
4. Calculation Results and Discussion
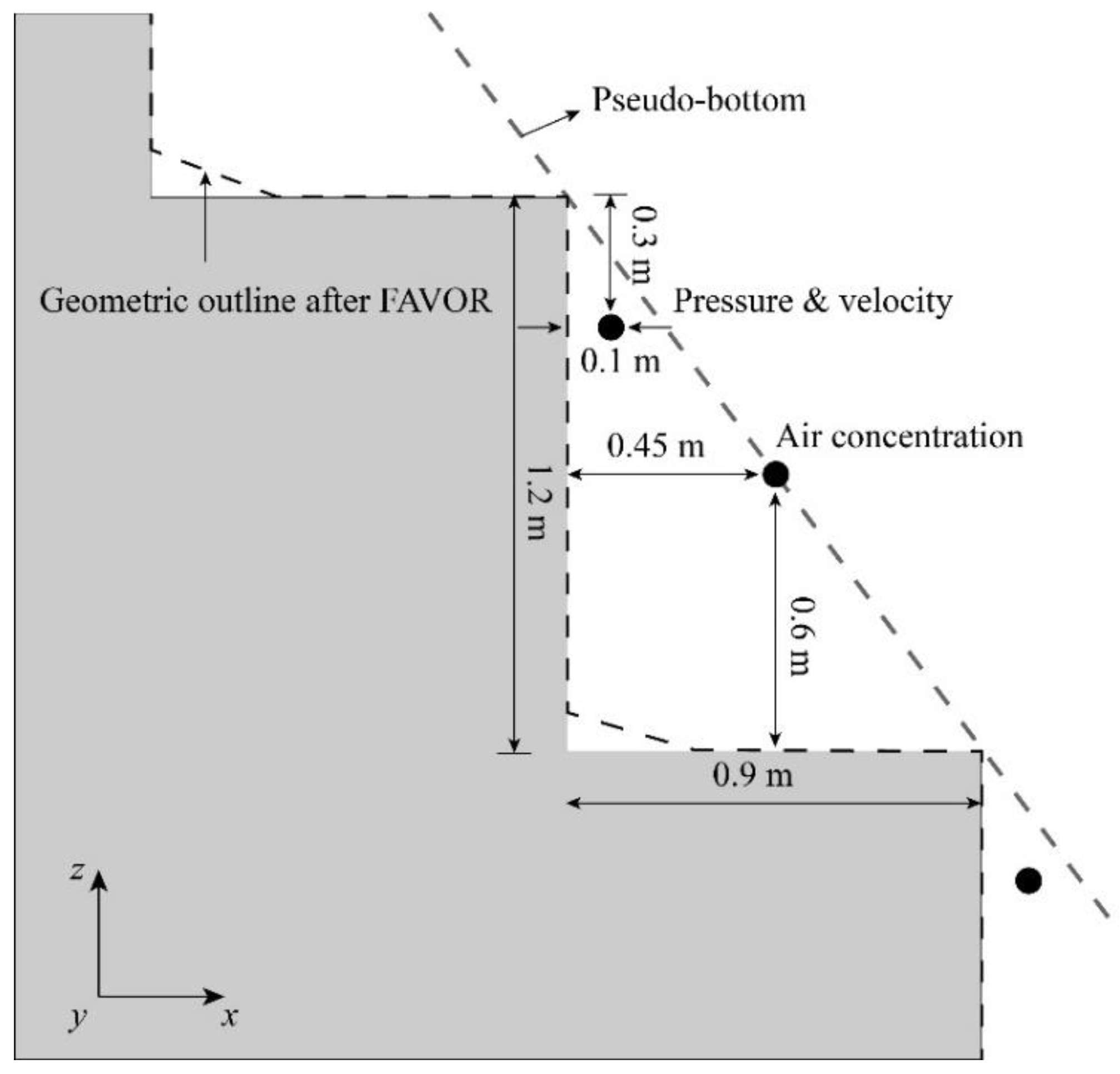
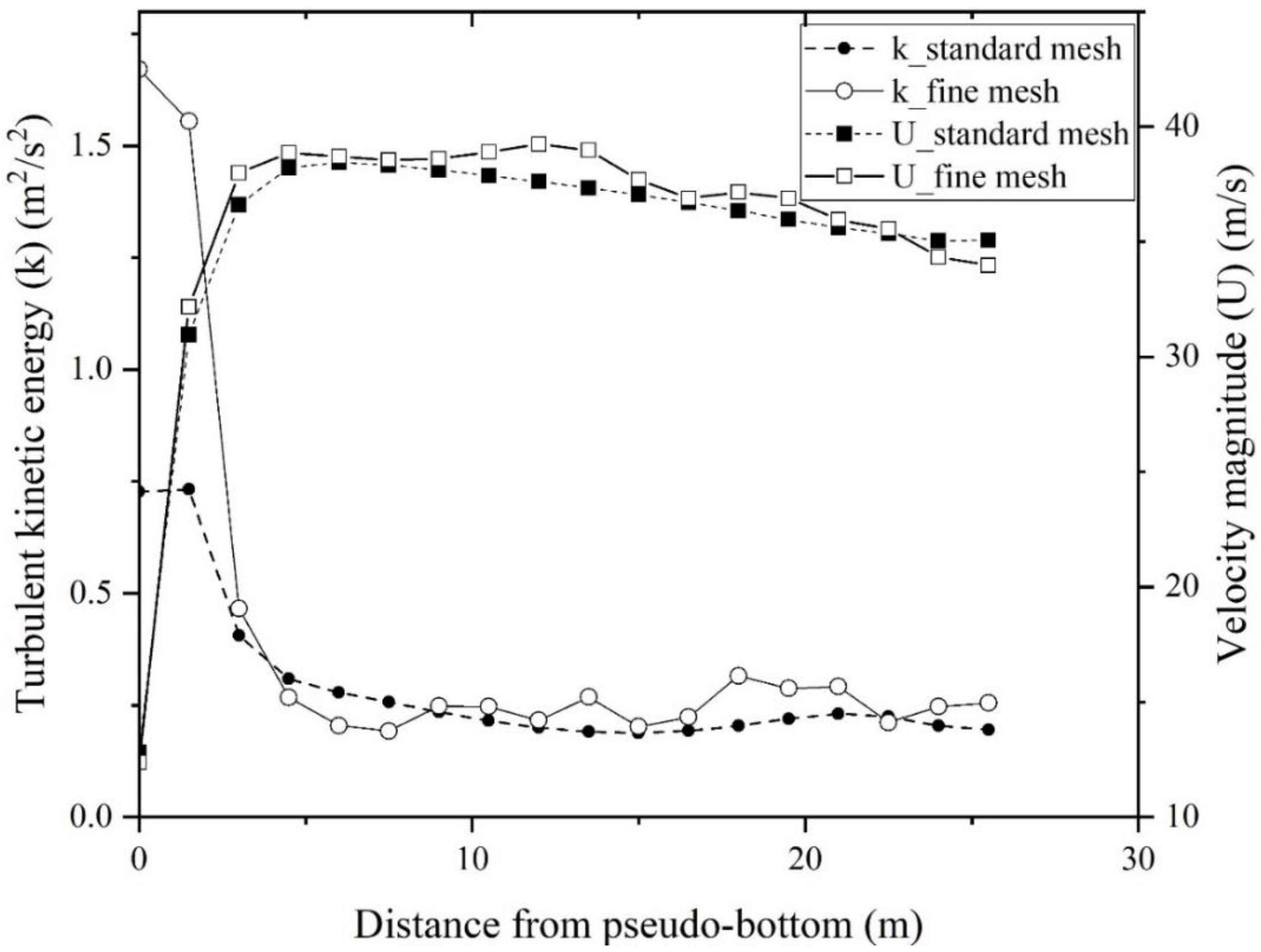
4.1. Mesh Sensitivity Analysis and Model Validation
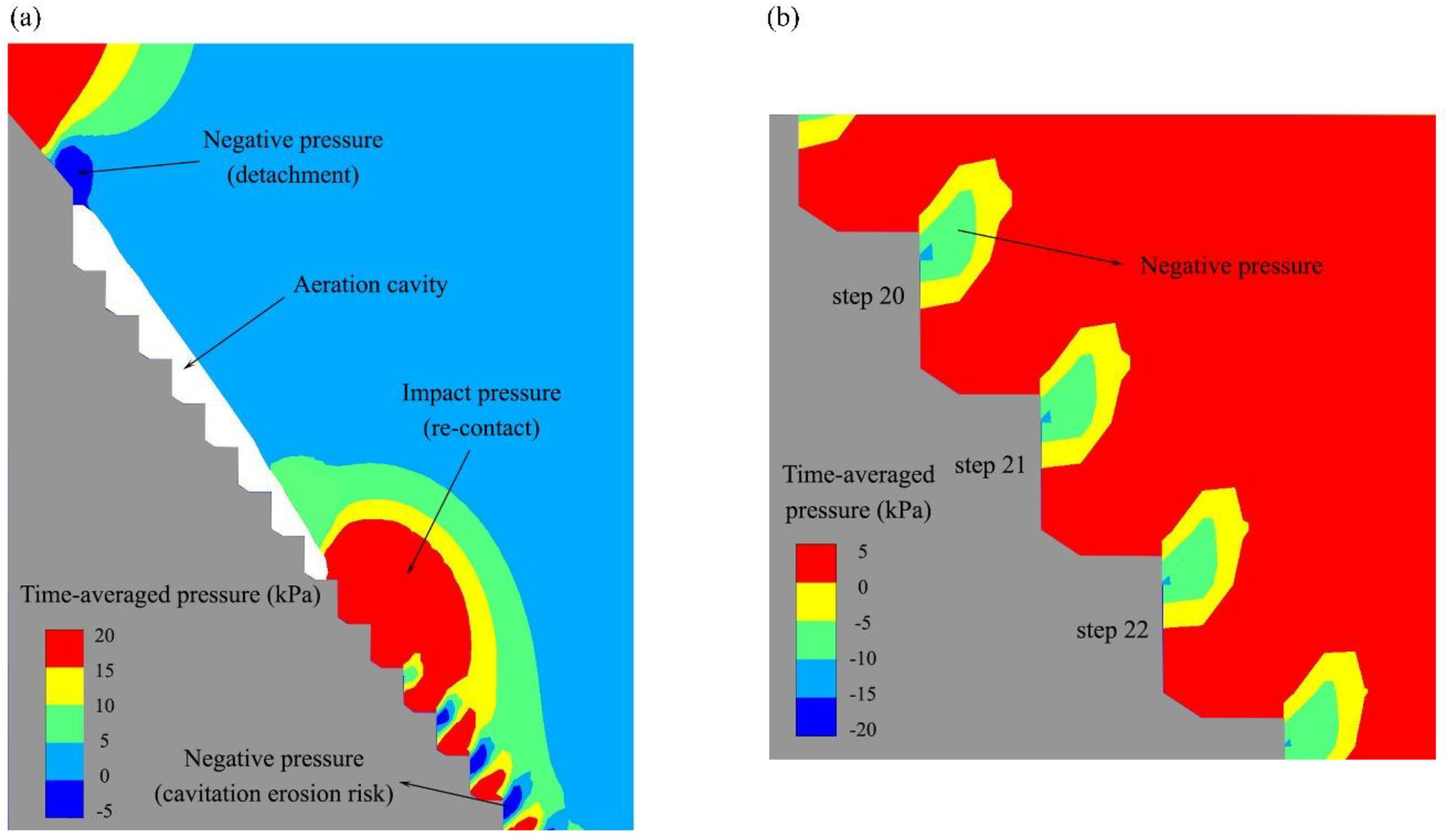
4.2. Pressure Distribution
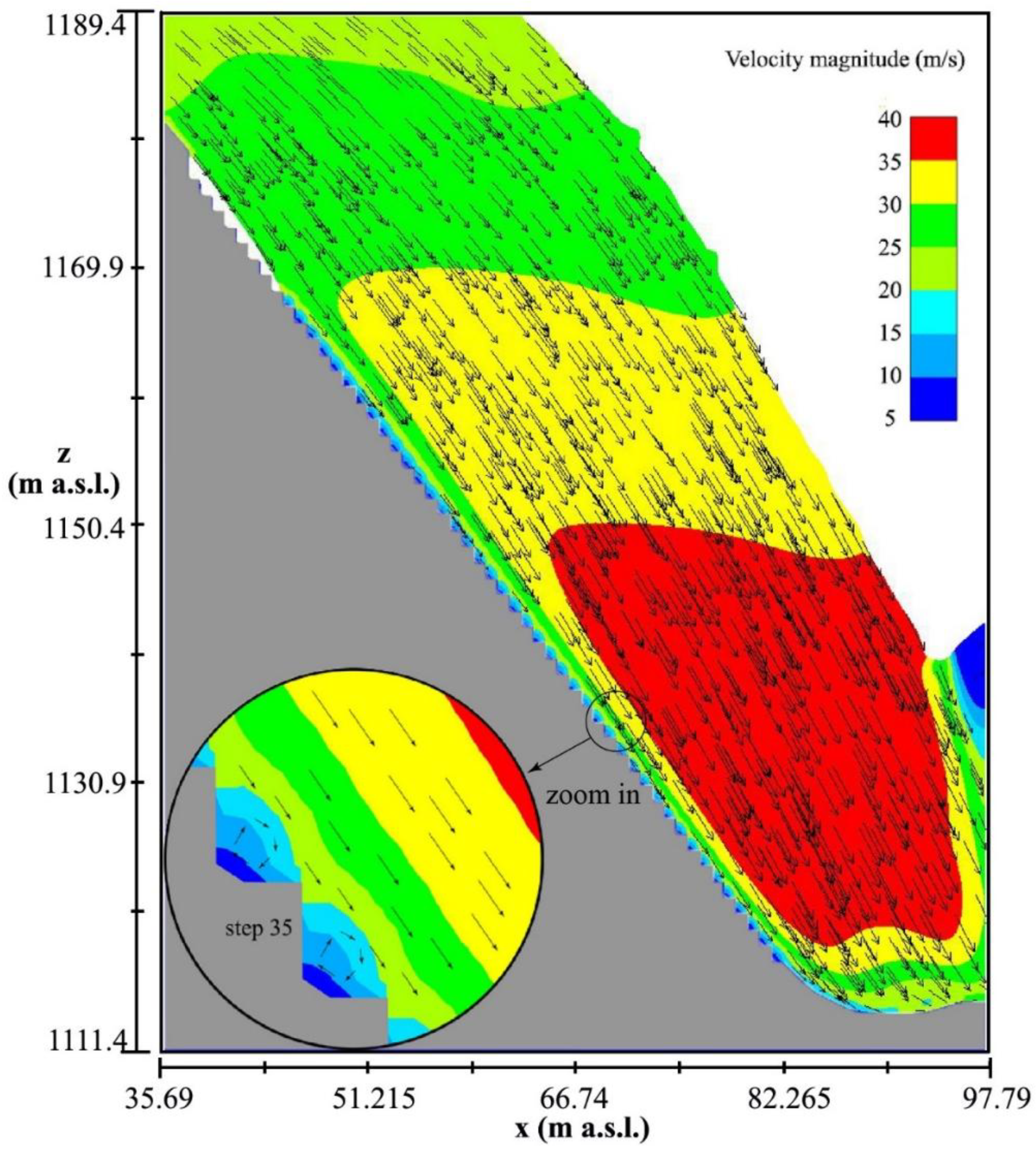
4.3. Velocity Magnitude
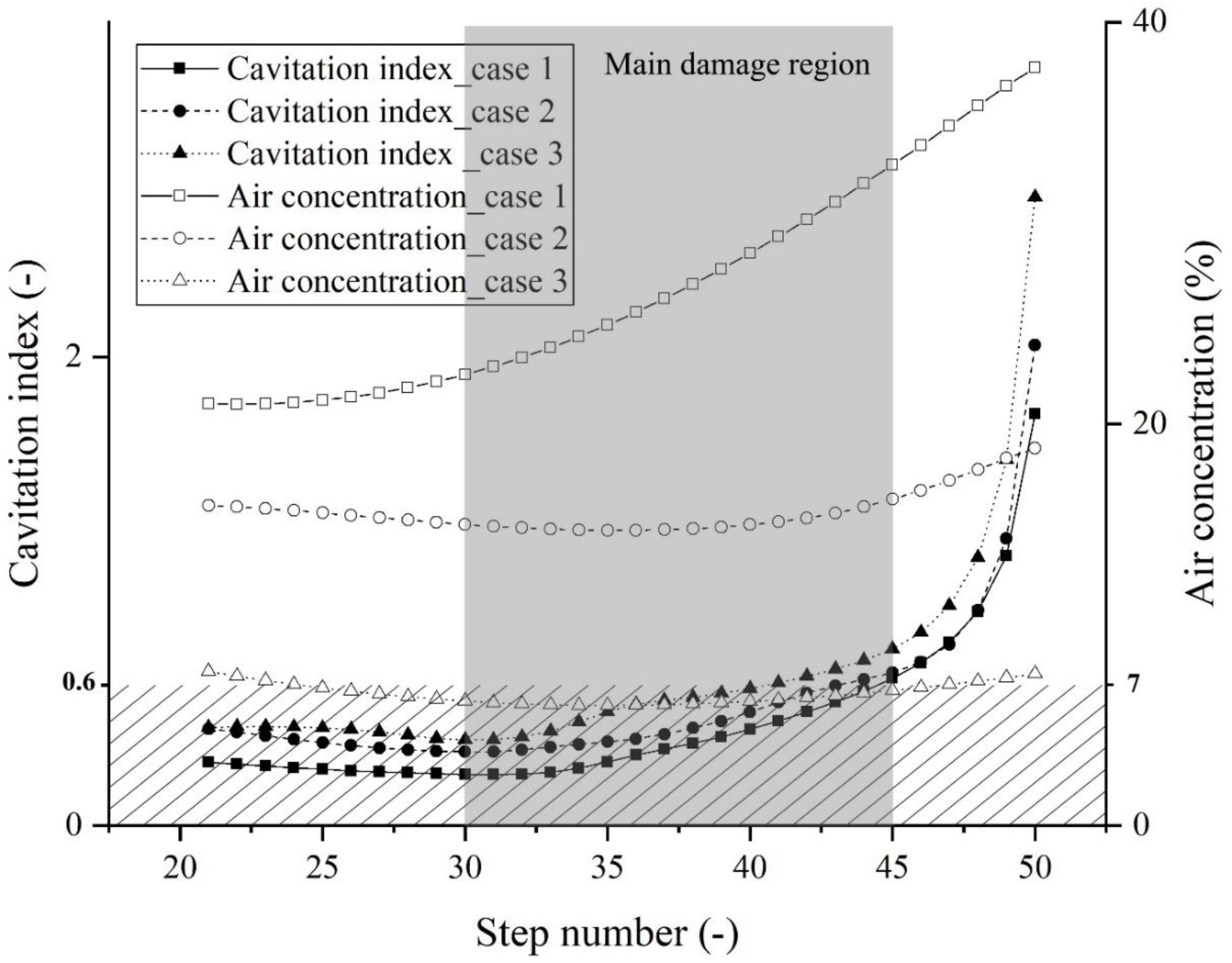
4.4. Step Surface Cavitation Index
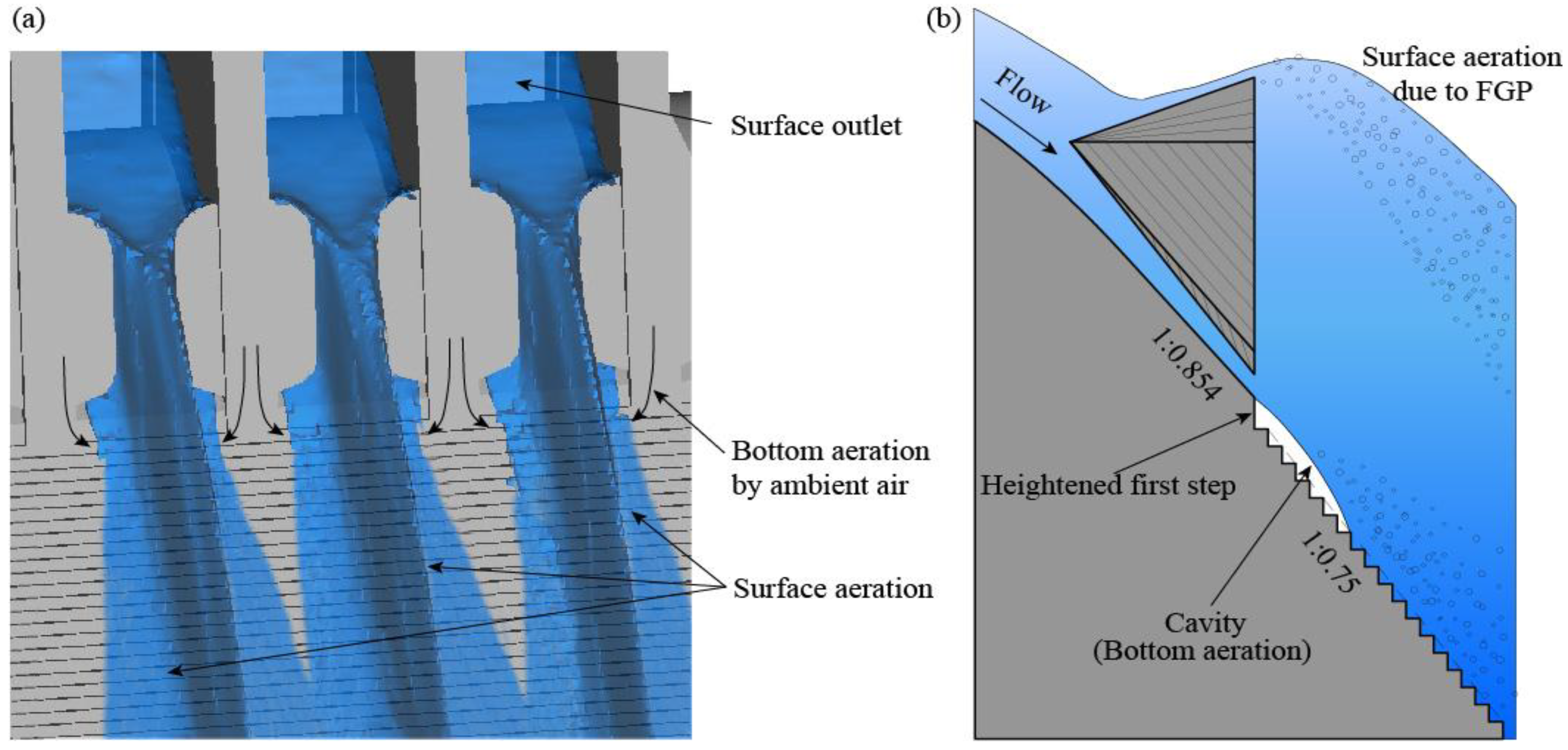
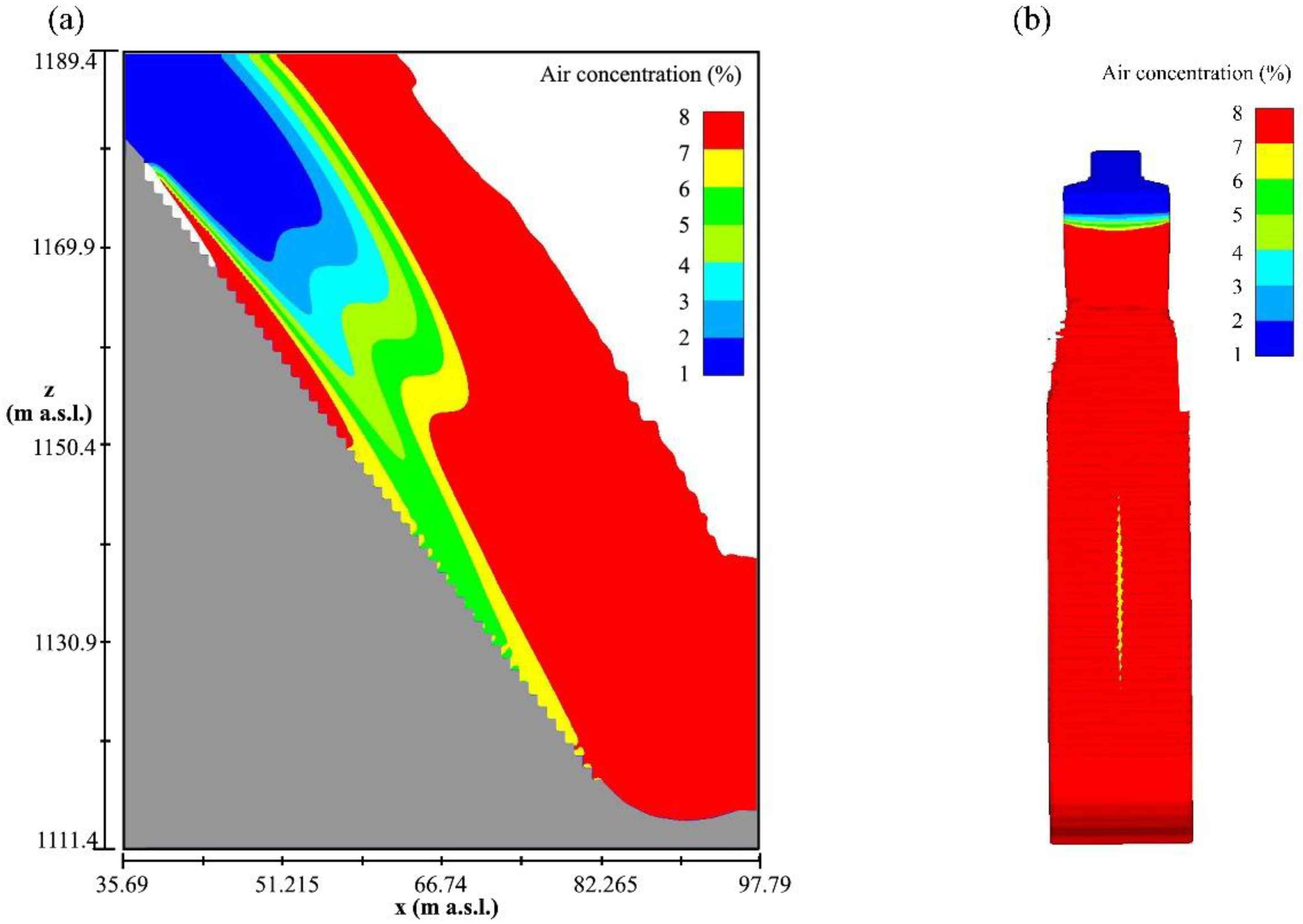
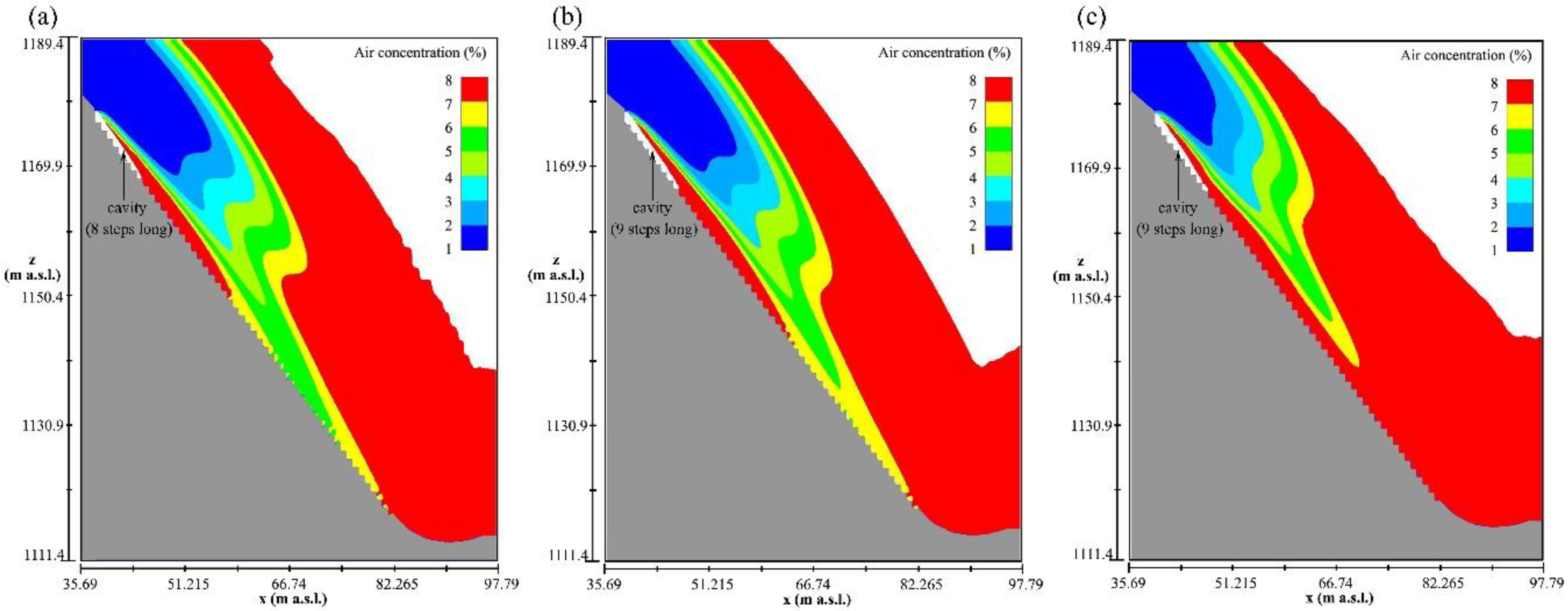
4.5. Air Concentration
4.6. Aerator Optimization
5. Conclusions
- The reliability of the involved models is considered satisfying, as the results are in good agreement with laboratory data.
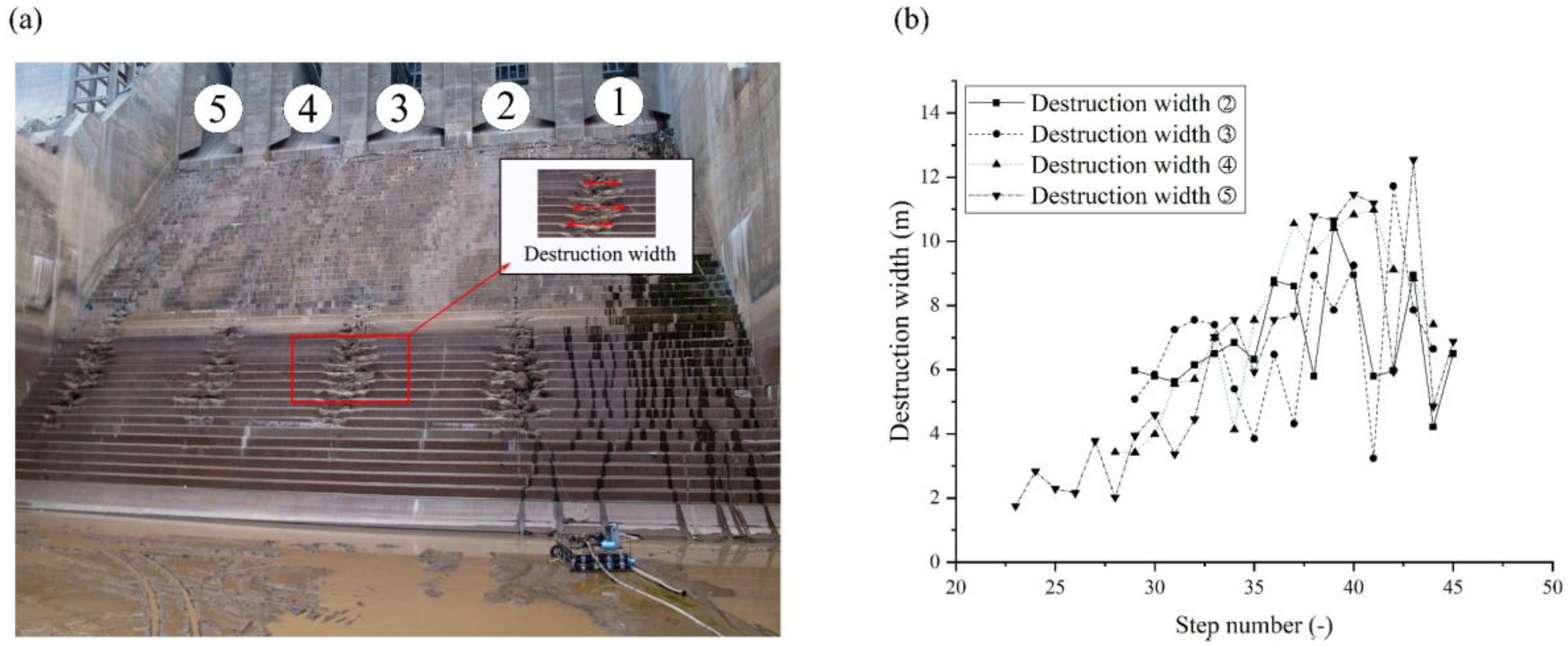
- The velocity close to the step tips was about 15 m/s, indicating potential cavitation occurrence for all investigated discharges. The negative pressure close to the step tips is a key factor that may cause cavitation erosion, since both analytical evidence of a low cavitation index and practical real-world step failure were discovered.
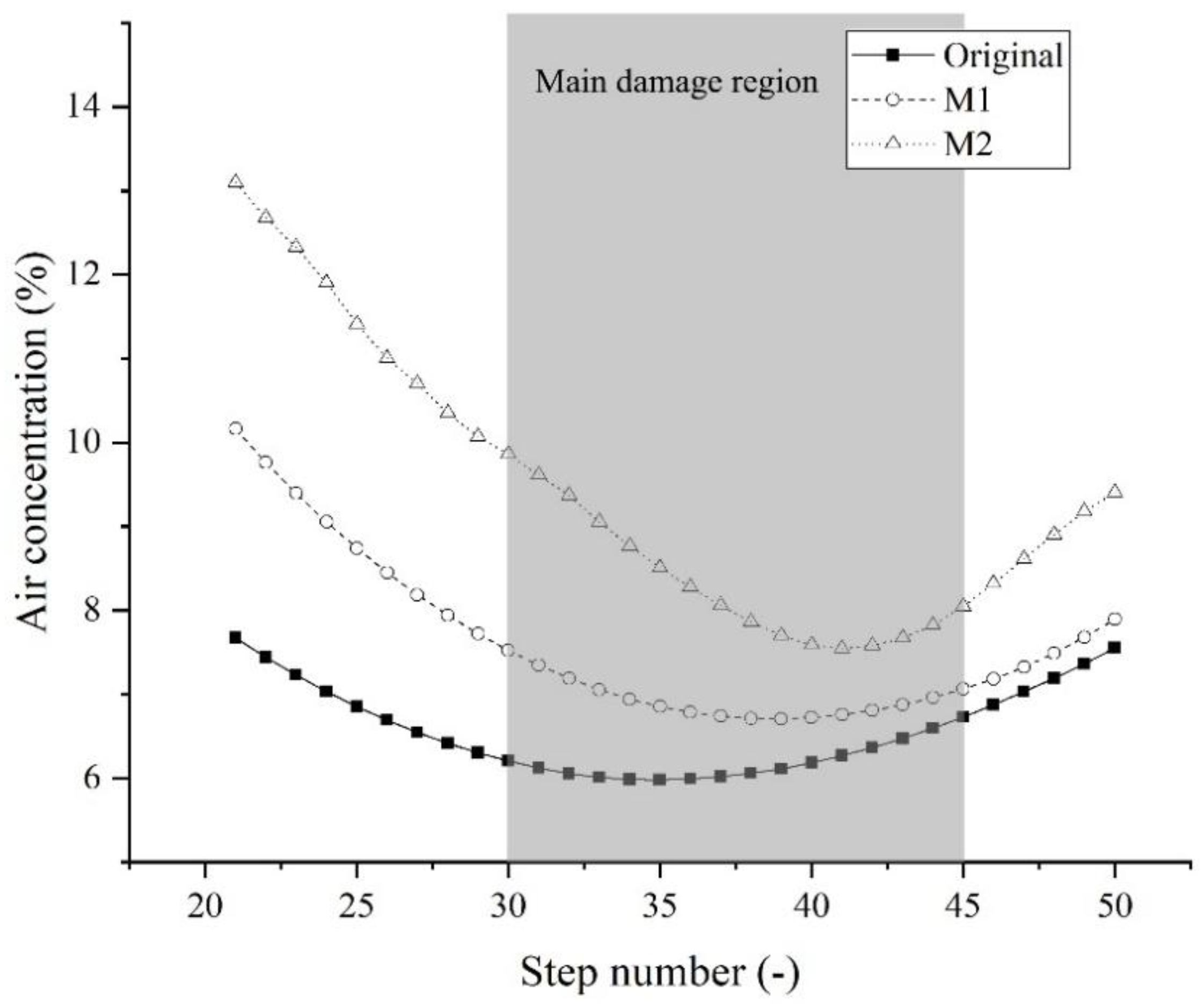
- The calculated air concentration data is rather reliable, considering the air concentration on the stepped surface behind the X-shaped FGP of roughly 5% to 6% and the reported scaled physical model value of 3% to 5% in [14]. In addition, the simulated air concentration and derived cavitation potential are plausible with regard to the prototype step failure. It was found that for a high unit discharge of 166 m2/s and flow depths up to 30 m (25 times the step height), free surface self-entrained air fails to reach the stepped surface before step 45. A bottom-aeration thus becomes very important but insufficient if a threshold of 7% for the air concentration is considered necessary for cavitation erosion avoidance.
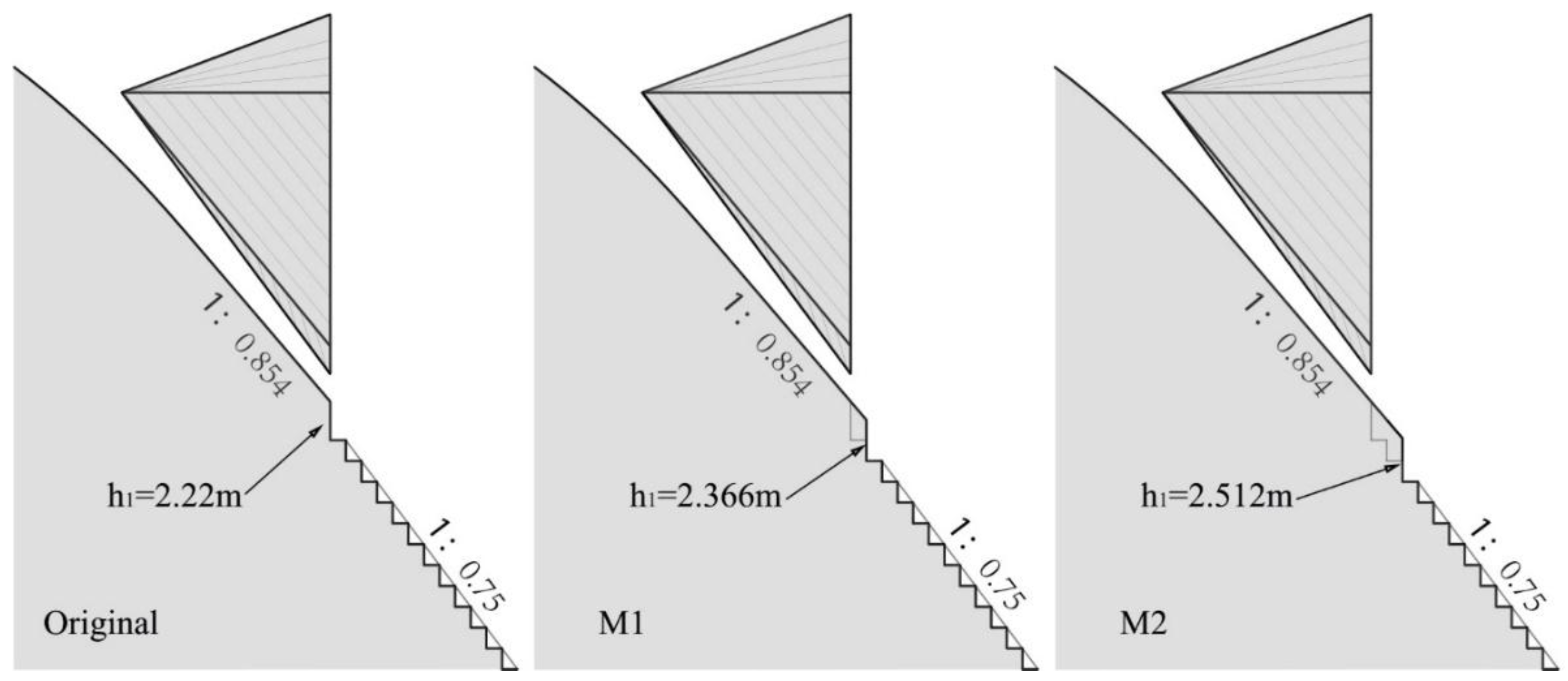
- The height of the first step of the spillway may affect the air concentration on the stepped surface to some degree. An increased air concentration along the steps for a larger first step height was found in the case study of Ludia dam spillway, especially upstream of step 35. Therefore, for aerator optimization of built projects, heightening the first step could be an economic and efficient measure to prevent cavitation erosion.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notation
| cross sectional area of air bubble (m2) | |
| As | area of surface disturbance (m2) |
| air concentration (–) | |
| user-defined drag coefficient (–) | |
| CNU | coefficient equal to 0.09 (–) |
| bubble diameter (m) | |
| effective diffusivity of k (kg m−1 s−1) | |
| effective diffusivity of (kg m−1 s−1) | |
| e | opening of radial gate (m) |
| f | water volume fraction (–) |
| gn | component of gravity normal to the free surface (m s−2) |
| Hd | design head of weir (m) |
| I | identity matrix |
| drag coefficient (kg m−3 s−1) | |
| drag coefficient for single particle (kg s−1) | |
| coefficient of proportionality (–) | |
| k | turbulent kinetic energy (m2 s−2) |
| Richardson–Zaki coefficient multiplier (-) | |
| LT | turbulent length (m) |
| P | gauge pressure in flow field (Pa) |
| ambient pressure (Pa) | |
| generation of k due to mean velocity gradient (kg m−1 s−3) | |
| vapor pressure (Pa) | |
| Pd | disturbance energy per unit volume (N m−2) |
| Pt | destabilization force per unit volume (N m−2) |
| q | unit width discharge (m2 s−1) |
| bubble radius (m) | |
| mixture velocity (m s−1) | |
| relative/slip velocity (m s−1) | |
| effective relative velocity (m s−1) | |
| magnitude of (m s−1) | |
| kinematic viscosity related to the turbulence Schmidt number (m2 s−1) | |
| effective kinematic viscosity (m2 s−1) | |
| We | Weber number (–) |
| Zup | upstream water elevation (m) |
| Zdown | downstream water elevation (m) |
| volume of air entrained to the flow (m3) | |
| Heightened height when extend curve end 0.9 m downstream (m) | |
| dissipation rate of k (m2 s−3) | |
| dynamic viscosity of air (Pa s−1) | |
| Richardson–Zaki coefficient (–) | |
| density of air, 1.225 kg m−3 | |
| macroscopic mixture density (kg m−3) | |
| density of water, 1000 kg m−3 | |
| coefficient of surface tension (N m−1) | |
| Reynolds stress tensor (kg m−1 s−2) |
Appendix A
References
- Christodoulou, G.C. Energy dissipation on stepped spillways. J. Hydraul. Eng. 1993, 119, 644–650. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Two-phase flow characteristics of stepped spillways. J. Hydraul. Eng. 2003, 129, 661–670. [Google Scholar] [CrossRef]
- Boes, R.M.; Hager, W.H. Hydraulic Design of Stepped Spillways. J. Hydraul. Eng. 2003, 129, 671–679. [Google Scholar] [CrossRef]
- Chanson, H. The Hydraulics of Stepped Chutes and Spillways; Balkema A.A. Publishers: Lisse, The Netherlands, 2002. [Google Scholar]
- Sánchez-Juny, M.; Bladé, E.; Dolz, J. Pressures on a stepped spillway. J. Hydraul. Res. 2007, 45, 505–511. [Google Scholar] [CrossRef]
- Ohtsu, I.; Yasuda, Y. Characteristics of flow conditions on stepped channels. In Proceedings of the 27th IAHR World Congress, San Francisco, CA, USA, 10–15 August 1997. [Google Scholar]
- Li, B.L. Experimental Study on the Pressure Characteristics in Stepped Spillway; Xi’an University of Technology: Xi’an, China, 2005. (In Chinese) [Google Scholar]
- Zhang, J.M.; Chen, J.G.; Wang, Y.R. Experimental study on time-averaged pressures in stepped spillway. J. Hydraul. Res. 2012, 50, 236–240. [Google Scholar] [CrossRef]
- Frizell, K.W.; Renna, F. Cavitation potential of flow on stepped spillways. J. Hydraul. Eng. 2013, 139, 630–636. [Google Scholar] [CrossRef]
- Boes, R.M. Guidelines on the design and hydraulic characteristics of stepped spillways. In Proceedings of the 24th ICOLD Congress, Kyoto, Japan, 6–8 June 2012; pp. 203–220. [Google Scholar]
- Falvey, H.T. Cavitation in Chutes and Spillways. Engineering Monograph 42; Bureau of Reclamation: Denver, CO, USA, 1990.
- Pfister, M.; Hager, W.H. Self-entrainment of air on stepped spillways. Int. J. Multiph. Flow 2011, 37, 99–107. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H.; Minor, H.E. Stepped chutes: Pre-aeration and spray reduction. Int. J. Multiph. Flow 2006, 32, 269–284. [Google Scholar] [CrossRef]
- Liang, Z.X.; Yin, J.B.; Zheng, Z.; Lu, H. Aeration of skimming flow on stepped spillway combined with flaring gate piers. J. Hydraul. Eng. 2009, 40, 564–568. (In Chinese) [Google Scholar]
- Pfister, M.; Hager, W.H.; Minor, H.E. Bottom aeration of stepped spillways. J. Hydraul. Eng. 2006, 132, 850–853. [Google Scholar] [CrossRef]
- Mateos, I.C.; Elviro, G.V. Initiation of aeration in stepped spillways. In Proceedings of the 27th IAHR World Congress, San Francisco, CA, USA, 10–15 August 1997. [Google Scholar]
- Amador, A.; Sanchez-Juny, M.; Dolz, J. Developing flow region and pressure fluctuations on steeply sloping stepped spillways. J. Hydraul. Eng. 2009, 135, 1092–1100. [Google Scholar] [CrossRef]
- Xie, X.Z.; Li, S.Q.; Li, G.F. Development of flaring gate piers in China I. Hongshui River 1995, 14, 3–11. (In Chinese) [Google Scholar]
- Xie, X.Z.; Li, S.Q.; Li, G.F. Development of flaring gate piers in China II. Hongshui River 1995, 15, 24–30. (In Chinese) [Google Scholar]
- He, G.T.; Zeng, X.K.; Li, Z.F.; Yang, S.L. Optimum design of new energy dissipators of Shuidong hydropower station. W. Power 1994, 9, 26–28. (In Chinese) [Google Scholar]
- Yin, J.B.; Liang, Z.X.; Gong, H.L. Experimental study on flow characteristics on 3D hydraulic jump of flaring gate piers. J. Hydraul. Eng. 2010, 41, 1333–1338. (In Chinese) [Google Scholar]
- Dong, Z.S.; Wang, J.X.; Zhang, W.C.; Da, J.R. Study on dissipation characteristics of incomplete flaring gate pier with low froude number. J. Sichuan Univ. (Eng. Sci. Ed.) 2016, 48, 9–15. (In Chinese) [Google Scholar]
- Nan, X.H.; Liang, Z.X.; Liu, H.S. New type of flaring pier for improving energy dissipation of stepped surface overflow dam. J. Hydraul. Eng. 2003, 8, 49–57. (In Chinese) [Google Scholar]
- Wang, B.; Wu, C.; Hu, Y.H.; Mo, Z.Y. Relationship of first step height, step slope and cavity in X-shaped flaring gate piers. J. Hydrodyn. 2007, 19, 349–355. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, C.; Liao, H.S.; Hu, Y.H. 3D numerical simulation on water and air two-phase flows of the steps and flaring gate piers. J. Hydrodyn. 2005, 17, 338–343. [Google Scholar]
- Li, S.; Zhang, J. Numerical Investigation on the Hydraulic Properties of the Skimming Flow over Pooled Stepped Spillway. Water 2018, 10, 1478. [Google Scholar] [CrossRef]
- Koh, C.G.; Luo, M.; Bai, W. Simulation of wave impact with compressible air entrainment based on consistent particle method. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, 31 May–5 June 2015. [Google Scholar]
- Wan, H.; Li, R.; Gualtieri, C.; Yang, H.; Feng, J. Numerical simulation of hydrodynamics and reaeration over a stepped spillway by the SPH method. Water 2017, 9, 565. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Zhou, C.; Dong, Z.; Zhou, Z. Numerical simulation of hydraulic characteristics in a vortex drop shaft. Water 2018, 10, 1393. [Google Scholar] [CrossRef]
- Chen, Q.; Dai, G.Q.; Liu, H.W. Volume of Fluid Model for Turbulence Numerical Simulation of Stepped Spillway Overflow. J. Hydraul. Eng. 2002, 128, 683–688. [Google Scholar] [CrossRef]
- Valentin, H. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar]
- Felder, S.; Chanson, H. Turbulence, dynamic similarity and scale effects in high-velocity free-surface flows above a stepped chute. Exp. Fluids 2009, 47, 1–18. [Google Scholar] [CrossRef]
- Takahashi, M.; Yasuda, Y.; Ohtsu, I. Effect of Reynolds number on characteristics of skimming flows in stepped channels. In Proceedings of the 31th IAHR World Congress, Seoul, Korea, 11–16 September 2005. [Google Scholar]
- Flow-3D, version 11.2; User Manual; Flow Science Inc.: Santa Fe, NM, USA, 2017.
- Yakhot, S.; Orszag, A. Renormalization group analysis of turbulence. I. Basic theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Hirt, C.W. Modeling Turbulent Entrainment of Air at a Free Surface; Technical Note FSI-01-12; Flow Science, Inc.: Santa Fe, NM, USA, 2003. [Google Scholar]
- Meireles, I.C.; Bombardelli, F.A.; Matos, J. Air entrainment onset in skimming flows on steep stepped spillways: An analysis. J. Hydraul. Res. 2014, 52, 375–385. [Google Scholar] [CrossRef]
- Brethour, J.M.; Hirt, C.W. Drift Model for Two-Component Flows; Technical Note FSI-09-TN83; Flow Science Inc.: Santa Fe, NM, USA, 2009. [Google Scholar]
- Hirt, C.W. Dynamic Droplet Sizes for Drift Fluxes; Technical Note FSI-11-16; Flow Science Inc.: Santa Fe, NM, USA, 2016. [Google Scholar]
- Richardson, J.F.; Zaki, W.N. Sedimentation and fluidisation: Part 1. Trans. Inst. Chem. Eng. 1954, 32, 35–53. [Google Scholar] [CrossRef]
- Hirt, C.W.; Sicilian, J.M. A porosity technique for the definition of obstacles in rectangular cell meshes. In Proceedings of the 4th International Conference Ship Hydrodynamics, National Academy of Science, Washington, DC, USA, 24–27 September 1985. [Google Scholar]
- Hirt, C.W. Volume-Fraction Techniques: Powerful Tools for Flow Modeling; Flow Science Report FSI-92-00-02; Flow Science Inc.: Santa Fe, NM, USA, 1992. [Google Scholar]
- Khosro, M.; Afshin, E. Study of inception point, void fraction and pressure over pooled stepped spillways using Flow-3D. Int. J. Numer. Methods Heat Fluid Flow 2017, 28, 982–998. [Google Scholar]
- Rajaratnam, N. Skimming flow in stepped spillways. J. Hydraul. Eng. 1990, 116, 587–591. [Google Scholar] [CrossRef]
- Chamani1, M.R.; Rajaratnam, N. Onset of skimming flow on stepped spillways. J. Hydraul. Eng. 1999, 125, 969–971. [Google Scholar] [CrossRef]
- Peterka, A.J. The effect of entrained air on cavitation pitting. In Proceedings of the 5th IAHR Congress, Minneapolis, MN, USA, 1–4 September 1953. [Google Scholar]

| Load Case No. | e (m) | q (m2 s−1) |
|---|---|---|
| 1 | 4.75 | 80 |
| 2 | 9.5 | 120 |
| 3 | 19 | 166 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Wang, J.; Vetsch, D.F.; Boes, R.M.; Tan, G. Numerical Simulation of Air–Water Two-Phase Flow on Stepped Spillways behind X-Shaped Flaring Gate Piers under Very High Unit Discharge. Water 2019, 11, 1956. https://doi.org/10.3390/w11101956
Dong Z, Wang J, Vetsch DF, Boes RM, Tan G. Numerical Simulation of Air–Water Two-Phase Flow on Stepped Spillways behind X-Shaped Flaring Gate Piers under Very High Unit Discharge. Water. 2019; 11(10):1956. https://doi.org/10.3390/w11101956
Chicago/Turabian StyleDong, Zongshi, Junxing Wang, David Florian Vetsch, Robert Michael Boes, and Guangming Tan. 2019. "Numerical Simulation of Air–Water Two-Phase Flow on Stepped Spillways behind X-Shaped Flaring Gate Piers under Very High Unit Discharge" Water 11, no. 10: 1956. https://doi.org/10.3390/w11101956
APA StyleDong, Z., Wang, J., Vetsch, D. F., Boes, R. M., & Tan, G. (2019). Numerical Simulation of Air–Water Two-Phase Flow on Stepped Spillways behind X-Shaped Flaring Gate Piers under Very High Unit Discharge. Water, 11(10), 1956. https://doi.org/10.3390/w11101956






