Abstract
In this paper we present a computational model for the fluid structure interaction of a buoyant rigid body immersed in a free surface flow. The presence of a free surface and its interaction with buoyant bodies make the problem very challenging. In fact, with light (compared to the fluid) or very flexible structures, fluid forces generate large displacements or accelerations of the solid and this enhances the artificial added mass effect. Such a problem is relevant in particular in naval and ocean engineering and for wave energy harvesting, where a correct prediction of the hydrodynamic loading exerted by the fluid on buoyant structures is crucial. To this aim, we develop and validate a tightly coupled algorithm that is able to deal with large structural displacement and impulsive acceleration typical, for instance, of water entry problems. The free surface flow is modeled through the volume of fluid model, the finite volume method is utilized is to discretize the flow and solid motion is described by the Newton-Euler equations. Fluid structure interaction is modeled through a Dirichlet-Newmann partitioned approach and tight coupling is achieved by utilizing a fixed-point iterative procedure. As most experimental data available in literature are limited to the first instants after the water impact, for larger hydrodynamic forces, we specifically designed a set of dedicated experiments on the water impact of a buoyant cylinder, to validate the proposed methodology in a more general framework. Finally, to demonstrate that the proposed numerical model could be used for a wide range of engineering problems related to FSI in multiphase flows, we tested the proposed numerical model for the simulation of a floating body.
1. Introduction
Fluid structure interaction (FSI) studies the physical phenomena related to the motion of a solid body, possibly compliant, within an encompassing fluid [1]. The development of reliable models for FSI is relevant for several engineering fields [2,3], including naval or marine engineering [4,5,6,7,8,9,10,11,12], bio-engineering [13,14,15,16,17], fluid machinery [1,18], energy harvesting [16,19,20,21,22,23], environmental engineering [24,25] and micro-mechanical systems and sensing devices [26,27,28,29] and a large scientific literature deals with the numerical evaluation of the fluid forces caused by the prescribed motion of a solid structure [9,10,19,20,21,30,31,32,33,34].
Recently, due to the increased availability of computational power, significant research efforts head towards the development of numerical methods that simultaneously model the fluid flow and the solid motion and deformation [35,36,37,38]. Such methodologies require the modeling of two non-overlapping domains, the fluid and the solid, separated by a common interface. Each field of application has different modeling requirements. For instance, aero-elasticity couples a stiff structure with a light and possibly compressible fluid [39], while in bio-engineering a very flexible structure and an incompressible fluid with comparable densities are coupled [13]. In naval or marine engineering structures interact with a free surface flows and are subject to a slamming pressure impulsive load [12,40,41,42].
When one of the two domains is predominant, as for example when a very stiff structure immersed in a light fluid, weakly or loosely coupled partitioned approaches are usually employed [43]. In this case, the two domains are solved sequentially through separate models that exchange informations through the fluid-structure interface. The dominant one (e.g., the solid) is modeled first, determining the boundary conditions for the other one whose reaction is lagged in time. In the conventional serial staggered approach (CSS) [44], at each time-step, the solid motion is predicted using the fluid flow from the previous time-step, then such a motion is utilized to determine the fluid flow and, finally, the solid motion is corrected utilizing the actual fluid flow [1,44]. Such a strategy is called Dirichlet-Neumann partitioning [2,45]. The flow field is the Dirichlet partition subject to the prescribed interface displacement and the solid is the Neumann partition subject to the interface forces [2].
However, loosely coupled partitioned algorithms do not guarantee convergence [1,2,45]. In particular, the artificial added mass effect is a well known issue for these approaches [1,46,47], especially at certain fluid to structure density ratios and certain geometries. This effect becomes relevant when the fluid forces generate large displacements or accelerations, in the solid, that is for light (compared to the fluid) or very flexible structures [1,2,45]. In such cases, strong or tight coupling, is needed [1,2,45] and can be achieved through both partitioned and monolithic algorithms.
In the realm of Dirichlet-Neumann partitioned methodologies, tight coupling is achieved through iterative algorithms that solve each domain multiple times until convergence within the same time-step. Different approaches such as fixed-point (also known as Block-Gauss-Seidel) [48] and interface Newton-Krylov [49] iterations are possible. Fixed-point iteration is the most straightforward, yet very effective, coupling strategy [2]. It allows to reuse existing solvers for the solid and fluid domains, reducing the modeling effort. Dynamic under-relaxation is often employed to improve the convergence speed of fixed-point iterations [2].
Monolithic algorithms obtain the strong coupling by solving simultaneously the non-linear system of equations that represents the fluid flow and solid displacement [38,50,51]. These methodologies are reliable and robust but partitioned approaches are far more popular for FSI problems [1]. In fact, monolithic solvers are more computationally intensive compared to partitioned ones and lack modularity hindering the code reuse that, on the contrary, is a characteristic of partitioned methods.
The fluid-structure interaction modelling becomes even more challenging in the presence of free surface flows, which is a common occurrence in several relevant engineering problems, in ocean engineering, aerospace and energy harvesting applications [52]. In particular, water entry problems [50,53], which occur when a solid body impacts the water, represent a challenging issue involving fluid-structure interaction in the presence of a free surface. A correct prediction of the impulsive loads originating from such an impact, as well as of the responses of the fluid and the structure, are crucial in the design of marine vessels and aerospace structures, such that several analytical, experimental and numerical studies have been published so far. In energy harvesting, when the fluid being treated as a source of exploitable energy rather than a mere source of mechanical damping, a proper simulation of fluid-structure interaction is crucial and in some cases involves solid bodies interacting with a free surface (i.e., wave energy harvesting). In such a case, the interaction between the solid and the water may be responsible for large impulsive loadings, with the humbling presence of the free-surface, which represents a jump of density of approximately three orders of magnitude and whose dynamics is very complex to be predicted. Therefore, the development of reliable numerical methods and experimental techniques to characterize such impulsive loading is crucial for the design of several kind of engineering devices, such as marine vessels and hydraulic structures. Several works are available in literature dealing with the simulation of fluid-structure interaction in the presence of a free surface [6,9,35,36,37]. Different numerical models, alternative to Navier-Stokes, may be also employed to simulate the fluid flow with a free surface, such as Smoothed Particles Hydrodynamics (SPH) [54,55], Lattice Boltzmann Method (LBM) [8,56] and constrained interpolation profile (CIP) method [57,58]. However, only few reliable numerical methods with strong coupling modelling techniques have been proposed in the scientific literature so far and only part of them refer to buoyant rigid bodies (e.g., References [59,60]), a problem relevant to the design of marine vessels [7,61,62,63] and aerospace structures [64] that are often designed to resist to large displacements and impulsive accelerations.
In this paper, we propose a computational model for the FSI of buoyant rigid bodies in the presence of free surface flows and we validate it with literature and custom designed experimental data for different fluid structure interaction problems. We adopt tightly coupled algorithm through a Dirichlet-Neumann partitioned approach with fixed-point iterations. The incompressible free surface flow is modelled through the volume of fluid approach (VOF), the partial differential flow equations are discretised thorugh the finite volume method and solid displacement is described by the Newton-Euler equations. The proposed algorithm is implemented within the foam-extend-3.2 open source framework [65], allowing a substantial code reutilization. Specifically, the flow solution is based on the interDyMFoam solver that utilizes the Arbitrary Lagrangian Eulerian method (ALE) and the PIMPLE algorithm [66] to solve the multiphase flow equations in a deformable domain, while we implement the solution algorithm for the Newton-Euler equations and the coupling procedure.
The rest of the paper is organized as follows. In Section 2 we describe the proposed methodology. In particular, in Section 2.1 and Section 2.2 we discuss on the fluid and the structure modeling, respectively, while in Section 2.3 we describe the proposed coupling algorithm. The methodology is experimentally validated in Section 3, by comparing numerical results to literature ones and ad-hoc experiments. Conclusions are drawn in Section 4.
2. Methodology
The problem in study is schematically represented in Figure 1. Solving an FSI problem requires the physical modeling of two non-overlapping domains, the fluid, and the solid, , ones, separated by an interface .
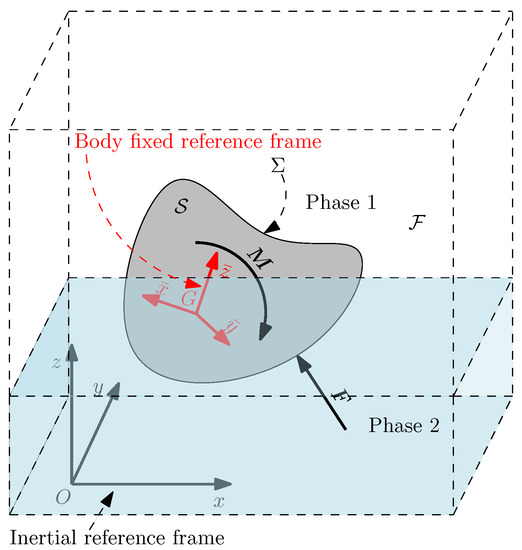
Figure 1.
Schematic representation of the problem.
Herein we consider two immiscible fluid phases, namely phase 1 and phase 2 and we assume that the flow is incompressible. The solid domain is rigid and free to move subject to fluid, gravity or other external forces.
We consider an inertial reference frame and a body fixed frame , which defines the orientation of with respect to (see Figure 1). G is the center of mass of and the superimposed bar () identifies the vectors expressed in body fixed coordinates.
We solve the FSI problem through a partitioned Dirichlet-Neumann approach with fixed-point iteration [2,45]. Thereafter separate models are utilized for (see Section 2.1) and , (see Section 2.2).
2.1. Fluid Flow
The incompressible flow of two immiscible fluids is described by the following continuity and momentum conservations:
where is the fluid velocity, p is the pressure, is the dynamic viscosity, is the density, is the gravitational acceleration and denotes the material derivative. Despite the flow is incompressible, and vary in space and time according to the fluid phase.
The force exerted by the fluid on the solid body is,
where is the identity matrix, is the body surface and is the unit normal to the solid body. The moment of with respect to G is
being the distance of each surface element from the center of gravity of the body.
The flow is numerically approximated utilizing the interDyMFoam algorithm included within the foam-extend-3.2 software package [65]. It implements the volume of fluid (VOF) [67,68,69,70] and models the incompressible flow of two immiscible fluids through a single set of the Navier-Stokes and continuity equations (Equation (1)). The interface between the two phases is tracked by solving Equation (4) [69]:
where is the water volume fraction and is the relative velocity of the two phases. The second term of Equation (4) is introduced to contrast the numerical diffusion of the fluid interface [69].
Equations (1) and (4) are discretized through a generalized unstructured finite volume approach with a collocated variable arrangement [71]. The pressure velocity coupling and the non linearity of Equation (1) are solved using the PIMPLE algorithm [72]. The discrete version of Equation (4) is solved through the Multidimensional Universal Limiter with Explicit Solution (MULES) procedure [66].
Turbulent flows can be modeled with different levels of approximations including Reynolds averaged Navier Stokes (RANS), large eddy simulation (LES) and direct numerical simulation (DNS) [66]. The most common turbulence models for RANS and LES are already included in the foam-extend-3.2 environment.
As the motion of the solid body distorts the fluid domain, the computational nodes are re-allocated after each time-step to avoid depletion of the mesh quality. Several procedures for the mesh deformation are implemented within the foam-extend library [45,73,74,75]. The numerical solution of Equations (1) and (4) accounts for the mesh deformation through the arbitrary Lagrangian Eulerian (ALE) procedure [45,74].
2.2. Rigid Body Dynamics in Space
The position () of the generic point p in can be expressed as
where is the position vector of G and is the rotation matrix that defines the orientation of with respect to . The motion in space of an unconstrained body follows the Newton-Euler equations [76],
being m the mass, the external force, the inertia matrix, the external moment, and the angular velocity of . The system of Equation (6) can be regarded as a system of differential equations in and . Since cannot be directly integrated, we introduce the four component vector
containing the Euler parameters to obtain the orientation of the body as follows [76,77]:
where and is the skew matrix associated to . The following equation provides the relation between and :
where .
The system of ordinary differential equations from (5) to (9) is numerically integrated through the Euler explicit method.
Equations from (5) to (9) describe the 6 degrees of freedom (6-DOF) motion of an unconstrained body. Reduced order models (i.e., 1-DOF, 2-DOF or 3-DOF) are obtained by assuming zero the proper components of and . For instance, 3-DOF motion in the -plane is obtained by setting and . Similarly, 2-DOF motion in the -plane is obtained by setting and . Finally, 1-DOF, for instance along the y-direction, is achieved by setting and .
2.3. Coupling Algorithm
The FSI problem is solved through a partitioned (or segregated) approach, which means that the mathematical models for the fluid flow (i.e., Equations (1) and (4)) and for the solid motion (i.e., Equations (5)–(9)) are integrated separately [2]. To accomplish the interaction between the fluid and the structure, communicates and to the solid and communicates the displacement to . A strong or tight, coupling is required to ensure convergence when the density of the solid is comparable or lower, than the fluid density [1,2]. Being the algorithm segregated, such a coupling is accomplished through the iterative procedure reported in Figure 2 [1,2].
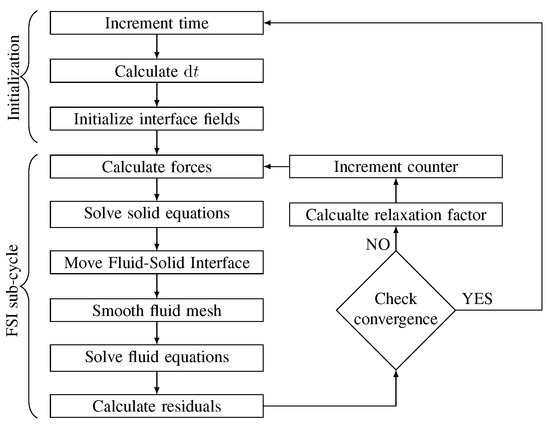
Figure 2.
Flow chart of the FSI solution algorithm.
At the beginning of each time step, , the time step duration is calculated according to the Courant condition, assuming that the fluid flow determines the most stringent stability constraint. Then, the interface fields are initialized. In particular, the residuals of the FSI sub-cycle and the interface displacement are set to zero (i.e., , ) and the relaxation factor is initialized , with the superscripts referring to the FSI subcycle.
After initialization, the FSI sub-cycle, identified in the followings by the superscript n, begins with the calculation of the interface forces. Fluid force and moment are calculated through Equations (2) and (3) and then utilized to solve the system of Equations (5)–(9). The displacement of the points on the fluid-solid interface is then estimated as:
The algorithm proceeds with the calculation of the interface displacement. The displacement of the generic node i on with respect to the previous time-step is estimated as:
Under-relaxation is necessary to guarantee the convergence of the segregated algorithm, as widely recognized in the literature [1,2]. Having determined the displacement of , the computational mesh for the fluid domain can be adjusted to meet the new boundary configuration. For each FSI sub-cycle, the flow equations have to be integrated within the same time-step. The ALE procedure calculates the convective fluxes accounting for the displacement of the faces of each computational cell within a time-step. A correct estimation of such fluxes requires that each computational node is displaced from its position at time-step to the final position at sub-cycle n of time-step . Within the foam-extend-3.2 framework, this is accomplished by first moving back the mesh to its configuration at time-step and then smoothing the nodes to their final position. The procedure described in Section 2.1 is then utilized to solve the flow equations. At any step, mass is updated guaranteeing continuity.
The residuals are defined as:
The convergence of the FSI sub-cycle is assessed by comparing the magnitude of the residuals to a user-defined threshold
where is the number of computational nodes in the fluid solid interface. If the inequality reported in Equation (13) is not verified, the relaxation factor is estimated before cycling the FSI sub-cycle starting from the flow solution (see Figure 2), according to the Aitken’s procedure [1,2]:
where is a limiting value that can be varied for each application.
3. Validation
The methodology described in Section 2 is validated by comparison against experimental data. Both independent literature data [40,78,79] and custom designed experiments are considered in this validation.
Despite the proposed methodology is able to simulate 3D hydrodynamics and 6-DOF motions, for validation we concentrate on 2D hydrodynamics and 1-DOF structure motion to facilitate the comparison between numerical results and experimental data.
We assume that the densities and the viscosities of water and air are kg/m, kg/m, Pa·s and Pa·s. For all the cases we considered and .
3.1. Water Entry of a Non-Buoyant Wedge
Zhao et al. [78] experimentally studied the water impact of a rigid wedge characterized by a total mass of 241 kg, a deadrise angle of , a width of m and a breadth of 1 m. The specimen is bounded to move in the vertical direction and impacts the water at a velocity of m/s.
Following the indications in Reference [80], we assume that the flow is two dimensional (2D), being the breadth of the specimen larger than its width. Thereafter the fluid domain is discretized through a 2D structured mesh with about 5200 computational cells. Moreover, according to References [10,32], we assumed that turbulence modeling is not required for impulsive impact phenomena.
Temporal discretization, is performed through the first order accurate Euler implicit scheme [66]. The Gauss upwind [66] scheme is utilized to discretize the convective terms in Equation (1) and the Gauss interface compression scheme is employed for the convective term in Equation (4) [69]. Other spatial discretizations are performed through the Gauss linear procedure.
In Figure 3 we compare the numerical and experimental results for the vertical velocity of the wedge. We note that numerical results compare very well with the experiments. Specifically, the average relative error is
being the number of the considered experimental samples, the numerical approximation vertical component of the velocity of the specimen center and its experimental evaluation.
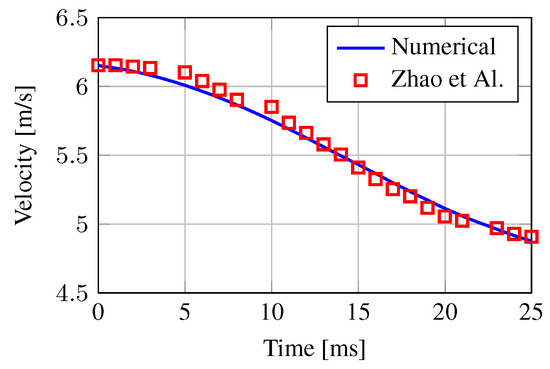
Figure 3.
Comparison between numerical and experimental results for the specimen velocity during the water impact of a rigid wedge. Experimental data are retrieved from Reference [78].
3.2. Water Entry of a Buoyant Wedge
The test performed in the previous section is not particularly challenging, as the specimen is relatively heavy and not buoyant, being the maximum mass of the displaced water 144 kg much lower than the mass of the specimen (241 kg). In this section, the proposed numerical model is verified against the water impact of buoyant bodies performed by Panciroli et al. [79]. Therein, the water impact of several buoyant wedges with different average deadrise angles, curvatures and impact velocities are reported. All the wedges have a square base of width m. Here, we focus on the specimens with a flat wetted surface, a constant deadrise angle of and a mass of 0.412 kg. The impact velocity varies between m/s and m/s as a function of the drop height h and is reported in Figure 4 together with its theoretical value, for all the considered experiments.
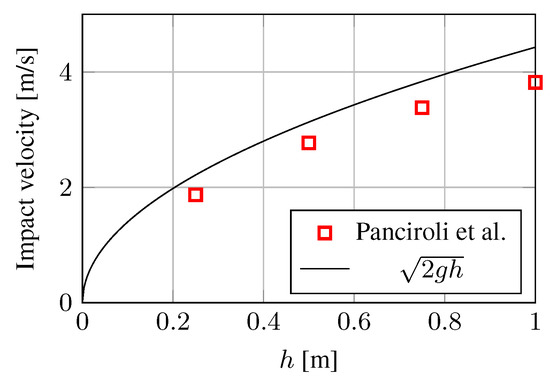
Figure 4.
Impact velocity of the specimen as a function of the drop height. Experimental data retrieved from Reference [79].
Analogously to the numerical test described in Section 3.1, we consider a 2D flow [80] and we utilize a laminar modeling approach [10,32]. A hexa-dominant unstructured mesh, with about 15,000 computational cells is used to discretize the fluid domain. We utilized the same numerical setting described in Section 3.1 except for the discretization of the convective term of Equation (1b) that is now performed through the linear-upwind procedure.
Numerical results are compared to experimental measurement from Reference [79] in terms of vertical displacement of the center of mass. We denote with and the experimental and numerical displacement, respectively. Figure 5 and Table 1 show the good agreement between the proposed numerical model and the experimental data for all the considered cases. The accuracy of CFD is quantitatively assessed by the average relative error, evaluated as
and reported in Table 1. Notably, is always below .
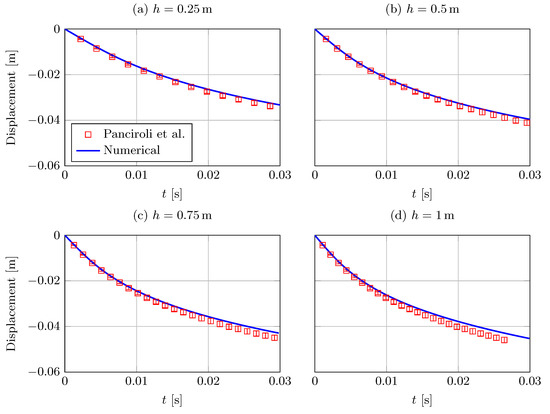
Figure 5.
Displacement of the specimen center of mass. Comparison between CFD and experiments [79] for different h: (a) m; (b) m; (c) m; (d) m.

Table 1.
Relative average error evaluated comparing and .
Figure 5 shows that CFD slightly underestimates the wedge penetration. This behavior can be explained by the 2D approximation that overestimates the fluid forces on the specimen. In fact, border effects, which are not considered in the 2D simulation, are expected to decrease the pressure close to the wedge borders, thus decreasing the fluid reaction [80].
Figure 6 depicts the free surface evolution for m, qualitatively demonstrating the capability of the proposed methodology to capture the most relevant features of hull water entry. In fact, bulk flow and pile-up can be clearly identified in Figure 6.

Figure 6.
Evolution of the free surface during water impact for m. CFD results for: (a) ms; (b) ms; (c) ms; (d) ms; (e) ms.
3.3. Water Entry and Exit of a Buoyant Cylinder
The test cases proposed in Section 3.1 and Section 3.2 focus on the water entry problem. Experimental data are, in fact, limited to the first instants after the water impact, when hydrodynamic forces are larger. To validate the proposed methodology in a more general framework, we specifically designed a set of dedicated experiments on the water entry and exit of a buoyant cylinder [81].
3.3.1. Experimental Setup
The experimental setup consists of a water tank made of stainless steel and Lexan®, with an internal volume of . The tank is filled with water up to a level of . Two transparent sides grant optical access to the tank. The specimen, a hollow PVC cylinder filled with polystyrene with a diameter m and a breadth m, is rigidly connected to a wood sledge that is allowed to move along two vertical aluminum rails. We consider four drop heights of m, m, m and m and two specimen masses, and kg, being kg.
The specimen position over time is measured through two Spectrasymbol thinpot linear potentiometers embedded in one of the rails. A wiper with tip diameter of mm is connected to the sledge and actuates the position sensor.
The optical acquisition of the experiments is performed via a Phantom® Miro 110 monochromatic high speed camera operating at a frame-rate of 2500 Hz for and of 2700 Hz for kg.
A capacitive accelerometer Adafruit ADXL335-5V is rigidly connected to the sledge and measures the specimen acceleration before water impact. Acceleration data are acquired only before the water impact because the measurement range of the accelerometer is ±3 g, while acceleration ensuing from the water impact is expected to be much larger.
The analogue signals from the accelerometer and the displacement sensor are synchronously acquired by a National Instrument NI USB-6009 acquisition board at a sampling rate of kHz at a resolution of 14 bits. The acquisition system is controlled through an ad-hoc realized LabVIEW [82] dashboard.
Each drop test is repeated three times to assess the data fidelity against random and systematic errors. We average the data from the three repetitions and apply a smoothing average filtering to obtain the effective position and acceleration as functions of time. We set when the specimen impacts the water free surface.
The impact velocity is of paramount importance in water entry problems, as discussed in Reference [83] and we obtain a robust estimation of it averaging the values yielded by three procedures:
- (i)
- Numerical differentiation of the displacement measurement through central difference approximation;
- (ii)
- Numerical integration of the measured acceleration through the trapezoid rule;
- (iii)
- Least square fitting of the specimen displacement to a second order function and algebraic differentiation.
The obtained impact velocity is reported in Figure 7, as a function of the specimen mass and drop height. For more details on the experimental setup, the reader can refer to References [81,84,85].
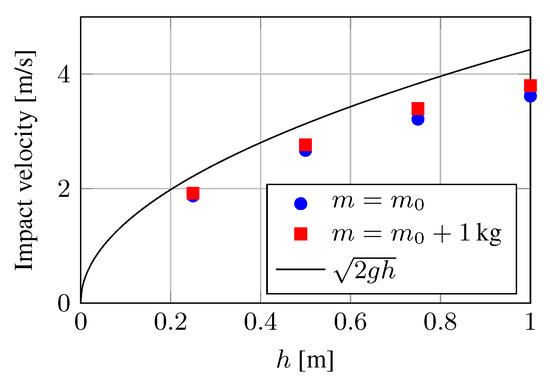
Figure 7.
Impact velocity of the specimen as a function of the drop height and of the mass of the impacting cylinder.
3.3.2. Numerical Setup
We consider here a 2D flow [80] and we utilize a laminar modeling approach [10,32]. We adopt the same numerical setup described in Section 3.2. In this case the hexa-dominant computational mesh is characterized by about 19,000 computational cells.
3.3.3. Results and Dicussion
Numerical and experimental evaluations of the cylinder displacement are reported in Figure 8 for all the combinations of h and m. We observe a general good agreement between CFD and experiments. A visual estimation of the cylinder position through the high speed camera is also reported in Figure 8 as a further confirmation of the accuracy of the proposed methodology. The reliability of the present simulations is quantitatively assessed by the percent relative errors estimated through Equation (16) and reported in Table 2. Remarkably, for all the considered tests.
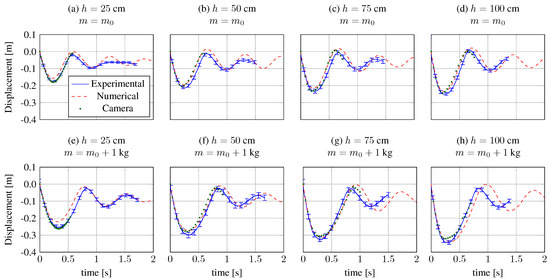
Figure 8.
Displacement of the specimen center of mass. Comparison between CFD and experiments for different h and m: (a) m and ; (b) m and ; (c) m and ; (d) m and ; (e) m and kg; (f) m and kg; (g) m and kg; (h) m and kg.

Table 2.
Percent error on the displacement of the center of mass of the buoyant cylinder as a function of h and m.
We note that the differences between numerical results and experimental data may be generally related to an overestimation of the fluid forces by the numerical model. In fact, numerical simulations underpredict the maximum penetration of the specimen and larger fluid forces also cause a higher rebound after motion inversion (see Figure 8). As already highlighted in Section 3.1 and Section 3.2, the 2D approximation may explain such an underprediction. Moreover, we discarded any friction dissipation on the experimental setup after water impact. Such a dissipation also concur in reducing the specimen momentum, in particular after the motion inversion, thus smearing the amplitude of the specimen oscillations.
Figure 9 represents the free surface dynamics ensuing from the water impact, by comparing the high speed camera images to the CFD evaluation of the water volume fraction for different time instants. The proposed numerical model correctly captures the most relevant features of the hydrodynamics related to the water impact of the cylinder, such as the pile-up and water jet formation (Figure 9b), the air cavity formation (Figure 9c) and closure ((Figure 9d,e) in the proximity of the maximum penetration. Slight differences between CFD and experiments are detected for the free surface pattern in Figure 9b,c, before the closure of the air cavity. Images from the high speed camera show a larger cavity compared to CFD. Moreover, the cavity closure is slightly anticipated in the CFD with respect to the experiments, as evidenced in Figure 9c, where the experimental air cavity borders points away from the cylinder, while the proposed numerical model predicts that the air cavity borders are directed inward. In this respect, we comment that such a discrepancy may be related to a poor prediction of the air flow. As a matter of facts, we focused on the hydrodynamics ensuing from water impact, that largely influence the cylinder motion, rather than on the modeling of the air flow. In particular, initial conditions are not realistic for the air flow, as the fluid domain is initialized with a constant null velocity and the cylinder is impulsively started at the impact onset. On the contrary, in the experiments the air flow at the impact onset is already completely developed, as a result of the specimen free fall path in air. We also note that the lack of turbulence modeling may also hinder the correct evaluation of the air flow behind the cylinder.

Figure 9.
Evolution of the free surface for and m. Comparison between CFD and experiments for different times after water impact: (a) S; (b) s; (c) s; (d) s; (e) (s).
Figure 10 shows the convergence history for m and . For sake of clarity we reported only 25 equally spaced time-steps from to s. Convergence is relatively fast being reached with a number of FSI subcycles comprised between 4 and 7. We also comment that is equal to for the first 3 iterations (see Equation (14)) and is then increased up to thanks to the Aitken’s procedure. Similar convergence histories are obtained also for the other cases.
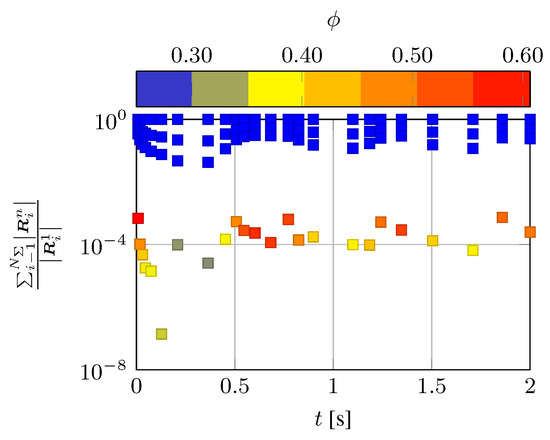
Figure 10.
Convergence history for m and . Note that only 25 time-steps are represented for clarity. Each mark represents a FSI subcycle.
3.4. Roll Motion of a Rectangular Structure
The previous tests are all focused on hull slamming problems. However, the proposed numerical model could be used for many other engineering problems related to FSI in multiphase flows and, among them, for the simulation of floating structures and their response to wave actions, which have attracted much interest in the hydraulic and ocean scientific community in the last decades [86,87,88,89].
In this section, we test the proposed numerical model for the simulation of a floating body. Jung et al. [40] experimentally studied the roll motion of a rectangular acrylic structure m large, m high and m wide (normal to the motion plane). The structure is hinged on a water tank 35 m long, m deep and m wide and is free to roll about its center of gravity. Translations, as well as yaw and pitch, are not permitted. The water depth is m. At equilibrium the width of the rectangle is horizontal and the draft of the body is m. The moment of inertia with respect to an axis normal to the motion plane through G is kgm.
The free roll decay test was performed by releasing the structure from an initial roll angle of 15 degrees in calm water and measuring the roll angle variation as a function of time with a rotary sensor [40].
We utilize the numerical setup described in Section 3.2 and the same mesh structure. In this case the domain discretization results in about 7000 computational cells.
As evidenced in Reference [41], contrarily to the hull slamming problems described in the previous sections, the turbulent eddy dissipation is expected to significantly impact the amplitude of the roll motion. Thereafter, a proper turbulence treatment is necessary to capture the hydrodynamics induced by the solid body motion and, in turn, the rotation amplitude. To this aim, we adopt a RANS modeling approach with a standard closure [90,91]. Standard wall functions [91] are utilized for the solution of the turbulent kinetic energy and turbulent kinetic energy dissipation velocity equations at solid boundaries.
The reliability of the proposed methodology is assessed in Figure 11 that reports the rotation angle () as a function of time. The agreement between CFD and experimental results from Reference [40] is remarkable. Specifically, the average relative error is
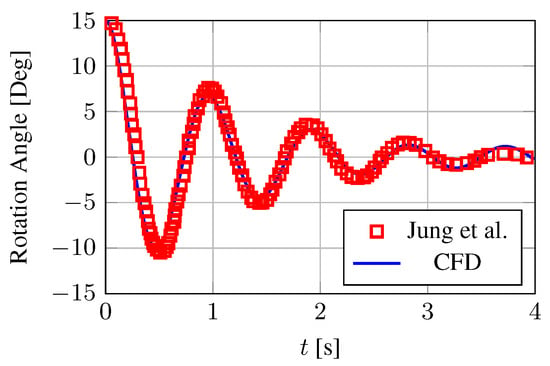
Figure 11.
Rotation of the specimen about its center of mass. Comparison between CFD and experiments from Reference [40].
To demonstrate the potentiality of the proposed methodology in terms of flow analysis we represent the flow field generated by the solid body motion in Figure 12. Therein, the velocity vectors are represented only within water to allow the visualization of the vortex structures ensuing from the rotation of the rectangle. We comment that, is this case, the air motion is expected to have a minor impact on the structure dynamics, with respect to water. As expected, the fluid velocity is maximized at the onset of the motion, when the angular velocity of the solid structure is larger. Two counter-rotating vortexes are generated at the corners of the rotating box. Such vortexes subtract mechanical energy from the structure contributing to the reduction of the oscillation amplitude. This mechanical energy is dissipated through a turbulent dissipation mechanism [41].
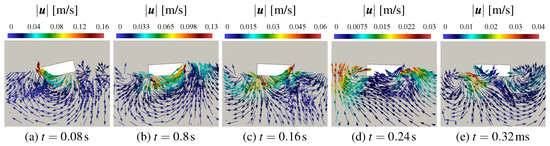
Figure 12.
Representation of the flow field in the vicinity of the oscillating box for different times. For clarity, vectors are represented only in water. (a) s, (b) s, (c) s, (d) s and (e) s.
4. Conclusions
In this paper we develop a computational methodology to model the FSI of rigid bodies in free surface flows. We adopt a tightly coupled partitioned approach to cope with structures whose density is comparable or lower to the fluid one.
The methodology is implemented within the foam-extend-3.2 open-source framework that allows a significant model re-utilization. The solution of the flow equation relies on the interDyMFoam solver that implements the VOF model and approximates Equations (1) and (4) through a generalized finite volume method. The 6-DOF solid body motion is described through the Newton-Euler equations that are numerically integrated utilizing the Euler explicit method. Quaternions or Euler parameters, are employed to parametrize the solid body orientation with respect to an inertial reference frame. Simplified solid body motions are obtained by nullifying the proper acceleration components in the Newton-Euler equations. Within the Dirichlet-Newmann approach, the tight coupling is obtained through fixed point iterations, whose convergence is boosted utilizing the Aitken’s dynamic under-relaxation.
We validate the proposed methodology by comparing numerical results to experiments in four different simplified 2D geometries (i.e., 2D flow field and 1-DOF solid body motion), yet computationally demanding test cases. Specifically, we select three different water impact problems and the free decay of the roll motion of a buoyant rectangle.
Both literature and custom designed experiments are considered. We first studied the water impact of elongated wedges varying the deadrise angle, the mass and the impact velocity. Comparison with experiments from the literature is very satisfactory with an average relative error below 4%. Nevertheless, literature data were limited to a relatively short time after the water impact. Thereafter, we performed a dedicated set of experiments to assess the capabilities of the proposed methodology also for the water exit. By contrasting CFD with those experiments, we note that the average relative error is around or below 10%. Moreover, the method is capable of correctly describing the initial water impact, the motion inversion and the successive oscillations about its equilibrium position of a buoyant cylinder. Finally, since rotations were not included in the previous tests, we simulated the natural decay of the roll motion of a buoyant rectangle to assess the capability of the proposed methodology to simulate floating bodies. Also in this case the agreement between numerical predictions and experimental data is very good, being the average relative error below 4%. Summarizing, the proposed numerical model performs remarkably well for all the tests cases. Even in the worst case, the discrepancies fall within the confidence interval expected for the adopted numerical models. The simplifying hypotheses in the computation, such as 2D flow, laminar modeling or the eddy viscosity model for the turbulent closure may explain the differences between CFD and experiments.
We comment that, despite we considered only 1-DOF cases for validation, due to the availability of experimental results, the combinations of the four proposed test cases includes both pure translations and rotations. Thus, the proposed methodology can be considered reliable also in the general 6-DOF case.
Besides demonstrating the reliability of the proposed methodology, the test cases described throughout the paper also evidence its relevance for engineering applications. In fact, such problems are important in several engineering fields such as naval, civil and hydraulic engineering. Moreover, FSI combined with multiphase flow modeling can be useful for other applications such as bio-engineering or energy harvesting.
Future work will be devoted to implementing kinematic constraints that limit the solid body motion and to modeling compliant bodies.
Author Contributions
Conceptualization, A.L.F. and G.F.; methodology, A.L.F. and G.F.; formal analysis and investigation, A.L.F. and G.F.; original CFD coding, A.L.F. and G.F.; coding implementation, A.A.; writing original draft preparation, A.L.F.; writing review and editing, A.A. and C.B.; supervision, S.U., C.B. and E.J.
Funding
This research has been supported by the Italian Ministry Program PRIN, grant n. 20154EHYW9 “Combined numerical and experimental methodology for fluid structure interaction in free surface flows under impulsive loading”, with Chiara Biscarini as the Principal Investigator.
Acknowledgments
The authors would like to thank two Anonymous Reviewers are also acknowledged for constructive comments to this paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Campbell, R.; Paterson, E. Fluid–structure interaction analysis of flexible turbomachinery. J. Fluids Struct. 2011, 27, 1376–1391. [Google Scholar] [CrossRef]
- Küttler, U.; Wall, W.A. Fixed-point fluid–structure interaction solvers with dynamic relaxation. Comput. Mech. 2008, 43, 61–72. [Google Scholar] [CrossRef]
- Montessori, A.; Falcucci, G. Lattice Boltzmann Modeling of Complex Flows for Engineering Applications; Morgan & Claypool Publishers: London, UK, 2018. [Google Scholar]
- Faltinsen, O.M. Hydroelastic slamming. J. Mar. Sci. Technol. 2000, 5, 49–65. [Google Scholar] [CrossRef]
- Wu, M.; Moan, T. Numerical prediction of wave-induced long-term extreme load effects in a flexible high-speed pentamaran. J. Mar. Sci. Technol. 2006, 11, 39–51. [Google Scholar] [CrossRef]
- Panciroli, R.; Abrate, S.; Minak, G.; Zucchelli, A. Hydroelasticity in water-entry problems: Comparison between experimental and SPH results. Compos. Struct. 2012, 94, 532–539. [Google Scholar] [CrossRef]
- Abrate, S. Hull Slamming. Appl. Mech. Rev. 2013, 64, 060803. [Google Scholar] [CrossRef]
- De Rosis, A.; Falcucci, G.; Porfiri, M.; Ubertini, F.; Ubertini, S. Hydroelastic analysis of hull slamming coupling lattice Boltzmann and finite element methods. Comput. Struct. 2014, 138, 24–35. [Google Scholar] [CrossRef]
- Zarghami, A.; Falcucci, G.; Jannelli, E.; Succi, S.; Porfiri, M.; Ubertini, S. Lattice Boltzmann modeling of water entry problems. Int. J. Mod. Phys. C 2014, 25, 1441012. [Google Scholar] [CrossRef]
- Facci, A.L.; Panciroli, R.; Ubertini, S.; Porfiri, M. Assessment of PIV-based analysis of water entry problems through synthetic numerical datasets. J. Fluids Struct. 2015, 55, 484–500. [Google Scholar] [CrossRef]
- Panciroli, R.; Falcucci, G.; Erme, G.; De Santis, E.; Jannelli, E. Fluid-structure interaction during the water entry of flexible cylinders. AIP Conf. Proc. 2015, 1648, 570011. [Google Scholar]
- Zhao, X.; Gao, Y.; Cao, F.; Wang, X. Numerical modeling of wave interactions with coastal structures by a constrained interpolation profile/immersed boundary method. Int. J. Numer. Methods Fluids 2016, 81, 265–283. [Google Scholar] [CrossRef]
- De Tullio, M.; Cristallo, A.; Balaras, E.; Verzicco, R. Direct numerical simulation of the pulsatile flow through an aortic bileaflet mechanical heart valve. J. Fluid Mech. 2009, 622, 259–290. [Google Scholar] [CrossRef]
- Chen, Z.; Shatara, S.; Tan, X. Modeling of biomimetic robotic fish propelled by an ionic polymer-metal composite caudal fin. IEEE/ASME Trans. Mechatron. 2010, 13, 519–529. [Google Scholar]
- Aureli, M.; Kopman, V.; Porfiri, M. Free-locomotion of underwater vehicles actuated by ionic polymer metal composites. IEEE/ASME Trans. Mechatron. 2010, 15, 603–614. [Google Scholar] [CrossRef]
- Erturk, A.; Delporte, G. Underwater thrust and power generation using flexible piezoelectric composites: An experimental investigation toward self-powered swimmer-sensor platforms. Smart Mater. Struct. 2011, 20, 125013. [Google Scholar] [CrossRef]
- Rosis, A.D.; Falcucci, G.; Ubertini, S.; Ubertini, F. Aeroelastic study of flexible flapping wings by a coupled lattice Boltzmann-finite element approach with immersed boundary method. J. Fluids Struct. 2014, 49, 516–533. [Google Scholar] [CrossRef]
- Amirante, D.; Hills, N.; Barnes, C. A moving mesh algorithm for aero-thermo-mechanical modelling in turbomachinery. Int. J. Numer. Methods Fluids 2012, 70, 1118–1138. [Google Scholar] [CrossRef]
- Falcucci, G.; Aureli, M.; Ubertini, S.; Porfiri, M. Transverse harmonic oscillations of laminae in viscous fluids: A lattice Boltzmann study. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2011, 369, 2456–2466. [Google Scholar] [CrossRef] [PubMed]
- Facci, A.L.; Porfiri, M. Nonlinear hydrodynamic damping of sharp-edged cantilevers in viscous fluids undergoing multi-harmonic base excitation. J. Appl. Phys. 2012, 112, 124908. [Google Scholar] [CrossRef]
- Facci, A.L.; Porfiri, M. Analysis of three-dimensional effects in oscillating cantilevers immersed in viscous fluids. J. Fluids Struct. 2013, 38, 205–222. [Google Scholar] [CrossRef]
- Brufau-Penella, J.; Puig-Vidal, M.; Giannone, P.; Graziani, S.; Strazzeri, S. Characterization of the harvesting capabilities of an ionic polymer metal composite device. Smart Mater. Struct. 2008, 17, 015009. [Google Scholar] [CrossRef]
- Aureli, M.; Prince, C.; Porfiri, M.; Peterson, S.D. Energy harvesting from base excitation of ionic polymer metal composites in fluid environments. Smart Mater. Struct. 2010, 19, 015003. [Google Scholar] [CrossRef]
- Biscarini, C. Computational fluid dynamics modelling of landslide generated water waves. Landslides 2010, 7, 117–124. [Google Scholar] [CrossRef]
- Fritz, H.; Hager, W.; Minor, H.E. Near field characteristics of landslide generated impulse waves. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 287–302. [Google Scholar] [CrossRef]
- Batra, R.C.; Porfiri, M.; Spinello, D. Review of modeling electrostatically actuated microelectromechanical systems. Smart Mater. Struct. 2007, 16, R23–R31. [Google Scholar] [CrossRef]
- Ihara, A.; Watanabe, H. On the flow around flexible plates, oscillating with large amplitude. J. Fluids Struct. 1994, 8, 601–619. [Google Scholar] [CrossRef]
- Kimber, M.; Garimella, S.V.; Raman, A. Local heat transfer coefficients induced by piezoelectrically actuated vibrating cantilevers. Trans. ASME J. Heat Transf. 2007, 129, 1168–1176. [Google Scholar] [CrossRef]
- Bidkar, R.A.; Kimber, M.; Raman, A.; Bajaj, A.K.; Garimella, S.V. Nonlinear aerodynamic damping of sharp-edged flexible beams oscillating at low Keulegan-Carpenter numbers. J. Fluid Mech. 2009, 634, 269–289. [Google Scholar] [CrossRef]
- Hay, A.; Leroyer, A.; Visonneau, M. H-adaptive Navier–Stokes simulations of free-surface flows around moving bodies. J. Mar. Sci. Technol. 2006, 11, 1–18. [Google Scholar] [CrossRef]
- Carcaterra, A.; Ciappi, E. Prediction of the compressible stage slamming force on rigid and elastic systems impacting on the water surface. Nonlinear Dyn. 2000, 21, 193–220. [Google Scholar] [CrossRef]
- Seng, S.; Jensen, J.J.; Pedersen, P.T. Numerical prediction of slamming loads. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2012, 226, 120–134. [Google Scholar] [CrossRef]
- Facci, A.L.; Porfiri, M.; Ubertini, S. Three-dimensional water entry of a solid body: A computational study. J. Fluids Struct. 2016, 66, 36–53. [Google Scholar] [CrossRef]
- Hermundstad, O.A.; Moan, T. Numerical and experimental analysis of bow flare slamming on a Ro–Ro vessel in regular oblique waves. J. Mar. Sci. Technol. 2005, 10, 105–122. [Google Scholar] [CrossRef]
- Panahi, R. Simulation of water-entry and water-exit problems using a moving mesh algorithm. J. Theor. Appl. Mech. 2012, 42, 79–92. [Google Scholar] [CrossRef]
- Uddin, E.; Sung, H.J. Simulation of flow-flexible body interactions with large deformation. Int. J. Numer. Methods Fluids 2012, 70, 1089–1102. [Google Scholar] [CrossRef]
- Zhang, Y.; Pin, F.; Yim, S. A heterogeneous flow model based on DD method for free surface fluid-structure interaction problems. Int. J. Numer. Methods Fluids 2014, 74, 292–312. [Google Scholar] [CrossRef]
- Eken, A.; Sahin, M. A parallel monolithic algorithm for the numerical simulation of large-scale fluid structure interaction problems. Int. J. Numer. Methods Fluids 2016, 80, 687–714. [Google Scholar] [CrossRef]
- Farhat, C.; Lesoinne, M.; Tallec, P.L. Load and motion transfer algorithms for fluid/structure interaction problems with non-matching discrete interfaces: Momentum and energy conservation, optimal discretization and application to aeroelasticity. Comput. Methods Appl. Mech. Eng. 1998, 157, 95–114. [Google Scholar] [CrossRef]
- Jung, K.H.; Chang, K.A.; Jo, H.J. Viscous effect on the roll motion of a rectangular structure. J. Eng. Mech. 2006, 132, 190–200. [Google Scholar] [CrossRef]
- Chen, Q.; Zang, J.; Dimakopoulos, A.S.; Kelly, D.M.; Williams, C.J. A Cartesian cut cell based two-way strong fluid–solid coupling algorithm for 2D floating bodies. J. Fluids Struct. 2016, 62, 252–271. [Google Scholar] [CrossRef]
- Cheon, J.S.; Jang, B.S.; Yim, K.H.; Lee, H.D.; Koo, B.Y.; Ju, H. A study on slamming pressure on a flat stiffened plate considering fluid-structure interaction. J. Mar. Sci. Technol. 2016, 21, 309–324. [Google Scholar] [CrossRef]
- Kassiotis, C. Nonlinear Fluid-Structure Interaction: A Partitioned Approach and Its Application through Component Technology. Ph.D. Thesis, Université Paris-Est, Champs-sur-Marne, France, 2009. [Google Scholar]
- Piperno, S.; Farhat, C. Partitioned procedures for the transient solution of coupled aeroelastic problems—Part II: Energy transfer analysis and three-dimensional applications. Comput. Methods Appl. Mech. Eng. 2001, 190, 3147–3170. [Google Scholar] [CrossRef]
- Habchi, C.; Russeil, S.; Bougeard, D.; Harion, J.L.; Lemenand, T.; Ghanem, A.; Della Valle, D.; Peerhossaini, H. Partitioned solver for strongly coupled fluid–structure interaction. Comput. Fluids 2013, 71, 306–319. [Google Scholar] [CrossRef]
- Causin, P.; Gerbeau, J.F.; Nobile, F. Added-mass effect in the design of partitioned algorithms for fluid–structure problems. Comput. Methods Appl. Mech. Eng. 2005, 194, 4506–4527. [Google Scholar] [CrossRef]
- Förster, C.; Wall, W.A.; Ramm, E. Artificial added mass instabilities in sequential staggered coupling of nonlinear structures and incompressible viscous flows. Comput. Methods Appl. Mech. Eng. 2007, 196, 1278–1293. [Google Scholar] [CrossRef]
- Wood, C.; Gil, A.; Hassan, O.; Bonet, J. Partitioned block-Gauss–Seidel coupling for dynamic fluid–structure interaction. Comput. Struct. 2010, 88, 1367–1382. [Google Scholar] [CrossRef]
- Ángel Fernández, M.; Moubachir, M. A Newton method using exact jacobians for solving fluid-structure coupling. Comput. Struct. 2005, 83, 127–142. [Google Scholar] [CrossRef]
- Walhorn, E.; Kölke, A.; Hübner, B.; Dinkler, D. Fluid-structure coupling within a monolithic model involving free surface flows. Comput. Struct. 2005, 83, 2100–2111. [Google Scholar] [CrossRef]
- Degroote, J.; Bathe, K.J.; Vierendeels, J. Performance of a new partitioned procedure versus a monolithic procedure in fluid–structure interaction. Comput. Struct. 2009, 87, 793–801. [Google Scholar] [CrossRef]
- Scruggs, J.; Jacob, P. Harvesting ocean wave energy. Science 2009, 323, 1176–1178. [Google Scholar] [CrossRef]
- Wall, W.A.; Genkinger, S.; Ramm, E. A strong coupling partitioned approach for fluid–structure interaction with free surfaces. Comput. Fluids 2007, 36, 169–183. [Google Scholar] [CrossRef]
- Antoci, C.; Gallati, M.; Sibilla, S. Numerical simulation of fluid–structure interaction by SPH. Comput. Struct. 2007, 85, 879–890. [Google Scholar] [CrossRef]
- Potapov, S.; Maurel, B.; Combescure, A.; Fabis, J. Modeling accidental-type fluid–structure interaction problems with the SPH method. Comput. Struct. 2009, 87, 721–734. [Google Scholar] [CrossRef]
- Di Francesco, S.; Biscarini, C.; Manciola, P. Numerical simulation of water free-surface flows through a front-tracking lattice Boltzmann approach. J. Hydroinform. 2015, 17, 1–6. [Google Scholar] [CrossRef]
- Hu, C.; Kashiwagi, M. A CIP-based method for numerical simulations of violent free-surface flows. J. Mar. Sci. Technol. 2004, 9, 143–157. [Google Scholar] [CrossRef]
- Takizawa, K.; Yabe, T.; Tsugawa, Y.; Tezduyar, T.E.; Mizoe, H. Computation of free-surface flows and fluid–object interactions with the CIP method based on adaptive meshless soroban grids. Comput. Mech. 2007, 40, 167–183. [Google Scholar] [CrossRef]
- Aly, A.M.; Asai, M.; Sonoda, Y. Simulation of free falling rigid body into water by a stabilized incompressible SPH method. Ocean Syst. Eng. 2011, 1, 207–222. [Google Scholar] [CrossRef]
- Vandamme, J.; Zou, Q.; Reeve, D.E. Modeling floating object entry and exit using smoothed particle hydrodynamics. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 213–224. [Google Scholar] [CrossRef]
- Faltinsen, O. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1993; Volume 1. [Google Scholar]
- Korobkin, A. Water impact problems in ship hydrodynamics. In Advances in Marine Hydrodynamics; Computational Mechanics Publications: Norwich, UK, 1996; pp. 323–371. [Google Scholar]
- Carrica, P.; Huang, J.; Noack, R.; Kaushik, D.; Smith, B.; Stern, F. Large-scale DES computations of the forward speed diffraction and pitch and heave problems for a surface combatant. Comput. Fluids 2010, 39, 1095–1111. [Google Scholar] [CrossRef]
- Seddon, C.; Moatamedi, M. Review of water entry with applications to aerospace structures. Int. J. Impact Eng. 2006, 32, 1045–1067. [Google Scholar] [CrossRef]
- Extend Project. 2016. Available online: http://www.extend-project.de/ (accessed on 19 May 2017).
- Greenshields, C.J. OpenFOAM User’s Guide, 2.4.0 ed.; OpenFOAM Foundation Ltd.: London, UK, 2015. [Google Scholar]
- Rider, W.J.; Kothe, D.B. Reconstructing Volume Tracking. J. Comput. Phys. 1998, 141, 112–152. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 1999, 31, 567–603. [Google Scholar] [CrossRef]
- Rusche, H. Computational Fluid Dynamiccs of Dispersed Two-Phase Flows at High Phase Fractions. Ph.D. Thesis, University of London, London, UK, 2002. [Google Scholar]
- Cavalagli, N.; Biscarini, C.; Facci, A.; Ubertini, F.; Ubertini, S. Experimental and numerical analysis of energy dissipation in a sloshing absorber. J. Fluids Struct. 2017, 68, 466–481. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Periç, M. Computational Methods for Fluid Dynamics, 3rd rev. ed.; Springer: Berlin, Germany; Tokyo, Japan, 2002. [Google Scholar]
- Jasak, H. Error Analysis and Estimation for Finite Volume Method with Applications to Fluid Flow. Ph.D. Thesis, University of London, London, UK, 1996. [Google Scholar]
- Jasak, H. Dynamic Mesh Handling in OpenFOAM. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2008. [Google Scholar]
- Jasak, H.; Tukovic, Z. Automatic Mesh Motion for the Unstructured Finite Volume Method. Trans. FAMENA 2007, 30, 1–18. [Google Scholar]
- Kassiotis, C. Which Strategy to Move the Mesh in the Computational Fluid Dynamic Code OpenFOAM; Technical Report; WiRe, LMT-Cachan: Braunschweig, Germany, 2008; Available online: http://perso.crans.org/kassiotis/openfoam/movingmesh.pdf (accessed on 19 May 2017).
- Haug, E.J. Computer Aided Kinematics and Dynamics of Mechanical Systems; Allyn and Bacon: Boston, MA, USA, 1989; Volume 1. [Google Scholar]
- Sherif, K.; Nachbagauer, K.; Steiner, W. On the rotational equations of motion in rigid body dynamics when using Euler parameters. Nonlinear Dyn. 2015, 81, 343–352. [Google Scholar] [CrossRef]
- Zhao, R.; Faltinsen, O.; Aarsnes, J. Water entry of arbitrary two-dimensional sections with and without flow separation. In Proceedings of the 21st Symposium on Naval Hydrodynamics, Trondheim, Norway, 24–28 June 1996; The National Academies Press: Washington, DC, USA, 1996; pp. 408–423. [Google Scholar]
- Panciroli, R.; Shams, A.; Porfiri, M. Experiments on the water entry of curved wedges: High speed imaging and particle image velocimetry. Ocean Eng. 2015, 94, 213–222. [Google Scholar] [CrossRef]
- Jalalisendi, M.; Osma, S.J.; Porfiri, M. Three-dimensional water entry of a solid body: A particle image velocimetry study. J. Fluids Struct. 2015, 59, 85–102. [Google Scholar] [CrossRef]
- Russo, S.; Biscarini, C.; Facci, A.L.; Falcucci, G.; Jannelli, E.; Ubertini, S. Experimental assessment of buoyant cylinder impacts through high-speed image acquisition. J. Mar. Sci. Technol. 2017, 23, 67–80. [Google Scholar] [CrossRef]
- NationalInstruments. Version 2014. Available online: www.ni.com/labview (accessed on 19 May 2017).
- Facci, A.L.; Ubertini, S. Numerical assessment of similitude parameters and dimensional analysis for water entry problems. Math. Probl. Eng. 2015, 2015, 324961. [Google Scholar] [CrossRef]
- Panciroli, R.; Biscarini, C.; Falcucci, G.; Jannelli, E.; Ubertini, S. Live monitoring of the distributed strain field in impulsive events through fiber Bragg gratings. J. Fluids Struct. 2016, 61, 60–75. [Google Scholar] [CrossRef]
- Russo, S.; Krastev, V.; Jannelli, E.; Falcucci, G. Design and optimization of an experimental test bench for the study of impulsive fluid-structure interactions. AIP Conf. Proc. 2016, 1738, 270020. [Google Scholar]
- Goggins, J.; Finnegan, W. Numerical simulation of linear water waves and wave-structure interaction. Ocean Eng. 2012, 43, 23–31. [Google Scholar]
- Xing-Kaeding, Y.; Jensen, G.; Technical University of Hamburg-Harburg; Hadžić, I.; Perić, M.; CD Adapco Group. Simulation of flow-induced ship motions in waves using a RANSE method. Ship Technol. Res. 2004, 51, 56–68. [Google Scholar] [CrossRef]
- Hadžić, I.; Hennig, J.; Perić, M.; Xing-Kaeding, Y. Computation of flow-induced motion of floating bodies. Appl. Math. Model. 2005, 29, 1196–1210. [Google Scholar] [CrossRef]
- Yan, S.; Ma, Q. Numerical simulation of fully nonlinear interaction between steep waves and 2D floating bodies using the QALE-FEM method. J. Comput. Phys. 2007, 221, 666–692. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1998; Volume 2. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).