Abstract
Water–rock interactions can alter rock properties through chemical reactions during subsurface transport processes like geological CO2 sequestration (GCS), matrix acidizing, and waterflooding in carbonate formations. Dynamic changes in rock properties cause a failure of waterflooding and GCS and could also dramatically affect the efficiency of the acidizing. Efficient numerical simulations are thus essential to the optimized design of those subsurface processes. In this paper, we develop a three-dimensional (3D) numerical model for simulating the coupled processes of fluid flow and chemical reactions in fractured carbonate formations. In the proposed model, we employ the Stokes–Brinkman equation for momentum balance, which is a single-domain formulation for modeling fluid flow in fractured porous media. We then couple the Stokes–Brinkman equation with reactive-transport equations. The model can be formulated to describe linear as well as radial flow. We employ a decoupling procedure that sequentially solves the Stokes–Brinkman equation and the reactive transport equations. Numerical experiments show that the proposed method can model the coupled processes of fluid flow, solute transport, chemical reactions, and alterations of rock properties in both linear and radial flow scenarios. The rock heterogeneity and the mineral volume fractions are two important factors that significantly affect the structure of conductive channels.
1. Introduction
Subsurface water–rock interactions involve the coupled phenomena of chemical reactions and fluid transport, in which the chemical reactions between minerals and water can cause mineral dissolution and precipitation. Mineral dissolution is a process in which the chemical elements in the solid phase transform into ions in the aqueous phase through various chemical reactions, and consequently lead to a decrease in mineral mass and volume. In contrast, mineral precipitation occurs when aqueous species transform to solid phases, resulting in an increase of mass and volume in solid phases. In carbonate rocks, the carbonate minerals calcite and dolomite can react with acid fluids, leading to carbonate rock dissolution and precipitation [1]. The couplings of fluid flow and mineral dissolution/precipitation may significantly change rock properties in carbonate formations. Mineral dissolution/precipitation can occur in many subsurface processes in carbonate formations, for example in waterflooding processes for improving oil recovery [2], geological CO2 sequestration (GCS) for reducing CO2 emissions [3,4], and matrix acidizing for improving oil production by changing the permeability near wellbores [5,6].
In waterflooding processes in carbonate formations, the chemical reactions between hydrogen ions in water phase and carbonate minerals can cause mineral dissolution. The mineral dissolution process may be enhanced by coupling with fluid flow to form large-scale conductive channels from both natural and factitious fractures [2]. Such conductive channels can cause early water breakthrough and limited hydrocarbon production, resulting in the failure of the waterflooding program. In a GCS process, the dissolved CO2 in situ brine, via various geochemical reactions, can form a carbonate acid that may then dissolve carbonate rocks [7,8]. Such CO2–rock–brine interactions cause mineral dissolutions that could enhance the existing fracture system and form highly conductive or leakage pathways, which may present environmental risks [9,10,11]. In a matrix acidizing treatment, the rock–fluid interaction creates highly conductive pathways, the so-called wormholes, around well-bores for enhancing hydrocarbon flow into wells [12,13,14,15]. It is thus vitally important to well understand the underlying mineral dissolution/precipitation processes happened in the above-mentioned subsurface processes for the successful implementations.
Mathematical modeling of the coupled physical processes of fluid flow, solute transport, and underline chemical reactions is vital for successful implementation of those subsurface processes, and also is challenging as rock porosity and permeability change due to fluid–rock interactions. The key challenges are the modeling of fluid flow in the free-flow regions that are dynamically changing due to the coupling effect of mineral dissolution and fluid transport. Over the last few decades, extensive studies have been performed on the coupled processes of fluid flow and mineral dissolution using the coupled reactive-transport models [16,17,18,19,20,21,22,23]. These mathematical models include conservations of momentum and solute mass [22], which developed from early studies on one-dimensional models for a single chemical reaction system [24,25] to the later studies on multi-component multi-dimensional reactive-transport systems [23,26]. The Navier–Stokes equation or the Stokes equation has been employed as a momentum equation to describe fluid flow in pore space for numerical modeling at pore-scale in which the characterization of changing mineral surface is critical in binary domains (solid and pore space) [19,22,27]. Molins [27] employed the embedded boundary and the level set methods to obtain an accurate representation of the calcite surface on the Cartesian grid. The lattice Boltzmann approach has also been used to study the reactive transport process and fracture evolution at the pore scale [28,29]. At the continuum scale and field scale, Darcy’s equation has usually been applied as a momentum equation [30,31,32]. Darcy’s equation can be inaccurate for modeling fluid flow in carbonate formation due to its large-scale void space features that can also be enhanced dynamically due to dissolution processes. To address such issues, Yuan et al. [33,34] presented a mathematical model that couples the Stokes–Brinkman equation and reactive-transport equations to describe calcite dissolution in both single and multiple mineral systems at the continuum scale. This model is capable of describing the fracture evolution as well due to the advantage of the Stokes–Brinkman formulation for modeling flow in fractured porous media.
The Stokes–Brinkman model uses a single set of equations in the entire domain (porous media and free-flow regions) for fluid flow [35,36,37] and can be considered as a modified Darcy’s law by adding the viscous shear stress term to account for the effect of shear stress near the boundary layer [38,39,40]. In the Stokes–Brinkman equation, the effective viscosity of the fluid work as a parameter for matching the shear stress interface condition between porous media and free-flow regions [33], which can be regarded as the fluid viscosity throughout the physical domain [33,34,36,37,41]. Applying the Stokes–Brinkman equation in reactive transport process offers several advantages. First, this equation can be reduced to the Stokes or Darcy equations by choosing appropriate coefficients. In such a way, a no interface condition, for example, the Beavers–Joseph condition [42], is needed between the porous media and free-flow regions. In addition, it can model the transitional flow pattern from a Darcy-dominated region to a Stokes-dominated region, a feature that allows us to efficiently model the alterations of the rock porosity and permeability caused by the mineral dissolution.
The existing mathematical models in the previous studies [33,34] focused on the 2-D case studies in the Cartesian coordinate system only, which limits their applications in modeling the real-world scenarios. For example, the actual matrix acidizing treatments are performed by acidic fluid injection through a wellbore, the fluid flows into porous media is radial, and the velocity decreases rapidly away from the wellbore. Therefore, a 3D mathematical model on both Cartesian coordinate and cylindrical coordinate systems is desirable for simulating the mineral dissolution process in the subsurface as well as the acidizing process at exact downhole environments. In this paper, we develop a 3D numerical simulator for modeling the coupling processes of fluid flow and mineral dissolution during the reactive transport processes. The proposed numerical model includes the Stokes–Brinkman equation for fluid flow, reactive-transport equations for solute transport and chemical reactions, and a rock property model for alterations of rock properties, which can be applied to simulate mineral dissolution under both linear flow and radial flow. The mathematical model is discretized and solved on both Cartesian coordinate and cylindrical coordinate systems sequentially. In the numerical solution procedure, the Stokes–Brinkman equation is solved by the staggered grid finite difference method, which was proposed by Harlow and Welsh [43] and was widely applied for solving the Navier–Stokes equation [44,45]. The reactive-transport equations are solved by the control volume finite difference method [23].
Effective linear solvers play a key role in scientific computing and many different types of numerical algorithms have been developed for solving linear systems. In this paper, we employ the Fast Auxiliary Space Preconditioning (FASP) package [46], which includes several efficient iterative solvers for solving linear systems of equations. In our proposed sequentially numerical procedure, we employ two linear algebraic preconditioning strategies from the FASP package for the Stokes–Brinkman and reactive transport equations, respectively. These methods are accelerated by a Krylov subspace method, the Variable-Restarting Flexible Generalized Minimal Residual (GMRES) method [47]. The numerical model for radial flow is validated using a 3D radial core-flooding experiment from the existing publication [48]. Two 3D synthetic case studies in both linear and radial core flooding are performed to investigate the alterations of rock properties and dissolution patterns. The first case study is for linear core flooding in a multi-mineral system, which is consist of calcite, quartz, and clay, and the second case study is for radial core flooding in a single calcite system. The numerical results demonstrate that the proposed numerical model is capable of modeling the coupled processes under investigation. And the rock heterogeneity and the mineral volume fractions affect the structure of conductive channels significantly.
The rest of this paper is organized as follows. First, the mathematical model is briefly presented. Second, the numerical solution methods and linear algebraic solvers are discussed. The numerical experiments of synthetic core-flooding case studies are then presented. We close with the concluding remarks.
2. The Mathematical Models
In our previous studies [33,34], we have developed a similar 2D mathematical model for the geochemical coupling of fluid flow in fractured reservoirs. In this paper, we focus on the 3D multicomponent flow in fractured carbonate formations on both Cartesian coordinate and cylindrical coordinate systems. In this section, we briefly present the coupled mathematical model. The readers are referred to Yuan et al. [33,34] for discussions on the coupled model and involved chemical reactions.
2.1. The Stokes–Brinkman Model
The Stokes–Brinkman equation has been widely applied to model fluid flow in fractured porous media [33,34,36,37,41], as it employs a single set of equations for simulating fluid flow in the entire domain. The general formulations of the Stokes–Brinkman equation for incompressible single-phase fluid are expressed as follows [33,34,36,37,38,41]:
where denotes the entire computational domain, is the physical velocity of the fluid in free-flow regions and the Darcy velocity in porous media, is pressure, is a permeability tensor, and is the body force, which is ignored in this study for simplicity of presentation. is the fluid viscosity, and is the so-called effective viscosity, which is the critical parameter for matching the shear stress at the interface between porous media and free-flow regions [49]. The effective viscosity is set to the fluid viscosity, in most applications [33,34,36,37,41]. The readers are referred to Yuan et al. [33] for more details of the Stokes–Brinkman equation.
2.2. The Reactive-Transport Model
We use the reactive-transport equations to describe solute transport coupled with geochemical reactions in the geological subsurface. In our model, the aqueous species are classified into primary and secondary species [23]. The general mass conservation equations for the primary species read as follows:
In Equation (3), is the fluid velocity defined in Equation (1), is the dispersion/diffusion coefficient, and is the porosity. is the number of primary species. is the kinetic reaction rate of primary species for mineral–water reactions. represents the total concentrations of primary species. and are nonlinear functions of the concentrations of primary species. For more details, the reader is referred to [26,33].
Equation (3) presents a general reactive transport model to describe solute transport and chemical reactions. In our previous studies, the reactive transport model has been applied to describe mineral dissolution processes in both a single mineral (calcite) system [33] and a multi-mineral (calcite, quartz, and clay) system [34]. In this study, we consider both scenarios in 3D. The detailed chemical reactions and related parameters can be found in [1,33,34].
2.3. The Rock Property Models
The porosity of porous media can be obtained by:
The change in the individual mineral volume fraction can be calculated from [23,26]:
where is the molar volume of the mineral.
The prediction of the absolute rock permeability is another challenge because of the difficulties in measuring it directly. As an alternative method to direct measurement, empirical models can be applied to predict the absolute rock permeability from the porosity [50,51,52,53,54]. Among these models, the most widely used one is the so-called Kozeny–Carman equation [31,32,55,56,57,58,59,60,61,62], which is written as per [51]:
where denotes the grain size. If we ignore changes in grain size, the permeability can then be given as:
where and are the initial permeability and porosity, respectively.
3. Numerical Solution Strategies
In this paper, the proposed 3D numerical model is solved numerically using a decoupled approach by the finite difference method. Within each time step, our numerical method contains four main steps:
- (1)
- Firstly, the Stokes–Brinkman equation (Equation (1)) and the continuity equation (Equation (2)) are solved by a staggered grid finite difference method for velocities and pressure.
- (2)
- Secondly, the velocities at grid-cell centers are calculated by averaging the velocities of grid faces obtained from the solution of the Stokes–Brinkman equation.
- (3)
- Thirdly, based on the calculated velocities at cell centers, the concentrations of primary species are determined by solving the reactive-transport equations using an implicit control-volume upwinding finite difference scheme.
- (4)
- The last step is then to update the rock porosities and absolute permeabilities based on the concentrations of primary species.
For more details on the numerical solution procedure of the sequential method, the readers are referred to [33]. Note that the above scheme can be embedded in a nonlinear iteration until the desired accuracy. For simplicity, we do not use such nonlinear iterations in our current study. The numerical discretization and solutions for the Stokes–Brinkman equation and reactive transport equations in the 3D Cartesian coordinates are discussed as follows. The numerical discretization and solutions of Stokes–Brinkman equation in the 3D cylindrical coordinates are discussed in Appendix A.
3.1. Numerical Solution of the Stokes–Brinkman Model
The Stokes–Brinkman equation and the continuity equation are discretized using the staggered grid method, also known as the Marker-and-Cell (MAC) scheme. In Cartesian coordinates, the idea of MAC is to place the unknowns of , , , and in different locations. More specifically, the pressure is located at the center of each cell (), and velocities are located at the center of grid faces as indicated by the subscripts , , and (see Figure 1).
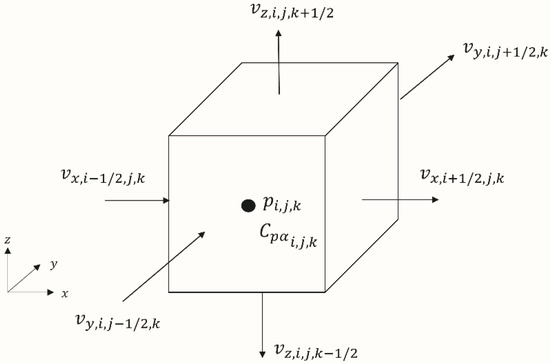
Figure 1.
Definition of pressure, velocities, and concentrations on a grid with indices i, j, k.
With the definitions of the pressure and velocities in Figure 1, the finite difference approximations of Equations (1) and (2) in the 3D Cartesian coordinates system are given as:
where the permeability at the interface is calculated as the harmonic average of the permeability values of the two neighboring blocks.
In this paper, we set constant velocity on the inlet boundary, constant pressure, and free-flows at the outlet boundary, and no-slip boundary condition on the other boundaries. The boundary conditions in the Cartesian system are expressed as:
where is the injected velocity at the inlet, is the outlet pressure, is the unit normal vector on the boundary, is the length of the domain in the flow direction, is the width of the domain, and is the depth of the domain.
The simplest way of treating the boundary is to use the reflection technique. In Figure 2, and denote the inlet and bottom boundaries, respectively. The two dashed lines are the ghost boundaries out of the domain. On the bottom boundary , the boundary condition is imposed exactly at the “▲” point: . Using the reflection technique, the value of at the “O” point on the dash line can be determined approximately: . On the inlet boundary , the boundary condition is imposed exactly at the “▲” point: . Similarly, we have .
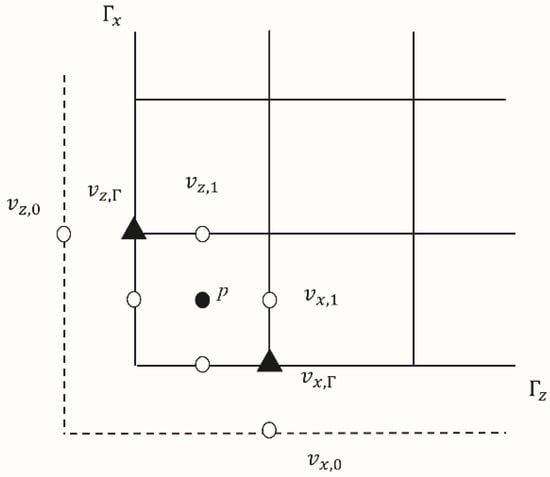
Figure 2.
Projection formulation of the Marker-and-Cell (MAC) scheme.
In the Cartesian coordinates, when the entire domain is divided into , , and grid blocks in the corresponding directions, respectively, the total numbers of , , , and are , , , and , respectively. By imposing the defined boundary conditions, we have unknown variables and the same number of discretized equations, which can be written as a block linear system:
where , , , and are unknown vectors, and all of them go through the indices , , in the same order. and are the submatrices resulting from the terms of and in the Equation (8), respectively. and are the submatrices resulting from the terms of and in the Equation (9), respectively. and are the submatrices resulting from the terms of and in the Equation (10), respectively. , , and are the submatrices resulting from the terms of , , and in the Equation (11), respectively. , , , and are the right-hand side vectors resulting from the defined boundary conditions.
Therefore, the velocity and pressure can be approximated simultaneously by solving the linear systems (Equations (17) and (A9) in Appendix A) for the finite difference approximations of the Stokes–Brinkman equation and continuity equation in Cartesian and cylindrical coordinates systems, respectively. The saddle-point systems from the MAC discretization of the Stokes–Brinkman equation are usually large-scale, ill-conditioned, and symmetric. Efficient preconditioning methods for such problems include the geometric multigrid schemes with the distributed Gauss–Seidel smoother [63] and the block preconditioners [64]. In this study, we employ the block lower triangular preconditioner in the following form:
where .
In our simulations, the inverses of , , and are obtained by a few fixed steps of classical algebraic multigrid (AMG) methods as they behave like the Poisson’s equation. Furthermore, the Schur complement can be replaced by
or a better approximation (see for example [65]).
3.2. Numerical Solution of the Reactive Transport Model
We followed our previous numerical method to solve the reactive-transport equations [33]. The advective mass flux term of Equation (3) is discretized using a first-order upwinding method. The nonlinear terms and are linearized using the classical Newton–Raphson method. A fully implicit finite difference scheme is employed for the reactive-transport equations. For more details on numerical solving reactive-transport equations, the readers are referred to see Yuan et al. [33].
The reactive transport equations give rise to nonsymmetric linear equations upon discretization. When the advection term is relatively small, the equations are Poisson-type diffusion-dominated equations. Hence, we can apply classical AMG as a preconditioner to solve such problems. The multilevel hierarchy in AMG is constructed based on the coefficient matrix only and can be applied to general meshes. The original AMG idea was developed under the assumption that the coefficient matrix being a symmetric M-matrix; see the recent review paper [66]. When the advection term dominates the equations, we apply the Incomplete LU factorization ILU(k) method as a preconditioner [67].
4. Numerical Experiments
The numerical solution method of the coupled model in a 2D Cartesian system has been extensively tested and validated in the previous studies [33,34]. In this paper, we present numerical experiments to validate the proposed numerical method in 3D.
4.1. Model Validation
In this numerical experiment, we compare our numerical results with the published experimental results by Tardy et al. [48]. The 15% HCL solution is injected into an Indiana Limestone core through the central borehole at an injection rate of 12 mL/min. The core has an average porosity of 0.11 and an average permeability of 19.6 mD, with dimensions of 2.77 in (0.07 m) in the outer radius, 0.125 in (0.0032 m) in the inner radius, and 2.25 in (0.057 m) in height, as indicated in [48]. The domain is partitioned into a mesh of 100 100 100 in the cylindrical coordinate system. The initial porosity values at grid nodes are uniformly distributed in the interval of with a mean value of 0.11 as indicated in [68]. The initial permeability is calculated from the initial porosity via the Kozeny–Carman equation (Equation (6)). Figure 3 shows the transient variations of the pressure at the inlet during acid injection, and the simulation result shows good agreement with the experimental results.
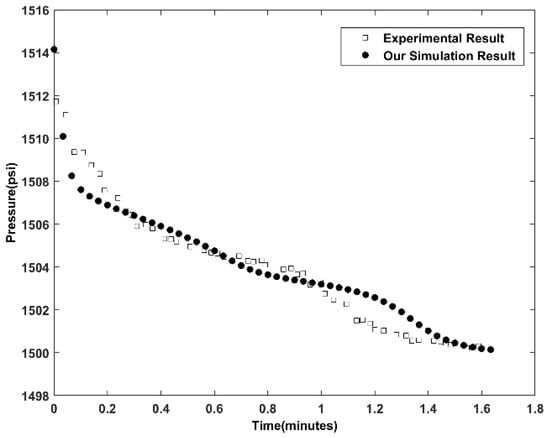
Figure 3.
Comparison of pressure at the inlet during acid injection.
4.2. Numerical Studies
Now we present two 3D synthetic core flooding case studies to investigate alterations of rock properties and dissolution patterns with different heterogeneities, volume fractions, and flow conditions. In the first case, the proposed numerical model is applied for 3D linear core flooding in a multi-mineral system, which is consist of calcite, quartz, and clay [34]. In order to examine the effects of heterogeneity of porous media and mineral volume fractions on the alterations of rock properties and dissolution patterns, sensitivity studies have been performed. In the second case study, the proposed numerical model is applied for 3D radial core flooding in a single calcite system, which can be applied to simulate the matrix acidizing process at exact downhole environments.
Case Study 1: 3D linear flow core flooding. In this case, we use a 3D synthetic core sample, which is 10-cm long, 5-cm wide, and 5-cm tall, as shown in Figure 4. The minerals are assumed to be homogeneously distributed, which indicates the initial mineral volume fractions are the same throughout the entire sample. As indicated in [30], the initial porosity values at grid nodes in the porous media are defined as: , where is the mean value of porosity, the fluctuations are uniformly distributed in the interval , and the magnitude of heterogeneity is defined as . We consider three scenarios with the different magnitudes of heterogeneity in the porous media. In this case study, three disconnected fractures representing natural fractures are embedded in the porous media. We set and choose large values in fractures. Acidic fluid with a pH value of 3 is injected from the inlet boundary at 25 °C at a constant rate. The outlet pressure is fixed at 100 kPa. The initial and injected values of primary species concentrations are given in Table 1.
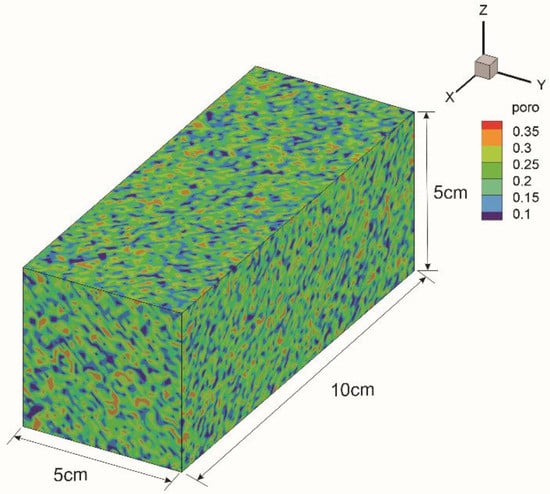
Figure 4.
The dimension of the core sample and the initial porosity distribution with fluctuation in the interval [−0.15, 0.15].

Table 1.
Initial and injected concentrations of aqueous species.
Heterogeneity of the porous media is an important factor that affects structures of the flow channel during reactive transport processes. In a realistic case, natural heterogeneities could trigger very complicated flow paths, which in turn causes complex structures in the transport of acid fluid. The various flow paths lead to different dissolution patterns. The initial mineral volume fraction is another important parameter that can affect alterations of rock properties significantly due to the different chemical reactivity with acidic fluid among the minerals.
4.2.1. The Effect of Heterogeneity
In this section, we have three different intervals of fluctuations of , , and , respectively, to investigate the effects of heterogeneity on dissolution patterns and variations of rock properties. The corresponding magnitudes of heterogeneity are chosen to be 0.25, 0.5, and 0.75, respectively. The initial mineral volume fractions of 90% calcite, 5% quartz, and 5% clay is fixed. The other initial conditions and boundary conditions are the same as shown in Table 1.
We consider three disconnected fractures with the same aperture of 1 mm as shown in Figure 5a, Figure 6a and Figure 7a. The computational domain is meshed using a 100 100 50 Cartesian grid system. Figure 5, Figure 6 and Figure 7 illustrate the initial porosity distributions and wormhole structures at the breakthrough. The definition of a breakthrough is the situation when the ratio of the pressure drop to the initial pressure drop decreases to 1% [18,30,33,34]. Figure 5b, Figure 6b and Figure 7b demonstrate that the heterogeneity of porous media has significant effects on the structure of the conductive pathways in the fractured porous media. Without heterogeneity, the dissolution front should propagate uniformly. In Figure 5b with a lower magnitude of heterogeneity, the wormhole structures tend to be more straight and smooth at breakthrough, because the permeability is almost uniform throughout the core and the flow direction of injected acidic fluid remains almost the same. As the magnitude of heterogeneity increases, the dominant wormholes become highly branched and irregular, as shown in Figure 7b.
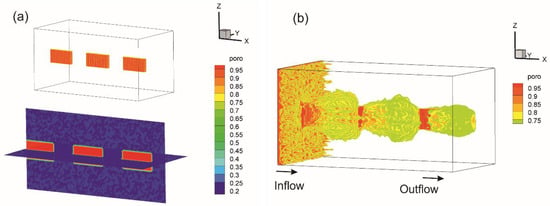
Figure 5.
Porosity profile of fractured rock with fluctuations in the interval [−0.05, 0.05]. (a) Initial condition; (b) dominant wormhole.
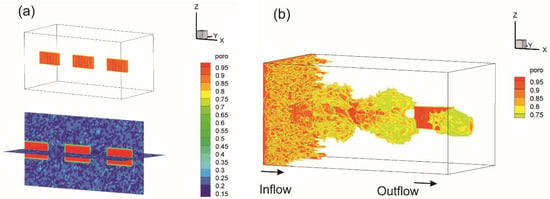
Figure 6.
Porosity profile of fractured rock with fluctuations in the interval [−0.10, 0.10]. (a) Initial condition; (b) dominant wormhole.
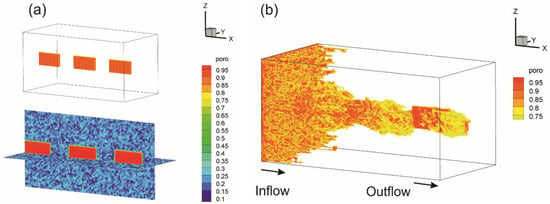
Figure 7.
Porosity profile of fractured rock with fluctuations in the interval [−0.15, 0.15]. (a) Initial condition; (b) dominant wormhole.
4.2.2. The Effect of the Mineral Volume Fraction
In this section, the mineral volume fractions are initially set to 80% calcite, 15% quartz, and 5% clay, and 70% calcite, 25% quartz, and 5% clay, respectively. The fluctuations are fixed in the interval , and the corresponding magnitude of heterogeneity is 0.75. Other initial and boundary conditions are the same among these three scenarios. The changes in average porosity are compared to investigate the effects of the mineral composition on the alterations of rock properties (Figure 8). Figure 8 illustrates a comparison of the average porosity of the fracture porous media from the beginning to the breakthrough among these three scenarios. The calcite has the highest chemical reactivity with the hydrogen ion among calcite, quartz, and clay, which consequently cause the highest chemical reaction rate. Therefore, an increased volume fraction of calcite at the beginning can lead to an expanded volume of dissolved calcite and can augment the mineral dissolution rate. As a result, a larger average porosity and an earlier breakthrough can be obtained, as shown in Figure 8.
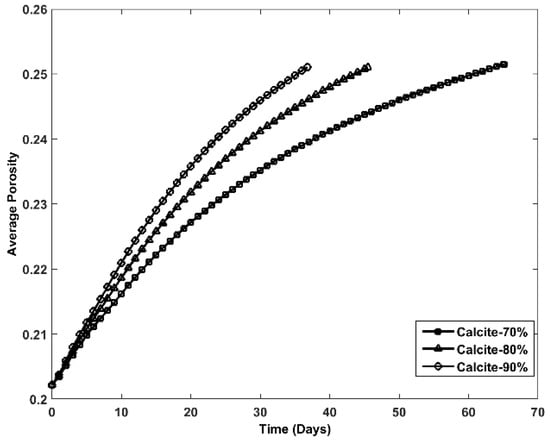
Figure 8.
Comparison results of the average porosity.
Case Study 2: 3D radial flow core flooding. In this case, we present the synthetic 3D radial flow core flooding case studies to simulate a matrix acidizing process. A 3D synthetic core sample has a dimension of 2 cm in inner diameter, 20 cm in outer diameter, and 10 cm in height. Several disconnected fractures with a uniform aperture of 2 mm are randomly distributed inside of the porous media, as shown in the low two figures of Figure 9. The initial porosity in the porous media is uniformly distributed in the interval of with a mean value of 0.2. The acidic fluid with a pH value of 1 is injected into the porous media through the central borehole at a constant rate. The pressure at the outer boundary is fixed at 10 Mpa. The core sample contains only one mineral, calcite, with a specific surface area of 0.039 [69], and the reaction rate constant was adjusted to based on the results of model validation.
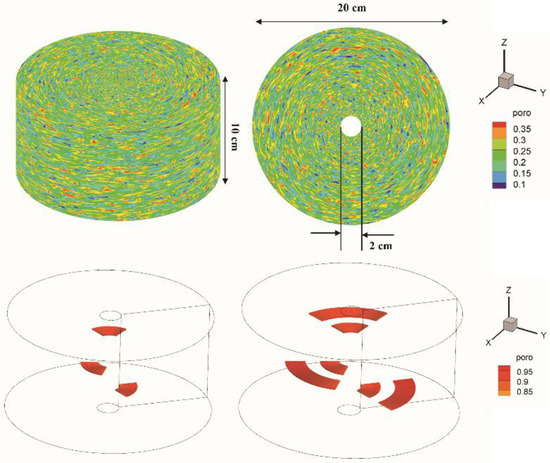
Figure 9.
The dimension of the core sample, initial porosity profile, and randomly distributed fractures.
Figure 10 and Figure 11 represent the porosity profiles at different times with 3 and 6 originally disconnected fractures under the radial flooding condition, respectively. During the flooding process, the injected acid fluid flows preferentially through the fractures due to the good fluid conductivity. Chemical reactions which occur at the mineral surface under the action of the acidic fluid then leads to the dissolution of the mineral rock. As a consequence, the conductive pathways are formed nearby the initial fractures (Figure 10b–d and Figure 11b–d). Comparing Figure 10 and Figure 11, the more initially disconnected fractures are embedded into the porous media, the greater the number of ramified structures will be, and the formation of conductive pathways will be obtained more quickly.
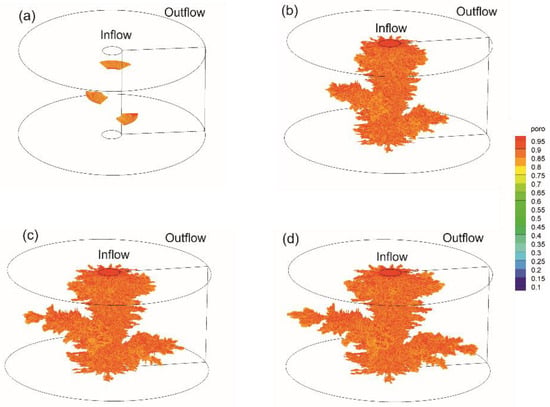
Figure 10.
Temporal and spatial evolution of porosity. (a) initial condition; (b) 14.4 min; (c) 28.8 min; (d) 48 min (breakthrough).
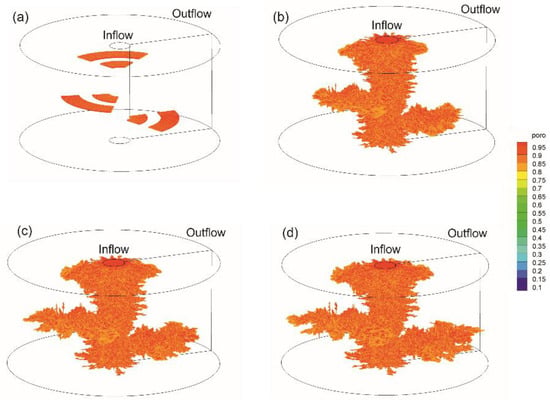
Figure 11.
Temporal and spatial evolution of porosity. (a) initial condition; (b) 14.4 min; (c) 28.8 min; (d) 47.4 min (breakthrough).
5. Conclusions
In this study, we developed a 3D mathematical model that couples the Stokes–Brinkman, reactive-transport, and rock properties equations to simulate fluid flow, solute transport, chemical reactions, and alterations of porosity and permeability in a fractured porous media. The coupled model can be applied to simulate the mineral dissolution processes in both linear and radial flow. We have developed and implemented a sequential numerical solution procedure to solve this coupled model. We applied the newly developed numerical simulator for three dimensional simulation study on the coupled processes of fluid transport and mineral dissolution both on Cartesian and cylindrical grids. The preliminary simulation results can be highlighted as follows:
- Firstly, the proposed numerical model is applied for 3D linear core flooding in a multi-mineral system, which consists of calcite, quartz, and clay. Sensitivity studies clearly show the effects of heterogeneity of porous media and mineral volume fractions on the rock properties and dissolution patterns. The numerical results demonstrate that the magnitude of heterogeneity has a significant impact on the structure of the dominant wormholes: Without heterogeneity, the dissolution front propagates uniformly. The higher initial calcite content has a significant impact on porosity and fracture evolution via an increase in the reactive surface area and the subsequent augmentation of the chemical reaction rate.
- In the second case study, the proposed numerical model is applied for 3D radial core flooding in a single calcite system. Several disconnected fractures are randomly distributed inside of porous media. During the flooding process, the fractures propagate radially within the porous media and eventually form the conductive channels, wormholes. Therefore, the proposed numerical model can be applied to simulate the matrix acidizing process in fractured carbonate formations at exact downhole environments.
However, it should be noted that the model developed in this work is mainly focused on the reactive transport processes at the core scale. Challenges arise when simulating this process at the field scale due to the treatment of fractures in this model. More efficient numerical models for field applications will be developed in the future.
Author Contributions
T.Y. conducted the research work under the supervision of G.Q., T.Y. developed the numerical model and numerical solution procedure, performed the numerical experiments, and wrote the paper. C.W. discussed the results, and reviewed and edited the paper. C.-S.Z. developed the linear solver Package (FASP), wrote the content of FASP, and reviewed and edited the paper. G.Q. conceived this study, discussed the results, and reviewed and edited the paper. All authors give the final approval of the manuscript to be submitted.
Funding
This research is partially supported by the US National Science Foundation through NSF Grant DMS-1209124, the Society of Petroleum Engineers—Gulf Coast Section through its distinguished professorship endowment, the Institute of Petroleum Exploration & Development, Langfang Branch, the PetroChina Company Limited, CNPC Chuanqing Drilling Engineering Company Limited, Sinopec Tech Houston LLC, the Key Research Program of Frontier Sciences of CAS, and the National Science Foundation of China (11971472). The authors thank PetroChina Company Limited and Sinopec Corp for their permission to publish this paper.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this paper, the unknowns of , , , and in 3-D cylindrical coordinates are defined in Figure A1. The pressure is located in the center of each cell (), and velocities are located in the center of grid faces as indicated by the subscripts , , and .
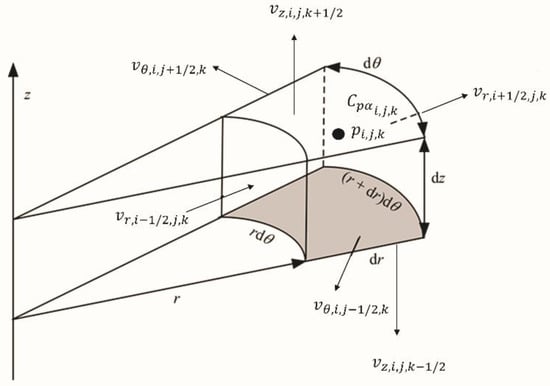
Figure A1.
Definition of pressure, velocities, and concentrations on a grid with indices i, j, k.
With the definitions of the pressure and velocities in Figure A1, the finite difference approximations of Equations (1) and (2) in the 3D cylindrical coordinate system are given as:
where the permeability at the cell interface is calculated as the harmonic average of the permeabilities of the two neighboring cells.
In this paper, we set constant velocity at the inlet boundary, constant pressure and free-flows at the outlet boundary, and no-slip boundary condition at the other boundaries. The boundary conditions in the cylindrical system are expressed as:
where denotes the wellbore radius, denotes the radius of the outer boundary, is the injected velocity at the wellbore, is the outlet pressure, is the unit normal vector on the boundary, and is the depth of the domain.
In the cylindrical coordinates system, when the entire domain is divided into , , and grid blocks in the corresponding directions, respectively, the total number of , , , and is , , , and , respectively. By imposing the defined boundary conditions, we have unknown variables and the same number of discretized equations, which can be expressed as a system of linear equations:
where , , , and are unknown vectors, and all of them go through the indices , , in the same order. , , and are the submatrices resulting from the terms of , , and in the Equation (A1), respectively. , , and are the submatrices resulting from the terms of , , and in the Equation (A2), respectively. and are the submatrices resulting from the terms of and in the Equation (A3), respectively. , , and are the submatrices resulting from the terms of , , and in the Equation (A4), respectively. , , , and are the right-hand side vectors resulting from the defined boundary conditions.
References
- Wolery, T.J.; Jackson, K.J.; Bourcier, W.L.; Bruton, C.J.; Viani, B.E.; Knauss, K.G.; Delany, J.M. Current Status of the EQ3/6 Software Package for Geochemical Modeling. Chem. Model. Aqueous Syst. II 1990, 416, 104–116. [Google Scholar]
- Smith, D.; Giraud, M.; Kemp, C.; McBee, M.; Taitano, J.; Winfield, M.; Protwood, J.; Everett, D. The successful evolution of anton irish conformance efforts. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. SPE 103044. [Google Scholar]
- Metz, B.; Davidson, O.; de Coninck, H.C.; Loos, M.; Meyer, L. IPCC Special Report on Carbon Dioxide Capture and Storage; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2005. [Google Scholar]
- Harvey, OR.; Cantrell, KJ.; Qafoku, NP.; Brown, C. Geochemical Implications of CO2 Leakage Associated with Geologic Storage: A Review; Pacific Northwest National Lab. (PNNL): Richland, WA, USA, 2012. [Google Scholar]
- McLeod, H.O. Matrix Acidizing. J. Pet. Technol. 1984, 36, 2055–2069. [Google Scholar] [CrossRef]
- Hung, K.M.; Hill, A.D.; Sepehrnoori, K. A Mechanistic Model of Wormhole Growth in Carbonate Matrix Acidizing and Acid Fracturing. J. Pet. Technol. 1989, 41, 59–66. [Google Scholar] [CrossRef]
- Assayag, N.; Matter, J.; Ader, M.; Goldberg, D.; Agrinier, P. Water–rock interactions during a CO2 injection field-test: Implications on host rock dissolution and alteration effects. Chem. Geol. 2009, 265, 227–235. [Google Scholar] [CrossRef]
- Gaus, I.; Azaroual, M.; Czernichowski-Lauriol, I. Preliminary Modelling of the Geochemical Impact of CO2-Injection on the Cap Rock at Sleipner; Rep. BRGM/RP-52081-FR; 2002. [Google Scholar]
- Jun, Y.S.; Giammar, D.E.; Werth, C.J. Impacts of geochemical reactions on geologic carbon sequestration. Environ. Sci. Technol. 2013, 47, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Lions, J.; Devau, N.; De Lary, L.; Dupraz, S.; Parmentier, M.; Gombert, P.; Dictor, M.C. Potential impacts of leakage from CO2 geological storage on geochemical processes controlling fresh groundwater quality: A review. Int. J. Greenh. Gas Control 2014, 22, 165–175. [Google Scholar] [CrossRef]
- Kharaka, Y.K.; Thordsen, J.J.; Hovorka, S.D.; Seay Nance, H.; Cole, D.R.; Phelps, T.J.; Knauss, K.G. Potential environmental issues of CO2 storage in deep saline aquifers: Geochemical results from the Frio-I Brine Pilot test, Texas, USA. Appl. Geochem. 2009, 24, 1106–1112. [Google Scholar] [CrossRef]
- Dong, C.; Zhu, D.; Hill, A.D. Modeling of the acidizing process in naturally fractured carbonates. SPE J. 2002, 7, 400–408. [Google Scholar] [CrossRef]
- Golfier, F.; Bazin, B.; Zarcone, C.; Lernormand, R.; Lasseux, D.; Quintard, M. Acidizing Carbonate Reservoirs: Numerical Modelling of Wormhole Propagation and Comparison to Experiments. In Proceedings of the SPE European Formation Damage Conference, The Hague, The Netherlands, 20–22 May 2001; pp. 1–11. [Google Scholar]
- Huang, T.; Zhu, D.; Hill, A.D. Prediction of Wormhole Population Density in Carbonate Matrix Acidizing. In Proceedings of the SPE European Formation Damage Conference, The Hague, The Netherlands, 31 May–1 June 1999. [Google Scholar]
- McDuff, D.; Shuchart, C.E.; Jackson, S.; Postl, D.; Brown, J.S. Understanding Wormholes in Carbonates: Unprecedented Experimental Scale and 3-D Visualization. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010; pp. 78–81. [Google Scholar]
- Daccord, G.; Lenormand, R.; Liétard, O. Chemical dissolution of a porous medium by a reactive fluid-I. Model for the “wormholing” phenomenon. Chem. Eng. Sci. 1993, 48, 169–178. [Google Scholar] [CrossRef]
- Daccord, G.; Liétard, O.; Lenormand, R. Chemical dissolution of a porous medium by a reactive fluid-II. Convection vs reaction, behavior diagram. Chem. Eng. Sci. 1993, 48, 179–186. [Google Scholar] [CrossRef]
- Fredd, C.N.; Fogler, H.S. Influence of transport and reaction on wormhole formation in porous media. AIChE J. 1998, 44, 1933–1949. [Google Scholar] [CrossRef]
- Li, L.; Steefel, C.I.; Yang, L. Scale dependence of mineral dissolution rates within single pores and fractures. Geochim. Cosmochim. Acta 2008, 72, 360–377. [Google Scholar] [CrossRef]
- Li, L.; Steefel, C.I.; Kowalsky, M.B.; Englert, A.; Hubbard, S.S. Effects of physical and geochemical heterogeneities on mineral transformation and biomass accumulation during biostimulation experiments at Rifle, Colorado. J. Contam. Hydrol. 2010, 112, 45–63. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Gawande, N.; Kowalsky, M.B.; Steefel, C.I.; Hubbard, S.S. Physicochemical heterogeneity controls on uranium bioreduction rates at the field scale. Environ. Sci. Technol. 2011, 45, 9959–9966. [Google Scholar] [CrossRef] [PubMed]
- Steefel, C.I.; DePaolo, D.J.; Lichtner, P.C. Reactive transport modeling: An essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 2005, 240, 539–558. [Google Scholar] [CrossRef]
- Steefel, C.I.; Lasaga, A.C. A Coupled Model for Transport of Multiple Chemical-Species and Kinetic Precipitation Dissolution Reactions with Application to Reactive Flow in Single-Phase Hydrothermal Systems. Am. J. Sci. 1994, 294, 529–592. [Google Scholar] [CrossRef]
- Lasaga, A.C. Kinetic Theory in the Earth Sciences; Princeton University Press: Princeton, NJ, USA, 1998; ISBN 0691037485. [Google Scholar]
- Lichtner, P.C. The quasi-stationary state approximation to coupled mass transport and fluid-rock interaction in a porous medium. Geochim. Cosmochim. Acta 1988, 52, 143–165. [Google Scholar] [CrossRef]
- Steefel, C.I. CrunchFlow Software for Modeling Multicomponent Reactive Flow and Transport. User’s Manual; Earth Science Division. Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2009. [Google Scholar]
- Molins, S. Reactive Interfaces in Direct Numerical Simulation of Pore-Scale Processes. Rev. Mineral. Geochem. 2015, 80, 461–481. [Google Scholar] [CrossRef]
- Kang, Q.; Lichtner, P.C.; Zhang, D. Lattice Boltzmann pore-scale model for multicomponent reactive transport in porous media. J. Geophys. Res. 2006, 111, 1–12. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Carey, B.; Tao, W.-Q. International Journal of Heat and Mass Transfer Pore-scale study of diffusion—Reaction processes involving dissolution and precipitation using the lattice Boltzmann method. Int. J. Heat Mass Transf. 2014, 75, 483–496. [Google Scholar] [CrossRef]
- Panga, M.K.R.; Ziauddin, M.; Balakotaiah, V. Two-scale continuum model for simulation of wormholes in carbonate acidization. AIChE J. 2005, 51, 3231–3248. [Google Scholar] [CrossRef]
- Qiao, C.; Li, L.; Johns, R.T.; Xu, J. A Mechanistic Model for Wettability Alteration by Chemically Tuned Waterflooding in Carbonate Reservoirs. SPE J. 2015, 20, 767–783. [Google Scholar] [CrossRef]
- Liu, P.; Yao, J.; Couples, G.D.; Huang, Z.; Sun, H.; Ma, J. Numerical modelling and analysis of reactive flow and wormhole formation in fractured carbonate rocks. Chem. Eng. Sci. 2017, 172, 143–157. [Google Scholar] [CrossRef]
- Yuan, T.; Ning, Y.; Qin, G. Numerical Modeling and Simulation of Coupled Processes of Mineral Dissolution and Fluid Flow in Fractured Carbonate Formations. Transp. Porous Media 2016, 114, 747–775. [Google Scholar] [CrossRef]
- Yuan, T.; Ning, Y.; Qin, G. Numerical Modeling of Mineral Dissolution of Carbonate Rocks During Geological CO2 Sequestration Processes. In Proceedings of the SPE Europec Featured at 79th EAGE Conference and Exhibition, Paris, France, 12–15 June 2017. [Google Scholar]
- Popov, P.; Efendiev, Y.; Qin, G. Multiscale modeling and simulations of flows in naturally fractured Karst reservoirs. Commun. Comput. Phys. 2009, 6, 162–184. [Google Scholar] [CrossRef]
- Bi, L.; Qin, G.; Popov, P. An Efficient Upscaling Process Based on a Unified Fine-scale Multi-Physics Model for Flow Simulation in Naturally Fracture Carbonate Karst Reservoirs. In Proceedings of the SPE/EAGE Reservoir Characterization and Simulation Conference, Abu Dhabi, UAE, 19–21 October 2009. [Google Scholar]
- Qin, G.; Bi, L.; Popov, P.; Efendiev, Y.; Espedal, M.S. An Efficient Upscaling Process Based on a Unified Fine-scale Multi-Physics Model for Flow Simulation in Naturally Fracture Carbonate Karst Reservoirs. In Proceedings of the CPS/SPE International Oil & Gas Conference and Exhibition in China, Beijing, China, 8–10 June 2010. [Google Scholar]
- Brinkman, H.C. A Calculation of the Viscous Force Exerted By a Flowing Fluid on a Dense Swarm of Particles. Appl. Sci. Res. 1947, 1, 27–34. [Google Scholar] [CrossRef]
- Durlofsky, L.; Brady, J.F. Analysis of the Brinkman equation as a model for flow in porous media. Phys. Fluids 1987, 30, 3329–3341. [Google Scholar] [CrossRef]
- Hwang, W.R.; Advani, S.G. Numerical simulations of Stokes-Brinkman equations for permeability prediction of dual scale fibrous porous media. Phys. Fluids 2010, 22, 113101. [Google Scholar] [CrossRef]
- Popov, P.; Qin, G.; Bi, L.; Efendiev, Y.; Kang, Z.; Jianglong, L. Multiphysics and multiscale methods for modeling fluid flow through naturally fractured carbonate karst reservoirs. SPE Reserv. Eval. Eng. 2009, 12, 218–231. [Google Scholar] [CrossRef]
- Beavers, G.S.; Joseph, D.D. Boudary conditions at a naturally permeable wall. J. Fluid Mech. 1967, 30, 197–207. [Google Scholar] [CrossRef]
- Harlow, F.H.; Welch, J.E. Numerical Calculation of Time-Dependent Viscous Incompressible Flow of Fluid with Free Surface. Phys. Fluids 1965, 8, 2182–2189. [Google Scholar] [CrossRef]
- Bell, J.B.; Colella, P.; Glaz, H.M. A Second-Order Incompressible Projection Method for the Navier-Stokes Equations. J. Comput. Phys. 1989, 283, 257–283. [Google Scholar] [CrossRef]
- Ge, L.; Fotis, S. A Numerical Method for Solving the 3D Unsteady Incompressible Navier-Stokes Equations in Curvilinear Domains with Complex Immersed Boundaries. J. Comput. Phys. 2007, 225, 1782–1809. [Google Scholar] [CrossRef] [PubMed]
- FASP User Guide. 2018. Available online: www.multigrid.org/fasp (accessed on 20 December 2018).
- Baker, A.H.; Jessup, E.R.; Kolev, T.V. A simple strategy for varying the restart parameter in GMRES(m). J. Comput. Appl. Math. 2009, 230, 751–761. [Google Scholar] [CrossRef]
- Tardy, P.; Lecerf, B.; Christanti, Y. An Experimentally Validated Wormhole Model for Self-Diverting and Conventional Acids in Carbonate Rocks Under Radial Flow Conditions. In Proceedings of the European Formation Damage Conference, Scheveningen, The Netherlands, 30 May–1 June 2007. [Google Scholar]
- Martys, N.; Bentz, D.P.; Garboczi, E.J. Computer simulation study of the effective viscosity in Brinkman’s equation. Phys. Fluids 1994, 6, 1434–1439. [Google Scholar] [CrossRef]
- Berg, R.R. Method for determining permeability from reservoir rock properties. Trans. Coast Assoc. Geol. Soc. 1970, 20, 303–317. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Pub. Co.: New York, NY, USA, 1972. [Google Scholar]
- Van Baaren, J.P. Quick-look permeability estimates using sidewall samples and porosity logs. In Proceedings of the Trans, 6th Annual European Logging Symposium, Society of Professional Well Log Analysts, London, UK, 26–27 March 1979. [Google Scholar]
- Glover, P.W.J.; Zadjali, I.I.; Frew, K.A. Using an Electrokinetic Approach. Geophysics 2006, 71, F49–F60. [Google Scholar] [CrossRef]
- Rashid, F.; Glover, P.W.J.; Lorinczi, P.; Collier, R.; Lawrence, J. Porosity and permeability of tight carbonate reservoir rocks in the north of Iraq. J. Pet. Sci. Eng. 2015, 133, 147–161. [Google Scholar] [CrossRef]
- Mavis, F.T.; Wilsey, E.F. A Study of the Permeability of Sand; State Univeristy Iowa Bullletin: Iowa, IA, USA, 1936. [Google Scholar]
- Nelson, P.H. Permeability-porosity relationships in sedimentary rocks. Log Anal. 1994, 35, 38–62. [Google Scholar]
- Chapuis, R.P. Sand–bentonite liners: Predicting permeability from laboratory tests. Can. Geotech. J. 1990, 27, 47–57. [Google Scholar] [CrossRef]
- Chapuis, R.P. The 2000 R.M. Hardy Lecture: Full-scale hydraulic performance of soil-bentonite and compacted clay liners. Can. Geotech. J. 2002, 39, 417–439. [Google Scholar] [CrossRef]
- Chapuis, R.P.; Aubertin, M. Predicting the Coefficient Permeability of Soils Using the Kozeny-Carman Équation; École Polytech. Montréal: Montreal, QC, Canada, 2003. [Google Scholar]
- Ehrenberg, S.N.; Eberli, G.P.; Baechle, G. Porosity-permeability relationships in Miocene carbonate platforms and slopes seaward of the Great Barrier Reef, Australia (ODP Leg 194, Marion Plateau). Sedimentology 2006, 53, 1289–1318. [Google Scholar] [CrossRef]
- Ghommem, M.; Zhao, W.; Dyer, S.; Qiu, X.; Brady, D. Carbonate acidizing: Modeling, analysis, and characterization of wormhole formation and propagation. J. Pet. Sci. Eng. 2015, 131, 18–33. [Google Scholar] [CrossRef]
- Brunet, J.P.L.; Li, L.; Karpyn, Z.T.; Huerta, N.J. Fracture opening or self-sealing: Critical residence time as a unifying parameter for cement-CO2-brine interactions. Int. J. Greenh. Gas Control 2016, 47, 25–37. [Google Scholar] [CrossRef]
- Brandt, A.; Dinar, N. Multigrid Solutions to Elliptic Flow Problems. In Numerical Methods for Partial Differential Equations; Parter, S., Ed.; Academic Press: Cambridge, MA, USA, 1979; pp. 53–147. [Google Scholar]
- Bramble, J.H.; Pasciak, J.E. Iterative techniques for time dependent Stokes problems. Comput. Math. Applic. 1997, 33, 13–30. [Google Scholar] [CrossRef]
- Shen, L.; Xu, J. On A Schur Complement Operator Arisen from Navier-Stokes Equations and Its Preconditioning. In Proceedings of the Guangzhou International Symposium on Computational Mathematics; Chen, Z., Li, Y., Micchelli, C., Xu, Y., Eds.; Marcel Dekker: New York, NY, USA, 1998; pp. 481–490. [Google Scholar]
- Xu, J.; Zikatanov, L.T. Algebraic Multigrid Methods. Acta Numer. 2016, 1–128. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2 ed.; SIAM: Philadelphia, PA, USA, 2003; Volume 3, ISBN 0898715342. [Google Scholar]
- Ghommem, M.; Brady, D. Multifidelity Modeling and Analysis of Matrix Acidizing Under Radial Flow Conditions. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 25–28 April 2016. [Google Scholar]
- Suarez, D.; Wood, J. Simultaneous determination of calcite surface area and content in soils. Soil Sci. Soc. Am. J. 1984, 48, 1232–1235. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).