Field Water Balance Closure with Actively Heated Fiber-Optics and Point-Based Soil Water Sensors
Abstract
1. Introduction
2. Materials and Methods
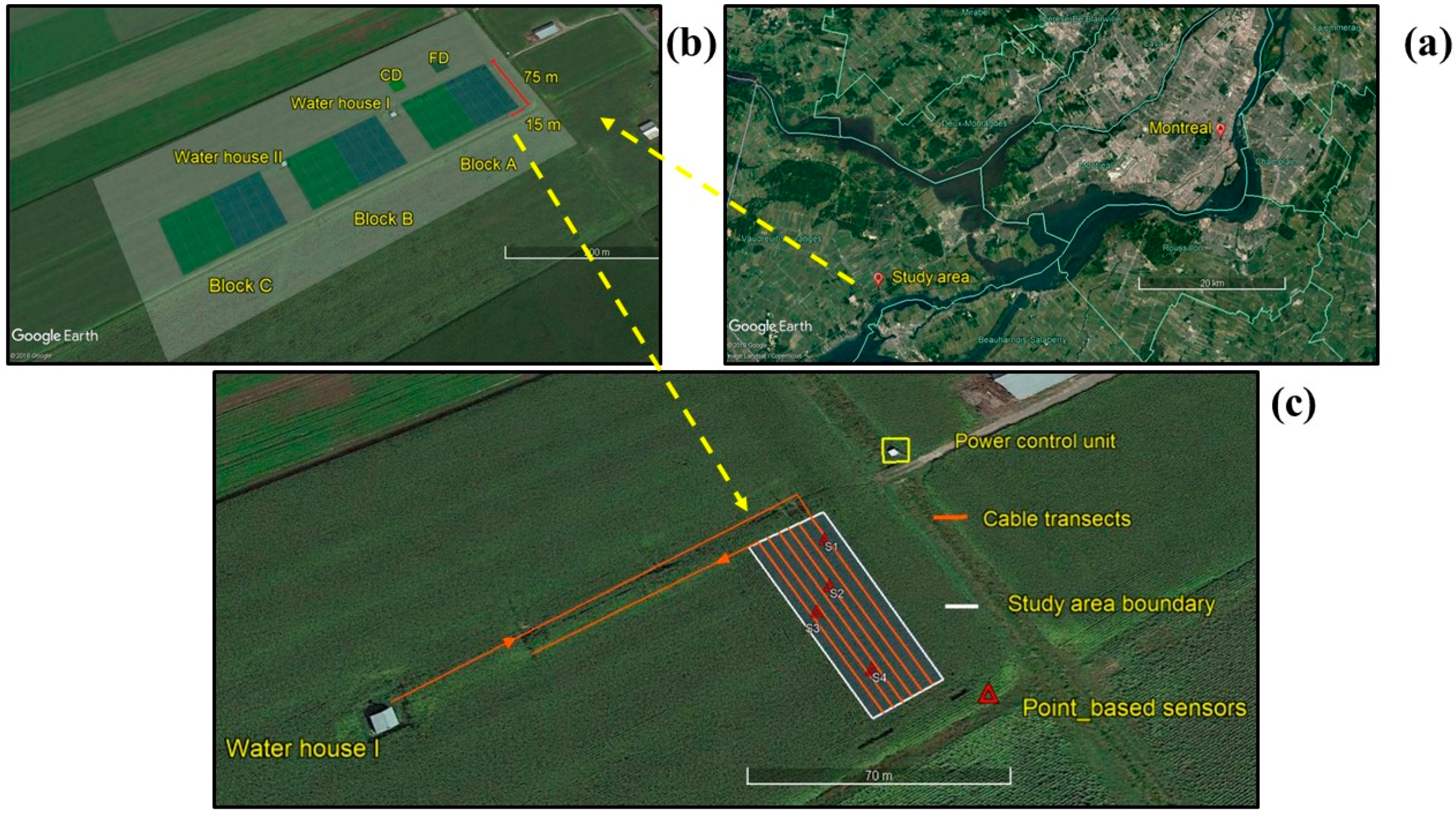
2.1. Study Site
2.2. Soil Water Measurement
2.3. Development of the Distributed Soil Water Sensor Using Actively Heated Fiber-Optics
2.4. Weather and Drainage Data
2.5. Soil Water Balance
3. Results and Discussion
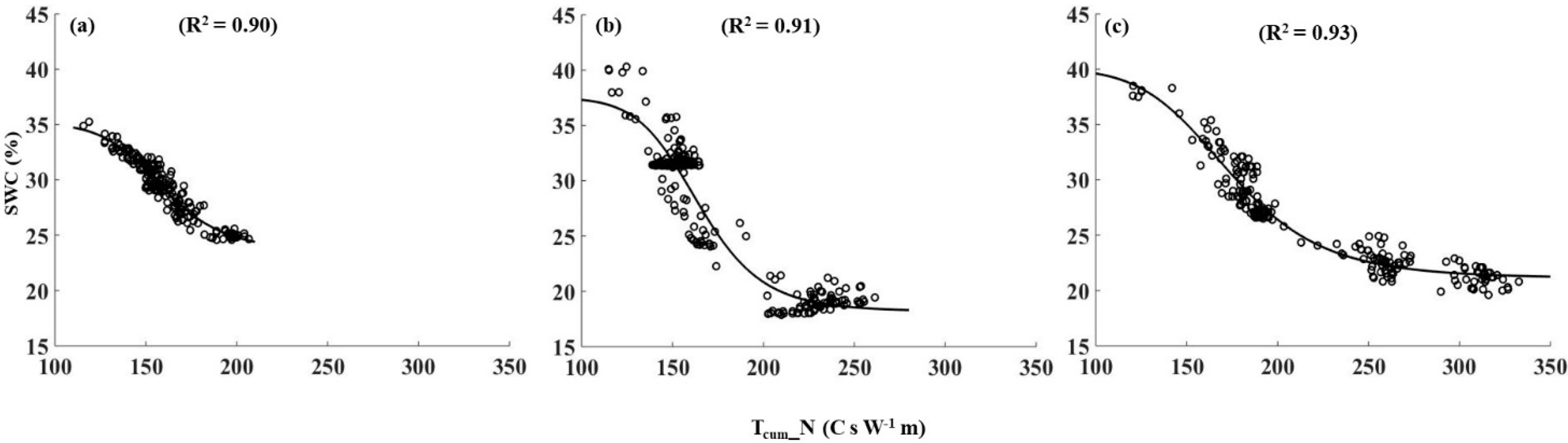
3.1. Calibration and Validation of the Soil Water Sensors
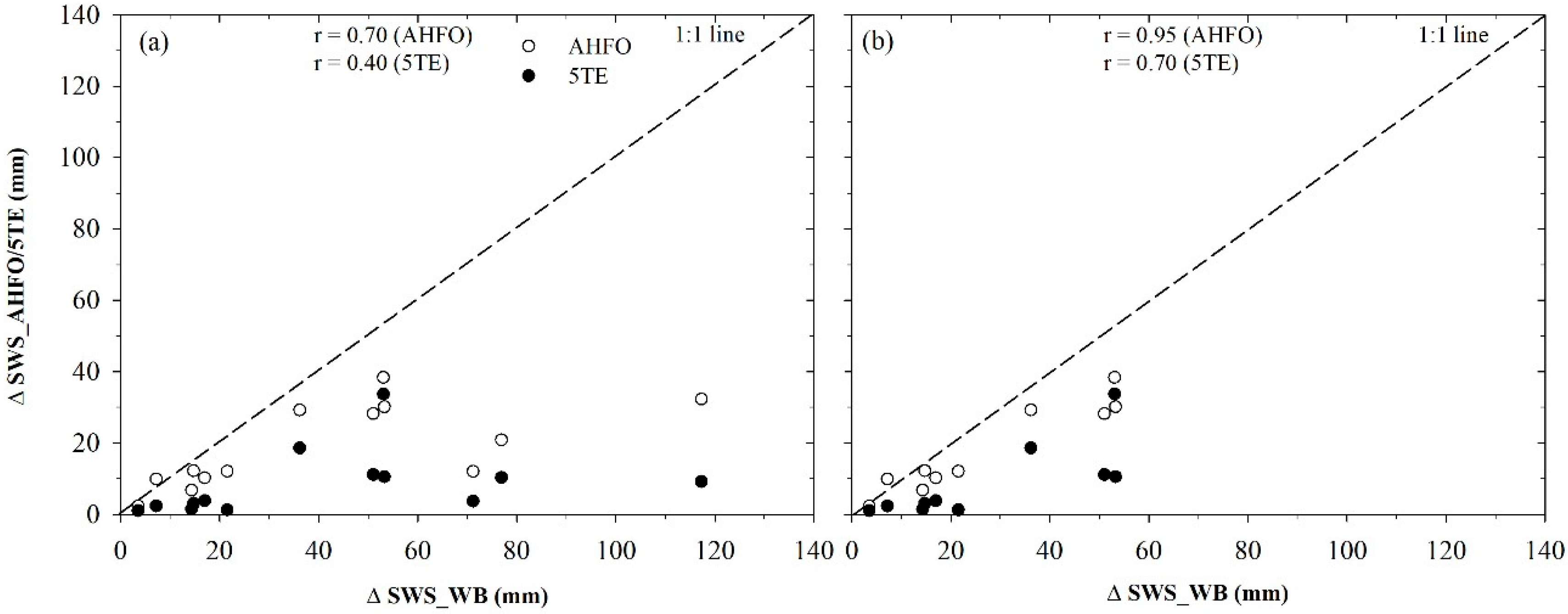
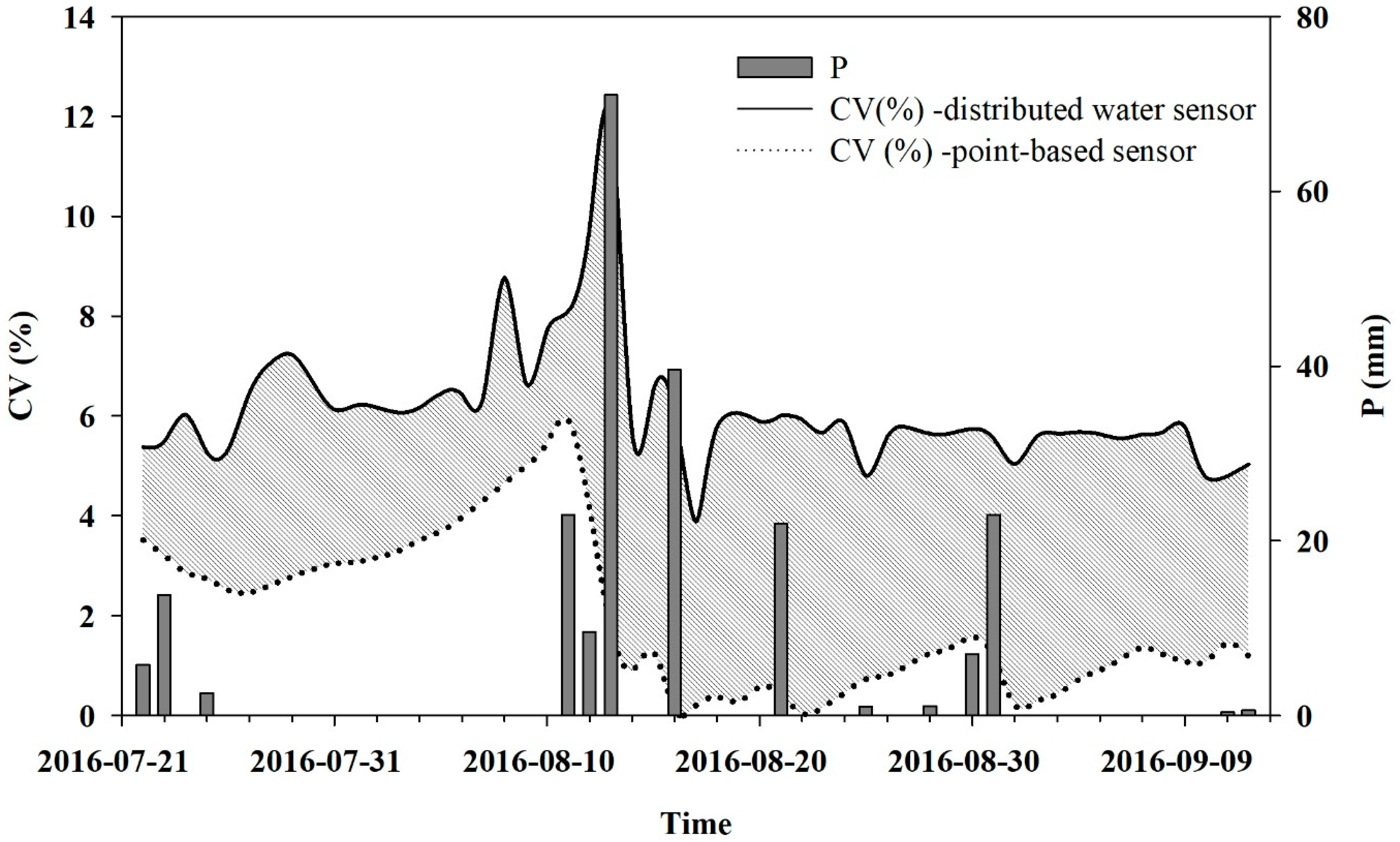
3.2. Comparison of the Distributed Sensor with the Point-Based Sensor
3.3. Comparison of Evapotranspiration Estimates
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- BaldocchI, D.D. Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: Past, present and future. Glob. Chang. Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Evett, S.R.; Schwartz, R.C.; Casanova, J.J.; Heng, L.K. Soil water sensing for water balance, et and wue. Agric. Water Manag. 2012, 104, 1–9. [Google Scholar] [CrossRef]
- Singh, S.; Boote, K.J.; Angadi, S.V.; Grover, K.K. Estimating water balance, evapotranspiration and water use efficiency of spring safflower using the cropgro model. Agric. Water Manag. 2017, 185, 137–144. [Google Scholar] [CrossRef]
- Aggarwal, P.; Bhattacharyya, R.; Mishra, A.K.; Das, T.K.; Šimůnek, J.; Pramanik, P.; Sudhishri, S.; Vashisth, A.; Krishnan, P.; Chakraborty, D.; et al. Modelling soil water balance and root water uptake in cotton grown under different soil conservation practices in the indo-gangetic plain. Agric. Ecosyst. Environ. 2017, 240, 287–299. [Google Scholar] [CrossRef]
- Entekhabi, D. Recent advances in land-atmosphere interaction research. Rev. Geophys. 1995, 33, 995–1003. [Google Scholar] [CrossRef]
- Moran, M.S.; Hymer, D.C.; Qi, J.; Sano, E.E. Soil moisture evaluation using multi-temporal synthetic aperture radar (sar) in semiarid rangeland. Agric. For. Meteorol. 2000, 105, 69–80. [Google Scholar] [CrossRef]
- Akbar, R.; Short Gianotti, D.; McColl, K.A.; Haghighi, E.; Salvucci, G.D.; Entekhabi, D. Hydrological storage length scales represented by remote sensing estimates of soil moisture and precipitation. Water Resour. Res. 2018, 54, 1476–1492. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Farahmand, A.; Melton, F.; Teixeira, J.; Anderson, M.; Wardlow, B.D.; Hain, C. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Zreda, M.; Desilets, D.; Ferré, T.P.A.; Scott, R.L. Measuring soil moisture content non-invasively at intermediate spatial scale using cosmic-ray neutrons. Geophys. Res. Lett. 2008, 35, L21402. [Google Scholar] [CrossRef]
- Ragab, R.; Evans, J.G.; Battilani, A.; Solimando, D. The cosmic-ray soil moisture observation system (cosmos) for estimating the crop water requirement: New approach. Irrig. Drain. 2017, 66, 456–468. [Google Scholar] [CrossRef]
- Zhu, X.; Cao, R.; Shao, M.; Liang, Y. Footprint radius of a cosmic-ray neutron probe for measuring soil-water content and its spatiotemporal variability in an alpine meadow ecosystem. J. Hydrol. 2018, 558, 1–8. [Google Scholar] [CrossRef]
- Moghadas, D.; Jadoon, K.Z.; McCabe, M.F. Spatiotemporal monitoring of soil water content profiles in an irrigated field using probabilistic inversion of time-lapse emi data. Adv. Water Resour. 2017, 110, 238–248. [Google Scholar] [CrossRef]
- Abdu, H.; Robinson, D.A.; Seyfried, M.; Jones, S.B. Geophysical imaging of watershed subsurface patterns and prediction of soil texture and water holding capacity. Water Resour. Res. 2008, 44, W00D18. [Google Scholar] [CrossRef]
- Saito, H.; Kitahara, M. Analysis of changes in soil water content under subsurface drip irrigation using ground penetrating radar. J. Arid Land Stud. 2012, 22, 283–286. [Google Scholar]
- Satriani, A.; Loperte, A.; Soldovieri, F. Integrated geophysical techniques for sustainable management of water resource. A case study of local dry bean versus commercial common bean cultivars. Agric. Water Manag. 2015, 162, 57–66. [Google Scholar] [CrossRef]
- Consoli, S.; Stagno, F.; Vanella, D.; Boaga, J.; Cassiani, G.; Roccuzzo, G. Partial root-zone drying irrigation in orange orchards: Effects on water use and crop production characteristics. Eur. J. Agron. 2017, 82, 190–202. [Google Scholar] [CrossRef]
- Puy, A.; García Avilés, J.M.; Balbo, A.L.; Keller, M.; Riedesel, S.; Blum, D.; Bubenzer, O. Drip irrigation uptake in traditional irrigated fields: The edaphological impact. J. Environ. Manag. 2017, 202, 550–561. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.D.; Bilich, A.L.; Braun, J.J.; Zavorotny, V.U. Use of gps receivers as a soil moisture network for water cycle studies. Geophys. Res. Lett. 2008, 35, L24405. [Google Scholar] [CrossRef]
- Gil-Rodríguez, M.; Rodríguez-Sinobas, L.; Benítez-Buelga, J.; Sánchez-Calvo, R. Application of active heat pulse method with fiber optic temperature sensing for estimation of wetting bulbs and water distribution in drip emitters. Agric. Water Manag. 2013, 120, 72–78. [Google Scholar] [CrossRef]
- Sayde, C.; Gregory, C.; Gil-Rodriguez, M.; Tufillaro, N.; Tyler, S.; van de Giesen, N.; English, M.; Cuenca, R.; Selker, J.S. Feasibility of soil moisture monitoring with heated fiber optics. Water Resour. Res. 2010, 46, W06201. [Google Scholar] [CrossRef]
- Ciocca, F.; Lunati, I.; Van de Giesen, N.; Parlange, M.B. Heated optical fiber for distributed soil-moisture measurements: A lysimeter experiment. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Sayde, C.; Benitez Buelga, J.; Rodriguez-Sinobas, L.; El Khoury, L.; English, M.; van de Giesen, N.; Selker, J.S. Mapping variability of soil water content and flux across 1–1000 m scales using the actively heated fiber optic method. Water Resour. Res. 2014, 50, 7302–7317. [Google Scholar] [CrossRef]
- Striegl, A.M.; Loheide, I.; Steven, P. Heated distributed temperature sensing for field scale soil moisture monitoring. Groundwater 2012, 50, 340–347. [Google Scholar] [CrossRef] [PubMed]
- Vidana Gamage, D.N.; Biswas, A.; Strachan, I.B. Active heat pulse method with fiber optic temperature sensing to monitor three dimensional wetting patterns under drip irrigation. In Canadian Soil Science Society Annual Meeting; Canadian Society of Soil Science Trent University: Peterborough, ON, Canada, 2017; p. 102. [Google Scholar]
- Vidana Gamage, D.N.; Biswas, A.; Strachan, I.B. Actively heated fiber optics method to monitor three-dimensional wetting patterns under drip irrigation. Agric. Water Manag. 2018, 210, 243–251. [Google Scholar] [CrossRef]
- Vidana Gamage, D.; Biswas, A.; Strachan, I.; Adamchuk, V. Soil water measurement using actively heated fiber optics at field scale. Sensors 2018, 18, 1116. [Google Scholar] [CrossRef] [PubMed]
- Laio, F.; Porporato, A.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress: Ii. Probabilistic soil moisture dynamics. Adv. Water Resour. 2001, 24, 707–723. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Moreno, H.A.; Mascaro, G.; Rodriguez, J.C.; Watts, C.J.; Garatuza-Payan, J.; Scott, R.L. Observed relation between evapotranspiration and soil moisture in the north american monsoon region. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Detto, M.; Montaldo, N.; Albertson, J.D.; Mancini, M.; Katul, G. Soil moisture and vegetation controls on evapotranspiration in a heterogeneous mediterranean ecosystem on Sardinia, Italy. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Watts, C.J.; Rodríguez, J.C.; Garatuza-Payan, J.; Méndez-Barroso, L.A.; Saiz-Hernández, J.A. Improved land–atmosphere relations through distributed footprint sampling in a subtropical scrubland during the north american monsoon. J. Arid Environ. 2010, 74, 579–584. [Google Scholar] [CrossRef]
- Alfieri, J.G.; Blanken, P.D. How representative is a point? The spatial variability of surface energy fluxes across short distances in a sand-sagebrush ecosystem. J. Arid Environ. 2012, 87, 42–49. [Google Scholar] [CrossRef]
- Lajoie, P.G.; Stobbe, P.C. Soils Study of Soulanges and Vaudreuil Counties in the Province of Quebec; Edmond Cloutier: Ottawa, ON, Canada, 1951; p. 73. [Google Scholar]
- Kaluli, J.W.; Madramootoo, C.A.; Zhou, X.; MacKenzie, A.F.; Smith, D.L. Subirrigation systems to minimize nitrate leaching. J. Irrig. Drain. Eng. 1999, 125, 52–58. [Google Scholar] [CrossRef]
- Winter, T.C. Uncertainties in estimating the water balance of lakes1. J. Am. Water Resour. Assoc. 1981, 17, 82–115. [Google Scholar] [CrossRef]
- Adam, J.C.; Lettenmaier, D.P. Adjustment of global gridded precipitation for systematic bias. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Nešpor, V.; Sevruk, B. Estimation of wind-induced error of rainfall gauge measurements using a numerical simulation. J. Atmos. Ocean. Technol. 1999, 16, 450–464. [Google Scholar] [CrossRef]
- Horst, T.; Weil, J. Footprint estimation for scalar flux measurements in the atmospheric surface layer. Bound.-Lay. Meteorol. 1992, 59, 279–296. [Google Scholar] [CrossRef]
- Baldocchi, D.; Finnigan, J.; Wilson, K.; Falge, E. On measuring net ecosystem carbon exchange over tall vegetation on complex terrain. Bound.-Lay. Meteorol. 2000, 96, 257–291. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Rudnicki, J.W.; Rodell, M. Variability in surface moisture content along a hillslope transect: Rattlesnake hill, texas. J. Hydrol. 1998, 210, 259–281. [Google Scholar] [CrossRef]
- Pan, F.; Peters-Lidard, C.D. On the relationship between mean and variance of soil moisture fields. J. Am. Water Resour. Assoc. 2008, 44, 235–242. [Google Scholar] [CrossRef]
- Vereecken, H.; Kamai, T.; Harter, T.; Kasteel, R.; Hopmans, J.; Vanderborght, J. Explaining soil moisture variability as a function of mean soil moisture: A stochastic unsaturated flow perspective. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Cornelissen, T.; Diekkrüger, B.; Bogena, H.R. Significance of scale and lower boundary condition in the 3d simulation of hydrological processes and soil moisture variability in a forested headwater catchment. J. Hydrol. 2014, 516, 140–153. [Google Scholar] [CrossRef]
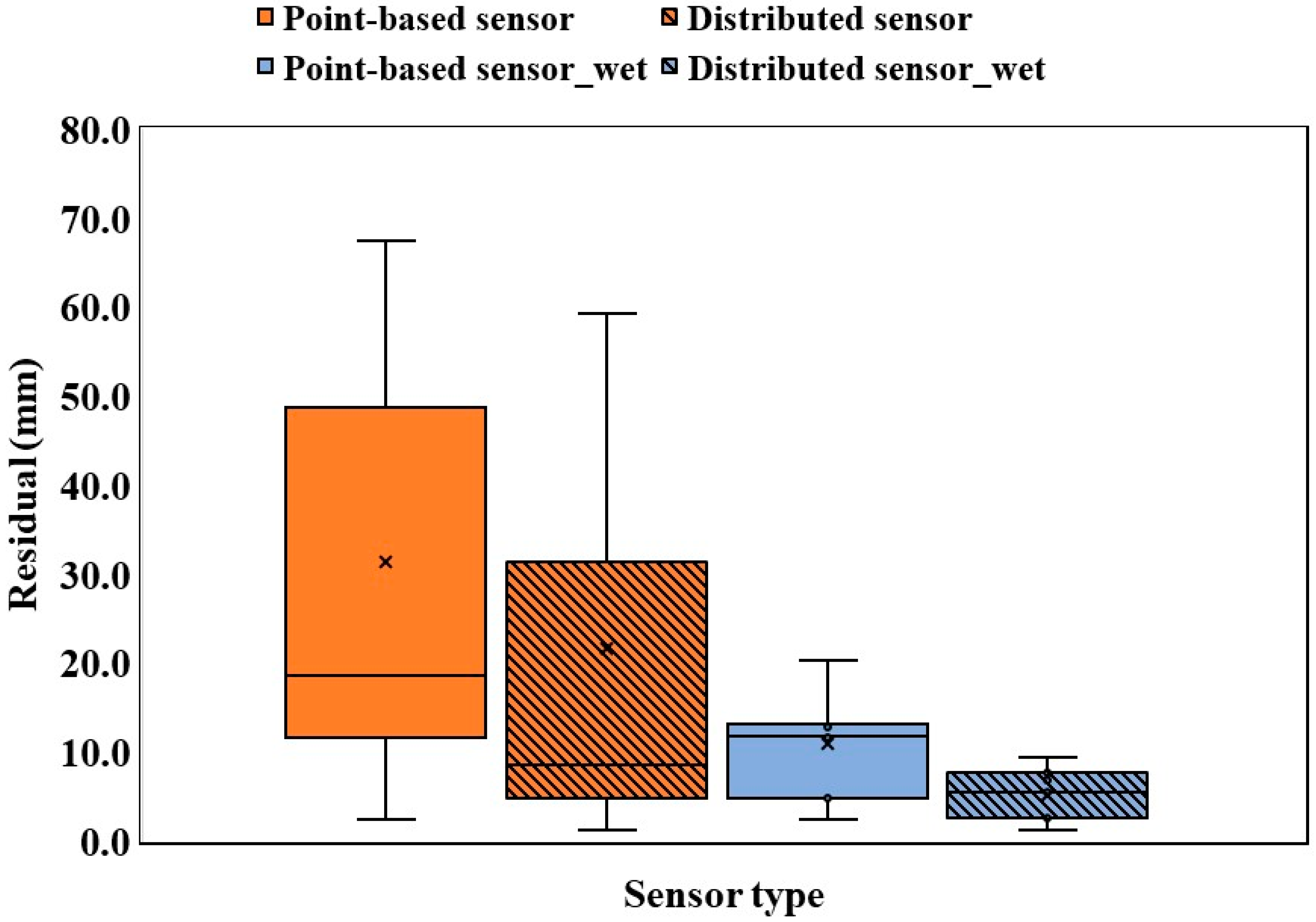
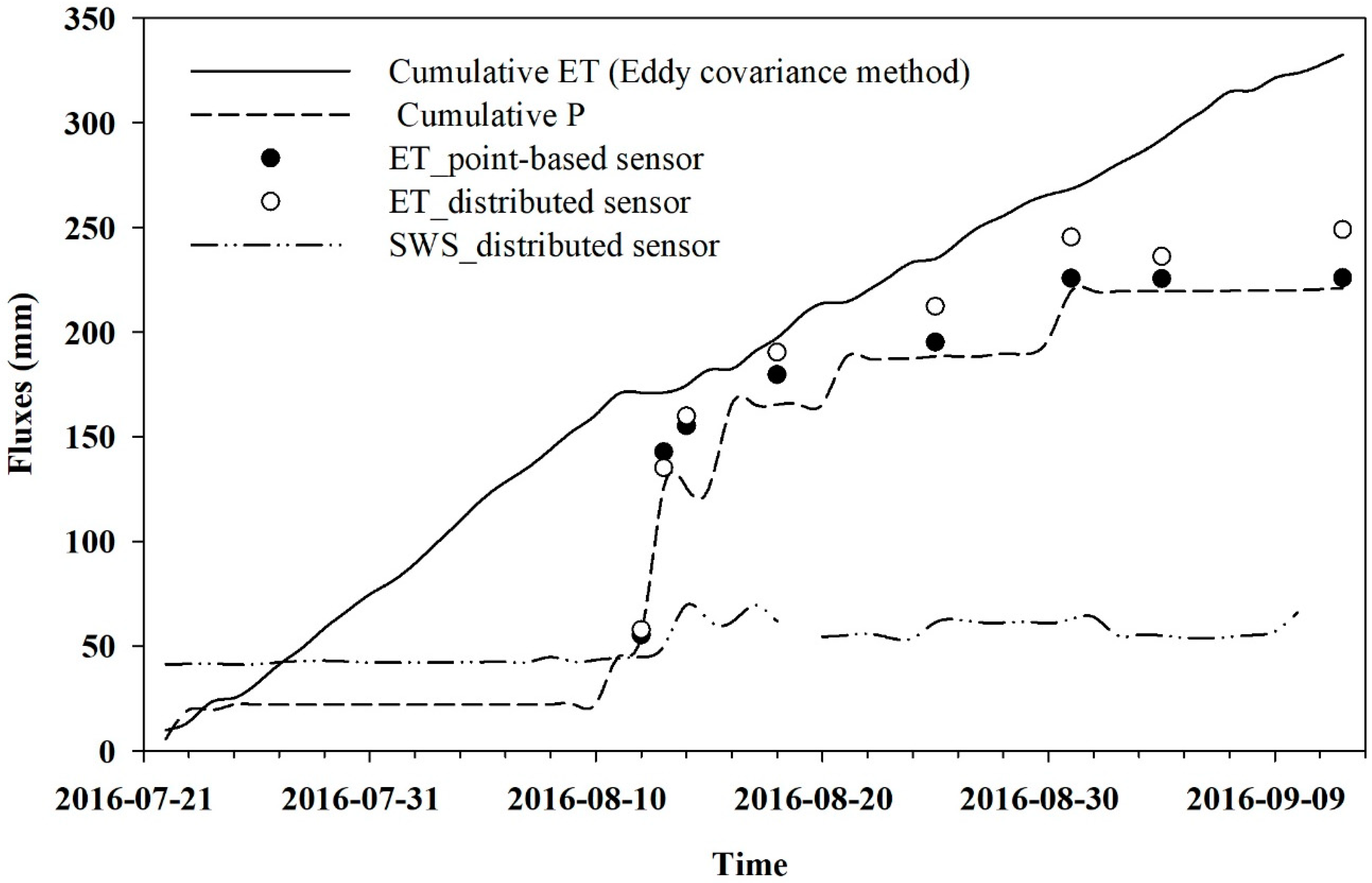
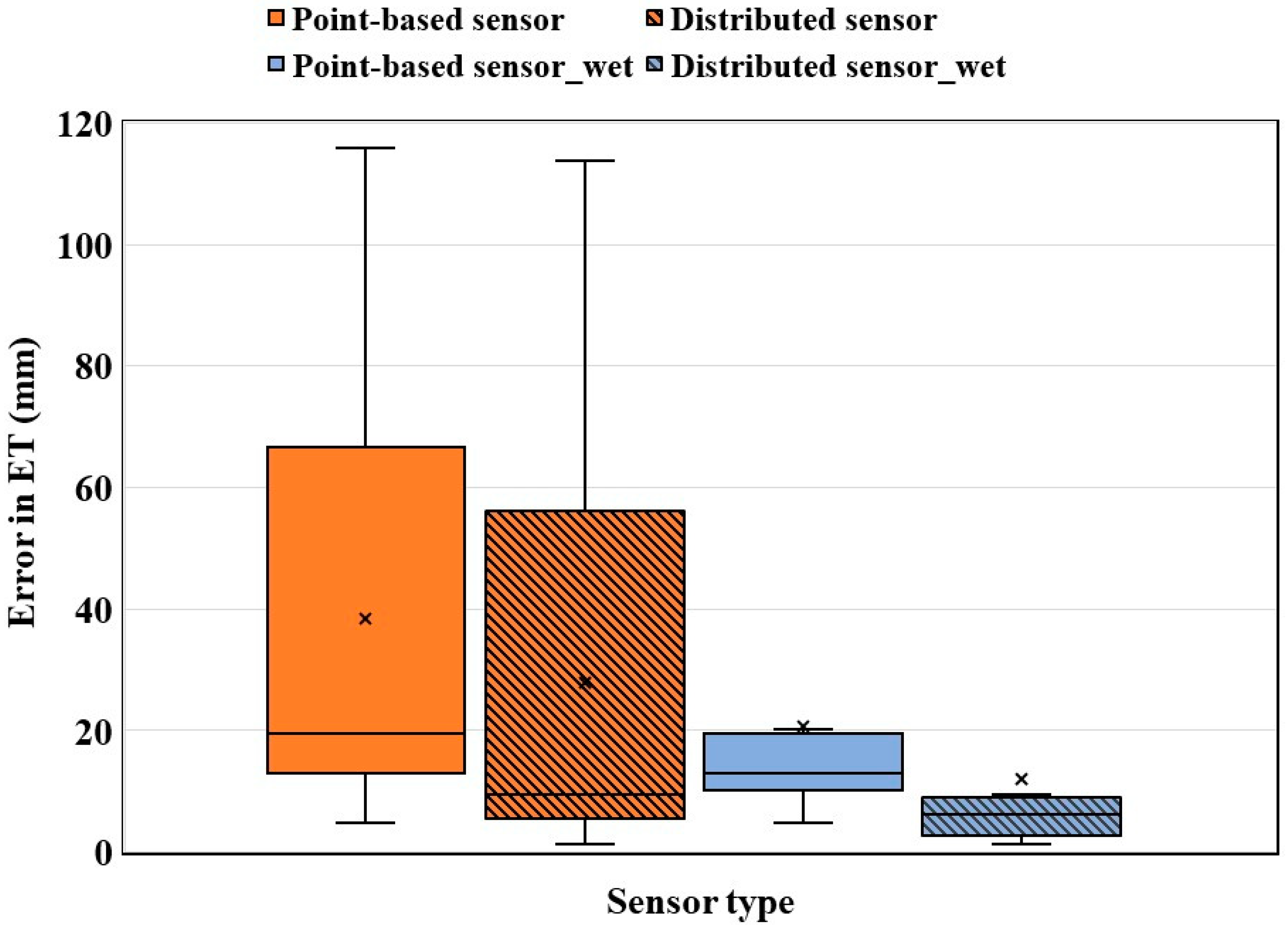
| Period (2016) | Observations (mm) | Residual (mm) | RRE (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| P | ET | D | ΔSWS | Re = P − ET − D − ΔSWS | |||||
| WB | 5TE | AHFO | 5TE | AHFO | |||||
| 22 July–14 August | 125.8 | 174.6 | 4.3 | −53.1 | −33.7 | −38.4 | −19.4 | −14.7 | 8.8 |
| 22 July–18 August | 165.4 | 197.2 | 4.4 | −36.2 | −18.6 | −29.3 | −17.5 | −6.9 | 29.4 |
| 22 July–25 August | 188.4 | 235.0 | 4.4 | −51.0 | −11.2 | −28.2 | −39.8 | −22.8 | 33.4 |
| 22 July–31 August | 219.5 | 268.4 | 4.4 | −53.3 | −10.6 | −30.2 | −42.7 | −23.1 | 36.8 |
| 22 July–4 September | 219.5 | 292.0 | 4.4 | −76.9 | −10.3 | −20.9 | −66.6 | −56.0 | 13.7 |
| 22 July–12 September | 219.5 | 332.4 | 4.4 | −117.3 | −9.2 | −32.3 | −108.1 | −85.0 | 19.7 |
| 23 August–25 August | 1.0 | 15.2 | 0.0 | −14.2 | −2.7 | −8.7 | −11.5 | −5.5 | 42.2 |
| 1 September–3 September | 0.0 | 17.0 | 0.0 | −17.0 | −3.9 | −10.3 | −13.1 | −6.7 | 37.7 |
| 24 August–1 September | 32.1 | 46.9 | 0.0 | −14.8 | −3.1 | −12.2 | −11.7 | −2.5 | 62.0 |
| 20 August–12 September | 54.1 | 125.3 | 0.0 | −71.2 | −3.7 | −12.1 | −67.5 | −59.1 | 11.7 |
| 9 August–11 August | 23.0 | 26.5 | 0.0 | −3.5 | −1.1 | −2.3 | −2.4 | −1.2 | 34.0 |
| 20 August–31 August | 54.1 | 61.3 | 0.0 | −7.2 | −2.4 | −9.9 | −4.8 | 2.7 | 28.5 |
| 25 August–2 September | 32.1 | 46.4 | 0.0 | −14.3 | −1.5 | −6.8 | −12.8 | −7.6 | 36.5 |
| Period (2016) | Observations (mm) | Estimations (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| P | ET | D | ΔSWS | ET* = P − D − ΔSWS | ETε = ET − ET* | ||||
| 5TE | AHFO | 5TE | AHFO | 5TE | AHFO | ||||
| 22 July–12 August | 54.8 | 171.0 | 2.1 | −2.7 | −5.7 | 55.4 | 57.8 | 115.6 | 113.2 |
| 22 July–14 August | 125.8 | 174.6 | 4.3 | −33.7 | −38.4 | 155.2 | 159.9 | 19.4 | 14.7 |
| 22 July–18 August | 165.4 | 197.2 | 4.4 | −18.6 | −29.3 | 179.7 | 190.3 | 17.5 | 6.9 |
| 22 July–25 August | 188.4 | 235.0 | 4.4 | −11.2 | −28.2 | 195.2 | 212.2 | 39.8 | 22.8 |
| 22 July–31 August | 219.5 | 268.4 | 4.4 | −10.6 | −30.2 | 225.7 | 245.3 | 42.7 | 23.1 |
| 22 July–4 September | 219.5 | 292.0 | 4.4 | −10.3 | −20.9 | 225.4 | 236.0 | 66.6 | 56.0 |
| 22 July–12 September | 219.5 | 332.4 | 4.4 | −9.2 | −32.3 | 224.3 | 247.4 | 108.1 | 85.0 |
| 9 August–11 August | 23.0 | 26.5 | 0.0 | 1.1 | −2.3 | 21.9 | 25.3 | 4.6 | 1.2 |
| 23 August–25 August | 1.0 | 15.2 | 0.0 | 2.7 | −8.7 | −1.7 | 9.7 | 16.9 | 5.5 |
| 24 August–1 September | 32.1 | 46.9 | 0.0 | −3.1 | −12.2 | 35.2 | 44.3 | 11.7 | 2.5 |
| 20 August–12 September | 54.1 | 125.3 | 0.0 | 3.7 | −12.1 | 50.4 | 66.2 | 74.9 | 59.1 |
| 20 August–31 August | 54.1 | 61.3 | 0.0 | 2.4 | −9.9 | 51.7 | 64.0 | 9.6 | −2.7 |
| 25 August–2 September | 32.1 | 46.4 | 0.0 | −1.5 | −6.8 | 33.6 | 38.9 | 12.8 | 7.6 |
| 1 September–3 September | 0.0 | 17.0 | 0.0 | −3.9 | −10.3 | 3.9 | 10.3 | 13.1 | 6.7 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vidana Gamage, D.N.; Biswas, A.; Strachan, I.B. Field Water Balance Closure with Actively Heated Fiber-Optics and Point-Based Soil Water Sensors. Water 2019, 11, 135. https://doi.org/10.3390/w11010135
Vidana Gamage DN, Biswas A, Strachan IB. Field Water Balance Closure with Actively Heated Fiber-Optics and Point-Based Soil Water Sensors. Water. 2019; 11(1):135. https://doi.org/10.3390/w11010135
Chicago/Turabian StyleVidana Gamage, Duminda N., Asim Biswas, and Ian B. Strachan. 2019. "Field Water Balance Closure with Actively Heated Fiber-Optics and Point-Based Soil Water Sensors" Water 11, no. 1: 135. https://doi.org/10.3390/w11010135
APA StyleVidana Gamage, D. N., Biswas, A., & Strachan, I. B. (2019). Field Water Balance Closure with Actively Heated Fiber-Optics and Point-Based Soil Water Sensors. Water, 11(1), 135. https://doi.org/10.3390/w11010135






