1. Introduction
A variety of agricultural pollutants resulting from farming and ranching operations (e.g., sediment, nutrients, pathogens, pesticides, metals, and salts) can lead to impairments of local and far-field water quality. These diffuse nonpoint sources can directly harm ecosystem and watershed water quality, and adversely affect our drinking water supply. Agricultural runoff, generated by rainfall or irrigation events, can transfer pollutants accumulated at the land surface into receiving water bodies. This process has been identified as one of the major causes of water impairment in agricultural settings [
1,
2,
3]. The amount of pollutants transported to surface runoff water is dependent on local soil and crop management, climatic conditions, contaminant properties and environmental factors. The discharge of pollutants from agricultural activities to surface waters can be minimized by locally implementing Best Management Practices (BMPs). However, obtaining monitoring data using field investigations is very time consuming and expensive, and associated with many experimental difficulties. Furthermore, simple field observations may be difficult to interpret to obtain a complete picture of potential contaminant transport routes and mechanisms, and to extrapolate findings to other environmental conditions and climates.
Alternatively, physically-based and data-driven models are potential tools for examining and optimizing the effects of land-use changes and BMPs on surface water quality [
4,
5,
6,
7]. Indeed, numerical experiments can be cheaply conducted using a physically-based model (PBM) to predict runoff water quality over a wide range of agricultural fields, weather patterns, and BMPs. PBMs explicitly account for main hydrologic and contaminant transport processes using mathematical descriptions. Complex numerical or analytical techniques are commonly used to solve these mathematical descriptions, which may require significant computational time as the spatial and temporal scale of the considered problem increases.
In contrast to PBMs, data-driven models are based on functional relationships between input and output variables. Artificial intelligence approaches, such as Machine Learning (ML) techniques, are increasingly being used in data-driven models to quantify input-output functional relations for complex systems in hydrology [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19]. Several ML algorithms for modeling rainfall-runoff processes include Linear Regression (LR), K-Nearest Neighbor Regression (kNN), Feed-forward Neural Networks (NN), and Support Vector Machine (SVM) models [
20,
21,
22,
23,
24,
25]. The NN technique consists of a neural network with a single or multiple hidden layer (Deep Neural Network) to describe complex, nonlinear structures in data. NN with multiple hidden layers have been successfully applied in many commercial products that are already available to the public, such as computer vision and speech recognition, language translation, and self-driving cars [
26,
27,
28]. While there are some studies investigating the applicability of NN with multiple hidden layers in hydrology/contaminant transport problems (e.g., [
19,
29,
30,
31,
32]), only limited experience exists with using ML algorithms in environmental applications involving surface runoff water quantity and quality. It is thus important to investigate the strengths and limitations of data-driven models and compare their predictions with robust PBMs.
As discussed above, while PBMs are powerful tools for simulating spatial and temporal distributions of various physical and chemical environmental variables, they require large amounts of data and computational resources. On the other hand, machine learning algorithms trained using PBMs, or the so-called “metamodels” [
33,
34], make predictions almost instantly. The overall objective of this research thus was to investigate the limitations and strengths of ML-based metamodels in comparison with the HYDRUS overland flow module [
35] in predicting contaminant loads in runoff water from agricultural fields. We synthetically generated an extensive database using the HYDRUS overland flow module that uses standard descriptions of overland flow and transport processes that have been extensively verified to properly represent real field processes (e.g., [
35,
36,
37,
38,
39]). This numerically generated database was used to generate metamodels that contained information about the impact of a wide range of physical factors on surface runoff quantity and quality in agricultural fields. Inputs included information about the agricultural field (slope, length, and area), the soils (type, roughness, initial water content, and initial contaminant concentration), and precipitation events (rainfall intensity and duration). Outputs included the cumulative water volume and the contaminant mass in runoff water. This database was then used in conjunction with ML techniques to develop correlation relationships between model inputs and outputs using various ML algorithms.
2. Database Preparation
2.1. Physically-Based Model
The one-dimensional diffusion-wave and advection-dispersion equations, which are commonly used for describing overland flow and solute transport, respectively, have recently been implemented into the popular HYDRUS-1D code [
35]. This code has previously been used to numerically solve the Richards equation, which simulates water flow, and the convection-dispersion equation, which simulates contaminant transport in the subsurface [
40]. Recent studies indicated that the governing overland flow equation can be written in a similar mathematical formulation as the Richards equation [
35,
41,
42,
43] so that existing numerical schemes of HYDRUS-1D can be used to solve the following 1D-diffusion wave equation:
where
x is a space coordinate in direction of flow (L; where L denotes units of length),
zb is a vertical coordinate of the soil surface,
t is time (T; where T denotes units of time),
h is the surface water depth (L),
R is rainfall or the irrigation rate (LT
−1), and
I is the infiltration rate (LT
−1),
S is the mean local slope (defined as d
zb/d
x) (-), and
k is a unit conversion factor (L
1/3T
−1). The parameter
nman is a Manning’s roughness coefficient for overland flow, and it is dimensionless when
k = 1 m
1/3s
−1 or has units of TL
−1/3 when
k is not equal to unity. See the graphical abstract for a schematic of some of these variables.
In this work, the infiltration rate
I is described using the Green-Ampt infiltration model [
44]. This model is a simplified physically-based approach that is based on fundamental physics to describe the infiltration process as a function of the soil suction head, water content, and soil hydraulic conductivity:
where
ψ is the wetting front soil suction head (L), ∆
θ is the water content difference (L
3L
−3),
KS is the saturated hydraulic conductivity (LT
−1), and
F is the cumulative depth of infiltration (L). The value of ∆
θ is defined by using the following equations:
where
Se is the effective saturation (-),
θe is the effective water content (L
3L
−3),
n is the porosity (L
3L
−3),
θi is the initial water content (L
3L
−3), and
θr is the residual water content (L
3L
−3).
Solute transport in overland flow is usually described using the advection-dispersion equation (ADE) of the form:
where
c is the solute concentration in the aqueous phase (ML
−3; where M denotes units of mass),
cr is the concentration in rainfall water (ML
−3);
s is the sorbed solute concentration at the soil surface area (ML
−2),
D is the effective dispersion coefficient accounting for both molecular diffusion and hydrodynamic dispersion (L
2T
−1),
ϕ is a sink/source term that accounts for various zero- and first-order or other reactions (ML
−3T
−1), and
Q is the runoff flow rate (L
2T
−1). The parameter
Q is given as:
where
is a depth-averaged velocity (LT
−1) calculated using the Manning–Strickler uniform flow formula [
41]. The effect of diffusion on the dispersion coefficient can often be ignored and in this case the value of
D can be defined as the product of the dispersivity (
λ, (L)) and
. Kinetic sorption/desorption between the solid and aqueous phases can be described using the following equation:
where
KD is the linear equilibrium partition coefficient (L) and
ω is the first-order desorption rate coefficient (T
−1). The product of
KD and
ω is proportional to the sorption rate coefficient. Details about the numerical solutions of flow and transport models are provided in the HYDRUS-1D manual [
45].
2.2. Numerical Simulations
A large number of numerical simulations was carried out to develop a database containing information about the impact of various relevant factors on surface runoff quantity and quality. In agricultural settings, land surface contaminants can be easily picked up and transported by surface runoff or can seep into the soil by infiltration. Therefore, simulation scenarios considered in this work mainly focused on the transport of various contaminants in overland flow over different soil and land surfaces under different rainfall rates.
At first, numerous water flow simulations were run with various input parameters shown in
Table 1. In order to build a realistic training database, a wide range of input parameter values was selected. In these simulations, precipitation was distributed uniformly over the land surface and lasted one hour. Historical records of precipitation frequency for the San Jacinto, CA watershed (
http://hdsc.nws.noaa.gov/hdsc/pfds) were employed to generate precipitation-frequency estimates that were employed in simulations. Seven different percent probabilities of exceedance were selected: 1%, 2%, 4%, 10%, 20%, 50%, and 100%. Various agricultural field conditions were obtained by assigning different values of the Manning’s roughness coefficient, slope, and length. As a result, 150 different field conditions (6 Manning’s roughness coefficients × 5 slopes × 5 lengths) were considered. Additionally, four different initial water contents were considered: max(
θr, 0.1), 0.2, 0.3, and the saturated water content (
θs), for each soil type. Selected Green-Ampt infiltration parameters (soil porosity, residual water content, suction head, and hydraulic conductivity) were taken from Rawls et al. [
46] (
Table 2). In all water flow simulations, cumulative water volumes at the bottom outlet at 25 evenly spaced times were outputs. The resulting water flow database thus contained 2,310,000 entries (22 soils × 7 rainfall rates × 150 field conditions × 4 initial water contents × 25 print times).
Solute transport simulations were subsequently conducted for the previously described water flow simulations. In these simulations, it was assumed that a unit concentration (
ci = 1 g/cm
2) of solute was initially distributed along the soil profile. Since the solute transport equation is a linear equation, the results obtained for a unit initial solute concentrations can be simply multiplied by other initial concentrations to get corresponding results. Runoff water generated by rainfall events “mobilized” solutes from the land surface and transported them to the bottom outlet of the field. The “mobilization” process was described using different sorption and desorption rates. The exchange of solute concentrations between solid and liquid phases is controlled by the overland water flow rate and kinetic sorption/desorption parameters (
ω and
KD) in Equation (8). The kinetic sorption model approaches equilibrium conditions when
ω is large, whereas non-equilibrium conditions prevail when
ω is small and solute release is slow. In this study, the database considered transport processes and solute desorption for near-equilibrium conditions (
ω = 8640 day
−1) to mitigate the complexity of these transport processes. Hence, two additional input parameters, variable
KD shown in
Table 1 and constant
ω = 8640 day
−1, were accounted for in these simulations. Solute transport simulations generated the output that included the cumulative solute mass at the bottom outlet at 25 evenly spaced times. The inclusion of two additional parameters to describe transport of mobilized solutes (
KD and
ω) resulted in a database that was five times bigger than the water flow database. Furthermore, the variance in the solute transport database was higher than the water flow database.
3. Data-Driven Models
In this section, we briefly describe the data-driven models used in this paper. They are divided into two broad classes, linear and nonlinear models. The selected linear data-driven models include Linear Regression (LR) and Linear Support Vector Machine (SVM-L). Nonlinear models include K-Nearest Neighbor Regression (kNN), Support Vector Machines with nonlinear kernel (SVM-NL), and Deep Neural Networks (DNN) with different numbers of hidden layers. We used the previously generated synthetic databases from the PBM to train the selected data-driven models to predict surface runoff water quantity and quality. All these models were implemented using the open-source Scikit-learn and Keras Libraries in Python 3.5 (Python Software Foundation, Wilmington, DE, USA) [
47,
48].
3.1. Linear Regression
LR is the simplest ML model, which is often treated as the baseline method. It applies linear mapping to minimize the sum of least square errors between input data (either experimental or derived from a PBM model) and output data (of the regression model). Suppose we have a set of training data set (
yi, xij), where
i =1, 2, 3, …,
N and
j =1, 2, 3, …,
k. In here,
i is the index for training samples in the data set,
j is the index for the input parameters. A general linear regression problem can be developed by assuming that output variables
yi are influenced by input parameters
xij as:
where
βj are regression coefficients,
β0 is intercept, and
ei represent a deviation between actual and predicted values. The ordinary least squares procedure seeks to minimize the total sum of the residuals. However, since this approach treats data as a matrix, the process will be very computational intensive when we have large data sets. Therefore, gradient-based optimization approaches, which optimize the values of the coefficients by iteratively minimizing the sum of the squared errors for each pair of input and output values are used here [
49].
3.2. Support Vector Machine
The SVM is another widely used model for both classification and regression tasks. The SVM model was originally developed for classification problems to find a hyperplane, which can separate a data set into one class from those of another class [
50,
51]. The SVM models have been successfully extended to solve regression problems by the introduction of the so-called
ε-insensitive loss function. This loss function is used to penalize errors that are greater than the threshold
ε (an insensitivity zone). A version of the SVM for regression problems is called support vector regression (SVR) and it depends on a subset of the training data. The
ε-SVR aims to find the flattest regression function
f(
xij) that has at most a deviation
ε from actual
yi for all training points
xij:
where
wj are weights and
bi is the bias term that should be estimated from the training data. One great benefit of using
ε-SVR is the use of kernels, which inherently map the data into a nonlinear space depending on the chosen kernel function. Therefore, the above regression can be formulated as [
52]:
where Φ(
xij) denotes nonlinear transformation (kernel functions). Several nonlinear kernel functions are available, such as polynomial, radial basis, and sigmoid functions. In this study, we tested both SVR with linear (SVM-L) and nonlinear (SVM-NL) sigmoid kernel functions.
The optimization of
ε-SVR is more complicated than the LR model because there is a linear constraint. In this case, the penalty factor
C and the slack variables
and
are introduced to cope with infeasible constraints [
51]. Hence,
wj and
bi are estimated by minimizing the following objective function:
subject to
where
. The penalty factor
C determines the trade-off between the flatness of the function
f(
xij) and the amount up to which deviations larger than
ε are tolerated. The slack variables
and
determine the degree to which data points will be penalized if the error is larger than
ε.
3.3. K-Nearest Neighbor Regression
K-Nearest Neighbor (kNN) Regression is another machine learning method for regression problems. The kNN is a non-parametric regression type of analysis. Predictions are made by computing the distance between all the data points in the database and searching for the number of neighbors (
Knn) which are most similar to a new instance. Once the nearest-neighbor list is obtained, the prediction of output
y is achieved by assigning weights to the contributions of the neighbors, so that the nearer neighbors contribute more to the average than the more distant ones. For example, the Euclidean distance
d between
lth training sample
xlj and
ith test sample
xij is defined as [
53]:
The weight
wd can be defined by a selected
Knn value and a distance between
lth and
ith samples:
Thus, the output
yi can be predicted by
3.4. Deep Feed-Forward Network
Neural networks (NN) are the most popular ML models used nowadays. The classical feed-forward network is a neural network that has been widely used in the hydrologic and water quality problems [
22,
23,
54,
55,
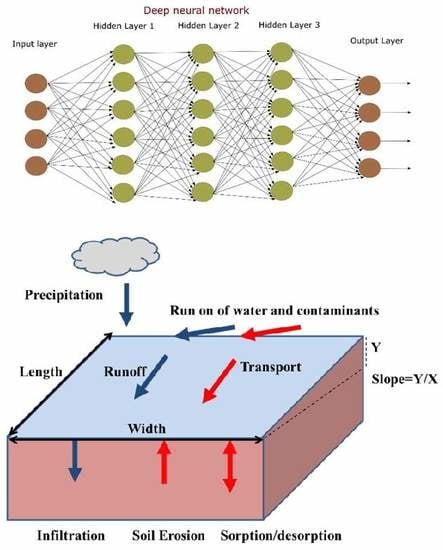
56]. The fundamental components of these algorithms include the input layer, intermediate layers, output layer, and neurons. Adjustable parameters characterize the neurons that are connected to the input and transmit the information from one neuron to another in one direction: from an input layer, through one or more hidden layers, to an output layer.
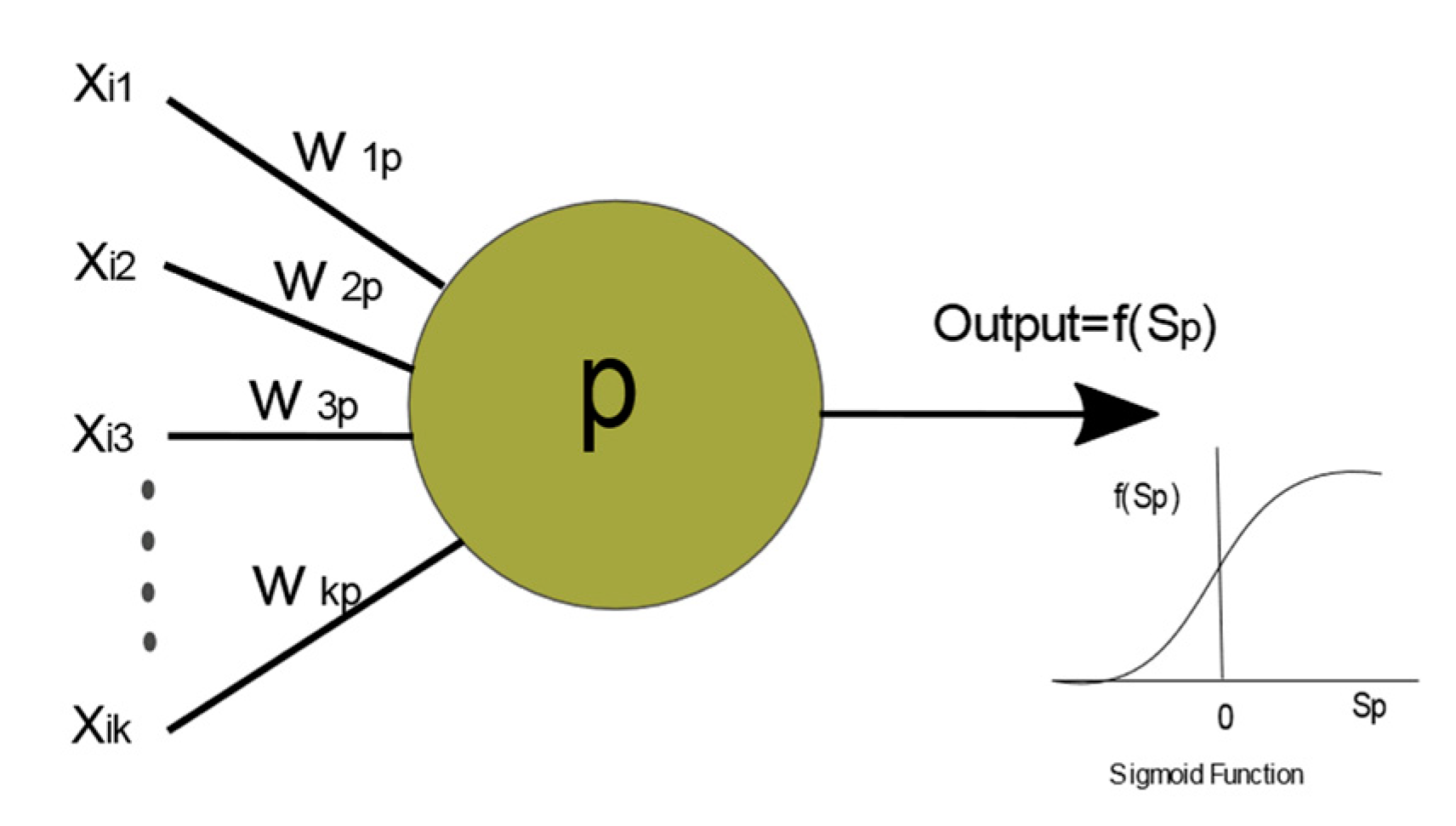
Figure 1 illustrates the adjustable parameters for an individual neuron. In a network, the input variables
xij are weighted and summed up to produce the hidden neurons
Sp (
p = 1, 2, …,
P):
where
p is the number of hidden neurons. A neuron computes an output, based on the weighted sum of all its inputs (
Sp), according to an activation function (
f(
Sp)). Finally, an activation function, which is applied to
Sp, provides the final output from this logistic sigmoid [
10] (see
Figure 1). The sigmoid activation function is given as:
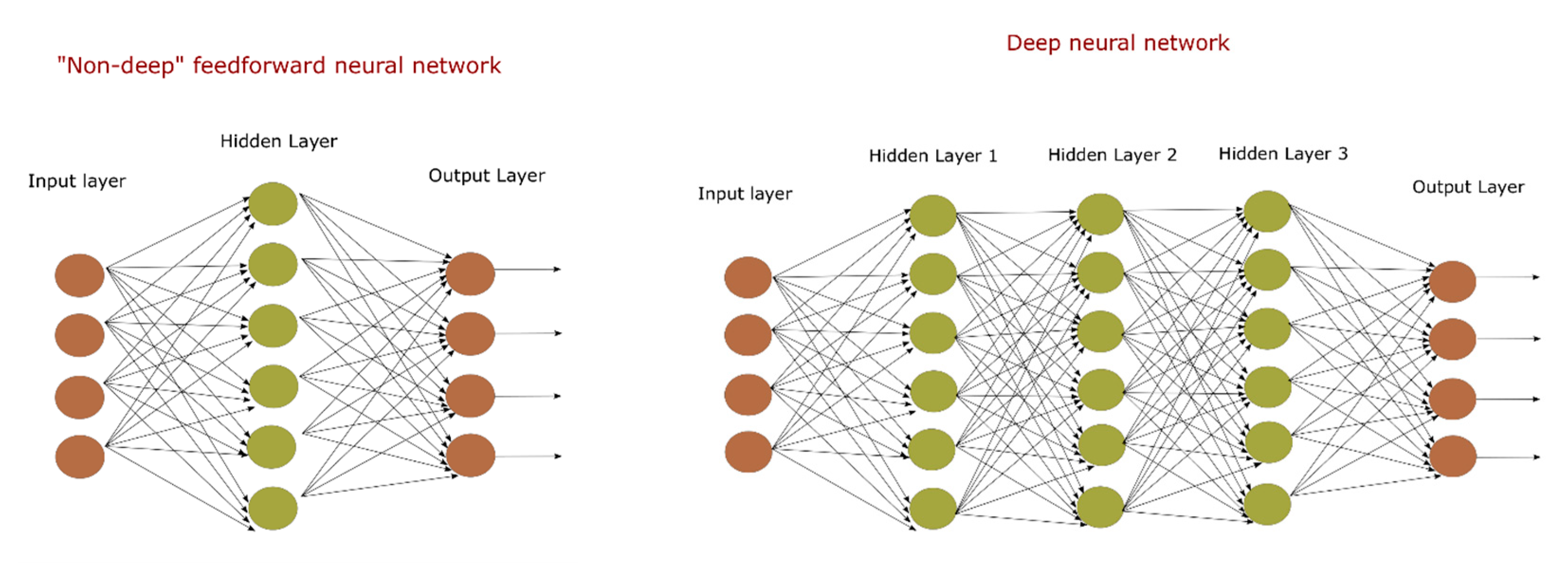
The so-called Deep Neural Networks (DNN) model is a direct extension of the feed-forward network that contains multiple hidden layers that are stacked as shown in
Figure 2 [
57]. The DNN model becomes “deeper” as the number of hidden layers increases. Deeper NN models allow for simulating more complicated, nonlinear mapping functions between input and output data. However, DNN models often suffer from overfitting when using too many hidden layers. This problem can be mitigated by dropping layers. We have tested the DNN model with one, two, and three hidden layers to determine the optimum number of hidden layers and to minimize overfitting.
4. Model Training and Evaluation
The runoff water database generated using the PBM was divided into training (80% of the entire database) and test (20% of the entire database) data sets for the data-driven models. Variable input parameters and output values were used to train the data-driven models by randomly selecting 18 out of 22 soil types. Each data-driven model was tuned using cross validation and further evaluated using the left-out test data set. After the training was completed, data-driven models were tested on the remaining four soil types over many different scenarios. The accuracy and predictive capability were first assessed by making scatter plots of cumulative runoff water volumes (Qc) for data-driven models and the PBM. The calculated R2 and the best-fitted regression line were shown in these scatter plots to quantify the goodness of the data-driven model prediction.
In addition, two examples were chosen to show the accuracy between observed and predicted cumulative runoff hydrographs between the PBM and data-driven models, respectively, over a range of initial water contents and soil types. The first example considered four different initial water contents and the following conditions: the rainfall rate of 69.6 cm/day for 1 h, the surface length of 240 m, a Silt Loam soil, the Manning’s roughness coefficient of 0.24 (dense grass), and a steep slope of 16%. The total simulation time was 1 h and 10 min so that the water recession process could be fully captured in these simulations. The second example considered surface runoff from Silt Loam, Clay, tilled Silt Clay, and tilled Clay soils under the following conditions: an initially saturated soil, the rainfall rate of 105.4 cm/day for 1 h, a surface length of 48 m, a slope of 16%, and the Manning’s roughness coefficient of 0.24.
Statistical measures were used to quantify the ability of various ML models to predict an output from the PBMs. Calculated statistical parameters included the root mean square error (RMSE), the mean absolute error (MAE), the mean bias error (MBE), the model efficiency (EF), and the
Relative Error . These statistical parameters were determined as:
where
Pi and
Oi are the output values predicted by data-driven models and observed data obtained from the PBM, respectively,
is the average of observed data, and
N is the number of observations. It should be noted that data with zero values of surface runoff were removed from this analysis for model inter-comparison.
A database for transport of mobilized solute with runoff water (e.g., the cumulative solute mass at the outlet) was developed using the PBM that encompassed a wide range in rainfall rates, soil physical properties, initial water contents, slopes, field size, Manning’s roughness coefficients, and kinetic sorption/desorption parameters. As we mentioned before, the solute transport database in this study considered transport processes and solute desorption for near-equilibrium conditions with a constant desorption rate coefficient (ω = 8640 day−1) and different KD values. The solute transport database had a similar structure as the water flow database but was five times bigger in size.
The contaminant transport is highly related to water flow. The data-driven model with the best performance in predicting the runoff water volume was therefore selected for training with the solute transport databases. Data-driven models were trained against 80% of the entire solute transport database using Qc, KD, and other input parameters associated with the water flow database. The remaining 20% of the solute transport database were employed for testing the model. Two simulation examples were chosen to further investigate the predictive ability of the trained data-driven models. These simulation scenarios considered the same input variables as for the water flow model (e.g., differences in initial water contents or soil texture) with KD = 2 cm and ω = 8640 day−1.
5. Results and Discussion
5.1. Surface Runoff Quantity
5.1.1. Linear Regression
A scatter plot of estimated
Qc using the LR model versus observed
Qc for the PBM test data set are shown in
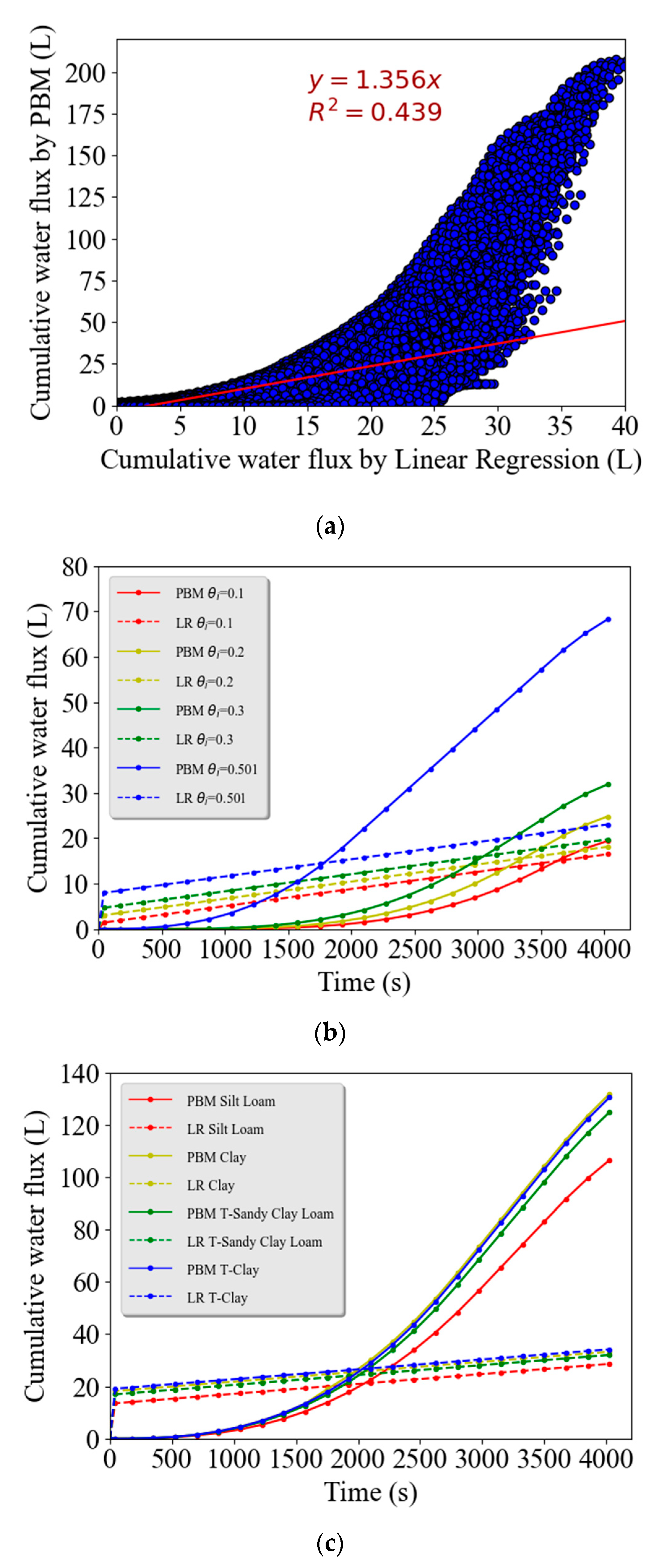
Figure 3a. We can see that
R2 is equal to 0.439, which indicates that the LR model failed to accurately describe the PBM data. The LR algorithm usually works well with high-bias and low variance data. However, the PBM describes real-world scenarios with complex, nonlinear relationships between input and output variables that generate high variance data sets.
The observed (PBM) runoff water volume in
Figure 3b decreased and was increasingly delayed when the initial soil water content was lower. The observed (PBM) simulations in
Figure 3c demonstrate that the Clay and tilled Clay textured soils produced the most runoff water because of their lower saturated hydraulic conductivity and infiltration. After rainfall stops, the cumulative runoff water flux continues to increase because water flows slowly over the rough surface before reaching the bottom boundary. The LR model failed to accurately describe runoff water dynamic for these two selected examples, especially when the initial water content was higher (
Figure 3b) and the hydraulic conductivity was lower (
Figure 3c). In particular, the LR model tended to overestimate
Qc for early times and underestimate
Qc for later times. Other authors (e.g., [
18]) similarly found that the linear regression model does not provide enough flexibility to represent complex nonlinear hydrological phenomena.
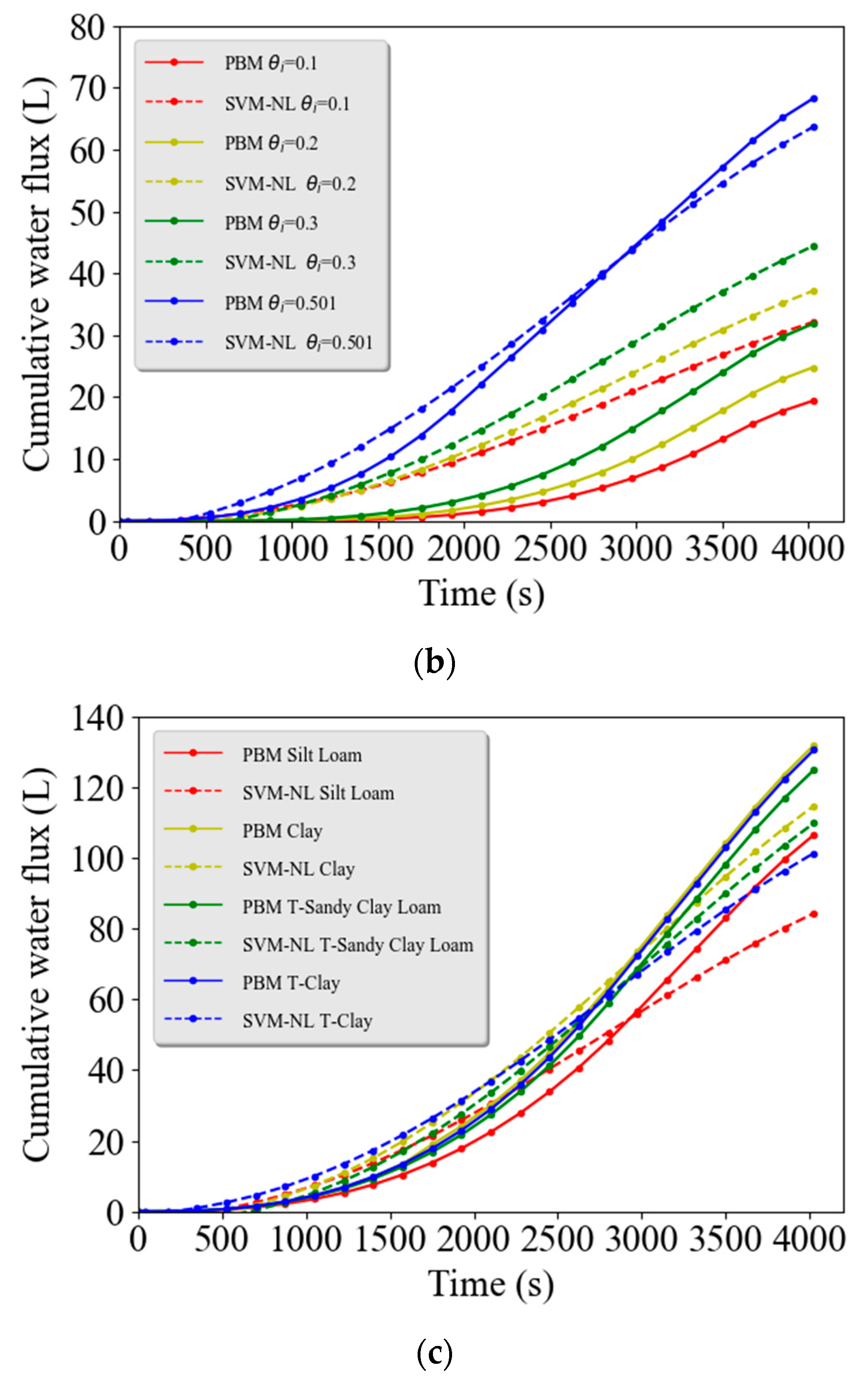
5.1.2. Support Vector Machine
Similar to the LR model, the Support Vector Machine model with linear kernel functions (SVM-L) produced a linear input-output relationship. Two user-defined parameters for the SVM-L model were the penalty parameter
C on the error term, which was set to 1, and the maximum number of iterations, which was 2000 [
58].
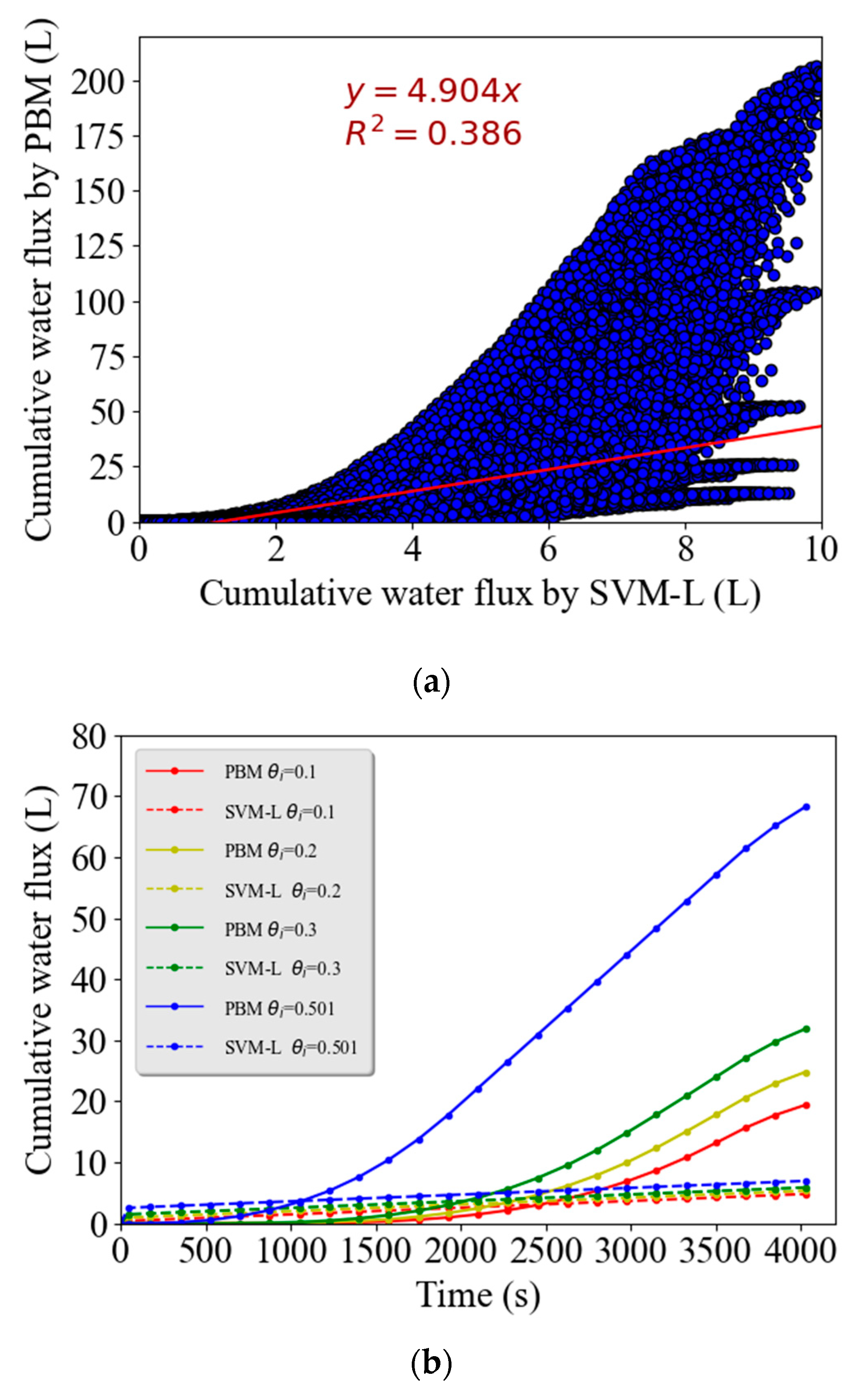
Figure 4a indicates that this SVM-L model had an even lower
R2 (
R2 = 0.386) than the LR model (
R2 = 0.439). Similarly, simulation examples shown in
Figure 4b (different initial water contents) and
4c (different textures) indicate that the SVM-L model completely failed to capture the large values of
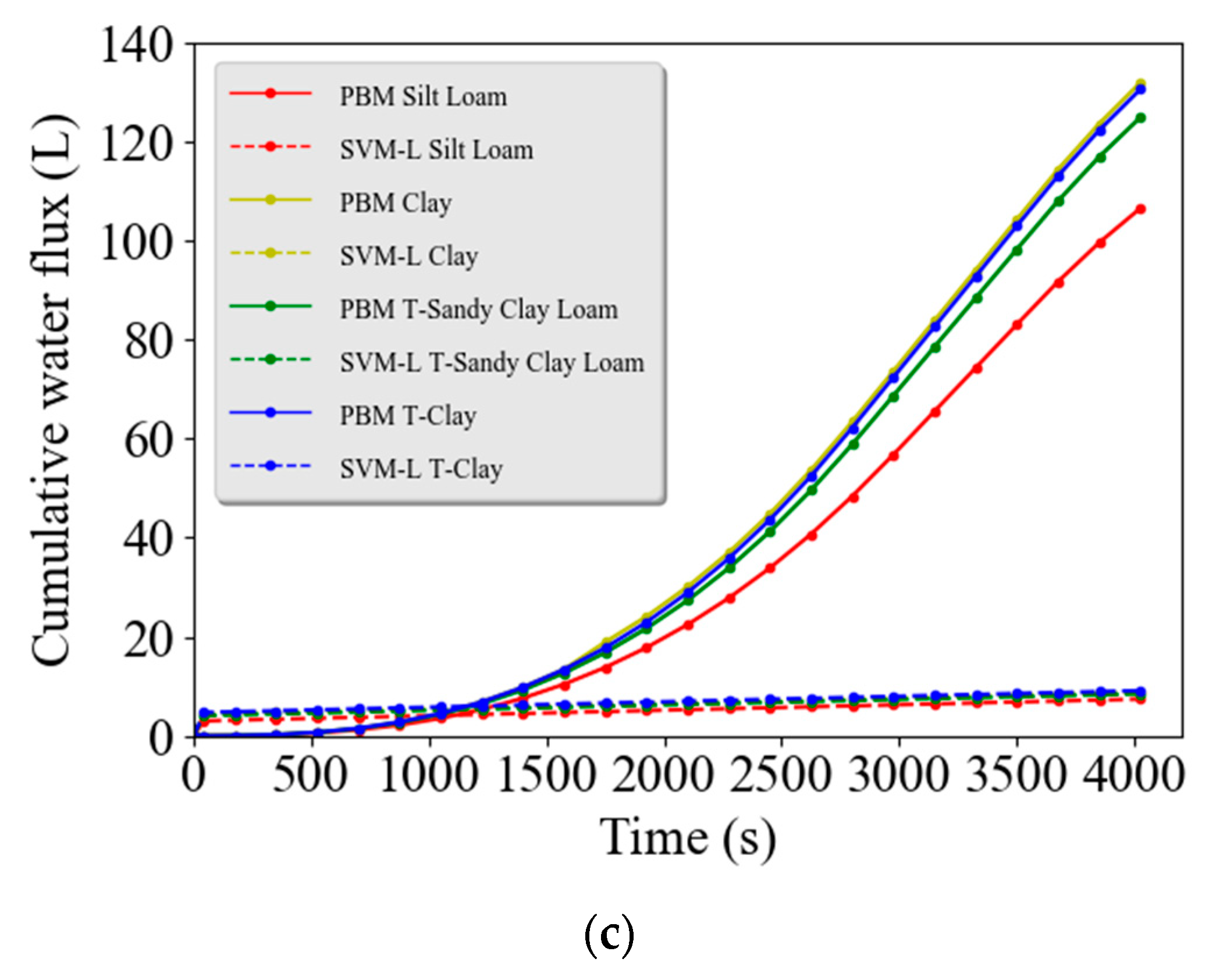
Qc at later times. Linear models (LR and SVM-L) are therefore not well suited to describe complex nonlinear runoff problems.
Many researchers have indicated that the SVM model with nonlinear kernels (SVM-NL) can successfully describe surface/subsurface hydrology problems [
18,
59,
60]. However, previous SVM-NL applications have considered only a relatively small training and test data set. Training the SVM-NL model takes a tremendous amount of computational time because of the complexity of this model. For example, we estimated that training the SVM-NL model to our complete runoff water database would take somewhere between a few days and a month. Consequently, only about 20% of the original runoff water training data set were randomly selected to train the SVM-NL model. The trained model was then used for testing against the test data set with
C = 1 and
ε = 0.2.
Figure 5a shows the scatter plot of estimated
Qc using the SVM-NL model versus observed
Qc from the test set. The
R2 (
R2 = 0.952) for the SVM-NL model was much higher than for the LR and SVM-L models. The SVM-NL model also provided a much-improved description of the PBM results for the two examples shown in
Figure 5b,c. However, there were still considerable deviations between the SVM-NL model and the PBM, especially for larger print times, higher initial water contents (
Figure 5b), and for the Silt Loam soil (
Figure 5c).
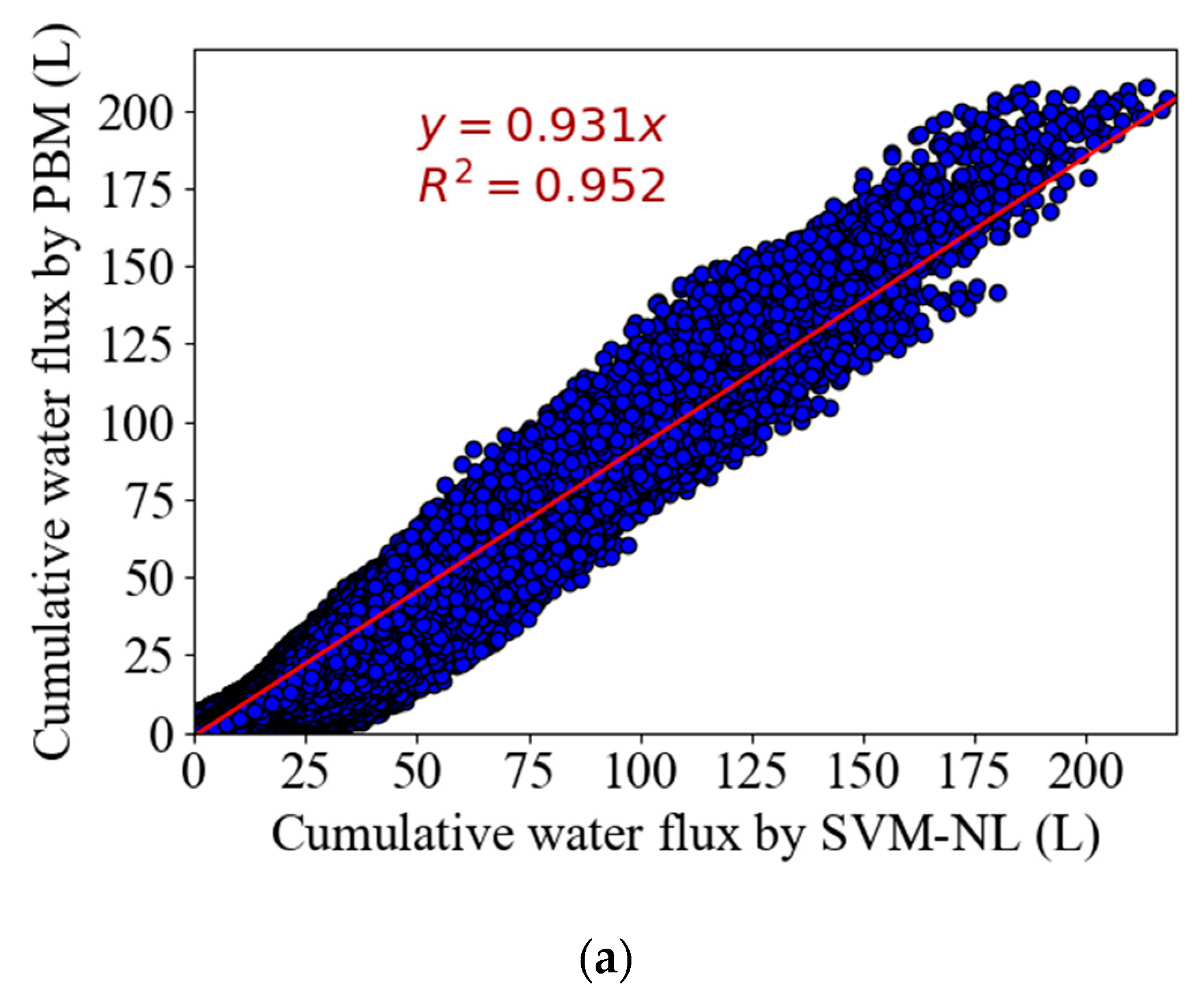
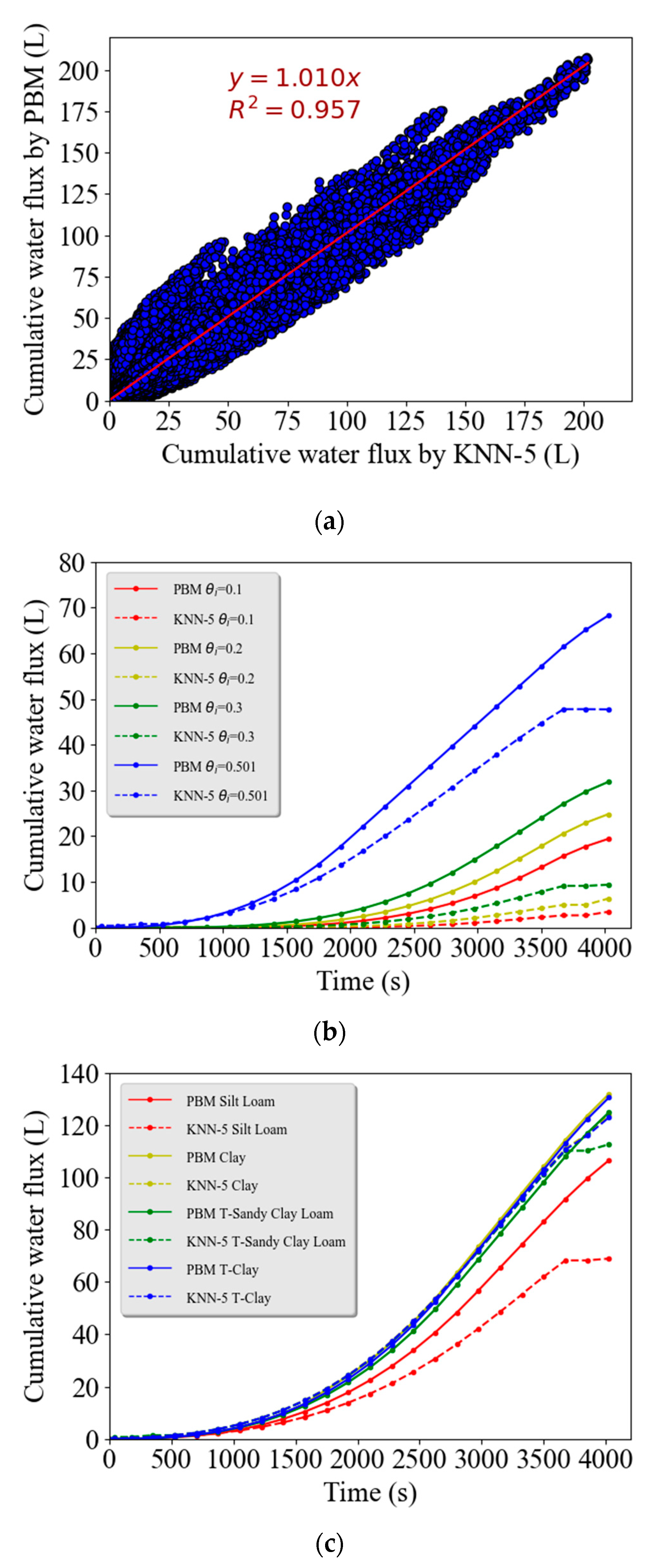
5.1.3. K-Nearest Neighbor Regression
The kNN models with different numbers of neighbors (the
K value) were tested while all points in each neighborhood were weighted equally. We observed that the optimal
K value is equal to 5. The results of calculations with the kNN model are summarized in
Figure 6. The
R2 (
R2 = 0.957) for the kNN-5 model was slightly higher than that for the SVM-NL model (
R2 = 0.952). However, there were more predicted outliers when the observed
Qc was relatively small. Although the overall runoff trends were correctly captured in
Figure 6b, the kNN-5 model underestimated the cumulative water flux at every print time and incorrectly predicted that
Qc stopped increasing when rainfall ended. Furthermore, this deviation tended to increase for smaller initial water contents. However,
Figure 6c shows that the kNN-5 model did a much better job of predicting large values of
Qc than the SVM-NL model.
5.1.4. Deep Feed-Forward Neural Network
The DNN models with one, two, and three hidden layers were tested to determine the optimum number of hidden layers and to minimize overfitting. In this study, the optimal number of neurons in each hidden layer was determined by trial and error. We tested possible numbers of neuron from 3 to 20 to see if the model performance was improved. The R2 and the Root Mean Squared Error (RMSE) were not improved when neuron numbers were increased beyond 16. Therefore, the number of neurons in each hidden layer was set to 16.
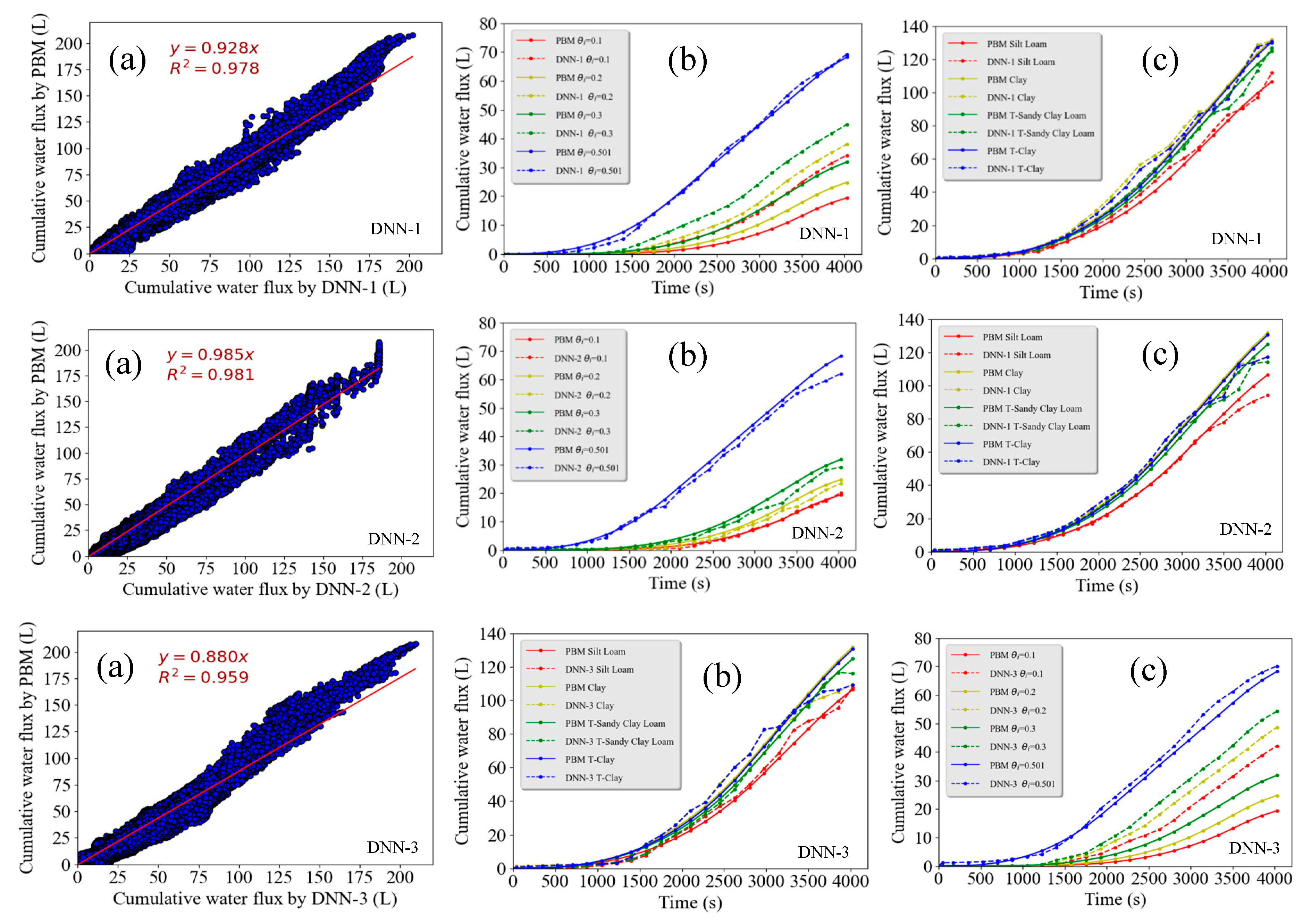
Figure 7a shows the scatter plot of estimated
Qc using DNN models with three different layers versus observed
Qc for the PBM data set. Values of
R2 were equal to 0.978, 0.981, and 0.959 for the DNN-1, DNN-2, and DNN-3 models, respectively. The DNN models provided a description of runoff that was fairly accurate and obtained higher
R2 values than the other ML models. However, the top and bottom rows of
Figure 7 indicate that the DNN-1 and DNN-3 models tended to underestimate and overestimate observed values of
Qc, respectively, whereas the DNN-2 model provided the best prediction. This result suggests that the one hidden layer model was not “deep” enough, whereas a three-layer model probably was too complicated and results in overfitting. A more quantitative comparison of various ML models is given below.
5.1.5. Comparison of Data-Driven Models
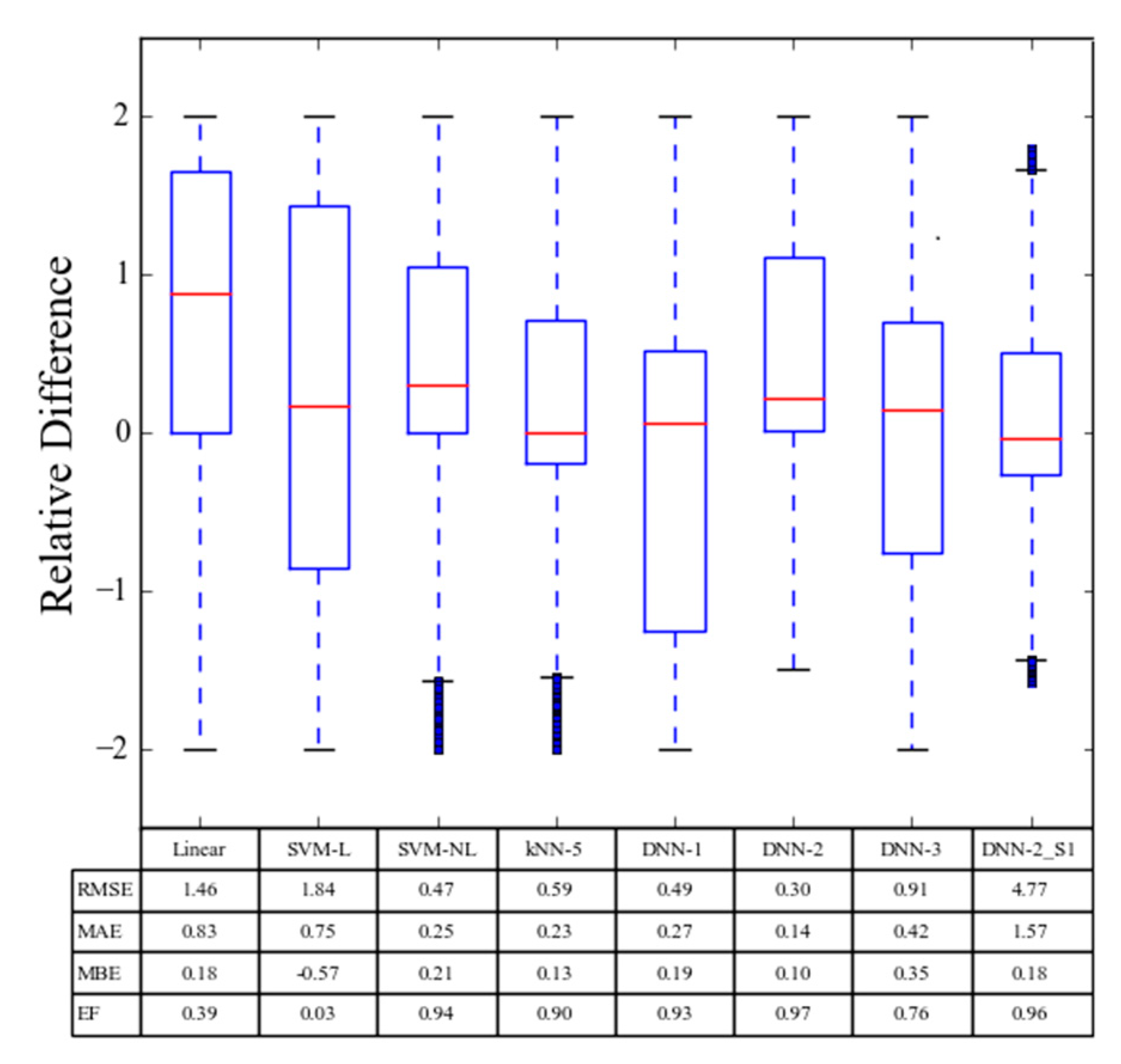
Figure 8 presents a box plot of the relative error distribution for various data-driven models, as well as other statistical parameters for their agreement with the PBM. The LR and SVM-L models show big error distributions, which indicates that these models were not well suited to predict runoff. The SVM-NL model performed much better than the SVM-L and LR models, but not as well as kNN-5 and DNN models. It is possible that the performance of the SVM-NL model could be further improved if the training data size was increased, but this would also dramatically increase the computational time. The boxplot of relative errors for the kNN-5 model was narrow, but it included a lot of outliers which indicated that the model performance may be different under other conditions.
Figure 7a and
Figure 8 indicate that outliers of the relative error for DNN-1 appeared when
Qc was over 100 L, whereas the DNN-3 model slightly underestimated large
Qc values. The DNN-2 model shows the narrowest box plot of relative errors and the best performance statistics for the considered ML models. This indicates that the DNN-2 model provided the best prediction of runoff water volumes.
5.2. Surface Runoff Quality
We discovered that the DNN-2 model structure with fine adjusted model parameters performs best among all selected data-driven models for predicting the runoff water volume. We therefore trained the DNN-2 model with the near equilibrium solute transport database. The DNN-2 model for water flow could be directly adjusted to produce a data-driven model that relates physical factors and the cumulative solute mass.
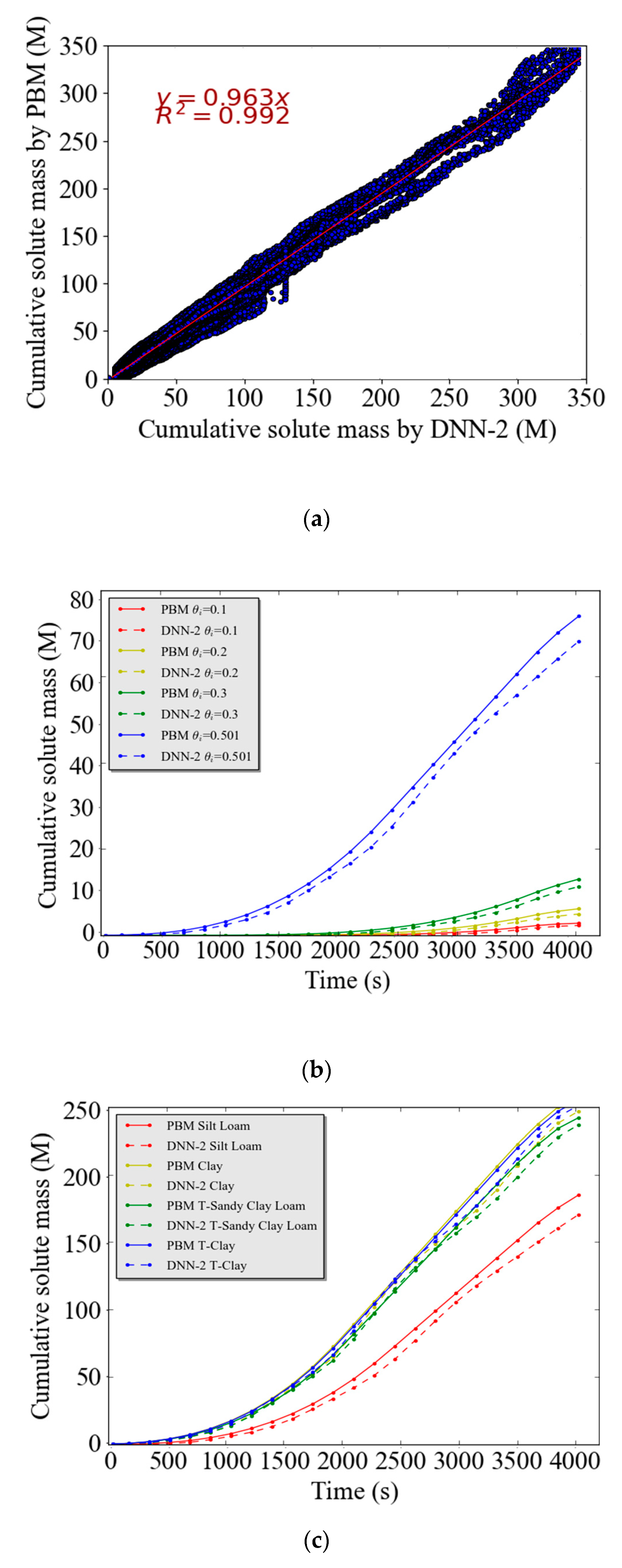
Figure 9a presents a scatter plot of the cumulative solute mass predicted by the DNN-2 model and observed by the PBM under near equilibrium conditions. The constructed DNN-2 relationship between input and output variables for near equilibrium conditions was very accurate. The goodness of the DNN-2 predictions for solute transport near equilibrium conditions is reflected by the statistical parameters (RMSE = 4.77 g, MAE =1.57 g, MBE = 0.18 g, and EF = 0.96 g) in
Figure 8, the value
R2 = 0.992 in
Figure 9a, and the agreement between observed (PBM) and predicted results for the example simulations for various water contents (
Figure 9b) and soil types (
Figure 9c).
6. Conclusions and Outlook
This study tested the ability of data-driven models to mimic PBMs to predict surface runoff water quantity and quality in agricultural settings. A physically-based overland flow and transport model was used to develop a large database containing information about the impact of various factors on surface runoff quantity and quality. In order to build a realistic training database, a wide range of input parameter values was selected. The input factors included: a) rainfall intensities (for seven different percent probabilities of exceedance of 1%, 2%, 4%, 10%, 20%, 50%, and 100% for the San Jacinto Watershed, Southern California), b) Manning’s roughness coefficients (reflecting management practices; 6 values), c) field slopes (5 values), d) field lengths (5 values), e) soil properties (affecting infiltration; 11 soil types with and without tillage), f) initial water contents (4 values), and g) solute sorption parameters (5 conditions). The resulting water flow database thus contained 2,310,000 entries, whereas the solute transport database was 5 times larger.
Multiple data-driven models were tested on their ability to relate/correlate model inputs with outputs. The following data-driven models were used in the analysis: Linear Regression (LR), k-Nearest Neighbor Regression (kNN), Support Vector Machine with linear (SVM-L) and nonlinear (SVM-NL) kernels, and Deep Neural Networks (DNN) (Neural Networks with multiple hidden layers). The LR and SWM-L models failed to accurately describe runoff water dynamics, having the regression coefficient (R2) less than 0.5. In particular, both linear models tended to overestimate the runoff water volume for early times and underestimate it for later times. Both SVM-NL and kNN models performed much better than linear models, having R2 of 0.93 and 0.96, respectively. However, there were still considerable deviations between the SVM-NL and kNN models and PBM predictions, especially for larger times, higher initial water contents, and for some textures (such as Silt Loam). Finally, the DNN models with one, two, and three hidden layers (DNN-1, DNN-2, and DNN-3) were tested to determine the optimum number of hidden layers and to minimize overfitting of output variables. The best performance was obtained by the DNN model with two hidden layers (DNN-2) (R2 = 0.98). The DNN-1 and DNN-3 models tended to underestimate, and overestimate observed values of runoff water volumes, respectively.
In conclusion, DNN techniques exhibited a better capability to reproduce the results of the PBM compare with traditional ML techniques. In particular, results indicate that the simple linear models are not well suited to develop correlations for runoff from agricultural lands because runoff is a complex nonlinear hydrological process. Although nonlinear models like kNN and SVM-NL can fairly accurately capture the surface water flow dynamic, the DNN models are more promising for dealing with complex hydrologic problems. Applications of the DNN models with additional hidden layers provide a possibility to further improve the model performance. Similarly, the trained DNN-2 model provided an excellent prediction of near equilibrium solute transport.
It should be noted that the training databases from the PBM could also be augmented to include real monitoring data and/or more complex model formulations (e.g., multidimensional simulations, stochastic simulations, other reactive transport processes, and physical non-equilibrium flow and transport). This approach would preserve the benefits of data-driven models over PBMs (e.g., faster execution times and ability to incorporate real data), while constraining data-driven models to the underlying physics of hydrological processes.