Coastal Flooding Hazard Due to Overflow Using a Level II Method: Application to the Venetian Littoral
Abstract
1. Introduction
2. Methodology
2.1. GPU-Based Swallow Water Equation Model
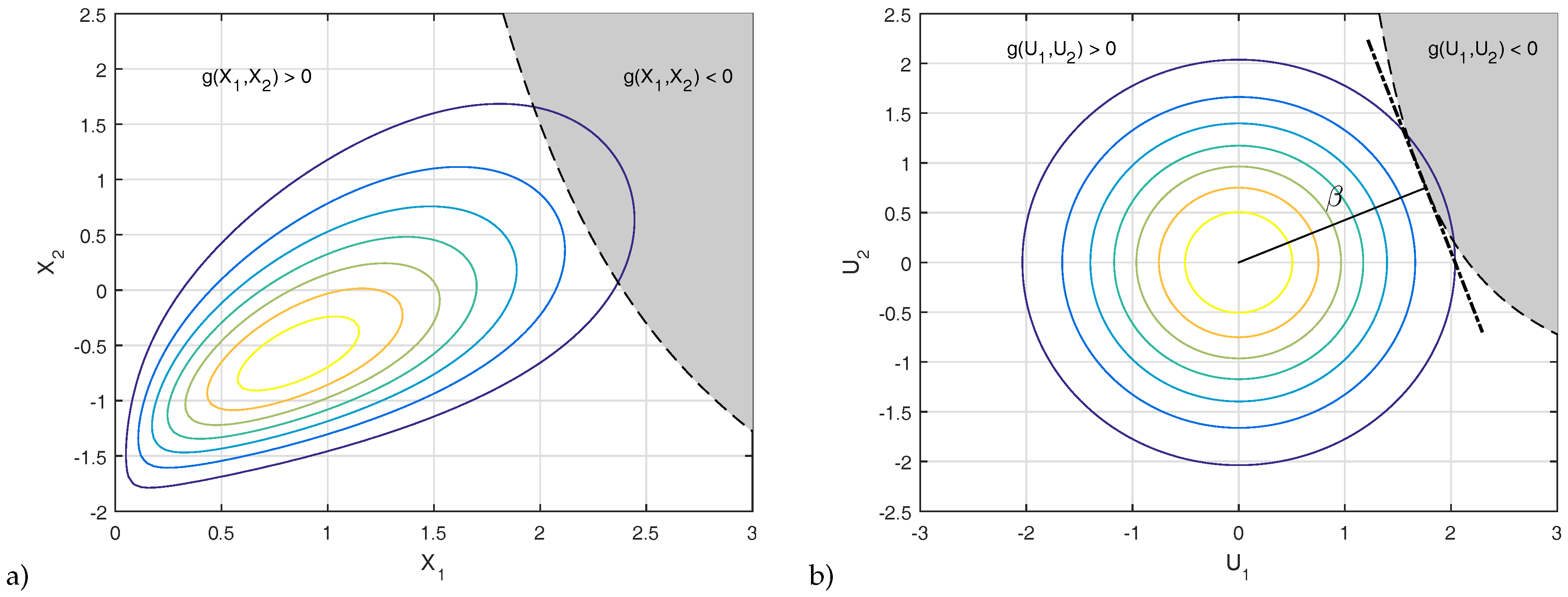
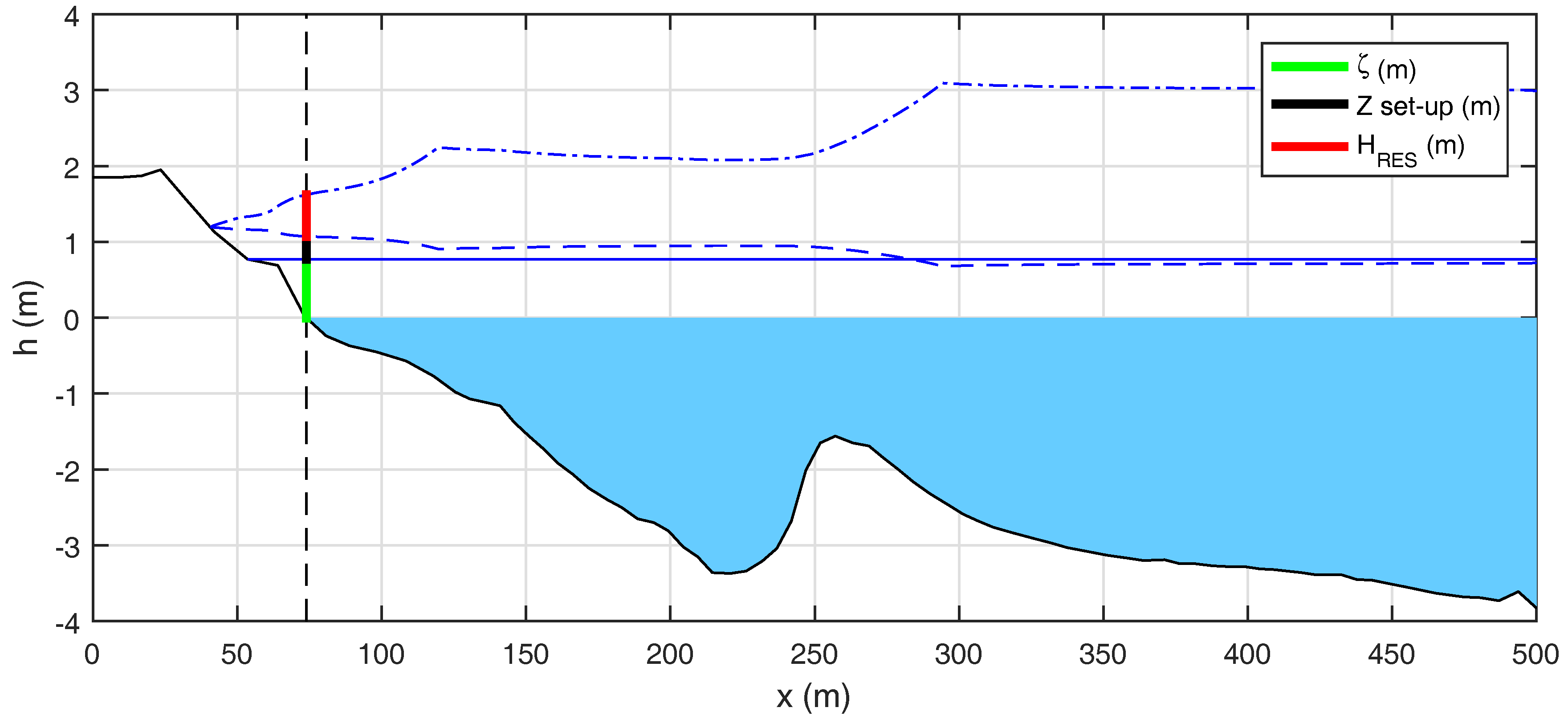
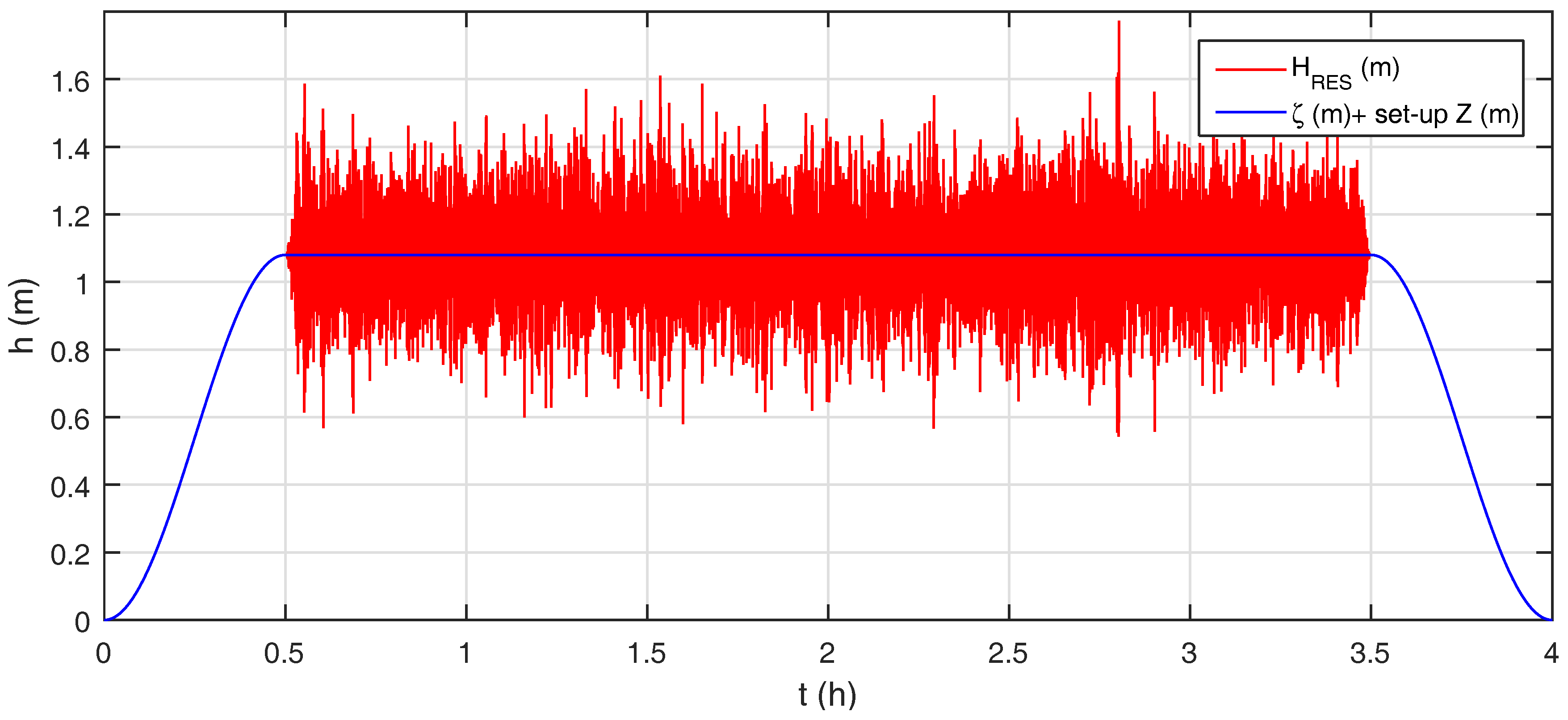
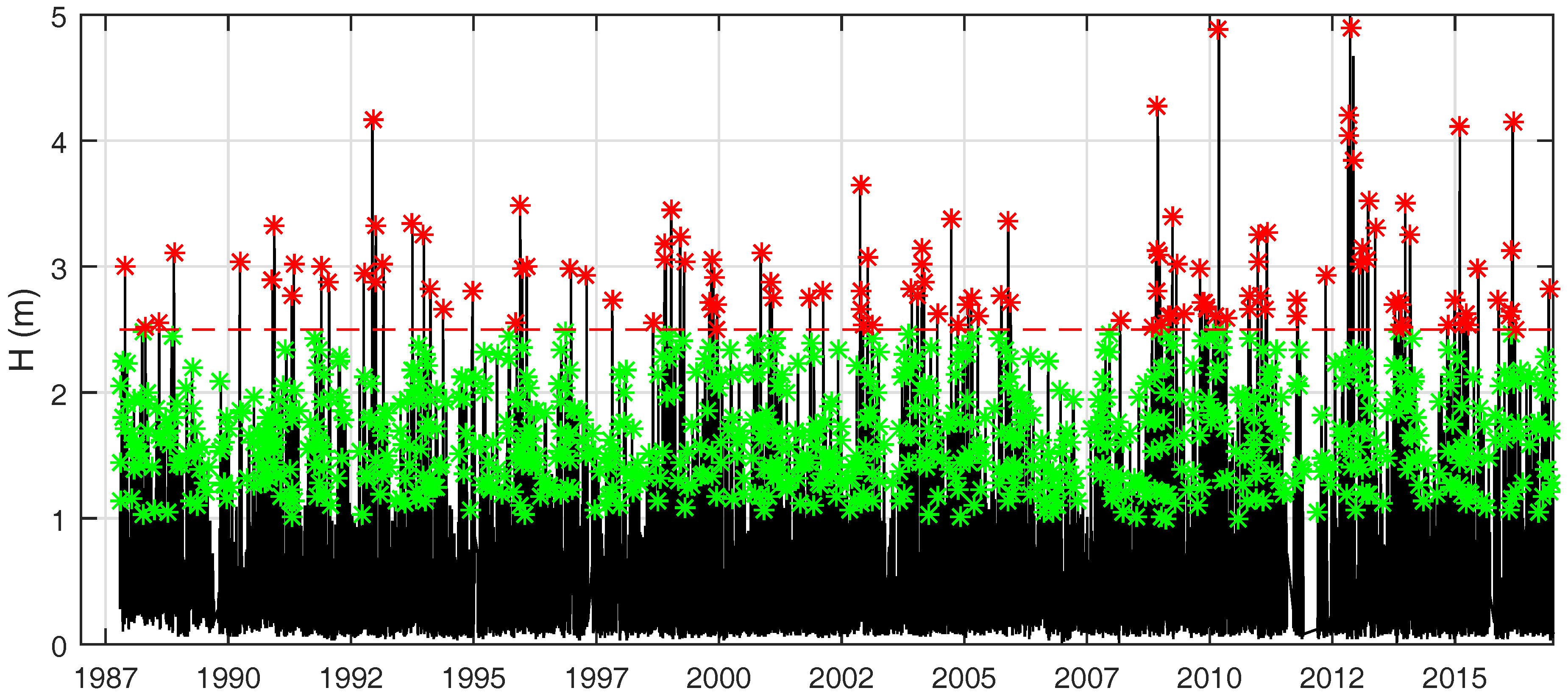
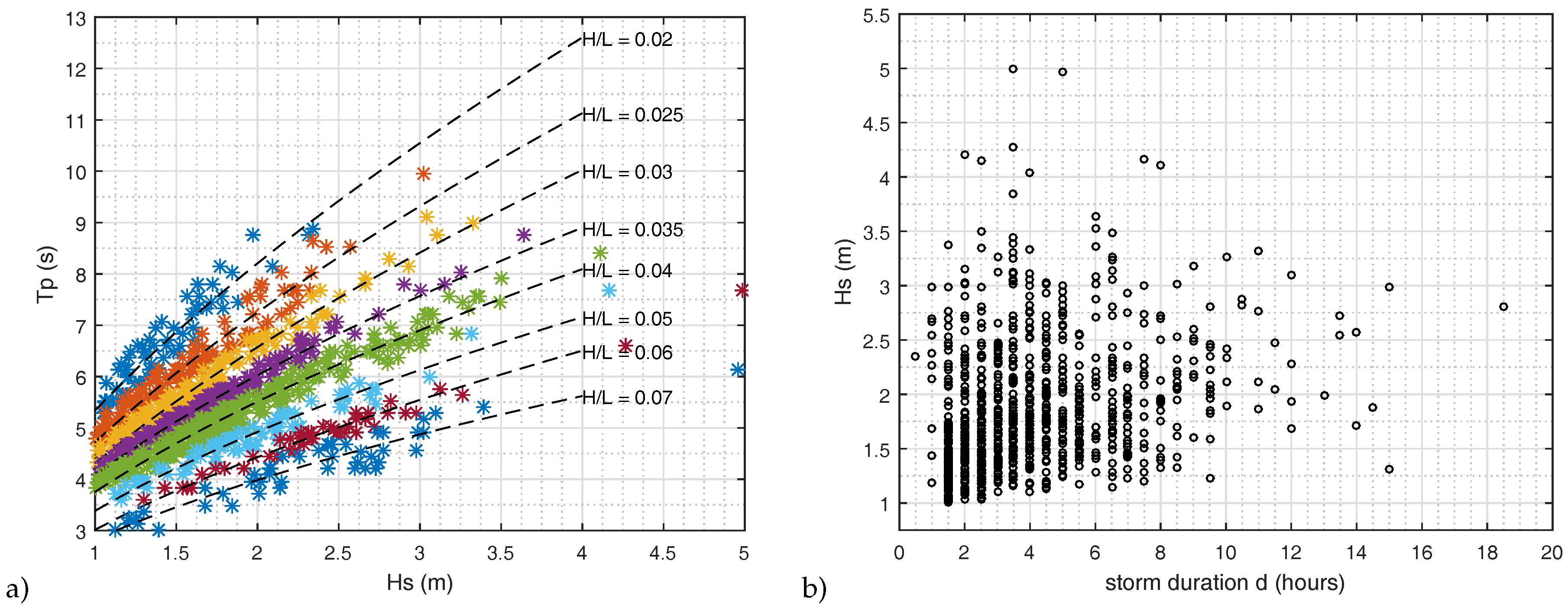
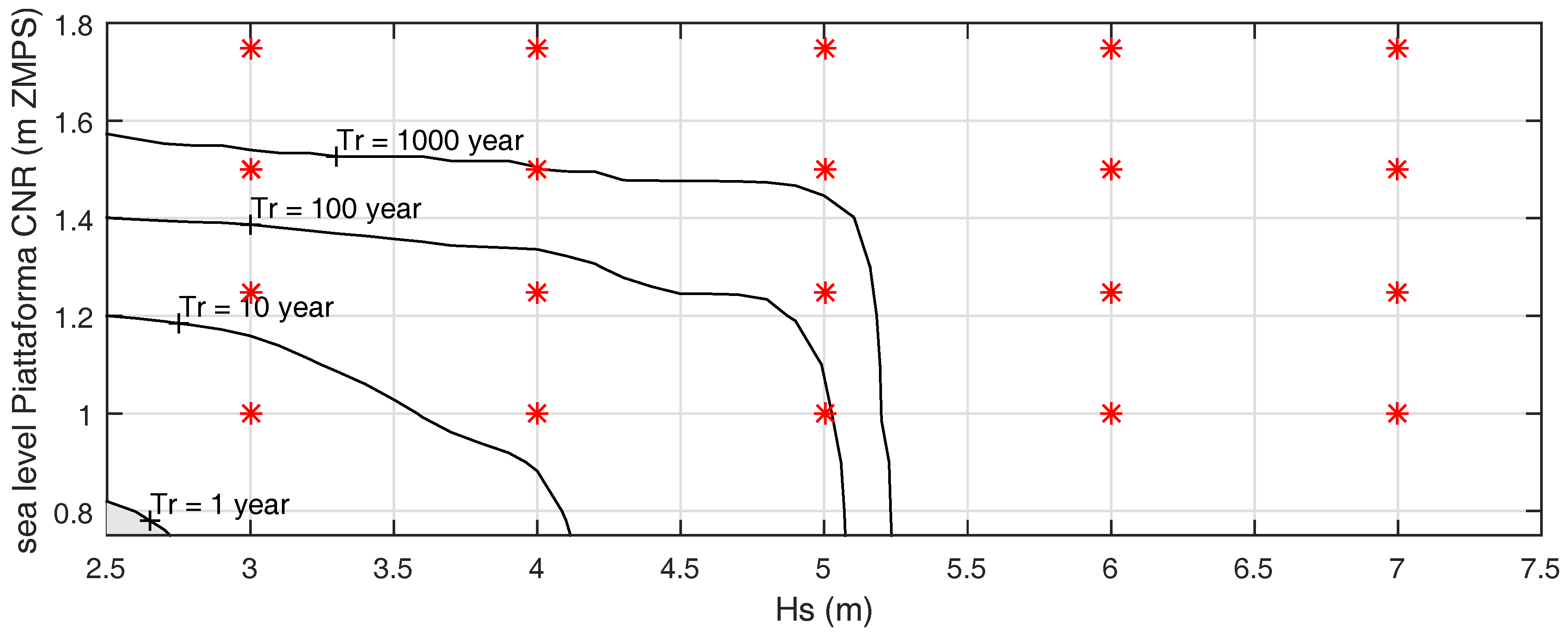
2.2. Procedure for the Assessment of Coastal Flooding Hazard Maps
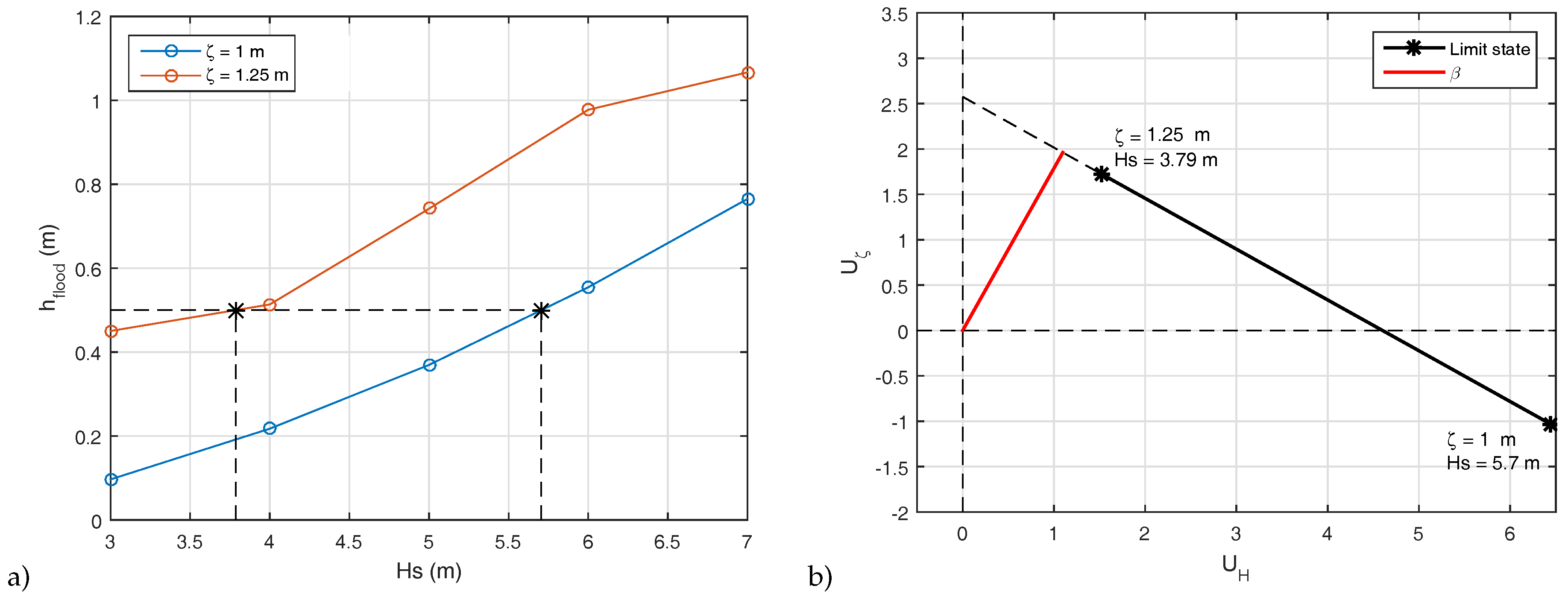
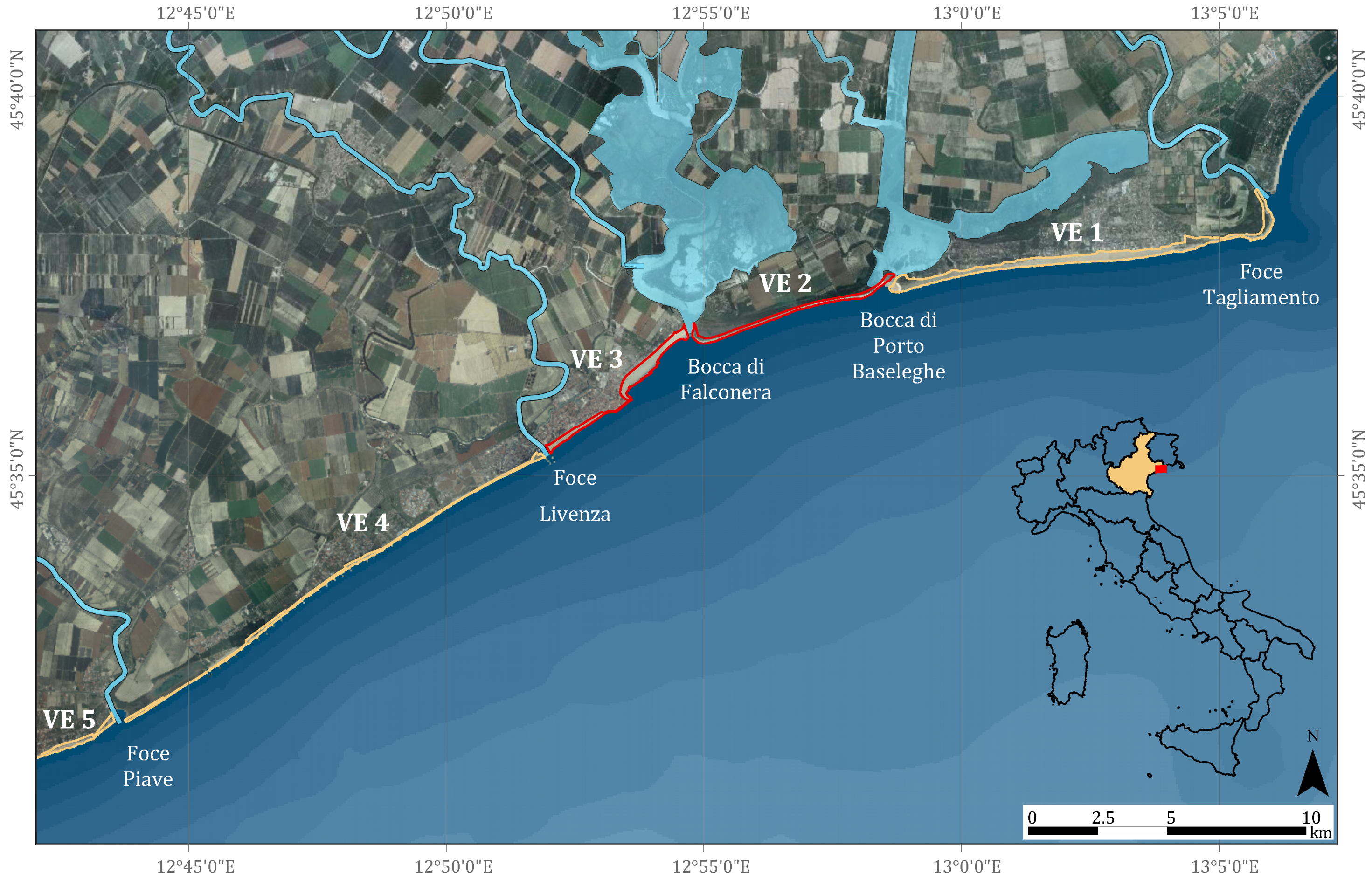
3. An Application to Two Stretches of the Venetian Littoral
3.1. Valle Vecchia Littoral Cell
3.2. Caorle Littoral Cell
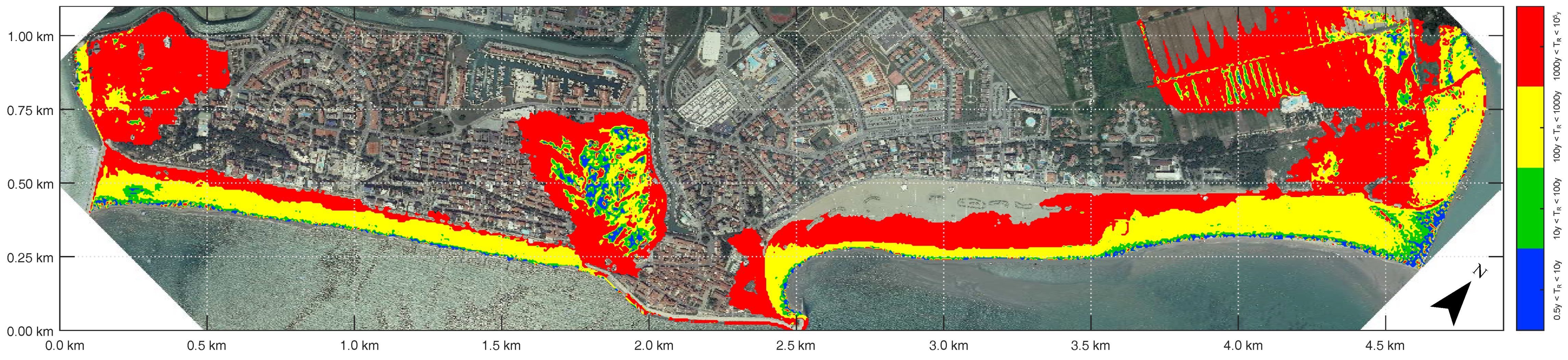
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cazenave, A.; Cozannet, G.L. Sea level rise and its coastal impacts. Earth’s Future 2014, 2, 15–34. [Google Scholar] [CrossRef]
- Pomaro, A.; Cavaleri, L.; Lionello, P. Climatology and trends of the Adriatic Sea wind waves: Analysis of a 37-year long instrumental data set. Int. J. Climatol. 2017, 37, 4237–4250. [Google Scholar] [CrossRef]
- Rahmstorf, S. Rising hazard of storm-surge flooding. Proc. Natl. Acad. Sci. USA 2017, 114, 11806–11808. [Google Scholar] [CrossRef] [PubMed]
- Nicholls, R.J.; Cazenave, A. Sea-level rise and its impact on coastal zones. Science 2010, 328, 1517–1520. [Google Scholar] [CrossRef] [PubMed]
- Vafeidis, A.T.; Nicholls, R.J.; McFadden, L.; Tol, R.S.; Hinkel, J.; Spencer, T.; Grashoff, P.S.; Boot, G.; Klein, R.J. A new global coastal database for impact and vulnerability analysis to sea-level rise. J. Coast. Res. 2008, 24, 917–924. [Google Scholar] [CrossRef]
- Zanuttigh, B.; Simcic, D.; Bagli, S.; Bozzeda, F.; Pietrantoni, L.; Zagonari, F.; Hoggart, S.; Nicholls, R.J. THESEUS decision support system for coastal risk management. Coast. Eng. 2014, 87, 218–239. [Google Scholar] [CrossRef]
- Zachry, B.C.; Booth, W.J.; Rhome, J.R.; Sharon, T.M. A national view of storm surge risk and inundation. Weather Clim. Soc. 2015, 7, 109–117. [Google Scholar] [CrossRef]
- Wadey, M.P.; Nicholls, R.J.; Hutton, C. Coastal flooding in the Solent: An integrated analysis of defences and inundation. Water 2012, 4, 430–459. [Google Scholar] [CrossRef]
- Spaulding, M.L.; Grilli, A.; Damon, C.; Fugate, G.; Oakley, B.A.; Isaji, T.; Schambach, L. Application of state of art modeling techniques to predict flooding and waves for an exposed coastal area. J. Mar. Sci. Eng. 2017, 5, 10. [Google Scholar] [CrossRef]
- Aucelli, P.P.C.; Di Paola, G.; Incontri, P.; Rizzo, A.; Vilardo, G.; Benassai, G.; Buonocore, B.; Pappone, G. Coastal inundation risk assessment due to subsidence and sea level rise in a Mediterranean alluvial plain (Volturno coastal plain–southern Italy). Estuarine Coast. Shelf Sci. 2017, 198, 597–609. [Google Scholar] [CrossRef]
- Di Luccio, D.; Benassai, G.; Di Paola, G.; Rosskopf, C.; Mucerino, L.; Montella, R.; Contestabile, P. Monitoring and modelling coastal vulnerability and mitigation proposal for an archaeological site (Kaulonia, Southern Italy). Sustainability (Switzerland) 2018, 10, 2017. [Google Scholar] [CrossRef]
- Di Risio, M.; Bruschi, A.; Lisi, I.; Pesarino, V.; Pasquali, D. Comparative Analysis of Coastal Flooding Vulnerability and Hazard Assessment at National Scale. J. Mar. Sci. Eng. 2017, 5, 51. [Google Scholar] [CrossRef]
- Gallien, T. Validated coastal flood modeling at Imperial Beach, California: Comparing total water level, empirical and numerical overtopping methodologies. Coast. Eng. 2016, 111, 95–104. [Google Scholar] [CrossRef]
- Lerma, A.; Bulteau, T.; Elineau, S.; Paris, F.; Durand, P.; Anselme, B.; Pedreros, R. High-resolution marine flood modelling coupling overflow and overtopping processes: Framing the hazard based on historical and statistical approaches. Nat. Hazards Earth Syst. Sci. 2018, 18, 207–229. [Google Scholar] [CrossRef]
- Simeoni, U.; Corbau, C. A review of the Delta Po evolution (Italy) related to climatic changes and human impacts. Geomorphology 2009, 107, 64–71. [Google Scholar] [CrossRef]
- Carbognin, L.; Teatini, P.; Tosi, L. Eustacy and land subsidence in the Venice Lagoon at the beginning of the new millennium. J. Mar. Syst. 2004, 51, 345–353. [Google Scholar] [CrossRef]
- Martinelli, L.; Zanuttigh, B.; Corbau, C. Assessment of coastal flooding hazard along the Emilia Romagna littoral, IT. Coast. Eng. 2010, 57, 1042–1058. [Google Scholar] [CrossRef]
- Pescaroli, G.; Magni, M. Flood warnings in coastal areas: How do experience and information influence responses to alert services? Nat. Hazards Earth Syst. Sci. 2015, 15, 703–714. [Google Scholar] [CrossRef]
- Wolshon, B.; Urbina, E.; Wilmot, C.; Levitan, M. Review of policies and practices for hurricane evacuation. I: Transportation planning, preparedness, and response. Nat. Hazards Rev. 2005, 6, 129–142. [Google Scholar] [CrossRef]
- Jia, X.; Morel, G.; Martell-Flore, H.; Hissel, F.; Batoz, J.L. Fuzzy logic based decision support for mass evacuations of cities prone to coastal or river floods. Environ. Model. Softw. 2016, 85, 1–10. [Google Scholar] [CrossRef]
- Kunreuther, H.; Pauly, M. Rules rather than discretion: Lessons from Hurricane Katrina. J. Risk Uncertain. 2006, 33, 101–116. [Google Scholar] [CrossRef]
- Burcharth, H.F.; Zanuttigh, B.; Andersen, T.L.; Lara, J.L.; Steendam, G.J.; Ruol, P.; Sergent, P.; Ostrowski, R.; Silva, R.; Martinelli, L.; et al. Chapter 3—Innovative Engineering Solutions and Best Practices to Mitigate Coastal Risk. In Coastal Risk Management in a Changing Climate; Butterworth-Heinemann: Boston, MA, USA, 2015; pp. 55–170. [Google Scholar]
- Vanderlinden, J.P.; Baztan, J.; Coates, T.; Dávila, O.G.; Hissel, F.; Kane, I.O.; Koundouri, P.; McFadden, L.; Parker, D.; Penning-Rowsell, E.; et al. Chapter 5—Nonstructural Approaches to Coastal Risk Mitigations. In Coastal Risk Management in a Changing Climate; Butterworth-Heinemann: Boston, MA, USA, 2015; pp. 237–274. [Google Scholar]
- Kusumo, A.; Reckien, D.; Verplanke, J. Utilising volunteered geographic information to assess resident’s flood evacuation shelters. case study: Jakarta. Appl. Geogr. 2017, 88, 174–185. [Google Scholar] [CrossRef]
- Coastal Flooding Hazard—Community information and participation. Available online: https://coastalfloodinghazard.wordpress.com/community-information (accessed on 7 January 2019).
- Hoggart, S.; Hawkins, S.J.; Bohn, K.; Airoldi, L.; van Belzen, J.; Bichot, A.; Bilton, D.T.; Bouma, T.J.; Colangelo, M.A.; Davies, A.J.; et al. Chapter 4–Ecological Approaches to Coastal Risk Mitigation. In Coastal Risk Management in a Changing Climate; Butterworth-Heinemann: Boston, MA, USA, 2015; pp. 171–236. [Google Scholar]
- Gómez-Pina, G.; Muñoz-Pérez, J.J.; Ramírez, J.L.; Ley, C. Sand dune management problems and techniques, Spain. J. Coast. Res. 2002, 36, 325–332. [Google Scholar] [CrossRef]
- Favaretto, C.; Martinelli, L.; Ruol, P. A Model of Coastal Flooding Using Linearized Bottom Friction and its Application to a Case Study in Caorle, Venice Italy. Int. J. Off. Polar Eng. 2019, 29, 1–9. [Google Scholar]
- Favaretto, C.; Martinelli, L.; Ruol, P. Raster Based Model of Inland Coastal Flooding Propagation Using Linearized Bottom Friction and Application to a Real Case Study in Caorle, Venice (IT). In Proceedings of the 28th International Ocean and Polar Engineering Conference, Sapporo, Japan, 10–15 June 2018. [Google Scholar]
- Bates, P.D.; Horritt, M.S.; Fewtrell, T.J. A simple inertial formulation of the shallow water equations for efficient two-dimensional flood inundation modelling. J. Hydrol. 2010, 387, 33–45. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; Wilson, M.D. Simple spatially-distributed models for predicting flood inundation: A review. Geomorphology 2007, 90, 208–225. [Google Scholar] [CrossRef]
- Khorshid, S.; Mohammadian, A.; Nistor, I. Extension of a well-balanced central upwind scheme for variable density shallow water flow equations on triangular grids. Comput. Fluids 2017, 156, 441–448. [Google Scholar] [CrossRef]
- Brodtkorb, A.R.; Sætra, M.L.; Altinakar, M. Efficient shallow water simulations on GPUs: Implementation, visualization, verification, and validation. Comput. Fluids 2012, 55, 1–12. [Google Scholar] [CrossRef]
- Liang, W.Y.; Hsieh, T.J.; Satria, M.T.; Chang, Y.L.; Fang, J.P.; Chen, C.C.; Han, C.C. A GPU-based simulation of tsunami propagation and inundation. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 593–603. [Google Scholar]
- Synolakis, C. The runup of solitary waves. J. Fluid Mech. 1987, 185, 523–545. [Google Scholar] [CrossRef]
- Briggs, M.J.; Synolakis, C.E.; Harkins, G.S.; Green, D.R. Laboratory experiments of tsunami runup on a circular island. Pure Appl. Geophys. 1995, 144, 569–593. [Google Scholar] [CrossRef]
- Kottegoda, N.; Rosso, R. Probability, Statistics, and Reliability for Civil and Environmental Engineers; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Madsen, H.O.; Krenk, S.; Lind, N.C. Methods of Structural Safety; Courier Corporation: North Chelmsford, MA, USA, 2006. [Google Scholar]
- Du, X. First order and second reliability methods. In Probabilistic Engineering Design; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2005; pp. 1–33. [Google Scholar]
- Hasofer, A.M.; Lind, N.C. Exact and invariant second-moment code format. J. Eng. Mech. Div. 1974, 100, 111–121. [Google Scholar]
- Group, T.W. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Armaroli, C.; Ciavola, P.; Perini, L.; Calabrese, L.; Lorito, S.; Valentini, A.; Masina, M. Critical storm thresholds for significant morphological changes and damage along the Emilia-Romagna coastline, Italy. Geomorphology 2012, 143, 34–51. [Google Scholar] [CrossRef]
- Boccotti, P. On coastal and offshore structure risk analysis. Excerpta Ital. Contrib. Field Hydraul. Eng. 1986, 1, 19–36. [Google Scholar]
- Mendoza, E.; Jimenez, J.; Mateo, J.; Salat, J. A coastal storms intensity scale for the Catalan sea (NW Mediterranean). Nat. Hazards Earth Syst. Sci. 2011, 11, 2453–2462. [Google Scholar] [CrossRef]
- Archetti, R.; Paci, A.; Carniel, S.; Bonaldo, D. Optimal index related to the shoreline dynamics during a storm: The case of Jesolo beach. Nat. Hazards Earth Syst. Sci. 2016, 16, 1107–1122. [Google Scholar] [CrossRef]
- Lin-Ye, J.; García-León, M.; Gràcia, V.; Ortego, M.I.; Stanica, A.; Sánchez-Arcilla, A. Multivariate hybrid modelling of future wave-storms at the northwestern Black Sea. Water 2018, 10, 221. [Google Scholar] [CrossRef]
- Dally, W.R.; Dean, R.G.; Dalrymple, R.A. Wave height variation across beaches of arbitrary profile. J. Geophys. Res. Oceans 1985, 90, 11917–11927. [Google Scholar] [CrossRef]
- Ruol, P.; Martinelli, L.; Favaretto, C. Vulnerability Analysis of the Venetian Littoral and Adopted Mitigation Strategy. Water 2018, 10, 984. [Google Scholar] [CrossRef]
- Ruol, P.; Martinelli, L.; Favaretto, C. Gestione Integrata Della Zona Costiera. Studio e Monitoraggio per la Definizione Degli Interventi di Difesa dei Litorali Dall’Erosione Nella Regione Veneto—Linee Guida; Edizioni Libreria Progetto; University of Padua: Padova, Italy, 2016. [Google Scholar]
- Nataf, A. Determination des Distribution don’t les marges sont Donnees. C. R. Acad. Sci. 1962, 225, 42–43. [Google Scholar]
- Prinos, P.; Kortenhaus, A.; Swerpel, B.; Jiménez, J.A. Review of Flood Hazard Mapping; Floodsite Report, No. T03-07-01,54; University of Athens: Athens, Greece, 2008. [Google Scholar]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Favaretto, C.; Martinelli, L.; Ruol, P. Coastal Flooding Hazard Due to Overflow Using a Level II Method: Application to the Venetian Littoral. Water 2019, 11, 134. https://doi.org/10.3390/w11010134
Favaretto C, Martinelli L, Ruol P. Coastal Flooding Hazard Due to Overflow Using a Level II Method: Application to the Venetian Littoral. Water. 2019; 11(1):134. https://doi.org/10.3390/w11010134
Chicago/Turabian StyleFavaretto, Chiara, Luca Martinelli, and Piero Ruol. 2019. "Coastal Flooding Hazard Due to Overflow Using a Level II Method: Application to the Venetian Littoral" Water 11, no. 1: 134. https://doi.org/10.3390/w11010134
APA StyleFavaretto, C., Martinelli, L., & Ruol, P. (2019). Coastal Flooding Hazard Due to Overflow Using a Level II Method: Application to the Venetian Littoral. Water, 11(1), 134. https://doi.org/10.3390/w11010134






