Catchment Hydrological Modeling with Soil Thermal Dynamics during Seasonal Freeze-Thaw Cycles
Abstract
1. Introduction
2. Study Area and Data
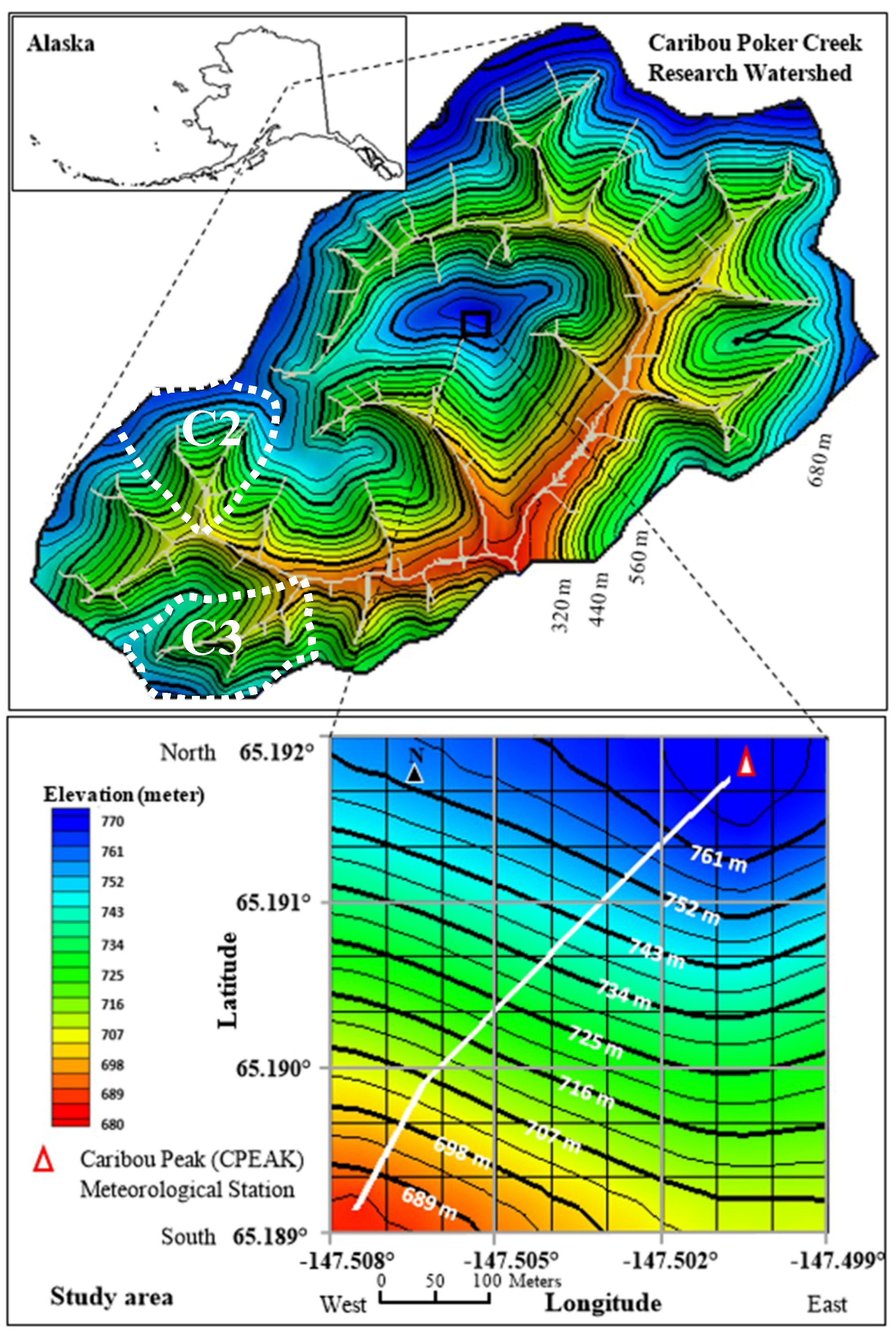
2.1. Description of the Study Site
2.2. Data Acquisition
2.2.1. Topography
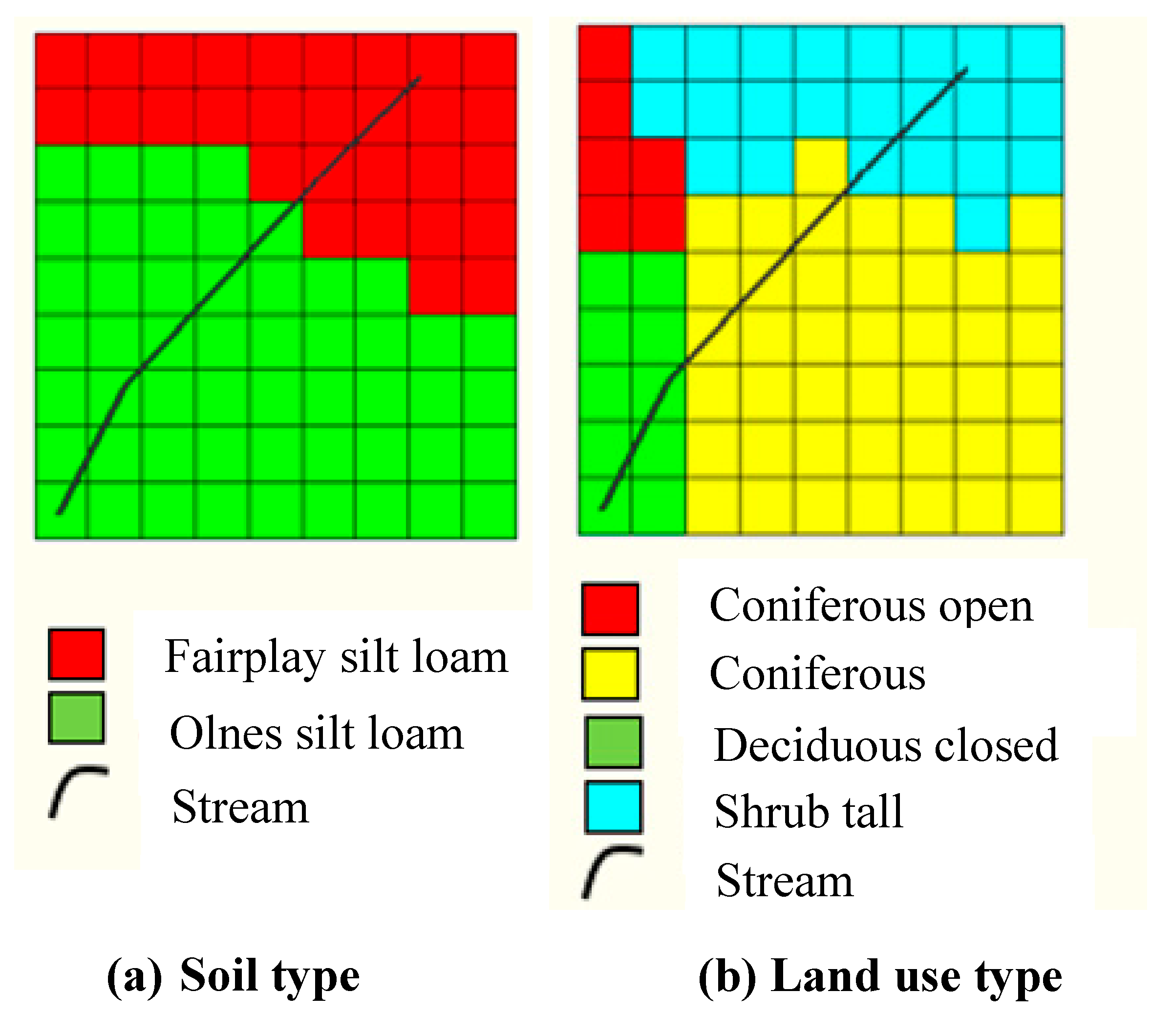
2.2.2. Soil and Land Use
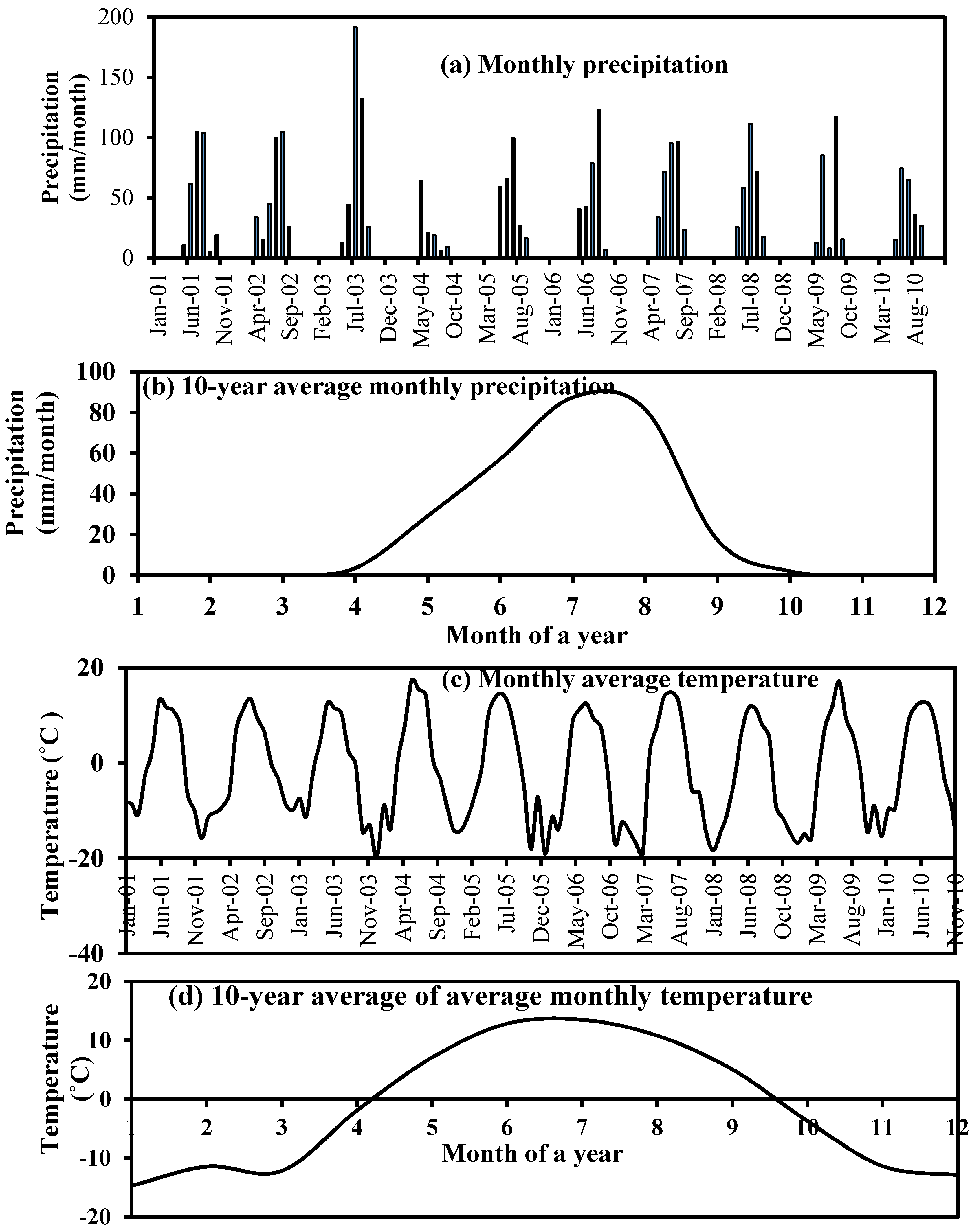
2.2.3. Climate of the Study Area
3. Methodology
3.1. Process Model Development of the Seasonal Change of the Soil Moisture Phase
3.2. Numerical Model of Soil Heat Transfer
3.3. Numerical Model of Soil Moisture
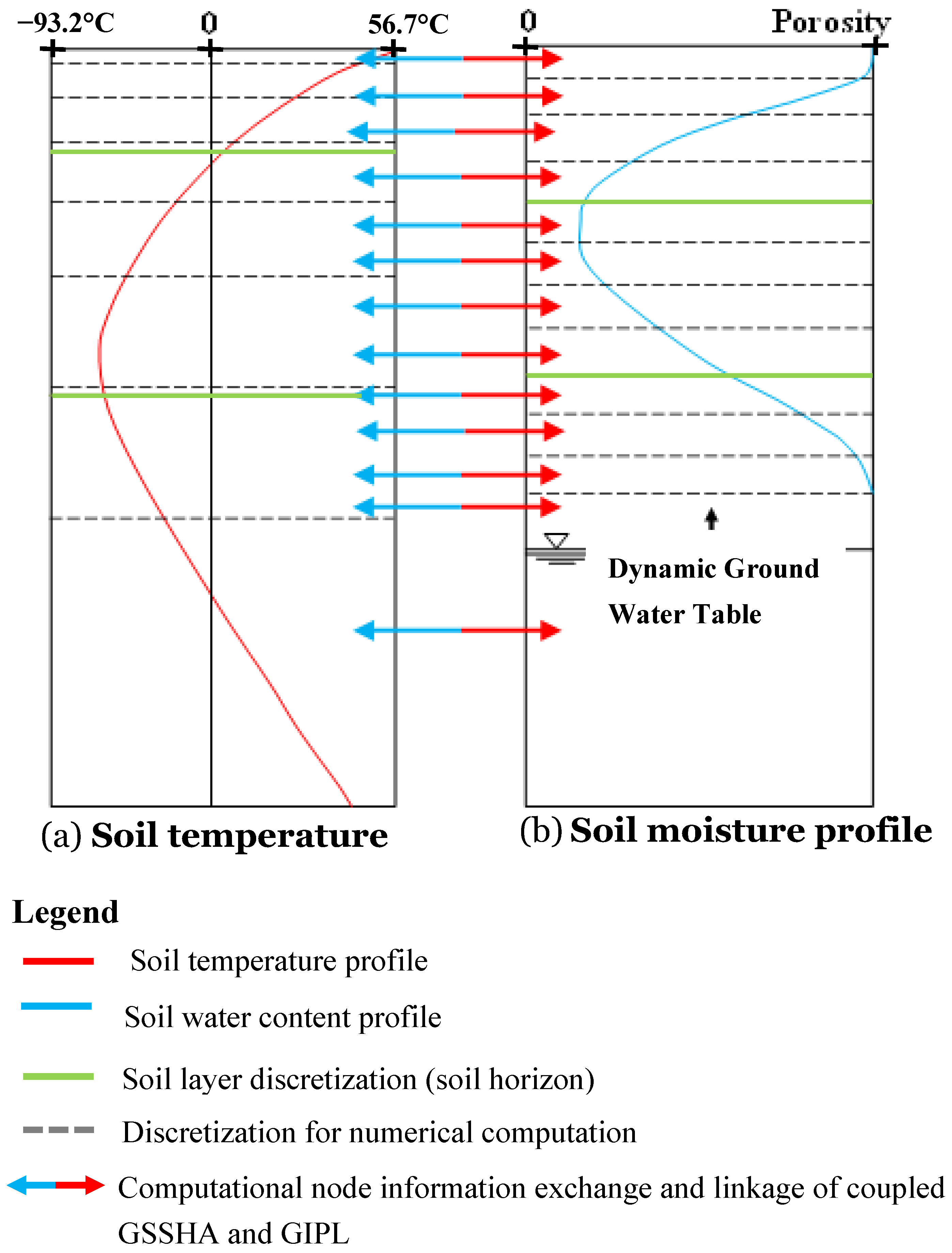
3.4. Linking Soil Temperature and Soil Water Computational Nodes
3.5. Linking Soil Thermodynamics with Soil Moisture Hydrodynamics
3.6. Linking Soil Temperature and Hydraulic Conductivity
4. Model Development of the Study Area
4.1. Initial Condition
4.2. Overall Model Processes and Parameter Values
4.2.1. Thermodynamic Process
4.2.2. Routing Process
4.2.3. Infiltration Process
4.2.4. Evapotranspirational Process for the Long-Term Simulation
5. Result and Discussion
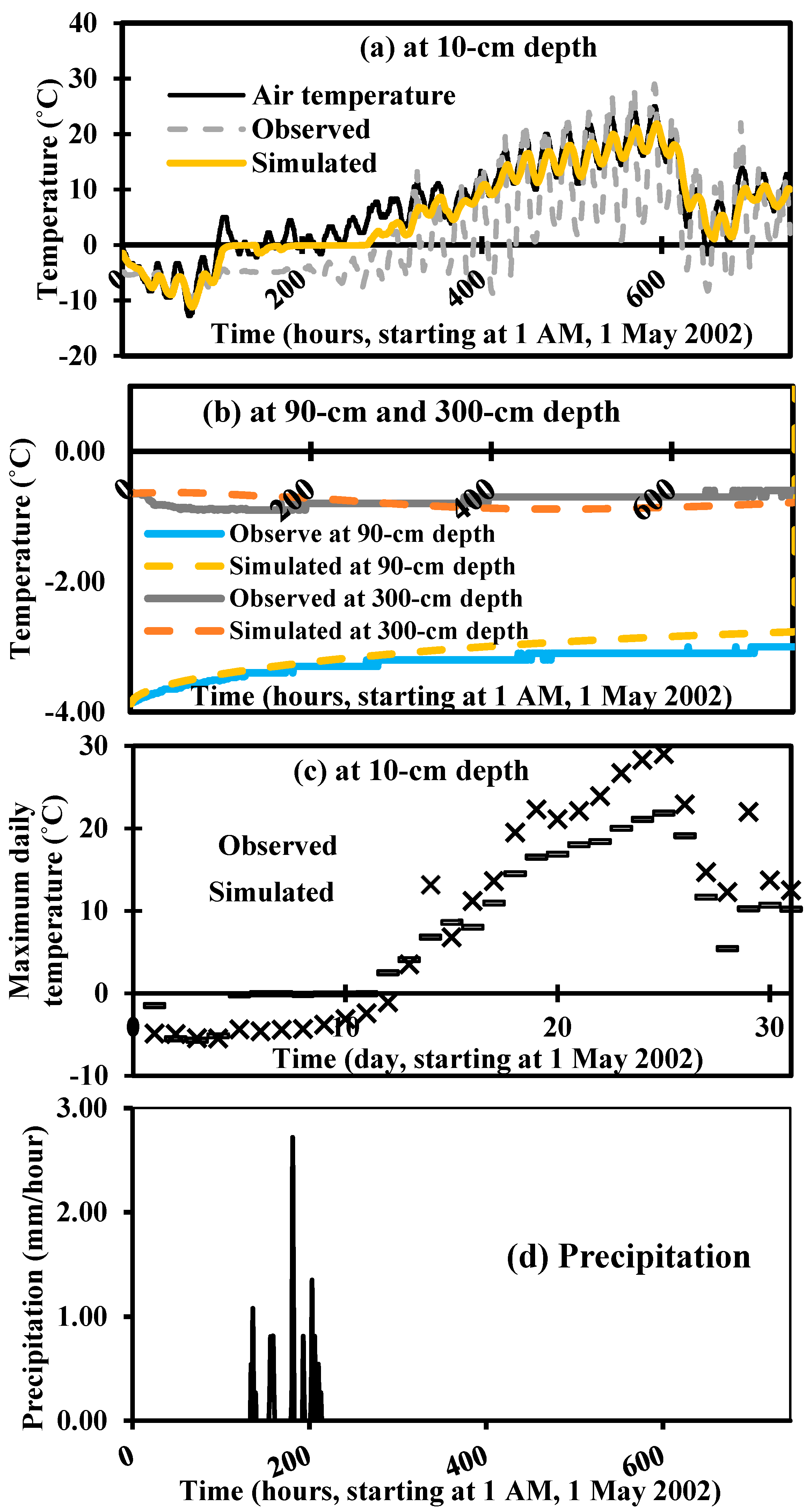
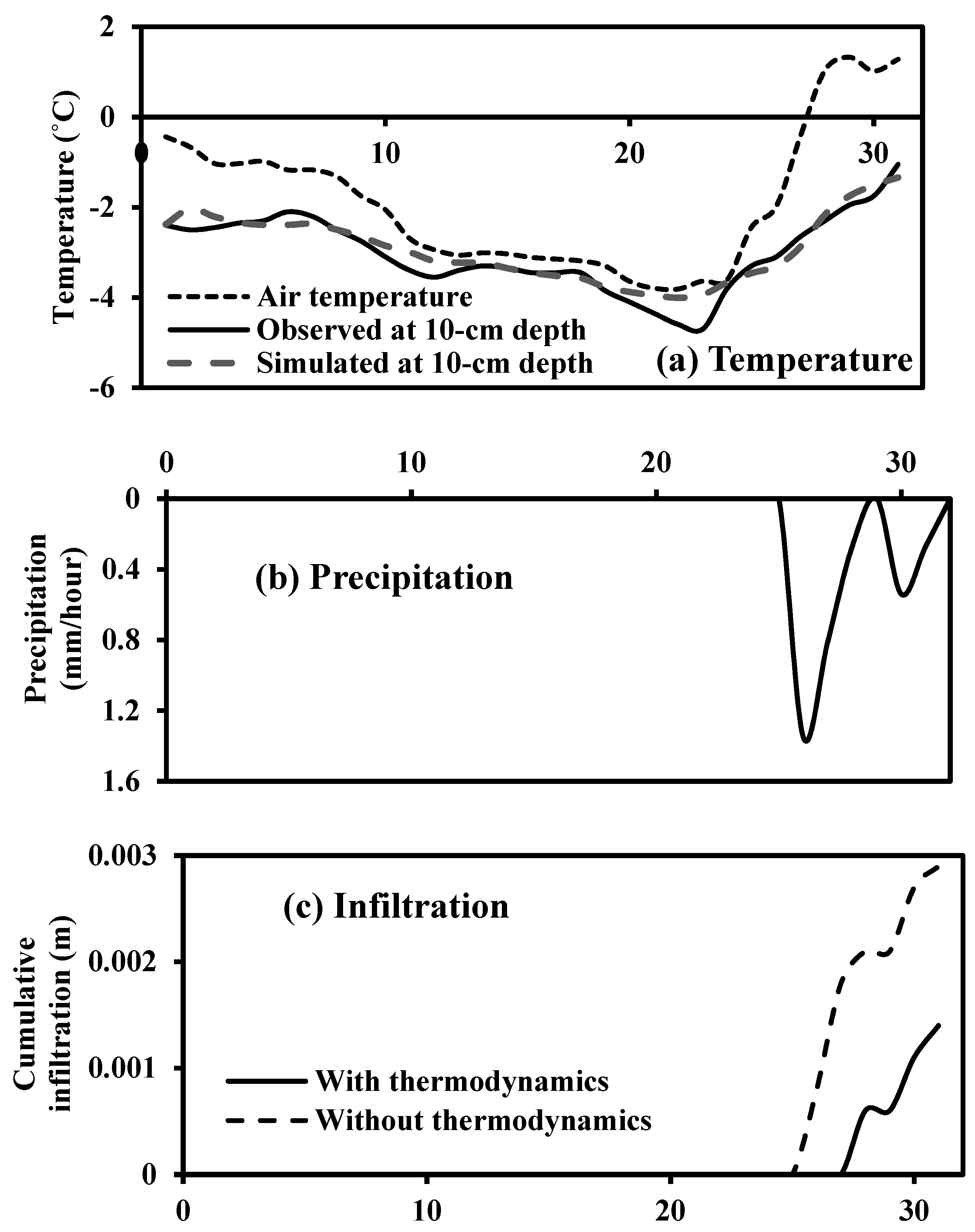
5.1. Observed and Simulated Soil Profile Temperature
5.2. Catchment Hydrological Dynamics under Freezing and Thawing
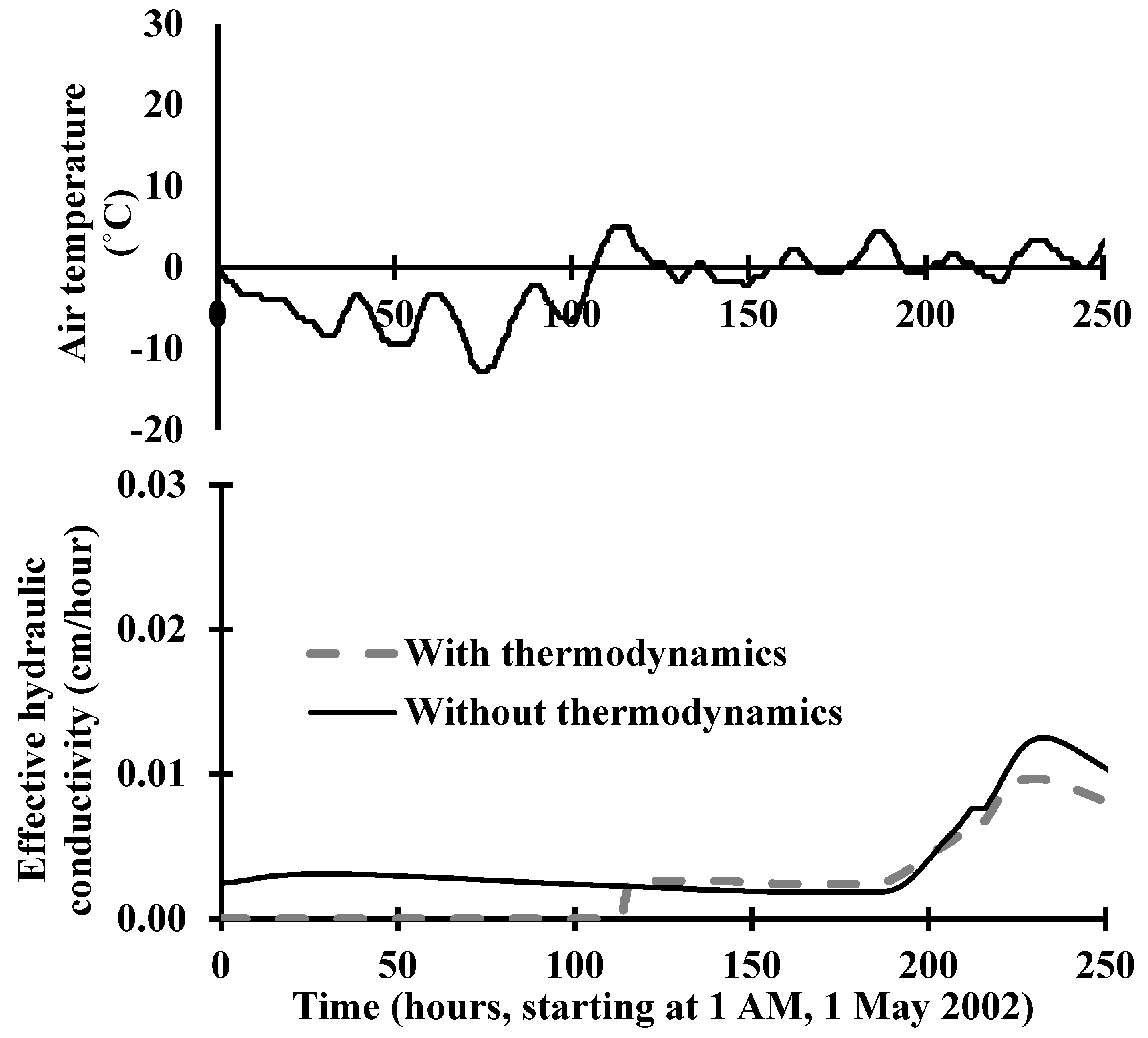
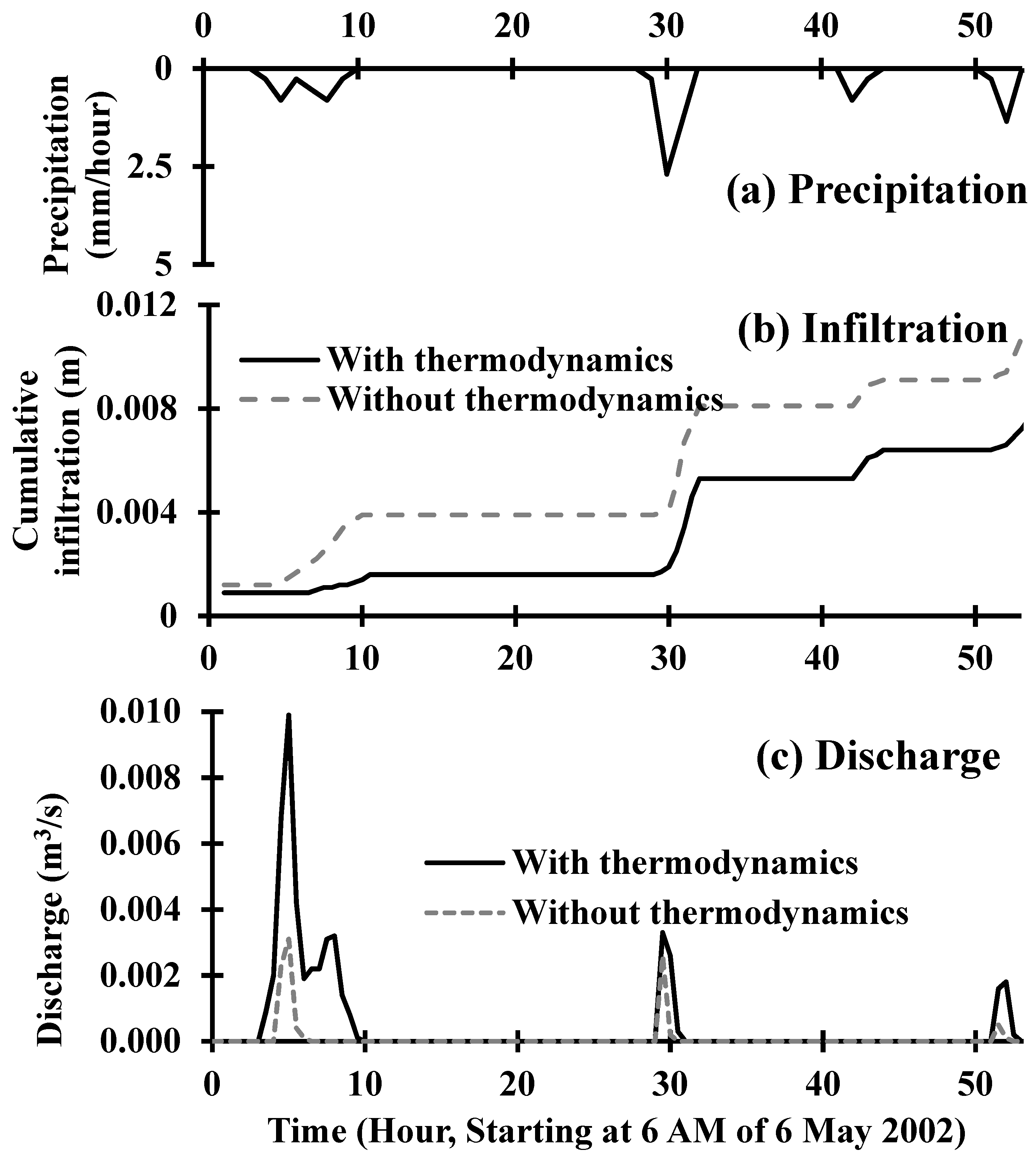
5.2.1. Effective Hydraulic Conductivity with and without Thermodynamics
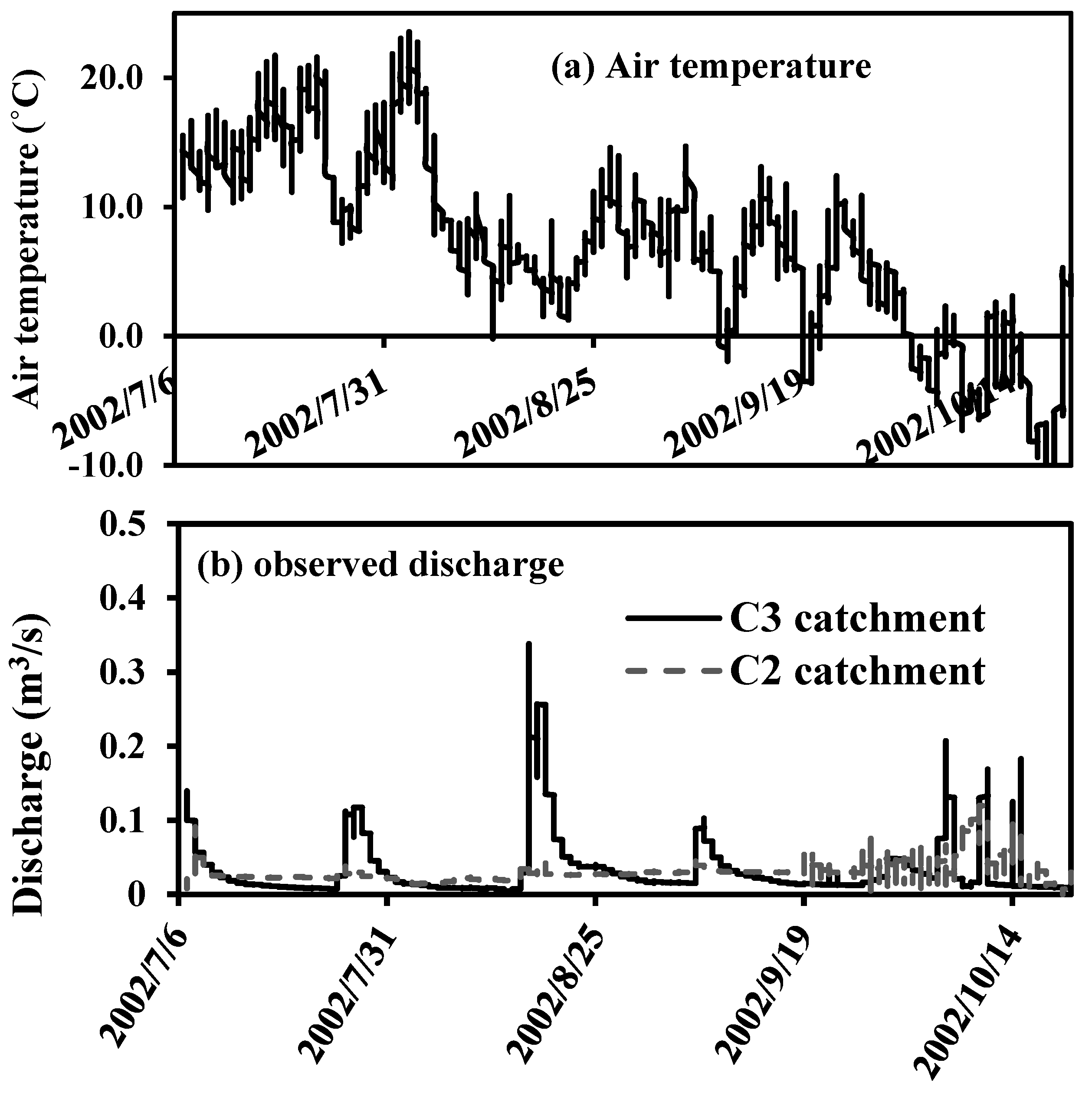
5.2.2. Hydrologic Runoff Response
5.3. Discussion
- Although C2 and C3 are the watersheds of similar size, 5.2 km2 and 5.7 km2, respectively, C3 discharge is significantly higher than C2 discharge.
- From 19 September 2002, C2 discharge rapidly increases to a value roughly equal to C3 discharge.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- U.S. Global Change Research Program. Climate Science Special Report: Fourth National Climate Assessment, Volume I; Wuebbles, D.J., Fahey, D.W., Hibbard, K.A., Dokken, D.J., Stewart, B.C., Maycock, T.K., Eds.; USGCRP: Washington, DC, USA, 2017; 470p. [Google Scholar] [CrossRef]
- Qian, B.; Gregorich, E.G.; Gameda, S.; Hopkins, D.W.; Wang, X.L. Observed soil temperature trends associated with climate change in Canada. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Schipper, L.A.; Hobbs, J.K.; Rutledge, S.; Arcus, V.L. Thermodynamic theory explains the temperature optima of soil microbial processes and high Q10 values at low temperatures. Glob. Chang. Biol. 2014, 20, 3578–3586. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, Q.; Melillo, J.M.; McGuire, A.D.; Kicklighter, D.W.; Prinn, R.G.; Steudler, P.A.; Felzer, B.S.; Hu, S. Net emissions of CH4 and CO2 in Alaska: Implications for the region’s greenhouse gas budget. Ecol. Appl. 2007, 17. [Google Scholar] [CrossRef]
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 65–173. [Google Scholar] [CrossRef] [PubMed]
- Melvina, A.M.; Larsenb, P.; Boehlertc, B.; Neumannc, J.E.; Chinowskye, P.; Espinete, X.; Martinichf, J.; Baumannc, M.S.; Rennelsc, L.; Bothnerc, A.; et al. Climate change damages to Alaska public infrastructure and the economics of proactive adaptation. Proc. Natl. Acad. Sci. USA 2017, 114, E122–E131. [Google Scholar] [CrossRef] [PubMed]
- Interagency Climate Adaptation Team. Adapting to Climate Change in Minnesota, Minnesota Pollution Control Agency; Document Number: p-gen4 -0; Interagency Climate Adaptation Team: MN, USA, 2017. [Google Scholar]
- Dunne, T.; Black, R.D. Runoff processes during snowmelt. Water Resour. Res. 1971, 7, 1160–1172. [Google Scholar] [CrossRef]
- Stähli, M.; Jansson, P.E.; Lundin, L.C. Soil moisture redistribution and infiltration in frozen sandy soils. Water Resour. Res. 1999, 35, 95–103. [Google Scholar] [CrossRef]
- Stähli, M. Hydrological significance of soil frost for pre-alpine areas. J. Hydrol. 2017, 546, 90–102. [Google Scholar] [CrossRef]
- Downer, C.W.; Ogden, F.L. Gridded Surface Subsurface Hydrologic Analysis (GSSHA) User’s Manual, Version 1.43 for Watershed Modeling System 6.1; ERDC/CHL SR-06-1; System Wide Water Resources Program, Coastal and Hydraulics Laboratory, U.S. Army Corps of Engineers, Engineer Research and Development Center: Vicksburg, MS, USA, 2006; 207p. [Google Scholar]
- Pradhan, N.R.; Downer, C.W.; Marchenko, S.; Lijedahl, A.; Douglas, T.A.; Byrd, A. Development of a Coupled Framework for Simulating Interactive Effects of Frozen Soil Hydrological Dynamics in Permafrost Regions; ERDC TR-13-15; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2013. [Google Scholar]
- Jafarov, E.E.; Marchenko, S.S.; Romanovsky, V.E. Numerical modeling of permafrost dynamics in Alaska using a high spatial resolution dataset. Cryosphere Discuss. 2012, 6, 89–124. [Google Scholar] [CrossRef]
- Marchenko, S.; Romanovsky, V.; Tipenko, G. Numerical modeling of spatial permafrost dynamics in Alaska. In Proceedings of the Nineth International Conference on Permafrost, Willey, Institute of Northern Engineering, University of Alaska, Fairbanks, AK, USA, 29 June–3 July 2008. [Google Scholar]
- Bolton, W.R.; Hinzman, L.D.; Yoshikawa, K. Stream flow studies in a watershed underlain by discontinuous peramafrost. In Water Resources in Extreme Environments; Kane, D.L., Ed.; American Water Resources Association: Anchorage, AK, USA, 2000; pp. 31–36. [Google Scholar]
- Rieger, S.; Furbush, C.E.; Schoephorster, D.; Sumnmerfield, H.; Geiger, L.C. Soils of the Caribou-Poker Creeks Research Watershed, Alaska; CRREL Technical Report 236, AD 744451; Cold Regions Research and Engineering Lab: Hanover, NH, USA, 1972. [Google Scholar]
- Farouki, O.T. The thermal properties of soils in cold regions. Cold Reg. Sci. Technol. 1981, 5, 67–75. [Google Scholar] [CrossRef]
- Konovalov, A.A.; Roman, L.T. The thermophysical properties of peat soils. Soil Mech. Found. Eng. 1973, 10, 179–181. [Google Scholar] [CrossRef]
- Nicolsky, D.J.; Romanovsky, V.E.; Tipenko, G.S. Using in-situ temperature measurements to estimate saturated soil thermal properties by solving a sequence of optimization problems. Cryosphere 2007, 1, 41–58. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D. Prediction of soil water properties for hydrologic modelling. In Watershed Management in the Eighties; Ward, T.J., Ed.; American Society of Civil Engineers: Reston, VI, USA, 1985; pp. 293–299. [Google Scholar]
- Viereck, L.A.; Dyrness, C.T. A Preliminary Classification Systems for Vegetation of Alaska; USDA Pacific Northwest Forest and Range Experiment Station, General Technical Report PNW-106; USDA: Washington, DC, USA, 1980.
- U.S. Department of Commerce. Monthly Normals of Temperature, Precipitation, and Heating and Cooling Degree-Days, 1941–1970; National Oceanic and Atmospheric Adminstration: Asheville, NC, USA, 1973.
- U.S. Department of Commerce. Local Climatological Data Annual Summary with Comparative Data, Fairbanks, Alaska; National Oceanic and Atmospheric Adminstration: Asheville, NC, USA, 1980.
- Downer, C.W.; Skahill, B.E.; Graulau-Santiago, J.A.; Weston, D.; Pradhan, N.R.; Byrd, A.R. Gridded Surface Subsurface Hydrologic Analysis Modeling for Analysis of Flood Design Features at the Picayune Strand Restoration Project; ERDC/CHL TR-15-X; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2015. [Google Scholar]
- Massey, T.C.; Pradhan, N.R.; Byrd, A.R.; Cresitello, D.E. USACE-ERDC coastal storm modelling systems in support of hurricane sandy operations. Flood Risk Manag. Newslett. 2013, 6, 2–3. [Google Scholar]
- Ogden, F.L.; Pradhan, N.R.; Downer, C.W.; Zahner, J.A. Relative importance of impervous area, drainage density, width function, and subsurface storm drainage on flood runoff from an urbanized catchment. Water Resour. Res. 2011, 47, W12503. [Google Scholar] [CrossRef]
- Pradhan, N.R.; Downer, C.W.; Johnson, B.E. A physics based hydrologic modeling approach to simulate non-point source pollution for the purposes of calculating TMDLs and designing abatement measures. In Practical Aspects of Computational Chemistry III; Leszczynski, J., Shukla, M.K., Eds.; Springer: New York, NY, USA, 2014; Chapter 9; pp. 249–282. [Google Scholar]
- Downer, C.W.; Pradhan, N.R.; Byrd, A. Modeling Subsurface Storm and Tile Drain Systems in GSSHA with Superlink; ERDC TR-14-11; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2014. [Google Scholar]
- Alexiades, V.; Solomon, A.D. Mathematical Modeling of Melting and Freezing Processes; Hemisphere: Washington, DC, USA, 1993; 325p. [Google Scholar]
- Verdi, C. Numerical Aspects of Parabolic Free Boundary and Hysteresis Problems; Lecture Notes in Mathematics; Springer: New York, NY, USA, 1994; pp. 213–284. [Google Scholar]
- Sergueev, D.; Tipenko, G.; Romanovsky, V.; Romanovskii, N. Mountain permafrost thickness evolution under the influence of long-term climate fluctuations (results from numerical simulation). In Proceedings of the 8th International Conference on Permafrost, Zürich, Switzerland, 21–25 July 2003; Taylor and Francis: Philadelphia, PA, USA, 2003; pp. 1017–1021. [Google Scholar]
- Marchuk, G.I.; Kuznetsov, Y.A.; Matsokin, A.M. Fictitious domain and domain decomposition methods. Sov. J. Num. Anal. Math. Modell. 1986, 1, 1–86. [Google Scholar] [CrossRef]
- Pollack, H.N.; Hurter, S.J.; Johnson, J.R. Heat flow from the earth’s interior: Analysis of the global data set. Rev. Geophys. 1993, 31, 267–280. [Google Scholar] [CrossRef]
- Lovell, C.W. Temperature effects on phase composition and strength of partially frozen soil. Highw. Res. Board Bull. 1957, 168, 74–95. [Google Scholar]
- Richards, L.A. Capillary conduction of liquids in porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Downer, C.W. Identification and Modeling of Important Stream Flow Producing Processes in Watersheds. Ph.D. Thesis, University of Connecticut, Storrs, CT, USA, 2002. [Google Scholar]
- Downer, C.W.; Ogden, F.L. Appropriate vertical discretization of Richards’ equation for two-dimensional watershed-scale modeling. Hydrol. Process. 2004, 18, 1–22. [Google Scholar] [CrossRef]
- Haverkamp, R.; Vauclin, M.; Touma, J.; Wierenga, P.J.; Vachaud, G. A Comparison of Numerical Simulation Models for One-Dimensional Infiltration. Soil Sci. Soc. Am. J. 1977, 41, 2. [Google Scholar] [CrossRef]
- Brooks, R.J.; Corey, A.T. Hydraulic Properties of Porous Media; Hydrology Paper 3; Colorade State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Huston, J.L.; Cass, A. A retentivity function for use in soil-water simulation models. J. Soil Sci. 1987, 38, 105–113. [Google Scholar]
- Downer, C.W.; Ogden, F.L. Prediction of runoff and soil moisture at the watershed scale: Effects of model complexity and parameter assignment. Water Resour. Res. 2003, 39, 1045. [Google Scholar] [CrossRef]
- Zhang, Y.; Carey, S.K.; Quinton, W.L.; Janowicz, J.R.; Pomeroy, J.W.; Flerhinger, G.N. Comparison of algorithms and parameterisations for infiltration into organic-covered permafrost soils. Hydrol. Earth Syst. Sci. 2010, 14, 729–750. [Google Scholar] [CrossRef]
- Schulla, J. Model Description WaSiM. 2017. Available online: http://www.wasim.ch/downloads/doku/wasim/wasim_2017_en.pdf (accessed on 2 January 2019).
- Monteith, J. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Monteith, J. Evaporation and surface temperature. R. J. Q. Meteorol. Soc. 1981, 107, 1–27. [Google Scholar] [CrossRef]
- Chapin, F.S.; Ruess, R.W. Caribou-Poker Creeks Research Watershed: Hourly Soil Moisture at Varying Depths from 2000 to Present. 2018. Available online: https://doi.org/10.6073/pasta/5207a6643bae4f9792aa21180bc1c08d (accessed on 9 December 2018).
- Senarath, S.U.S.; Ogden, F.L.; Downer, C.W.; Sharif, H.O. On the calibration and verification of two-dimensional, distributed, Hortonian, continuous watershed models. Water Resour. Res. 2000, 36, 1495–1510. [Google Scholar] [CrossRef]
- Engman, E.T. Roughness coefficients for routing surface runoff. J. Irrig. Drain. Eng. 1986, 112, 39–53. [Google Scholar] [CrossRef]
- Eagleson, P.S. Dynamic Hydrology; McGraw-Hill: New York, NY, USA, 1970; 461p. [Google Scholar]
- Sutton, O.G. Micrometeorology; McGraw Hill: New York, NY, USA, 1953; p. 68. [Google Scholar]
- Downer, C.W.; Wahl, M. EGU2017-10350 Conceptualizing Peatlands in a Physically-Based Spatially Distributed Hydrologic Model; European Geophysical Union: Munich, Germany, 2017. [Google Scholar]
- Whitfield, P.H.; Kamp, G.V.D.; St-Hilaire, A. Introduction to peatlands special issue: Improving hydrological prediction in Canadian peatlands. Can. Water Resour. J. 2009, 34, 303–310. [Google Scholar] [CrossRef]
- Bolton, W.R.; Hinzman, L.; Yoshikawa, K. Water balance dynamics of three small catchments in a Sub-Arctic boreal forest. In Northern Research Basins Water Balance (Proceedings of a Workshop Held at Victoria, Canada, March 2004); Kane, D.L., Yang, D., Eds.; IAHS: London, UK, 2004; pp. 213–223. [Google Scholar]
- Haugen, R.K.; Slaughter, C.W.; KEHowe, K.E.; Dingman, S.L. Hydrology and Climatology of the Caribou-Poker Creeks Research Watershed, Alaska; CRREL Report 82-26; U.S. Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1982. [Google Scholar]


| Soil Series | USDA Texture | Drainage | Soil Heat Conductivity (W/mK) | Soil Volumetric Heat Capacity (J/m3K) | Saturated Hydraulic Conductivity (cm/hour) |
|---|---|---|---|---|---|
| Fairplay | Silt loam and gravelly silt loam | Moderately well drained | 0.1–2.8 | 1,600,000–2,800,000 | 0.6 |
| Olnes | Silt loam and very gravelly silt loam | Well drained | 0.1–2.8 | 1,600,000–2,800,000 | 0.6 |
| Soil Heat Conductivity (W/mK) | Soil Volumetric Heat Capacity (J/m3K) |
|---|---|
| 3.0 | 2,800,000 |
| Land Use Type | Manning’s Roughness Values |
|---|---|
| Coniferous open | 0.17 |
| Coniferous woodland | 0.19 |
| Deciduous closed | 0.2 |
| Shrub tall | 0.25 |
| Infiltration Parameter | Soil Layer | ||
|---|---|---|---|
| Top | Middle | Lower | |
| Soil thickness (m) | 0.20 | 0.50 | - |
| Saturated hydraulic conductivity (m/s) | 0.00008 | 0.00008 | 0.00008 |
| Pore size distribution index | 0.60 | 0.694 | 0.694 |
| Bubbling Pressure head (m) | 0.08 | 0.06 | 0.06 |
| Porosity (m3/m3) | 0.42 | 0.40 | 0.40 |
| Residual soil moisture content (m3/m3) | 0.04 | 0.045 | 0.045 |
| Land Use Type | Albedo | Vegetation Height (m) | Canopy Resistance (s/m) | Transmission Coefficient |
|---|---|---|---|---|
| Coniferous open | 0.15 | 10 | 120 | 0.18 |
| Coniferous woodland | 0.15 | 10 | 120 | 0.18 |
| Deciduous closed | 0.2 | 12 | 200 | 0.18 |
| Shrub tall | 0.2 | 1.3 | 150 | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pradhan, N.R.; Downer, C.W.; Marchenko, S. Catchment Hydrological Modeling with Soil Thermal Dynamics during Seasonal Freeze-Thaw Cycles. Water 2019, 11, 116. https://doi.org/10.3390/w11010116
Pradhan NR, Downer CW, Marchenko S. Catchment Hydrological Modeling with Soil Thermal Dynamics during Seasonal Freeze-Thaw Cycles. Water. 2019; 11(1):116. https://doi.org/10.3390/w11010116
Chicago/Turabian StylePradhan, Nawa Raj, Charles W. Downer, and Sergei Marchenko. 2019. "Catchment Hydrological Modeling with Soil Thermal Dynamics during Seasonal Freeze-Thaw Cycles" Water 11, no. 1: 116. https://doi.org/10.3390/w11010116
APA StylePradhan, N. R., Downer, C. W., & Marchenko, S. (2019). Catchment Hydrological Modeling with Soil Thermal Dynamics during Seasonal Freeze-Thaw Cycles. Water, 11(1), 116. https://doi.org/10.3390/w11010116






