Abstract
The study investigates the hierarchical uncertainty of multi-ensemble hydroclimate projections for the Southern Hills-Gulf region, USA, considering emission pathways and a global climate model (GCM) as two main sources of uncertainty. Forty projections of downscaled daily air temperature and precipitation from 2010 to 2099 under four emission pathways and ten CMIP5 GCMs are adopted for hydroclimate modeling via the HELP3 hydrologic model. This study focuses on evapotranspiration (ET), surface runoff, and groundwater recharge projections in this century. Climate projection uncertainty is characterized by the hierarchical Bayesian model averaging (HBMA) method, which segregates emission pathway uncertainty and climate model uncertainty. HBMA is able to derive ensemble means and standard deviations, arising from individual uncertainty sources, for ET, runoff, and recharge. The model results show that future recharge in the Southern Hills-Gulf region is more sensitive to different climate projections and exhibits higher variability than ET and runoff. Overall, ET is likely to increase and runoff is likely to decrease in this century given the current emission path scenarios. Runoff are predicted to have an 18% to 20% decrease and ET is predicted to have around a 3% increase throughout the century. Groundwater recharge is likely to increase in this century with a decreasing trend. Recharge would increase about 13% in the early century and will have only a 3% increase in the late century. All hydrological projections have increasing uncertainty towards the end of the century. The HBMA result suggests that the GCM uncertainty dominates the overall hydrological projection uncertainty in the early century and the mid-century. The emission pathway uncertainty becomes important in the late century.
1. Introduction
Uncertainties in hydroclimate projections provide necessary information to support the planning and management of future water recourses, but those uncertainties have not been sufficiently addressed in the IPCC (Intergovernmental Panel on Climate Change) Fifth Assessment [1]. It is imperative to quantify the uncertainty associated with climate projections in order for detection and attribution as well as for adaptation and mitigation strategies [2]. The anthropogenic forcing impacts are investigated through future climate projections using general circulation models or global climate models (GCMs). There are different types uncertainties associated with GCM projections, which are mainly from model representations, scenarios, and internal model variability [3,4]. In addition to the various sources of uncertainty inherent in GCMs, additional uncertainties are also introduced during downscaling of raw GCM output for hydrologic simulation. Uncertainties resulting from GCMs and greenhouse gas (GHG) emissions generally have been given more attention in the uncertainty assessment of hydrological impacts of climate change [5]. There has been a growing interest in evaluating total uncertainty in future hydrologic projections using combinations of emission scenarios, climate models, downscaling methods, and hydrologic models [6,7,8,9,10,11,12,13,14,15].
Assessment using a single model is prone to underestimate uncertainty. There is no single model proclaimed as the best model due to the inaccuracy of each individual GCM. Hence, future climate projections should take into account multiple GCMs [16,17]. Compared to a single GCM approach, a multi-model ensemble of GCMs often increases reliability of information, and its average shows more consistency with climate observations [16,18]. The IPCC suggests using multi-model ensembles for evaluating climate projections [19]. In addition, weighting models based on some indices of performance might further increase the reliability of projections. Model weights can be defined based on model performance in simulating historical climate [20,21,22,23,24,25,26].
To integrate projections and quantify uncertainty from using multiple prediction models, Bayesian model averaging (BMA) [27] takes into account observational data evidence to determine model weights for averaging, and it performs better than other multi-model methods [28,29]. Many studies, such as weather forecasting [30,31], ensemble of climate models [32,33,34,35], and hydrological prediction [36,37,38,39,40,41,42], have adopted BMA for ensemble prediction and uncertainty analysis.
Moving forward, it is of great importance to better understand the influence of individual sources of uncertainty [43] as well as their relative contribution to the full hydroclimate uncertainty space. To address this issue, we utilize a hierarchical Bayesian model averaging (HBMA) method [44] that can systematically segregate sources of uncertainty in a hierarchical structure (known as the BMA tree).
We target hydroclimate modeling uncertainties arising from downscaled precipitation and air temperature (hereafter as temperature) projections and use hydroclimate modeling on the Southern Hills-Gulf region for illustration. This study uses the downscaled precipitation and temperature projections from References [45,46], where there are 21 Coupled Model Intercomparison Project phase 5 (CMIP5) GCMs developed by 16 organizations. Some downscaled data were derived by the same GCM with different initial conditions. Some GCMs were not run for the entire four representative concentration pathways (RCP2.6, RCP4.5, RCP6.0, and RCP8.5). This study selects 10 GCMs (see Table 1) that were run for all four RCPs with one initial condition. A HELP3 model [47] was built to simulate future surface runoff, evapotranspiration, and groundwater recharge based on the selected downscaled precipitation and temperature projections.

Table 1.
Modeling centers/groups and the corresponding downscaled data of 10 GCMs under the four representative concentration pathways (RCP2.6, RCP4.5, RCP6.0, and RCP8.5) [45,46] for the Southern Hills-Gulf region.
2. A Hierarchical Uncertainty Analysis Framework
2.1. Bayesian Model Averaging (BMA) Tree
To organize the multiple sources of uncertainty embedded in hydroclimate projections, a BMA tree [44] is adopted. Figure 1 shows a hierarchical structure of CMIP5 multi-model ensembles considering the choices of emission pathways and GCMs as the two main sources of uncertainty. Each source of uncertainty creates a number of mutually exclusive propositions (i.e., unique modeling choices). The future emission scenario is placed at the first level, which contains four propositions: RCP2.6, RCP4.5, RCP6.0, and RCP8.5. Under each emission pathway, different GCMs are placed at the second level. When other sources of uncertainty are considered (e.g., different downscaling approaches, hydrologic models, or model parameter sets), the uncertainty structure in Figure 1 can be further expanded.
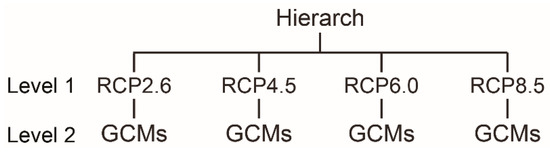
Figure 1.
Hierarchical structure of sources of uncertainty in the CMIP5 multi-model ensembles.
In the BMA tree, a parent model is a model at a vertex of a level, and a model one level below the parent model is a child model. The model at the apex of the BMA tree is called the hierarch model, which is a union of all sub-models. Each source of uncertainty corresponds to each level in the BMA tree and builds on top of other sources of uncertainty lower on the tree. The base level of the BMA tree depicts base models resulting from combinations of propositions at all different levels. Increasing the number of sources of uncertainty increases the number of levels of the BMA tree and the number of models. Through a BMA tree, the collective uncertainty from all child models can be hierarchically summarized into their parent models. This approach may enable the illustration of different sources of uncertainty in a clear and organized fashion.
2.2. Hierarchical Bayesian Model Averaging (HBMA)
Given p sources of uncertainty, base models, at level p are created, where the subscript locates a base model top down in the hierarchy (see Figure 1 for an example) from the first level to the second level and so forth to reach to base level p. For instance, the ith model at the first level of a BMA tree is denoted by , the jth model at level 2, a child model of , is denoted by , and so forth, until the base level p is reached. Furthermore, models at level p − 1 are BMA models of their corresponding child base models at level p, models at level p − 2 are BMA models of their corresponding child BMA models at level p − 1, and so forth, until the hierarch level is reached [44]. At the hierarch level (level zero), it is called “the hierarch BMA model”, where predictions are based on all base models and thus ensemble averaging results are the same as using the BMA model in Hoeting et al. [27].
The posterior probability for a predicted quantity Δ at level n given observational data D and models at level n + 1 is:
where is the expectation operator, which calculates the mean over models as follows:
where are the conditional posterior model probabilities for models at level n + 1 under their parent models at level n, which are calculated by:
where are the posterior model probabilities for models at level n + 1, and posterior model probabilities at level n are given by:
Equation (4) shows that posterior model probabilities at level n can be calculated as long as the posterior model probabilities of base models are known.
Note that the posterior model probabilities in the BMA paradigm do not represent absolute importance, but they are relative probabilities for the models selected by the analyst. Posterior model probabilities change when the pool of models changes. Moreover, Using BMA or HBMA takes place under the mutually exclusive and collectively exhaustive (MECE) principle, where models are considered to be mutually independent of each other and the combination of all models covers all possible outcomes. Analysts should exhaust all possible models for ensemble analysis.
Since Equation (1) is a recursive equation, one can expand the right-hand side of Equation (1) up to the base models:
Using the law of total expectation and law of total variance, the expectation and variance of predicted quantity Δ at level n are:
where is the prediction mean of Δ given observational data D and models at level p. is the prediction variance using models at level n + 1. It includes the within-model variance and the between-model variance . is the variance operator, which calculates the between-model variance using models at level n + 1. For example, given an RCP at level 1 (see Figure 1), is the projection variance for Δ using various GCMs () at level 2 under the same RCP. The within-model variance is the expectation of projection variances of individual GCMs, , under the same RCP. The between-model variance is due to the variation of the mean predicted Δ by different GCMs at level 1.
Since Equation (7) is a recursive equation, the within-model variance is obtained using:
which contains the within-model variance and the between-model variance for Δ using models at level n + 2. The between-model variance is:
2.3. Mean and Variance at the Hierarch Level
The prediction mean of Δ at the hierarch level can be obtained by averaging the prediction means of models at level 1 or using Equation (2) recursively from the base level to level 1:
The total prediction variance of Δ at the hierarch level is:
Equation (11) is used to evaluate the contribution of individual sources of uncertainty to the total uncertainty. Using Figure 1 as an example, the total variance of multi-model hydroclimate projections can be decomposed into three components:
The first term on the right-hand side of Equation (12) is the projection variance due to emission pathway. The second term is the projection variance caused by different GCMs. The third term is the projection variance caused by parameter uncertainty in individual climate models, which can be assessed by the perturbations of parameters over the range of plausible values [48]. However, given that such information is unavailable for most of the CMIP5 models, the third term is not considered in this study.
The relative contributions of these sources of uncertainty are defined as the proportions of their corresponding variance terms to the total variance. Building upon the conventional BMA method [27], this HBMA method provides a theoretical sound foundation for the quantification of relative contributions from different sources of uncertainty in multi-ensemble hydroclimate projections.
3. Case Study
3.1. Study Area and Model Data
Figure 2 shows the study area, the Southern Hills-Gulf region. The study area covers the Southern Hills regional aquifer system [49] and the Gulf region of southeastern Louisiana. We analyze hydroclimate projection uncertainty due to emission scenarios and GCM uncertainties. The study area lies between latitudes 28.93° N and 33.06° N and between longitudes 88.81° W and 91.98° W and covers 79,126 km2. It includes 28 parishes of Louisiana and 20 counties of Mississippi. The area contains 26 U.S. Geological Survey (USGS) 8-digit hydrologic units (HUC8 or subbasin) and 728 12-digit hydrologic units (HUC12 or subwatershed) with average sizes of 588 and 33 km2, respectively. Precipitation at the outcrops in southwestern Mississippi is the main source of water to the deep aquifers in southeastern Louisiana.
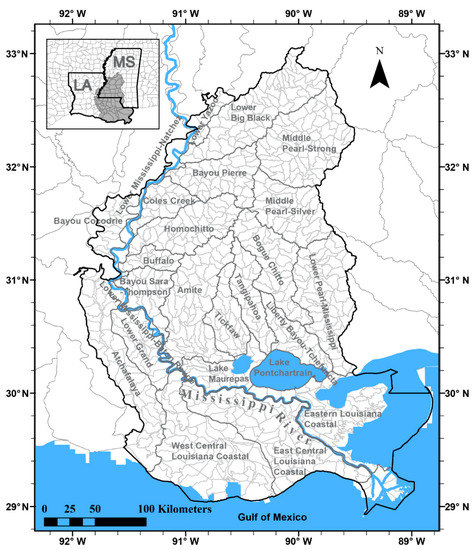
Figure 2.
The study area of the Southern Hills-Gulf region, which includes 26 HUC8 (dark gray lines) and 728 HUC12 (light gray lines).
To evaluate the posterior model probability for each GCM, the gridded 1950–2006 monthly precipitation and temperature observation over the study area were obtained from Maurer et al. [50] and Maurer [51]. The horizontal grid resolution of precipitation and temperature is 1/8° (≈12 km), which covers 439 cells in the study area.
To enable high spatial-resolution hydrologic projections, this study created vector-based data maps that included land use/land cover, topographic slope, base flow index, HUC8 boundaries, surficial soil type, leaf area index (LAI), lithology, precipitation, and temperature, and intersected the data maps using Esri ArcGIS 10.2. As a result, the study area was divided into 2,669,533 subdivisions, each of which had homogeneous model parameters for high-performance hydrologic simulation. Detailed information on the various data and maps for the study area can be found in Beigi and Tsai [52,53].
3.2. Climate Projections
3.2.1. Downscaled Climate Projection Data Set
The downscaled daily precipitation and temperature projections from 1950 to 2099 were obtained from the Downscaled CMIP3 and CMIP5 Climate and Hydrology Projections data archive [45,46], where the bias corrected constructed analogs (BCCA) method was used to downscale the raw GCM outputs to 1/8° (≈12 km) horizontal resolution, which is consistent with the gridded observations [50,51]. The archive integrates the state-of-the-art climate models and the most recent GHG emission scenarios [54]. The historical GHG forcing was used during the baseline control simulation (before 2006), and followed by four RCPs—RCP2.6, RCP4.5, RCP6.0, and RCP8.5—representing the lowest, lower, midrange, and highest emission pathways, respectively. RCP2.6 is the most optimistic scenario that features the least warming (0.3–1.7 °C) and the lowest GHG concentration. On the contrary, RCP8.5 portrays the most pessimistic scenario that features the highest GHG concentration and the greatest warming (2.6–4.8 °C) across the 21st century [55].
A total of 40 sets of climate projections that are combinations of four RCPs and 10 CMIP5 GCMs were comprehensively collected (see Table 1). Referring to the hierarchical structure illustrated in Figure 1, there are four propositions (RCPs) in the first level. Under each RCP, there are 10 propositions (GCMs) in the second level. Note also that because downscaled climate projections were available only under the BCCA downscaling method, this case study did not consider uncertainty from other downscaling techniques.
3.2.2. Climate Model Evaluation
Although there are various approaches to evaluating the reasonableness of a GCM from different perspectives (e.g., using observed sea surface temperature [56,57]), given our specific hydrologic simulation needs, we focused on examining the similarity of simulated 1950–2006 monthly temperature and precipitation observations to historical observations. Based on the CMIP5 experimental design, the climate projections across different RCPs from a particular GCM will have a common baseline period (before 2006). Therefore, we evaluated the 10 GCMs listed in Table 1 as a basis to estimate the posterior model probabilities in Equation (4). Because statistical bias-correction has been a part of BCCA (i.e., the long-term mean has been corrected by observation), the performance evaluated herein was mainly governed by the similarity of interannual variability of temperature and precipitation to historical observations. The study also assumed equal prior model probability for the 10 climate models before their outputs were compared to the historical precipitation and temperature data.
By adopting the Bayesian information criterion (BIC) and the variance window [58], the posterior model probabilities of the climate models were approximated as follows:
where and α is the scaling factor that determines the size of the variance window. is the BIC value of climate model , and BICmin is the minimum BIC value among the climate models. Focusing on monthly precipitation and temperature, the BIC can be written as:
where and are the ith simulated monthly precipitation and temperature by model , and are the ith observed monthly precipitation and temperature, and are the ith error variance of precipitation and temperature, N is the total number of monthly data from the 439 cells and from 1950 to 2006 (N = 439 × 57 × 12), and is the number of model (GCM) parameters. The first two terms on the right-hand side of Equation (14) are the weighted fitting residuals. The term represents the complexity of climate model . Due to the lack of information on the complexity term in Equation (14), this study assumed equal model complexity for all climate models such that the complexity term had no effect on values or posterior model probabilities.
3.3. Hydrologic Modeling
In this study, HELP3 [47] was adopted to estimate evapotranspiration (ET), surface runoff, and groundwater recharge in the Southern Hills-Gulf region given the aforementioned climate projections. HELP3 is a quasi-two-dimensional hydrologic model that simulates processes including ET, surface runoff, soil moisture storage, and vertical unsaturated drainage for individual layered soil columns. The HELP3 model has been used in many hydrological studies to estimate groundwater recharge, runoff, and ET (e.g., References [59,60,61,62,63]) and has been extensively verified to be a suitable model for hydrologic studies [47,64,65].
3.3.1. HELP3 Input Data
Daily precipitation, temperature, solar radiation, annual wind speed, and quarterly relative humidity are required inputs to the HELP3 model. For this study, we compiled historical daily precipitation and temperature data from 1950 to 2009 at a 12-km resolution from Maurer et al. [50] and Maurer [51]. We also compiled averaged quarterly relative humidity and annual wind speed that were obtained from the Southern Regional Climate Center [66]. The downscaled solar radiation data were generated synthetically using the weather generator (WGEN) model of Richardson and Wright [67].
Detailed surficial soil texture classes were obtained from the Natural Resources Conservation Service [68] for each soil layer in the HELP3 model. Land use and land cover data at high spatial resolution (30 m) were obtained from the National Land Cover Dataset 2011 [69], which is the latest national land cover product produced by the Multi-Resolution Land Characteristics (MRLC) Consortium [70]. The status quo of land use/land cover and soil type is assumed as inputs to HELP3 for 2010–2099.
3.3.2. Parallel Computation for High-Resolution Hydrologic Prediction
Forty sets of downscaled daily precipitation and temperature projections were used as input to drive the HELP3 model that projects future evapotranspiration, surface runoff and groundwater recharge. For each of the 40 climate projections, a large number (2,669,533) of HELP3 model runs were needed for hydrologic prediction for the study area. It was computationally impractical to execute millions of HELP3 model runs in a single-core processor. The Python programming language was used in this study to feed 2,669,533 HELP3 model runs to SuperMike-II, a supercomputer with multiple cores at Louisiana State University for parallel computation. SuperMike-II is a 146-TFlop Peak Performance cluster running on the Red Hat Enterprise Linux 6 operating system. SuperMike-II contains 440 compute nodes, each of which consists of two 8-Core Sandy Bridge Xeon 64-bit processors with 2.6 GHz core frequency.
We used the USGS WaterWatch runoff data of the hydrologic units (see Figure 2) to adjust the curve number (CN) for each subdivision in the HELP3 model. Yearly USGS computed runoffs from 1950 to 2009 (60 years) were used for model calibration. Based on the regression Equation (34) in HELP Engineering Documentation for Version 3 [47], an equation was proposed to adjust user-specified antecedent moisture condition II (AMC-II) curve number for different topographic slope and slope length conditions for each subdivision. The optimal curve numbers (CNs) for each hydrologic unit were obtained by minimizing the sum of squared errors of the HELP3 calculated to USGS computed direct runoffs as follows:
where is the calculated direct runoff at year t for hydrologic unit u from the HELP3 model and is the computed direct runoff at year t for hydrologic unit u from the USGS WaterWatch database. Readers are referred to Beigi and Tsai [52] for detailed model calibration techniques. The root mean square error (RMSE) on yearly runoff ranges from 90.32 to 137.45 mm, which are much smaller than the range of the WaterWatch yearly runoff data. The Nash–Sutcliffe model efficiency coefficient (NSE) ranged from −0.10 to 0.50. The lowest three NSE values are −0.10, 0.10, and 0.11 for Coles Creek, Bayou Cocodrie, and Lake Maurepas HUC8s, respectively. Other HUC8s have an NSE higher than 0.15. Watersheds with low NSE show high runoff variability in the WaterWatch data. Low NSE indicates that the HELP3 predictions are as accurate as the mean of the WaterWatch data but cannot capture the data variability. The highest three NSE values are 0.50, 0.47, and 0.44 for Tangipahoa, Middle Pearl-Silver, and Middle Pearl-Strong HUC8s, respectively.
We used the estimated ET from the MOD16 evapotranspiration dataset [71,72] to verify the calibrated HELP3 model. The RMSE of the HELP3 yearly estimated ET from 2000 to 2010 versus the MOD16 yearly computed ET is 93.52 mm, which is much smaller than the range of the MOD16 ET estimates. The NSE is 0.59.
4. Results and Discussion
4.1. Posterior Model Probabilities
Based on Equations (13) and (14), we evaluated the posterior model probabilities for the 10 GCMs listed in Table 1 using simulated and observed 1950–2006 monthly temperature and precipitation observations. Table 2 summarizes the weighted fitting residuals and ΔBIC values for the 10 climate models with individual posterior model probabilities. The GCM model, gfdl-esm2g.1, had the highest posterior model probability (23.0%), followed by miroc-esm-chem.1 (19.4%) and miroc5.1 (14.7%).

Table 2.
Posterior model probabilities of 10 climate models based on monthly precipitation and temperature data 1950–2006 in the Southern Hills-Gulf region.
The posterior model probabilities of GCMs in Table 2 represent conditional posterior model probabilities at level 2 under each RCP shown in Figure 3. The GCM probability distributions were the same under each RCP; therefore, each RCP had a posterior model probability 25% at level 1. The posterior model probabilities of GCMs at level 2, according to Equation (3), are shown in Figure 3.
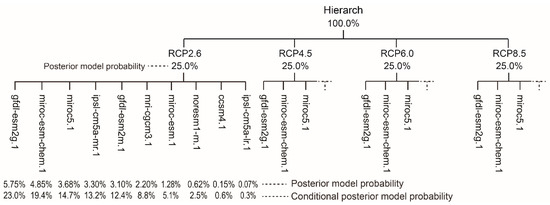
Figure 3.
A BMA tree of posterior model probabilities for emission pathways and GCMs at levels 1 and 2.
4.2. Temporal Analysis with HBMA
Recharge, runoff, and ET projections in the Southern Hills-Gulf region for 2010–2099 using the first and the second best GCM members at level 2 for four emission pathways are shown in Figure 4. Projected recharge showed much larger variability compared to runoff and ET projections. Recharge quantities projected by different climate models were quite different. The ET projection for the 21st century was consistently high regardless of climate models and emission pathways.
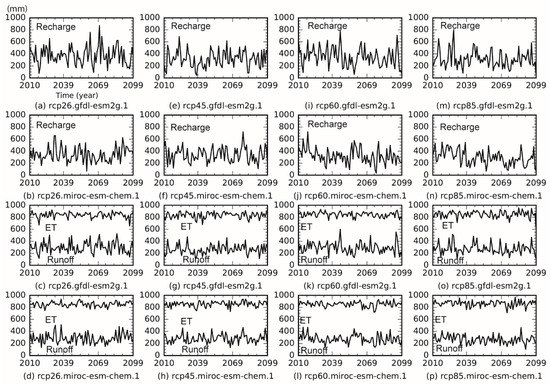
Figure 4.
Annual recharge, ET and runoff projections (2010–2099) in Southern Hills-Gulf region using the best and the second-best climate models at level 2.
Using BMA at level 1, the mean projection and standard deviation of recharge, runoff, and ET due to using the 10 GCMs are shown in Figure 5. Recharge projection showed the highest uncertainty, and ET projection showed the lowest uncertainty. Using linear trend analysis, RCP2.6 projected an increasing trend (the slope of a linear model = 0.31 mm/year) in recharge while RCP4.5 (slope = −0.46 mm/year), RCP6.0 (slope = −1.01 mm/year), and RCP8.5 (slope = −1.16 mm/year) each showed a decreasing trend in recharge. For runoff projection, RCP2.6 projected an increasing trend (slope = 0.25 mm/year), and RCP4.5 (slope = −0.06 mm/year), RCP6.0 (slope = −0.31 mm/year), and RCP8.5 (slope = −0.24 mm/year) each showed a decreasing trend. None of the emission pathways showed a noticeable trend (slope was positive, but less than 0.1 mm/year) in the ET projections. Generally speaking, ET tended to increase as recharge and runoff were likely to decrease as RCP tended toward more pessimistic scenarios.
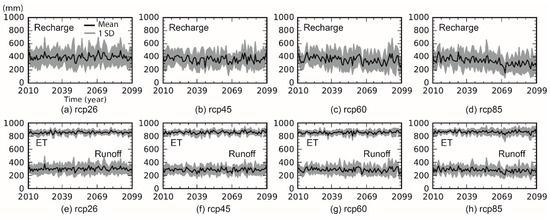
Figure 5.
Means and one standard deviation (SD) intervals of annual recharge, ET and runoff projections (2010−2099) in the Southern Hills-Gulf region using all climate models under corresponding emission pathways at level 1.
Figure 6 shows the annual recharge, runoff, and ET predictions from 2010 to 2099. The BMA mean and one standard deviation interval resulted from the 10 GCMs and 4 emission pathways in a hierarchical order (Figure 3). The results of all 40 climate projections indicate that mean recharge would slightly decrease while mean runoff and ET would remain the same throughout 2099. The temporal averages (and ranges) of the coefficient of variation (CV) for yearly recharge, runoff, and ET projections were 40.1% (31.5–54.1%), 28.6% (23.3–35.6%), and 5.4% (3.6–8.9%), respectively. Projected ET and runoff have smaller CVs than projected recharge, indicating that recharge estimation was more sensitive to climate projections. Moreover, as shown in Figure 4, Figure 5 and Figure 6, the loss in the variability of mean hydrologic projections compared to individual hydrologic projections was compensated by the increase in projection variances. Therefore, the variability of future projections was implicitly preserved in the HBMA method.
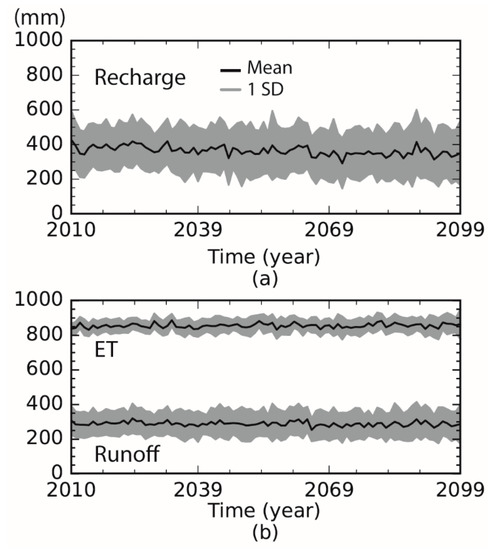
Figure 6.
Means and one standard deviation (SD) intervals of (a) annual recharge, and (b) ET and runoff projections (2010–2099) in the Southern Hills-Gulf region at the hierarch level.
4.3. Future Hydrologic Projection Anomalies
Future hydrologic projection anomalies with respect to historical means were assessed by looking into the future 30-year mean projected changes with respect to the mean annuals between 1950 and 2009. The future recharge, runoff, and ET projection anomalies at different BMA levels is shown in Table 3. The estimated mean annual ET, runoff, and recharge between 1950 and 2009 were 832.9, 352.8, and 337.4 mm, respectively, which accounted for 54.4%, 23.1%, and 22.1% of the mean annual precipitation. The best and the second-best climate models at level 2 in Table 3 under each emission pathway gave more positive recharge anomalies than negative recharge anomalies in 2010–2069, indicating that recharge is likely to increase in this 60-year period. From 2070 to 2099, recharge is likely to increase under RCP2.6 and is likely to decrease under RCPs 6.0 and 8.5. The rcp26.gfdl-esm2g.1 model projected the highest recharge increase (13.49%), while the rcp85.miroc-esm-chem.1 model projected the largest recharge decrease (−33.0%) between 2070 and 2099. With respect to the historical mean, the runoff is predicted to decrease and ET is predicted to increase throughout 2099.

Table 3.
Anomalies of mean annuals in 2010–2039, 2040–2069, and 2070–2099 to mean annuals of 1950–2009 in recharge, runoff, and evapotranspiration (ET) in the Southern Hills-Gulf region. Only the best and the second best GCMs under each emission path are listed in level 2.
Consistent results were found between the projection anomalies at level 1 (Table 3) and the established future emissions. Under the assumption of lesser warming and lower GHG concentration, the RCP2.6 and RCP4.5 projected recharge increase was between 4.5% and 19.6% in the 21st century. RCP6.0 and RCP8.5 also projected more than a 10% recharge increase in 2010–2039. However, the recharge could be significantly reduced by as much as 16% toward the end of the century. All emission pathways (level 1) showed consistent projections that runoff is predicted to decrease between 15% and 25%, while ET is predicted to increase between 2% and 4% in this century.
Using all the 40 climate projections (the hierarch model), the modeling results show that recharge in the Southern Hills-Gulf region is likely to increase 13% in 2010–2039. This is due to increase in precipitation and decrease in surface runoff in 2010–2039. However, the recharge increase would reduce to only 3% in 2070–2099 because of the decrease in precipitation. Runoff is likely to decrease between 18% and 20% and ET is likely to increase around 3% in this century.
4.4. Spatial Analysis
Figure 7 shows the mean annual ET, recharge, and runoff distributions over the 728 HUC12s using all 40 climate projections. The maximum changes of ET, runoff, and recharge projections over the three 30-year periods were only 38.6 mm, 56.2 mm, and 44.7 mm, respectively. Outcrops of Miocene deposits in southwestern Mississippi showed a high recharge rate, which indicated good future groundwater recharge to deep sands (e.g., the “2000-foot” sand and the “2400-foot” sand) in southeastern Louisiana. Figure 8 shows the spatial distributions of BMA standard deviations. Projection uncertainty increased toward the end of the century for all hydrologic projections. Annual recharge projection had the greatest uncertainty. In 2070–2099, the standard deviation of projected annual recharge had a large range from 4.1 to 123.2 mm, followed by runoff (1.7–96.7 mm) and ET (7.8–45.6 mm).
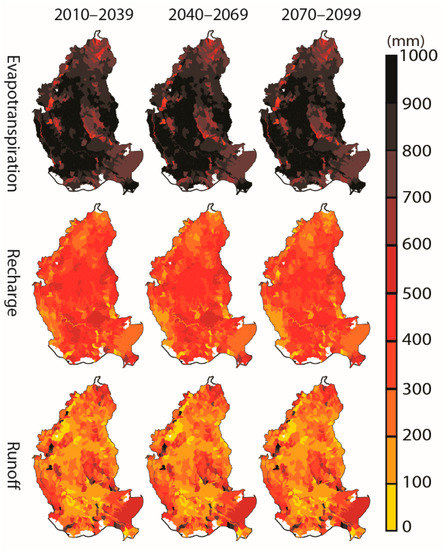
Figure 7.
Means of annual ET, recharge, and runoff projections in 2010–2039, 2040–2069, and 2070–2099 at the hierarch level for the Southern Hills-Gulf region.
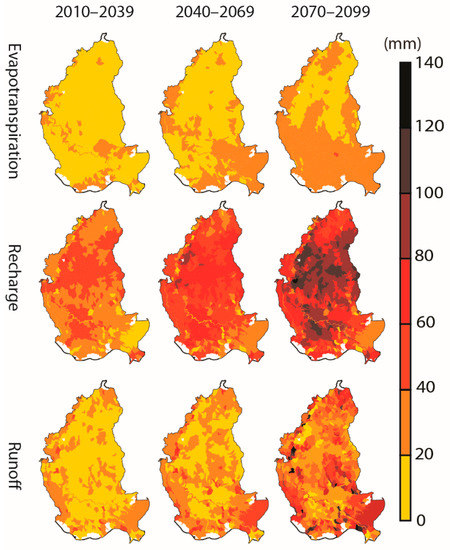
Figure 8.
Standard deviations of annual ET, recharge, and runoff projections in 2010–2039, 2040–2069, and 2070–2099) at the hierarch level for the Southern Hills-Gulf region.
4.5. Contributions of Sources of Uncertainty
Contributions of individual sources of uncertainty from the emission paths and climate models to the total recharge projection uncertainty are shown in Figure 9. The contributions are the proportions of variances in the first and the second terms in Equation (12) to the sum of the three variances. Figure 9 shows that the dominant source of uncertainty in hydrologic projections came from GCM uncertainty. Moreover, emission pathway uncertainty increased toward the end of the century because under different emission paths, hydrologic projections started to diverge significantly after the mid-century. Table 4 shows the uncertainty contributions from GCMs and emission paths to the projected recharge. In 2010–2039, almost all uncertainty in recharge projection came from GCM uncertainty, which reduced to 66.0% in 2070–2099. Emission path uncertainty grew from 5.4% in 2010–2039 to 34% in 2070–2099. The standard deviations were small, indicating that variations of individual source uncertainty contributions across the 728 HUC12s were small. Although not presented, the GCM and emission path uncertainties had similar contributions to the projected runoff and ET.
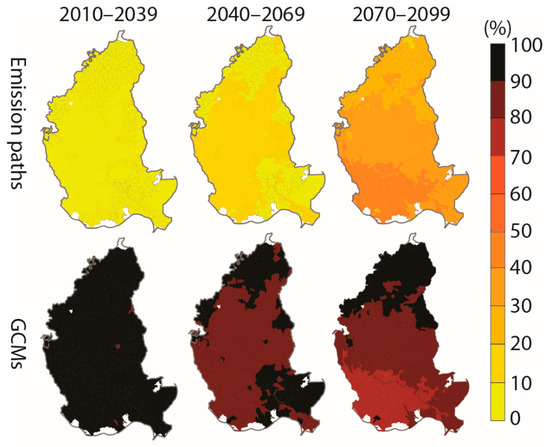
Figure 9.
Uncertainty contribution (%) in 2010–2039, 2040–2069, and 2070–2099 from emission paths and GCMs to the projected recharge in the Southern Hills-Gulf region.

Table 4.
Means and standard deviations (SD) of uncertainty contributions in 2010–2039, 2040–2069, and 2070–2099 from emission paths and GCMs to the projected recharge (including all 728 HUC12) in the Southern Hills-Gulf region.
The finding that GCM uncertainty dominated in hydrological projections is consistent with many studies [6,8,73,74,75], although numerical quantification of contributions in the literature is not as available as in this study. Hosseinzadehtalaei et al. [76] found that the choice of GCMs is the major contributor (up to 65% for some cases) toward intensifying precipitation change uncertainty for all return periods. Also, Mandal et al. [77] concluded that the choice of GCMs is the largest sources of uncertainty of the climate change impacts on total monthly precipitation when uncertainty arising from downscaling methods are excluded. Taylor and Kingston [78] found that GCM-related uncertainty substantially dominates uncertainty associated with climate sensitivity and hydrological model parametrization. Also, Teng et al. [75] indicated that uncertainty due to GCMs is significantly greater than uncertainty sources from rainfall-runoff models in assessing climate change impacts on runoffs. Kay et al. [8] investigated six different sources of uncertainty including: GCM structure, downscaling method, hydrological model structure, hydrological model parameters, and internal variability of climate system. Their results suggested that uncertainty arising from GCM structure is the largest source of uncertainty in studying impacts of climate change on flood frequency in England. In summary, regardless of the number of sources contributing to total uncertainty, there is a consensus among previous studies that GCM uncertainty is the major source of uncertainty when assessing the impact of climate change on hydrologic projections (e.g., References [8,79]).
The other finding is also consistent with Northrop and Chandler [80] where uncertainty resulting from the choice of emission pathways becomes more important toward the end of the twenty-first century. This indicates that climate model parameterizations, sensitivities, and responses to greenhouse gases and other forcings grow over time and become evident. Although the contribution of GCM uncertainty to the total uncertainty decreases every 30-year period, this does not mean that GCM uncertainty decreases over time, but reflects the significant growth of emission pathway uncertainty. The total uncertainty actually increased towards the end of the century as shown in Figure 8.
5. Conclusions
The hierarchical Bayesian model averaging (HBMA) method is able to characterize the hierarchical natural of sources of uncertainties in climate projections. The HBMA was shown be to a good approach to analyze 40 sets of CMIP5 BCCA-downscaled daily precipitation and temperature projections that were generated using 10 GCMs and 4 emission paths. Through the HELP3 model, the HBMA was able to derive means and variances of ET, runoff, and groundwater recharge projections under climate model uncertainty and emission path scenario uncertainty.
This study conducted hydroclimate modeling for the Southern Hills-Gulf region, which is computationally demanding because the HELP3 model is highly parameterized, where 40 sets of daily precipitation and temperature projections are used, and the simulation period is a century long. By using the CPU-based multi-core supercomputer, this study was able to efficiently execute several million runs of the HELP3 model in order to quantify climate-related hydrologic projection uncertainty.
Projected groundwater recharge shows higher spatial and temporal variability and variance than ET and runoff in the Southern Hills-Gulf region, indicating that recharge estimation is more sensitive to climate projections. Evapotranspiration projection shows the least variability and variance in space and time. The uncertainty (in terms of standard deviation) in projected ET, runoff, and recharge increased toward the end of the century, indicating that the 40 climate projections diverge chronologically.
The anomalies with respect to the past record (1950–2009) show that groundwater recharge in the Southern Hills-Gulf region is predicted to increase 13% in the early century, but is predicted to reduce to 3% increase in the late century. Runoff is predicted to decrease between 18% and 20% and ET is predicted to increase around 3% throughout the century.
The study found that the GCM uncertainty prevailed the total uncertainty in future hydrologic projections in the Southern Hills-Gulf region. For recharge projection in the early century, 95% of total uncertainty came from the GCM uncertainty. The recharge project uncertainty in the late century had 66% from the GCM uncertainty. The emission pathway uncertainty was negligible in the early century, but become significant towards the end of the century.
Author Contributions
Conceptualization, E.B., F.T.-C.T., V.P.S. and S.-C.K.; methodology, F.T.-C.T.; software, E.B.; validation, E.B. and F.T.-C.T.; formal analysis, E.B. and F.T.-C.T.; investigation, E.B., F.T.-C.T., V.P.S. and S.-C.K.; resources, F.T.-C.T.; data curation, E.B. and S.-C.K.; writing—original draft preparation, E.B. and F.T.-C.T.; writing—review and editing, V.P.S. and S.-C.K.; visualization, E.B.; supervision, F.T.-C.T.; project administration, F.T.-C.T.; funding acquisition, F.T.-C.T.
Funding
This research was funded by the U.S. Geological Survey through the Louisiana Water Resources Research Institute, Grant/Cooperative Agreement Numbers G10AP00136 and G11AP20082.
Acknowledgments
This paper was coauthored by an employee of the Oak Ridge National Laboratory, managed by UT Battelle, LLC, under contract DE-AC05-00OR22725 with the U.S. Department of Energy. Accordingly, the publisher, by accepting the article for publication, acknowledges that the United States government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States government purposes.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Katz, R.W.; Craigmile, P.F.; Guttorp, P.; Haran, M.; Sansó, B.; Stein, M.L. Uncertainty analysis in climate change assessments. Nat. Clim. Chang. 2013, 3, 769–771. [Google Scholar] [CrossRef]
- Solomon, S.; Qin, D.; Manning, M.; Marquis, M.; Averyt, K.B.; Tignor, M.; Miller, H.L.; Chen, Z. Climate Change 2007-the Physical Science Basis. Working Group I Contribution to the Fourth Assessment Report of the IPCC; Cambridge University Press: Cambridge, UK, 2007; Volume 4. [Google Scholar]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in regional climate predictions. Bull. Am. Meteorol. Soc. 2009, 90, 1095–1107. [Google Scholar] [CrossRef]
- Yip, S.; Ferro, C.A.T.; Stephenson, D.B.; Hawkins, E. A simple, coherent framework for partitioning uncertainty in climate predictions. J. Clim. 2011, 24, 4634–4643. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Uncertainty of downscaling method in quantifying the impact of climate change on hydrology. J. Hydrol. 2011, 401, 190–202. [Google Scholar] [CrossRef]
- Wilby, R.L.; Harris, I. A framework for assessing uncertainties in climate change impacts: Low-flow scenarios for the River Thames, UK. Water Resour. Res. 2006, 42, W02419. [Google Scholar] [CrossRef]
- Déqué, M. Frequency of precipitation and temperature extremes over France in an anthropogenic scenario: Model results and statistical correction according to observed values. Glob. Planet. Chang. 2007, 57, 16–26. [Google Scholar] [CrossRef]
- Kay, A.L.; Davies, H.N.; Bell, V.A.; Jones, R.G. Comparison of uncertainty sources for climate change impacts: Flood frequency in England. Clim. Chang. 2009, 92, 41–63. [Google Scholar] [CrossRef]
- Görgen, K.; Beersma, J.; Brahmer, G.; Buiteveld, H.; Carambia, M.; Keizer, O.D.; Krahe, P.; Nilson, E.; Lammersen, R.; Perrin, C.; et al. Assessment of Climate Change Impacts on Discharge in the Rhine River Basin: Results of the RheinBlick2050 Project; CHR Rep I-23; CHR: Lelystad, The Netherlands, 2010; 229p. [Google Scholar]
- Bosshard, T.; Carambia, M.; Goergen, K.; Kotlarski, S.; Krahe, P.; Zappa, M.; Schär, C. Quantifying uncertainty sources in an ensemble of hydrological climate-impact projections. Water Resour. Res. 2013, 49, 1523–1536. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Poulin, A.; Leconte, R. Overall uncertainty study of the hydrological impacts of climate change for a Canadian watershed. Water Resour. Res. 2011, 47, W12509. [Google Scholar] [CrossRef]
- Kwon, H.H.; Assis de Souza Filho, F.; Block, P.; Sun, L.; Lall, U.; Reis, D.S. Uncertainty assessment of hydrologic and climate forecast models in Northeastern Brazil. Hydrol. Process. 2012, 26, 3875–3885. [Google Scholar] [CrossRef]
- Habets, F.; Boé, J.; Déqué, M.; Ducharne, A.; Gascoin, S.; Hachour, A.; Martin, E.; Pagé, C.; Sauquet, E.; Terray, L.; et al. Impact of climate change on the hydrogeology of two basins in Northern France. Clim. Chang. 2013, 121, 771–785. [Google Scholar] [CrossRef]
- Surfleet, C.G.; Tullos, D. Uncertainty in hydrologic modelling for estimating hydrologic response due to climate change (Santiam River, Oregon). Hydrol. Process. 2013, 27, 3560–3576. [Google Scholar] [CrossRef]
- Dessu, S.B.; Melesse, A.M. Impact and uncertainties of climate change on the hydrology of the Mara River basin, Kenya/Tanzania. Hydrol. Process. 2013, 27, 2973–2986. [Google Scholar] [CrossRef]
- Knutti, R.; Furrer, R.; Tebaldi, C.; Cermak, J.; Meehl, G.A. Challenges in combining projections from multiple climate models. J. Clim. 2010, 23, 2739–2758. [Google Scholar] [CrossRef]
- McAvaney, B.J.; Covey, C.; Joussaume, S.; Kattsov, V.; Kitoh, A.; Ogana, W.; Pitman, A.J.; Weaver, A.J.; Wood, R.A.; Zhao, Z.-C.; et al. Model evaluation. In Climate Change 2001: The Scientific Basis; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: New York, NY, USA, 2001; Volume 8, pp. 471–524. [Google Scholar]
- Pierce, D.W.; Barnett, T.P.; Santer, B.D.; Gleckler, P.J. Selecting global climate models for regional climate change studies. Proc. Natl. Acad. Sci. USA 2009, 106, 8441–8446. [Google Scholar] [CrossRef]
- Stocker, T.; Dahe, Q.; Plattner, G.-K.; Tignor, M.; Midgley, P. IPCC Expert Meeting on Assessing and Combining Multi Model Climate Projections. In Proceedings of the Intergovernmental Panel on Climate Change, Boulder, CO, USA, 25–27 January 2010; IPCC: Bern, Switzerland, 2010. [Google Scholar]
- Doblas-Reyes, F.J.; Pavan, V.; Stephenson, D.B. The skill of multi-model seasonal forecasts of the wintertime North Atlantic Oscillation. Clim. Dyn. 2003, 21, 501–514. [Google Scholar] [CrossRef]
- Yun, W.T.; Stefanova, L.; Krishnamurti, T.N. Improvement of the multimodel superensemble technique for seasonal forecasts. J. Clim. 2003, 16, 3834–3840. [Google Scholar] [CrossRef]
- Schmittner, A.; Latif, M.; Schneider, B. Model projections of the North Atlantic thermohaline circulation for the 21st century assessed by observations. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Connolley, W.M.; Bracegirdle, T.J. An Antarctic assessment of IPCC AR4 coupled models. Geophys. Res. Lett. 2007, 34, L22505. [Google Scholar] [CrossRef]
- Murphy, J.M.; Booth, B.B.; Collins, M.; Harris, G.R.; Sexton, D.M.; Webb, M.J. A methodology for probabilistic predictions of regional climate change from perturbed physics ensembles. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 365, 1993–2028. [Google Scholar] [CrossRef]
- Tebaldi, C.; Knutti, R. The use of multi-model ensemble in probabilistic climate projections. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 365, 2053–2075. [Google Scholar] [CrossRef]
- Waugh, D.W.; Eyring, V. Quantitative performance metrics for stratospheric-resolving chemistry-climate models. Atmos. Chem. Phys. 2008, 8, 5699–5713. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial. Stat. Sci. 1999, 14, 382–401. [Google Scholar]
- Clyde, M.A. Bayesian model averaging and model search strategies. Bayesian Stat. 1999, 6, 157–185. [Google Scholar]
- Raftery, A.E.; Zheng, Y. Discussion: Performance of Bayesian model averaging. J. Am. Stat. Assoc. 2003, 98, 931–938. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef]
- Sloughter, J.M.L.; Raftery, A.E.; Gneiting, T.; Fraley, C. Probabilistic quantitative precipitation forecasting using Bayesian model averaging. Mon. Weather Rev. 2007, 135, 3209–3220. [Google Scholar] [CrossRef]
- Tebaldi, C.; Smith, R.L.; Nychka, D.; Mearns, L.O. Quantifying uncertainty in projections of regional climate change: A Bayesian approach to the analysis of multi-model ensembles. J. Clim. 2005, 18, 1524–1540. [Google Scholar] [CrossRef]
- Min, S.K.; Simonis, D.; Hense, A. Probabilistic climate change predictions applying Bayesian model averaging. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 365, 2103–2116. [Google Scholar] [CrossRef]
- Buser, C.M.; Künsch, H.R.; Lüthi, D.; Wild, M.; Schär, C. Bayesian multi-model projection of climate: Bias assumptions and interannual variability. Clim. Dyn. 2009, 33, 849–868. [Google Scholar] [CrossRef]
- Smith, R.L.; Tebaldi, C.; Nychka, D.; Mearns, L.O. Bayesian modeling of uncertainty in ensembles of climate models. J. Am. Stat. Assoc. 2009, 104, 97–116. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.; Gao, X.; Sorooshian, S. Multimodel combination techniques for analysis of hydrological simulations: Application to distributed model intercomparison project results. J. Hydrometeorol. 2006, 7, 755–768. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Treatment of uncertainty using ensemble methods: Comparison of sequential data assimilation and Bayesian model averaging. Water Resour. Res. 2007, 43, W01411. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Bosch, D. Calibration and uncertainty analysis of the SWAT model using genetic algorithms and Bayesian model averaging. J. Hydrol. 2009, 374, 307–317. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H.; Jung, W.I. Combined effect of global climate projection and hydrologic model uncertainties on the future changes of Streamflow. In Proceedings of the World Environmental and Water Resources Congress 2010, Rhode, Island, 16–20 May 2010; pp. 81–91. [Google Scholar] [CrossRef]
- Dong, L.; Xiong, L.; Yu, K.X. Uncertainty analysis of multiple hydrologic models using the Bayesian model averaging method. J. Appl. Math. 2013, 2013, 346045. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, D.; Guo, Y.; Zhang, Y.; Dai, R. Application of Bayesian model averaging approach to multimodel ensemble hydrologic forecasting. J. Hydrol. Eng. ASCE 2013, 18, 1426–1436. [Google Scholar] [CrossRef]
- Wagener, T.; Gupta, H.V. Model identification for hydrological forecasting under uncertainty. Stoch. Environ. Res. Risk Assess. 2005, 19, 378–387. [Google Scholar] [CrossRef]
- Tsai, F.T.-C.; Elshall, A.S. Hierarchical Bayesian model averaging for hydrostratigraphic modeling: Uncertainty segregation and comparative evaluation. Water Resour. Res. 2013, 49, 5520–5536. [Google Scholar] [CrossRef]
- Maurer, E.P.; Brekke, L.; Pruitt, T.; Duffy, P.B.; Thrasher, B.; Long, J.; Arnold, J. An enhanced archive facilitating climate impacts and adaptation analysis. Bull. Am. Meteorol. Soc. 2013, 95, 1011–1019. [Google Scholar] [CrossRef]
- USBR. Downscaled CMIP3 and CMIP5 Climate and Hydrology Projections: Release of Downscaled CMIP5 Climate Projections, Comparison with preceding Information, and Summary of User Needs, prepared by the U.S.; Department of the Interior, Bureau of Reclamation (USBR), Technical Services Center: Denver, CO, USA, 2013; 47p.
- Schroeder, P.R.; Dozier, T.S.; Zappi, P.A.; McEnroe, B.M.; Sjostrom, J.W.; Peyton, R.L. The Hydrologic Evaluation of Landfill Performance (HELP) Model: Engineering Documentation for Version 3; EPA/600/R-94/168b; U.S. Environmental Protection Agency Office of Research and Development: Washington, DC, USA, 1994.
- Murphy, J.M.; Sexton, D.M.; Barnett, D.N.; Jones, G.S.; Webb, M.J.; Collins, M.; Stainforth, D.A. Quantification of modelling uncertainties in a large ensemble of climate change simulations. Nature 2004, 430, 768–772. [Google Scholar] [CrossRef]
- Buono, A. The Southern Hills Regional Aquifer System of Southeastern Louisiana and Southwestern Mississippi; U.S. Geological Survey, Water-Resources Investigations Report 83-4189; US Geological Survey: Reston, VA, USA, 1983; 38p.
- Maurer, E.P.; Wood, A.W.; Adam, J.C.; Lettenmaier, D.P.; Nijssen, B. A long-term hydrologically based dataset of land surface fluxes and states for the conterminous United States. J. Clim. 2002, 15, 3237–3251. [Google Scholar] [CrossRef]
- Maurer, E.P. Gridded Meteorological Data: 1949–2010, Santa Clara University. 2013. Available online: http://www.engr.scu.edu/~emaurer/gridded_obs/index_gridded_obs.html (accessed on 2 February 2019).
- Beigi, E.; Tsai, F.T.-C. A GIS-based water budget framework for high-resolution groundwater recharge estimation of large-scale humid regions. J. Hydrol. Eng.-ASCE 2014, 19, 8. [Google Scholar] [CrossRef]
- Beigi, E.; Tsai, F.T.-C. Comparative study of climate-change scenarios on groundwater recharge, southwestern Mississippi and southeastern Louisiana, USA. Hydrogeol. J. 2015, 23, 789–806. [Google Scholar] [CrossRef]
- Rogelj, J.; Meinshausen, M.; Knutti, R. Global warming under old and new scenarios using IPCC climate sensitivity range estimates. Nat. Clim. Chang. 2012, 2, 248–253. [Google Scholar] [CrossRef]
- Meinshausen, M.; Smith, S.J.; Calvin, K.; Daniel, J.S.; Kainuma, M.L.; Lamarque, J.F.; Matsumoto, K.; Montzka, S.A.; Raper, S.C.; Riahi, K.; et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Chang. 2011, 109, 213–241. [Google Scholar] [CrossRef]
- Johnson, F.; Westra, S.; Sharma, A.; Pitman, A.J. An assessment of GCM skill in simulating persistence across multiple time scales. J. Clim. 2011, 24, 3609–3623. [Google Scholar] [CrossRef]
- Khan, M.Z.K.; Sharma, A.; Mehrotra, R.; Schepen, A.; Wang, Q.J. Does improved SSTA prediction ensure better seasonal rainfall forecasts? Water Resour. Res. 2015, 51, 3370–3383. [Google Scholar] [CrossRef]
- Tsai, F.T.-C.; Li, X. Inverse groundwater modeling for hydraulic conductivity estimation using Bayesian model averaging and variance window. Water Resour. Res. 2008, 44, W09434. [Google Scholar] [CrossRef]
- Khire, M.V.; Benson, C.H.; Bosscher, P.J. Water balance modeling of earthen final covers. J. Geotech. Geoenviron. Eng. 1997, 123, 744–754. [Google Scholar] [CrossRef]
- Jyrkama, M.I.; Sykes, J.F. The impact of climate change on spatially varying groundwater recharge in the grand river watershed (Ontario). J. Hydrol. 2007, 338, 237–250. [Google Scholar] [CrossRef]
- Scibek, J.; Allen, D.M.; Cannon, A.J.; Whitfield, P.H. Groundwater–surface water interaction under scenarios of climate change using a high-resolution transient groundwater model. J. Hydrol. 2007, 333, 165–181. [Google Scholar] [CrossRef]
- Toews, M.W.; Allen, D.M. Evaluating different GCMs for predicting spatial recharge in an irrigated arid region. J. Hydrol. 2009, 374, 265–281. [Google Scholar] [CrossRef]
- Calderhead, A.I.; Martel, R.; Garfias, J.; Rivera, A.; Therrien, R. Pumping dry: An increasing groundwater budget deficit induced by urbanization, industrialization, and climate change in an over-exploited volcanic aquifer. Environ. Earth Sci. 2012, 66, 1753–1767. [Google Scholar] [CrossRef]
- Peyton, R.L.; Schroeder, P.R. Field verification of HELP model for landfills. J. Environ. Eng. ASCE 1988, 114, 247–269. [Google Scholar] [CrossRef]
- Schroeder, P.R.; Peyton, R.L. Verification of the Hydrologic Evaluation of Landfill Performance (HELP) Model Using Field Datha; EPA/600/S2-87/050; Hazardous Waste Engineering Research Laboratory, Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 1987.
- Robbins, K. Southern Regional Climate Center, Louisiana State University. Available online: http://www.srcc.lsu.edu (accessed on 2 February 2019).
- Richardson, C.W.; Wright, D.A. WGEN: A Model for Generating Daily Weather Variables; ARS-8; U.S. Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1984; p. 83.
- NRCS. Soil Survey Geographic (SSURGO). Soil Survey Staff, Natural Resources Conservation Service; U.S. Department of Agriculture: Washington, DC, USA, 2014. Available online: http://sdmdataaccess.nrcs.usda.gov/ (accessed on 2 February 2019).
- NLCD. USDA/NRCS National Geospatial Center of Excellence. National Land Cover Dataset. 2011. Available online: http://datagateway.nrcs.usda.gov/ (accessed on 2 February 2019).
- Jin, S.; Yang, L.; Danielson, P.; Homer, C.; Fry, J.; Xian, G. A comprehensive change detection method for updating the National Land Cover Database to circa 2011. Remote Sens. Environ. 2013, 132, 159–175. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Prudhomme, C.; Davies, H. Assessing uncertainties in climate change impact analyses on the river flow regimes in the, U.K. Part 2: Future climate. Clim. Chang. 2009, 93, 197–222. [Google Scholar] [CrossRef]
- Woldemeskel, F.M.; Sharma, A.; Sivakumar, B.; Mehrotra, R. An error estimation method for precipitation and temperature projections for future climates. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Teng, J.; Vaze, J.; Chiew, F.H.S.; Wang, B.; Perraud, J.M. Estimating the relative uncertainties sourced from GCMs and hydrological models in modeling climate change impact on runoff. J. Hydrometeorol. 2012, 13, 122–139. [Google Scholar] [CrossRef]
- Hosseinzadehtalaei, P.; Tabari, H.; Willems, P. Uncertainty assessment for climate change impact on intense precipitation: How many model runs do we need? Int. J. Climatol. 2017, 37, 1105–1117. [Google Scholar] [CrossRef]
- Mandal, S.; Breach, P.A.; Simonovic, S.P. Uncertainty in Precipitation Projection under Changing Climate Conditions: A Regional Case Study. Am. J. Clim. Chang. 2016, 5, 116–132. [Google Scholar] [CrossRef]
- Taylor, R.G.; Kingston, D.G. Sources of uncertainty in climate change impacts on river discharge and groundwater in a headwater catchment of the Upper Nile Basin, Uganda. Hydrol. Earth Syst. Sci. 2010, 14, 1297–1308. [Google Scholar] [CrossRef]
- Vetter, T.; Reinhardt, J.; Flörke, M.; van Griensven, A.; Hattermann, F.; Huang, S.; Koch, H.; Pechlivanidis, I.G.; Plötner, S.; Seidou, O.; et al. Evaluation of sources of uncertainty in projected hydrological changes under climate change in 12 large-scale river basins. Clim. Chang. 2017, 141, 419–433. [Google Scholar] [CrossRef]
- Northrop, P.J.; Chandler, R.E. Quantifying Sources of Uncertainty in Projections of Future Climate. J. Clim. 2014, 27, 8793–8808. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).