Impact of Main Pipe Flow Velocity on Leakage and Intrusion Flow: An Experimental Study
Abstract
1. Introduction
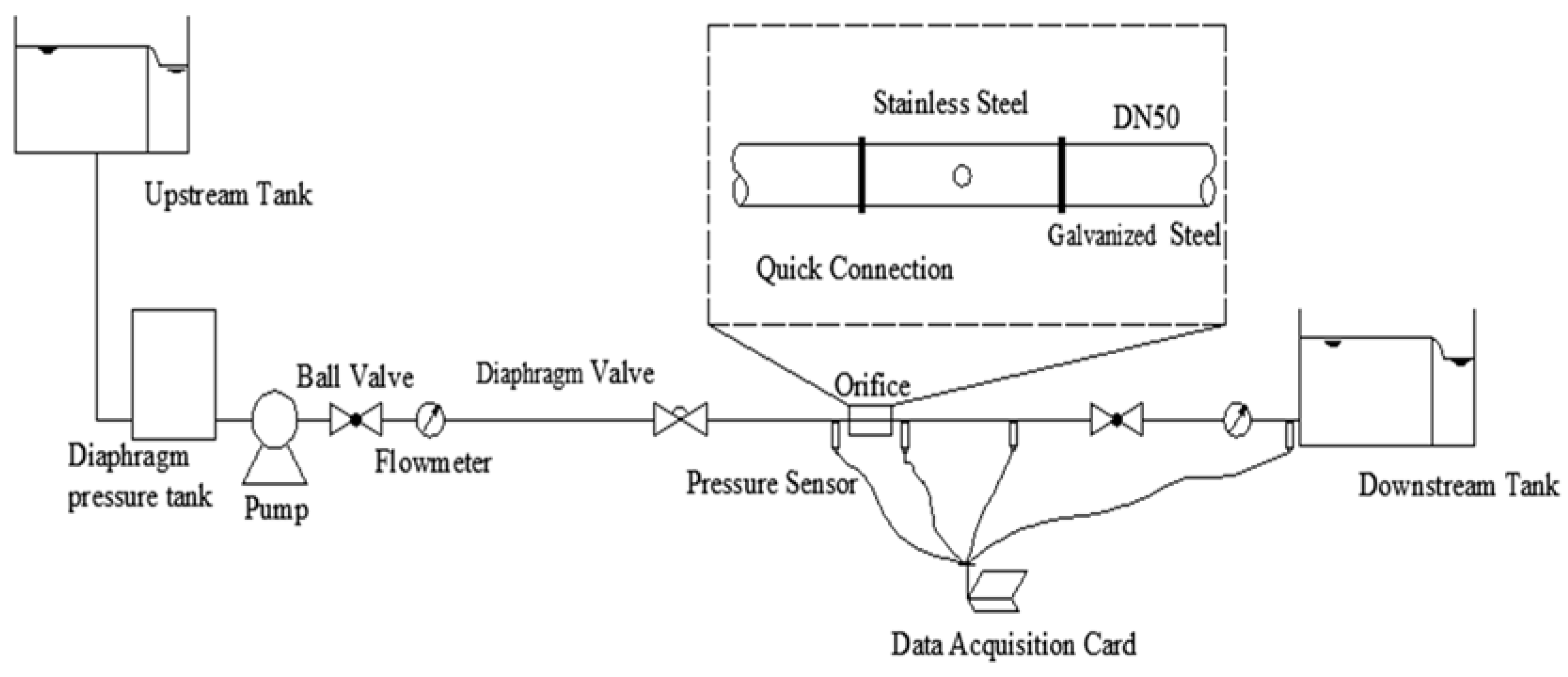
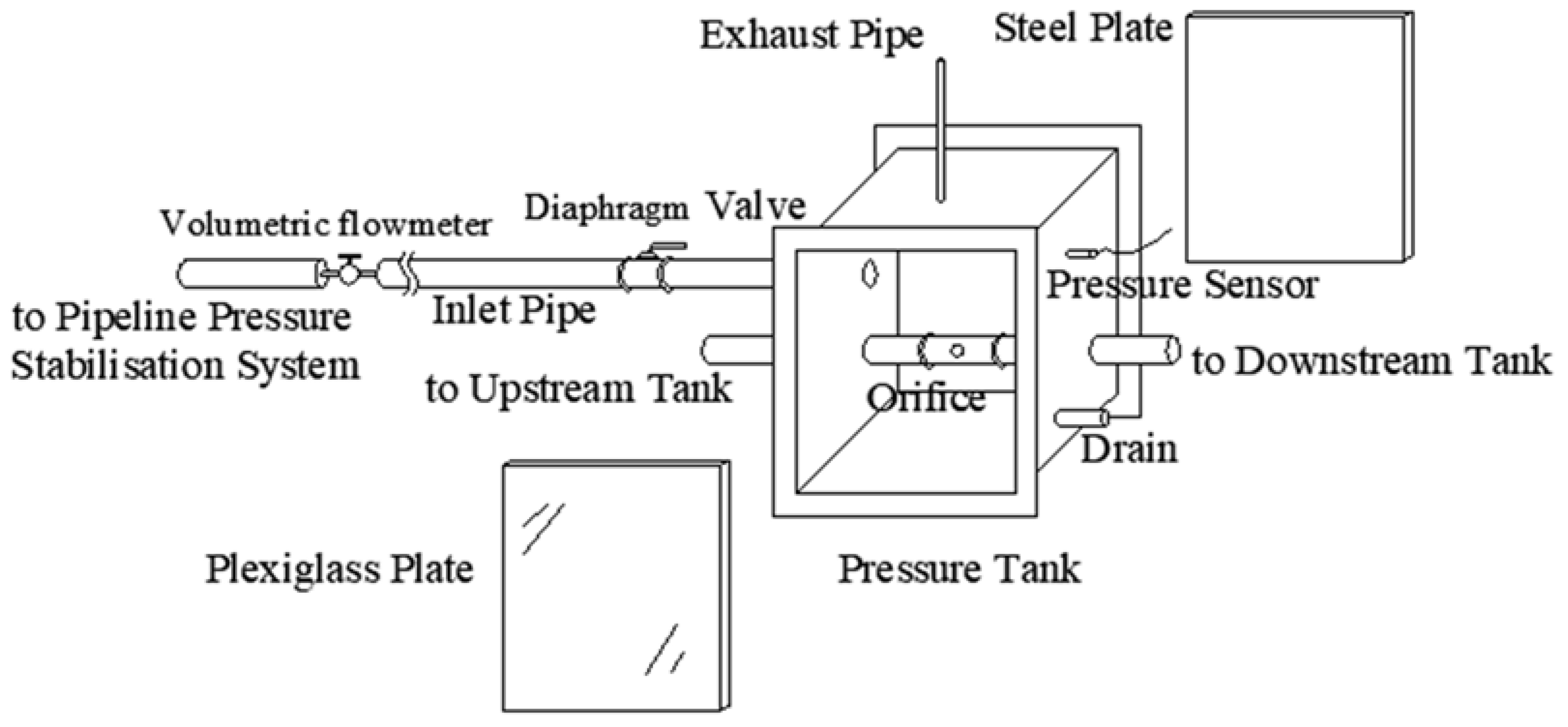
2. Experimental Apparatus
3. Results of the Orifice Outflow Study
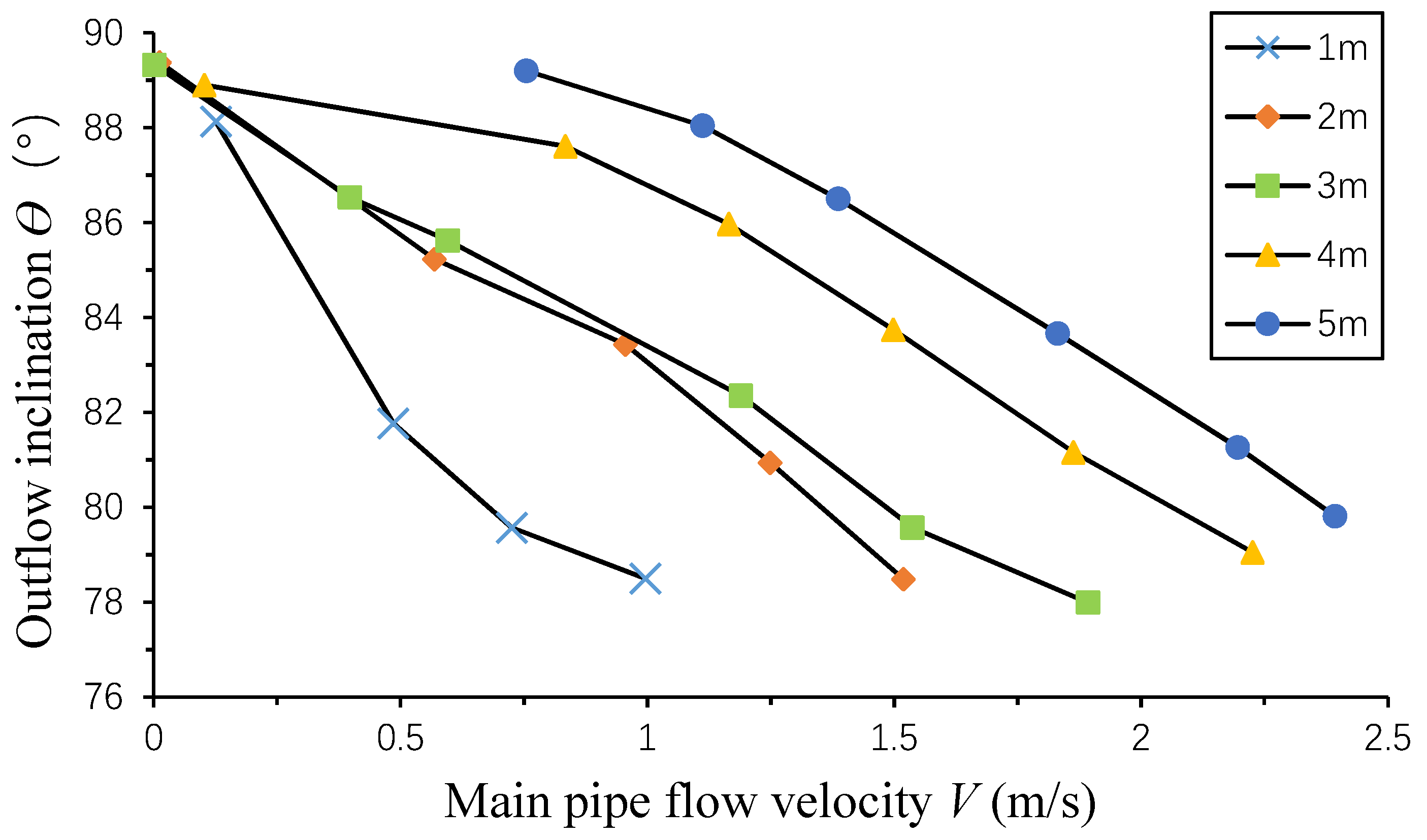
3.1. Inclination of the Circular Orifice Outflow
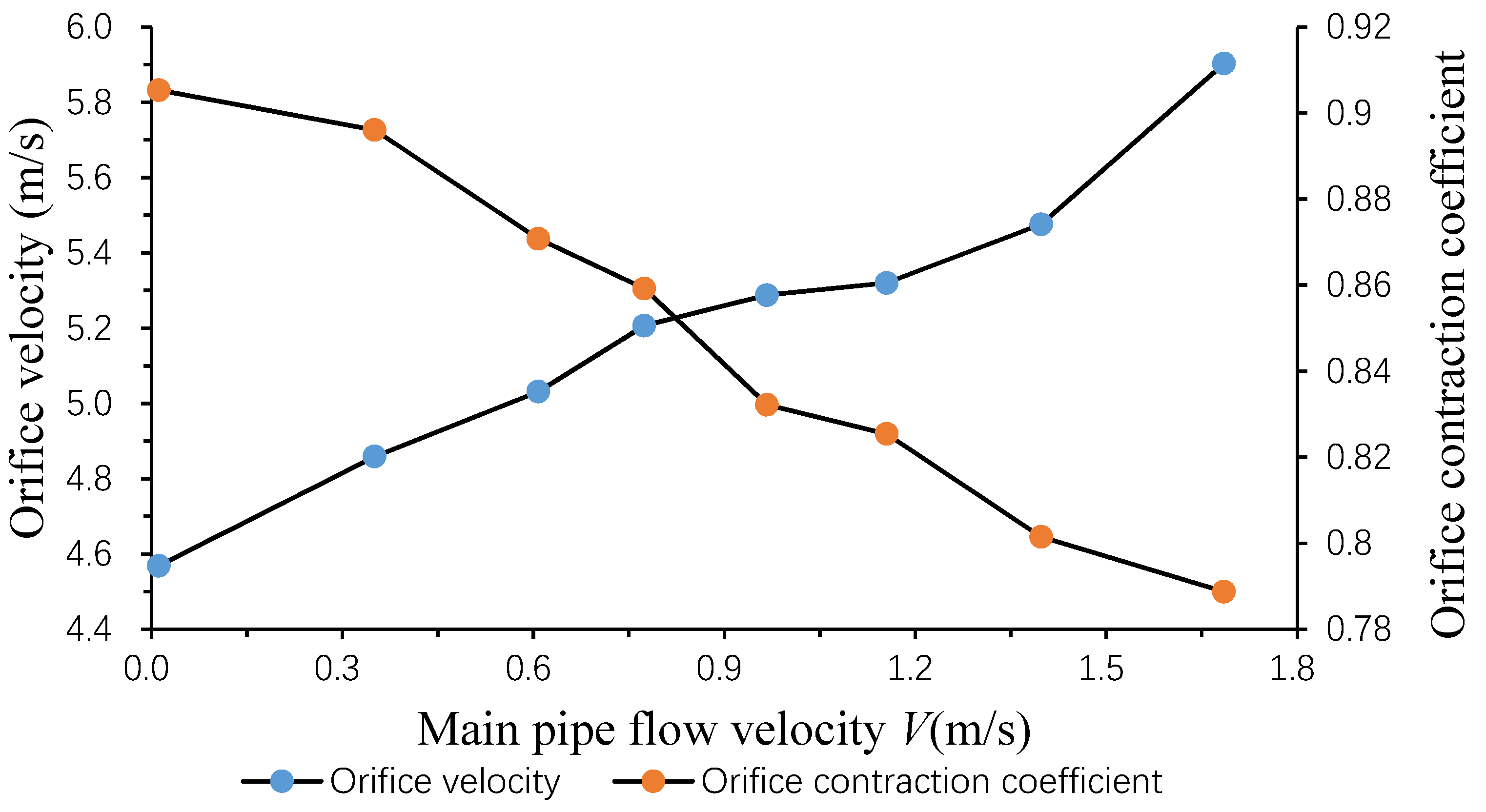
3.2. Cross-Sectional Area and Velocity of the Circular Orifice Outflow
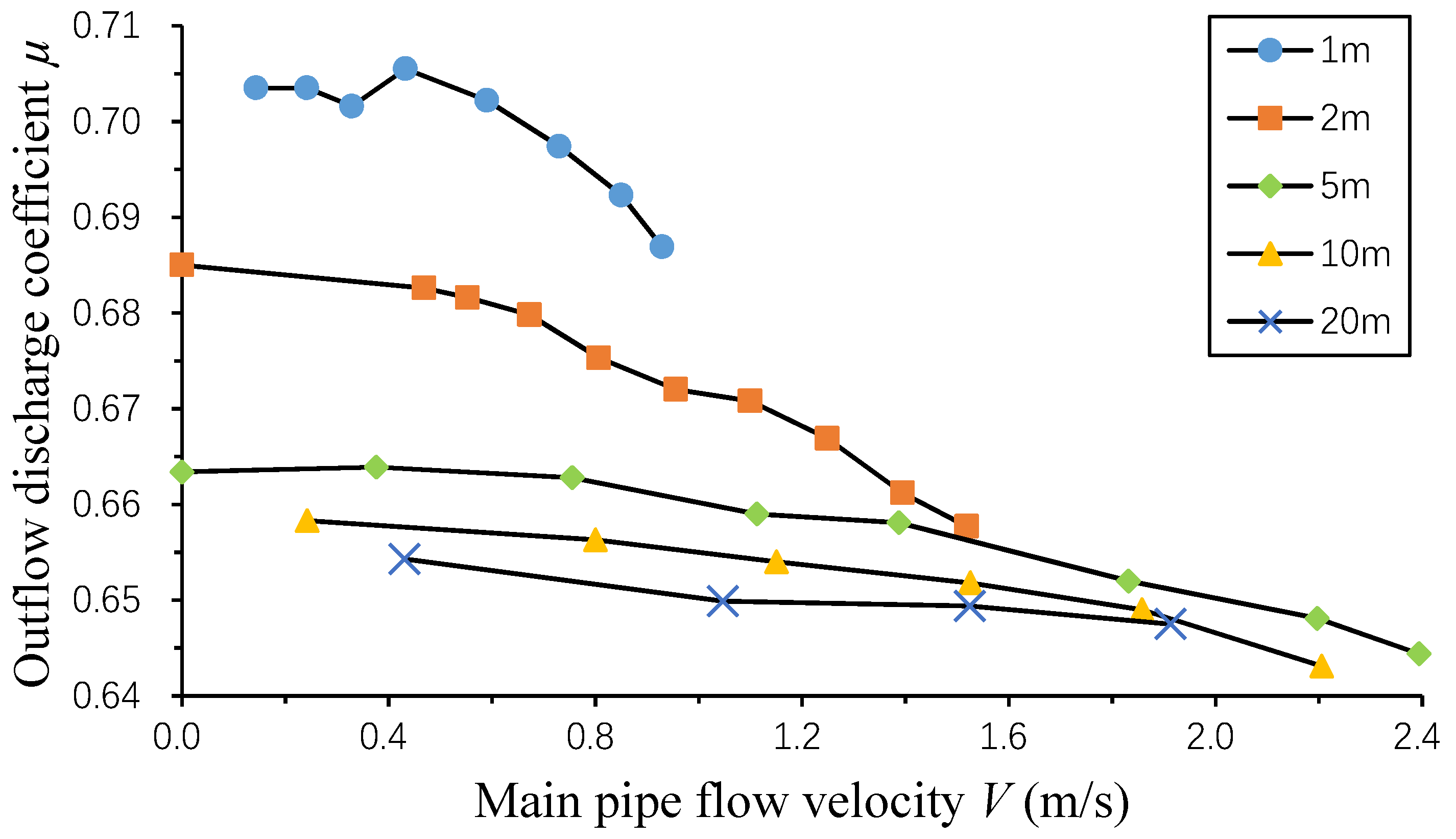
3.3. Discharge Coefficient of the Circular Orifice
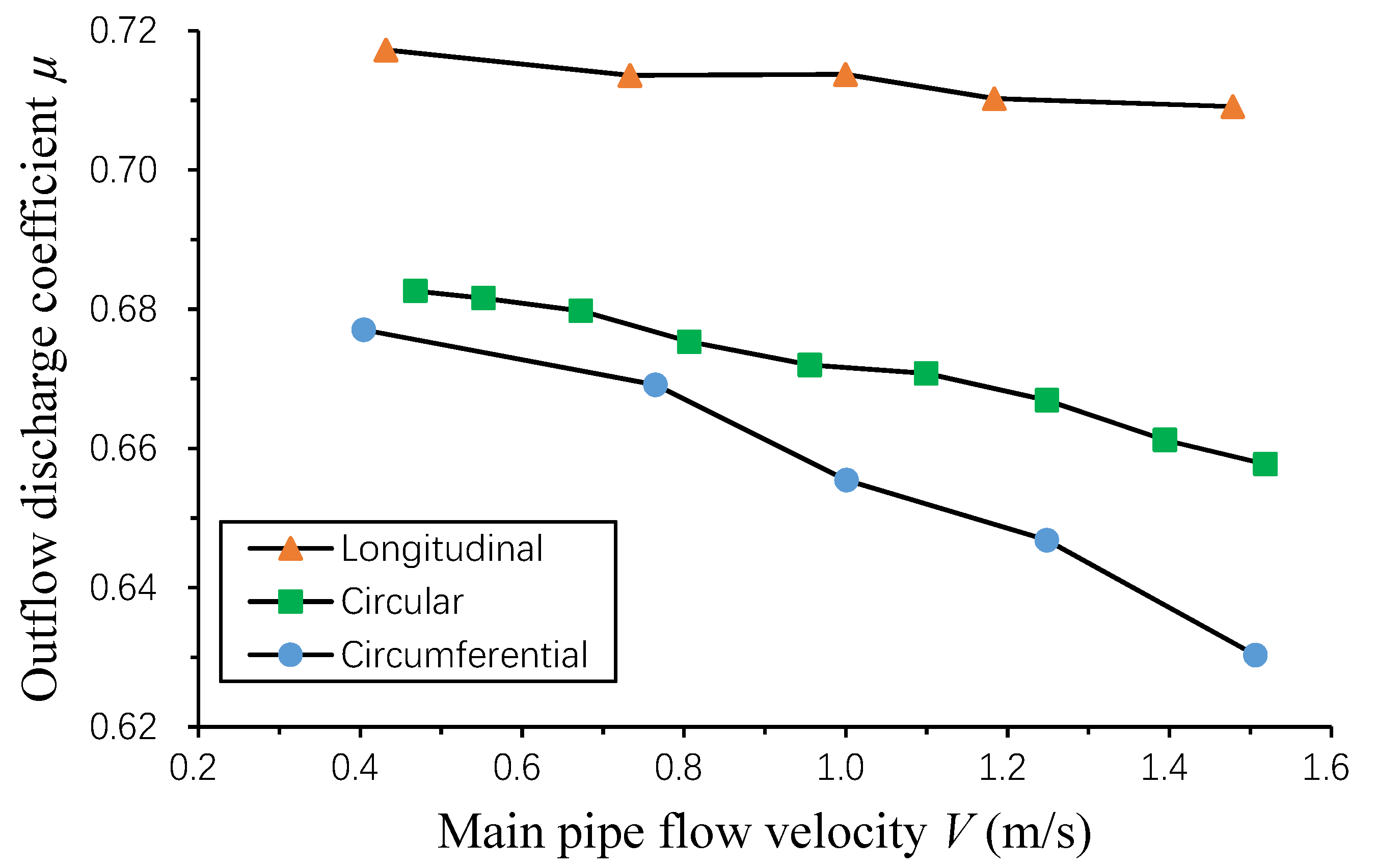
3.4. Effect of the Shape of the Orifice
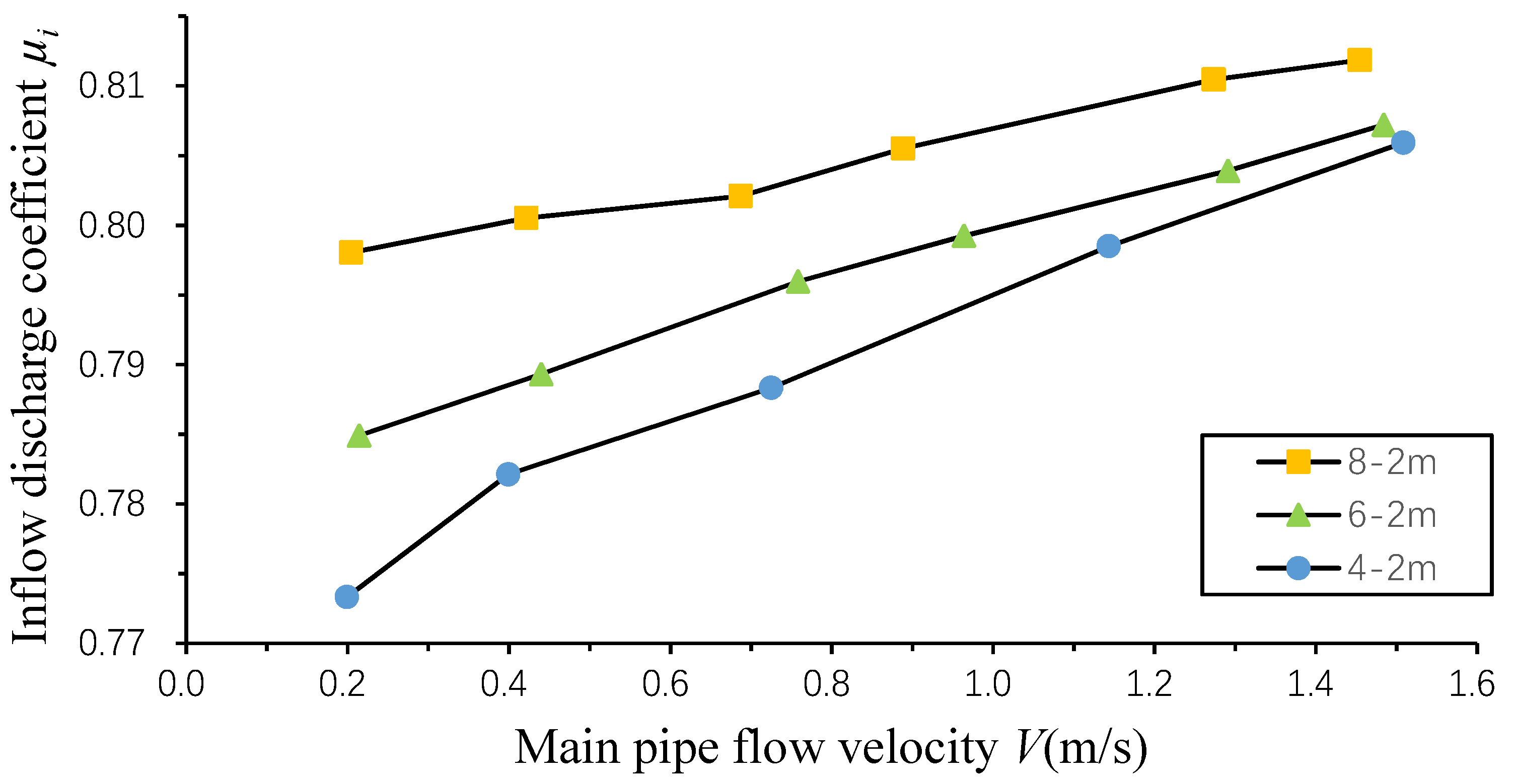
4. Results of the Orifice Inflow Study
5. Conclusions
- The main pipe flow velocity influenced the orifice outflow. When the pressure difference across the orifice was constant, with the increase of the main pipe flow velocity, the outflow velocity increased, but the contraction area of the jet and the outflow discharge coefficient (as calculated using the conventional orifice equation) decreased.
- For the orifice outflow, three types of orifices were considered: a circular orifice to simulate a pinhole leak, a rectangular orifice to simulate a longitudinal crack in a pipe wall, and a rectangular orifice to simulate a circumferential crack. When the orifice pressures and the orifice opening areas were the same, the discharge of the circumferential orifice was the most sensitive to the main pipe flow velocity, and the discharge of the longitudinal orifice was the least sensitive.
- The main pipe flow velocity promoted the orifice inflow. When the pressure difference across the orifice was constant, with the increase of the main pipe flow velocity, the inflow discharge coefficient increased, which the opposite pattern to that of the orifice outflow. For the same pressure difference and the main pipe velocity, the inflow discharge coefficient was larger than the outflow counterpart.
- For both the orifice inflow and outflow, the impact of the main pipe flow velocity was more significant for the lower pressure head difference across the orifice.
Author Contributions
Funding
Conflicts of Interest
References
- Beuken, R.H.S.; Lavooij, C.S.W.; Bosch, A.; Schaap, P.G. Low leakage in the Netherlands confirmed. In Proceedings of the 8th Annual Water Distribution Systems Analysis Symposium (WDSA 2006), Cincinnati, OH, USA, 27–30 August 2006. [Google Scholar]
- Mutikanga, H.E.; Sharma, S.; Vairavamoorthy, K. Water loss management in developing countries: Challenges and prospects. J. Am. Water Works Assn. 2009, 101, 57–68. [Google Scholar] [CrossRef]
- Besner, M.C.; Prevost, M.; Regli, S. Assessing the public health risk of microbial intrusion events in distribution systems: Conceptual model, available data, and challenges. Water Res. 2011, 45, 961–979. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.C.; Jin, H.F.; Zhang, T.Q.; Shao, Y.; Wu, X. Experimental observation on factors affecting intrusion volumes during low or negative pressure events. J. Water Supply Res. Technol.-Aqua 2016, 65, 396–406. [Google Scholar] [CrossRef]
- Mora-Rodriguez, J.; Delgado-Galvan, X.; Ramos, H.M.; Lopez-Jimenez, P.A. An overview of leaks and intrusion for different pipe materials and failures. Urban Water J. 2014, 11, 1–10. [Google Scholar] [CrossRef]
- Lambert, A.O. International report: Water losses management and techniques. Water Sci. Technol. Water Supply 2002, 2, 1–20. [Google Scholar] [CrossRef]
- Van Zyl, J.E.; Clayton, C.R.I. The effect of pressure on leakage in water distribution systems. Proc. Inst. Civ. Eng.-Water Manag. 2007, 160, 109–114. [Google Scholar] [CrossRef]
- Cassa, A.M.; van Zyl, J.E.; Laubscher, R.F. A numerical investigation into the effect of pressure on holes and cracks in water supply pipes. Urban Water J. 2010, 7, 109–120. [Google Scholar] [CrossRef]
- Ferrante, M.; Massari, C.; Brunone, B.; Meniconi, S. Experimental Evidence of Hysteresis in the Head-Discharge Relationship for a Leak in a Polyethylene Pipe. J. Hydraul. Eng-ASCE 2011, 137, 775–780. [Google Scholar] [CrossRef]
- Massari, C.; Ferrante, M.; Brunone, B.; Meniconi, S. Is the leak head-discharge relationship in polyethylene pipes a bijective function? J. Hydraul. Res. 2012, 50, 409–417. [Google Scholar] [CrossRef]
- De Marchis, M.; Fontanazza, C.M.; Freni, G.; Notaro, V.; Puleo, V. Experimental Evidence of Leaks in Elastic Pipes. Water Resour. Manag. 2016, 30, 2005–2019. [Google Scholar] [CrossRef]
- Ssozi, E.N.; Reddy, B.D.; van Zyl, J.E. Numerical Investigation of the Influence of Viscoelastic Deformation on the Pressure-Leakage Behavior of Plastic Pipes. J. Hydraul. Eng. 2016, 142, 04015057. [Google Scholar] [CrossRef]
- Fox, S.; Collins, R.; Boxall, J. Experimental Study Exploring the Interaction of Structural and Leakage Dynamics. J. Hydraul. Eng. 2017, 143, 04016080. [Google Scholar] [CrossRef]
- Lin, C.C. A Hybrid Heuristic Optimization Approach for Leak Detection in Pipe Networks Using Ordinal Optimization Approach and the Symbiotic Organism Search. Water 2017, 9, 812. [Google Scholar] [CrossRef]
- van Zyl, J.E.; Lambert, A.O.; Collins, R. Realistic Modeling of Leakage and Intrusion Flows through Leak Openings in Pipes. J. Hydraul. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Mora-Rodriguez, J.; Delgado-Galvan, X.; Ortiz-Medel, J.; Ramos, H.M.; Fuertes-Miquel, V.S.; Lopez-Jimenez, P.A. Pathogen intrusion flows in water distribution systems: According to orifice equations. J. Water Supply Res. Technol.-AQUA 2015, 64, 857–869. [Google Scholar] [CrossRef]
- Jan, C.-D.; Nguyen, Q.-T. Discharge Coefficient for a Water Flow through a Bottom Orifice of a Conical Hopper. J. Irrig. Drain Eng 2010, 136, 567–572. [Google Scholar] [CrossRef]
- McLemore, A.J.; Tyner, J.S.; Yoder, D.C.; Buchanan, J.R. Discharge Coefficients for Orifices Cut into Round Pipes. J. Irrig. Drain Eng. 2013, 139, 947–954. [Google Scholar] [CrossRef]
- Noack, C.; Ulanicki, B. Modelling of Soil Diffusibility on Leakage Characteristics of Buried Pipes. In Proceedings of the 8th Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006; pp. 1–9. [Google Scholar]
- Collins, R.; Boxall, J. Influence of Ground Conditions on Intrusion Flows through Apertures in Distribution Pipes. J. Hydraul. Eng. 2013, 139, 1052–1061. [Google Scholar] [CrossRef]
- Yu, H.F.; Li, X.G.; Sui, H.; Xu, C.C.; Li, H. Simulation of Orifice Flow Influenced by Lateral Flow in a Trough-Type Liquid Distributor. Chem. Eng. Technol. 2013, 36, 1975–1984. [Google Scholar] [CrossRef]
- Patterson, J.; Page, N.W.; Ritchie, J.B. Contraction coefficients for compressible flow through axisymmetric orifices. Int. J. Mech. Sci. 1970, 12, 405–415. [Google Scholar] [CrossRef]
- International Organization for Standardization. Measurement of Fluid Flow by Means of Orifice Plates, Nozzles, and Venturi Tubes Inserted in Circular Cross Section Conduits Running Full; International Organization for Standardization: Geneva, Switzerland, 1976. [Google Scholar]
- Wang, X.; Li, A.; Sobey, A.J.; Tan, M. Investigation into the effects of two immiscible fluids on coefficient of discharge during Compartment Flooding. Ocean Eng. 2016, 111, 254–266. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, Y.; Yao, T.; Gong, J.; Liu, J.; Zhang, T.; Yu, T. Impact of Main Pipe Flow Velocity on Leakage and Intrusion Flow: An Experimental Study. Water 2019, 11, 118. https://doi.org/10.3390/w11010118
Shao Y, Yao T, Gong J, Liu J, Zhang T, Yu T. Impact of Main Pipe Flow Velocity on Leakage and Intrusion Flow: An Experimental Study. Water. 2019; 11(1):118. https://doi.org/10.3390/w11010118
Chicago/Turabian StyleShao, Yu, Tian Yao, Jinzhe Gong, Jinjie Liu, Tuqiao Zhang, and Tingchao Yu. 2019. "Impact of Main Pipe Flow Velocity on Leakage and Intrusion Flow: An Experimental Study" Water 11, no. 1: 118. https://doi.org/10.3390/w11010118
APA StyleShao, Y., Yao, T., Gong, J., Liu, J., Zhang, T., & Yu, T. (2019). Impact of Main Pipe Flow Velocity on Leakage and Intrusion Flow: An Experimental Study. Water, 11(1), 118. https://doi.org/10.3390/w11010118





