Developing Hydro-Meteorological Thresholds for Shallow Landslide Initiation and Early Warning
Abstract
1. Introduction
2. Materials and Methods
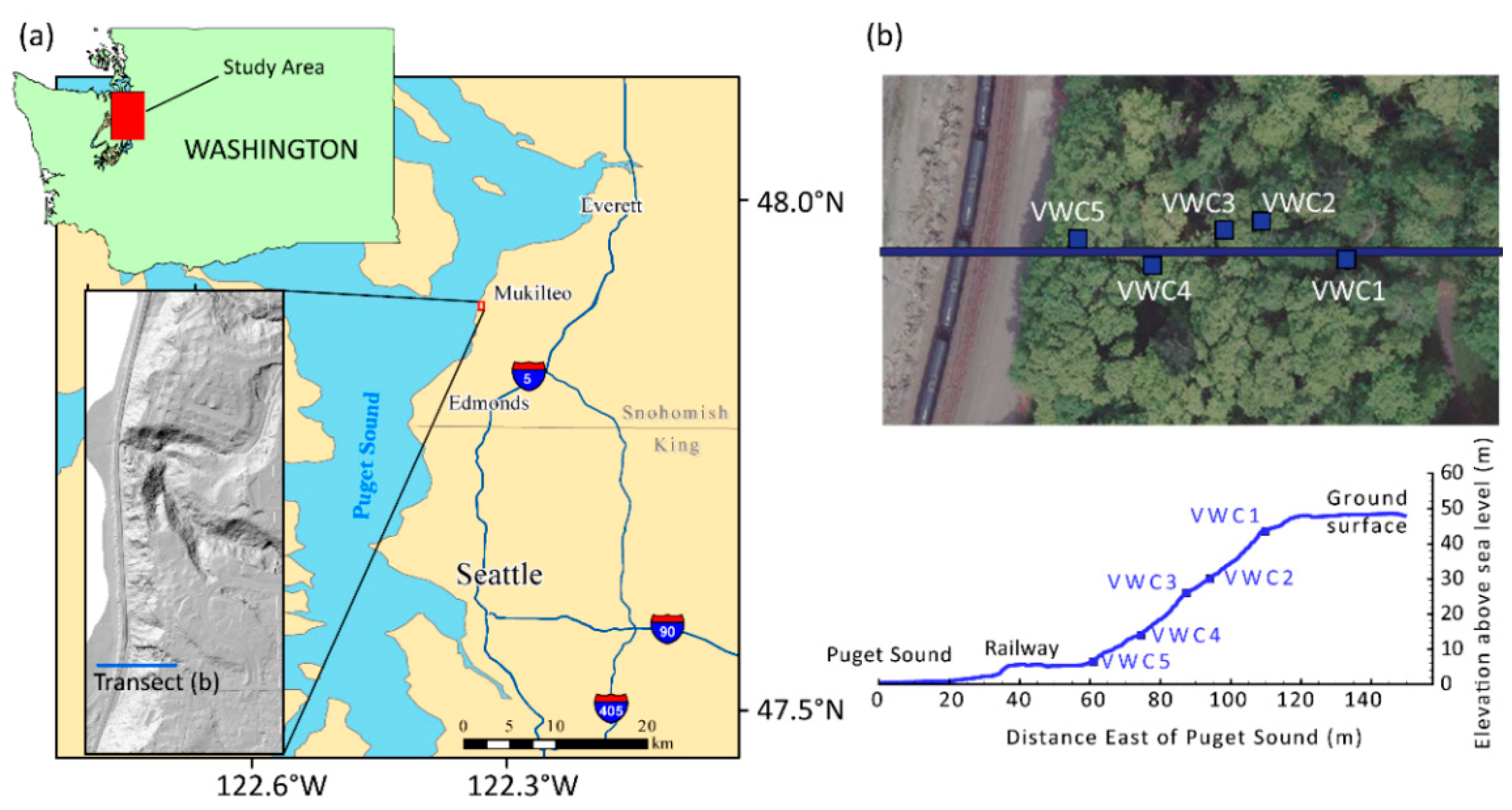
2.1. Field Monitoring Sites
2.2. Data Inputs
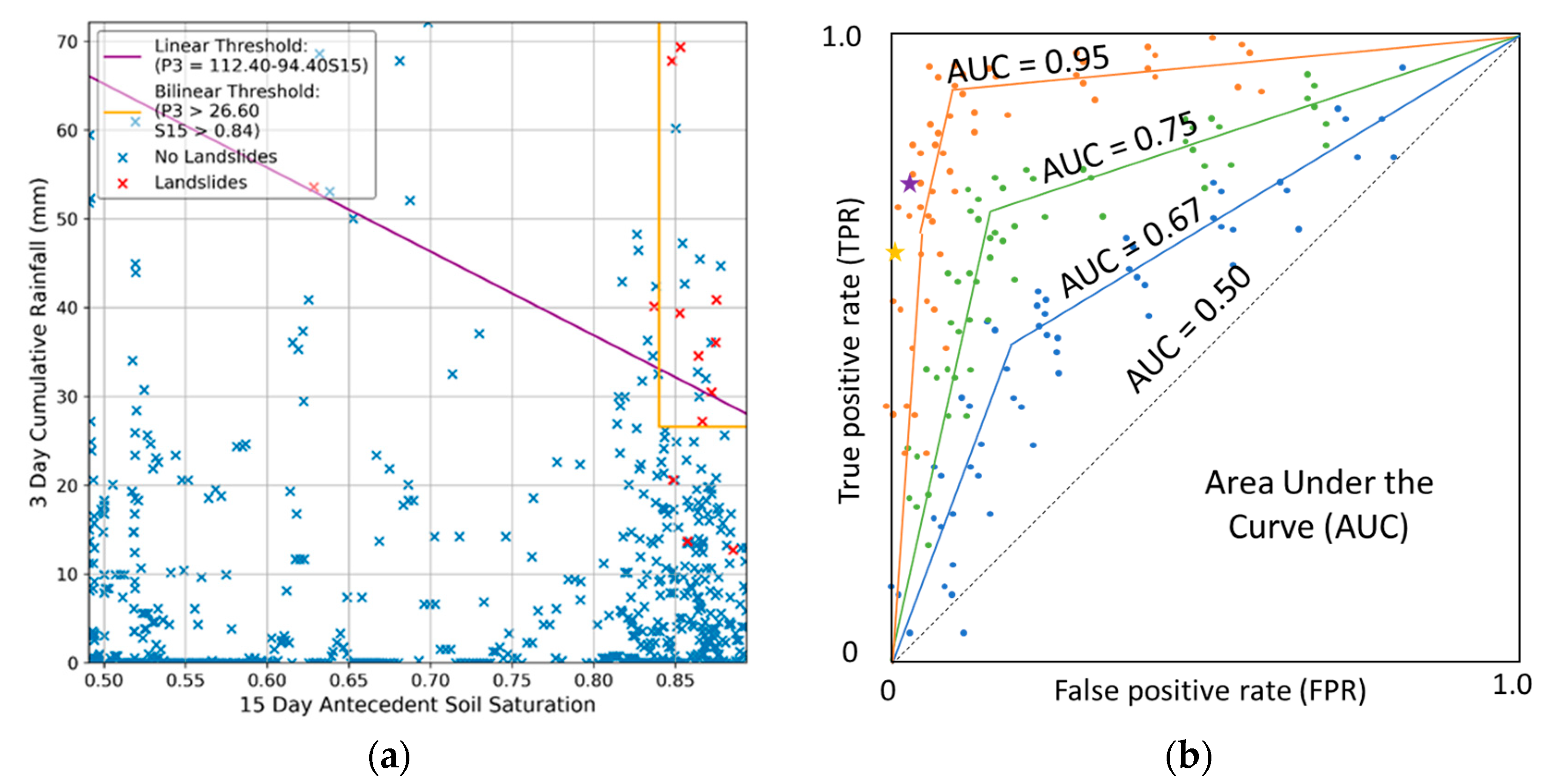
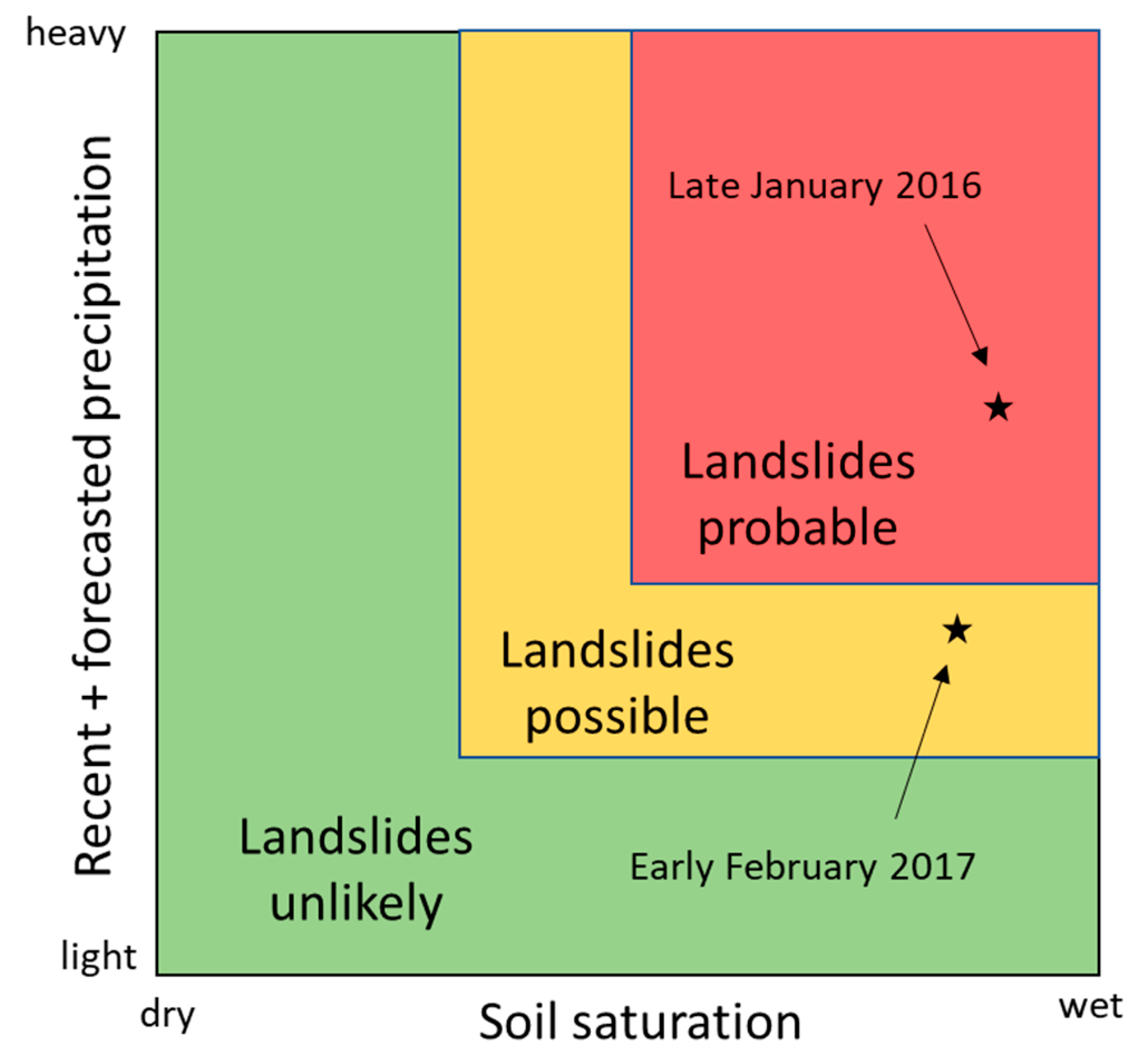
2.3. Threshold Formats, Variables and Timescales
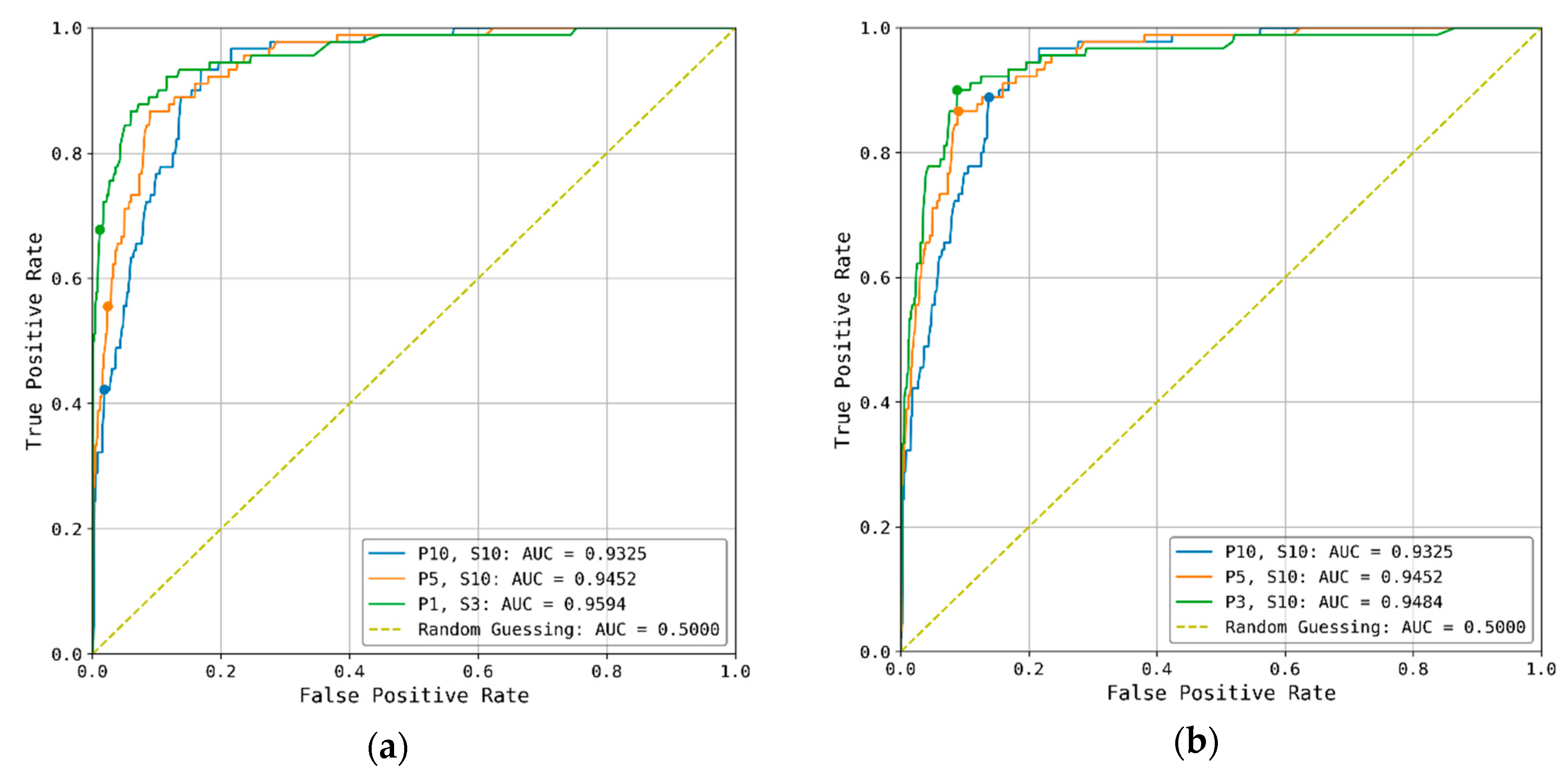
2.4. Threshold Optimization Metrics
2.5. Iterative Threshold Development
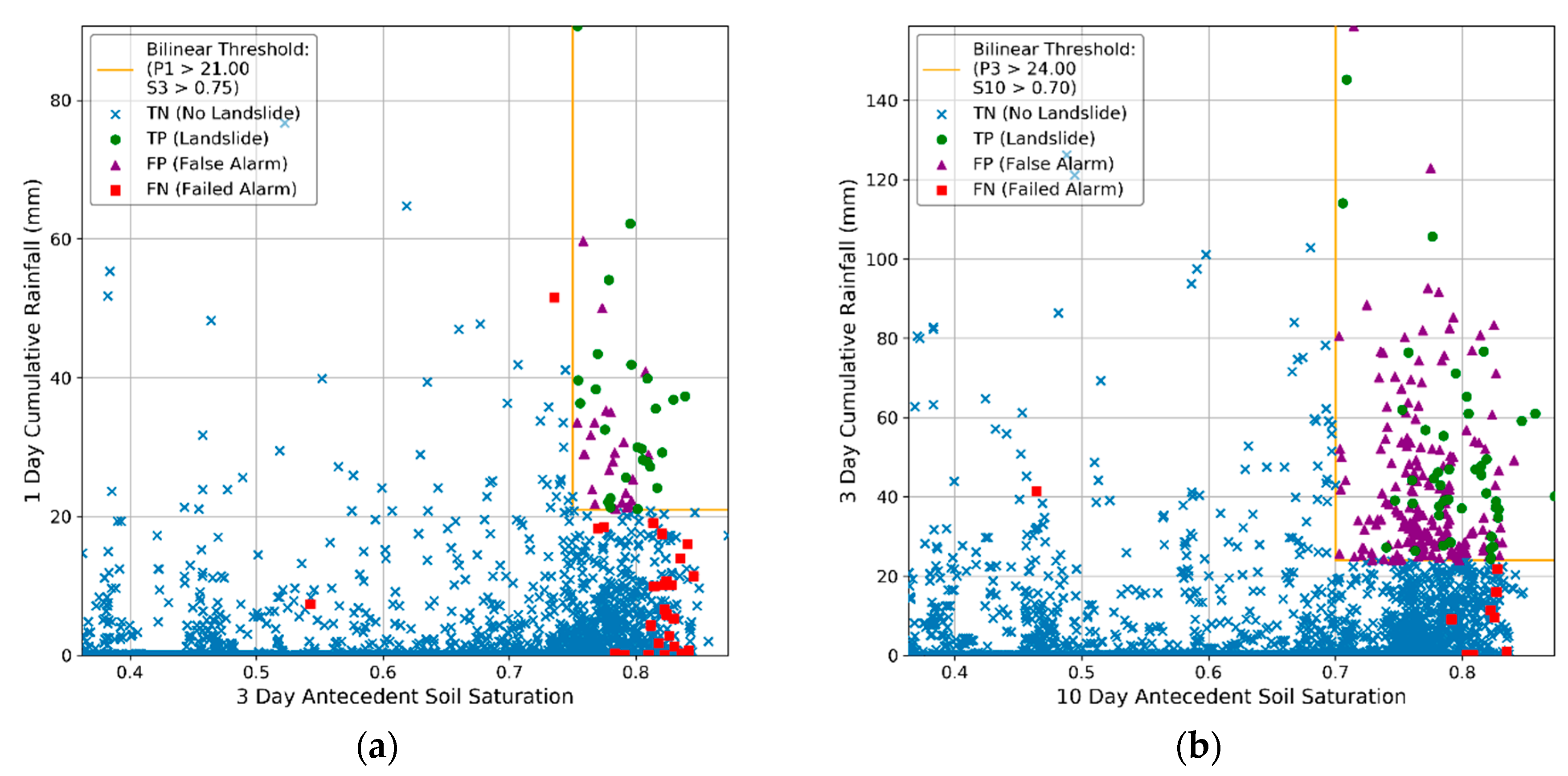
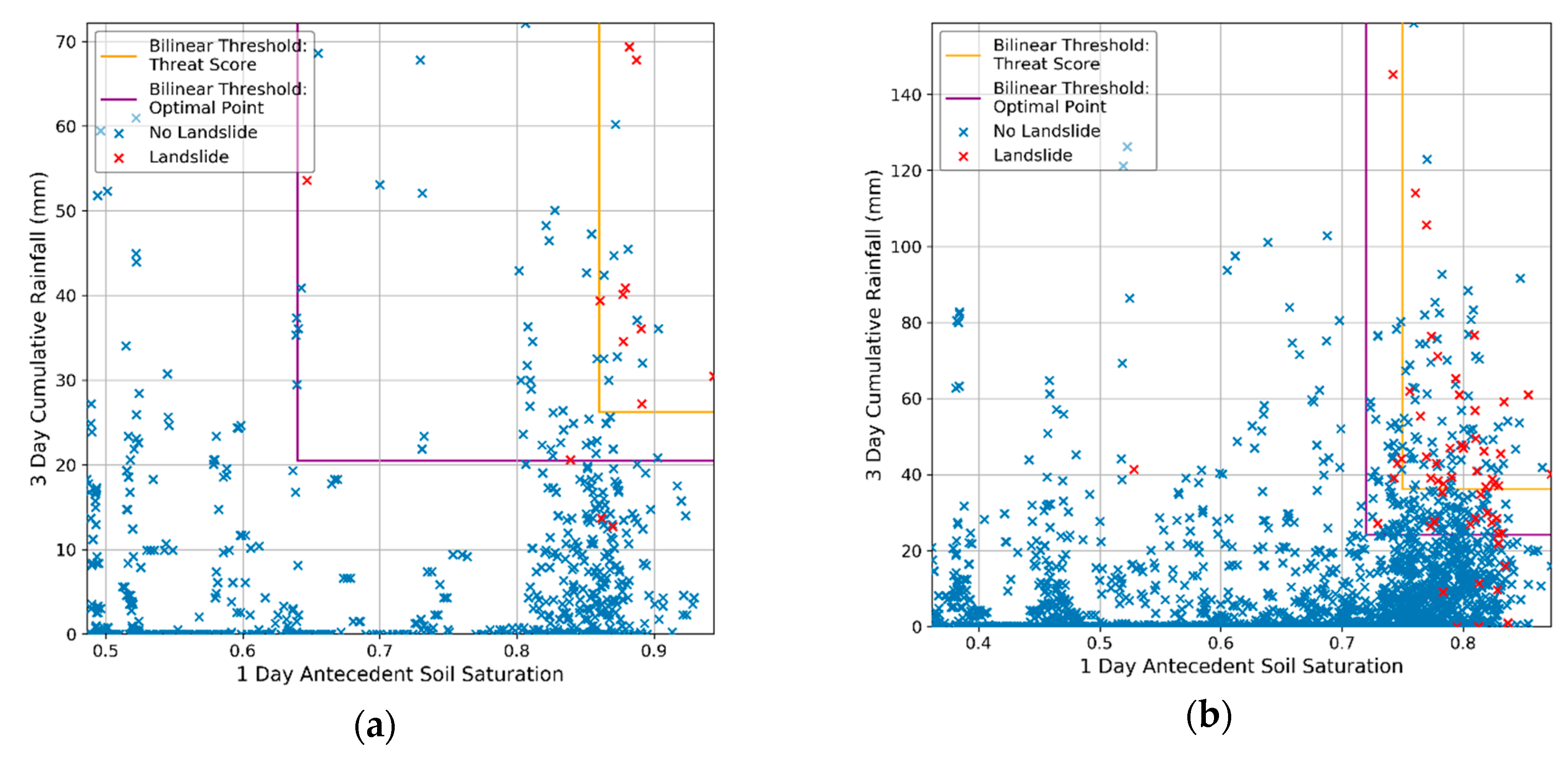
3. Results
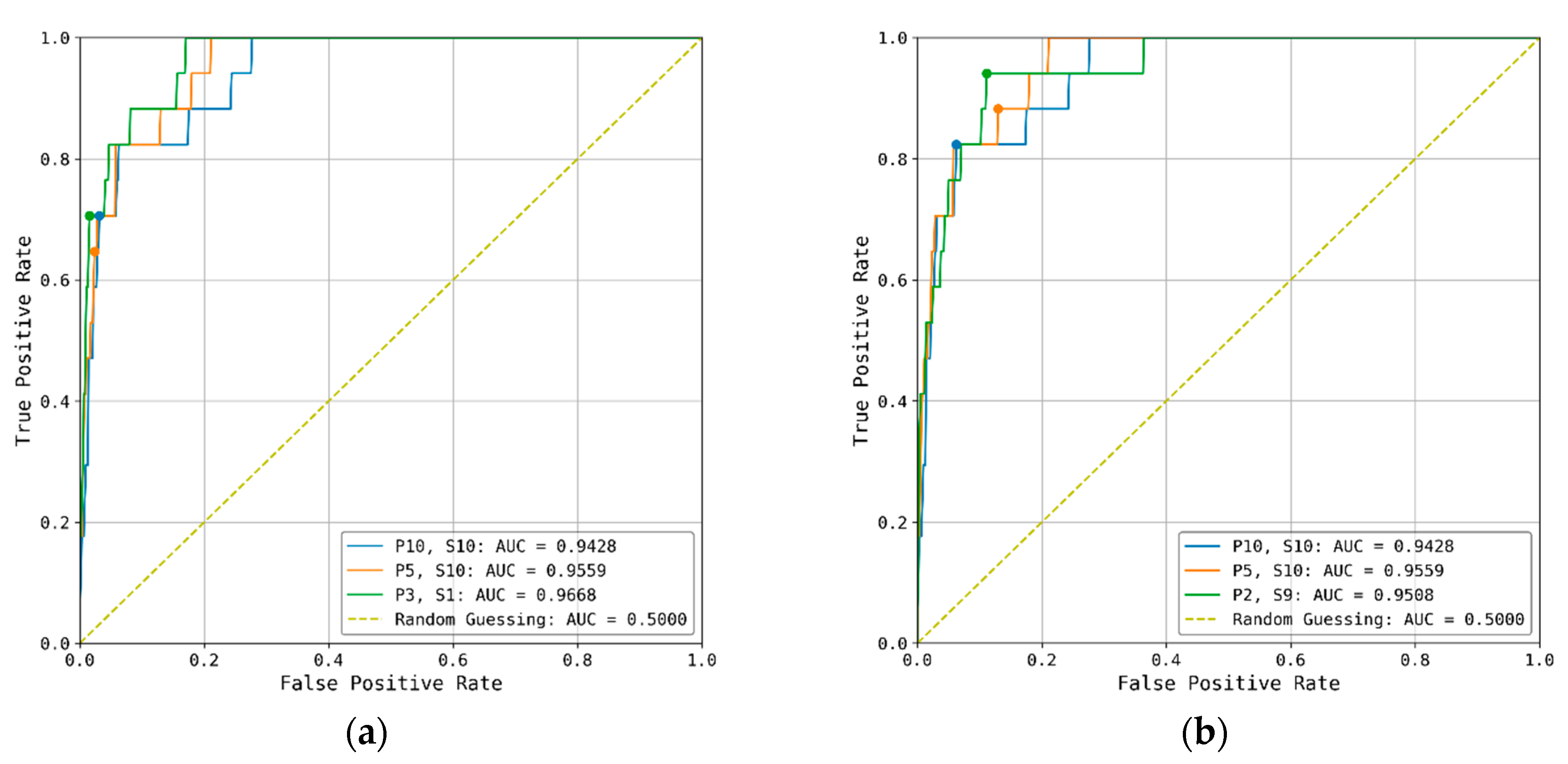
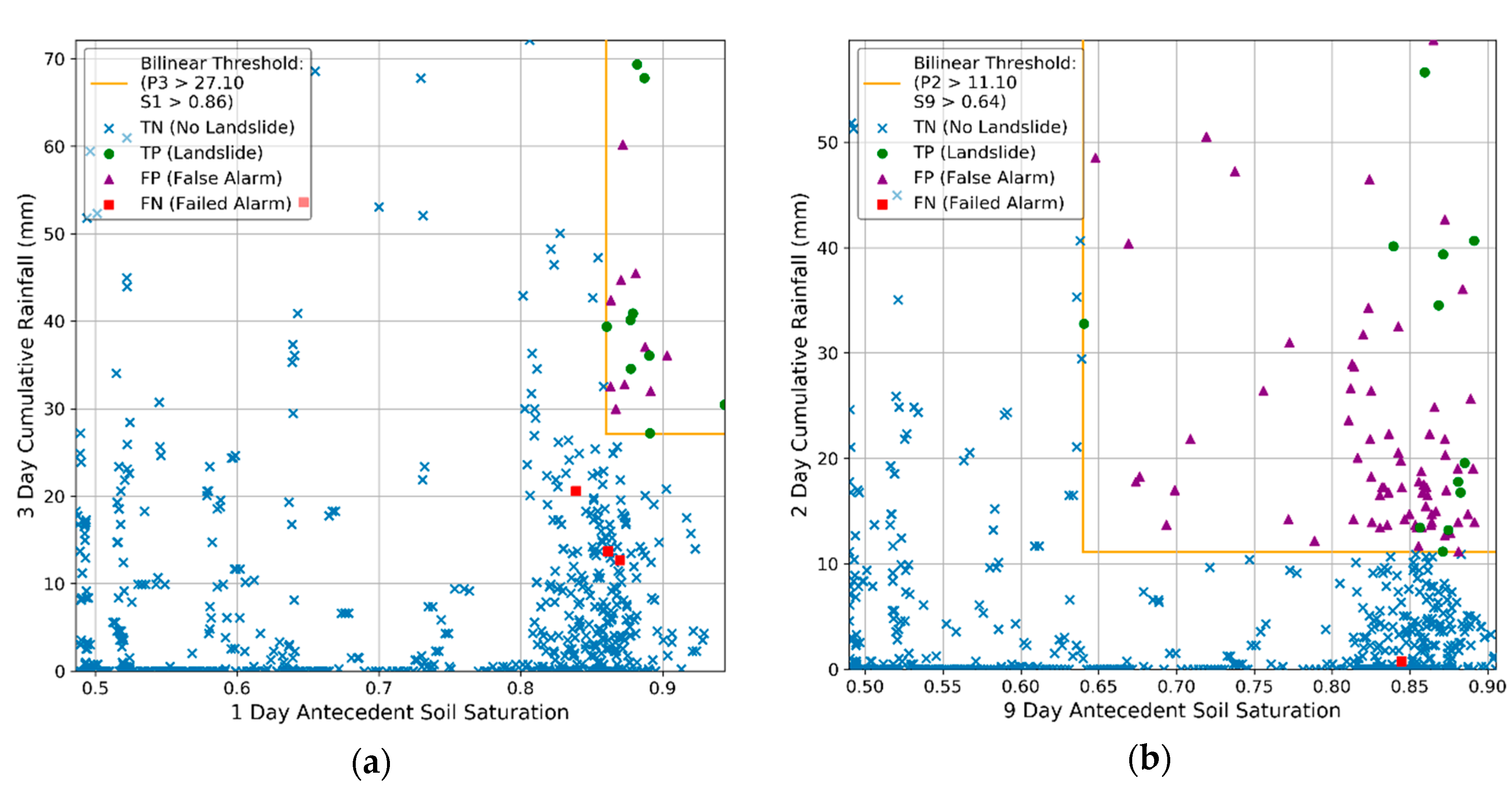
3.1. Seattle Area Thresholds
3.2. Portland Thresholds
4. Discussion
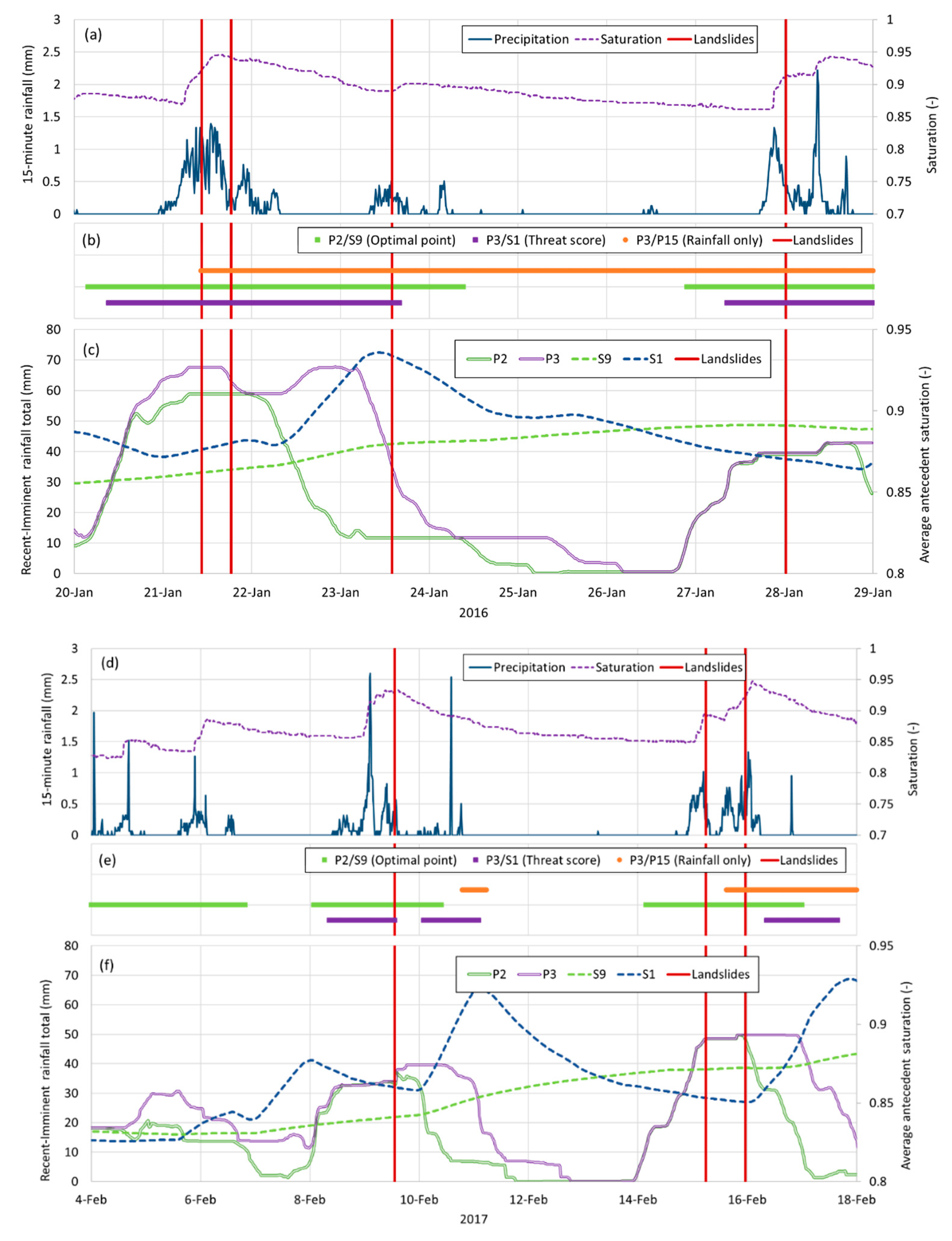
4.1. Comparing Operational Utility of Competing Thresholds
4.2. Dual Alert Systems, Threshold Exceedence and Landslide Occurrence
4.3. Improvements over Established Rainfall-Only Approaches
4.4. Versatility of the Hydro-Meterological Threshold Approach
4.5. Avenues for Further Investigation and Improvements
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Baum, R.L.; Godt, J.W. Early warning of rainfall-induced shallow landslides and debris flows in the USA. Landslides 2010, 7, 259–272. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Staley, D.M.; Kean, J.W.; Cannon, S.H.; Schmidt, K.M.; Laber, J.L. Objective definition of rainfall intensity-duration thresholds for the initiation of post-fire debris flows in southern California. Landslides 2013, 10, 547–562. [Google Scholar] [CrossRef]
- Jakob, M.; Owen, T.; Simpson, T. A regional real-time debris-flow warning system for the District of North Vancouver, Canada. Landslides 2012, 9, 165–178. [Google Scholar] [CrossRef]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows. Geogr. Ann. Ser. A Phys. Geogr. 1980, 62, 23–27. [Google Scholar] [CrossRef]
- Leonarduzzi, E.; Molnar, P.; McArdell, B.W. Predictive performance of rainfall thresholds for shallow landslides in Switzerland from gridded daily data. Water Resour. Res. 2017, 53, 6612–6625. [Google Scholar] [CrossRef]
- Rosi, A.; Peternel, T.; Jemec-Auflič, M.; Komac, M.; Segoni, S.; Casagli, N. Rainfall thresholds for rainfall-induced landslides in Slovenia. Landslides 2016, 13, 1571–1577. [Google Scholar] [CrossRef]
- Glade, T.; Crozier, M.J.; Smith, P. Applying Probability Determination to Refine Landslide-triggering Rainfall Thresholds Using an Empirical “Antecedent Daily Rainfall Model”. Pure Appl. Geophys. 2000, 157, 1059–1079. [Google Scholar] [CrossRef]
- Crozier, M.J. Prediction of rainfall-triggered landslides: A test of the antecedent water status model. Earth Surf. Process. Landf. 1999, 24, 825–833. [Google Scholar] [CrossRef]
- Godt, J.W.; Baum, R.L.; Chleborad, A.F. Rainfall characteristics for shallow landsliding in Seattle, Washington, USA. Earth Surf. Process. Landf. 2006, 31, 97–110. [Google Scholar] [CrossRef]
- Chleborad, A.F.; Baum, R.L.; Godt, J.W.; Powers, P.S. A prototype system for forecasting landslides in the Seattle, Washington, area. In Landslides and Engineering Geology of the Seattle, Washington, Area; Baum, R.L., Godt, J.W., Highland, L., Eds.; Geological Society of America: Boulder, CO, USA, 2008; pp. 103–120. [Google Scholar]
- Segoni, S.; Rosi, A.; Lagomarsino, D.; Fanti, R.; Casagli, N. Brief communication: Using averaged soil moisture estimates to improve the performances of a regional-scale landslide early warning system. Nat. Hazards Earth Syst. Sci. 2018, 18, 807–812. [Google Scholar] [CrossRef]
- Thomas, M.A.; Mirus, B.B.; Collins, B.D. A physics-based approach to identify thresholds for rainfall-induced shallow landsliding. Geophys. Res. Lett. 2018, GRL58002. [Google Scholar] [CrossRef]
- Salvatici, T.; Tofani, V.; Rossi, G.; D’Ambrosio, M.; Tacconi Stefanelli, C.; Masi, E.B.; Rosi, A.; Pazzi, V.; Vannocci, P.; Petrolo, M.; et al. Application of a physically based model to forecast shallow landslides at a regional scale. Nat. Hazards Earth Syst. Sci. 2018, 18, 1919–1935. [Google Scholar] [CrossRef]
- Fusco, F.; De Vita, P.; Baum, R.L.; Mirus, B.B.; Allocca, V.; Tufano, R.; Calcaterra, D. Hydrological monitoring and modeling approaches for assessing timing of shallow landslide in the volcanic area of the Phlegrean Fields (southern Italy). Landslides 2018. in review. [Google Scholar]
- Napolitano, E.; Fusco, F.; Baum, R.L.; Godt, J.W.; De Vita, P. Effect of antecedent-hydrological conditions on rainfall triggering of debris flows in ash-fall pyroclastic mantled slopes of Campania (southern Italy). Landslides 2016, 13, 967–983. [Google Scholar] [CrossRef]
- Bogaard, T.; Greco, R. Invited perspectives: A hydrological look to precipitation intensity duration thresholds for landslide initiation: Proposing hydro-meteorological thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 31–39. [Google Scholar] [CrossRef]
- Mirus, B.B.; Becker, R.; Baum, R.L.; Smith, J.B. Integrating real-time subsurface hydrologic monitoring with empirical rainfall thresholds to improve landslide early warning. Landslides 2018, 15, 1909–1919. [Google Scholar] [CrossRef]
- Scheevel, C.R.; Baum, R.L.; Mirus, B.B.; Smith, J.B. Precipitation Thresholds for Landslide Occurrence Near Seattle, Mukilteo, and Everett, Washington; GSGS: Reston, VA, USA, 2017. [Google Scholar]
- Ciavoletta, M.; Bogaard, T.; Gargano, R.; Greco, R. Is there predictive power in hydrological catchment information for regional landslide hazard assessment? Procedia Earth Planet. Sci. 2016, 16, 195–203. [Google Scholar] [CrossRef]
- Torres, R.; Dietrich, W.E.; Montgomery, D.R.; Anderson, S.P.; Loague, K. Unsaturated zone processes and the hydrological response of a steep unchanneled catchment. Water Resour. Res. 1998, 34, 1865–1879. [Google Scholar] [CrossRef]
- Baum, R.L.; McKenna, J.P.; Godt, J.W.; Harp, E.L.; McMullen, S.R. Hydrologic Monitoring of Landslide-Prone Coastal Bluffs near Edmonds and Everett, Washington, 2001–2004; GSGS: Reston, VA, USA, 2005. Available online: https://pubs.usgs.gov/of/2005/1063/ (accessed on 27 January 2005).
- Smith, J.B.; Baum, R.L.; Mirus, B.B.; Michel, A.; Stark, B. Results of Hydrologic Monitoring on Landslide Prone Coastal Bluffs near Mukilteo, Washington; GSGS: Reston, VA, USA, 2017. [Google Scholar]
- Smith, J.B.; Godt, J.W.; Baum, R.L.; Coe, J.A.; Ellis, W.L.; Jones, E.S.; Burns, S.F. Results of Hydrologic Monitoring of a Landslide-Prone Hillslope in Portland’s West Hills, Oregon, 2006–2017; GSGS: Reston, VA, USA, 2017. [Google Scholar]
- Statewide Landslide Information Database for Oregon (SLIDO), Release 3.2. Available online: https://www.oregongeology.org/slido/ (accessed on 26 July 2018).
- Seattle Area, Washington. Available online: https://www.usgs.gov/natural-hazards/landslide-hazards/science/seattle-area-washington?qt-science_center_objects=0#qt-science_center_objects (accessed on 7 September 2018).
- Portland, Oregon. Available online: https://www.usgs.gov/natural-hazards/landslide-hazards/science/portland-oregon?qt-science_center_objects=0#qt-science_center_objects (accessed on 7 September 2018).
- Mirus, B.B.; Smith, J.B.; Stark, B.; Lewis, Y.; Michel, A.R.; Baum, R.L. Assessing Landslide Potential on Coastal Bluffs near Mukilteo, Washington—Geologic Site Characterization for Hydrologic Monitoring; GSGS: Reston, VA, USA, 2016. [Google Scholar]
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Postance, B.; Hillier, J.; Dijkstra, T.; Dixon, N. Comparing threshold definition techniques for rainfall-induced landslides: A national assessment using radar rainfall. Earth Surf. Process. Landf. 2018, 43, 553–560. [Google Scholar] [CrossRef]
- Piciullo, L.; Gariano, S.L.; Melillo, M.; Brunetti, M.W.; Peruccacci, S.; Guzetti, F.; Calvello, M. Definition and performance of a threshold-based regional early warning model for rainfall-induced landslides. Landslides 2017, 14, 995–1008. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Moramarco, T.; Ponziani, F.; Berni, N.; Wagner, W. Use of Satellite Soil Moisture Products for the Operational Mitigation of Landslides Risk in Central Italy. In Satellite Soil Moisture Retrievals: Techniques & Applications; Petropoulos, G.P., Srivastava, P., Kerr, Y.H., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 231–247. [Google Scholar] [CrossRef]
- Mirus, B.B.; Smith, J.B.; Baum, R.L. Hydrologic Impacts of Landslide Disturbances: Implications for Remobilization and Hazard Persistence. Water Resour. Res. 2017, WRCR22885. [Google Scholar] [CrossRef]
- National Weather Service. Available online: https://weather.gov (accessed on 7 September 2018).



| Timescale 1 | Equation | TPR | Threat Score | Precision | True Skill Statistic | Radial Distance |
|---|---|---|---|---|---|---|
| P10/S10 | P10 > 69.8, S10 > 0.82 | 0.71 | 0.32 | 0.38 | 0.67 | 0.30 |
| P5/S10 | P5 > 39.3, S10 > 0.84 | 0.64 | 0.34 | 0.42 | 0.62 | 0.35 |
| P3/S1 | P3 > 27.1, S1 > 0.86 | 0.71 | 0.44 | 0.55 | 0.69 | 0.29 |
| P10/S10 | P10 > 70.1, S10 > 0.57 | 0.82 | 0.25 | 0.26 | 0.76 | 0.19 |
| P5/S10 | P5 > 25.2, S10 > 0.63 | 0.88 | 0.15 | 0.15 | 0.75 | 0.18 |
| P2/S9 | P2 > 11.1, S9 > 0.64 | 0.94 | 0.18 | 0.18 | 0.83 | 0.13 |
| Timescale 1 | Equation | TPR | Threat Score | Precision | True Skill Statistic | Radial Distance |
|---|---|---|---|---|---|---|
| P10/S10 | P10 > 123, S10 > 0.68 | 0.42 | 0.29 | 0.49 | 0.40 | 0.58 |
| P5/S10 | P5 > 76.0, S10 > 0.69 | 0.56 | 0.35 | 0.50 | 0.53 | 0.45 |
| P1/S3 | P3 > 21.0, S1 > 0.75 | 0.68 | 0.53 | 0.71 | 0.67 | 0.32 |
| P10/S10 | P10 > 61.0, S10 > 0.68 | 0.89 | 0.20 | 0.21 | 0.75 | 0.18 |
| P5/S10 | P5 > 39.0, S10 > 0.69 | 0.87 | 0.27 | 0.28 | 0.78 | 0.16 |
| P2/S9 | P2 > 24.0, S9 > 0.70 | 0.90 | 0.29 | 0.30 | 0.81 | 0.13 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mirus, B.B.; Morphew, M.D.; Smith, J.B. Developing Hydro-Meteorological Thresholds for Shallow Landslide Initiation and Early Warning. Water 2018, 10, 1274. https://doi.org/10.3390/w10091274
Mirus BB, Morphew MD, Smith JB. Developing Hydro-Meteorological Thresholds for Shallow Landslide Initiation and Early Warning. Water. 2018; 10(9):1274. https://doi.org/10.3390/w10091274
Chicago/Turabian StyleMirus, Benjamin B., Michael D. Morphew, and Joel B. Smith. 2018. "Developing Hydro-Meteorological Thresholds for Shallow Landslide Initiation and Early Warning" Water 10, no. 9: 1274. https://doi.org/10.3390/w10091274
APA StyleMirus, B. B., Morphew, M. D., & Smith, J. B. (2018). Developing Hydro-Meteorological Thresholds for Shallow Landslide Initiation and Early Warning. Water, 10(9), 1274. https://doi.org/10.3390/w10091274





