The Effect of Bedrock Topography on Timing and Location of Landslide Initiation Using the Local Factor of Safety Concept
Abstract
1. Introduction
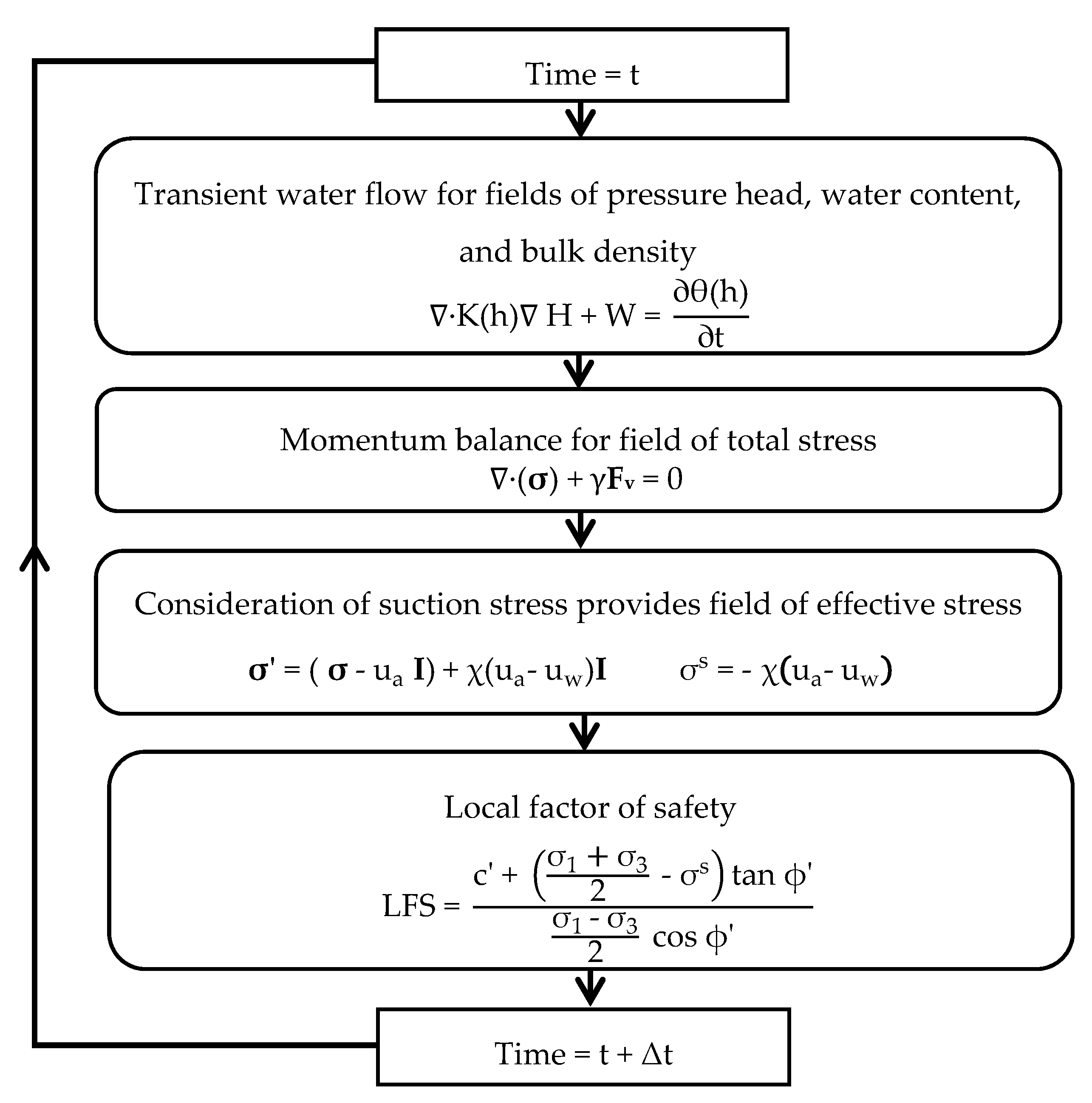
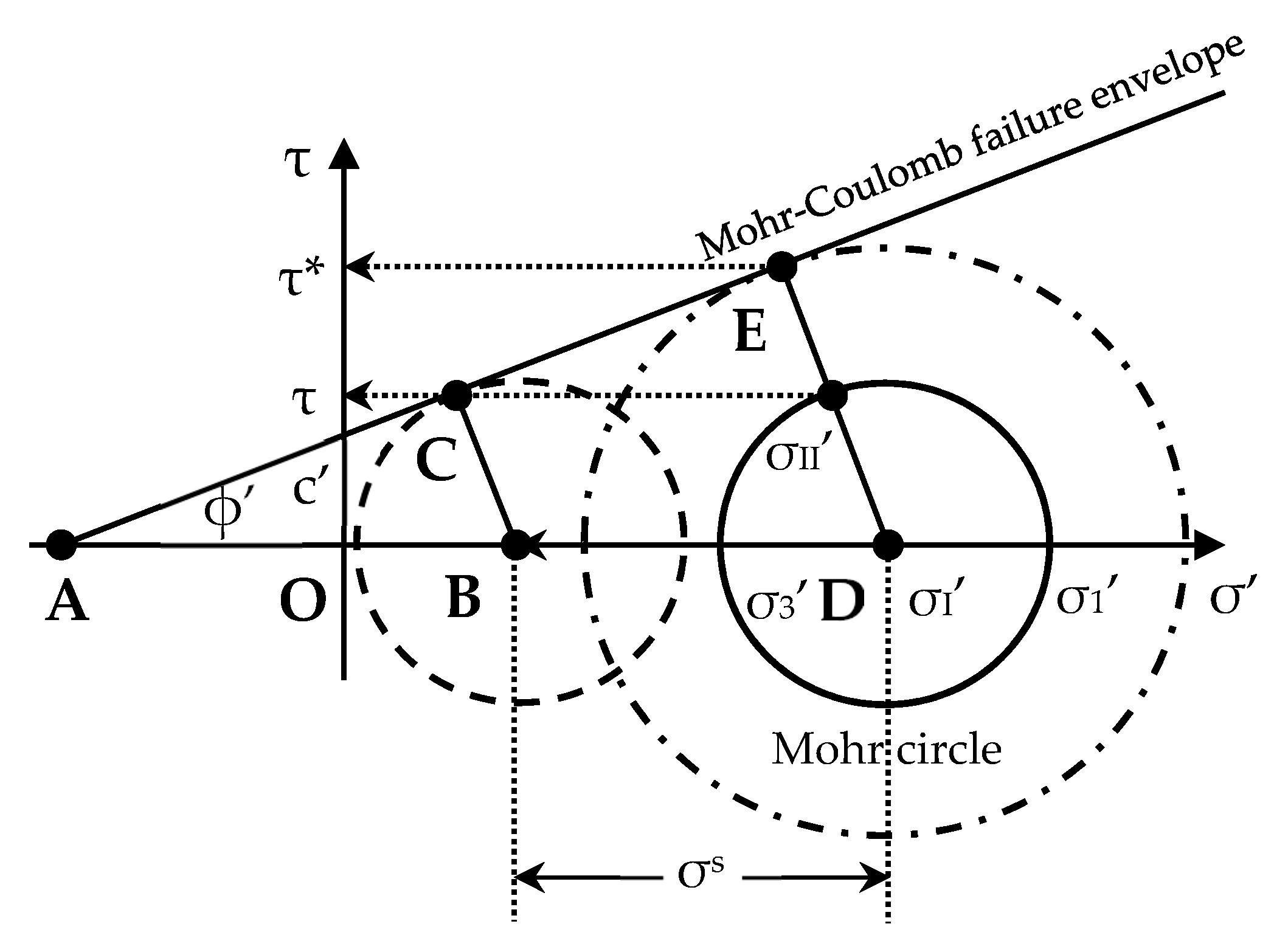
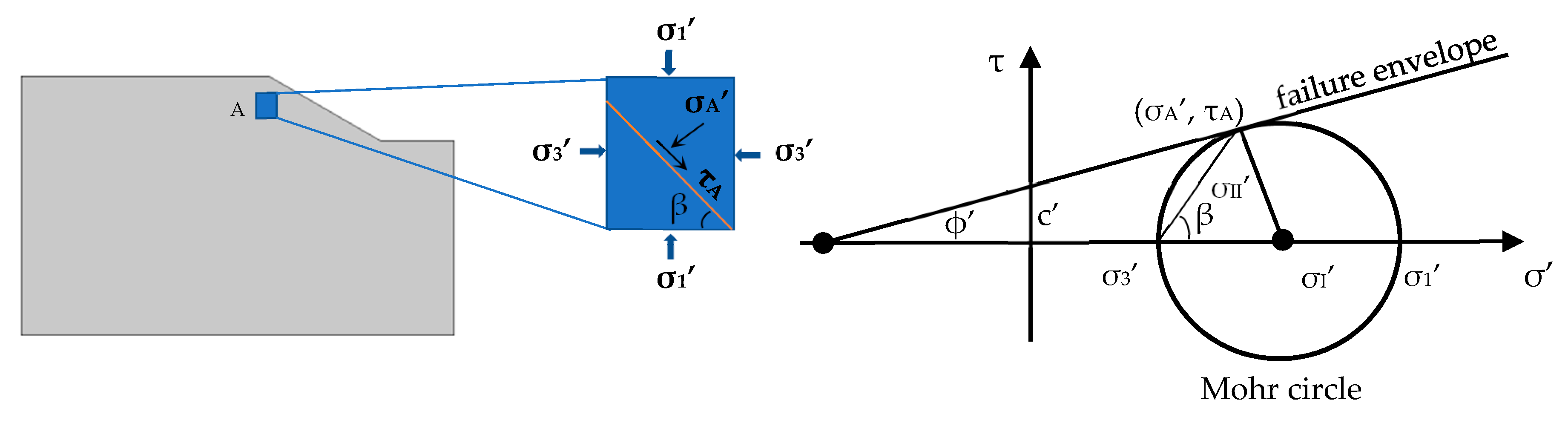
2. Coupled Hydromechanical Framework
3. Materials and Methods
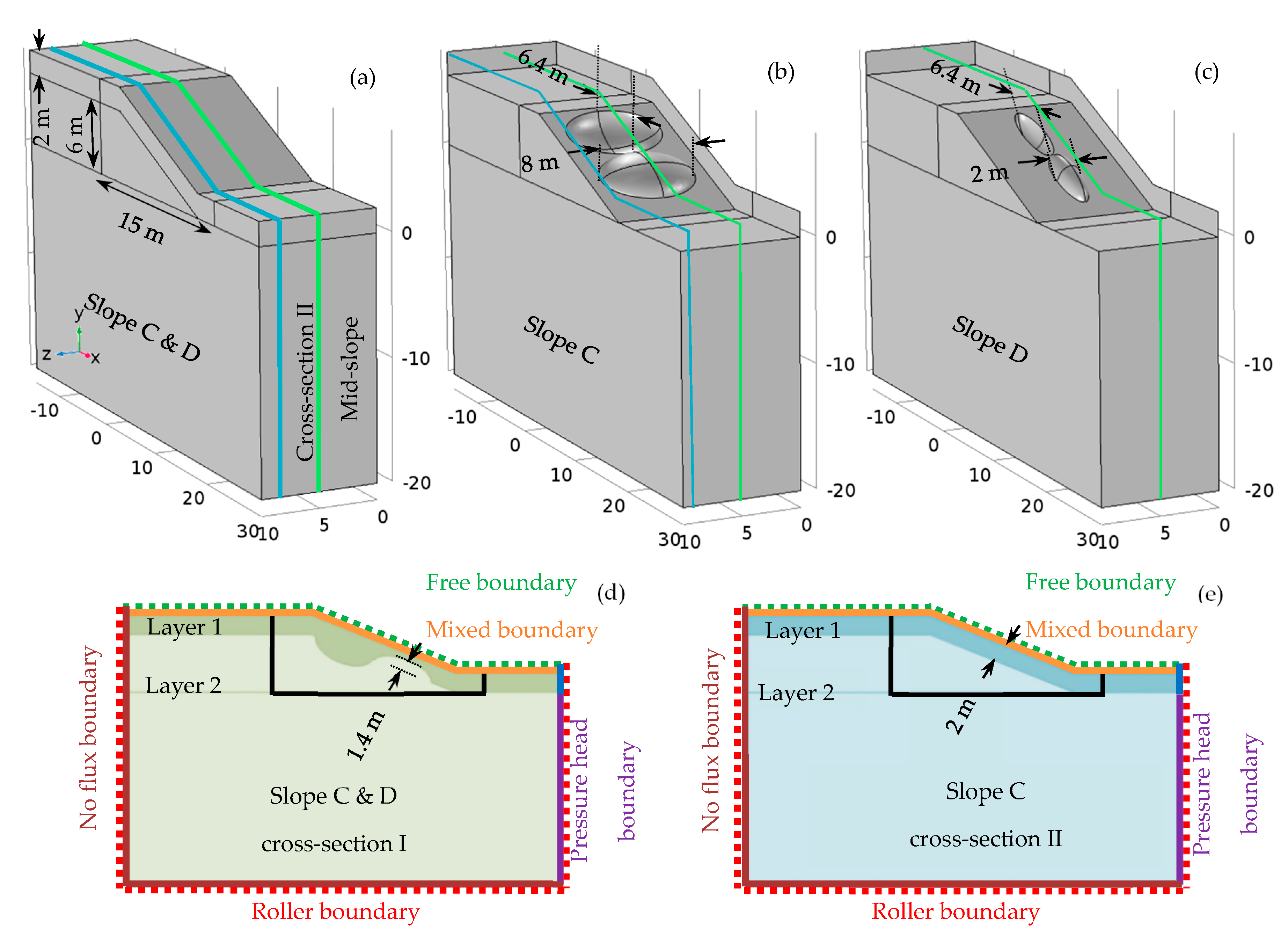
3.1. Set-Up of the Benchmark Model
3.2. Numerical Experiments
4. Results and Discussion
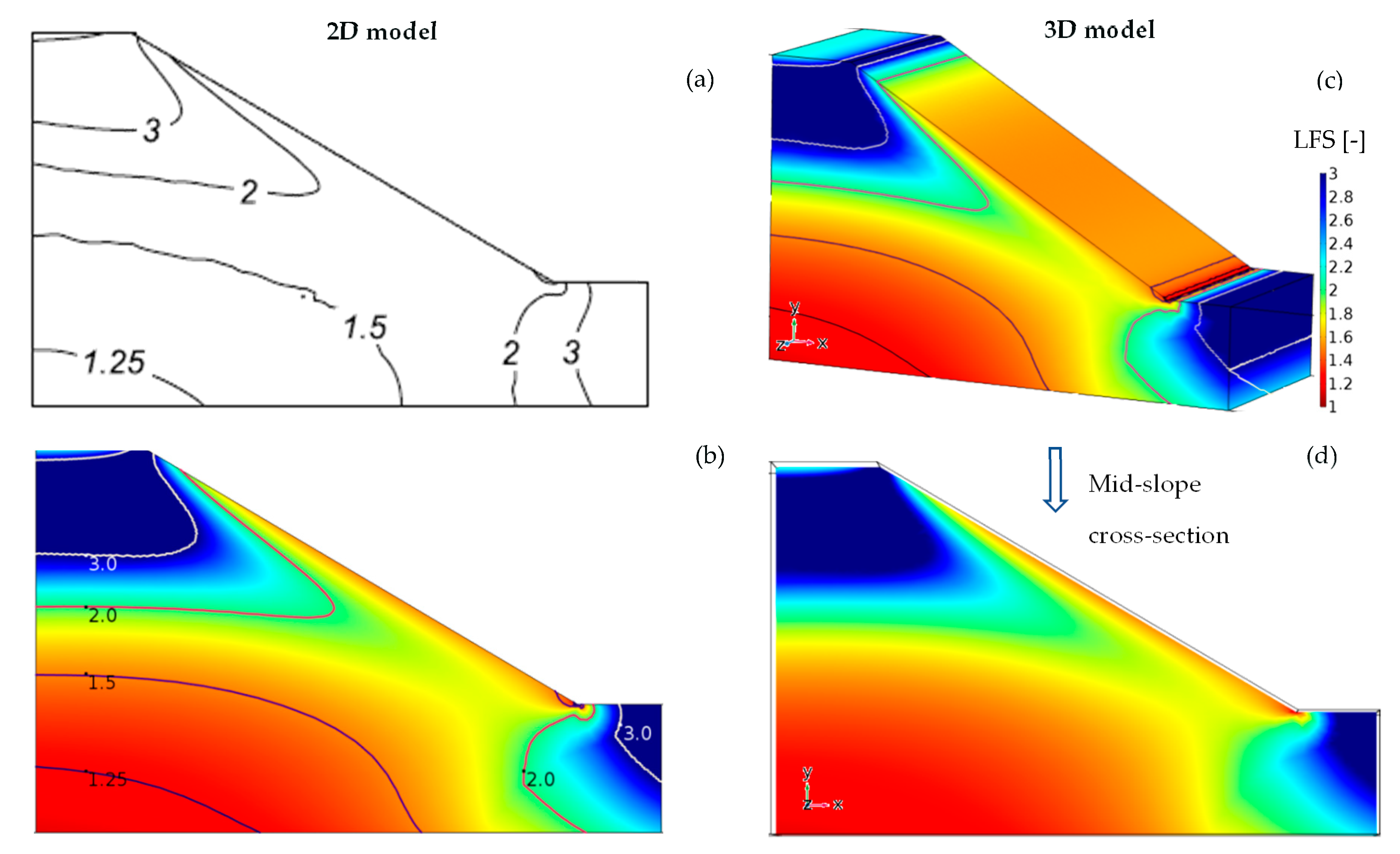
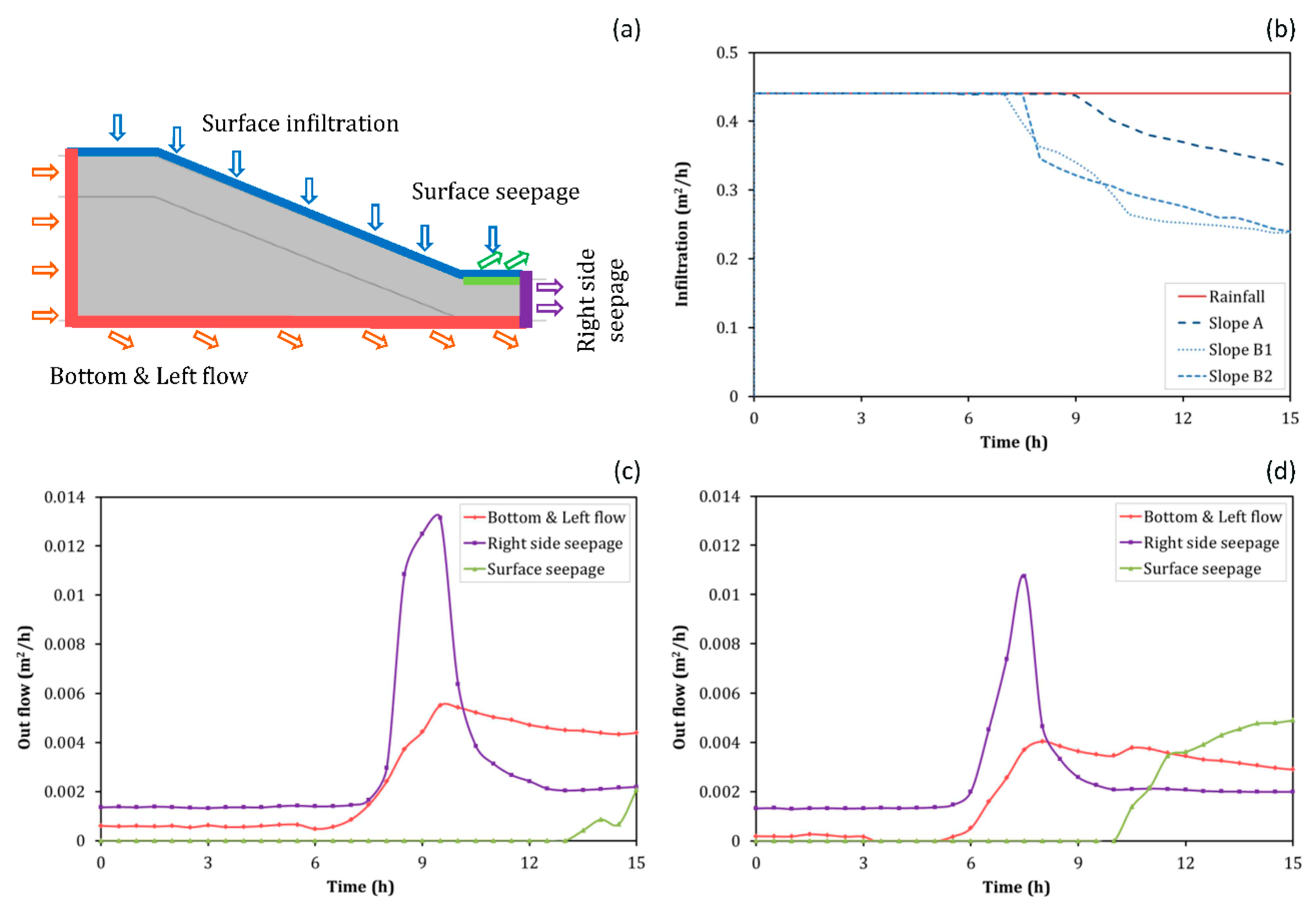
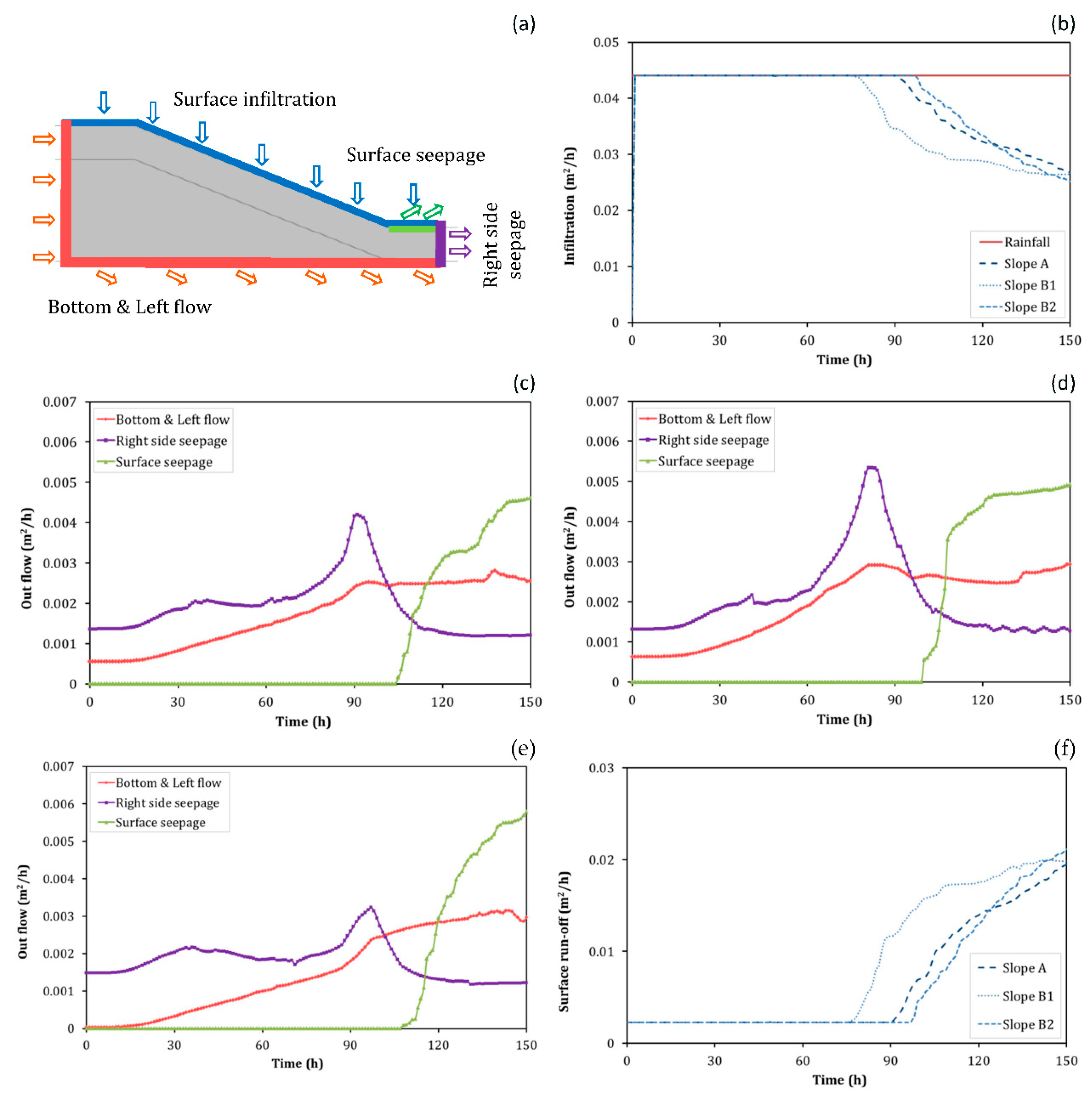
4.1. Results for the Benchmark Model
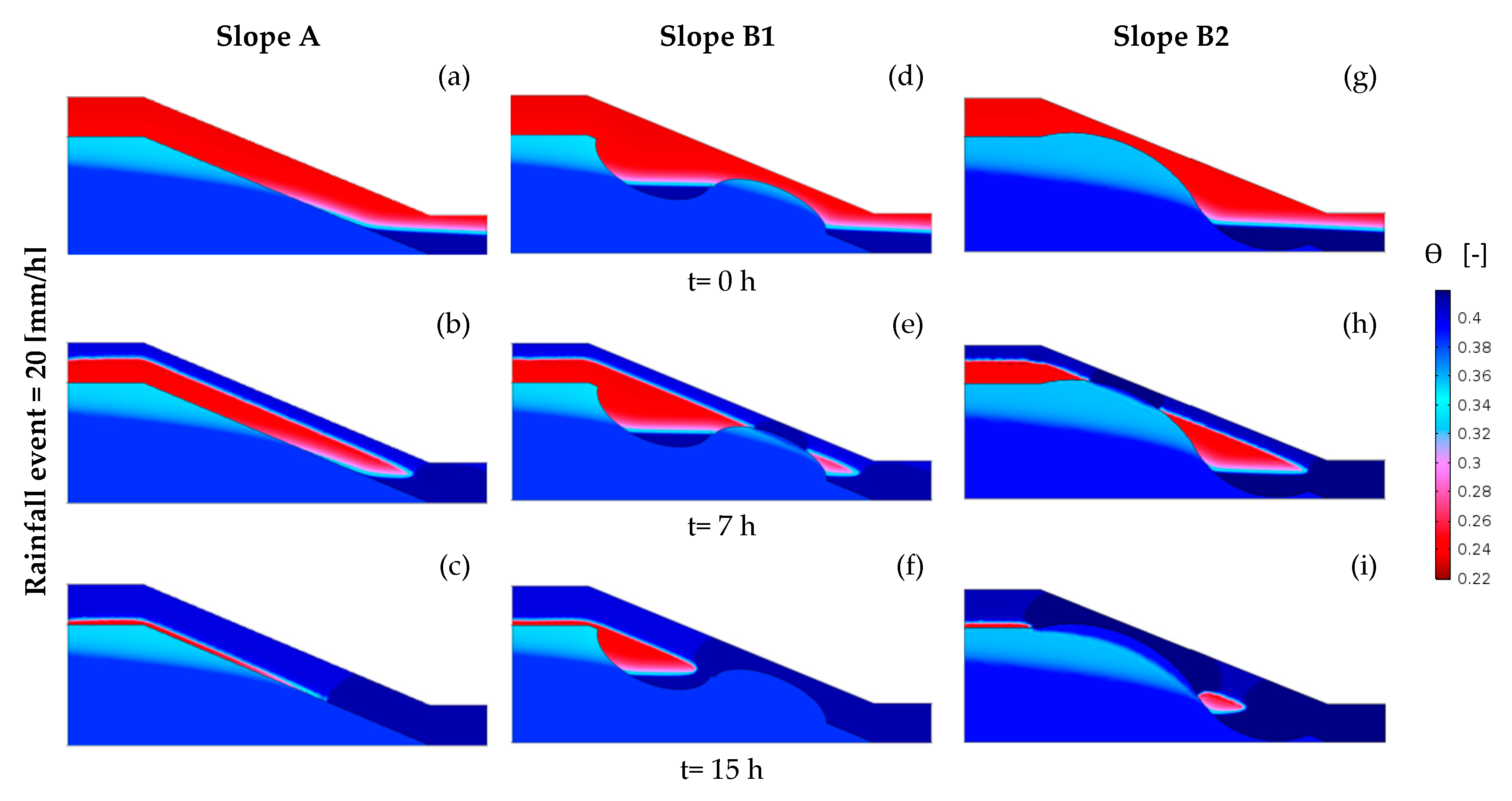
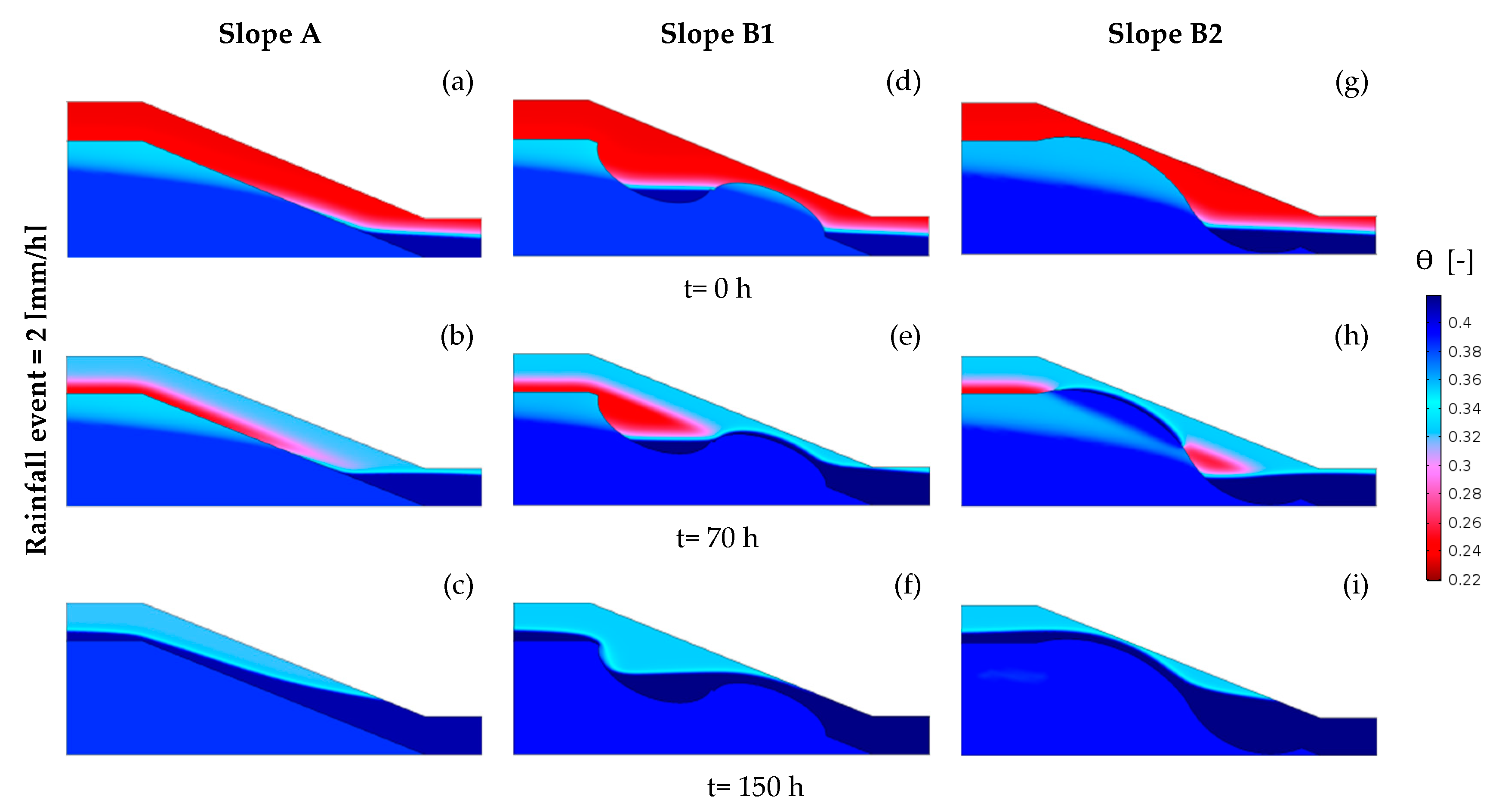
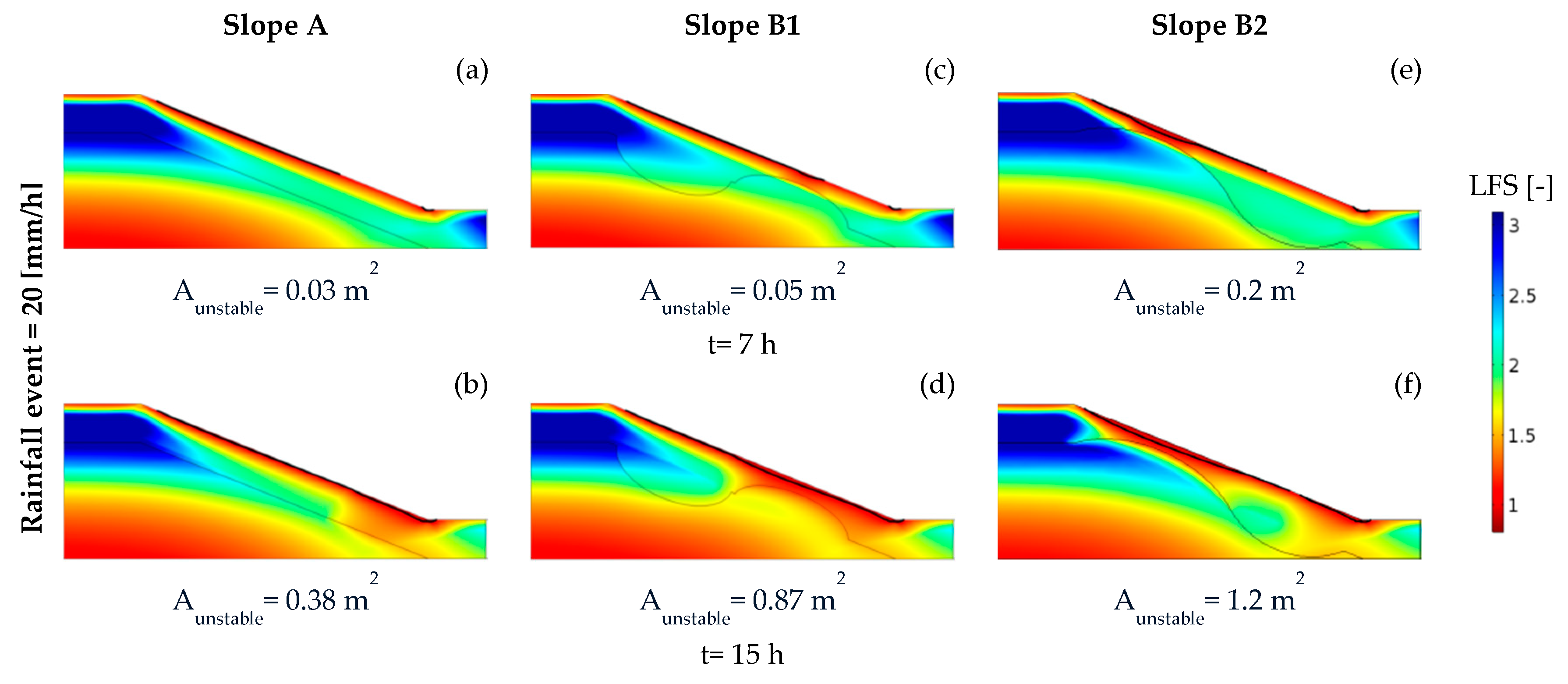
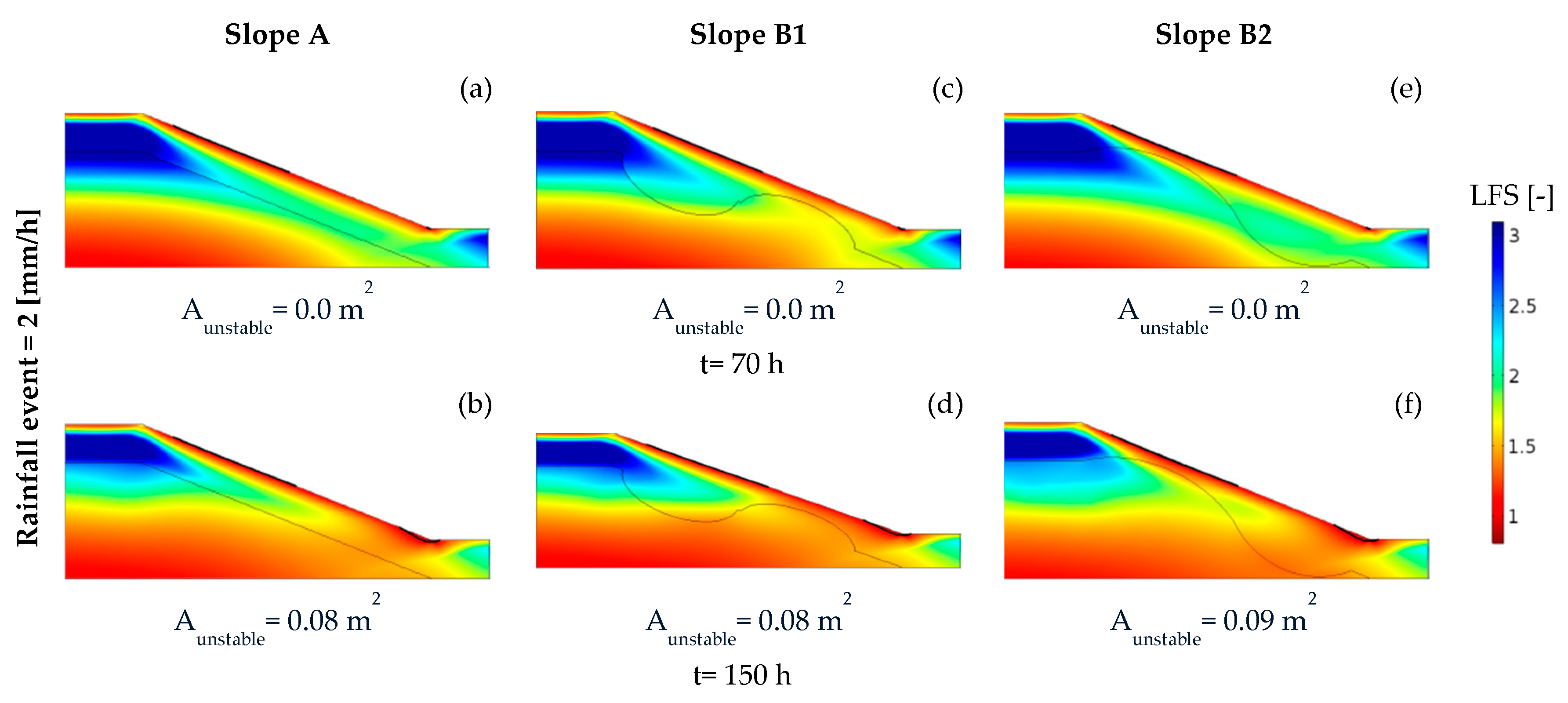
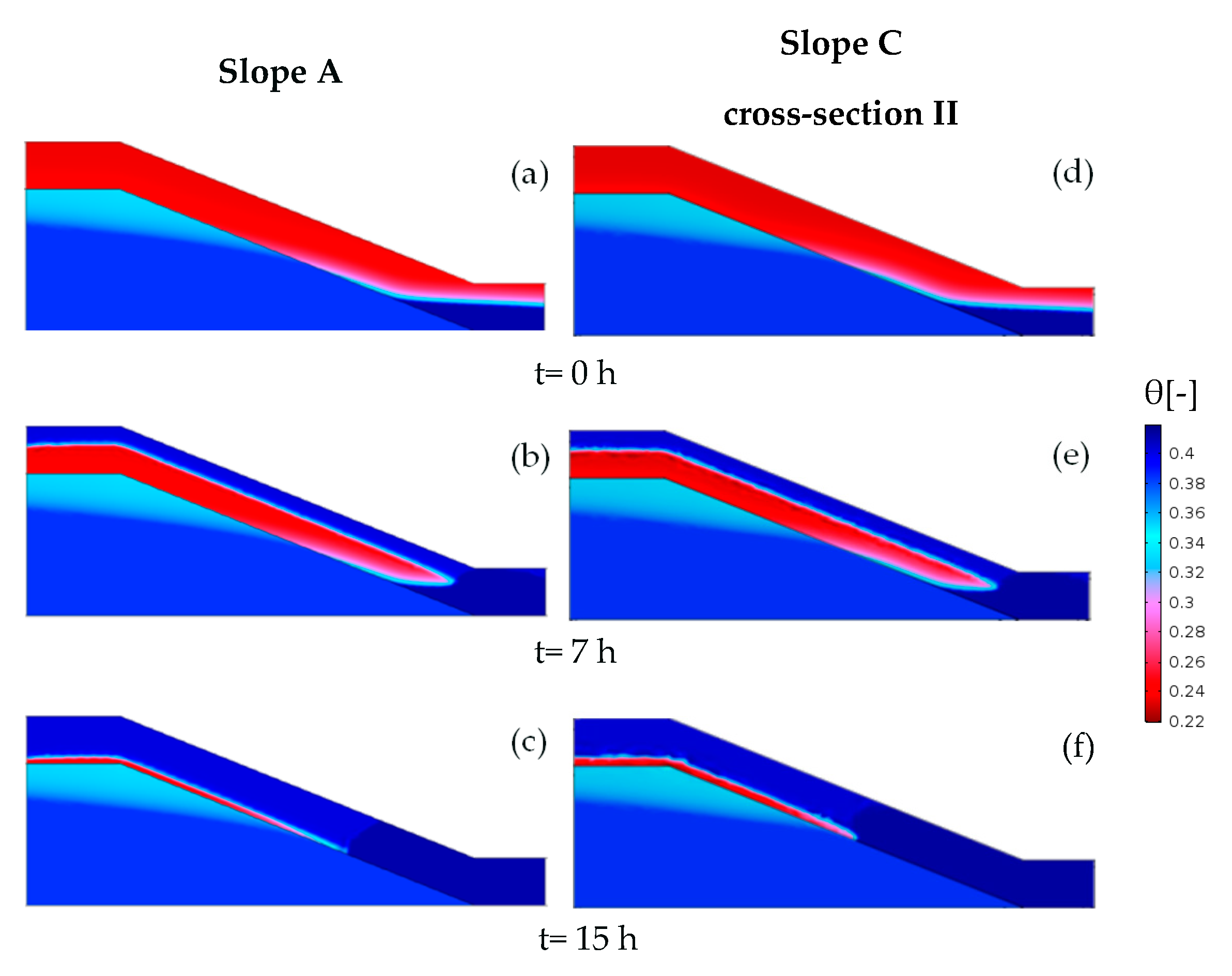
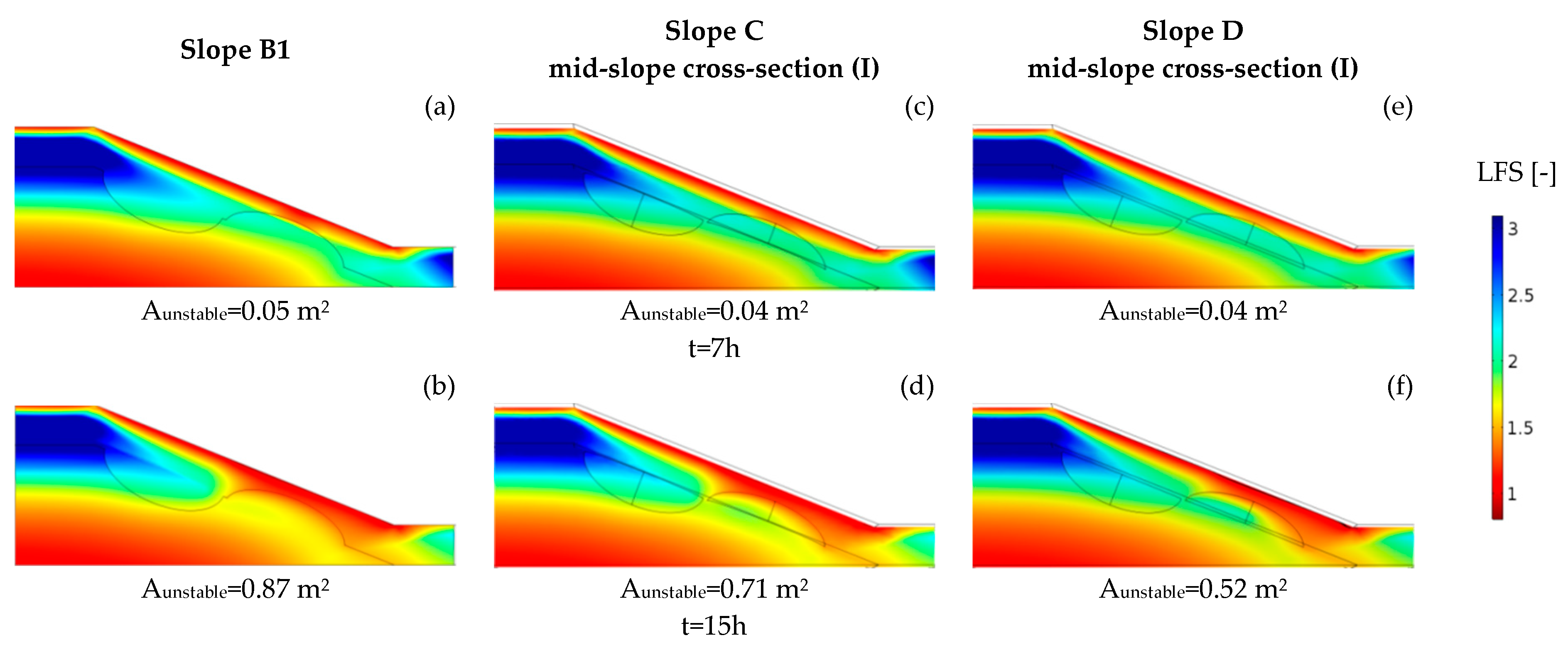
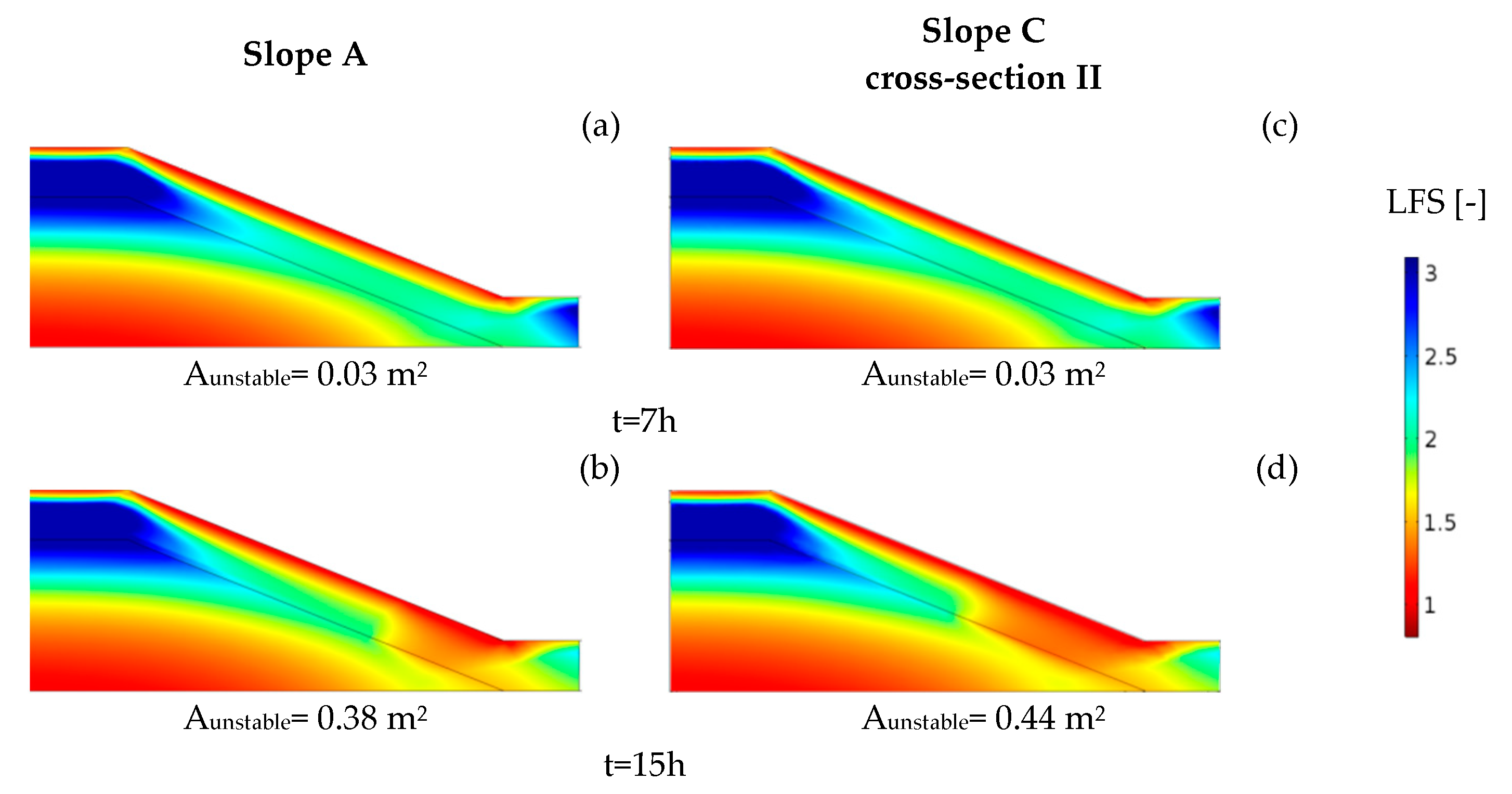
4.2. Results of the 2D Numerical Experiments
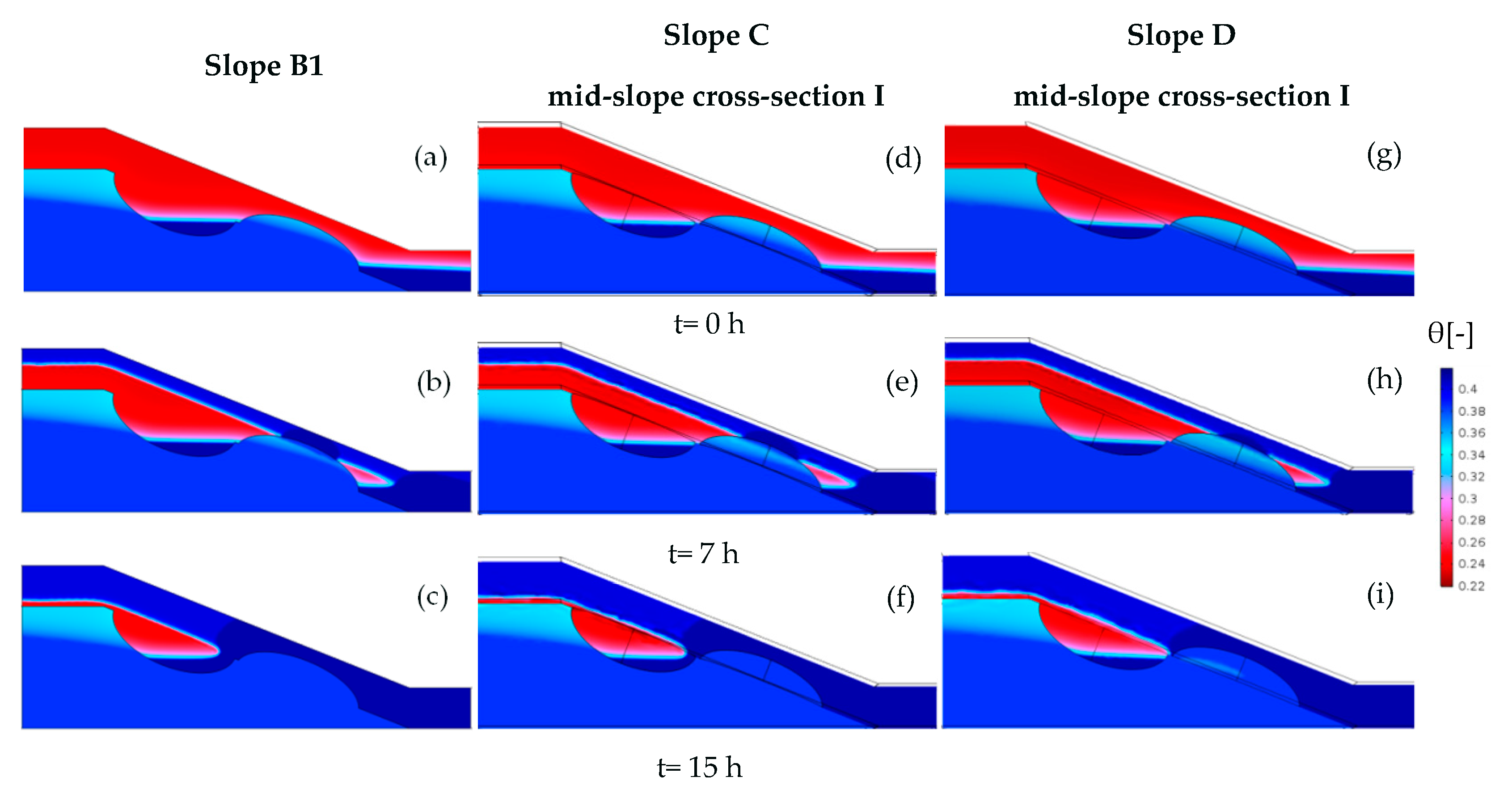
4.3. Results of the 3D Numerical Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cuomo, S.; Della Sala, M. Large-area analysis of soil erosion and landslides induced by rainfall: A case of unsaturated shallow deposits. J. Mt. Sci. 2015, 12, 783–796. [Google Scholar] [CrossRef]
- Cuomo, S.; Della Sala, M. Rainfall-induced infiltration, runoff and failure in steep unsaturated shallow soil deposits. Eng. Geol. 2013, 162, 118–127. [Google Scholar] [CrossRef]
- Borja, R.I.; White, J.A. Continuum deformation and stability analyses of a steep hillside slope under rainfall infiltration. Acta Geotech. 2010, 5, 1–14. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P. Rainfall-induced landslides and debris flows—Preface. Hydrol. Process. 2008, 22, 473–477. [Google Scholar] [CrossRef]
- Matsushi, Y.; Matsukura, Y. Rainfall thresholds for shallow landsliding derived from pressure-head monitoring: Cases with permeable and impermeable bedrocks in Boso Peninsula, Japan. Earth Surf. Process. Landf. 2007, 32, 1308–1322. [Google Scholar] [CrossRef]
- Lu, N.; Wayllace, A.; Oh, S. Infiltration-induced seasonally reactivated instability of a highway embankment near the Eisenhower Tunnel, Colorado, USA. Eng. Geol. 2013, 162, 22–32. [Google Scholar] [CrossRef]
- Godt, J.W.; Baum, R.L.; Lu, N. Landsliding in partially saturated materials. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Keefer, D.K.; Larsen, M.C. Assessing landslide hazards. Science 2007, 316, 1136–1138. [Google Scholar] [CrossRef] [PubMed]
- Petley, D.N. On the impact of climate change and population growth on the occurrence of fatal landslides in South, East and SE Asia. Q. J. Eng. Geol. Hydrogeol. 2010, 43, 487–496. [Google Scholar] [CrossRef]
- Klose, M.; Maurischat, P.; Damm, B. Landslide impacts in Germany: A historical and socioeconomic perspective. Landslides 2016, 13, 183–199. [Google Scholar] [CrossRef]
- Sidle, R.C.; Ochiai, H. Landslides: Processes, Prediction and Land Use; American Geophysical Union: Washington, DC, USA, 2006. [Google Scholar]
- Lu, N.; Godt, J.W. Hillslope Hydrology and Stability; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Montgomery, D.R.; Dietrich, W.E. A physically-based model for the topographic control on shallow landsliding. Water Resour. Res. 1994, 30, 1153–1171. [Google Scholar] [CrossRef]
- Kim, M.S.; Onda, Y.; Kim, J.K.; Kim, S.W. Effect of topography and soil parameterisation representing soil thicknesses on shallow landslide modelling. Quat. Int. 2015, 384, 91–106. [Google Scholar] [CrossRef]
- Lehmann, P.; Or, D. Hydromechanical triggering of landslides: From progressive local failures to mass release. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Gabet, E.J.; Dunne, T. Landslides on coastal sage-scrub and grassland hillslopes in a severe El Nino winter: The effects of vegetation conversion on sediment delivery. Geol. Soc. Am. Bull. 2002, 114, 983–990. [Google Scholar] [CrossRef]
- Schiliro, L.; Esposito, C.; Mugnozza, G.S. Evaluation of shallow landslide-triggering scenarios through a physically based approach: An example of application in the southern Messina area (northeastern Sicily, Italy). Nat. Hazards Earth Syst. Sci. 2015, 15, 2091–2109. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Estimating return period of landslide triggering by Monte Carlo simulation. J. Hydrol. 2016, 541, 256–271. [Google Scholar] [CrossRef]
- Stahli, M.; Sattele, M.; Huggel, C.; McArdell, B.W.; Lehmann, P.; Van Herwijnen, A.; Berne, A.; Schleiss, M.; Ferrari, A.; Kos, A.; et al. Monitoring and prediction in early warning systems for rapid mass movements. Nat. Hazards Earth Syst. Sci. 2015, 15, 905–917. [Google Scholar] [CrossRef]
- Lehmann, P.; Gambazzi, F.; Suski, B.; Baron, L.; Askarinejad, A.; Springman, S.M.; Holliger, K.; Or, D. Evolution of soil wetting patterns preceding a hydrologically induced landslide inferred from electrical resistivity survey and point measurements of volumetric water content and pore water pressure. Water Resour. Res. 2013, 49, 7992–8004. [Google Scholar] [CrossRef]
- Srinivasan, K.; Howell, B.; Anderson, E.; Flores, A. A low cost wireles sensor network for landslide hazard monitoring. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 4793–4796. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Eichenberger, J.; Ferrari, A.; Laloui, L. Early warning thresholds for partially saturated slopes in volcanic ashes. Comput. Geotech. 2013, 49, 79–89. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W.J. Suction stress characteristic curve for unsaturated soil. J. Geotech. Geoenviron. Eng. 2006, 132, 131–142. [Google Scholar] [CrossRef]
- Godt, J.W.; Sener-Kaya, B.; Lu, N.; Baum, R.L. Stability of infinite slopes under transient partially saturated seepage conditions. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Baum, R.; Godt, J. Early warning of rainfall-induced shallow landslides and debris flows in the USA. Landslides 2010, 7, 259–272. [Google Scholar] [CrossRef]
- Raia, S.; Alvioli, M.; Rossi, M.; Baum, R.L.; Godt, J.W.; Guzzetti, F. Improving predictive power of physically based rainfall-induced shallow landslide models: A probabilistic approach. Geosci. Model Dev. 2014, 7, 495–514. [Google Scholar] [CrossRef]
- Arnone, E.; Noto, L.V.; Lepore, C.; Bras, R.L. Physically-based and distributed approach to analyze rainfall-triggered landslides at watershed scale. Geomorphology 2011, 133, 121–131. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J. Infinite slope stability under steady unsaturated seepage conditions. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Lu, N.; Sener-Kaya, B.; Wayllace, A.; Godt, J.W. Analysis of rainfall-induced slope instability using a field of local factor of safety. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Hovland, H.J. Three-dimensional slope stability analysis method. J. Geotech. Eng. Div. 1977, 103, 971–986. [Google Scholar]
- Wong, F.S. Uncertainties in modeling of slope stability. Comput. Struct. 1984, 19, 777–791. [Google Scholar] [CrossRef]
- Rabie, M. Comparison study between traditional and finite element methods for slopes under heavy rainfall. HBRC J. 2014, 10, 160–168. [Google Scholar] [CrossRef]
- Hammah, R.E.; Yacoub, T.E.; Corkum, B.; Curran, J. (2005) A comparison of finite element slope stability analysis with conventional limit-equilibrium investigation. In Proceedings of the 58th Canadian Geotechnical and 6th Joint IAH-CNC and CGS Groundwater Specialty Conferences—GeoSask 2005, Saskatoon, SK, Canada, 18–21 September 2005; pp. 480–487. [Google Scholar]
- Shao, W.; Bogaard, T.A.; Bakker, M.; Greco, R. Quantification of the influence of preferential flow on slope stability using a numerical modelling approach. Hydrol. Earth Syst. Sci. 2015, 19, 2197–2212. [Google Scholar] [CrossRef]
- Lanni, C.; McDonnell, J.; Hopp, L.; Rigon, R. Simulated effect of soil depth and bedrock topography on near-surface hydrologic response and slope stability. Earth Surf. Process. Landf. 2013, 38, 146–159. [Google Scholar] [CrossRef]
- Freer, J.; McDonnell, J.J.; Beven, K.J.; Peters, N.E.; Burns, D.A.; Hooper, R.P.; Aulenbach, B.; Kendall, C. The role of bedrock topography on subsurface storm flow. Water Resour. Res. 2002, 38. [Google Scholar] [CrossRef]
- Tromp-van Meerveld, H.J.; McDonnell, J.J. On the interrelations between topography, soil depth, soil moisture, transpiration rates and species distribution at the hillslope scale. Adv. Water Resour. 2006, 29, 293–310. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.A.; Franssen, H.J.H.; Bruggemann, N.; Bogena, H.R.; Kollet, S.; Javaux, M.; van der Kruk, J.; Vanderborght, J. Soil hydrology: Recent methodological advances, challenges, and perspectives. Water Resour. Res. 2015, 51, 2616–2633. [Google Scholar] [CrossRef]
- Talebi, A.; Troch, P.A.; Uijlenhoet, R. A steady-state analytical slope stability model for complex hillslopes. Hydrol. Process. 2008, 22, 546–553. [Google Scholar] [CrossRef]
- Tromp-van Meerveld, H.J.; McDonnell, J.J. Threshold relations in subsurface stormflow: 2. The fill and spill hypothesis. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Mualem, Y. Hysteretical models for prediction of hydraulic conductivity of unsaturated porous-media. Water Resour. Res. 1976, 12, 1248–1254. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, A. Hydraulic Properties of Porous Media; Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Oh, S.; Lu, N. Slope stability analysis under unsaturated conditions: Case studies of rainfall-induced failure of cut slopes. Eng. Geol. 2015, 184, 96–103. [Google Scholar] [CrossRef]
- Iverson, R.M.; Reid, M.E. Gravity-driven groundwater-flow and slope failure potential. 1. Elastic effective-stress model. Water Resour. Res. 1992, 28, 925–938. [Google Scholar] [CrossRef]
- Bishop, A.W. The principle of effective stress. Tek. Ukebl. 1959, 106, 859–863. [Google Scholar]
- Greco, R.; Gargano, R. A novel equation for determining the suction stress of unsaturated soils from the water retention curve based on wetted surface area in pores. Water Resour. Res. 2015, 51, 6143–6155. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Fellenius, W. Erdstatische Berechnungen mit Reibung und Kohäsion (Adhäsion) und unter Annahme Kreiszylindrischer Gleitflächen; W. Ernst & Sohn: Berlin, Germany, 1927. [Google Scholar]
- Zhang, K.; Cao, P.; Liu, Z.Y.; Hu, H.H.; Gong, D.P. Simulation analysis on three-dimensional slope failure under different conditions. Trans. Nonferrous Met. Soc. China 2011, 21, 2490–2502. [Google Scholar] [CrossRef]
- Shen, J.Y.; Karakus, M. Three-dimensional numerical analysis for rock slope stability using shear strength reduction method. Can. Geotech. J. 2014, 51, 164–172. [Google Scholar] [CrossRef]
- Shao, W.; Bogaard, T.; Bakker, M. Third Italian Workshop on Landslides: Hydrological Response of Slopes through Physical Experiments, Field Monitoring and Mathematical Modeling; Picarelli, L., Greco, R., Urciuoli, G., Eds.; Elsevier Science Bv: Amsterdam, The Netherlands, 2014; pp. 83–90. [Google Scholar]




| Symbol | Parameter Name | Units | Value |
|---|---|---|---|
| Saturated water content | - | 0.46 | |
| Residual water content | - | 0.034 | |
| Ks | Saturated hydraulic conductivity | m s−1 | 1.39 × 10−6 |
| van Genuchten fitting parameter | m−1 | 1.6 | |
| van Genuchten fitting parameter | - | 1.37 | |
| Dry unit weight | kN m−1 | 20 | |
| E | Young’s modulus | MPa | 10 |
| ν | Poisson’s ratio | - | 0.33 |
| ϕ′ | Friction angle | ° | 30 |
| c′ | Effective cohesion | kPa | 15 |
| Symbol | Parameter | Units | Value for Top Layer (Sandy Loam) | Value for Bottom Layer (Clay) |
|---|---|---|---|---|
| Saturated water content | - | 0.412 | 0.385 | |
| Residual water content | - | 0.041 | 0.090 | |
| Ks | Saturated hydraulic conductivity | m s−1 | 7.20 × 10−6 | 1.67 × 10−7 |
| Brooks-Corey fitting parameter | m−1 | 0.068 | 0.027 | |
| Brooks-Corey fitting parameter | - | 0.322 | 0.131 | |
| Dry unit weight | kN m−1 | 15.5 | 15.5 | |
| E | Young’s modulus | MPa | 10 | 10 |
| ν | Poisson’s ratio | - | 0.35 | 0.35 |
| ϕ′ | Friction angle | ° | 35 | 35 |
| c′ | Effective cohesion | kPa | 5 | 5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradi, S.; Huisman, J.A.; Class, H.; Vereecken, H. The Effect of Bedrock Topography on Timing and Location of Landslide Initiation Using the Local Factor of Safety Concept. Water 2018, 10, 1290. https://doi.org/10.3390/w10101290
Moradi S, Huisman JA, Class H, Vereecken H. The Effect of Bedrock Topography on Timing and Location of Landslide Initiation Using the Local Factor of Safety Concept. Water. 2018; 10(10):1290. https://doi.org/10.3390/w10101290
Chicago/Turabian StyleMoradi, Shirin, Johan Alexander Huisman, Holger Class, and Harry Vereecken. 2018. "The Effect of Bedrock Topography on Timing and Location of Landslide Initiation Using the Local Factor of Safety Concept" Water 10, no. 10: 1290. https://doi.org/10.3390/w10101290
APA StyleMoradi, S., Huisman, J. A., Class, H., & Vereecken, H. (2018). The Effect of Bedrock Topography on Timing and Location of Landslide Initiation Using the Local Factor of Safety Concept. Water, 10(10), 1290. https://doi.org/10.3390/w10101290






