Abstract
Land use has significant impact on the hydrologic and hydraulic processes in a catchment. This work applies a hydrodynamic based numerical model to quantitatively investigate the land use effect on the flood patterns under various rainfall and terrain conditions in an ideal V-shaped catchment and a realistic catchment, indicating the land use could considerably affect the rainfall-flood process and such effect varies with the catchment terrain, land use scenario and the rainfall events. The rainfall-flood process is less sensitive for the side slope than the channel slope. For a channel slope lower than the critical value in this work, the forest located in the middle of the catchment slope could most effectively attenuate the flood peak. When the channel slope is higher than the critical one, forest located in the downstream of the catchment could most significantly mitigate the peak discharge. Moreover, the attenuation effect becomes more obvious as the rainfall becomes heavier. The fragmentation of vegetation does not reduce the flood peak in a more obvious way, compared with the integral vegetation patterns with the same area proportion. The research can help more reasonably guide the land use plan related to flood risk.
1. Introduction
As averaged temperatures increase globally, the probability for extreme rainfall events increases [1,2], leading to sever flood with more casualties and property loss and becomes a major concern world widely [3,4]. Land use could impact the rainfall-runoff process by changing the catchment property in term of hydrological and hydraulic parameters [5,6]. For example, comparing to the bare land, the forest could slow down the surface runoff by increasing the friction, meanwhile, it raises the infiltration through changing the soil structure, inducing less stream flow and lower intensity of flooding [7]. It in turn influences the ecosystem, environment and local economy in a catchment, e.g., reconstruction of ecological environment and synthetic control of environment in large scale by changing cultivated land into grass land or forest are carried out in Loess Plateau, China, where suffering from sever flash floods and erosion [8,9]. Therefore, a better understanding and assessment of land use impacts on catchment rainfall-runoff process is of great importance for the mitigation of flood hazards, and has become a crucial issue for planning, management, and sustainable development of the catchment. However, how to properly guide the land use to mitigate the flood in a more efficient way is still under investigation.
Recently, many researchers have paid attentions to the relations between land use and rainfall-runoff processes. Most of the studies have focused on the land use effects on hydrological process due to human activities [10,11,12]. For instance, Chaves et al. [13] used an end-member mixing analysis approach evaluating potential contributing sources of stream flow from pasture and forest during an entire rain season in the lowland Amazon region, where the forest is clearing and converting to cattle pasture. Yira et al. [14] applied land use conditions of different years in the process of urbanization as inputs to models, establishing a strong relationship between reduction of vegetation and the total runoff increase. All those studies, however, just analyze roughly the trend of the runoff variety among the different land use conditions and do not systematically point out how to plan and design the optimal land use.
As the catchment hydrology is a very complex process, choosing an effective methodology to investigate the impacts of land use change on storm-runoff is very important. In recent years, many of hydrological models have been developed to evaluate such impacts [15]. These models differ, in part, based on their spatial aggregation levels-ranging from lumped, semi-distributed to fully distributed and the physical processes incorporated into the model. Siriwardena et al. [16] used a simple conceptual rainfall-runoff model to investigate the effects of natural forest cover reduction on runoff, but the lumped hydrological model is difficult to obtain accurate results. Liu et al. [17] applied a grid-based physical-conceptual hydrological model to a catchment in Luxembourg and simulated the storm runoff contributions from different land use types. Notter et al. [18] used a semi-distributed grid-based water balance model to predict the discharge in a mesoscale catchment in Kenya. And other more complex fully-distributed hydrological models such as the precipitation runoff modeling system (PRMS) [19], European Hydrological System Model (MIKE-SHE) [7,20], and soil and water assessment tool (SWAT) [8,21,22,23,24] become a common approach to assess the impact of land use on hydrological process. Although the above-mentioned hydrological models are capable of assessing such influence, the models may fail to accurately simulate the surface runoff process as they cannot reliably predict the important dynamical variables, velocities, because the physical processes are not fully taken into account [25,26].
In this work, through two test cases, a hydrodynamic based model is used to systematically and reliably investigate the effect of the land use patterns under different rainfall and topographic conditions on rainfall-flood processes. The results are analyzed to determine the optimal land use type for flood mitigation. The research can help guide the catchment and flood management. The remainder of the paper is structured as following: the numerical model is presented in Section 2; Section 3 simulates the land use effects in an ideal V-shaped catchment and analyzes the relations between the land use and flood; Section 4 demonstrates land use effects on flood patterns in a realistic catchment and conclusions are briefly drawn in Section 5.
2. Numerical Model
The shallow water equations (SWEs) are derived from the conservation of mass and momentum by assuming hydrostatic pressure distribution. In a vector form, a conservation law of the 2D shallow water equations can be written as [27,28]:
where t represents the time; x and y are the Cartesian coordinates; t denotes the vector of conserved flow variables consisting of h, qx and qy, i.e., the water depth, unit-width discharges in x- and y- direction, respectively; qx = uh and qy = vh and u and v are depth-averaged velocities in x- and y- directions; f and g dare the flux vectors in x- and y- directions; S is the source vector that may be further subdivided into slope source terms Sb and friction source terms Sf; Zb represents the bed elevation; Cf is the bed roughness coefficient that is generally computed by gn2/h1/3 with n being the Manning coefficient. i is the mass source or sink term equal to ir−ii, where ir is the rainfall rate while ii denotes the infiltration rate. When the rainfall rate ir is larger than infiltration rate ii, i is the source term. On the contrary, i is the sink term. Moreover, the water level η = h + zb is also used in the numerical scheme adopted in this work.
This section describes the numerical model for solving the SWEs within the framework of a Godunov-type cell-centered finite volume scheme based on the structured grids. The SWEs are discretized into algebraic equations by the finite volume method. The fluxes of mass and momentum are computed by the HLLC (Harten Lax van Leer Contact) approximate Riemann solver (i.e., Harten, Lax and van Leer approximate Riemann solver with contact wave restored). The slope source terms are evaluated by the slope flux method as proposed in Hou et al. [29]. The friction source terms are calculated by the improved explicit method. When computing the fluxes and the slope source terms, the values at the midpoints of the cell edges are required. The two-stage explicit Runge-Kutta approach is applied to update the flow variables to a new time level. These values are evaluated by a novel 2D edge-based MUSCL (Monotonic Upwind Scheme for Conservation Laws) scheme. The code is programmed by using C++ and CUDA (Compute Unified Device Architecture), which could run on GPUs (Graphics Processing Unit) to substantially accelerate the computation.
3. Evaluation of Land Use Effects on Rainfall-Flood Process in a V-Shaped Catchment
A classic theoretical V-shaped catchment proposed by Overton and Brakensiek [30], see Figure 1, is applied to systematically investigate the land use effects on rainfall-runoff process by using various rainfall, slopes and land use patterns. It also helps determine the optimised land use scenario mitigating the flood. There are two symmetrical side slopes and a channel in the middle of the catchment.
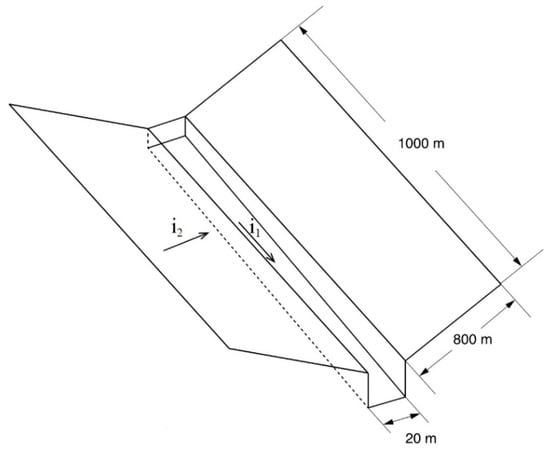
Figure 1.
Geometry of the V-shaped channel.
Figure 2 shows the land use conditions on the left-hand side slope of the catchment, including forest and grass land; the channel is considered as bare land. Land use scenarios of the other slope of the catchment are symmetrical. To evaluate the land use effects on hydrological process using numerical model, the different land use type can be presented by different hydrological. After uncertainty analysis, the coefficients don’t obviously affect the land use effect. The hydrological or hydraulic parameters such as infiltration rate and Manning coefficient are based on those recommended by Engman [31] and Li [32], as shown in Table 1.

Figure 2.
Different land use scenarios on the left-hand side slope. (a) Case 1; (b) Case 2; (c) Case 3.

Table 1.
The parameters for different land use.
Regarding the same land use pattern, different catchment slope and channel slope will lead to different flow pattern, because the flow momentum is very sensitive to the terrain especially for over land flows [33]. This work therefore looks at the land use effect on different terrain slopes.
The design storms from Suide County, Shaanxi Province is employed as a rainfall input data with the return periods of 2, 10, 50, 100 years and the duration time of 2 h (Figure 3). The storm formula is expressed as follows [34]:
where i represents rainfall intensity, mm/min; p is the return periods, year; t denotes rainfall duration, min.
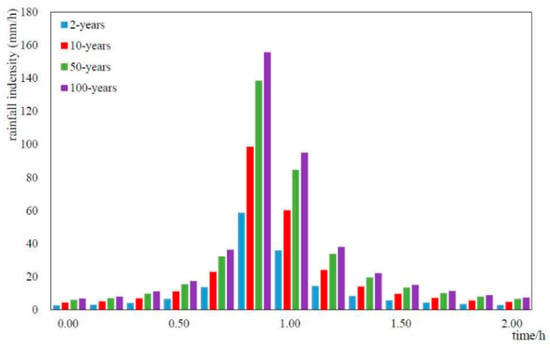
Figure 3.
The hyetography of design storms with different return periods.
The validation is conducted for a rainfall event with a constant intensity of 10.8 mm/h lasting for 1.5 h. All parameters used in this simulation are applied the same as that in Di Giammarco et al. [35] and Simons et al. [36], which used the n = 0.015 s/m1/3 for the side slope and n = 0.15 s/m1/3 for the main channel. i1 and i2 of the catchment are 0.02 and 0.05, respectively. The computational domain is discretized by uniform grid with the cell size of 5 m. Regarding the boundary condition, all boundaries are closed boundaries, except the outlet. Figure 4 shows the comparison between the analytical (Overton and Brakensiek [30]) and simulation hydrographs. The root mean square error (RMSE) values of the simulated data and the standard deviation of analytical solution in side slope and channel are 0.085 and 0.844, 0.365 and 1.758, respectively. The RMSE values is smaller than the half of the standard deviation of analytical solution, demonstrating the reliable simulation of rainfall-flood processes [37].
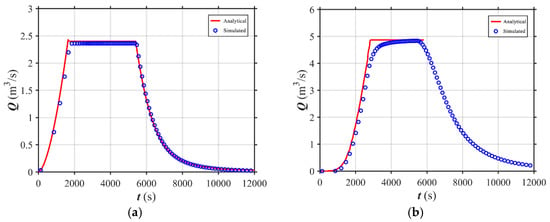
Figure 4.
Comparison between the analytical and simulated hydrographs. (a) Side slope; (b) Channel.
In this section, three land use factors are explored in detail: (i) channel slop (i1); (ii) side slope (i2) and (iii) vegetation cover patterns.
3.1. Land Use Effects on Flood Mitigation for Different Channel Slopes
Three land use patterns in the V-shaped catchment with the side slope of 0.58 and four different channel slopes termed as i1 of 0.01 (Scenario 1), 0.02 (Scenario 2), 0.05 (Scenario 3) and 0.08 (Scenario 4) are used in the simulation. As plotted in Figure 2, three land use patterns which divide a slope plane into three parts consisting of forest or grass land are employed in this section. The model is run under the rainfall condition with 4 return periods (2, 10, 50 and 100 years). The water depth and velocities are computed all over the domain and the flow discharge at the catchment outlet is recorded in this event. It should be noted that surface landform is not changed with the different land use patterns. Interception (accounting for a relatively small proportion) and the ecological restoration influence on channel morphology is not considered.
The computed hydrographs at the outlet under different land use and slope scenarios are illustrated in Figure 5, Figure 6, Figure 7 and Figure 8. The simulated peak discharges corresponding to the different land use scenarios exhibit high variations. The peak discharge among different land use cases (Case 1, Case 2 and Case 3) for different scenarios of channel slope are presented in Figure 9 and Table 2. For Scenario 1 (i1 = 0.01), the Case 2 shows more obvious effects in mitigating the peak discharge compared with the Case 1 and Case 3. The Case 3 has the highest peak discharge. The peak discharge of Case 2 can reduce by 7.02%, 3.94%, 4.22% and 4.19% for the rainfall events with different return periods, respectively, in contrast to Case 1. Comparing to Case 3, the peak discharge of Case 2 reduces by 19.58%, 15.15%, 13.52% and 12.94% for the rainfall events with different return periods, respectively. The same phenomenon can be observed for Scenario 2 (i1 = 0.02). The peak discharge reduction of Case 2 can reach 7.55–20.58%, compared to other land use types. However, for Scenario 3 (i1 = 0.05), the results clearly demonstrate that the Case 3 mitigates the peak discharge in a most efficient way. The Case 1 and the Case 2 do not show obvious effect on flood mitigation. The peak discharge of Case 3 can reduce by 5.87%, 9.09%, 7.93% and 9.22% for the rainfall events with different return periods, respectively, in comparison to Case 1. The reduction percentage between Case 3 and Case 2 reaches 10.22–15.10% for different rainfall events. For Scenario 4 (i1 = 0.08), the same phenomenon as Scenario 3 is observed, and the reduction percentage between Case 3 and others can reach 28.16%. In term of water level, the peak value among different land use scenarios (Case 1, Case 2 and Case 3) for different scenarios of channel slope are presented in Table 3. From the above, it can be seen that the return period of rainfall will not affect the conclusion, so the 100-year rainfall event is selected to investigate the land use effects on water level. As shown in Figure 10, for Scenario 1 (i1 = 0.01) and Scenario 2 (i1 = 0.02), Case 2 could attenuate the peak values most effectively and Case 3 has the highest water level. On the contrary, for Scenario 3 (i1 = 0.05) and Scenario 4 (i1 = 0.08), Case 3 is the safest scenario and Case 2 causes the highest flood risk. With the rainfall becomes intenser, the peak discharge mitigation among different land use scenarios become larger. For instance, the peak discharge of Case 3 can reduce by 3.16 m3/s, 6.72 m3/s, 11.57 m3/s and 13.78 m3/s for the rainfall events with the return periods of 2, 10, 50, 100 years, respectively, in contrast to Case 2 with i1 = 0.08. And the slight time lag (3–10 min) in which flood peak occurs can be observed from Figure 5, Figure 6, Figure 7 and Figure 8, which means Case 2 (i1 ≤ 0.02) and Case 3 (i1 ≥ 0.05) could detain flood peaks as well.
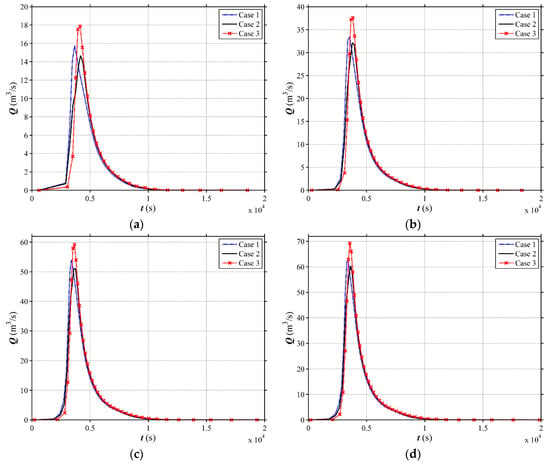
Figure 5.
Simulated hydrographs at the outlet for different land use scenarios in the V-shaped catchment with i1 = 0.01. (a) 2-year; (b) 10-year; (c) 50-year; (d) 100-year.
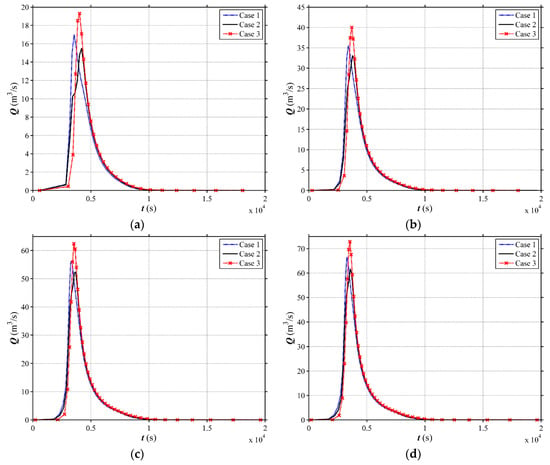
Figure 6.
Simulated hydrographs at the outlet for different land use scenarios in the V-shaped catchment with i1 = 0.02. (a) 2-year; (b) 10-year; (c) 50-year; (d) 100-year.
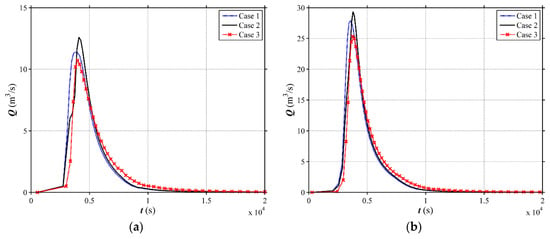
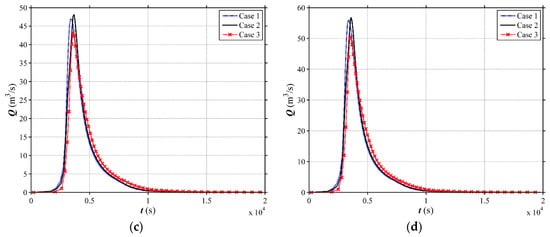
Figure 7.
Simulated hydrographs at the outlet for different land use scenarios in the V-shaped catchment with i1 = 0.05. (a) 2-year; (b) 10-year; (c) 50-year; (d) 100-year.
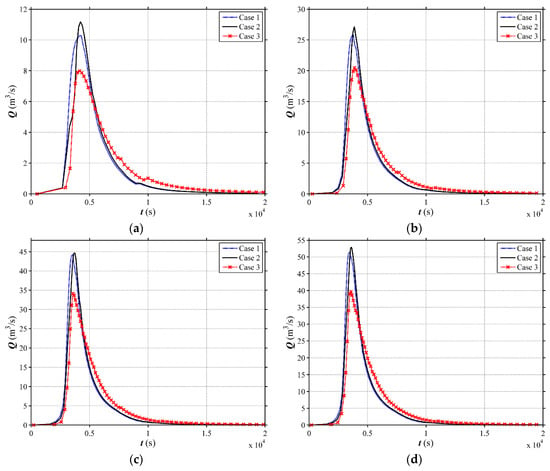
Figure 8.
Simulated hydrographs at the outlet for different land use scenarios in the V-shaped catchment with i1 = 0.08. (a) 2-year; (b) 10-year; (c) 50-year; (d) 100-year.
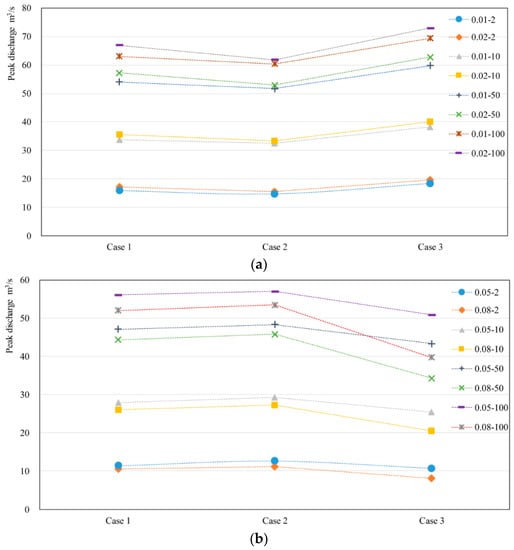
Figure 9.
Simulated peak discharge at the outlet for different land use scenarios in the V-shaped catchment (0.01-2 in legend means i1 = 0.01 and the return period of rainfall is 2). (a) i1 = 0.01 and i1 = 0.02; (b) i1 = 0.05 and i1 = 0.08.

Table 2.
Comparison of peak discharge for different land use scenarios.

Table 3.
Comparison water level peak values for different land use scenarios.
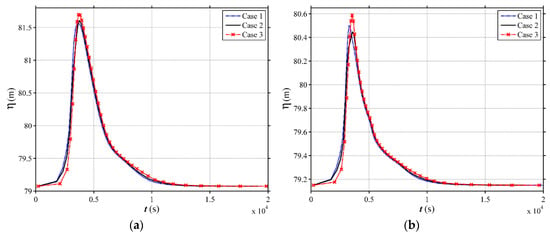
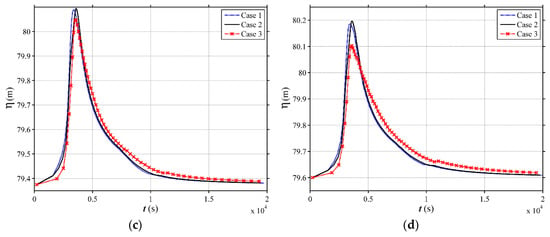
Figure 10.
Simulated water level evolution at the outlet for different land use scenarios in the V-shaped catchment under the 100-year rainfall event. (a) i1 = 0.01; (b) i1 = 0.02; (c) i1 = 0.05; (d) i1 = 0.08.
In a sum, with the channel slope (i1) lower than 0.05, the forest located in the middle of the catchment slope could most effectively attenuate the flood, while that in the downstream causes the most severe flood. When the channel slope (i1) higher than 0.05, the forest located in the downstream of the catchment slope mitigates the most peak discharge, meanwhile, that in the upper and middle part cause higher flood risk. Meanwhile, the flood mitigation rate becomes higher as the rainfall becomes heavier. The same phenomenon can be found for any rainfall events, so the 100-year rainfall event is selected to investigate the land use effects in the following sections.
3.2. Land Use Effects on Flood Mitigation for Different Side Slopes
On the basis of the previous section, the rainfall-flood processes of the V-shaped catchment with the different side slopes (i2) classified into three Scenarios (Scenario I: i2 = 0.18, Scenario II: i2 = 0.58, Scenario III: i2 = 1.19,) are simulated. Figure 11 shows the simulated discharge at the outlet for different land use scenarios under 100-year rainfall. For the three side slope scenarios with the same channel slope (i1) of 0.01, the peak flood discharge can be mitigated by 5.91%, 4.17% and 3.27% for Case 2, respectively, in contrast to Case 1. Comparing to Case 3, the peak discharge of Case 2 can reduce by 15.97%, 12.93% and 11.24%, respectively. The similar phenomenon can be found for the channel slope (i1) of 0.02. On this slope, the peak flood discharge reduction in Case 2 can reach 6.37%–17.87% in contrast to other land use scenarios. For that with the same channel slope (i1) of 0.05, the peak flood discharge can be decreased by 8.53%, 9.20% and 7.44% for Case 3, respectively for three side slope scenarios, comparing with Case 1. The peak flood discharge can be mitigated by 13.35%, 10.72% and 9.02% for Case 3, respectively, compared to Case 2. A similar situation occurs for channel slope (i1) of 0.08 and the reduction of Case 2 can reach 16.73%–25.73%.
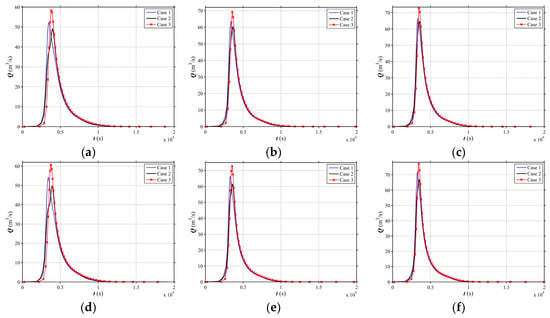
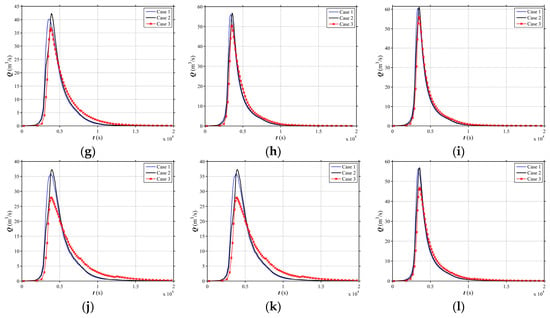
Figure 11.
Simulated hydrographs at the outlet for different land use scenarios under the 100-year rainfall event. (a) i1 = 0.01, i2 = 0.18; (b) i1 = 0.01, i2 = 0.58; (c) i1 = 0.01, i2 = 1.19; (d) i1 = 0.02, i2 = 0.18; (e) i1 = 0.02, i2 = 0.58; (f) i1 = 0.02, i2 = 1.19; (g) i1 = 0.05, i2 = 0.18; (h) i1 = 0.05, i2 = 0.58; (i) i1 = 0.05, i2 = 1.19; (j) i1 = 0.08, i2 = 0.18; (k) i1 = 0.08, i2 = 0.58; (l) i1 = 0.08, i2 = 1.19.
The above results indicate that land use effect on flood process are very similar for different slopes gradient (i2) when the channel slope (i1) lower than 0.05, i.e., the forest located in the middle of the catchment slope could most effectively attenuate the flood. If i1 is higher than 0.05, the forest located in the downstream of the catchment slope is the safest scenario. The effect of the side slope is less sensitive than that of the channel slope for the same land use and rainfall patterns.
From the analysis, a critical channel slope (i1c) is defined in this work to determine the optimal type of land use on side slopes, i.e., when the i1 is lower than i1c, the forest located in the middle of the catchment is the optimal land use type for flood mitigation. Otherwise, the downstream forest could mitigate the most of the flood. As plotted in Figure 12, the i1c is 0.035, 0.039 and 0.038, respectively for Scenarios I, II, and III.
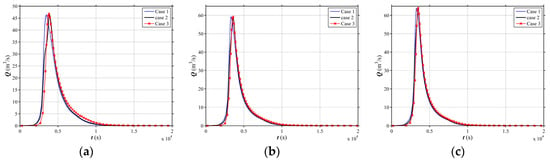
Figure 12.
Simulated hydrographs at the outlet of the critical channel slopes () in the V-shaped catchment with different slopes (i2) (a) i2 = 0.18 (b) i2 = 0.58 (c) i2 = 1.19.
3.3. Land Use Effects on Flood Mitigation for Different Vegetation Cover Patterns
To more systematically investigate the land use effects on flood patterns, more land use scenarios in terms of different vegetation patterns are calculated in this section. Figure 13 shows the considered vegetation patterns in the left hand of slope in the V-shaped catchment and that in the right-hand side is symmetric. Those patterns consider the fragmentation of vegetation across the slope and the integral vegetation blocks. Patterns 1 to 5 present the side slopes covered by 50% forest and 50% grass land. Among which, the forest in Patterns 1, 2, and 3 are located in the upper, middle and lower part of the slope, respectively. The forest is in stripped pattern for Patterns 4 and 5 with the band width of 200 m and 100 m, respectively. Patterns 6 to 10 are similar to the Patterns 1 to 5 but the forest cover rate is 75%. The width of the stripe in Patterns 9 and 10 is 200 m and 300 m, respectively.
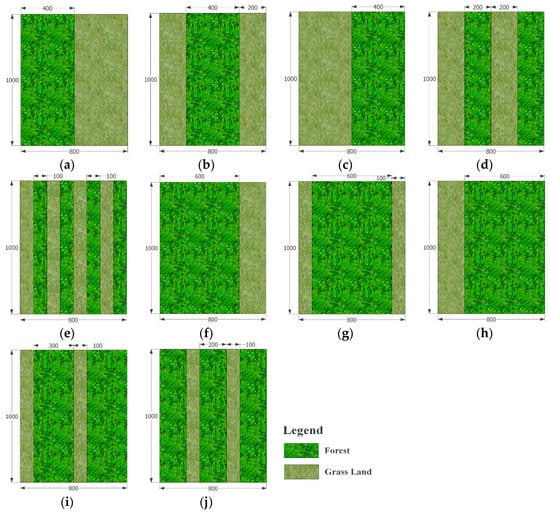
Figure 13.
Different vegetation cover patterns on the left hand of slope in the V-shaped catchment (unit: m). (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4; (e) Case 5; (f) Case 6; (g) Case 7; (h) Case 8; (i) Case 9; (j) Case 10.
Figure 14 and Figure 15 plotted the computed flow discharge processes of different land use scenarios with the two side and channel slopes (i1 = 0.01, i2 = 0.58 and i1 = 0.08, i2 = 0.58) under a 100-year rainfall event. Obviously, the bigger area of the forest could induce the lower peak discharge and the distinction of hydrographs among different forest locations is smaller, i.e., the runoff process is less sensitive to the forest locations.
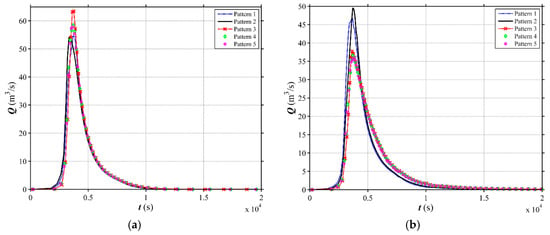
Figure 14.
Simulated hydrographs at the outlet for different vegetation cover patterns of the V-shaped catchment under 100-year rainfall event (vegetation cover is 50%). (a) i1 = 0.01, i2 = 0.58; (b) i1 = 0.08, i2 = 0.58.
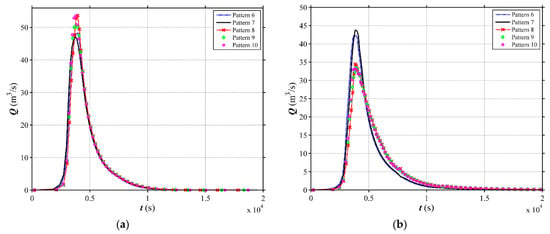
Figure 15.
Simulated hydrographs at the outlet for different vegetation cover patterns in the V-shaped catchment under 100-year rainfall event (vegetation cover is 70%). (a) i1 = 0.01, i2 = 0.58; (b) i1 = 0.08, i2 = 0.58.
When the forest cover is 50%, with i1 = 0.01, the peak discharges of the separated Patterns 4 and 5 are 58.44 m3/s and 58.08 m3/s (Figure 14a), which are higher than that of the integral Patterns 1 and 2, indicating the separated pattern is not the most suitable scenario for mitigating flood hazard. When the i1 = 0.08, as shown in Figure 14b, Pattern 4 and Pattern 5 attenuate slightly more peak discharge than other patterns, i.e., 1.65 m3/s and 1.78 m3/s in comparison to the Pattern 3, respectively, showing the separated pattern performs a little better in terms of flood mitigation. The very similar phenomenon can be observed for the forest cover of 70% (Figure 15). However, considering the separated patterns (Patterns 4, 5, 9 and 10) are sometimes difficult to implement, and do not show more obvious effects than the integral vegetation patterns, the integral Pattern 3 or Pattern 8, with the forest in the downstream slope, might be the most suitable one when the channel slope (i1) is higher than 0.05. For the channel slope lower than 0.05, the Patterns 2 and 7 are the most ideal land use.
4. Land Use Effects on Rainfall-Runoff Process in a Realistic Catchment
To investigate the land use effects on rainfall-runoff process in a real catchment, the numerical model is implemented for abovementioned land use scenarios in Wangmaogou catchment, China.
4.1. Calibration and Validation
Wangmaogou catchment (Figure 16) is applied to calibrate and validate the numerical model. It is a semiarid loessal hillslope with a catchment area of 5.9 km2, experienced cultivated land changed into grassland or forestland. The catchment is located in Suide County, Shaanxi Province, China. The regional climate is classified as monsoonal and more than 60% of the rainfall falls during July to September. The input data to the model include a digital elevation model (DEM) with resolution of 2 m (Figure 16a), land use information (Figure 16b), rainfall events (Figure 17), infiltration rate, and Manning coefficient (Table 4). With the high precision terrain data, there are 452,124 computational cells and it brings large computation costs. In this model, graphic processing units (GPU) parallel computing technique is applied to significantly accelerate the calculation speed. The rainfall and observed discharge data were collected by the Wangmaogou Hydrological Station from 0:25 15 July 2012 to 10:25 15 July 2012; and the return period of storm event is about 100 years. The infiltration rate and Manning coefficient of different land use are determined by trial method based on the range recommended by Engman [31] and Li [32]. The parameters are determined as Table 4, whose simulation result is closest to the observed one. Through calculation, the average channel slope (i1) of the Waomaogou catchment is about 0.05 and the average side slope (i2) is about 0.70.
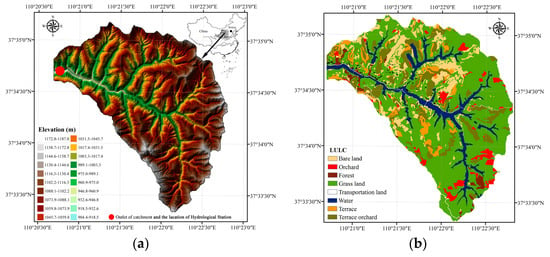
Figure 16.
Wangmaogou catchment on the Loess Plateau, China. (a) Digital elevation model (DEM); (b) land use map (Landsat TM, 2012).
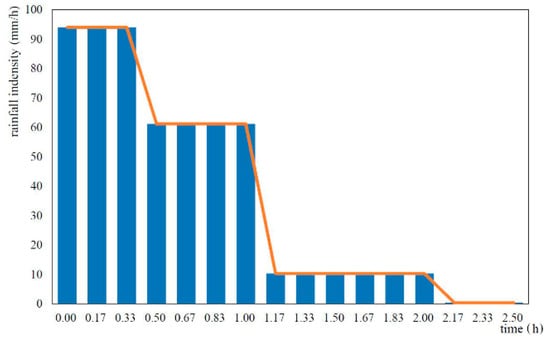
Figure 17.
The hyetography in the study area.

Table 4.
Infiltration rate (mm/h) and Manning coefficient (s/m1/3) under different land use types.
The comparison between the observed values and simulation values (Figure 18) shows that the model reproduced the hydrograph for fairly well storm event under consideration. Regarding the observed peak discharge, the simulated volume was overestimated by 3.2%. The simulated peak occurring time is delayed about 1h, accounting for 10% of the whole runoff process. The RMSE values of the simulated data and the standard deviation of observed data are 0.83 and 1.84, respectively. The RMSE values is smaller than the half of the standard deviation of observed data, indicating the model is able to reliably simulate the rainfall-runoff process and therefore can be used to evaluate the effects of land use on runoff generation in the considered real catchment [37].
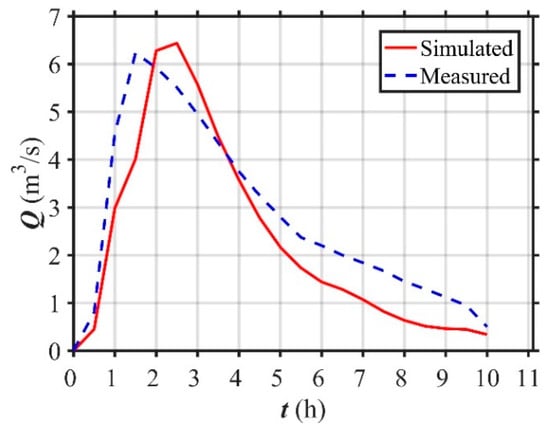
Figure 18.
Comparison between the observed and simulated hydrographs.
4.2. Land Use Effect Simulation on Flood Mitigation in Wangmaogou Catchment
To systematically compute the land use effects on runoff process, the land use data are reclassified into three types including forest, grass and bare land. As shown in Figure 19, the channel of the catchment is bare land and the slopes are composed by two types of land use, i.e., grass land and forest. The forest area on the slope are the same in the three different land use types and located in the upper (Case 1), middle (Case 2) and lower (Case 3) part of slope respectively, accounting for 1/3 of the slope area. The design storms from Suide County, Shaanxi Province with different return periods (2, 10, 50, 100 years) and three land use scenarios are imported into the model to simulate the runoff process. Figure 20 and Figure 21 show the inundated area (the blue area) and the flood process in the outlet of catchment under the return period of 100 year in Case 1.
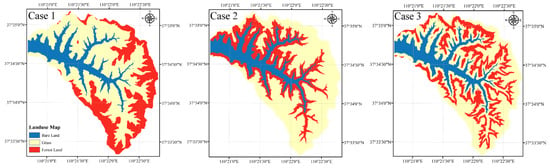
Figure 19.
Different land use scenarios in Wangmaogou catchment.
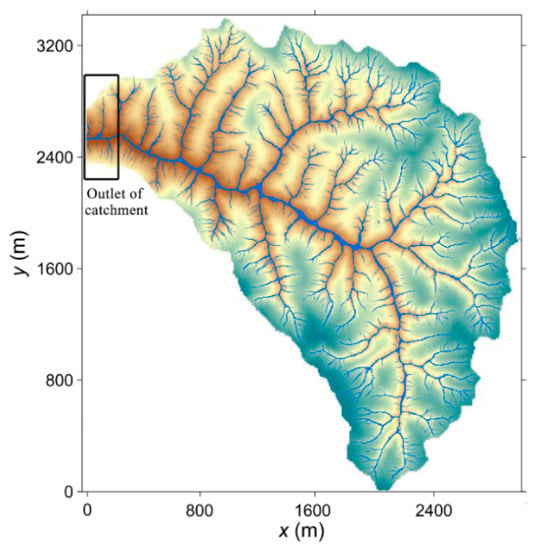
Figure 20.
Inundated area of Wangmaogou catchment at the peak time of the discharge (t = 6000 s).
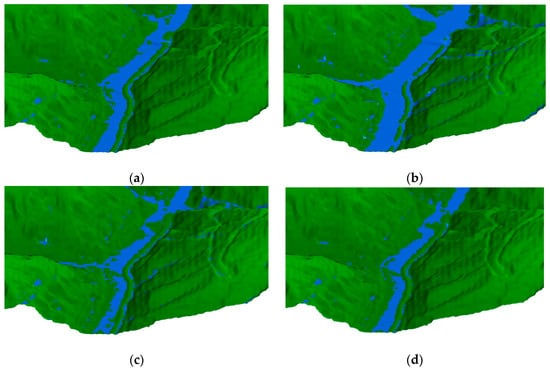
Figure 21.
Flood process in the outlet of catchment. (a) t = 3600 s; (b) t = 6000 s (Peak time); (c) t = 10,800 s; (d) t = 18,000 s.
The discharge process at the outlet of Wangmaogou catchment and the peak discharge among different land use scenarios (Case 1, Case 2 and Case 3) are presented in Figure 22 and Table 5. The results clearly demonstrate that Case 3 mitigates the peak discharge in the most effective way but Case 1 and Case 2 do not show obvious effect. Comparing to Case 1, the peak discharge of Case 3 can reduce by 12.28%, 8.95%, 13.02% and 11.95% for the rainfall events with the return periods of 2, 10, 50 and 100 years, respectively. The reduction percentage between Case 2 and Case 3 reaches 12.66%, 9.24%, 13.26% and 12.31%, respectively. In other words, the forest located in the downstream of the catchment slope could most significantly mitigate the peak discharge, while that in the upper and middle part causes higher flood risk. The computed land use effect on flood is very similar to that in the V-shaped catchment with the slopes i1 = 0.05 and i1 = 0.58, proving the reasonability of the research.
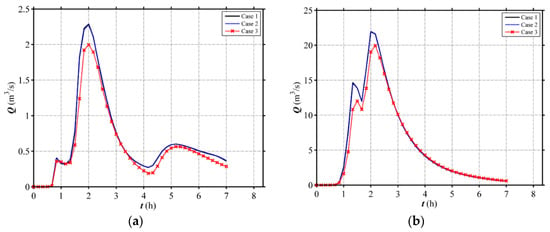
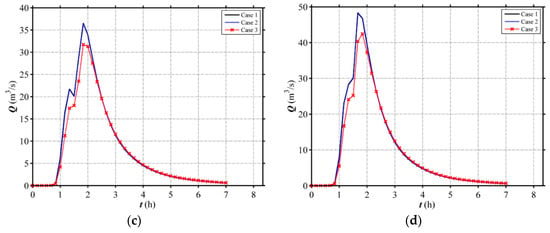
Figure 22.
Simulated hydrographs at the outlet for different land use scenarios of Wangmaogou catchment under (a) 2-year, (b) 10-year, (c) 50-year, (d) 100-year rainfall event.

Table 5.
Comparison water level peak values for different land use scenarios.
5. Conclusions
Through using a hydrodynamic based numerical model, this work quantitatively investigates the land use effect on the flood patterns in catchment, finding that different land use could cause different rainfall-flood process and the effect vary with the catchment terrain, land use scenario and the rainfall events.
- The effect of the side slope gradient is less sensitive than that of the channel slope for the same land use and rainfall patterns;
- When the channel slope () is smaller than the critical channel slope termed as , the forest located in the middle of the catchment slope could most effectively attenuate the flood peak, while that in the downstream causes the most sever flood;
- On the contrary, if the channel slope () is higher than critical channel slope, the forest located in the downstream of the catchment slope mitigates the peak discharge in a most effective way, while that in the upper and middle part have slight difference;
- The fragmentation of vegetation does not show more obvious effects on flood reduction compared with the integral vegetation patterns with the same area proportion;
- Meanwhile, the flood mitigation extent becomes higher as the rainfall becomes more intense, indicating the optimal land use has better performance for heavier flood.
The research could be used to guide the land use plan in a catchment with consideration of the flood mitigation, especially for the ongoing ecological engineering constructions in some provinces in China suffering from flash floods and soil erosion. Considering the different parameters of different catchment, the land use effect may be different. The further study will be carried out later.
Author Contributions
J.H. conducted the analyses and conceive the manuscript. K.G. completed the numerical simulation and draft the manuscript. F.L. and H.H. helped to calculate and analyse. Q.L. polished the manuscript. And P.L. provided the basic data of Wangmaogou catchment. Y.T. helped to recalculate and polish the manuscript in the revision. J.H. and K.G. contributed equally.
Funding
This work is partly supported by the National Key Research Program of China (2016YFC0402704); National Natural Science Foundation of China (19672016); State Key Program of National Natural Science Foundation of China (Grant No. 41330858) and the UK Natural Environment Research Council (NERC) (Grant No. NE/K008781/1).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ali, M.; Khan, S.J.; Aslam, I.; Khan, Z. Simulation of the impacts of land-use change on surface runoff of Lai Nullah Basin in Islamabad, Pakistan. Landsc. Urban Plan. 2011, 102, 271–279. [Google Scholar] [CrossRef]
- Becker, A.; Gruenewald, U. Disaster Management: Flood Risk in Central Europe. Science 2003, 300, 1099. [Google Scholar] [CrossRef] [PubMed]
- Wilkinson, M.; Quinn, P.; Barber, N.; Jonczyk, J. A framework for managing runoff and pollution in the rural landscape using a Catchment Systems Engineering approach. Sci. Total Environ. 2014, 468–469, 1245–1254. [Google Scholar] [CrossRef] [PubMed]
- Schroeter, K.; Kreibich, H.; Vogel, K.; Riggelsen, C.; Scherbaum, F.; Merz, B. How useful are complex flood damage models? Water Resour. Res. 2014, 50, 3378–3395. [Google Scholar] [CrossRef]
- Yu, M.; Li, Q.; Liu, X.; Zhang, J. Quantifying the effect on flood regime of land-use pattern changes via hydrological simulation in the upper Huaihe River basin, China. Nat. Hazards 2016, 84, 2279–2297. [Google Scholar] [CrossRef]
- Zope, P.E.; Eldho, T.I.; Jothiprakash, V. Hydrological impacts of land use-land cover change and detention basins on urban flood hazard: A case study of Poisar River basin, Mumbai, India. Nat. Hazards 2017, 87, 1267–1283. [Google Scholar] [CrossRef]
- Ozturk, M.; Copty, N.K.; Saysel, A.K. Modeling the impact of land use change on the hydrology of a rural watershed. J. Hydrol. 2013, 497, 97–109. [Google Scholar] [CrossRef]
- Zhang, L.; Karthikeyan, R.; Bai, Z.; Srinivasan, R. Analysis of streamflow responses to climate variability and land use change in the Loess Plateau region of China. Catena 2017, 154, 1–11. [Google Scholar] [CrossRef]
- Persichillo, M.G.; Bordoni, M.; Meisina, C. The role of land use changes in the distribution of shallow landslides. Sci. Total Environ. 2017, 574, 924–937. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Guan, D.; Jin, C.; Wang, A.; Wu, J.; Yuan, F. Impacts of climate change and land use change on runoff of forest catchment in northeast China. Hydrol. Process. 2012, 28, 186–196. [Google Scholar] [CrossRef]
- Khoi, D.N.; Suetsugi, T. The responses of hydrological processes and sediment yield to land use and climate change in the Be River Catchment, Vietnam. Hydrol. Process. 2012, 28, 640–652. [Google Scholar] [CrossRef]
- Sun, N.; Yearsley, J.; Baptiste, M.; Cao, Q.; Lettenmaier, D.P.; Nijssen, B. A spatially distributed model for assessment of the effects of changing land use and climate on urban stream quality. Hydrol. Process. 2016, 30, 4779–4798. [Google Scholar] [CrossRef]
- Chaves, J.; Neill, C.; Germer, S.; Neto, S.G.; Krusche, A.; Elsenbeer, H. Land management impacts on runoff sources in small Amazon watersheds. Hydrol. Process. 2008, 22, 1766–1775. [Google Scholar] [CrossRef]
- Yira, Y.; Diekkruger, B.; Steup, G.; Bossa, A.Y. Modeling land use change impacts on water resources in a tropical West African catchment (Dano, Burkina Faso). J. Hydrol. 2016, 537, 187–199. [Google Scholar] [CrossRef]
- Semenova, O.; Beven, K. Barriers to progress in distributed hydrological modelling. Hydrol. Process. 2015, 29, 2074–2078. [Google Scholar] [CrossRef]
- Siriwardena, L.; Finlayson, B.L.; Mcmahon, T.A. The impact of land use change on catchment hydrology in large catchments: The Comet River, Central Queensland, Australia. J. Hydrol. 2006, 326, 199–214. [Google Scholar] [CrossRef]
- Liu, Y.B.; Gebremeskel, S.; de Smedt, F.; Hoffmann, L.; Pfister, L. Predicting storm runoff from different land use classes using a geographical information system-based distributed model. Hydrol. Process. 2006, 20, 533–548. [Google Scholar] [CrossRef]
- Notter, B.; Macmillan, L.; Viviroli, D.; Weingartner, R.; Liniger, H.P. Impacts of environmental change on water resources in the Mt. Kenya region. J. Hydrol. 2007, 343, 266–278. [Google Scholar] [CrossRef]
- Qi, S.; Sun, G.; Wang, Y.; Mcnulty, S.G.; Myers, J.A.M. Streamflow response to climate and land use changes in a coastal watershed in North Carolina. Trans. ASABE 2009, 52, 739–749. [Google Scholar] [CrossRef]
- Stoll, S.; Franssen, H.J.H.; Butts, M.; Kinzelbach, W. Analysis of the impact of climate change on groundwater related hydrological fluxes: A multi-model approach including different downscaling methods. Hydrol. Earth Syst. Sci. Discuss. 2010, 7, 7521–7561. [Google Scholar] [CrossRef]
- Yan, B.; Fang, N.F.; Zhang, P.C.; Shi, Z.H. Impacts of land use change on watershed streamflow and sediment yield: An assessment using hydrologic modelling and partial least squares regression. J. Hydrol. 2013, 484, 26–37. [Google Scholar] [CrossRef]
- Niraula, R.; Meixner, T.; Norman, L.M. Determining the importance of model calibration for forecasting absolute/relative changes in streamflow from LULC and climate changes. J. Hydrol. 2015, 522, 439–451. [Google Scholar] [CrossRef]
- Marhaento, H.; Booij, M.J.; Rientjes, T.H.M.; Hoekstra, A.Y. Attribution of changes in the water balance of a tropical catchment to land use change using the SWAT model. Hydrol. Process. 2017, 31, 2029–2040. [Google Scholar] [CrossRef]
- Shrestha, M.K.; Recknagel, F.; Frizenschaf, J.; Meyer, W. Future climate and land uses effects on flow and nutrient loads of a Mediterranean catchment in South Australia. Sci. Total Environ. 2017, 590–591, 186–193. [Google Scholar] [CrossRef] [PubMed]
- Liang, Q.; Xia, X.; Hou, J. Catchment-scale High-resolution Flash Flood Simulation Using the GPU-based Technology. Procedia Eng. 2016, 154, 975–981. [Google Scholar] [CrossRef]
- Xia, X.; Liang, Q.; Ming, X.; Hou, J. An efficient and stable hydrodynamic model with novel source term discretization schemes for overland flow and flood simulations. Water Resour. Res. 2017, 53, 3730–3759. [Google Scholar] [CrossRef]
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Liang, Q. Flood simulation using a well-balanced shallow flow model. J. Hydraul. Eng. 2010, 136, 669–675. [Google Scholar] [CrossRef]
- Hou, J.; Simons, F.; Mahgoub, M.; Hinkelmann, R. A robust well-balanced model on unstructured grids for shallow water flows with wetting and drying over complex topography. Comput. Methods Appl. Mech. Eng. 2013, 257, 126–149. [Google Scholar] [CrossRef]
- Overton, D.E.; Brakensiek, D.L. A kinematic model of surface runoff response. In Proceedings of the Wellington Symposium; Unesco/IAHS: Paris, France, 1970; pp. 100–112. [Google Scholar]
- Engman, E.T. Roughness Coefficients for Routing Surface Runoff. J. Irrig. Drain. Eng. 1986, 112, 39–53. [Google Scholar] [CrossRef]
- Li, G. Comparative Study of Soil Infiltration under Different Land Uses in Loess Hilly Regions; Northwest A&F University: Yangling, China, 2007. (In Chinese) [Google Scholar]
- Reaney, S.M.; Bracken, L.J.; Kirkby, M.J. The importance of surface controls on overland flow connectivity in semi-arid environments: Results from a numerical experimental approach. Hydrol. Process. 2014, 28, 2116–2128. [Google Scholar] [CrossRef]
- Shao, Y.; Shao, D. A New Generation of Urban Rainstorm Intensity Formula China; China Architecture & Building Press: Beijing, China, 2014; p. 82. ISBN 978-7-112-16847-7. [Google Scholar]
- Giammarco, P.D.; Todini, E.; Lamberti, P. A conservative finite elements approach to overland flow: The control volume finite element formulation. J. Hydrol. 1996, 175, 267–291. [Google Scholar] [CrossRef]
- Simons, F.; Busse, T.; Hou, J.; Özgen, I.; Hinkelmann, R. A model for overland flow and associated processes within the Hydroinformatics Modelling System. J. Hydroinform. 2014, 16, 375–391. [Google Scholar] [CrossRef]
- Singh, J.; Altinakar, M.S.; Ding, Y. Two-dimensional numerical modeling of dam-break flows over natural terrain using a central explicit scheme. Adv. Water Resour. 2011, 34, 1366–1375. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).