Energy Efficient Operation of Variable Speed Submersible Pumps: Simulation of a Ground Water Well Field
Abstract
1. Introduction
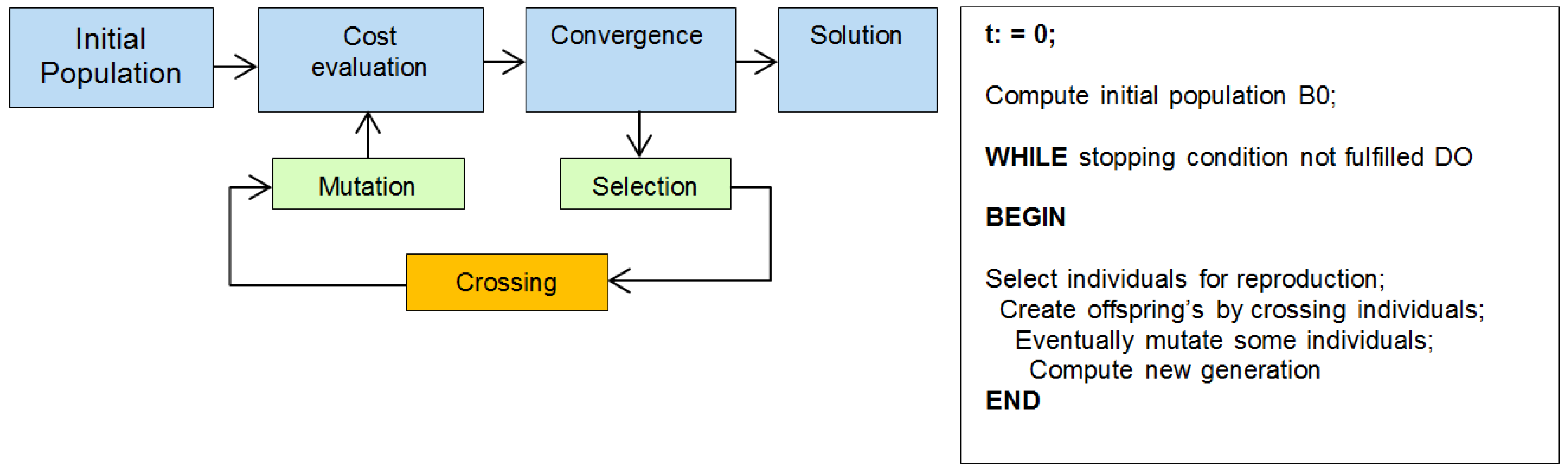
Optimization Using Genetic Algorithms
- Initialization (initial population): An initial population is created. This population is generated, in principle, randomly and can be of the desired size, from a couple of individuals to thousands.
- Cost evaluation (aptitude): Each member of the population is evaluated and the adjustment or aptitude for that individual is calculated. The adjustment value is calculated based on how well the individual are adjusted to the established requirements.
- Selection: This procedure is executed to constantly improve the population. The selection discards bad solutions in a way that keeps the best individuals in the population.
- Crossing: During crossing, new individuals are created by combining aspects of the individuals selected in the previous stage.
- Mutation: It is required to add some randomness to the genetics of the population; otherwise, every combination of solutions that could be created would be in the initial population, that is, it would be trapped in a local optimum.
- Iteration/convergence: Once there is a new generation, the process starts from step two until a stopping criterion is reached.
2. Materials and Methods
2.1. Hydraulic Modeling of Groundwater Abstraction and Transport
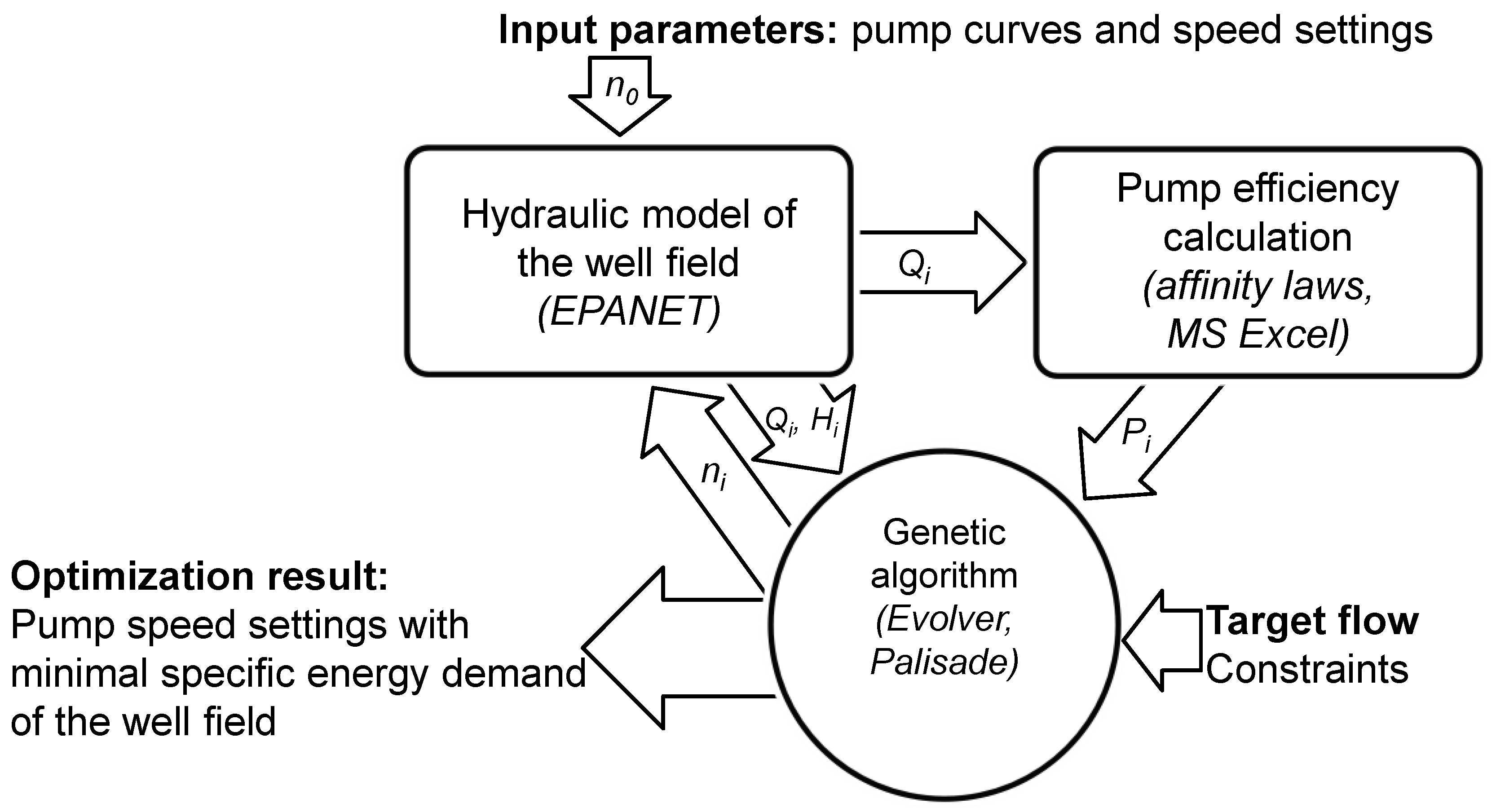
2.2. Optimization Through Genetic Algorithms Using Evolver
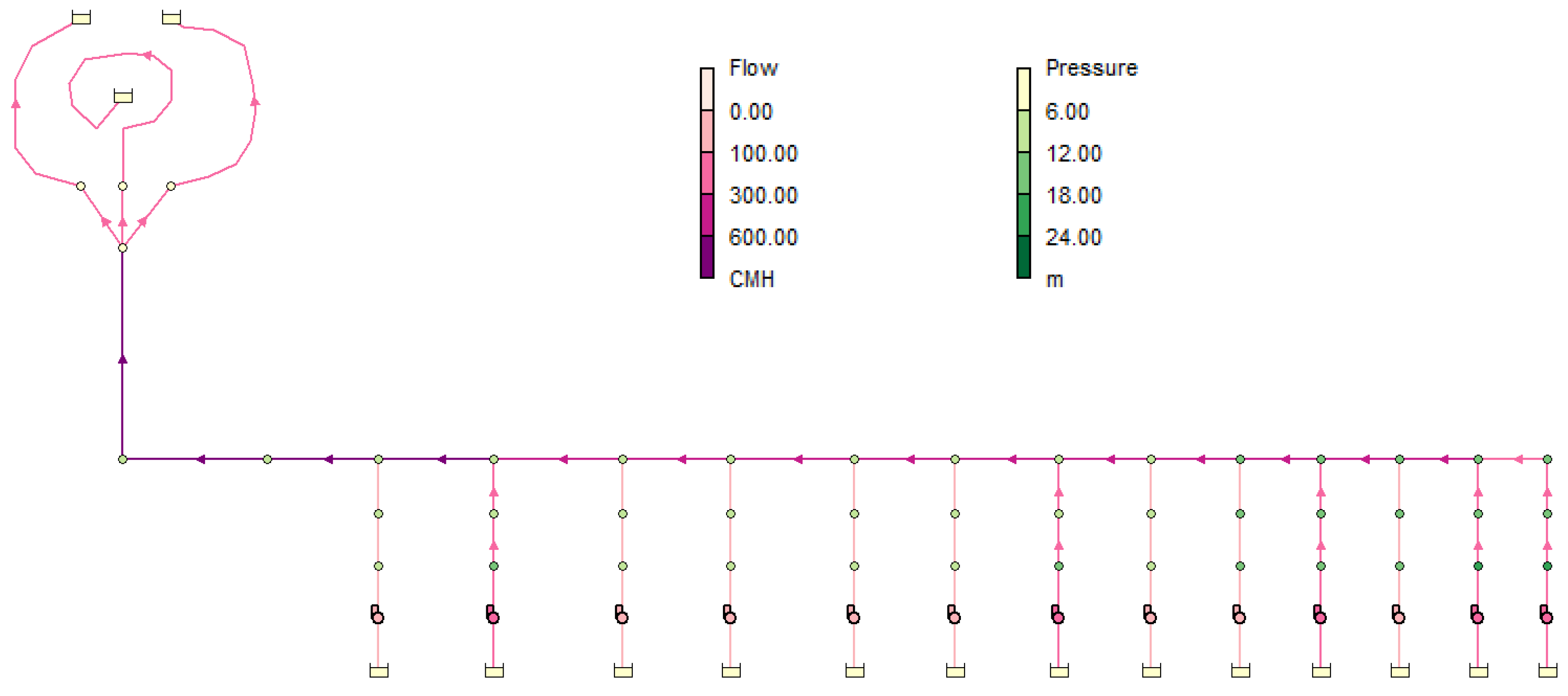
2.3. Case Study: Well Field Tegel-Ost
2.4. Monitoring Campaign
3. Results and Discussion
3.1. Simulation of Different Operational Scenarios Using Variable Speed Submersible Pumps in a Well Field
3.2. Analysis of Seasonal Variations in Groundwater Abstraction
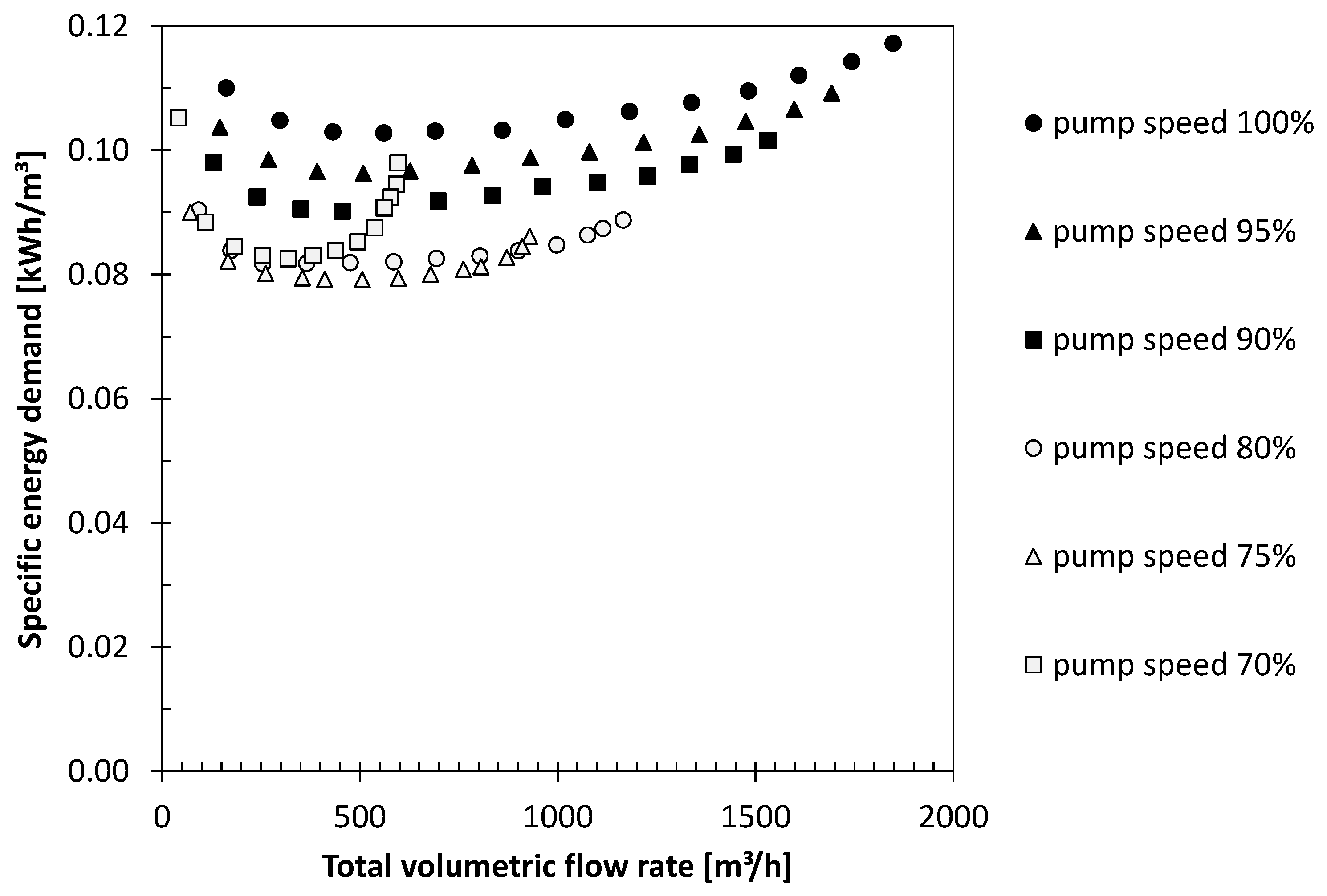
3.3. Simulation of Typical Operational Scenarios and Optimal Pump Speed
3.4. Comparison of Simulation and Measurements
4. Conclusions
- The combination of hydraulic simulation models such as EPANET and genetic algorithm optimization can be used to determine the best efficiency scenario of variable speed pump operation in a groundwater well field.
- Simulation results show that, using speed control, significant energy savings can be achieved. For the simulated well field, the total specific energy demand required for pumping was 20–30% lower at reduced pump speed than at nominal pump speed.
- Depending on the well field, transport pipe system and pump characteristics, significant energy savings can be achieved, especially in systems characterized by low static head.
- The simulation results were compared to real world operation of variable speed pumps and the projected reduction in specific energy demand was confirmed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Burgschweiger, J.; Gnädig, B.; Steinbach, M.C. Optimization models for operative planning in drinking water networks. Optim. Eng. 2009, 10, 43–73. [Google Scholar] [CrossRef]
- Ormsbee, L.E.; Lansey, K.E. Optimal control of water supply pumping systems. J. Water Resour. Plan. Manag. 1994, 120, 237–252. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Tabesh, M.; Ataeekia, B. Ant-colony optimization of pumping schedule to minimize the energy cost using variable-speed pumps in water distribution networks. Urban Water J. 2014, 11, 335–347. [Google Scholar] [CrossRef]
- López-Ibáñez, M.; Prasad, T.D.; Paechter, B. Ant colony optimization for optimal control of pumps in water distribution networks. J. Water Resour. Plan. Manag. 2008, 134, 337–346. [Google Scholar] [CrossRef]
- Van Zyl, J.E.; Savic, D.A.; Walters, G.A. Operational optimization of water distribution systems using a hybrid genetic algorithm. J. Water Resour. Plan. Manag. 2004, 130, 160–170. [Google Scholar] [CrossRef]
- Beck, M.; Sperlich, A.; Blank, R.; Meyer, E.; Binz, R.; Ernst, M. Increasing energy efficiency in water collection systems by modern well pumps. Water 2018. submitted. [Google Scholar]
- Fuchsloch, J.F.; Finley, W.R.; Walter, R.W. The next generation motor. IEEE Ind. Appl. Mag. 2008, 14, 37–43. [Google Scholar] [CrossRef]
- Marchi, A.; Simpson, A.R.; Ertugrul, N. Assessing variable speed pump efficiency in water distribution systems. Drink. Water Eng. Sci. 2012, 5, 15–21. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2: Users Manual; EPANET: Cincinnati, OH, USA, 2000. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- Rojas, R. Neural Networks: A Systematic Introduction; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Palisade, N. Guide to Evolver—The Genetic Algorithm Solver for Microsoft Excel; Palisade Corporation: Newfield, NY, USA, 1998. [Google Scholar]
- Coley, D.A. An Introduction to Genetic Algorithms for Scientists and Engineers; World Scientific Publishing Company: Singapore, 1999. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Yadav, P.K.; Prajapati, N.L. An overview of Genetic algorithm and modelling. Int. J. Sci. Res. Publ. 2012, 2, 1–4. [Google Scholar]
- Worm, G.I.; Mesman, G.A.; van Schagen, K.M.; Borger, K.J.; Rietveld, L.C. Hydraulic modelling of drinking water treatment plant operations. Drink. Water Eng. Sci. 2009, 2, 15–20. [Google Scholar] [CrossRef]
- Sárbu, I.; Borza, I. Energetic optimization of water pumping in distribution systems. Periodica Polytech. Mech. Eng. 1998, 42, 141–152. [Google Scholar]
- Marchi, A.; Simpson, A.R. Correction of the EPANET Inaccuracy in Computing the Efficiency of Variable Speed Pumps. J. Water Resour. Plan. Manag. 2013, 139, 456–459. [Google Scholar] [CrossRef]
- Georgescu, A.-M.; Cosoiu, C.-I.; Perju, S.; Georgescu, S.-C.; Hasegan, L.; Anton, A. Estimation of the efficiency for variable speed pumps in EPANET compared with experimental data. Procedia Eng. 2014, 89, 1404–1411. [Google Scholar] [CrossRef]
- Brentan, B.M.; Campbell, E.; Meirelles, G.L.; Luvizotto, E.; Izquierdo, J. Social network community detection for DMA creation: criteria analysis through multilevel optimization. Math. Probl. Eng. 2017, 2017, 9053238. [Google Scholar] [CrossRef]
- Campbell, E.; Izquierdo, J.; Montalvo, I.; Pérez-García, R. A novel water supply network sectorization methodology based on a complete economic analysis, including uncertainties. Water 2016, 8, 179. [Google Scholar] [CrossRef]
- Gonzalez, E.C. Sectorización de redes de Abastecimiento de agua potable basada en detección de comunidades en redes sociales y optimización heurística. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, 2017. [Google Scholar]
- Marchi, A.; Salomons, E.; Ostfeld, A.; Kapelan, Z.; Simpson, A.R.; Zecchin, A.C.; Maier, H.R.; Wu, Z.Y.; Elsayed, S.M.; Song, Y. Battle of the water networks II. J. Water Resour. Plan. Manag. 2013, 140, 4014009. [Google Scholar] [CrossRef]
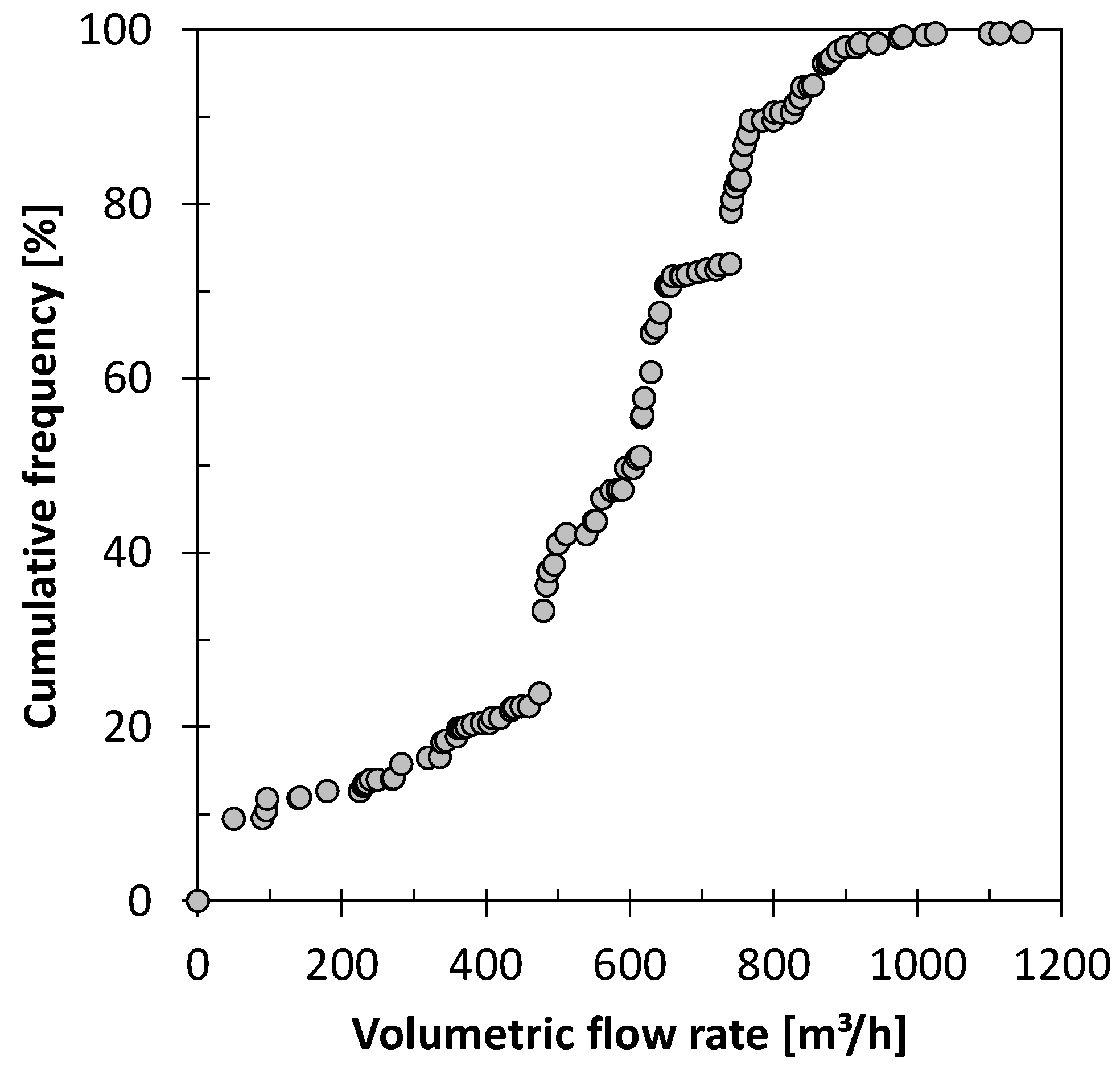
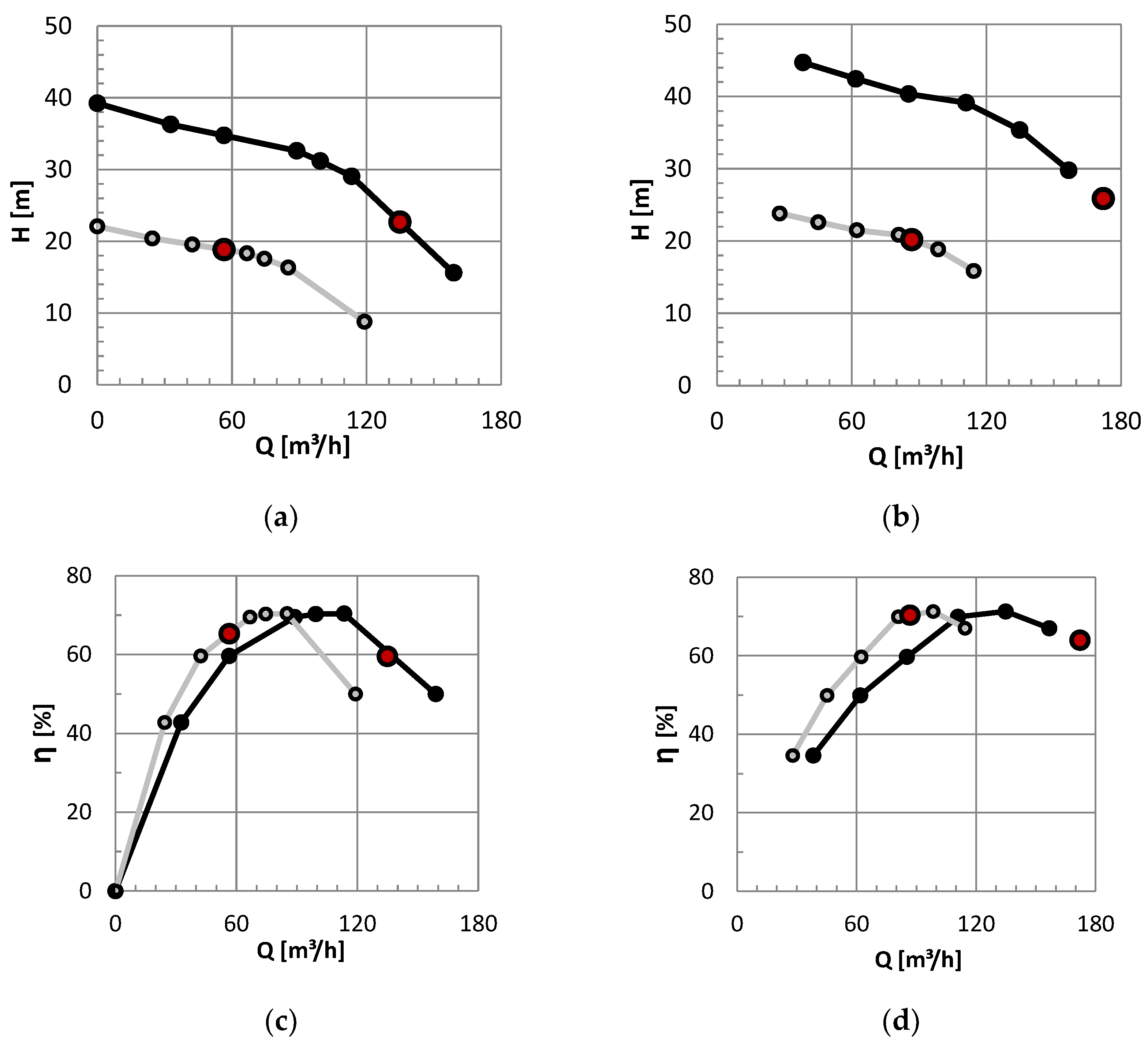
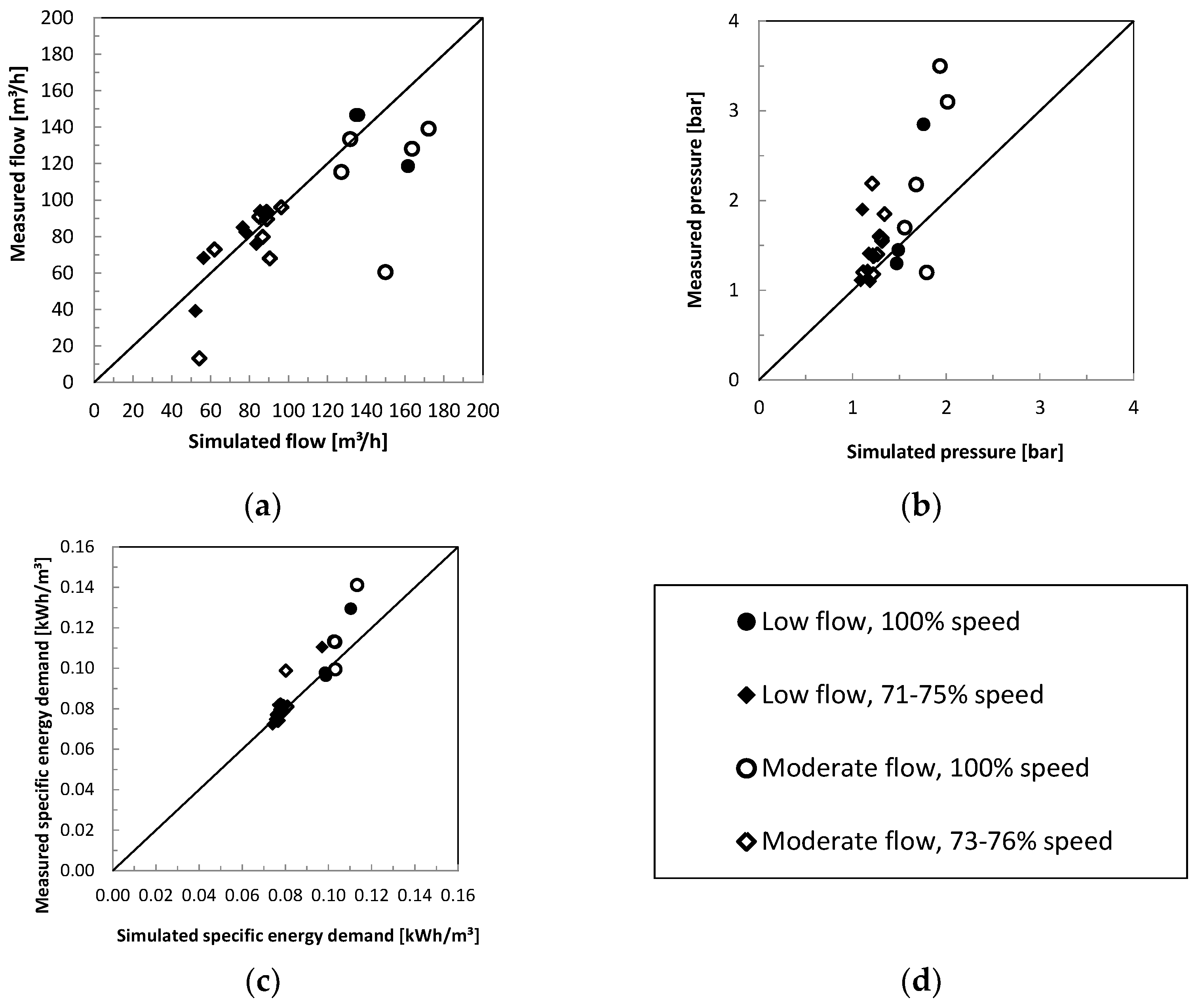
| Low Flow Scenario | Moderate Flow Scenario | |||||||
|---|---|---|---|---|---|---|---|---|
| Nominal Speed | Variable Speed | Nominal Speed | Variable Speed | |||||
| Pump | Pump Speed (rpm) | Pump Speed (%) | Pump Speed (rpm) | Pump Speed (%) | Pump Speed (rpm) | Pump Speed (%) | Pump Speed (rpm) | Pump Speed (%) |
| 1 | 3000 | 100 | 2250 | 75 | - | - | 2280 | 76 |
| 2 | 2160 | 72 | 3000 | 100 | 2190 | 73 | ||
| 3 | 2130 | 71 | 2190 | 73 | ||||
| 4 | 3000 | 100 | ||||||
| 5 | 2220 | 74 | ||||||
| 6 | 2130 | 71 | 2280 | 76 | ||||
| 7 | 2850 | 100 | ||||||
| 8 | 2220 | 74 | ||||||
| 9 | 2160 | 72 | 2220 | 74 | ||||
| 10 | 3000 | 100 | ||||||
| 11 | ||||||||
| 12 | 3000 | 100 | 2250 | 75 | ||||
| 13 | 2850 | 100 | 2052 | 72 | 2850 | 100 | 2109 | 74 |
| Total well field flow (m3/h) | 432 | 432 | 744 | 740 | ||||
| Specific energy (kWh/m3) | 0.10 | 0.08 | 0.11 | 0.08 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sperlich, A.; Pfeiffer, D.; Burgschweiger, J.; Campbell, E.; Beck, M.; Gnirss, R.; Ernst, M. Energy Efficient Operation of Variable Speed Submersible Pumps: Simulation of a Ground Water Well Field. Water 2018, 10, 1255. https://doi.org/10.3390/w10091255
Sperlich A, Pfeiffer D, Burgschweiger J, Campbell E, Beck M, Gnirss R, Ernst M. Energy Efficient Operation of Variable Speed Submersible Pumps: Simulation of a Ground Water Well Field. Water. 2018; 10(9):1255. https://doi.org/10.3390/w10091255
Chicago/Turabian StyleSperlich, Alexander, Dino Pfeiffer, Jens Burgschweiger, Enrique Campbell, Marcus Beck, Regina Gnirss, and Mathias Ernst. 2018. "Energy Efficient Operation of Variable Speed Submersible Pumps: Simulation of a Ground Water Well Field" Water 10, no. 9: 1255. https://doi.org/10.3390/w10091255
APA StyleSperlich, A., Pfeiffer, D., Burgschweiger, J., Campbell, E., Beck, M., Gnirss, R., & Ernst, M. (2018). Energy Efficient Operation of Variable Speed Submersible Pumps: Simulation of a Ground Water Well Field. Water, 10(9), 1255. https://doi.org/10.3390/w10091255






