Abstract
Currently research on joint operation of a large reservoir and its re-regulating reservoir focuses on either water quantity regulation or water head regulation. The accuracy of relevant models is in need of improvement if the influence of factors such as water flow hysteresis and the aftereffect of tail water level variation are taken into consideration. In this paper, given the actual production of Pankou-Xiaoxuan cascade hydropower stations that combines two operation modes (‘electricity to water’ and ‘water to electricity’), a coupling model of their short-term optimal operation is developed, which considers Xiaoxuan reservoir’s regulating effect on Pankou reservoir’s outflow volume and water head. Factors such as water flow hysteresis and the aftereffect of tail water level variation are also considered to enhance the model’s accuracy. The Backward Propagation (BP) neural network is employed for precise calculation of the downstream reservoir’s inflow and the upstream reservoir’s tail water level. Besides, we put forth Accompanying Progressive Optimality Algorithm (APOA) to solve the coupling model with aftereffect. An example is given to verify the scientificity of the proposed model and the advantages of APOA. Through analysis of the model calculation results, the optimal operation rules of the cascade reservoirs are obtained in terms of water quantity regulation and water head regulation, which can provide scientific reference for cascade reservoirs’ optimal operation.
1. Introduction
In the downstream of a large reservoir, the construction of a small re-regulating reservoir can not only ensure the upstream hydropower station’s peak-regulating capability in the power grid, but also exert a positive effect on downstream water supply, ecology, shipping, etc., spawning significant comprehensive utilization benefits. Therefore, this kind of development mode has been widely adopted in water conservancy construction across the world, e.g., the Three Gorges-Gezhouba cascade reservoirs in China [1], the Xiaolangdi-Xixiayuan cascade reservoirs in China [2], the Bigge-Ahausen cascade reservoirs in Germany [3], the Srinagarindra-Tha Thung Na cascade reservoirs in Thailand, and so forth [4].
The downstream reservoir’s reverse regulation effect on the upstream reservoir is mainly embodied in two facets: (1) water quantity regulation, i.e., using the downstream reservoir’s storage capacity to optimize the upstream reservoir’s outflow; (2) water head regulation, i.e., controlling the downstream reservoir’s water level to optimize the overall output given its backwater effect on the upstream reservoir’s tail water level. To date, many scholars have studied the joint operation of a large reservoir and its re-regulating reservoir. For example, Richter, B. D. proposed that the re-regulating reservoir can readjust the upstream reservoir’s outflow to eliminate the unnatural fluctuations caused by hydropower operation, so that water discharge to the downstream channel can move in a way much closer to natural flow, thus protecting the downstream ecological environment [5]. Bai, T. et al. established a model of Xiaolangdi-Xixiayuan cascade hydropower stations’ joint peak-regulating operation, which used Xixiayuan reservoir to regulate Xiaolangdi reservoir’s outflow volume, thus alleviating the conflict between water regulation and power dispatching during Xiaolangdi hydropower station’s operation process [6]. Taking the Three Gorges-Gezhouba cascade reservoirs as an example, Cai, Z. et al. analyzed the law of the influence of Gezhouba reservoir’s water level on the cascade hydropower generation during different operation states of the Three Gorges reservoir, and obtained the control table of optimal water levels [7]. However, the above studies have only considered either water quantity regulation or water head regulation. For instance, Bai, T. did not consider Xixiayuan reservoir’s influence on Xiaolangdi reservoir’s tail water level in calculation. For simplification, Cai, Z. used the ‘runoff operation’ hypothesis on Gezhouba reservoir, whose water level stayed unchanged during calculation. So far, there has been no research that considers the combination of water quantity regulation and water head regulation; hence the above models somewhat deviate from the actual operation of cascade reservoirs, with limitations in their conclusions.
Additionally, in previous studies, to solve the cascade reservoirs’ short-term optimal operation model, the calculation of such variables as downstream reservoir’s inflow and upstream reservoir’s tail water level was often simplified (e.g., the upstream reservoir’s outflow was directly used as the downstream reservoir’s inflow [8], the upstream reservoir’s tail water level was calculated via the stage-discharge relation method [9], etc.). These simplifications neglect the impact of factors such as water flow hysteresis and the aftereffect of tail water level variation, which makes model variables deviate from reality and reduces model accuracy. Yet, in the study of reverse regulation, downstream reservoir’s inflow and upstream reservoir’s tail water level are the key variables during calculation, as they can reflect the connection of water quantity and water head between the upstream and the downstream reservoirs. Therefore, it is important to accurately calculate these two variables. Research about water flow hysteresis is focused mainly on flow travel time, which is generally treated as a fixed value in primary studies [10]. In recent years, some scholars have proposed that flow travel time varies dynamically with the change of upstream reservoir outflow [11]. Although this improvement takes into consideration the influence of reservoir outflow’s rate on its travel speed, it is still regarded as a steady flow without considering flow attenuation during travel. Consequently, there is still a certain deviation between the study results and the actual situation. Apart from the stage-discharge relation method, research on the variation rule of tail water level mostly adopts hydraulic methods that determine reservoir tail water level by constructing and solving a hydrodynamic model of open-channel unsteady flow [12,13]. However, hydraulic models are unsuitable for practical production due to their stringent requirements for boundary condition data and slow calculation speed. Accordingly, to seek a universal and efficient method for further exploration and accurate simulation of cascade reservoirs’ operation process with various complex factors is of great significance in improving model accuracy.
Short-term optimal operation is mostly applied to reservoirs’ practical production. Therefore, besides model accuracy, there is also high demand for solving methods of the model in terms of computation time, calculation results, and so on. Among the many methods to work out reservoir optimal operation models, Dynamic Programming (DP) is widely used thanks to its advantages such as global convergence and high stability [14,15]. However, DP is restricted by the ‘curse of dimensionality’ [16], which means that the amount of calculation increases exponentially with the growing number of reservoirs. Moreover, the no-aftereffect condition is no longer satisfied in cascade reservoirs’ short-term optimal operation when factors such as water flow hysteresis and the aftereffect of tail water level variation are taken into account, which makes DP inapplicable. In this regard, Ji, C. et al. tried to solve the model of cascade reservoirs’ short-term optimal operation with aftereffect by using Multi-Stage Dynamic Programming (MSDP) [17]. This method has global convergence, but its problem of ‘dimensionality curse’ is even more serious, which renders it inapplicable to practical production. Mei, Y. proposed Multi-Dimensional Dynamic Programming Approximation Algorithm [18], which has a small amount of calculation, but may not produce the actual global optimal solution due to approximation in the calculation process. Although modern intelligent algorithms, such as Genetic Algorithm [19,20], Particle Swarm Optimization Algorithm [21,22], and Ant Colony Optimization Algorithm [23,24], can solve problems with aftereffect in a short period of time, they tend to get stuck in the local optimal solution. Until now, there has been no mature method that can fully meet the requirements of actual production, so presently it is necessary to develop a method that can accurately figure out the model’s global optimal solution in a relatively short time.
In view of the above problems in the study of short-term optimal operation of cascade reservoirs under the effect of reverse regulation, this paper combines the two operation modes (‘electricity to water’ and ‘water to electricity’) of Pankou-Xiaoxuan cascade hydropower stations to build a coupling model of their short-term optimal operation, which considers both Xiaoxuan reservoir’s regulating effect on Pankou reservoir’s outflow and the former’s backwater effect on the latter’s tail water level. Through the BP neural network, factors such as water flow hysteresis and the aftereffect of tail water level variation are studied. Furthermore, Accompanying Progressive Optimality Algorithm (APOA) is put forward to solve the proposed coupling model, so as to provide scientific guidance for the short-term optimal operation of cascade reservoirs under the effect of reverse regulation.
2. Coupling Model
2.1. Objective Function
The subject of this paper is Pankou-Xiaoxuan cascade hydropower stations located in Hubei province in China. With an installed capacity of 500 MW, the Pankou hydropower station is an important peak-regulating power station in the province. Its regular power operation is controlled by Hubei Provincial Power Dispatching Center (a typical ‘electricity to water’ mode). With an installed capacity of 50 MW, Xiaoxuan hydropower station, as the re-regulating hydropower station for Pankou, mainly regulates Pankou’s outflow for power generation (a typical ‘water to electricity’ mode), which is controlled by Han Jiang Hydropower Development Co., Ltd. (hereafter referred to as the Company, Shiyan, China). Although the two hydropower stations have different dispatching superordinates, they both belong to the Company as their decision maker. The Company hopes that through Xianxuan reservoir’s reverse regulation over Pankou reservoir, the overall power generation efficiency of the whole cascade hydropower stations can be improved. Long-term production practice has proved that Xiaoxuan reservoir’s water level has a certain backwater effect on Pankou reservoir’s tail water level. On one hand, while maintaining a high water level of Xiaoxuan reservoir is apparently beneficial to its own power generation, it will raise the tail water level of Pankou reservoir, thus lowering its productive water head and affecting its power generation efficiency, which means consuming more water to complete the same power generation quota. On the other hand, Xiaoxuan reservoir can operate at a low water level to enhance the power generation efficiency of Pankou hydropower station, but at the cost of losing some of its own power generation benefits. Plus, when Pankou hydropower station is in operation to regulate peak load, its outflow is so uneven that Xiaoxuan reservoir has to re-regulate it to meet the demand for downstream ecological flow. Hence, for the economic operation of the cascade hydropower stations, it is of crucial importance to determine the operation mode of Xiaoxuan hydropower station that can reversely regulate Pankou reservoir’s outflow and water head in a scientific manner.
Against the backdrop of coupling the two operation modes (‘electricity to water’ and ‘water to electricity’), the aim of the cascade hydropower stations is to balance Pankou’s power generation efficiency with Xiaoxuan’s generated energy. Accordingly, from the angle of the whole cascade hydropower stations’ total energy, two optimization criteria—minimum energy consumption and maximum generated energy—are integrated to develop the objective function in the coupling model of Pankou-Xiaoxuan cascade reservoirs’ short-term optimal operation [25,26], as shown by Equation (1). Unlike the traditional objective function that involves water quantity, this one calculates water energy, with Pankou’s power generation efficiency reflected by its hydroenergy consumption for power generation (meaning that the less hydroenergy consumption, the higher its power generation efficiency). In this way, the operation goals of both Pankou and Xiaoxuan are unified in the form of energy, which avoids the emergence of a multi-objective problem. In addition, as the two optimization criteria conflict with each other, the objective function is the subtraction of the former from the latter, finally seeking the maximum power generation benefits of the whole cascade hydropower stations:
where E is the remainder of Xiaoxuan’s generated energy after deducting Pankou’s hydroenergy consumption in the operation period, unit: kWh; T is the number of calculation periods over the entire operation period; N2,t(q2,t, H2,t) is Xiaoxuan’s power output when its power generation flow and water head are q2,t and H2,t respectively in period t, unit: kW, and is obtained according to the power characteristic curve of its generator set; Δt is the length of the calculation period, unit: h, and Δt = 0.25 h; λ1,t is the energy efficiency coefficient of Pankou hydropower station in period t, unit: kWh/m3, and its physical meaning is the amount of energy contained in every cubic meter of Pankou reservoir’s water in period t; q1,t(N1,t, H1,t) is Pankou’s power generation discharge when its output and water head are N1,t and H1,t respectively in period t, unit: m3/s, and is also obtained according to the power characteristic curve of its generator set.
2.2. Constraint Conditions
Now that the coupling model combines the two operation modes, the constraint conditions must contain particular constraints specific to these two modes, as shown by Equations (2) and (3), while other regular constraints are expressed by Equations (4)–(10).
(1) Output command constraint
Because Pankou hydropower station operates in the ‘electricity to water’ mode, its output in each period is already determined:
where Ni,t is the output of hydropower station i in period t, unit: kW (i = 1 for Pankou, i = 2 for Xiaoxuan and the same hereafter); Nt is the output command from the superior dispatching center for Pankou hydropower station in period t, unit: kW.
(2) Water level constraint at the end of the operation period
Because Xiaoxuan hydropower station operates in the ‘water to electricity’ mode, its water level at the end of the operation period is already determined:
where Zi,t is the water level of reservoir i at moment t, unit: m; Z2,end is Xiaoxuan reservoir’s controlled water level at the end of the operation period, unit: m.
(3) The upper and lower bounds of water level:
where , are the upper and lower bounds of water level of reservoir i, respectively, unit: m.
(4) The upper and lower bounds of output:
where , are the upper and lower bounds of output of hydropower station i, respectively, unit: kW.
(5) The upper and lower bounds of flow rate:
where qi,t is the power generation discharge of hydropower station i in period t, unit: m3/s, and in this paper, it equals to reservoir outflow because water abandonment is not taken into consideration; , are the upper and lower bounds of power generation discharge of hydropower station i, respectively, unit: m3/s.
(6) Water balance constraint:
where Vi,t, Vi,t+1 are the storage capacity of reservoir i at respectively the beginning and the end of period t (i.e., moment t and moment t + 1), unit: m3; Qi,t is the inflow of reservoir i in period t, unit: m3/s.
(7) Vibration zone constraint:
where Ni,j is the output of generator unit j in hydropower station i, unit: kW; , are the upper and lower bounds of the vibration zone of generator unit j in hydropower station i, unit: kW.
(8) Ecological flow constraint
To meet the demand for downstream ecological flow [27], Xiaoxuan reservoir’s outflow should not be less than 16.7 m3/s:
where qe is the demand for downstream ecological flow, unit: m3/s, and qe = 16.7 m3/s.
(9) Auxiliary power constraint
To prevent the occurrence of inverse power transmission, when Pankou hydropower station halts production, it is Xiaoxuan hydropower station that undertakes the auxiliary power supply mission for the running of both stations:
where Ns is the auxiliary power need of the cascade hydropower stations, unit: kW, and Ns = 2000 kW.
The ecological flow constraint and the auxiliary power constraint can well reflect Xiaoxuan reservoir’s regulation effect on Pankou reservoir’s discharge volume. Since the completion of Xiaoxuan reservoir, Pankou reservoir no longer bears the task of downstream ecological water supply, and the task of auxiliary power supply has been transferred to Xiaoxuan hydropower station. Therefore, when Pankou hydropower station does not undertake peak-regulating tasks, all its generator units can stop running instead of operating in the low efficiency zone just to meet the constraints of ecological flow and auxiliary power supply.
3. Calculation of the Model’s Key Variables
Between the upstream and the downstream reservoirs, there is a certain hydraulic connection in terms of water quantity and water head [28], as shown in Figure 1. Water quantity connection refers to the upstream reservoir’s outflow turning into the downstream reservoir’s inflow after travelling through the interval river channel. Water head connection refers to that the downstream reservoir’s backwater raises the water level of the interval channel, causing a jacking effect on the upstream reservoir’s tail water level. Due to these two kinds of connections, the re-regulating reservoir can adjust the upstream reservoir’s discharge volume and water head. Thus, the downstream reservoir’s inflow and the upstream reservoir’s tail water level, which can respectively reflect these two types of connections, become the key variables in the coupling model of Pankou-Xiaoxuan cascade reservoirs’ short-term optimal operation under the effect of reverse regulation. Computation of the key variables has a critical influence on the model’s accuracy in that an error in their calculations will cause the model’s results to deviate from reality, losing its instructive significance to practical production. Thus, it is very important to calculate them accurately.
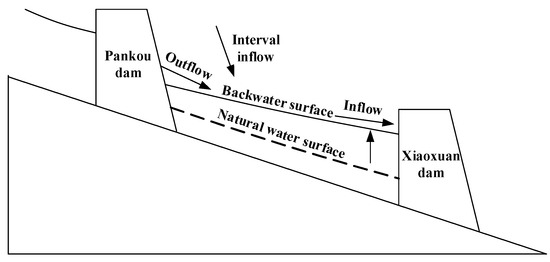
Figure 1.
Schematic diagram of the cascade reservoirs’ hydraulic connection.
3.1. The Downstream Reservoir’s Inflow Considering Water Flow Hysteresis and Interval Inflow
In the cascade reservoirs, the downstream reservoir’s inflow is composed of the upstream reservoir’s outflow and the interval inflow. The upstream reservoir’s outflow arrives at the downstream reservoir with water flow hysteresis that mainly involves two parts. (1) It takes some time for the water flow to travel from the upstream reservoir to the downstream reservoir. (2) During this travel process, the upstream reservoir’s outflow, which is an unsteady flow, goes through not only displacement but also attenuation to some degree [29]. Figure 2 illustrates the comparison between Pankou reservoir’s outflow and Xiaoxuan reservoir’s inflow during a certain power generation process, from which it can be seen that in contrast to Pankou reservoir’s outflow, Xiaoxuan reservoir’s inflow somewhat lags behind and gets smoother. Water flow hysteresis makes it a complicated hydraulics problem as to when and how Pankou reservoir’s outflow will reach Xiaoxuan reservoir.
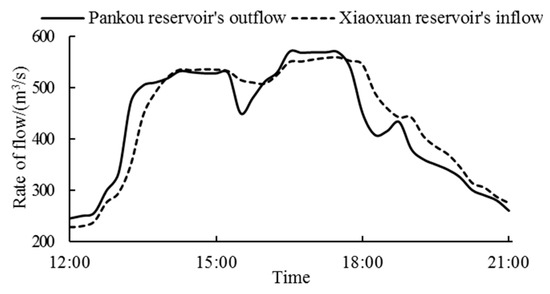
Figure 2.
Pankou’s outflow and Xiaoxuan’s inflow.
The dam sites of Pankou and Xiaoxuan are only 10.4 km apart, without any tributary in between, and the interval catchment area is fairly small, so the interval inflow is often neglected in practical production. However, long-term monitoring data show that on average Xiaoxuan reservoir’s inflow is slightly greater than Pankou reservoir’s outflow, so the existence of the interval inflow cannot be ignored in order to improve the model’s accuracy. The interval inflow between Pankou and Xiaoxuan is mainly formed by runoff generation and confluence in the interval basin, which largely depends on the basin’s rainfall [30]. When the interval inflow is taken into consideration, the calculation of Xiaoxuan reservoir’s inflow will become more complicated in that not only the evolution of water current in the river but also the hydrologic cycle from precipitation to runoff is involved. Since the physical mechanisms of these natural processes are not fully understood, it is difficult to accurately simulate them. Hence in this paper, with masses of data, the BP neural network is used to figure out the relationship between Xiaoxuan reservoir’s inflow and Pankou reservoir’s outflow as well as the interval basin’s rainfall, so that the accurate value of Xiaoxuan reservoir’s inflow can be worked out [31].
The BP neural network is a multilayer feedforward network trained by the error backward propagation algorithm. As one of the most widely-used neural networks, it can approximate any nonlinear function with any precision. Structurally, the BP neural network is divided into one input layer, one output layer, and several hidden layers [32]. In the calculation of Xiaoxuan reservoir’s inflow, the output layer is represented by Xiaoxuan reservoir’s inflow in the current period (Q2,t). As for the input layer, Pankou reservoir’s outflow (q1,t~q1,t−4) as well as the interval basin’s precipitation (Pt~Pt−4) in the current and the previous four periods are chosen as the primary data and screened by the correlation coefficient method. It is demonstrated in Table 1 that the correlation coefficient between Pankou reservoir’s outflow and Xiaoxuan reservoir’s inflow is smaller in the earlier period. For q1,t, q1,t−1 and q1,t−2, their correlation coefficients with Q2,t are similar, whereas the correlation coefficients of q1,t−3 and q1,t−4 with Q2,t are noticeably smaller. Therefore, q1,t, q1,t−1 and q1,t−2 are selected as the input layer data. Compared with Pankou reservoir’s outflow, the interval basin’s precipitation has a much smaller correlation coefficient, which changes little over time. Considering that the interval inflow accounts for only a small portion of Xiaoxuan reservoir’s inflow, the precipitation Pt−1, with the largest correlation coefficient with Q2,t in this regard, is selected as the input layer data. In 1989, Cybenko, G. and Hornik, K. proved that the three-layer network (with one input layer, one output layer, and one hidden layer) can simulate any complex nonlinear problems [33,34]. Therefore, one hidden layer is set up whose node numbers are determined according to Equation (11) [35]:
where h is the number of nodes in the hidden layer; u is the number of nodes in the input layer; v is the number of nodes in the output layer; a is an adjustment coefficient between 0 and 10, and according to tentative calculation when a = 4 the neural network yields the best training results in this study.

Table 1.
Correlation coefficients between input layer data and the output layer.
After the structure of the neural network is established, the historical data of 2012–2016 are input into the neural network for training. The neuron transfer function is a hyperbolic tangent function, and after 10,000 times of training, the network is saved for later calculation of Xiaoxuan reservoir’s inflow. Figure 3 shows the calculated Xiaoxuan reservoir’s inflow during the power generation process mentioned before. Compared with the actual inflow, the inflow produced by the BP neural network has a relative error of 1.11%, which is more accurate than that obtained by the translation method (relative error: 3.84%), which only considers the travel time (i.e., Pankou reservoir’s outflow merely translates into Xiaoxuan reservoir’s inflow).
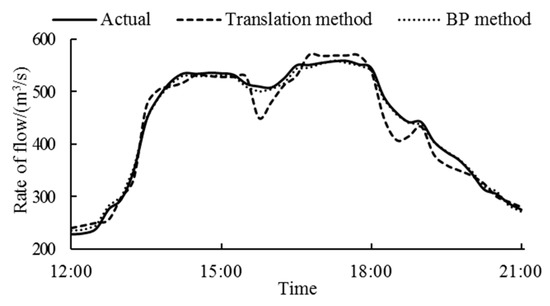
Figure 3.
Calculation results of Xiaoxuan’s inflow.
3.2. The Upstream Reservoir’s Tail Water Level Considering the Influence of Dual Aftereffect Factors
During the operation of cascade reservoirs, under the backwater effect of the downstream reservoir, the upstream reservoir’s tail water level is closely related to the downstream reservoir’s water level. Different water levels of the downstream reservoir have different degrees of backwater effect on the upstream reservoir’s tail water level. Figure 4 is the stage-discharge curve of Pankou reservoir corresponding to different water levels of Xiaoxuan reservoir. Long-term practical production shows that Pankou reservoir’s tail water level obtained by the stage-discharge relation method still deviates from the actual value. This kind of deviation can be explained by two reasons. For one thing, the tail water level-discharge curve is based on the assumption that the reservoir outflow is a steady flow. However, in fact, it is an unsteady flow whose characteristics result in a certain aftereffect of tail water level variation [36], that is, the tail water level in the current period is related to that in the previous period. For another, it takes some time for Xiaoxuan reservoir’s backwater to reach Pankou dam, meaning that Pankou reservoir’s tail water level in the current period is not necessarily influenced by Xiaoxuan reservoir’s water level in the current period but the previous several periods [37], which is another aftereffect of Pankou’s tail water level variation. Under the influence of such dual aftereffect factors, Pankou’s tail water level in the current period is affected by three kinds of variables: Pankou’s outflow in the current period, Pankou’s tail water level in the previous period, and Xiaoxuan’s water level in the previous n (n is determined by the travel time of Xiaoxuan’s backwater) periods. As the physical mechanism is very complicated, the BP neural network is again used for calculation.
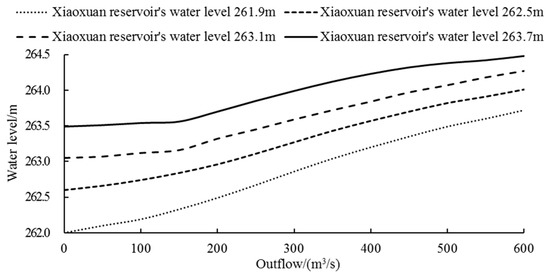
Figure 4.
Pankou’s stage-discharge curve.
Here, Pankou reservoir’s tail water level in the current period (DZ1,t) represents the output layer. As for the input layer data, aside from Pankou reservoir’s outflow in the current period (q1,t) and its tail water level in the previous period (DZ1,t−1), it is also needed to decide which periods of Xiaoxuan reservoir’s water level are concerned. Similarly, Xiaoxuan reservoir’s water levels in the current and the previous four periods (Z2,t~Z2,t−4) are chosen as the primary data to be filtered by the correlation coefficient method. From Table 2 it can be seen that the correlation coefficient between Xiaoxuan’s water level and Pankou’s tail water level gradually decreases with time. For Z2,t, Z2,t−1 and Z2,t−2, their correlation coefficients have little difference, while for Z2,t−3 and Z2,t−4 their correlation coefficients are apparently smaller, which indicates that the time it takes for Xiaoxuan reservoir’s backwater to reach Pankou is between 0 and 2 periods. Thus, Z2,t, Z2,t−1 and Z2,t−2 are selected as the input layer data. The configuration of the hidden layer and the training parameters is similar to that described in Section 3.1. After the training is completed, the network is saved for later calculation of Pankou reservoir’s tail water level. Figure 5 shows the resulted tail water level variation of Pankou reservoir in the same power generation process mentioned before. Compared with the actual variation, the results of the BP neural network only produce a calculation error of 0.001 m, which is notably smaller than the calculation error (0.027 m) produced by the stage-discharge relation method, thus proving the advantage of the BP neural network.

Table 2.
Correlation coefficients between input layer data and the output layer.
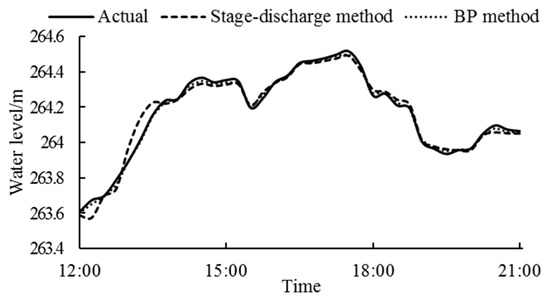
Figure 5.
Calculation results of Pankou’s tail water level.
4. Model Solution
When factors such as water flow hysteresis and the aftereffects of tail water level variation are taken into account, the decision variable (power generation flow) of the current period for the cascade reservoirs is not only related to the state (reservoir water level) of this period but also the state of the previous several periods. Since the ‘no aftereffect’ condition is not satisfied, the proposed model of short-term optimal operation cannot be solved by DP. Although MSDP can deal with the problem with aftereffect, it is restricted by a serious ‘curse of dimensionality’ [17]. The subject of this study is taken as an example for further explanation. The short-term optimal operation of Pankou-Xiaoxuan cascade reservoirs is an issue about the joint operation of two reservoirs. Nonetheless, as Pankou hydropower station operates in the ‘electricity to water’ model, once the operation state of Xiaoxuan hydropower station is determined, Pankou’s operation state will also be settled (by in-plant economic operation calculation), which reduces the issue to an essentially one-dimensional problem. In this one-dimensional scenario, suppose that the number of discrete points of the reservoir water level is M and the number of interrelated periods is N (i.e., the state of the former N − 1 periods influences the decision of the current period), then in each multi-stage calculation of MSDP there are MN+1 combinations of Xiaoxuan’s water level and the total amount of calculation is T·MN+1 with T times of multi-stage calculation. Since the value of T·MN+1 grows exponentially with the increase in N, even in a one-dimensional circumstance the dimensionality curse still emerges due to the interconnection of N periods. As the number of dimensions increases to L (L > 1), the total amount of calculation will become T·(MN+1)L with (MN+1)L combinations of water level at each multistage, which is a more serious problem of dimensionality curse. In view of this, we come up with an improved POA (i.e., APOA) to solve the model of the cascade reservoirs’ short-term optimal operation with aftereffect.
4.1. Basic Principle of APOA
POA is an improved DP that simplifies a complicated multi-stage decision problem into a series of two-stage decision problems, considerably reducing the complexity and effectively mitigating the dimensionality curse [38]. In contrast to POA, APOA has two facets of improvements.
(1) When Xiaoxuan hydropower station is being optimized, Pankou reservoir’s water level is taken as the variable that spatially accompanies Xiaoxuan reservoir’s water level for calculation. In each discrete computation where Xiaoxuan’s water levels in the current and the previous n periods are known, the magnitude of Xiaoxuan’s backwater effect on Pankou’s tail water level is definite. In addition, because Pankou’s tail water level in the previous one period is already known, in the current period, Pankou’s tail water level is only related to Pankou’s outflow. Under the condition of a definite output of Pankou hydropower station, its reservoir outflow can be obtained through trial calculation. Its water level can then be figured out according to its inflow and outflow. Hence, for each discrete water level of Xiaoxuan, there is only one corresponding water level of Pankou and accordingly, one hydrograph of Pankou corresponding to each hydrograph of Xiaoxuan in the operation period.
(2) In each two-stage calculation, the variables of the preceding related N − 1 periods are taken as the temporally-accompanying variables of the current period for calculation. Considering the interrelation of N periods, the decision of the current two-stage calculation is affected by those decisions made in the previous N − 1 periods. APOA divides the problem with T periods into T − 1 sub problems, each of which includes two main calculation periods accompanied by N − 1 related periods. As shown in Figure 6, in the calculation of period t and period t + 1, the state and the decision of other periods (including the accompanying N − 1 related periods) are known, thereby effectively tackling the aftereffect problem. In each two-stage calculation, there are M combinations of Xiaoxuan’s water level and T − 1 times of two-stage calculation for one iteration, so the amount of calculation is (T − 1)·M. If the precision requirement is satisfied after K times of iteration, the total amount of calculation will be K·(T − 1)·M, evidently smaller than T·MN+1 produced by MSDP. As a result, APOA can effectively alleviate the problem of dimensionality curse.
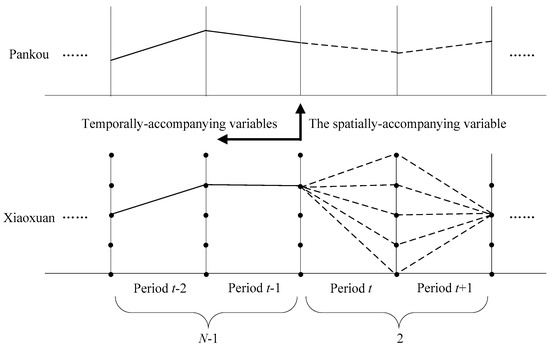
Figure 6.
Schematic diagram of APOA.
4.2. Calculation Procedure of APOA
The calculation procedure of APOA is detailed as follows:
Step 1: Determine the number of associated periods. Use the correlation coefficient method to calculate the number of periods connected with the current period in terms of water quantity and water head. If the first m periods are related to the current period in terms of Xiaoxuan reservoir’s inflow and the first n periods are related to the current period in terms of Pankou reservoir’s tail water level, then the number of the related periods can be calculated by Equation (12), where m = 2, n = 2 and N = 3 in this article:
Step 2: Train the BP neural networks. The BP neural networks are trained by inputting training data, including the type of training data, starting and ending time, as well as the structure and parameters of the neural networks, which are detailed in Section 3.1 and Section 3.2. After the training is completed, the neural network for calculating Xiaoxuan reservoir’s inflow (net1) and that for Pankou reservoir’s tail water level (net2) are obtained.
Step 3: Set the initial solution. The selection of initial solutions has a major influence on the convergence speed and computation time of APOA [39]. Long-term experience of the dispatchers is often embodied in the operation rule of the hydropower station, according to which a relatively optimal solution can be obtained. Thus, in this paper, such a solution is used as the initial solution. It should be noted that in the initial solution, the initial water level of Xiaoxuan reservoir ( = {, , …, }) is the most critical variable while that of Pankou reservoir ( = {, , …, }) is only the variable accompanying it.
Step 4: Optimize progressively. Carry out the optimization step by step from period 1 to period T. When the calculation progresses to period t and period t + 1 (accompanied by the two related periods of t − 2 and t − 1), fix Xiaoxuan reservoir’s water levels at all moments except that at moment t + 1 and calculate all the discrete points of its water level at that moment. Xiaoxuan reservoir’s inflow and Pankou reservoir’s tail water level are calculated by the BP neural networks, as shown in Equation (13), with Pankou reservoir’s water level acting as the variable accompanying Xiaoxuan’s water level. After running through all the discrete points, select the optimal water level of Xiaoxuan reservoir () and correspondingly the optimal water level of Pankou () at moment t + 1. Make = and = .
Step 5: Iterative calculation. After Step 4 is executed, the first iteration completes and produces a new solution = {, , …, } accompanied by = {, , …, }. Compare with in terms of the value of the objective function. If the difference between their values is less than the calculation precision (ε), then the convergence condition is satisfied and (accompanied by ) is the final solution. Otherwise replace the initial solution with and repeat Step 4 until the convergence condition is satisfied.
5. Case Study
The Du River, the largest tributary of the Hanjiang River, is located across Shaanxi province and Hubei province in China. Pankou-Xiaoxuan cascade hydropower stations, whose basic information is listed in Table 3, lie in the upper reaches of the Du River, as shown in Figure 7. Under the ‘electricity to water mode, Pankou hydropower station generates electricity in accordance with the daily instructions (in the form of a 96-point load curve) from the superior dispatching center. In this paper, the operation period is one day with 96 calculation periods lasting 15 min each. Considering the different conditions among flood season, dry season, and transition season, 10 representative days are selected from each season of 2016–2017 for calculation. The results are analyzed in terms of model solving methods and the patterns of reverse regulation.

Table 3.
Parameters of Pankou-Xiaoxuan cascade hydropower stations.
Figure 7.
The location of Pankou-Xiaoxuan cascade reservoirs.
5.1. Comparative Analysis of Model Solving Methods
Take 10 December 2016 as an example to develop the coupling model of Pankou-Xiaoxuan cascade reservoirs’ short-term optimal operation and use DP, POA, MSDP and APOA, respectively, to work it out. While water flow hysteresis and the aftereffect of tail water level variation are taken into account in MSDP and APOA by using BP neural network to calculate Xiaoxuan reservoir’s inflow and Pankou reservoir’s tail water level, the two factors are not considered in DP and POA where Pankou’s outflow is directly taken as Xiaoxuan’s inflow and Pankou’s tail water level is obtained by the stage-discharge relation method. The calculated results of each method are statistically summarized in Table 4, in which the optimization margin refers to the ratio of the energy increase after optimization (the difference between the two objective functions) to the actual generated energy.

Table 4.
The statistics of calculated results.
5.1.1. Comparative Analysis of the Objective Function Value of Each Method
MSDP has been theoretically proved to have global convergence, so on the premise of the same calculation conditions (taking into account the water flow hysteresis, the aftereffect of tail water level variation and the with same amount of discrete points), the objective function calculated by APOA is compared with that calculated by MSDP in order to assess the calculated results of APOA. It can be seen from Table 4 that for 10 December 2016, the objective function of APOA equals that of MSDP. Among the other 29 representative days, there are 20 days where their objective functions are equal and 9 days where their objective functions are very close. According to the results of the 30 representative days, the average optimization margin of APOA is 0.93%, only 0.03% less than that of MSDP, which demonstrates the advantage of APOA.
Similarly, the comparative analysis of POA and DP can also illustrate the advantage of POA. It is shown from Table 4 that the objective functions of DP and POA are different from those of MSDP and APOA. This is due to their different calculation conditions. Thus, there is no point in comparing the objective functions between the former two and the latter two. Instead, we make comparisons in terms of the length of computation time and the calculation accuracy.
5.1.2. Analysis of Computation Time
In this case, the amount of calculation is T·M2 for DP and T·MN+1 for MSDP with the aftereffect factors taken into consideration. With the number of discrete points M = 560 and the number of related periods N = 3, the amount of calculation of MSDP is 313,600 times that of DP. However, Table 4 shows that the computation time of MSDP is about 1400 times that of DP, far fewer than 313,600 times. This is because MSDP imposes constraint on the feasible domain and leaves out those discrete points that do not satisfy the constraints, saving a great deal of calculation time. Nevertheless, its computation time of 262 h still cannot meet the efficiency requirement in practical production.
As an improved algorithm for alleviating the dimensionality curse of DP, POA is characterized by an obviously smaller amount of calculation compared with DP, as demonstrated by the statistical results from Table 4. Unlike the contrast between DP and MSDP, APOA has the same form of calculation amount as POA (K·(T − 1)·M) despite considering aftereffect factors. No matter how the number of iterations (K) may change, the change in the amount of calculation is linear rather than exponential, so the amount of calculation for APOA and POA is in the same order of magnitude. Table 4 shows that the calculation time of APOA is 156.37 s, which is 1.8 times that of POA but only 1/6000 that of MSDP. This means that with the same calculation results, APOA substantially shortens the computation time in comparison with MSDP, which can meet the efficiency requirement in actual production.
5.1.3. Analysis of Calculation Accuracy
The accuracy of calculation depends on how close the calculation result is to the actual process. As is shown in Figure 8a, the outflow graphs of Pankou reservoir obtained by APOA and POA basically coincide, with merely a slight difference that can be seen from the partially enlarged detail (the reason will be analyzed in detail in Section 5.2). While the difference of Pankou’s outflow processes obtained by the two methods is small, the calculated tail water level graphs differ distinctly, as is displayed in Figure 8b. For POA, the shape of Pankou’s tail water level graph resembles that of the reservoir’s outflow graph, with steep rises and falls. However, Pankou’s tail water level variation is a continuous and slow process. The stage-discharge relation method used in POA only takes into account the impact of Pankou’s outflow and Xiaoxuan’s water level in the current period and neglects the aftereffect of tail water level variation, making the calculation results inconsistent with the reality. On the contrary, the BP neural network used in APOA considers various factors that influence Pankou’s tail water level and produces a relatively smooth graph, which tallies more with the actual situation. Therefore, APOA has higher calculation accuracy than POA with respect to Pankou’s tail water level.
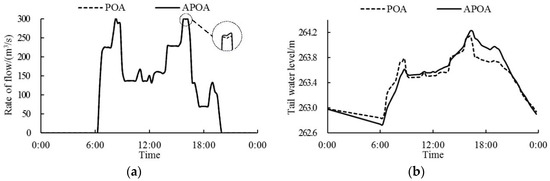
Figure 8.
Comparison of Pankou’s calculated results between POA and APOA. (a) Pankou’s outflow process; (b) Pankou’s tail water level process.
Next, we analyze from the angle of Xiaoxuan reservoir’s inflow. As the BP neural network adopted in APOA takes water flow hysteresis into consideration, the corresponding inflow of Xiaoxuan reservoir, as shown in Figure 9a, slightly lags behind and is smoother compared to POA. Due to water flow hysteresis, Xiaoxuan’s operation strategy obtained by APOA, as signified by Xiaoxuan’s water level process in Figure 9b and its output process in Figure 9c, also lags behind that obtained by POA, especially around the periods when Pankou starts power generation. On that day, it is Pankou hydropower station’s downtime until 6:30 when power generation begins, spurring an increase in its outflow. In the calculation of POA, Pankou’s outflow is directly used as Xiaoxuan’s inflow, causing Xiaoxuan to receive inflow at the exact moment and gradually increase its output as well as water level. Yet actually, when Pankou starts operation, its generator units are at the climbing stage with a relatively small outflow that travels a long time (about two periods) to reach Xiaoxuan. Accordingly, during the two periods of 6:30–6:45 and 6:45–7:00 Xiaoxuan’s inflow is too little to keep the reservoir water level rising while discharging water for power generation. Because of the low accuracy in calculating Xiaoxuan reservoir’s inflow, the operation scheme produced by POA is against the natural law and impractical in actual production. The calculation results of APOA, however, show that Xiaoxuan reservoir’s water level does not rise until 7:00 when Pankou’s outflow from the previous two periods has already got to Xiaoxuan. Therefore, Xiaoxuan does follow the rule of water balance, discharging water for power generation and meanwhile raising reservoir water level. To sum up, owing to the excellent performance of the BP neural network in the calculation of Xiaoxuan reservoir’s inflow, the accuracy of APOA is higher than that of POA.
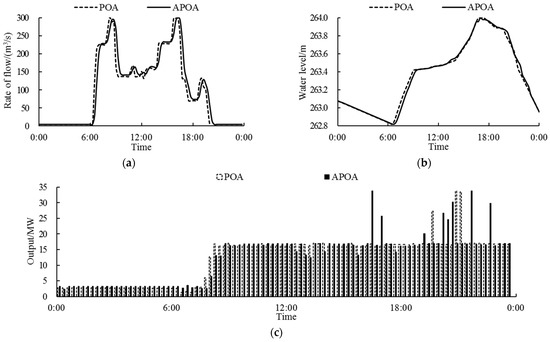
Figure 9.
Comparison of Xiaoxuan’s calculated results between POA and APOA. (a) Xiaoxuan’s inflow process; (b) Xiaoxuan’s water level process; (c) Xiaoxuan’s output process.
5.2. Analysis of the Reverse Regulation Rule
The optimal operation scheme obtained by APOA is compared to the actual operation scheme in order to find out the reverse regulation rule and get the optimal operation mode of the cascade reservoirs. Figure 10 is a comparison chart of the optimal and the actual operation schemes on 10 December 2016. During the actual operation, Pankou generates electricity as instructed, with its water level and output process shown in Figure 10a, while Xiaoxuan’s water level and output process are shown in Figure 10b. Between 0:00 and 6:30, the downtime of Pankou hydropower station, Xiaoxuan hydropower station keeps operating with about 2 MW of output to meet the requirements for auxiliary power and ecological flow, and its water level drops steadily and slowly. After 6:30, as Pankou begins power generation, Xiaoxuan also increases its output until Pankou halts operation at 20:00. Then Xiaoxuan’s operation returns to about 2 MW of output until the end of the operation period.
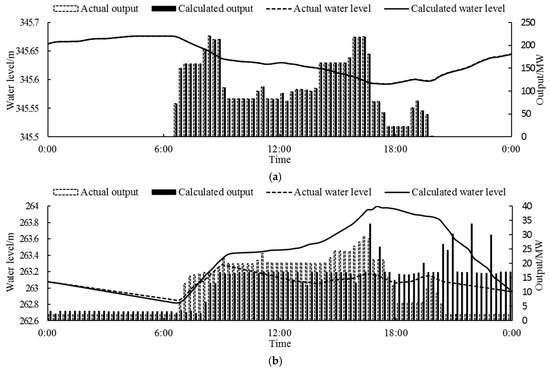
Figure 10.
Comparison between the optimal and the actual operation schemes. (a) Pankou; (b) Xiaoxuan.
In contrast to the actual operation scheme, the optimal operation scheme produces a markedly different operation strategy for Xiaoxuan. For one thing, after Pankou commences power generation, Xiaoxuan’s water level steadily rises and nearly reaches the normal water level at 17:00, and keeping a high water level yields greater output with the same flow rate. For another, after Pankou halts operation at 20:00, Xiaoxuan’s power generation remains efficient with about 16 MW of output as its water level is still high. As a result, Xiaoxuan’s generated energy in the optimal operation scheme is 307.4 thousand kWh, an increase of 39.7 thousand kWh from the actual situation (267.7 thousand kWh).
As for Pankou, the elevated water level of Xiaoxuan increases the backwater effect on its tail water level and affects its power generation efficiency. However, it can be seen from Figure 10a that the calculated hydrograph of Pankou virtually coincides with the actual one. In addition, it can be obtained from Table 4 that the hydroenergy consumption of Pankou in the optimal operation scheme is 1518.9 thousand kWh, only 0.4 thousand kWh more than the actual situation (1518.5 thousand kWh), meaning that the backwater effect of Xiaoxuan on Pankou’s power generation efficiency is insignificant.
As far as the whole cascade hydropower stations are concerned, the elevated water level of Xiaoxuan creates a growth in generated energy that is remarkably greater than the hydroenergy consumption increase of Pankou caused by its fall in power generation efficiency. Moreover, the optimization of Xiaoxuan’s storage and discharge leads to more efficient utilization of Pankou’s outflow. Consequently, the value of objective function in the optimal operation scheme is 39.3 thousand kWh greater than the actual value, with an optimization margin of 2.19%.
A primary conclusion can be drawn from these calculated results—to raise Xiaoxuan’s water level (water head regulation) and keep its generator units working within the high-efficiency zone (water quantity regulation) can boost the power generation benefits of the cascade hydropower stations.
Thus, to make the above conclusion more convincing, the other 29 representative days are also analyzed. As the above analyses have involved the representative day in the dry season, Figure 11 only displays the results of 1 July 2017 (flood season) and 12 June 2017 (transition season). Besides, it can be seen from Figure 10a that in the optimal scheme and the actual scheme, Pankou’s operation processes are basically the same, and the focus of this article is Xiaoxuan’s re-regulating effect on Pankou. Therefore, only Xiaoxuan’s operation schemes are displayed in Figure 11. It can be seen from Figure 10b and Figure 11 that whatever the season is, the calculated hydrographs of Xiaoxuan are above the actual ones and that in the optimal operation scheme, Xiaoxuan hydropower station’s output is around 16 MW, 32 MW or 48 MW. When such output is assigned to its generator units, the generator units operate in the high-efficiency zone (the rated output of Xiaoxuan’s generator unit is 16.7 MW, near which the power generation efficiency is relatively high), which also verifies the above conclusion.
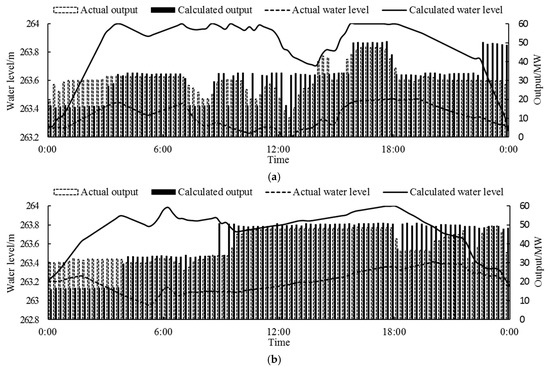
Figure 11.
Comparison between optimal and actual operation schemes of Xiaoxuan, (a) 1 July; (b) 12 June.
It should be noted that during Pankou’s downtime, if Xiaoxuan discharges water by efficiently operating one generator unit, its water level will decline continually because of its small reservoir capacity. If the downtime lasts long, to prevent the situation of a too low water level with no water for use, Xiaoxuan has to generate electricity inefficiently with a flow that just satisfies the needs of ecological flow and auxiliary power.
It is easy to understand that keeping Xiaoxuan’s generators operating in the high-efficiency zone benefits the power generation of the cascade hydropower stations. As for the reason why raising Xiaoxuan’s water level can boost the power generation benefits of the cascade hydropower stations, it is discussed from two aspects: the efficiency of the generator units and the total water head of the cascade hydropower stations. From the angle of generators’ efficiency, while Pankou hydropower station with a high water head is affected mainly by power generation flow and insignificantly by a minor change in water head, Xiaoxuan hydropower station with a low water head is sensitive to changes in water head. Suppose the impact of Xiaoxuan’s water level variation on the cascade hydropower stations’ total water head is neglected (i.e., when Xiaoxuan’s water level is raised by 1 m, Pankou’s tail water level will also rise by 1 m correspondingly and the cascade hydropower stations’ total water head stays unchanged), then we design two operation schemes as shown in Table 5. On the basis of Scheme 1, Scheme 2 raises Xiaoxuan’s water level by 2 m, thus increasing the water head of Xiaoxuan from 12 to 14 m while decreasing that of Pankou from 80 to 78 m. The calculation results show that with the same power generation flow of 100 m3/s, Xiaoxuan sees an increase of 0.0198 in power generation efficiency, much greater than the reduction of 0.0063 that Pankou suffers. Therefore, to raise Xiaoxuan’s water level by 2 m means an increase of 0.0021 in the overall power generation efficiency.

Table 5.
Comparison of different operation schemes η = N/(9.81qH).
In fact, the water level variation of Xiaoxuan reservoir has some influence on the total water head of the cascade hydropower stations. As is shown in Figure 1, the farther the backwater is from Xiaoxuan dam, the closer the backwater surface gets to the natural water surface. It is found from statistical analysis of historical data that an increase of 1 m in Xiaoxuan reservoir’s water level will raise Pankou reservoir’s tail water level by about 0.6 m. Therefore, Scheme 1 should actually become Scheme 3 after Xiaoxuan’s water level is raised by 2 m, as shown in Table 5. From the angle of the cascade hydropower stations’ total water head, Scheme 3 uses 0.8 m more of water head than Scheme 1 and further elevates the overall efficiency compared to Scheme 2.
In summary, when Xiaoxuan hydropower station raises its operation water level, even though Pankou’s water head will fall due to the backwater effect, the impact on the efficiency of Pankou’s generator units is unnoticeable. Besides, the increment in Xiaoxuan’s water head can greatly enhance the efficiency of its generator units and thus considerably increase its generated energy. In contrast, the improvement of Xiaoxuan’s power generation benefits is more significant. Therefore, it is beneficial for the cascade hydropower stations to raise Xiaoxuan’s operation water level.
6. Conclusions
In this paper, Pankou-Xiaoxuan cascade reservoirs are taken as an example and integrated with their practical production, a coupling model of their short-term optimal operation under the effect of reverse regulation is developed and solved. Through analysis of the model’s calculation results, Xiaoxuan reservoir’s reverse regulation effect on Pankou reservoir is studied from two facets (water quantity and water head) and the optimal operation rules of the cascade reservoirs are obtained, with the following conclusions:
- On the basis of considering Xiaoxuan reservoir’s regulation on both water quantity and water head of Pankou reservoir, the model takes into account both Pankou’s power generation efficiency and Xiaoxuan’s generated energy to seek the maximum of overall power generation benefits from the angle of the cascade hydropower stations’ total energy, which fits the requirements of actual production. The calculation results show that the model can effectively enhance power generation benefits of the cascade hydropower stations, which also verifies the model’s validity.
- The BP neural network has excellent performance in exploring water flow hysteresis and the aftereffect of tail water level variation, so that the accurate values of downstream reservoir’s inflow and upstream reservoir’s tail water level can be obtained, which significantly improves the coupling model’s accuracy. The proposed APOA can efficiently work out the short-term optimal operation model of cascade reservoirs with aftereffect. With the merits and accuracy of its calculation results demonstrated, APOA is proved to meet the demand of actual production.
- As for the rule of reverse regulation, from the aspect of water quantity regulation, Xiaoxuan reservoir should strategically store and discharge the inflow from Pankou reservoir and try to discharge flow in the mode where its generator units are in the high-efficiency zone, so that this portion of water can be utilized more efficiently; from the aspect of water head regulation, the increase in Xiaoxuan’s generated energy brought by raising its operation water level is greater than Pankou’s hydroenergy loss caused by the fall in its power generation efficiency. Therefore, to raise Xiaoxuan’s operation water level is beneficial to power generation of the whole cascade hydropower stations.
It should be noted that we need to balance water quantity regulation with water head regulation. Excessive elevation of Xiaoxuan’s operation water level may result in lack of space for water quantity regulation and even water abandonment of Xiaoxuan. Thus, it will be the focus of future research to study how high Xiaoxuan’s operation water level should be raised, considering the uncertainty of Pankou’s output.
Author Contributions
C.J. conceived and designed the experiments; H.Y. and X.Y. performed the experiments; H.Y. and J.W. analyzed the data; H.Y., J.W. and R.L. wrote the paper.
Acknowledgments
This study was financially supported by the National Key Research and Development Program of China (2016YFC0402208) and the National Natural Science Foundation of China (51709105). The authors are grateful to the reviewers for their comments and valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mo, L.; Lu, P.; Wang, C.; Zhou, J. Short-term hydro generation scheduling of Three Gorges-Gezhouba cascaded hydropower plants using hybrid MACS-ADE approach. Energy Convers. Manag. 2013, 76, 260–273. [Google Scholar] [CrossRef]
- Liao, X.; Li, Y.; Zhu, X.; Zhao, K.; Bai, T.; Gao, K. Research on peak regulation capacity of Xiaolangdi-Xixiayuan cascade hydropower station. Int. J. Hydroelectr. Energy 2011, 29, 29–31. [Google Scholar]
- Dickel, K.; Klein, P.; Nielinger, A. Rehabilitation of the weir at Ahausen reservoir. Hydropower Dam 2001, 4, 94–97. [Google Scholar]
- Tospornsampan, J.; Kita, I.; Ishii, M.; Kitamura, Y. Optimization of a multiple reservoir system operation using a combination of genetic algorithm and discrete differential dynamic programming: A case study in Mae Klong system, Thailand. Paddy Water Environ. 2005, 3, 29–38. [Google Scholar] [CrossRef]
- Richter, B.D.; Thomas, G.A. Restoring environmental flows by modifying dam operations. Ecol. Soc. 2007, 12, 181–194. [Google Scholar] [CrossRef]
- Bai, T.; Chang, J.; Fang, J.; Huang, Q.; Zhu, X.; Liao, X. Study on short-term peak load of Xiaolangdi and Xixiayuan cascade hydropower stations. J. Hydroelectr. Eng. 2012, 31, 83–88. [Google Scholar]
- Cai, Z.; Zhang, A.; Zhang, J. Optimized control on water level between Three Gorges dam and Gezhouba dam and its benefit analysis. J. Hydroelectr. Eng. 2010, 29, 10–17. [Google Scholar]
- Shawwash, Z.K.; Siu, T.K.; Russell, S.O.D. The B.C. hydro short term hydro scheduling optimization model. IEEE Trans. Power Syst. 2000, 15, 1125–1131. [Google Scholar] [CrossRef]
- Habert, J.; Ricci, S.; Papa, E.L.; Thual, O.; Piacentini, A.; Goutal, N.; Jonville, G.; Rochoux, M. Reduction of the uncertainties in the water level-discharge relation of a 1D hydraulic model in the context of operational flood forecasting. J. Hydrol. 2016, 532, 52–64. [Google Scholar] [CrossRef]
- Li, A.; Wang, L.; Lin, W.; Ji, C. Application of immune particle swarm optimization algorithm to short-term optimal dispatch of cascade hydropower stations. J. Hydraul. Eng. 2008, 39, 426–432. [Google Scholar]
- Ge, X.; Zhang, L.; Shu, J.; Xu, N. Short-term hydropower optimal scheduling considering the optimization of water time delay. Electr. Power Syst. Res. 2014, 110, 188–197. [Google Scholar] [CrossRef]
- Shang, Y.; Liu, R.; Li, T.; Zhang, C.; Wang, G. Transient flow control for an artificial open channel based on finite difference method. Sci. China Technol. Sci. 2011, 54, 781–792. [Google Scholar] [CrossRef]
- Wang, N.; Wang, C.; Du, S.; Le, H.; Li, J. Application of dynamic relationship between water level and discharge in hydrodynamic flood forecasting model. Int. J. Hydroelectr. Energy 2014, 32, 68–72. [Google Scholar]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef] [PubMed]
- Saadat, M.; Asghari, K. Reliability improved stochastic dynamic programming for reservoir operation optimization. Water Resour. Manag. 2017, 31, 1795–1807. [Google Scholar] [CrossRef]
- Chu, W.; Yang, T.; Gao, X. Comment on “High-dimensional posterior exploration of hydrologic models using multiple-try DREAM (ZS) and high-performance computing” by Eric Laloy and Jasper A. Vrugt. Water Resour. Res. 2014, 50, 2775–2780. [Google Scholar] [CrossRef]
- Ji, C.; Li, C.; Wang, B.; Liu, M.; Wang, L. Multi-stage dynamic programming method for short-term cascade reservoirs optimal operation with flow attenuation. Water Resour. Manag. 2017, 31, 4571–4586. [Google Scholar] [CrossRef]
- Mei, Y. Dynamic programming model without Markovin property of cascade reservoirs operation and its application. Adv. Water Sci. 2000, 11, 194–198. [Google Scholar]
- Prasanchum, H.; Kangrang, A. Optimal reservoir rule curves under climatic and land use changes for Lampao Dam using Genetic Algorithm. KSCE J. Civ. Eng. 2017, 22, 351–364. [Google Scholar] [CrossRef]
- Chang, L.C. Guiding rational reservoir flood operation using penalty-type genetic algorithm. J. Hydrol. 2008, 354, 65–74. [Google Scholar] [CrossRef]
- Kumar, D.N.; Reddy, M.J. Multipurpose reservoir operation using particle swarm optimization. J. Water Resour. Plan. Manag. 2007, 2006, 192–201. [Google Scholar] [CrossRef]
- Xie, W.; Ji, C.; Wu, Y.; Li, X. Particle swarm optimization based on cultural algorithm for flood optimal scheduling of hydropower reservoir. J. Hydraul. Eng. 2010, 41, 452–457. [Google Scholar]
- Afshar, M.H.; Ketabchi, H.; Rasa, E. Elitist continuous ant colony optimization algorithm: Application to reservoir operation problems. Int. J. Civ. Eng. 2006, 4, 274–285. [Google Scholar]
- Jalali, M.R.; Afshar, A.; Marino, M.A. Multi-reservoir operation by adaptive pheromone re-initiated ant colony optimization algorithm. Int. J. Civ. Eng. 2007, 5, 284–301. [Google Scholar]
- Chen, J.; Wu, Y.; Hu, B.; Cheng, T. Improved mathematical model of minimum energy consumption for load distribution of cascade hydropower plants. Automat. Electr. Power Syst. 2017, 41, 155–160. [Google Scholar]
- Jiang, Z.; Qin, H.; Ji, C.; Feng, Z.; Zhou, J. Two dimension reduction methods for multi-dimensional dynamic programming and its application in cascade reservoirs operation optimization. Water 2017, 9, 634. [Google Scholar] [CrossRef]
- Suen, J.P.; Eheart, J.W. Reservoir management to balance ecosystem and human needs: Incorporating the paradigm of the ecological flow regime. Water Resour. Res. 2016, 42, 178–196. [Google Scholar] [CrossRef]
- Yuan, B. Short-Term Optimization Dispatching of Cascaded Hydropower Daily-Optimized Dispatching for YILIHE Cascaded Hydropower. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2012. [Google Scholar]
- Barbetta, S.; Moramarco, T.; Perumal, M. A Muskingum-based methodology for river discharge estimation and rating curve development under significant lateral inflow conditions. J. Hydrol. 2017, 554, 216–232. [Google Scholar] [CrossRef]
- Papazafiriou, Z.G. Linear and nonlinear approaches for short-term runoff estimations in time-invariant open hydrologic systems. J. Hydrol. 1976, 30, 63–80. [Google Scholar] [CrossRef]
- Othman, F.; Naseri, M. Reservoir inflow forecasting using artificial neural network. Int. J. Phys. Sci. 2011, 6, 433–440. [Google Scholar]
- Coulibaly, P.; Anctil, F.; Bobée, B. Daily reservoir inflow forecasting using artificial neural network with stopped training approach. J. Hydrol. 2000, 230, 244–257. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superposition of sigmoidal function. Math. Control Signal. 1989, 2, 304–314. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Shen, H.; Wang, Z.; Gao, C.; Qin, J.; Yao, F.; Xu, W. Determining the number of BP neural network hidden layer units. J. Tianjin Univ. Technol. 2008, 24, 13–15. [Google Scholar]
- Liu, J.; Wang, J. Exploration of empirical calculation method about tailwater level in Gezhouba hydropower station. Hydropower Autom. Dam Monit. 2011, 35, 77–80. [Google Scholar]
- Tang, H.; Chen, S.; Zhao, Y. Model and algorithm of short-term optimal scheduling of Three Gorges cascaded hydropower stations. Int. J. Hydroelectr. Energy 2008, 26, 133–136. [Google Scholar]
- Lucas, N.J.D.; Perera, P.J. Short-term hydroelectric scheduling using the progressive optimality algorithm. Water Resour. Res. 1985, 21, 1456–1458. [Google Scholar] [CrossRef]
- Zhong, P.; Zhang, J.; Xu, B.; Zhang, M. Daily optimal operation model of cascade reservoirs considering delay of flow propagation. J. Hydroelectr. Eng. 2012, 31, 34–38. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).