Characterization of the Infiltration Capacity of Porous Concrete Pavements with Low Constant Head Permeability Tests

Abstract

Porous concrete (PC) has been extensively used as a surface layer in permeable pavements. The effectiveness of this material in managing stormwater runoff depends not only on subsurface storage, but on infiltration capacity during rainfall events. A variety of tests have been traditionally used for assessing their infiltration capacity, however, there is still uncertainty about whether these tests produce representative performance results under real conditions. This study aims to propose a methodology based on saturated and unsaturated low constant head (LCH) permeability tests, in order to characterize in detail the infiltration performance of PC materials during storm events and predict their infiltration behavior over time. To this end, three different infiltration tests were performed on PC specimens, both in newly built conditions and after being clogged. These experiments included unsaturated LCH, Laboratorio Caminos Santander (LCS) (one falling head permeameter) and saturated LCH tests. The results achieved were analyzed to describe the infiltration performance of the PC pavements tested. Finally, the correlation between the results obtained from on-site tests and laboratory scale devices was studied, providing the regression equations required to apply the infiltration models developed with easily measurable parameters. Consequently, the outputs of this research showed the suitability of the proposed methodology for assessing the infiltration behavior of PC pavements during storm events.

1. Introduction

Porous concrete (PC) pavements have been widely used as a surface layer in permeable pavement systems (PPS) [1,2], providing important benefits in terms of runoff attenuation, pollutant filtration, and Urban Heat Island (UHI) mitigation, among others [3,4,5,6]. PC is basically composed by a granular skeleton coated by a cementitious binder, sometimes including additives or polymers for improved strength characteristics. Water infiltration in PC pavements is produced by the water flow through the interconnected air voids of the porous matrix of the material, being influenced by the pore structure and geometry. Thus, fine aggregate materials are normally reduced, if not eliminated in order to maintain high air void contents, normally above 18–20%, for allowing water infiltration without compromising the required bearing capacity and durability to withstand traffic loads during a reasonable service life [7].

Porous pavement materials like PC can be conceptualized as porous materials, and generally follows the governing principles of infiltration in a porous media. The infiltration process of porous materials is governed by the Darcy Law, and can be furtherly examined by using Richards Equations, considered the governing equations of the infiltration process in a porous media [8,9]. The numerical solution of the Richards equation allows for a precisely quantified vertical percolation of water in a variety of conditions, but requires numerous measurements to adequately describe variations in materials properties [9]. Approximate physical models apply the physical principles governing infiltration for simplified boundary conditions. Other equations are empirical or semi-empirical, and use parameters obtained from measured infiltration data yielding satisfactory results in most applications [10].

Recently, there has been an increase on the search for precise and reliable methods for measuring the infiltration capacity on porous surfaces [1,3,11,12,13,14]. Different methods have been conceived to measure the infiltration capacity of PC pavements directly, such as single-ring and double-ring infiltrometers [12,15], rainfall simulators [1,3,16,17], and permeameters [11,12]. The results provided by permeability tests vary among the devices used. Some of them provide a permeability coefficient or infiltration capacity, while others focus on discharge times or runoff coefficients through which the infiltration capacity of the pavement is directly assessed. Falling head and constant head permeameters have been widely used in permeability measurements on PC pavements [11,12]. However, some studies have pointed out that the different apparatus and test procedures used might lead to different permeability values, so that the results obtained cannot be comparable to each other [11]. Furthermore, the coefficient of permeability measured by different tests is rather a qualitative value than a real quantification of the infiltration capacity of the pavement in on-site applications under real climatic conditions [18]. As water head increases, the flow through the porous matrix switches from laminar to transitional or turbulent, also increasing the resulting permeability coefficient obtained [18,19]. In fact, recent studies [19] showed that the higher the applied water head, the higher the permeability coefficient obtained for both constant and falling head methods, especially for the latter. Ranieri and others [18] found that ΔH values between 0.1 cm and 1 cm over a specimen surface in constant head permeameters lead to laminar flow through the specimen and are suitable for use in Darcy’s Law to obtain permeability values that correctly describe the performance of porous surfaces.

For managing stormwater runoff, PC pavements must provide the necessary infiltration capacity for managing rainfall events during their operational life, considering the runoff contribution from impervious surrounding areas. Reference standards such as the NCAT report 2000/01 [20,21] recommend that the minimum infiltration capacity of porous surfaces used in pavements should be higher than 100 m/day. Although the infiltration capacities of newly built PC pavements normally exceed this minimum level, clogging effects tend to reduce their infiltration rates throughout time [1,3]. Sediments deposited on the pavement and/or transported by the runoff that pass through the porous matrix during storm events progressively block its interconnected pores and, consequently, reduce the infiltration capacity of the PPS dramatically [22]. Usually, the clogging layer produced is located near the surface, mainly in the first 1.5 cm, with consolidation in the first 6–7 mm [23]. The sediment particle sizes, together with the average daily traffic, pavement age and nearness of vegetated areas are considered the main external factors that influence the clogging rate of PPS [24]. In addition, although PC pavements are commonly designed considering a constant infiltration rate during storm events, some authors suggested that their infiltration capacity is affected by external conditions like the degree of saturation of the pavement or rainfall intensity [25]. These findings are consistent with theories related to the infiltration behavior of porous materials like soils, which found a downward trend in measured infiltration capacities due to the progressive soil water uptake and the further increase in the soil saturation degree.

Under these circumstances, the aim of this paper was to study the infiltration behavior of PC pavements using different tests and devices in order to develop a methodology that enables describing, comparing, and predicting their infiltration capacity during storm events. To this end, three different permeability tests were conducted at the laboratory scale in newly built and clogged PC specimens. Hence, short-term and long-term infiltration tests were carried out using laboratory and on-site devices. Measured infiltration rates were modelled according to several empirical infiltration models to enable predicting the infiltration capacity evolution of PC during specific storm events in both clogging scenarios. Empirical relationships between on-site infiltration tests and laboratory measured parameters were also established to allow the estimation of the infiltration model parameters used from easy on-site infiltration measurements.

2. Materials and Methods

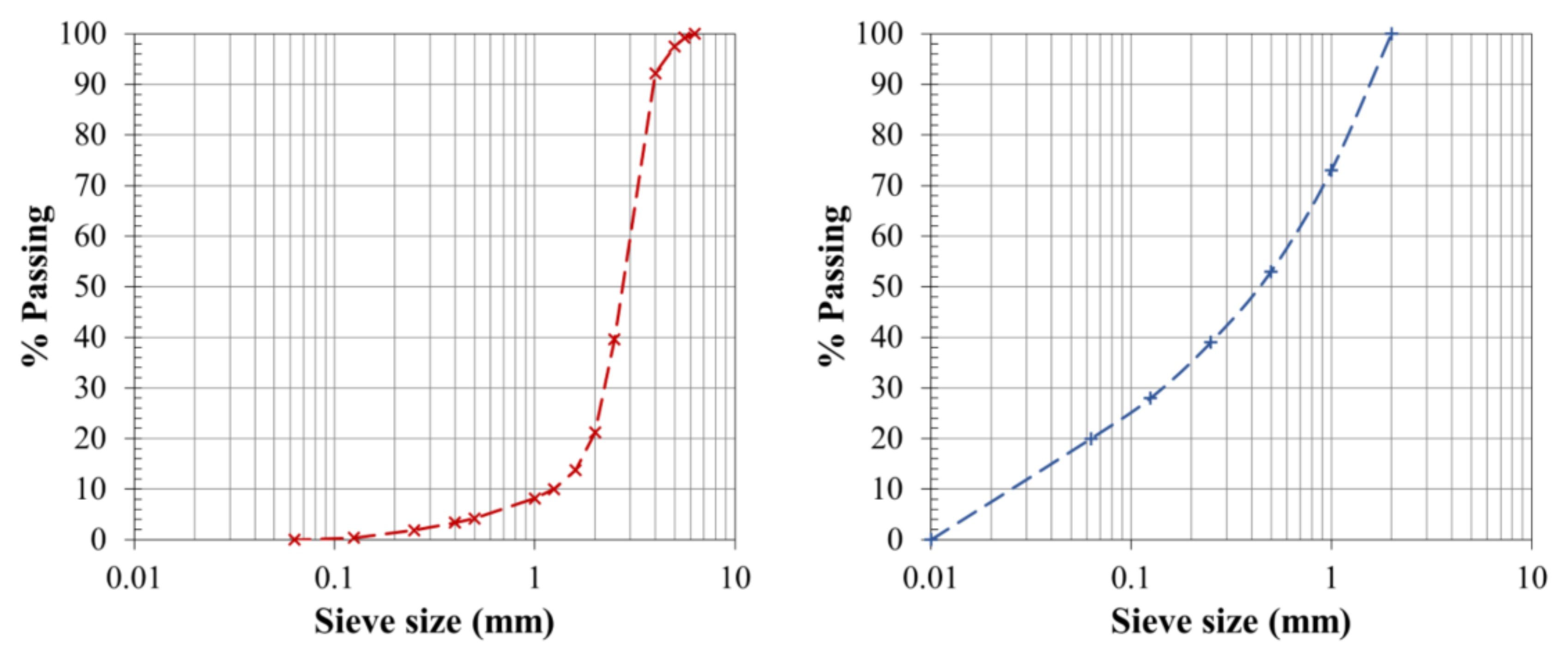
Eight PC specimens of 20 × 20 cm and 8 cm in height were tested in this research, named P1 to P8. The eight specimens were made with a PC mixture with an average air void content of 23 ± 1%, a water to cement ratio of 0.3 and using Portland cement and granitic aggregates (ρ = 2.69 T/m³) with the gradation shown in Figure 1a. The specimens were studied in newly built conditions and after clogging simulation at laboratory scale. A mix of limestone with 10% of replacement by sawdust in the fraction lower than 0.5 mm was used as clogging agent on the basis of previous research [1], using the gradation depicted in Figure 1b [3,26]. This sediment gradation has been used on the basis of various street sediments studies and looking for the maximum compactness of sediments in the range of the gradations observed according the Federal Highway Administration (FHWA) 0.45 power gradation curve as summarized in Andrés-Valeri and others [3].

Specimens were tested for newly built infiltration measurements according to the various tests described below. After that, they were clogged by applying 2000 g/m² of sediments over the wetted surfaces of the specimens and manually compacted by a steel roller according to previous studies [1,3,26]. This quantity of sediments can be estimated to be equivalent to 5 to 10 years of continuous use, considering a climate with 50% of dry days according to the results provided by Zafra and others [27]. After that, 1200 mm of rainfall were simulated over the specimens using a rainfall simulator with intensities ranging from 50 to 150 mm/h, resulting in a total of 4 wet–dry cycles.

Table 1. Characteristics of wet and dry cycles applied over the specimens in terms of rainfall intensity, and duration of each cycle.

Cycle	Characteristics of Wet–Dry Cycles (Rainfall Intensity and Duration)
Wet cycle	50 mm/h (1 h) + 100mm/h (1 h) + 150 mm/h (1 h)
Dry cycle	24 h

summarizes the applied cycles and in Figure 2 the used rainfall simulation set-up is shown. Rainfall simulations enabled both favoring the penetration of the sediments in the pore structure of the PC specimens and washing off the excess of particles over the specimens’ surface. Finally, the specimens were air-dried for one week prior to being tested for infiltration measurements in clogged conditions.

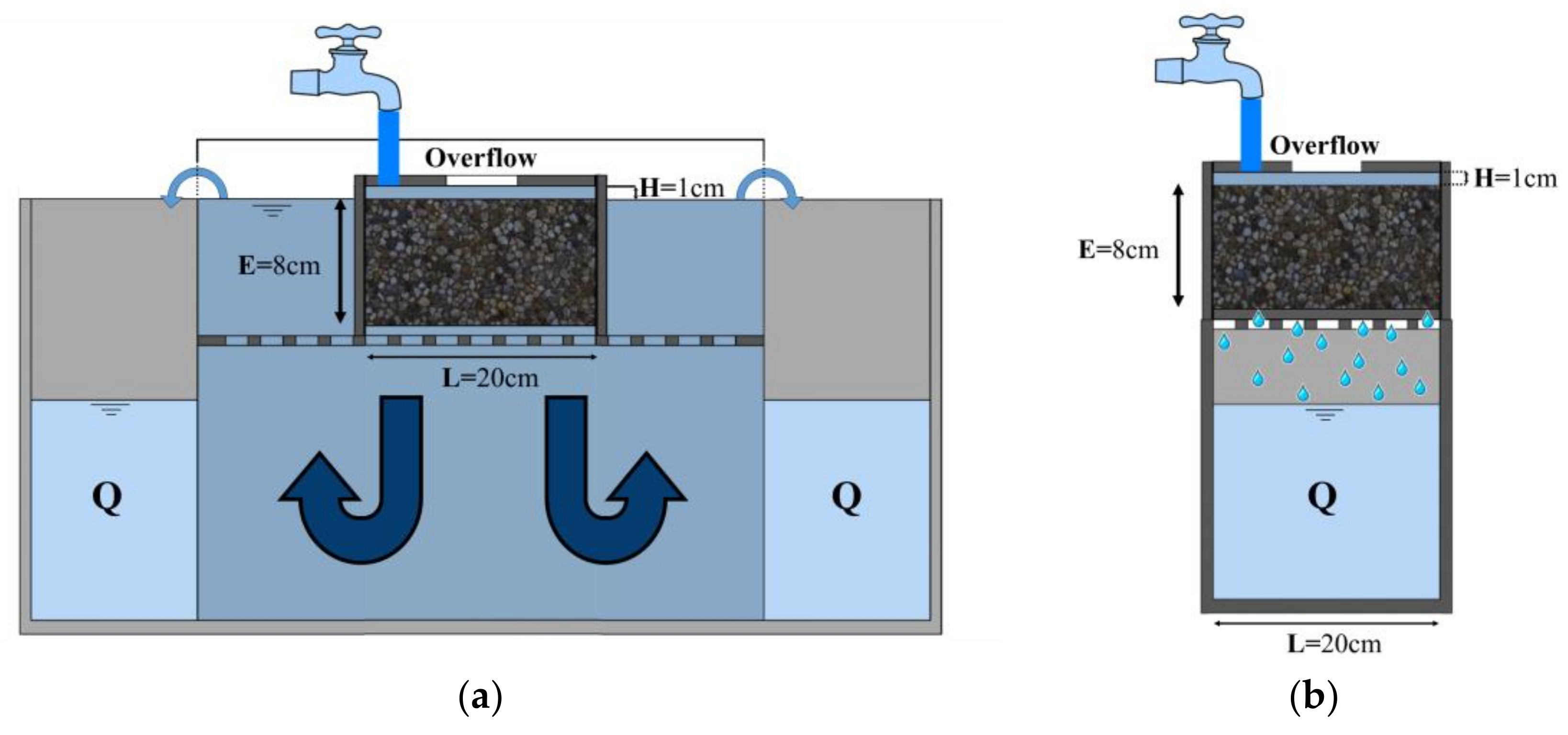
The infiltration capacity of the laboratory specimens was assessed using a Constant Head (CH) permeameter (Figure 3a). This device performance is based on the permeameter used in the European norm EN 12697-19 [28] for measuring vertical permeability in porous asphalt pavements, but adapted to prismatic specimens and modified to maintain the water head 1 cm over the pavements’ surface (low constant head—LCH). This value was established on the basis of previous studies [11,19] that suggested that this experimental setup can provide more accurate and suitable permeability values for porous pavement materials than the use of higher water heads as those reported in commonly used permeability standards for these materials.

The CH device was used for determining the saturated permeability (K_Sat) of the test specimens, submerging the specimens in water at 25 °C for 120 min prior to testing, and measuring infiltration rates three consecutive times per specimen. Then, the water volume (Q) infiltrated was converted into permeability (mm/s) through Equation (1).

$$K_{Sat}=\frac{Q·E}{L^2·H·t}$$

(1)

where E (mm) is the specimen height, L² the surface area (mm²), H the height of the water head (mm) and t the time (s) in which Q infiltrated through the specimen.

As for the unsaturated permeability test, base and sub-base layers were assumed to have greater infiltration capacities than the surface in common permeable pavements. This hypothesis enabled conceptualizing the infiltration process as a free discharge process. Consequently, the experimental setup previously described was modified to allow infiltrated water to freely discharge from the test specimens (Figure 3b). The test lasted 120 min, during which the volume of water infiltrated was measured every 5 min in order to evaluate the infiltration capacity evolution of the specimens over time. This capacity (f(t)) was directly obtained by calculating the amount of water infiltrated in each interval according to Equation (2).

$$f\left(t\right)=\frac{Q }{t ·L^2 }$$

(2)

where Q is the volume of the infiltrated water, t is the time needed for infiltrating water and L² the area of infiltration. The results achieved were mathematically modelled to maximize the fit with the measured data, in order to enable predicting the infiltration capacity of the studied PC material over time.

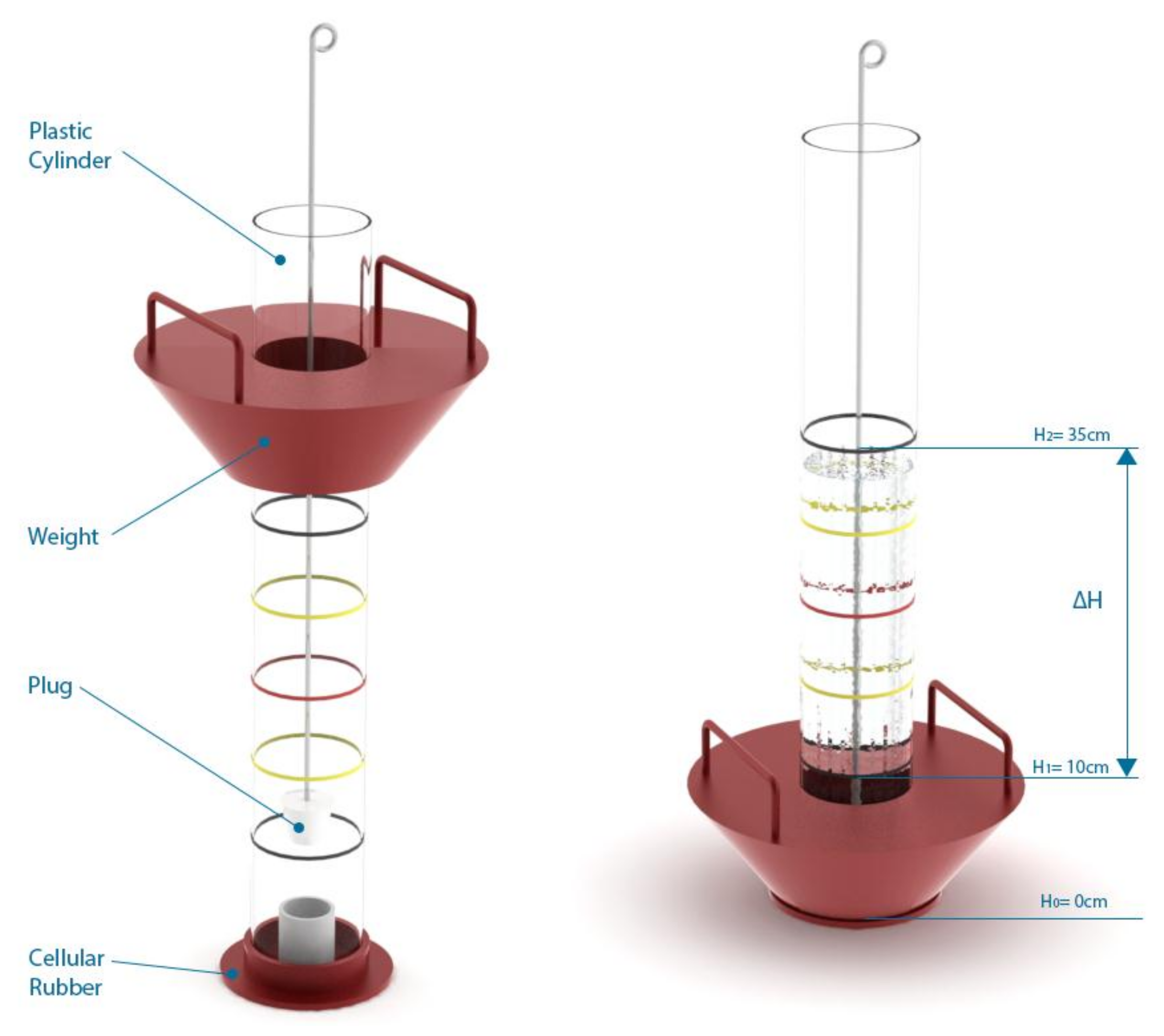
As a control experiment, the infiltration capacity of the tested PC specimens were also assessed through the Laboratorio Caminos Santander (LCS) permeameter, in order to evaluate its suitability for making predictions. The LCS device (Figure 4) is a falling head permeameter commonly used for on-site measurements of the drainage capacity of porous asphalt pavements according to the Spanish standard NLT 327/00 [29], being also similar to the permeameter included in the European norm EN 12697-40 [30].

The LCS device is basically composed by a cylindrical tube with a diameter of 94 mm and a rounded bottom hole of 30 mm of diameter with a plug. The test measures the time needed for infiltrating the amount of water contained in the device from a height of 35 cm until the level of 10 cm. The experimental procedure consists of repeating the test in 5 different points of the specimen surface, including two initial null-tests at each point for wetting the surface as suggested by NLT 327/00 [29] before doing the real measurements. The highest and lowest measured values in each specimen were discarded to reduce variability, such that the average time of discharge was obtained for each specimen from the three remaining tests. The results obtained with LCS permeameter were correlated with those achieved through the previous infiltration tests, in order to establish a useful relationship between on-site infiltration tests and laboratory measured infiltration rates.

3. Results and Discussion

Initial measurements of the infiltration capacity of the PC specimens were carried out at laboratory scale with the three different infiltration tests defined above, in newly built conditions and after being artificially clogged with sediments following the methodology described above. The results obtained for newly built and clogged specimens are summarized in

Table 2. Infiltration test results for clogged porous concrete (PC) specimens. Results are unsaturated infiltration rates at different times of the unsaturated constant head experiment and P1 through P8 indicate the tested specimens. The saturated value (K_Sat) indicates results from the saturated constant head experiment and the LCS discharge time and equivalent infiltration rate.

Infiltration Measurements	Units	P1	P2	P3	P4	P5	P6	P7	P8	Average
f0–5min	(mm/s)	1.25	1.93	1.17	2.58	3.07	2.36	2.33	1.89	2.07
f5–10min		1.01	1.54	0.96	2.18	2.70	2.10	2.05	1.64	1.77
f10–15min		0.81	1.29	0.83	1.76	2.27	1.78	1.76	1.42	1.49
f15–20min		0.70	1.10	0.70	1.43	1.84	1.45	1.51	1.23	1.24
f20–25min		0.60	0.95	0.61	1.15	1.52	1.21	1.29	1.07	1.05
f25–30min		0.53	0.83	0.53	0.97	1.29	0.99	1.11	0.93	0.90
f30–35min		0.47	0.73	0.46	0.82	1.11	0.80	0.94	0.82	0.77
f35–40min		0.43	0.68	0.40	0.71	0.97	0.67	0.77	0.70	0.67
f40–45min		0.39	0.62	0.36	0.63	0.87	0.58	0.71	0.65	0.60
f45–50min		0.36	0.57	0.32	0.54	0.78	0.50	0.62	0.57	0.53
f50–55min		0.34	0.50	0.29	0.50	0.71	0.43	0.56	0.52	0.48
f55–60min		0.32	0.48	0.26	0.44	0.65	0.38	0.50	0.48	0.44
f60–65min		0.30	0.46	0.25	0.42	0.62	0.35	0.45	0.44	0.41
f65–70min		0.29	0.42	0.22	0.38	0.57	0.32	0.41	0.41	0.38
f70–75min		0.28	0.39	0.20	0.37	0.55	0.29	0.39	0.39	0.36
f75–80min		0.26	0.38	0.18	0.35	0.56	0.28	0.34	0.35	0.34
f80–85min		0.25	0.35	0.17	0.33	0.52	0.25	0.32	0.32	0.31
f85–90min		0.24	0.32	0.17	0.32	0.50	0.24	0.31	0.32	0.30
f90–95min		0.22	0.33	0.15	0.30	0.49	0.23	0.28	0.31	0.29
f95–100min		0.23	0.31	0.15	0.29	0.48	0.23	0.28	0.29	0.28
f100–105min		0.23	0.31	0.14	0.29	0.46	0.21	0.26	0.29	0.27
f105–110min		0.23	0.31	0.13	0.28	0.44	0.21	0.24	0.28	0.26
f110–115min		0.22	0.30	0.12	0.28	0.42	0.21	0.25	0.28	0.26
f115–120min		0.22	0.29	0.11	0.27	0.42	0.21	0.23	0.26	0.25
KSat	(mm/s)	0.13	0.19	0.10	0.19	0.26	0.13	0.17	0.15	0.17
LCS Discharge Time	(s)	31.2	29.4	47.2	31.1	25.7	36.4	34.7	37.4	34.1
LCS Infiltration rate	(mm/s)	8.01	8.50	5.30	8.04	9.73	6.87	7.20	6.68	7.33

and

Table 3. Infiltration test results for clogged porous concrete (PC) specimens. Results are unsaturated infiltration rates at different times of the unsaturated constant head experiment and P1 through P8 indicate the tested specimens. The saturated value (K_Sat) indicates results from the saturated constant head experiment and the LCS discharge time and equivalent infiltration rate.

Infiltration Measurements	Units	P1	P2	P3	P4	P5	P6	P7	P8	Average
f0–5min	(mm/s)	0.21	0.34	0.16	0.30	0.37	0.60	0.20	0.38	0.32
f5–10min		0.18	0.30	0.14	0.29	0.34	0.53	0.19	0.38	0.29
f10–15min		0.16	0.26	0.11	0.26	0.31	0.47	0.19	0.38	0.27
f15–20min		0.14	0.22	0.12	0.23	0.30	0.42	0.18	0.34	0.24
f20–25min		0.12	0.20	0.11	0.22	0.28	0.38	0.17	0.28	0.22
f25–30min		0.11	0.15	0.10	0.19	0.27	0.34	0.16	0.22	0.19
f30–35min		0.10	0.16	0.09	0.17	0.27	0.28	0.15	0.22	0.18
f35–40min		0.09	0.15	0.08	0.16	0.27	0.27	0.15	0.21	0.17
f40–45min		0.08	0.13	0.08	0.16	0.25	0.25	0.14	0.20	0.16
f45–50min		0.08	0.12	0.08	0.14	0.25	0.23	0.13	0.19	0.15
f50–55min		0.08	0.11	0.07	0.14	0.24	0.20	0.13	0.18	0.15
f55–60min		0.08	0.11	0.06	0.14	0.23	0.19	0.13	0.17	0.14
f60–65min		0.07	0.10	0.07	0.13	0.23	0.19	0.12	0.15	0.13
f65–70min		0.07	0.10	0.06	0.13	0.22	0.18	0.11	0.15	0.13
f70–75min		0.07	0.09	0.06	0.12	0.21	0.17	0.11	0.14	0.12
f75–80min		0.07	0.10	0.05	0.11	0.20	0.15	0.11	0.15	0.12
f80–85min		0.06	0.10	0.05	0.11	0.20	0.14	0.10	0.15	0.11
f85–90min		0.06	0.10	0.05	0.12	0.19	0.14	0.10	0.15	0.11
f90–95min		0.06	0.10	0.05	0.10	0.19	0.13	0.10	0.14	0.11
f95–100min		0.05	0.09	0.05	0.11	0.18	0.13	0.10	0.15	0.11
f100–105min		0.06	0.09	0.05	0.11	0.19	0.12	0.10	0.14	0.11
f105–110min		0.05	0.09	0.04	0.11	0.18	0.12	0.10	0.14	0.10
f110–115min		0.05	0.09	0.04	0.11	0.18	0.12	0.10	0.14	0.10
f115–120min		0.04	0.09	0.04	0.11	0.18	0.12	0.10	0.13	0.10
KSat	(mm/s)	0.03	0.09	0.03	0.10	0.17	0.12	0.10	0.12	0.10
LCS Discharge Time	(s)	204.0	158.5	223.7	199.4	116.6	110.0	170.5	135.7	164.8
LCS Infiltration Rate	(mm/s)	1.22	1.58	1.12	1.25	2.14	2.27	1.47	1.84	1.52

, respectively, which report the obtained results for each infiltration test.

The initial infiltration of PC specimens was near 2 mm/s, which is in the range of permeability values reported in previous literature [31,32]. However, the unsaturated infiltration capacity measured in the specimens showed a constant downward tendency with time in all cases. After 120 min of testing, the results indicated that the infiltration capacity of the specimens decayed around one order of magnitude in relation to the initial value. A similar phenomenon is seen in soils and other porous media research, where infiltration rates move towards a steady value over time and is due to increasing saturation. Despite being in the same order of magnitude as saturated permeability (K_Sat), the final value measured through the unsaturated infiltration capacity test (f_115–120) was nearly double the saturated test. This discrepancy has also been seen in soil infiltration research, where a factor ranging from 0.3 [33,34] to 0.67 [35] was applied to relate saturated hydraulic conductivity to the Philip steady infiltration parameter [36]. These results indicated that the infiltration capacity of PC materials was about 8–10 times higher and more than the double than K_Sat for storm events with a duration of 5–15 min and less than 2 h, respectively. Moreover, the discharge time measured with the LCS permeameter proved to be inversely correlated to both initial and final unsaturated permeability and saturated permeability, indicating a logical relationship between both variables.

The average initial infiltration capacity in clogged specimens was found to be 74.5% lower than in newly built specimens. These results were in agreement with those observed in previous works with similar sediment dosages [1,3,24] and gradation [3,24], highlighting the impact of clogging in the formation of runoff at very early stages of the storm event. Saturated permeability and the last results in unsaturated tests (f_115–120min) were very similar and less sensitive to clogging, resulting in a reduction of 41.2% and 60% in relation to the newly built scenario, respectively. These results indicated that the higher the degree of saturation of the specimens, the lower their sensitivity to clogging effects in permeability tests. Since water flows freely through the porous matrix in unsaturated conditions, the effect of clogging on infiltration rates could be more influential in these cases than in saturated scenarios, where water may provide resistance to infiltration. As the level of saturation of the specimens increases, some of the air voids were filled with water, and since the amount of water applied over the specimens exceed their infiltration capacity, the trapped water in the air voids reduce the water infiltration velocity, and hence the infiltration rate. These inferences also suggested that clogging effects are less important in long rainfall conditions than in short events.

The downward tendency of the unsaturated test results with time resembled an exponential function decay, similarly to what occurs in soils. Several infiltration models have been assessed for describing the observed tendency on the basis of the measured PC parameters. Three traditionally used empirical models were assessed: the Horton [37], Kostiakov [38], and Mezencev [39] infiltration models. Additionally, the Philips [40] and Green and Ampt [41] physical infiltration models were also assessed for describing the observed tendency, even though the boundary conditions of the performed test limited their physical significance.

Table 4. Infiltration models used in the research.

Infiltration Model	Equation
Horton’s Equation	$f\left(t\right)=f_C+\left(f_0-f_C\right)·e^{-k·t}$	(3)
Kostiakov’s Equation	$f\left(t\right)=\alpha ·t^{-\beta }$	(4)
Mezencev’s Equation	$f\left(t\right)=f_C+\alpha ·t^{-\beta }$	(5)
Philips Equation	$f\left(t\right)=\frac{S}{2}·t^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+f_c$	(6)
Green–Ampt Equation	$f\left(t\right)=K_{sat}·\left(1+\frac{\left|\psi \right|·\Delta \theta }{F}\right)$	(7)

summarized the infiltration models analyzed.

In equations showed in Table 4, f₀ is the initial infiltration rate, fc the ultimate or steady state infiltration rate, t is the time elapsed since the beginning of the rainfall event, K_Sat is the saturated permeability, ψ is the matric pressure, Δθ the effective porosity, F the cumulated infiltration, S the sorptivity, α and β are constants related to the material characteristics and k is the so called constant of decay, also dependent of the material. The regression analyses were performed by fixing f_c = K_Sat and fitting the infiltration equations to the measured data by iterating the material-related constants of each equation (k, α, β, S and ψ) as well as f₀ until maximizing the determination coefficients of each model. 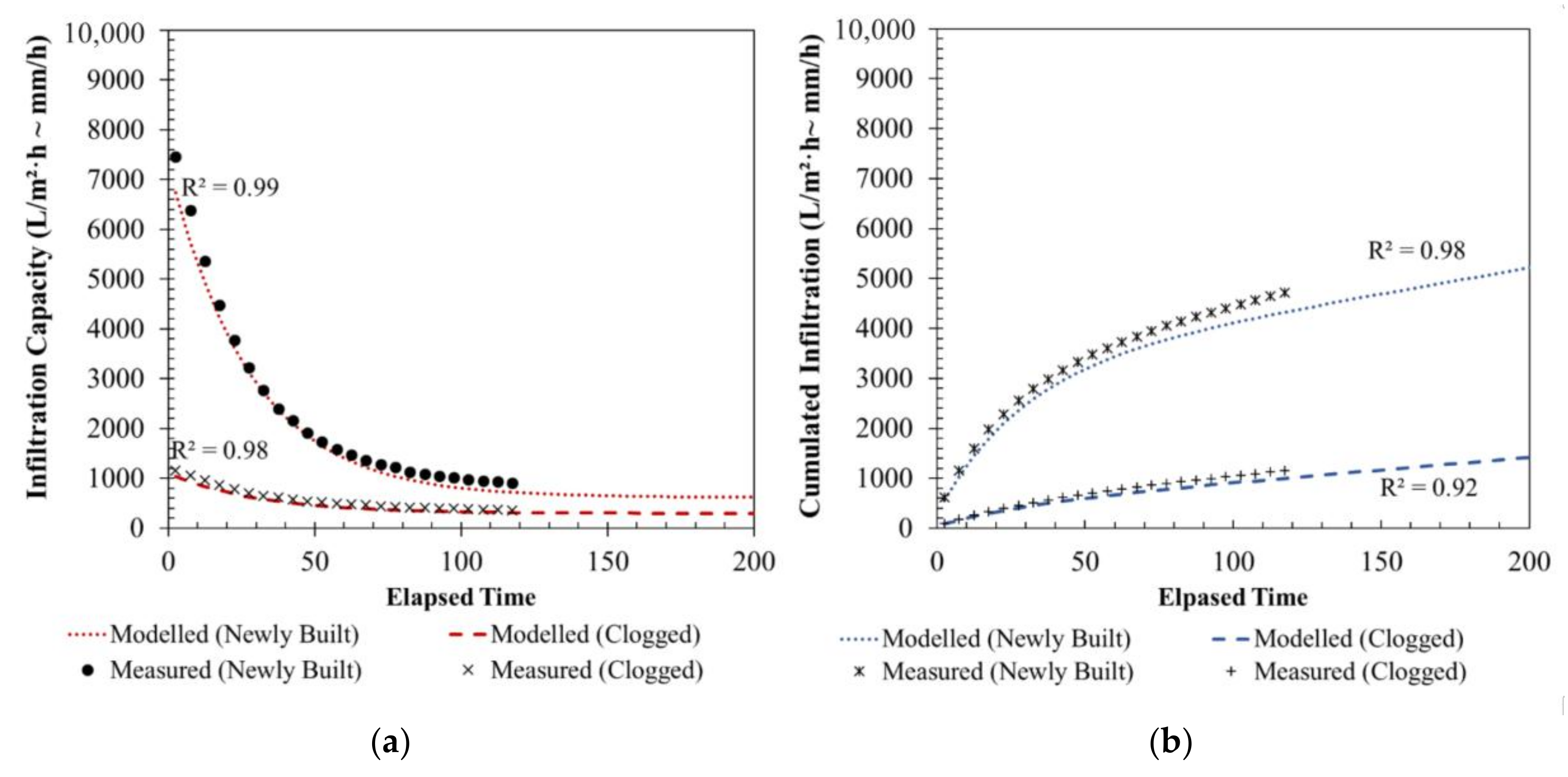The resulting infiltration models, their parameters and the fit to measured data are shown in Figure 5.

The obtained results showed that the Horton infiltration model (Equation (3)) provided the best fit to the measured infiltration rate. Modelled infiltration rates over time in unsaturated LCH permeability tests provided an excellent fit to the measured data, reaching coefficients of determination higher than 0.99 for both new and clogged scenarios. Similar values were also obtained for cumulated infiltration, indicating that the proposed model can describe the infiltration capacity evolution of PC pavements with high accuracy. The decay constant of the modelled infiltration capacity (k) was reduced by the clogging effects, as a consequence of the higher reduction in initial infiltration rates in relation to their ultimate values and saturated permeability measurements. According to the proposed model, the average infiltration rate decays after 5 to 6 h of testing from initial values of 7991 mm/h to the ultimate values defined by the measured K_Sat.

In order to evaluate the hydrological response of the tested PC materials under steady-state extreme rainfall events, a set of performance graphs was developed and are showed in Figure 6. The graphs were developed according to the modelled infiltration rates, showing the estimated percentage of runoff and the percentage of cumulated runoff for various stationary rainfall intensities represented by the different lines in the graph. Additionally, the rain intensity related to some of the lines have been also directly plotted in order to easily use the proposed graphs. In order to estimate the percentage of runoff produced and the cumulated runoff, the averaged infiltration rates of the tested specimens were directly compared with steady-state rainfall events for different durations in 5 min intervals. A Semi-logarithmic horizontal axis was used to better visualize short events, where higher variation in infiltration rates was found. Although the infiltration rates measured in the tested materials allowed managing extremely high rainfall intensities in relation to the magnitude of natural storm events, the performance graphs shown in Figure 6 can also consider runoff received from the surrounding areas. Furthermore, this value might be estimated even if runoff contribution is variable over time by determining the equivalent rainfall intensity (I_eq) through Equation (8).

$$I_{eq}=I\times \left(1+\frac{A_{imp}\times F}{A_{per}}\right)$$

(8)

where I is the rainfall intensity, A_imp is the area draining to the PC, which can include pervious or impervious surfaces, F is the weighted runoff coefficient, according to the Rational method (0.1 to 0.95 depending on the land use, soil type and slope) and A_per is the PC area. For using the graphs shown in Figure 6 it was only necessary to enter with a defined rain duration in order to obtain the amount of instantaneous runoff and the cumulated runoff produced depending on the rain intensity. On the other hand, it was also possible to directly enter with a rain intensity and assess for each duration the runoff and cumulated runoff produced for a storm event.

Considering the performance graphs obtained for the used specimens, the newly built PC tested on this research was found to manage equivalent rainfall intensities higher than 7000 mm/h without producing runoff for very short storm events. As the duration of the event increases, the infiltration rate decreases, which in turn results in an increase in the amount of runoff produced for a stationary rainfall event. For instance, no runoff would be expected for a short storm event, resulting in an equivalent rainfall intensity of 4000 mm/h. However, increased amounts of runoff are predicted for durations higher than 25 min, so that near 70% of the cumulated equivalent rainfall height would be transformed into runoff at the end of a theoretical storm event of 250 min, while the instantaneously produced runoff would be near to 85% at the end of the storm. The analysis of the clogged specimens revealed that their infiltration capacity for short events was dramatically reduced after clogging, so that an equivalent rainfall intensity of 1200 mm/h produced runoff from the beginning of the storm event, resulting in more than 60% of cumulated runoff production after 250 min of continuous storm. A similar event in newly built conditions only produced runoff after 80 min of continuous rainfall, resulting in about 30% of total cumulated runoff after 250 min.

Furthermore, the graphs shown in Figure 6 emerged as an effective way for comparing the infiltration performance of porous pavement materials such as PC, as well as for predicting and evaluating their infiltration behavior over time under specific storm events, including clogging conditions. Thus, this methodology is proposed as an easy-to-use approach for characterizing PC materials, providing more useful information to practitioners than the representation of permeability.

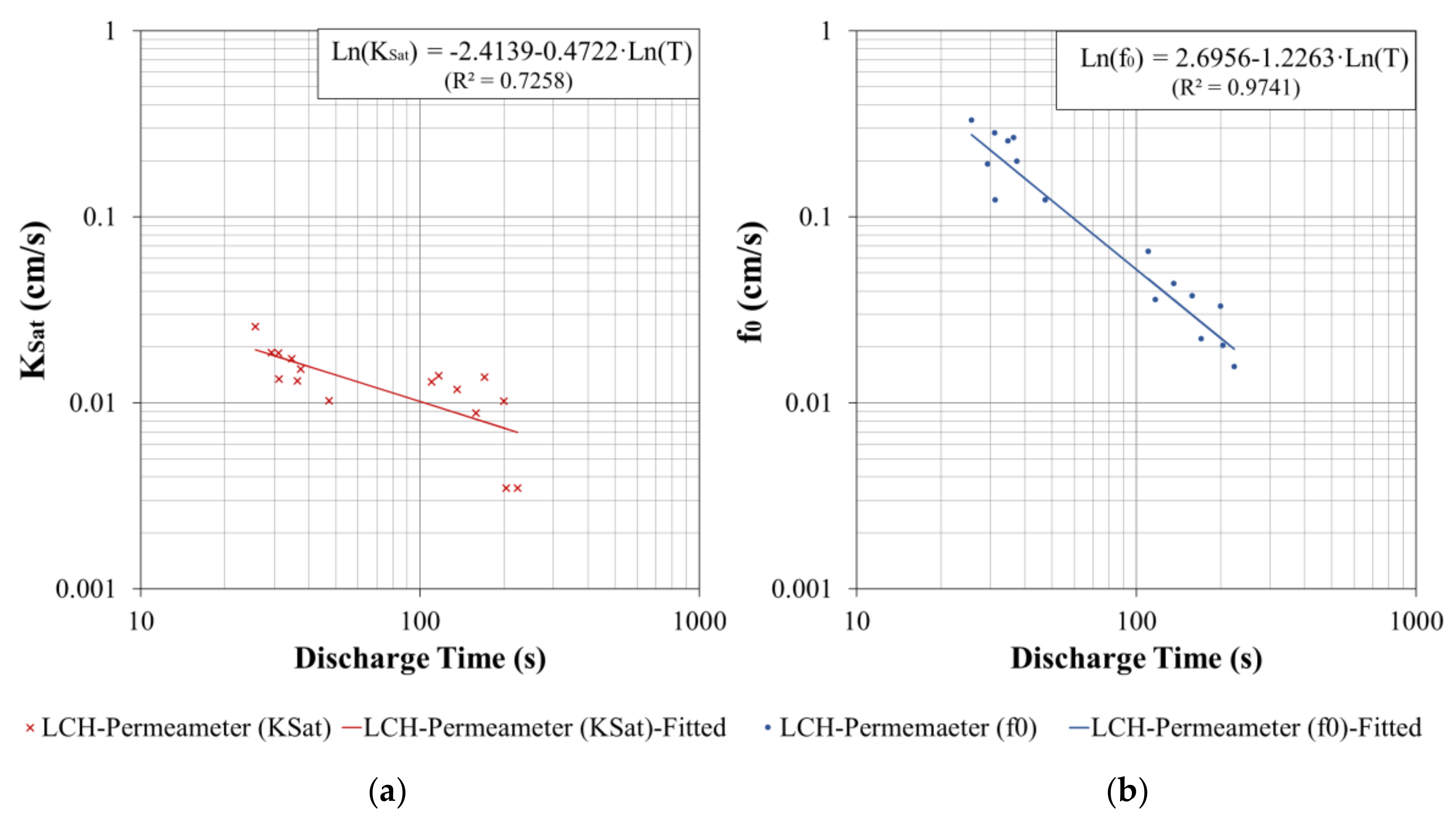
In an attempt to extend the scope of the research from laboratory to on-site tests, a correlation study was developed to compare the results achieved through the LCS permeameter and those obtained using unsaturated and saturated LCH permeability tests. These analyses revealed high and moderate significant Pearson linear correlations (Sig < 0.05) of LCS results with initial and saturated permeability values, showing correlation coefficients (R) of −0.854 and −0.767 respectively. It should be noted that R ranges between −1 and 1, where values near to 0 indicates no correlation, while values of 1 and −1 indicate a total linear correlation, direct or inverse respectively. Since the LCS permeameter measured the time of discharge in very similar conditions than the unsaturated permeability test, the initial infiltration rates measured by the unsaturated permeability test reached higher correlation than that associated with the saturated permeability test. Subsequent regression analyses showed that the best fit was reached by transforming the measured infiltration rates at laboratory scale and the time of discharge measured with LCS permeameter using a logarithmic scale. According to this analysis, regression models between time of discharge, initial infiltration rates and saturated permeability values were built as shown in Figure 7a,b.

To assess the suitability of using LCS results for predicting the infiltration capacity of the tested PC specimens, the regression equations depicted in Figure 7 were applied to the times of discharge shown in Table 2 and Table 3. The values of f₀ and K_Sat obtained were used in the infiltration models developed in Figure 5, in order to evaluate the precision when modelling the infiltration evolution over time on the basis of on-site drainability tests like the LCS. The infiltration rates obtained were further compared to measured data as illustrated in order to assess the precision of the modelled infiltration using LCS results.

Modelled infiltration rates based on the results of the LCS drainability test showed an excellent fit with measured data, reaching coefficients of determination higher than 0.98 in both scenarios, with slightly better values for newly built specimens. Moreover, cumulated runoff also proved to be well represented by the regression models in both cases (R² > 0.92), again with a better fit for the newly built specimens as showed in Figure 8. These results demonstrated that the combination of the infiltration model based on laboratory-scale infiltration tests with the estimation of the main parameters from LCS drainability tests can provide an accurate description of the infiltration rate evolution of PC materials over time during stationary storm events. Furthermore, once the materials have been characterized at laboratory scale and the fixed terms of the model have been obtained, the performance graphs developed in Figure 6 can be adequately replicated considering only LCS test results.

4. Conclusions

The infiltration behavior of PC specimens was assessed through three different tests: saturated and unsaturated LCH permeability tests, and LCS on-site drainability test. The results of these tests were used for developing a reasonably simple methodology that can help to evaluate, describe, and compare the infiltration capacity of porous pavements.

Initial infiltration rates measured in unsaturated conditions were near to ten times higher than the values corresponding to saturated permeability conditions (K_Sat), indicating that the infiltration capacity of the tested PC materials could be more than two times higher than K_Sat in storm events with durations shorter than 120 min.

Clogging effects proved to be more influential in unsaturated conditions than in saturated tests, producing average reductions in initial and final infiltration rates of 75% and 42%, respectively. In fact, the reduction in infiltration capacity due to clogging decreased as the unsaturated infiltration test progressed, suggesting a relationship between the sensitivity to clogging and the degree of saturation in which the test was performed.

Infiltration rates of PC specimens measured in unsaturated conditions were adequately modelled by an infiltration approach based on the Horton equation in both scenarios, reaching coefficients of determination close to 0.99. Hence, the proposed approach was based on developing initial laboratory scale infiltration tests to specific materials in various clogging scenarios for obtaining infiltration model parameters. The application of these models on the basis of on-site measurements with the LCS permeameter demonstrated to adequately describe the infiltration behavior of the tested PC materials.

The time of discharge measured with the LCS drainability test was found to be correlated with both laboratory-scale infiltration tests, however, a better fit was observed when considering initial unsaturated permeability values (R² = 0.97), being increasingly reduced as the test progressed until the minimum fit achieved under saturated permeability test (R² = 0.73).

The infiltration model developed for predicting the infiltration rate evolution over time proved to be applicable on the basis of the LCS results with precision, providing an easy and simple way for assessing the infiltration of PC pavements.

Further research is required to extend the proposed methodology to more clogging levels and types of permeable pavement systems in order to evaluate the evolution of the model parameters and develop an easy-to-use tool to evaluate maintenance needs for particular surface materials under specific climate conditions. Additional research fields include the study of the materials response under non-stationary rainfall events, including more variables to the analysis like rainfall abstractions or surface slope using stormwater computer models.