Tracers Reveal Recharge Elevations, Groundwater Flow Paths and Travel Times on Mount Shasta, California
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Collection and Data Reduction
2.2. Spatial Analysis
2.3. Flow Path Analysis
3. Results
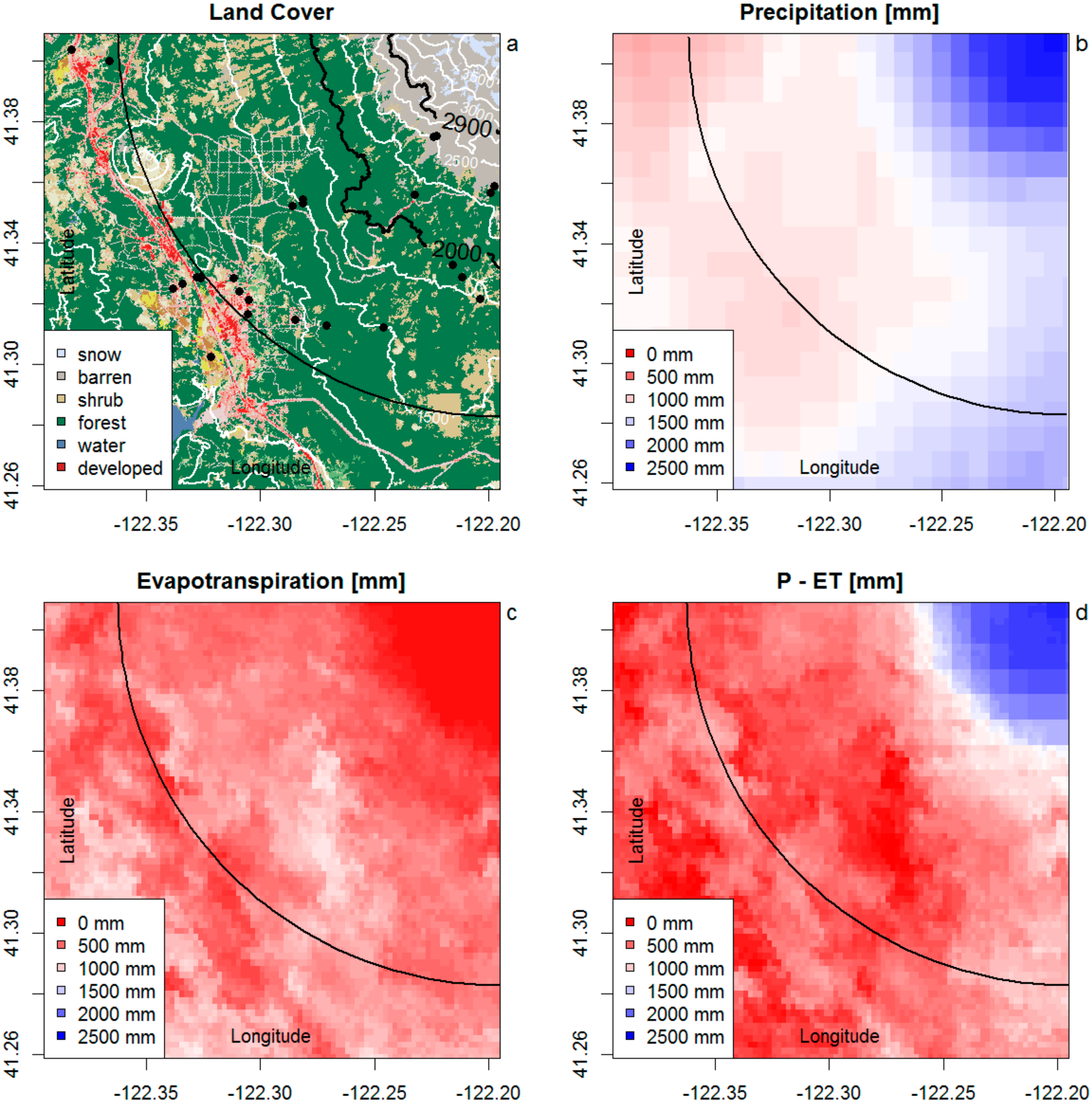
3.1. Recharge Source Area
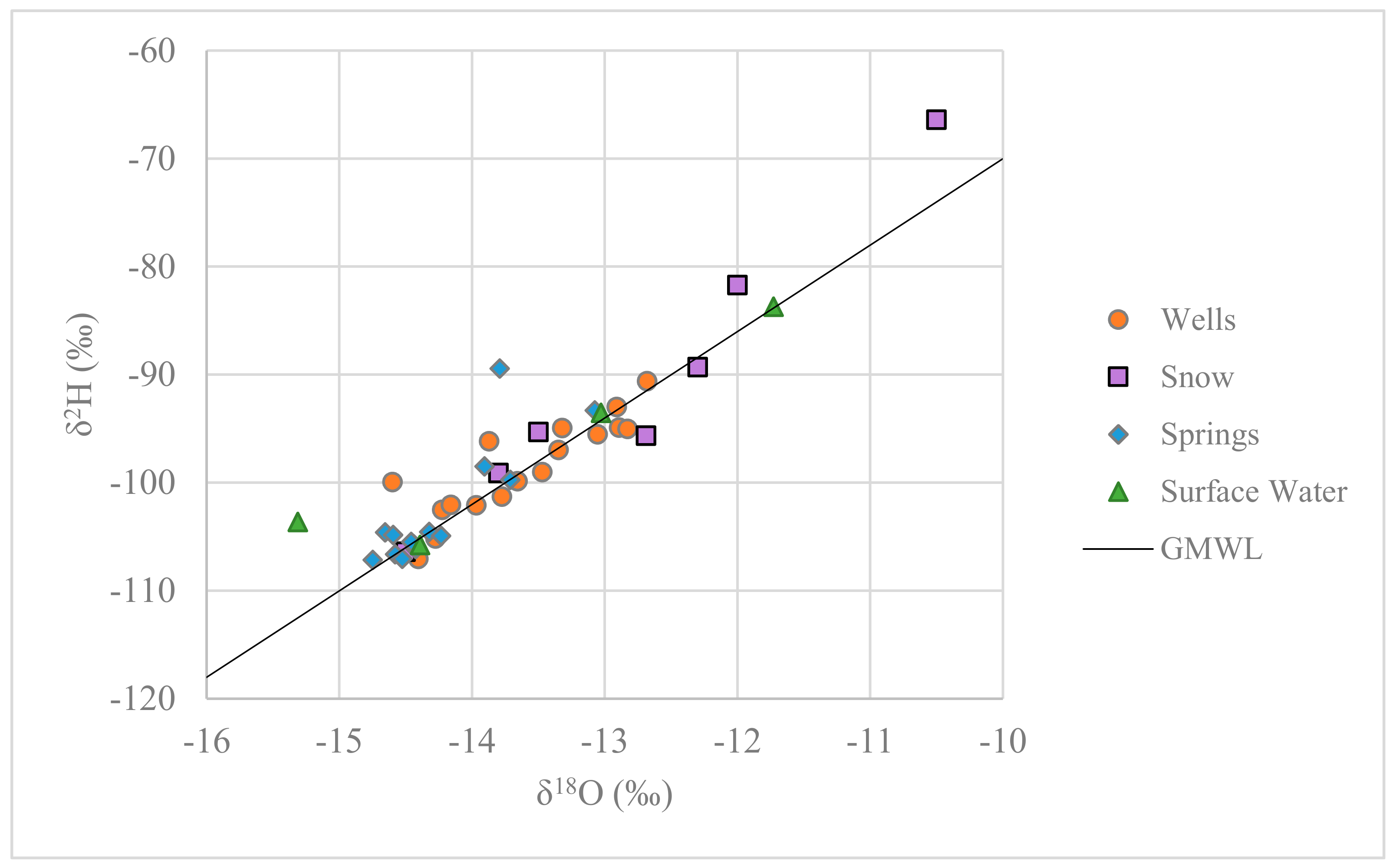
3.1.1. Stable Isotopes of Water
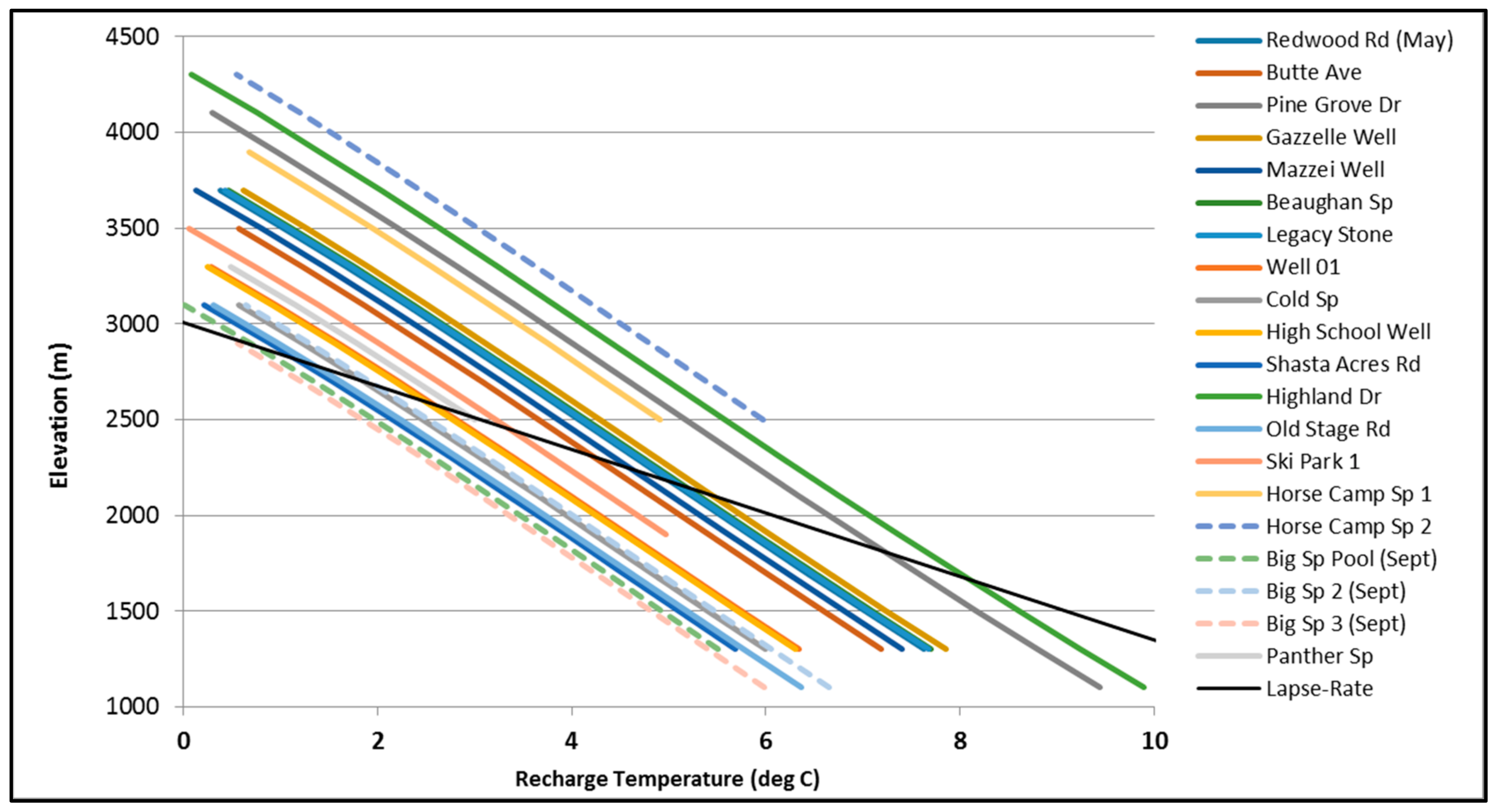
3.1.2. Noble Gas Recharge Conditions
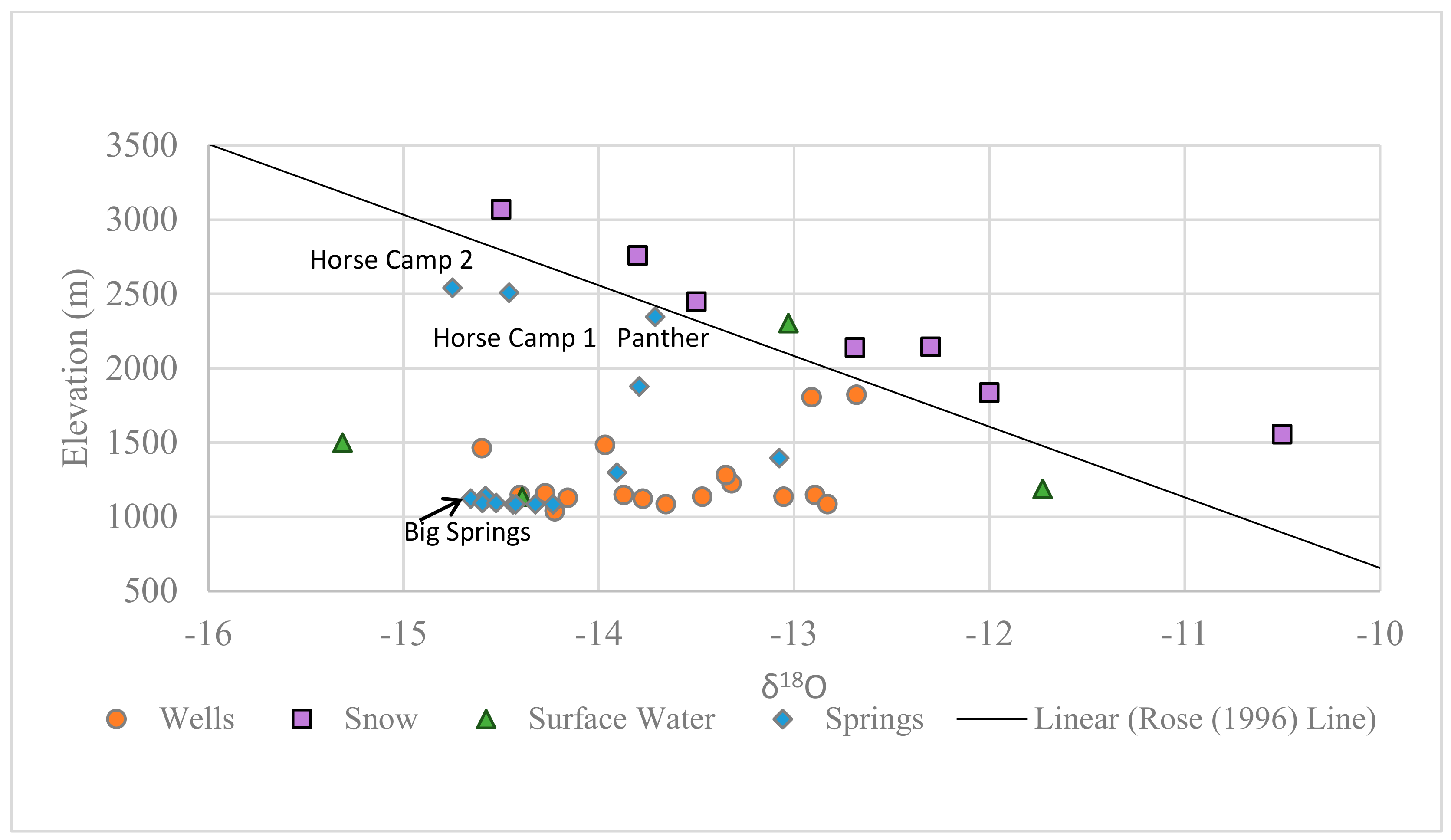
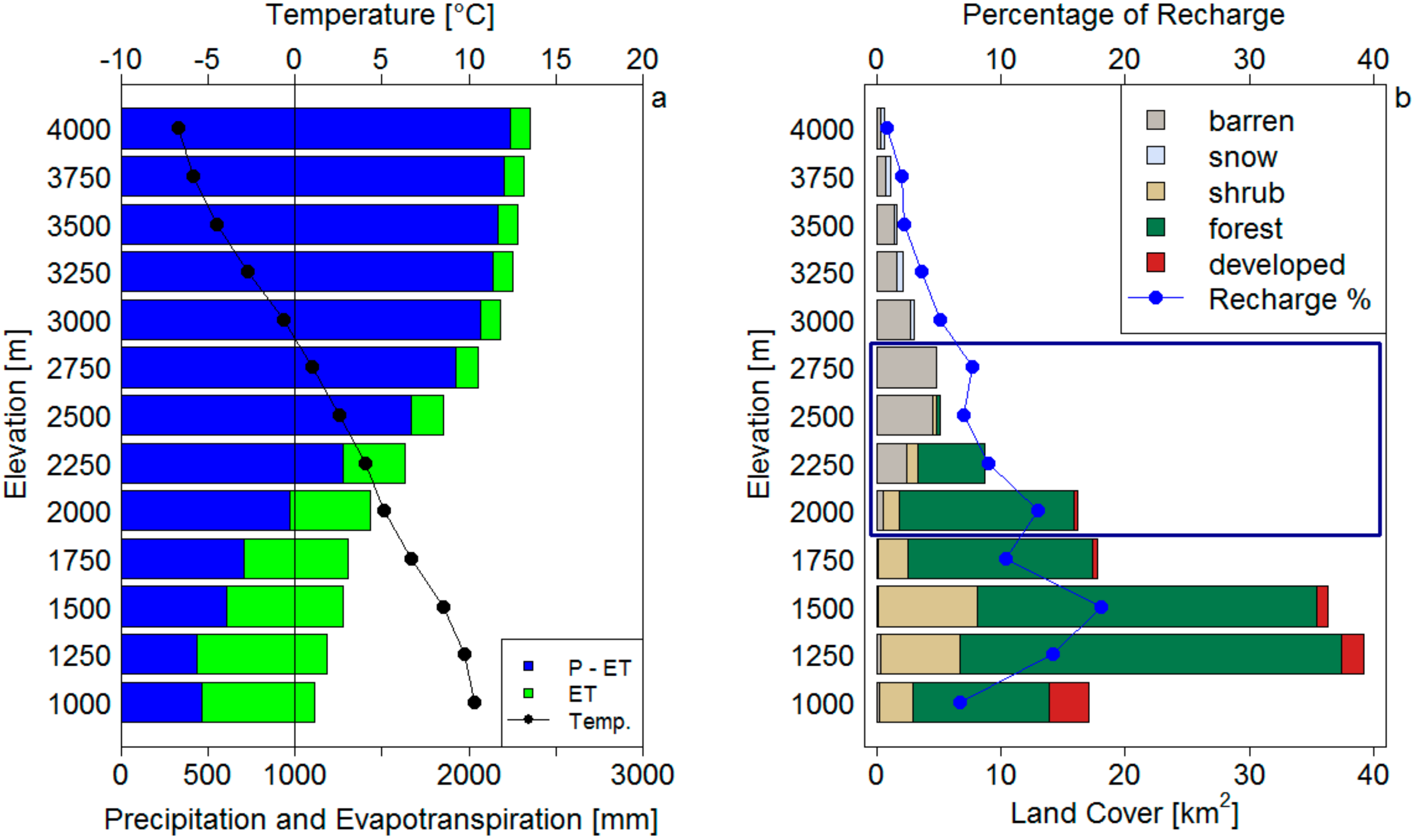
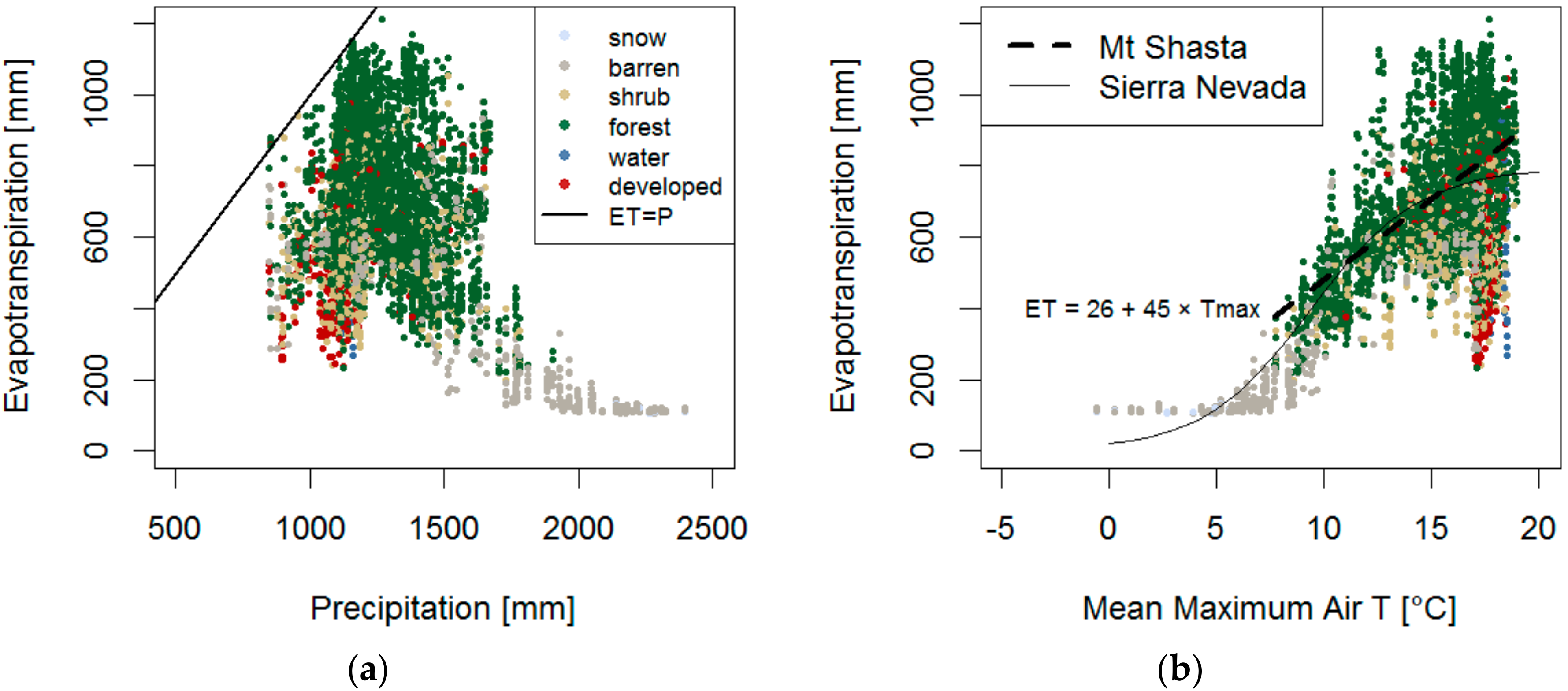
3.1.3. Spatial Analysis
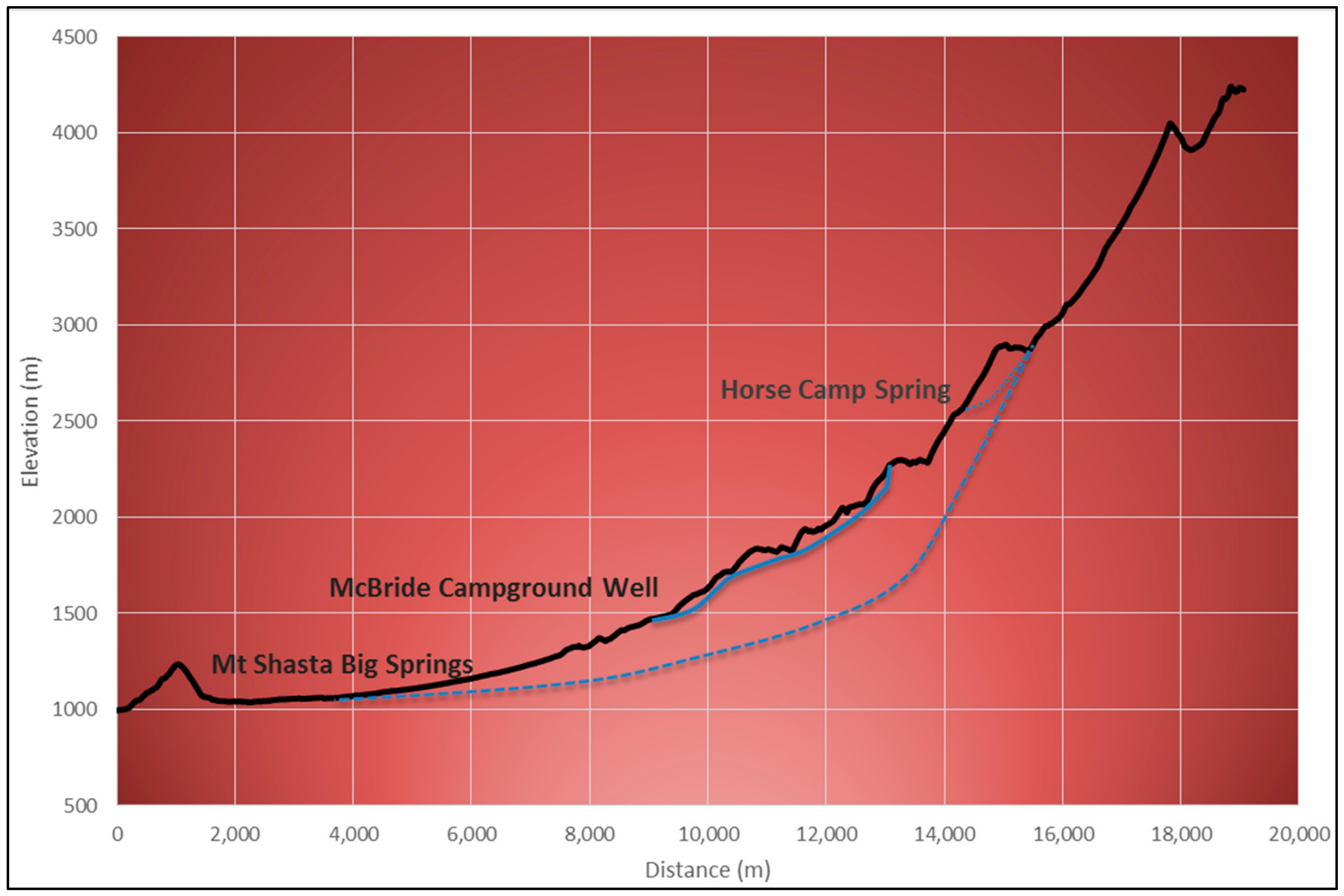
3.2. Groundwater Flow Paths
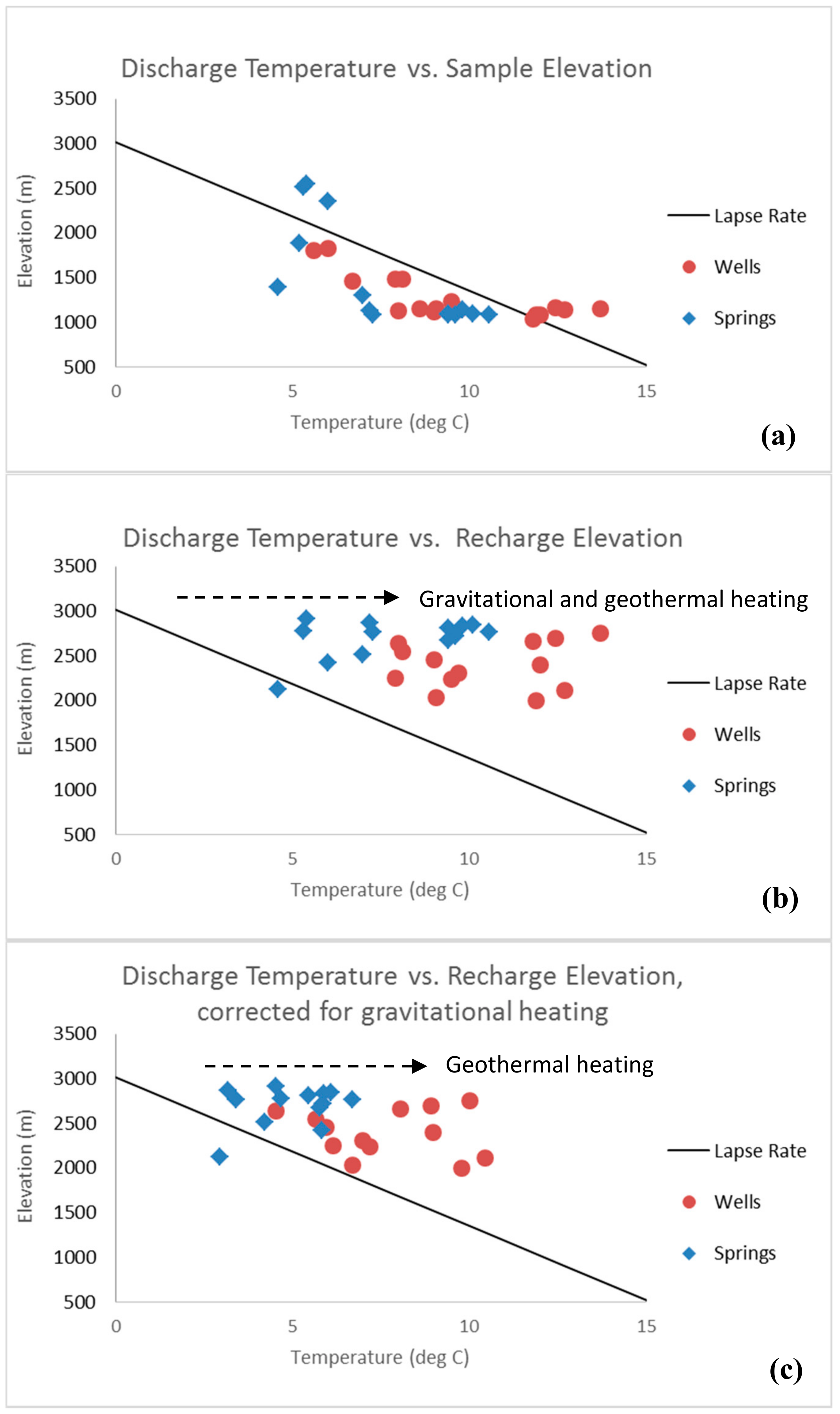
3.2.1. Temperature Changes between Recharge and Discharge
3.2.2. Groundwater Travel Times
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Data Tables
| Site Name | Sample Date | Sample Time | Sample Type | Elevation (m) | GPS Latitude (Decimal °N) | GPS Longitude (Decimal °W) | Field Temp (°C) | Field Conductivity (uS/cm) | Field pH | Field DO (mg/L) | Field ORP (mV) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Old Stage Rd | 20150501 | 1650 | Domestic | 1036 | 41.3025 | −122.3219 | 11.8 | 121.6 | 7.22 | 9.5 | −12.6 |
| Big Springs Main | 20150428 | 1400 | Spring | 1085 | 41.3287 | −122.3265 | 7.3 | 166 | 6.5 | 12.3 | −55.2 |
| Big Springs B | 20150428 | 1630 | Spring | 1085 | 41.3287 | −122.3265 | 10.6 | 218 | NM | 11.7 | −27.2 |
| Big Springs C | 20150428 | 1645 | Spring | 1085 | 41.3287 | −122.3265 | 9.6 | 146 | NM | 11.4 | −23.2 |
| Big Springs D | 20150428 | 1725 | Spring | 1085 | 41.3287 | −122.3265 | 9.4 | 146 | NM | 11.0 | −1.7 |
| Big Springs 2 | 20150918 | 1000 | Spring | 1094 | 41.3290 | −122.3281 | 10.1 | 142.5 | NM | 4.1 | NM |
| Big Springs 3 | 20150918 | 1025 | Spring | 1094 | 41.3290 | −122.3281 | 9.4 | 131.4 | NM | 9.0 | NM |
| Big Springs Pool | 20150918 | 945 | Spring | 1123 | 41.3287 | −122.3264 | 7.2 | 88 | NM | 10.3 | NM |
| Pine Grove Dr | 20150428 | 1810 | Domestic | 1085 | 41.3267 | −122.3345 | 11.9 | 25.3 | NM | 10.2 | 1.2 |
| Highland Drive | 20150501 | 1540 | Domestic | 1085 | 41.3250 | −122.3386 | 12.0 | 162.8 | 6.8 | 8.3 | 11.4 |
| Mt Shasta Well 01 | 20150501 | 830 | Public Supply | 1122 | 41.3167 | −122.3058 | 9.0 | 96.21 | 6.98 | 7.7 | 1.3 |
| Mt Shasta High School Well | 20150501 | 1500 | Public Supply | 1128 | 41.3214 | −122.3053 | 8.0 | 81.4 | 7.2 | NM | 2.5 |
| Butte Ave | 20150428 | 1100 | Domestic | 1134 | 41.3243 | −122.3093 | 9.7 | 80 | NM | 14.0 | NM |
| Gazelle Well | 20150429 | 1340 | Public Supply | 1134 | 41.4038 | −122.3831 | 12.7 | 109 | NM | 11.4 | 11.4 |
| Beaughan Springs | 20150430 | 1000 | Spring | 1140 | 41.4207 | −122.3558 | 9.8 | 101.7 | 6.94 | 9.7 | NM |
| Redwood Rd | 20150428 | 1025 | Domestic | 1146 | 41.3284 | −122.3118 | 9.1 | 87 | 7.34 | 2.1 | −53.7 |
| Redwood Rd | 20150917 | 1445 | Domestic | 1146 | 41.3284 | −122.3118 | 8.6 | 10.16 | 7.01 | 11.0 | 5.1 |
| Legacy Stone Property | 20150430 | 1500 | Domestic | 1146 | 41.4220 | −122.3523 | 13.7 | 152.5 | 6.9 | 9.4 | 5.6 |
| Mazzei Well | 20150429 | 1410 | Public Supply | 1158 | 41.4001 | −122.3665 | 12.4 | 159 | NM | 8.9 | 41 |
| Shasta Acres Rd | 20150501 | 1430 | Domestic | 1225 | 41.3147 | −122.2847 | 9.5 | 87.22 | 7 | 9.7 | 0.2 |
| Mt Shasta Cold Spring | 20150501 | 1100 | Spring | 1298 | 41.3128 | −122.2712 | 7.0 | 42.04 | 6.92 | 10.1 | 4.4 |
| Shasta Retreat | 20150917 | 1830 | Domestic | 1461 | 41.3524 | −122.2859 | 6.7 | 65.66 | 6.57 | 8.4 | 30.1 |
| McBride Campground Well | 20150502 | 940 | Domestic | 1483 | 41.3546 | −122.2816 | 7.9 | 68.8 | 6.96 | 9.3 | 2.2 |
| McBride Campground Well | 20150917 | 1600 | Public Supply | 1483 | 41.3546 | −122.2816 | 8.1 | 68.35 | NM | 9.5 | NM |
| Ski Park 2 | 20150918 | 940 | Domestic | 1805 | 41.3290 | −122.2117 | 5.6 | 52.91 | 6.22 | 10.3 | NM |
| Ski Park 1 | 20150917 | 830 | Domestic | 1821 | 41.3216 | −122.2035 | 6.0 | 86.29 | 7.18 | 10.2 | −1.8 |
| McGinnis Spring | 20150917 | 1130 | Spring | 1878 | 41.3328 | −122.2159 | 5.2 | 56.07 | 6.95 | 9.6 | 9.3 |
| Panther Spring | 20150918 | 1230 | Spring | 2346 | 41.3589 | −122.1976 | 6.0 | 15.39 | NM | 9.5 | NM |
| Horse Camp Spring 1 | 20150918 | 1415 | Spring | 2509 | 41.3752 | −122.2239 | 5.3 | 13.51 | NM | 11.6 | NM |
| Horse Camp Spring 2 | 20150918 | 1500 | Spring | 2542 | 41.3755 | −122.2229 | 5.4 | 27.49 | NM | 10.8 | NM |
| McCloud Intake Spring | 20150429 | 845 | Spring | 1396 | 41.3179 | −122.1168 | 4.6 | NM | 7.2 | 14.1 | −16.2 |
| McCloud R at Lower Falls | 20150429 | 1050 | Surface Water | 1189 | 41.3142 | −122.1065 | 12.0 | 82 | NM | 11.9 | −30.8 |
| Panther Meadow Creek | 20150502 | 1210 | Surface Water | 2304 | 41.3566 | −122.1990 | 2.3 | 14.12 | 7.26 | 10.4 | −14.3 |
| Beaughan Creek at Roseberg Bridge | 20150430 | 1100 | Surface Water | 1134 | 41.4216 | −122.3565 | NM | NM | NM | NM | NM |
| Big Canyon Creek Middlefork | 20150917 | 1344 | Surface Water | 1500 | 41.3124 | −122.2461 | 5.6 | 49.76 | 6.71 | 11.4 | 22.5 |
| Bunny Flat snow | 20150502 | 1030 | Snow | 2140 | 41.3559 | −122.2322 | NA | NA | NA | NA | NA |
| Mt Shasta Snow 1 | 20160214 | Snow | 1554 | 41.3411 | −122.2739 | NA | NA | NA | NA | NA | |
| Mt Shasta Snow 2 | 20160214 | Snow | 1835 | 41.3394 | −122.2594 | NA | NA | NA | NA | NA | |
| Mt Shasta Snow 3 | 20160214 | Snow | 2143 | 41.3561 | −122.2328 | NA | NA | NA | NA | NA | |
| Mt Shasta Snow 4 | 20160214 | Snow | 2448 | 41.3714 | −122.2281 | NA | NA | NA | NA | NA | |
| Mt Shasta Snow 5 | 20160214 | Snow | 2758 | 41.3736 | −122.2075 | NA | NA | NA | NA | NA | |
| Mt Shasta Snow 6 | 20160214 | Snow | 3069 | 41.3842 | −122.2058 | NA | NA | NA | NA | NA |
| Site Name | 3He/ 4He | ± | 4He | ± | Ne | ± | Ar | ± | Kr | ± | Xe | ± | Pχ2 a | Recharge Temp. | 4HeTERb | RNA/Ra c |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ×10−7 | ×10−8 cm3STP/g | ×10−8 cm3STP/g | ×10−5 cm3STP/g | ×10−8 cm3STP/g | ×10−9 cm3STP/g | % | °C | ×10−9 cm3STP/g | ||||||||
| Redwood Rd | 6.41 | 0.23 | 17.88 | 0.36 | 26.49 | 0.53 | 39.60 | 0.79 | 9.17 | 0.28 | 12.93 | 0.39 | 63% | 5.0 | 113.4 | 0.16 |
| Butte Ave | 19.88 | 0.32 | 5.07 | 0.10 | 21.84 | 0.44 | 37.95 | 0.76 | 8.75 | 0.26 | 12.91 | 0.39 | 49% | 4.2 | 0.0 | - |
| Pine Grove Dr | 4.33 | 0.08 | 62.47 | 1.25 | 19.88 | 0.52 | 35.97 | 0.72 | 8.47 | 0.25 | 12.09 | 0.36 | 58% | 7.2 | 578.0 | 0.26 |
| Gazelle Well | 16.33 | 0.27 | 4.61 | 0.09 | 20.06 | 0.40 | 36.53 | 0.73 | 8.57 | 0.26 | 12.52 | 0.38 | 58% | 5.4 | 0.0 | - |
| Mazzei Well | 69.82 | 1.14 | 26.62 | 0.53 | 20.56 | 0.41 | 36.76 | 0.74 | 8.74 | 0.26 | 12.75 | 0.38 | 67% | 4.6 | 217.9 | 5.94 |
| Beaughan Springs | 14.73 | 0.24 | 4.93 | 0.10 | 19.74 | 0.39 | 36.14 | 0.72 | 8.59 | 0.26 | 12.57 | 0.38 | 73% | 5.2 | 3.3 | 2.15 |
| Legacy Stone Property | 14.64 | 0.24 | 4.05 | 0.08 | 18.25 | 0.37 | 35.60 | 0.71 | 8.74 | 0.26 | 12.51 | 0.38 | 39% | 5.1 | 0.0 | - |
| Mt Shasta Well 01 | 58.75 | 0.96 | 12.80 | 0.26 | 22.22 | 0.44 | 38.12 | 0.76 | 8.99 | 0.27 | 13.34 | 0.40 | 73% | 2.6 | 75.3 | 6.53 |
| Mt Shasta Cold Spring | 13.23 | 0.22 | 4.15 | 0.08 | 18.93 | 0.38 | 37.36 | 0.75 | 8.89 | 0.27 | 13.36 | 0.40 | 33% | 1.9 | 0.0 | - |
| Mt Shasta High School Well | 26.81 | 0.24 | 5.40 | 0.11 | 20.19 | 0.40 | 37.40 | 0.75 | 9.09 | 0.27 | 13.26 | 0.40 | 40% | 2.5 | 7.1 | 8.26 |
| Shasta Acres Rd | 26.13 | 0.23 | 5.23 | 0.10 | 19.93 | 0.40 | 37.23 | 0.74 | 9.12 | 0.27 | 13.56 | 0.41 | 67% | 1.2 | 6.3 | 8.49 |
| Highland Drive | 5.91 | 0.17 | 129.32 | 2.59 | 19.17 | 0.38 | 33.86 | 0.68 | 8.25 | 0.25 | 11.87 | 0.36 | 74% | 8.1 | 1248.4 | 0.41 |
| Old Stage Rd | 77.24 | 0.69 | 20.37 | 0.41 | 22.23 | 0.44 | 40.40 | 0.81 | 9.52 | 0.29 | 13.63 | 0.41 | 2% | 1.4 | 151.1 | 7.18 |
| Ski Park 1 | 13.54 | 0.15 | 4.02 | 0.08 | 18.36 | 0.37 | 35.92 | 0.72 | 8.83 | 0.27 | 12.96 | 0.39 | 56% | 3.4 | 0.0 | - |
| Big Springs Pool | NC | NC | 5.00 | 0.25 | 22.66 | 1.13 | 38.36 | 0.77 | 9.08 | 0.18 | 13.79 | 0.28 | 96% | 0.7 | 0.0 | NC |
| Big Springs 2 | NC | NC | 5.83 | 0.29 | 22.89 | 1.14 | 37.96 | 0.76 | 8.90 | 0.18 | 13.52 | 0.27 | 96% | 2.0 | 3.7 | NC |
| Big Springs 3 | NC | NC | 6.39 | 0.32 | 23.48 | 1.17 | 38.74 | 0.77 | 8.99 | 0.18 | 13.89 | 0.28 | 83% | 0.5 | 7.8 | NC |
| Panther Spring | NC | NC | 4.21 | 0.21 | 20.97 | 1.05 | 35.97 | 0.72 | 8.62 | 0.17 | 13.19 | 0.26 | 75% | 2.9 | 0.0 | NC |
| Horse Camp Spring 1 | NC | NC | 4.22 | 0.21 | 20.65 | 1.03 | 34.70 | 0.69 | 8.21 | 0.16 | 12.25 | 0.24 | 58% | 6.7 | 0.0 | NC |
| Horse Camp Spring 2 | NC | NC | 4.01 | 0.20 | 19.49 | 0.97 | 33.52 | 0.67 | 8.07 | 0.16 | 11.71 | 0.23 | 56% | 9.0 | 0.0 | NC |
| Site Name | SampleDate | Site Elevation (m) | δ18O SMOW (‰) | δD SMOW (‰) | δ18O Recharge Elevation (m) |
|---|---|---|---|---|---|
| Old Stage Rd | 20150501 | 1036 | −14.2 | −102.5 | 2665 |
| Pine Grove Dr | 20150428 | 1085 | −12.8 | −95.0 | 2001 |
| Highland Drive | 20150501 | 1085 | −13.7 | −99.9 | 2395 |
| Big Springs Main | 20150428 | 1085 | −14.4 | −105.7 | 2767 |
| Big Springs B | 20150428 | 1085 | −14.4 | −106.1 | 2761 |
| Big Springs C | 20150428 | 1085 | −14.3 | −104.5 | 2713 |
| Big Springs D | 20150428 | 1085 | −14.2 | −104.9 | 2669 |
| Big Springs Pool | 20150918 | 1123 | −14.7 | −104.6 | 2870 |
| Big Springs 2 | 20150918 | 1094 | −14.6 | −104.8 | 2841 |
| Big Springs 3 | 20150918 | 1094 | −14.5 | −107.0 | 2809 |
| Mt Shasta Well 01 | 20150501 | 1122 | −13.8 | −101.3 | 2451 |
| Mt Shasta High School Well | 20150501 | 1128 | −14.2 | −102.0 | 2633 |
| Butte Ave | 20150428 | 1134 | −13.5 | −99.0 | 2306 |
| Gazelle Well | 20150429 | 1134 | −13.1 | −95.5 | 2108 |
| Beaughan Springs | 20150430 | 1140 | −14.6 | −106.6 | 2834 |
| Redwood Rd | 20150428 | 1146 | −12.9 | −94.9 | 2031 |
| Redwood Rd | 20150917 | 1146 | −12.9 | −94.9 | 2031 |
| Legacy Stone Property | 20150430 | 1146 | −14.4 | −107.1 | 2750 |
| Mazzei Well | 20150429 | 1158 | −14.3 | −105.2 | 2689 |
| Shasta Acres Rd | 20150501 | 1225 | −13.3 | −95.0 | 2235 |
| Mt Shasta Cold Spring | 20150501 | 1298 | −13.9 | −98.5 | 2514 |
| McCloud Intake Spring | 20150429 | 1396 | −13.1 | −93.3 | 2119 |
| Shasta Retreat | 20150917 | 1461 | −14.6 | −99.7 | 2844 |
| McBride Campground Well | 20150502 | 1483 | −13.3 | −97.0 | 2248 |
| McBride Campground Well | 20150917 | 1483 | −14.0 | −102.1 | 2543 |
| Ski Park 2 | 20150918 | 1805 | −13.0 | −92.3 | 2083 |
| Ski Park 1 | 20150917 | 1821 | −12.9 | −93.9 | 2035 |
| McGinnis Spring | 20150917 | 1878 | −13.8 | −92.1 | 2463 |
| Panther Spring | 20150918 | 2346 | −13.7 | −99.7 | 2421 |
| Horse Camp Spring 1 | 20150918 | 2509 | −14.5 | −105.5 | 2777 |
| Horse Camp Spring 2 | 20150918 | 2542 | −14.7 | −107.1 | 2914 |
| McCloud R at Lower Falls | 20150429 | 920 | −11.7 | −83.7 | NA |
| Beaughan Creek at Roseberg Bridge | 20150430 | 1134 | −14.4 | −105.7 | NA |
| Panther Meadow Creek | 20150502 | 2304 | −13.0 | −93.5 | NA |
| Mt Shasta Snow 1 | 20160214 | 1554 | −10.5 | −66.4 | NA |
| Mt Shasta Snow 2 | 20160214 | 1835 | −12.0 | −81.7 | NA |
| Mt Shasta Snow 3 | 20160214 | 2143 | −12.3 | −89.3 | NA |
| Mt Shasta Snow 4 | 20160214 | 2448 | −13.5 | −93.5 | NA |
| Mt Shasta Snow 5 | 20160214 | 2758 | −13.8 | −99.1 | NA |
| Mt Shasta Snow 6 | 20160214 | 3069 | −14.5 | −106.4 | NA |
| Bunny Flat snow | 20150502 | 2140 | −12.9 | −97.3 | NA |
| Elevation Range (m) | Area (%) | Distance to Summit (km) | Precipitation (mm) | P (%) | ET (mm) | ET (%) | P−ET (mm) | P−ET (%) | Temperature (°C) | Precipitation (mm) | ET (mm) | P−ET Norm |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1000–1250 | 11.1 | 13.2 | 1112 | 9% | 644 | 13% | 468 | 6% | 10.3 | 123.4 | 71.5 | 51.9 |
| 1250–1500 | 25.1 | 11.8 | 1190 | 22% | 746 | 33% | 444 | 14% | 9.7 | 298.7 | 187.2 | 111.4 |
| 1500–1750 | 23.4 | 10.5 | 1281 | 22% | 673 | 28% | 608 | 18% | 8.5 | 299.8 | 157.5 | 142.3 |
| 1750–2000 | 11.6 | 8.3 | 1306 | 11% | 596 | 12% | 710 | 10% | 6.7 | 151.5 | 69.1 | 82.4 |
| 2000–2250 | 10.5 | 6.9 | 1431 | 11% | 464 | 9% | 967 | 13% | 5.1 | 150.3 | 48.7 | 101.5 |
| 2250–2500 | 5.8 | 5.5 | 1629 | 7% | 351 | 4% | 1278 | 9% | 4.1 | 94.5 | 20.4 | 74.1 |
| 2500–2750 | 3.4 | 4.5 | 1853 | 5% | 181 | 1% | 1672 | 7% | 2.6 | 63.0 | 6.2 | 56.8 |
| 2750–3000 | 3.2 | 3.7 | 2050 | 5% | 130 | 1% | 1920 | 8% | 1 | 65.6 | 4.2 | 61.4 |
| 3000–3250 | 2 | 3 | 2177 | 3% | 115 | 0% | 2062 | 5% | −0.7 | 43.5 | 2.3 | 41.2 |
| 3250–3500 | 1.5 | 2.4 | 2238 | 2% | 112 | 0% | 2126 | 4% | −2.6 | 33.6 | 1.7 | 31.9 |
| 3500–3750 | 1.1 | 1.9 | 2270 | 2% | 114 | 0% | 2156 | 3% | −4.4 | 25.0 | 1.3 | 23.7 |
| 3750–4000 | 0.8 | 1.2 | 2309 | 1% | 113 | 0% | 2196 | 2% | −5.8 | 18.5 | 0.9 | 17.6 |
| >4000 | 0.4 | 0.6 | 2352 | 1% | 112 | 0% | 2240 | 1% | −6.9 | 9.4 | 0.4 | 9.0 |
| Site Name | 3H (pCi/L) | +/− (pCi/L) | Model Age (Year) |
|---|---|---|---|
| Old Stage Rd | 0.09 | 0.16 | >50 |
| Big Springs Main | 3.03 | 0.29 | 19.4 |
| Big Springs B | 1.05 | 0.22 | 38.3 |
| Big Springs C | 1.22 | 0.22 | 35.6 |
| Big Springs D | 0.17 | 0.75 | >50 |
| Big Springs Pool | 3.32 | 0.19 | 17.8 |
| Big Springs 2 | 1.33 | 0.13 | 34.0 |
| Big Springs 3 | 1.25 | 0.12 | 35.2 |
| Highland Drive | 4.56 | 0.32 | 12.2 |
| Pine Grove Dr | 5.81 | 0.35 | 7.9 |
| Mt Shasta Well 01 | 3.89 | 0.27 | 15.0 |
| Mt Shasta High School Well | 3.21 | 0.24 | 18.4 |
| Butte Ave | 6.45 | 0.50 | 6.0 |
| Gazelle Well | 6.50 | 0.42 | 5.9 |
| Beaughan Springs | 3.25 | 0.26 | 18.2 |
| Legacy Stone Property | 3.80 | 0.27 | 15.4 |
| Redwood Rd (April) | 4.94 | 0.52 | 10.8 |
| Redwood Rd (September) | 5.64 | 0.55 | 8.4 |
| Mazzei Well | 0.69 | 0.17 | >50 |
| Shasta Acres Rd | 6.65 | 0.55 | 5.5 |
| Mt Shasta Cold Spring | 6.81 | 0.46 | 5.1 |
| McCloud Intake Spring | 7.27 | 0.40 | 3.9 |
| Shasta Retreat | 6.57 | 0.54 | 5.7 |
| McBride Campground Well (May) | 6.02 | 0.15 | 7.2 |
| McBride Campground Well (September) | 6.33 | 0.96 | 6.4 |
| Big Canyon Creek Middlefork | 7.31 | 0.93 | 3.8 |
| Ski Park 2 | 7.96 | 0.60 | 2.3 |
| Ski Park 1 | 7.57 | 0.64 | 3.2 |
| McGinnis Spring | 8.57 | 0.63 | 1.0 |
| Panther Spring | 9.74 | 0.40 | −1.3 |
| Horse Camp Spring 1 | 8.78 | 0.37 | 0.5 |
| Horse Camp Spring 2 | 9.03 | 0.42 | 0.0 |
| Bunny Flat snow | 9.05 | 0.46 | 0.0 |
References
- López-Moreno, J.I.; Pomeroy, J.W.; Revuelto, J.; Vicente-Serrano, S.M. Response of snow processes to climate change: Spatial variability in a small basin in the spanish pyrenees. Hydrol. Process. 2013, 27, 2637–2650. [Google Scholar] [CrossRef]
- Hayhoe, K.; Cayan, D.; Field, C.B.; Frumhoff, P.C.; Maurer, E.P.; Miller, N.L.; Moser, S.C.; Schneider, S.H.; Cahill, K.N.; Cleland, E.E.; et al. Emissions pathways, climate change and impacts on California. PNAS 2004, 101, 12422–12427. [Google Scholar] [CrossRef] [PubMed]
- Mote, P.W.; Hamlet, A.F.; Clark, M.P.; Lettenmaier, D.P. Declining mountain snowpack in western North America. Bull. Am. Meteorol. Soc. 2005, 86, 39–49. [Google Scholar] [CrossRef]
- Fritze, H.; Stewart, I.T.; Pebesma, E. Shifts in western North American snowmelt runoff regimes for the recent warm decades. J. Hydrometeorol. 2011, 12, 989–1006. [Google Scholar] [CrossRef]
- Surfleet, C.G.; Tullos, D. Variability in Effect of Climate change on rain-on-snow peak flow events in a temperate climate. J. Hydrol. 2013, 479, 24–34. [Google Scholar] [CrossRef]
- Gershunov, A.; Shulgina, T.; Ralph, F.M.; Lavers, D.A.; Rutz, J.J. Assessing the climate-scale variability of atmospheric rivers affecting western North America. Geophys. Res. Lett. 2017, 44, 2017GL074175. [Google Scholar] [CrossRef]
- Polade, S.D.; Pierce, D.W.; Cayan, D.R.; Gershunov, A.; Dettinger, M.D. The key role of dry days in changing regional climate and precipitation regimes. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef] [PubMed]
- Rapacciuolo, G.; Maher, S.P.; Schneider, A.C.; Hammond, T.T.; Jabis, M.D.; Walsh, R.E.; Iknayan, K.J.; Walden, G.K.; Oldfather, M.F.; Ackerly, D.D.; et al. Beyond a warming fingerprint: Individualistic biogeographic responses to heterogeneous climate change in California. Glob. Chang. Biol. 2014, 20, 2841–2855. [Google Scholar] [CrossRef] [PubMed]
- Sundqvist, M.K.; Sanders, N.J.; Wardle, D.A. Community and ecosystem responses to elevational gradients: Processes, mechanisms and insights for global change. Annu. Rev. Ecol. Evol. Syst. 2013, 44, 261–280. [Google Scholar] [CrossRef]
- Goulden, M.L.; Bales, R.C. Mountain runoff vulnerability to increased evapotranspiration with vegetation expansion. Proc. Natl. Acad. Sci. USA 2014, 111, 14071–14075. [Google Scholar] [CrossRef] [PubMed]
- Segal, D.C.; Moran, J.E.; Visser, A.; Singleton, M.J.; Esser, B.K. Seasonal variation of high elevation groundwater recharge as indicator of climate response. J. Hydrol. 2014, 519, 3129–3141. [Google Scholar] [CrossRef]
- Singleton, M.J.; Moran, J.E. Dissolved noble gas and isotopic tracers reveal vulnerability of groundwater in a small, high-elevation catchment to predicted climate changes: Vulnerability of high elevation groundwater. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Tague, C.; Grant, G.E. Groundwater dynamics mediate low-flow response to global warming in snow-dominated alpine regions. Water Resour. Res. 2009, 45, W07421. [Google Scholar] [CrossRef]
- Rose, T.P.; Lee Davisson, M.; Criss, R.E. Isotope hydrology of voluminous cold springs in fractured rock from an active volcanic region, northeastern California. J. Hydrol. 1996, 179, 207–236. [Google Scholar] [CrossRef]
- Nathenson, M.; Thompson, J.M.; White, L.D. Slightly thermal springs and non-thermal springs at Mount Shasta, California: Chemistry and recharge elevations. J. Volcanol. Geotherm. Res. 2003, 121, 137–153. [Google Scholar] [CrossRef]
- Jefferson, A.; Grant, G.; Rose, T. Influence of volcanic history on groundwater patterns on the west slope of the Oregon High Cascades. Water Resour. Res. 2006, 42, W12411. [Google Scholar] [CrossRef]
- Saar, M.O.; Manga, M. Depth dependence of permeability in the Oregon Cascades inferred from hydrogeologic, thermal, seismic and magmatic modeling constraints. J. Geophys. Res. 2004, 109, B04204. [Google Scholar] [CrossRef]
- Surano, K.; Hudson, G.; Failor, R.; Sims, J.; Holland, R.; MacLean, S.; Garrison, J. Heliuim-3 mass spectrometry for low-level tritium analysis of environmental samples. J. Radioanal. Nucl. Chem. 1992, 161, 443–453. [Google Scholar] [CrossRef]
- Clarke, W.B.; Jenkins, W.J.; Top, Z. Determination of tritium by mass spectrometric measurement of 3He. Int. J. Appl. Radiat. Isotopes 1976, 27, 515–522. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Dansgaard, W. The Isotopic Composition of Natural Waters with Special Reference to the Greenland Ice Cap. Meddelelser Om GrÒ©Nland Vol 165 No 2; C. A. Reitzel: Copenhagen, Denmark, 1961. [Google Scholar]
- Rademacher, L.K.; Clark, J.F.; Hudson, G.B.; Erman, D.C.; Erman, N.A. Chemical evolution of shallow groundwater as recorded by Springs, Sagehen Basin; Nevada County, California. Chem. Geol. 2001, 179, 37–51. [Google Scholar] [CrossRef]
- Cey, B.D.; Hudson, G.B.; Moran, J.E.; Scanlon, B.R. Impact of artificial recharge on dissolved noble gases in groundwater in California. Environ. Sci. Technol. 2008, 42, 1017–1023. [Google Scholar] [CrossRef] [PubMed]
- Visser, A.; Singleton, M.J.; Hillegonds, D.J.; Velsko, C.A.; Moran, J.E.; Esser, B.K. A membrane inlet mass spectrometry system for noble gases at natural abundances in gas and water samples. Rapid Commun. Mass Spectrom. 2013, 27, 2472–2482. [Google Scholar] [CrossRef] [PubMed]
- Visser, A.; Fourré, E.; Barbecot, F.; Aquilina, L.; Labasque, T.; Vergnaud, V.; Esser, B.K. Intercomparison of tritium and noble gases analyses, 3H/3He ages and derived parameters excess air and recharge temperature. Appl. Geochem. 2014, 50 (Suppl. C), 130–141. [Google Scholar] [CrossRef]
- Heaton, T.H.E.; Vogel, J.C. “Excess Air” in groundwater. J. Hydrol. 1981, 50 (Suppl. C), 201–216. [Google Scholar] [CrossRef]
- Visser, A.; Moran, J.E.; Hillegonds, D.; Singleton, M.J.; Kulongoski, J.T.; Belitz, K.; Esser, B.K. Geostatistical analysis of tritium, groundwater age and other noble gas derived parameters in California. Water Res. 2016, 91, 314–330. [Google Scholar] [CrossRef] [PubMed]
- Aeschbach-Hertig, W.; Peeters, F.; Beyerle, U.; Kipfer, R. Palaeotemperature Reconstruction from noble gases in ground water taking into account equilibration with entrapped air. Nature 2000, 405, 1040–1044. [Google Scholar] [CrossRef] [PubMed]
- Manning, A.H.; Solomon, D.K. Using noble gases to investigate mountain-front recharge. J. Hydrol. 2003, 275, 194–207. [Google Scholar] [CrossRef]
- Cederberg, J.R.; Gardner, P.M.; Thiros, S.A. Hydrology of Northern Utah Valley, Utah County, Utah; 2008–5197; U.S. Geological Survey: Reston, VA, USA, 2009. [Google Scholar]
- Althaus, R.; Klump, S.; Onnis, A.; Kipfer, R.; Purtschert, R.; Stauffer, F.; Kinzelbach, W. Noble gas tracers for characterisation of flow dynamics and origin of groundwater: A Case study in Switzerland. J. Hydrol. 2009, 370, 64–72. [Google Scholar] [CrossRef]
- Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the Conterminous United States—Representing a Decade of Land Cover Change Information; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2015; Volume 81. [Google Scholar]
- Spruce, J.P.; Gasser, G.E.; Hargrove, W.W. MODIS NDVI Data, Smoothed and Gap-Filled, for the Conterminous US: 2000–2013; ORNL Distributed Active Archive Center: Oak Ridge, TN, USA, 2015. [Google Scholar]
- Stoklosa, J.; Daly, C.; Foster, S.D.; Ashcroft, M.; Warton, D. A Climate of uncertainty: accounting for error in climate variables for species distribution models. Methods Ecol. Evol. 2014, 6. [Google Scholar] [CrossRef]
- California Irrigation Management Information System. Available online: http://www.cimis.water.ca.gov/ (accessed on 30 October 2017).
- Multi-Resolution Land Characteristics Consortium (MRLC). Available online: https://www.mrlc.gov/ (accessed on 30 October 2017).
- Manga, M.; Kirchner, J.W. Interpreting the temperature of water at cold springs and the importance of gravitational potential energy. Water Resour. Res. 2004, 40, W05110. [Google Scholar] [CrossRef]
- Blackwell, D.D.; Steele, J.L.; Carter, L.C. Heat Flow Patterns of the North American Continent: A Discussion of the DNAG Geothermal Map of North America; DOEEEGTP (USDOE Office of Energy Efficiency and Renewable Energy Geothermal Tech Pgm): Washington, DC, USA, 1990. [Google Scholar]
- Schlosser, P.; Stute, M.; Dörr, H.; Sonntag, C.; Münnich, K.O. Tritium/3He dating of shallow groundwater. Earth Planet. Sci. Lett. 1988, 89, 353–362. [Google Scholar] [CrossRef]
- Saar, M.O.; Castro, M.C.; Hall, C.M.; Manga, M.; Rose, T.P. Quantifying magmatic, crustal and atmospheric helium contributions to volcanic aquifers using all stable noble gases: Implications for magmatism and groundwater flow. Geochem. Geophys. Geosyst. 2005, 6, Q03008. [Google Scholar] [CrossRef]
- Harms, P.; Visser, A.; Moran, J.; Esser, B. Distribution of tritium in precipitation and surface water in California. J. Hydrol. 2016, 534. [Google Scholar] [CrossRef]
- Goulden, M.L.; Anderson, R.G.; Bales, R.C.; Kelly, A.E.; Meadows, M.; Winston, G.C. Evapotranspiration along an elevation gradient in California’s Sierra Nevada. J. Geophys. Res. 2012, 117, G03028. [Google Scholar] [CrossRef]
- Hoch, G.; Körner, C. Global Patterns of mobile carbon stores in trees at the high-elevation tree line. Glob. Ecol. Biogeogr. 2012, 21, 861–871. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peters, E.; Visser, A.; Esser, B.K.; Moran, J.E. Tracers Reveal Recharge Elevations, Groundwater Flow Paths and Travel Times on Mount Shasta, California. Water 2018, 10, 97. https://doi.org/10.3390/w10020097
Peters E, Visser A, Esser BK, Moran JE. Tracers Reveal Recharge Elevations, Groundwater Flow Paths and Travel Times on Mount Shasta, California. Water. 2018; 10(2):97. https://doi.org/10.3390/w10020097
Chicago/Turabian StylePeters, Elizabeth, Ate Visser, Bradley K. Esser, and Jean E. Moran. 2018. "Tracers Reveal Recharge Elevations, Groundwater Flow Paths and Travel Times on Mount Shasta, California" Water 10, no. 2: 97. https://doi.org/10.3390/w10020097
APA StylePeters, E., Visser, A., Esser, B. K., & Moran, J. E. (2018). Tracers Reveal Recharge Elevations, Groundwater Flow Paths and Travel Times on Mount Shasta, California. Water, 10(2), 97. https://doi.org/10.3390/w10020097







