Numerical Analysis on Hydraulic Characteristics of U-shaped Channel of Various Trapezoidal Cross-Sections
Abstract
1. Introduction
2. Numerical Model
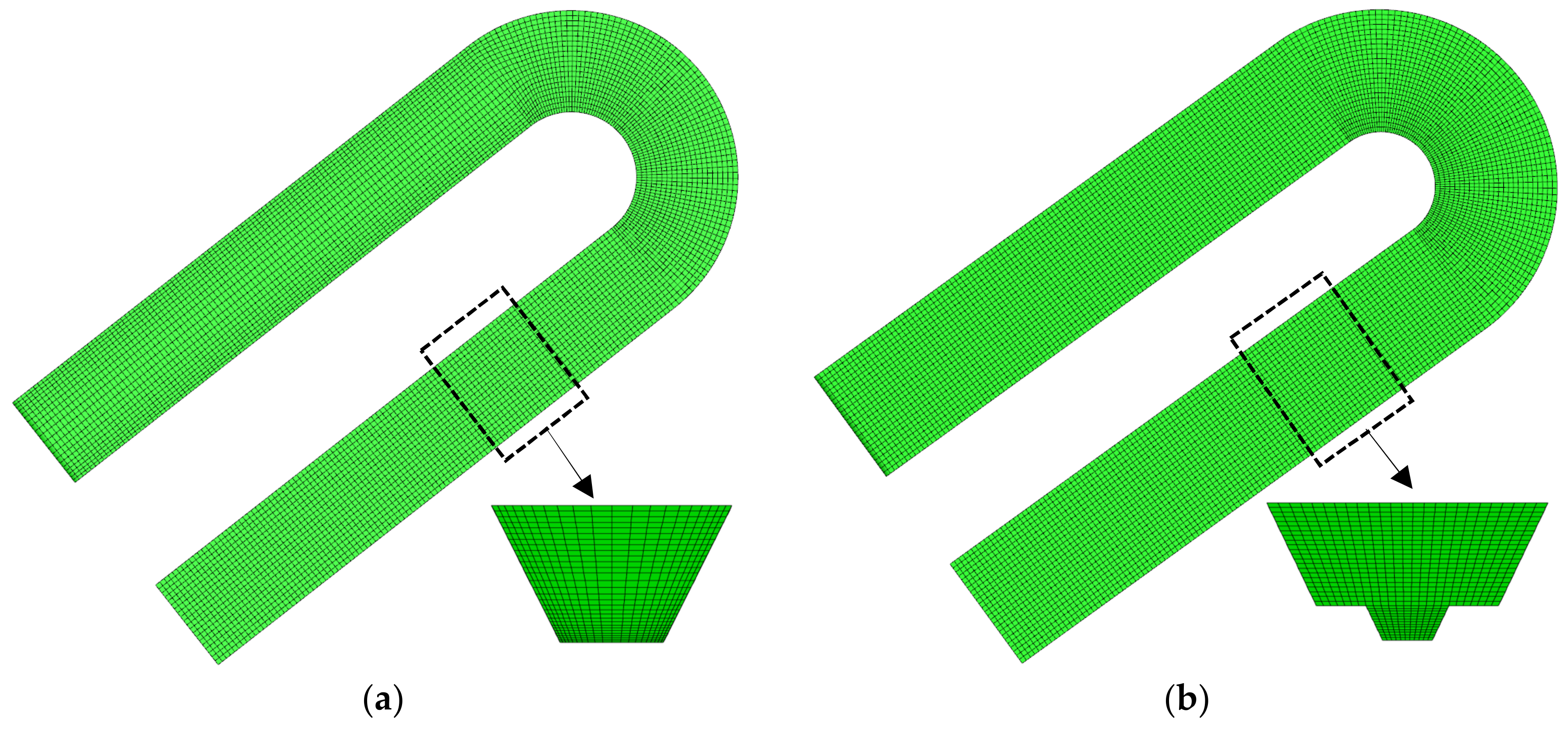
2.1. Numerical Methods
2.2. Governing Equations
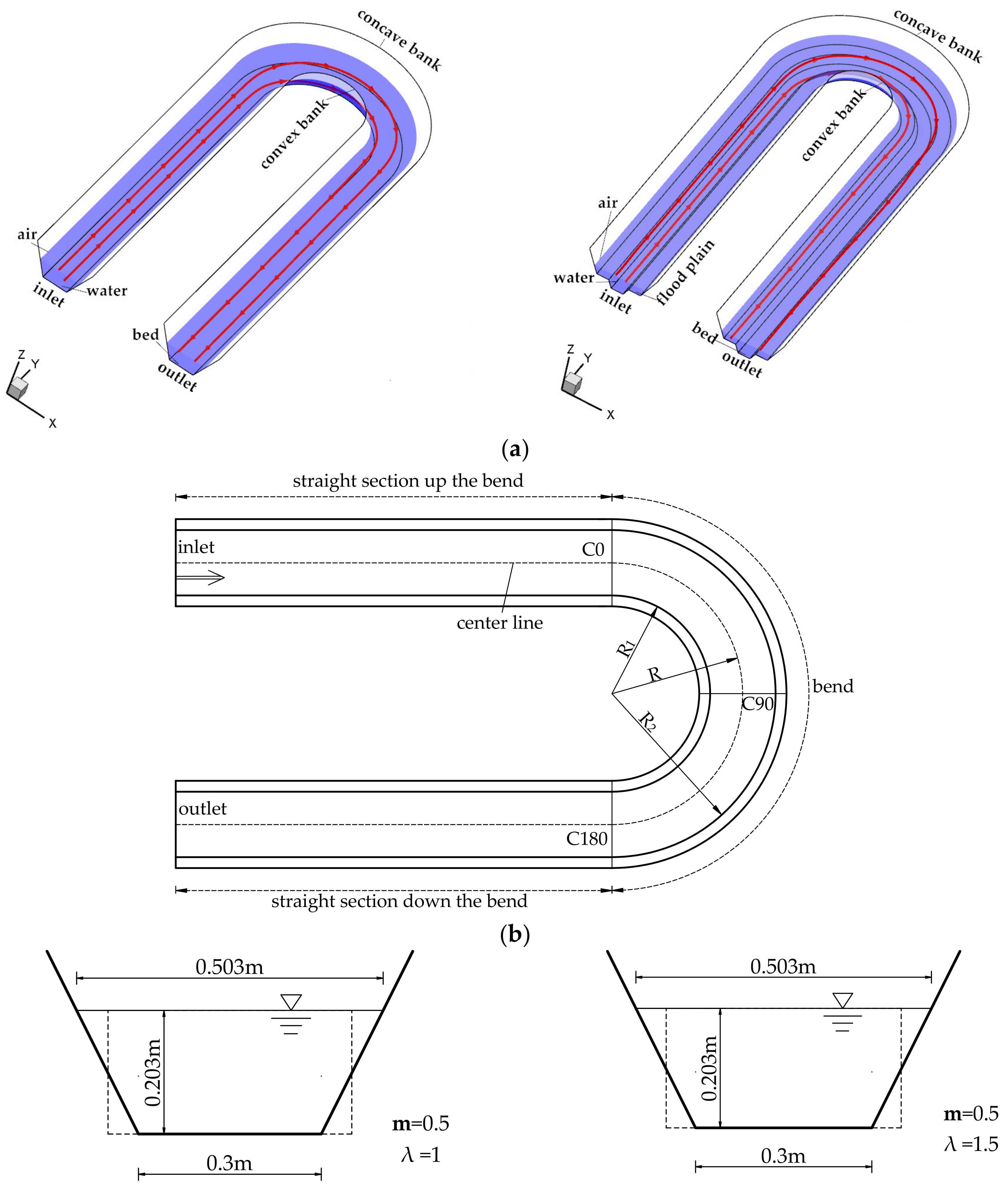
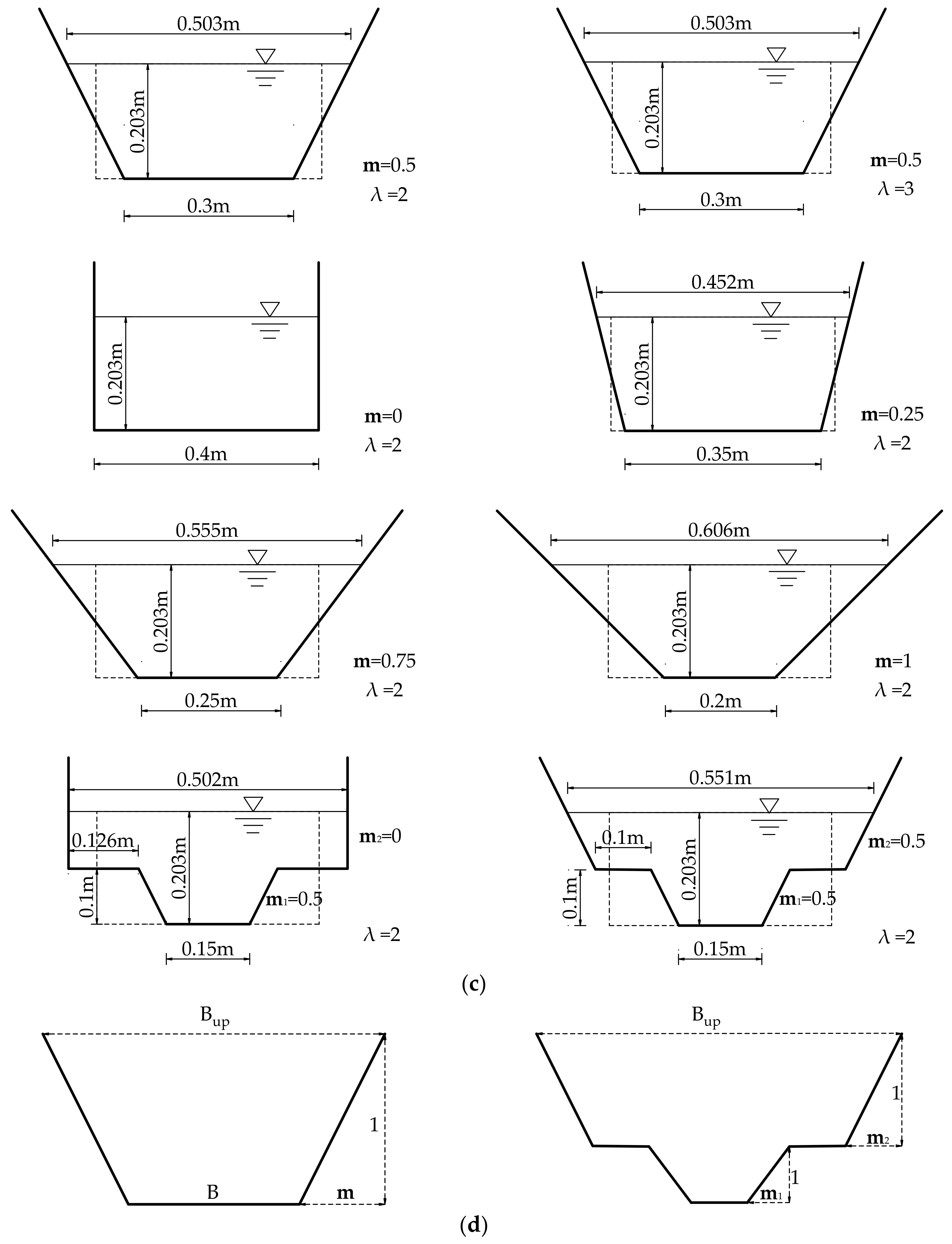
2.3. Boundary Conditions and Assumptions
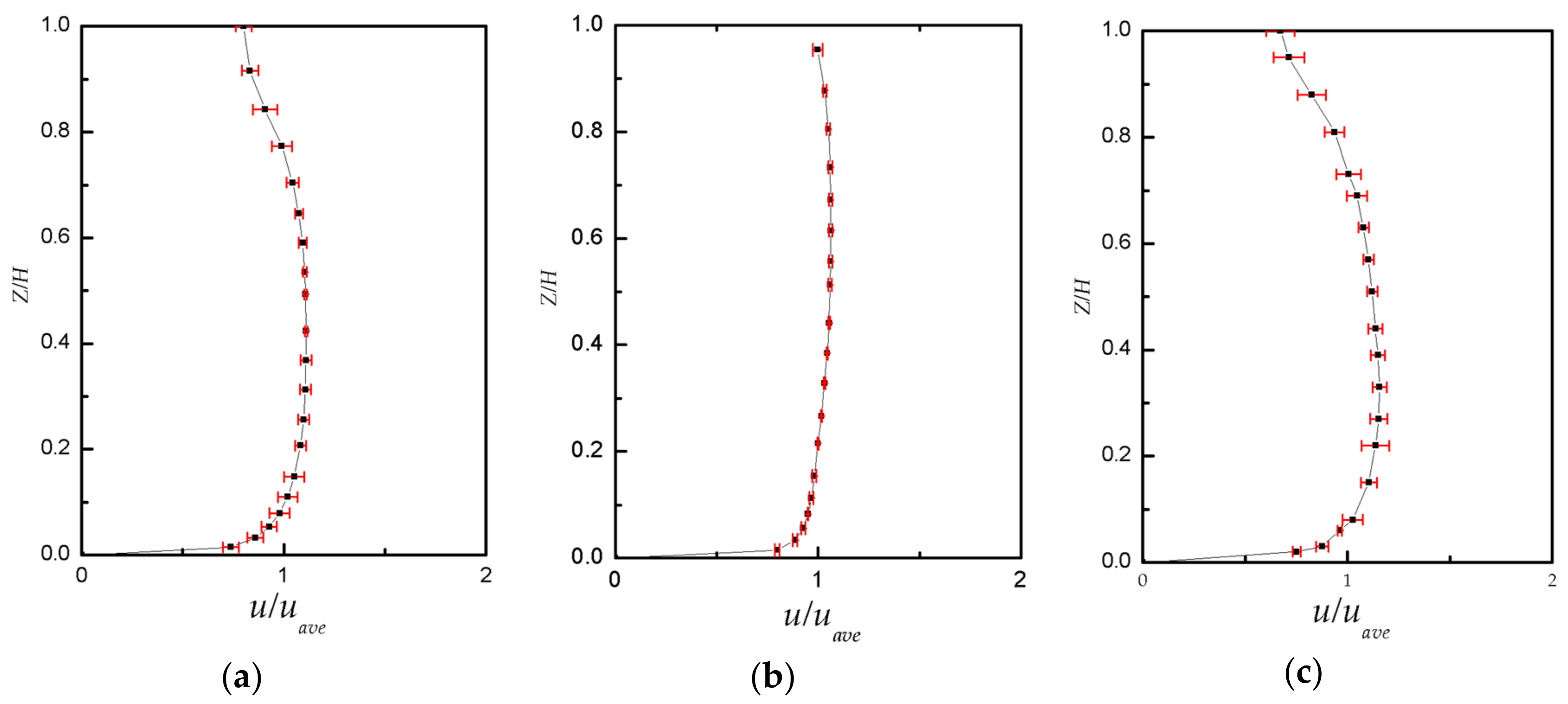
2.4. Model Verification
3. Results and Discussion
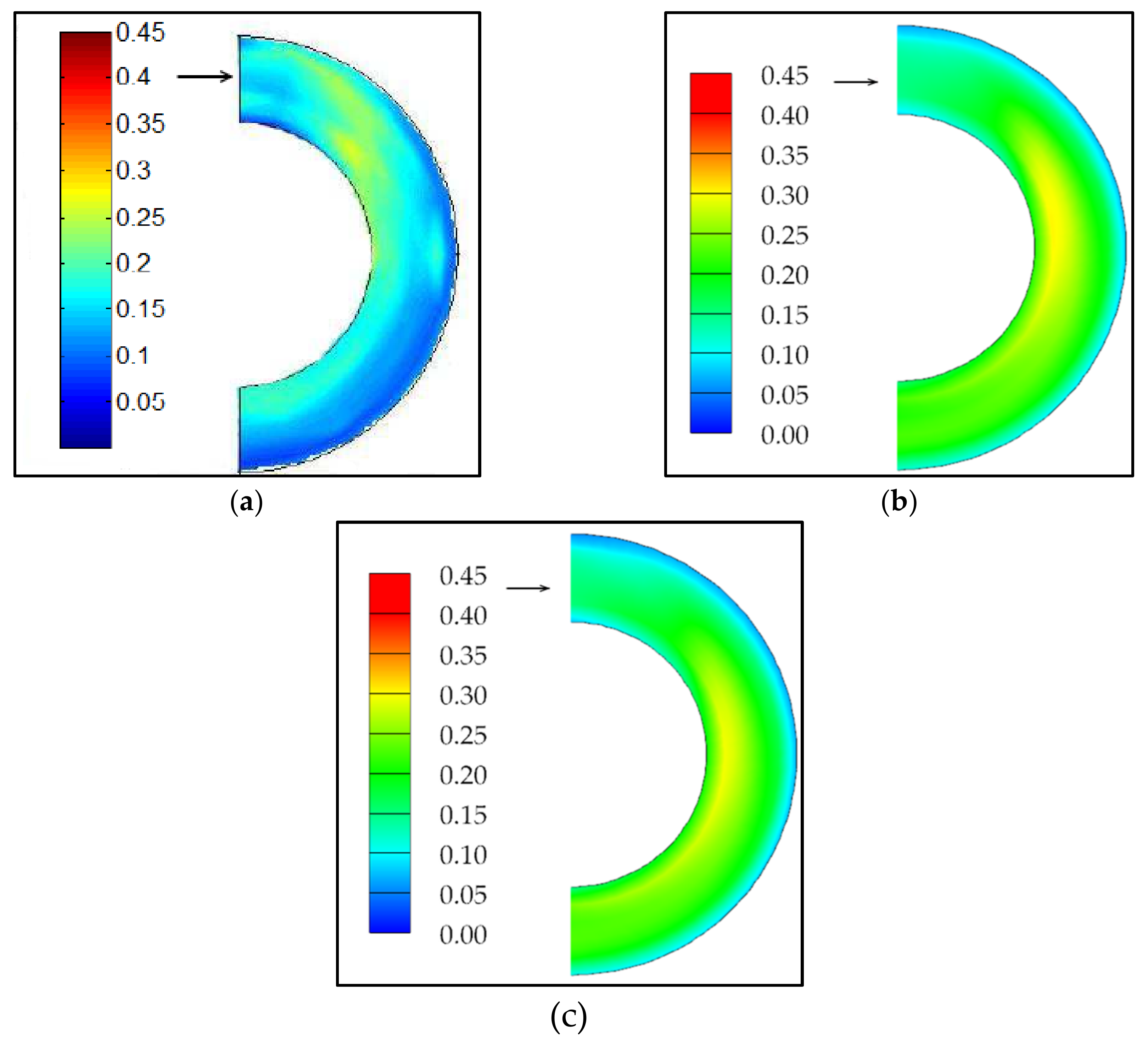
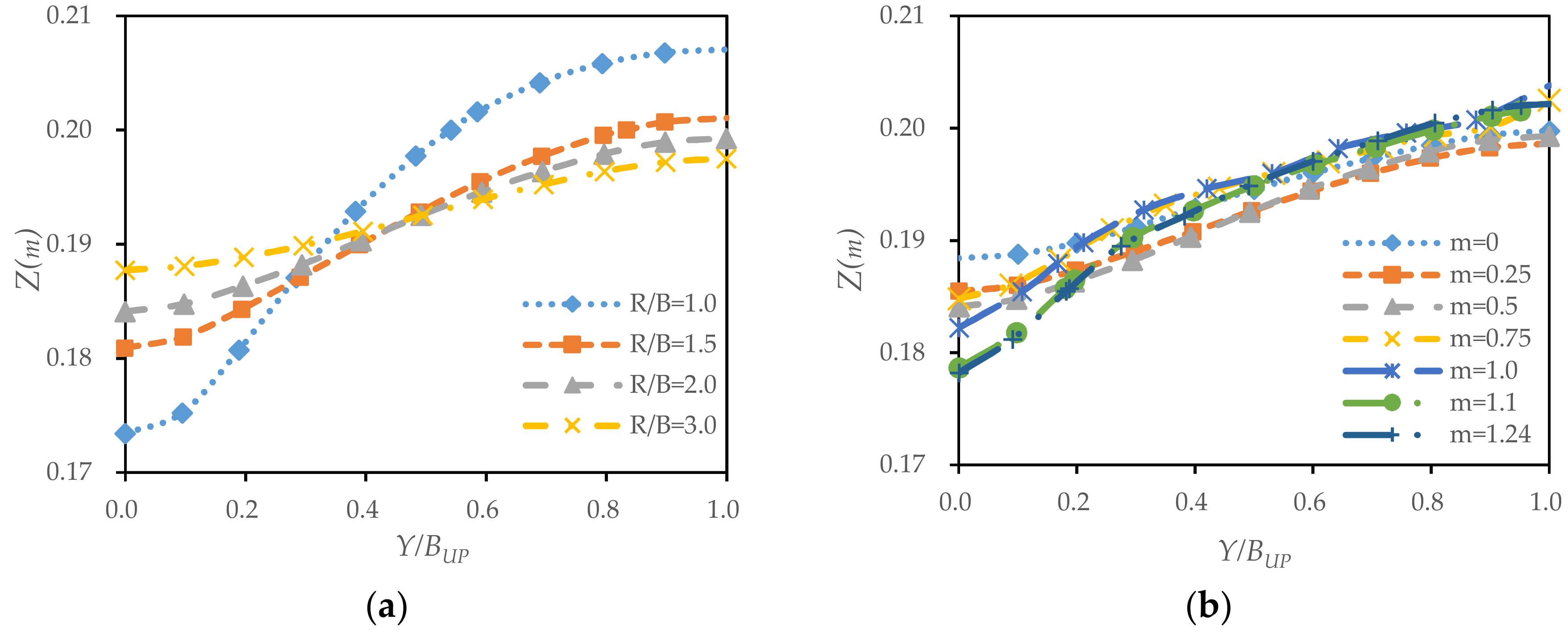
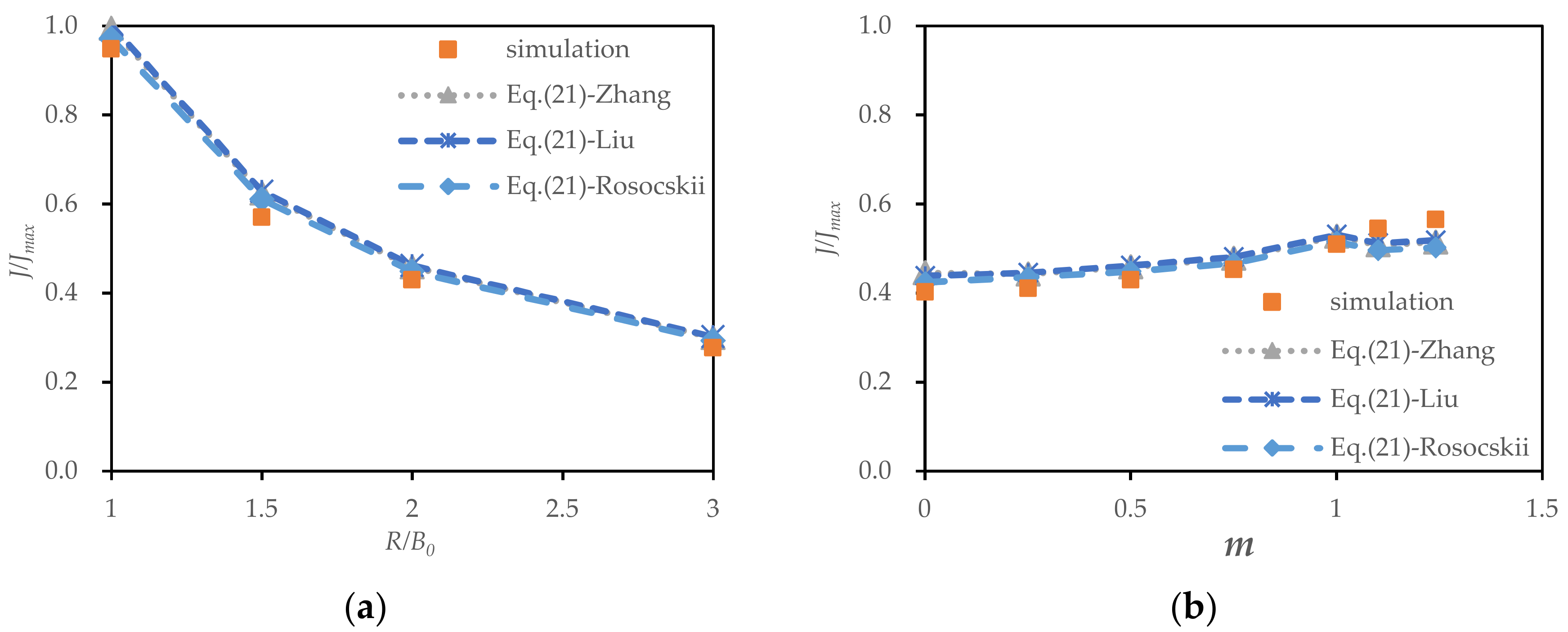
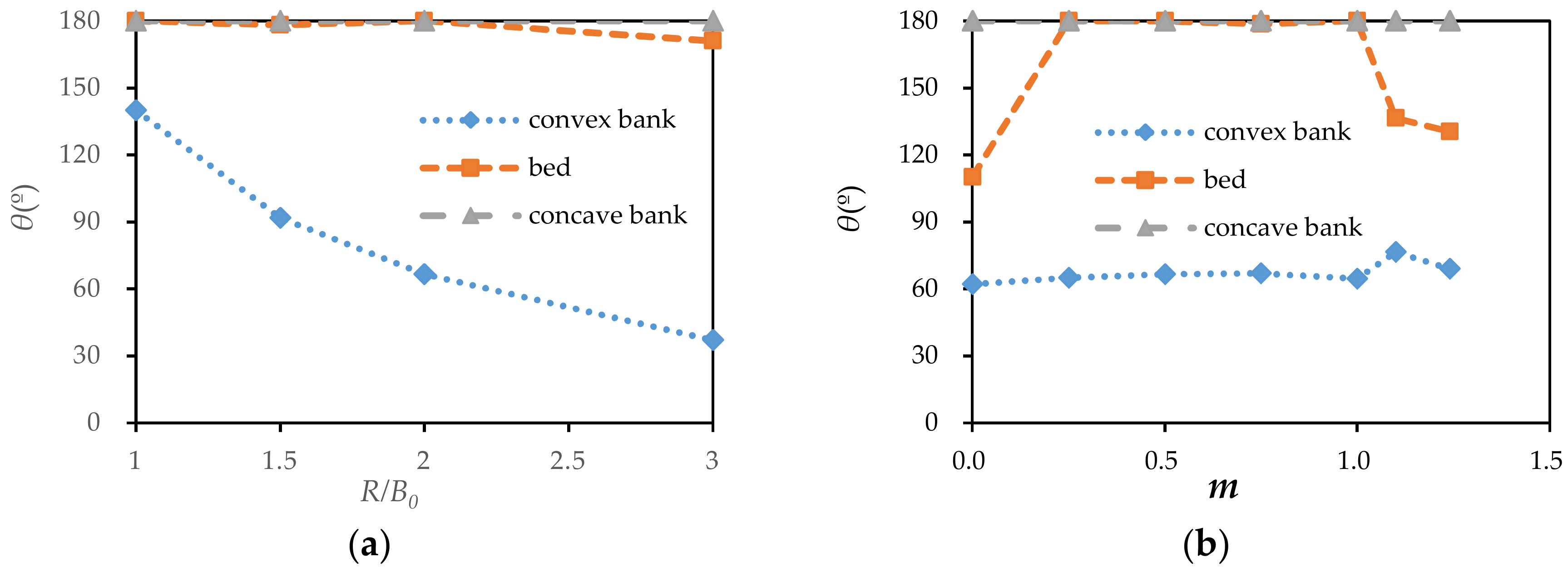
3.1. Analysis of the Water Surface Transverse Slope in Bend Apex
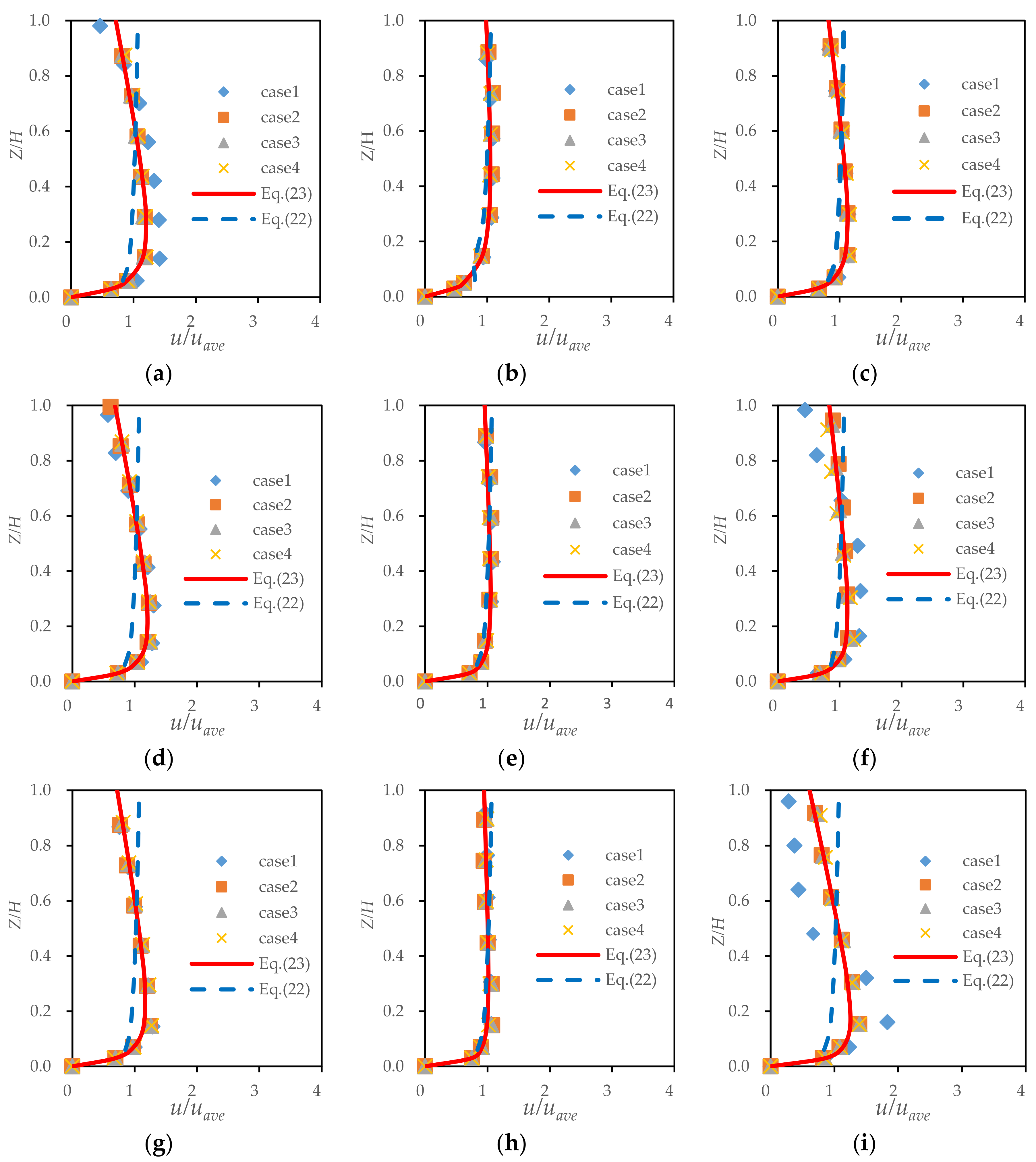
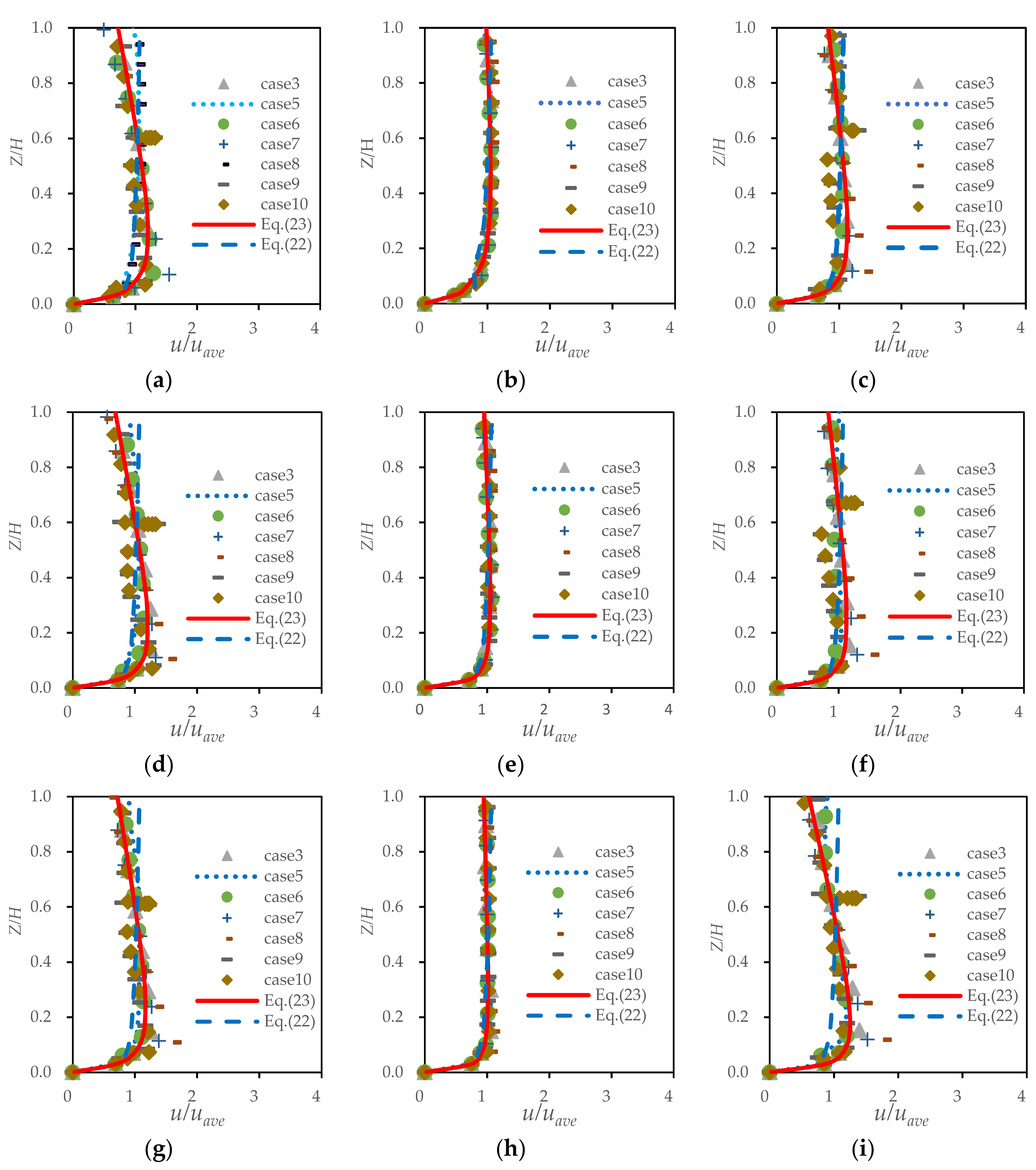
3.2. Analysis of the Longitudinal Velocity
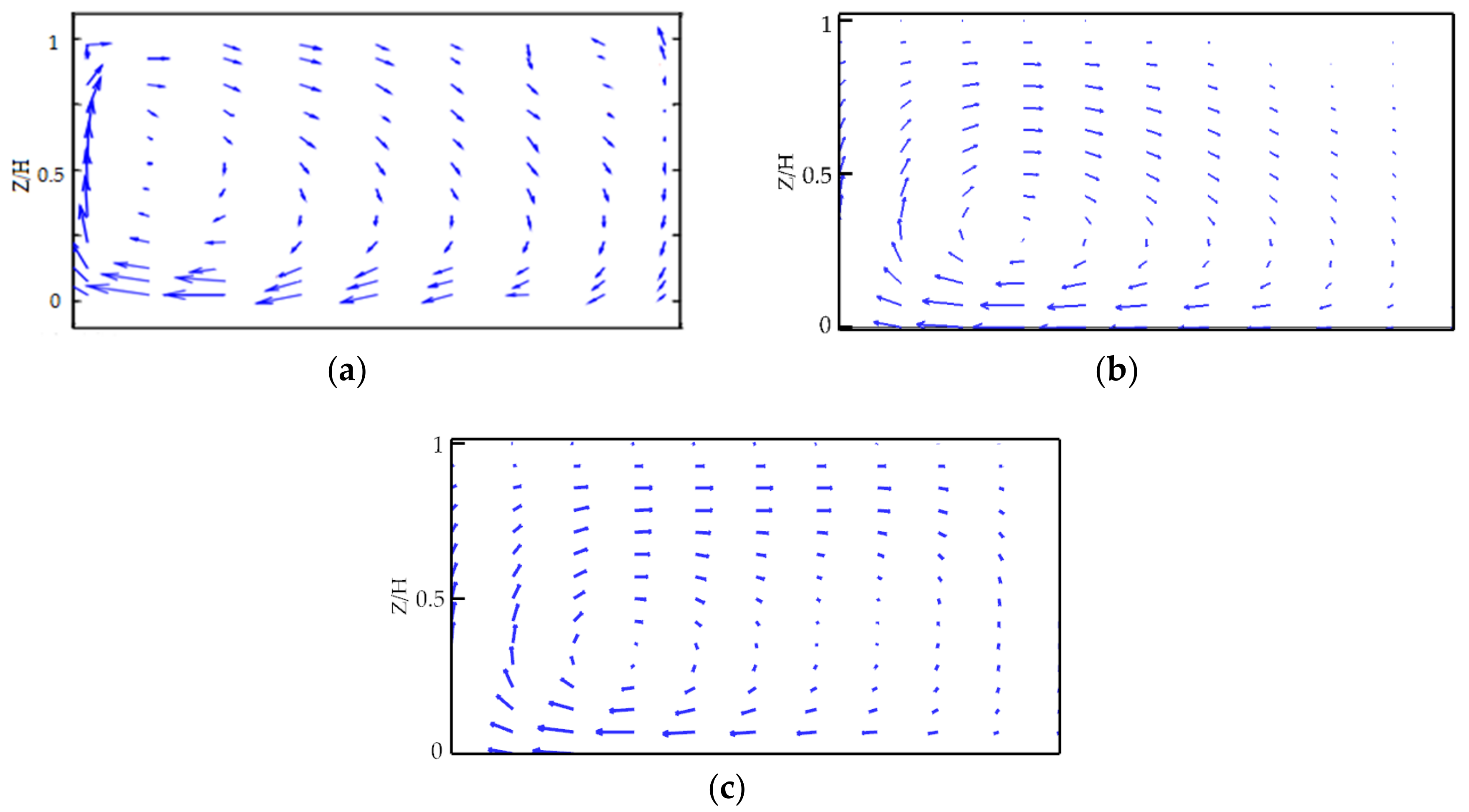
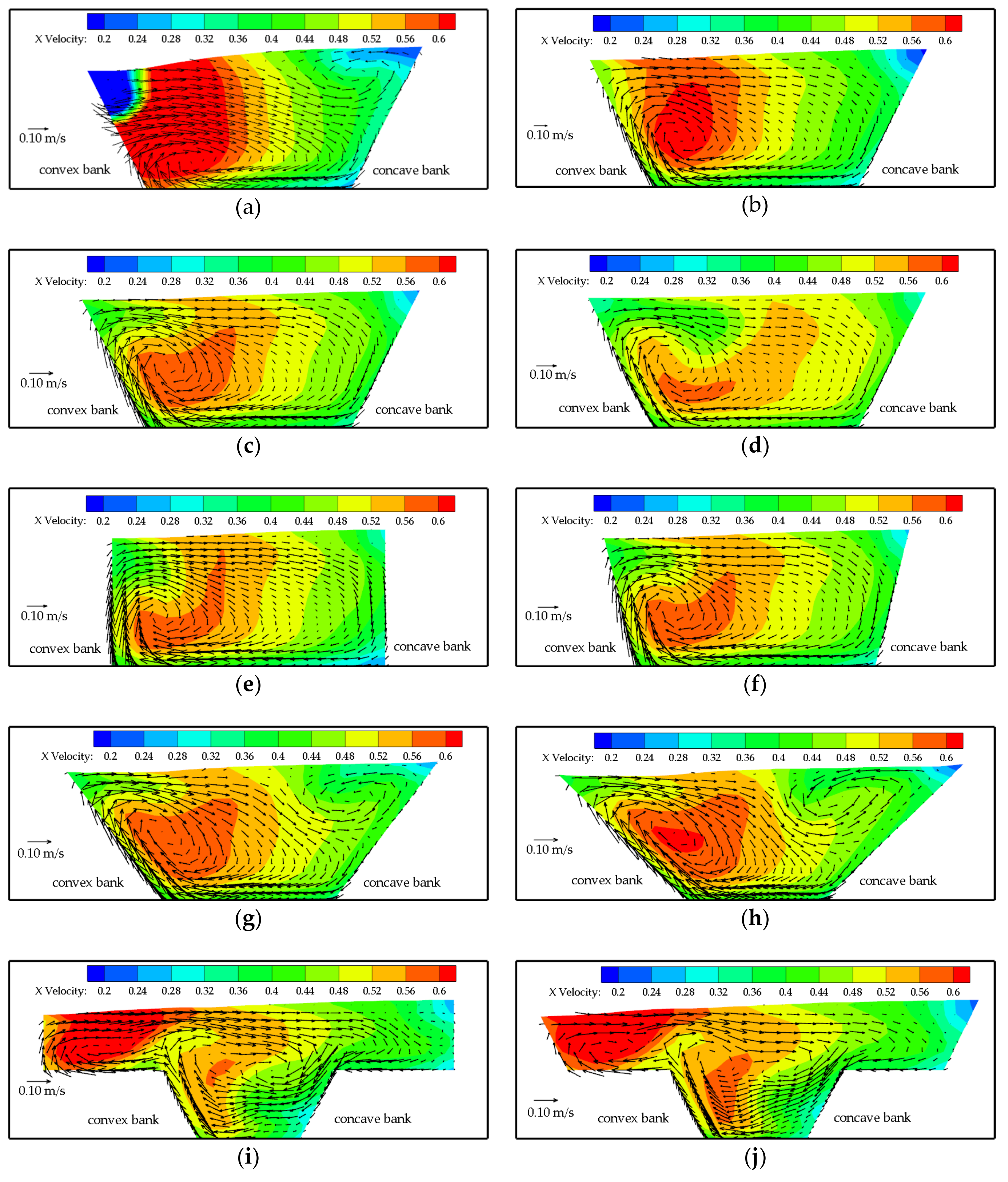
3.3. Analysis of the Secondary Flow
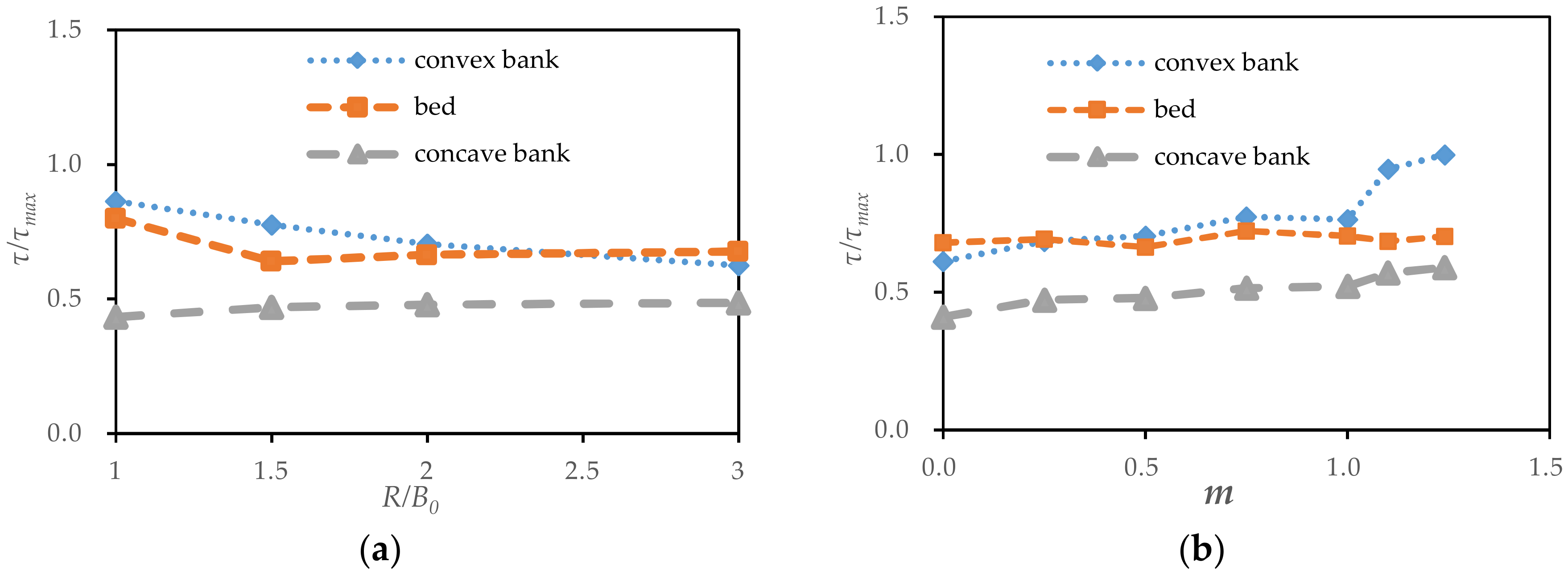
3.4. Analysis of the Shear Stress
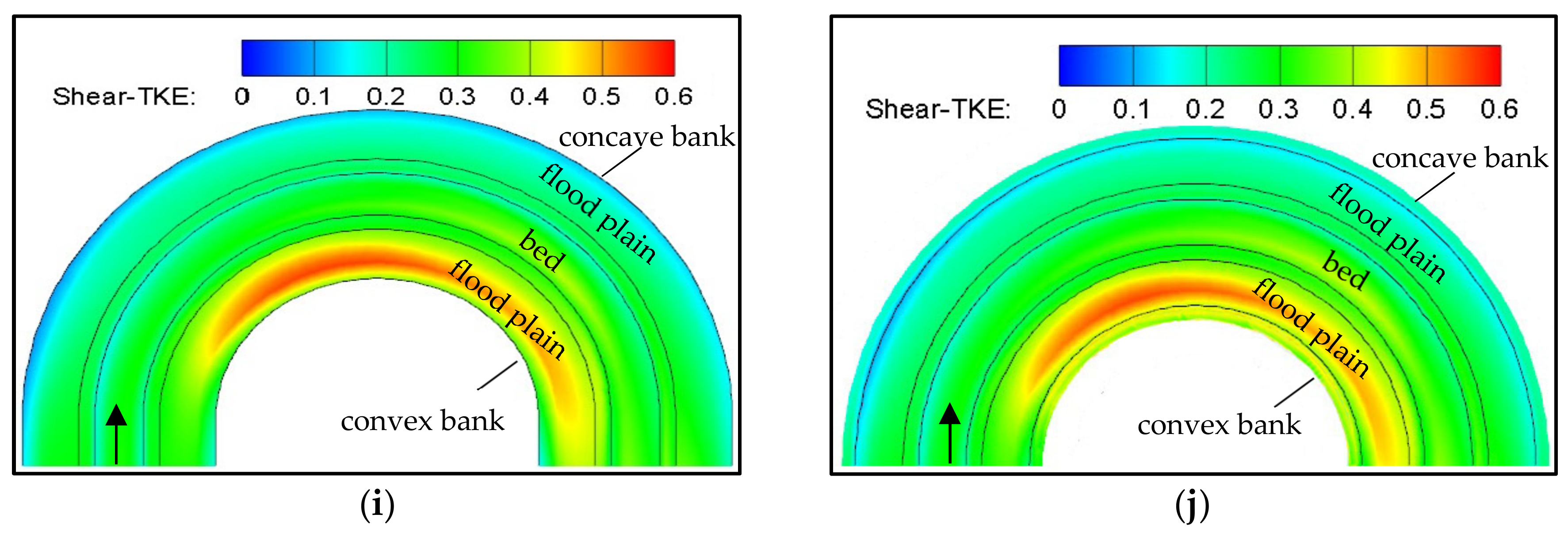
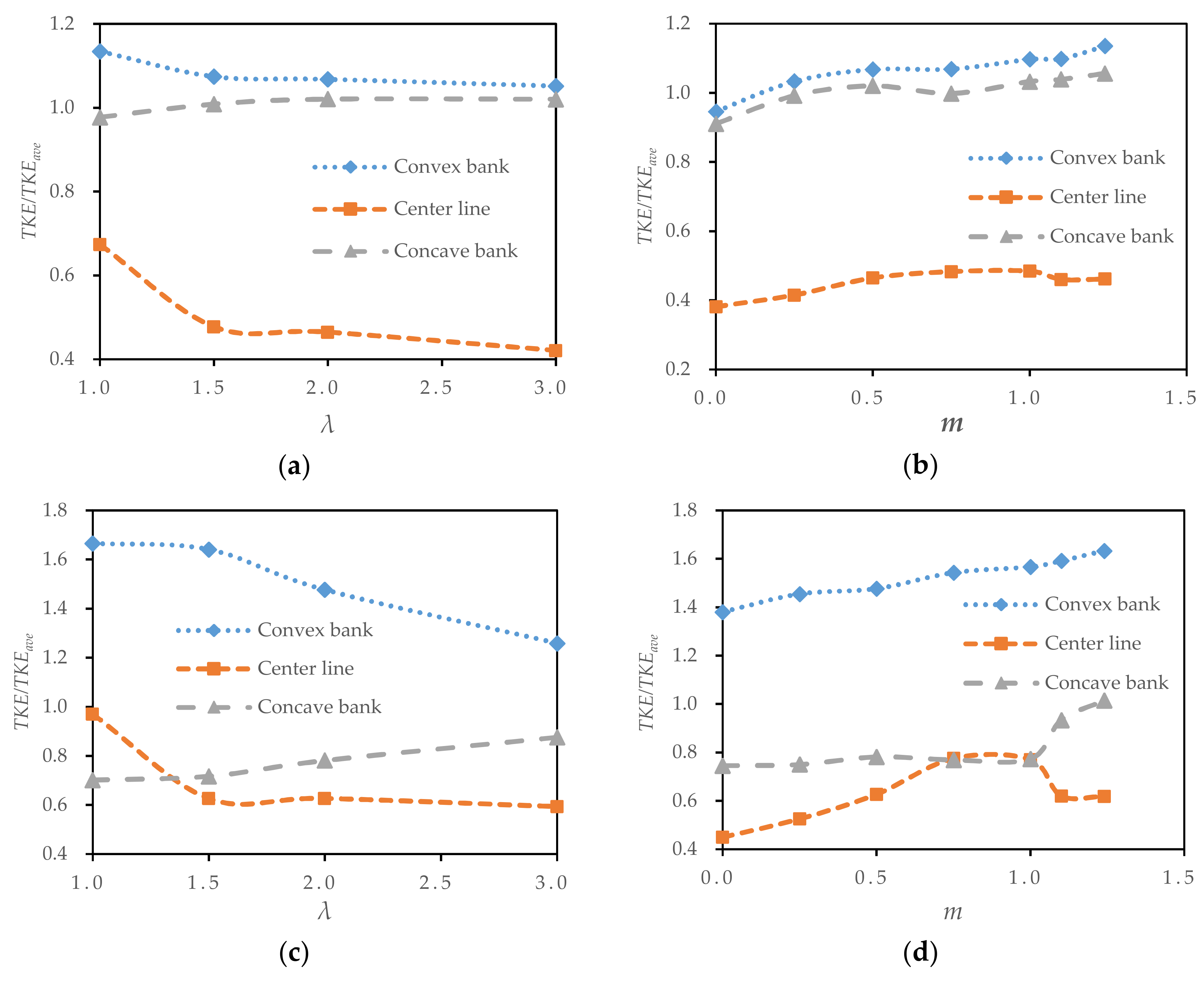
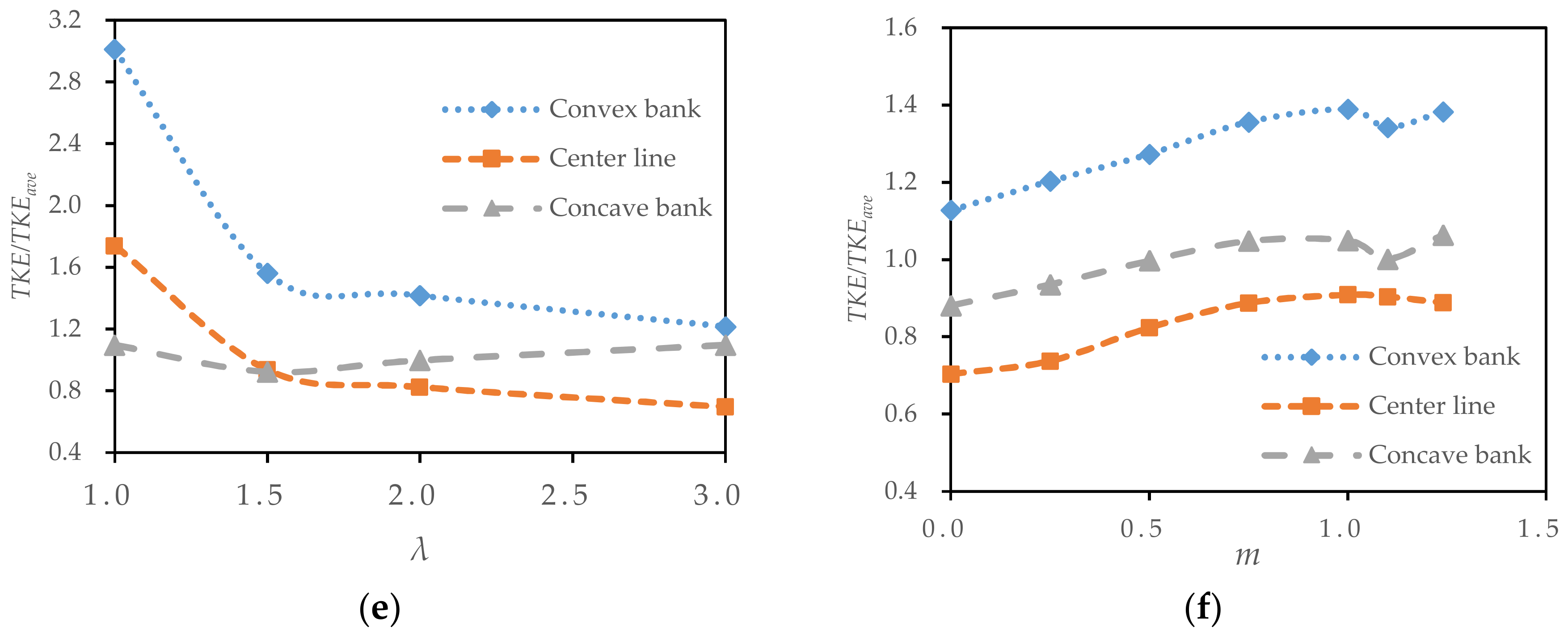
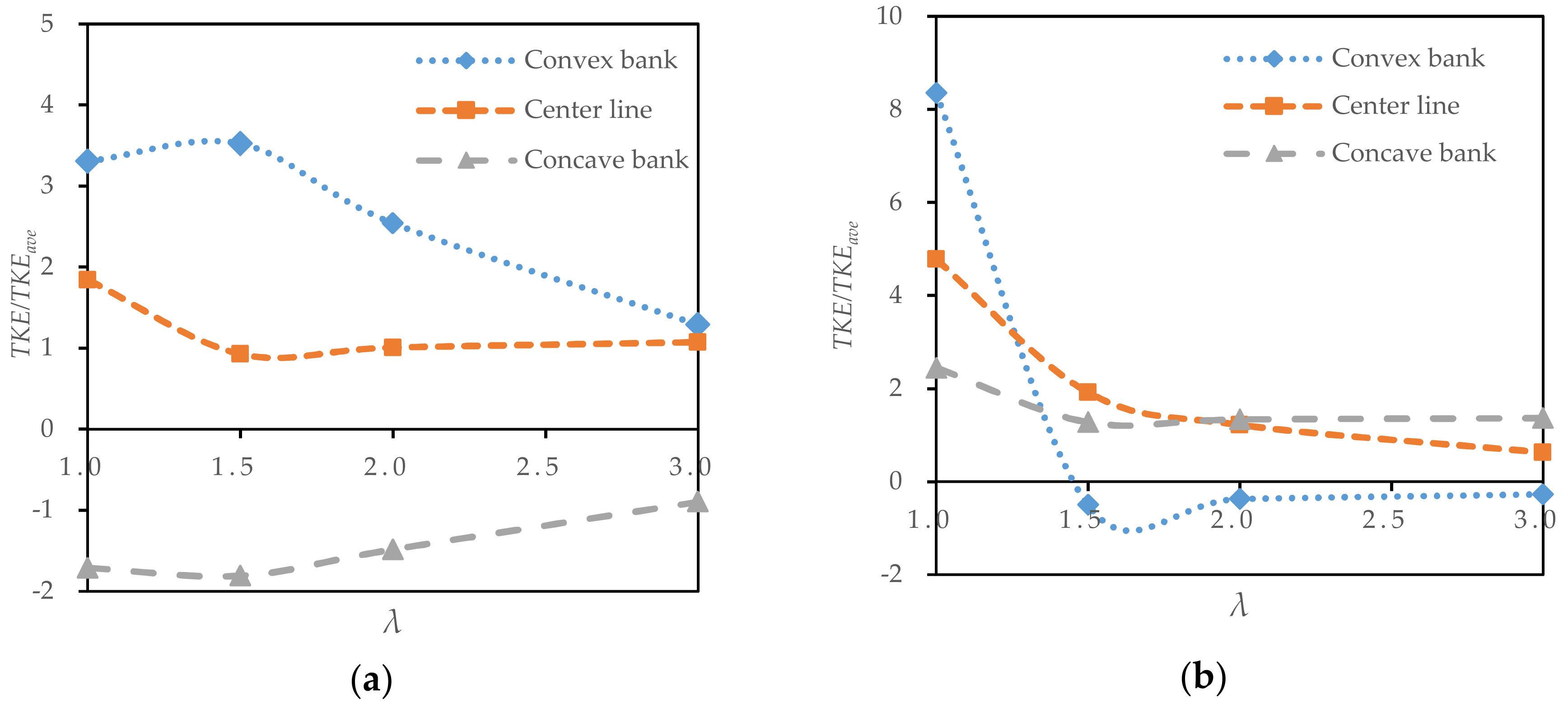
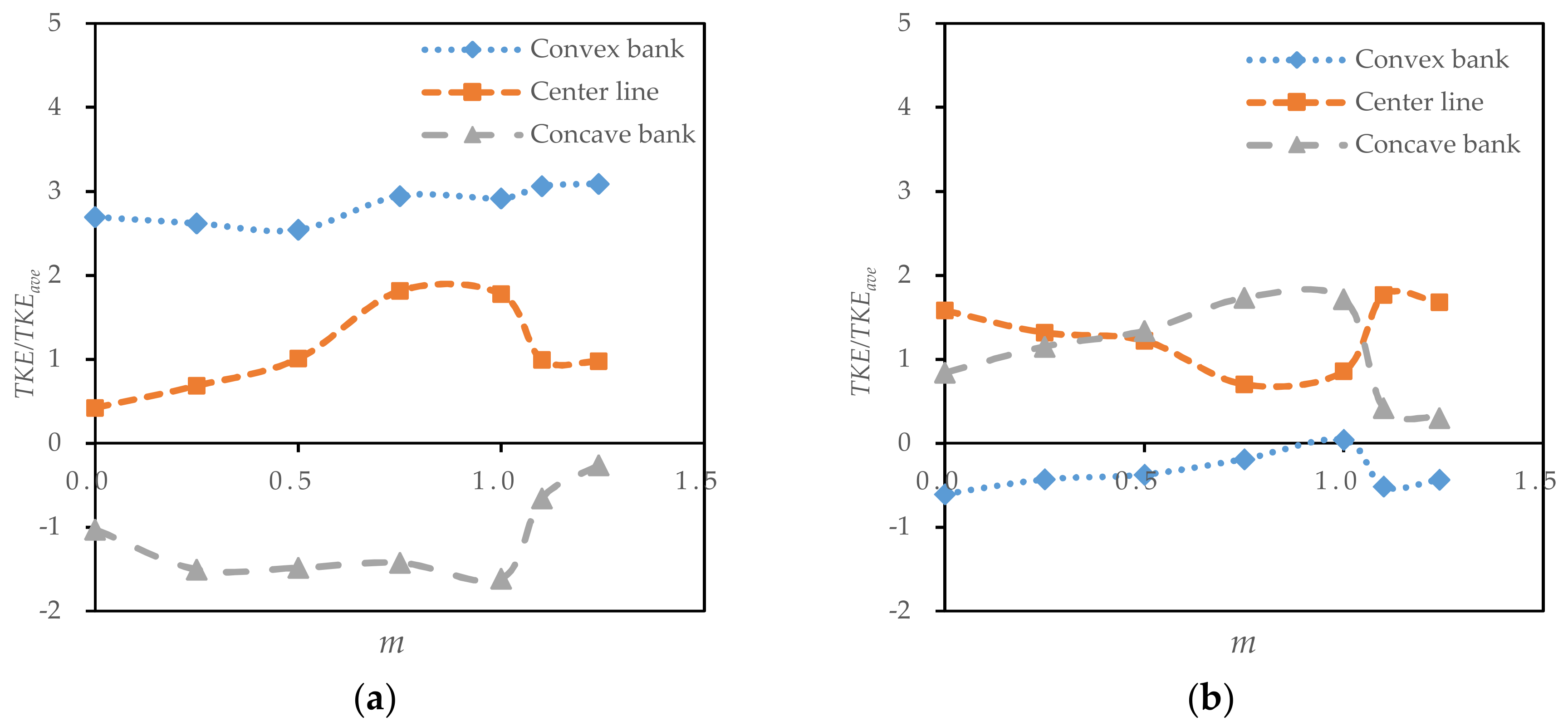
3.5. Analysis of the TKE
4. Conclusions
- (1)
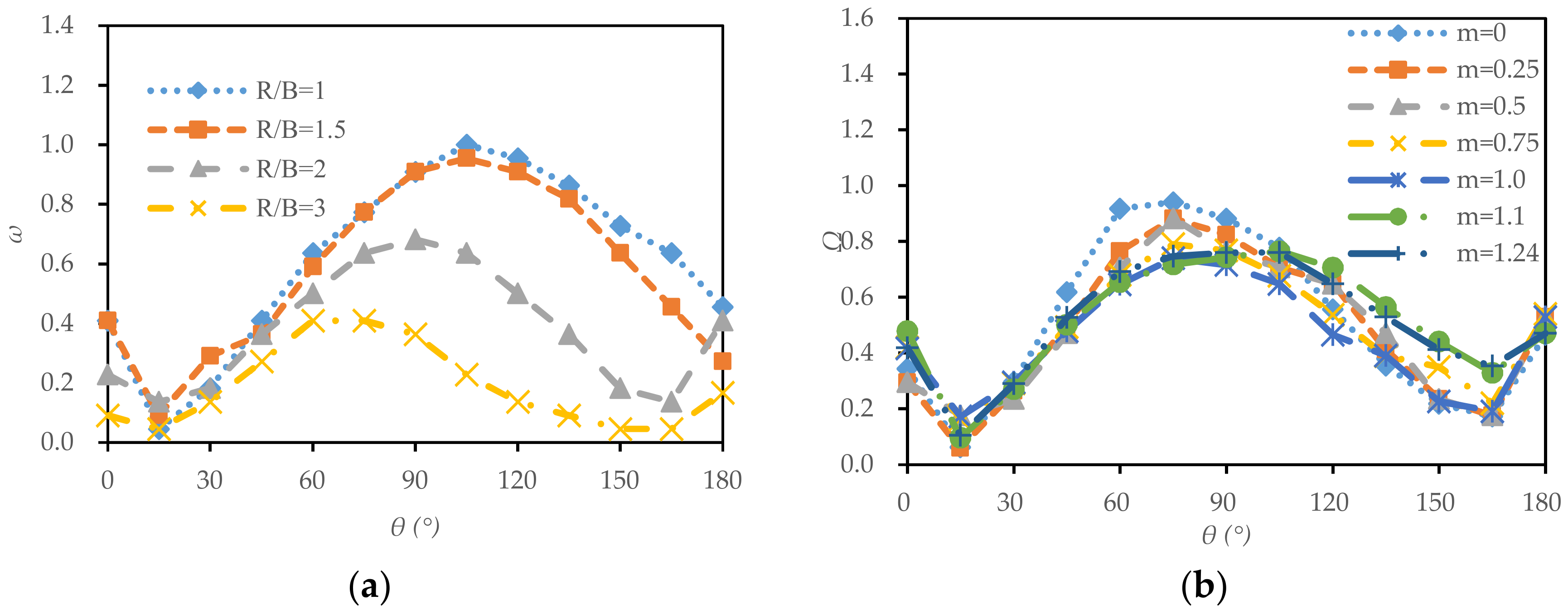
- The transverse slope decreased with increasing radius-to-width ratios and increased with increasing slope coefficients. The effect of the radius-to-width ratio on the WTS in the bend apex was greater than that of the slope coefficient.
- (2)
- A new equation concerning the vertical distribution of the longitudinal velocity in trapezoidal cross-section channel was proposed. The influence of the slope coefficient on the distribution of the longitudinal velocity was higher than that of the radius-to-width ratio.
- (3)
- The slope coefficient had an effect on the structure of secondary flow in the bend. When the slope coefficient was large enough (m = 0.75 in the present study), obvious double vortexes were captured in the bend apex. The corresponding angle of the maximum intensity of secondary flow in the bend gradually moved to the upstream with increasing radius-to-width ratios. The intensity of secondary flow in the bend gradually decreased with the increase in slope coefficients.
- (4)
- The maximum of the shear stress of the bend was observed in the convex bank, which decreased gradually and the corresponding angle decreased with increasing radius-to-width ratios. As the slope coefficient increased, the maximum of the shear stress in the convex bank gradually increased.
- (5)
- The maximum TKE of the section in the bend decreased with increasing radius-to-width ratios and increased with increasing slope coefficients.
Author Contributions
Funding
Conflicts of Interest
References
- Blanckaert, K.; Graf, W.H. Momentum transport in sharp open-channel bends. J. Hydraul. Eng. 2004, 130, 186–198. [Google Scholar] [CrossRef]
- Hey, R.D.; Thorne, C.R. Secondary flows in river channels. Area 1975, 7, 191–195. [Google Scholar]
- Kabiri, S.A.; Farshi, F.; Chamani, M.R. Boundary shear stress in smooth trapezoidal open channel flows. J. Hydraul. Eng. 2013, 139, 205–212. [Google Scholar] [CrossRef]
- Knight, D.W.; Omran, M.; Tang, X.N. Modeling depth-averaged velocity and boundary shear in trapezoidal channels with secondary flows. J. Hydraul. Eng. 2007, 133, 39–47. [Google Scholar] [CrossRef]
- Shiono, K.; Muto, Y. Complex flow mechanisms in compound meandering channels with overbank flow. J. Fluid Mech. 1998, 376, 221–261. [Google Scholar] [CrossRef]
- Knight, D.W.; Shiono, K. Turbulence measurements in a shear layer region of a compound channel. J. Hydraul. Res. 1990, 28, 175–196. [Google Scholar] [CrossRef]
- Tominaga, A.; Nezu, L.; Ezaki, K.; Nakagawa, H. Three-dimensional turbulent structure in straight open channel flows. J. Hydraul. Res. 1989, 27, 149–173. [Google Scholar] [CrossRef]
- Yang, S.Q.; Lim, S.Y. Boundary shear stress distributions in trapezoidal channels. J. Hydraul. Res. 2005, 43, 98–102. [Google Scholar] [CrossRef]
- Ansar, K.; Morvan, H.P.; Hargreaves, D.M. Numerical Investigation into Secondary flow and Wall Shear in Trapezoidal Channels. J. Hydraul. Eng. 2011, 137, 432–440. [Google Scholar] [CrossRef]
- Farhadi, A.; Sindelar, C.; Tritthart, M.; Glas, M.; Blanckaert, K.; Habersack, H. An investigation on the outer bank cell of secondary flow in channel bends. J. Hydro-Envrion. Res. 2018, 18, 1–11. [Google Scholar] [CrossRef]
- Termini, D.; Piraino, M. Experimental analysis of cross-sectional flow motion in a large amplitude meandering bend. Earth Surf. Process. Landf. 2011, 36, 244–256. [Google Scholar] [CrossRef]
- Shukla, D.R.; Shiono, K. CFD modelling of meandering channel during floods. Water Manag. 2008, 161, 1–12. [Google Scholar] [CrossRef]
- Mosalman, A.; Mosalman, M.; Yazdi, H.M. Equations of unsteady flow in curved trapezoidal channels. Int. J. Phys. Sci. 2011, 6, 671–676. [Google Scholar] [CrossRef]
- Shao, S.D. Simulation of breaking wave by SPH method coupled with k-epsilon model. Int. J. Numer. Methods Fluids 2006, 44, 338–349. [Google Scholar] [CrossRef]
- Shao, S.D.; Ji, C.M. SPH computation of plunging waves using a 2-D sub-particle scale (SPS) turbulence model. J. Hydraul. Res. 2010, 51, 913–936. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Burrows, R. Modelling the free surface flow in rectangular shallow basins by lattice Boltzmann method. J. Hydraul. Eng. 2011, 137, 1680–1685. [Google Scholar] [CrossRef]
- Peng, Y.; Zhou, J.G.; Burrows, R. Modelling solute transport in shallow water with the lattice Boltzmann method. Comput. Fluids 2011, 50, 181–188. [Google Scholar] [CrossRef]
- Peng, Y.; Mao, Y.F.; Wang, B.; Xie, B. Study on C-S and P-R EOS in pseudo-potential lattice Boltzmann model for two-phase flows. Int. J. Mod. Phys. C 2017, 28, 1750120. [Google Scholar] [CrossRef]
- Bai, R.; Liu, S.; Tian, Z.; Wang, W.; Zhang, F. Experimental investigations of air-water flow properties of offse-aerator. J. Hydraul. Eng. 2017, 144, 04017059. [Google Scholar] [CrossRef]
- Bai, R.; Zhang, F.; Liu, S.; Wang, W. Air concentration and bubble characteristics downstream of a chute aerator. Int. J. Multiph. Flow 2016, 87, 156–166. [Google Scholar] [CrossRef]
- Ducoin, A.; Shadloo, M.S.; Roy, S. Direct Numerical Simulation of flow instabilities over Savonius style wind turbine blades. Renew. Energy 2017, 105, 374–385. [Google Scholar] [CrossRef]
- Mendez, M.; Shadloo, M.S.; Hadjadj, A.; Ducoin, A. Boundary layer transition over a concave surface caused by centrifugal instabilities. Comput. Fluids 2018, 171, 135–153. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Hadjadj, A.; Hussain, F. Statistical behavior of supersonic turbulent boundary layers with heat transfer at M∞= 2. Int. J. Heat Fluid Flow 2015, 53, 113–134. [Google Scholar] [CrossRef]
- Ma, M. Flow Characteristics and Influence of Geometric Factors in a Bend. Ph.D. Thesis, Xi’an University of Technology, Xi’an, China, 2017. (In Chinese). [Google Scholar]
- Bai, Z.L.; Peng, Y.; Zhang, J.M. Three-Dimensional Turbulence Simulation of Flow in a V-Shaped Stepped Spillway. J. Hydraul. Eng. 2017, 143, 06017011. [Google Scholar] [CrossRef]
- Sun, X.; Shiono, K.; Rameshwaran, P. Modelling vegetation effects in irregular meandering river. J. Hydraul. Res. 2010, 48, 775–783. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization group analysis of turbulence: I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Han, Z.; Reitz, R.D. Turbulence modeling of internal combustion engines using RNG k~ε models. Combust. Sci. Technol. 1995, 106, 267–295. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure of estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001–078004. [Google Scholar] [CrossRef]
- Liu, H.F. The study of water surface in curved channel. J. Hydraul. Eng. 1990, 4, 46–50. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, H.W.; Lv, X. Hydraulics in the Curved Channel, 1st ed.; China Water Power Press: Beijing, China, 1993; pp. 48–49. ISBN 7–120-02333-0/TV•835. (In Chinese) [Google Scholar]
- Chang, H.H. Fluvial Processes in River Engineering; John Wiley and Sons: New York, NY, USA, 1988. [Google Scholar]
- Sarma, K.V.N.; Lakshminatayana, P.; Rao, N.S.L. Velocity distribution in smooth rectangular open channels. J. Hydraul. Eng. 1988, 109, 270–289. [Google Scholar] [CrossRef]
- Yan, J.; Tang, H.W.; Xiao, Y.; Li, K.J.; Tian, Z.J. Experimental study on influence of boundary on location of maximum velocity in open channel flows. Water Sci. Eng. 2011, 4, 185–191. [Google Scholar] [CrossRef]
- Song, T.; Graf, W.H. Velocity and turbulence distribution in unsteady open-channel flows. J. Hydraul. Eng. 1996, 122, 141–154. [Google Scholar] [CrossRef]
- Kirkgoz, M.S. Turbulent Velocity Profiles for Smooth and Rough Open Channel Flow. J. Hydraul. Eng. 1989, 115, 1543–1561. [Google Scholar] [CrossRef]
- Abhari, M.N.; Ghodsian, M.; Vaghefi, M.; Panahpur, N. Experimental and numerical simulation of flow in a 90° bend. Flow Meas. Instrum. 2010, 21, 292–298. [Google Scholar] [CrossRef]
- Vaghefi, M.; Akbari, M.; Fiouz, A.R. An Experimental Study of Mean and Turbulent Flow in a 180 Degree Sharp Open Channel Bend: Secondary Flow and Bed Shear Stress. KSCE J. Civ. Eng. 2016, 20, 1582–1593. [Google Scholar] [CrossRef]
- Koopaei, K.B.; Ervine, D.A.; Carling, P.A.; Cao, Z. Velocity and turbulence measurements for two overbank flow events in River Severn. J. Hydraul. Eng. 2002, 128, 891–900. [Google Scholar] [CrossRef]
- Williams, J.J.; Rose, C.P.; Thorne, P.D.; O’connor, B.A.; Humphery, J.D.; Hardcastle, P.J.; Moores, S.P.; Cooke, J.A.; Wilson, D.J. Field observations and predictions of bed shear stresses and vertical suspended sediment concentration profiles in wave-current conditions. Cont. Shelf Res. 1999, 19, 507–536. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flow, 1st ed.; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kim, S.C.; Friedrichs, C.T.; Ma, J.P.Y.; Wright, L.D. Estimating bottom stress in tidal boundary layer from acoustic Doppler velocimeter data. J. Hydraul. Eng. 2000, 126, 399–406. [Google Scholar] [CrossRef]
- Biron, P.M.; Robson, C.; Lapointe, M.F.; Gaskin, S.J. Comparing various methods of bed shear stress estimates in simple and complex flow fields. Earth Surf. Process. Landf. 2010, 29, 1403–1415. [Google Scholar] [CrossRef]
- Blanckaert, K.; Vriend, H.J. Turbulence characteristics in sharp open-channel bends. Phys. Fluids 2005, 17, 717–731. [Google Scholar] [CrossRef]
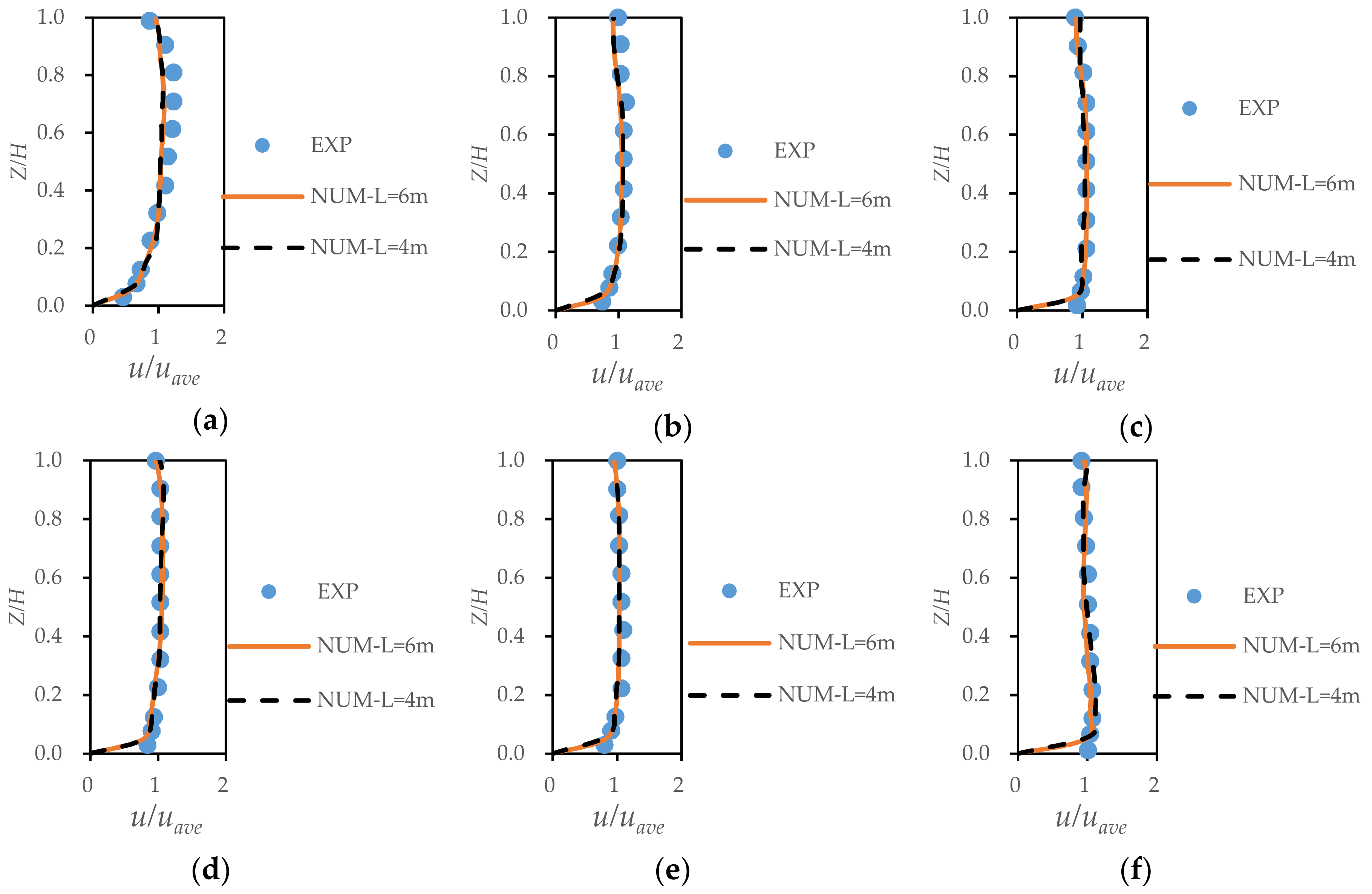
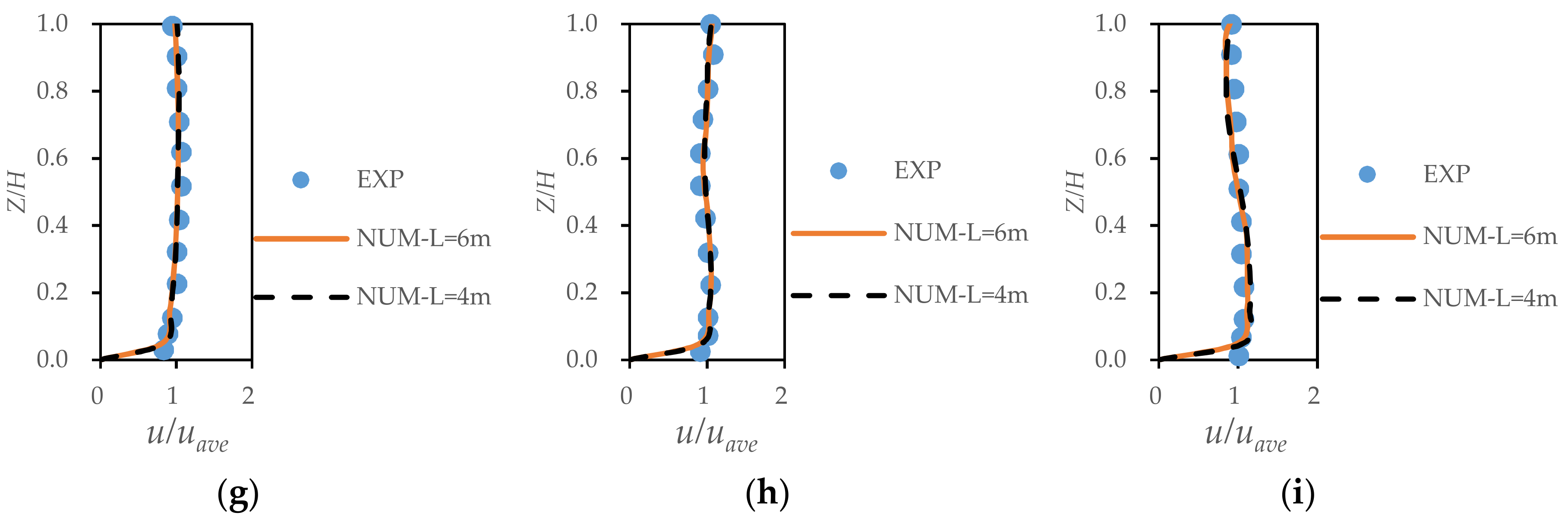
| Series | m | B | R | R1 | R2 | Q | B0 | Fr | Re | B0/H | Cells | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (°) | (m) | (m) | (m) | (m) | (L s−1) | (m) | |||||||
| case1 | 0.50 | 1.0 | 180 | 0.30 | 0.40 | 0.25 | 0.55 | 38 | 0.40 | 0.33 | 1.73 | 180,000 | |
| case2 | 0.50 | 1.5 | 180 | 0.30 | 0.60 | 0.45 | 0.75 | 38 | 0.40 | 0.33 | 1.73 | 180,000 | |
| case3 | 0.50 | 2.0 | 180 | 0.30 | 0.80 | 0.65 | 0.95 | 38 | 0.40 | 0.33 | 1.73 | 180,000 | |
| case4 | 0.50 | 3.0 | 180 | 0.30 | 1.20 | 1.05 | 1.35 | 38 | 0.40 | 0.33 | 1.73 | 180,000 | |
| case5 | 0.00 | 2.0 | 180 | 0.30 | 0.80 | 0.60 | 1.00 | 38 | 0.40 | 0.33 | 1.73 | 180,000 | |
| case6 | 0.25 | 2.0 | 180 | 0.35 | 0.80 | 0.625 | 0.975 | 38 | 0.40 | 0.33 | 1.73 | 180,000 | |
| case7 | 0.75 | 2.0 | 180 | 0.25 | 0.80 | 0.675 | 0.925 | 38 | 0.40 | 0.33 | 1.73 | 180,000 | |
| case8 | 1.00 | 2.0 | 180 | 0.20 | 0.80 | 0.70 | 0.90 | 38 | 0.40 | 0.33 | 1.73 | 180,000 | |
| case9 | 1.10 | 2.0 | 180 | 0.15 | 0.80 | 0.725 | 0.875 | 38 | 0.40 | 0.33 | 1.73 | 262,500 | |
| case10 | 1.24 | 2.0 | 180 | 0.15 | 0.80 | 0.725 | 0.875 | 38 | 0.40 | 0.33 | 1.73 | 262,500 |
| a | b | c | d | e | f | g | h | i | ||
|---|---|---|---|---|---|---|---|---|---|---|
| L = 6 m | Absolute error (m/s) | 0.03 | 0.05 | 0.06 | 0.04 | 0.06 | 0.05 | 0.01 | 0.06 | 0.07 |
| Relative error (%) | 12 | 10.8 | 13.9 | 15.4 | 12 | 12.5 | 4.6 | 13.3 | 14.6 | |
| L = 4 m | Absolute error (m/s) | 0.03 | 0.04 | 0.05 | 0.04 | 0.07 | 0.06 | 0.02 | 0.06 | 0.06 |
| Relative error (%) | 12 | 8.7 | 11.6 | 15.4 | 14 | 15 | 7.6 | 13.3 | 12.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, R.; Zhang, J. Numerical Analysis on Hydraulic Characteristics of U-shaped Channel of Various Trapezoidal Cross-Sections. Water 2018, 10, 1788. https://doi.org/10.3390/w10121788
Hu R, Zhang J. Numerical Analysis on Hydraulic Characteristics of U-shaped Channel of Various Trapezoidal Cross-Sections. Water. 2018; 10(12):1788. https://doi.org/10.3390/w10121788
Chicago/Turabian StyleHu, Ruichang, and Jianmin Zhang. 2018. "Numerical Analysis on Hydraulic Characteristics of U-shaped Channel of Various Trapezoidal Cross-Sections" Water 10, no. 12: 1788. https://doi.org/10.3390/w10121788
APA StyleHu, R., & Zhang, J. (2018). Numerical Analysis on Hydraulic Characteristics of U-shaped Channel of Various Trapezoidal Cross-Sections. Water, 10(12), 1788. https://doi.org/10.3390/w10121788





