Study on the Best Depth of Stilling Basin with Shallow-Water Cushion
Abstract
1. Introduction
2. Materials and Methods
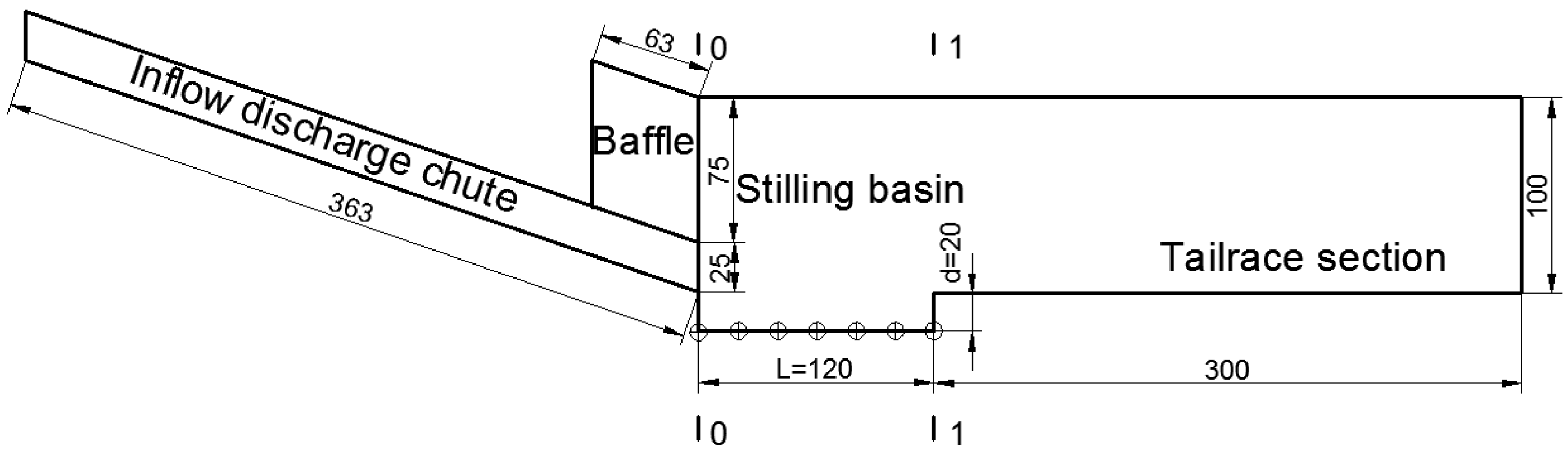
2.1. Experimental Setup
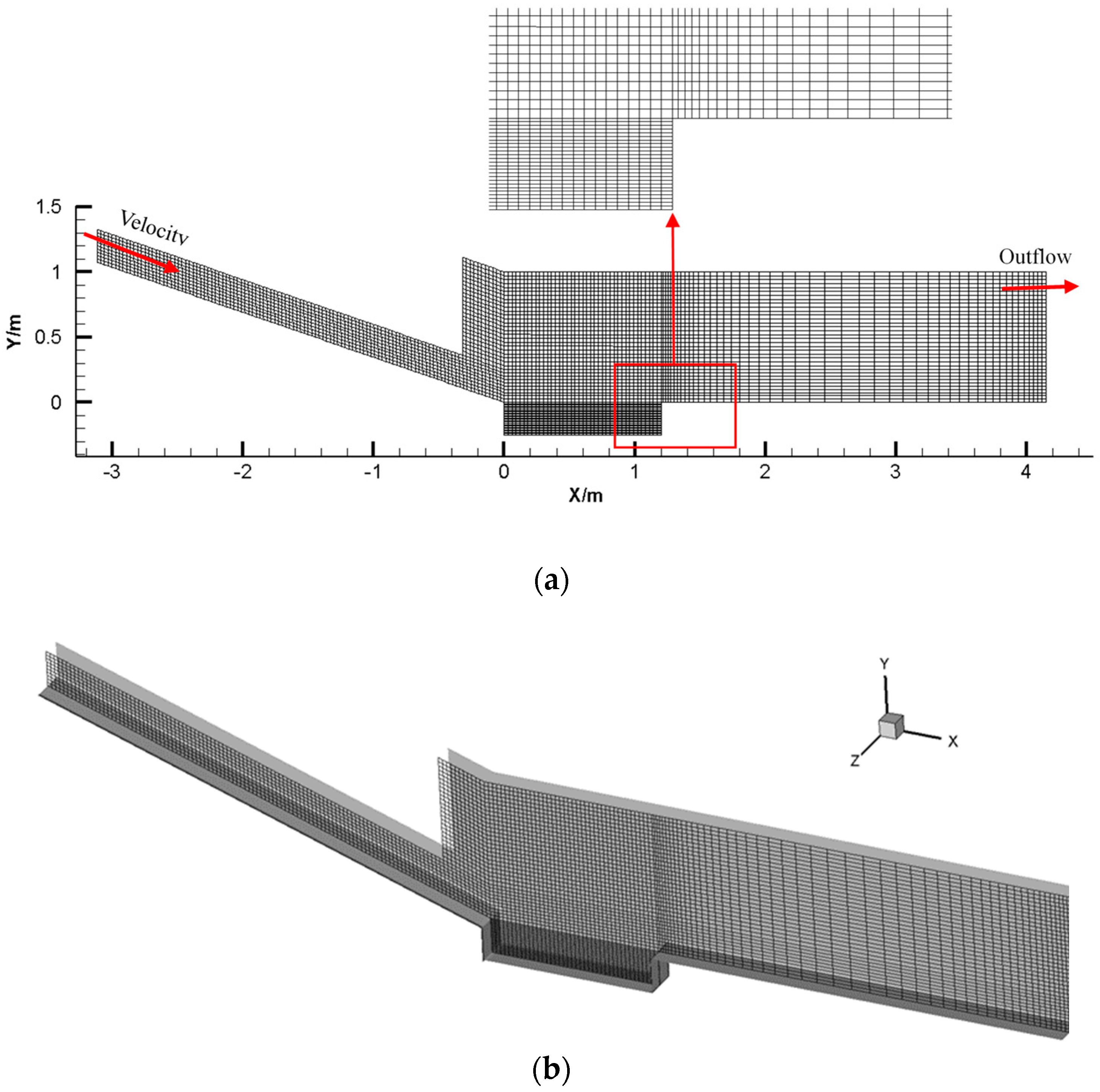
2.2. Mathematical Model
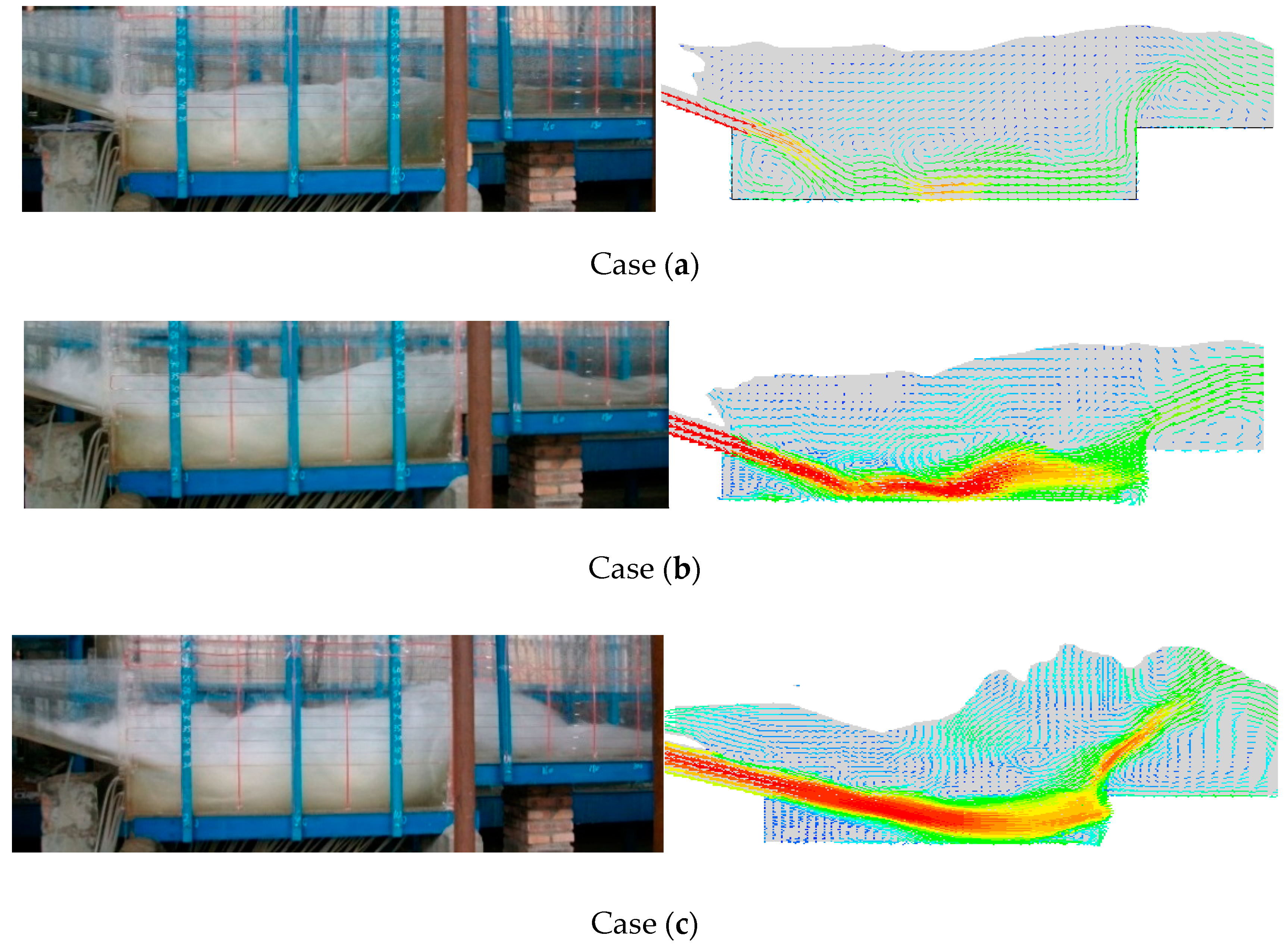
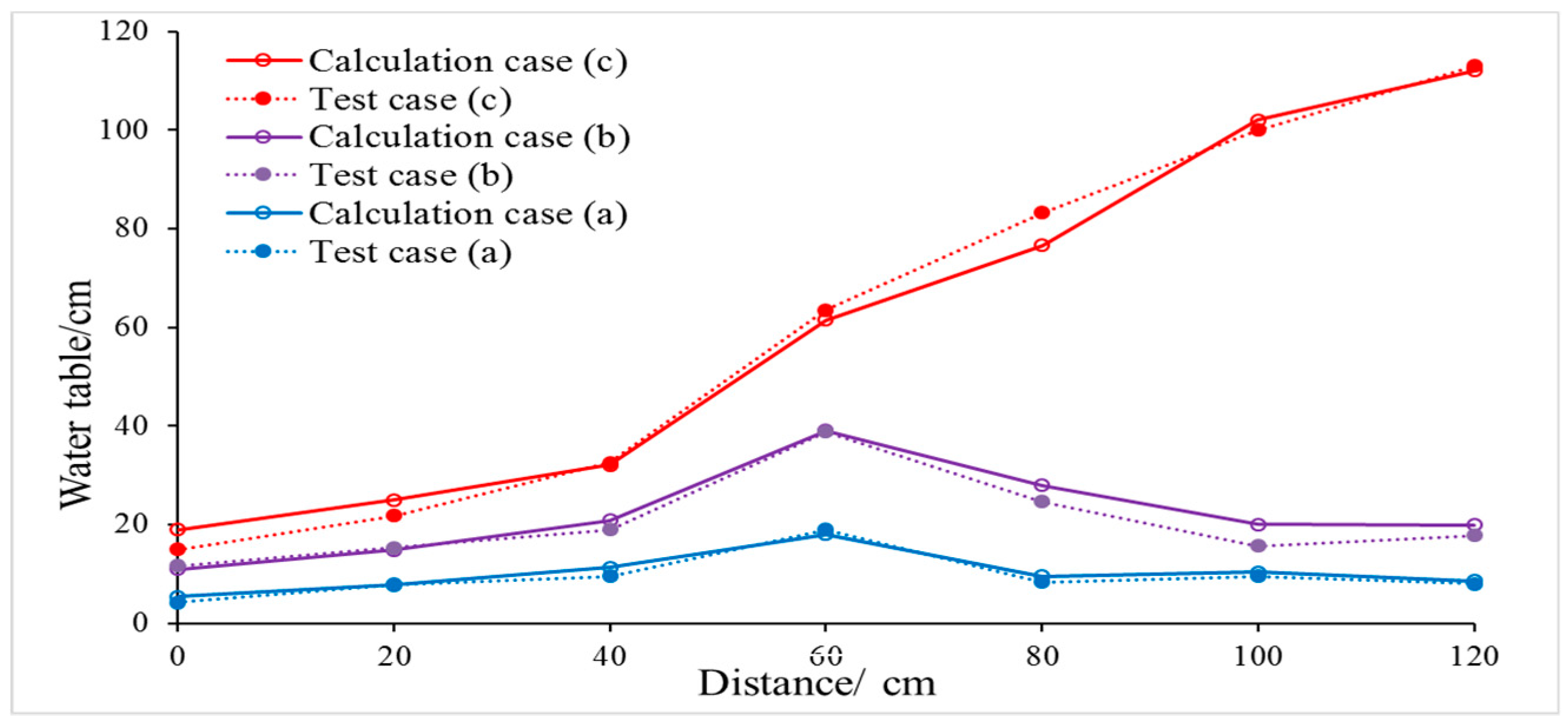
2.3. Verification of Mathematical Model
3. Results and Discussion
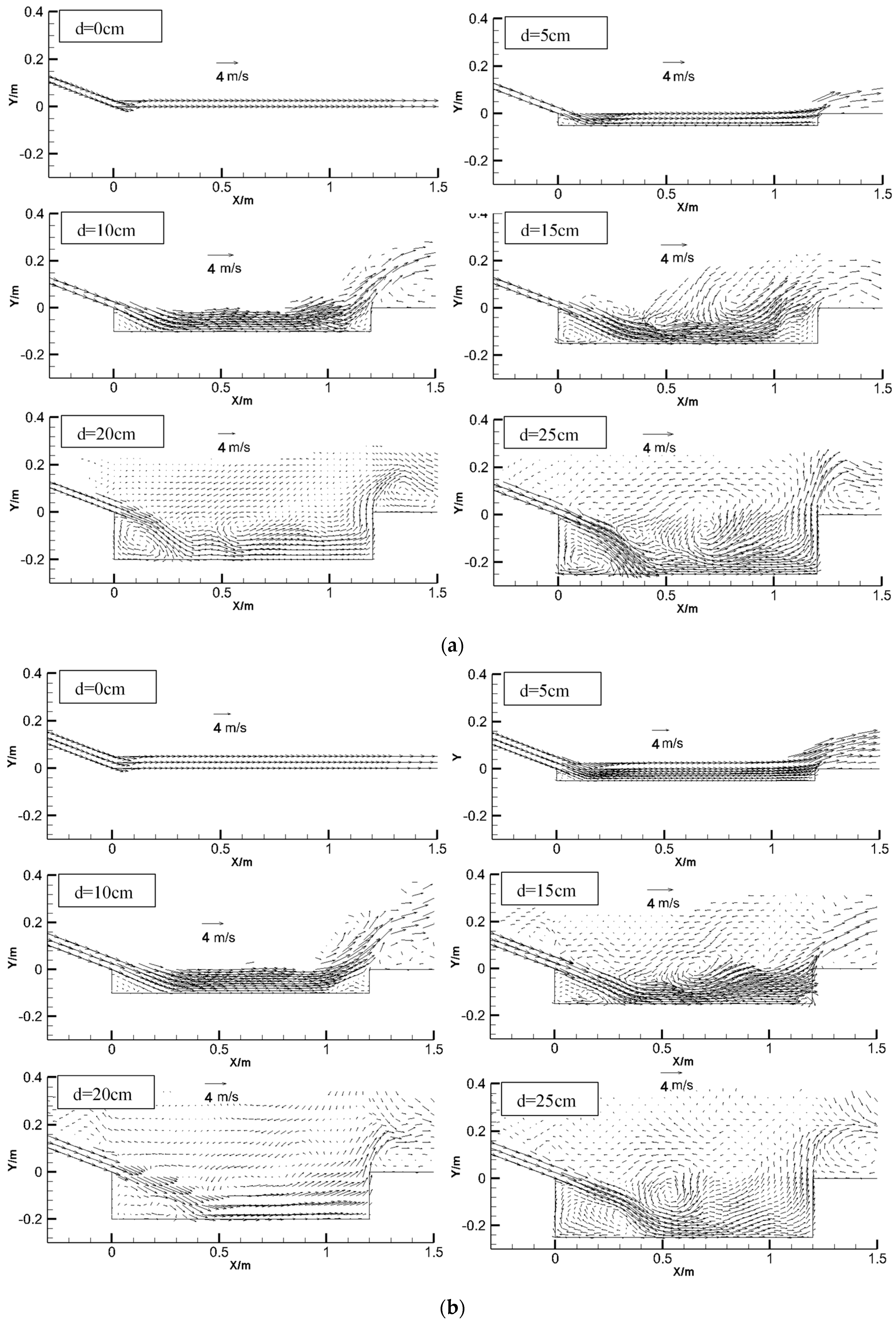
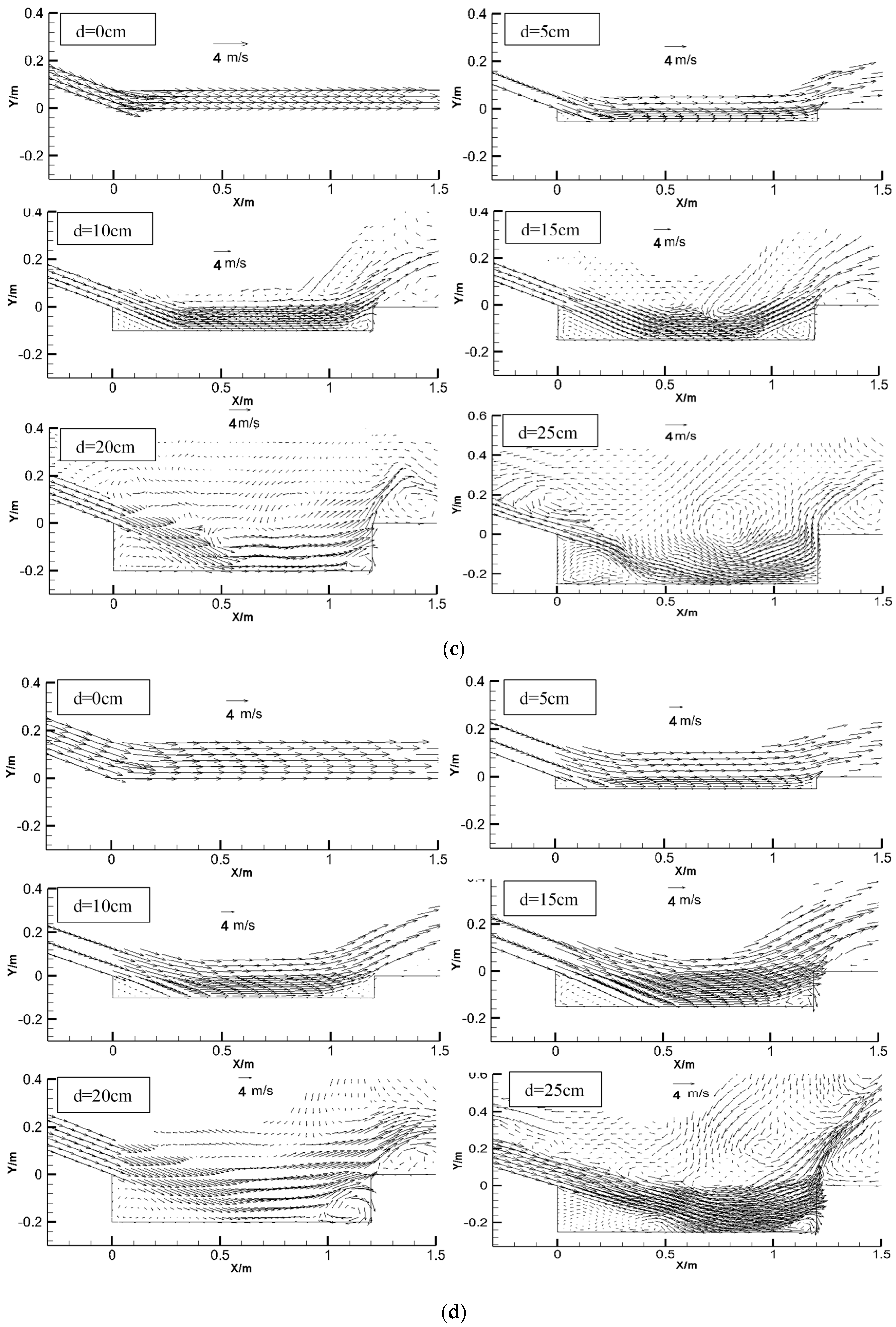
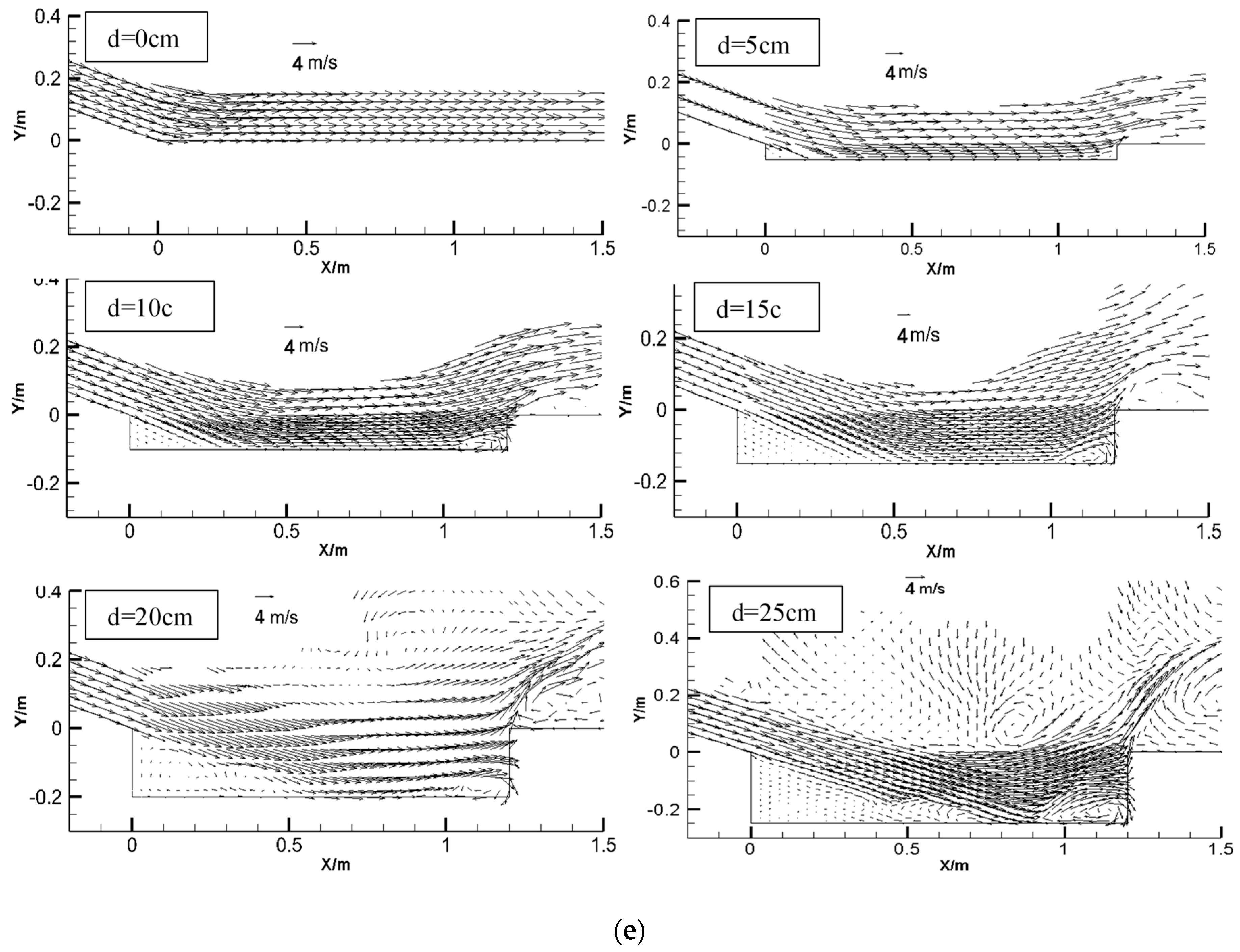
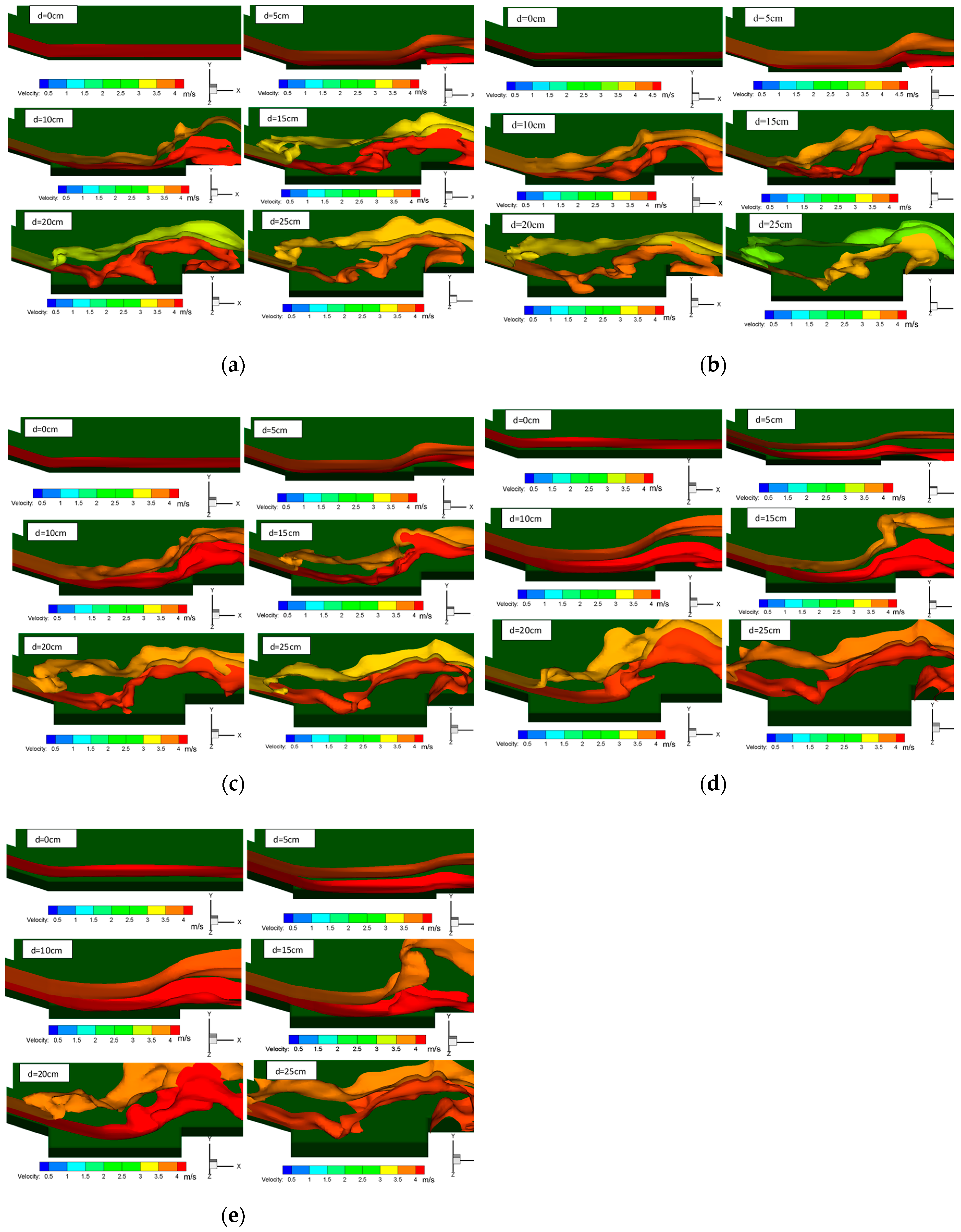
3.1. Flow Regime
3.2. Main Stream Location
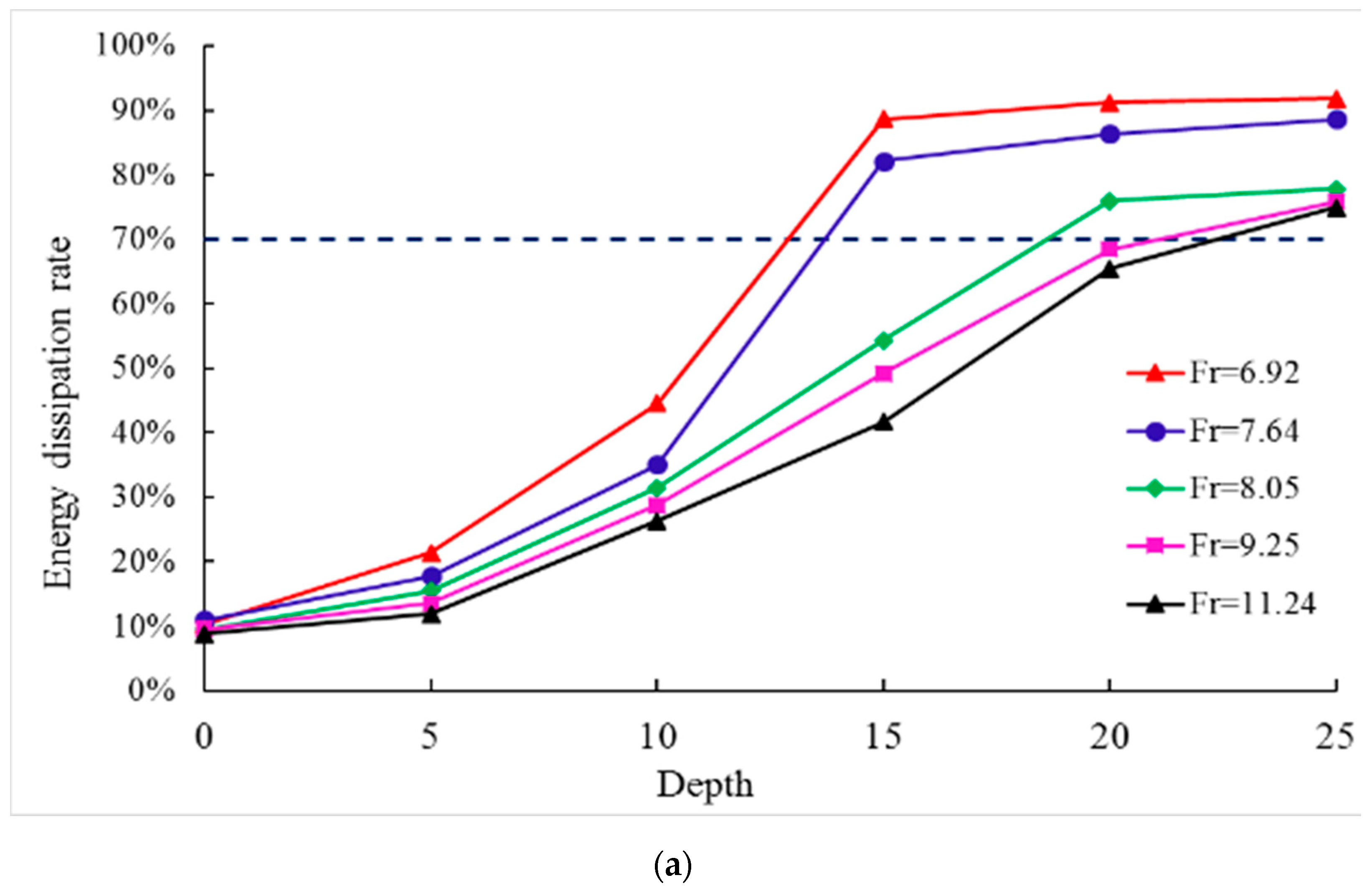
3.3. Energy Dissipation Rate
3.4. The Best Depth of the Stilling Basin
4. Conclusions
- After comparing large eddy simulation calculation results and model tests, the computation of the flow profile and hydraulic jumps were similar to the test, and the differences of the average pressure between test results and calculated results were very small except for individual locations. The numerical data and experimental results were in good agreement, indicating the reliability and accuracy of LES in the present work.
- Based on the experimental results of flow regime of hydraulic jump, the location of the main stream and the energy dissipation rate, for the first time three standards of the best depth of stilling basin with shallow water cushion (SBSWC) are proposed in this paper; namely, (1) a complete hydraulic jump must occur in the basin (2) the thickness of water cushion is about 1/10–1/3 deep of the basin, and (3) the energy dissipation rate is more than 70% and the unit volume energy dissipation rate is as high as possible.
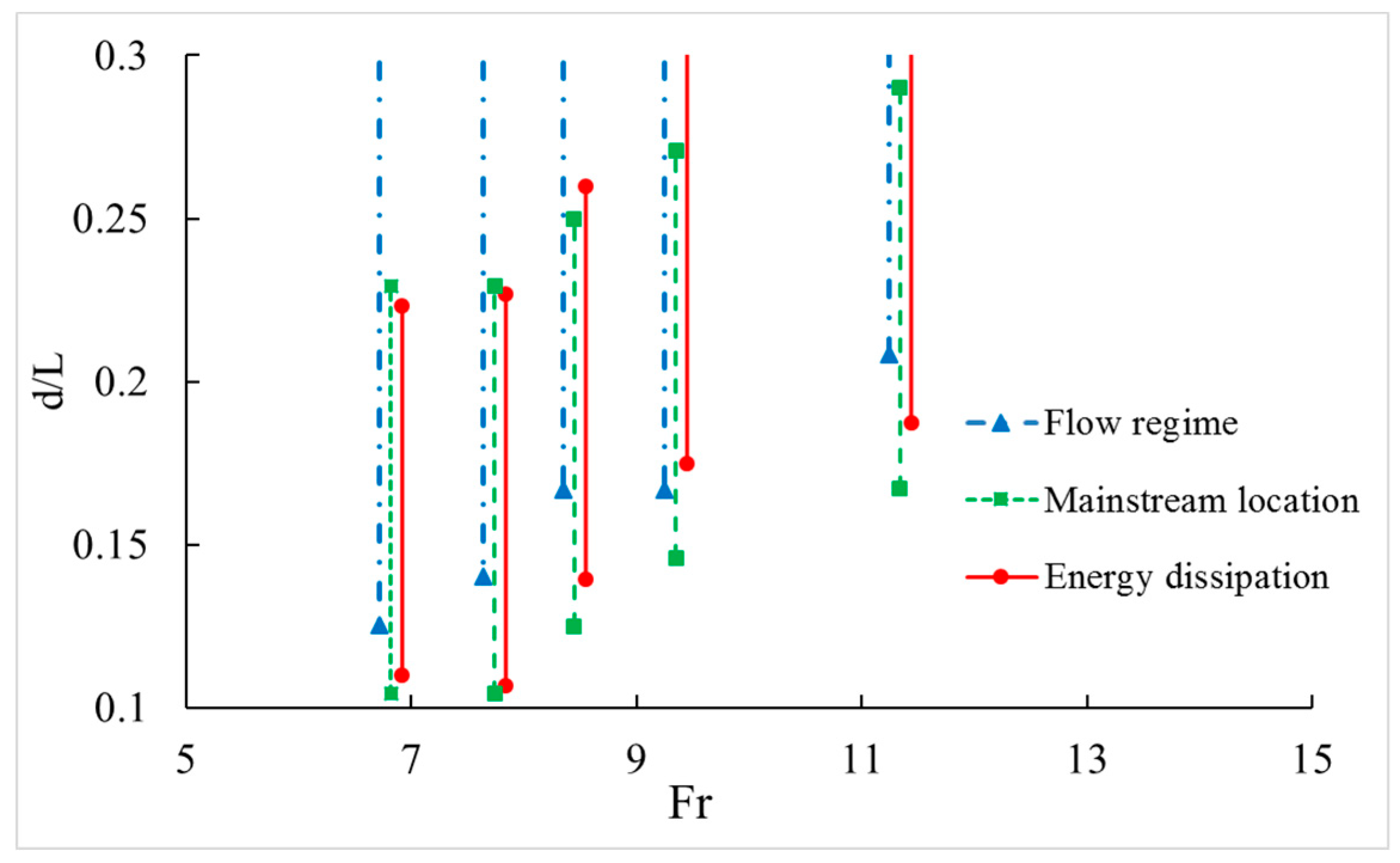
- According to the definition for the best depth of SBSWC, three ranges of the depth were depicted in the 5 different Froude numbers respectively. Therefore, the overlapping sections are the range of the best depth of stilling basin with shallow water cushion for this study.
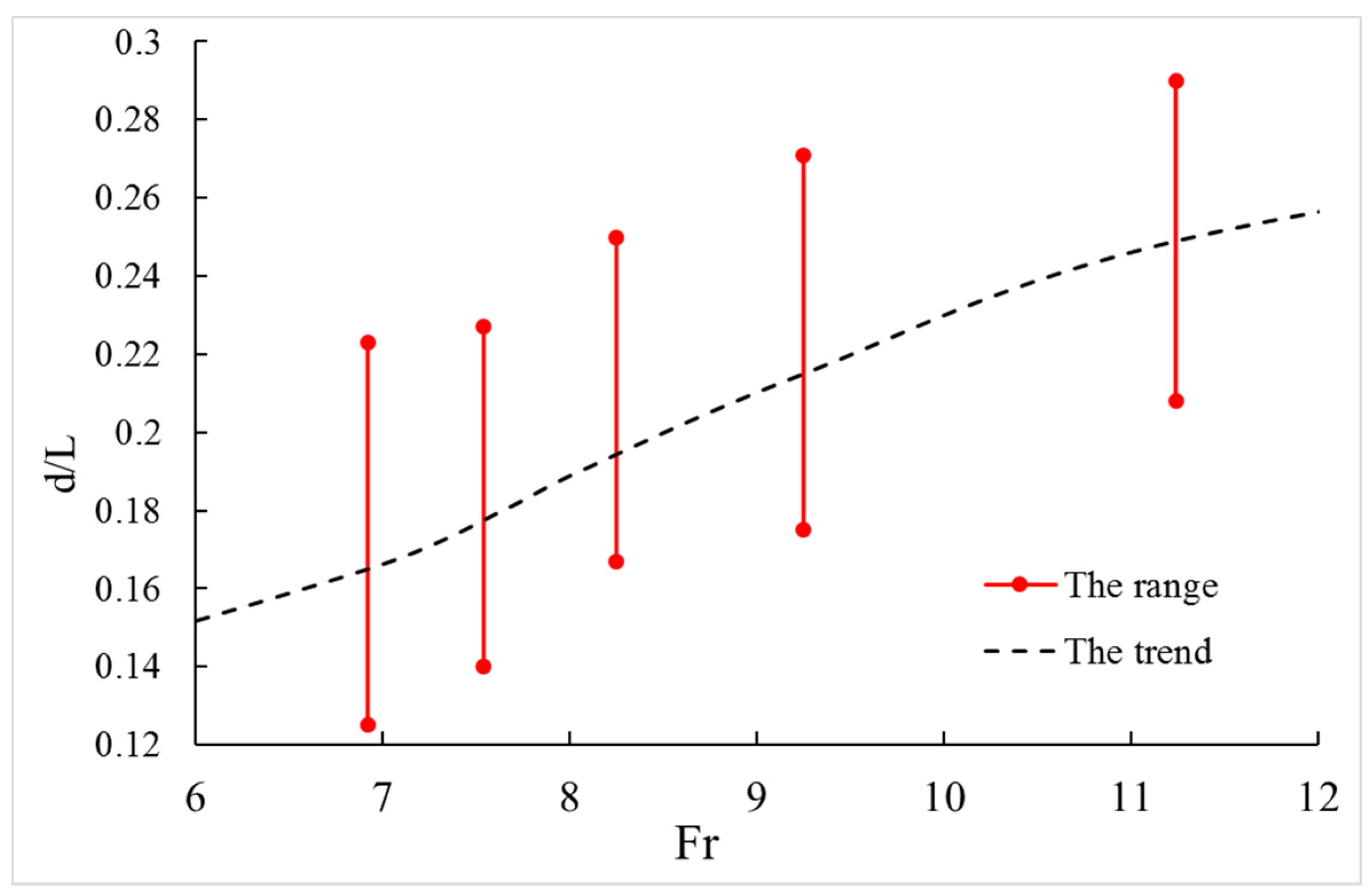
- It showed that the best depth radio of stilling basin with shallow-water cushion (depth to length ratio) was between 0.1 and 0.3 and it also indicated that the best depth of the stilling basin with shallow water cushion increased with the increase of Froude number. The results in this paper are of significance for design and optimizing of SBSWC.
Author Contributions
Funding
Conflicts of Interest
References
- Chanson, H. Current knowledge in hydraulic jumps and related phenomena. A survey of experimental results. Eur. J. Mech. B Fluids 2009, 28, 191–210. [Google Scholar] [CrossRef]
- Alikhani, A.; Behrozi-Rad, R.; Fathi-Moghadam, M. Hydraulic jump in stilling basin with vertical end sill. Int. J. Phys. Sci. 2010, 5, 25–29. Retrieved from http://www.academicjournals.org/IJPS.
- Chanson, H. Hydraulic condition for undular-jump formations. J. Hydraul. Res. 2001, 39, 203–209. [Google Scholar] [CrossRef]
- Zare, H.K.; Doering, J.C. Forced Hydraulic Jumps below Abrupt Expansions. J. Hydraul. Eng. 2011, 137, 825–835. [Google Scholar] [CrossRef]
- Champagne, T.M.; Barlock, R.R.; Ghimire, S.R.; Barkdoll, B.D.; Gonzalez-Castro, J.A.; Deaton, L. Scour Reduction by Air Injection Downstream of Stilling Basins: Optimal Configuration Determination by Experimentation. J. Irrig. Drain. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Tianxiang, L.I. Investigation on Hydraulic Performances of Stilling Basin with Shallow-Water Cushion. Master’s Thesis, State Key Laboratory of Hydraulics and Mountain River R & D in Sichuan University, Chengdu, China, 2006. [Google Scholar]
- Li, L.X.; Liao, H.S.; Liu, D.; Jiang, S.Y. Experimental investigation of the optimization of stilling basin with shallow water cushion used for low Froude number energy dissipation. J. Hydrodyn. B Ser. 2015, 27, 522–529. [Google Scholar] [CrossRef]
- Liu, D.; Li, L.X.; Huang, B.S.; Liao, H.S. Numerical Simulation and Experimental Investigation on Stilling Basin with Double Shallow-water Cushions. J. Hydraul. Eng. 2012, 623–630. [Google Scholar] [CrossRef]
- Hager, W.H.; Kawagoshi, N. Hydraulic jumps at rounded drop. Proc. Inst. Civ. Eng. Part Res. Theory 1990, 89, 443–470. [Google Scholar] [CrossRef]
- Eroǧlu, N.; Tokyay, N. Statistical approach to geometric properties of wave-type flow occurring at an abrupt drop. J. Fac. Eng. Archit. Gazi Univ. 2012, 27, 911–919. [Google Scholar]
- Rice, C.E.; Kadavy, K.C. Riprap design upstream of straight drop spillways. Trans. Asae 1992, 34, 1715–1725. [Google Scholar] [CrossRef]
- Ram, K.V.; Prasad, S.; Spatial, R. B-Jump at Sudden Channel Enlargements with Abrupt Drop. J. Hydraul. Eng. 1998, 124, 643–646. [Google Scholar] [CrossRef]
- Sabzkoohi, A.M.; Kashefipour, S.M.; Bina, M. Investigation of effective parameters on stepped and straight drops energy dissipation using physical modeling. J. Food Agric. Environ. 2011, 9, 748–753. Retrieved from https://www.researchgate.net/publication/286803391.
- Riazi, R.; Bejestan, M.S.; Kashkouli, H.; Khosrojerdi, A. Effect of roughness on characteristics of bed B-jump in stilling basin with abrupt drop. Res. Crops 2012, 13, 1137–1141. Retrieved from https://www.researchgate.net/publication/287059975.
- Ilie, M. Fluid-structure interaction in turbulent flows; a CFD based aeroelastic algorithm using LES. Appl. Math. Comput. 2018, 342, 309–321. [Google Scholar] [CrossRef]
- Wanik, A.; Schnell, U. Some remarks on the PISO and SIMPLE algorithms for steady turbulent flow problems. Comput. Fluids 1989, 17, 555–570. [Google Scholar] [CrossRef]
- Wang, T.; Gu, C.G.; Yang, B. PISO algorithm for unsteady flow field. J. Hydrodyn. 2003. [Google Scholar] [CrossRef]
- Moeng, C.H. A Large-Eddy-Simulation Model for the Study of Planetary Boundary-Layer Turbulence. J. Atmos. Sci. 1984, 41, 2052–2062. [Google Scholar] [CrossRef]
- Moin, P.; Kim, J. Numerical investigation of turbulent channel flow. J. Fluid Mech. 2006, 118, 1280–1284. [Google Scholar] [CrossRef]
- Sarfaraz, M. Numerical Computation of Inception Point Location for Steeply Sloping Stepped Spillways. In Proceedings of the 9th International Congress on Civil Engineering, Isfahan University of Technology (IUT), Isfahan, Iran, 18–20 December 2012. [Google Scholar]
- Smagorinsky, J.S.; Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Song, C.C.S. A weakly compressible flow model and rapid convergence methods. J. Fluids Eng. 1988, 110, 441–445. [Google Scholar] [CrossRef]
- Canuto, V.M.; Cheng, Y. Determination of the Smagorinsky–Lilly constant CS. Phys. Fluids 1997, 9, 1368–1378. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the Implicitly Discretised Fluid Flow Equations by Operator-Splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D.; Romero, N.C. SOLA: A Numerical Solution Algorithm for Transient Fluid Flows (LA-5852); Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1988. [CrossRef]
- Nichols, B.D.; Hirt, C.W.; Hotchkiss, R.S. SOLA-VOF: A Solution Algorithm for Transient Fluid Flow with Multiple Free Boundaries (LA-8355); Nasa Sti/recon Technical Report N.; Los Alamos Scientific Laboratory: Los Alamos, NM, USA, 1980.
- Nichols, B.D.; Hirt, C.W.; Hotchkiss, R.S. A fractional volume of fluid method for free boundary dynamics. In Seventh International Conference on Numerical Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Mossa, M.; Petrillo, A.; Chanson, H. Tail-water level effects on flow conditions at an abrupt drop. J. Hydraul. Res. 2003, 41, 39–51. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Air-water flow patterns of hydraulic jumps on uniform beds macroroughness. J. Hydraul. Eng. 2017, 144. [Google Scholar] [CrossRef]
- Pagliara, S.; Palermo, M. Hydraulic jumps on rough and smooth beds: Aggregate approach for horizontal and adverse-sloped beds. J. Hydraul. Res. 2015, 53, 243–252. [Google Scholar] [CrossRef]
- Palermo, M.; Pagliara, S. Semi-theoretical approach for energy dissipation estimation at hydraulic jumps in rough sloped channels. J. Hydraul. Res. 2018. [Google Scholar] [CrossRef]



| Fr | d (cm) | d/L | Fr | d (cm) | d/L | Fr | d (cm) | d/L | Fr | d (cm) | d/L | Fr | d (cm) | d/L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.64 | 0 | 0.000 | 6.92 | 0 | 0.000 | 8.05 | 0 | 0.000 | 9.25 | 0 | 0.000 | 11.24 | 0 | 0.000 |
| 5 | 0.042 | 5 | 0.042 | 5 | 0.042 | 5 | 0.042 | 5 | 0.042 | |||||
| 10 | 0.083 | 10 | 0.083 | 10 | 0.083 | 10 | 0.083 | 10 | 0.083 | |||||
| 15 | 0.125 | 15 | 0.125 | 15 | 0.125 | 15 | 0.125 | 15 | 0.125 | |||||
| 20 | 0.167 | 20 | 0.167 | 20 | 0.167 | 20 | 0.167 | 20 | 0.167 | |||||
| 25 | 0.208 | 25 | 0.208 | 25 | 0.208 | 25 | 0.208 | 25 | 0.208 |
| Group | Fr | d = 0 | d = 5 cm | d = 10 cm | d = 15 cm | d = 20 cm | d = 25 cm |
|---|---|---|---|---|---|---|---|
| 1 | 6.92 | 0 | 0.08 | 0.09 | 0.13 | 0.15 | 0.16 |
| 2 | 7.64 | 0 | 0.08 | 0.08 | 0.13 | 0.14 | 0.14 |
| 3 | 8.05 | 0 | 0.07 | 0.09 | 0.12 | 0.13 | 0.13 |
| 4 | 9.25 | 0 | 0.06 | 0.07 | 0.09 | 0.11 | 0.12 |
| 5 | 11.24 | 0 | 0.06 | 0.04 | 0.08 | 0.10 | 0.11 |
| Fr (1) | d (cm) (2) | d/L (3) | V (m/s) at Different Sections | e (11) | (12) | (13) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 (4) | 20 (5) | 40 (6) | 60 (7) | 80 (8) | 100 (9) | 120 (10) | ||||||
| 7.64 | 0.00 | 0.00 | 4.25 | 4.25 | 4.28 | 4.18 | 4.13 | 4.10 | 4.01 | 10.98% | 0.00 | / |
| 5.00 | 0.04 | 4.19 | 3.87 | 4.30 | 4.20 | 4.20 | 4.05 | 3.80 | 17.75% | 0.76 | 0.30 | |
| 10.00 | 0.08 | 3.60 | 3.30 | 3.50 | 3.70 | 3.81 | 3.40 | 2.90 | 35.11% | 0.72 | 0.55 | |
| 15.00 | 0.13 | 2.84 | 3.15 | 2.30 | 1.48 | 1.36 | 1.25 | 1.20 | 82.15% | 0.56 | 1.46 | |
| 20.00 | 0.02 | 2.60 | 1.55 | 1.33 | 0.96 | 1.09 | 0.99 | 0.96 | 86.37% | 0.43 | 2.10 | |
| 25.00 | 0.21 | 1.66 | 1.75 | 1.23 | 0.76 | 0.77 | 0.68 | 0.56 | 88.62% | 0.45 | 2.05 | |
| 6.92 | 0.00 | 0.00 | 4.37 | 4.38 | 4.37 | 4.29 | 4.22 | 4.20 | 4.14 | 10.25% | 0.00 | / |
| 5.00 | 0.04 | 4.32 | 4.17 | 4.11 | 4.08 | 3.90 | 3.90 | 3.83 | 21.40% | 0.54 | 0.25 | |
| 10.00 | 0.08 | 4.07 | 3.89 | 3.85 | 3.88 | 3.80 | 3.50 | 3.03 | 44.58% | 0.62 | 0.50 | |
| 15.00 | 0.13 | 4.03 | 3.85 | 3.13 | 2.77 | 2.15 | 1.53 | 1.36 | 88.61% | 0.48 | 1.85 | |
| 20.00 | 0.02 | 3.30 | 1.73 | 1.55 | 1.13 | 0.91 | 0.73 | 0.98 | 91.18% | 0.44 | 2.20 | |
| 25.00 | 0.21 | 2.30 | 1.83 | 1.44 | 1.16 | 0.88 | 0.72 | 0.66 | 91.77% | 0.46 | 1.99 | |
| 8.05 | 0.00 | 0.00 | 7.78 | 7.63 | 7.54 | 7.43 | 7.51 | 7.46 | 7.40 | 9.53% | 0.00 | / |
| 5.00 | 0.04 | 7.90 | 7.55 | 7.49 | 7.43 | 7.35 | 7.30 | 7.26 | 15.55% | 0.42 | 0.37 | |
| 10.00 | 0.08 | 7.55 | 7.45 | 7.29 | 6.98 | 6.85 | 6.33 | 6.25 | 31.47% | 0.42 | 0.60 | |
| 15.00 | 0.13 | 7.53 | 7.20 | 6.70 | 6.50 | 6.29 | 5.94 | 5.09 | 54.31% | 0.46 | 1.19 | |
| 20.00 | 0.02 | 5.81 | 5.01 | 4.53 | 4.01 | 3.82 | 3.15 | 2.85 | 75.94% | 0.36 | 2.01 | |
| 25.00 | 0.21 | 4.73 | 4.16 | 3.86 | 3.38 | 3.19 | 2.65 | 2.23 | 77.77% | 0.37 | 2.10 | |
| 9.25 | 0.00 | 0.00 | 10.39 | 10.14 | 10.01 | 10.02 | 9.97 | 9.91 | 9.88 | 9.58% | 0.00 | / |
| 5.00 | 0.04 | 10.36 | 9.89 | 9.93 | 9.76 | 9.71 | 9.64 | 9.63 | 13.60% | 0.27 | 0.46 | |
| 10.00 | 0.08 | 10.20 | 9.77 | 9.53 | 9.52 | 9.44 | 9.29 | 8.61 | 28.75% | 0.45 | 0.65 | |
| 15.00 | 0.13 | 10.42 | 9.56 | 9.44 | 9.36 | 9.20 | 8.09 | 7.43 | 49.16% | 0.53 | 1.05 | |
| 20.00 | 0.02 | 9.44 | 9.49 | 9.26 | 8.79 | 7.85 | 6.25 | 5.30 | 68.48% | 0.43 | 1.80 | |
| 25.00 | 0.21 | 7.89 | 6.18 | 6.03 | 5.82 | 5.33 | 4.85 | 3.88 | 75.82% | 0.35 | 2.27 | |
| 11.24 | 0.00 | 0.00 | 13.36 | 13.11 | 13.12 | 13 | 12.92 | 12.88 | 12.76 | 8.78% | 0.00 | / |
| 5.00 | 0.04 | 13.23 | 12.96 | 12.88 | 12.69 | 12.43 | 12.42 | 12.42 | 11.87% | 0.26 | 0.50 | |
| 10.00 | 0.08 | 13.2 | 12.91 | 12.8 | 12.56 | 12.21 | 11.52 | 11.33 | 26.33% | 0.43 | 0.70 | |
| 15.00 | 0.13 | 13.19 | 12.88 | 12.62 | 12.12 | 11.63 | 11.15 | 10.07 | 41.71% | 0.31 | 0.92 | |
| 20.00 | 0.02 | 13.26 | 12.56 | 11.45 | 10.62 | 9.53 | 8.05 | 7.79 | 65.49% | 0.32 | 1.60 | |
| 25.00 | 0.21 | 12.21 | 11.64 | 10.88 | 9.48 | 8.38 | 7.23 | 6.11 | 74.96% | 0.32 | 2.34 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Li, L.; Liao, H. Study on the Best Depth of Stilling Basin with Shallow-Water Cushion. Water 2018, 10, 1801. https://doi.org/10.3390/w10121801
Li Q, Li L, Liao H. Study on the Best Depth of Stilling Basin with Shallow-Water Cushion. Water. 2018; 10(12):1801. https://doi.org/10.3390/w10121801
Chicago/Turabian StyleLi, Qiulin, Lianxia Li, and Huasheng Liao. 2018. "Study on the Best Depth of Stilling Basin with Shallow-Water Cushion" Water 10, no. 12: 1801. https://doi.org/10.3390/w10121801
APA StyleLi, Q., Li, L., & Liao, H. (2018). Study on the Best Depth of Stilling Basin with Shallow-Water Cushion. Water, 10(12), 1801. https://doi.org/10.3390/w10121801




