Copula-Based Hazard Risk Assessment of Winter Extreme Cold Events in Beijing
Abstract
1. Introduction
2. Materials and Methods
2.1. Descriptions of Study Area and Meteorological Data
2.2. Selection of Extreme Cold Events
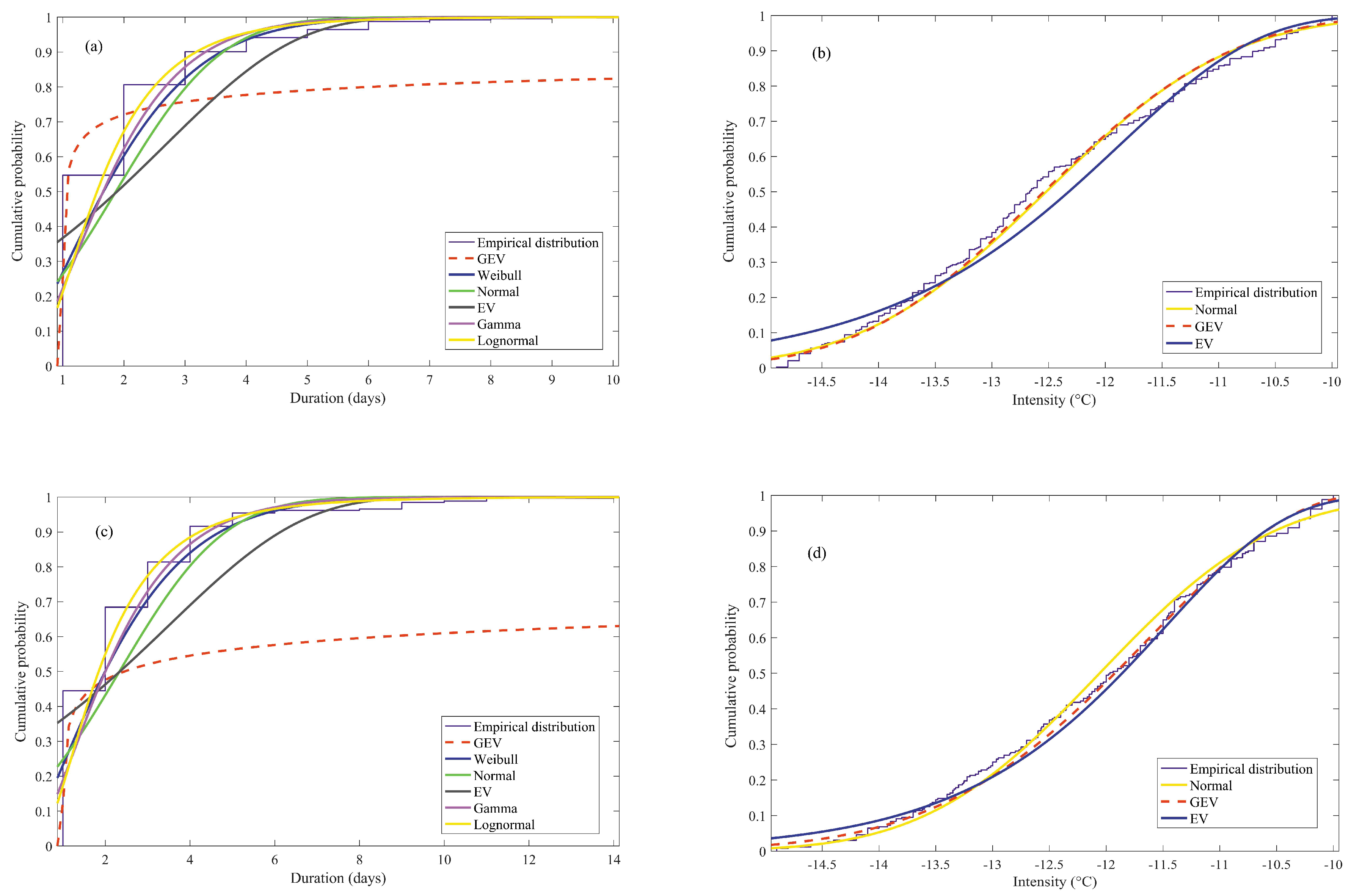
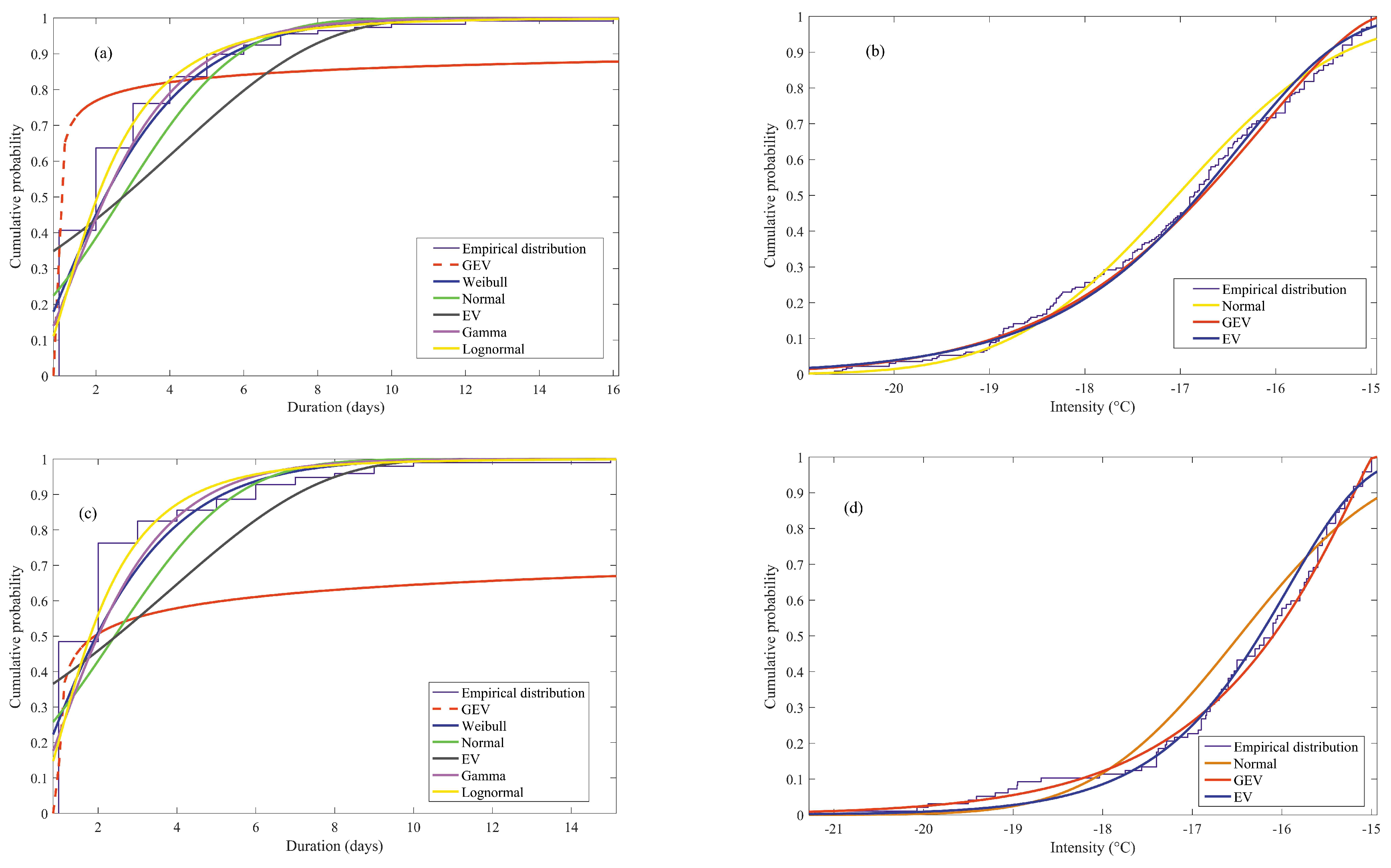
2.3. Estimation of Marginal Probability Distributions
2.4. Copula Functions
2.4.1. Bivariate Archimedean Copulas
2.4.2. Goodness-of-Fit Tests for Copula Functions
2.5. Return Periods
3. Results
3.1. Low Temperature Events
3.1.1. Statistics of Low Temperature Events
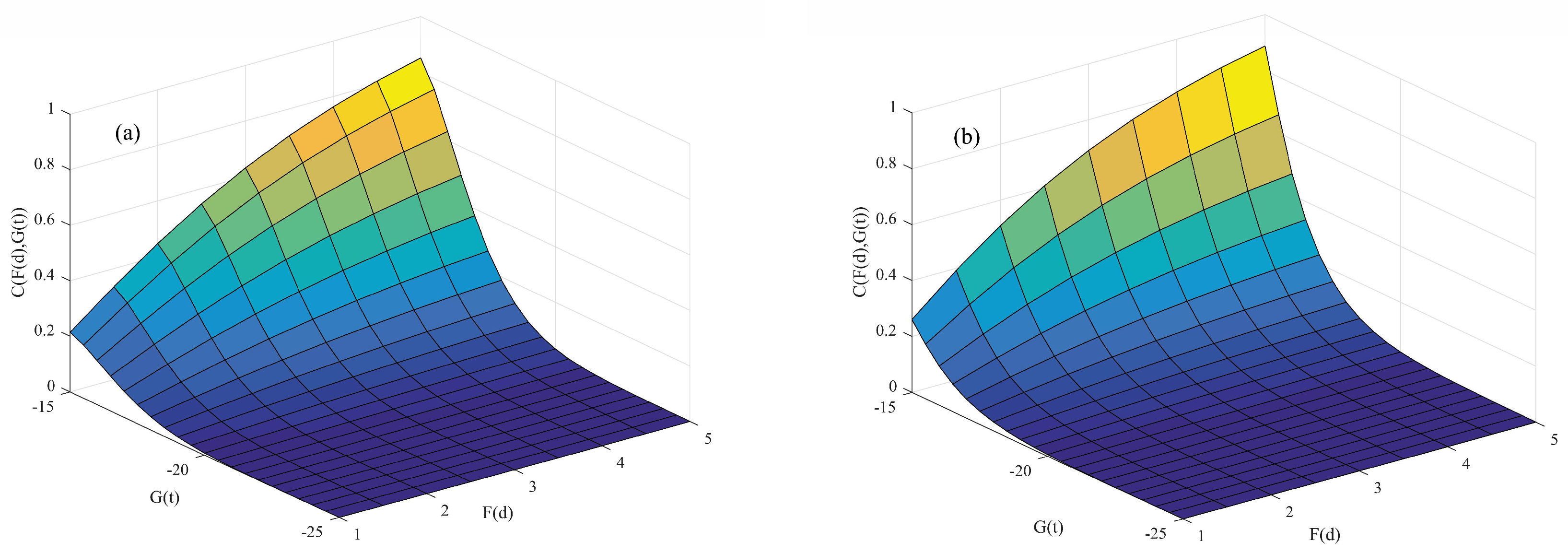
3.1.2. Joint Distribution of Winter Low Temperature Based on the Copula Function
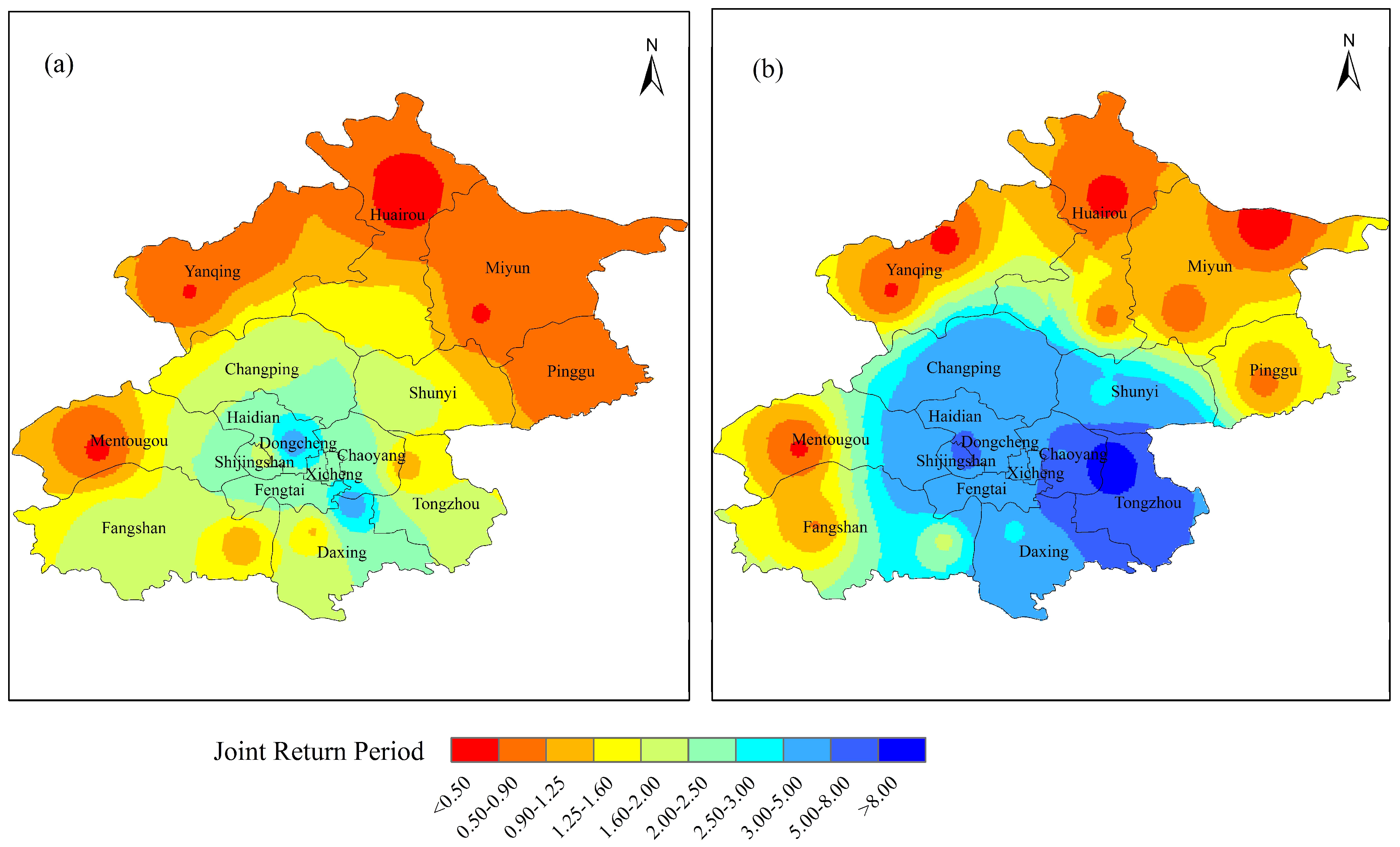
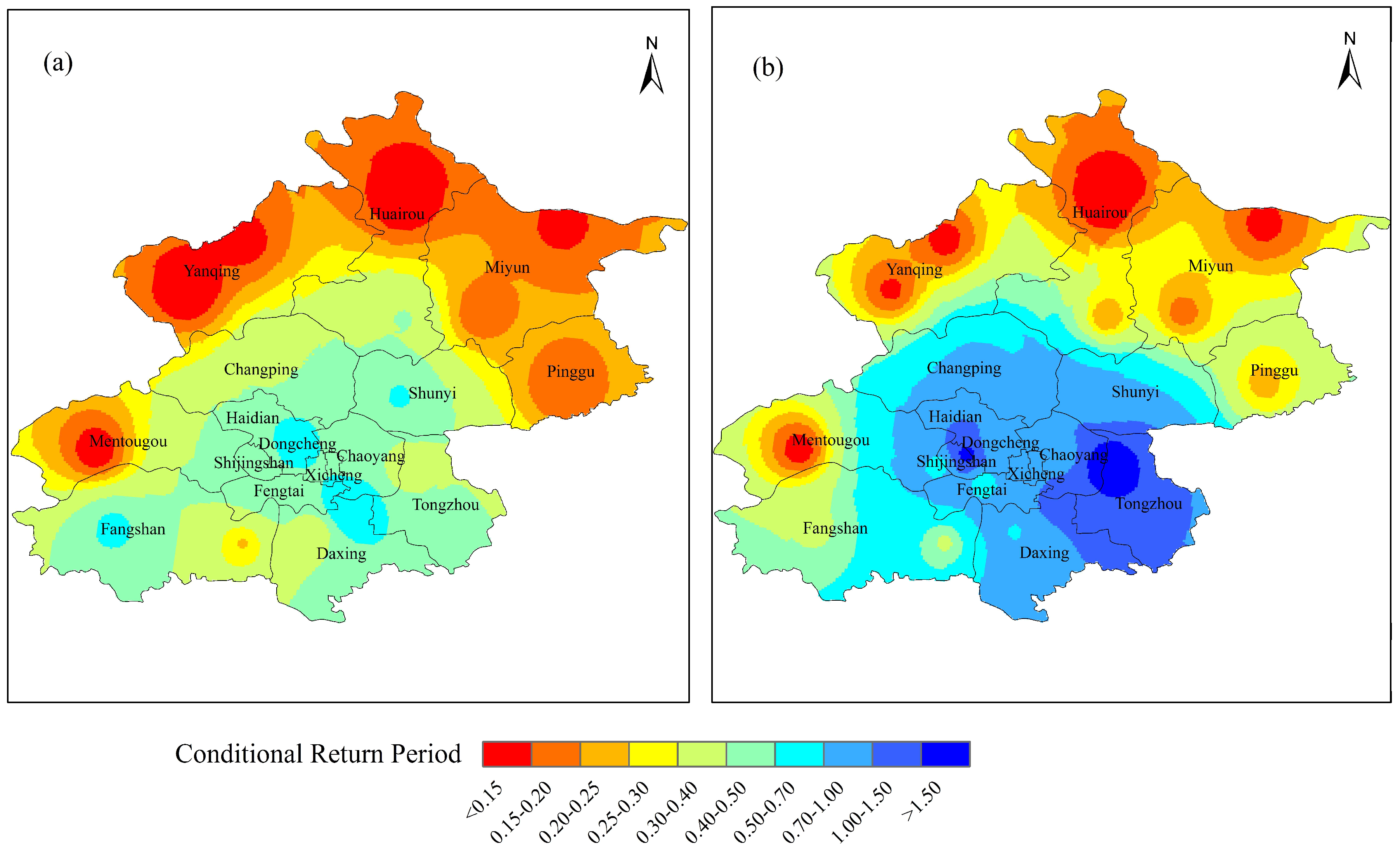
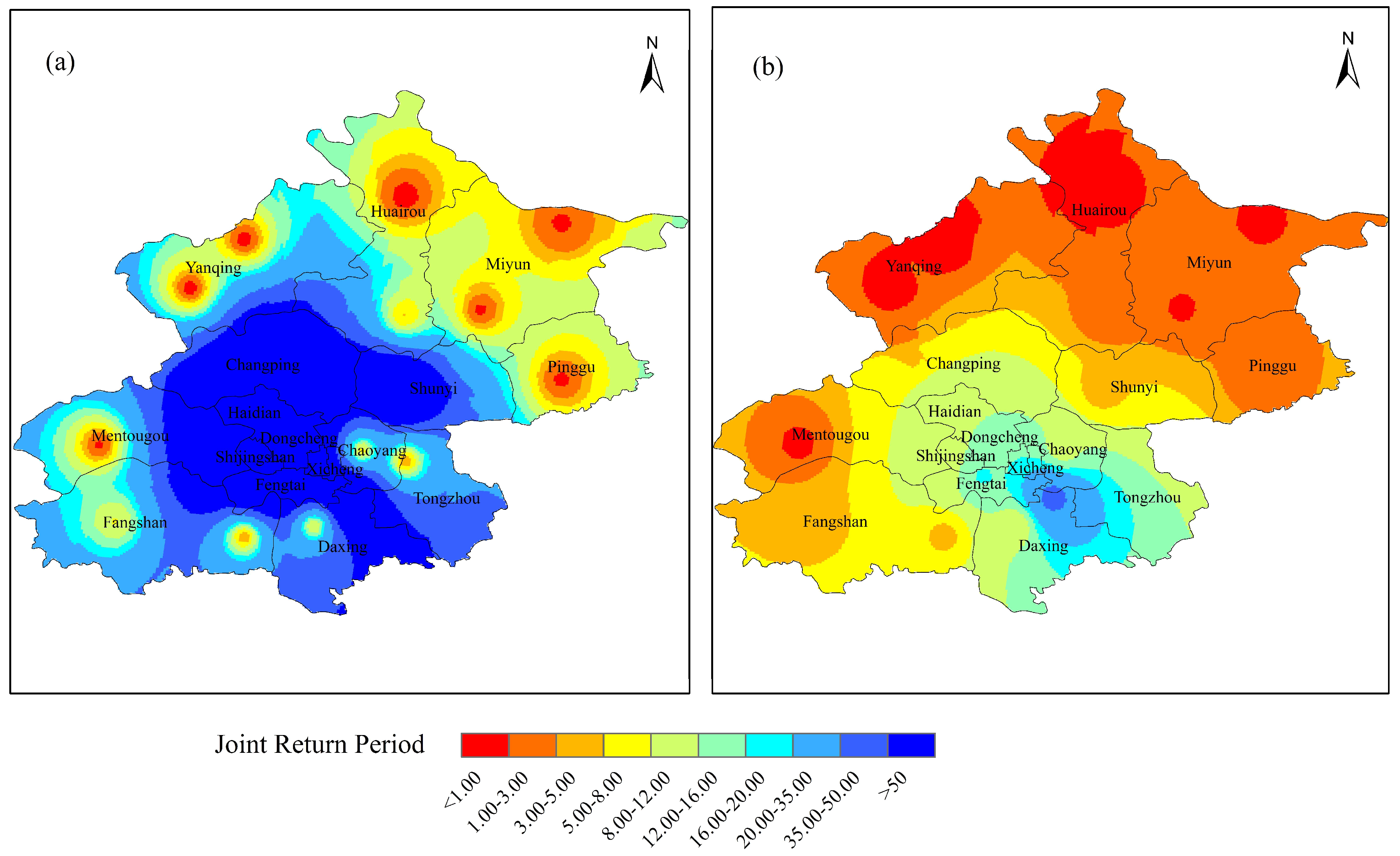
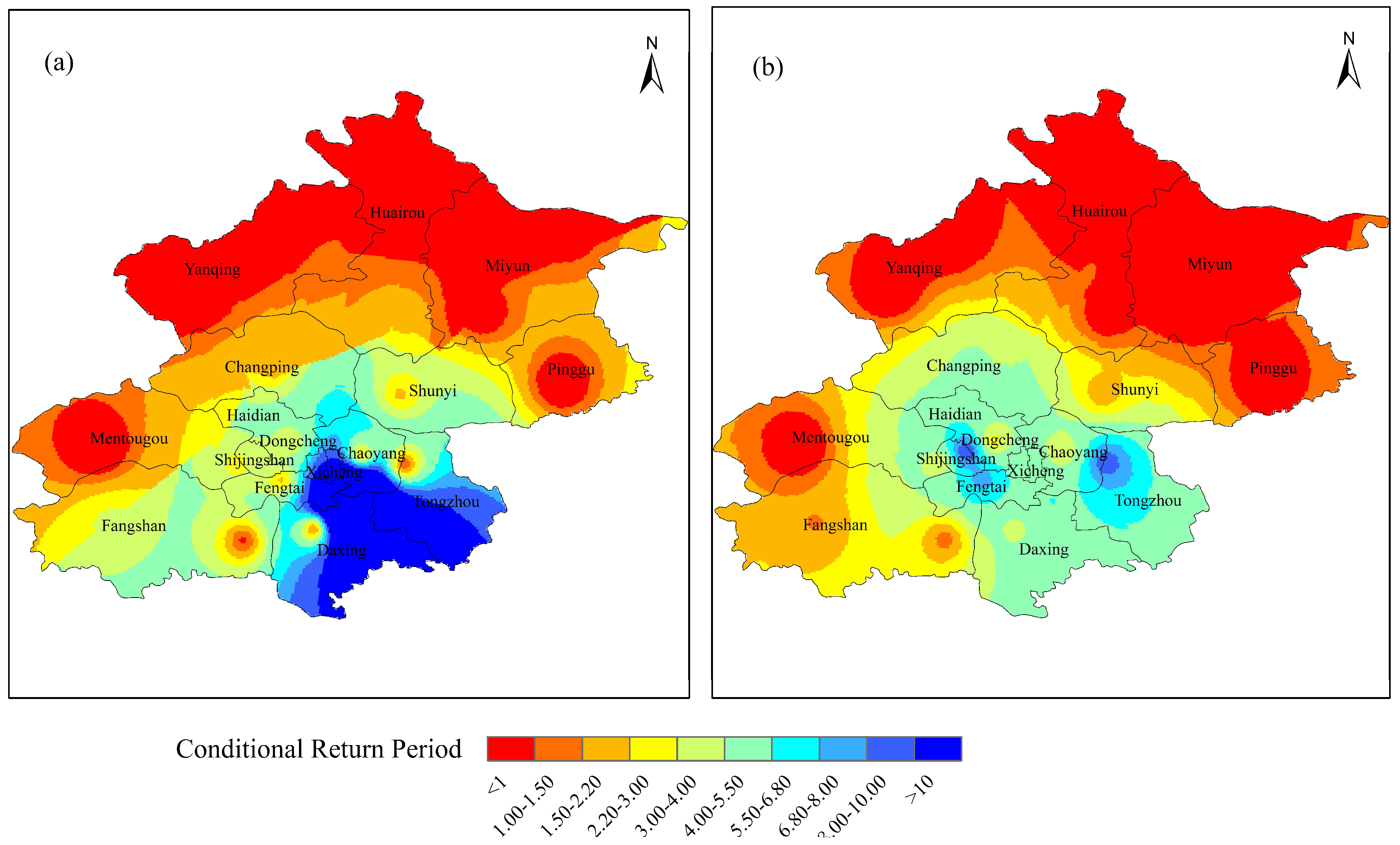
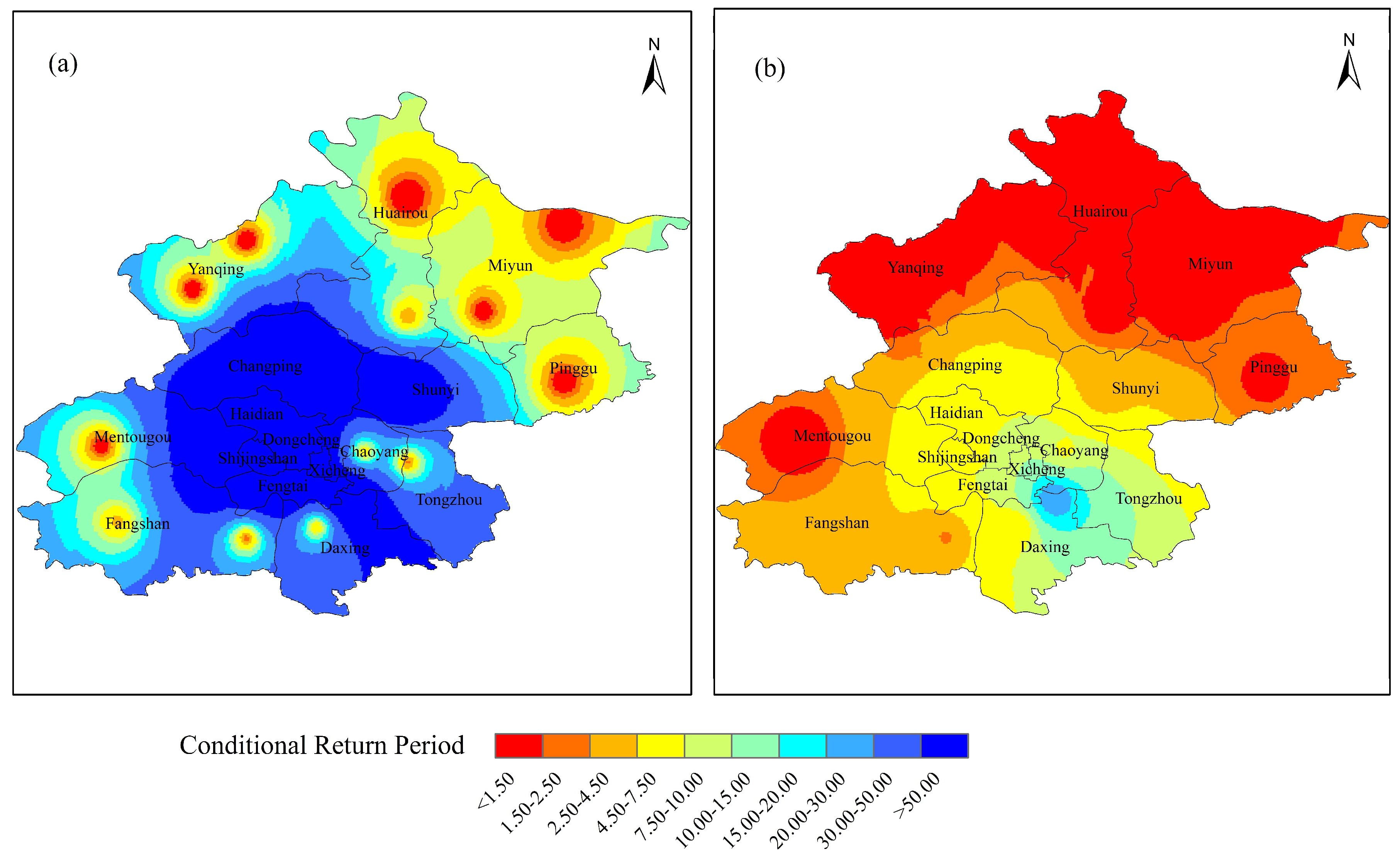
3.1.3. Return Period and Risk Analysis
3.2. Extreme Low Temperature Events
3.2.1. Statistics of Extreme Low Temperature Events
3.2.2. Joint Distribution of Winter Extreme Low Temperature Based on the Copula Functions
3.2.3. Return Period and Risk Analysis
4. Discussion and Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Screen, J.A.; Deser, C.; Sun, L. Reduced risk of North American cold extremes due to continued Arctic sea ice loss. Bull. Am. Meteorol. Soc. 2015, 96, 1489–1503. [Google Scholar] [CrossRef]
- Cohen, J.; Screen, J.A.; Furtado, J.C.; Barlow, M.; Whittleston, D.; Coumou, D.; Francis, J.; Dethloff, K.; Entekhabi, D.; Overland, J. Recent Arctic amplification and extreme mid-latitude weather. Nat. Geosci. 2014, 7, 627–637. [Google Scholar] [CrossRef]
- Jennifer, A.; Francis, S.J.V. Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys. Res. Lett. 2012, 39, L06801. [Google Scholar]
- Screen, J.A. Arctic amplification decreases temperature variance in northern mid- to high-latitudes. Nat. Clim. Chang. 2014, 4, 577–582. [Google Scholar] [CrossRef]
- Zuo, Z.; Zhang, R.; Huang, Y.; Xiao, D.; Guo, D. Extreme cold and warm events over China in wintertime. Int. J. Climatol. 2015, 35, 3568–3581. [Google Scholar] [CrossRef]
- Jing-Bei, P.; Cholaw, B. The definition and classification of extensive and persistent extreme cold events in China. Atmos. Ocean. Sci. Lett. 2011, 4, 281–286. [Google Scholar] [CrossRef]
- Wen, M.; Yang, S.; Arun, K.; Zhang, P. An analysis of the large-scale climate anomalies associated with the snowstorms affecting China in January 2008. Mon. Weather Rev. 2009, 137, 1111–1131. [Google Scholar] [CrossRef]
- Marengo, J.A.; Jones, R.; Alves, L.M.; Valverde, M.C. Future change of temperature and precipitation extremes in South America as derived from the precis regional climate modeling system. Int. J. Climatol. 2010, 29, 2241–2255. [Google Scholar] [CrossRef]
- Zheng, J.; Ding, L.; Hao, Z.; Ge, Q. Extreme cold winter events in southern China during AD 1650–2000. Boreas 2015, 41, 1–12. [Google Scholar] [CrossRef]
- Sun, W.; Mu, X.; Song, X.; Wu, D.; Cheng, A.; Qiu, B. Changes in extreme temperature and precipitation events in the loess plateau (China) during 1960–2013 under global warming. Atmos. Res. 2016, 168, 33–48. [Google Scholar] [CrossRef]
- Choi, G.; Collins, D.; Ren, G.; Trewin, B.; Baldi, M.; Fukuda, Y.; Afzaal, M.; Pianmana, T.; Gomboluudev, P.; Huong, P.T.T.; et al. Changes in means and extreme events of temperature and precipitation in the Asia-Pacific network region, 1955–2007. Int. J. Climatol. 2009, 29, 1906–1925. [Google Scholar] [CrossRef]
- Cholaw, B.; Xian-Yue, F.U.; Xie, Z.W. Large-scale circulation features typical of wintertime extensive and persistent low temperature events in China. Atmos. Ocean. Sci. Lett. 2011, 4, 235–241. [Google Scholar] [CrossRef]
- Honda, M.; Inoue, J.; Yamane, S. Influence of low Arctic sea-ice minima on anomalously cold Eurasian winters. Geophys. Res. Lett. 2009, 36, 262–275. [Google Scholar] [CrossRef]
- Beguería, S. Mapping the hazard of extreme rainfall by peaks-over-threshold extreme value analysis and spatial regression techniques. J. Appl. Meteorol. Climatol. 2006, 45, 108–124. [Google Scholar] [CrossRef]
- Hanel, M.; Buishand, T.A.; Ferro, C.A.T. A nonstationary index flood model for precipitation extremes in transient regional climate model simulations. J. Geophys. Res. Atmos. 2009, 114, D15107. [Google Scholar] [CrossRef]
- Krishnamurthy, C.K.B.; Lall, U.; Hyunhan, K. Changing frequency and intensity of rainfall extremes over India from 1951 to 2003. J. Clim. 2009, 22, 4737–4746. [Google Scholar] [CrossRef]
- Salvadori, G.; Michele, C.D. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour. Res. 2004, 40, 229–244. [Google Scholar] [CrossRef]
- Rauf, U.F.A.; Zeephongsekul, P. Copula based analysis of rainfall severity and duration: A case study. Theor. Appl. Climatol. 2014, 115, 153–166. [Google Scholar] [CrossRef]
- Vandenberghe, S.; Verhoest, N.E.C.; Onof, C.; De Baets, B. A comparative copula-based bivariate frequency analysis of observed and simulated storm events: A case study on Bartlett-Lewis modeled rainfall. Water Resour. Res. 2011, 47, 197–203. [Google Scholar] [CrossRef]
- Singh, V.P.; Zhang, L. Bivariate flood frequency analysis using the copula method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar]
- Zhang, Y.; Meng, W.; Chen, D.; Guo, W.; Wang, J. The trend of variation for low temperature days over Beijing and its surrounding area. Chin. J. Agrometeorol. 2011, 32, 33–37. (In Chinese) [Google Scholar]
- Frich, P.; Alexander, L.; Dellamarta, P.; Gleason, B.; Haylock, M.; Klein Tank, A.; Peterson, T. Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Kostopoulou, E.; Jones, P.D. Assessment of climate extremes in the Eastern Mediterranean. Meteorol. Atmos. Phys. 2005, 89, 69–85. [Google Scholar] [CrossRef]
- Russo, S.; Sterl, A. Global changes in indices describing moderate temperature extremes from the daily output of a climate model. J. Geophys. Res. Atmos. 2011, 116, D03104. [Google Scholar] [CrossRef]
- Frank, J.; Massey, J. The kolmogorov-smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar]
- Sklar, M. Fonctions de Répartition À n Dimensions et Leurs Marges; Publications de l’Institut de Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas (Springer Series in Statistics); Springer: New York, NY, USA, 2006; p. 315. [Google Scholar]
- Zhang, D.D.; Yan, D.H.; Lu, F.; Wang, Y.C.; Feng, J. Copula-based risk assessment of drought in Yunnan province, China. Nat. Hazards 2015, 75, 2199–2220. [Google Scholar] [CrossRef]
- Kao, S.-C.; Govindaraju, R.S. A bivariate frequency analysis of extreme rainfall with implications for design. J. Geophys. Res. Atmos. 2007, 112, D13119. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; Chapman and Hall/CRC: New York, NY, USA, 1997. [Google Scholar]
- Joe, H. Asymptotic efficiency of the two-stage estimation method for copula-based models. J. Multivar. Anal. 2005, 94, 401–419. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O'Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Oceans 1985, 90, 8995–9005. [Google Scholar] [CrossRef]
- Shiau, J.T. Return period of bivariate distributed extreme hydrological events. Stoch. Environ. Res. Risk Assess. 2003, 17, 42–57. [Google Scholar] [CrossRef]
- Watson, D.F. A refinement of inverse distance weighted interpolation. Geo-Processing 1985, 2, 315–327. [Google Scholar]
- IPCC. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Summaries, Frequently Asked Questions, and Cross-Chapter Boxes. A Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; World Meteorological Organization: Geneva, Switzerland, 2014; pp. 81–111. [Google Scholar]
- Sun, Y.; Zhang, X.; Zwiers, F.W.; Song, L.; Wan, H.; Hu, T.; Yin, H.; Ren, G. Rapid increase in the risk of extreme summer heat in Eastern China. Nat. Clim. Chang. 2014, 4, 1082–1085. [Google Scholar] [CrossRef]
- Spinoni, J.; Lakatos, M.; Szentimrey, T.; Bihari, Z.; Szalai, S.; Vogt, J.; Antofie, T. Heat and cold waves trends in the carpathian region from 1961 to 2010. Int. J. Climatol. 2015, 35, 4197–4209. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Nicholls, N.; Easterling, D.; Goodess, C.M.; Kanae, S.; Kossin, J.; Luo, Y.; Marengo, J.; McInnes, K.; Rahimi, M.; et al. 2012: Changes in climate extremes and their impacts on the natural physical environment. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK, 2012; pp. 109–230. [Google Scholar]
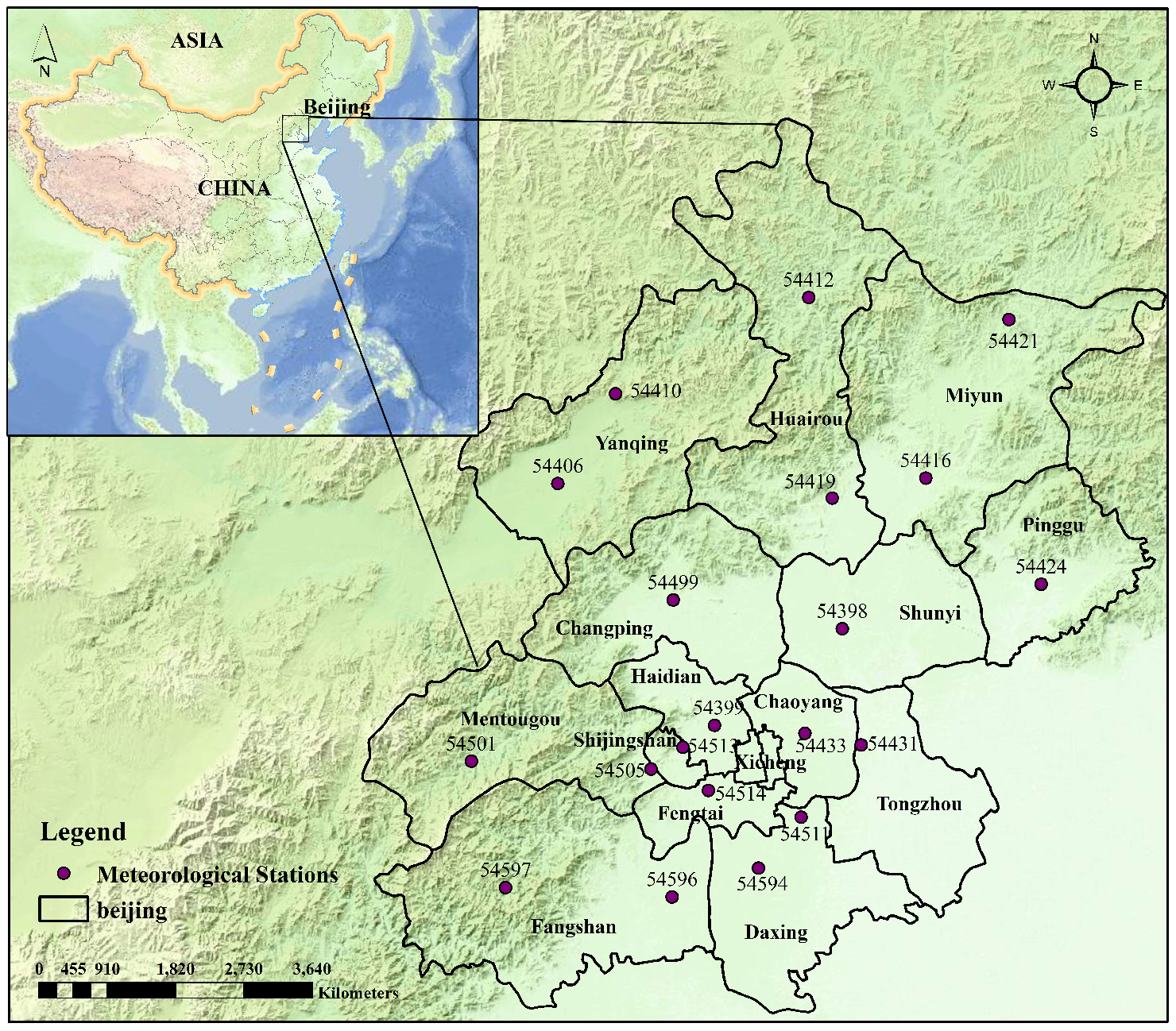


| Station Identity (ID) | Name | Longitude (°) | Latitude (°) | Elevation (m) |
|---|---|---|---|---|
| 54398 | Shunyi | 116.37 | 40.8 | 28.6 |
| 54399 | Haidian | 116.17 | 39.59 | 45.8 |
| 54406 | Yanqing | 115.58 | 40.27 | 487.9 |
| 54410 | Foyeding | 116.08 | 40.36 | 1224.7 |
| 54412 | Tanghekou | 116.38 | 40.44 | 331.6 |
| 54416 | Miyun | 116.52 | 40.23 | 71.8 |
| 54419 | Huairou | 116.38 | 40.22 | 75.7 |
| 54421 | Shangdianzi | 117.07 | 40.39 | 293.3 |
| 54424 | Pinggu | 117.07 | 40.10 | 32.1 |
| 54431 | Tongzhou | 116.38 | 39.55 | 43.3 |
| 54433 | Chaoyang | 116.30 | 39.57 | 35.3 |
| 54499 | Changping | 116.13 | 40.13 | 76.2 |
| 54501 | Zhaitang | 115.41 | 39.58 | 440.3 |
| 54505 | Mentougou | 116.07 | 39.55 | 92.7 |
| 54511 | Beijing | 116.28 | 39.48 | 31.3 |
| 54513 | Shijingshan | 116.12 | 39.57 | 65.6 |
| 54514 | Fengtai | 116.15 | 39.52 | 55.2 |
| 54594 | Daxing | 116.21 | 39.43 | 37.6 |
| 54596 | Fangshan | 116.08 | 39.41 | 39.2 |
| 54597 | Xiayunling | 115.44 | 39.44 | 407.7 |
| Copula Type | Function |
|---|---|
| Clayton | |
| GH | |
| Frank |
| Stations | Frequency | The Maximum Duration (Days) | Mean Intensity (°C) | ||||
|---|---|---|---|---|---|---|---|
| ID | Name | 1978–1998 | 1999–2015 | 1978–1998 | 1999–2015 | 1978–1998 | 1999–2015 |
| 54398 | Shunyi | 148 | 97 | 13 | 12 | −11.53 | −11.43 |
| 54399 | Haidian | 170 | 105 | 7 | 6 | −11.35 | −11.31 |
| 54406 | Yanqing | 393 | 263 | 10 | 14 | −12.52 | −12.06 |
| 54410 | Foyeding | 323 | 255 | 9 | 8 | −12.45 | −12.32 |
| 54412 | Tanghekou | 354 | 288 | 10 | 10 | −12.60 | −12.68 |
| 54416 | Miyun | 311 | 239 | 14 | 9 | −11.97 | −11.87 |
| 54419 | Huairou | 180 | 196 | 8 | 13 | −11.56 | −11.92 |
| 54421 | Shangdianzi | 310 | 266 | 10 | 12 | −12.09 | −12.06 |
| 54424 | Pinggu | 319 | 208 | 10 | 15 | −11.97 | −11.74 |
| 54431 | Tongzhou | 196 | 51 | 10 | 9 | −11.66 | −11.17 |
| 54433 | Chaoyang | 187 | 103 | 10 | 8 | −11.48 | −11.28 |
| 54499 | Changping | 211 | 96 | 11 | 8 | −11.48 | −11.41 |
| 54501 | Zhaitang | 379 | 288 | 9 | 10 | −12.14 | −12.13 |
| 54505 | Mentougou | 184 | 102 | 10 | 9 | −11.49 | −11.51 |
| 54511 | Beijing | 138 | 74 | 6 | 8 | −11.36 | −11.31 |
| 54513 | Shijingshan | 159 | 70 | 14 | 8 | −11.57 | −11.14 |
| 54514 | Fengtai | 194 | 105 | 11 | 8 | −11.35 | −11.43 |
| 54594 | Daxing | 198 | 104 | 9 | 8 | −11.66 | −11.41 |
| 54596 | Fangshan | 223 | 135 | 9 | 6 | −11.81 | −11.71 |
| 54597 | Xiayunling | 176 | 125 | 13 | 13 | −11.37 | −11.64 |
| Stations | The Period 1978–1998 | The Period 1999–2015 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Duration | Intensity | Duration | Intensity | ||||||
| ID | Name | K–S D | Distributions | K–S D | Distributions | K–S D | Distributions | K–S D | Distributions |
| 54398 | Shunyi | 0.1318 | Weibull | 0.0796 | GEV | 0.1246 | Weibull | 0.0799 | GEV |
| 54399 | Haidian | 0.1228 | Weibull | 0.0706 | EV | 0.1255 | EV | 0.1080 | EV |
| 54406 | Yanqing | 0.0789 | Weibull | 0.0544 | GEV | 0.1001 | Weibull | 0.0463 | GEV |
| 54410 | Foyeding | 0.0905 | Weibull | 0.0406 | GEV | 0.1019 | Normal | 0.0511 | Normal |
| 54412 | Tanghekou | 0.0872 | Normal | 0.0402 | Normal | 0.0954 | Weibull | 0.0394 | GEV |
| 54416 | Miyun | 0.0928 | Normal | 0.0522 | GEV | 0.1043 | Normal | 0.0451 | GEV |
| 54419 | Huairou | 0.1210 | Weibull | 0.0697 | EV | 0.1118 | Weibull | 0.0581 | GEV |
| 54421 | Shangdianzi | 0.0924 | Weibull | 0.0413 | GEV | 0.0950 | Weibull | 0.0371 | GEV |
| 54424 | Pinggu | 0.0909 | Normal | 0.0422 | GEV | 0.1112 | Weibull | 0.0668 | GEV |
| 54431 | Tongzhou | 0.1061 | Weibull | 0.0852 | GEV | 0.1005 | Weibull | 0.1388 | Normal |
| 54433 | Chaoyang | 0.1155 | Weibull | 0.0647 | GEV | 0.1532 | Weibull | 0.0944 | GEV |
| 54499 | Changping | 0.1107 | Weibull | 0.0742 | Normal | 0.1601 | Weibull | 0.0708 | GEV |
| 54501 | Zhaitang | 0.0836 | Weibull | 0.062 | GEV | 0.0907 | Weibull | 0.0467 | GEV |
| 54505 | Mentougou | 0.1134 | Weibull | 0.0682 | GEV | 0.1602 | Weibull | 0.0890 | GEV |
| 54511 | Beijing | 0.1373 | Weibull | 0.0683 | GEV | 0.1447 | Weibull | 0.0764 | EV |
| 54513 | Shijingshan | 0.1229 | Weibull | 0.0614 | GEV | 0.1696 | Weibull | 0.0873 | EV |
| 54514 | Fengtai | 0.1128 | Weibull | 0.0675 | GEV | 0.1104 | Weibull | 0.0844 | Normal |
| 54594 | Daxing | 0.1159 | Normal | 0.0635 | GEV | 0.1580 | Normal | 0.0681 | GEV |
| 54596 | Fangshan | 0.1084 | Weibull | 0.0494 | GEV | 0.1360 | Weibull | 0.0948 | GEV |
| 54597 | Xiayunling | 0.1224 | Gamma | 0.0736 | GEV | 0.1340 | Weibull | 0.0710 | Normal |
| Stations | 1978–1998 | 1999–2015 | |||||
|---|---|---|---|---|---|---|---|
| ID | Name | RMSE | Copula | RMSE | Copula | ||
| 54398 | Shunyi | 1.0135 | 0.0883 | GH | 1.0001 | 0.0886 | GH |
| 54399 | Haidian | 1.0001 | 0.0122 | GH | −2.2989 | 0.0506 | Frank |
| 54406 | Yanqing | 0.1197 | 0.0154 | Clayton | 1.0000 | 0.0807 | GH |
| 54410 | Foyeding | 0.3651 | 0.0107 | Clayton | 0.1610 | 0.0150 | Clayton |
| 54412 | Tanghekou | 0.2985 | 0.0144 | Clayton | 0.3024 | 0.1158 | Clayton |
| 54416 | Miyun | 1.0000 | 0.1048 | GH | 1.0000 | 0.0150 | GH |
| 54419 | Huairou | 1.0136 | 0.0871 | GH | 1.0001 | 0.1030 | GH |
| 54421 | Shangdianzi | 0.0118 | 0.0921 | Clayton | 0.0310 | 0.1156 | Clayton |
| 54424 | Pinggu | 1.0000 | 0.1062 | GH | 1.0000 | 0.0855 | GH |
| 54431 | Tongzhou | 1.0001 | 0.0775 | GH | 1.0000 | 0.0174 | GH |
| 54433 | Chaoyang | 1.0013 | 0.0166 | GH | 1.0013 | 0.0168 | GH |
| 54499 | Changping | 1.4500 | 0.1061 | GH | 1.0001 | 0.0218 | GH |
| 54501 | Zhaitang | −0.9643 | 0.0979 | Frank | −1.3006 | 0.0997 | Frank |
| 54505 | Mentougou | 1.0001 | 0.1091 | GH | 1.0000 | 0.1090 | GH |
| 54511 | Beijing | 1.0017 | 0.1114 | GH | 1.0000 | 0.1084 | GH |
| 54513 | Shijingshan | 1.0000 | 0.0849 | GH | 1.0000 | 0.0130 | GH |
| 54514 | Fengtai | 1.0001 | 0.1046 | GH | −2.3676 | 0.0247 | Frank |
| 54594 | Daxing | −2.0774 | 0.1111 | Frank | 1.0000 | 0.1094 | GH |
| 54596 | Fangshan | 1.0000 | 0.0933 | GH | −1.8516 | 0.0190 | Frank |
| 54597 | Xiayunling | −2.6704 | 0.0870 | Frank | 1.0001 | 0.0616 | GH |
| Stations | Frequency | The Maximum Duration (Days) | Mean Intensity (°C) | ||||
|---|---|---|---|---|---|---|---|
| ID | Name | 1978–1998 | 1999–2015 | 1978–1998 | 1999–2015 | 1978–1998 | 1999–2015 |
| 54398 | Shunyi | 14 | 10 | 2 | 7 | −16.20 | −16.63 |
| 54399 | Haidian | 10 | 9 | 2 | 2 | −15.97 | −16.06 |
| 54406 | Yanqing | 226 | 97 | 16 | 15 | −17.03 | −16.48 |
| 54410 | Foyeding | 203 | 138 | 21 | 17 | −17.65 | −17.38 |
| 54412 | Tanghekou | 221 | 190 | 17 | 23 | −16.69 | −17.28 |
| 54416 | Miyun | 94 | 59 | 9 | 11 | −16.45 | −16.46 |
| 54419 | Huairou | 18 | 37 | 4 | 11 | −15.93 | −16.36 |
| 54421 | Shangdianzi | 101 | 85 | 11 | 11 | −16.29 | −16.34 |
| 54424 | Pinggu | 102 | 38 | 5 | 7 | −16.32 | −16.28 |
| 54431 | Tongzhou | 25 | 2 | 3 | 1 | −16.14 | −15.65 |
| 54433 | Chaoyang | 12 | 7 | 3 | 4 | −15.94 | −15.94 |
| 54499 | Changping | 19 | 6 | 2 | 3 | −15.99 | −16.08 |
| 54501 | Zhaitang | 118 | 98 | 9 | 11 | −16.26 | −16.45 |
| 54505 | Mentougou | 15 | 9 | 1 | 4 | −15.94 | −15.95 |
| 54511 | Beijing | 7 | 5 | 1 | 2 | −15.3 | −15.73 |
| 54513 | Shijingshan | 14 | 2 | 2 | 2 | −15.70 | −15.95 |
| 54514 | Fengtai | 15 | 5 | 2 | 6 | −15.73 | −15.79 |
| 54594 | Daxing | 24 | 7 | 3 | 4 | −15.96 | −15.77 |
| 54596 | Fangshan | 34 | 22 | 4 | 4 | −16.05 | −16.19 |
| 54597 | Xiayunling | 13 | 16 | 5 | 4 | −15.49 | −15.92 |
| Stations | The Period 1978–1998 Duration | The Period 1978–1998 Mean Temperature | The Period 1999–2015 Duration | The Period 1999–2015 Mean Temperature | |||||
|---|---|---|---|---|---|---|---|---|---|
| ID | Name | K–S D | Distributions | K–S D | Distributions | K–S D | Distributions | K–S D | Distributions |
| 54398 | Shunyi | 0.1974 | EV | 0.1617 | GEV | 0.2020 | Normal | 0.1640 | GEV |
| 54399 | Haidian | 0.1937 | EV | 0.1521 | GEV | 0.1570 | EV | 0.1086 | EV |
| 54406 | Yanqing | 0.1064 | Weibull | 0.0542 | GEV | 0.1615 | Weibull | 0.0680 | GEV |
| 54410 | Foyeding | 0.1102 | Weibull | 0.0488 | EV | 0.1248 | Gamma | 0.0751 | GEV |
| 54412 | Tanghekou | 0.1093 | Weibull | 0.0668 | GEV | 0.1162 | Gamma | 0.0575 | EV |
| 54416 | Miyun | 0.1632 | Normal | 0.0613 | GEV | 0.1148 | Normal | 0.0678 | GEV |
| 54419 | Huairou | 0.1868 | EV | 0.1126 | GEV | 0.1700 | Weibull | 0.0733 | GEV |
| 54421 | Shangdianzi | 0.1630 | Weibull | 0.0626 | GEV | 0.1623 | Weibull | 0.0892 | GEV |
| 54424 | Pinggu | 0.1254 | EV | 0.1017 | EV | 0.1944 | Weibull | 0.0669 | EV |
| 54431 | Tongzhou | 0.1729 | EV | 0.0967 | GEV | 0.2997 | Normal | 0.2602 | Normal |
| 54433 | Chaoyang | 0.1563 | EV | 0.1330 | EV | 0.2753 | EV | 0.1995 | EV |
| 54499 | Changping | 0.1210 | EV | 0.0626 | GEV | 0.2762 | Weibull | 0.1811 | Normal |
| 54501 | Zhaitang | 0.1401 | Weibull | 0.0794 | GEV | 0.1476 | Weibull | 0.0759 | EV |
| 54505 | Mentougou | 0.2602 | Normal | 0.2002 | GEV | 0.1338 | EV | 0.1245 | GEV |
| 54511 | Beijing | 0.2595 | Normal | 0.1549 | Normal | 0.2673 | Lognormal | 0.1276 | Normal |
| 54513 | Shijingshan | 0.1974 | Weibull | 0.1874 | GEV | 0.2466 | Normal | 0.1602 | Normal |
| 54514 | Fengtai | 0.1898 | Weibull | 0.1237 | Normal | 0.2246 | Weibull | 0.1232 | GEV |
| 54594 | Daxing | 0.1764 | EV | 0.1102 | GEV | 0.2105 | EV | 0.1117 | EV |
| 54596 | Fangshan | 0.1734 | EV | 0.0974 | GEV | 0.1950 | Weibull | 0.1422 | GEV |
| 54597 | Xiayunling | 0.3980 | EV | 0.2614 | Normal | 0.2450 | Weibull | 0.1032 | Normal |
| Stations | 1978–1998 | 1999–2015 | |||||
|---|---|---|---|---|---|---|---|
| ID | Name | RMSE | Copula | RMSE | Copula | ||
| 54398 | Shunyi | −0.8500 | 0.0957 | Frank | 0.0448 | 0.1815 | Clayton |
| 54399 | Haidian | 1.0001 | 0.0826 | GH | 1.0001 | 0.1319 | GH |
| 54406 | Yanqing | 1.0000 | 0.0688 | GH | 1.0000 | 0.1046 | GH |
| 54410 | Foyeding | 1.0015 | 0.0676 | GH | 1.0000 | 0.0571 | GH |
| 54412 | Tanghekou | 1.0000 | 0.0581 | GH | 1.0000 | 0.0760 | GH |
| 54416 | Miyun | 1.0135 | 0.1233 | GH | 1.1400 | 0.1520 | GH |
| 54419 | Huairou | 1.1157 | 0.0445 | GH | 1.0000 | 0.1157 | GH |
| 54421 | Shangdianzi | −2.3067 | 0.0276 | Frank | 1.0013 | 0.1111 | GH |
| 54424 | Pinggu | 1.0000 | 0.0204 | GH | −2.2779 | 0.1010 | Frank |
| 54431 | Tongzhou | −1.7019 | 0.1288 | Frank | 0.1749 | 0.2002 | Clayton |
| 54433 | Chaoyang | −2.9860 | 0.1394 | Frank | 1.0000 | 0.2104 | GH |
| 54499 | Changping | −2.4250 | 0.1043 | Frank | 1.0000 | 0.2213 | GH |
| 54501 | Zhaitang | 1.0013 | 0.0550 | GH | 1.0003 | 0.08858 | GH |
| 54505 | Mentougou | −0.5220 | 0.1168 | Frank | −3.3670 | 0.1824 | Frank |
| 54511 | Beijing | 0.0210 | 0.0762 | Frank | 1.0000 | 0.2241 | GH |
| 54513 | Shijingshan | −1.7901 | 0.1804 | Frank | 0.1749 | 0.2002 | Clayton |
| 54514 | Fengtai | 1.0046 | 0.1159 | GH | 1.0001 | 0.2008 | GH |
| 54594 | Daxing | 0.0972 | 0.0471 | Clayton | 1.0000 | 0.2031 | GH |
| 54596 | Fangshan | −1.0530 | 0.1263 | Frank | 1.0001 | 0.1833 | GH |
| 54597 | Xiayunling | 1.0001 | 0.2294 | GH | 1.0001 | 0.1201 | GH |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Hu, H. Copula-Based Hazard Risk Assessment of Winter Extreme Cold Events in Beijing. Atmosphere 2018, 9, 263. https://doi.org/10.3390/atmos9070263
Zhang X, Hu H. Copula-Based Hazard Risk Assessment of Winter Extreme Cold Events in Beijing. Atmosphere. 2018; 9(7):263. https://doi.org/10.3390/atmos9070263
Chicago/Turabian StyleZhang, Xiya, and Haibo Hu. 2018. "Copula-Based Hazard Risk Assessment of Winter Extreme Cold Events in Beijing" Atmosphere 9, no. 7: 263. https://doi.org/10.3390/atmos9070263
APA StyleZhang, X., & Hu, H. (2018). Copula-Based Hazard Risk Assessment of Winter Extreme Cold Events in Beijing. Atmosphere, 9(7), 263. https://doi.org/10.3390/atmos9070263




