Modeling of Aerosol Radiation-Relevant Parameters in the Troposphere of Siberia on the Basis of Empirical Data
Abstract
1. Introduction
2. Construction of the Empirical Model
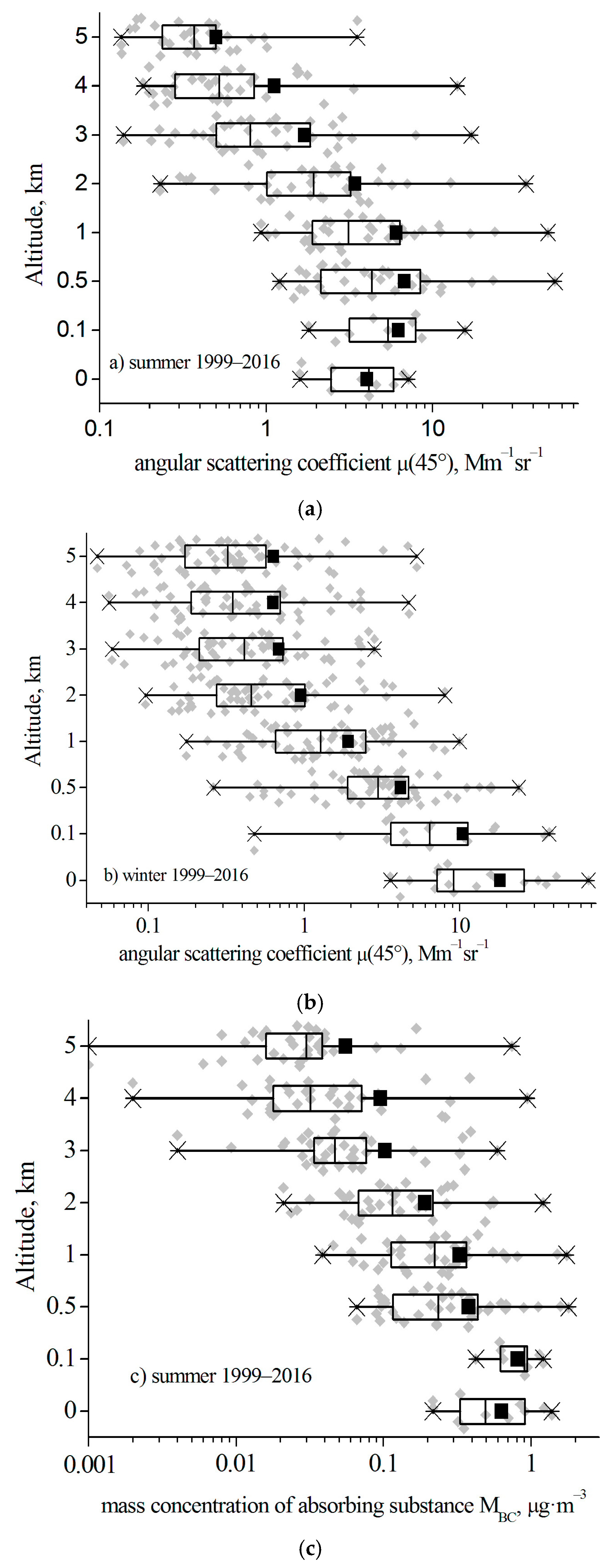
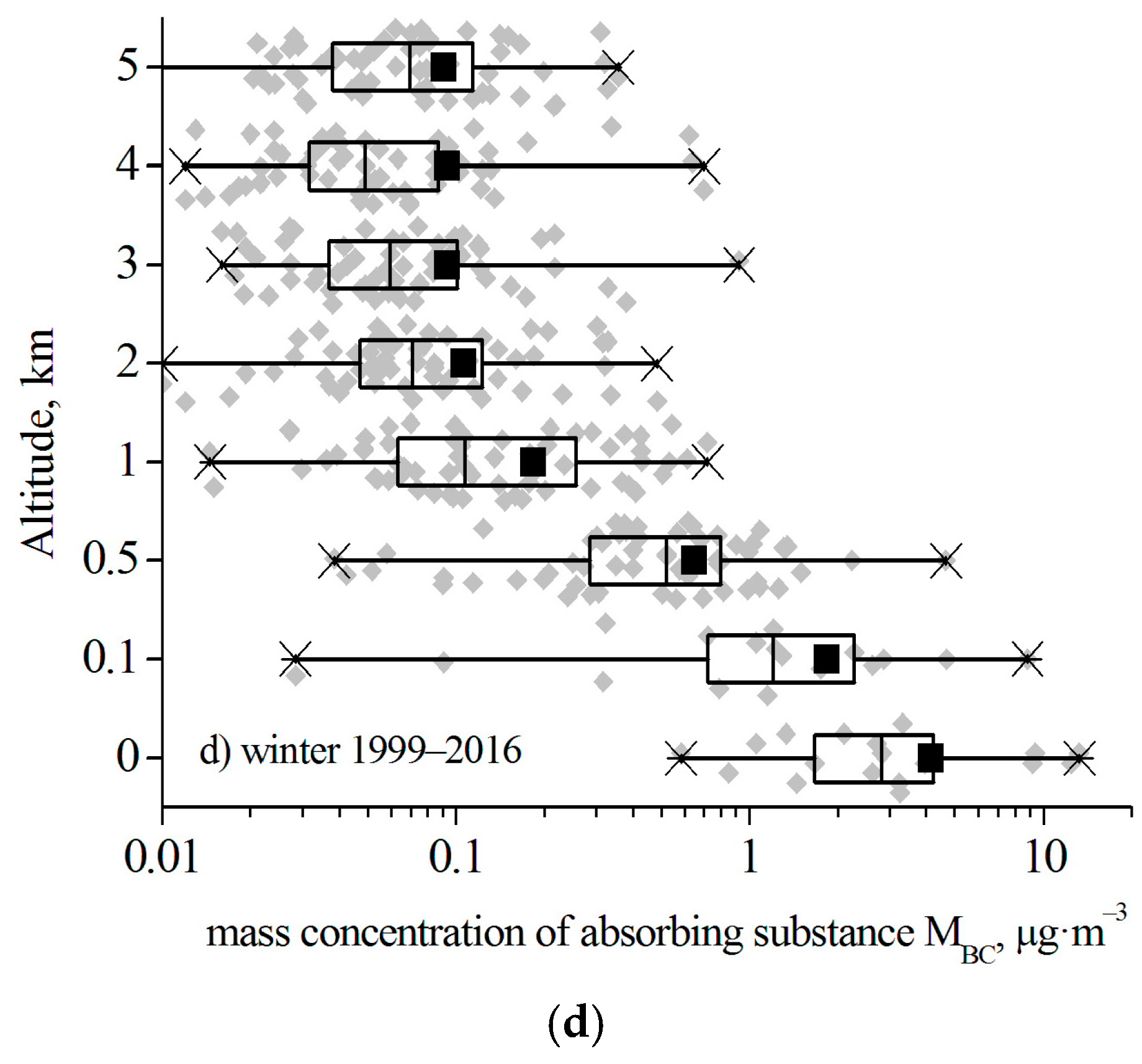
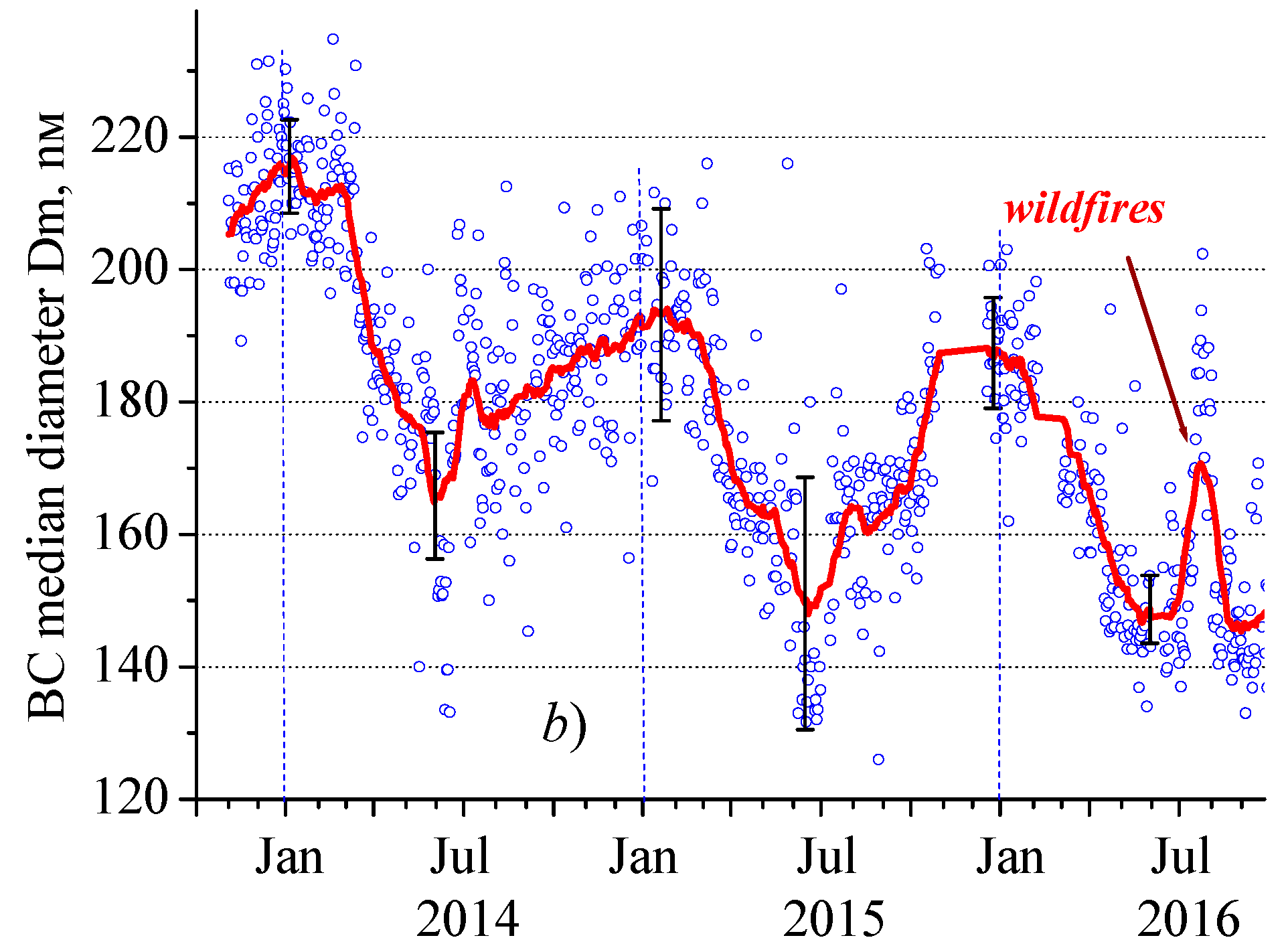
2.1. Experimental Data
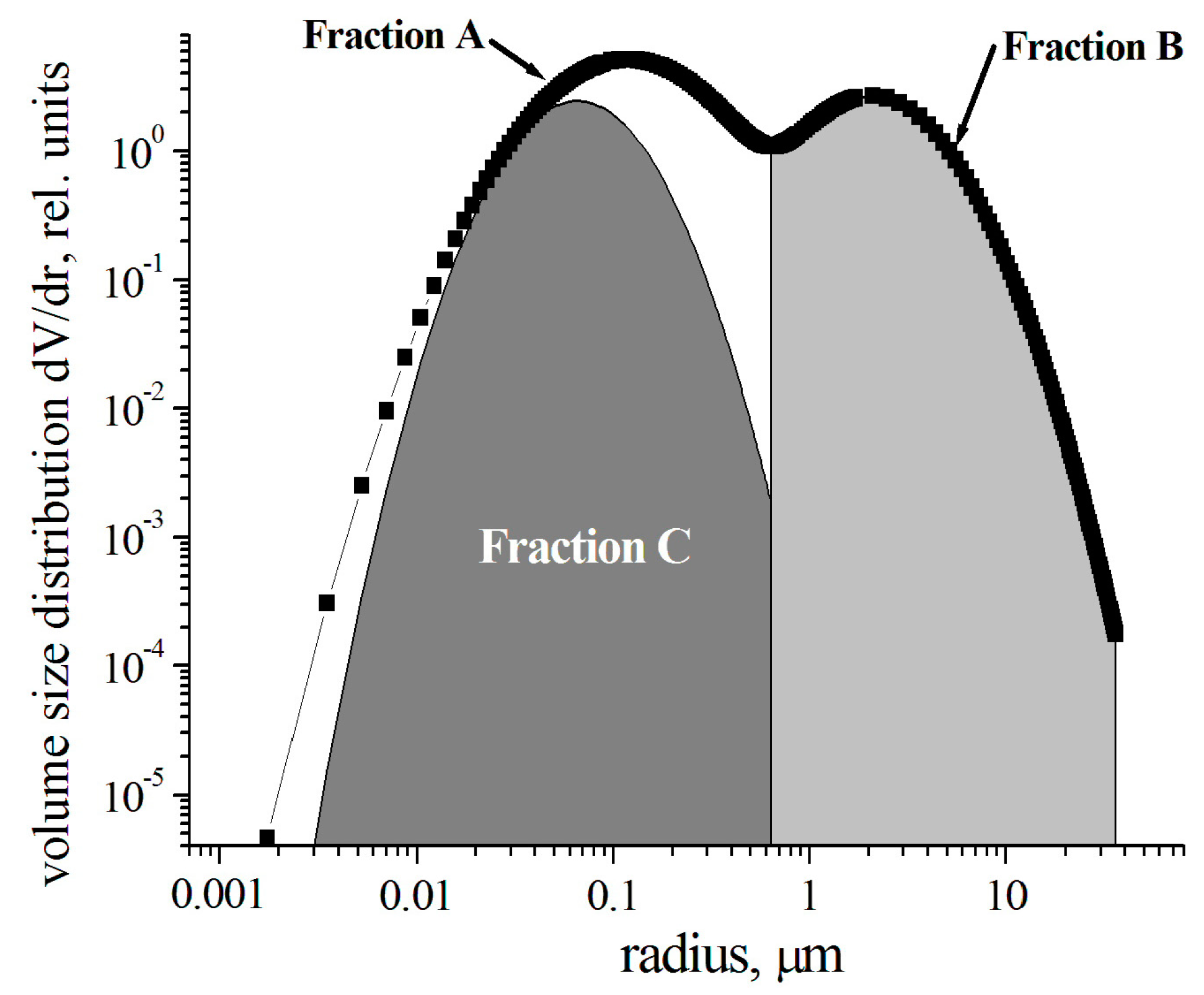
2.2. Modeling of the Aerosol Size Distribution and Complex Refractive Index
2.3. Relative Humidity in the Model
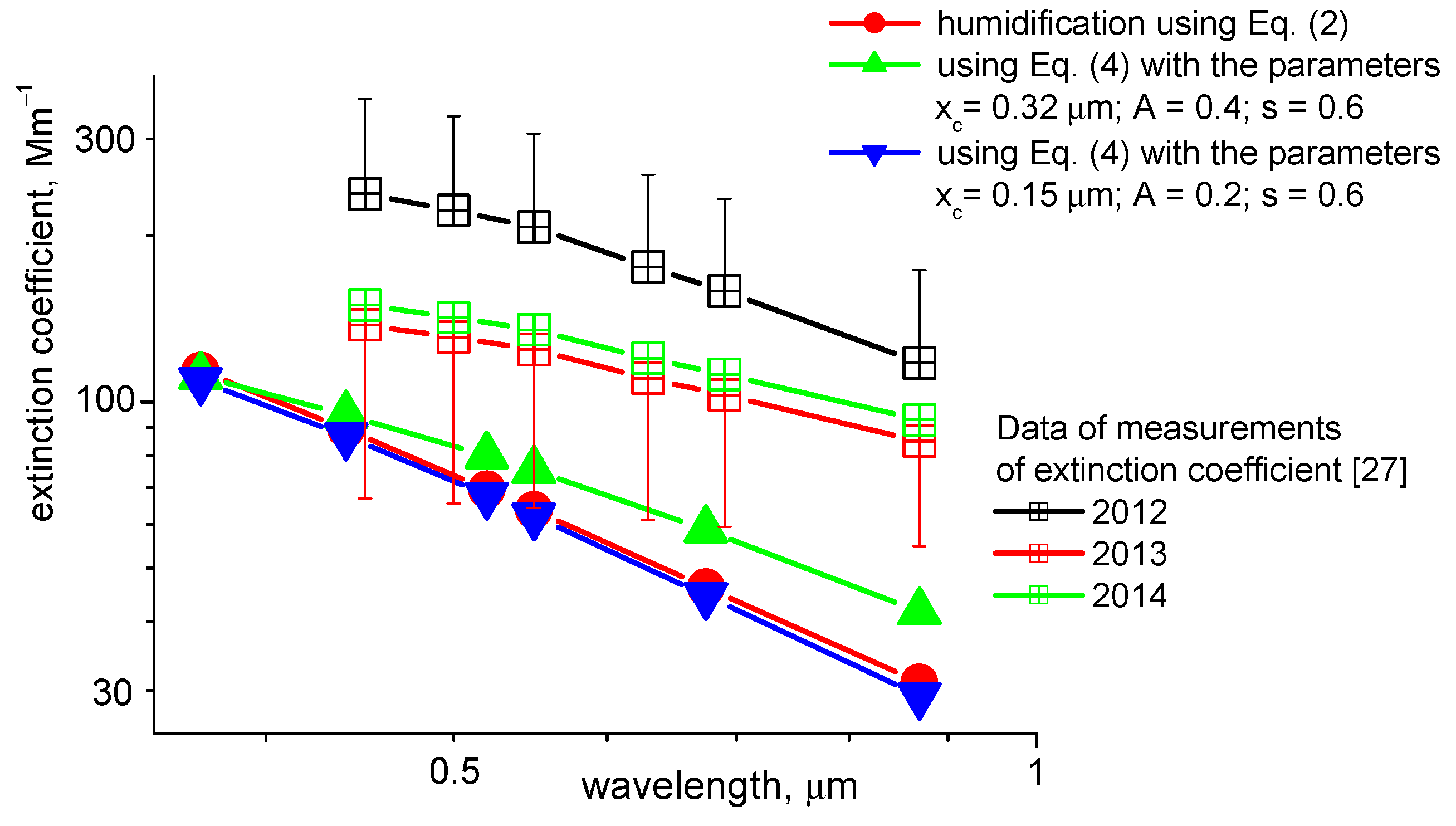
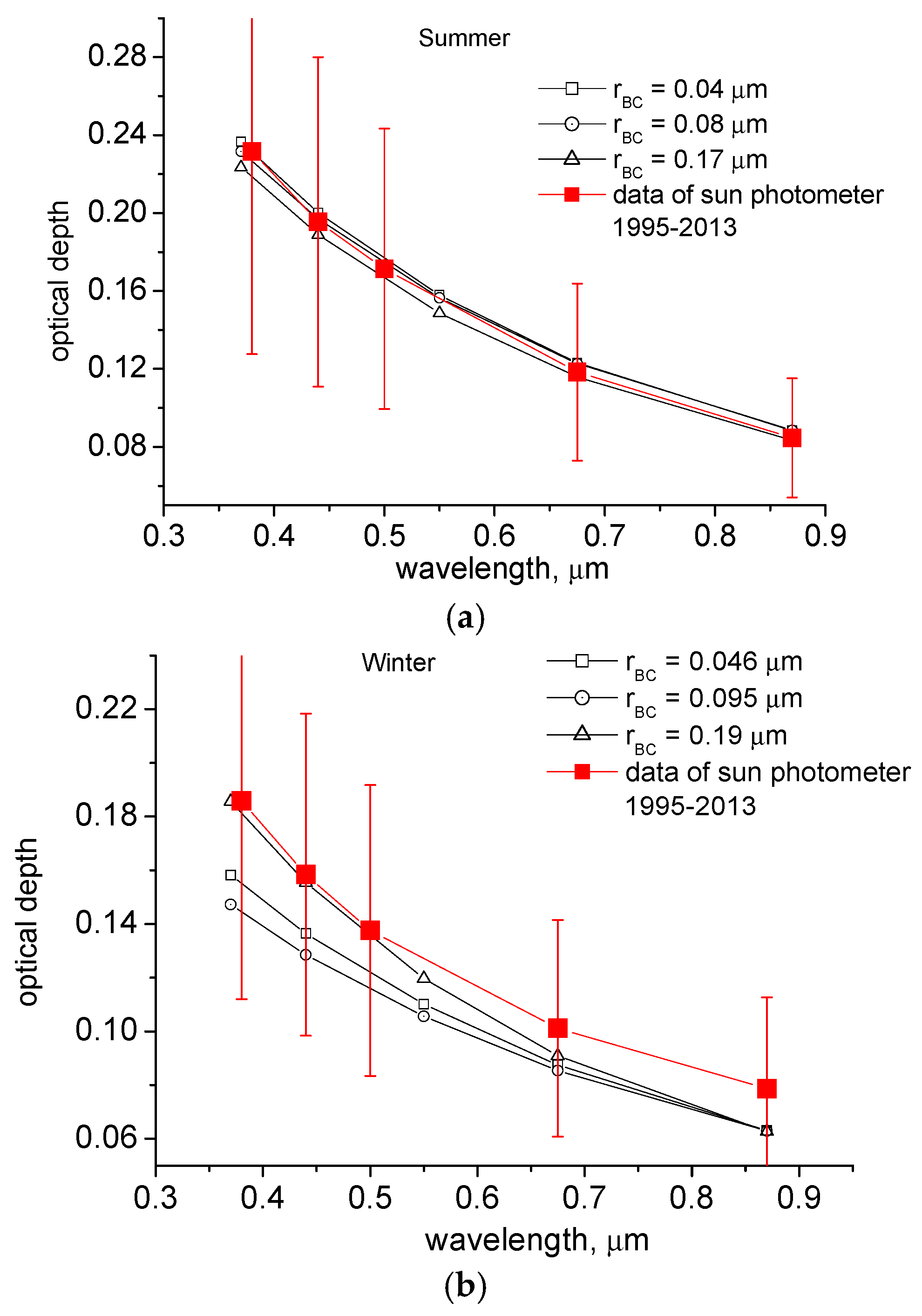
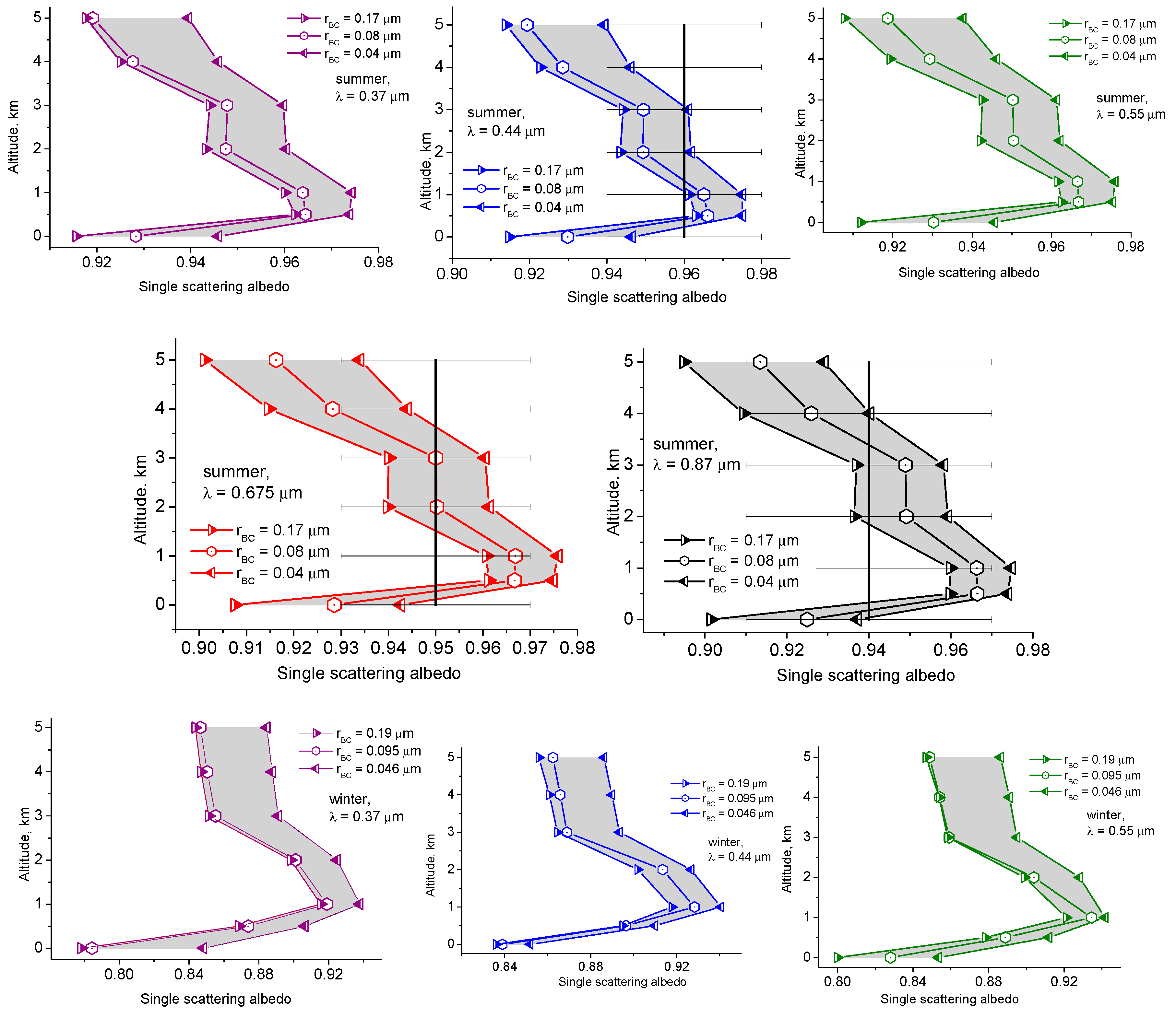
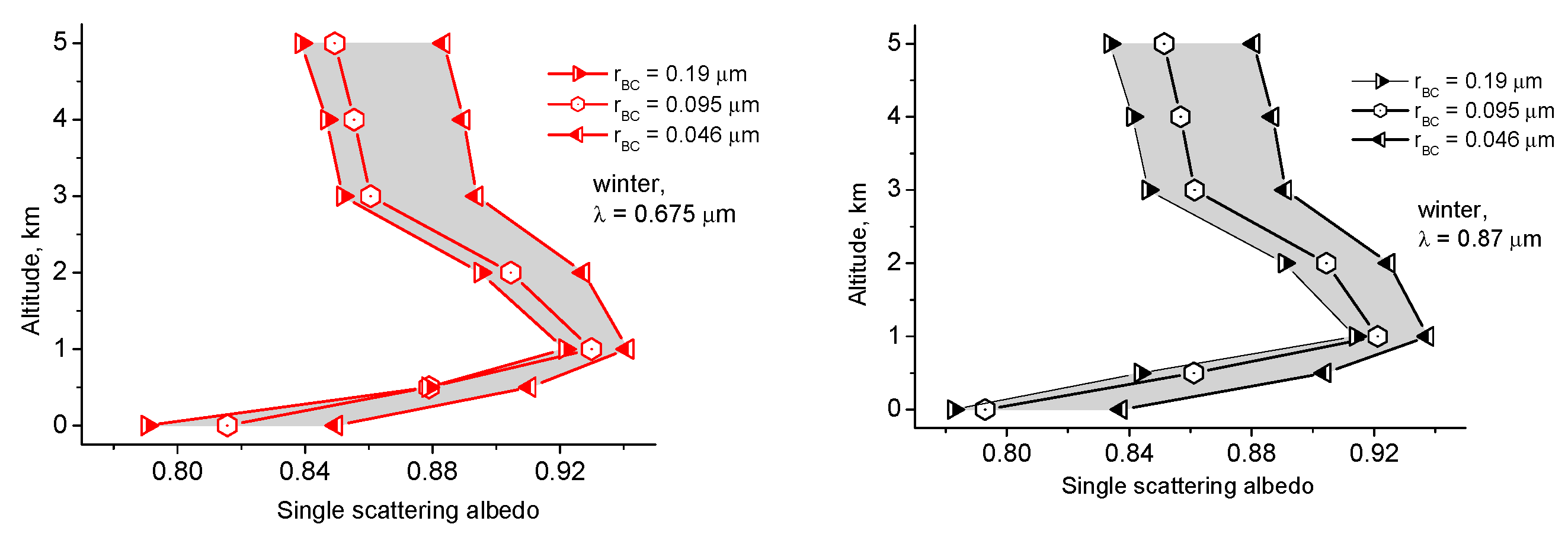
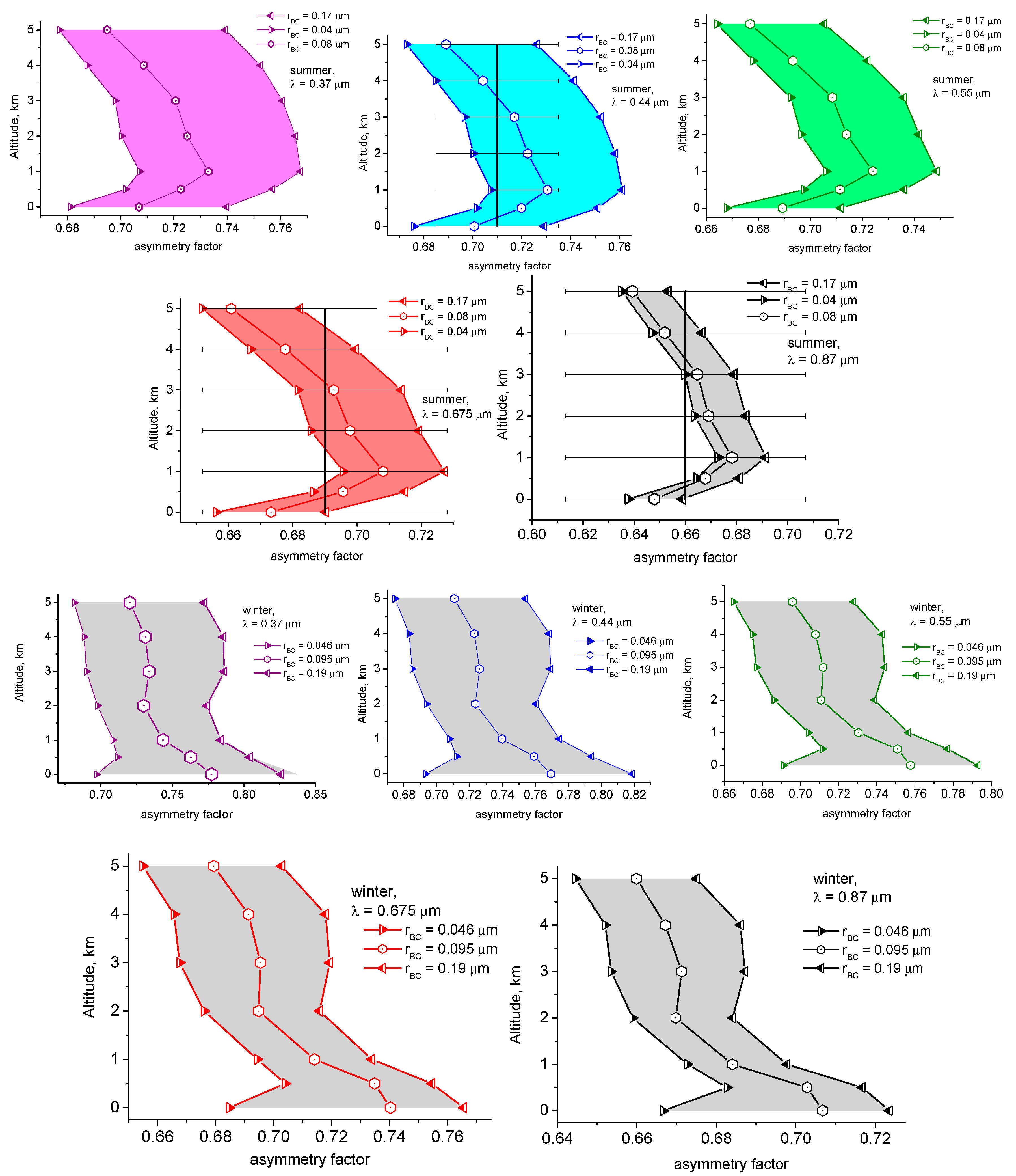
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seinfield, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Haywood, J.; Boucher, O. Estimates of the direct and indirect radiative forcing due to tropospheric aerosols: A review. Rev. Geophys. 2000, 38, 513–543. [Google Scholar] [CrossRef]
- Andrews, E.; Sheridan, P.J.; Ogren, J.A. Seasonal differences in the vertical profiles of aerosol optical properties over rural Oklahoma. Atmos. Chem. Phys. 2011, 11, 10661–10676. [Google Scholar] [CrossRef]
- Jaenicke, R. Atmospheric aerosol and global climate. J. Aerosol Sci. 1980, 11, 577–588. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. IPCC Fifth Assessment Report: Climate Change. 2013. Available online: http://www.ipcc.ch/report/ar5/ (accessed on 24 July 2018).
- Hansen, J.; Sato, M.; Ruedy, R.; Nazarenko, L.; Lacis, A.; Schmidt, G.A.; Russell, G.; Aleinov, I.; Bauer, M.; Bauer, S.; et al. Eficacy of climate forcings. J. Geophys. Res. 2005, 110, D18104. [Google Scholar] [CrossRef]
- Takemura, T.; Nakajima, T.; Dubovik, O.; Holben, B.; Kinne, S. Single-scattering albedo and radiative forcing of various aerosol species with a global three-dimensional model. J. Clim. 2002, 15, 333–352. [Google Scholar] [CrossRef]
- Yu, H.; Kaufman, Y.; Chin, M.; Feingold, G.; Remer, L.; Anderson, T.; Balkanski, Y.; Bellouin, N.; Boucher, O.; Christopher, S.; et al. A review of measurement-based assessments of the aerosol direct radiative effect and forcing. Atmos. Chem. Phys. 2006, 6, 613–666. [Google Scholar] [CrossRef]
- Hartley, S.W.; Hobbs, P.V.; Ross, J.L.; Russell, P.B.; Livingston, J.M. Properties of aerosols aloft relevant to direct radiative forcing of the mid-Atlantic coast of the United States. J. Geophys. Res. 2000, 105, 9859–9885. [Google Scholar] [CrossRef]
- Haywood, J.M.; Ramaswamy, V. Global sensitivity studies of the direct radiative forcing due to anthropogenic sulphate and black carbon aerosols. J. Geophys. Res. 1998, 103, 6043–6058. [Google Scholar] [CrossRef]
- Zhuravleva, T.B. Simulation of solar radiative transfer under different atmospheric conditions. Part I: Deterministic atmosphere. Atmos. Ocean. Opt. 2008, 21, 99–114. [Google Scholar]
- Zhuravleva, T.B.; Kabanov, D.M.; Sakerin, S.M.; Firsov, K.M. Simulation of direct aerosol radiative forcing for typical summer conditions of Siberia. Part 1: Method of calculation and choice of the input parameters. Atmos. Ocean. Opt. 2009, 22, 63–73. [Google Scholar] [CrossRef]
- Gorchakov, G.I.; Karpov, A.V.; Vasiliev, A.V.; Gorchakova, I.A. Brown and black carbons in megacity smogs. Atmos. Ocean. Opt. 2017, 30, 248–254. [Google Scholar] [CrossRef]
- Bates, T.S.; Anderson, T.L.; Baynard, T.; Bond, T.; Boucher, O.; Carmichael, G.; Clarke, A.; Erlick, C.; Guo, H.; Horowitz, L.; et al. Aerosol direct radiative effects over the northwest Atlantic, northwest Pacific, and North Indian Oceans: Estimates based on in-situ chemical and optical measurements and chemical transport modeling. Atmos. Chem. Phys. 2006, 6, 1657–1732. [Google Scholar] [CrossRef]
- Penner, J.E.; Zhang, S.Y.; Chuang, C.C. Soot and smoke aerosol may not warm climate. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Sviridenkov, M.A.; Mikhailov, E.F.; Nebos’ko, E.Y. Parameterization of asymmetry factor of atmospheric aerosol scattering phase function. Atmos. Ocean. Opt. 2017, 30, 435–440. [Google Scholar] [CrossRef]
- Andrews, E.; Sheridan, P.J.; Fiebig, M.; McComiskey, M.; Ogren, J.A.; Arnott, P.; Covert, D.; Elleman, R.; Gasparini, R.; Collins, D.; et al. Comparison of methods for deriving aerosol asymmetry parameter. J. Geophys. Res. 2006, 111, D05S04. [Google Scholar] [CrossRef]
- Bedareva, T.V.; Zhuravleva, T.B. Retrieval of aerosol scattering phase function and single scattering albedo according to data of radiation measurements in solar almucantar: Numerical simulation. Atmos. Ocean. Opt. 2011, 24, 373–385. [Google Scholar] [CrossRef]
- Panchenko, M.V.; Terpugova, S.A.; Tumakov, A.G. Annual variations of submicron aerosol fraction as assessed from the data of airborne nephelometric measurements. Atmos. Res. 1996, 41, 203–215. [Google Scholar] [CrossRef]
- Panchenko, M.V.; Terpugova, S.A. Reconstruction of the scattering coeffcient in the lower troposphere using ground-based measurement. J. Atmos. Sci. 2002, 59, 581–589. [Google Scholar] [CrossRef]
- Panchenko, M.V.; Terpugova, S.A.; Pol’kin, V.V. Empirical model of the aerosol optical properties in the troposphere over West Siberia. Atmos. Ocean. Opt. 1998, 11, 532–539. [Google Scholar]
- Panchenko, M.V.; Zhuravleva, T.B.; Terpugova, S.A.; Polkin, V.V.; Kozlov, V.S. An empirical model of optical and radiative characteristics of the tropospheric aerosol over West Siberia in summer. Atmos. Meas. Tech. 2012, 5, 1513–1527. [Google Scholar] [CrossRef]
- Kozlov, V.S.; Shmargunov, V.P.; Panchenko, M.V. Seasonal Variability of the Vertical Profiles of Absorption Parameters of Submicron Aerosol in the Troposphere. Atmos. Ocean. Opt. 2009, 22, 413–420. [Google Scholar] [CrossRef]
- Panchenko, M.V.; Terpugova, S.A.; Tumakov, A.G.; Belan, B.D.; Rasskazchikova, T.M. Some aspects of a technique for airborne nephelometric studies of the tropospheric aerosol on a regional scale. Atmos. Ocean. Opt. 1994, 7, 546–551. [Google Scholar]
- Fuchs, N.A. The Mechanics of Aerosol; The McMillan Company: New York, NY, USA, 1964. [Google Scholar]
- Zhuravleva, T.; Kabanov, D.; Nasrtdinov, I.; Russkova, T.; Sakerin, S.; Smirnov, A.; Holben, B. Radiative characteristics of aerosol under smoke mist conditions in Siberia during summer 2012. Atmos. Meas. Tech. 2017, 10, 179–198. [Google Scholar] [CrossRef]
- Panchenko, M.V.; Zhuravleva, T.B.; Kozlov, V.S.; Nasrtdinov, I.M.; Pol’kin, V.V.; Terpugova, S.A.; Chernov, D.G. Estimation of Aerosol Radiation Effects under Background and Smoke-haze Atmospheric Conditions over Siberia from Empirical Data. Russ. Meteorol. Hydrol. 2016, 41, 104–111. [Google Scholar] [CrossRef]
- Zuev, V.E.; Krekov, G.M. Optical Models of the Atmosphere; Gidrometeoizdat: Leningrad, Russia, 1986. [Google Scholar]
- Terpugova, S.A.; Panchenko, M.V.; Kozlov, V.S. Estimation of the effect of black carbon on the single scattering albedo of submicron aerosol. In Proceedings of the Abstracts of European Aerosol Conference, Ghent, Belgium, 28 August–2 September 2005; p. 704. [Google Scholar]
- Hitzenberger, R.; Tohno, S. Comparison of black carbon (BC) aerosols in two urban areas–concentrations and size distributions. Atmos. Environ. 2001, 35, 2153–2167. [Google Scholar] [CrossRef]
- Reischl, G.P.; Majerovicz, A.; Ankilov, A.; Baklanov, A.; Eremenko, S.I.; Mavliev, R.A. Comparison of the Novosibirsk automated diffusion battery with Vienna electromobility spectrometer. J. Aerosol Sci. 1991, 22, 325–331. [Google Scholar] [CrossRef]
- Hőler, R.; Tohno, S.; Kasahara, M.; Hitzenberger, R. Long–term characterization of carboneous aerosol in Uji, Japan. Atmos. Environ. 2002, 36, 1267–1275. [Google Scholar] [CrossRef]
- Kristjansson, J.E. Studies of the aerosol indirect effect from sulfate and black carbon aerosols. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Magi, B.I.; Hobbs, P.V.; Schmid, B.; Redemann, J. Vertical profiles of light scattering, light absorption and single scattering albedo during the dry, biomass burning season in southern Africa and comparisons of in-situ and remote sensing measurements of aerosol optical depth. J. Geophys. Res. 2003, 108, 8504. [Google Scholar] [CrossRef]
- Sheridan, P.J.; Arnott, W.P.; Ogren, J.A.; Andrews, E.; Atkinson, D.B.; Covert, D.S.; Moosmuller, H. The Reno Aerosol Optics Study: An evaluation of aerosol absorption measurement methods. Aerosol. Sci. Technol. 2005, 39, 1–16. [Google Scholar] [CrossRef]
- Tikhomirov, A.B.; Firsov, K.M.; Kozlov, V.S.; Panchenko, M.V.; Ponomarev, Y.N.; Tikhomirov, B.A. Investigation of spectral dependence of shortwave radiation absorption by ambient aerosol using time-resolved photoacoustic technique. Opt. Eng. 2005, 4, 071203. [Google Scholar] [CrossRef]
- Virkkula, A.; Ahlquist, N.C.; Covert, D.S.; Arnott, W.P.; Sheridan, P.J.; Quinn, P.K.; Coffman, D.J. Modification, calibration and a field test of an instrument for measuring light absorption by particles. Aerosol. Sci. Technol. 2005, 36, 68–83. [Google Scholar] [CrossRef]
- Bond, T.C.; Bergstrom, R.W. Light absorption by carbonaceous particles: An investigative review. Aerosol Sci. Technol. 2006, 40, 27–67. [Google Scholar] [CrossRef]
- Kecorius, S.; Madueño, L.; Vallar, E.; Alas, H.; Betito, G.; Birmili, W.; Cambaliza, M.O.; Catipay, G.; Gonzaga-Cayetano, M.; Galvez, M.C.; et al. Aerosol particle mixing state, refractory particle number size distributions and emission factors in a polluted urban environment: Case study of Metro Manila, Philippines. Atmos. Environ. 2017, 170, 169–183. [Google Scholar] [CrossRef]
- He, C.; Liou, K.-N.; Takano, Y.; Zhang, R.; Levy Zamora, M.; Yang, P.; Li, Q.; Leung, L.R. Variation of the radiative properties during black carbon aging: Theoretical and experimental intercomparison. Atmos. Chem. Phys. 2015, 15, 11967–11980. [Google Scholar] [CrossRef]
- Bauer, S.E.; Menon, S.; Koch, D.; Bond, T.C.; Tsigaridis, K. A global modeling study on carbonaceous aerosol microphysical characteristics and radiative effects. Atmos. Chem. Phys. 2010, 10, 7439–7456. [Google Scholar] [CrossRef]
- Kozlov, V.S.; Shmargunov, V.P.; Panchenko, M.V.; Chernov, D.G.; Kozlov, A.S.; Malyshkin, S.B. Seasonal variability of Black Carbon size distribution in the atmospheric aerosol. Russ. Phys. J. 2016, 58, 1804–1810. [Google Scholar] [CrossRef]
- Kozlov, V.S.; Shmargunov, V.P.; Panchenko, M.V. Modified aethalometer for monitoring of black carbon concentration in atmospheric aerosol and technique for correction of the spot loading effect. Proceed. SPIE 2016, 10035, 1003530. [Google Scholar] [CrossRef]
- Available online: http://aerosol.iao.ru (accessed on 17 April 2018).
- Panchenko, M.V.; Terpugova, S.A.; Kozlov, V.S.; Pol’kin, V.V.; Yausheva, E.P. Annual behavior of the condensation activity of submicron aerosol in the atmospheric surface layer of Western Siberia. Atmos. Ocean. Opt. 2005, 18, 607–611. [Google Scholar]
- Gassfio, S.; Hegg, D.A.; Covert, D.S.; Noone, K.J.; Ostrom, E.; Schmid, B.; Russell, P.B.; Livingston, J.M.; Durkee, P.A.; Jonsson, H.H. Influence of humidity on the aerosol scattering coeffcient and its effect on the upwelling radiance during ACE-2. Tellus 2000, 52B, 546–567. [Google Scholar] [CrossRef]
- Meszaros, A. On the concentration and size distribution of atmospheric sulfate particles under rural conditions. Atmos. Environ. 1978, 12, 2425–2428. [Google Scholar] [CrossRef]
- Laktionov, A.G. Equilibrium Heterogeneous Condensation; Gidrometeoizdat: Leningrad, Russia, 1988. [Google Scholar]
- Wang, Z.; Cheng, Y.; Ma, N.; Mikhailov, E.; Pöschl, U.; Su, H. Dependence of the hygroscopicity parameter κ on particle size, humidity and solute concentration: Implications for laboratory experiments, field measurements and model studies. Atmos. Chem. Phys. Discuss. 2017. [Google Scholar] [CrossRef]
- Gruzdev, A.N.; Isakov, A.A.; Shukurova, L.M. Analysis of relationship between condensation activity of surface aerosol and its chemical composition and relative air humidity according to measurements at the Zvenigorod Scientific Station. Atmos. Ocean Opt. 2014, 27, 169–175. [Google Scholar] [CrossRef]
- Isakov, A.A.; Tikhonov, A.V. Relationship between aerosol parameters and air masses in central Russia. Atmos. Ocean Opt. 2014, 27, 475–478. [Google Scholar] [CrossRef]
- Terpugova, S.A.; Panchenko, M.V.; Sviridenkov, M.A.; Dokukina, T.A. Relationships between optical and microphysical parameters of the near-ground aerosol condensation variability. Atmos. Oceanic Opt. 2009, 22, 405–412. [Google Scholar] [CrossRef]
- Panchenko, M.V.; Polkin, V.V.; Terpugova, S.A.; Uzhegov, V.N.; Pkhalagov, Y.A. Testing the algorithms for taking into account relative humidity of air in the model of optical characteristics of absorbing aerosol. Proceed. SPIE 2015, 9680, 96802R. [Google Scholar] [CrossRef]
- Uzhegov, V.N.; Kabanov, D.M.; Pkhalagov, Y.A.; Sakerin, S.M. Correlation between variations of aerosol extinction of visible and IR radiation in the near-ground layer and atmospheric column. Atmos. Ocean. Opt. 2009, 22, 338–345. [Google Scholar] [CrossRef]
- Sakerin, S.M.; Beresnev, S.A.; Kabanov, D.M.; Kornienko, G.I.; Nikolashkin, S.V.; Poddubny, V.A.; Tashchilin, M.A.; Turchinovich, Y.S.; Holben, B.N.; Smirnov, A. Analysis of Approaches to Modeling the Annual and Spectral Behaviors of Atmospheric Aerosol Optical Depth in Siberia and Primorye. Atmos. Ocean. Opt. 2015, 28, 145–157. [Google Scholar] [CrossRef]
- Kabanov, D.M.; Beresnev, S.A.; Gorda, S.Yu.; Holben, B.N.; Kornienko, G.I.; Nikolashkin, S.V.; Sakerin, S.M.; Smirnov, A.; Taschilin, M.A. Annual behavior of the aerosol optical depth in some regions of Asian part of Russia. Proceed. SPIE 2014, 9292, 929241. [Google Scholar]
- Kabanov, D.M.; Zhamsueva, G.S.; Zayakhanov, A.S.; Kornienko, G.I.; Naguslaev, S.A.; Pavlov, A.N.; Panchenko, M.V.; Pestunov, D.A.; Sakerin, S.M.; Shmirko, K.A. About results of two-site measurements of the aerosol optical depth of the atmosphere in certain regions of Russia. Atmos. Ocean. Opt. 2016, 29, 960–971. [Google Scholar]
- Sakerin, S.M.; Kabanov, D.M. Spectral dependence of the atmosphere aerosol optical depth near 0.37–4 μm. Atmos. Ocean. Opt. 2007, 20, 141–149. [Google Scholar]
- Tomsk, Version 3, Level 2.0. Available online: https://aeronet.gsfc.nasa.gov (accessed on 12 March 2018).

| Winter | |||||
| Fraction A | |||||
| H (km) | rA | νA | VA × 1012 | n | χ |
| 0 | 0.093 | 0.8 | 16.8274 | 1.5 | 0 |
| 0.5 | 0.093 | 0.8 | 3.8644 | 1.5 | 0 |
| 1 | 0.093 | 0.8 | 2.0938 | 1.5 | 0 |
| 2 | 0.093 | 0.8 | 1.0645 | 1.5 | 0 |
| 3 | 0.093 | 0.8 | 0.6574 | 1.5 | 0 |
| 4 | 0.093 | 0.8 | 0.5487 | 1.5 | 0 |
| 5 | 0.093 | 0.8 | 0.5357 | 1.5 | 0 |
| Fraction B | |||||
| H (km) | rB | νB | VB × 1012 | n | χ |
| 0 | 3.63 | 0.75 | 20.0553 | 1.503 | 0.00685 |
| 0.5 | 1.774 | 0.75 | 1.8454 | 1.503 | 0.0086 |
| 1 | 1.778 | 0.75 | 1.217 | 1.5015 | 0.0038 |
| 2 | 1.786 | 0.75 | 0.8809 | 1.501 | 0.003 |
| 3 | 1.794 | 0.75 | 0.6175 | 1.502 | 0.0042 |
| 4 | 1.802 | 0.75 | 0.5154 | 1.502 | 0.0044 |
| 5 | 1.81 | 0.75 | 0.5032 | 1.502 | 0.0042 |
| Summer | |||||
| Fraction A | |||||
| H (km) | rA | νA | VA × 1012 | n | χ |
| 0 | 0.099 | 0.8 | 9.0096 | 1.5 | 0 |
| 0.5 | 0.078 | 0.8 | 9.43 | 1.5 | 0 |
| 1 | 0.078 | 0.8 | 7.66 | 1.5 | 0 |
| 2 | 0.078 | 0.8 | 3.22 | 1.5 | 0 |
| 3 | 0.078 | 0.8 | 1.608 | 1.5 | 0 |
| 4 | 0.078 | 0.8 | 1.11 | 1.5 | 0 |
| 5 | 0.078 | 0.8 | 0.932 | 1.5 | 0 |
| Fraction B | |||||
| H (km) | rB | νB | VB × 1012 | n | χ |
| 0 | 2.078 | 0.65 | 5.8215 | 1.5011 | 0.00266 |
| 0.5 | 1.803 | 0.65 | 7.9639 | 1.5004 | 0.000937 |
| 1 | 1.797 | 0.65 | 6.2687 | 1.5004 | 0.001 |
| 2 | 1.784 | 0.65 | 2.4649 | 1.5007 | 0.00164 |
| 3 | 1.771 | 0.65 | 1.1961 | 1.5007 | 0.00163 |
| 4 | 1.758 | 0.65 | 0.7304 | 1.5010 | 0.00237 |
| 5 | 1.745 | 0.65 | 0.5625 | 1.5011 | 0.0027 |
| Summer | |||||||||||
| Altitude (km) | RH (%) | Fraction A | Fraction B | Fraction C | |||||||
| rBC = 0.04 μm | rBC = 0.08 μm | rBC = 0.17 μm | |||||||||
| n | χ | n | χ | n | χ | n | χ | n | χ | ||
| 0 | 72 | 1.451 | 0 | 1.501 | 0.0027 | 1.526 | 0.088 | 1.468 | 0.017 | 1.439 | 0.021 |
| 0.5 | 70 | 1.435 | 0 | 1.500 | 0.00094 | 1.488 | 0.015 | 1.439 | 0.006 | 1.409 | 0.012 |
| 1 | 75 | 1.425 | 0 | 1.50 | 0.001 | 1.484 | 0.019 | 1.429 | 0.006 | 1.400 | 0.011 |
| 2 | 71 | 1.433 | 0 | 1.50 | 0.0016 | 1.493 | 0.029 | 1.439 | 0.009 | 1.410 | 0.019 |
| 3 | 69 | 1.437 | 0 | 1.50 | 0.016 | 1.494 | 0.029 | 1.443 | 0.009 | 1.414 | 0.019 |
| 4 | 62 | 1.447 | 0 | 1.50 | 0.024 | 1.501 | 0.038 | 1.454 | 0.013 | 1.428 | 0.028 |
| 5 | 53 | 1.457 | 0 | 1.501 | 0.027 | 1.506 | 0.041 | 1.465 | 0.015 | 1.441 | 0.033 |
| Winter | |||||||||||
| Altitude (km) | RH (%) | Fraction A | Fraction B | Fraction C | |||||||
| rBC = 0.046 μm | rBC = 0.095 μm | rBC = 0.19 μm | |||||||||
| n | χ | n | χ | n | χ | n | χ | n | χ | ||
| 0 | 84 | 1.413 | 0 | 1.503 | 0.0068 | 1.5413 | 0.1884 | 1.4304 | 0.0470 | 1.51 | 0.163 |
| 0.5 | 78 | 1.411 | 0 | 1.503 | 0.0086 | 1.5012 | 0.0935 | 1.4183 | 0.0229 | 1.4010 | 0.0321 |
| 1 | 72 | 1.424 | 0 | 1.501 | 0.0038 | 1.4936 | 0.0534 | 1.4283 | 0.0144 | 1.4102 | 0.0269 |
| 2 | 62 | 1.439 | 0 | 1.501 | 0.003 | 1.5065 | 0.0645 | 1.4467 | 0.0193 | 1.4296 | 0.0368 |
| 3 | 61 | 1.441 | 0 | 1.502 | 0.0042 | 1.5224 | 0.1023 | 1.4528 | 0.0309 | 1.4398 | 0.0589 |
| 4 | 60 | 1.442 | 0 | 1.502 | 0.0044 | 1.5245 | 0.1059 | 1.4546 | 0.0322 | 1.4423 | 0.0617 |
| 5 | 50 | 1.453 | 0 | 1.502 | 0.0042 | 1.5287 | 0.1053 | 1.4665 | 0.0342 | 1.4566 | 0.0674 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panchenko, M.V.; Terpugova, S.A.; Pol’kin, V.V.; Kozlov, V.S.; Chernov, D.G. Modeling of Aerosol Radiation-Relevant Parameters in the Troposphere of Siberia on the Basis of Empirical Data. Atmosphere 2018, 9, 414. https://doi.org/10.3390/atmos9110414
Panchenko MV, Terpugova SA, Pol’kin VV, Kozlov VS, Chernov DG. Modeling of Aerosol Radiation-Relevant Parameters in the Troposphere of Siberia on the Basis of Empirical Data. Atmosphere. 2018; 9(11):414. https://doi.org/10.3390/atmos9110414
Chicago/Turabian StylePanchenko, Mikhail V., Svetlana A. Terpugova, Victor V. Pol’kin, Valerii S. Kozlov, and Dmitry G. Chernov. 2018. "Modeling of Aerosol Radiation-Relevant Parameters in the Troposphere of Siberia on the Basis of Empirical Data" Atmosphere 9, no. 11: 414. https://doi.org/10.3390/atmos9110414
APA StylePanchenko, M. V., Terpugova, S. A., Pol’kin, V. V., Kozlov, V. S., & Chernov, D. G. (2018). Modeling of Aerosol Radiation-Relevant Parameters in the Troposphere of Siberia on the Basis of Empirical Data. Atmosphere, 9(11), 414. https://doi.org/10.3390/atmos9110414





