Sensitivity Study of WRF Numerical Modeling for Forecasting Heavy Rainfall in Sri Lanka
Abstract
1. Introduction
2. Method
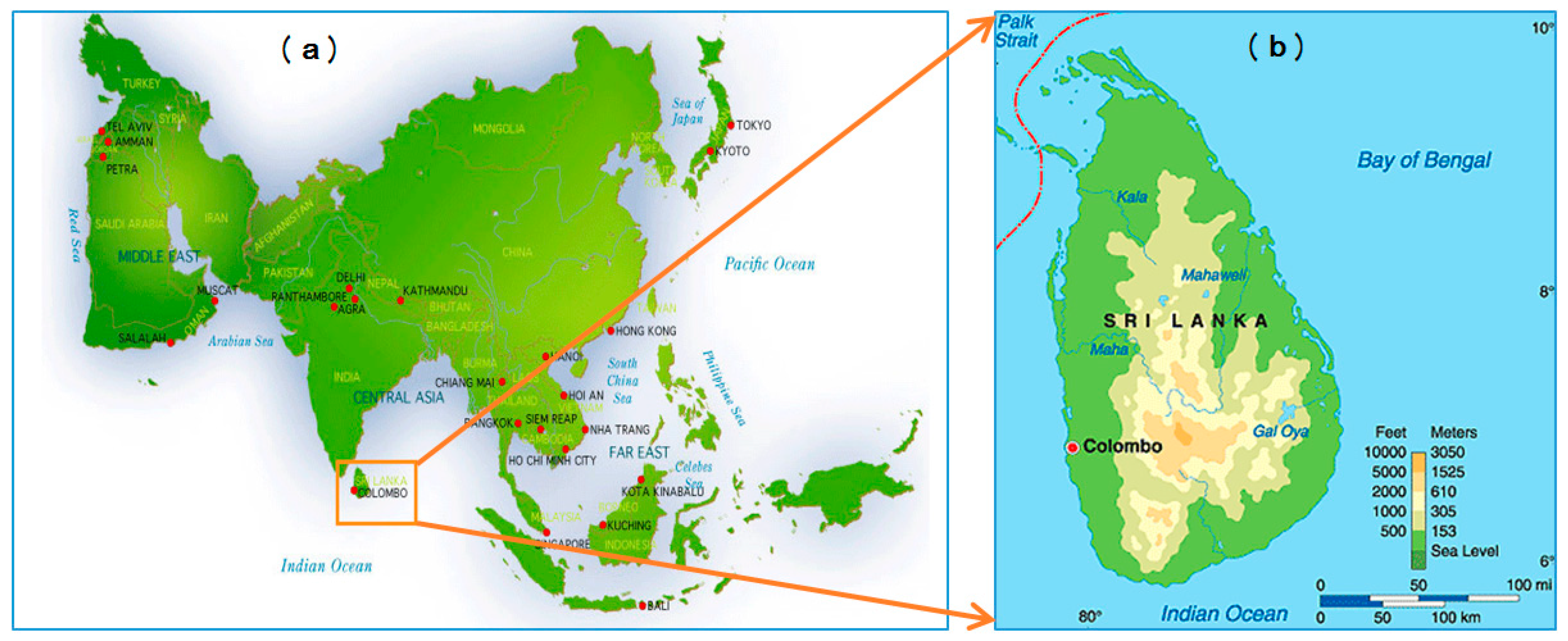
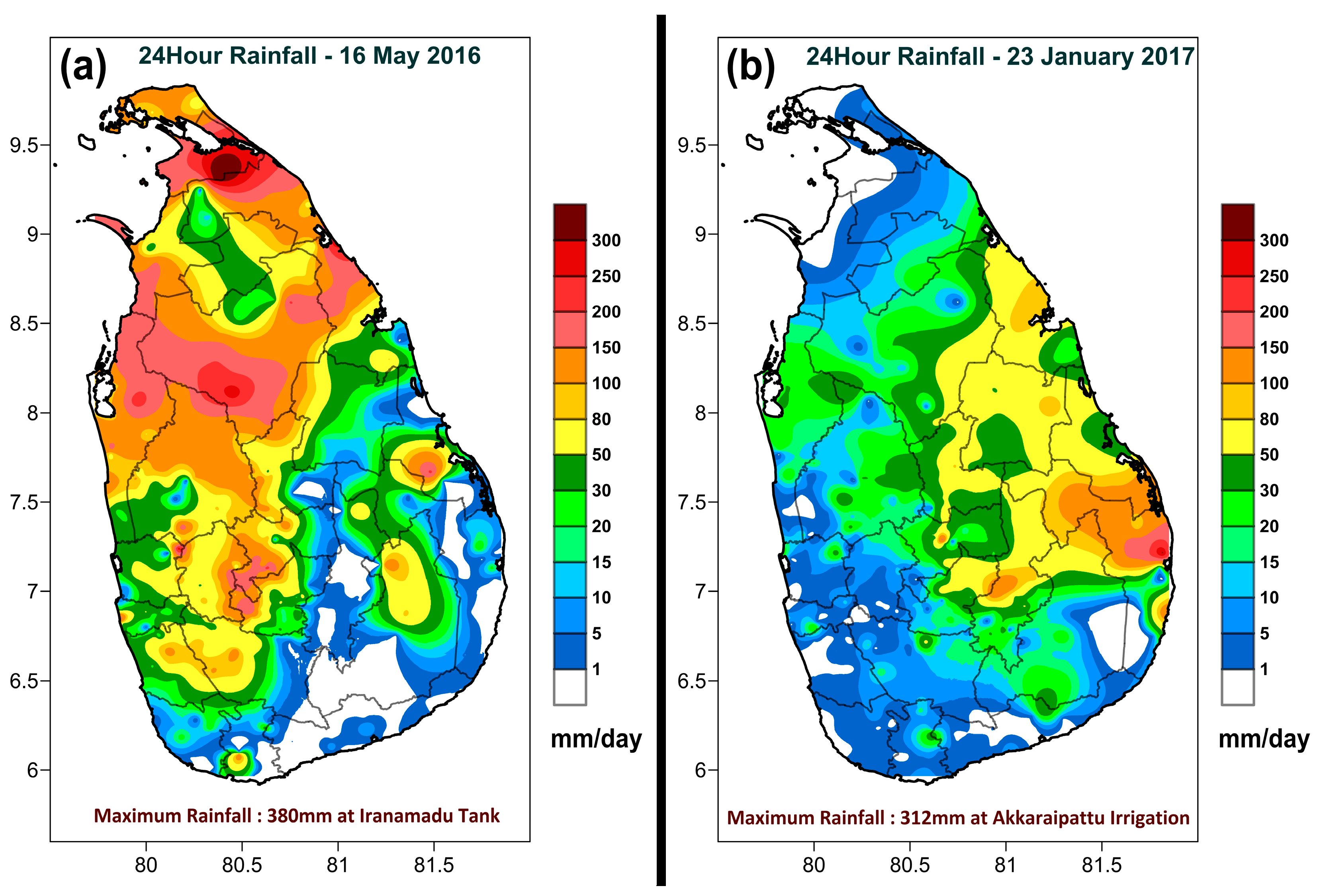
2.1. Study Area and Events
2.2. Method and Materials
2.2.1. Basic Model Configuration
2.2.2. Experimental Set-up
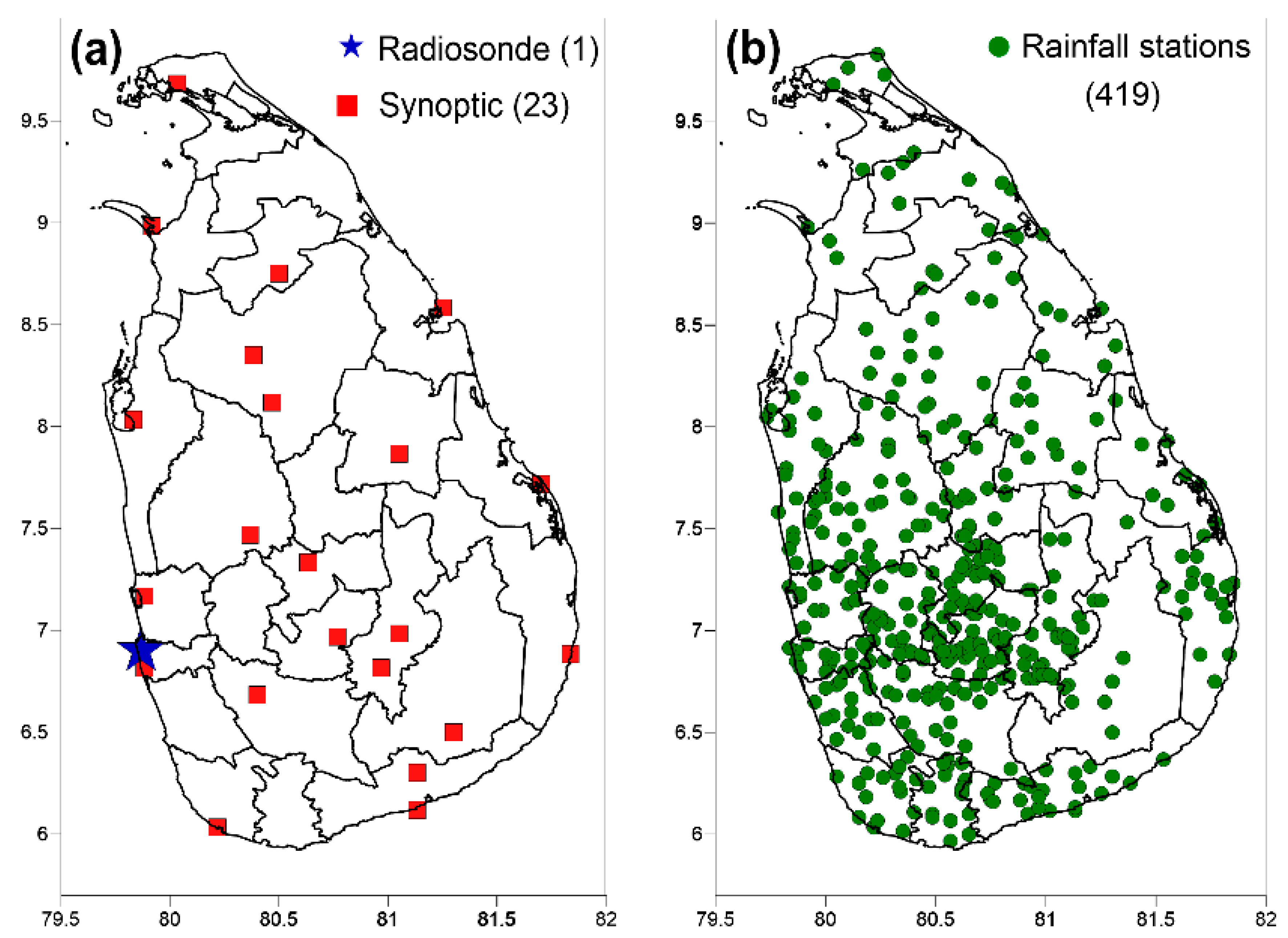
2.3. Data
2.4. Statistical Skill Scores
3. Results and Discussion
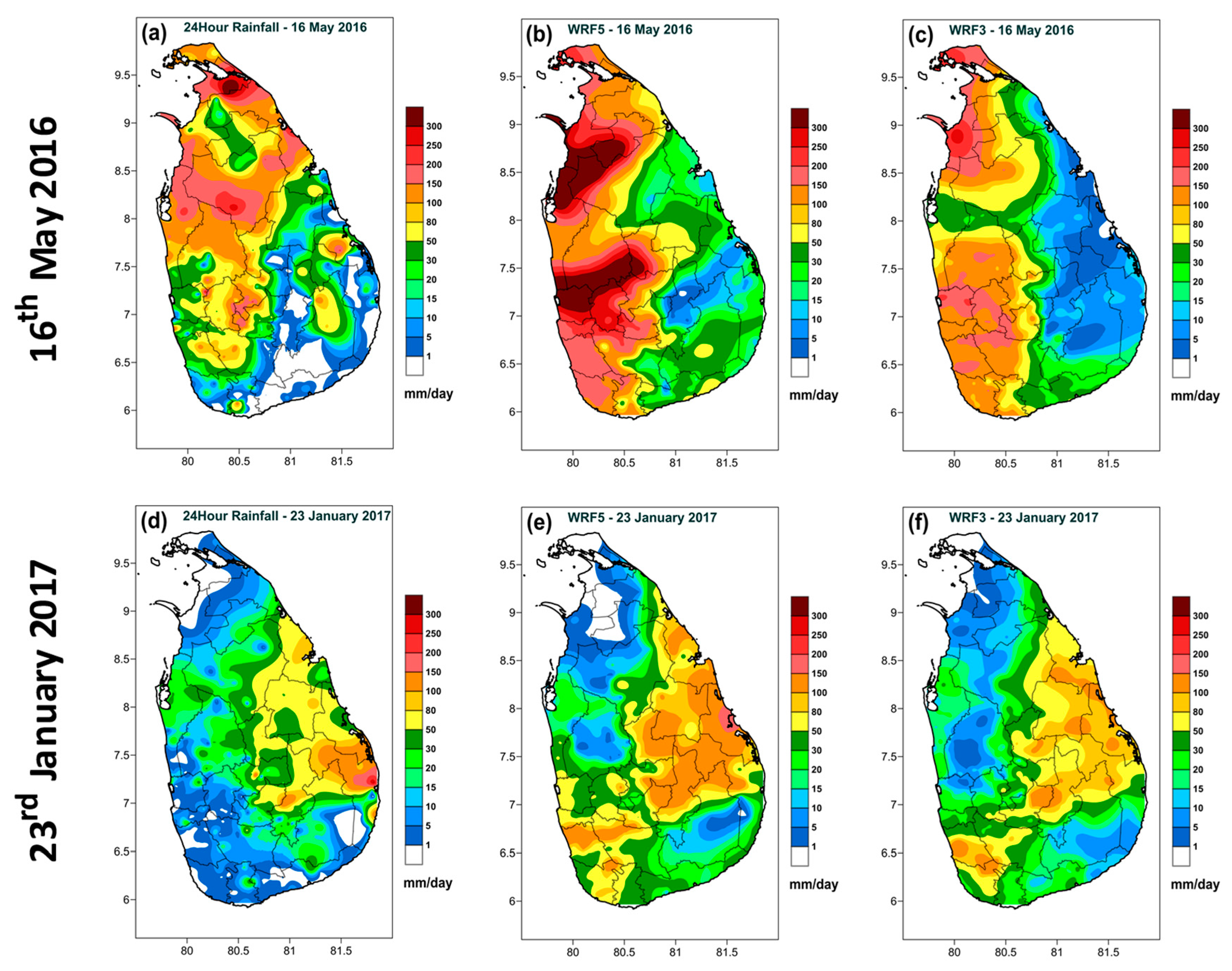
3.1. Model Horizontal Resolution
3.2. Impact of Physical Parameterization
4. Summaries and Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hapuarachchi, H.A.S.U.; Jayawardena, I.M.S.P. Modulation of seasonal rainfall in Sri Lanka by ENSO extremes. Sri Lanka J. Meteorol. 2015, 1, 3–11. [Google Scholar]
- Rasmusson, E.M.; Carpenter, T.H. The relationship between eastern equatorial Pacific sea surface temperatures and rainfall over India and Sri Lanka. Mon. Weather Rev. 1983, 111, 517–528. [Google Scholar] [CrossRef]
- Zubair, L.; Ropelewski, C.F. The strengthening relationship between ENSO and Northeast Monsoon rainfall over Sri Lanka and Southern India. J. Clim. 2006, 19, 1567–1575. [Google Scholar] [CrossRef]
- Jayawardene, H.K.W.I.; Sonnadara, D.U.J.; Jayewardene, D.R. Trends of rainfall in Sri Lanka over the last century. Sri Lankan J. Phys. 2005, 6, 7–17. [Google Scholar] [CrossRef]
- Vuillaume, J.F.; Dorji, S.; Komolafe, A.; Herath, S. Sub-seasonal extreme rainfall prediction in the Kelani River basin of Sri Lanka by using self-organizing map classification. Nat. Hazards 2018, 94, 385–404. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; Technical Report, (June); National Center For Atmospheric Research: Boulder, CO, USA, 2005; p. 113. [Google Scholar]
- Kain, J.S. The Kain-Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Lim, K.-S.S.; Hong, S.-Y. Development of an effective double-moment cloud microphysics scheme with prognostic cloud condensation nuclei (CCN) for weather and climate models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
- Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.A.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.P.; Cuenca, R.H. Implementation and verification of the unified noah land surface model in the WRF model. Bull. Am. Meteorol. Soc. 2004, 27, 2165–2170. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- NCEP. The GFS Atmospheric Model, Note 442., (November); NCEP: Washington, DC, USA, 2003; p. 14. Available online: http://www.emc.ncep.noaa.gov/officenotes/newernotes/on442.pdf (accessed on 30 June 2017).
- Hong, S.-Y.; Dudhia, J.; Chen, S.-H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather. Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Hong, S.; Lim, J. The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Pan, H.-L.; Wu, W.-S. Implementing a mass flux convective parameterization package for the NMC medium-range forecast model. NMC Off. Note 1995, 409. Available online: http://www.emc.ncep.noaa.gov/officenotes/FullTOC.html (accessed on 27 September 2017).
- Janjić, Z.I. The Step-Mountain Eta Coordinate Model: Further developments of the convection, viscous sublayer, and turbulence closure schemes. Mon. Weather Rev. 1994, 927–945. [Google Scholar] [CrossRef]
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2014, 14, 5233–5250. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. Multiscale convective overturning in mesoscale convective systems: Reconciling observations, simulations, and theory. Mon. Weather. Rev. 1998, 126, 2254–2273. [Google Scholar] [CrossRef]
- Grell, G.A.; Dévényi, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Tiedtke, M. A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon. Weather Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Hamilton, K. Improved representation of boundary layer clouds over the southeast Pacific in ARW-WRF using a modified Tiedtke cumulus parameterization scheme. Mon. Weather Rev. 2011, 139, 3489–3513. [Google Scholar] [CrossRef]
- Han, J.; Pan, H.-L. Revision of convection and vertical diffusion schemes in the NCEP Global Forecast System. Weather Forecast. 2011, 26, 520–533. [Google Scholar] [CrossRef]
- Pearson, K. On the Theory of Contingency and Its Relation to Association and Normal Correlation; Drapers’ Company Research Memoirs Biometric Series I; Cambridge University Press: Cambridge, UK, 1904. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: San Diego, CA, USA, 1995. [Google Scholar]
- Done, J.; Davis, C.A.; Weisman, M. The next generation of NWP: Explicit forecasts of convection using the weather research and forecasting (WRF) model. Atmos. Sci. Lett. 2004, 5, 110–117. [Google Scholar] [CrossRef]
- Wang, W.; Seaman, N.L. A comparison study of convective parameterization schemes in a mesoscale model. Mon. Weather Rev. 1997, 125, 252–278. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]

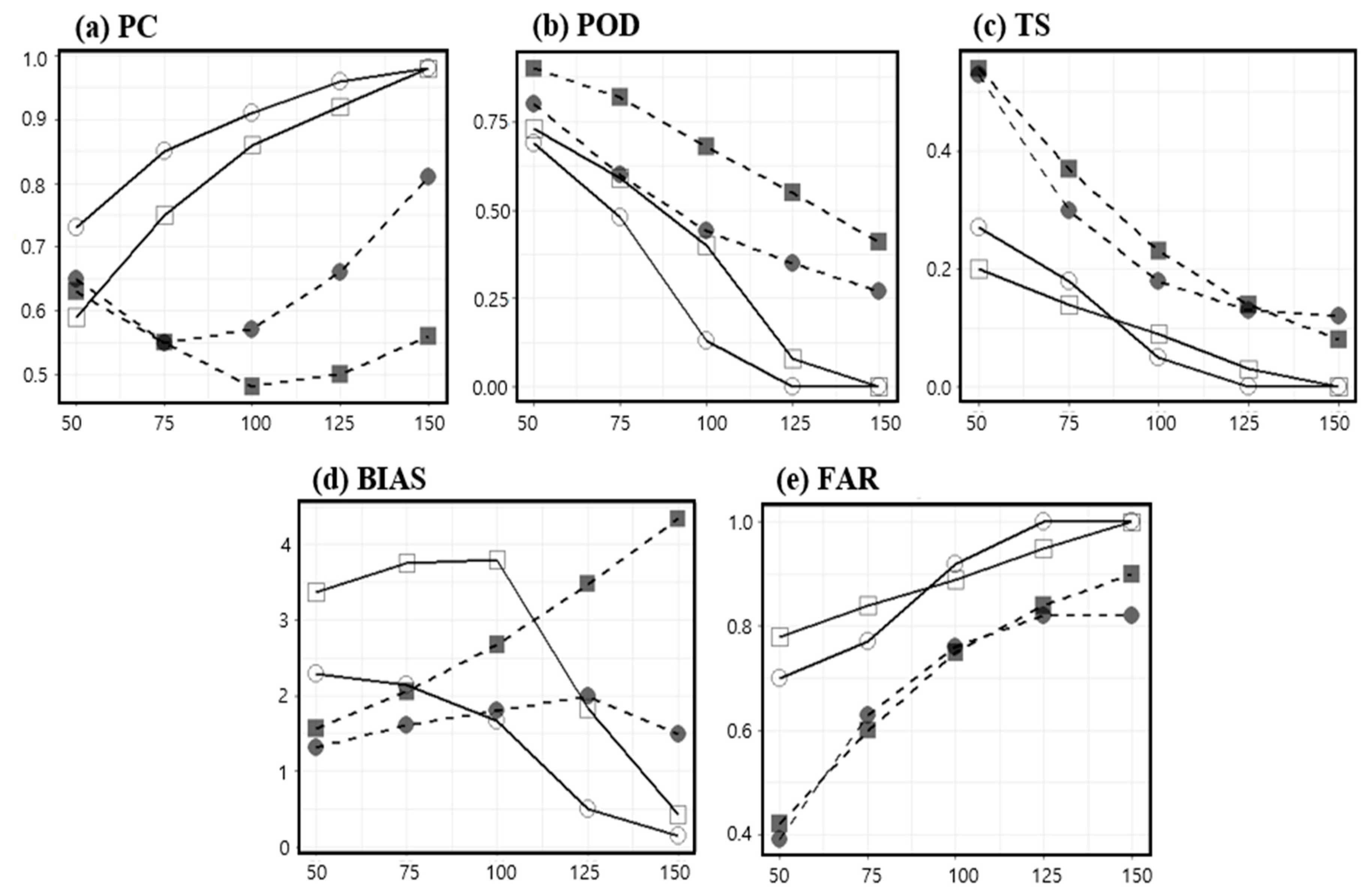
 ,
,  ,
,  ,
,  , O,
, O,  ,
,  ,
,  ,
,  ) indicate KF, BMJ, New SAS, Grell 3D, Old SAS, Grell–Freitas, Kain–Fritch, NEW SAS, and Multi-scale KF, respectively.
) indicate KF, BMJ, New SAS, Grell 3D, Old SAS, Grell–Freitas, Kain–Fritch, NEW SAS, and Multi-scale KF, respectively.
 ,
,  ,
,  ,
,  , O,
, O,  ,
,  ,
,  ,
,  ) indicate KF, BMJ, New SAS, Grell 3D, Old SAS, Grell–Freitas, Kain–Fritch, NEW SAS, and Multi-scale KF, respectively.
) indicate KF, BMJ, New SAS, Grell 3D, Old SAS, Grell–Freitas, Kain–Fritch, NEW SAS, and Multi-scale KF, respectively.
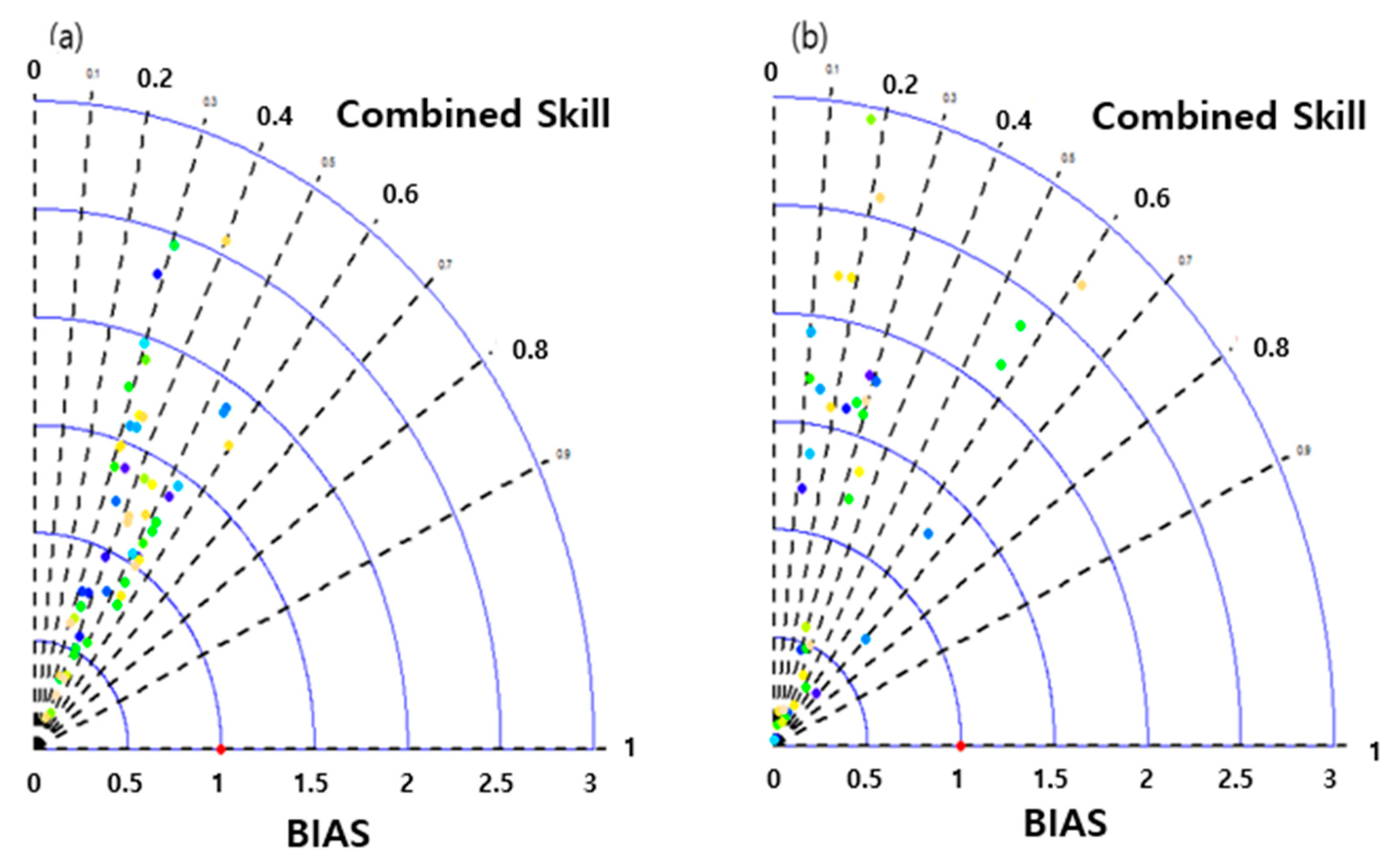
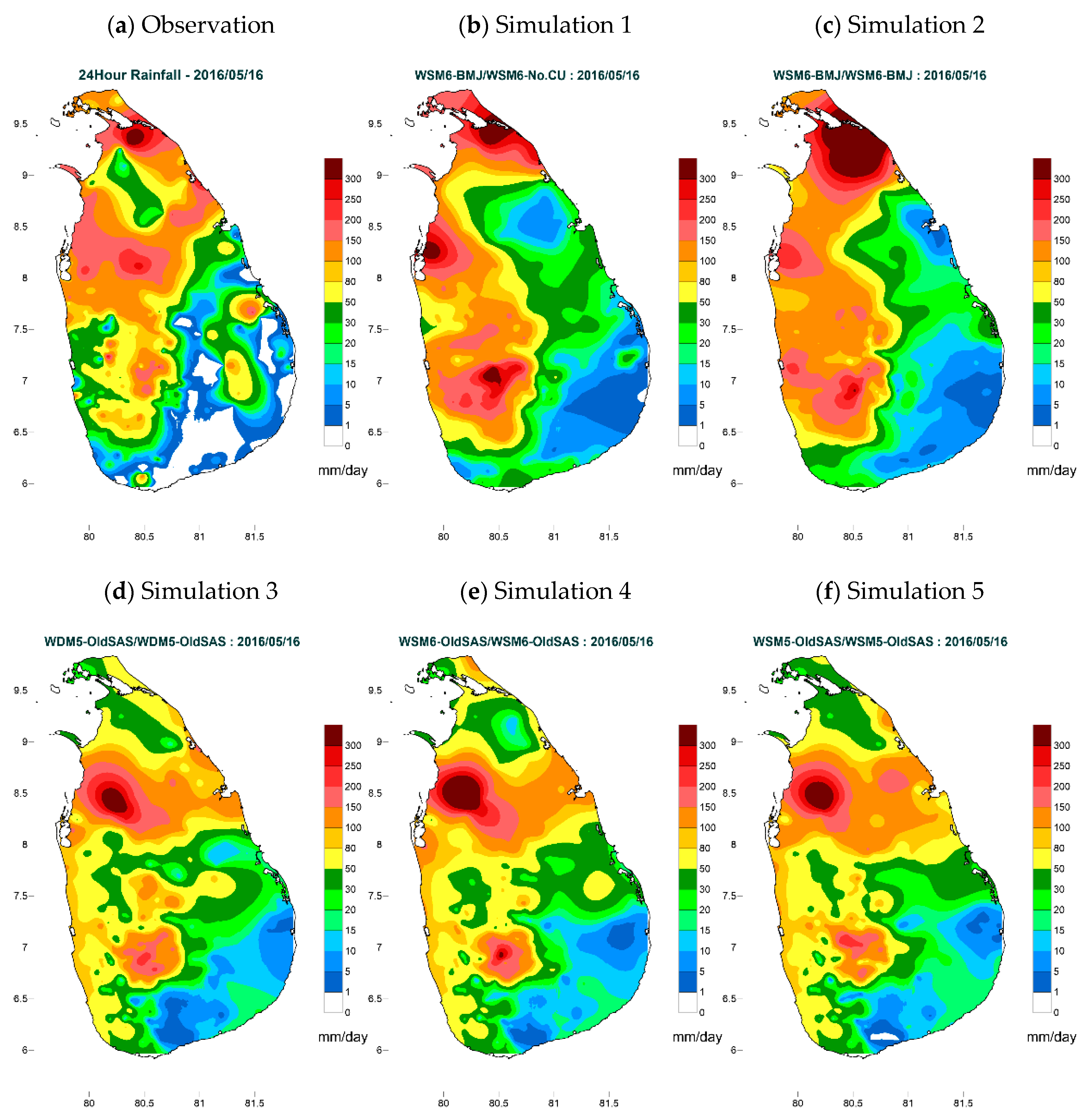
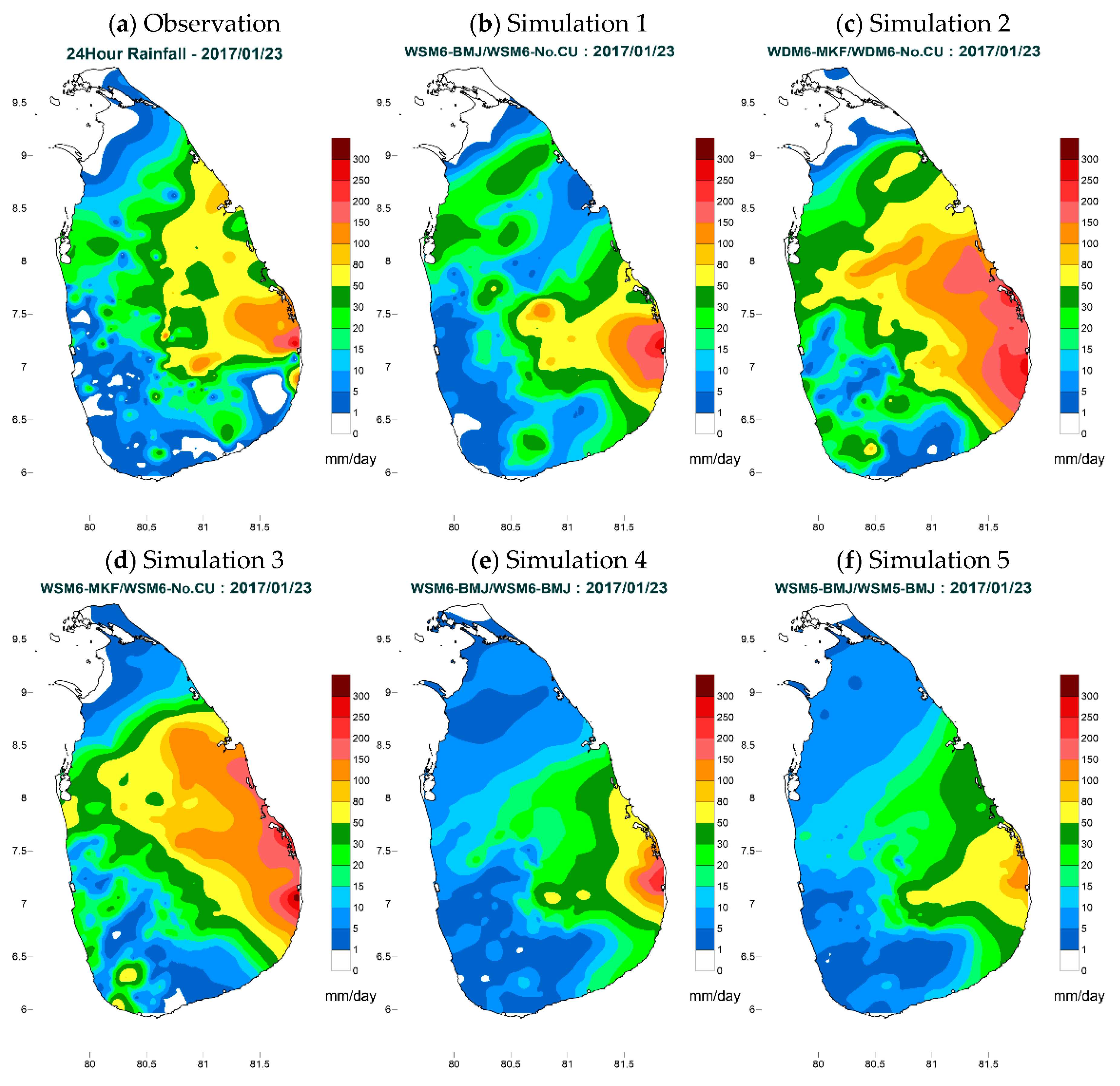
| Event | Date/Time | Season | Duration (hours) | Max. 24-h Rainfall (mm) |
|---|---|---|---|---|
| 1 | 0300 UTC 16 May–0300 UTC 17 May 2016 | Southwest monsoon | 24 | 380 |
| 2 | 0300 UTC 23 January–0300 UTC 24 January 2017 | Northeast monsoon | 24 | 312 |
| Configuration | Outer Domain | Inner Domain |
|---|---|---|
| WRF version | 3.8.1 | |
| Horizontal grids | 100 × 80 | 70 × 106 |
| Grid spacing (km) | 15 | 5 |
| Vertical grids | 42 layer/Top 50 hPa | |
| Integration time (s) | 90 | 30 |
| Radiation | Dudhia shortwave/RRTM longwave Integration time: 10 min | |
| Microphysics | WDM 5-class | WDM 6-class |
| Surface layer | MM5 Similarity scheme | |
| Land surface | Unified Noah LSM | |
| Planetary boundary layer | Yonsei University (YSU) scheme Integration time: every time step | |
| Land use and topography data | 2 m/MODIS 21 | 30 s/MODIS 21 |
| Cumulus | Kain–Fritsch scheme | |
| Initial boundary condition | Global Forecasting System (GFS) Model Forecast Fields (27 km resolution, NCEP) | |
| Observed | ||||
|---|---|---|---|---|
| Yes | No | |||
| Forecast | Yes | Hits (YY) | False alarms (YN) | # (Forecast yes) |
| No | Misses (NY) | Correct rejections (NN) | # (Forecast no) | |
| # (observed yes) | # (observed no) | Total = N | ||
| Variable | Evaluation Method | Formula | Range | Perfect Score |
|---|---|---|---|---|
| Rainfall occurrence | Frequency bias index (BIAS) | 0~ | 1 | |
| Probability of detection (POD) | 0~1 | 1 | ||
| Threat score (TS) | 0~1 | 1 | ||
| False alarm ratio (FAR) | 0~1 | 0 | ||
| Proportion correct (PC) | 0~1 | 1 | ||
| Rainfall amount | Pearson correlation coefficient (r) | −1~1 | 1 |
| Evaluation Method | Range | Perfect Score | |
|---|---|---|---|
| Overall performance of rainfall prediction | Combined score | −0.2~1 | 1 |
| BIAS | 0~∞ | 1 |
| Rainfall Event | 5-km (Default) Configuration | 3-km (New) Configuration | ||
|---|---|---|---|---|
| Combined Score | BIAS | Combined Score | BIAS | |
| 16 May 2016 | 0.35 | 2.82 | 0.34 | 1.64 |
| 23 Jan 2017 | 0.31 | 2.64 | 0.34 | 1.35 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigo, C.; Kim, S.; Jung, I.H. Sensitivity Study of WRF Numerical Modeling for Forecasting Heavy Rainfall in Sri Lanka. Atmosphere 2018, 9, 378. https://doi.org/10.3390/atmos9100378
Rodrigo C, Kim S, Jung IH. Sensitivity Study of WRF Numerical Modeling for Forecasting Heavy Rainfall in Sri Lanka. Atmosphere. 2018; 9(10):378. https://doi.org/10.3390/atmos9100378
Chicago/Turabian StyleRodrigo, Channa, Sangil Kim, and Il Hyo Jung. 2018. "Sensitivity Study of WRF Numerical Modeling for Forecasting Heavy Rainfall in Sri Lanka" Atmosphere 9, no. 10: 378. https://doi.org/10.3390/atmos9100378
APA StyleRodrigo, C., Kim, S., & Jung, I. H. (2018). Sensitivity Study of WRF Numerical Modeling for Forecasting Heavy Rainfall in Sri Lanka. Atmosphere, 9(10), 378. https://doi.org/10.3390/atmos9100378




