A Comprehensive Approach to Assess the Hydrological Drought of Inland River Basin in Northwest China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data
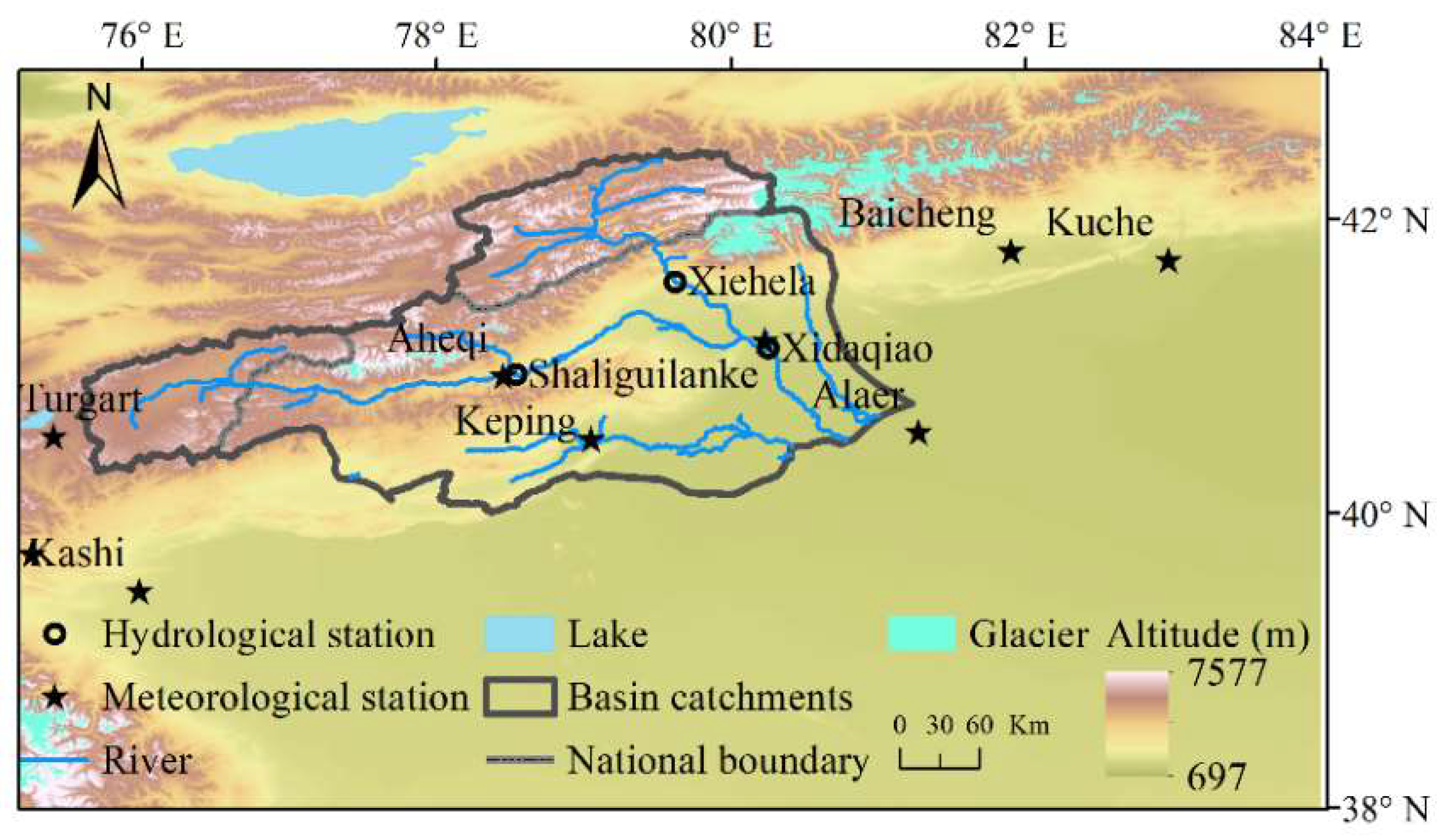
2.1.1. Study Area
2.1.2. Data
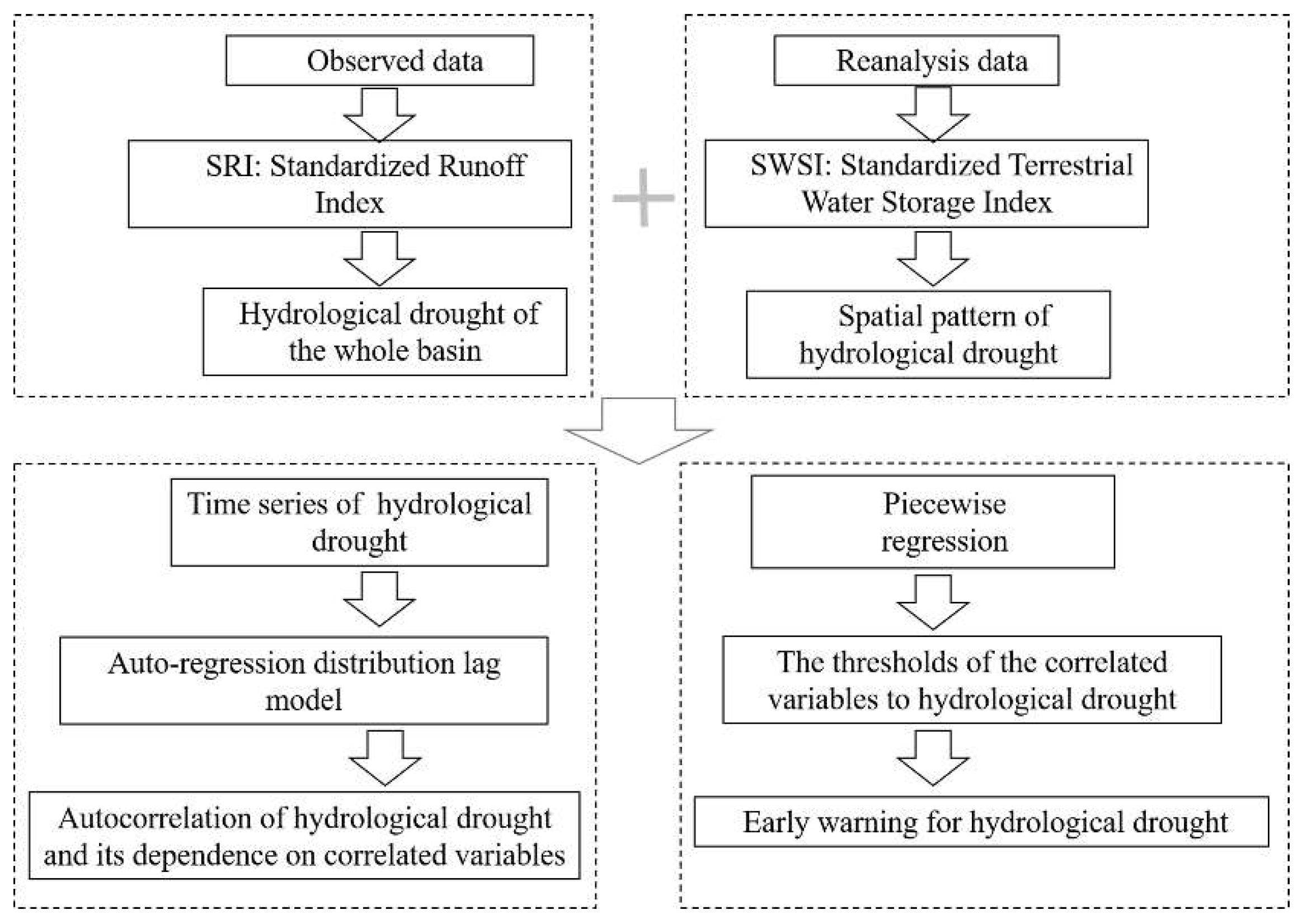
2.2. Methods
2.2.1. Drought Indices
Standardized Runoff Index (SRI)
Standardized Terrestrial Water Storage Index (SWSI)
2.2.2. Auto-Regressive Distribution Lag Model (ARDL)
2.2.3. Threshold Analysis
3. Results
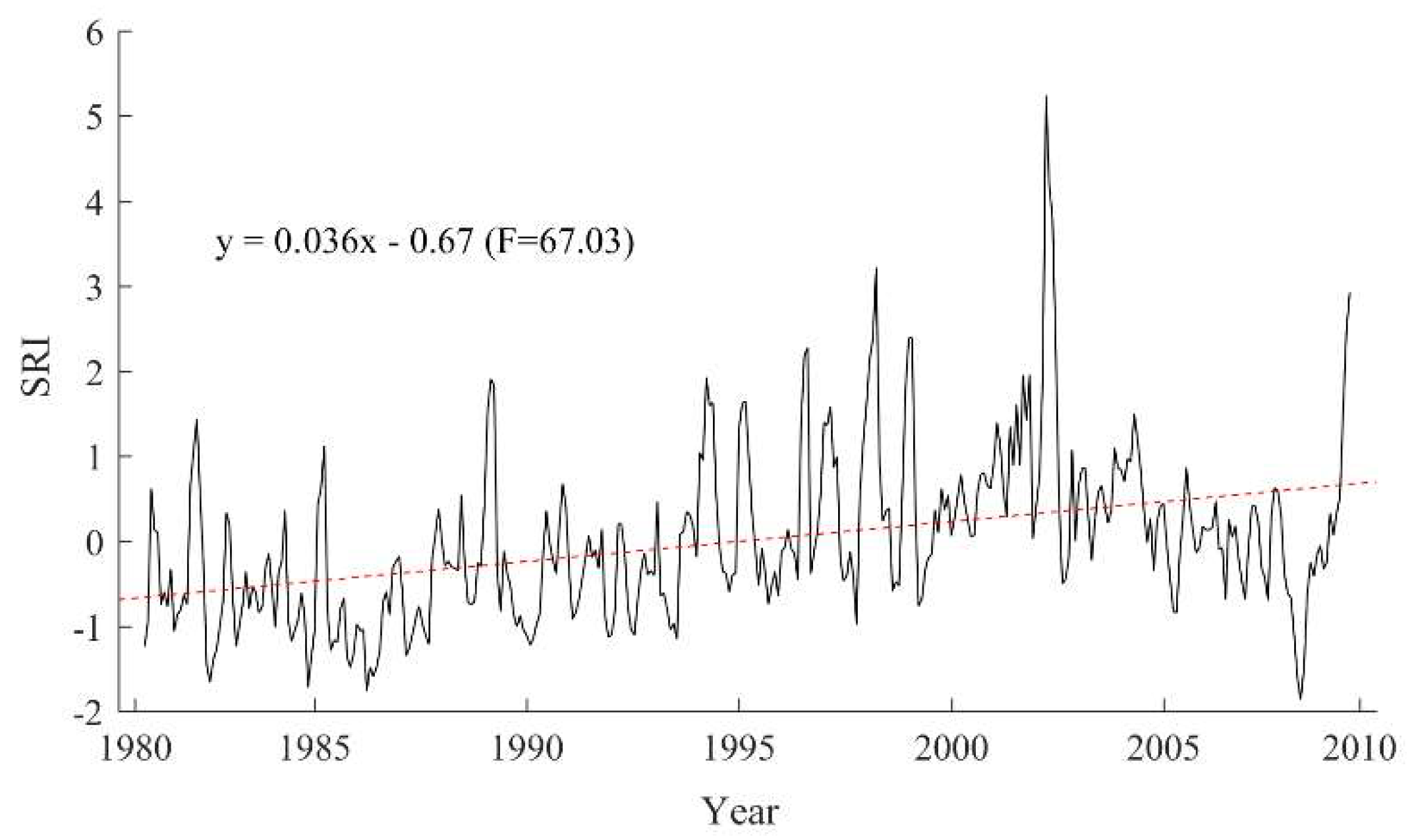
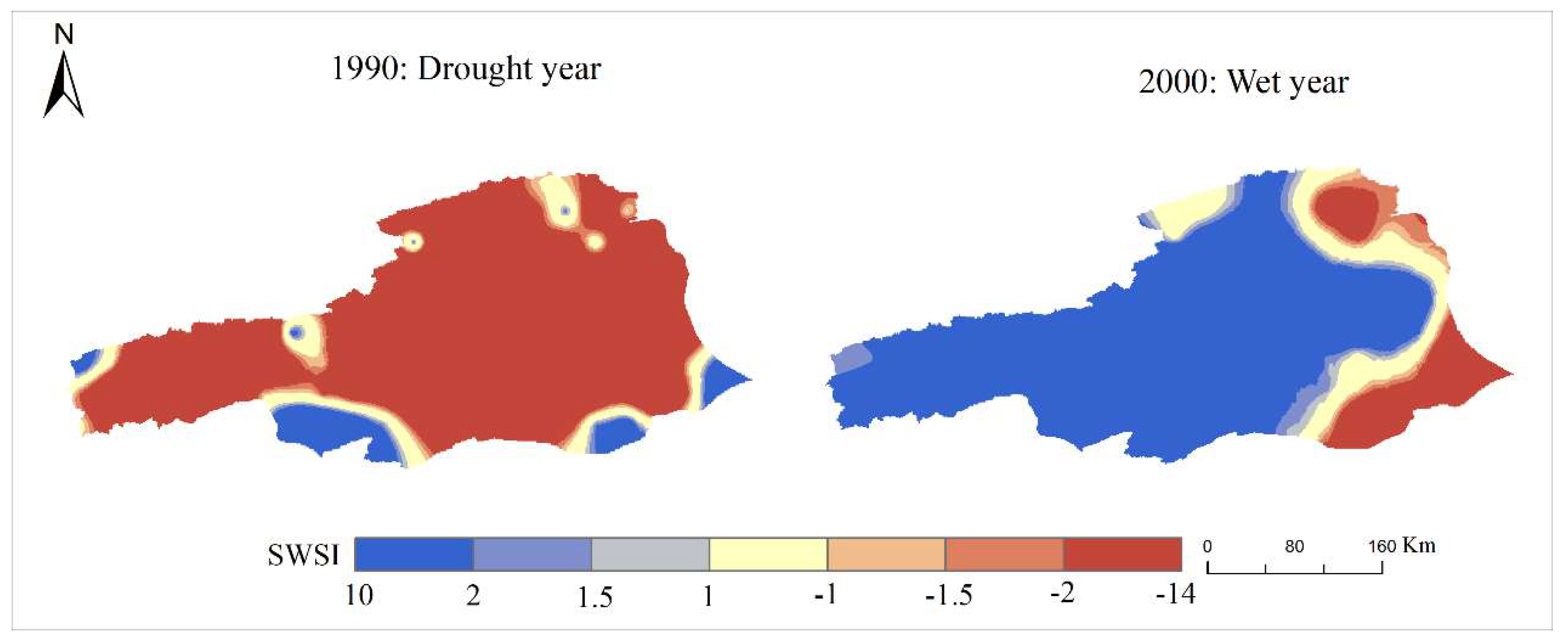
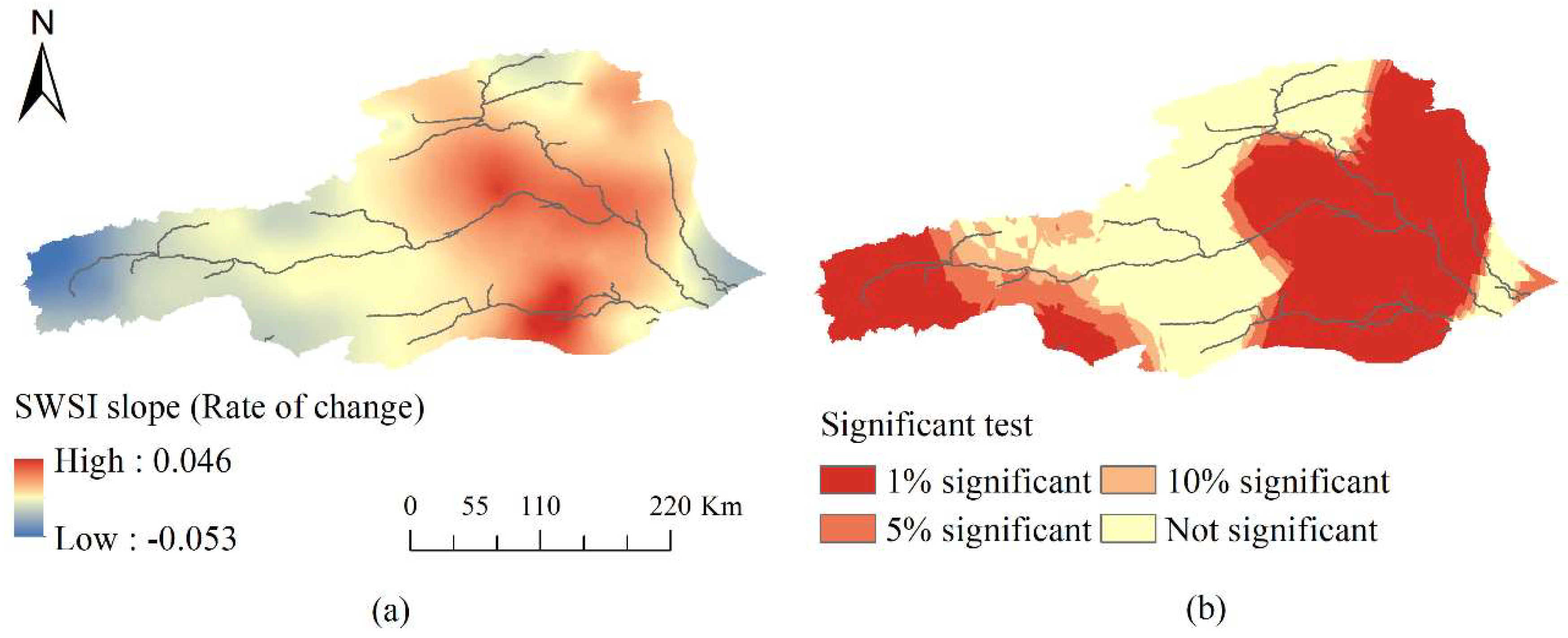
3.1. The Spatio-Temporal Pattern of HD
3.2. The Autocorrelation of HD and Its Dependence on Precipitation, PET and Soil Moisture
3.3. The Thresholds of the Correlated Variables to HD
4. Discussion
5. Conclusions
- The spatio-temporal pattern of HD was complex in the ARB. There was a tendency to become wet in the entire basin during the study periods. The high frequency of drought occurred in the east and west, whereas the low frequency of drought occurred in the middle. In addition, the drought year did not mean that drought would occur in the entire basin, and vice versa.
- The autocorrelation of HD and its dependence on precipitation, PET, and soil moisture were found. The occurrence of a drought was not only related to the contemporaneous correlated variables, but also related to historical drought and historically correlated variables. Among them, HD presents significant autocorrelation with two months’ lag, and soil moisture is correlated with SWSI with two months’ lag, whereas PET and precipitation are correlated with SWSI with one month’s lag.
- We developed a new early warning system according to the threshold range of the correlated variables to HD. One of the correlated variables achieve the corresponding threshold range to perform a three-level early warning, two correlated variables achieve the corresponding threshold range at the same time to perform a two-level early warning, and three correlated variables achieve the corresponding threshold range at the same time to perform a one-level early warning.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Council, A.M.S. AMS statement on meteorological drought. Bull. Am. Meteorol. Soc. 2004, 85, 6. [Google Scholar]
- Keyantash, J.; Dracup, J.A. The quantification of drought: An evaluation of drought indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Tallaksen, L.M.; Van Lanen, H.A. (Eds.) Hydrological Drought: Processes and Estimation Methods for Streamflow and Groundwater; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, 1–7. [Google Scholar] [CrossRef]
- Linsley, R.K., Jr.; Kohler, M.A.; Paulhus, J.C.H. Hydrology for Engineers, 2nd ed.; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Bhuiyan, C.; Singh, R.P.; Kogan, F.N. Monitoring drought dynamics in the Aravalli region (India) using different indices based on ground and remote sensing data. Int. J. Appl. Earth Obs. 2006, 8, 289–302. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-lacruz, J.; Azorin-Molina, C.; Morán-Tejeta, E. Accurate computation of a streamflow drought index. J. Hydrol. Eng. 2011, 17, 318–332. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Moghaddasi, M. Comparison of seven meteorological indices for drought monitoring in Iran. Int. J. Climatol. 2006, 26, 971–985. [Google Scholar] [CrossRef]
- Mo, K.C. Model-based drought indices over the United States. J. Hydrometeorol. 2008, 9, 1212–1230. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Application of the extreme learning machine algorithm for the prediction of monthly Effective Drought Index in eastern Australia. Atmos. Res. 2015, 153, 512–525. [Google Scholar] [CrossRef]
- Zhu, J.W.; Zhou, L.N.; Huang, S.Z. A hybrid drought index combining meteorological, hydrological, and agricultural information based on the entropy weight theory. Arab. J. Geosci. 2018, 11, 91. [Google Scholar] [CrossRef]
- Van Rooy, M.P. A rainfall anomaly index independent of time and space. Notos 1965, 14, 6. [Google Scholar]
- Karl, T.R. The sensitivity of the Palmer drought severity index and Palmer’s Z-index to their calibration coefficients including potential evapotranspiration. J. Clim. Appl. Meteorol. 1986, 25, 77–86. [Google Scholar] [CrossRef]
- Hisdal, H.; Tallaksen, L.M. Estimation of regional meteorological and hydrological drought characteristics: A case study for Denmark. J. Hydrol. 2003, 281, 230–247. [Google Scholar] [CrossRef]
- Fleig, A.K.; Tallaksen, L.M.; Hisdal, H.; Hannah, D.M. Regional hydrological drought in north-western Europe: Linking a new Regional Drought Area Index with weather types. Hydrol. Process. 2011, 25, 1163–1179. [Google Scholar] [CrossRef]
- Xu, J.H.; Chen, Y.N.; Bai, L.; Xu, Y.W. A hybrid model to simulate the annual runoff of the Kaidu River in northwest China. Hydrol. Earth Syst. Sci. 2016, 20, 1447–1457. [Google Scholar] [CrossRef]
- Xu, J.H.; Chen, Y.N.; Li, W.H.; Nie, Q.; Song, C.N.; Wei, C.M. Integrating wavelet analysis and BPANN to simulate the annual runoff with regional climate change: A case study of Yarkand River, Northwest China. Water Resour. Manag. 2014, 28, 2523–2537. [Google Scholar] [CrossRef]
- Xu, J.H.; Wang, C.; Li, W.H.; Zuo, J.P. Multi-temporal scale modeling on climatic-hydrological processes in data-scarce mountain basins of Northwest China. Arab. J. Geosci. 2018, 11, 423. [Google Scholar] [CrossRef]
- Li, J.B.; Gou, X.H.; Cook, E.R.; Chen, F.H. Tree-ring based drought reconstruction for the central Tien Shan area in northwest China. Geophys. Res. Lett. 2006, 33, 1–5. [Google Scholar] [CrossRef]
- Fang, K.Y.; Gou, X.H.; Chen, F.H.; Yang, M.X.; Li, J.B.; He, M.S.; Zhang, Y.; Tian, Q.H.; Peng, J.F. Drought variations in the eastern part of northwest China over the past two centuries: Evidence from tree rings. Clim. Res. 2009, 38, 129–135. [Google Scholar] [CrossRef]
- Zhai, L.X.; Feng, Q. Spatial and temporal pattern of precipitation and drought in Gansu Province, Northwest China. Nat. Hazards 2009, 49, 1–24. [Google Scholar] [CrossRef]
- Wang, D.; Hejazi, M.; Cai, X.; Volocchi, A.J. Climate change impact on meteorological, agricultural, and hydrological drought in central Illinois. Water. Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Xu, J.H.; Chen, Y.N.; Li, W.H.; Ji, M.H.; Dong, S. The complex nonlinear systems with fractal as well as chaotic dynamics of annual runoff processes in the three headwaters of the Tarim River. J. Geogr. Sci. 2009, 19, 25–35. [Google Scholar] [CrossRef]
- Li, S.N.; Weng, B.S.; Yan, C.M.; Wang, J.W. Applicability analysis of SPI and SPEI in Aksu River basin. J. Water Resour. Water Eng. 2016, 27, 101–107. [Google Scholar]
- Xu, J.H.; Chen, Y.N.; Lu, F.; Li, W.H.; Zhang, L.J.; Hong, Y.L. The nonlinear trend of runoff and its response to climate change in the Aksu River, western China. Int. J. Climatol. 2011, 31, 687–695. [Google Scholar] [CrossRef]
- Hu, X.X.; Zhang, Y.H.; Liu, X. The Characteristics of Meteorological Drought in Aksu in Xinjiang. J. Anhui Agric. Sci. 2015, 43, 96–100. (In Chinese) [Google Scholar]
- Chen, Y.N.; Xu, C.; Chen, Y.P.; You, Y.B.; Li, W.H. Progress, challenges and prospects of eco-hydrological studies in the Tarim River Basin of Xinjiang, China. Envirom. Manag. 2013, 51, 138–153. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.P.; Wang, G.Y.; Zhan, J.G. Human activity impacts on local climate and water environments of the Aksu River oasis, South Xinjiang. Arid Land Geogr. 2008, 31, 524–534. (In Chinese) [Google Scholar]
- Zhou, D.C.; Luo, G.P.; Yin, C.Y.; Xu, W.Q.; Feng, Y.X. Land Use/Cover Change of the Aksu River Watershed in the Period of 1960–2008. J. Glaciol. Geocryol. 2010, 32, 275–284. [Google Scholar]
- Chen, X.; Luo, G.; Xia, J.; Zhou, K.; Lou, S.; Ye, M. Ecological response to the climate change on the northern slope of the Tianshan Mountains in Xinjiang. Sci. China Ser. D 2005, 48, 765–777. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, 1–4. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.L.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Zhang, S.H.; Liu, S.X.; Mo, X.G.; Shu, C.; Sun, Y.; Zhang, C. Assessing the impact of climate change on potential evapotranspiration in Aksu River Basin. J. Geogr. Sci. 2011, 21, 609–620. [Google Scholar] [CrossRef]
- Chen, Y.N.; Yang, K.; He, J.; Qin, J.; Shi, J.C.; Du, J.Y.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. Atmos. 2011, 116, 1–15. [Google Scholar] [CrossRef]
- Yang, K.; Zhang, J.Y. Evaluation of reanalysis datasets against observational soil temperature data over China. Clim. Dyn. 2018, 50, 317–337. [Google Scholar] [CrossRef]
- Madadgar, S.; Moradkhani, H. Spatio-temporal drought forecasting within Bayesian networks. J. Hydrol. 2014, 512, 134–146. [Google Scholar] [CrossRef]
- Tao, H.; Borth, H.; Fraedrich, K.; Su, B.; Zhu, X.H. Drought and wetness variability in the Tarim River Basin and connection to large-scale atmospheric circulation. Int. J. Climatol. 2014, 34, 2678–2684. [Google Scholar] [CrossRef]
- Wang, Y.X.; Li, J.Z.; Feng, P.; Chen, F.L. Effects of large-scale climate patterns and human activities on hydrological drought: A case study in the Luanhe River basin, China. Nat. Hazards 2015, 76, 1687–1710. [Google Scholar] [CrossRef]
- Wang, W.; Wang, P.; Cui, W. A comparison of terrestrial water storage data and multiple hydrological data in the Yangtze River basin. Adv. Water Sci. 2015, 26, 759–768. (In Chinese) [Google Scholar]
- Nkoro, E.; Uko, A.K. Autoregressive Distributed Lag (ARDL) cointegration technique: Application and interpretation. J. Stat. Econom. Methods 2016, 5, 63–91. [Google Scholar]
- Hassler, U.; Wolters, J. Autoregressive distributed lag models and cointegration. In Modern Econometric Analysis; Springer: Berlin/Heidelberg, Germany, 2006; pp. 57–72. [Google Scholar]
- Shahbaz, M.; Loganathan, N.; Zeshan, M.; Zaman, K. Does renewable energy consumption add in economic growth? An application of auto-regressive distributed lag model in Pakistan. Renew. Sustain. Energy Rev. 2015, 44, 576–585. [Google Scholar] [CrossRef]
- Kiviet, J.F.; Dufour, J.M. Exact tests in single equation autoregressive distributed lag models. J. Econ. 1997, 80, 325–353. [Google Scholar] [CrossRef]
- Toms, J.D.; Lesperance, M.L. Piecewise regression: A tool for identifying ecological thresholds. Ecology 2003, 84, 2034–2041. [Google Scholar] [CrossRef]
- Hawkins, D.M. Point estimation of the parameters of piecewise regression models. Appl. Stat. 1976, 25, 51–57. [Google Scholar] [CrossRef]
- Seber, G.A.F.; Wild, C.J. Nonlinear Regression: Wiley Series in Probability and Mathematical Statistics; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Barrowman, N.; Myers, R. Still more spawner-recruitment curves: The hockey stick and its generalizations. Can. J. Fish. Aquat. Sci. 2000, 57, 665–676. [Google Scholar] [CrossRef]
- Dracup, J.A.; Lee, K.S.; Paulson, E.G., Jr. On the definition of droughts. Water Resour. Res. 1980, 16, 297–302. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Cai, W.Y.; Chen, Q.H.; Yao, Y.J.; Liu, K.L. Analysis of changes in precipitation and drought in Aksu River Basin, Northwest China. Adv. Meteorol. 2015, 2015, 215840. [Google Scholar] [CrossRef]
- Wang, C.; Xu, J.H.; Chen, Y.N.; Bai, L.; Chen, Z.S. A hybrid model to assess the impact of climate variability on streamflow for an ungauged mountainous basin. Clim. Dyn. 2017, 50, 1–16. [Google Scholar] [CrossRef]
- Hanson, R.L. Evapotranspiration and droughts. US Geol. Surv. Water-Supply Pap. 1991, 2375, 99–104. [Google Scholar]
- Dai, A.G.; Trenberth, K.E.; Qian, T.T. A global dataset of Palmer Drought Severity Index for 1870–2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Hutchinson, C.F. Uses of satellite data for famine early warning in sub-Saharan Africa. Int. J. Remote Sens. 1991, 12, 1405–1421. [Google Scholar] [CrossRef]
- Lohani, V.K.; Loganathan, G.V. An early warning system for drought management using the Palmer drought index. J. Am. Water Resour. Assoc. 1997, 33, 1375–1386. [Google Scholar] [CrossRef]
- Paulo, A.A.; Ferreira, E.; Coelho, C. Drought class transition analysis through Markov and Loglinear models, an approach to early warning. Agric. Water Manag. 2005, 77, 59–81. [Google Scholar] [CrossRef]
- Tomé, A.R.; Miranda, P.M.A. Piecewise linear fitting and trend changing points of climate parameters. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Zhang, L.; Wylie, B.K.; Ji, L.; Gilmanov, T.G.; Tieszen, L.L. Climate-driven interannual variability in net ecosystem exchange in the northern Great Plains grasslands. Rangel. Ecol. Manag. 2010, 63, 40–50. [Google Scholar] [CrossRef]
- Greenville, A.C.; Wardle, G.M.; Dickman, C.R. Extreme climatic events drive mammal irruptions: Regression analysis of 100-year trends in desert rainfall and temperature. Ecol. Evol. 2012, 2, 2645–2658. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.N.; Li, Z.; Fan, Y.T.; Wang, H.J.; Fang, G.H. Research progress on the impact of climate change on water resources in the arid region of Northwest China. Acta Geogr. Sin. 2014, 69, 1295–1304. (In Chinese) [Google Scholar]
- Qian, W.; Lin, X. Regional trends in recent precipitation indices in China. Meteorol. Atmos. Phys. 2005, 90, 193–207. [Google Scholar] [CrossRef]
- Shi, Y.F.; Shen, Y.P.; Kang, E.; Li, D.L.; Ding, Y.J.; Zhang, G.W.; Hu, R.J. Recent and future climate change in northwest China. Clim. Chang. 2007, 80, 379–393. [Google Scholar] [CrossRef]
- Biatwright, G.O.; Whitehead, V.S. Early warning and crop condition assessment research. IEEE. Trans. Geosci. Remote Sens. 1986, 1, 54–64. [Google Scholar] [CrossRef]
- Kumar, V. An early warning system for agricultural drought in an arid region using limited data. J. Arid. Environ. 1998, 40, 199–209. [Google Scholar] [CrossRef]
- Morgan, R. The development and applications of a drought early warning system in Botswana. Disasters 1985, 9, 44–50. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.C.; Yuan, L.C. A drought early warning system on real-time multireservoir operations. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Kogan, F.N. Contribution of remote sensing to drought early warning. In Early Warning Systems for Drought Preparedness and Drought Management; World Meteorological Organization: Geneva, Switzerland, 2000; pp. 75–87. [Google Scholar]
- Boken, V.K. Improving a drought early warning model for an arid region using a soil-moisture index. Appl. Geogr. 2009, 29, 402–408. [Google Scholar] [CrossRef]

| Category | SRI Value | Cumulative Probability (%) |
|---|---|---|
| Extremely wet | SRI ≥ 2 | 2.28 |
| Moderately wet | 1.5 ≤ SRI< 2 | 6.68 |
| Slightly wet | 1 ≤ SRI< 1.5 | 15.87 |
| Near normal | −1 < SRI < 1 | 50.00 |
| Mild drought | −1.5 < SRI ≤ −1 | 84.13 |
| Moderate drought | −2 < SRI ≤ −1.5 | 93.32 |
| Extremely drought | SRI ≤ −2 | 97.72 |
| Year | Drought/Non-Drought Year | Year | Drought/Non-Drought Year |
|---|---|---|---|
| 1980 | Y | 1996 | Y |
| 1981 | Y | 1997 | N |
| 1982 | Y | 1998 | N |
| 1983 | Y | 1999 | N |
| 1984 | Y | 2000 | N |
| 1985 | Y | 2001 | N |
| 1986 | Y | 2002 | N |
| 1987 | Y | 2003 | N |
| 1988 | Y | 2004 | N |
| 1989 | Y | 2005 | N |
| 1990 | Y | 2006 | N |
| 1991 | Y | 2007 | N |
| 1992 | Y | 2008 | Y |
| 1993 | Y | 2009 | Y |
| 1994 | N | 2010 | N |
| 1995 | N | Sum of drought years | 17 |
| ADF | p-Value | ADF | P-Value | ||
|---|---|---|---|---|---|
| SWSI | −2.5443 ** | 0.0108 | Precipitation | −4.8042 *** | 0.0005 |
| PET | −6.6351 *** | 0.0000 | Soil moisture | −2.6259 * | 0.0887 |
| Variable | Coefficient | Prob. |
|---|---|---|
| SWSI (−1) | 0.9476 *** | 0.0000 |
| SWSI (−2) | 0.3192 *** | 0.0000 |
| PET | −0.0016 ** | 0.0184 |
| PET (−1) | −0.0021 *** | 0.0065 |
| Precipitation | −0.0009 | 0.4726 |
| Precipitation (−1) | 0.0027 ** | 0.0338 |
| Soil Moisture | 0.0898 *** | 0.0000 |
| Soil Moisture (−1) | -0.0959 *** | 0.0000 |
| Soil Moisture (−2) | 0.0595 *** | 0.0000 |
| Constant | −20.7678 | 0.0000 |
| R-squared | 0.9592 | |
| Akaike info criterion | −0.3402 | |
| Durbin-Watson stat | 1.9313 | |
| F-statistic | 936.4129 *** | 0.0000 |
| Breakpoint | 95% Confidence Intervals | |
|---|---|---|
| Annual PET (mm) | 891.242 | (844.048, 938.435) |
| Annual Precipitation (mm) | 113.037 | (91.5564, 134.518) |
| Annual average Soil moisture (kg/m2) | 397.98 | (384.89, 411.071) |
| Correlated Variable | Threshold Range (95% Confidence Interval) | Actual Value |
|---|---|---|
| Annual PET (mm) | >844.05 | 824.00 |
| Annual Precipitation (mm) | <134.52 | 157.61 |
| Annual average Soil Moisture (kg/m2) | <411.07 | 385.30 |
| Early Warning Level | Annual PET > 844.05 mm | Annual Precipitation < 134.52 mm | Annual Average Soil Moisture < 411.07 kg/m2 |
|---|---|---|---|
| 1 | √ | √ | √ |
| 2 | √ | √ | × |
| × | √ | √ | |
| √ | × | √ | |
| 3 | √ | × | × |
| × | √ | × | |
| × | × | √ |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, N.; Xu, J.; Li, W.; Li, K.; Zhou, C. A Comprehensive Approach to Assess the Hydrological Drought of Inland River Basin in Northwest China. Atmosphere 2018, 9, 370. https://doi.org/10.3390/atmos9100370
Zhu N, Xu J, Li W, Li K, Zhou C. A Comprehensive Approach to Assess the Hydrological Drought of Inland River Basin in Northwest China. Atmosphere. 2018; 9(10):370. https://doi.org/10.3390/atmos9100370
Chicago/Turabian StyleZhu, Nina, Jianhua Xu, Weihong Li, Kaiming Li, and Cheng Zhou. 2018. "A Comprehensive Approach to Assess the Hydrological Drought of Inland River Basin in Northwest China" Atmosphere 9, no. 10: 370. https://doi.org/10.3390/atmos9100370
APA StyleZhu, N., Xu, J., Li, W., Li, K., & Zhou, C. (2018). A Comprehensive Approach to Assess the Hydrological Drought of Inland River Basin in Northwest China. Atmosphere, 9(10), 370. https://doi.org/10.3390/atmos9100370






