Evaluation of Phenology Models for Predicting Full Bloom Dates of ‘Niitaka’ Pear Using Orchard Image-Based Observations in South Korea
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. “Niitaka” Pear Full Bloom Prediction Model
- DVR(T) = (1/(A × B^ T)) × 100, for T > 5
- Case 1: DVR1(T) = 0, for T ≤ 0
- Case 2: DVR1(T) = 1.333 × 10−3, for 0 < T ≤ 6
- Case 3: DVR1(T) = 2.276 × 10−3 − 1.571 × 10−4 × T, for 6 < T ≤ 9
- Case 4: DVR1(T) = 3.448 × 10−3 − 2.874 × 10−4 × T, for 9 < T ≤ 12
- Case 5: DVR1(T) = 0, for T > 12
- Case 1: DVR2(T) = exp [35.27 − 12094/(T + 273)−1], for T ≤ 20
- Case 2: DVR2(T) = exp[5.82 − 3474/(T + 273) −1], for T > 20(based on Sugiura [45])
- Case 1: Cd = 0, for 0 ≤ Tc ≤ Tn ≤ Tx
- Case 2: Cd = −[(TM − Tn) − (Tx − Tc)/2], for 0 ≤ Tn < Tc ≤ Tx
- Case 3: Cd = −(TM − Tn), for 0 ≤ Tn ≤ Tx ≤ Tc
- Case 4: Cd = −[(Tx/(Tx − Tn)) × (Tx/2)], for Tn ≤ 0 ≤ Tc ≤ Tx
- Case 5: Cd = −[(Tx/(Tx − Tn)) × (Tx/2) − (Tx − Tc)/2], for Tn ≤ 0 ≤ Tx ≤ Tc
- Case 1: Ca = TM − Tc, for 0 ≤ Tc ≤ Tn ≤ Tx
- Case 2: Ca = (Tx − Tc)/2, for 0 ≤ Tn < Tc ≤ Tx
- Case 3: Ca = 0, for 0 ≤ Tn ≤ Tx ≤ Tc
- Case 4: Ca = 0, for Tn ≤ 0 ≤ Tc ≤ Tx
- Case 5: Ca = (Tx − Tc)/2, for Tn ≤ 0 ≤ Tx ≤ Tc(based on Cesaraccio et al. [30])
2.3. Analysis of Chill and Heat Units
- (1)
- (2)
- DVR1 values from the mDVR model;
- (3)
- Chill values from the CD model.
- (1)
- Hours above 5 °C, based on the DVR model;
- (2)
- DVR2 values from the mDVR model;
- (3)
- Heat values from the CD model.
2.4. “Niitaka” Pear Full Bloom Prediction and Model Evaluation
3. Results and Discussion
3.1. Comparison of Chill and Heat Units by Region
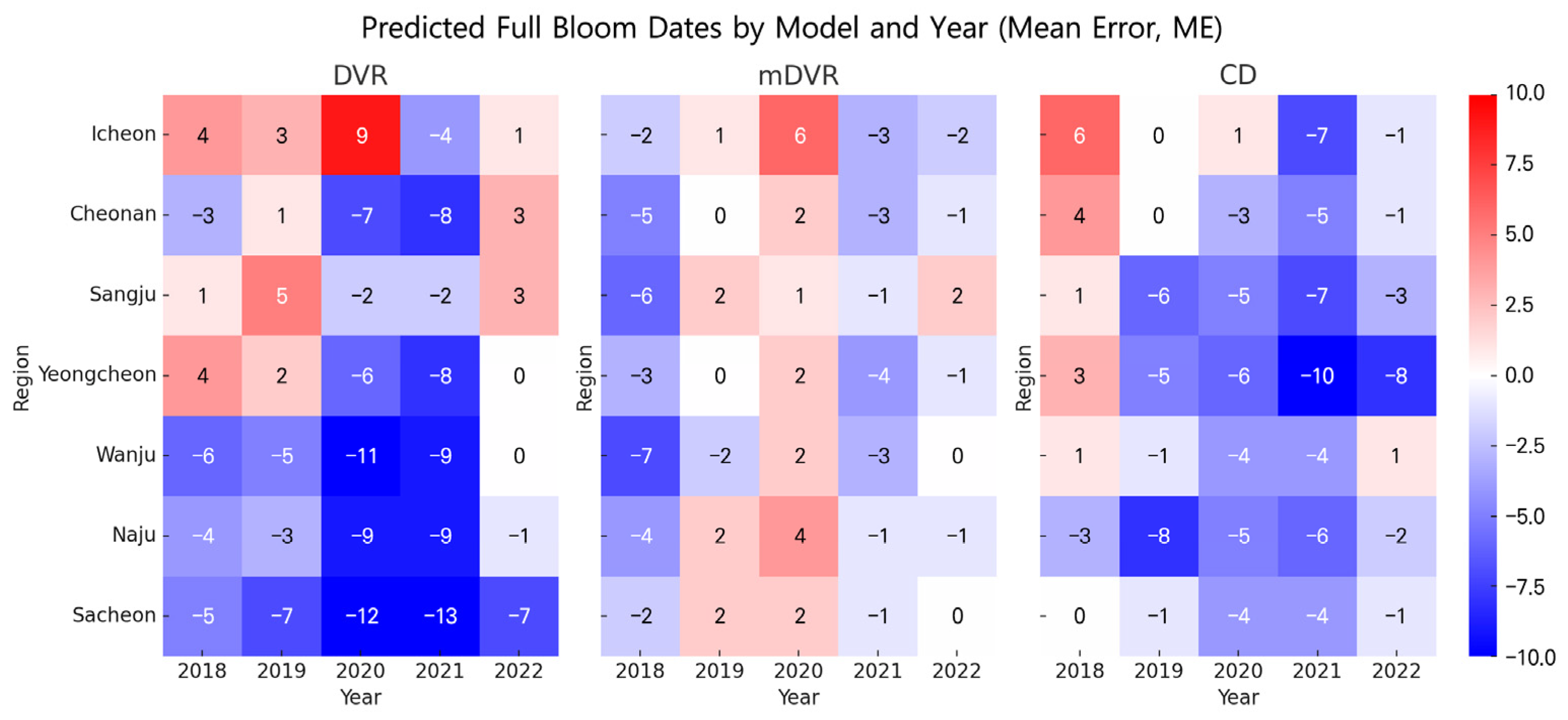
3.2. Evaluation of the Full Bloom Prediction Models for “Niitaka” Pear
4. Conclusions and Future Study
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zavalloni, C.; Andresen, J.A.; Winkler, J.A.; Black, J.R.; Beedy, T.L.; Flore, J.A. The Pileus Project: Climatic Impacts on Sour Cherry Production in the Great Lakes Region in Past and Projected Future Time Frames. Acta Hortic. 2006, 707, 101–108. [Google Scholar] [CrossRef]
- Salazar, M.R.; Jones, J.W.; Chaves, B.; Cooman, A.; Fischer, G. Base Temperature and Simulation Model for Nodes Appearance in Cape Gooseberry (Physalis peruviana, L.). Rev. Bras. Frutic. 2008, 30, 862–867. [Google Scholar] [CrossRef]
- Whiting, M.D.; Salazar, M.R.; Hoogenboom, G. Development of bloom phenology models for tree fruits. Acta Hortic. 2015, 1068, 107–112. [Google Scholar] [CrossRef]
- Valentini, N.; Me, G.; Ferrero, R.; Spanna, F. Use of Bioclimatic Indexes to Characterize Phenological Phases of Apple Varieties in Northern Italy. Int. J. Biometeorol. 2001, 45, 191–195. [Google Scholar] [CrossRef] [PubMed]
- Viator, R.P.; Nuti, R.C.; Edmisten, K.L.; Wells, R. Predicting Cotton Boll Maturation Period Using Degree Days and Other Climatic Factors. Agron. J. 2005, 97, 494–499. [Google Scholar] [CrossRef]
- Legave, J.M.; Farrera, I.; Almeras, T.; Calleja, M. Selecting Models of Apple Flowering Time and Understanding How Global Warming Has Had an Impact on This Trait. J. Hortic. Sci. Biotechnol. 2008, 83, 76–84. [Google Scholar] [CrossRef]
- Oh, S.D.; Kang, S.M.; Kim, D.I.; Kim, M.S.; Kim, W.S. Fruit Tree Physiology in Relation to Temperature; Gilmogeum: Seoul, Republic of Korea, 2004. [Google Scholar]
- Kim, J.-H.; Lee, E.-J.; Yun, J.I. Prediction of Blooming Dates of Spring Flowers by Using Digital Temperature Forecasts and Phenology Models. Kor. J. Agric. For. Meteorol. 2013, 15, 40–49. [Google Scholar] [CrossRef][Green Version]
- Menzel, A.; Fabian, P. Growing Season Extended in Europe. Nature 1999, 397, 659. [Google Scholar] [CrossRef]
- Ou, S.; Chen, C. Estimation of the Chilling Requirement and Development of a Low-Chill Model for Local Peach Trees in Taiwan. J. Chin. Soc. Hortic. Sci. 2000, 46, 337–350. [Google Scholar]
- Cook, B.I.; Wolkovich, E.M.; Parmesan, C. Divergent Responses to Spring and Winter Warming Drive Community Level Flowering Trends. Proc. Natl. Acad. Sci. USA 2012, 109, 9000–9005. [Google Scholar] [CrossRef]
- Guo, L.; Dai, J.; Wang, M.; Xu, J.; Luedeling, E. Responses of Spring Phenology in Temperate Zone Trees to Climate Warming: A Case Study of Apricot Flowering in China. Agric. For. Meteorol. 2015, 201, 1–7. [Google Scholar] [CrossRef]
- Atkinson, C.J.; Brennan, R.M.; Jones, H.G. Declining Chilling and Its Impact on Temperate Perennial Crops. Environ. Exp. Bot. 2013, 91, 48–62. [Google Scholar] [CrossRef]
- Guo, L.; Dai, J.; Ranjitkar, S.; Yu, H.; Xu, J.; Luedeling, E. Chilling and Heat Requirements for Flowering in Temperate Fruit Trees. Int. J. Biometeorol. 2014, 58, 1195–1206. [Google Scholar] [CrossRef] [PubMed]
- Legave, J.M.; Guédon, Y.; Malagi, G.; El Yaacoubi, A.; Bonhomme, M. Differentiated Responses of Apple Tree Floral Phenology to Global Warming in Contrasting Climatic Regions. Front. Plant Sci. 2015, 6, 1054. [Google Scholar] [CrossRef] [PubMed]
- Scorza, R.; Okie, W.R. PEACHES (PRUNUS). Acta Hortic. 1991, 290, 177–234. [Google Scholar] [CrossRef]
- Burroughs, W.J. Gardening and Climate Change. Weather 2002, 57, 151–157. [Google Scholar] [CrossRef][Green Version]
- Kim, J.-H.; Kim, D.; Kim, S.; Yun, E.; Ju, O.; Sun Park, J.; Soon Shin, Y. Estimation of Freeze Damage Risk According to Developmental Stage of Fruit Flower Buds in Spring. Kor. J. Agric. For. Meteorol. 2019, 21, 55–64. [Google Scholar] [CrossRef]
- Baldocchi, D.; Wong, S. Accumulated Winter Chill Is Decreasing in the Fruit Growing Regions of California. Clim. Change 2008, 87, 153–166. [Google Scholar] [CrossRef]
- Luedeling, E.; Zhang, M.; Girvetz, E.H. Climatic Changes Lead to Declining Winter Chill for Fruit and Nut Trees in California during 1950–2099. PLoS ONE 2009, 4, e6166. [Google Scholar] [CrossRef]
- Darbyshire, R.; Webb, L.; Goodwin, I.; Barlow, E.W.R. Impact of Future Warming on Winter Chilling in Australia. Int. J. Biometeorol. 2013, 57, 355–366. [Google Scholar] [CrossRef]
- Lang, G.A.; Early, J.D.; Martin, G.C.; Darnell, R.L. Endo-, Para-, and Ecodormancy: Physiological Terminology and Classification for Dormancy Research. HortScience 1987, 22, 371–377. [Google Scholar] [CrossRef]
- Rural Development Administration. The Agrometeorological Early Warning System. Available online: https://agmet.kr/ (accessed on 17 August 2025).
- Heuvelink, E. Re-Interpretation of an Experiment on the Role of Assimilate Transport Resistance in Partitioning in Tomato. Ann. Bot. 1996, 78, 467–470. [Google Scholar] [CrossRef]
- Richardson, E.A.; Seeley, S.D.; Walker, D.R. A Model for Estimating the Completion of Rest for ‘Redhaven’ and ‘Elberta’ Peach Trees1. HortScience 1974, 9, 331–332. [Google Scholar] [CrossRef]
- Gilreath, P.R.; Buchanan, D.W. Rest Prediction Model for Low-Chilling ‘Sungold’ Nectarine1. J. Am. Soc. Hortic. Sci. 1981, 106, 426–429. [Google Scholar] [CrossRef]
- Aron, R. Availability of Chilling Temperatures in California. Agric. Meteorol. 1983, 28, 351–363. [Google Scholar] [CrossRef]
- Shaltout, A.D.; Unrath, C.R. Effect of Some Growth Regulators and Nutritional Compounds as Substitutes for Chilling of “Delicious” Apple Leaf and Flower Buds. J. Am. Soc. Hortic. Sci. 1983, 108, 898–901. [Google Scholar] [CrossRef]
- Ono, S.; Konno, T. Estimation of Flowering Date and Temperature Characteristics of Fruit Trees by DTS Method. Jpn. Agric. Res. Q. 1999, 33, 105–108. [Google Scholar]
- Cesaraccio, C.; Spano, D.; Snyder, R.L.; Duce, P. Chilling and Forcing Model to Predict Bud-Burst of Crop and Forest Species. Agric. For. Meteorol. 2004, 126, 1–13. [Google Scholar] [CrossRef]
- Dennis, F.G. Problems in Standardizing Methods for Evaluating the Chilling Requirements for the Breaking of Dormancy in Buds of Woody Plants. HortScience 2003, 38, 347–350. [Google Scholar] [CrossRef]
- Kim, S.-O.; Kim, J.-H.; Chung, U.-R.; Kim, S.-H.; Park, G.-H.; Yun, J.-I. Quantification of Temperature Effects on Flowering Date Determination in Niitaka Pear. Kor. J. Agric. For. Meteorol. 2009, 11, 61–71. [Google Scholar] [CrossRef][Green Version]
- Han, J.H.; Cho, K.S.; Choi, J.J.; Hwang, H.S.; Gook Kim, C.; Kim, T.-C. Estimation of Changes in Full Bloom Date of “Niitaka” Pear Tree with Global Warming. Hortic. Sci. Technol. 2010, 28, 937–941. [Google Scholar][Green Version]
- Chuine, I.; Cour, P.; Rousseau, D.D. Selecting Models to Predict the Timing of Flowering of Temperate Trees: Implications for Tree Phenology Modelling. Plant Cell Environ. 1999, 22, 1–13. [Google Scholar] [CrossRef]
- Primack, R.B.; Ibáñez, I.; Higuchi, H.; Lee, S.D.; Miller-Rushing, A.J.; Wilson, A.M.; Silander, J.A. Spatial and Interspecific Variability in Phenological Responses to Warming Temperatures. Biol. Conserv. 2009, 142, 2569–2577. [Google Scholar] [CrossRef]
- Wang, J.; Song, G.; Liddell, M.; Morellato, P.; Lee, C.K.F.; Yang, D.; Alberton, B.; Detto, M.; Ma, X.; Zhao, Y.; et al. An Ecologically-Constrained Deep Learning Model for Tropical Leaf Phenology Monitoring Using PlanetScope Satellites. Remote. Sens. Environ. 2023, 286, 113429. [Google Scholar] [CrossRef]
- Toomey, M.; Friedl, M.A.; Frolking, S.; Hufkens, K.; Klosterman, S.; Sonnentag, O.; Baldocchi, D.D.; Bernacchi, C.J.; Biraud, S.C.; Bohrer, G.; et al. Greenness Indices from Digital Cameras Predict the Timing and Seasonal Dynamics of Canopy-scale Photosynthesis. Ecol. Appl. 2015, 25, 99–115. [Google Scholar] [CrossRef]
- Richardson, A.D.; Braswell, B.H.; Hollinger, D.Y.; Jenkins, J.P.; Ollinger, S.V. Near-surface Remote Sensing of Spatial and Temporal Variation in Canopy Phenology. Ecol. Appl. 2009, 19, 1417–1428. [Google Scholar] [CrossRef]
- Rural Development Administration. The Fruit Tree Growth and Quality Management System. Available online: https://fruit.nihhs.go.kr/ (accessed on 31 October 2023).
- Meier, U. Growth Stages of Mono-and Dicotyledonous Plants—BBCH Monograph; Julius Kühn-Institut: Berlin, Germany, 2001. [Google Scholar]
- Miller, P.; Lanier, W.; Assistant, I.; Brandt, S.; Canada, A. Using Growing Degree Days to Predict Plant Stages. In Ag/Extension Communications Coordinator, Communications Services; Montana State University-Bozeman: Bozeman, MO, USA, 2001; Volume 59717, pp. 994–2721. [Google Scholar]
- Müller, M.; Braun, P. Development of Phenological Models over Time–a Review. Acta Hortic. 2008, 803, 111–116. [Google Scholar] [CrossRef]
- National Agricultural Technology Research Institute. Climatic Characteristics of Major Fruit Growing Areas; Rural Development Administration: Jeonju, Republic of Korea, 1990. [Google Scholar]
- Sugiura, T.; Honjo, H. The Effects of Temperature on Endodormancy Completion in Japanese Pear (Pyrus Pyrifolia Nakai) and Modeling the Relationship. J. Agric. Meteorol. 1997, 53, 285–290. [Google Scholar] [CrossRef]
- Sugiura, T. Prediction of Full Bloom Date of Pear Using Air Temperature. Agric. Hortic. 1999, 54, 146–149. [Google Scholar]
- Hauagge, R.; Cummins, J.N. Phenotypic Variation of Length of Bud Dormancy in Apple Cultivars and Related Malus Species. J. Am. Soc. Hortic. Sci. 1991, 116, 100–106. [Google Scholar] [CrossRef]
- Erez, A. Means to Compensate for Insufficient Chilling to Improve Bloom and Leafing. Acta Hortic. 1994, 395, 81–96. [Google Scholar] [CrossRef]
- Chandler, W.H.; Kimball, M.H.; Philp, G.L.; Tufts, W.P.; Weldon, G.P. Chilling Requirements for Opening of Buds on Deciduous Orchard Trees and Some Other Plants in California. Univ. Calif. Agr. Expt. Sta. Bull. 1937, 611, 63. [Google Scholar]
- Alburquerque, N.; García-Montiel, F.; Carrillo, A.; Burgos, L. Chilling and Heat Requirements of Sweet Cherry Cultivars and the Relationship between Altitude and the Probability of Satisfying the Chill Requirements. Environ. Exp. Bot. 2008, 64, 162–170. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Nossent, J.; Bauwens, W. Application of a Normalized Nash-Sutcliffe Efficiency to Improve the Accuracy of the Sobol’ Sensitivity Analysis of a Hydrological Model. In Proceedings of the EGU general assembly conference abstracts, Vienna, Austria, 22–27 April 2012; Volume 14, p. 237. [Google Scholar]
- Taylor, K.E. Summarizing Multiple Aspects of Model Performance in a Single Diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Hunter, A.F.; Lechowicz, M.J. Predicting the Timing of Budburst in Temperate Trees. J. Appl. Ecol. 1992, 29, 597. [Google Scholar] [CrossRef]
- Chuine, I.; Cour, P.; Rousseau, D.D. Fitting Models Predicting Dates of Flowering of Temperate-zone Trees Using Simulated Annealing. Plant Cell Environ. 1998, 21, 455–466. [Google Scholar] [CrossRef]

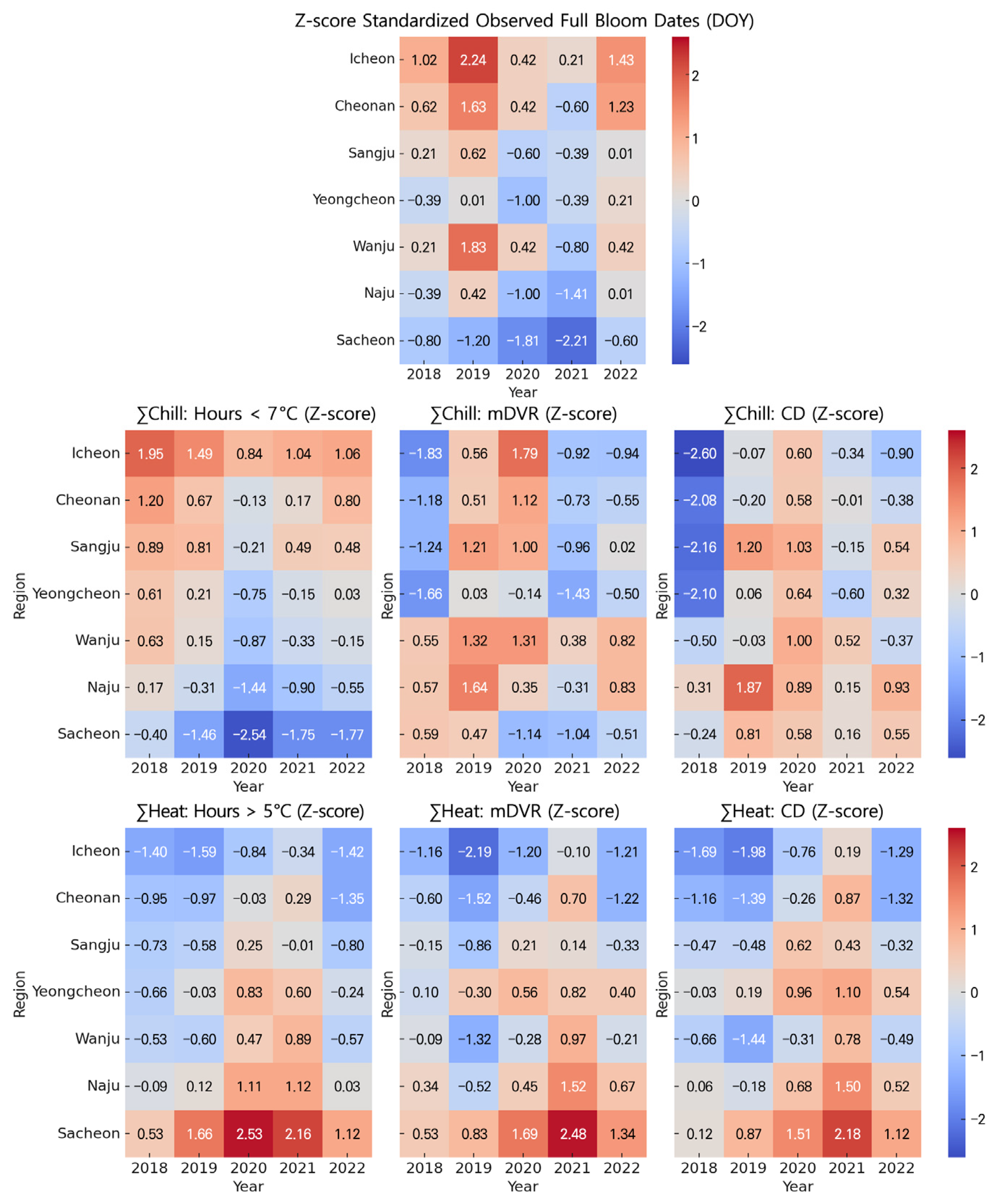

| Region | Chill Units (CV, %) | Heat Units (CV, %) | ||||
|---|---|---|---|---|---|---|
| Hours < 7 °C | mDVR Model | CD Model | Hours > 5 °C | mDVR Model | CD Model | |
| Icheon | 5.1 | 9.2 | 15.9 | 13 | 18.5 | 17.2 |
| Cheonan | 6.5 | 6.1 | 12.7 | 15.4 | 18.8 | 17.7 |
| Sangju | 5.4 | 7 | 16.3 | 9.8 | 8.7 | 8.7 |
| Yeongcheon | 6.7 | 5 | 13.7 | 11.7 | 7.9 | 7.3 |
| Wanju | 7.5 | 2.6 | 7.5 | 13.8 | 13.8 | 14.1 |
| Naju | 8.7 | 4.3 | 7.4 | 10.8 | 12.9 | 9.8 |
| Sacheon | 13 | 5.3 | 4.8 | 11.9 | 11.6 | 10.5 |
| Avg. | 13.3 | 6.3 | 12.1 | 19.5 | 19.3 | 16.4 |
| Region | DVR | mDVR | CD | |||
|---|---|---|---|---|---|---|
| RMSE | EF | RMSE | EF | RMSE | EF | |
| Icheon | 5 | −0.90 | 3.3 | 0.17 | 4.2 | −0.34 |
| Cheonan | 5.1 | −0.86 | 2.8 | 0.45 | 3.2 | 0.28 |
| Sangju | 2.9 | −0.89 | 3 | −1.02 | 4.9 | −4.26 |
| Yeongcheon | 4.9 | −4.66 | 2.4 | −0.42 | 6.8 | −10.04 |
| Wanju | 7.3 | −2.06 | 3.6 | 0.23 | 2.6 | 0.59 |
| Naju | 6.1 | −2.53 | 2.8 | 0.29 | 5.3 | −1.59 |
| Sacheon | 9.3 | −8.65 | 1.6 | 0.71 | 2.6 | 0.25 |
| Average | 6.1 | −0.57 | 2.9 | 0.66 | 4.5 | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-H.; Yun, E.-J.; Kang, D.G.; Han, J.-H.; Shim, K.-M.; Kim, D.-J. Evaluation of Phenology Models for Predicting Full Bloom Dates of ‘Niitaka’ Pear Using Orchard Image-Based Observations in South Korea. Atmosphere 2025, 16, 996. https://doi.org/10.3390/atmos16090996
Kim J-H, Yun E-J, Kang DG, Han J-H, Shim K-M, Kim D-J. Evaluation of Phenology Models for Predicting Full Bloom Dates of ‘Niitaka’ Pear Using Orchard Image-Based Observations in South Korea. Atmosphere. 2025; 16(9):996. https://doi.org/10.3390/atmos16090996
Chicago/Turabian StyleKim, Jin-Hee, Eun-Jeong Yun, Dae Gyoon Kang, Jeom-Hwa Han, Kyo-Moon Shim, and Dae-Jun Kim. 2025. "Evaluation of Phenology Models for Predicting Full Bloom Dates of ‘Niitaka’ Pear Using Orchard Image-Based Observations in South Korea" Atmosphere 16, no. 9: 996. https://doi.org/10.3390/atmos16090996
APA StyleKim, J.-H., Yun, E.-J., Kang, D. G., Han, J.-H., Shim, K.-M., & Kim, D.-J. (2025). Evaluation of Phenology Models for Predicting Full Bloom Dates of ‘Niitaka’ Pear Using Orchard Image-Based Observations in South Korea. Atmosphere, 16(9), 996. https://doi.org/10.3390/atmos16090996







