Spatiotemporal Graph Convolutional Network-Based Long Short-Term Memory Model with A* Search Path Navigation and Explainable Artificial Intelligence for Carbon Monoxide Prediction in Northern Cape Province, South Africa

Abstract

Background: The emission of air pollutants into the atmosphere is a global issue as it contributes to global warming and climate-related issues. Human activities like the burning of fossil fuel influence changes in weather patterns—resulting in issues such as a rise in sea levels, among other things. Identifying road network routes within Northern Cape Province in South Africa that are less exposed to air pollutants like carbon monoxide is the issue this study seeks to address. Methods: The method used for our predictions is based on a graph convolutional network (GCN) and long short-term memory (LSTM). The GCN extracts geospatial characteristics, and the LSTM captures both nonlinear relationships and temporal dependencies in an air pollutant and meteorological dataset. Furthermore, an A* search strategy identifies the path from one location to another with the lowest carbon monoxide concentrations within a road network. The explainable artificial intelligence (xAI) technique is used to describe the nonlinear relationship between the target variable and features. Meteorological and air pollutant data in the form of statistical mean, minimum, and maximum values were leveraged, and a random sampling technique was utilized to fill the data gap to help train the predictive model (GCN-LSTM-A*). Results: The predictive model was evaluated with mean squared error (MSE) and root mean squared error (RMSE) values within two multi-time steps (8 and 16 h) with MSEs of 0.1648 and 0.1701, respectively. The LIME technique, which provides explanations of features, shows that Wind_speed and NO₂ and NOx concentrations decreased the predicted CO, whereas PM_2.5, PM₁₀, relative humidity, and O₃ increased the predicted CO of the route.

1. Introduction

Air pollution a major problem in most countries. In recent times, countries with high levels of pollution are embracing mitigation measures to minimize the impact of air pollution on their country. While pollutants such as particulate matter (PM_2.5) and nitrogen dioxide (NO₂), among others, have received considerable attention in both scientific research and policy, carbon monoxide (CO) remains comparatively under-studied, despite its importance within the discourse of air pollution analysis. CO is a colorless, odorless gas with well-known health effects, such as reduced oxygen transport in the human bloodstream, impaired cardiovascular function, and increased health risks in vulnerable populations. From a modeling perspective, CO is challenging because its concentration levels are highly influenced by local meteorological conditions, atmospheric chemistry, and traffic emissions, making it an important but technically complex target for any predictive modeling task. While traditional models such as those based on statistics and regression are used as predictive models that capture nonlinear relationships in air pollutants and meteorological datasets, they are largely not transparent which is a limitation of these models. Furthermore, while temporal models are largely used to capture nonlinearity, the lack of spatial models that handle dependencies across towns and locations needs to be addressed.

Explainable AI is an emerging domain that seeks to address the challenge of model interpretability. Explainable AI describes “why” a set of AI models make predictions about a task in a certain manner, whereas interpretable AI explains “how” the model makes predictions in that manner. Thus, explainable AI answers key questions about why and how models make decisions in a certain manner. Graph-based neural networks handle the processing of graph data; however, the black-box nature of this neural model is considered a challenge that hinders it use, leading to the utilization of graph-based artificial intelligence models that offer some explanation of the model’s structure [1].

The underrepresentation of CO in spatiotemporal modeling, particularly in data-scare provinces such as the Northern Cape, South Africa, represents a major research gap. Current navigation systems do not incorporate CO concentration predictions and therefore cannot provide optimal, pollution-aware routing recommendations. Moreover, the adoption of graph-based deep learning models for spatiotemporal prediction is limited by their black-box nature, which limits interpretability and reduces trust among users and policymakers. Therefore, this study aims to address these gaps by developing a predictive and explainable geospatial intelligence-based graph convolutional network long short-term memory with A* search (GeoxAI-GCN-LSTM-A*) model for CO concentration modeling and pollution-aware navigation. Specifically, the objectives are as follows: (1) to design a spatiotemporal prediction model for CO that integrates both spatial dependencies across towns and temporal trends in pollutant dynamics; (2) to enhance the transparency of graph-based neural models through explainable AI (xAI) techniques, making the prediction interpretable to end-users; (3) to integrate pollution predictions into navigation systems using A* search, enabling users to avoid CO hotspots while engaging in open-air activities such as driving, biking, sprinting, exercising, trekking, and others on the road network.

In terms of the contribution and novelty, the novelty of this research lies in the integration of the explainable graph neural network model into spatiotemporal modeling and navigation systems. This contribution can be summarized as follows: (1) A GeoxAI-GCN-LSTM-A* model is proposed, combining graph convolutional networks (GCNs) for spatial dependencies, LSTM for temporal dynamics, and A* search for optimal path-finding. (2) The model introduces explainability into graph-based neural networks, revealing how meteorological and air pollutant features contribute to CO prediction. (3) A geospatial-intelligence framework is developed for Northern Cape Province, addressing the lack of CO-focused studies in data-scarce regions. (4) The integration of predicted CO concentrations with road network navigation allows for health-conscious route recommendations, ensuring that users can avoid pollution hotspots in real time. The sections are organized as follows: Section 2 describes the study area, Section 3 is the literature review, Section 4 comprises the methods and materials, Section 5 contains the results, Section 6 outlines the discussion, and the conclusion can be found in Section 7.

2. Study Area

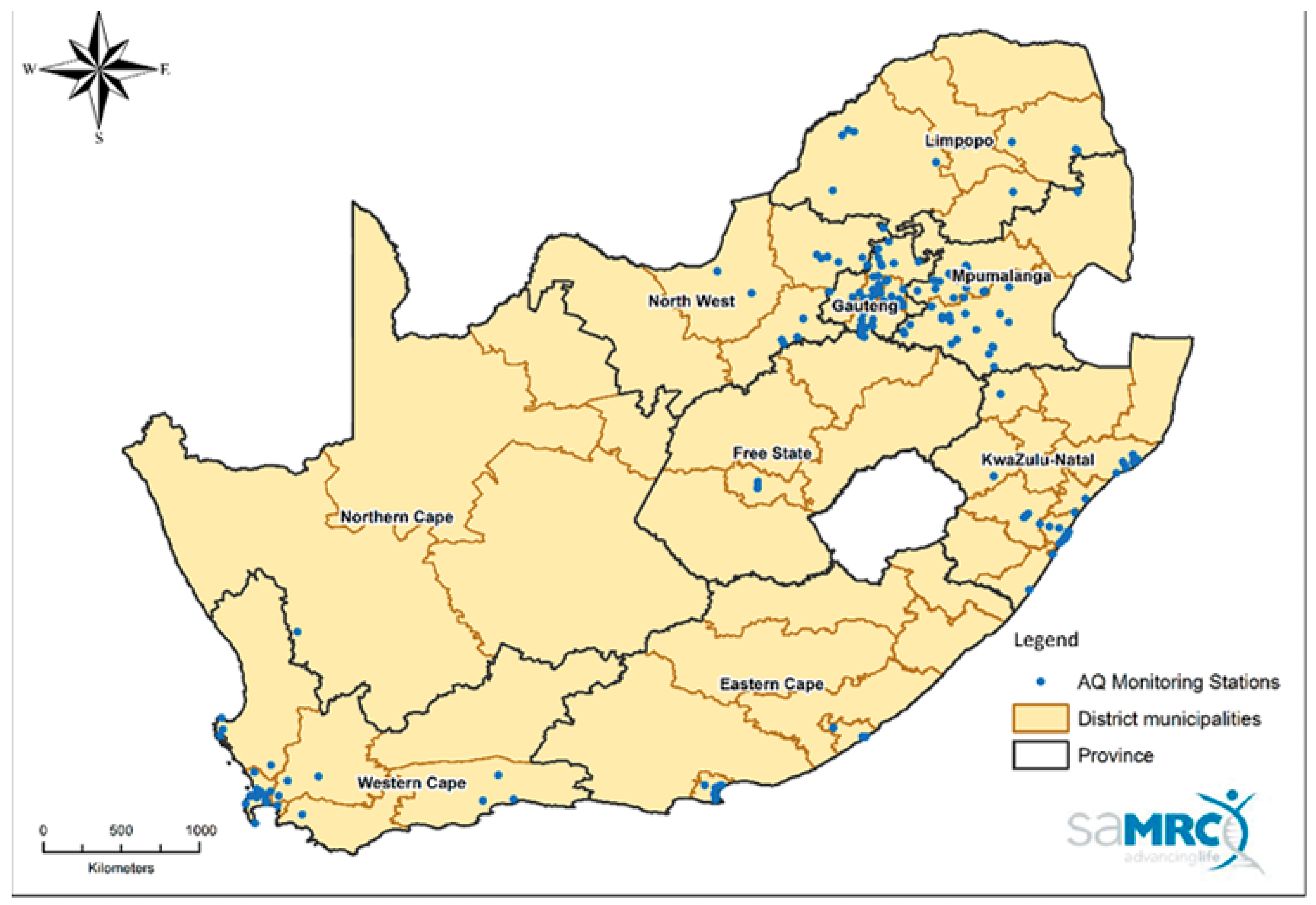
In South Africa, several challenges confront air-monitoring stations, such as theft of air-monitoring tools; vandalism of air-monitoring stations, which leads to the relocation of monitoring stations; power cuts leading to a loss of data from monitoring stations; and non-functional air-monitoring stations. Some stations are non-operational because of resource constraints and the lack of skilled personnel in the affected provinces. Out of the 130 state-owned air-monitoring stations in South Africa, 36 are operational up to the minimum data need, 55 are operational but unable to meet the minimum data need, and 39 are not operational (

Table 1. Status of air-monitoring stations in SA, Sept 2023.

Province	Number of Stations	Meeting Data Requirements	Not Meeting Data Requirements	Stations Not Operational
Eastern Cape	8	0	8	0
Free State	3	1	0	2
Gauteng	30	2	20	8
Kwa-Zulu Natal	27	7	10	10
Limpopo	5	0	4	1
Mpumalanga	6	1	4	1
North-West	10	0	8	2
SAWS	17	9	8	0
Western Cape	26	5	20	1
National Total	132	25	82	25 (37 in 2021)

Source: [2].

). Given these challenges, stakeholders’ rationale is to have fewer and reliable monitoring stations rather than all stations operating and generating intermittent data. Consequently, air pollution data are not collected from other monitoring stations, which create an air pollution data gap. In recognizing this gap, private participation in monitoring air pollution in South Africa (SA) was critical, leading to the establishment of 66 private-led air pollution monitoring stations, which are operated by companies such as Sasol, Eskom, industries, and mining. Unfortunately, the participation of private companies in harnessing air pollution data has raised some concerns about data independence [2]. These concerns have raised issues of air pollution data collected from locations that are not covered by both private and state-owned monitoring stations.

Table 1 shows the status of the air-monitoring stations, which further suggests that state-owned monitoring stations are either not providing reliable scientific data or are not functional. Figure 1: Location of air quality monitoring stations in South Africa.

Additionally, power cuts or load shedding contribute to the data loss from the monitoring station at Diepkloof, in Soweto, which leads to significant data loss for PM_2.5, nitrogen dioxide, and sulfur dioxide [3]. As load shedding contributes to the insufficiency of data, monitoring stations are handicapped; therefore, the need to resolve this is more pressing. Again, the insufficiency of data can be a challenge when new monitoring stations are established. Thus, having to relocate a monitoring station to a new location because of vandalism also creates the issue of data insufficiency. Consequently, the role of a data-driven model is increasingly being championed to help in filling the data insufficiency gap [4]. Fong, Li [5] indicated that transfer learning and pre-trained models provide a surety of accurate prediction in data insufficiency situations. Building a robust air prediction model requires a voluminous amount of data so that when any pre-trained model is used in the target location, it can effectively predict with even a limited amount of data [6].

The National Air Quality Indicator (NAQI) report on carbon monoxide concentration recorded from Karoo air-monitoring station in Northern Cape Province in South Africa [7] indicates null recording of CO concentration for several months as presented in

Table 2. Karoo CO concentration recordings from 2023 to 2024.

Month	Year	Average	Min	Max
Jan	2023	0.02	0.00	1.49
February	2023	0.00	0.00	0.00
March	2023	0.01	−0.01	1.45
April	2023	0.05	−0.04	0.15
May	2023	0.02	0.00	1.33
June	2023	-	-	-
July	2023	-	-	-
August	2023	-	-	-
September	2023	-	-	-
October	2023	-	-	-
November	2023	-	-	-
December	2023	-	-	-
February	2024	-	-	-

. Northern Cape Province is a large and sparsely populated province, which includes towns like Kuruman, Upington, and many more. Kimberley is a city in the Northern Cape.

Table 2 shows the CO concentration recorded from 2023 to February 2024 at Karoo air-monitoring station. Furthermore,

Table 3. Unprocessed air pollutant data from SAAQIS.

Station Name	Date/Time	PM10	PM2.5	NO2	NOX	NO	SO2	O3	CO	Benzene	H2S
		µg/m3	µg/m3	ppb	ppb	ppb	ppb	ppb	ppm	ppb	ppb
-	8 April 2025 11:00	28.551	13.391	-	-	-	-	-	-	-	-
-	11 April 2025 12:00	-	-	-	-	-	-	-	-	-	-
-	11 December 2024 03:00	-	-	-	-	-	-	-	-	-	-
-	26 January 2025 21:00	0.560	-	-	-	-	-	5.563	0.620	-	-
-	11 April 2025 12:00	20.114	12.559	10.877	18.132	7.255	25.065	33.871	0.311	-	-
-	11 April 2025 12:00	0.276	0.253	3.111	0.719	-	1.571	-	0.189	-	-
-	11 April 2025 12:00	-	-	16.407	19.554	3.148	3.569	38.053	1.271	-	-
-	11 April 2025 12:00	15.878	10.641	2.895	4.495	1.600	1.785	56.437	0.339	-	2.418
-	11 April 2025 12:00	10.484	6.812	6.111	8.271	2.160	1.445	31.73	0.127	-	-
-	26 January 2025 21:00	14.200	15.967	3.845	5.709	1.868	0.618	14.507	0.121	-	-
-	11 April 2025 12:00	17.624	4.825	4.543	6.928	2.385	0.507	23.664	0.146	-	-
-	20 March 2025 09:00	3.277	2.841	-	-	-	4.562	-	-	-	-
-	11 April 2025 12:00	39.983	12.336	7.270	9.442	2.172	5.067	39.977	0.230	-	-

shows the recent unprocessed air pollutant data for South Africa (accessed on https://saaqis.environment.gov.za/ 11 April 2025).

Table 2 and Table 3 demonstrate a data gap on the South Africa Air Quality Information System (SAAQIS). While Table 3 lacks station name data, Table 2 also lacks subsequent data on CO concentration specific to the Karoo air-monitoring station located in Northern Cape Province. The aforementioned challenge with data insufficiency is the motivation to conduct research that seek to develop a geospatial intelligence model that utilizes the best navigation path and deep learning techniques such as long short-term memory and graph convolutional networks to understand the spatiotemporal dependencies and predict CO concentration from the available meteorological and air pollutant dataset. This contributes to providing CO concentration information in locations with a data insufficiency problem. Such a model combination introduces an additional internal layer to the deep learning model, making it complex. Thus, understanding the internal architecture and how each feature contributes to the model’s prediction at each location and time offers a useful contribution to the air prediction task.

3. Literature Review

This section reviews geospatial models and graph convolutional LSTM models applicable in air pollution prediction.

3.1. Geographic Artificial Intelligence and Explainable AI Models

Geographic artificial intelligence, or geospatial artificial intelligence (GeoAI) which is essentially the same concept, refers to the use of AI techniques to analyze and interpret spatial data. GeoAI leverages machine learning and other AI methods to extract meaningful insights from geographical data, like satellite imagery and location data [8]. Thus, GeoAI is intelligence derived from images or location data. Such intelligence is uncovered through the use of machine learning or deep learning models which are integrated with geospatial data for spatial pattern prediction. Thus, GeoAI models geospatial relationships and interactions, predicts spatial phenomena, shows spatiotemporal trends, and provides spatial reasoning [9]. Deep learning in geospatial analysis captures the complex spatiotemporal relationship inherent in air quality data. While Chadalavada, Faust [10] highlighted the significance of leveraging multiple data sources to enhance model predictions, model interpretability helps to enhance the understanding of how each variable considered in the model contributes to the understanding of users. Geospatial systems are experiencing transformative change in the advent of deep learning models equipped with interpretability [11]. Geospatial artificial intelligence (GeoAI) contributes immensely to solving spatial problems by helping to extract information from complex data through geospatial intelligence [12,13]. In recent times, the word GeoxAI is used in research to refer to xAI and GeoAI. In this regard, geographic explainable AI (GeoxAI) is employed to enhance spatial interpretability. For instance, Foroutan, Hu [14] used the GeoXAI GeoShapley to understand spatial heterogeneity in terms of how geographic location influences factors of extreme weather that leads to heat-related emergency department visits (EDVs) across different regions in Texas.

The fundamental distinction between GeoAI and traditional AI is data handling. While GeoAI considers data as dependent spatial and heterogeneously distinct features ingrained in geographic information, traditional AI models consider data as independent features that are identically distributed with aspatial variables such as text and demographics. Data handling in these two techniques (GeoAI and conventional AI) is often different. For instance, during data transformation, GeoAIs use methods such as spatial encoding to transform geographic attributes like road networks and towns into a machine-readable format, showing them as adjacent metrics or by graph embedding. Furthermore, modeling techniques ensure the preservation of the spatial relationship in GeoAI-based models. GeoShapley is a game theory method for assessing spatial effects in machine learning (ML) models [15]. Liu [16] indicated that the GeoShapley method integrates ML with Shapley values to explain the contribution of geographical features. This notwithstanding, geospatial ML models lack exploration of nonlinear interactions between geographical features and explanatory variables. GeoShapley is a model-agnostic approach which can be applied to different ML and statistical models, which are considered as black-box, to understand the various structures in these models [15]. Furthermore, the interpretation of GeoShapley can be directly linked with spatially varying coefficient models to explain the spatial effects, whereas additive models can be used to explain the non-spatial effects.

While machine learning and artificial intelligence (ML/AI) were considered black-box models because they lack explainability, recent advances in explainable AI (xAI) offer more interpretable models in geospatial systems in terms of how to extract spatial effects from machine learning models [17]. Explainable AI models for local interpretation methods, such as SHAP (Shapley additive explanations), offer the opportunity to interpret and visualize complex geographical phenomena and processes. For instance, SHAP interprets XGBoost (extreme gradient boosting) [17].

Table 4. Summary of geospatial intelligence and xAI models.

Author	Research Focus	Approach/Method	Dataset	xAI Model
Gianquintieri, Oxoli [18]	PM2.5.	GEOAI (Geomatics and Earth Observation Artificial Intelligence) with Shapley additive explanation algorithm.	-	Shapley additive explanation
Razavi-Termeh, Sadeghi-Niaraki [19]	Variability of air and noise pollution levels. The absence of xAI for model interpretability.	Geospatial artificial intelligence (GeoAI) techniques.	Spatial database.
Hsu and Li [20]	Interpretability of geospatial models.	Occlusion method, integrated gradients method, class activation map method, and deep learning.	Image datasets.
Lee and Li [21]	Interpretability of deep learning models in remote sensing.	Interpretable deep active learning for flood inundation mapping (IDAL-FIM).	Sen1Floods11 dataset, and adopts U-Net with MC-dropout.
Liu, Zhang [22]	Interpretability and algorithmic biases.	Explainable spatially explicit GeoAI GCN, graph-based xAI (GNNExplainer), features of urban roads.	Street View Imagery (SVI) data source.	GNNExplainer
Li [23]	Carpool-style ridesharing.	Machine learning and xAI.	Big-trip data.	SHAP
Li [15]	Interpretability of ML model and location quantification.	GeoShapley.		GeoShapley
Liu [16]	Interpretability of spatial variables.	An ensemble framework (xAI and ML).	Synthetic datasets.	GeoShapley
Razavi-Termeh, Sadeghi-Niaraki [24]	Noise pollution.	GeoAI, categorical boosting (CatBoost), Firefly algorithm (CatBoost-FA), and fruit fly optimization algorithm (CatBoost-FOA).	Spatial database enriched with spatial criteria.	SHAP
Jin, Park [25]	Explainability of human mobility AI models.	Explainable GeoAI (GLIME and LSTM).		GLIME
Chang, Chern [26]	Atmospheric CH4 concentrations.	GeoAI, ML predict CH4 concentration.		-

presents a summary of GeoAI models and the focus of research.

Though xAI provides explanations, Xing and Sieber [27] indicate that the challenge with xAI computation is the choice of reference model, data, and the challenge to attribute explanatory power to gradients. Furthermore, applying xAI to geospatial tasks is also challenged by how to accommodate geographical scales and geographical data structures. Explainable AI methods often describe models’ input and outcome. Often, different deep learning or machine learning models have information on their underlying algorithms and how they are written and also how the algorithms (DL and ML) are stress-tested on different datasets [28]. Thus, xAI is not merely giving a model’s output to an AI process for an explanation.

Rajabi and Etminani [29] argued that a knowledge graph (KG) provides semantic network information regarding geographic objects, locations, and spatial events together with their labeled relationship, which is very useful in GeoAI, such that the integration of KG with xAI can provide very useful explainable data in GeoxAI systems. Xu, Uszkoreit [30] indicated that xAI algorithms require a reference point as a baseline to offer some explanation of a model. Such a reference could be a dataset or data points provided to an xAI model for explanation. Aside from local interpretable model-agnostic explanations (LIME) and Shapley additive explanations (SHAP) techniques, other xAI models include class activation mapping (CAM), gradient CAM (Grad-CAM), and Grad-CAM++ which are gradient-based approaches to increase spatial context and preserve geographic structures like coordinates, distances, and projections. Mostly, gradient-based approaches have their bias term, in gradient-based explanations, distributed across input features and input gradient. Sources of bias include skewed data, tainted data (e.g., wrong feature labeling), limited features, sample size disparity, and proxy features (e.g., some feature may correlate with other sensitive features, thereby inducing a bias) in the dataset [31]. The model-agnostic capability of xAI techniques suggests that regardless of the internal structure of any model (ML or DL) and how it was trained, xAI could offer an explanation as it operates on the input–output relationship of a model and does not require access to the internal parameters of the model. Thus, xAI glass-boxes “black-box” DL or ML models. Knowledge of the geographic structure and its scope is useful in GeoxAI explanation, suggesting a shift from model-agnostic xAI to model-specific or location-specific model explanations [27]. Therefore, having a model to capture both spatial–temporal dependencies for further explanation is beneficial in air pollutant prediction. Zou, Goh [32] presented a framework that hybridized SHAP and Grad-CAM++ to provide a visual explanation of the DL prognostic model. However, such combinations also incur a high computational cost in providing visual explanations. Nambiar, Harikrishnaa [33] indicated that xAI techniques (e.g., LIME and SHAP) augment the performance of AI-based systems with expert knowledge and reasoning which can enhance the trustworthiness of DL and ML models.

3.2. Geographic Artificial Intelligence (GeoAI) and Graph Convolutional Network-Based Long Short-Term Memory

GeoAI systems are especially useful in modeling spatiotemporal dynamics and generating intelligent insights over geographical spaces. For instance, graph neural networks (GNNs) have been used for spatial networks and long short-term memory (LSTM) models for temporal modeling. The graph convolutional network belongs to the family of GNNs which are designed to work on graph network data and capture the relationship and interaction between non-Euclidean spatial points like cities, roads, and air-monitoring sensors. The LSTM model is adapted to handle long-range temporal dependencies using its gated mechanism which allows it to remember or forget past information based on its relevance to the data inputs. In this context, models that are developed based on LSTM for air pollution prediction can handle the time-varying nature of pollutants in different geographical locations better than traditional machine learning models. Though there may be challenges with monitoring air pollutants from monitoring stations, several locations may also not be monitored due to logistical reasons leading to the use of AI-driven models to forecast air quality [34].

Wu, Wang [35] suggested a multi-scaled graph-based approach to simultaneously predict pollutant (PM_2.5) concentrations from multiple cities by leveraging the geo-sensory nature of pollutants. In this approach, a deep convolutional network model was proposed to address the multi-scaled nature of air pollutants. The multi-scaled approach combines three different models: T-net, S-net, and F-net. S-net is a created from the combination of graph convolutional neural frameworks (GCNs) at different spatial scales because it is adaptive to irregular spatial features. F-net is a dense network that fuses features to make a final prediction, whereas T-net is a dilated network that extracts multi-scale temporal features.

Table 5. GeoAI and graph convolutional network-based LSTM models.

Author	Air Pollutant/Domain	Challenge	Model	Evaluation Metrics
Li, Chen [36]	Traffic forecast	Traffic flow prediction.	Spatiotemporal dynamically fused graph convolutional network (STDFGCN) for traffic prediction.	-
Li and Zhang [37]	Traffic forecast	Heterogeneous correlations between regions pose high computational costs on spatial–temporal graph models.	Spatial–temporal graph model, spatial–temporal dynamic graph diffusion convolutional network (SDGDN).	Performance and computation efficiency
Zhang, Zhang [38]	PM2.5 learn long-term temporal dependencies prediction	Air quality prediction.	Temporal difference graph transformer networks (TDGTN).	RMSE, MAE, MAPE
Alrige, Bitar [39]	-	Merge user profile with geospatial information.	GeoAI technique referred as “space–time cube” (STC) and user profile information to the local map.	-
Chen, Sun [40]	-	Road network information.	Bidirectional feature pyramid network (BiFPN) model to capture road junctions and boundaries.	IoU
Liang, Zhu [41]	-	Community detection models lack attribute information.	GeoAI-enhanced unsupervised community detection methods (region2vec based on graph attention networks (GATs) and graph convolutional networks (GCNs)).	Cosine, synthetic score, intra-flow ratio, normalized inequality
Matthes, Jeschor [42]	Air pollution, noise	Mobility-related problems such as space limitations, air pollution, and noise levels.	Geospatial artificial intelligence (GeoAI).	F1
Wang and Zhu [43]	-	Human activity intensity prediction.	Hyper graph-based hybrid graph convolutional network (HyGCN).	-
Augustin and Kiliroor [44]	PM 2.5	Real-time monitoring of dust particle concentration levels periodically.	Long short-term memory (LSTM) and multi-layer perceptron (MLP) for accurate prediction.	-
Crivellari and Shi [45]	-	Location-based services data leads to privacy issues and regulation on it use and sharing.	Generative adversarial network (GAN) and LSTM. Dataset (synthetic dataset and real-world large-scale dataset).	Multiple metrics
Rao, Gao [46]	-	The prevalence of location-based services.	LSTM-TrajGAN.
Li, Hu [47]	-	DL’s data dependence and lack of process understanding.	Physics-encoded neural network model (dNN) was used.	-
Chen, Ding [48]	PM2.5, PM10, and O3	Spatial–temporal correlations of air pollutants.	An adaptive adjacency matrix-based graph convolutional recurrent network (AAMGCRN) and LSTM.	Hourly multi-step
Cheng and Fan [49]	PM2.5, PM10, SO2	Long-term PM2.5 concentrations prediction and impact health.	Spatial–temporal synchronous graph convolutional network (STSGCN).	Hourly multi-step
Ehteram, Najah Ahmed [50]	Ozone (O3)	Difficult and complex to predict ozone concentration.	Graph convolutional network (GCN), LSTM, MLP, Gaussian progress models (GPR), and convolutional neural network (CNN).	MAE
Gao, Mo [51]	PM2.5 concentrations	Neglecting the dual needs for accuracy and stability in PM2.5 forecast.	LSTM, GCN, transformer, and graph sample and aggregation network (GraphSAGE).	-
Kunar and Nithish [52]	PM2.5	Air quality prediction.	Graph convolutional networks (GCNs), and bidirectional long short-term memory (Bi-LSTM).	MAE, MSE, RMSE
Mao, Jiao [53]	PM2.5, PM10, O3, CO, SO2, and NO2	Complexity and differences in spatiotemporal changes for air pollution.	Graph convolutional temporal sliding long short-term memory (GT-LSTM) model to predict next 24 h.	-
Muthukumar, Cocom [54]	Air pollution (nitrogen dioxide)	Patterns and sources of air pollutant advance concentration prediction.	Graph convolutional network combined with deep convolutional LSTM.	-
Zhao, Liu [55]	PM2.5	PM2.5 forecasting.	Combines GCN with LSTM.	-

presents a summary of the models and their challenges.

Table 5 shows that several spatiotemporal models have been employed to address various challenges including traffic and air pollutant predictions. The challenge with spatiotemporal prediction is the non-Euclidean nature, suggesting that the relationship between data points depends not only on physical proximity but also on topological networks like road networks or meteorological dependencies. Furthermore, the time-varying nature of data captured in geospace introduces complexity which traditional machine learning models are challenged by. In view of this limitation, deep learning models have effectively handled such spatial and temporal complexities. For instance, the LSTM model has been employed to address the time-varying correlations within location data. Again, graph convolutional network (GCN)-LSTM-MLP-GPR has also been leveraged to predict ozone concentration. Graph convolutional networks (GCNs) and the Bi-LSTM model have also been leveraged to predict PM_2.5. Furthermore, Zhao, Liu [55] combined GCN with LSTM to extract both spatial and temporal correlations to predict the PM_2.5 concentration level. Wang and Zhu [43] proposed the adaptive graph and hypergraph generation methods to interpret edge weights and learned high-order geographic relationships. While air quality prediction with geospatial artificial intelligence (GeoAI) is an emerging research field [44], the complexity and time-varying nature of air pollutants suggest that at each time, knowing the hotspot of air pollutant could inform people so that the best navigation path is provided by the GeoAI model which we are proposing.

3.3. Geospatial Path Navigation Strategies

Path navigation describes an ordered path for a user to view so as to arrive at their destination. Path navigation is a search optimization problem with its inherent constraints including time and road network constraints. Classical search strategies help to find an optimal search from one node to another within given constraints such as cost, distance, and other environmental factors. Fusic, Kanagaraj [56] looked at finding a collision-free path for automated guided vehicles (AGVs) in an outdoor environment using satellite images with the classical optimization technique of the particle swarm optimization algorithm. Chen, Guo [57] attempted to overcome the lengthy search time in finding an optimal path with the traditional A* search method combined with the traditional ant colony search for a dynamic navigation path search. It was suggested that the A* algorithm speeds up the search and elevates the precision of the local optimum search. Yang [58] compared A* with the classical Dijkstra’s algorithm and suggested that A* search is faster in local search with a smaller storage space and less time complexity. In this regard, the A* search algorithm is one of the most effective heuristic search algorithms for path optimization.

AI-driven path navigation strategies have also contributed towards modeling robust predictive spatiotemporal models. These models predict the air pollutant level, which is then embedded into a routing decision. Example of AI-driven models for spatiotemporal prediction include GCN, convolutional LSTM (ConvLSTM), and LSTM. Thus, the routing decisions are ranked based on their impact.

In this study, we employ a graph convolutional network (GCN) in combination with a long short-term memory (LSTM) network. This design reflects the dual nature of the problem, where pollutant concentrations are influenced by both spatial dependencies across towns/monitoring stations and temporal dynamics driven by atmospheric processes.

The motivation behind the choice of GCN and LSTM stems from both a theoretical and a practical perspective. In terms of GCN, its design is more suitable in handing non-Euclidean data structures like graphs. Theoretically, it hinges on convolutional neural network structures that support graph operations. Practically, it leverages the existing road networks and the closeness of locations or spatial features. In terms of LSTM, the design is more based on learning sequential patterns and improving on learning over time using filters or gate mechanisms. Theoretically, it hinges on learning nonlinear characteristics of patterns and their long-term interdependencies. Practically, it is suitable for data that exhibit different seasons and meteorological cycles. Hybridizing these two architectures provides a robust unified structure to address spatial and temporal issues such that location data are combined with meteorological and environmental data to develop a robust predictive system. The rationale to choose GCN and LSTM as the proposed model is theoretically and practically grounded.

4. Materials and Methods

The method is based on a graph convolutional network and long short-term memory for spatial dependencies and temporal evolution learning. Additionally, the A star (A*) search algorithm was applied to compute the optimal or best path that avoids high-CO areas with A* CO-influenced weights. The predicted CO concentration is then indicated on the local map with its connecting locations. The choice to consider CO as the primary air pollutant for this study is motivated by the following: (a) The data availability gap existing within Northern Cape Province. (b) The methodological focus which aims to evaluate the feasibility of integrating the proposed model for air pollution navigation instead of privileging one air pollutant over another. Most importantly, the model can be extended to other equally common air pollutants as data quality improves. (c) CO serves as one of the useful indicators on incomplete combustion sources in traffic and wildfires in Northern Cape Province. Furthermore, given that deep learning models are combined with A* search, explaining the model’s internal structures offers trust and transparency to geospatial artificial intelligence researchers. In this regard, the LIME and SHAP techniques are implemented in this research to offer both local agnostic and global explanations to aid expert knowledge. Thus, the proposed model is referred as the GeoxAI-GCN-LSTM-A* model. With this model, the LSTM model trains per town, then predicts the CO concentration which is integrated into the spatial graph for A* routing. The phases of the proposed model are expressed as follows.

4.1. Dataset

In this study, the dataset was leveraged from the South African Air Quality Information System (SAAQIS) platform. As mentioned earlier (see Table 2), there was a lack of monthly recording of CO concentration. Furthermore, Table 3 also lacks spatial information and daily recording on some pollutants for the entire country. The statistical information recorded in terms of the average, minimum, and maximum values for each parameter that ranges within 8 h is presented in Table 2. To have substantial data for training, we synthesized 8 h daily data within this minimum and maximum range from 2008 to 2024 for Northern Cape Province. This statistical information based on Karoo was used as the baseline for data synthesis for the towns and city in the Northern Cape.

In this study, data preprocessing strategies were adopted including handling of missing values through mean imputation where no issue of missing value was identified, issuing outliers using the z-score, and feature normalization addressed using the MinMaxscaler. The data dimension was 16 columns by 208,889 rows.

To ensure synchronization of synthetic data with the limited observed data such that it approximates a real-world context, three procedures were followed to help develop a robust model: (a) An inter-variable correlation procedure ensured the preservation of the covariance which was achieved by the method of correlation and preserving sampling based on the empirical covariance matrix of the observed variables. In this regard, air pollutants and their meteorological variables retain a realistic dependency (for example, the co-variation between Wind_speed and CO). Therefore this procedure avoids the sampling of each variable independently. (b) Spatial heterogeneity ensured the sampled data were stratified according to town to show the pollutant distribution across the locations. Thus, the characteristics of the location were ensured. (c) Temporal autocorrelation helped to maintain the short-term temporal dependencies of the sample data. This was achieved through the use of block boot-strapping of subsequent observation, instead of independent random selection, to preserve lag-1 autocorrelation patterns. These procedures ensured that the synthetic dataset retained statistical, spatial, and temporal characteristics of the real observations, reducing the risk of unrealistic patterns.

To further strengthen the reliability of our results, we performed cross-validation checks. First, wherever real observations were available, we compared synthetic samples against observed distributions, finding strong alignment in mean, variance, and correlation structures. Second, robustness tests were conducted by training models on different ratios of real and synthetic data, which demonstrated stable performance and suggested that the model did not overfit artifacts from synthetic generation.

The dataset contained meteorological and air pollutant datasets. The land area is 372,889 km². Appendix A.1 show the cities and major towns in the Northern Cape. Kabanda [59] identified attributes of the spatial road network structure of Northern Cape Province and the centrality or closeness of cities using geometric and topology attributes to analyze the transportation planning that supports mobility in terms of driving, walking, and biking at different scales. The road infrastructure in the Northern Cape is composed of national (N) and regional (R) routes that connect cities and towns.

4.2. Input Layer

To fill this data gap, we applied a random sampling approach to fill this data gap so as to train the proposed model. Thus, the baseline average, minimum, and maximum recording was based on the May 2023 recorded values of CO concentration. The dataset on air pollutants and meteorological data consists of PM_2.5, PM₁₀, CO, O₃, SO₂, NO₂, NOx, NO, wind speed, ambient temperature, relative humidity, and solar radiation. The dataset on road network structures is presented in Appendix A.2, found in “OpenStreetMap”. Thus, we have geospatial data about streets and intersections, which are in the “GeoJSON” data format. These datasets were loaded as input into the proposed model for training and to build the graph network.

4.3. GCN-LSTM Model for CO Prediction

The GCN model is integrated with the LSTM model to form the GCN-LSTM model. The GCN layer(s) extracts the spatial features or correlation from graph structured data where information is aggregated from neighboring nodes. With respect to the graph, towns are represented as nodes and the edges between them as roads, with each edge’s weight determined by the CO concentration predicted in each town. Then, the dynamic edge weights dynamically adjust the edge weights (CO levels) based on real-time predictions. Afterwards, the graph representation stores the towns as nodes, with edges weighted by CO concentration in each town. In this regard, to model the spatiotemporal dynamics of CO across a graph, we assume the graph G = (V, E) to be a weighted graph where

• V is the set of locations (nodes).
• E: Edges indicating spatial proximity (e.g., road links, geographic neighbors), $E\subseteq V\times V$ is the set of edges representing the possible paths.
• $X_t\in R^{N\times F}$: Node feature matrix at time t with

  ○

  N: Number of nodes.

  ○

  F: Number of input features (NO₂, NO, PM_2.5, etc.).

• $A\in {\mathbb{R}}^{N\times N}$: Adjacency matrix representing graph structure.

For the spatial learning, the graph convolution network (GCN) is expressed, where each input $X_t$ is passed through a graph convolutional layer ${\mathrm{H}}_{\mathrm{t}}$ by Equation (1):

$${\mathrm{H}}_t=\mathsf{\sigma }\left({\tilde{\mathrm{D}}}^{-{\displaystyle \frac{1}{2}}}{\tilde{\mathrm{A}}\tilde{\mathrm{D}}}^{-{\displaystyle \frac{1}{2}}}{\mathrm{X}}_t{\mathrm{W}}_g\right)$$

(1)

where

• $\tilde{A}=A+I$: Adjacency matrix with self-loops.
• $\tilde{\mathrm{D}}$: Degree matrix of $\tilde{A}$.
• ${\tilde{\mathrm{D}}}^{-{\displaystyle \frac{1}{2}}}$ is the symmetric normalization of the adjacency matrix, where the coefficient −1/2 is from the symmetric normalization of the graph. The rationale is to normalize the contribution of neighbors with a degree while preserving symmetry. The coefficient −1/2 ensures the operator is well-bounded.
• $W_g\in {\mathbb{R}}^{F\times F\mathrm{\text{'}}}$ is the learnable weight matrix for GCN.
• $H_t\in {\mathbb{R}}^{N\times F\mathrm{\text{'}}}$ is the spatial feature embedding at time t = 1, …, T.
• σ is the non-linear activation (e.g., ReLU).

In terms of temporal learning, the LSTM layer(s) processes the spatial features across multiple time steps to learn the temporal patterns. The time-evolving spatial features $H{=\mathrm{H}}_1,{\mathrm{H}}_2,\dots ,{\mathrm{H}}_T$ are fed into the LSTM layer for temporal dependency learning. Thus, the input sequence is expressed by Equation (2):

$$\mathrm{LSTM}:H\in {\mathbb{R}}^{T\times N\times F\mathrm{\text{'}}}$$

(2)

For each $v_1\in V$, the temporal evolution is expressed by Equation (3):

$$h_t^i,c_t^i=LSTM(H_t^i,h_{t-1}^i,c_{t-1}^i)$$

(3)

where $h_t^i\in {\mathbb{R}}^d$ represents the hidden state for node i, $c_t^i$ represents the cell state, and d represents the LSTM hidden dimension. The output layer for CO prediction at the final time step T is expressed by Equation (4):

$${\widehat{y}}_T^i=W_o{h}_T^i+b_o$$

(4)

where $y_T^i$ represents the predicted CO concentration for node i at time step T+1, $W_o\in {\mathbb{R}}^{d\times 1}$ represents the output layer weights, and $b_o\in \mathbb{R}$ represents the bias term.

The loss function during the training of the model is expressed using the mean squared error (MSE) between the predicted CO and the actual CO concentration. MSE is expressed by Equation (5):

$$\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left({{\widehat{y}}_T^i-y}_T^i\right)}^2$$

(5)

where N represents the total data points, T is the final time step, ${\widehat{y}}_T^i$ is the predicted CO concentration, and $y_T^i$ is the actual CO concentration.

4.4. A* Search with CO-Influence Weights

The A* search algorithm helps to efficiently navigate and find an optimal path through graph structures. In this context, A* search finds the optimal path considering the road network structure, predicted CO concentration (as edge weights), and distance between towns (in terms of coordinates). The algorithm searches for the optimal route from a start node (or town) to an end node (another town) using the predicted CO concentrations as weights and the Euclidean distance as the heuristic. The A* algorithm works by considering both the cost to reach a node (g(n)) and the estimated cost to the goal (h(n)). Thus, the following assumption underlines the A* search process:

• g(n) is the cost from the start node to the current node; in this case, the CO concentration at that town.
• h(n) is the heuristic estimate of the cost from the current node to the goal node. This is computed as the straight-line distance (Euclidean distance) between two towns.
• The A* algorithm assesses the cost from the current node n to the target node using the heuristic function, that is, to evaluate the path length between the two nodes.
• The following represent the steps for A* search:

• Step 1: Graph representation

• Let graph G = (V, E) be the weighted graph where V is the set of locations (nodes) and $E\subseteq V\times V$ is the set of edges representing the possible paths.
• Each edge $e_{ij}\in E$ has

  ○

  A geographical distance $d_{ij}$;

  ○

  A predicted CO concentration $c_{ij}$ associated with node j or averaged over (i, j).

• Step 2: A* evaluationfunction

For each node n, compute in Equation (6)

$$f\left(n\right)=g\left(n\right)+h\left(n\right)$$

(6)

where g(n) represents the actual cost from the start to n, and h(n) represents the heuristic estimated distance from n to the goal (heuristic, such as Euclidean distance).

• Step 3: CO-influenceedgeweight

Define a CO-augmented edge cost in Equation (7).

$$w_{ij}=\alpha ·d_{ij}+\beta ·c_{ij}$$

(7)

where α is the weighting coefficient for physical distance, β is the weighting coefficient for CO pollution (e.g., to penalize high pollution), $c_{ij}$ represents the predicted CO value at or between nodes i and j, $w_{ij}$ is the final cost for traversing edge (i, j), and $d_{ij}$ is the distance between (i, j).

• Step 4: g(n) function

Let $g\left(n\right)=[v_0,v_1,\dots v_n]$ represent the path from the start node n to another node as presented in Equation (8).

$$g\left(n\right)={\sum }_{i=0}^{n-1}{w}_{i,i+1}={\sum }_{i=0}^{n-1}(\alpha ·d_{i,i+1}+\beta ·c_{i,i+1})$$

(8)

• Step 5: Heuristic function h(n)

For the spatial graph h(n), the Euclidean distance (n, goal) is expressed by Equation (9).

$$h\left(n\right)=\sqrt{{\left(x_n-x_g\right)}^2+{\left(y_n-y_g\right)}^2}$$

(9)

In choosing weights, if avoiding CO is critical (set β > α), and for the shortest path regardless of pollution (set α >> β), normalize the distance and predicted CO concentration to similar ranges for meaningful weight tuning.

4.5. GeoXAI: SHAP and LIME

The SHAP model explanation is expressed in Equation (10), and for a model f and an input x, the SHAP $f\left(x\right)$ explanation for node i’s prediction is given in Equation (10):

$$f\left(x\right)={\mathsf{\varphi }}_0+{\sum }_{j=1}^{T-F}{\varphi }_j^i$$

(10)

where ${\mathsf{\varphi }}_0$ represents the model output with no input features, ${\mathsf{\varphi }}_j^i$ is the SHAP value of the feature j (at some time step) from node i, and each ${\mathsf{\varphi }}_j^i$ reflects the contribution of features j (e.g., CO, PM_2.5, etc.) at a particular time step to the prediction at location i. In terms of SHAP within space–time, for spatial SHAP, we aggregated ${\mathsf{\varphi }}_j^i$ over time to see feature importance per location. Furthermore, for temporal SHAP we aggregated ${\mathsf{\varphi }}_j^i$ across nodes to see the importance per time step.

The LIME model explanation is expressed by Equation (11), where LIME approximates a complex model $f\left(\right)$ near an instance x with a simple interpretable model $g\left(\right).$

$$LIME\left(x\right)=\mathit{arg}\underset{g\in G}{\mathit{min}}\mathcal{L}\left(f,g,{\pi }_x\right)+\Omega \left(g\right)$$

(11)

where G represents the family of simple (that is, linear regression) interpretable models, $\mathcal{L}$ is the loss function that measures how well g approximates f locally, ${\mathsf{\pi }}_x$ represents a locality measure around input x, and $\Omega \left(\mathrm{g}\right)$ represents a complexity penalty on the explanation model g. In terms of LIME in space–time, the input features were perturbed at different times and nodes, and then we observed the change in prediction. Afterwards, we fit a simple model (that is, linear regression) to map feature changes to their output as in Equation (12):

$$f\left(x\right)\approx g{\left(x\right)}_i=w_0+{\sum }_{j=1}^{T.F}{w}_j{x}_j$$

(12)

where weight w_j indicates the importance of feature j in predicting CO at node i. Thus, LIME was adopted in this paper.

4.6. Model Evaluation

The model was evaluated in multiple time steps (M) with mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE). The multi-time step represents the data from M number of previous days used for model training. The MSE is expressed in Equation (13).

$$\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(y_i-\overline{y}\right)}^2$$

(13)

where $\overline{y}$ is the predicted value from the model and $y_i$ is the actual value of the target pollutant. The interpretation is that a lower MSE value means a better model, and a higher MSE suggests the model is worse. MSE equal to zero means the model’s prediction is perfect. RMSE is expressed in Equation (14).

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{MSE}$$

(14)

4.7. Uncertainty Estimation

Let the predicted CO concentration be ${\widehat{y}}_{t+1|t}$ for each edge/town node. Uncertainty is modeled with aleatoric (data noise) and Monte Carlo dropout components.

Aleatoric:

$$\mathcal{L}={\displaystyle \frac{1}{2}}\sum _i[\mathit{log}{\sigma }_{\theta }^2\left(x_i\right)+{\displaystyle \frac{{\left(y_i-{\mu }_{\theta }\left(x_i\right)\right)}^2}{{\sigma }_{\theta }^2\left(x_i\right)}}]$$

(15)

Monte Carlo dropout:

$${{\{\widehat{y}}^{\left(s\right)}\}}_{s=1}^S⟹\widehat{\mu }={\displaystyle \frac{1}{S}}{\sum }_s{\widehat{y}}^{\left(s\right)}$$

(16)

$${\widehat{\sigma }}^2={\displaystyle \frac{1}{S-1}}{\sum }_s{{(\widehat{y}}^{\left(s\right)}-\widehat{\mu })}^2$$

(17)

where ${\widehat{\sigma }}^2$ represents the standard deviation, $\widehat{\mu }$ is the mean, $\widehat{y}$ is the observed value, and S is the drawn stochastic forward pass.

4.8. Model Parameter Description

Build the Navigation Graph: Each node = location (e.g., GPS point, street segment); each edge = possible route (e.g., road, trail, path). The data split was 20% (test) and 80% (training).

Table 6. Hyperparameters.

Model	Parameter Values
LSTM	Hidden units = 128; Batch size = 32
GCN	Hidden units = 64
Learning rate	0.001
Network structure	Name of location, geometry, type of road, etc.
Multi-time step	M: 8, 16
Start node	City: Kimberley
End node	Kuruman

presents the hyperparameters.

Table 7. Model architecture.

Layer (Type)	Output Shape	Param #	Connected to
Node_features (InputLayer)	(None, 100, 10)	0	-
Adjacency_matrix (InputLayer)	(None, 100, 100)	0	-
Graph_conv_1 (GraphConvolution)	[(None, 100, 32), (None, 100, 100)]	352	Node_features [0]_ adjacency_matrix_
Dropout_1 (Dropout)	(None, 100, 32)	0	graph_conv_1 [0][0]
Graph_conv_2 (GraphConvolution)	[(None, 100, 16), (None, 100, 100)]	528	dropout_1 [0][0], graph_conv_1 [0][0]
Dropout_2 (Dropout)	(None, 100, 16)	0	graph_conv_2 [0][0]
Output_layer (Dense)	(None, 100, 1)	17	dropout_2 [0][0]

shows the model architecture consisting of the layers, output shape, and parameters.

Figure 2 depicts the flowchart of the GeoxAI-GCN-LSTM-A* search model for CO concentration prediction.

5. Results

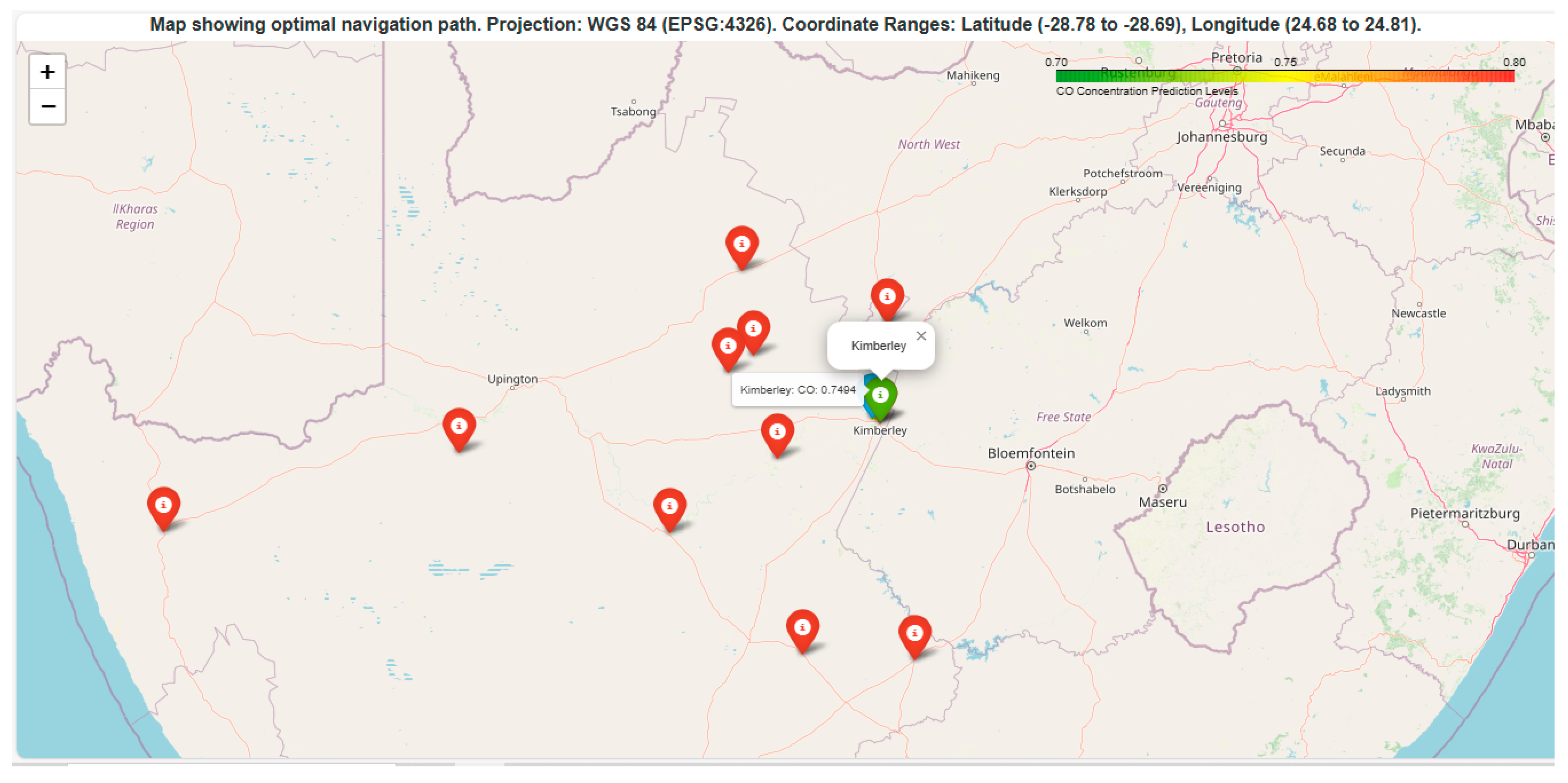
The “OSMnx” library was used to generate the road network graph “networkx.MultiDiGraph” for deriving and extracting the main network connecting the target towns to ensure it is routable. Here, the target location is “Kimberley” and the start location is Kuruman. And we compute the A* path using the “Networkx” to plot the map. The predicted CO concentration is added as a weight. Figure 3 shows the extracted map with its latitude and longitudinal data. The library to support the implementation of the A* search is “OSMnx + NetworkX”.

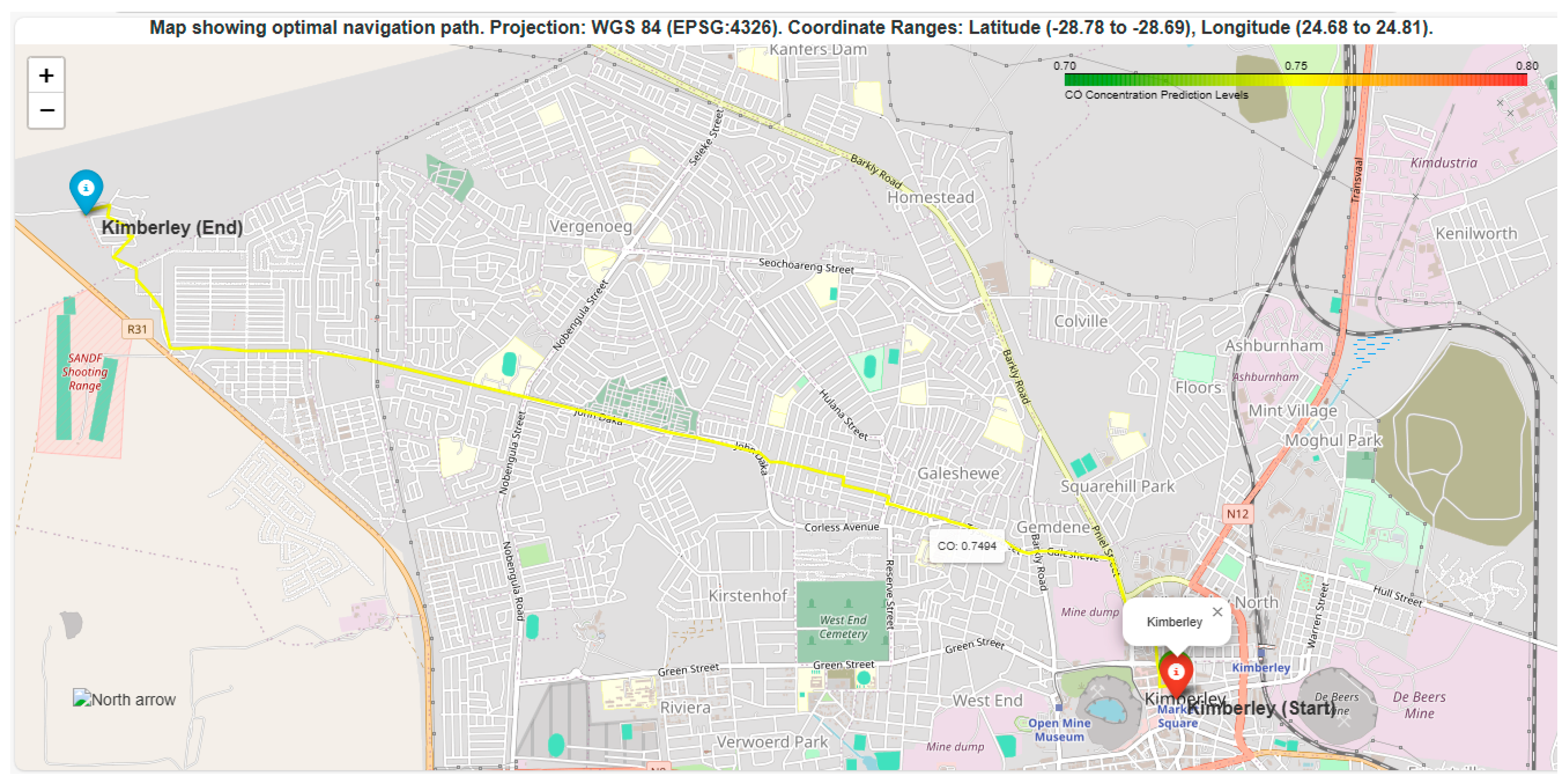
The GCN-LSTM model’s prediction using different time steps such as 8- and 16-hour time steps was assessed to gain insight into the prediction using the GCN-LSTM model. Figure A1 (Appendix B) show the plot of location on the map of the Northern Cape, with the optimal path shown in “red” on the map. Figure A2 and Figure A3 (Appendix B) show the navigation paths that have less CO prediction from the start city/node of Kimberley and the end node/town (that is, Kuruman) for both 8 h and 16 h time steps.

Table 8. Multi-time step results of GCN-LSTM-A* model.

Multi-Time Step	Model Loss	RMSE	MSE	Prediction
8 h	0.0046	0.4059	0.1648	0.69
16 h	0.0825	0.4124	0.1701	0.74

shows the performance metrics for the different time steps for predictions on the road network focusing on Kimberley to Kuruman.

Geospatial explainable AI based on LIME is provided in Figure 4. This shows the features that contribute to CO prediction.

Figure 4 shows the LIME explanation. Basically, the LIME value indicates how much the feature, in this specific case, pushed the prediction up or down. Thus, it can be observed that features on the negative side of the vertical line have LIME values that decrease the CO prediction. On the other hand, the features on the positive side increase the CO prediction.

To evaluate whether the synthetic data adequately captured the structure of the observed dataset adequately, the experiment was conducted on the temporal autocorrelation, spatial autocorrelation with Moran’s I values, and inter-variable dependencies.

Table 9. Spatial autocorrelation with Moran’s I (synthetic CO).

Variable	Value
I	0.00097
p-value	0.152
Expected I	−4.787 × 10−6
Variable (Simulated)	1.068 × 10−6
z-score (Simulated)	0.966

shows the spatial autocorrelation with Moran’s I.

Table 9 shows the explanation of Moran’s I and spatial autocorrelation. Moran’s I is a measure of spatial autocorrelation which describes the degree to which nearby locations have similar values. It is observed that a positive Moran’s I value was guaranteed, indicating a positive spatial autocorrelation (that is, clustering of similar values). Again, the synthetic CO Moran’s I shows a computed Moran’s I of approximately 0.0010 and a p-value of 0.1520, which is greater than the significance level of 0.05, indicating that the observed spatial pattern is not statistically significant. Therefore, it cannot be concluded that there is significant spatial autocorrelation in the synthetic CO data.

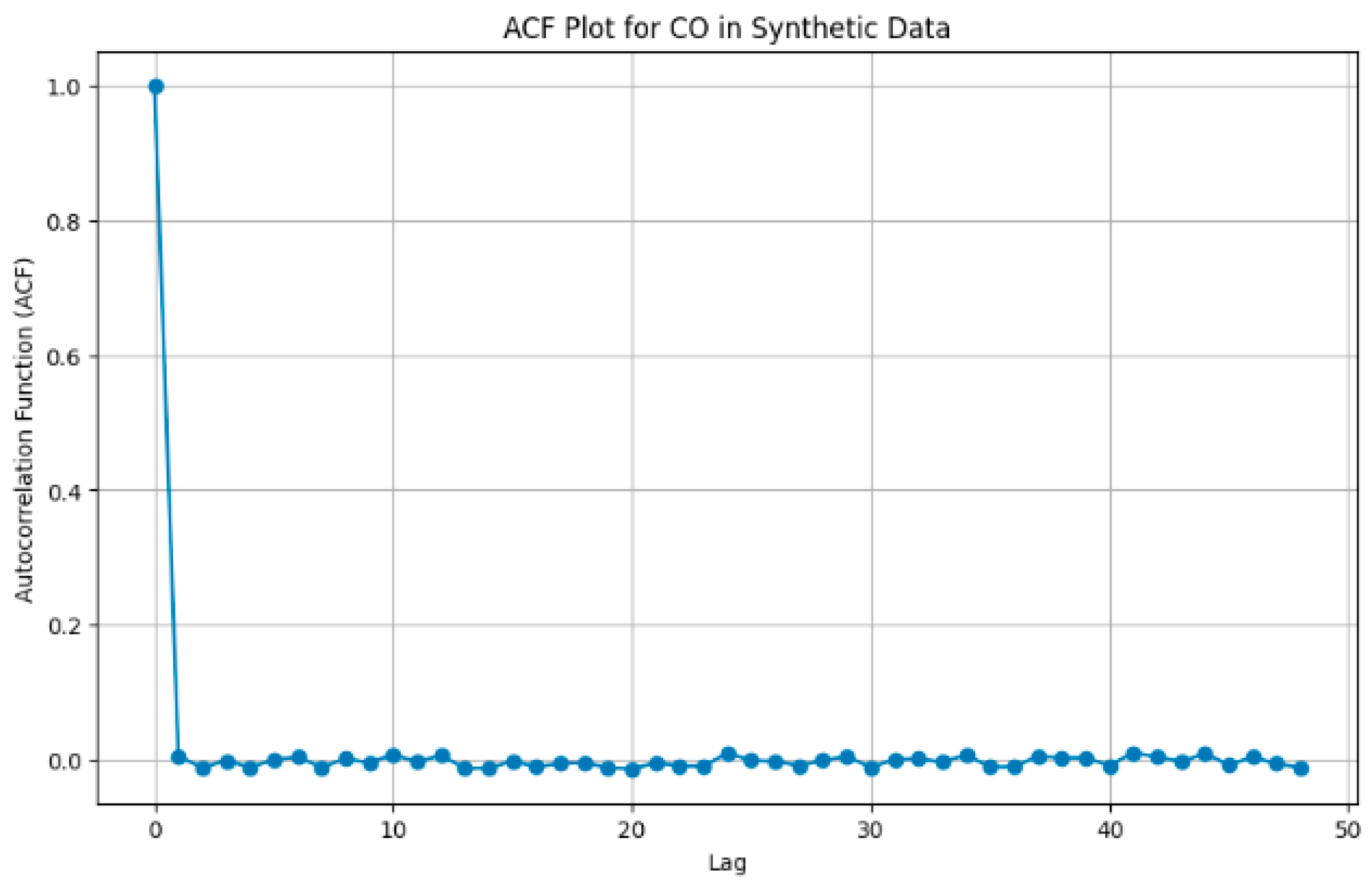
Figure 5 shows the temporal autocorrelation plot of CO concentration in the synthetic dataset. It shows 48 lags for 8 h data over approximately 16 days. It is observed that the autocorrelation function (ACF) plot for CO concentration in the synthetic data (e.g., Kimberley) indicates a significant positive autocorrelation at lag 1, which sharply drops to near zero for subsequent lags. This suggests that the CO concentration at a given time is positively correlated with the concentration in the immediately preceding 8 h interval; however, this correlation reduces rapidly over longer periods. Again, it suggests that values are influenced by immediate past data.

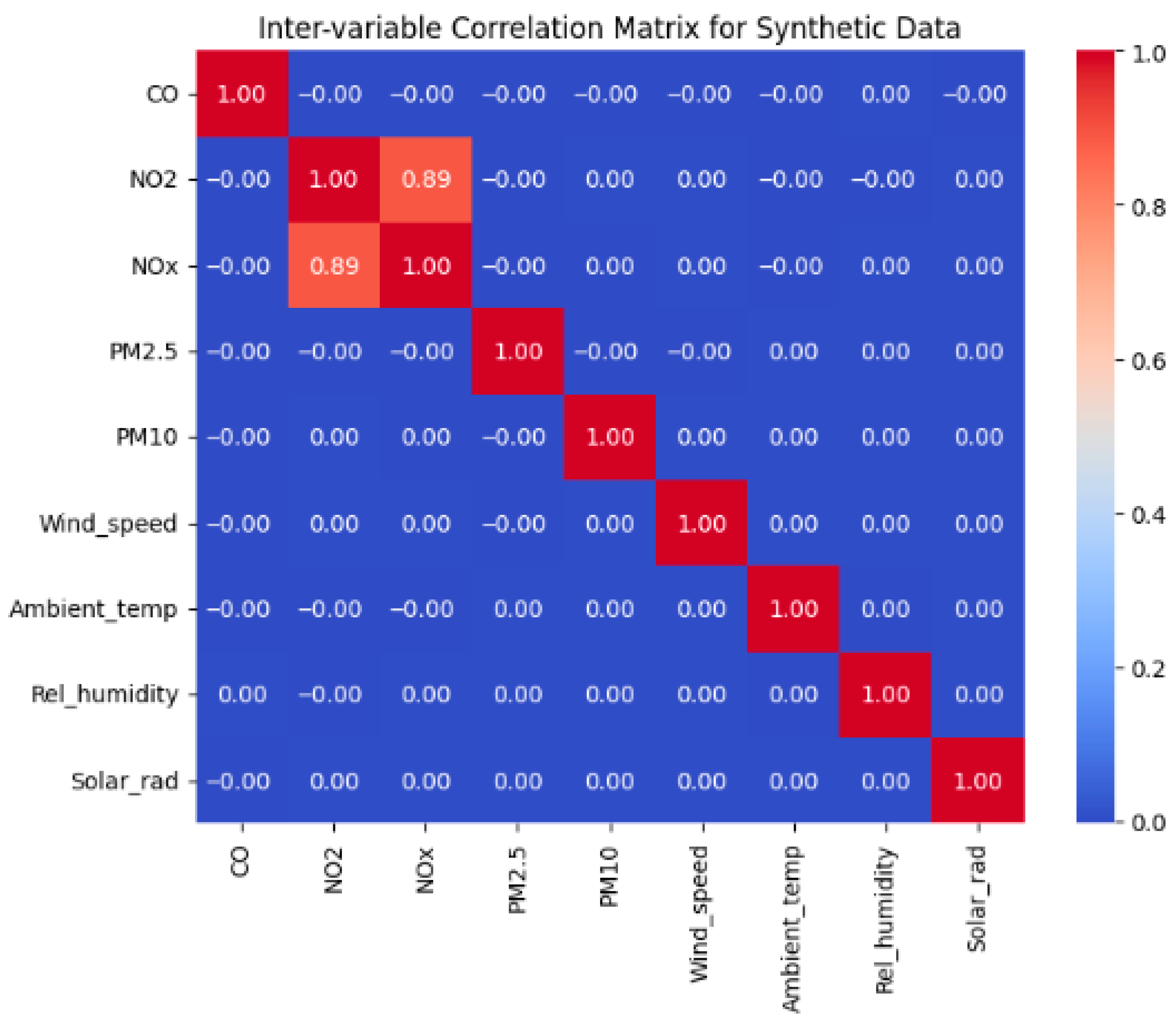
Figure 6 shows the inter-variable dependencies of air pollutants and meteorological variables. The correlation heatmap shows the correlation coefficients between different pollutants and meteorological variables in the synthetic data. It can be observed that the synthetic data revealed a strong positive linear correlation, for example, between ‘NO₂’ and ‘NOx’ (approximately 0.89), which is scientifically expected. However, most paired variables show very weak linear correlations (values close to zero). Thus, there are no strong linear dependencies, for instance, between CO and the other pollutants or meteorological variables, aside from the relationship between NO₂ and NOx.

Uncertainty estimation in the route for each location is presented for each town (

Table 10. Uncertainty estimation with Monte Carlo.

Town	Predicted CO (Mean)	Uncertainty (Std Dev)
Colesberg	0.6981	0.0600
Danielskuil	0.7176	0.0552
De Aar	0.8181	0.0595
Douglas	0.7551	0.0753
Jan Kempdorp	0.8394	0.0591
Kakamas	0.7433	0.0516
Kimberley	0.8014	0.0579
Kuruman	0.7560	0.0542
Postmasburg	0.7595	0.0614
Prieska	0.7507	0.0502
Springbok	0.8609	0.0652

). It was observed that by using Monte Carlo dropout, the CO prediction mean and uncertainty were shown.

With respect to hyperparameter tuning, the results after the grid search showed the best loss of 0.0585 and the best parameters: ‘dropout_rate’ of 0.3, gcn_layers of 32, L2 regularization factor of 0.0001, and learning_rate of 0.01.

Ablation experiment results indicate baseline (best parameter) loss of 0.0585, No Dropout loss of 0.0503 (difference from baseline: −0.0083); ‘No L2 Regularization’ loss of 0.0796 (difference from baseline: 0.0211); ‘More GCN Layers (32, 16)’ loss: 0.0990 (difference from baseline: 0.0405); ‘Fewer GCN Layers (None)’ loss: NaN (difference from baseline: NaN). Thus, a positive difference from the baseline loss indicates that removing or modifying the component in that experiment led to worse performance, whereas a negative difference indicates improved performance (though this might suggest the baseline tuning was not exhaustive or the ablated component was detrimental). The magnitude of the difference quantifies the contribution of the ablated component to the model’s performance. The final performance of the GCN model shows RMSE (0.2834) and MAE (0.2603).

Sensitivity analysis is performed across different synthesized-data fractions, reporting mean performance and confidence intervals over multiple experiment runs subject to a confidence interval (CI) of 95%, which is the range where the true mean performance is likely to fall.

Table 11. Sensitivity analysis across experimental runs and folds.

Synthetic Data Proportion (Train)	Mean RMSE	95% CI RMSE	Mean MAE	95% CI MAE
0.2	0.424724	0.051660	0.391754	0.051658
0.5	0.420008	0.052997	0.392730	0.054272
0.8	0.452957	0.059384	0.419094	0.060274
1.0	0.446586	0.061659	0.411695	0.062064

shows the results of experiments across different proportions.

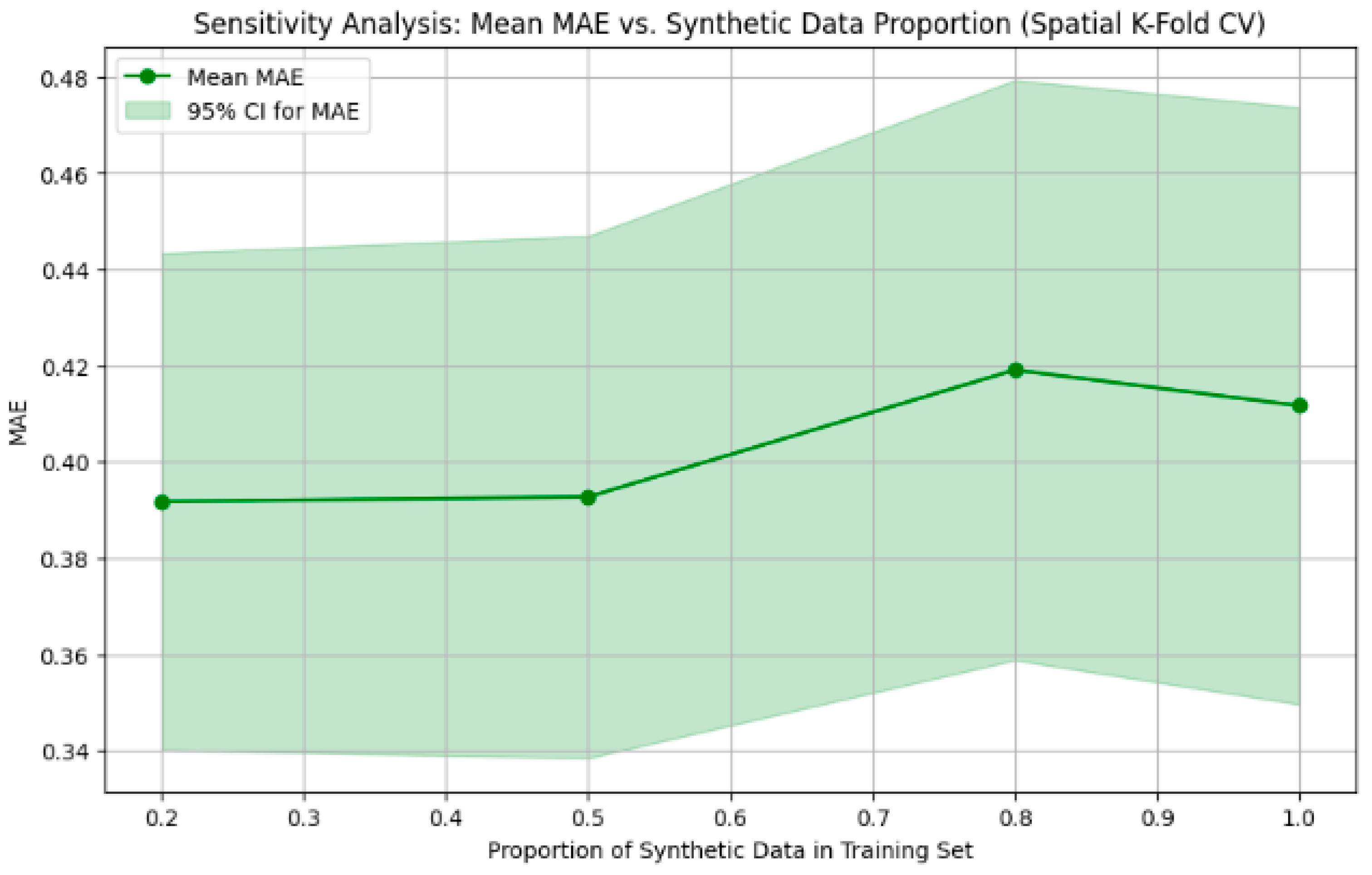
Table 11 presents the sensitivity analysis showing the average RMSE and MAE of the GCN model’s performance for different proportions of synthetic data included in the training set. By comparing the mean RMSE and MAE values across the different synthetic data proportions, we assess the influence of including varying samples of synthetic data on the model’s generalization performance. The deciding factor on the synthetic data proportion is having a smaller mean RMSE, which suggests a better performance. Hence, the least mean RMSE is approx. 0.42 which is between proportions 0.2 and 0.5. Figure 7 shows the sensitivity analysis results.

From Figure 7, it can be observed that the lowest mean RMSE (0.4200) is observed at a synthetic data proportion of 0.5, and the lowest mean MAE (0.3918) is observed at a synthetic data proportion of 0.2. It can be observed that the CIs for both RMSE and MAE overlap across different synthetic data proportions. This suggests that the observed differences in mean performance might not be statistically significant, given the number of experimental runs and folds. The width of the CI indicates variability in performance across different folds and experimental runs.

6. Discussion

The GCN-LSTM-A* model with xAI was developed and experimented with pollutant concentrations and meteorological datasets to predict CO concentration. Figure A2 and Figure A3 showed path navigation for 8 and 16 h time steps. The performance results showed MSE values of 0.1648 (8 h) and 0.1701 (16 h), respectively. Figure 4 presented the LIME values which showed that Wind_speed, NO₂, and NOx concentrations decreased the CO prediction, whereas PM_2.5, PM₁₀, relative humidity, and O₃ increase the CO prediction on the road path.

In this research, although the use of random sampling addresses the data limitation in terms of pollutant and meteorological data, future research should create a single pool that harmonizes a variable dataset from each location so that each point of location live data can be fed into GCN-LSTM-A* with the xAI model at 8 h time. In the event that time variability is required, our model can take into consideration this time variability as evident in the 16 h time prediction. Thus, the use of multi-time steps addresses the challenge of the time range. This means that if each location has different hours of data, the proposed model can dynamically address this. For instance, assuming location A requires 4 h prediction, and location B requires 8 h, then the proposed model can be deployed at a centralized location for the prediction. Afterwards, the predictions can be deployed to an end-user’s devices to aid in navigation decisions.

While synthetic data was leveraged for model training under sparse monitoring conditions, we caution against generalizing the findings as its application introduces some limitations in the real world. A reduction in long-term temporal autocorrelation using synthetic dataset suggests that the proposed model may learn patterns that are less reflective of true atmospheric persistence. Though the spatial characteristics of features were largely preserved, smoothing their effects could underestimate the fine-scaled heterogeneity across the towns in the Northern Cape. It is imperative to cautiously interpret the proposed model’s output and to avoid the limitation to overstate the physical representativeness. Furthermore, future work should consider enhancing the proposed model by testing it in other provinces in South Africa.

Due to the serial pipeline structure of the proposed model (GCN→LSTM→A*), there is a possibility of amplified bias from the top to the bottom streams of the pipeline. This was addressed with the Monte Carlo method and Aleatoric uncertainty during route planning (Table 10).

While Figure 7 and Table 11 present the sensitivity analyses, the results imply that under a stricter spatial K-Fold cross-validation strategy, when the proportion of synthetic data in increased in the training set, it does not consistently lead to improved model performance on unseen locations. Another implication is that the synthetic data may not fully capture the spatial dependencies that are necessary to help in generalizing the model to a new location. Furthermore, the performance variability in the CI indicates that generalizing the proposed model to an unseen location is largely influenced by the specific town.

Due to the limitations of the real-world dataset, the model’s ability to learn robust representations is very limited, even when supplemented with a synthetic dataset. Therefore, the reason for spatial K-Fold cross-validation is to ensure the model can generalize to entirely new locations, which is a challenging than temporal generalization or random splits. Verification on a larger real-world dataset is important to further improve confidence and provide a stronger empirical confirmation of our findings.

While Foroutan, Hu [14] used GeoShapley for spatial heterogeneity comprehension, our study focused on hotspot avoidance during open-air activities. Again, while Liu [16] integrated GeoShapley with ML, our study went a step further to consider deep learning models such as LSTM. The current trend to enhance the black-box nature of artificial intelligence models (Table 4) is the use of explainable AI models as demonstrated in this study. While Table 5 shows some of the graph-based models, future work that compares the proposed model with the models identified in Table 5 is recommended.

Though CO was chosen for practical demonstration in this study, the proposed model is generalizable to other air pollutants including PM_2.5 and NO₂, among others. To this end, the study developed a geospatial intelligence model (GIM) based on deep learning (graph convolutional network long short-term memory) to predict CO concentration. Having used the A* search method and xAI, we proposed a model that provides the best navigation path on road networks such that hotspots or locations with high CO concentration levels can be avoided. Furthermore, the features that contribute to the model’s behavior were also explained using the LIME technique.

7. Conclusions

This study proposed a GeoxAI-GCN-LSTM-A* search model that predicts CO concentration and offers the ideal navigation path. The road network structures for the provinces and air pollutant and meteorological data were used for this study. While acknowledging data scarcity in the province, a random sampling approach was adopted subject to the available provincial recording of the min and max values of air pollutants and meteorological data. The Centre for Global Change suggests the use of this model, although it cautions against model generalization and suggests that future work is focused on enhancing the model’s performance. Furthermore, the proposed model is generalizable to other air pollutants.