Forecasting 7Be Concentrations Using Time Series Analysis: A Case Study of Panama City
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description
- A 570 mm × 460 mm polypropylene filter (3M, Saint Paul, MN, USA).
- Collection efficiency of 99.99% for particles with a diameter equal to or greater than 0.4 μm and 85% for particles with a diameter between 0.15 and 0.4 μm, at a flow rate of 980 m3 h−1 [35].
2.2. Methodology
- Step 1:
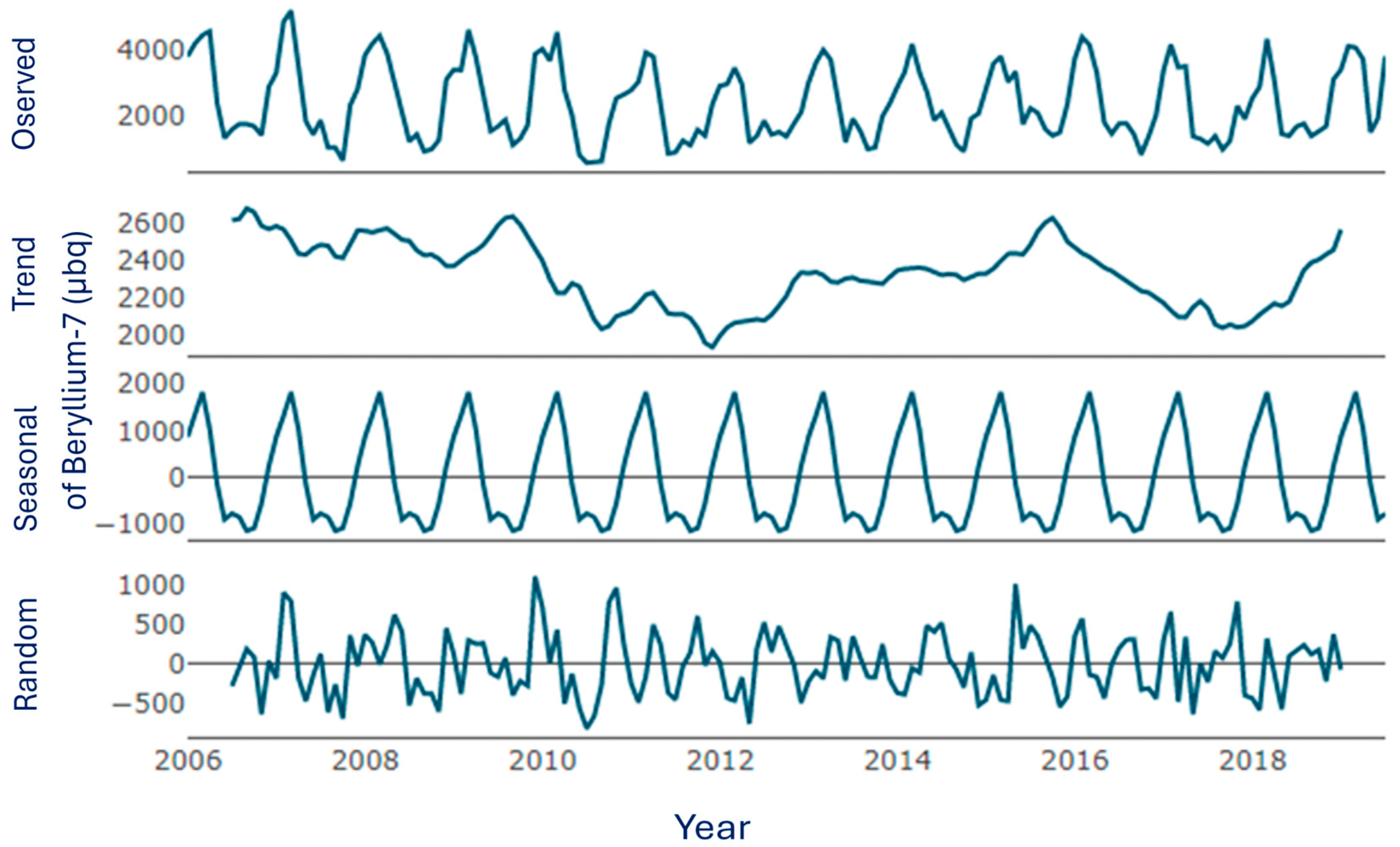
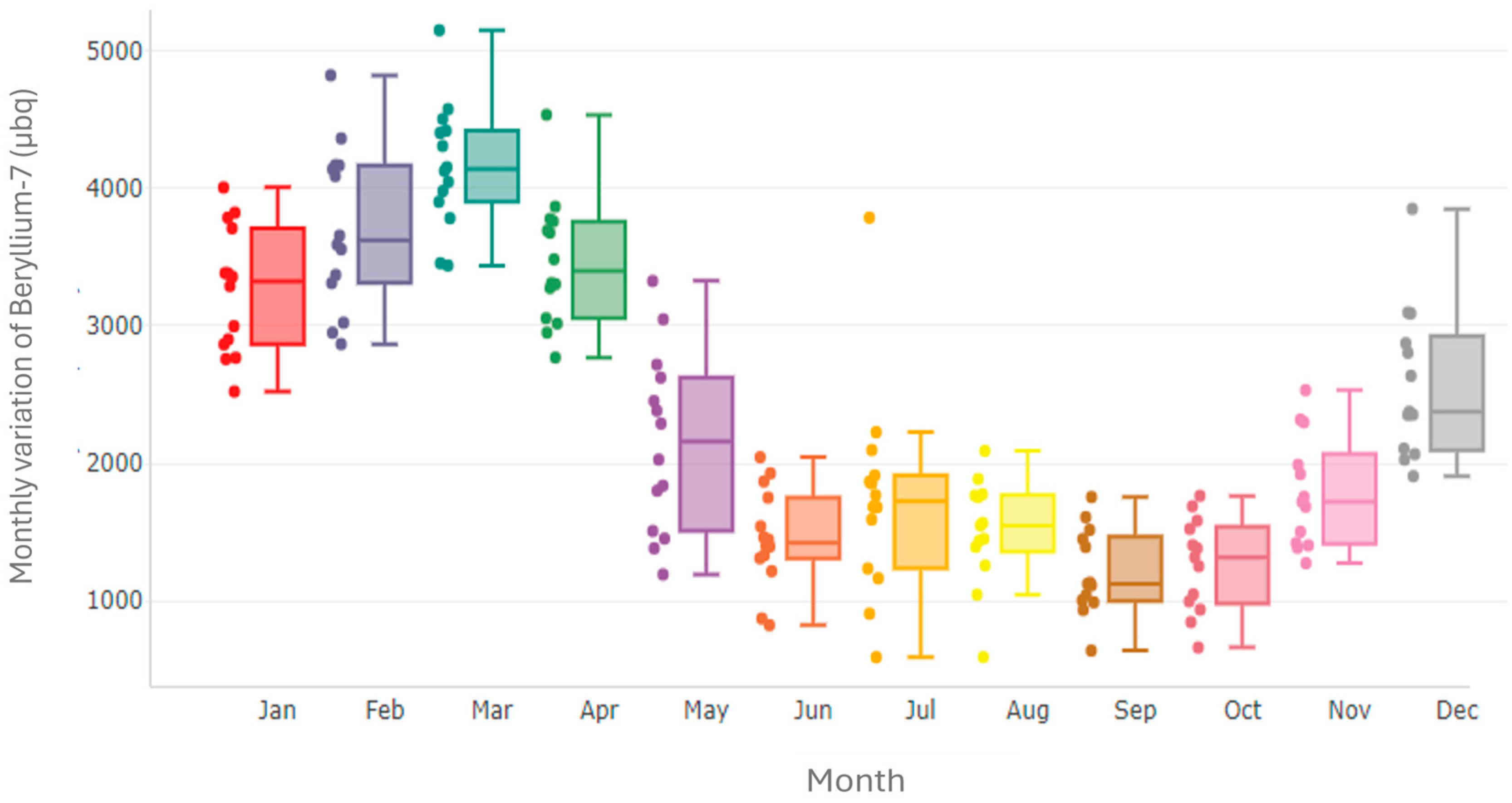
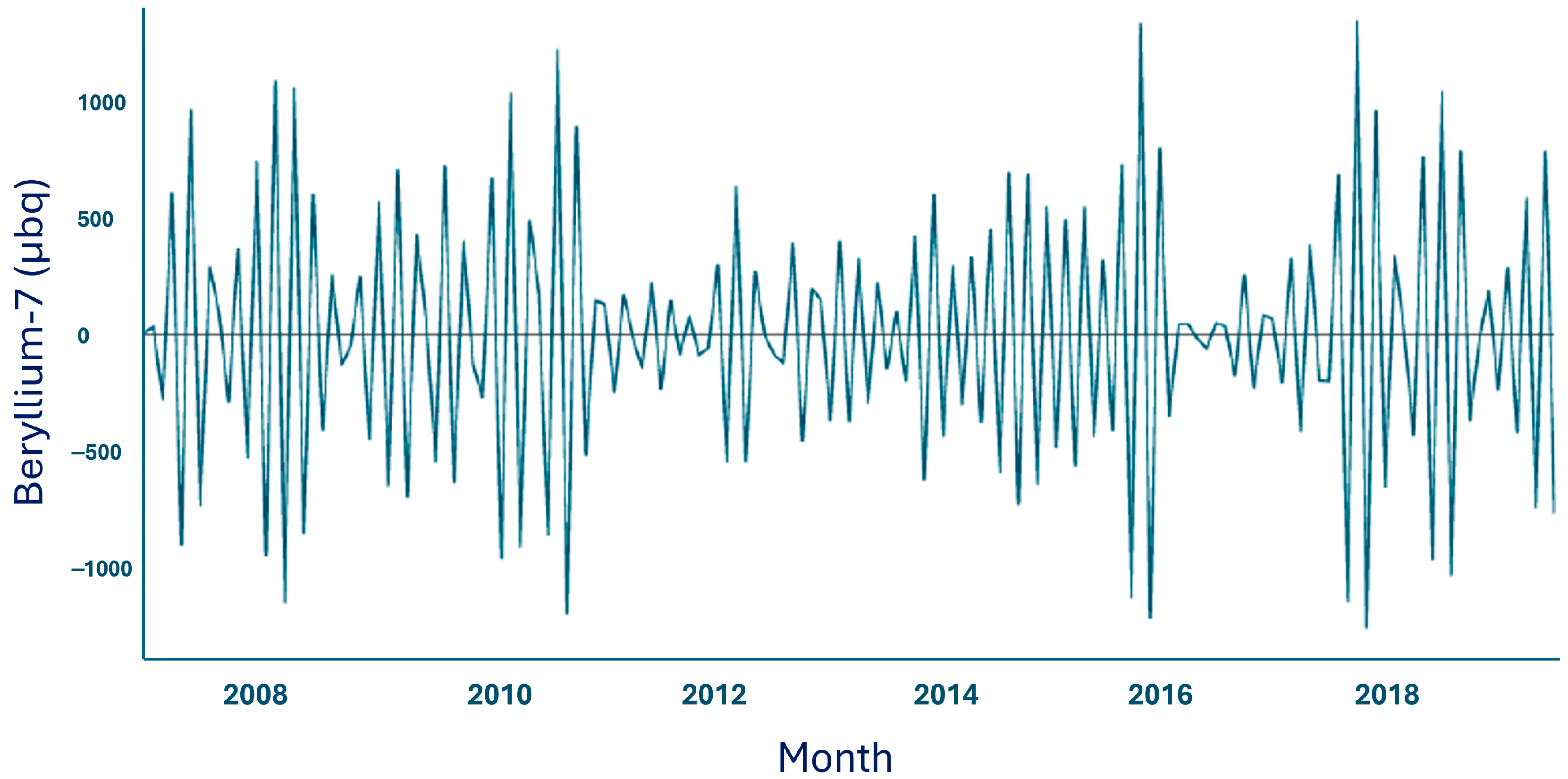
- The modeling begins with an exploratory analysis of the beryllium concentration time series, in order to identify patterns such as trends, seasonality, and irregularities. Visualization tools, statistical tests, and correlograms were employed.
- Step 2:
- The Dickey–Fuller test was applied to assess mean stationarity, and it was necessary to apply differencing to stabilize the seasonal component of the series.
- Step 3:
- At this stage, the Levene test was applied as a reference to explore the homogeneity of variance in the series. Since no significant differences were detected between temporal segments, the variance was considered stable, suggesting variance stationarity. Therefore, no additional transformations were necessary to stabilize it.
- Step 4:
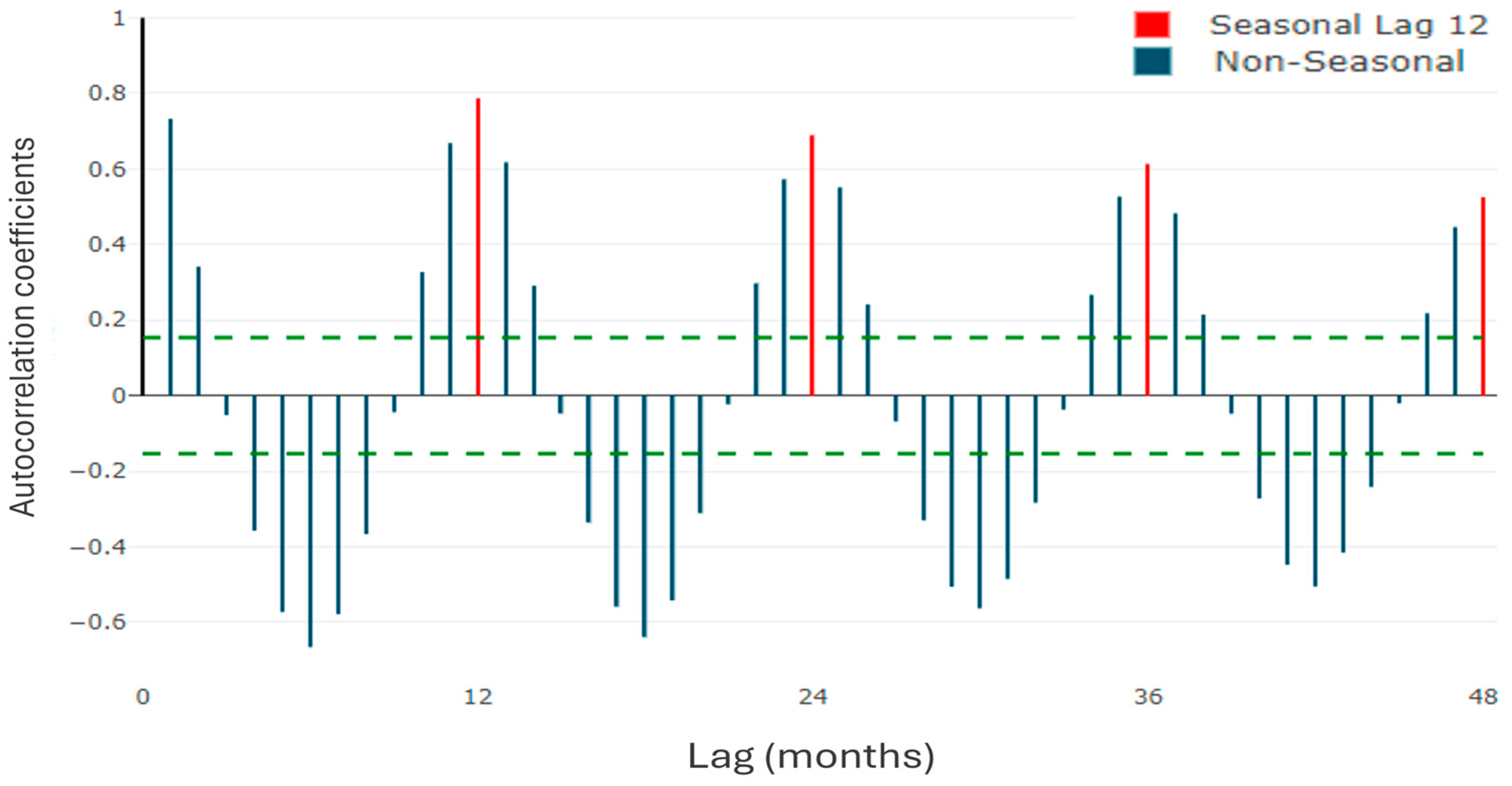
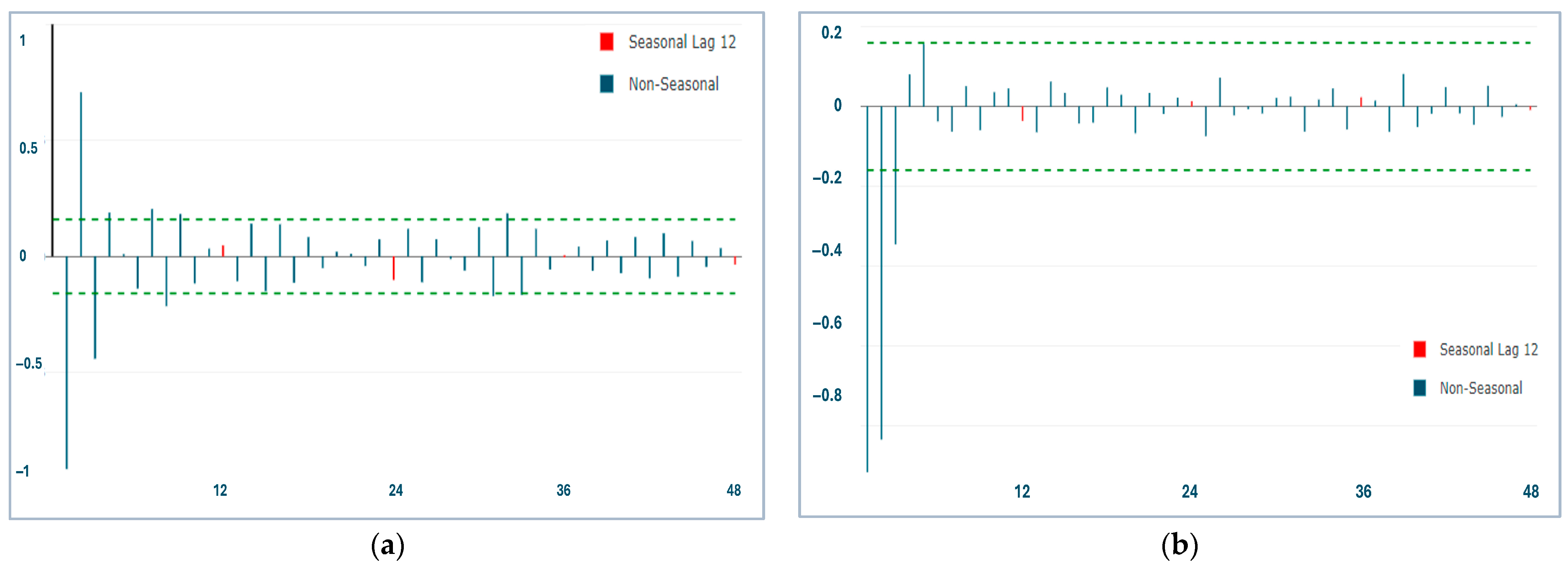
- To identify the SARIMA model parameters, the simple (ACF) and partial (PACF) correlograms were analyzed, which allowed establishing the initial values of the non-seasonal components (p, d, q) and seasonal components (P, D, Q).
- Step 5:
- Based on the structure observed in the correlograms and the results of the stationarity tests, different SARIMA model configurations were proposed, adjusting the parameters (p, d, q) (P, D, Q) to adequately capture the temporal dynamics of the beryllium series.
- Step 6:
- The performance of the models was evaluated using error metrics such as ME, RMSE, MAE, MAPE, and MASE, as detailed in Table 2.
- Step 7:
- The selected models were validated by verifying that their estimated parameters were statistically significant.
- Step 8:
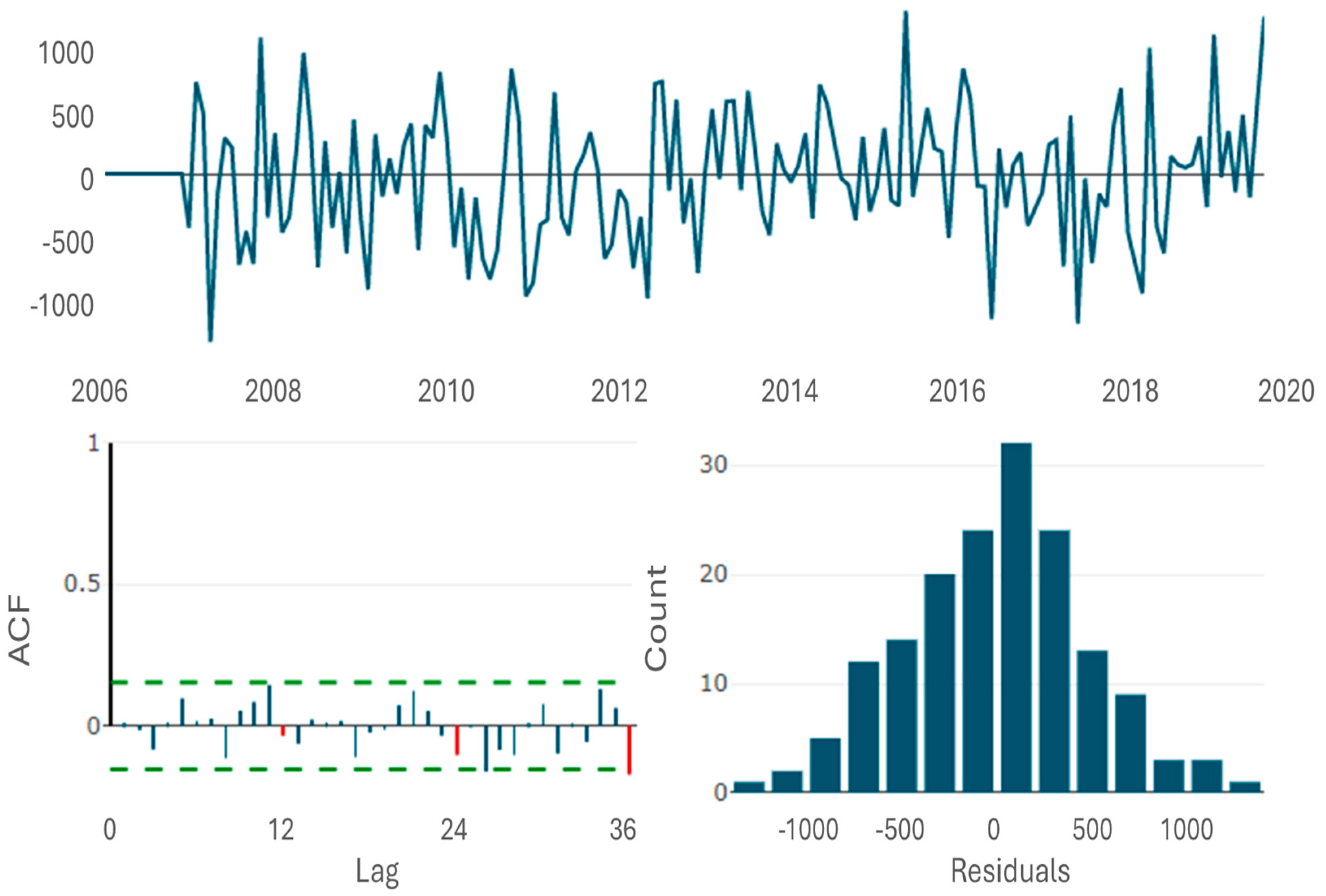
- The model’s performance was validated by checking that the residuals exhibited a white noise structure. Visualization tools and the Ljung–Box test were used.
- Step 9:
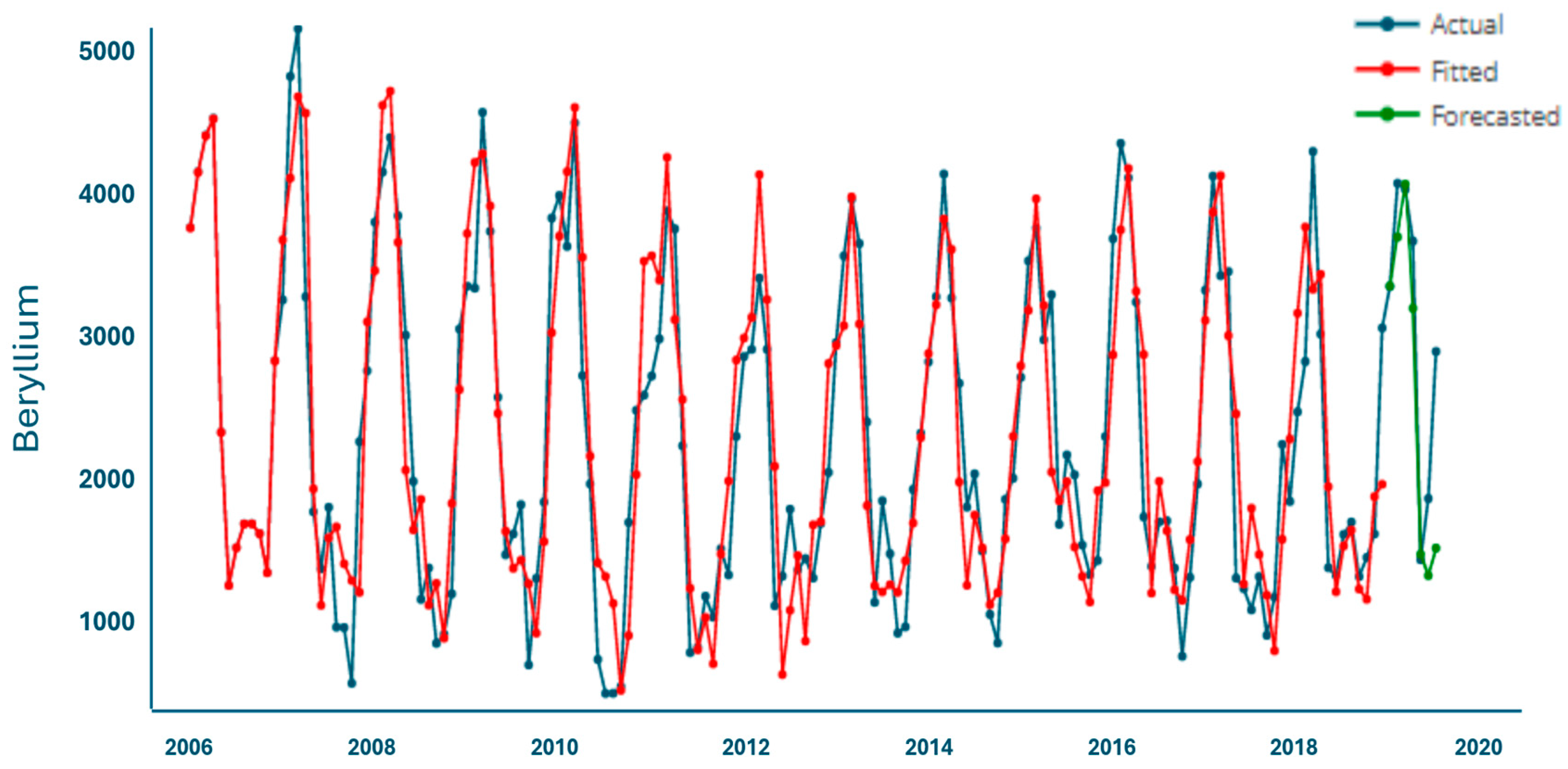
- Once the optimal model was selected, it was used to generate forecasts for the 7Be.
2.3. Error Metrics
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ren, X.; Luke, W.T.; Kelley, P.; Cohen, M.; Ngan, F.; Artz, R.; Walker, J.; Brooks, S.; Moore, C.; Swartzendruber, P.; et al. Mercury Speciation at a Coastal Site in the Northern Gulf of Mexico: Results from the Grand Bay Intensive Studies in Summer 2010 and Spring 2011. Atmosphere 2014, 5, 230–251. [Google Scholar] [CrossRef]
- Janković, M.M.; Todorović, D.J.; Nikolić, J.D.; Rajačić, M.M.; Pantelić, G.K.; Sarap, N.B. Aktivnost Berilijuma-7 i Olova-210 u Prizemnom Sloju Atmosfere u Srbiji. Hem. Ind. 2014, 68, 83–88. [Google Scholar] [CrossRef]
- Lal, D.; Peters, D. Cosmic Ray Produced Radioactivity on the Earth. In Kosmische Strahlung II/cosmic rays II; Springer: Berlin/Heidelberg, Germany, 1967; pp. 551–612. [Google Scholar]
- Kaste, J.M.; Norton, S.A. Environmental Chemistry of Beryllium-7. Rev. Miner. Geochem. 2002, 50, 271–289. [Google Scholar] [CrossRef]
- Yoshimori, M.; Hirayama, H. Production of 7Be Nuclei in the Earth’s Upper Atmosphere from Galactic Cosmic Rays and Solar Energetic Particles. In Proceedings of the 28th International Cosmic Ray Conference, Tsukuba, Japan, 31 July–7 August 2003. [Google Scholar]
- Papastefanou, C.; Ioannidou, A. Aerodynamic Size Association of 7Be in Ambient Aerosols. J. Environ. Radioact. 1995, 26, 273–282. [Google Scholar] [CrossRef]
- Lal, D.; Malhotra, P.K.; Peters, B. On the Production of Radioisotopes in the Atmosphere by Cosmic Radiation and Their Application to Meteorology. Atmos. Terr. Phys. 1958, 12, 306–328. [Google Scholar] [CrossRef]
- Bhandari, N.; Lal, D. Rama Vertical Structure of the Troposphere as Revealed by Radioactive Tracer Studies. J. Geophys. Res. 1970, 75, 2974–2980. [Google Scholar] [CrossRef]
- Cannizzaro, F.; Greco, G.; Raneli, M.; Spitale, M.C.; Tomarchio, E. Concentration Measurements of 7Be at Ground Level Air at Palermo, Italy—Comparison with Solar Activity over a Period of 21 Years. J. Env. Radioact. 2004, 72, 259–271. [Google Scholar] [CrossRef] [PubMed]
- Usoskin, I.G.; Bazilevskaya, G.A.; Kovaltsov, G.A. Solar Modulation Parameter for Cosmic Rays since 1936 Reconstructed from Ground-Based Neutron Monitors and Ionization Chambers. J. Geophys. Res. Space Phys. 2011, 116, A02104. [Google Scholar] [CrossRef]
- Nandy, D.; Martens, P.C.H.; Obridko, V.; Dash, S.; Georgieva, K. Solar Evolution and Extrema: Current State of Understanding of Long-Term Solar Variability and Its Planetary Impacts. Prog. Earth Planet. Sci. 2021, 8, 40. [Google Scholar] [CrossRef]
- Stozhkov, Y.; Makhmutov, V.; Svirzhevsky, N. About Cosmic Ray Modulation in the Heliosphere. Universe 2022, 8, 558. [Google Scholar] [CrossRef]
- Ioannidou, A.; Paatero, J. Activity Size Distribution and Residence Time of 7Be Aerosols in the Arctic Atmosphere. Atmos. Env. 2014, 88, 99–106. [Google Scholar] [CrossRef]
- Landis, J.D.; Feng, X.; Kaste, J.M.; Renshaw, C. Patterns and Processes in Aerosol Bulk Deposition: Insights from a 9-Year Study of 7Be, 210Pb, Sulfate and Major/Trace Elements. Authorea Prepr. 2022. [Google Scholar] [CrossRef]
- Alegría, N.; Hernández-Ceballos, M.Á.; Herranz, M.; Idoeta, R.; Legarda, F. Meteorological Factors Controlling 7Be Activity Concentrations in the Atmospheric Surface Layer in Northern Spain. Atmosphere 2020, 11, 1340. [Google Scholar] [CrossRef]
- You, C.F.; Lee, T.; Yi, Y.H. The Partition of Be between Soil and Water. Chem. Geol. 1989, 77, 105–118. [Google Scholar] [CrossRef]
- Ryken, N.; Al-Barri, B.; Blake, W.; Taylor, A. Rapid and Irreversible Sorption Behavior of 7Be Assessed to Evaluate Its Use as a Catchment Sediment Tracer. J. Env. Radioact. 2018, 182, 108–116. [Google Scholar] [CrossRef]
- Pérez, O.C.; Fernández, B.G. Trazadores Atmosféricos BE-7, K-40 Y PB-210 en la Ciudad de Panamá. Scientia 2019, 29, 44–67. [Google Scholar]
- Benchrif, A.; Khalfaoui, O.; Baghdad, B.; Jung, C.H.; Tahri, M.; Baghdad, B.; Bounakhla, M.; Cachier, H. Aerosols in Northern Morocco (Part 4): Seasonal Chemical Signatures of PM 2.5 and PM 10. Atmosphere 2025, 16, 982. [Google Scholar] [CrossRef]
- Olivares-Salazar, S.E.; Bahreini, R.; Lin, Y.H.; Castro, T.; Alvarez-Ospina, H.; Salcedo, D. Aerosol Composition in a Semi-Urban Environment in Central Mexico: Influence of Local and Regional Processes on Overall Composition and First Quantification of Nitroaromatics. Atmosphere 2025, 16, 827. [Google Scholar] [CrossRef]
- Guo, Q.; He, Z.; Wang, Z. The Characteristics of Air Quality Changes in Hohhot City in China and Their Relationship with Meteorological and Socio-Economic Factors. Aerosol Air Qual. Res. 2024, 24, 230274. [Google Scholar] [CrossRef]
- Papastefanou, C. Beryllium-7 Aerosols in Ambient Air. Aerosol Air Qual. Res. 2009, 9, 187–197. [Google Scholar] [CrossRef]
- Johnson, W.B.; Viezee, W. Stratospheric Ozone in the Lower Troposphere—I. Presentation and Interpretation of Aircraft Measurements. Atmos. Env. 1981, 15, 1309–1323. [Google Scholar] [CrossRef]
- Feely, H.; Larsen, R.; Sanderson, C.G. Factors That Cause Seasonal Variations in Beryllium-7 Concentrations in Surface Air. J. Env. Radioact. 1989, 9, 223–249. [Google Scholar] [CrossRef]
- Kremenchutskii, D.A. Influence of Precipitation on the Daily Beryllium-7 (7Be) Activity Concentration in the Atmospheric Surface Layer. J. Env. Radioact. 2021, 237, 106722. [Google Scholar] [CrossRef]
- Wallbrink, P.J.; Murray, A.S. Use of Fallout Radionuclides as Indicators of Erosion Processes. Hydrol. Process 1993, 7, 297–304. [Google Scholar] [CrossRef]
- Wallbrink, P.J.; Murray, A.S. Distribution and Variability of 7Be in Soils Under Different Surface Cover Conditions and Its Potential for Describing Soil Redistribution Processes. Water Resour. Res. 1996, 32, 467–476. [Google Scholar] [CrossRef]
- Blake, W.; Walling, D.; He, Q. Fallout Beryllium-7 as a Tracer in Soil Erosion Investigations. Elsevier 1999, 51, 599–605. [Google Scholar] [CrossRef]
- Schuller, P.; Iroumé, A.; Walling, D.E.; Mancilla, H.B.; Castillo, A.; Trumper, R.E. Use of Beryllium-7 to Document Soil Redistribution Following Forest Harvest Operations. J. Environ. Qual. 2006, 35, 1756–1763. [Google Scholar] [CrossRef]
- Yang, M.Y.; Walling, D.E.; Tian, J.L. Partitioning the Contributions of Sheet and Rill Erosion Using Beryllium-7 and Cesium-137. Soil. Sci. Soc. Am. J. 2006, 70, 1579–1590. [Google Scholar] [CrossRef]
- Saari, H.; Schmidt, S.; Castaing, P.; Blanc, G.; Sautour, B.; Masson, O.; Cochran, J.K. The Particulate 7Be/210Pbxs and 234Th/210Pbxs Activity Ratios as Tracers for Tidal-to-Seasonal Particle Dynamics in the Gironde Estuary (France): Implications for the Budget of Particle-Associated Contaminants. Sci. Total Environ. 2010, 408, 4784–4794. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lu, Y.; Nie, X.; Huang, B.; Ma, W.; Liu, C.; Xiao, H. Variability of Beryllium-7 and Its Potential for Documenting Soil and Soil Organic Carbon Redistribution by Erosion. Wiley Online Libr. 2016, 80, 693–703. [Google Scholar] [CrossRef]
- Martınez-Casasnovas, J.; Ramos, M.; Geoderma, M.R.-D. Soil Erosion Caused by Extreme Rainfall Events: Mapping and Quantification in Agricultural Plots from Very Detailed Digital Elevation Models. Geoderma 2002, 105, 125–140. [Google Scholar] [CrossRef]
- Fernández, B.; Juri Ayub, J.; Valladares, D.; Pérez, O.; Tejedor-Flores, N.; Esquivel-López, A. 7Be Atmospheric Concentration in Panama City: Influence of Climatic Conditions and Atmospheric Recovery Process. Isot. Env. Health Stud. 2025, 61, 351–370. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, G.M. Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1976. [Google Scholar]
- Ryabko, D. Asymptotic Nonparametric Statistical Analysis of Stationary Time Series; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Chintalapudi, N.; Battineni, G.; Amenta, F. COVID-19 Virus Outbreak Forecasting of Registered and Recovered Cases after Sixty Day Lockdown in Italy: A Data Driven Model Approach. J. Microbiol. Immunol. Infect. 2020, 53, 396–403. [Google Scholar] [CrossRef]
- Noor, T.H.; Almars, A.M.; Alwateer, M.; Almaliki, M.; Gad, I.; Atlam, E.S. SARIMA: A Seasonal Autoregressive Integrated Moving Average Model for Crime Analysis in Saudi Arabia. Electronics 2022, 11, 3986. [Google Scholar] [CrossRef]
- RStudio: Integrated Development for R, Version 4.2.1, [Computer Software]. RStudio PBC: Boston, MA, USA, 2020.
- Armstrong, J.S.; Collopy, F. Error Measures for Generalizing about Forecasting Methods: Empirical Comparisons. Int. J. Forecast. 1992, 8, 69–80. [Google Scholar] [CrossRef]
- St-Aubin, P.; Agard, B. Precision and Reliability of Forecasts Performance Metrics. Forecasting 2022, 4, 882–903. [Google Scholar] [CrossRef]
- Jierula, A.; Wang, S.; Oh, T.M.; Wang, P. Study on Accuracy Metrics for Evaluating the Predictions of Damage Locations in Deep Piles Using Artificial Neural Networks with Acoustic Emission Data. Appl. Sci. 2021, 11, 2314. [Google Scholar] [CrossRef]
- Yadav, B.K.; Srivastava, S.K.; Arasu, P.T.; Singh, P. Time Series Modeling of Tuberculosis Cases in India from 2017 to 2022 Based on the SARIMA-NNAR Hybrid Model. Can. J. Infect. Dis. Med. Microbiol. 2023, 2023, 5934552. [Google Scholar] [CrossRef] [PubMed]
- Cubilla-Montilla, M.; Ramírez, A.; Escudero, W.; Cruz, C. Analyzing and Forecasting Vessel Traffic Through the Panama Canal: A Comparative Study. Appl. Sci. 2025, 15, 8389. [Google Scholar] [CrossRef]
- Bas, M.d.C.; Ortiz, J.; Ballesteros, L.; Martorell, S. Evaluation of a Multiple Linear Regression Model and SARIMA Model in Forecasting 7Be Air Concentrations. Chemosphere 2017, 177, 326–333. [Google Scholar] [CrossRef]
- Bas, M.d.C.; Ortiz, J.; Ballesteros, L.; Martorell, S. Forecasting 7BE Concentrations in Surface Air Using Time Series Analysis. Atmos. Env. 2017, 155, 154–161. [Google Scholar] [CrossRef]
- Chham, E.; Piñero-García, F.; Brattich, E.; El Bardouni, T.; Ferro-García, M.A. 7Be Spatial and Temporal Pattern in Southwest of Europe (Spain): Evaluation of a Predictive Model. Chemosphere 2018, 205, 194–202. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, S.; Longo, A.; Plastino, W. A New Methodological Approach for Worldwide Beryllium-7 Time Series Analysis. Phys. A Stat. Mech. Its Appl. 2018, 501, 377–387. [Google Scholar] [CrossRef]
- Bianchi, S.; Plastino, W.; Brattich, E.; Djurdjevic, V.; Longo, A.; Hernández-Ceballos, M.A.; Sarvan, D.; Ajtić, J. Analysis of Trends, Periodicities, and Correlations in the Beryllium-7 Time Series in Northern Europe. Appl. Radiat. Isot. 2019, 148, 160–167. [Google Scholar] [CrossRef] [PubMed]
- Houali, A.; Azahra, M.; El Bardouni, T.; Ferro García, M.A.; Piňero García, F.; Chham, E. Impact of the Meteorological Parameters on the Behaviour of 7Be at Ground Level in Tetouan City, Morocco from June 2015 to February 2017. J. Radioanal. Nucl. Chem. 2019, 322, 271–280. [Google Scholar] [CrossRef]



| Variable | Definition |
|---|---|
| Beryllium-7 | Airborne particulate matter (PM10) samples were collected, and particulate analysis provided monthly measurements of Beryllium-7. |
| Year | Study period in years for Beryllium-7 concentrations: from 2006 to 2019. |
| Month | Study period (months) of Beryllium-7 concentrations: January 2006–July 2019. |
| Metric | Formula | Description |
|---|---|---|
| ME (Mean Error) | Measures the average deviation between predicted and observed values. | |
| RMSE (Root Mean Squared Error) | Provides information about the overall prediction accuracy. | |
| MAE (Mean Absolute Error) | Captures the average magnitude of errors, regardless of direction. | |
| MPE (Mean Percentage Error) | Indicates the average percentage deviation, useful for scale-independent comparisons | |
| MAPE (Mean Absolute Percentage Error) | Expresses the error in percentage terms, facilitating comparison across different dataset. | |
| MASE (Mean Absolute Scaled Error) | An error metric that allows comparison across models by benchmarking against a naïve forecast. A naïve forecast assumes that the future value will be equal to the last observed value. |
| Model | AIC | Ljung—Box p-Value |
|---|---|---|
| SARIMA (1,0,1) (0,1,0) | 2354.6 | 0.0002 |
| SARIMA (2,0,1) (0,1,0) | 2356.4 | 0.0002 |
| SARIMA (2,0,2) (0,1,0) | 2347.6 | 0.0008 |
| SARIMA (2,0,3) (0,1,0) | 2344.6 | 0.0042 |
| SARIMA (1,0,1) (1,1,0) | 2329.6 | 0.0298 |
| SARIMA (2,0,1) (1,1,0) | 2331.6 | 0.0231 |
| SARIMA (2,0,1) (2,1,0) | 2321.7 | 0.3411 |
| SARIMA (2,0,2) (2,1,0) | 2321.7 | 0.5680 |
| SARIMA (2,0,2) (2,1,1) | 2311.5 | 0.6785 |
| SARIMA (2,0,2) (2,1,2) | 2313.6 | 0.6750 |
| Model | ME | RMSE | MAE | MPE | MAPE | MASE |
|---|---|---|---|---|---|---|
| SARIMA (1,0,1) (0,1,0) | 558.51 | 756.72 | 634.13 | 18.37 | 20.24 | 1.31 |
| SARIMA (2,0,1) (0,1,0) | 567.88 | 759.08 | 630.87 | 18.62 | 20.18 | 1.30 |
| SARIMA (2,0,2) (0,1,0) | 568.88 | 732.66 | 617.10 | 18.09 | 19.28 | 1.27 |
| SARIMA (2,0,3) (0,1,0) | 533.48 | 714.12 | 559.64 | 16.44 | 17.09 | 1.15 |
| SARIMA (1,0,1) (1,1,0) | 482.85 | 662.92 | 482.85 | 16.83 | 16.83 | 1.00 |
| SARIMA (2,0,1) (1,1,0) | 492.57 | 668.10 | 492.57 | 17.13 | 17.13 | 1.02 |
| SARIMA (2,0,1) (2,1,0) | 375.88 | 591.85 | 397.91 | 13.06 | 14.05 | 0.82 |
| SARIMA (2,0,2) (2,1,0) | 388.67 | 589.98 | 426.59 | 12.09 | 14.46 | 0.88 |
| SARIMA (2,0,2) (2,1,1) | 284.88 | 614.73 | 467.88 | 7.74 | 18.69 | 0.96 |
| SARIMA (2,0,2) (2,1,2) | 281.58 | 616.17 | 474.12 | 7.52 | 18.94 | 0.98 |
| Month | Actual | Forecasted | 95% CI Lower | 95% CI Upper |
|---|---|---|---|---|
| January-2019 | 3382.27 | 3385.79 | 2394.24 | 4377.35 |
| February-2019 | 4091.31 | 3722.01 | 2686.62 | 4757.41 |
| March-2019 | 4048.48 | 4084.72 | 3044.73 | 5124.72 |
| April-2019 | 3694.41 | 3233.51 | 2193.13 | 4273.88 |
| May-2019 | 1507.94 | 1545.25 | 504.83 | 2585.67 |
| June-2019 | 1927.56 | 1398.96 | 358.53 | 2439.38 |
| July-2019 | 2937.00 | 1587.54 | 547.12 | 2627.96 |
| Month | Forecasted | 95% CI Lower | 95% CI Upper |
|---|---|---|---|
| August 2019 | 2121.22 | 1126.66 | 3115.77 |
| September 2019 | 1477.46 | 435.67 | 2519.24 |
| October 2019 | 1293.97 | 244.97 | 2342.97 |
| November 2019 | 1756.08 | 706.58 | 2805.59 |
| December 2019 | 2483.60 | 1433.96 | 3533.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esquivel-López, A.; Fernández, B.; Pérez, O.; Castillo, F.; Tejedor-Flores, N.; Cubilla-Montilla, M. Forecasting 7Be Concentrations Using Time Series Analysis: A Case Study of Panama City. Atmosphere 2025, 16, 1104. https://doi.org/10.3390/atmos16091104
Esquivel-López A, Fernández B, Pérez O, Castillo F, Tejedor-Flores N, Cubilla-Montilla M. Forecasting 7Be Concentrations Using Time Series Analysis: A Case Study of Panama City. Atmosphere. 2025; 16(9):1104. https://doi.org/10.3390/atmos16091104
Chicago/Turabian StyleEsquivel-López, Alexander, Bernardo Fernández, Omayra Pérez, Felipe Castillo, Nathalia Tejedor-Flores, and Mitzi Cubilla-Montilla. 2025. "Forecasting 7Be Concentrations Using Time Series Analysis: A Case Study of Panama City" Atmosphere 16, no. 9: 1104. https://doi.org/10.3390/atmos16091104
APA StyleEsquivel-López, A., Fernández, B., Pérez, O., Castillo, F., Tejedor-Flores, N., & Cubilla-Montilla, M. (2025). Forecasting 7Be Concentrations Using Time Series Analysis: A Case Study of Panama City. Atmosphere, 16(9), 1104. https://doi.org/10.3390/atmos16091104








