High-Resolution Daily XCH4 Prediction Using New Convolutional Neural Network Autoencoder Model and Remote Sensing Data
Abstract
1. Introduction
2. Materials and Methods
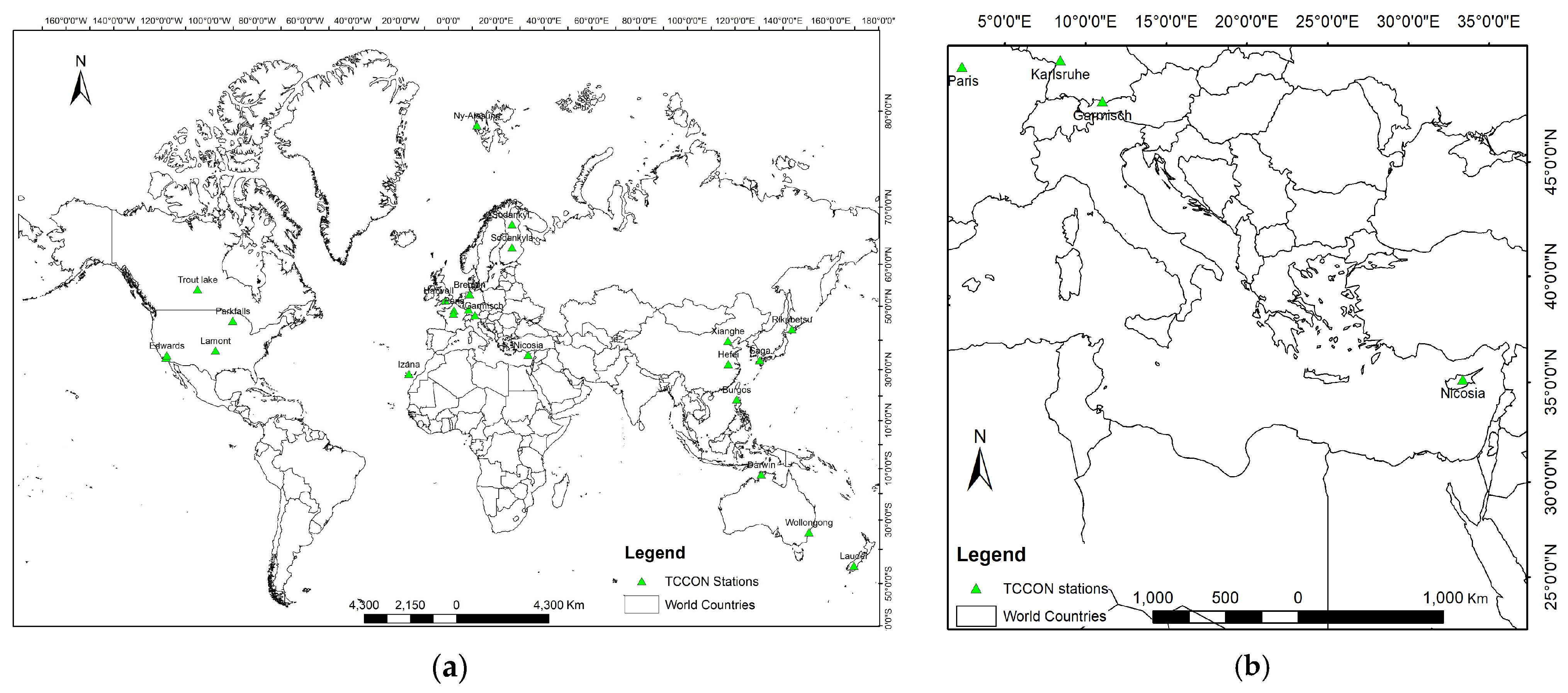
2.1. Materials
2.2. Methods
2.2.1. Acquire Data Using Google Earth Engine (GEE)
2.2.2. Testing Interpolation Techniques and Building the CNN-AE Model
- I
- Radial Basis Function (RBF)
- II
- Overview of Interpolation Algorithms in SciPy GridData
- III
- Random Forest Regression Method
- IV
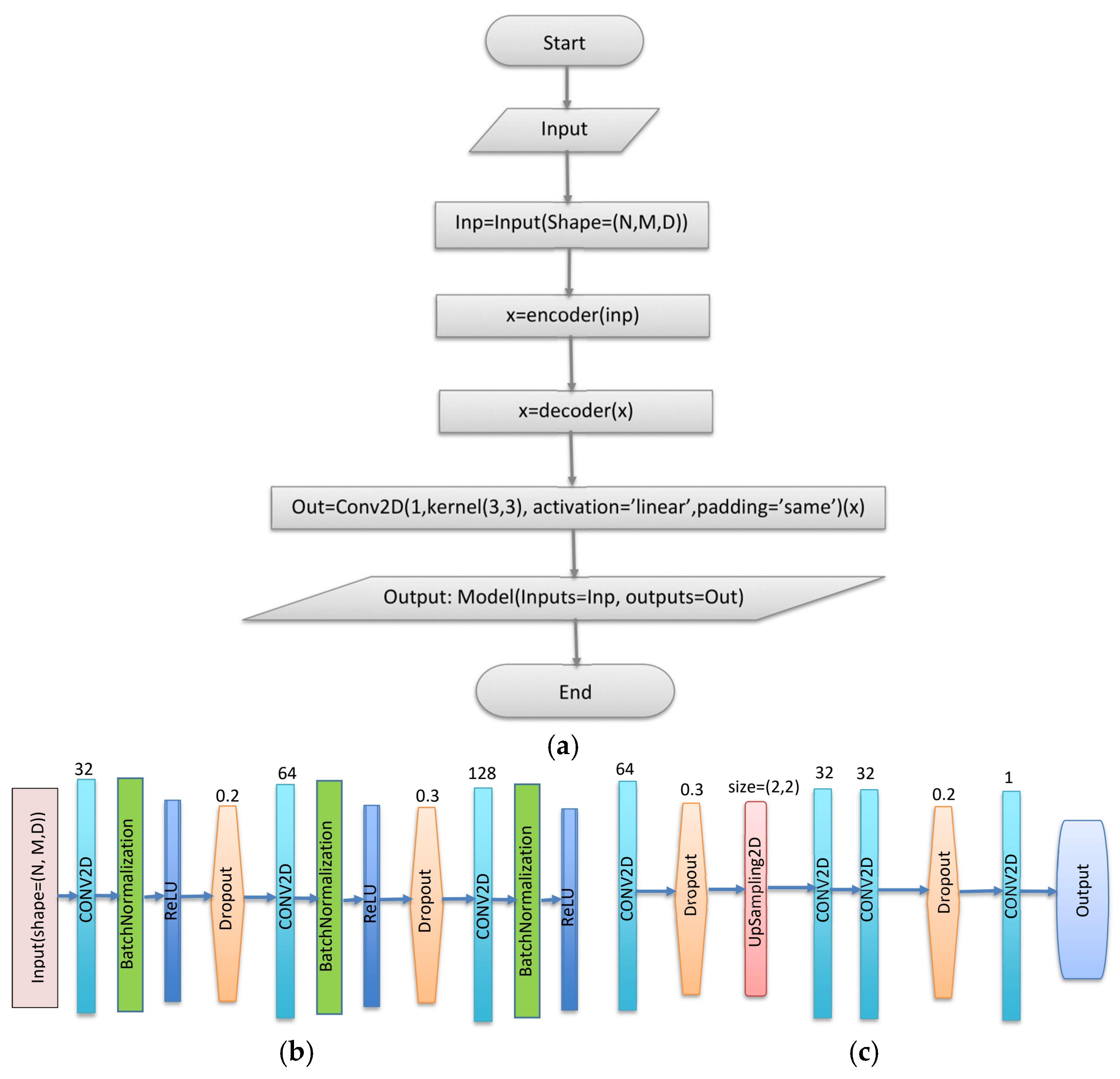
- A New CNN Autoencoder (CNN-AE) Model for the Prediction of XCH4
- represents the spatial resolution.
- = 2 channels correspond to two input features (e.g., longitude and latitude).
- -
- Convolution (Conv2D) that extracts spatial features using the following equation:
- -
- Batch Normalization (BatchNormalization) that normalizes activations using the following equation:
- V
- Verifying the Predicted and Interpolated Values
- Visual Comparison: Plotting the predicted, interpolated, and observed values on graphs to inspect how well the predictions match the observations visually.
- Statistical Comparison: Calculating statistical measures to quantify the differences between predicted/interpolated and observed values. Common metrics include
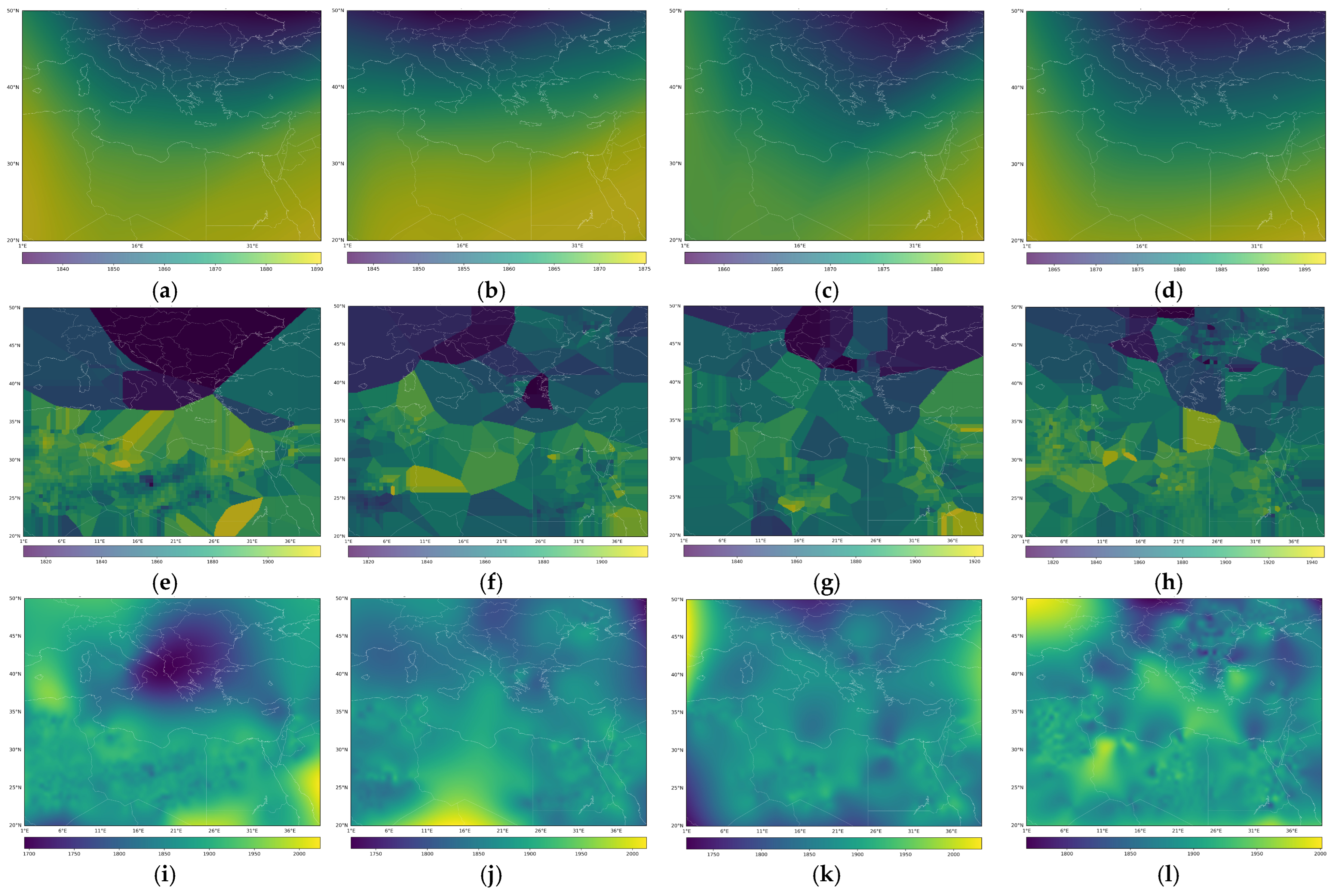
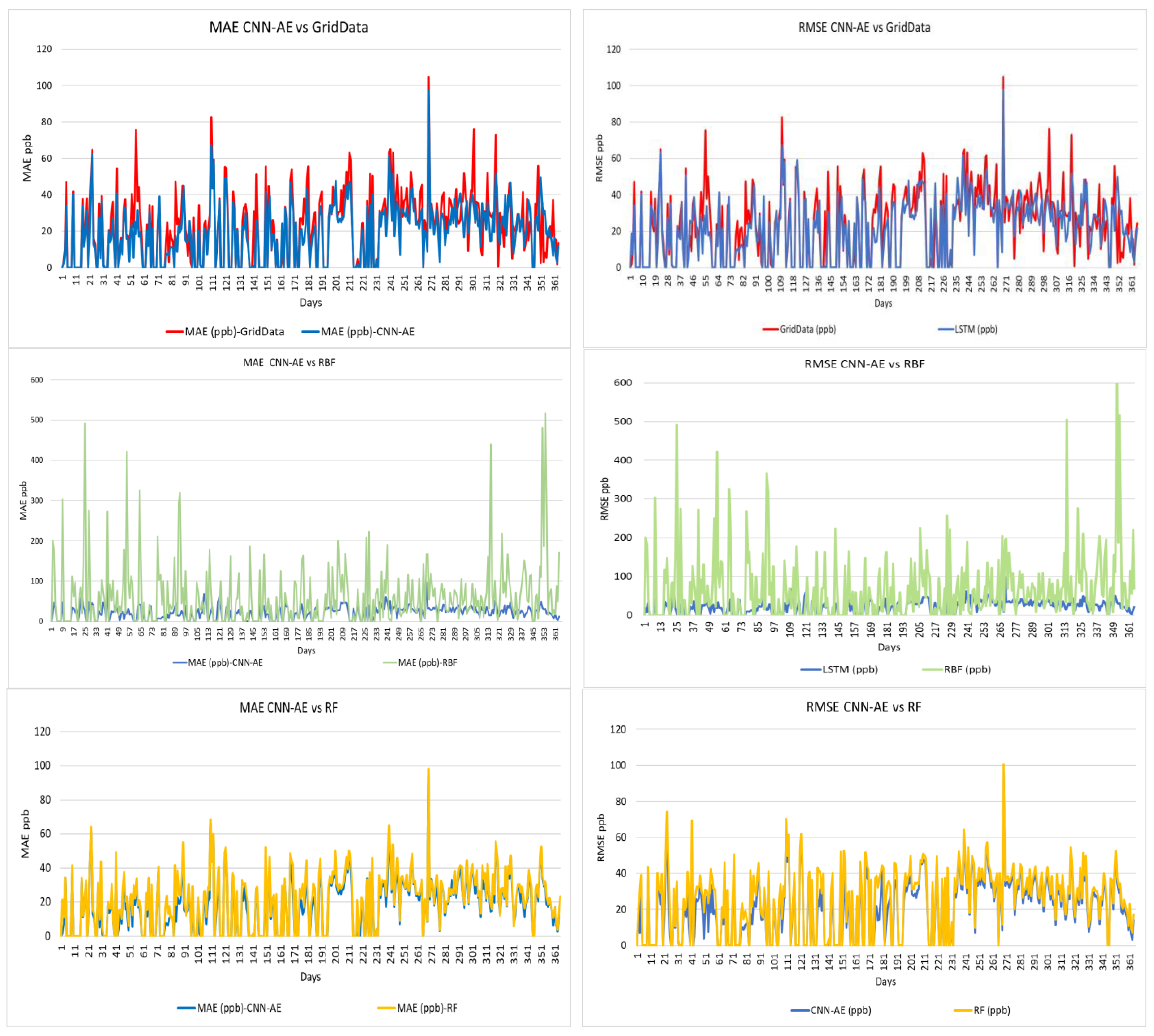
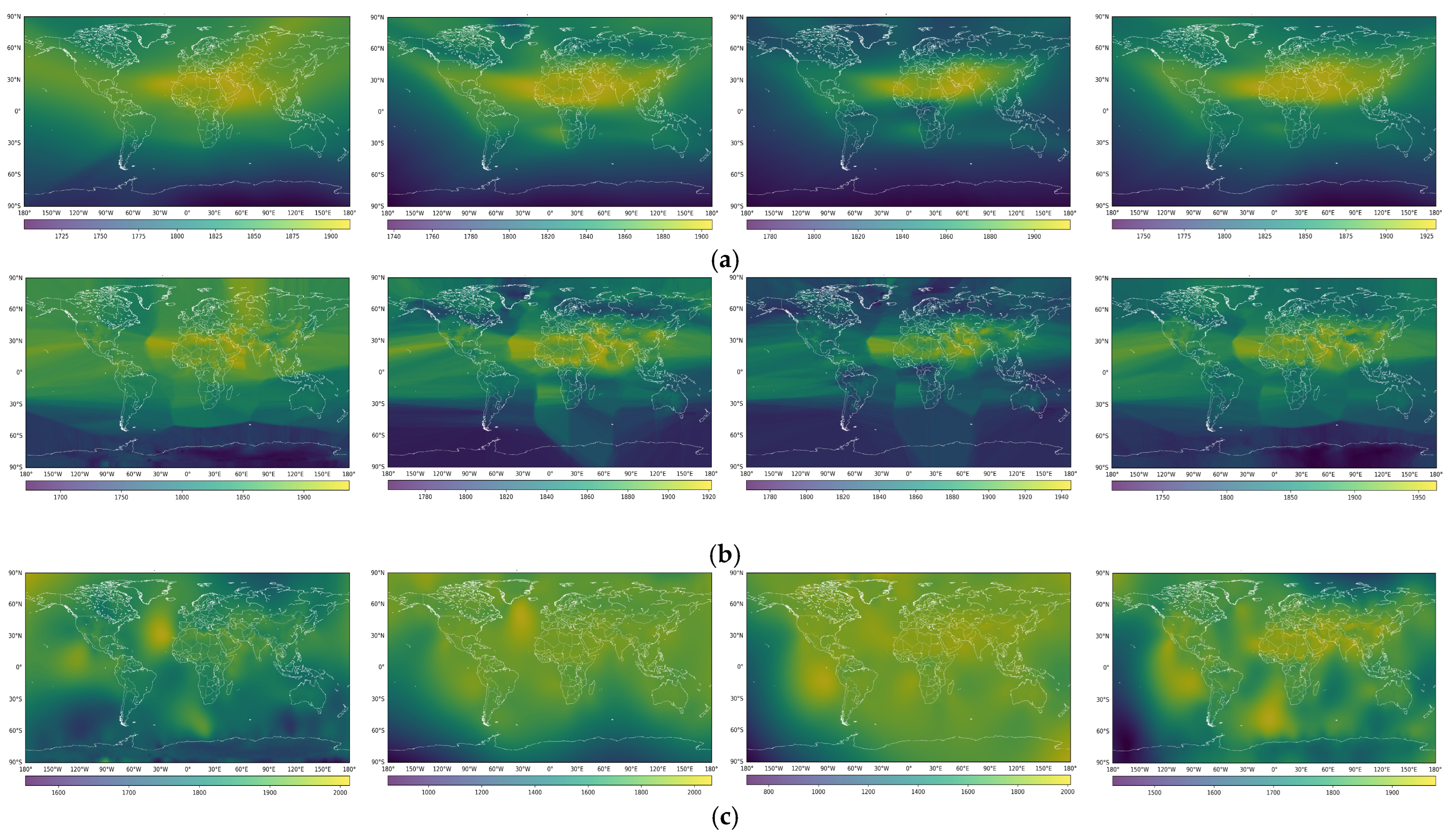
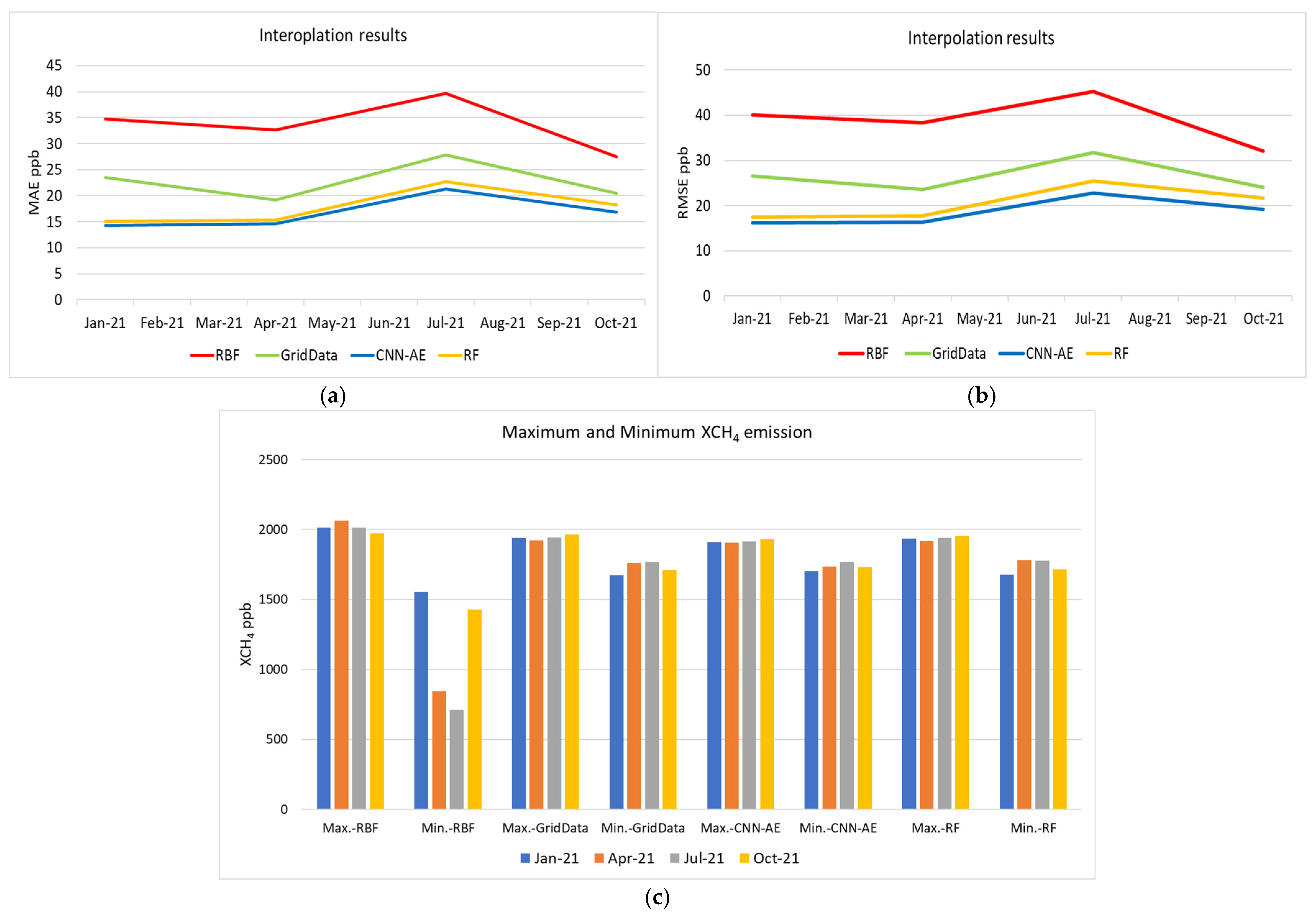
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schneising, O.; Buchwitz, M.; Reuter, M.; Heymann, J.; Bovensmann, H.; Burrows, J.P. Long-term analysis of carbon dioxide and methane column-averaged mole fractions retrieved from SCIAMACHY. Atmos. Chem. Phys. 2011, 11, 2863–2880. [Google Scholar] [CrossRef]
- Reuter, M.; Buchwitz, M.; Schneising, O.; Noel, S.; Bovensmann, H.; Burrows, J.P.; Boesch, H.; Di Noia, A.; Anand, J.; Parker, R.J.; et al. Ensemble-based satellite-derived carbon dioxide and methane column-averaged dry-air mole fraction data sets (2003–2018) for carbon and climate applications. Atmos. Meas. Tech. 2020, 13, 789–819. [Google Scholar] [CrossRef]
- Saunois, M.; Stavert, A.R.; Poulter, B.; Bousquet, P.; Canadell, J.G.; Jackson, R.B.; Raymond, P.A.; Dlugokencky, E.J.; Houweling, S.; Patra, P.K.; et al. The Global Methane Budget 2000–2017. Earth Syst. Sci. Data 2020, 12, 1561–1623. [Google Scholar] [CrossRef]
- Solomon, S. Climate Change 2013: The Physical Science Basis. Working Group 1 Contribution to the IPCC Fifth Assessment Report; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- European Space Agency (ESA), Sentinel-5P Tropomi. Available online: https://www.esa.int/Applications/Observing_the_Earth/Copernicus/Sentinel-5P (accessed on 21 April 2025).
- Kuze, A.; Suto, H.; Nakajima, M.; Hamazaki, T. Thermal and near infrared sensor for carbon observation Fourier-transform spectrometer on the Greenhouse Gases Observing Satellite for greenhouse gases monitoring. Appl. Opt. 2009, 48, 6716–6733. [Google Scholar] [CrossRef] [PubMed]
- Suto, H.; Kuze, A.; Shiomi, K.; Nakajima, M. Recent progress of GOSAT series for greenhouse gas monitoring. Remote Sens. 2021, 13, 689. [Google Scholar] [CrossRef]
- McLinden, C.A.; Griffin, D.; Davis, Z.; Hempel, C.; Smith, J.; Sioris, C.; Nassar, R.; Moeini, O.; Legault-Ouellet, E.; Malo, A. An Independent Evaluation of GHGSat Methane Emissions: Performance Assessment. J. Geophys. Res. Atmos. 2024, 129, e2023JD039906. [Google Scholar] [CrossRef]
- Jiang, Y.; Gao, Z.; He, J.; Wu, J.; Christakos, G. Application and Analysis of XCO2 Data from OCO Satellite Using a Synthetic DINEOF–BME Spatiotemporal Interpolation Framework. Remote Sens. 2022, 14, 4422. [Google Scholar] [CrossRef]
- Azcarate, A.A.; Barth, A.; Sirjacobs, D.; Lenartz, F.; Beckers, J.M. Data Interpolating Empirical Orthogonal Functions (DINEOF): A tool for geophysical data analyses. Mediterr. Mar. Sci. 2011, 12, 5–11. [Google Scholar] [CrossRef]
- Wefers, W.; Lehnert, L.; Schmidt, D.; Reuter, M.; Buchwitz, M.; Kammann, C.; Velten, K.; Hase, F.; Notholt, J.; Kubistin, D.; et al. Approximation of multi-year time series of XCO2 concentrations using satellite observations and statistical interpolation methods. Atmos. Res. 2023, 294, 106965. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, Q.; Feng, X.; Liu, Z.; Shao, P.; Xia, M.; Ye, X. An Interpolation and Prediction Algorithm for XCO2 Based on Multi-Source Time Series Data. Remote Sens. 2024, 16, 1907. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Chen, Y. A Symmetric Efficient Spatial and Channel Attention (ESCA) Module Based on Convolutional Neural Networks. Symmetry 2024, 16, 952. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Sheng, M.; Lei, L.; Zeng, Z.C.; Rao, W.; Song, H.; Wu, C. Global land 1° mapping dataset of XCO2 from satellite observations of GOSAT and OCO-2 from 2009 to 2020. Big Earth Data 2022, 7, 170–190. [Google Scholar] [CrossRef]
- Zeng, Z.-C.; Lei, L.; Strong, K.; Jones, D.B.A.; Guo, L.; Liu, M.; Lin, H. Global land mapping of satellite-observed CO2 total columns using spatio-temporal geostatistics. Int. J. Digit. Earth 2016, 10, 426–456. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Li, B.; Li, T.; Wang, Z.; Yang, X.; Jin, Y.; Zhang, L. Retrieval of Atmospheric XCH4 via XGBoost Method Based on TROPOMI Satellite Data. Atmosphere 2025, 16, 279. [Google Scholar] [CrossRef]
- Mueller, J.P.; Massaron, L. Python for Data Science for Dummies; John Wiley & Sons: Hoboken, NJ, USA, 2015; p. 432. [Google Scholar]
- Cardille, J.A.; Crowley, M.A.; Saah, D.; Clinton, N.E. (Eds.) Cloud-Based Remote Sensing with Google Earth Engine: Fundamentals and Applications; Springer: Cham, Switzerland, 2024; p. 1226. [Google Scholar] [CrossRef]
- Lorente, A.; Borsdorff, T.; Butz, A.; Hasekamp, O.; de Brugh, J.A.; Schneider, A.; Wu, L.; Hase, F.; Kivi, R.; Wunch, D.; et al. Methane retrieved from TROPOMI: Improvement of the data product and validation of the first 2 years of measurements. Atmos. Meas. Tech. 2021, 14, 665–684. [Google Scholar] [CrossRef]
- Rocha, H. On the selection of the most adequate radial basis function. Appl. Math. Model. 2009, 33, 1573–1583. [Google Scholar] [CrossRef]
- Lazzaro, D.; Montefusco, L. Radial basis functions for the multivariate interpolation of large scattered data sets. J. Comput. Appl. Math. 2002, 140, 521–536. [Google Scholar] [CrossRef]
- Winkel, B.; Lenz, D.; Flöer, L. Cygrid, A fast Cython-powered convolution-based gridding module for Python. Astron. Astrophys. 2016, 591, A12. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; Volume 37, pp. 448–456. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, 11–13 April 2011; Volume 15, pp. 315–323. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Mean squared error: A powerful performance measure for speech enhancement. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1–40. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or Mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Copernicus Climate Change Service. Climate Data Store. Methane data from 2002 to Present Derived from Satellite Observations. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018. Available online: https://doi.org/10.24381/cds.b25419f8 (accessed on 14 June 2025).





| 1. Import necessary libraries 2. Combine data frames into a single DataFrame 3. Convert the ‘date’ column to a date and time format 4. Calculate total hours from the start of the year and add them to the DataFrame 5. Normalize features 6. Prepare input–output data 7. Reshape input data for the CNN-AE model 8. Split data into training and testing sets 9. Build CNN-AE model 10. Compile the model with the Adam optimizer and the Huber error loss function 11. Train the model with an early stopping callback 12. Evaluate the model on test data 13. Predict using the trained model 14. Inverse transform the scaled data for actual and predicted values 15. Validate the results using TCCON data |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awad, M.M.; Homayouni, S. High-Resolution Daily XCH4 Prediction Using New Convolutional Neural Network Autoencoder Model and Remote Sensing Data. Atmosphere 2025, 16, 806. https://doi.org/10.3390/atmos16070806
Awad MM, Homayouni S. High-Resolution Daily XCH4 Prediction Using New Convolutional Neural Network Autoencoder Model and Remote Sensing Data. Atmosphere. 2025; 16(7):806. https://doi.org/10.3390/atmos16070806
Chicago/Turabian StyleAwad, Mohamad M., and Saeid Homayouni. 2025. "High-Resolution Daily XCH4 Prediction Using New Convolutional Neural Network Autoencoder Model and Remote Sensing Data" Atmosphere 16, no. 7: 806. https://doi.org/10.3390/atmos16070806
APA StyleAwad, M. M., & Homayouni, S. (2025). High-Resolution Daily XCH4 Prediction Using New Convolutional Neural Network Autoencoder Model and Remote Sensing Data. Atmosphere, 16(7), 806. https://doi.org/10.3390/atmos16070806










