A Signal Processing-Guided Deep Learning Framework for Wind Shear Prediction on Airport Runways
Abstract
1. Introduction
1.1. Wind Shear: Hidden Dangers
1.2. Impact of Wind Shear on Aircraft
1.3. Wind Shear Detection Technologies
1.4. Wind Shear Forecasting
1.5. Hong Kong International Airport as Wind Shear-Prone Airport
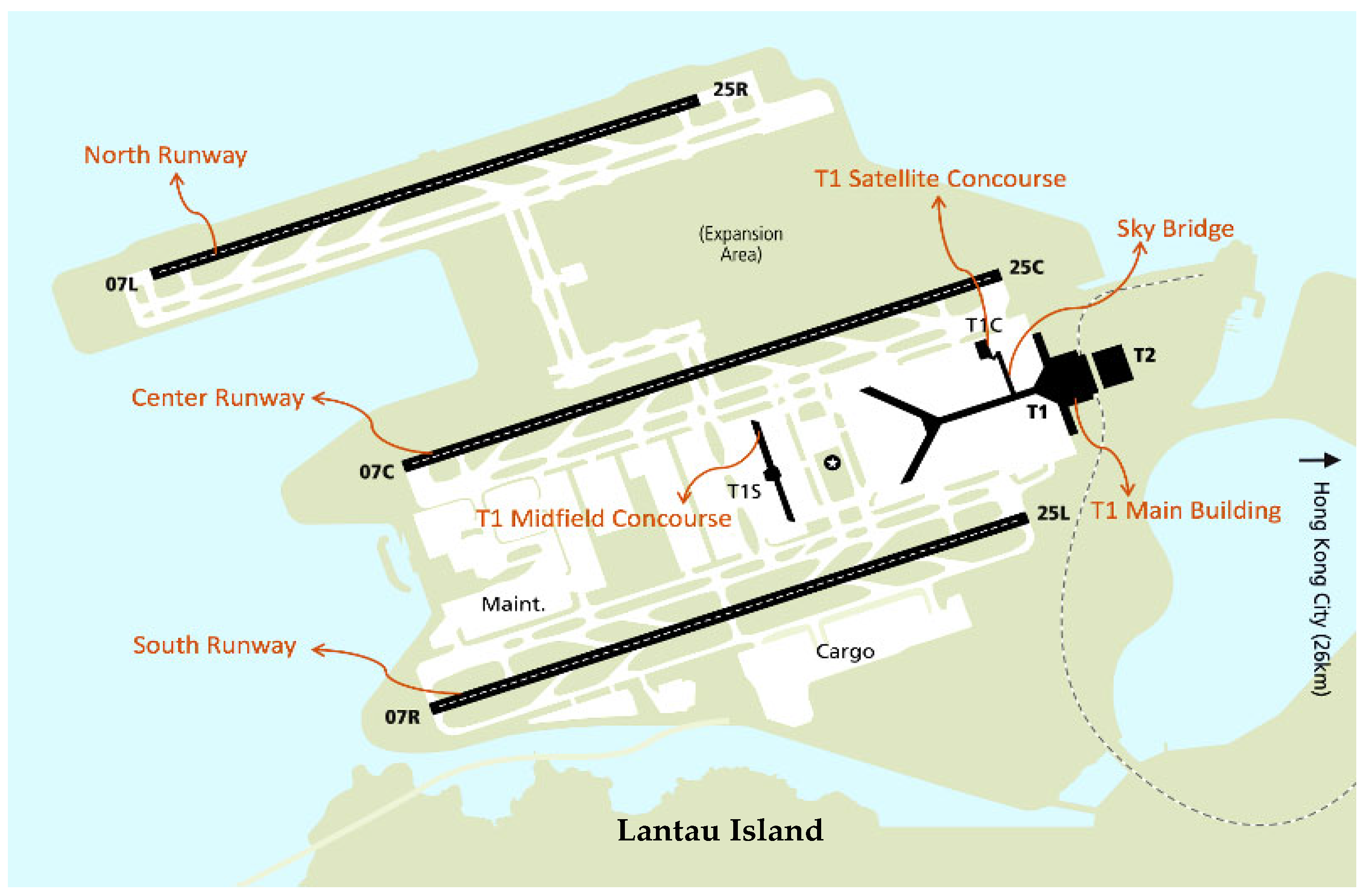
1.6. Research Contribution
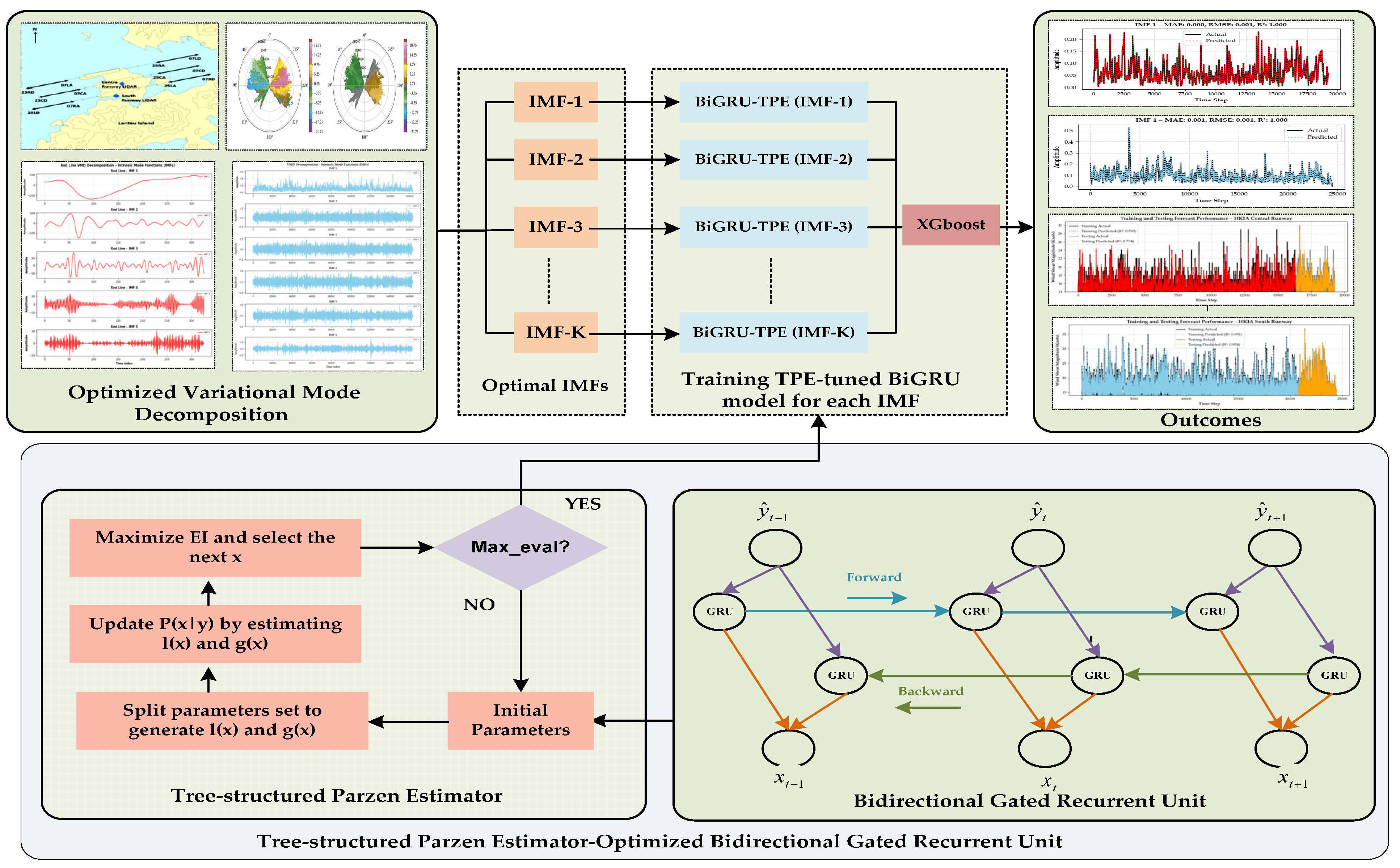
- Wind shear data recorded at the HKIA often displays abrupt changes and multi-scale variability influenced by terrain-induced disturbances. To address these characteristics, the study applies optimized variational mode decomposition (OVMD) to divide the original time series into intrinsic mode functions (IMFs), with each IMF representing a specific frequency component [29,30]. This decomposition enhances temporal resolution, reduces noise interference, and exposes features that are essential for modeling wind shear behavior more precisely.
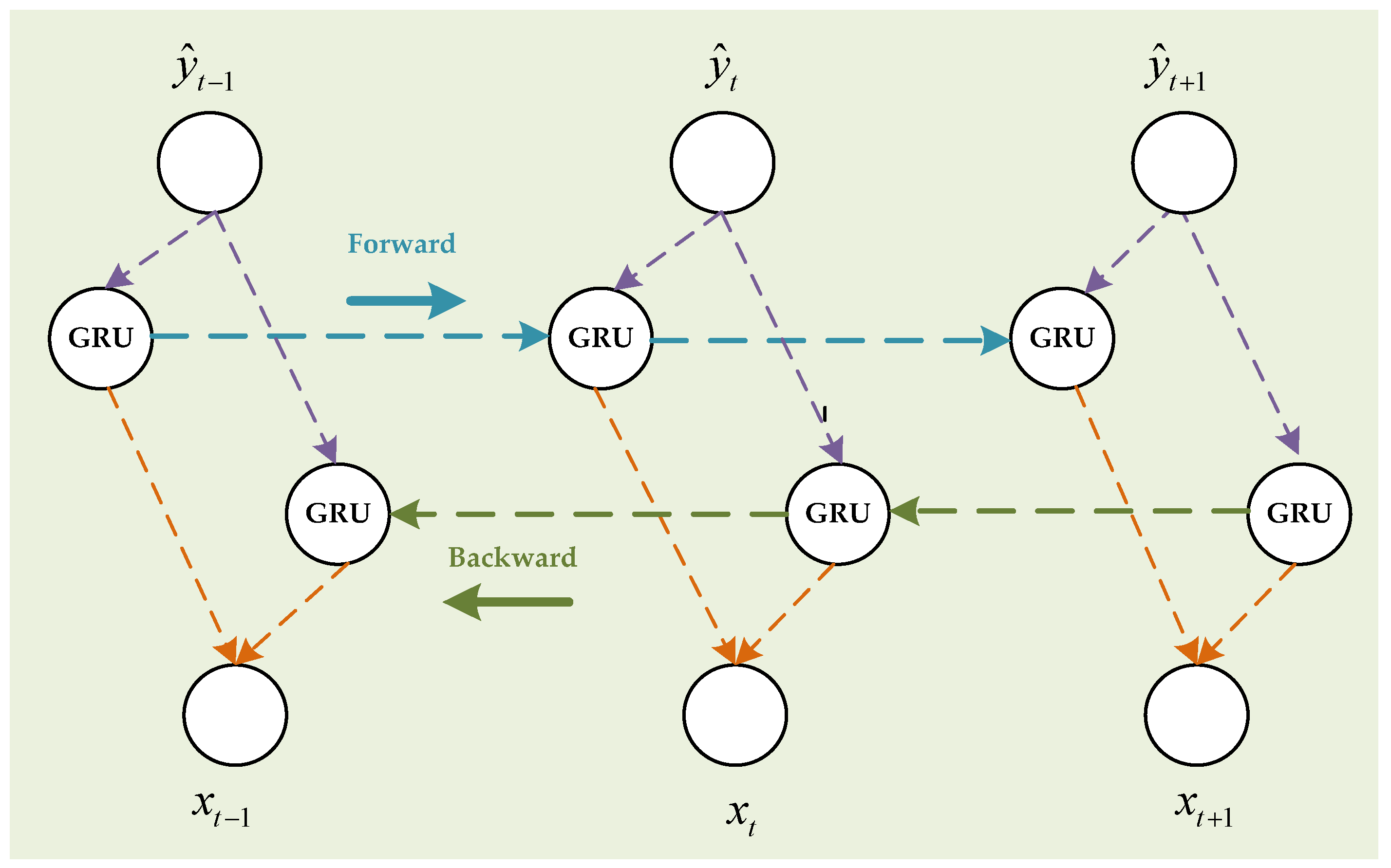
- Each IMF is modeled independently using a bidirectional gated recurrent unit (BiGRU) network [22,31,32]. This structure captures temporal dependencies in both forward and backward directions and adapts to the evolving nature of the underlying patterns across different IMFs. Hyperparameters for BiGRUs are selected through the Tree-structured Parzen Estimator (TPE) [33,34] to maintain balance between generalization and responsiveness to localized fluctuations in the data.
- Residual prediction errors from the BiGRU stage are further refined using an Extreme Gradient Boosting (XGBoost) model [35]. This stage identifies non-linear deviations and remaining signal components that are not captured by the deep learning stage. XGBoost improves overall prediction accuracy by correcting these discrepancies, which often reflect the irregular and abrupt nature of wind shear near airport runways.
2. Materials and Methods
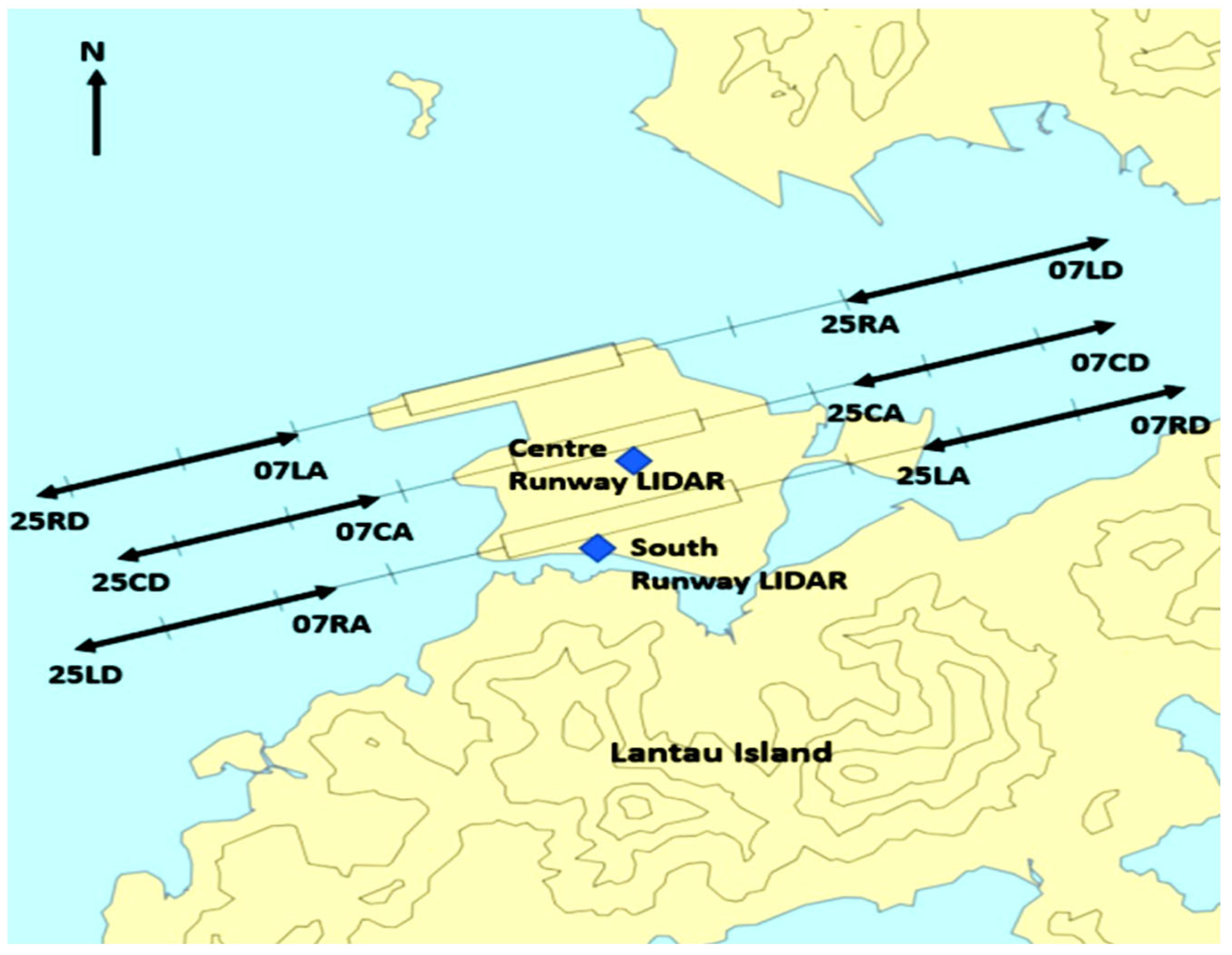
2.1. HKIA Doppler LiDAR System
2.2. Hybrid OVMD–GRU–XGBoost Framework for Time Series Analysis
2.2.1. Optimized Variational Mode Decomposition (OVMD)
2.2.2. BiGRU Component Optimized via TPE
2.2.3. Reconstruction and Residual Correction
2.3. Performance Metrics
3. Results and Discussion
3.1. VMD Decomposition of Wind Shear Data for Central and South Runways
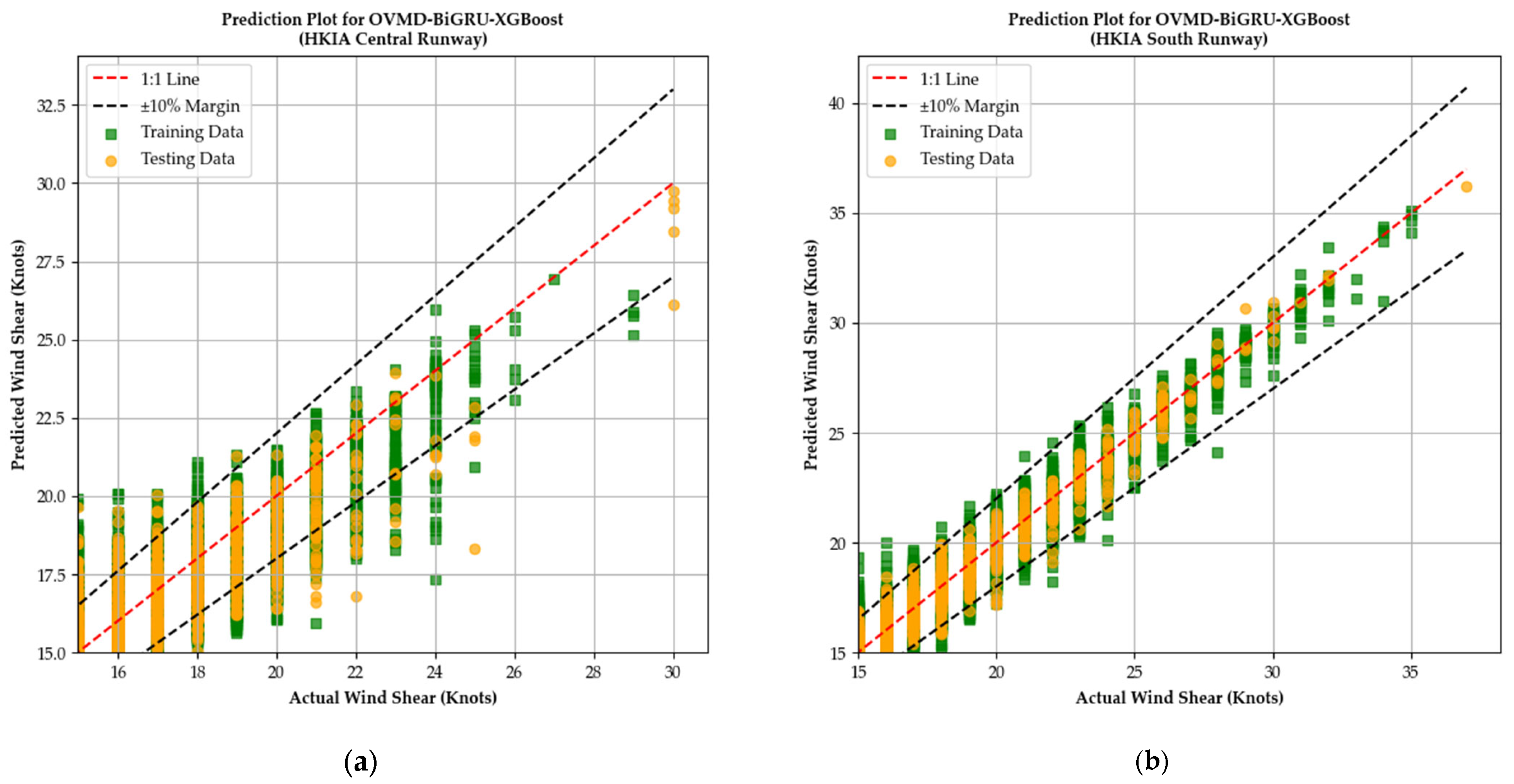
3.2. Comparison of Proposed OVMD–BiGRU–XGBoost with Other Competitive Models
4. Conclusions and Recommendations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, H.; Liu, X.; Wang, Q.; Zhang, J.; He, Z.; Zhang, X.; Li, R.; Zhang, K.; Tang, J.; Wu, S. Low-level wind shear identification along the glide path at BCIA by the pulsed coherent doppler LiDAR. Atmosphere 2020, 12, 50. [Google Scholar] [CrossRef]
- Bretschneider, L.; Hankers, R.; Schönhals, S.; Heimann, J.-M.; Lampert, A. Wind shear of low-level jets and their influence on manned and unmanned fixed-wing aircraft during landing approach. Atmosphere 2021, 13, 35. [Google Scholar] [CrossRef]
- International Civil Aviation Organization. Manual on Low-Level Wind Shear; International Civil Aviation Organization: Montreal, QC, Canada, 2005. [Google Scholar]
- Federal Aviation Administration. Wind Shear; FAA-P-8740-40; Federal Aviation Administration: Washington, DC, USA, 2008. [Google Scholar]
- Lin, C.; Zhang, K.; Chen, X.; Liang, S.; Wu, J.; Zhang, W. Overview of low-level wind shear characteristics over Chinese mainland. Atmosphere 2021, 12, 628. [Google Scholar] [CrossRef]
- Kusuma, L.K.N.A.; Pratiwi, I.; Ismanto, H.; Fitrianto, M.A. Utilization of Doppler Weather Surveillance Radar for Wind-Shear Detection in Airport. In Proceedings of the 2022 8th International Conference on Science and Technology (ICST), Yogyakarta, Indonesia, 7–8 September 2022; pp. 1–5. [Google Scholar]
- Ryan, M.; Saputro, A.H.; Sopaheluwakan, A. Review of low-level wind shear: Detection and prediction. AIP Conf. Proc. 2023, 2719, 020044. [Google Scholar]
- Liu, X.; Zhang, H.; Wu, S.; Wang, Q.; He, Z.; Zhang, J.; Li, R.; Liu, S.; Zhang, X. Effects of buildings on wind shear at the airport: Field measurement by coherent Doppler lidar. J. Wind Eng. Ind. Aerodyn. 2022, 230, 105194. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, S.; Wang, Q.; Liu, B.; Yin, B.; Zhai, X. Airport low-level wind shear lidar observation at Beijing Capital International Airport. Infrared Phys. Technol. 2019, 96, 113–122. [Google Scholar] [CrossRef]
- Gheitasi, N.; Mazlumi, F. A review on radar applications in civil aviation. In Proceedings of the 21st International Conference of Iranian Aerospace Society, Tehran, Iran, 20 February 2023; pp. 1–8. [Google Scholar]
- MORRIS, M.T.; Brewster, K.A.; Carr, F.H. Assessing the Impact of Non-Conventional Radar and Surface Observations on High-Resolution Analyses and Forecasts of a Severe Hailstorm. Electron. J. Sev. Storms Meteorol. (EJSSM) 2021, 16, 1–39. [Google Scholar] [CrossRef]
- Nechaj, P.; Gaál, L.; Bartok, J.; Vorobyeva, O.; Gera, M.; Kelemen, M.; Polishchuk, V. Monitoring of low-level wind shear by ground-based 3D lidar for increased flight safety, protection of human lives and health. Int. J. Environ. Res. Public Health 2019, 16, 4584. [Google Scholar] [CrossRef]
- Mizuno, S.; Ohba, H.; Ito, K. Machine learning-based turbulence-risk prediction method for the safe operation of aircrafts. J. Big Data 2022, 9, 29. [Google Scholar] [CrossRef]
- Khattak, A.; Chan, P.W.; Chen, F.; Peng, H. Interpretable ensemble imbalance learning strategies for the risk assessment of severe-low-level wind shear based on LiDAR and PIREPs. Risk Anal. 2024, 44, 1084–1102. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zhang, H.; Chan, P.-W.; Tai, H.; Deng, Z. A Machine Learning-Based Model for Flight Turbulence Identification Using LiDAR Data. Atmosphere 2023, 14, 797. [Google Scholar] [CrossRef]
- Williams, J.K. Using random forests to diagnose aviation turbulence. Mach. Learn. 2014, 95, 51–70. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Mahadevan, S. Ensemble machine learning models for aviation incident risk prediction. Decis. Support Syst. 2019, 116, 48–63. [Google Scholar] [CrossRef]
- Celikmih, K.; Inan, O.; Uguz, H. Failure prediction of aircraft equipment using machine learning with a hybrid data preparation method. Sci. Program. 2020, 2020, 8616039. [Google Scholar] [CrossRef]
- Nanduri, A.; Sherry, L. Anomaly detection in aircraft data using Recurrent Neural Networks (RNN). In Proceedings of the 2016 Integrated Communications Navigation and Surveillance (ICNS), Herndon, VA, USA, 19–21 April 2016; pp. 5C2-1–5C2-8. [Google Scholar]
- Mamdouh, M.; Ezzat, M.; Hefny, H. Improving flight delays prediction by developing attention-based bidirectional LSTM network. Expert Syst. Appl. 2024, 238, 121747. [Google Scholar] [CrossRef]
- Khan, W.A.; Ma, H.-L.; Chung, S.-H.; Wen, X. Hierarchical integrated machine learning model for predicting flight departure delays and duration in series. Transp. Res. Part C Emerg. Technol. 2021, 129, 103225. [Google Scholar] [CrossRef]
- Zhu, Q.; Zhang, F.; Liu, S.; Wu, Y.; Wang, L. A hybrid VMD–BiGRU model for rubber futures time series forecasting. Appl. Soft Comput. 2019, 84, 105739. [Google Scholar] [CrossRef]
- Khattak, A.; Chan, P.-w.; Chen, F.; Peng, H. Explainable Boosting Machine for Predicting Wind Shear-Induced Aircraft Go-around based on Pilot Reports. KSCE J. Civ. Eng. 2023, 27, 4115–4129. [Google Scholar] [CrossRef]
- Yuen, A.; Tsui, K.; Fung, M. Hong Kong Airport’s Competitiveness as an International Hub. In Aviation Law and Policy in Asia; Brill Nijhoff: Leiden, The Netherlands, 2020; pp. 118–142. [Google Scholar]
- Chan, P.; Hon, K. Observation and numerical simulation of terrain-induced windshear at the Hong Kong International Airport in a planetary boundary layer without temperature inversions. Adv. Meteorol. 2016, 2016, 1454513. [Google Scholar] [CrossRef]
- Hon, K.; Chan, P. Application of LIDAR-derived eddy dissipation rate profiles in low-level wind shear and turbulence alerts at H ong K ong I nternational A irport. Meteorol. Appl. 2014, 21, 74–85. [Google Scholar] [CrossRef]
- Chan, P. Severe wind shear at H ong K ong I nternational a irport: Climatology and case studies. Meteorol. Appl. 2017, 24, 397–403. [Google Scholar] [CrossRef]
- Turis.io. Hong Kong Airport Departure Gate Map: Where Is My Gate? Available online: https://blog.turis.io/en/2025/01/24/hong-kong-airport-departure-gate-map-where-is-my-gate/ (accessed on 19 April 2025).
- Lahmiri, S. A variational mode decompoisition approach for analysis and forecasting of economic and financial time series. Expert Syst. Appl. 2016, 55, 268–273. [Google Scholar] [CrossRef]
- Chen, H.; Lu, T.; Huang, J.; He, X.; Yu, K.; Sun, X.; Ma, X.; Huang, Z. An improved VMD-LSTM model for time-varying GNSS time series prediction with temporally correlated noise. Remote Sens. 2023, 15, 3694. [Google Scholar] [CrossRef]
- Huang, J.; Ding, W. Aircraft trajectory prediction based on bayesian optimised temporal convolutional network–bidirectional gated recurrent unit hybrid neural network. Int. J. Aerosp. Eng. 2022, 2022, 2086904. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, Y.; Wu, S.; Li, X.; Luo, H.; Yin, S. Prediction of remaining useful life based on bidirectional gated recurrent unit with temporal self-attention mechanism. Reliab. Eng. Syst. Saf. 2022, 221, 108297. [Google Scholar] [CrossRef]
- Chen, C.; Seo, H. Prediction of rock mass class ahead of TBM excavation face by ML and DL algorithms with Bayesian TPE optimization and SHAP feature analysis. Acta Geotech. 2023, 18, 3825–3848. [Google Scholar] [CrossRef]
- Khattak, A.; Zhang, J.; Chan, P.-W.; Chen, F. Turbulence along the runway glide path: The invisible hazard assessment based on a wind tunnel study and interpretable TPE-optimized KTBoost approach. Atmosphere 2023, 14, 920. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Zhang, J.; Chan, P.-W.; Ng, M.K.-P. Optimal-Transport-Based Positive and Unlabeled Learning Method for Windshear Detection. Remote Sens. 2024, 16, 4423. [Google Scholar] [CrossRef]
- Zhang, J.; Chan, P.W.; Ng, M.K. LiDAR-Based Windshear Detection via Statistical Features. Adv. Meteorol. 2022, 2022, 3039797. [Google Scholar] [CrossRef]
- Mohanty, S.; Gupta, K.K.; Raju, K.S. Comparative study between VMD and EMD in bearing fault diagnosis. In Proceedings of the 2014 9th International Conference on Industrial and Information Systems (ICIIS), Gwalior, India, 15–17 December 2014; pp. 1–6. [Google Scholar]
- Wang, L.; Liu, Y.; Li, T.; Xie, X.; Chang, C. Short-term PV power prediction based on optimized VMD and LSTM. IEEE Access 2020, 8, 165849–165862. [Google Scholar] [CrossRef]
- Dinda, B. Gated recurrent neural network with TPE Bayesian optimization for enhancing stock index prediction accuracy. arXiv 2024, arXiv:2406.02604. [Google Scholar]
- Xie, D.; Sun, H.; Qi, J. A new feature extraction method based on improved variational mode decomposition, normalized maximal information coefficient and permutation entropy for ship-radiated noise. Entropy 2020, 22, 620. [Google Scholar] [CrossRef] [PubMed]

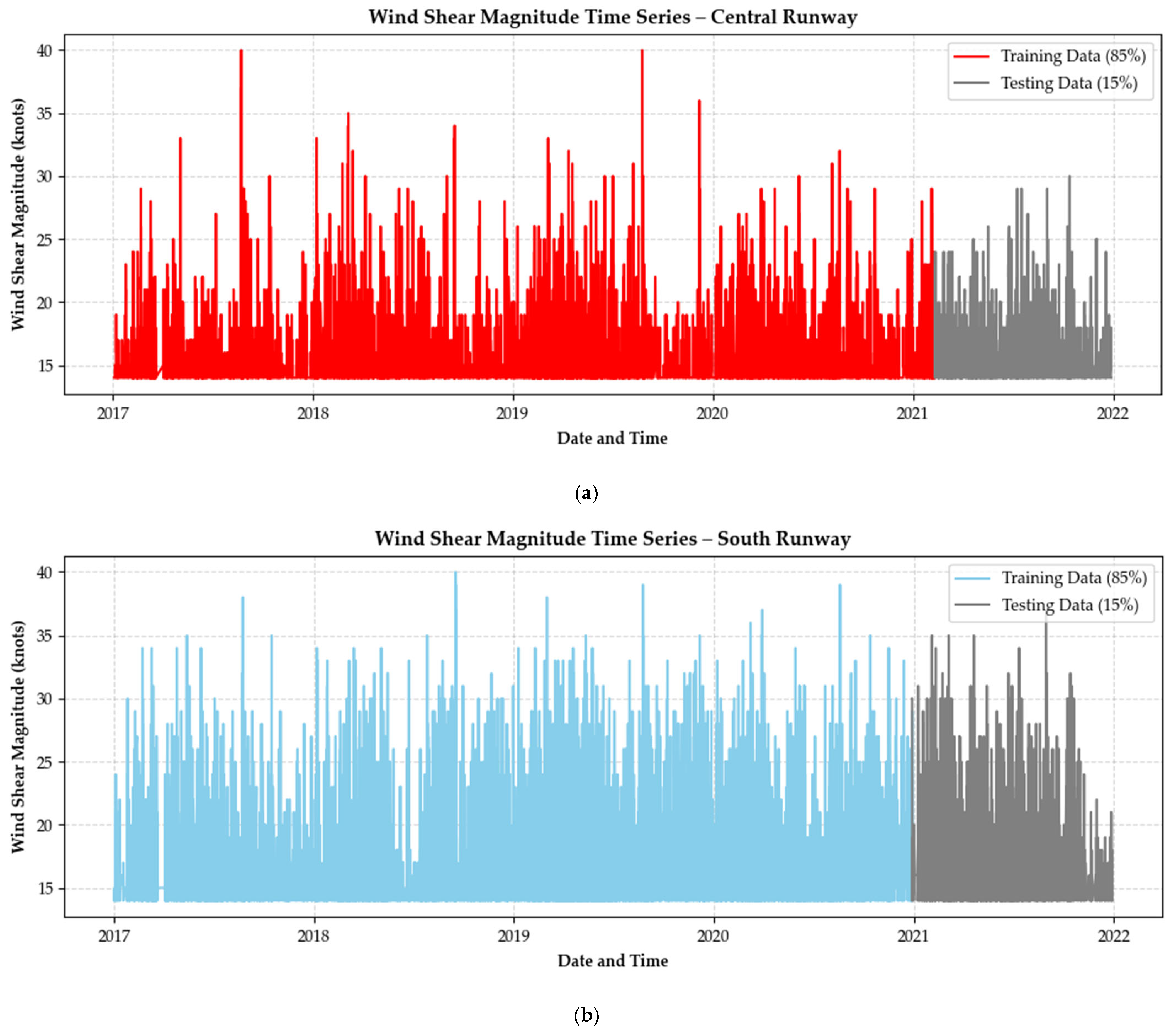
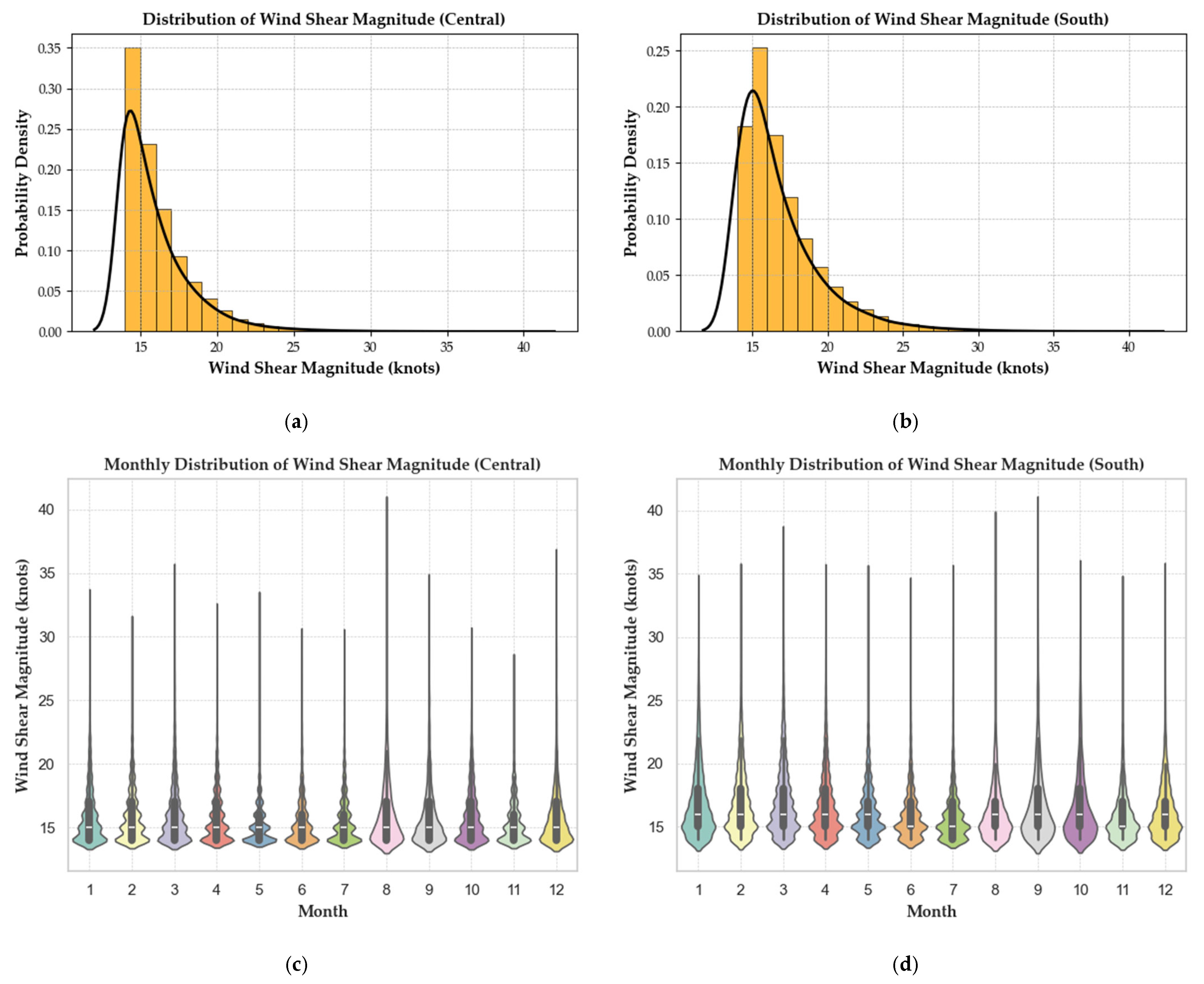
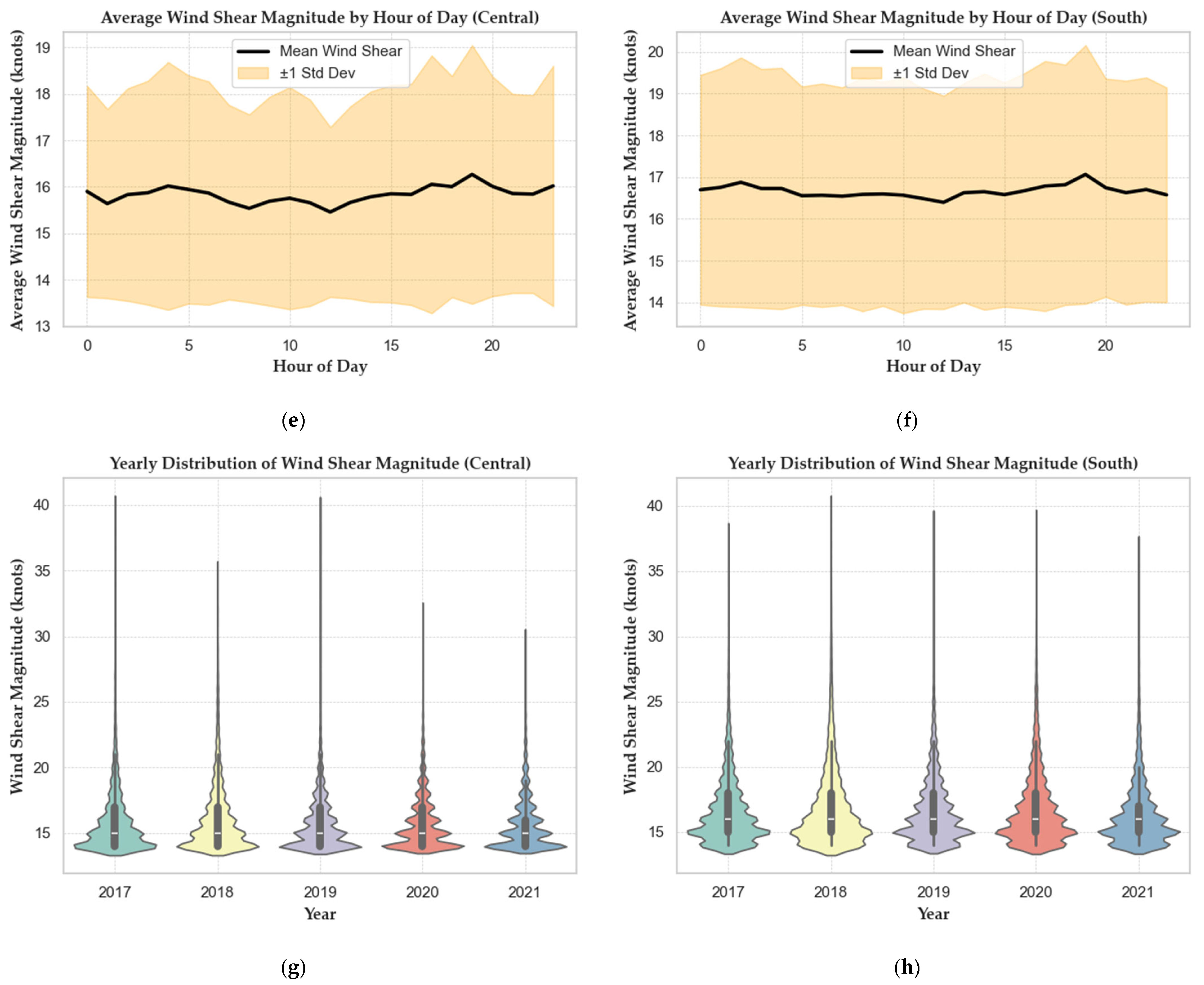


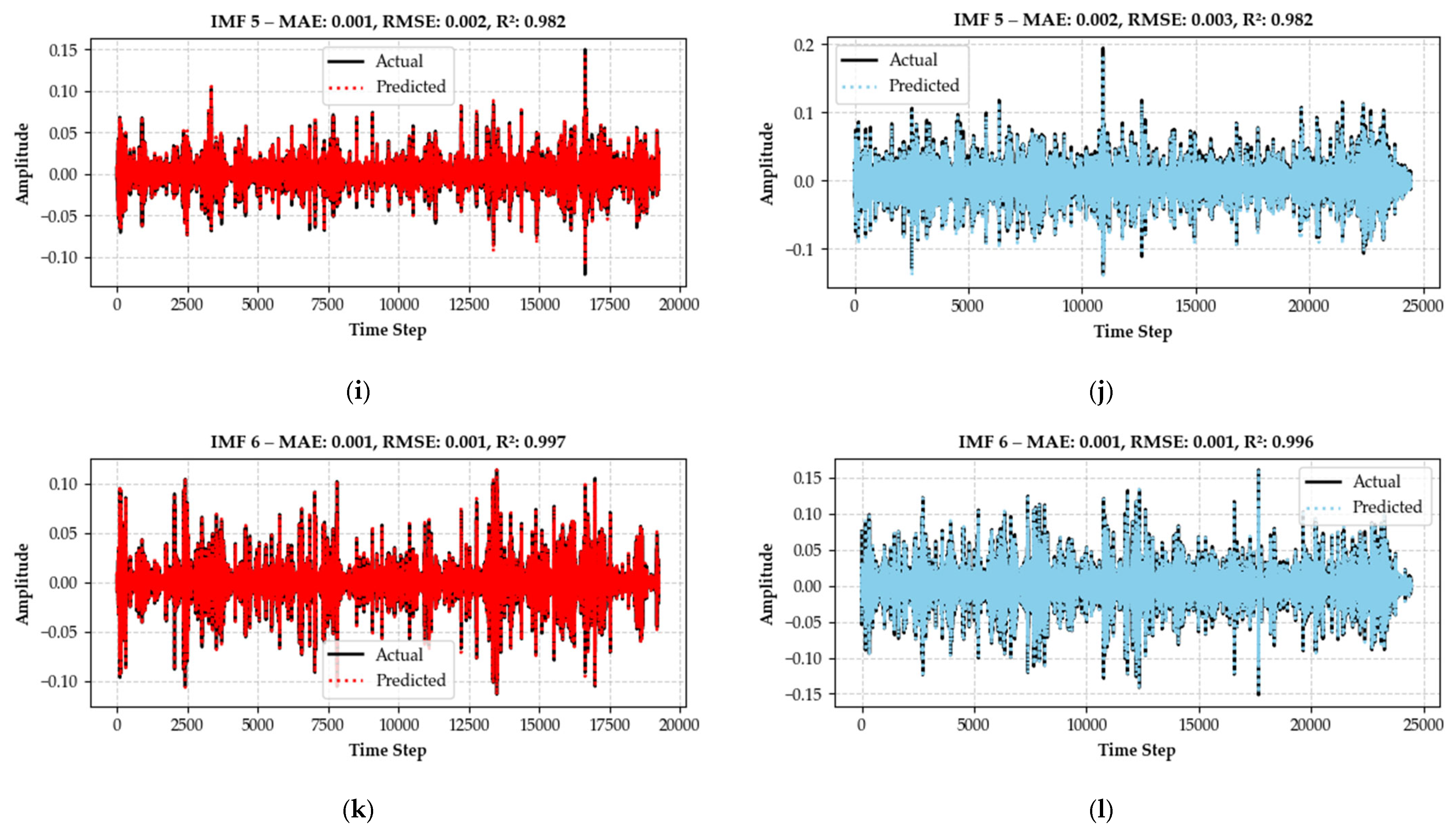

| Date and Time | Wind Shear Magnitude (Knots) | Elevation Angle (°) | Azimuth Angle (°) | Assigned Runway | Encounter Location |
|---|---|---|---|---|---|
| 29 January 2017 18:36 | 30 | (3.00 3.00) | (221, 271.5) | 25CA | 2 MF |
| 15 March 2018 15:41 | 24 | (3.00 3.00) | (278, 260.5) | 07CA | 1 MF |
| - | - | - | - | - | - |
| 27 January 2019 7:02 | 16 | (3.00 3.00) | (265, 242.5) | 07CD | RWY |
| - | - | - | - | - | - |
| 11 June 2020 21:08 | 24 | (3.00 3.00) | (225, 230.5) | 25CA | RWY |
| 15 October 2021 15:41 | 21 | (3.00 3.00) | (278, 260.5) | 07CA | 1 MD |
| Date and Time | Wind Shear Magnitude (Knots) | Elevation Angle (°) | Azimuth Angle (°) | Assigned Runway | Encounter Location |
|---|---|---|---|---|---|
| 27 May 2017 5:37 | 23 | (3.00 3.00) | (223, 248.5) | 07LA | 1 MD |
| 18 August 2019 18:42 | 35 | (3.00 3.00) | (262, 276.3) | 25LA | 1 MF |
| - | - | - | - | - | - |
| 11 March 2020 16:55 | 18 | (3.00 3.00) | (249, 273.5) | 25LA | 2 MD |
| - | - | - | - | - | - |
| 20 August 2021 11:03 | 30 | (3.00 3.00) | (280, 220.5) | 07RD | RWY |
| 18 October 2021 5:31 | 20 | (3.00 3.00) | (262, 269.5) | 07RA | 2 MF |
| Metric | Description | Expression |
|---|---|---|
| MSE | Calculates the mean of the squared deviations between the predicted and actual values. | |
| RMSE | Represents the square root of the mean squared differences between predicted outputs and actual observations. | |
| R2 | Indicates the proportion of variance in the actual values that is explained by the model’s predictions, reflecting how well the model fits the observed data. |
| IMF | Batch Size (Range) | Batch Size (Central) | Batch Size (South) | GRUs (Range) | GRUs (Central) | GRUs (South) | Learning Rate (Range) | Learning Rate (Central) | Learning Rate (South) |
|---|---|---|---|---|---|---|---|---|---|
| IMF-1 | 32–128 | 32 | 64 | 50–160 | 100 | 128 | 0.001–0.01 | 0.00167 | 0.00167 |
| IMF-2 | 80 | 32 | 64 | 70 | 0.00698 | 0.00588 | |||
| IMF-3 | 64 | 64 | 50 | 90 | 0.00217 | 0.00367 | |||
| IMF-4 | 40 | 35 | 60 | 90 | 0.00145 | 0.00234 | |||
| IMF-5 | 32 | 32 | 60 | 120 | 0.00105 | 0.00365 | |||
| IMF-6 | 60 | 85 | 50 | 55 | 0.00243 | 0.00163 |
| Hyperparameter | Range | Optimal Value (Central) | Optimal Value (South) |
|---|---|---|---|
| n_estimators | 100–1000 | 325 | 250 |
| max_depth | 3–10 | 3 | 6 |
| learning_rate | 0.01–0.3 | 0.17 | 0.09 |
| Model | Central Runway | South Runway | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | R2 | MAE | RMSE | R2 | |
| Training data | ||||||
| OVMD–BIGRU–XGBoost | 0.624 | 0.931 | 0.773 | 0.521 | 0.709 | 0.921 |
| OVMD–GRU–XGBoost | 0.705 | 1.042 | 0.712 | 0.593 | 0.821 | 0.884 |
| OVMD–ResNet–XGBoost | 0.794 | 1.201 | 0.648 | 0.681 | 0.933 | 0.836 |
| OVMD–LSTM–XGBoost | 0.682 | 1.015 | 0.719 | 0.571 | 0.789 | 0.895 |
| OVMD–BiLSTM–XGBoost | 0.643 | 0.964 | 0.755 | 0.538 | 0.738 | 0.913 |
| Testing data | ||||||
| OVMD–BIGRU–XGBoost | 0.624 | 0.931 | 0.729 | 0.521 | 0.709 | 0.926 |
| OVMD–GRU–XGBoost | 0.721 | 1.081 | 0.685 | 0.611 | 0.842 | 0.874 |
| OVMD–ResNet–XGBoost | 0.812 | 1.232 | 0.624 | 0.698 | 0.957 | 0.827 |
| OVMD–LSTM–XGBoost | 0.697 | 1.038 | 0.702 | 0.582 | 0.814 | 0.884 |
| OVMD–BiLSTM–XGBoost | 0.659 | 0.979 | 0.716 | 0.547 | 0.759 | 0.911 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khattak, A.; Chan, P.-w.; Chen, F.; Alyami, H.; Alajmi, M. A Signal Processing-Guided Deep Learning Framework for Wind Shear Prediction on Airport Runways. Atmosphere 2025, 16, 802. https://doi.org/10.3390/atmos16070802
Khattak A, Chan P-w, Chen F, Alyami H, Alajmi M. A Signal Processing-Guided Deep Learning Framework for Wind Shear Prediction on Airport Runways. Atmosphere. 2025; 16(7):802. https://doi.org/10.3390/atmos16070802
Chicago/Turabian StyleKhattak, Afaq, Pak-wai Chan, Feng Chen, Hashem Alyami, and Masoud Alajmi. 2025. "A Signal Processing-Guided Deep Learning Framework for Wind Shear Prediction on Airport Runways" Atmosphere 16, no. 7: 802. https://doi.org/10.3390/atmos16070802
APA StyleKhattak, A., Chan, P.-w., Chen, F., Alyami, H., & Alajmi, M. (2025). A Signal Processing-Guided Deep Learning Framework for Wind Shear Prediction on Airport Runways. Atmosphere, 16(7), 802. https://doi.org/10.3390/atmos16070802








