Increased Frequency of Central Pacific El Niño Events Since 2000 Caused by Frequent Anomalous Warm Zonal Advection
Abstract
1. Introduction
2. Data and Methods
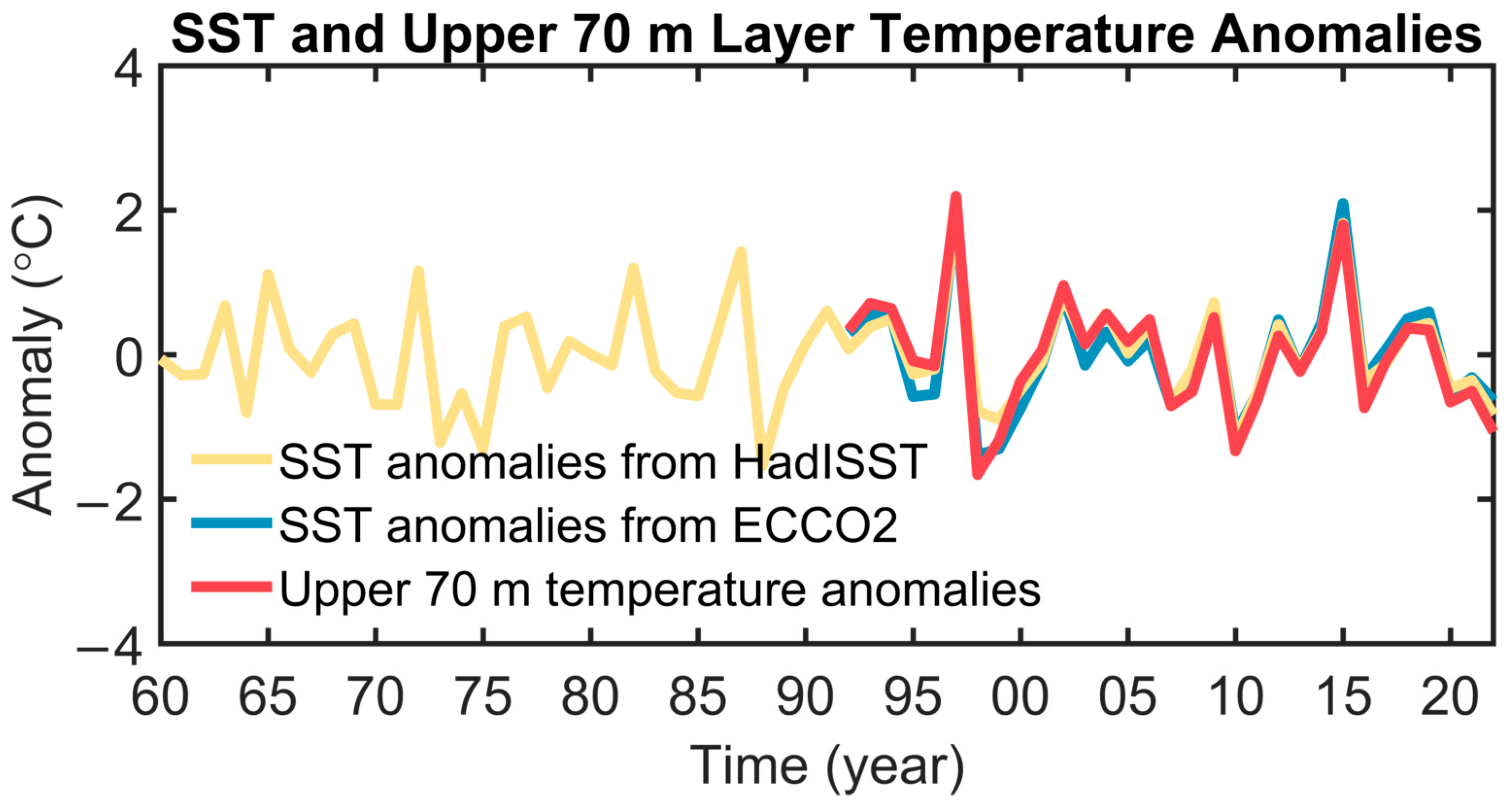
2.1. Data
2.2. Methods
2.2.1. Identification of CP and EP El Niño Events
2.2.2. Significance Tests
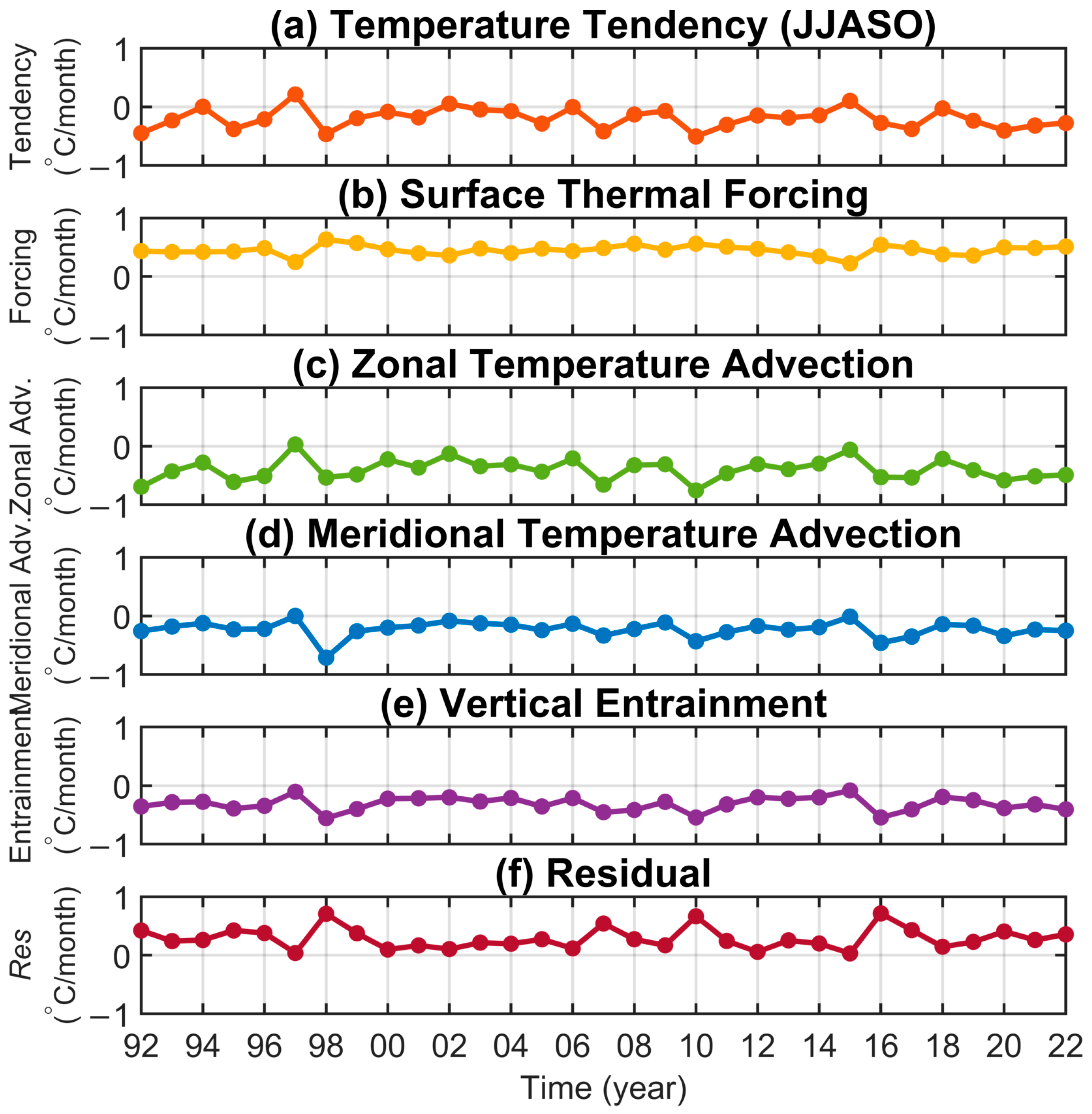
2.2.3. The Mixed Layer Heat Budget Equation
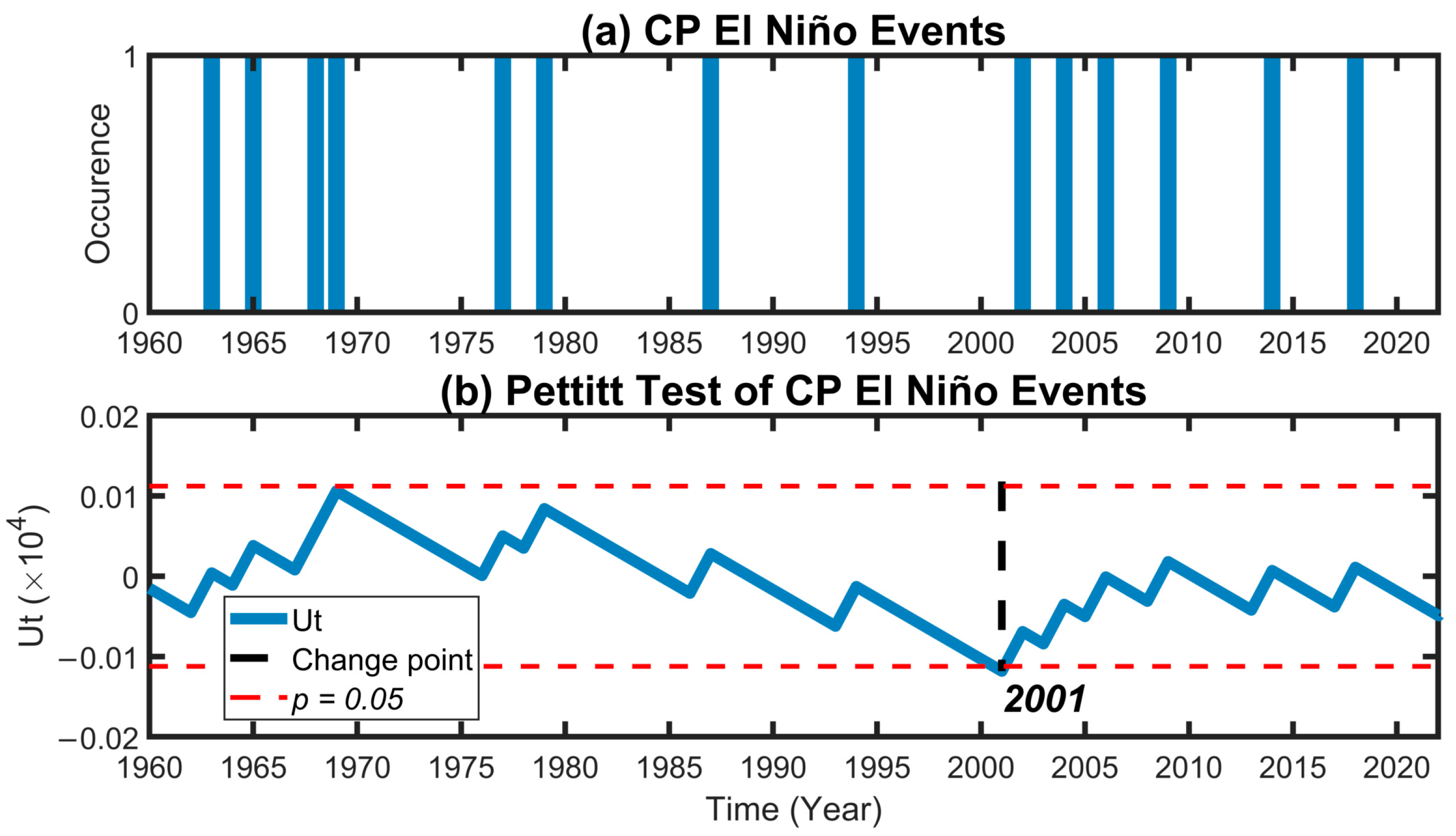
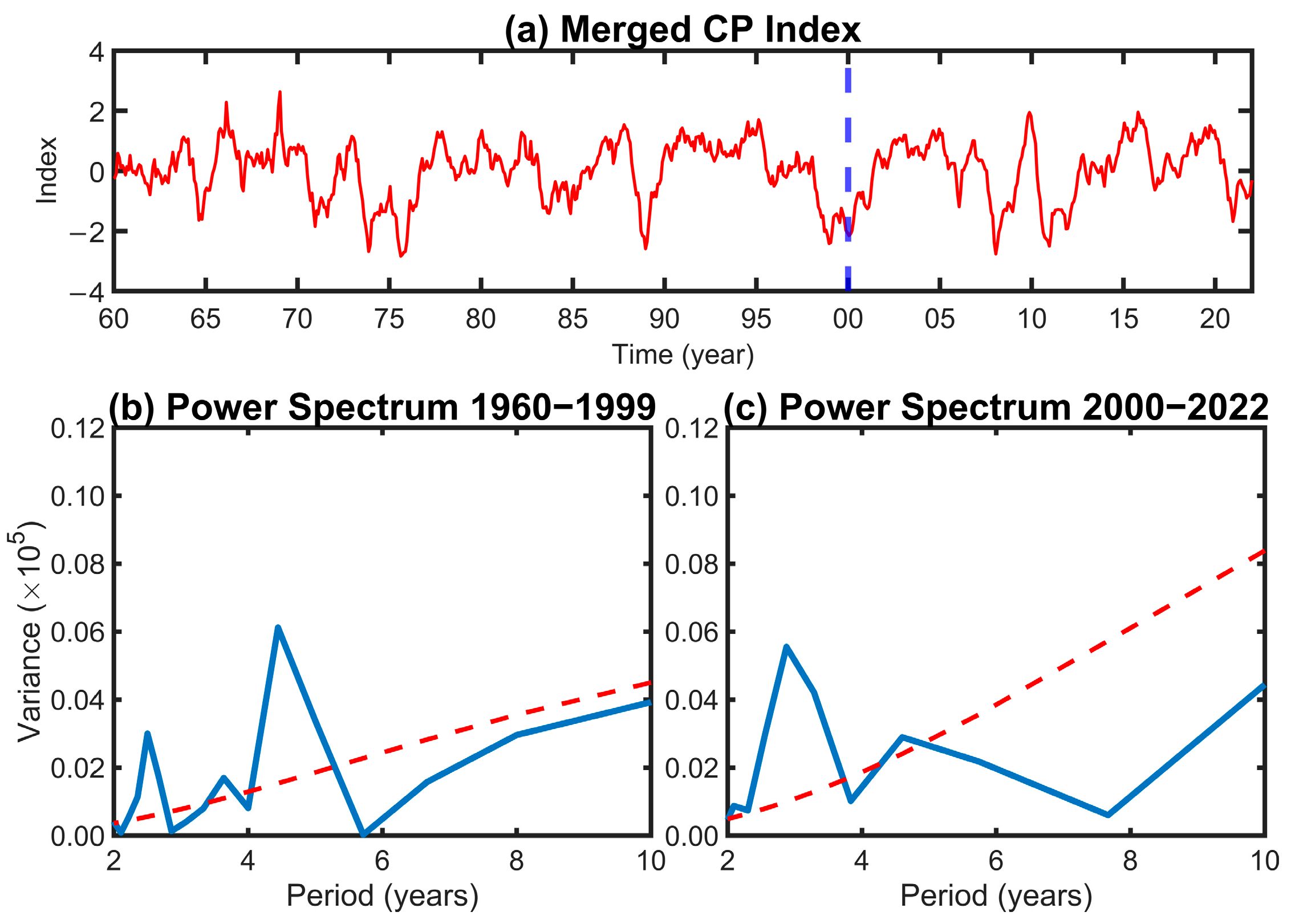
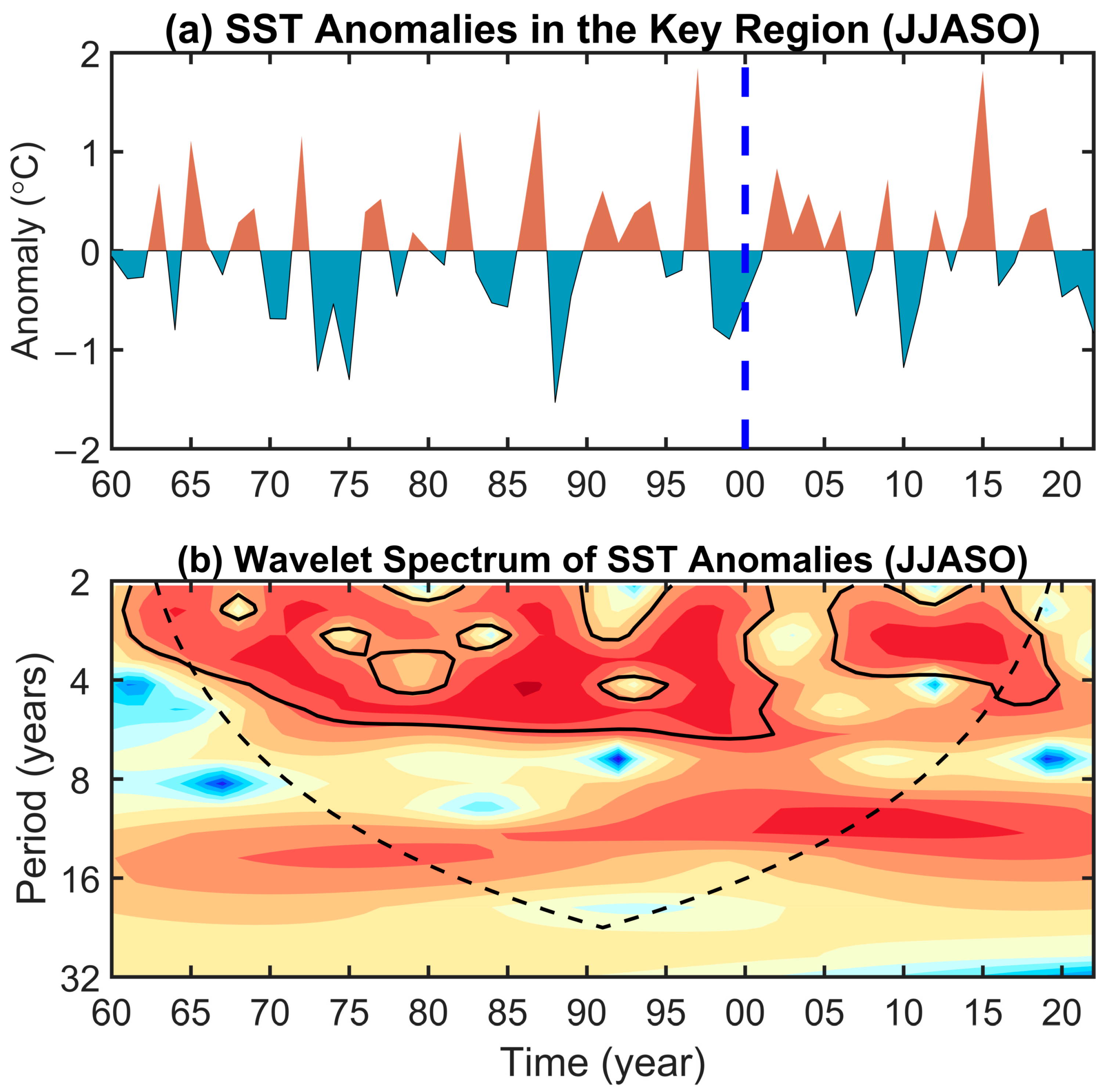
3. Increase in CP El Niño Frequency Since 2000
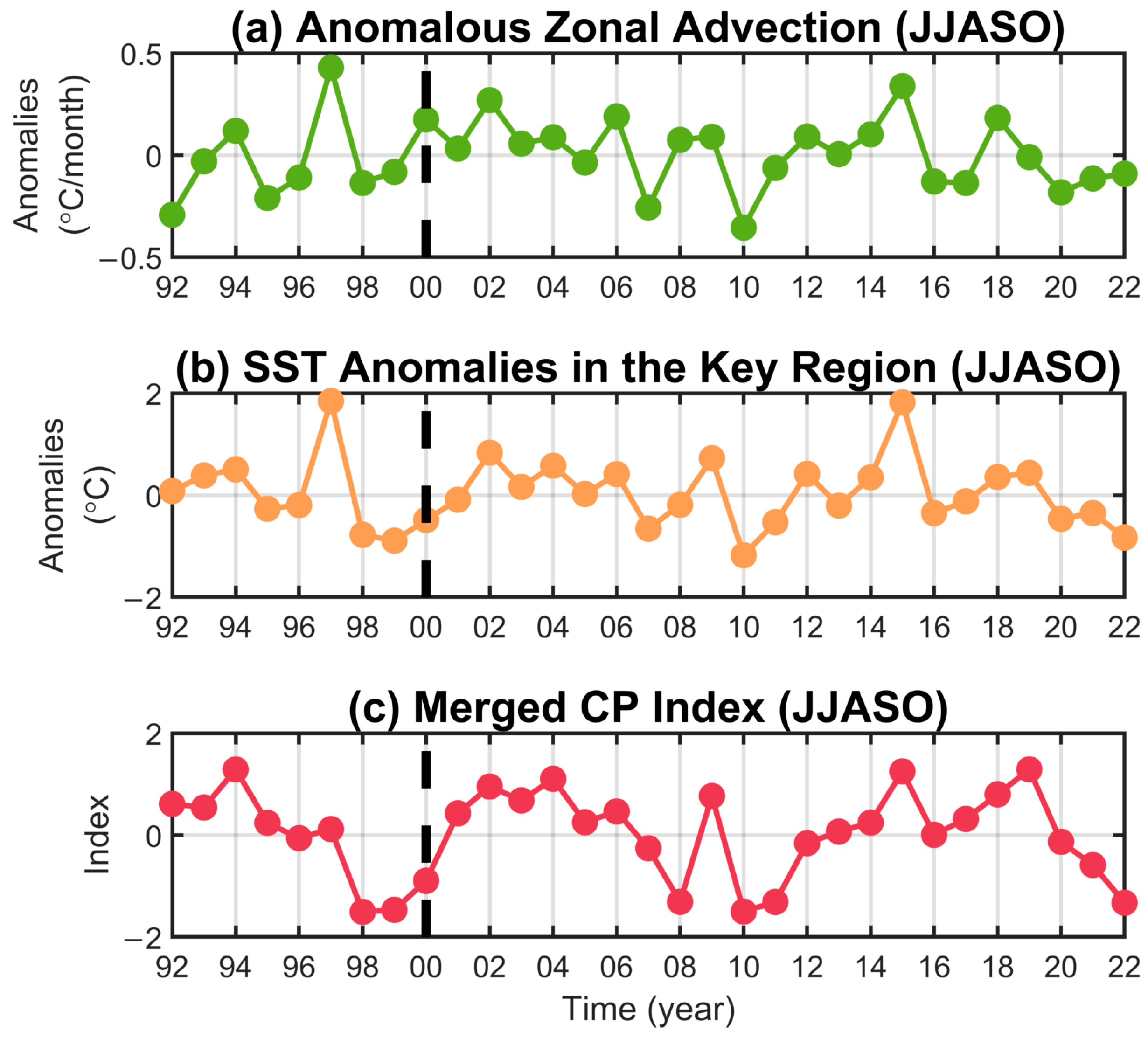
4. Mechanisms
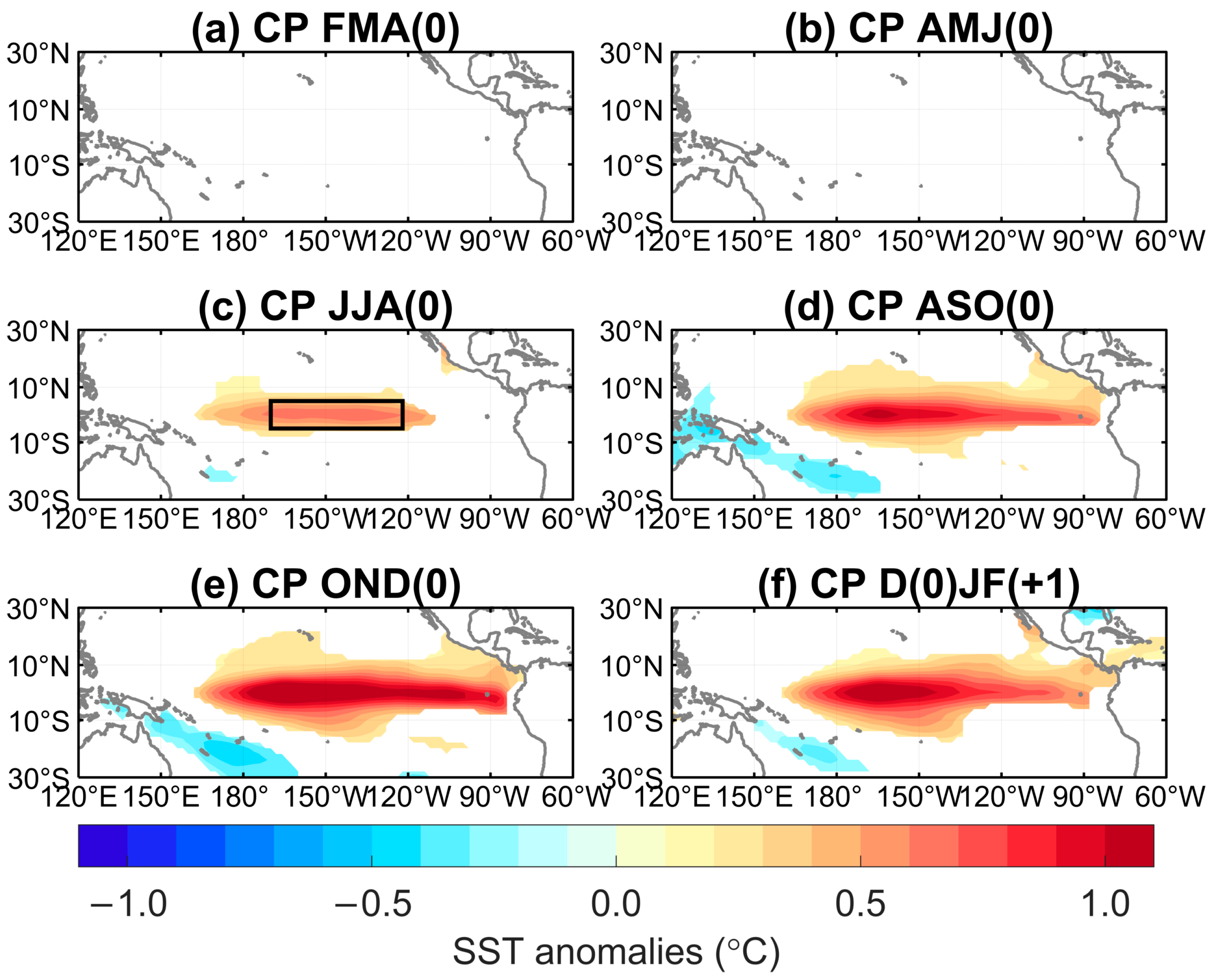
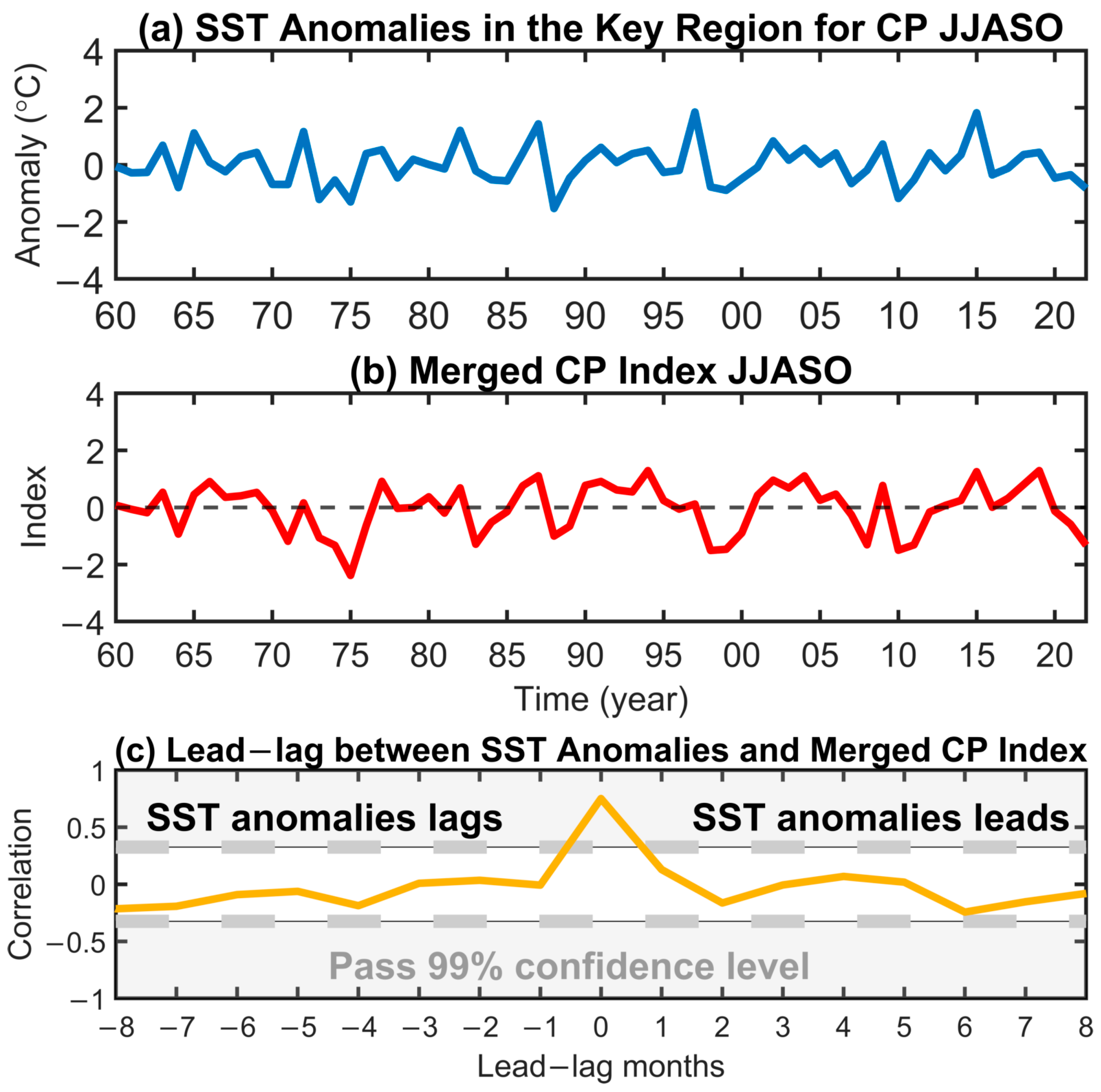
4.1. More Frequent Warm SST Anomalies in the Key Region
4.2. Role of Anomalous Warm Zonal Advection
5. Conclusions
6. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ENSO | El Niño–Southern Oscillation |
| SST | Sea surface temperature |
| EP | Eastern Pacific |
| CP | Central Pacific |
| ONI | Ocean Niño Index |
| NWP | Warm pool Niño index |
| NCT | Cold tongue Niño index |
| HadISST | The Hadley Centre Sea Ice and Sea Surface Temperature |
| FMA | February, March, and April |
| AMJ | April, May, and June |
| JJA | June, July, and August |
| ASO | August, September, and October |
| OND | October, November, and December |
| DJF | December, January, and February |
References
- Newman, M.; Shin, S.I.; Alexander, M.A. Natural variation in ENSO flavors. Geophys. Res. Lett. 2011, 38, L14705. [Google Scholar] [CrossRef]
- Bjerknes, J. Atmospheric Teleconnections from the Equatorial Pacific1. Mon. Weather Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P.J. Interdecadal Changes in the ENSO–Monsoon System. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Nicholls, N. Predictability of Interannual Variations of Australian Seasonal Tropical Cyclone Activity. Mon. Weather Rev. 1985, 113, 1144–1149. [Google Scholar] [CrossRef]
- Rasmusson, E.M.; Carpenter, T.H. Variations in Tropical Sea Surface Temperature and Surface Wind Fields Associated with the Southern Oscillation/El Niño. Mon. Weather Rev. 1982, 110, 354–384. [Google Scholar] [CrossRef]
- Jin, F.F.; Kug, J.S.; An, S.-I. Two Types of El Niño Events: Cold Tongue El Niño and Warm Pool El Niño. J. Clim. 2009, 22, 1499–1515. [Google Scholar] [CrossRef]
- Troup, A. The ‘southern oscillation’. Q. J. R. Meteorol. Soc. 1965, 91, 490–506. [Google Scholar] [CrossRef]
- Kim, H.M.; Webster, P.J.; Curry, J.A. Impact of shifting patterns of Pacific Ocean warming on North Atlantic tropical cyclones. Science 2009, 325, 77–80. [Google Scholar] [CrossRef]
- Wang, C.; Deser, C.; Yu, J.-Y.; DiNezio, P.; Clement, A. El Niño and Southern Oscillation (ENSO): A Review. In Coral Reefs of the Eastern Tropical Pacific; Coral Reefs of the World; Springer: Berlin/Heidelberg, Germany, 2017; pp. 85–106. [Google Scholar]
- Alexander, M.A.; Bladé, I.; Newman, M.; Lanzante, J.R.; Lau, N.-C.; Scott, J.D. The atmospheric bridge: The influence of ENSO teleconnections on air–sea interaction over the global oceans. J. Clim. 2002, 15, 2205–2231. [Google Scholar] [CrossRef]
- Jiang, T.; Kundzewicz, Z.W.; Su, B. Changes in monthly precipitation and flood hazard in the Yangtze River Basin, China. Int. J. Climatol. A J. R. Meteorol. Soc. 2008, 28, 1471–1481. [Google Scholar] [CrossRef]
- Changnon, S.A. Impacts of 1997–98 EI Niño–generated weather in the United States. Bull. Am. Meteorol. Soc. 1999, 80, 1819–1828. [Google Scholar] [CrossRef]
- Alizadeh-Choobari, O. Contrasting global teleconnection features of the eastern Pacific and central Pacific El Niño events. Dyn. Atmos. Ocean. 2017, 80, 139–154. [Google Scholar] [CrossRef]
- Shin, N.Y.; Kug, J.-S.; Stuecker, M.F.; Jin, F.F.; Timmermann, A.; Kim, G.-I. More frequent central Pacific El Niño and stronger eastern pacific El Niño in a warmer climate. NPJ Clim. Atmos. Sci. 2022, 5, 101. [Google Scholar] [CrossRef]
- Ashok, K.; Behera, S.K.; Rao, S.A.; Weng, H.; Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. 2007, 112, C11007. [Google Scholar] [CrossRef]
- Yu, J.Y.; Kao, H.Y. Contrasting Eastern-Pacific and Central-Pacific Types of ENSO. J. Clim. 2009, 22, 615–632. [Google Scholar] [CrossRef]
- Kim, S.T.; Yu, J.-Y. Reversed Spatial Asymmetries between El Niño and La Niña and Their Linkage to Decadal ENSO Modulation in CMIP3 Models. J. Clim. 2011, 24, 5423–5434. [Google Scholar] [CrossRef]
- Larkin, N.K.; Harrison, D. Global seasonal temperature and precipitation anomalies during El Niño autumn and winter. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Jia, L.; Guo, Y. Revisiting the differential impacts of Eastern-Pacific and Central-Pacific El Niño on late autumn to winter precipitation over South China. Dyn. Atmos. Ocean. 2025, 110, 101557. [Google Scholar] [CrossRef]
- Yu, J.Y.; Zou, Y.h.; Kim, S.T.; Lee, T. The changing impact of El Niño on US winter temperatures. Geophys. Res. Lett. 2012, 39, L15702. [Google Scholar] [CrossRef]
- Schopf, P.S.; Suarez, M.J. Vacillations in a Coupled Ocean–Atmosphere Model. J. Atmos. Sci. 1988, 45, 549–566. [Google Scholar] [CrossRef]
- Jin, F.-F. An equatorial ocean recharge paradigm for ENSO. Part II: A stripped-down coupled model. J. Atmos. Sci. 1997, 54, 830–847. [Google Scholar] [CrossRef]
- Weisberg, R.H.; Wang, C. A western Pacific oscillator paradigm for the El Niño-Southern Oscillation. Geophys. Res. Lett. 1997, 24, 779–782. [Google Scholar] [CrossRef]
- Picaut, J.; Masia, F.; du Penhoat, Y. An advective-reflective conceptual model for the oscillatory nature of the ENSO. Science 1997, 277, 663–666. [Google Scholar] [CrossRef]
- Battisti, D.S.; Hirst, A.C. Interannual Variability in a Tropical Atmosphere–Ocean Model: Influence of the Basic State, Ocean Geometry and Nonlinearity. J. Atmos. Sci. 1989, 46, 1687–1712. [Google Scholar] [CrossRef]
- Jin, F.F. An equatorial ocean recharge paradigm for ENSO. Part I: Conceptual model. J. Atmos. Sci. 1997, 54, 811–829. [Google Scholar] [CrossRef]
- Wang, C.Z.; Weisberg, R.H.; Virmani, J.I. Western Pacific interannual variability associated with the El Niño-Southern Oscillation. J. Geophys. Res. Ocean. 1999, 104, 5131–5149. [Google Scholar] [CrossRef]
- Yeh, S.W.; Kug, J.S.; Dewitte, B.; Kwon, M.H.; Kirtman, B.P.; Jin, F.-F. El Niño in a changing climate. Nature 2009, 461, 511–514. [Google Scholar] [CrossRef]
- Xiang, B.Q.; Wang, B.; Li, T. A new paradigm for the predominance of standing central Pacific warming after the late 1990s. Clim. Dyn. 2013, 41, 327–340. [Google Scholar] [CrossRef]
- Yu, J.-Y.; Kao, H.-Y.; Lee, T. Subtropics-related interannual sea surface temperature variability in the central equatorial Pacific. J. Clim. 2010, 23, 2869–2884. [Google Scholar] [CrossRef]
- Vimont, D.J.; Alexander, M.; Fontaine, A. Midlatitude excitation of tropical variability in the Pacific: The role of thermodynamic coupling and seasonality. J. Clim. 2009, 22, 518–534. [Google Scholar] [CrossRef]
- Vimont, D.J.; Wallace, J.M.; Battisti, D.S. The seasonal footprinting mechanism in the Pacific: Implications for ENSO. J. Clim. 2003, 16, 2668–2675. [Google Scholar] [CrossRef]
- Vimont, D.J.; Battisti, D.S.; Hirst, A.C. Footprinting: A seasonal connection between the tropics and mid-latitudes. Geophys. Res. Lett. 2001, 28, 3923–3926. [Google Scholar] [CrossRef]
- Cai, W.; Borlace, S.; Lengaigne, M.; Van Rensch, P.; Collins, M.; Vecchi, G.; Timmermann, A.; Santoso, A.; McPhaden, M.J.; Wu, L. Increasing frequency of extreme El Niño events due to greenhouse warming. Nat. Clim. Change 2014, 4, 111–116. [Google Scholar] [CrossRef]
- Gan, R.Y.; Liu, Q.; Huang, G.; Hu, K.M.; Li, X.C. Greenhouse warming and internal variability increase extreme and central Pacific El Niño frequency since 1980. Nat. Commun. 2023, 14, 394. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.Y.; Yu, J.Y.; Wang, X.; Chen, S. Distinct onset mechanisms of two subtypes of CP El Niño and their changes in future warming. Geophys. Res. Lett. 2021, 48, e2021GL093707. [Google Scholar] [CrossRef]
- Ng, B.; Cai, W.; Cowan, T.; Bi, D. Impacts of low-frequency internal climate variability and greenhouse warming on El Niño–Southern Oscillation. J. Clim. 2021, 34, 2205–2218. [Google Scholar] [CrossRef]
- Freund, M.B.; Henley, B.J.; Karoly, D.J.; McGregor, H.V.; Abram, N.J.; Dommenget, D. Higher frequency of Central Pacific El Niño events in recent decades relative to past centuries. Nat. Geosci. 2019, 12, 450–455. [Google Scholar] [CrossRef]
- Solomon, S.; Rosenlof, K.H.; Portmann, R.W.; Daniel, J.S.; Davis, S.M.; Sanford, T.J.; Plattner, G.-K. Contributions of stratospheric water vapor to decadal changes in the rate of global warming. Science 2010, 327, 1219–1223. [Google Scholar] [CrossRef]
- Lee, T.; McPhaden, M.J. Increasing intensity of El Niño in the central-equatorial Pacific. Geophys. Res. Lett. 2010, 37, L14603. [Google Scholar] [CrossRef]
- Chung, P.H.; Li, T. Interdecadal relationship between the mean state and El Niño types. J. Clim. 2013, 26, 361–379. [Google Scholar] [CrossRef]
- Barnston, A.G.; Chelliah, M.; Goldenberg, S.B. Documentation of a highly ENSO-related SST region in the equatorial Pacific. Atmos.-Ocean (Can. Meteorol. Oceanogr. Soc.) 1997, 35, 367. [Google Scholar] [CrossRef]
- Takahashi, K.; Montecinos, A.; Goubanova, K.; Dewitte, B. ENSO regimes: Reinterpreting the canonical and Modoki El Niño. Geophys. Res. Lett. 2011, 38, L10704. [Google Scholar] [CrossRef]
- Ren, H.L.; Jin, F.F. Niño indices for two types of ENSO. Geophys. Res. Lett. 2011, 38, L04704. [Google Scholar] [CrossRef]
- Huang, B.Y.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended reconstructed sea surface temperature, version 5 (ERSSTv5): Upgrades, validations, and intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.; Folland, C.K.; Alexander, L.V.; Rowell, D.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 2003, 108, 4407. [Google Scholar] [CrossRef]
- Marshall, J.; Adcroft, A.; Hill, C.; Perelman, L.; Heisey, C. A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers. J. Geophys. Res. Ocean. 1997, 102, 5753–5766. [Google Scholar] [CrossRef]
- Kalnay, E. The NCEP/NCAR 40-yr reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 431–477. [Google Scholar] [CrossRef]
- Larkin, N.K. On the definition of El Niño and associated seasonal average U.S. weather anomalies. Geophys. Res. Lett. 2005, 32, L13705. [Google Scholar] [CrossRef]
- Mallakpour, I.; Villarini, G. A simulation study to examine the sensitivity of the Pettitt test to detect abrupt changes in mean. Hydrol. Sci. J. 2016, 61, 245–254. [Google Scholar] [CrossRef]
- Das, P.K.; Chandra, S.; Das, D.K.; Midya, S.K.; Paul, A.; Bandyopadhyay, S.; Dadhwal, V.K. Understanding the interactions between meteorological and soil moisture drought over Indian region. J. Earth Syst. Sci. 2020, 129, 197. [Google Scholar] [CrossRef]
- Pyper, B.J.; Peterman, R.M. Comparison of methods to account for autocorrelation in correlation analyses of fish data. Can. J. Fish. Aquat. Sci. 1998, 55, 2127–2140. [Google Scholar] [CrossRef]
- Qu, T. Mixed layer heat balance in the western North Pacific. J. Geophys. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- Bond, N.A.; Cronin, M.F.; Freeland, H.; Mantua, N. Causes and impacts of the 2014 warm anomaly in the NE Pacific. Geophys. Res. Lett. 2015, 42, 3414–3420. [Google Scholar] [CrossRef]
- Kara, A.B.; Rochford, P.A.; Hurlburt, H.E. Mixed layer depth variability over the global ocean. J. Geophys. Res. Ocean. 2003, 108. [Google Scholar] [CrossRef]
- de Boyer Montégut, C.; Madec, G.; Fischer, A.S.; Lazar, A.; Iudicone, D. Mixed layer depth over the global ocean: An examination of profile data and a profile-based climatology. J. Geophys. Res. Ocean. 2004, 109. [Google Scholar] [CrossRef]
- Su, J.Z.; Li, T.; Zhang, R.H. The initiation and developing mechanisms of central Pacific El Niños. J. Clim. 2014, 27, 4473–4485. [Google Scholar] [CrossRef]
- Feng, J.; Chen, W.; Tam, C.; Zhou, W. Different impacts of El Niño and El Niño Modoki on China rainfall in the decaying phases. Int. J. Climatol. 2011, 31, 2091–2101. [Google Scholar] [CrossRef]
- Kousky, V.E. The global climate of December 1991–February 1992: Mature-phase warm (ENSO) episode conditions develop. J. Clim. 1993, 6, 1639–1655. [Google Scholar] [CrossRef]
- Iwakiri, T.; Watanabe, M. Multiyear La Niña impact on summer temperature over Japan. J. Meteorol. Soc. Jpn. Ser. II 2020, 98, 1245–1260. [Google Scholar] [CrossRef]
- Woolway, R.I.; Sharma, S.; Weyhenmeyer, G.A.; Debolskiy, A.; Golub, M.; Mercado-Bettín, D.; Perroud, M.; Stepanenko, V.; Tan, Z.; Grant, L. Phenological shifts in lake stratification under climate change. Nat. Commun. 2021, 12, 2318. [Google Scholar] [CrossRef]
- L’Heureux, M.L.; Takahashi, K.; Watkins, A.B.; Barnston, A.G.; Becker, E.J.; Di Liberto, T.E.; Gamble, F.; Gottschalck, J.; Halpert, M.S.; Huang, B. Observing and predicting the 2015/16 El Niño. Bull. Am. Meteorol. Soc. 2017, 98, 1363–1382. [Google Scholar] [CrossRef]
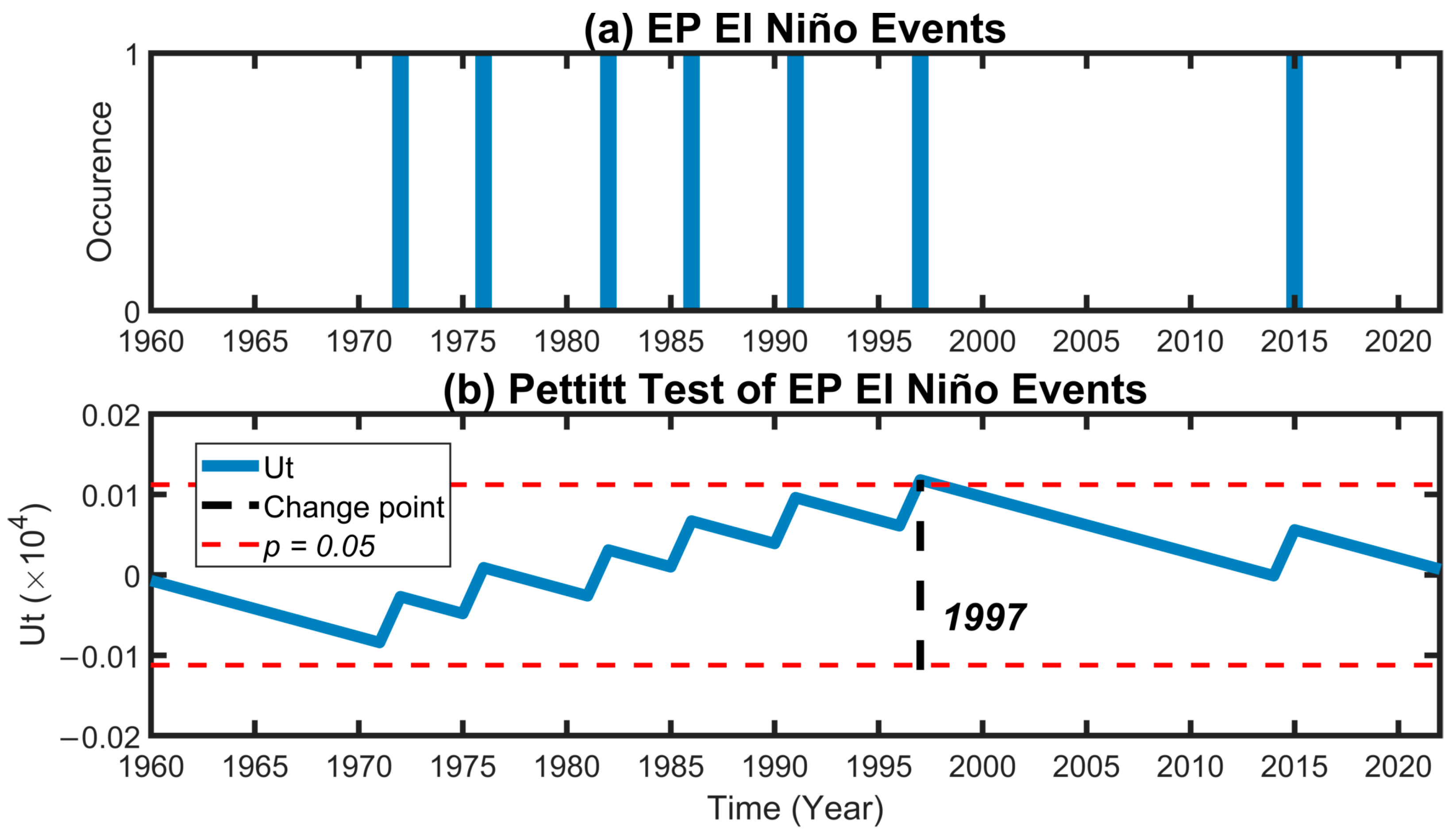
| CP El Niño Events | EP El Niño Events | |
|---|---|---|
| Years | 1963–1964; 1965–1966; 1968–1969; 1969–1970; 1977–1978; 1979–1980; 1987–1988; 1994–1995; 2002–2003; 2004–2005; 2006–2007; 2009–2010; 2014–2015; 2018–2019 | 1972–1973; 1976–1977; 1982–1983; 1986–1987; 1991–1992; 1997–1998; 2015–2016 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, L.; Guo, Y. Increased Frequency of Central Pacific El Niño Events Since 2000 Caused by Frequent Anomalous Warm Zonal Advection. Atmosphere 2025, 16, 654. https://doi.org/10.3390/atmos16060654
Jia L, Guo Y. Increased Frequency of Central Pacific El Niño Events Since 2000 Caused by Frequent Anomalous Warm Zonal Advection. Atmosphere. 2025; 16(6):654. https://doi.org/10.3390/atmos16060654
Chicago/Turabian StyleJia, Lanyu, and Yongqing Guo. 2025. "Increased Frequency of Central Pacific El Niño Events Since 2000 Caused by Frequent Anomalous Warm Zonal Advection" Atmosphere 16, no. 6: 654. https://doi.org/10.3390/atmos16060654
APA StyleJia, L., & Guo, Y. (2025). Increased Frequency of Central Pacific El Niño Events Since 2000 Caused by Frequent Anomalous Warm Zonal Advection. Atmosphere, 16(6), 654. https://doi.org/10.3390/atmos16060654






