Evaluation of Automated Spread–F (SF) Detection over the Midlatitude Ionosphere
Abstract
1. Introduction
2. Data
3. Analysis
3.1. Automated SF Detection
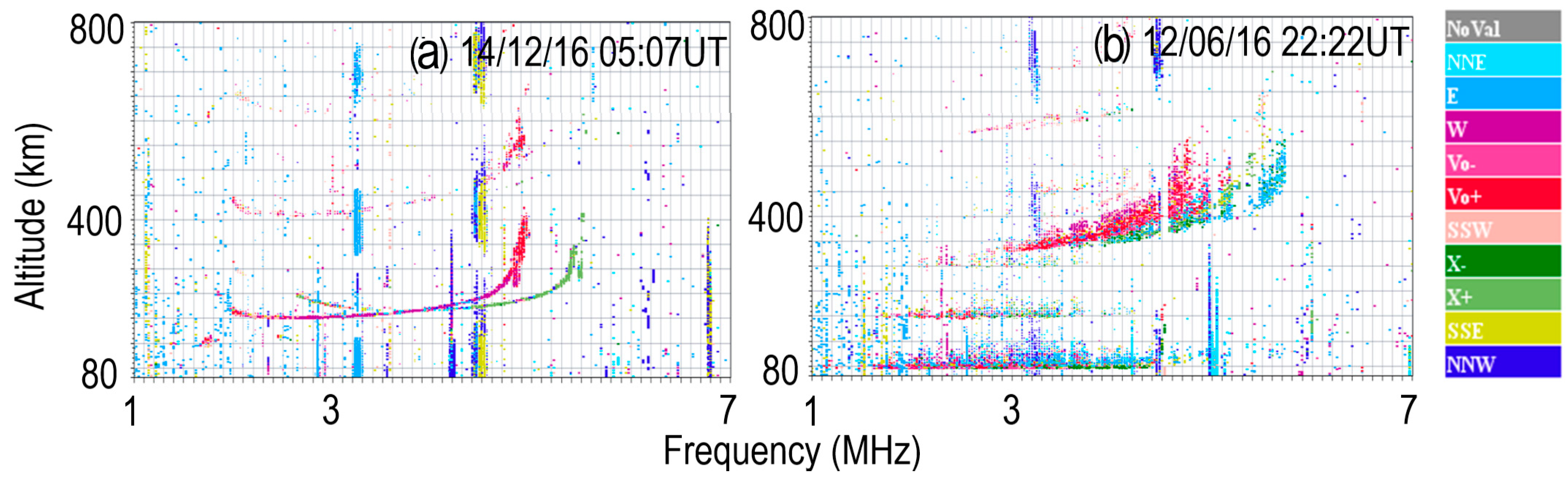
- QF > 0: This condition indicates the presence of RSF and specifies horizontal spreading in the F layer trace. QF is considered latitude independent and serves as a basic indicator of RSF activity [24].
- a < Δh′F < 200 km: h′F is a critical parameter, which indicates a sudden F layer uplift as an RSF driver. Δh′F exceeding a threshold value ‘a’ strongly suggests the likelihood of RSF. The value of ‘a’ (in km) is latitude dependent, as SF occurrence depends on latitude. We also apply an upper limit of 100 km to avoid spurious values caused by auto-scaling.
- hmF2 > b for FF < 1 MHz: hmF2 is commonly linked to FSF formation [1]. Here, we define ‘b’ (in km) as a latitude-dependent threshold, beyond which the probability of FSF increases under the condition that FF remains within realistic limits (FF < 1 MHz).
- FF > c and FF < 1 MHz, with hmF2 > b: While FF can indicate FSF, not all FF values confirm its presence. According to Paul and Haralambous (2025) [24], some FF values may result from unrelated irregularities. To address this, we calculated a threshold ‘c’ (in MHz), above which FF values pointed to confirmed FSF occurrence, particularly when accompanied by higher hmF2 values (hmF2 > b).
3.1.1. Algorithm Used for Automated SF Detection
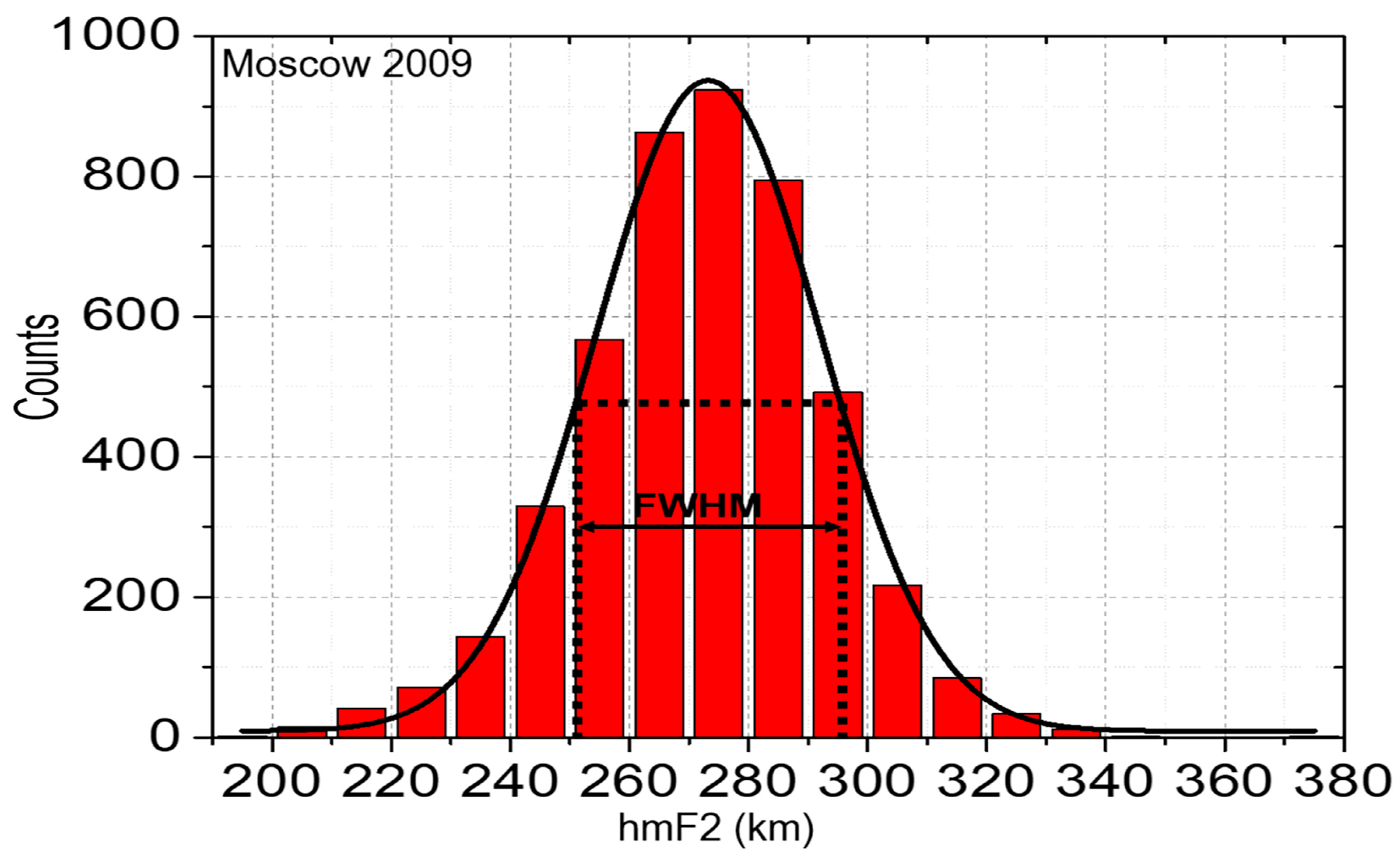
3.1.2. Calculation of Threshold Values
Threshold Estimation for Δh′F and hmF2
Threshold Estimation for FF
3.1.3. Statistics for Common Observation
- 35°–40° N: Thresholds were derived from Nicosia and validated over Athens and Nicosia.
- 40°–45° N: Thresholds were derived from Roquetes and validated over Roquetes and Rome.
- 50°–55° N: Thresholds were derived from Pruhonice and validated over Pruhonice, Dourbes, and Chilton.
- 55°–60° N: Thresholds were derived from Moscow and validated over Moscow and Juliusruh.
3.2. Manual SF Detection
4. Result and Discussion
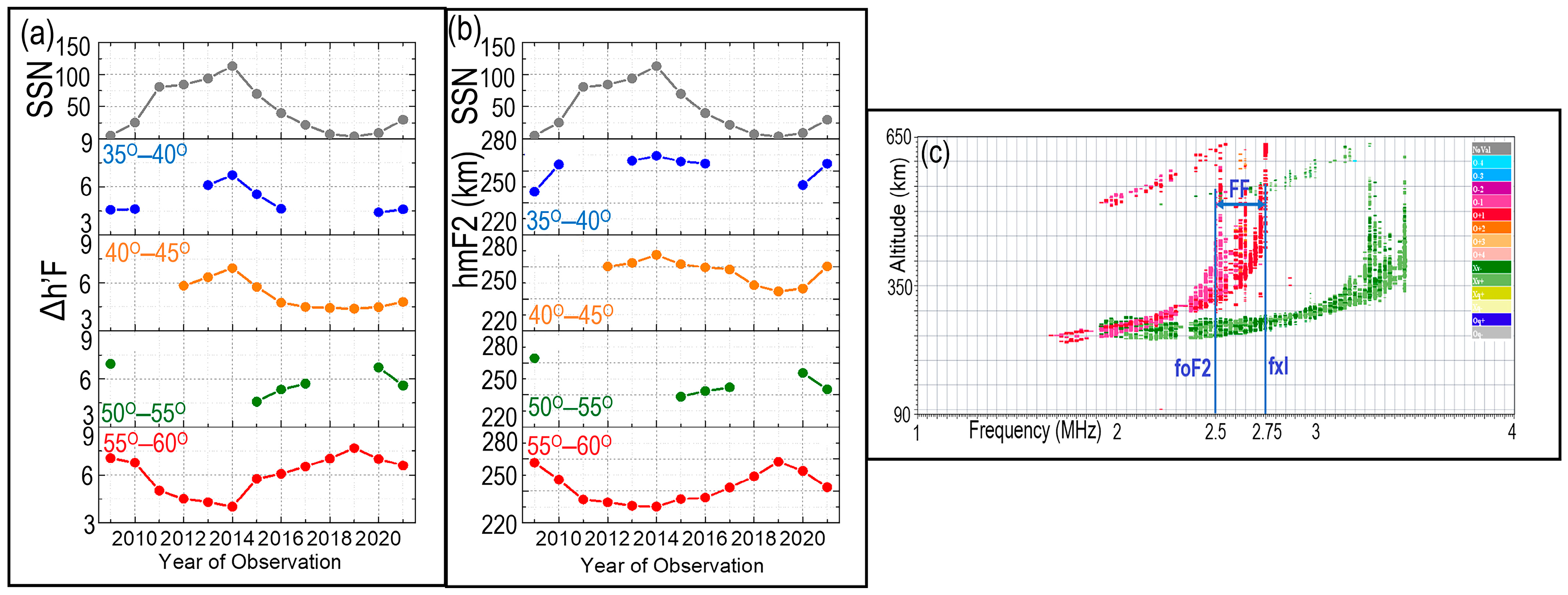
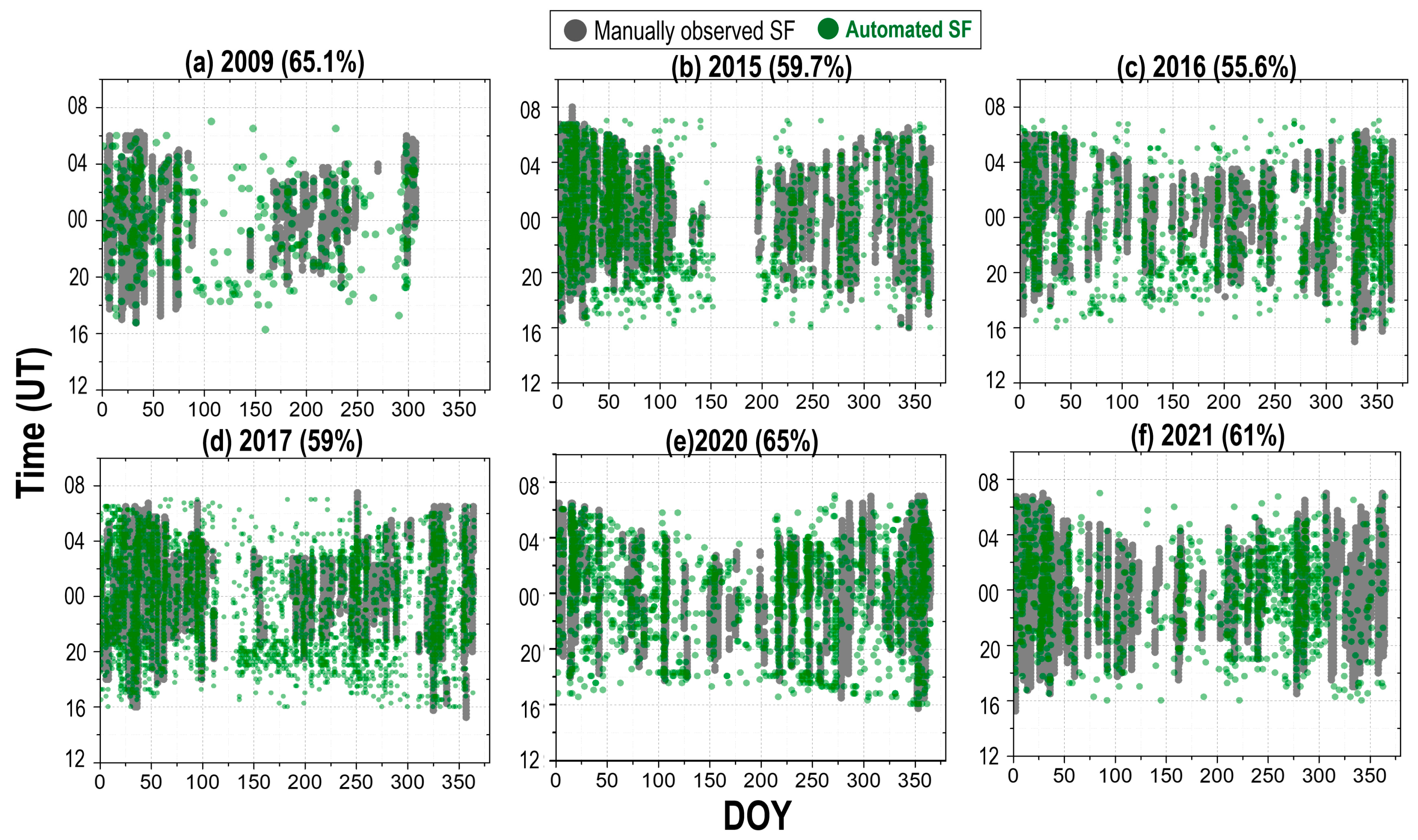
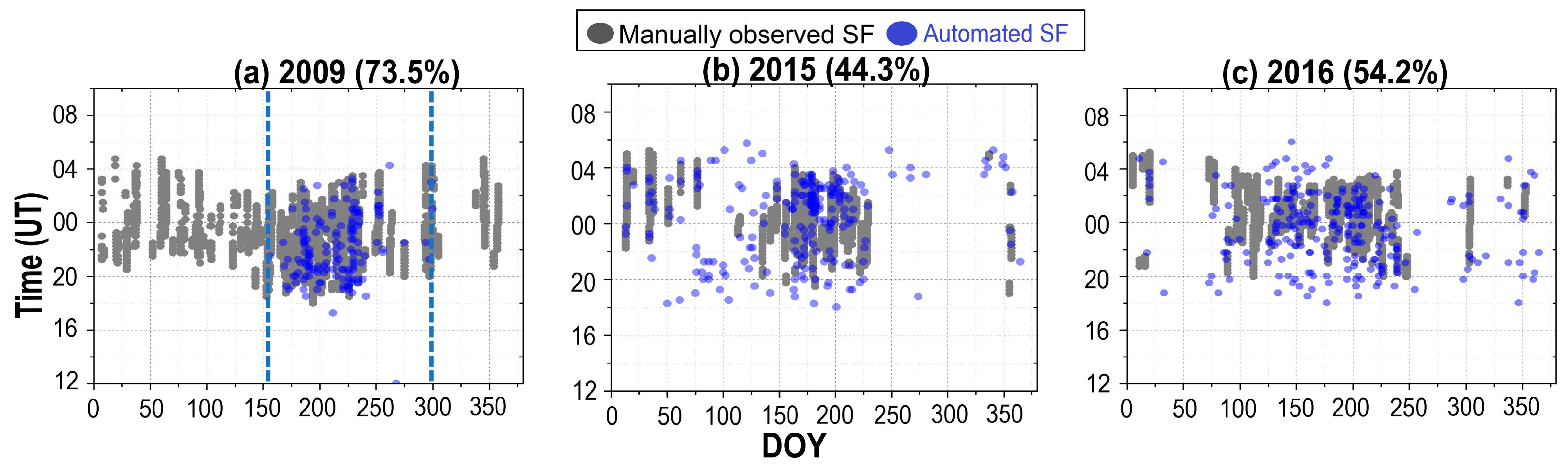
4.1. 55°–60° N Latitude
4.2. 50°–55° N Latitude
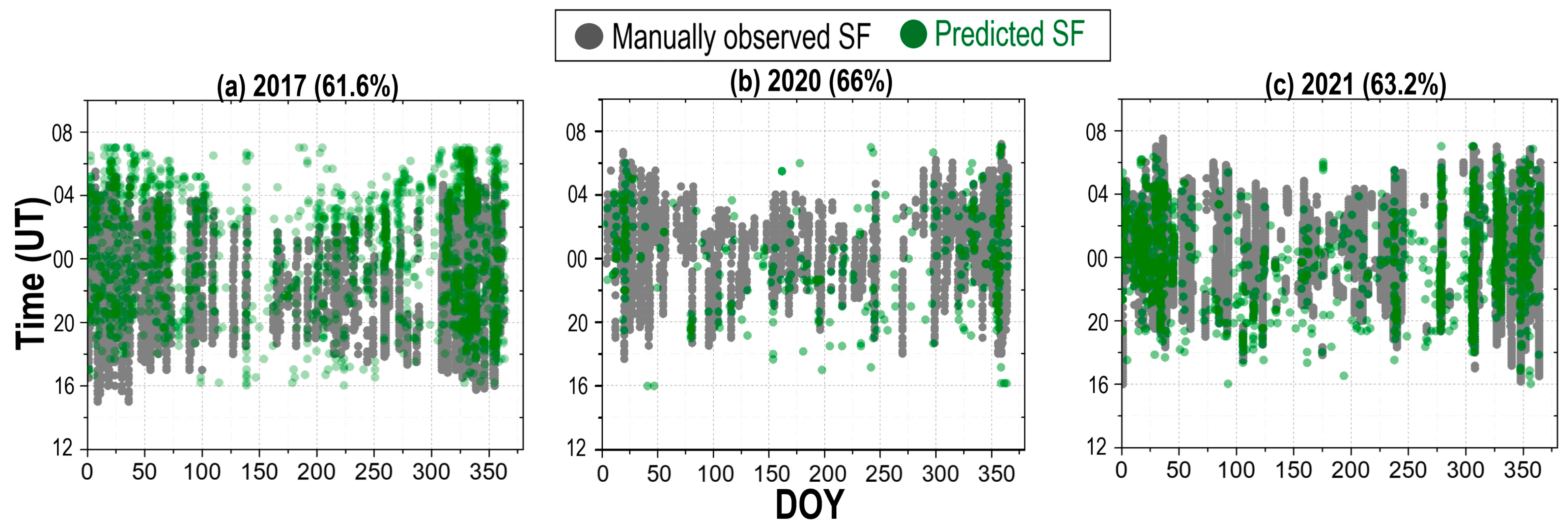
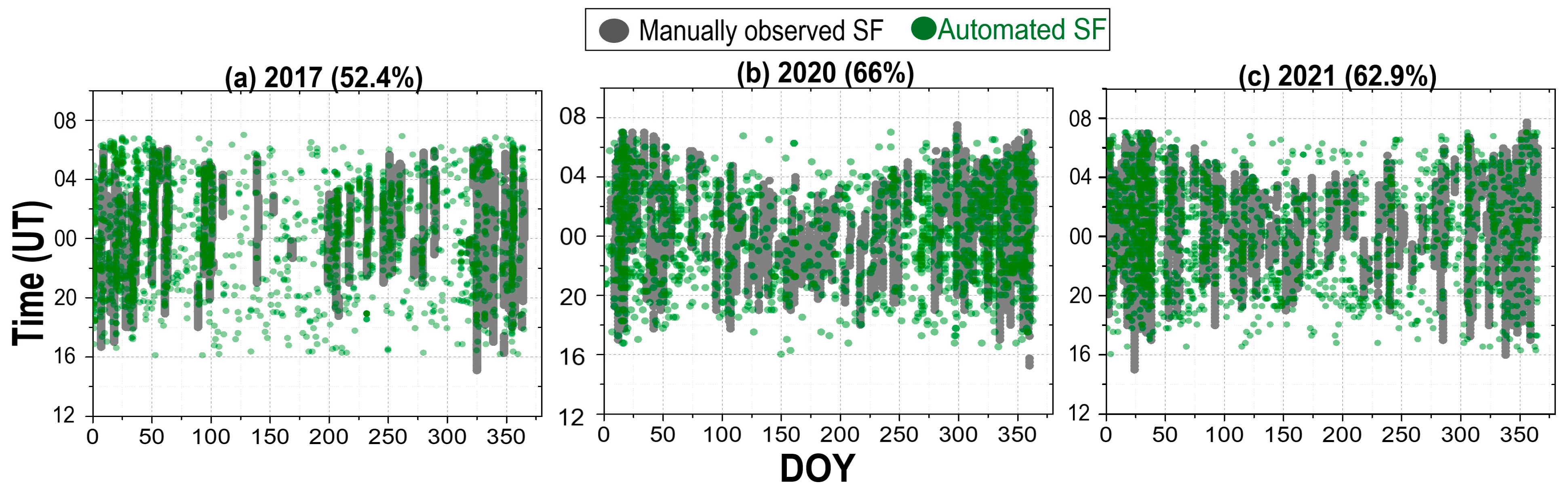
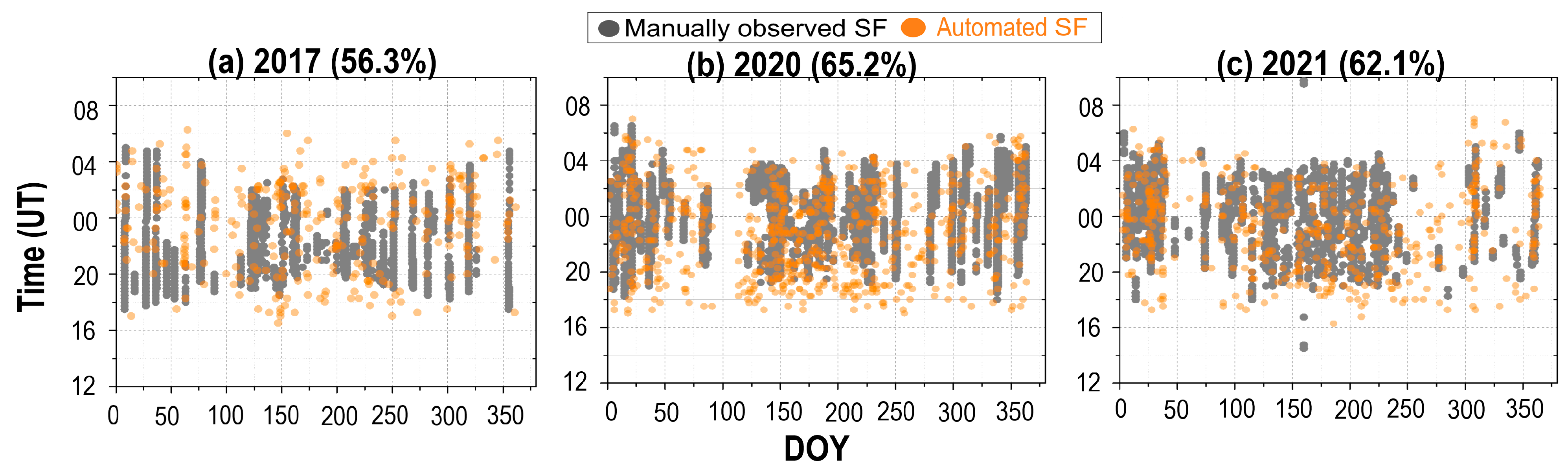
4.3. 45°–40° N Latitude
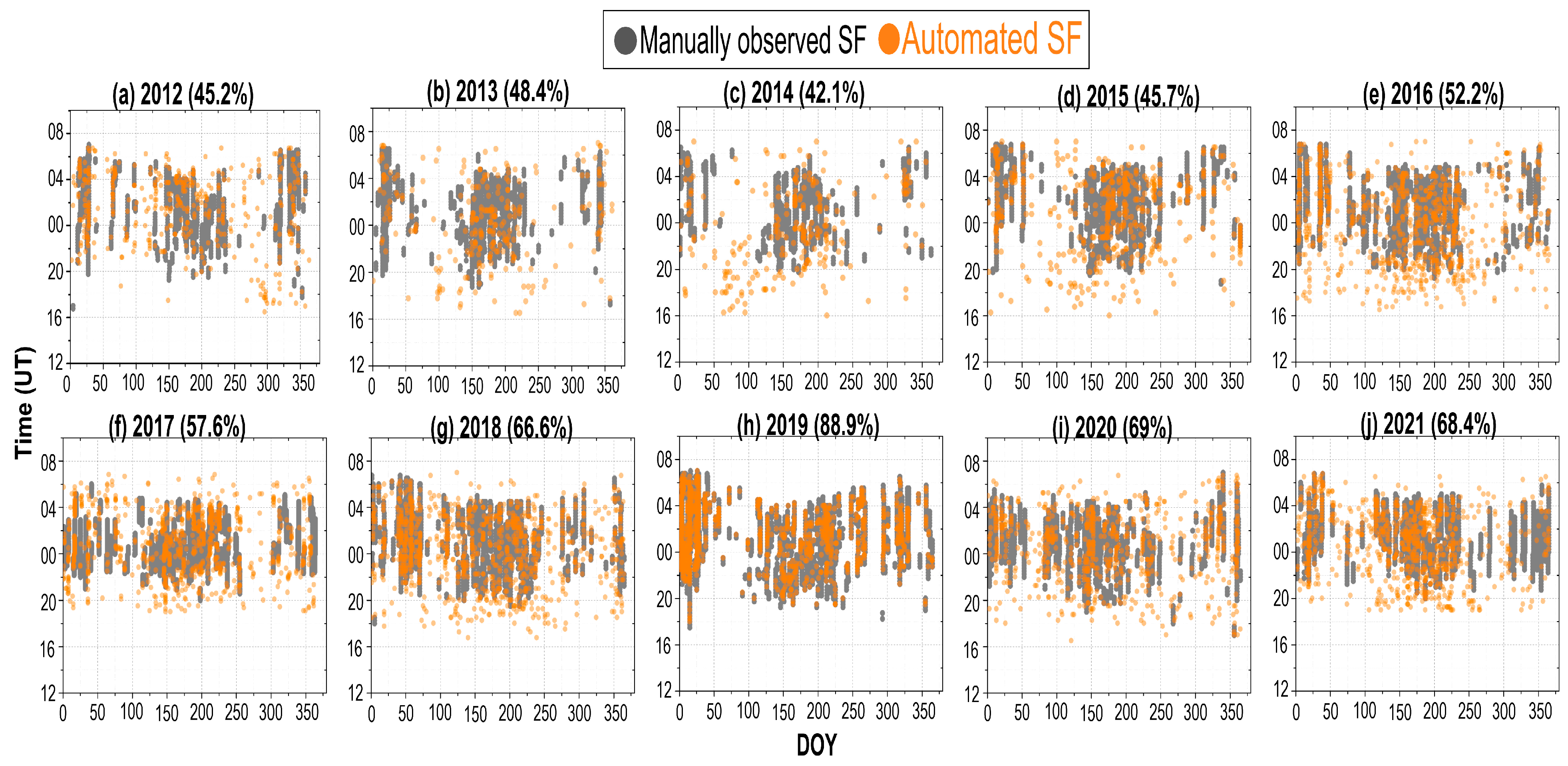
4.4. 35°–40° N Latitude
5. Conclusions
- i.
- In the 55°–60° N latitude sector, the association between automated SFP and SFM events ranged from a maximum of 71% during the solar minimum to a minimum of 47% during the solar maximum. The algorithm frequently overestimated SFP occurrences during periods of high solar activity, which is primarily attributed to LSTID activity that can mislead the detection algorithm.
- ii.
- The association between SFP and SFM in the 50°–55° N latitude sector reached a maximum of 66% during the solar minimum and a minimum of 56% during the solar maximum. Overestimation by SFP was predominantly observed during post-sunset hours during the equinox and summer under high solar activity. This overestimation is likely due to the presence of oblique traces or MSTIDs, which can interfere with accurate SF detection by resembling spread signatures in ionograms.
- iii.
- In the 40°–45° N latitude sector, the association between SFM and SFP reached a maximum of 89% during the solar minimum and dropped to a minimum of 42% during the solar maximum. SFP overestimated SFM, particularly during post-sunset hours in the equinoctial and summer months under high solar activity, likely due to the presence of STs and MREs, which can mimic SF signatures and confuse the auto-scaling algorithm. Conversely, during summer periods when SF occurrence is generally high in this region, SFP may have underestimated SFM. This underestimation is likely attributed to the presence of spread Es, which can blanket the F layer trace in ionograms, leading to scaling errors and the failure of the algorithm to detect actual SF events.
- iv.
- The SFM and SFP association in the 35°–40° N latitude sector varied from a maximum of 69% during the solar minimum to a minimum of 30% during the solar maximum. Overestimation by SFP was mostly noted during winter and high solar activity, which may have resulted from the STs and MREs that interfere with accurate SF detection. Additionally, during summer periods—when SF events are more frequent in this sector—SFP may have underestimated SFM, likely due to spread Es. These irregular Es layer structures can blanket the F trace in ionograms, preventing the auto-scaling algorithm from correctly identifying SF events and resulting in missed detections.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bowman, G.G. Frontal and non-frontal characteristics of mid-latitude spread-F structures. Indian J. Radio Space Phys. 1990, 19, 62–68. [Google Scholar]
- Bowman, G.G. The influence of 10.7-cm solar-flux variations on midlatitude daytime ionospheric disturbance conditions. J. Geophys. Res. 1996, 101, 10849–10854. [Google Scholar] [CrossRef]
- Paul, K.S.; Haralambous, H.; Oikonomou, C.; Paul, A.; Belehaki, A.; Ioanna, T.; Kouba, D.; Buresova, D. Multi-station investigation of spread F over Europe during low to high solar activity. J. Sp. Weather Sp. Clim. 2018, 8, A27. [Google Scholar] [CrossRef]
- Paul, K.S.; Haralambous, H.; Oikonomou, C.; Paul, A. Long-term aspects of nighttime spread F over a low mid-latitude European station. Adv. Space Res. 2019, 64, 1199–1216. [Google Scholar] [CrossRef]
- Paul, K.S.; Haralambous, H.; Singh, A.K.; Gulyaeva, T.L.; Panchenko, V.A. Mid-latitude Spread F long-term occurrence characteristics as a function of latitude over Europe. Adv. Space Res. 2022, 70, 710–722. [Google Scholar] [CrossRef]
- Paul, K.S.; Haralambous, H.; Oikonomou, C.; Singh, A.K.; Gulyaeva, T.L.; Panchenko, V.A.; Altadill, D.; Buresova, D.; Mielich, J.; Verhulst, T. A mid-latitude spread F over an extended European area. J. Atmos. Sol.-Terr. Phys. 2023, 248, 106093. [Google Scholar] [CrossRef]
- Vasylyev, D.; Béniguel, Y.; Volker, W.; Kriegel, M.; Berdermann, J. Modeling of ionospheric scintillation. J. Sp. Weather Sp. Clim. 2022, 12, 22. [Google Scholar] [CrossRef]
- Huang, W.Q.; Xiao, Z.; Xiao, S.G.; Zhang, D.H.; Hao, Y.Q.; Suo, Y.C. Case study of apparent longitudinal differences of spread F occurrence for two mid-latitude stations. Radio Sc. 2011, 46. [Google Scholar] [CrossRef]
- Bhaneja, P.; Earle, G.D.; Bishop, R.L.; Bullett, T.W.; Mabie, J.; Redmon, R. A statistical study of mid-latitude spread F at Wallops Island, Virginia. J. Geophys. Res. 2009, 114, A04301. [Google Scholar] [CrossRef]
- Miller, C.A.; Swartz, W.E.; Kelley, M.C.; Mendillo, M.; Nottingham, D.; Scali, J.; Reinisch, B. Electrodynamics of midlatitude spread F: 1. Observations of unstable, gravity wave-induced ionospheric electric fields at tropical latitudes. J. Geophys. Res. Sp. Phys. 1997, 102, 11521–11532. [Google Scholar] [CrossRef]
- Fejer, B.G.; Kelley, M.C. Ionospheric irregularities. Rev. Geophys. 1980, 18, 401–454. [Google Scholar] [CrossRef]
- Hajkowicz, L.A. June. Morphology of quantified ionospheric range spread-F over a wide range of midlatitudes in the Australian longitudinal sector. Ann. Geophys. 2007, 25, 1125–1130. [Google Scholar] [CrossRef]
- Dyson, P.L.; Newton, G.P.; Brace, L.H. In situ measurements of neutral and electron density wave structure from the Explorer 32 satellite. J. Geophys. Res. 1970, 75, 3200–3210. [Google Scholar] [CrossRef]
- Hines, C.O. The upper atmosphere in motion. Q. J. Roy. Meteorol. Soc. 1963, 89, 1–42. [Google Scholar] [CrossRef]
- Bowman, G.G. A relationship between ‘‘spread-F” and the height of the F2 ionospheric layer. Aust. J. Phys. 1960, 13, 69–72. [Google Scholar] [CrossRef]
- Singleton, D.G. The morphology of spread-F occurrence over half a sunspot cycle. J. Geophys. Res. 1968, 73, 295–308. [Google Scholar] [CrossRef]
- Igarashi, K.; Kato, H. Solar cycle variations and latitudinal dependence on the midlatitude spread F occurrence around Japan. In Proceedings of the XXIV General Assembly, Kyoto, Japan, 25 August–2 September 1993. [Google Scholar]
- Bowman, G.G. A comparison of nighttime TID characteristics between equatorial ionospheric-anomaly crest and midlatitude regions, related to spread F occurrence. J. Geophys Res. 2001, 106, 1761–1769. [Google Scholar] [CrossRef]
- Shimazaki, T. A statistical study of occurrence probability of spread F at high latitudes. J. Geophys. Res. 1962, 67, 4617–4634. [Google Scholar] [CrossRef]
- Singleton, D.G. Spread-F and the parameters of the F-layer of the ionosphere—II: Spread-F and F-layer height. J. Atmos. Terr. Phys. 1962, 24, 885–898. [Google Scholar] [CrossRef]
- Khmyrov, G.M.; Galkin, I.A.; Kozlov, A.V.; Reinisch, B.W.; McElroy, J.; Dozois, C. Exploring digisonde ionogram data with SAO-X and DIDBase. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2008; Volume 974, pp. 175–185. [Google Scholar]
- Reinisch, B.W.; Galkin, I.A. Global ionospheric radio observatory (GIRO). Earth Planets Sp. 2011, 63, 377–381. [Google Scholar] [CrossRef]
- Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere model: A review and description of an ionospheric benchmark. Rev. Geophys. 2022, 60, e2022RG000792. [Google Scholar] [CrossRef]
- Paul, K.S.; Haralambous, H. Assessment of the Midlatitude SF Detection. In Proceedings of the Remote Sensing and Geoinformation of Environment, Paphos, Cyprus, 17–19 March 2025. [Google Scholar]
- Galkin, I.A.; Reinisch, B.W. The new ARTIST 5 for all digisondes. Proc. Ionosonde Netw. Advis. Group Bull. 2008, 69, 1–8. [Google Scholar]
- Bamford, R.A.; Stamper, R.; Cander, L.R. A comparison between the hourly autoscaled and manually scaled characteristics from the Chilton ionosonde from 1996 to 2004. Radio Sci. 2008, 43, 1–11. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS–Global Navigation Satellite Systems: GPS, GLONASS, Galileo, and More; Springer Wien: NewYork, NY, USA, 2007. [Google Scholar]
- Scotto, C.; Ippolito, A.; Sabbagh, D. A method for automatic detection of equatorial spread-F in Ionograms. Adv. Space Res. 2019, 63, 337–342. [Google Scholar] [CrossRef]
- Rao, T.V.; Sridhar, M.; Ratnam, D.V. Auto-detection of sporadic E and spread F events from the digital ionograms. Adv. Space Res. 2022, 70, 1142–1152. [Google Scholar] [CrossRef]
- Deminov, M.G.; Nepomnyashchaya, E.V.; Sitnov, Y.S. Regularities of the midlatitude spread F occurrence probability during sunrises and sunsets. Geomag. Aeron. 2005, 45, 458–465. [Google Scholar]
- Liu, Y.; Xiong, C.; Wan, X.; Lai, Y.; Wang, Y.; Yu, X.; Ou, M. Instability mechanisms for the F-region plasma irregularities inside the midlatitude ionospheric trough: Swarm observations. Sp. Weather 2021, 19, e2021SW002785. [Google Scholar] [CrossRef]
- Otsuka, Y.; Suzuki, K.; Nakagawa, S.; Nishioka, M.; Shiokawa, K.; Tsugawa, A. GPS observations of medium-scale travelling ionospheric disturbances over Europe. Ann. Geophys. 2013, 31, 163–172. [Google Scholar] [CrossRef]
- Paul, K.S.; Haralambous, H. Investigation for Possible Association of the Topside and Bottomside Ionospheric Irregularities over the Midlatitude Ionosphere. Appl. Sci. 2025, 15, 506. [Google Scholar] [CrossRef]
- Paul, K.S.; Haralambous, H.; Oikonomou, C.; Paul, A. Investigation of Satellite Trace (ST) and Multi-reflected Echo (MRE) ionogram signatures and its possible correlation to nighttime spread F development from Cyprus over the solar mini-max (2009–2016). Adv. Space Res. 2021, 67, 1958–1967. [Google Scholar] [CrossRef]
- McNicol, R.W.E.; Webster, H.C.; Bowman, G.G. A study of ‘‘Spread-F‘‘ ionospheric echoes at night at Brisbane. I. Range spreading (Experimental). Aust. J. Phys. 1956, 9, 247–271. [Google Scholar] [CrossRef]
- Haldoupis, C.; Kelley, M.C.; Hussey, G.C.; Shalimov, S. Role of unstable sporadic-E layers in the generation of mid-latitude spread F. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
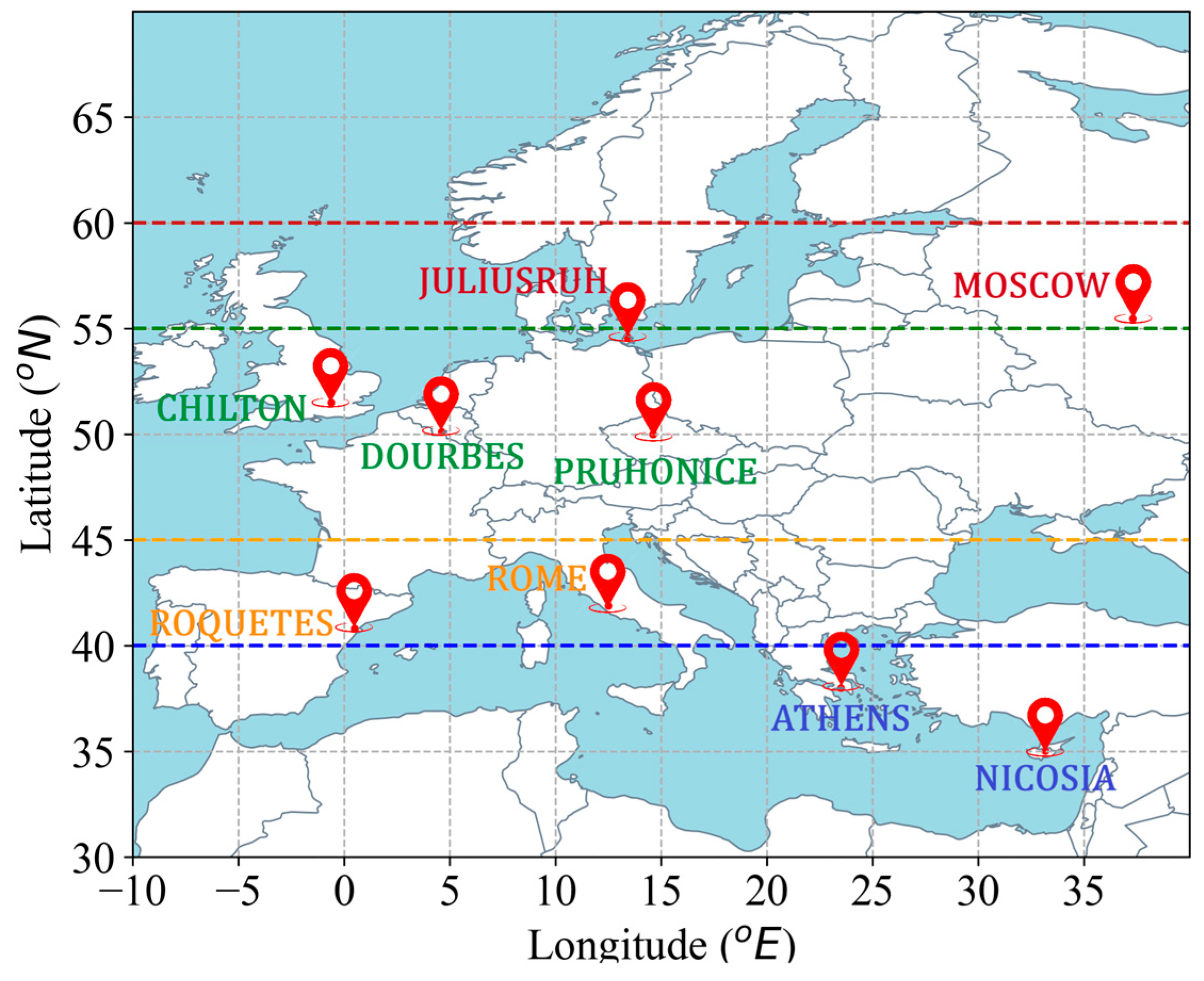




| Latitude Range | Stations | Latitude (° N) | Longitude (°E) | Manual SF Detected Years |
|---|---|---|---|---|
| 35°–40° | Nicosia | 35.03 | 33.16 | 2009–2010, 2013–2016, 2020–2021 |
| Athens | 38 | 23.5 | 2009, 2015–2016 | |
| 40°–45° | Rome | 41.8 | 12.5 | 2017, 2020–2021 |
| Roquetes | 40.8 | 0.5 | 2012–2021 | |
| 50°–55° | Pruhonice | 50 | 14.6 | 2009, 2015–2017, 2020–2021 |
| Dourbes | 50.1 | 4.6 | 2017, 2020–2021 | |
| Chilton | 51.5 | –0.6 | 2017, 2020–2021 | |
| 55°–60° | Juliusruh | 54.6 | 13.4 | 2017, 2020–2021 |
| Moscow | 55.47 | 37.3 | 2009–2021 |
| Latitude Zone | Stations Included | Threshold Candidate | SF Detection Time |
|---|---|---|---|
| 35°–40° N | Athens and Nicosia | Nicosia | 18:00–06:00 UT |
| 40°–45° N | Roquetes and Rome | Roquetes | 16:00–07:00 UT |
| 50°–55° N | Pruhonice, Dourbes and Chilton | Pruhonice | 16:00–07:00 UT |
| 55°–60° N | Moscow and Juliusruh | Moscow | 14:00–08:00 UT |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paul, K.S.; Biswas, T.; Haralambous, H. Evaluation of Automated Spread–F (SF) Detection over the Midlatitude Ionosphere. Atmosphere 2025, 16, 642. https://doi.org/10.3390/atmos16060642
Paul KS, Biswas T, Haralambous H. Evaluation of Automated Spread–F (SF) Detection over the Midlatitude Ionosphere. Atmosphere. 2025; 16(6):642. https://doi.org/10.3390/atmos16060642
Chicago/Turabian StylePaul, Krishnendu Sekhar, Trisani Biswas, and Haris Haralambous. 2025. "Evaluation of Automated Spread–F (SF) Detection over the Midlatitude Ionosphere" Atmosphere 16, no. 6: 642. https://doi.org/10.3390/atmos16060642
APA StylePaul, K. S., Biswas, T., & Haralambous, H. (2025). Evaluation of Automated Spread–F (SF) Detection over the Midlatitude Ionosphere. Atmosphere, 16(6), 642. https://doi.org/10.3390/atmos16060642






