Can GCMs Simulate ENSO Cycles, Amplitudes, and Its Teleconnection Patterns with Global Precipitation?
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
- (a)
- Observed sea surface temperature (SST) datasets to derive ENSO indices. Two different SST datasets are used in this study: the Extended Reconstruction of SST (ERSST) [18], and the Met Office Hadley Centre’s Sea Ice and SST (HADISST) [19]. They are chosen because previous studies with AR4 (CMIP3) models used them [9].
- (b)
- GCM data. A total of 48 CMIP5 GCMs are used in this study, and their names, acronyms, country, and horizontal and vertical resolutions are listed in Table 1.
- (c)
- Observed global precipitation. The Global Precipitation Climatology Centre (GPCC) monthly precipitation is used in this study. It comprises gridded datasets interpolated based on quality-controlled data from 67,200 stations globally [20]. For ENSO interdecadal variability, monthly data covering 115 years (1890–2004) are used because a few CMIP5 GCM historical runs end in 2004. The ENSO–precipitation teleconnection analysis is limited to 1950–2004 for two reasons: (1) to be consistent with National Weather Service La Niña and El Niño episodes by (http://www.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ensoyears.shtml, accessed on 30 September 2024), which started in 1950, and (2) because the quality of precipitation data in the early 1950s is relatively poor due to a limited number of stations.
2.2. Methods
3. Results
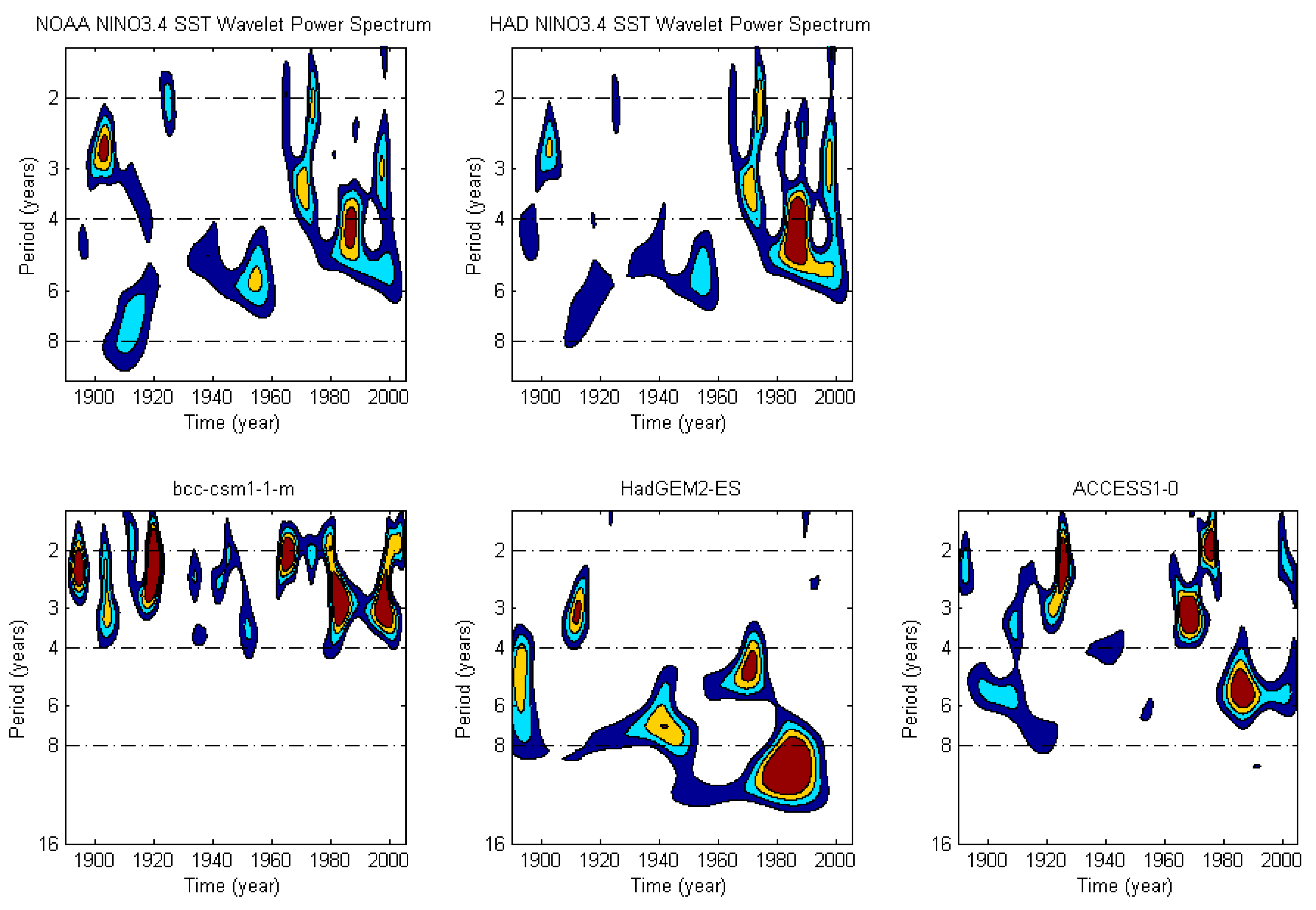
3.1. Interdecadal Variability of ENSO
- (a)
- Seven GCMs displayed a pronounced spectral peak with a period shorter than the observed ENSO period (first row);
- (b)
- Nine GCMs produced one prominent peak with a period longer than 7 years (second row);
- (c)
- Ten GCMs displayed a spectral peak that is similar to an ENSO-like 3–7-year period, but with a larger amplitude (third row);
- (d)
- The remaining twenty-two GCMs displayed a relatively good spectral peak with a 3–7-year period as well as a similar amplitude to the observed one (fourth row).
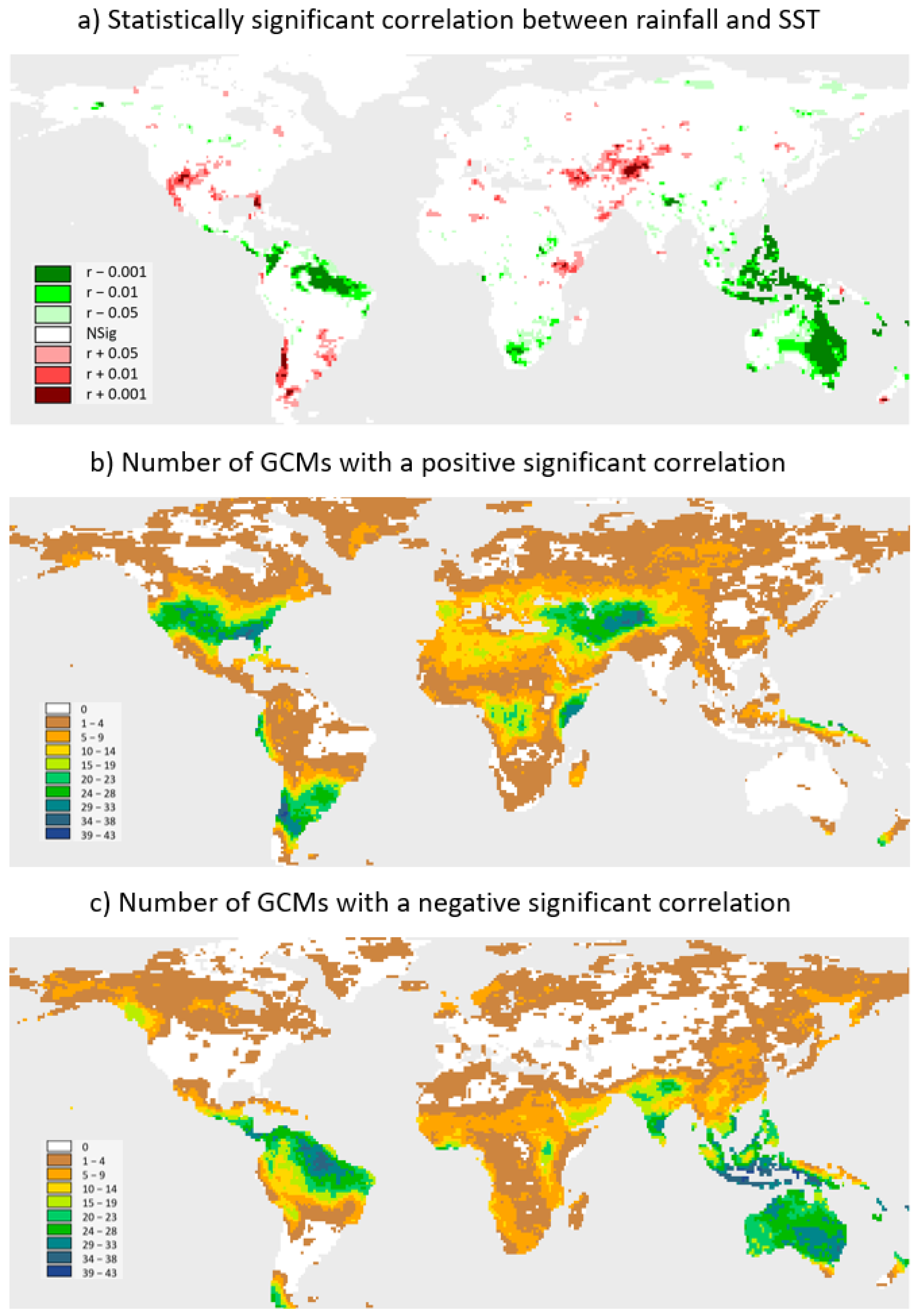
3.2. ENSO–Precipitation Teleconnections
4. Discussion
4.1. Implications of This Study
4.2. Uncertainties and Limitations
4.2.1. CMIP5 vs. CMIP6 GCMs
4.2.2. Data Quality
4.2.3. Physical Processes of GCMs
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMIP | Coupled Model Intercomparison Project |
| ENSO | El Niño–Southern Oscillation |
| GCM | General circulation model (or global climate model) |
| GPCC | Global Precipitation Climatology Centre |
| IPCC | Intergovernmental Panel on Climate Change |
| SST | Sea surface temperature |
References
- Ropelewski, C.F.; Halpert, M.S. Global and Regional Scale Precipitation Patterns Associated with the El-Nino Southern Oscillation. Mon. Weather. Rev. 1987, 115, 1606–1626. [Google Scholar] [CrossRef]
- Power, S.; Delage, F.; Chung, C.; Kociuba, G.; Keay, K. Robust twenty-first-century projections of El Nino and related precipitation variability. Nature 2013, 502, 541–545. [Google Scholar] [CrossRef]
- Yeh, S.W.; Cai, W.; Min, S.; McPhaden, M.J.; Dommenget, D.; Dewitte, B.; Collins, M.; Ashok, K.; An, S.; Yim, B.; et al. ENSO Atmospheric Teleconnections and Their Response to Greenhouse Gas Forcing. Rev. Geophys. 2018, 56, 185–206. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; McMahon, T.A. Global ENSO-streamflow teleconnection, streamflow forecasting and interannual variability. Hydrol. Sci. J.-J. Des Sci. Hydrol. 2002, 47, 505–522. [Google Scholar] [CrossRef]
- Ouyang, R.; Liu, W.; Fu, G.; Liu, C.; Hu, L.; Wang, H. Linkages between ENSO/PDO signals and precipitation, streamflow in China during the last 100 years. Hydrol. Earth Syst. Sci. 2014, 18, 3651–3661. [Google Scholar] [CrossRef]
- Yin, H.; Wu, Z.; Fowler, H.J.; Blenkinsop, S.; He, H.; Li, Y. The Combined Impacts of ENSO and IOD on Global Seasonal Droughts. Atmosphere 2022, 13, 1673. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Climate Change 2023: Synthesis Report. A Report of the Intergovernmental Panel on Climate Change. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; p. 36. [Google Scholar]
- Fu, G.; Charles, S.P.; Kirshner, S. Daily rainfall projections from general circulation models with a downscaling nonhomogeneous hidden Markov model (NHMM) for south-eastern Australia. Hydrol. Process. 2013, 27, 3663–3673. [Google Scholar] [CrossRef]
- Lin, J.L. Interdecadal variability of ENSO in 21 IPCC AR4 coupled GCMs. Geophys. Res. Lett. 2007, 34, L12702. [Google Scholar] [CrossRef]
- Jin, E.K.; Kinter, J.L.; Wang, B.; Park, C.-K.; Kang, I.-S.; Kirtman, B.P.; Kug, J.-S.; Kumar, A.; Luo, J.-J.; Schemm, J.; et al. Current status of ENSO prediction skill in coupled ocean–atmosphere models. Clim. Dyn. 2008, 31, 647–664. [Google Scholar] [CrossRef]
- Langenbrunner, B.; Neelin, J.D. Analyzing ENSO Teleconnections in CMIP Models as a Measure of Model Fidelity in Simulating Precipitation. J. Clim. 2013, 26, 4431–4446. [Google Scholar] [CrossRef]
- Jiang, P.; Gautam, M.R.; Zhu, J.; Yu, Z. How well do the GCMs/RCMs capture the multi-scale temporal variability of precipitation in the Southwestern United States? J. Hydrol. 2013, 479, 75–85. [Google Scholar] [CrossRef]
- Rowell, D.P. Simulating SST Teleconnections to Africa: What is the State of the Art? J. Clim. 2013, 26, 5397–5418. [Google Scholar] [CrossRef]
- King, A.D.; Donat, M.G.; Alexander, L.V.; Karoly, D.J. The ENSO-Australian rainfall teleconnection in reanalysis and CMIP5. Clim. Dyn. 2014, 44, 2623–2635. [Google Scholar] [CrossRef]
- Kristóf, E.; Barcza, Z.; Hollós, R.; Bartholy, J.; Pongrácz, R. Evaluation of Historical CMIP5 GCM Simulation Results Based on Detected Atmospheric Teleconnections. Atmosphere 2020, 11, 723. [Google Scholar] [CrossRef]
- Zhao, T.; Chen, H.; Tian, Y.; Yan, D.; Xu, W.; Cai, H.; Wang, J.; Chen, X. Quantifying overlapping and differing information of global precipitation for GCM forecasts and El Niño–Southern Oscillation. Hydrol. Earth Syst. Sci. 2022, 26, 4233–4249. [Google Scholar] [CrossRef]
- Trenberth, K.E. The definition of El Nino. Bull. Am. Meteorol. Soc. 1997, 78, 2771–2777. [Google Scholar] [CrossRef]
- Smith, T.M.; Reynolds, R.W. Improved Extended Reconstruction of SST (1854–1997). J. Clim. 2004, 17, 2466–2477. [Google Scholar] [CrossRef]
- Rayner, N.A.; Parker, D.E.; Horton, E.B.; Folland, C.K.; Alexander, L.V.; Rowell, D.P.; Kent, E.C.; Kaplan, A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. Atmos. 2003, 108, 4407. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC Full Data Reanalysis Version 6.0 at 1.0°: Monthly Land-Surface Precipitation from Rain-Gauges Built on GTS-Based and Historic Data. 2011. Available online: https://cir.nii.ac.jp/crid/1883679867557616512 (accessed on 30 September 2024).
- Riedel, K.; Sidorenko, A. Minimum bias multiple taper spectral estimation. IEEE Trans. Signal Process. 1995, 43, 188–195. [Google Scholar] [CrossRef]
- Barbour, A.J.; Parker, R.L. psd: Adaptive, sine multitaper power spectral density estimation for R. Comput. Geosci. 2014, 63, 1–8. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P.J. Interdecadal changes in the ENSO-monsoon system. J. Clim. 1999, 12, 2679–2690. [Google Scholar] [CrossRef]
- Gobena, A.K.; Gan, T.Y. The Role of Pacific Climate on Low-Frequency Hydroclimatic Variability and Predictability in Southern Alberta, Canada. J. Hydrometeorol. 2009, 10, 1465–1478. [Google Scholar] [CrossRef]
- Bellenger, H.; Guilyardi, E.; Leloup, J.; Lengaigne, M.; Vialard, J. ENSO representation in climate models: From CMIP3 to CMIP5. Clim. Dyn. 2013, 42, 1999–2018. [Google Scholar] [CrossRef]
- Zhang, W.; Jin, F.F. Improvements in the CMIP5 simulations of ENSO-SSTA meridional width. Geophys. Res. Lett. 2012, 39, L23704. [Google Scholar] [CrossRef]
- Kumar, S.; Merwade, V.; Kinter, J.L.; Niyogi, D. Evaluation of Temperature and Precipitation Trends and Long-Term Persistence in CMIP5 Twentieth-Century Climate Simulations. J. Clim. 2013, 26, 4168–4185. [Google Scholar] [CrossRef]
- Whetton, P.; Hennessy, K.; Clarke, J.; McInnes, K.; Kent, D. Use of Representative Climate Futures in impact and adaptation assessment. Clim. Change 2012, 115, 433–442. [Google Scholar] [CrossRef]
- Clarke, J.; Whetton, P.; Hennessy, K. Providing application-specific climate projections datasets: CSIROs climate futures framework. In Proceedings of the MODSIM, International Congress on Modelling and Simulation, Modelling and Simulation Society of Australia and New Zealand, Perth, Western Australia, 12–16 December 2011. [Google Scholar]
- Watterson, I.G. Improved Simulation of Regional Climate by Global Models with Higher Resolution: Skill Scores Correlated with Grid Length*. J. Clim. 2015, 28, 5985–6000. [Google Scholar] [CrossRef]
- Wittenberg, A.T.; Rosati, A.; Delworth, T.L.; Vecchi, G.A.; Zeng, F. ENSO Modulation: Is It Decadally Predictable? J. Clim. 2014, 27, 2667–2681. [Google Scholar] [CrossRef]
- McGregor, G.R.; Ebi, K. El Niño Southern Oscillation (ENSO) and Health: An Overview for Climate and Health Researchers. Atmosphere 2018, 9, 282. [Google Scholar] [CrossRef]
- Liao, H.; Wang, C.; Song, Z. ENSO phase-locking biases from the CMIP5 to CMIP6 models and a possible explanation. In Deep Sea Research Part II: Topical Studies in Oceanography; Elsevier: Amsterdam, The Netherlands, 2021; pp. 189–190. [Google Scholar]
- Brown, J.R.; Brierley, C.M.; An, S.-I.; Guarino, M.-V.; Stevenson, S.; Williams, C.J.R.; Zhang, Q.; Zhao, A.; Abe-Ouchi, A.; Braconnot, P.; et al. Comparison of past and future simulations of ENSO in CMIP5/PMIP3 and CMIP6/PMIP4 models. Clim. Past 2020, 16, 1777–1805. [Google Scholar] [CrossRef]
- Beobide-Arsuaga, G.; Bayr, T.; Reintges, A.; Latif, M. Uncertainty of ENSO-amplitude projections in CMIP5 and CMIP6 models. Clim. Dyn. 2021, 56, 3875–3888. [Google Scholar] [CrossRef]
- Fang, Y.; Screen, J.A.; Hu, X.; Lin, S.; Williams, N.C.; Yang, S. CMIP6 Models Underestimate ENSO Teleconnections in the Southern Hemisphere. Geophys. Res. Lett. 2024, 51, 16295. [Google Scholar] [CrossRef]
- Fu, G.; Clark, S.R.; Gonzalez, D.; Rojas, R.; Janardhanan, S. Spatial and Temporal Patterns of Groundwater Levels: A Case Study of Alluvial Aquifers in the Murray–Darling Basin, Australia. Sustainability 2023, 15, 16295. [Google Scholar] [CrossRef]
- Giorgi, F.; Francisco, R. Uncertainties in regional climate change prediction: A regional analysis of ensemble simulations with the HADCM2 coupled AOGCM. Clim. Dyn. 2000, 16, 169–182. [Google Scholar] [CrossRef]
- Stevenson, S.L. Significant changes to ENSO strength and impacts in the twenty-first century: Results from CMIP5. Geophys. Res. Lett. 2012, 39, 17703. [Google Scholar] [CrossRef]




| GCM | Institute | Lat | Lon |
|---|---|---|---|
| ACCESS1-0 | The Centre for Australian Weather and Climate Research (Commonwealth Scientific and Industrial Research Organisation, CSIRO, and Bureau of Meteorology, BoM) | 145 | 192 |
| ACCESS1-3 | 145 | 192 | |
| bcc-csm1-1 | Beijing Climate Centre, China Meteorological Administration | 64 | 128 |
| bcc-csm1-1-m | 160 | 320 | |
| BNU-ESM | Beijing Normal University | 64 | 128 |
| CanESM2 | Canadian Centre for Climate Modelling and Analysis | 64 | 128 |
| CCSM4 | National Center for Atmospheric Research, USA | 192 | 288 |
| CESM1-BGC | National Science Foundation, Department of Energy, National Center for Atmospheric Research, USA | 192 | 288 |
| CESM1-CAM5-1-FV2 | 96 | 144 | |
| CESM1-CAM5 | 192 | 288 | |
| CESM1-FASTCHEM | 192 | 288 | |
| CESM1-WACCM | 96 | 144 | |
| CMCC-CESM | Centro Euro-Mediterraneo per I Cambiamenti Climatici | 48 | 96 |
| CMCC-CM | 240 | 480 | |
| CMCC-CMS | 96 | 192 | |
| CNRM-CM5-2 | Centre National de Recherches Meteorologiques/Centre Europeen de Recherche et Formation Avancees en Calcul Scientifique | 128 | 256 |
| CNRM-CM5 | 128 | 256 | |
| CSIRO-Mk3-6-0 | Commonwealth Scientific and Industrial Research Organisation | 96 | 192 |
| EC-EARTH | EC-EARTH consortium | 160 | 320 |
| FGOALS-g2 | LASG, Institute of Atmospheric Physics, Chinese Academy of Sciences; and CESS, Tsinghua University | 60 | 128 |
| FGOALS-s2 | LASG, Institute of Atmospheric Physics, Chinese Academy of Sciences | 108 | 128 |
| FIO-ESM | The First Institute of Oceanography, SOA, China | 64 | 128 |
| GFDL-CM2p1 | Geophysical Fluid Dynamics Laboratory, USA | 90 | 144 |
| GFDL-CM3 | 90 | 144 | |
| GFDL-ESM2G | 90 | 144 | |
| GFDL-ESM2M | 90 | 144 | |
| GISS-E2-H-CC | NASA Goddard Institute for Space Studies, USA | 90 | 144 |
| GISS-E2-H | 90 | 144 | |
| GISS-E2-R-CC | 90 | 144 | |
| GISS-E2-R | 90 | 144 | |
| HadCM3 | Met Office Hadley Centre, UK | 73 | 96 |
| HadGEM2-AO | 145 | 192 | |
| HadGEM2-CC | 145 | 192 | |
| HadGEM2-ES | Met Office Hadley Centre (Realizations contributed by Instituto Nacional de Pesquisas Espaciais) | 145 | 192 |
| inmcm4 | Institute for Numerical Mathematics | 120 | 180 |
| IPSL-CM5A-LR | Institut Pierre-Simon Laplace | 96 | 96 |
| IPSL-CM5A-MR | 143 | 144 | |
| IPSL-CM5B-LR | 96 | 96 | |
| MIROC-ESM-CHEM | Japan Agency for Marine-Earth Science and Technology, Atmosphere and Ocean Research Institute (The University of Tokyo), and National Institute for Environmental Studies | 64 | 128 |
| MIROC-ESM | 64 | 128 | |
| MIROC5 | Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology | 128 | 256 |
| MPI-ESM-LR | Max Planck Institute for Meteorology (MPI-M) | 96 | 192 |
| MPI-ESM-MR | 96 | 192 | |
| MPI-ESM-P | 96 | 192 | |
| MRI-CGCM3 | Meteorological Research Institute, Japan | 160 | 320 |
| MRI-ESM1 | 160 | 320 | |
| NorESM1-ME | Norwegian Climate Centre | 96 | 144 |
| NorESM1-M | 96 | 144 |
| GCMs | Coincident Precipitation Anomaly | Non-Coincident Precipitation Anomaly | ||||||
|---|---|---|---|---|---|---|---|---|
| La Niña | El Niño | La Niña | El Niño | |||||
| P > 110% | P < 90% | P > 110% | P < 90% | P > 110% | P < 90% | P > 110% | P < 90% | |
| GPCC | 1962 | 1229 | 1463 | 1833 | ||||
| ACCESS1-0 | 40.9 | 41.6 | 42.9 | 35.3 | 32.4 | 113.8 | 99.6 | 47.0 |
| ACCESS1-3 | 36.1 | 43.3 | 48.2 | 44.5 | 36.1 | 86.7 | 82.6 | 50.4 |
| bcc-csm1-1 | 32.8 | 18.2 | 11.8 | 21.4 | 31.4 | 76.6 | 49.1 | 15.3 |
| bcc-csm1-1-m | 28.6 | 37.8 | 47.2 | 29.9 | 22.5 | 95.9 | 78.3 | 29.7 |
| BNU-ESM | 59.8 | 35.2 | 35.3 | 57.8 | 57.2 | 73.1 | 48.4 | 55.0 |
| CanESM2 | 44.7 | 57.2 | 63.7 | 48.9 | 60.8 | 133.8 | 90.2 | 71.0 |
| CCSM4 | 44.2 | 39.6 | 52.2 | 48.6 | 43.7 | 77.5 | 71.2 | 49.0 |
| CESM1-BGC | 31.9 | 31.1 | 46.1 | 42.2 | 43.2 | 49.3 | 54.8 | 37.9 |
| CESM1-CAM5-1-FV2 | 44.5 | 53.2 | 58.1 | 56.4 | 51.7 | 97.7 | 78.3 | 54.3 |
| CESM1-CAM5 | 0.7 | 9.5 | 1.6 | 1.1 | 6.8 | 17.6 | 3.9 | 13.9 |
| CESM1-FASTCHEM | 45.9 | 31.9 | 43.7 | 33.3 | 41.1 | 65.6 | 51.5 | 37.0 |
| CESM1-WACCM | 49.3 | 43.0 | 47.2 | 54.4 | 47.0 | 60.2 | 55.5 | 58.9 |
| CMCC-CESM | 52.7 | 30.8 | 57.7 | 53.9 | 50.1 | 55.6 | 99.3 | 48.4 |
| CMCC-CM | 33.6 | 49.1 | 30.4 | 17.2 | 54.9 | 172.5 | 76.1 | 30.0 |
| CMCC-CMS | 54.7 | 56.4 | 62.4 | 43.8 | 27.4 | 116.7 | 104.2 | 27.3 |
| CNRM-CM5-2 | 45.2 | 42.1 | 46.9 | 24.5 | 36.4 | 86.1 | 86.1 | 19.0 |
| CNRM-CM5 | 32.8 | 44.1 | 45.4 | 26.2 | 20.2 | 66.2 | 66.4 | 16.7 |
| CSIRO-Mk3-6-0 | 60.6 | 41.2 | 56.9 | 54.1 | 79.0 | 102.3 | 100.1 | 74.0 |
| EC-EARTH | 23.1 | 10.5 | 16.0 | 11.7 | 48.2 | 41.7 | 22.2 | 8.3 |
| FGOALS-g2 | 35.1 | 26.1 | 23.3 | 33.8 | 16.7 | 60.6 | 52.4 | 19.1 |
| FGOALS-s2 | 56.5 | 38.5 | 32.7 | 37.0 | 62.1 | 116.1 | 68.5 | 39.0 |
| FIO-ESM | 49.6 | 40.4 | 36.2 | 38.1 | 40.6 | 82.3 | 51.7 | 36.2 |
| GFDL-CM2p1 | 58.7 | 51.2 | 60.2 | 67.2 | 79.9 | 98.4 | 100.1 | 92.0 |
| GFDL-CM3 | 36.2 | 51.1 | 46.3 | 39.2 | 29.9 | 98.6 | 72.4 | 28.8 |
| GFDL-ESM2G | 50.6 | 49.4 | 47.1 | 43.0 | 48.1 | 104.1 | 71.5 | 30.9 |
| GFDL-ESM2M | 56.3 | 67.7 | 81.3 | 50.5 | 68.3 | 136.2 | 147.9 | 88.3 |
| GISS-E2-H-CC | 38.9 | 32.8 | 7.4 | 23.6 | 38.5 | 107.4 | 23.9 | 25.5 |
| GISS-E2-H | 21.3 | 26.8 | 30.7 | 8.3 | 24.4 | 84.9 | 74.8 | 15.3 |
| GISS-E2-R-CC | 19.3 | 21.0 | 7.9 | 15.8 | 46.9 | 79.1 | 19.9 | 40.8 |
| GISS-E2-R | 11.9 | 18.1 | 20.1 | 11.9 | 21.8 | 61.8 | 57.3 | 37.2 |
| HadCM3 | 26.8 | 46.2 | 23.0 | 33.0 | 33.3 | 96.4 | 36.6 | 44.6 |
| HadGEM2-AO | 44.7 | 43.4 | 20.4 | 35.4 | 56.8 | 98.4 | 63.0 | 37.0 |
| HadGEM2-CC | 32.2 | 27.8 | 23.8 | 23.2 | 46.2 | 76.6 | 37.2 | 43.3 |
| HadGEM2-ES | 32.1 | 28.5 | 28.9 | 19.5 | 39.3 | 74.3 | 51.5 | 22.5 |
| inmcm4 | 32.3 | 20.4 | 14.4 | 34.6 | 51.5 | 69.3 | 36.9 | 48.8 |
| IPSL-CM5A-LR | 44.6 | 40.2 | 23.8 | 37.8 | 51.7 | 97.6 | 53.5 | 41.1 |
| IPSL-CM5A-MR | 42.2 | 28.9 | 35.5 | 42.8 | 53.4 | 64.5 | 92.6 | 83.1 |
| IPSL-CM5B-LR | 28.6 | 48.7 | 54.3 | 18.3 | 33.4 | 160.2 | 147.7 | 20.3 |
| MIROC-ESM-CHEM | 32.2 | 6.1 | 16.8 | 44.6 | 69.7 | 46.9 | 40.3 | 128.5 |
| MIROC-ESM | 16.5 | 9.9 | 7.9 | 28.5 | 81.1 | 62.6 | 34.9 | 63.3 |
| MIROC5 | 46.3 | 32.6 | 74.8 | 46.8 | 37.8 | 79.3 | 105.3 | 67.5 |
| MPI-ESM-LR | 54.0 | 47.8 | 40.2 | 46.1 | 41.1 | 82.5 | 59.1 | 36.1 |
| MPI-ESM-MR | 53.7 | 58.5 | 38.3 | 48.0 | 27.0 | 117.7 | 83.3 | 40.5 |
| MPI-ESM-P | 4.0 | 21.7 | 16.4 | 17.1 | 16.6 | 66.4 | 39.5 | 28.3 |
| MRI-CGCM3 | 16.2 | 55.9 | 38.6 | 23.0 | 45.8 | 175.9 | 94.1 | 30.6 |
| MRI-ESM1 | 34.0 | 42.5 | 40.2 | 22.2 | 69.6 | 156.6 | 114.2 | 34.4 |
| NorESM1-ME | 48.7 | 37.6 | 39.5 | 48.8 | 48.5 | 69.6 | 55.8 | 39.4 |
| NorESM1-M | 40.6 | 34.7 | 42.1 | 48.9 | 54.0 | 77.8 | 52.2 | 38.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Li, J.; Zou, Y.; Liu, J.; Fu, G. Can GCMs Simulate ENSO Cycles, Amplitudes, and Its Teleconnection Patterns with Global Precipitation? Atmosphere 2025, 16, 507. https://doi.org/10.3390/atmos16050507
Ma C, Li J, Zou Y, Liu J, Fu G. Can GCMs Simulate ENSO Cycles, Amplitudes, and Its Teleconnection Patterns with Global Precipitation? Atmosphere. 2025; 16(5):507. https://doi.org/10.3390/atmos16050507
Chicago/Turabian StyleMa, Chongya, Jiaqi Li, Yuanchun Zou, Jiping Liu, and Guobin Fu. 2025. "Can GCMs Simulate ENSO Cycles, Amplitudes, and Its Teleconnection Patterns with Global Precipitation?" Atmosphere 16, no. 5: 507. https://doi.org/10.3390/atmos16050507
APA StyleMa, C., Li, J., Zou, Y., Liu, J., & Fu, G. (2025). Can GCMs Simulate ENSO Cycles, Amplitudes, and Its Teleconnection Patterns with Global Precipitation? Atmosphere, 16(5), 507. https://doi.org/10.3390/atmos16050507








