Abstract
Vegetation is a vital component of ecosystems and an indicator of global environmental change. It is significantly influenced by climate factors. Previous studies have often overlooked the nonlinear relationships, spatiotemporal variability, and interaction effects of climate factors on vegetation, focusing instead on simplistic trends or regional classifications based on vegetation type, climate zone, or ecosystem. In this study, a factorial-clustered copula covariate analysis model was developed to investigate the effects of climate factors on vegetation cover (NDVI) in China from 2000 to 2023. The results showed that temperature had the strongest correlation with NDVI (0.66), followed by precipitation and solar radiation (both 0.46), and soil moisture (0.14). The NDVI exhibited significant spatial variability, with low values (<0.1) in 17.6% and high values (>0.8) in 12.7% of the areas. Regional variations were observed: precipitation-dominated NDVI changes in arid regions (Cluster 1, 43%), solar radiation in tropical areas (Clusters 4 and 5, >79%), and soil moisture in humid zones (Cluster 2, 29%). Interaction effects, such as Pre:Temp and Pre:Temp:SM, further influenced NDVI dynamics. Joint probability analysis revealed diverse dependency patterns across clusters, highlighting the complex interplay between climatic and non-climatic factors. These findings emphasize the need for tailored management strategies to address region-specific vegetation dynamics under changing climatic conditions.
1. Introduction
Vegetation, as an important component of terrestrial ecosystems, plays a crucial role in regulating carbon balance, cycling of materials and energy, and maintaining ecosystem biodiversity [1]. It is a key indicator of global environmental change [2]. Climate is one of the main driving factors influencing vegetation cover [3]. Precipitation and temperature are the primary climatic factors driving vegetation changes. Variations in water and heat conditions can affect the physiological functions and distribution density of vegetation, thereby altering its structure [4]. Precipitation is an important source of water for vegetation growth, influencing the soil moisture and water absorption capacity of vegetation [5]. Temperature affects vegetation transpiration, thereby influencing the water demand of the vegetation. In addition, it directly impacts physiological processes, such as vegetation growth rate, photosynthesis, and respiration [6]. Soil moisture is the primary method by which vegetation acquires water and directly affects its growth. Surface net solar radiation provides energy for photosynthesis, influencing primary productivity. On the other hand. It heats the surface directly, affecting the local temperature, which in turn influences transpiration, soil moisture, and the growth environment of vegetation [7]. Practically, these climatic factors are interrelated. Precipitation and temperature together determine the moisture conditions and growing season, while soil moisture and temperature jointly affect the level of water stress experienced by vegetation [8]. Surface net solar radiation influences the physiological processes of vegetation through light conditions and temperature regulation. It is essential to consider the combined effects of these climatic factors in research [9]. In the context of climate change, studying vegetation dynamics and its response to climatic factors can provide a scientific basis for addressing climate change, protecting the ecological environment, and achieving sustainable regional development.
The normalized difference vegetation index (NDVI) is widely recognized as one of the most effective indicators for monitoring global and regional vegetation changes [10]. It is highly sensitive to the biophysical characteristics of vegetation and shows a significant linear correlation with vegetation cover [11]. As a crucial parameter for describing vegetation growth conditions, NDVI has been extensively used in studies of dynamic vegetation changes and the response of vegetation to climatic factors [12]. The correlation between NDVI and climatic factors provides a highly practical method for exploring the corresponding responses of ecosystems to climate change [13].
In recent years, many scholars have made substantial progress in studying the relationship between NDVI and climatic factors at both regional and global scales. Regional-scale studies have shown that vegetation responses to climatic factors vary significantly across different regions. Sun (2019) found that precipitation plays a decisive role in NDVI variations in the Yarlung Tsangpo River Basin on the Tibetan Plateau [12], while Peng (2012) identified temperature as the dominant factor influencing NDVI changes during the growing season in the permafrost region of northeastern China [14]. Sun (2019) explored changes in vegetation growth and their driving mechanisms in the Yarlung Zangbo River Basin, which is the largest basin in the world [12]. Wang (2021) explored the spatiotemporal changes in the growth season of the NDVI for different natural vegetation types in China using grid temperature, precipitation, drought, and the GIMMS NDVI data [15]. Feng (2023) characterized the spatiotemporal variation in vegetation coverage and its climatic driving factors in the Yellow River Basin [16]. Deng (2024) investigated the spatiotemporal dynamics of vegetation growth and its response to both individual and composite climatic factors in Sichuan Province, China [17]. Vegetation growth in northern China is primarily influenced by precipitation, while vegetation in southern China is more sensitive to temperature changes [13,15]. On a global scale, previous studies have shown an overall increasing trend in the global surface vegetation NDVI [18]. The influence of temperature and precipitation on NDVI varies across different spatiotemporal scales. Temperature is a driving factor for NDVI changes in most of the Northern Hemisphere, whereas precipitation drives NDVI changes in the Southern Hemisphere [19,20]. It is important to note that interactions between climate factors further complicate their impacts on vegetation growth.
In addition, the response of NDVI to climatic factors is also influenced by other factors, such as vegetation type, land use, climate zones, and ecosystems. Therefore, some studies have further classified and discussed the relationship between NDVI and climatic factors based on these influencing factors [21]. Previous studies have pointed out that vegetation cover of different types responds differently to the same climatic factors [22]. Bao (2021) utilized machine learning algorithms to study the sensitivity of vegetation cover in various climate zones to climate change and found that NDVI sensitivity to temperature and precipitation varied across different climate zones [21]. Moreover, vegetation growth in different ecosystems exhibits temporal response differences to climatic factors on a monthly scale. Precipitation has a cumulative effect on vegetation growth in forest ecosystems, while vegetation in agricultural ecosystems responds most quickly to precipitation changes.
However, previous studies have primarily focused on partitioning discussions based on natural characteristics, such as different vegetation types, climate zones, or ecosystems, and have classified and statistically analyzed data based on entire administrative regions or natural watersheds [22]. These studies have not fully considered the intrinsic relationship between NDVI and climatic factors within different regions. Moreover, most studies employ linear trend-fitting methods for simple analysis to reveal the relationship between NDVI and climatic factors [23]. Due to the complexity of ecosystems and the uncertainty of mechanisms driving vegetation dynamics under climate change [24], the above commonly used methods cannot reveal the complex nonlinear relationships in vegetation dynamics and lack consideration for the spatiotemporal variability of vegetation evolution [25]. Furthermore, few studies have considered the indirect effects of interactions between climatic factors on vegetation change [26].
Therefore, the objective of this study is to develop a factorial-clustered copula covariate analysis model to explore the interaction effects of multiple climate factors on vegetation cover in China. Specifically, the objectives are to (1) select the vegetation cover index (NDVI) as the target variable and investigate its relationship with key climate factors such as precipitation, temperature, soil moisture, and solar radiation to explore their impact mechanisms on vegetation cover change; (2) apply a stepwise clustering method to divide the country into several climate-ecological units, revealing the spatial variability of climate factors’ effects on vegetation cover; (3) construct regional multivariate dependency models based on marginal distribution fitting and Vine Copula to uncover the nonlinear relationships and tail dependence between climate factors; and (4) quantify the main and interactive effects of climate factors on vegetation cover change through multilevel factorial analysis. Through this series of analyses, this study aims to provide a deeper understanding of the complex impact mechanisms of multiple climate factors on vegetation cover in China and offers a novel and effective analytical framework for assessing ecosystem responses in the context of climate change.
2. Data Source and Methods
The framework of this study is shown in Figure 1. The trend of NDVI changes in China and the spatiotemporal heterogeneity of its correlation with precipitation, temperature, soil moisture, and net solar radiation at each grid point were analyzed. Given the spatial distribution of the correlation, the relationship between NDVI and climatic factors was classified into seven categories using K-means clustering analysis. The marginal distribution and multidimensional joint distribution of each cluster were fitted based on the copula. Climate combinations were input into a Vine Copula model, which was used to estimate the NDVI response under different climatic conditions. The climate factors and corresponding NDVI responses were subsequently input into a two-way factorial analysis to evaluate the main and interaction effects.
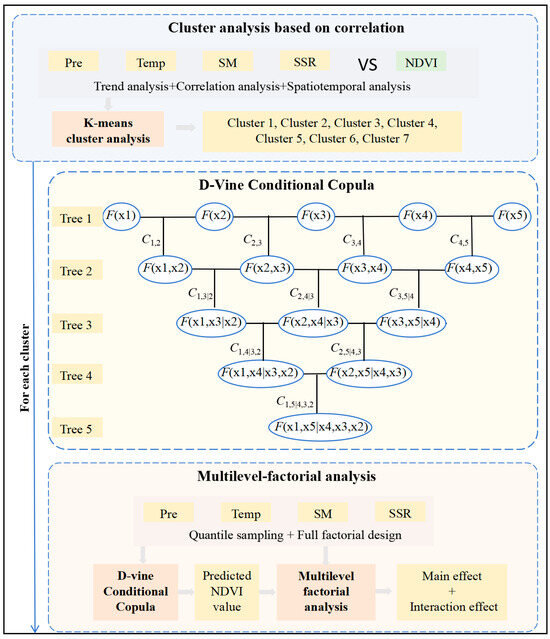
Figure 1.
Framework for factorial-clustered copula covariate analysis model.
2.1. Dataset
The NDVI data used in this study originates from the China regional 250 m normalized difference vegetation index dataset (2000–2023), provided by the National Tibetan Plateau/Third Pole Environment Data Center (http://data.tpdc.ac.cn (accessed on 5 August 2024)). This product is derived from Aqua/Terra-MODIS satellite sensor MOD13Q1 products and land use data. It was processed through several stages, including the preliminary reconstruction of noise pixels for similar land cover in single-period images, long-term series image S-G filtering, retaining high-quality pixels, 16-day composite monthly products, and mosaicking over the China region. The dataset has a spatial resolution of 250 m and uses maximum value compositing for monthly synthesis with 12 periods per year. In this study, the 250 m NDVI data were resampled to a 1° × 1° grid through interpolation. The annual-scale NDVI data were further aggregated using the maximum value composite (MVC) method. The data on average temperature, cumulative precipitation, soil moisture, and monthly net solar radiation are derived from the ERA5 dataset of the European Centre for Medium-Range Weather Forecasts (ECMWF) https://www.ecmwf.int/en/forecasts/dataset/ecmwf-reanalysis-v5?check_logged_in=1, accessed on 30 December 2024) with a spatial resolution of a 1° × 1° grid.
2.2. Methods
- (1)
- Theil-Sen trend analysis
Theil-Sen trend analysis is a non-parametric statistical trend analysis method [27]. This method calculates the median slope of all n(n − 1)/2 pairwise combinations of time series data. It does not require the analyzed data to follow a normal distribution and is robust against the influence of outliers [28], thereby avoiding errors caused by a few extreme values. In this study, a grid-point-by-grid-point analysis was performed for the study area. The calculation formula is as follows:
In the formula, β represents the interannual variation trend of NDVI, xi and xj are the NDVI values for year i and year j, respectively, and n is the length of the time series. If β > 0, it indicates an increasing trend in the vegetation index, while β < 0 indicates a decreasing trend in the vegetation index.
- (2)
- Pearson correlation analysis
Pearson’s correlation analysis is a statistical method used to calculate the degree of relationship between variables based on their covariance and variance [25]. In this study, the Pearson correlation coefficient is employed to analyze the correlation between vegetation cover (NDVI) and various climatic factors. According to Ahlgren et al. (2003), the Pearson correlation coefficient measures the strength and direction (decreasing or increasing, depending on the sign) of a linear relationship between two variables, X and Y [29]. It is defined as:
In the formula, x represents the climatic factor, y represents vegetation NDVI, and represent mean values of x and y, respectively, n denotes the number of data points, and i is the index of the data sequence. The correlation coefficient r ranges from −1 to 1. When r > 0, it indicates a positive correlation between x and y, and when r < 0, it indicates a negative correlation. The larger the absolute value of r, the stronger the correlation [9].
- (3)
- Vine Copula-based multivariate covariate analysis
The copula model can provide a statistical approach for modeling the dependent structure of random variables. It connects the marginal distribution functions of each random variable with their joint distribution functions, revealing their correlation structure without relying on specific marginal distribution forms. Copula has the advantage of handling any type of marginal distribution. It can measure the correlation of multivariate distributions under different marginal distributions, thus comprehensively describing the linear and nonlinear dependencies between variables [30]. Owing to its strong flexibility and applicability, copula has been widely applied in various fields such as climate, hydrology, and environment. This study employs Vine Copula-based multivariate covariate analysis to investigate the dependence structure between NDVI and various meteorological factors (e.g., temperature and precipitation). Vine Copula is a flexible high-dimensional copula model commonly represented by C-vine and D-vine structures. Its core principle is to decompose high-dimensional dependency structures into a series of lower-dimensional copulas (e.g., bivariate or trivariate), allowing for efficient modeling of complex dependencies, including nonlinear relationships and tail dependencies. The specific steps of Vine Copula-based analysis are as follows:
- (i)
- Marginal Distribution Fitting.
The marginal distribution of each variable is first fitted to accurately describe its univariate behavior. For the climate and NDVI data, multiple marginal distributions, including Gumbel, Gamma, log-normal, Weibull, normal, and generalized extreme value (GEV) distributions, are sequentially fitted to describe their univariate behavior. The fitting process estimates the parameters (e.g., location, scale, and shape) of each distribution and evaluates the model quality using the Akaike Information Criterion (AIC), with the lowest AIC indicating the best fit. Using the parameters of the optimal distribution, the cumulative distribution function (CDF) is computed over a specified data range to analyze the probability distribution characteristics and support risk assessment. The data are then transformed into [0, 1] quantiles via the probability integral transform for standardized input in copula modeling.
- (ii)
- Vine Copula Structure Selection.
Based on the dimensionality of the data and the relationships among variables, an appropriate Vine structure (C-Vine or D-Vine) is selected. Model selection criteria such as AIC are used to determine the optimal tree structure and choose suitable low-dimensional copula types (e.g., Gaussian, t-distribution, or Gumbel copulas). In detail, a d-dimensional copula is a function mapping from [0, 1]d to [0, 1]. Consider random vectors X1, X2, …, Xd with marginal distributions denoted as F1, F2, …, Fd, and the joint distribution denoted as F(x1, x2, …, xd). According to Sklar’s theorem, for all x ∈ R, R ∈ (−∞, +∞), there exists a copula C and the relationship between the joint distribution F(x1, x2, …, xd) and copula function C, which can be expressed as follows [31]:
where C(.) is a copula function; is a continuous function; and ; and for i = 1, 2, …, d. As modeling of marginal distributions can be conveniently separated from dependence modeling, it is flexible in selecting both the marginal and dependent models of copulas [32]. A number of bivariate copula functions have been developed, mainly including the Archimedean, elliptical, and extreme value copulas [33]. With the development of the pair-copula approach, multivariate copulas have recently been significantly extended through d(d − 1)/2 bivariate copulas [34]. Among the possible pair-copula constructions, vine copulas, including canonical vine (C-vine) and D-vine, have been widely used as decomposition structures. The structures of the C-vine and D-vine for the five random variables are shown in Figure 2.
F(y, x1, x2,x3, x4) = C(v, u1, u2, u3, u4)
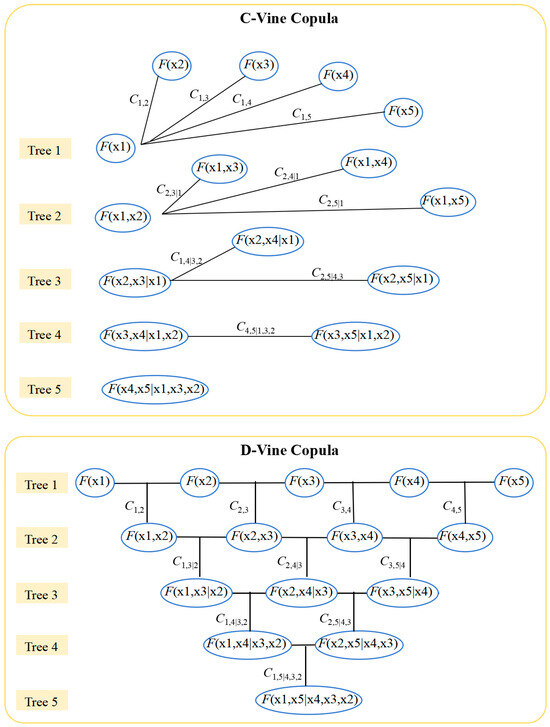
Figure 2.
The structures of C-vine and D-vine for five random variables.
For C-vine:
For D-vine:
For is the probability density corresponding to and c(.) is the density function corresponding to copula C(.). The pair-copula constructions decompose a multivariate probability density into a bivariate copula, with each pair-copula chosen independently from the others, which allows for enormous flexibility in dependence modeling.
- (4)
- Multilevel Factorial Analysis.
Multilevel factorial analysis (MFA) is a powerful statistical analysis method that has been widely used by researchers to investigate the individual effects of several independent variables (factors) and their interactions with a dependent variable (response). MFA has been used in many fields, such as water resource management [35], hydrological model parameter uncertainties [36], and water quality management [37]. Assume a generalized model Y = F(x1, x2, x3, x4). x1, x2, x3, and x4 represent the independent variables (e.g., climate variables), and Y represents the response (e.g., NDVI). Each variable xi has levels, where . According to the Analysis of variance (ANOVA) theory, the total sum of the squares (TSS) can be divided into the sum of squares due to individual model parameters and their interactions as follows:
where represents the squares due to the individual effect of xi; to represent the squares due to interactions among k factors. In this model, all interaction terms are summarized into the term SSint.
Then, for each effect, the variance fractions are derived as follows:
where:
The symbol “o” indicates the averaging over a particular index. The value of indicates the contribution of the independent variable to the total ensemble variance:
3. Results
3.1. The Spatiotemporal Variability of NDVI
The annual distribution and trend of NDVI in China from 2000 to 2023 are shown in Figure 3. The results reveal significant spatial heterogeneity in NDVI, with values gradually increasing from northwest to southeast, which is consistent with previous reports [38]. Low NDVI values (NDVI < 0.1) account for 17.6% of the area, predominantly distributed in inland river basins. In contrast, high NDVI values (NDVI > 0.8) make up 12.7% of the area, mainly concentrated in the eastern parts of the Southwest River basins, the central Yangtze River Basin, the Southeast River basins, and the Songliao River Basin. In addition, as shown in Figure 3b, the overall NDVI in China exhibits an improving trend from 2000 to 2023, indicating favorable vegetation growth nationwide. Areas with an NDVI change rate greater than 0.003/a and less than −0.003/a account for 23.9% and 1.4% of the total area, respectively. Regions with significant improvement (NDVI change rate greater than 0.009/a) represent 2.8% of the area and are mainly concentrated in the Pearl River basin, the central Yangtze River Basin, the central Yellow River Basin, the Songliao River Basin, and the southern parts of the Southwest River basins [1,16,38]. The increase in NDVI from northwest to southeast reflects the influence of regional climatic and hydrological conditions, with arid inland river basins showing lower vegetation cover and wetter regions exhibiting denser vegetation. The notable improvement in vegetation, particularly in areas with significant NDVI growth (e.g., the central Yangtze and Pearl River basins), can be attributed to reforestation efforts, ecological restoration projects, and favorable climate changes. However, areas with declining NDVI values require further attention to mitigate environmental degradation.
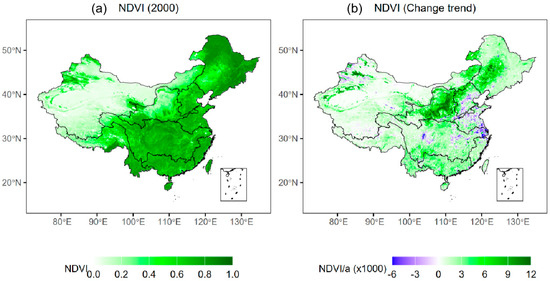
Figure 3.
The spatiotemporal variability of NDVI in China: (a) Spatial distribution of NDVI, (b) NDVI trend from 2000 to 2023.
Figure 4 presents the spatial distribution and trends from 2000 to 2023 of the main climatic variables influencing NDVI. Temp, PRE, SM, and SSR represent the surface temperature at 2 m, precipitation, soil moisture, and net solar radiation, respectively. The results indicate that China’s climate exhibits significant regional differences, with precipitation and soil moisture showing a pronounced pattern of being higher in the southeast and lower in the northwest, similar to previous reports [39]. Influenced by topography and altitude, the Qinghai-Tibet Plateau has the lowest annual average temperature and the highest net radiation intensity.
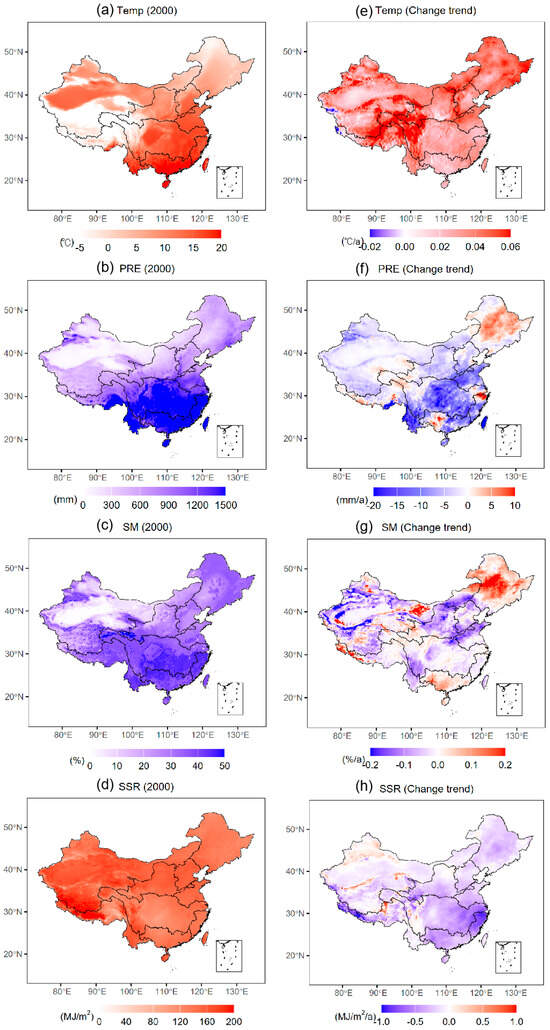
Figure 4.
Spatiotemporal analysis of major meteorological factors affecting NDVI (a–d) Spatial distribution of climate variables; (e–h) Trends of climate variables from 2000 to 2023. Temp, PRE, SM, and SSR represent surface temperature at 2 m, precipitation, soil moisture, and net solar radiation, respectively.
As shown in Figure 4, over the past two decades, 99.2% of China’s regions have experienced rising temperatures, with 38.1% showing an increase exceeding 0.04 °C per year, particularly concentrated in the upper reaches of the Yangtze River and the Qinghai-Tibet Plateau. Concurrently, the total annual precipitation across mainland China shows an overall declining trend, with an average decrease of 3.5 mm per year. This indicates a reduction in the overall water resource availability, potentially impacting agricultural production, water supply, and ecosystem health. The decline in precipitation could exacerbate drought conditions, especially in the northern and northwestern regions, intensifying water scarcity issues. However, 20.8% of the regions experienced increased precipitation, with 2.9% showing significant increases (exceeding 5 mm per year), mainly in the Songliao River Basin, upper reaches of the Pearl River Basin, Yangtze River Delta, and Three-River Source region. Similarly, from 2000 to 2023, the soil moisture across China’s land areas exhibited an overall declining trend, with an average reduction rate of 0.013% per year. About 11.8% of the area saw a decrease in soil moisture exceeding 0.1% per year, primarily in the Yellow River Basin, Huai River Basin, and Yunnan-Guizhou Plateau. Meanwhile, 7.5% of the area showed soil moisture increases above 0.1% per year, mainly in the Songliao River Basin, Pearl River Basin, eastern inland river basins, and the Three-River Source region. Net solar radiation exhibited an overall declining trend, especially in the southeastern coastal areas.
Previous studies have shown that the impacts of climate change on vegetation cover and restoration are highly complex and region-specific [20,22]. On the one hand, rising temperatures and decreasing precipitation could intensify vegetation degradation in arid northern and northwestern regions, leading to reduced NDVI values and increased risks of soil erosion and desertification. On the other hand, in regions with increasing precipitation and soil moisture, such as the Songliao River Basin and the Three-River Source region, vegetation recovery may occur due to improved water availability, potentially increasing NDVI values. Such recovery may be constrained by extreme weather events (e.g., floods and droughts) induced by climate change and anthropogenic disturbances [40]. Jin et al. (2021) proved that the state of vegetation coverage is affected by various conditions and human activities; different regions have different factors that play a leading role in vegetation [41]. Additionally, while rising temperatures may extend the growing season, they could also exceed the tolerance thresholds of certain plant species, affecting vegetation composition and biodiversity. Therefore, assessing the impacts of climate change on vegetation requires an integrated evaluation of water and thermal conditions, land use, and ecological resilience to guide effective adaptation strategies.
3.2. Correlation Between Climatic Factors and NDVI
To explore the relationship between vegetation dynamics and climatic factors, this study calculated the correlation coefficients between vegetation NDVI and climatic factors across China at each grid point from 2000 to 2023 (Figure 5). On a national scale, the annual vegetation NDVI shows correlations of 0.66, 0.46, 0.14, and 0.46 with temperature, precipitation, soil moisture, and net radiation, respectively. This indicates that temperature has the most significant impact on vegetation growth, serving as the primary limiting factor for vegetation change [15,41]. Precipitation and net radiation have moderate effects, contributing to vegetation growth to a certain extent. In contrast, the correlation with soil moisture is relatively low, suggesting that its influence might be more pronounced under local or specific conditions but weaker on a national scale. These findings reveal the combined effects of climatic and environmental factors on vegetation dynamics.
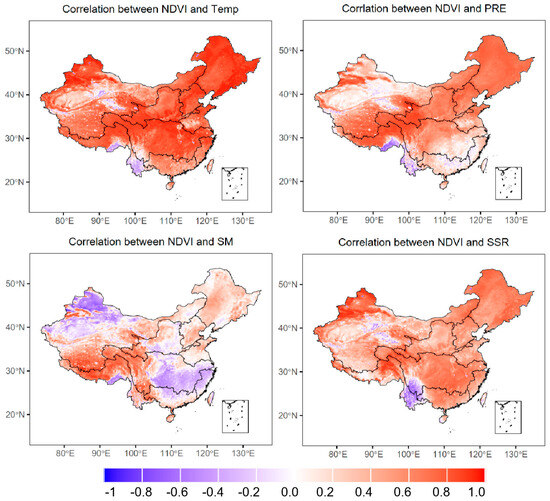
Figure 5.
Correlation analysis between NDVI and meteorological factors. (Temp, PRE, SM, and SSR represent the surface temperature at 2 m, precipitation, soil moisture, and net solar radiation, respectively. The number of data pairs analyzed is n = 12 × 24, representing monthly values over 24 years).
From a regional perspective, the correlation between vegetation NDVI and climatic factors during 2000–2023 exhibits significant spatial heterogeneity, a phenomenon that has also been reported in previous studies [8,42]. Overall, the area with a positive correlation between NDVI and climatic factors is larger than that with a negative correlation, indicating that climate change generally has a positive effect on vegetation growth. In detail, the correlation coefficients between annual vegetation NDVI and temperature show that regions with positive and negative correlations account for 95.87% and 4.13% of the total study area, respectively, suggesting that temperature promotes vegetation growth in most areas [43]. Regions with correlation coefficients greater than 0.8 account for 41.3% of the total area, mainly concentrated in the Songhua River Basin and the Yangtze River Basin. In these areas, temperature changes likely align closely with the vegetation growing season, with rising temperatures directly enhancing photosynthesis and biomass accumulation [9]. In contrast, the small negative correlation areas may be associated with vegetation stress caused by extreme heat events or drought [40], requiring further investigation. NDVI and precipitation show positive and negative correlations across 8.01% and 91.99% of the study area, respectively, reflecting significant spatial variability in precipitation’s impact on vegetation growth. The correlation coefficients range from −0.84 to 0.92. Regions with positive correlations are mainly distributed in the Himalayan region of Southwest China and eastern Northeast China [43], where increased precipitation effectively alleviates water stress and promotes vegetation growth. Positive and negative correlation areas between NDVI and soil moisture account for 66.30% and 33.70% of the total area, respectively, with correlation coefficients ranging from −0.85 to 0.95. Regions with high correlation coefficients (>0.8) are primarily located in the southern Tibetan Plateau, likely due to the critical role of soil moisture in limiting alpine vegetation growth. Areas with low or negative correlations are mainly distributed in the lower Yangtze River Basin and northwestern inland river basins, where excessive or insufficient soil moisture may stress vegetation. This highlights the complexity and spatial variability of soil moisture impacts. NDVI and net solar radiation show positive and negative correlations across 93.44% and 6.56% of the total area, respectively, with positive correlations dominating. Solar radiation has the strongest positive effect on NDVI in the Himalayan region of Southwest China and northwestern inland river basins, where vegetation has high light-use efficiency, and radiation changes significantly affect photosynthetic efficiency [44]. In contrast, the negative correlation areas are smaller and may be related to excessive radiation causing enhanced evapotranspiration and water stress in some regions.
In summary, these findings reveal the temporal and spatial complexity of climatic factors affecting vegetation growth. Temperature generally has a positive effect nationwide, while the impacts of precipitation and soil moisture are more regionalized and complex. Net solar radiation significantly promotes vegetation growth; however, its effects may be reversed under extreme climatic conditions. These results provide a scientific basis for understanding vegetation dynamics across different regions of China and offer valuable insights into regional ecological management and climate adaptation strategies.
3.3. Clustering Analysis
To reveal the relationship between NDVI and climatic factors, we can calculate the correlation for each grid point (e.g., using Pearson correlation coefficients) and classify the study area through clustering analysis, identifying the spatial distribution characteristics of each category and their main driving factors. K-means is one of the widely used clustering methods. The only parameter of the K-means algorithm is the number of clusters, K. In this study, we estimate the number of clusters based on the total within-cluster sum of squares. As shown in Figure 6, the total within-cluster sum of squares significantly decreased as the number of clusters increased from 1 to 6 and then decreased more slowly. Figure 7 shows the spatial clustering results for different values of K. It can be observed that as the number of clusters increases, for instance, from six to eight, the classification becomes more granular, resulting in a more fragmented spatial distribution. Therefore, after considering both the clustering outcomes and the spatial distribution of the geographical and climatic zones, K = 7 was selected for subsequent classification. This choice allows for a more balanced representation of spatial patterns. In the next phase, we will conduct a separate analysis of the influence of climate factors and NDVI within each identified class.
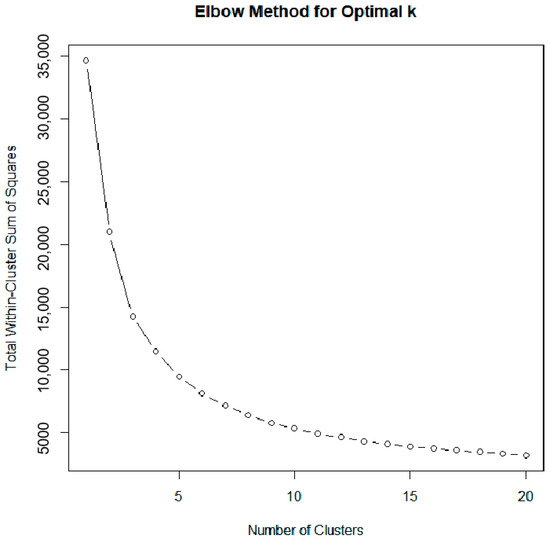
Figure 6.
Optimum number of clusters in K-means clustering based on the total within-cluster sum of squares.
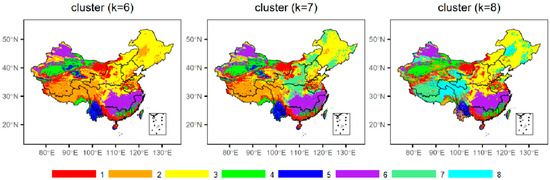
Figure 7.
Clustering results for K = 6, K = 7, and K = 8.
In the clustering results for K = 7, 23.7% of the grid points belong to Cluster 3, mainly distributed in the Songliao and Haihe River Basins, showing a banded spatial distribution. Cluster 7 accounts for 16.4% of the grid points, concentrated in central China, particularly at the intersection of the Yellow River Basin and the middle reaches of the Yangtze River. Cluster 2 contains 15.7% of the grid points, primarily located on the Qinghai-Tibet Plateau. Cluster 1 comprises 14.7% of the grid points, distributed in the western part of North China. Cluster 6 accounts for 14.4% of the grid points, mainly distributed in the middle and lower reaches of the Yangtze River. Cluster 4 contains 10.5% of the grid points, concentrated in the Tarim Basin and the southern Qinghai-Tibet Plateau. Finally, 4.5% of the grid points belong to Cluster 5, mainly distributed in the Yunnan-Guizhou Plateau.
Table 1 presents the mean correlations between NDVI and climatic variables for the different categories (when k = 7). It can be found that there are significant differences in the correlation distribution characteristics among different clusters. For instance, in Cluster 1, the mean correlations between NDVI and precipitation, temperature, soil moisture, and net solar radiation are 0.34, 0.53, 0.25, and 0.34 (as shown in Table 1), respectively, indicating that vegetation in these areas responds relatively evenly to multiple climatic factors, with moderate impacts from each factor on NDVI. In Cluster 2, NDVI exhibits high correlations with precipitation and temperature, with mean values of 0.75 and 0.78, respectively, while the correlations with soil moisture and net solar radiation are also relatively high (0.66 and 0.50). This suggests that vegetation dynamics in these regions are strongly driven by comprehensive climatic conditions, particularly precipitation and temperature. In Cluster 3, NDVI has the highest correlation with temperature (0.83), followed by precipitation (0.67) and net solar radiation (0.58), while the correlation with soil moisture is lower (0.26). This indicates that temperature is the primary driver of vegetation changes in these areas, with precipitation and net solar radiation also contributing to some extent. In Cluster 4, NDVI shows low or even negative correlations with climatic variables. The mean correlations with precipitation and soil moisture are −0.02 and −0.16, respectively, suggesting that the relationship between vegetation and climatic factors in these areas is more complex, possibly influenced by non-climatic factors (e.g., land use) or other unconsidered environmental variables. In Cluster 5, NDVI has negative correlations with temperature and net solar radiation (−0.08 and −0.34) and low correlations with precipitation and soil moisture (0.02 and 0.29), indicating that vegetation dynamics in these areas are less sensitive to climatic factors and may be primarily driven by non-climatic factors. In Cluster 6, NDVI shows high correlations with temperature and net solar radiation (0.76 and 0.63), while the correlation with precipitation is relatively low (0.21) and negative with soil moisture (−0.35). This suggests that vegetation in these regions is mainly driven by temperature and radiation conditions, while soil moisture may impose certain limitations on vegetation changes. In Cluster 7, NDVI exhibits the highest correlation with temperature (0.85), followed by net solar radiation (0.60) and precipitation (0.63), while the correlation with soil moisture is low and close to zero (−0.05). This indicates that vegetation changes in these regions are primarily driven by temperature, with precipitation and solar radiation also playing important roles. Overall, the different clusters reflect the distinct response characteristics of NDVI to climatic factors in various regions, providing valuable insights for further analysis of the driving mechanisms behind vegetation dynamics.

Table 1.
Mean correlations between NDVI and climatic variables for different categories (when k = 7).
Figure 8 presents box plots of the correlations between NDVI and climatic variables for different clusters. A comprehensive analysis of the correlations between NDVI and environmental factors (precipitation, temperature, soil moisture, and radiation) across different clusters reveals significant variations in the influence of these factors on NDVI. Firstly, regarding the correlation between NDVI and precipitation (PRE), most clusters exhibit a strong positive correlation. Notably, in Cluster 2 and Cluster 3, the influence of precipitation on NDVI is particularly significant, with the median correlation in Cluster 2 reaching 0.77, ranging from 0.51 to 0.92, indicating high stability. In contrast, Cluster 5 shows significant variability, with a median correlation close to 0, ranging from −0.68 to 0.71, suggesting that the influence of precipitation on NDVI is more complex or even negligible in this cluster. Secondly, the correlation between NDVI and temperature (temp) reveals a highly significant positive correlation. In Cluster 3, the median correlation is as high as 0.84, with a range from 0.58 to 0.97, indicating strong consistency and stability. Cluster 6 and Cluster 7 also exhibit significant positive correlations, with median values of 0.79 and 0.86, respectively. However, the temperature correlation in Cluster 5 shows a slight negative trend, with a median of −0.09, suggesting that in this region, NDVI may be influenced more by other factors. Notably, Cluster 4 shows the greatest fluctuation in correlation, ranging from −0.17 to 0.60, indicating that the influence of temperature on NDVI in this region is uncertain. Regarding the correlation between NDVI and soil moisture (SM), the results vary greatly across clusters. In Cluster 2, the correlation between NDVI and soil moisture is relatively high, with a median of 0.56, ranging from 0.38 to 0.74. However, in Cluster 6, the correlation is distinctly negative, with a median of −0.46, ranging from −0.76 to −0.25, suggesting that higher soil moisture may inhibit NDVI in this Cluster. Additionally, Cluster 5 shows a more neutral trend, with a median of 0.06, indicating that the influence of soil moisture on NDVI is minimal or confounded by other factors. Lastly, the correlation between NDVI and radiation (SSR) generally shows a consistent positive relationship. In Cluster 3 and Cluster 6, the median correlations are 0.58 and 0.64, respectively, indicating a significant promoting effect of radiation on NDVI. However, Cluster 5 is an outlier, with a median correlation of −0.33, ranging from −0.80 to 0.11, indicating a negative correlation that may be influenced by regional climate or topographical factors. Moreover, Cluster 1 shows a relatively weak positive correlation, with a median of only 0.35, suggesting a limited role of radiation in affecting NDVI in this group.
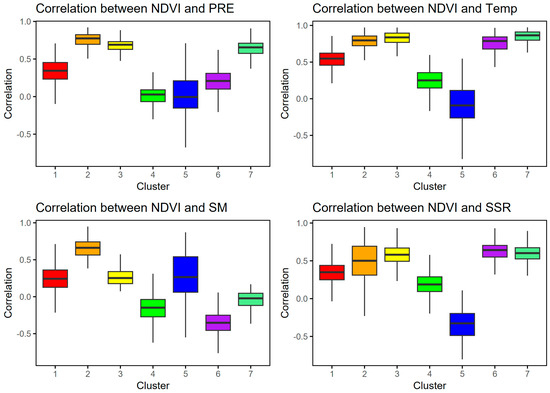
Figure 8.
Box plots of the correlations between NDVI and climatic variables for different clusters. (The number of data pairs analyzed for each grid is n = 12 × 24, representing monthly values over 24 years).
In conclusion, the influence of environmental factors on NDVI varies significantly across different clusters. Precipitation and temperature generally exhibit strong positive correlations, especially in Clusters 2 and 3. The effects of soil moisture and radiation are more region-specific, with Cluster 6 showing a negative correlation for soil moisture and Cluster 5 exhibiting considerable uncertainty in the impact of multiple factors. Future research could explore the mechanisms by which environmental factors influence NDVI, taking into account the specific characteristics of different regions, to provide a scientific basis for ecosystem management and sustainable development.
3.4. Multivariate Joint Probability Analysis
Table 2 presents the best-fit distribution types, corresponding parameters, and Akaike Information Criterion (AIC) values for various variables (precipitation pre, temperature Temp, soil moisture SM, solar radiation SSR, and normalized difference vegetation index NDVI) across different Clusters (Clusters 1–7). The results indicate that the best-fit distribution for precipitation across clusters is primarily the Weibull distribution, with some clusters following gamma and log-normal (lnorm) distributions. The AIC values range from 12,739,921 to 62,787,189, with Cluster 5 (gamma distribution) having the lowest AIC, indicating the best fit. For temperature, the best-fit distribution for all clusters is the normal distribution (norm), where parameter 1 and parameter 2 represent the mean and standard deviation, respectively. Cluster 5 has the lowest AIC value (9,572,931), showing the most optimal fit. For soil moisture (SM), the best-fit distributions include the generalized extreme value (gev), normal (norm), and Weibull distributions. Cluster 5 has the lowest AIC value (gev, −967,188.9), demonstrating the best fit. For solar radiation (SSR), the best-fit distribution for all clusters is the Weibull distribution, with parameters 1 and 2 describing its distribution characteristics. In the case of the normalized difference vegetation index (NDVI), the best-fit distribution for all clusters is the normal distribution, with Cluster 5 having the lowest AIC value (23,762,261), reflecting its superior fit. Overall, the best-fit distributions for precipitation and soil moisture exhibit greater variability, including Weibull, Gamma, and generalized extreme value distributions, while the distributions for temperature, solar radiation, and NDVI are more consistent, primarily following the normal and Weibull distributions. Additionally, the comparison of AIC values reveals that lower values indicate better model performance, with Cluster 5 consistently achieving the best-fit results across all variables.

Table 2.
The best distribution of climate variables and DNVI for different clusters.
Table 3 shows the results of the joint probability distribution fitting and optimization between NDVI and climate factors for different clusters, including tree structures (Tree), edge node information (Edge), copula distribution family types (Family), copula model parameters (Par1, Par2), and Kendall’s Tau correlation coefficient (Tau). Based on these two tables, the dependency structures, correlation patterns, and differences between each cluster are analyzed. The different trees (Tree) and edges (Edge) in each cluster correspond to five main climate factors: NDVI (normalized difference vegetation index), Pre (precipitation), Temp (temperature), SM (soil moisture), and SSR (solar radiation). These factors represent different edges in the model, and the correlation of each edge is measured by the tau value.

Table 3.
The best D-Vine Copula fit for clusters 1–7.
Specifically, in Cluster 1, the tau values vary significantly, reflecting notable dependency structures between different climate factors within this cluster. For example, the tau value between edge 1 (NDVI) and edge 2 (Precipitation) is 0.46, indicating a moderate positive correlation between these two factors. Meanwhile, the tau value between edge 4 (SSR) and edge 5 (Soil Moisture) is 0.37, showing a strong positive correlation between soil moisture and SSR. Cluster 2’s tau values show some strong correlations, particularly between NDVI and precipitation (tau = 0.39) and temperature (tau = 0.46). In this cluster, the F-type copula (e.g., edge 4) exhibits significant dependence, especially with a strong correlation between temperature and precipitation. Cluster 3’s data demonstrate a more complex dependency structure. For instance, the correlation between NDVI and precipitation (tau = 0.49) is strong, while the correlation between soil moisture and solar radiation (tau = 0.37) is moderately positive. Cluster 4’s results suggest relatively weak correlations between different climate factors, particularly between temperature and precipitation (tau = 0.11) and between soil moisture and solar radiation (tau = 0.50). Some edges show strong dependencies, particularly under the influence of F-type and SC-type copulas. In Cluster 5, the tau values are generally high, indicating strong correlations. For example, there is a strong correlation between NDVI and precipitation (tau = 0.60), and there is a weaker positive correlation between SSR and soil moisture (tau = 0.37). The C270-type copula here shows a more complex correlation pattern with other factors. Cluster 6’s tau values are relatively low, especially with weak correlations between temperature and precipitation (tau = 0.27) and between soil moisture and SSR (tau = 0.61). The dependency structure in this cluster is more dispersed, indicating a looser relationship between climate factors. Cluster 7 also exhibits strong dependencies, particularly with a high correlation between NDVI and precipitation (tau = 0.52). Compared with other clusters, Cluster 7 shows more complex dependency structures in some cases, especially in models using G90- and C270-type copulas.
3.5. Main and Interactive Impacts of Climate Factors on NDVI
To quantitatively analyze the main and interactive impacts of climate factors on NDVI changes, a combination of quantile sampling and full combination techniques was employed to generate climate combinations. These climate combinations were then input into a Vine Copula model, which was used to estimate the NDVI response under different climatic conditions. The climate factors and corresponding NDVI responses were subsequently input into a two-way factorial analysis to evaluate the main and interaction effects. The main and interactive impacts of climate factors on NDVI, both qualitatively and quantitatively, are illustrated in Figure 9, Figure 10, Figure 11 and Figures S1–S6.
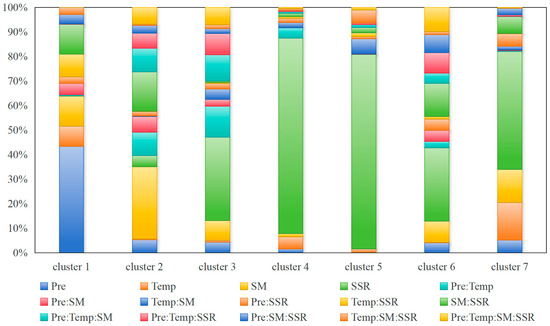
Figure 9.
Quantitative results of the main effects and interaction effects of climatic variables on NDVI.
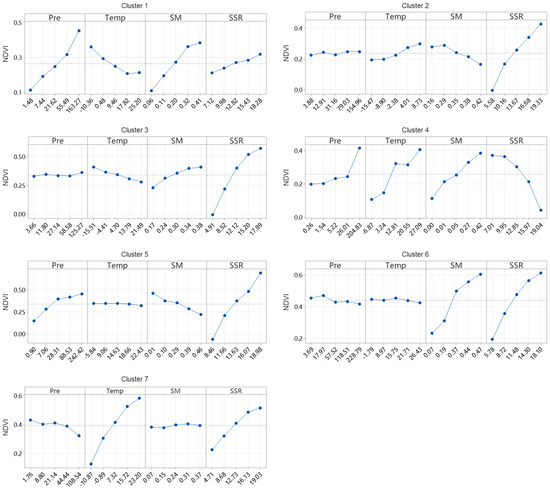
Figure 10.
The main effects of multiple climatic factors on NDVI for different clusters.
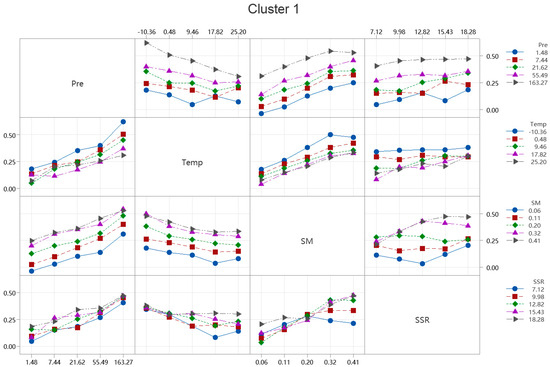
Figure 11.
Interactive effects of multiple climatic factors on NDVI in Cluster 1. The results for Clusters 2 through 7 are presented in the Supplementary Materials (Figures S1–S6).
Figure 9 presents an analysis of the major contributing factors and their interactions across different clusters. The results indicate significant regional differences in the drivers of NDVI, including precipitation (Pre), temperature (Temp), soil moisture (SM), and solar radiation (SSR). In Cluster 1, precipitation is the primary contributing factor, accounting for 43%, highlighting the high dependence of vegetation growth on water availability, which may be associated with arid or semi-arid regions. In contrast, the contribution of precipitation in Cluster 7 is only 5%, indicating a lower dependence on water in areas likely to have sufficient water supply. SSR dominates in Clusters 4 and 5, contributing 80% and 79%, respectively, suggesting that vegetation in these regions is primarily limited by solar energy, possibly in tropical or high-radiation environments. In Cluster 2, the direct contribution of soil moisture reaches 29%, emphasizing the importance of soil water availability in humid areas or irrigated agricultural regions. The influence of temperature is more evident in its interactions with other factors [41], such as Pre:Temp and Pre:Temp:SM, which show significant contributions in Clusters 3 and 6, reflecting the critical role of the synergy between precipitation, temperature, and soil moisture.
As shown in Figure 9 and Figure 11, the interactions among climatic factors significantly affect NDVI variations, a phenomenon also observed in previous studies [9]. However, in our study, we provide quantitative results to support these findings. In Cluster 6, the second-order interaction between soil moisture and solar radiation (SM:SSR) contributes 13%, underscoring the crucial role of their synergy in vegetation growth. In Cluster 3, the second-order interaction between precipitation and temperature (Pre:Temp) contributes 13%, likely influencing NDVI indirectly by regulating evapotranspiration and soil moisture. Moreover, third-order interactions, such as Pre:Temp:SM, contribute 10% and 11% in Clusters 2 and 3, respectively, while the fourth-order interaction, Pre:Temp:SM:SSR, contributes the most in Cluster 6 at 10%. The variations in contributing factors across clusters reflect the diversity of regional climatic conditions driving NDVI. For example, Cluster 1 is dominated by precipitation, suggesting a focus on water resource management; Clusters 4 and 5 are dominated by solar radiation, which could benefit from optimizing photosynthetic efficiency; and Cluster 6 highlights the comprehensive influence of multiple factors, including third- and fourth-order interactions. The differences in contributing factors across clusters underscore the complexity of the driving mechanisms and the need for tailored adaptive management strategies to address diverse climatic conditions.
4. Conclusions
This study developed a factorial-clustered copula covariate analysis model to explore the interaction effects of multiple climate factors on vegetation cover in China. Specifically, the copula model was used to analyze the response relationship of NDVI to precipitation, temperature, soil moisture, and surface net solar radiation. Given the relationship between NDVI and these climatic factors, regions with similar relationships are clustered into one category. The main and interaction effects of the climatic factors and corresponding NDVI responses are evaluated through multilevel factorial analysis. The main results are as follows:
- (1)
- From 2000 to 2023, NDVI in China showed significant spatial variability, with low values (<0.1) covering 17.6% and high values (>0.8) covering 12.7% of the area. Rising temperatures impacted 99.2% of the regions, with 38.1% showing increases above 0.04 °C/year. NDVI improved significantly in 2.8% of the areas (e.g., Pearl River and Yangtze basins), while 1.4% showed a decline. Temperature had the strongest correlation with NDVI (0.66), followed by precipitation (0.46), net radiation (0.46), and soil moisture (0.14).
- (2)
- NDVI responses to climatic factors exhibit distinct spatial heterogeneity. Temperature emerges as the dominant driver in Clusters 2, 3, 6, and 7, primarily located in the Qinghai-Tibet Plateau, Songliao and Haihe River Basins, the middle and lower Yangtze River, and central China, respectively, where correlations with precipitation and solar radiation are also notable. In contrast, Clusters 4 (Tarim Basin and southern Qinghai-Tibet Plateau) and 5 (Yunnan-Guizhou Plateau) show weak or negative correlations with climatic variables, suggesting that non-climatic factors, such as land use, play a more significant role in these areas. This highlights the complex interplay between climatic and non-climatic factors influencing vegetation dynamics across diverse regions.
- (3)
- The analysis of joint probability distributions between NDVI and climate factors reveals significant spatial heterogeneity in dependency structures across clusters. Strong correlations are observed in Clusters 5 and 7, particularly between NDVI and precipitation (tau = 0.60 and tau = 0.52, respectively), while weaker dependencies are evident in Clusters 4 and 6. The types of copulas and correlation strengths highlight distinct interaction patterns, with Clusters 1, 3, and 5 showing more complex and varied dependency structures compared to the others. This underscores the diverse climatic influences on vegetation dynamics across regions.
- (4)
- The results of the multilevel factorial analysis reveal significant regional variations in the climate factors driving NDVI changes. In Cluster 1, precipitation is the dominant factor, contributing 43%, while in Cluster 7, its contribution is only 5%. Solar radiation is the primary driver in Clusters 4 and 5, contributing 80% and 79%, respectively. Soil moisture plays a key role in Cluster 2, with a contribution of 29%. Additionally, interactions between climate factors, such as Pre:Temp and Pre:Temp:SM, significantly influence NDVI variations, emphasizing the need for tailored regional management strategies.
This study provides a deeper understanding of the complex impact mechanisms of multiple climate factors on vegetation cover in China and offers a novel and effective analytical framework for assessing ecosystem responses in the context of climate change. Future studies should focus on higher-resolution spatial and temporal data, incorporating land use and anthropogenic factors. Advanced modeling techniques, like machine learning, can enhance prediction accuracy. Additionally, exploring climate change scenarios can provide insights into the NDVI dynamics and guide regional adaptation strategies.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/atmos16020185/s1, Figure S1. Interactive effects of multiple climatic factors on NDVI for cluster 2; Figure S2. Interactive effects of multiple climatic factors on NDVI for cluster 3; Figure S3. Interactive effects of multiple climatic factors on NDVI for cluster 4; Figure S4. Interactive effects of multiple climatic factors on NDVI for cluster 5; Figure S5. Interactive effects of multiple climatic factors on NDVI for cluster 6; Figure S6. Interactive effects of multiple climatic factors on NDVI for cluster 7.
Author Contributions
F.W.: Conceptualization, Methodology, Software, Writing—original draft. Y.W.: Methodology, Writing—original draft. R.D.: Methodology. J.Z.: Writing—original draft. X.Z.: Methodology, Validation, review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the China Postdoctoral Science Foundation funded project (2023M730282, GZB20230069).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets analyzed in this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors have no relevant financial or non-financial interest to disclose.
References
- Zhu, L.; Sun, S.; Li, Y.; Liu, X.; Hu, K. Effects of climate change and anthropogenic activity on the vegetation greening in the Liaohe River Basin of northeastern China. Ecol. Indic. 2023, 148, 110105. [Google Scholar] [CrossRef]
- Lawley, V.; Lewis, M.; Clarke, K.; Ostendorf, B. Site-based and remote sensing methods for monitoring indicators of vegetation condition: An Australian review. Ecol. Indic. 2016, 60, 1273–1283. [Google Scholar] [CrossRef]
- Shen, X.; Xue, Z.; Jiang, M.; Lu, X. Spatiotemporal Change of Vegetation Coverage and its Relationship with Climate Change in Freshwater Marshes of Northeast China. Wetlands 2019, 39, 429–439. [Google Scholar] [CrossRef]
- He, B.; Chen, A.; Wang, H.; Wang, Q. Dynamic Response of Satellite-Derived Vegetation Growth to Climate Change in the Three North Shelter Forest Region in China. Remote Sens. 2015, 7, 9998–10016. [Google Scholar] [CrossRef]
- Jiapaer, G.; Liang, S.; Yi, Q.; Liu, J. Vegetation dynamics and responses to recent climate change in Xinjiang using leaf area index as an indicator. Ecol. Indic. 2015, 58, 64–76. [Google Scholar] [CrossRef]
- Gao, Q.; Guo, Y.; Xu, H.; Ganjurjav, H.; Li, Y.; Wan, Y.; Qin, X.; Ma, X.; Liu, S. Climate change and its impacts on vegetation distribution and net primary productivity of the alpine ecosystem in the Qinghai-Tibetan Plateau. Sci. Total. Environ. 2016, 554, 34–41. [Google Scholar] [CrossRef]
- Riihimaki, H.; Heiskanen, J.; Luoto, M. The effect of topography on arctic-alpine aboveground biomass and NDVI patterns. Int. J. Appl. Earth Obs. Geoinf. 2017, 56, 44–53. [Google Scholar] [CrossRef]
- Guo, B.; Xu, M.; Zhang, R.; Luo, W.; Yang, J. What Are the Variation Patterns of Vegetation and Its Influencing Factors in China from 2000–2020 from the Partition Perspective? Forests 2024, 15, 1409. [Google Scholar] [CrossRef]
- Fan, J.; Zhao, Y.; Wang, D.; Zhou, X.; Li, Y.; Zhang, W.; Xu, F.; Wei, S. A Stepwise Multifactor Regression Analysis of the Interactive Effects of Multiple Climate Factors on the Response of Vegetation Recovery to Drought. Atmosphere 2024, 15, 1094. [Google Scholar] [CrossRef]
- Lamchin, M.; Park, T.; Lee, J.-Y.; Lee, W.-K. Monitoring of Vegetation Dynamics in the Mongolia Using MODIS NDVIs and their Relationship to Rainfall by Natural Zone. J. Indian Soc. Remote Sens. 2015, 43, 325–337. [Google Scholar] [CrossRef]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol. 2005, 20, 503–510. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Wang, Y.; Fu, Y.H.; Xue, B.; Wang, G.; Yu, J.; Zuo, D.; Xu, Z. Spatial heterogeneity of changes in vegetation growth and their driving forces based on satellite observations of the Yarlung Zangbo River Basin in the Tibetan Plateau. J. Hydrol. 2019, 574, 324–332. [Google Scholar] [CrossRef]
- Yuan, X.; Li, L.; Chen, X. Increased grass NDVI under contrasting trends of precipitation change over North China during 1982–2011. Remote Sens. Lett. 2015, 6, 69–77. [Google Scholar] [CrossRef]
- Peng, J.; Dong, W.; Yuan, W.; Zhang, Y. Responses of grassland and forest to temperature and precipitation changes in Northeast China. Adv. Atmos. Sci. 2012, 29, 1063–1077. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z.; Cao, L.; Feng, R.; Pan, Y. Response of NDVI of natural vegetation to climate changes and drought in China. Land 2021, 10, 966. [Google Scholar] [CrossRef]
- Feng, X.; Tian, J.; Wang, Y.; Wu, J.; Liu, J.; Ya, Q.; Li, Z. Spatio-Temporal Variation and Climatic Driving Factors of Vegetation Coverage in the Yellow River Basin from 2001 to 2020 Based on kNDVI. Forests 2023, 14, 620. [Google Scholar] [CrossRef]
- Deng, Q.; Zhang, C.; Dong, J.; Li, Y.; Li, Y.; Huang, Y.; Zhang, H.; Fan, J. Variations over 20 Years in Vegetation Dynamics and Its Coupled Responses to Individual and Compound Meteorological Drivers in Sichuan Province, China. Atmosphere 2024, 15, 1384. [Google Scholar] [CrossRef]
- Kushwaha, A.; Bhatnagar, R.; Kumar, P.; Zucca, C.; Srivastava, S. Ajai Long Term Monitoring of Ecological Status of Major Deserts of the World. J. Indian Soc. Remote Sens. 2024, 52, 1819–1839. [Google Scholar] [CrossRef]
- Guo, J.; Wang, K.; Wang, T.; Bai, N.; Zhang, H.; Cao, Y.; Liu, H. Spatiotemporal Variation of Vegetation NDVI and Its Climatic Driving Forces in Global Land Surface. Pol. J. Environ. Stud. 2022, 31, 3541–3549. [Google Scholar] [CrossRef]
- Ichii, K.; Kawabata, A.; Yamaguchi, Y. Global correlation analysis for NDVI and climatic variables and NDVI trends: 1982-1990. Int. J. Remote Sens. 2002, 23, 3873–3878. [Google Scholar] [CrossRef]
- Bao, Z.; Zhang, J.; Wang, G.; Guan, T.; Jin, J.; Liu, Y.; Li, M.; Ma, T. The sensitivity of vegetation cover to climate change in multiple climatic zones using machine learning algorithms. Ecol. Indic. 2021, 124, 107443. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, J.; Chen, Y. NDVI-based vegetation responses to climate change in an arid area of China. Theor. Appl. Climatol. 2016, 126, 213–222. [Google Scholar] [CrossRef]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Liu, L.; Niu, Q.; Heng, J.; Li, H.; Xu, Z. Transition Characteristics of the Dry-Wet Regime and Vegetation Dynamic Responses over the Yarlung Zangbo River Basin, Southeast Qinghai-Tibet Plateau. Remote Sens. 2019, 11, 1254. [Google Scholar] [CrossRef]
- Wang, F.; Huang, G.; Cheng, G.; Li, Y. Impacts of climate variations on non-stationarity of streamflow over Canada. Environ. Res. 2021, 197, 111118. [Google Scholar] [CrossRef]
- Peng, J.; Liu, Z.; Liu, Y.; Wu, J.; Han, Y. Trend analysis of vegetation dynamics in Qinghai bet Plateau using Hurst Exponent. Ecol. Indic. 2012, 14, 28–39. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Shi, P.; Hou, P.; Gao, J.; Wan, H.; Wang, Y.; Sun, C. Spatial-Temporal Variation Characteristics and Influencing Factors of Vegetation in the Yellow River Basin from 2000 to 2019. Atmosphere 2021, 12, 1576. [Google Scholar] [CrossRef]
- Ahlgren, P.; Jarneving, B.; Rousseau, R. Requirements for a cocitation similarity measure, with special reference to Pearson’s correlation coefficient. J. Am. Soc. Inf. Sci. Technol. 2003, 54, 550–560. [Google Scholar] [CrossRef]
- Chen, L.; Qiu, H.; Zhang, J.; Singh, V.P.; Zhou, J.; Huang, K. Copula-based method for stochastic daily streamflow simulation considering lag-2 autocorrelation. J. Hydrol. 2019, 578, 123938. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de Répartition à n Dimensions et Leurs Marges; Publications de l’Institut de Statistique de l’Université de Paris: Paris, France, 1959; Volume 8, pp. 229–231. Available online: https://hal.science/hal-04094463/document (accessed on 30 December 2024).
- Brechmann, E.C.; Schepsmeier, U. Modeling dependence with C-and D-vine copulas: The R package CDVine. J. Stat. Softw. 2013, 52, 1–27. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-copula constructions of multiple dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Wang, F.; Huang, G.; Cheng, G.; Li, Y. Multi-level factorial analysis for ensemble data-driven hydrological prediction. Adv. Water Resour. 2021, 153, 103948. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Huang, G.; Chen, X.; Bao, A. Assessment of parameter uncertainty in hydrological model using a Markov-Chain-Monte-Carlo-based multilevel-factorial-analysis method. J. Hydrol. 2016, 538, 471–486. [Google Scholar] [CrossRef]
- Liu, J.; Li, Y.; Huang, G.; Fu, H.; Zhang, J.; Cheng, G. Identification of water quality management policy of watershed system with multiple uncertain interactions using a multi-level-factorial risk-inference-based possibilistic-probabilistic programming approach. Environ. Sci. Pollut. Res. 2017, 24, 14980–15000. [Google Scholar] [CrossRef]
- Jin, H.; Chen, X.; Wang, Y.; Zhong, R.; Zhao, T.; Liu, Z.; Tu, X. Spatio-temporal distribution of NDVI and its influencing factors in China. J. Hydrol. 2021, 603, 127129. [Google Scholar] [CrossRef]
- Chen, S.; Zhu, Z.; Liu, X.; Yang, L. Variation in Vegetation and Its Driving Force in the Pearl River Delta Region of China. Int. J. Environ. Res. Public Health 2022, 19, 10343. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Chen, Y.; Wang, A.; De Maeyer, P. The spatiotemporal response of soil moisture to precipitation and temperature changes in an arid region, China. Remote Sens. 2018, 10, 468. [Google Scholar] [CrossRef]
- Adhikari, S.; Zhou, W.; Dou, Z.; Sakib, N.; Ma, R.; Chaudhari, B.; Liu, B. Analysis of Flash Drought and Its Impact on Forest Normalized Difference Vegetation Index (NDVI) in Northeast China from 2000 to 2020. Atmosphere 2024, 15, 818. [Google Scholar] [CrossRef]
- Liang, J.; Marino, A.; Ji, Y. Spatial and Temporal Change Characteristics and Climatic Drivers of Vegetation Productivity and Greenness during the 2001–2020 Growing Seasons on the Qinghai–Tibet Plateau. Land 2024, 13, 1230. [Google Scholar] [CrossRef]
- Liu, B.; Tang, Q.; Zhou, Y.; Zeng, T.; Zhou, T. The sensitivity of vegetation dynamics to climate change across the Tibetan Plateau. Atmosphere 2022, 13, 1112. [Google Scholar] [CrossRef]
- Tuoku, L.; Wu, Z.; Men, B. Impacts of climate factors and human activities on NDVI change in China. Ecol. Inform. 2024, 81, 102555. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).