Improving the Prediction of Land Surface Temperature Using Hyperparameter-Tuned Machine Learning Algorithms
Abstract
1. Introduction
2. Materials and Methods
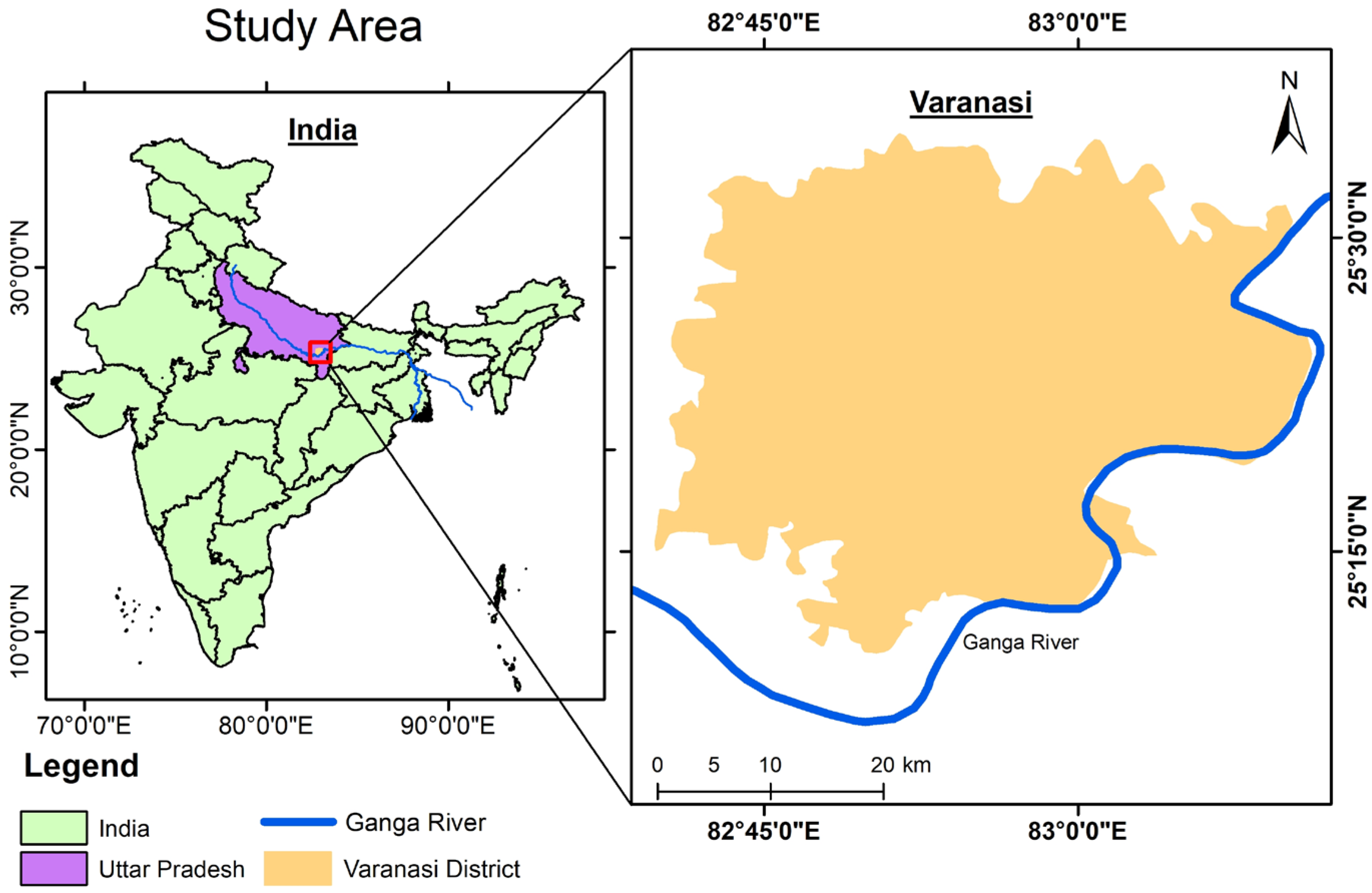
2.1. Study Area
2.2. Data Acquisition and Preprocessing
2.3. Land Surface Temperature (LST) Calculation
2.4. Spectral Indices
2.4.1. Normalised Difference Vegetation Index (NDVI)
2.4.2. Normalised Difference Water Index (NDWI)
2.4.3. Normalised Built-Up Index (NDBI)
2.4.4. Bare Soil Index (BSI)
2.5. Machine Learning Algorithms
2.5.1. Random Forest (RF)
2.5.2. Support Vector Regression (SVR)
2.5.3. K-Nearest Neighbours (kNN)
2.5.4. Gradient Boosting (GBM)
2.6. Statistical Indicators
- Top of Form
2.7. Hyperparameter Tuning
3. Results
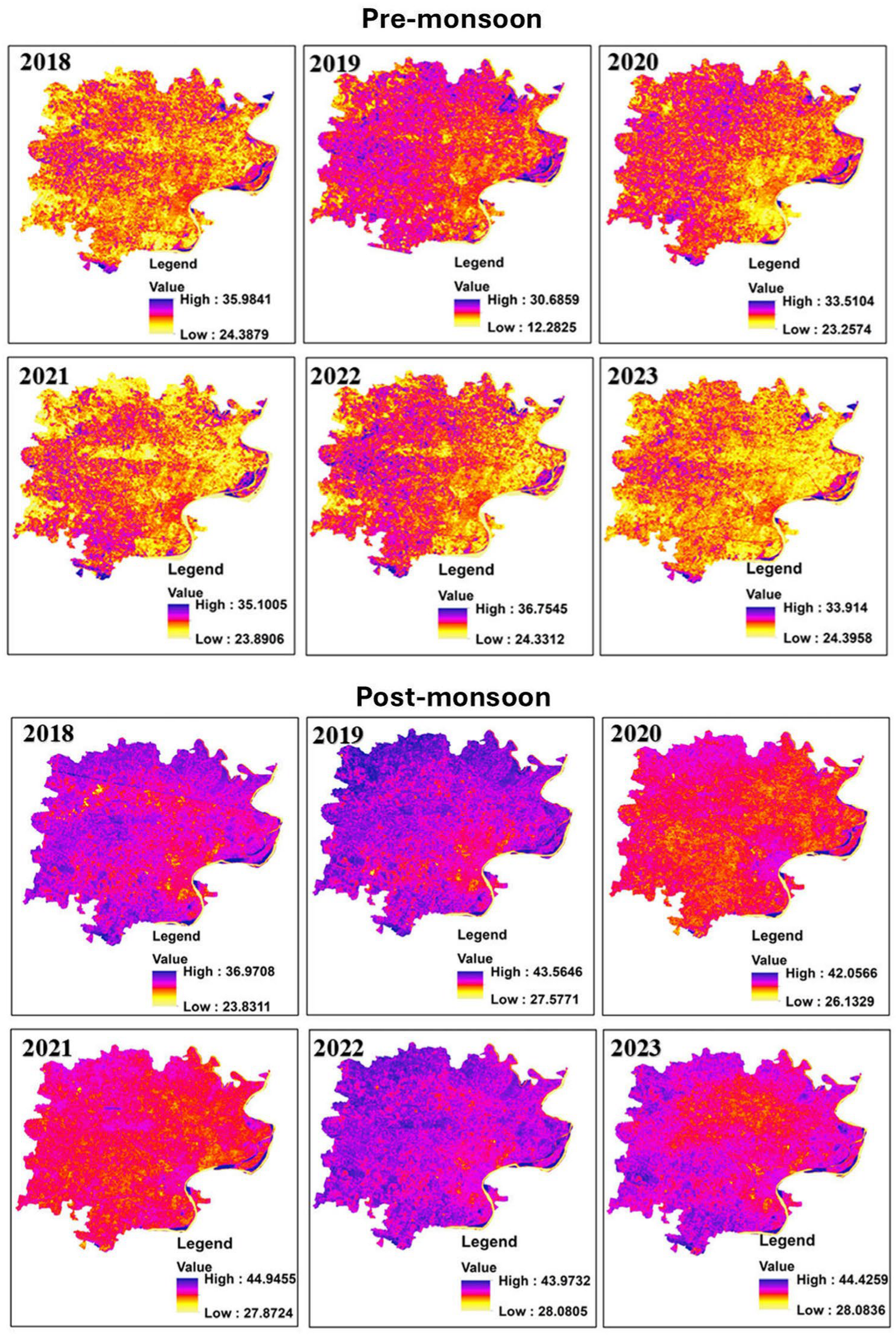
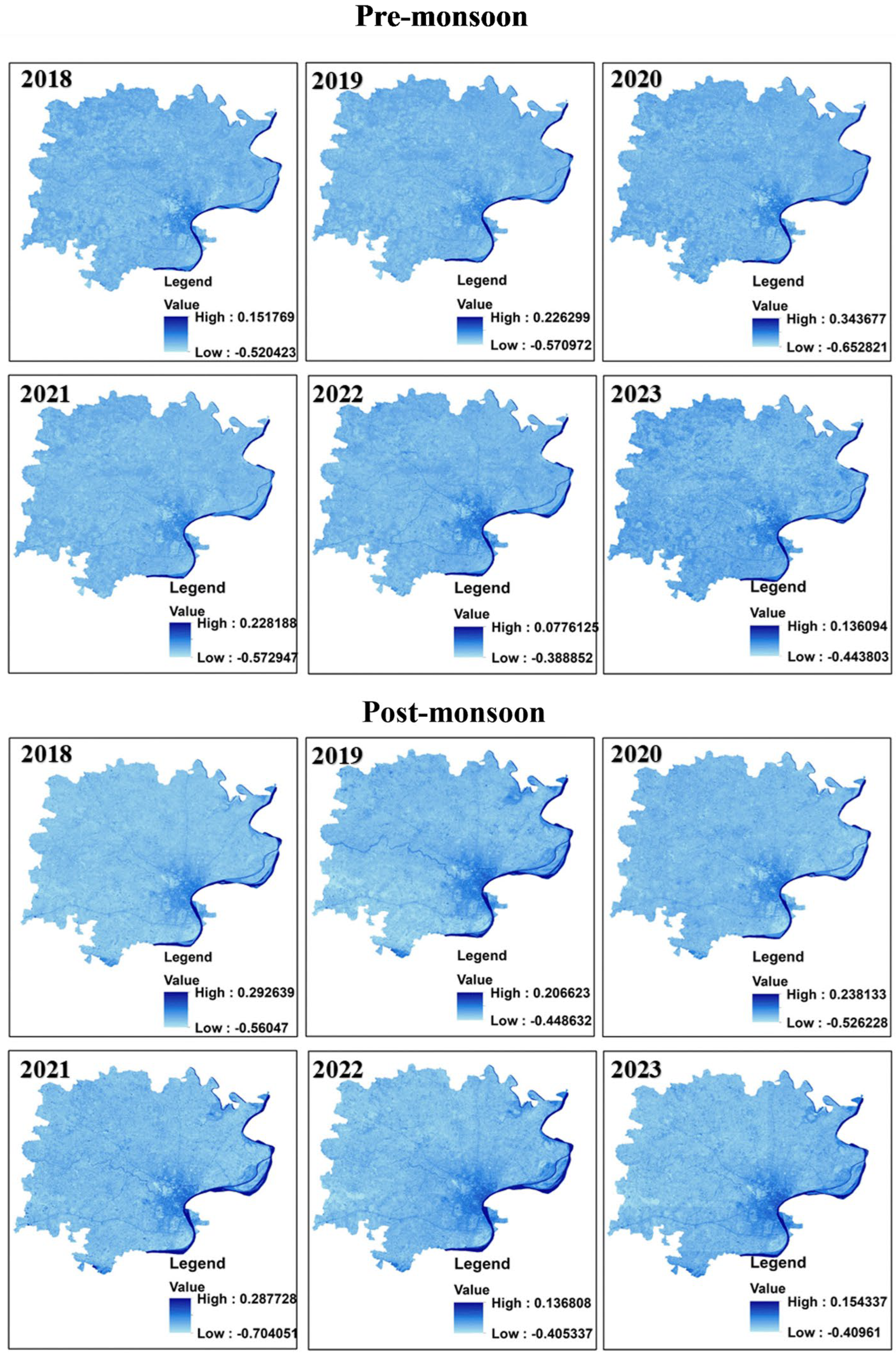
3.1. Seasonal Variations in LST Correlations Across Spectral Indices
3.1.1. Impact of Water Bodies on LST: Analysis of NDWI
3.1.2. Vegetation’s Complex Relationship with LST: Insights from NDVI
3.1.3. Urbanisation and LST: Strong Correlation with NDBI
3.1.4. Role of Bare Soil in Elevating LST: Analysis of BSI
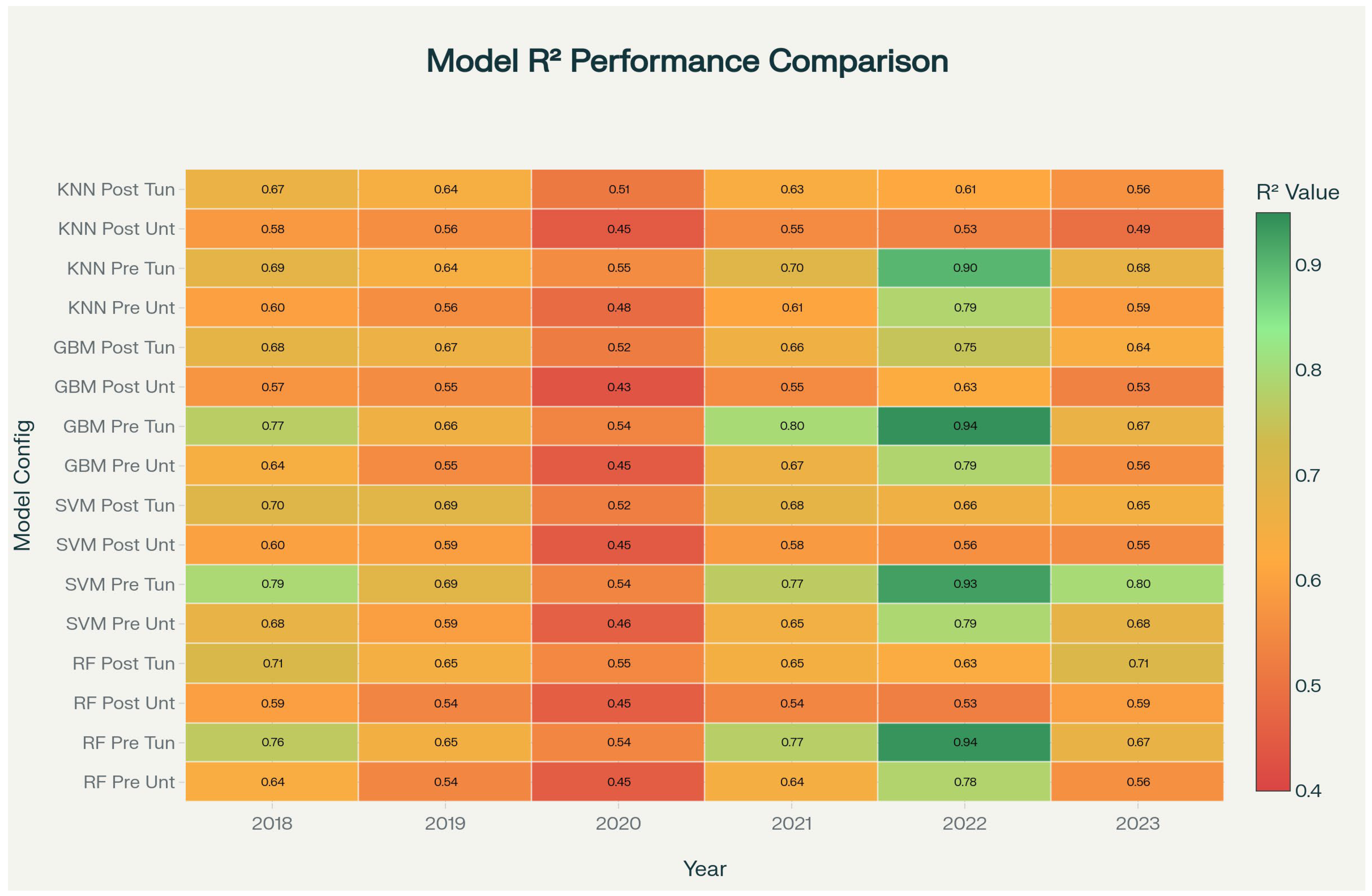
3.2. Performance of ML Algorithms for LST Prediction
4. Discussion
4.1. Importance of LST Prediction in Environmental Management
4.2. Societal Implications of LST Management
4.3. Limitations and Future Research Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LST | Land Surface Temperature |
| NDVI | Normalised Difference Vegetation Index |
| NDBI | Normalized Difference Built-up Index |
| NDWI | Normalized Difference Water Index |
| BSI | Bare Soil Index |
| RF | Random Forest |
| SVM | Support Vector Machine |
| KNN | K-Nearest Neighbours |
| GBM | Gradient Boosting Machine |
References
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Crago, R.D.; Qualls, R.J. Use of land surface temperature to estimate surface energy fluxes: Contributions of Wilfried Brutsaert and collaborators. Water Resour. Res. 2014, 50, 3396–3408. [Google Scholar] [CrossRef]
- Faisal, A.A.; Al Kafy, A.; Al Rakib, A.; Akter, K.S.; Jahir, D.M.A.; Sikdar, M.S.; Ashrafi, T.J.; Mallik, S.; Rahman, M.M. Assessing and predicting land use/land cover, land surface temperature and urban thermal field variance index using Landsat imagery for Dhaka Metropolitan area. Environ. Chall. 2021, 4, 100192. [Google Scholar] [CrossRef]
- Frahmand, A.S.; Akyuz, D.E.; Sanli, F.B.; Balcik, F.B. Can remote sensing and sebal fill the gap on evapotranspiration? A case study: Kunduz catchment, Afghanistan. J. Environ. Prot. Ecol. 2020, 21, 423–432. [Google Scholar]
- de Almeida, C.R.; Teodoro, A.C.; Gonçalves, A. Study of the urban heat island (Uhi) using remote sensing data/techniques: A systematic review. Environments 2021, 8, 105. [Google Scholar] [CrossRef]
- Mathew, A.; Sreekumar, S.; Khandelwal, S.; Kumar, R. Prediction of land surface temperatures for surface urban heat island assessment over Chandigarh city using support vector regression model. Sol. Energy 2019, 186, 404–415. [Google Scholar] [CrossRef]
- Megna, Y.S.; Pallarés, S.; Sánchez-Fernández, D. Conservation of aquatic insects in Neotropical regions: A gap analysis using potential distributions of diving beetles in Cuba. Aquat. Conserv. Mar. Freshw. Ecosyst. 2021, 31, 2714–2725. [Google Scholar] [CrossRef]
- Sánchez, J.M.; Galve, J.M.; González-Piqueras, J.; López-Urrea, R.; Niclòs, R.; Calera, A. Monitoring 10-m LST from the combination MODIS/Sentinel-2, validation in a high contrast semi-arid agroecosystem. Remote Sens. 2020, 12, 1453. [Google Scholar] [CrossRef]
- Reiners, P.; Sobrino, J.; Kuenzer, C. Satellite-Derived Land Surface Temperature Dynamics in the Context of Global Change—A Review. Remote Sens. 2023, 15, 1857. [Google Scholar] [CrossRef]
- Li, Z.L.; Wu, H.; Duan, S.B.; Zhao, W.; Ren, H.; Liu, X.; Leng, P.; Tang, R.; Ye, X.; Zhu, J.; et al. Satellite Remote Sensing of Global Land Surface Temperature: Definition, Methods, Products, and Applications. Rev. Geophys. 2023, 61, e2022RG000777. [Google Scholar] [CrossRef]
- Taloor, A.K.; Manhas, D.S.; Chandra Kothyari, G. Retrieval of land surface temperature, normalized difference moisture index, normalized difference water index of the Ravi basin using Landsat data. Appl. Comput. Geosci. 2021, 9, 100051. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
- Kim, M.; Cho, K.; Kim, H.; Kim, Y. Spatiotemporal Fusion of High Resolution Land Surface Temperature Using Thermal Sharpened Images from Regression-Based Urban Indices. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, V-3-2020, 247–254. [Google Scholar] [CrossRef]
- Zhang, L.; Yao, Y.; Bei, X.; Li, Y.; Shang, K.; Yang, J.; Guo, X.; Yu, R.; Xie, Z. ERTFM: An Effective Model to Fuse Chinese GF-1 and MODIS Reflectance Data for Terrestrial Latent Heat Flux Estimation. Remote Sens. 2021, 13, 3703. [Google Scholar] [CrossRef]
- Pu, R. Assessing scaling effect in downscaling land surface temperature in a heterogenous urban environment. Int. J. Appl. Earth Obs. Geoinf. 2021, 96, 102256. [Google Scholar] [CrossRef]
- Zegaar, A.; Telli, A.; Ounoki, S.; Shahabi, H.; Rueda, F. Data-driven approach for land surface temperature retrieval with machine learning and sentinel-2 data. Remote Sens. Appl. Soc. Environ. 2024, 36, 101357. [Google Scholar] [CrossRef]
- Shirgholami, M.R.; Masoodian, S.A.; Montazeri, M. Investigation of environmental changes in arid and semi-arid regions based on MODIS LST data (case study: Yazd province, central Iran). Arab. J. Geosci. 2023, 16, 514. [Google Scholar] [CrossRef]
- Shukla, K.K.; Attada, R.; Kumar, A.; Kunchala, R.K.; Sivareddy, S. Comprehensive analysis of thermal stress over northwest India: Climatology, trends and extremes. Urban Clim. 2022, 44, 101188. [Google Scholar] [CrossRef]
- Kumar, A.; Agarwal, V.; Pal, L.; Chandniha, S.K.; Mishra, V. Effect of Land Surface Temperature on Urban Heat Island in Varanasi City, India. J 2021, 4, 420–429. [Google Scholar] [CrossRef]
- Onačillová, K.; Gallay, M.; Paluba, D.; Péliová, A.; Tokarčík, O.; Laubertová, D. Combining Landsat 8 and Sentinel-2 Data in Google Earth Engine to Derive Higher Resolution Land Surface Temperature Maps in Urban Environment. Remote Sens. 2022, 14, 4076. [Google Scholar] [CrossRef]
- Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. In Proceedings of the Image and Signal Processing for Remote Sensing XXIII, Warsaw, Poland, 11–14 September 2017; p. 3. [Google Scholar] [CrossRef]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ. 1996, 57, 167–184. [Google Scholar] [CrossRef]
- Rad, A.M.; Kreitler, J.; Sadegh, M. Augmented Normalized Difference Water Index for improved surface water monitoring. Environ. Model. Softw. 2021, 140, 105030. [Google Scholar] [CrossRef]
- Yao, Y.; Lu, L.; Guo, J.; Zhang, S.; Cheng, J.; Tariq, A.; Liang, D.; Hu, Y.; Li, Q. Spatially Explicit Assessments of Heat-Related Health Risks: A Literature Review. Remote Sens. 2024, 16, 4500. [Google Scholar] [CrossRef]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature–vegetation abundance relationship for urban heat island studies. Remote Sens. Environ. 2004, 89, 467–483. [Google Scholar] [CrossRef]
- Mzid, N.; Pignatti, S.; Huang, W.; Casa, R. An Analysis of Bare Soil Occurrence in Arable Croplands for Remote Sensing Topsoil Applications. Remote Sens. 2021, 13, 474. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Raj, D.K.; Gopikrishnan, T. Machine learning models for predicting vegetation conditions in Mahanadi River basin. Environ. Monit. Assess. 2023, 195, 1401. [Google Scholar] [CrossRef]
- Song, Y.; Liang, J.; Lu, J.; Zhao, X. An efficient instance selection algorithm for k nearest neighbor regression. Neurocomputing 2017, 251, 26–34. [Google Scholar] [CrossRef]
- Ferreira, A.J.; Figueiredo, M.A.T. Boosting Algorithms: A Review of Methods, Theory, and Applications BT—Ensemble Machine Learning: Methods and Applications; Zhang, C., Ma, Y., Eds.; Springer: New York, NY, USA, 2012; pp. 35–85. [Google Scholar]
- Wang, B.; Hipsey, M.R.; Oldham, C. ML-SWAN-v1: A hybrid machine learning framework for the concentration prediction and discovery of transport pathways of surface water nutrients. Geosci. Model Dev. 2020, 13, 4253–4270. [Google Scholar] [CrossRef]
- Guha, S.; Govil, H.; Taloor, A.K.; Gill, N.; Dey, A. Land surface temperature and spectral indices: A seasonal study of Raipur City. Geod. Geodyn. 2022, 13, 72–82. [Google Scholar] [CrossRef]

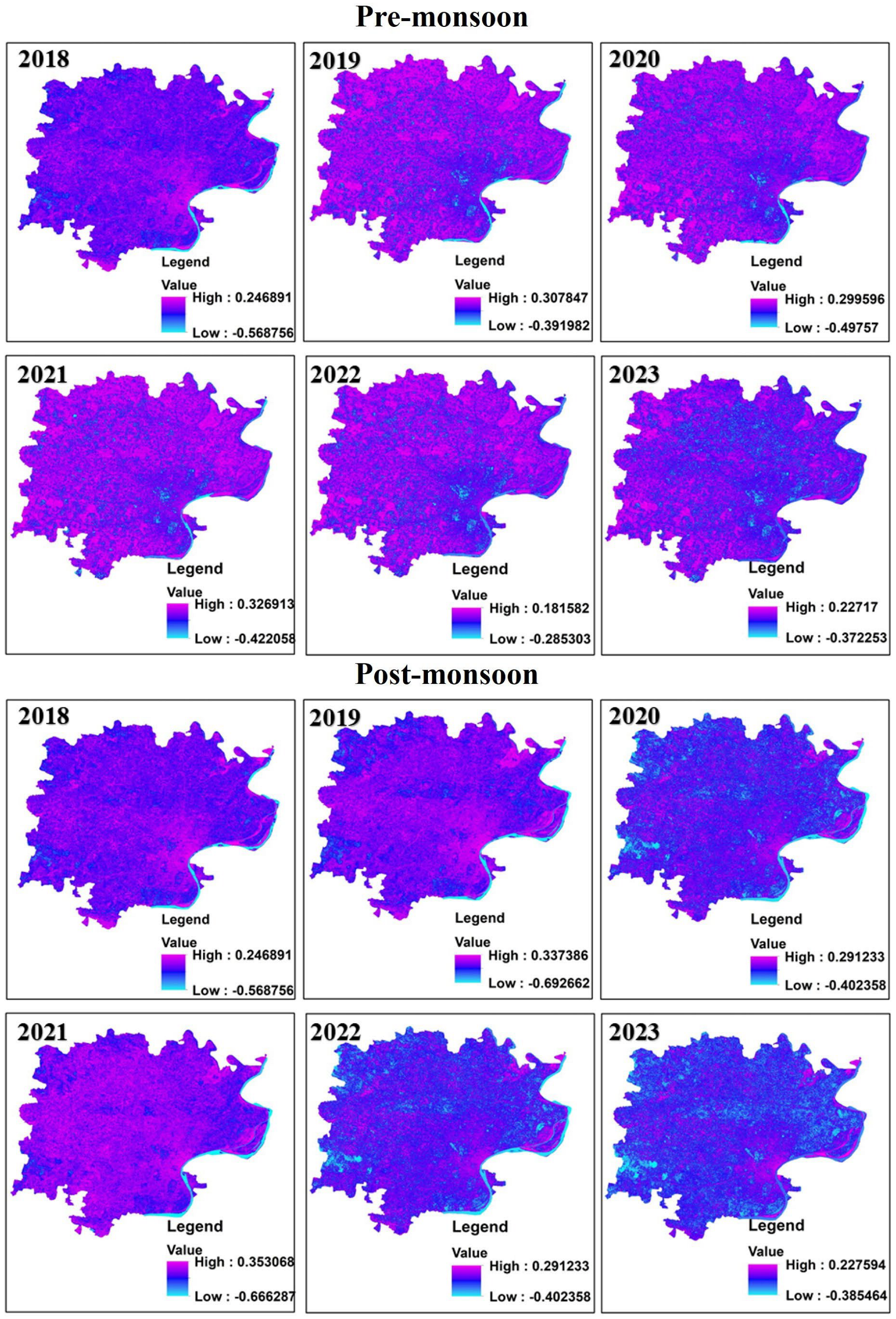

| Pre-Monsoon | Post-Monsoon | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 | |
| NDWI | −0.17 | −0.27 | −0.2 | −0.23 | −0.35 | −0.29 | −0.03 | −0.28 | −0.12 | −0.01 | −0.15 | −0.23 |
| NDVI | −0.17 | 0.14 | 0.03 | −0.06 | −0.04 | −0.13 | −0.18 | 0.14 | −0.05 | −0.14 | 0.03 | −0.09 |
| NDBI | 0.69 | 0.72 | 0.53 | 0.55 | 0.71 | 0.73 | 0.69 | 0.72 | 0.48 | 0.67 | 0.65 | 0.68 |
| BSI | 0.73 | 0.67 | 0.59 | 0.68 | 0.78 | 0.59 | 0.74 | 0.79 | 0.53 | 0.68 | 0.53 | 0.64 |
| Model | Season | Optimum Hyperparameters |
|---|---|---|
| Random Forest | Pre-monsoon | n_estimators = 300–500, max_depth = 8–10, min_samples_split = 2, min_samples_leaf = 1 |
| Post-monsoon | n_estimators = 300–500, max_depth = 8–10, min_samples_split = 2, min_samples_leaf = 1 | |
| Gradient Boosting Machine | Pre-monsoon | n_estimators = 400–500, max_depth = 6–8, learning rate = 0.01–0.05, min_samples_split = 2, min_samples_leaf = 1 |
| Post-monsoon | n_estimators = 400–500, max_depth = 6–8, learning rate = 0.01–0.05, min_samples_split = 2, min_samples_leaf = 1 | |
| Support Vector Machine | Pre-monsoon | Kernel = ‘rbf’, C = 10–100, epsilon = 0.01–0.05, gamma = ‘scale’/’auto’ |
| Post-monsoon | Kernel = ‘rbf’, C = 10–100, epsilon = 0.01–0.05, gamma = ‘scale’/’auto’ | |
| k-Nearest Neighbours | Pre-monsoon | n_neighbors = 5–7, weights = ‘distance’, p = 2, algorithm = ‘auto’ |
| Post-monsoon | n_neighbors = 5–7, weights = ‘distance’, p = 2, algorithm = ‘auto’ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mishra, A.; Ohri, A.; Singh, P.K.; Singh, N.; Calay, R.K. Improving the Prediction of Land Surface Temperature Using Hyperparameter-Tuned Machine Learning Algorithms. Atmosphere 2025, 16, 1295. https://doi.org/10.3390/atmos16111295
Mishra A, Ohri A, Singh PK, Singh N, Calay RK. Improving the Prediction of Land Surface Temperature Using Hyperparameter-Tuned Machine Learning Algorithms. Atmosphere. 2025; 16(11):1295. https://doi.org/10.3390/atmos16111295
Chicago/Turabian StyleMishra, Anurag, Anurag Ohri, Prabhat Kumar Singh, Nikhilesh Singh, and Rajnish Kaur Calay. 2025. "Improving the Prediction of Land Surface Temperature Using Hyperparameter-Tuned Machine Learning Algorithms" Atmosphere 16, no. 11: 1295. https://doi.org/10.3390/atmos16111295
APA StyleMishra, A., Ohri, A., Singh, P. K., Singh, N., & Calay, R. K. (2025). Improving the Prediction of Land Surface Temperature Using Hyperparameter-Tuned Machine Learning Algorithms. Atmosphere, 16(11), 1295. https://doi.org/10.3390/atmos16111295







