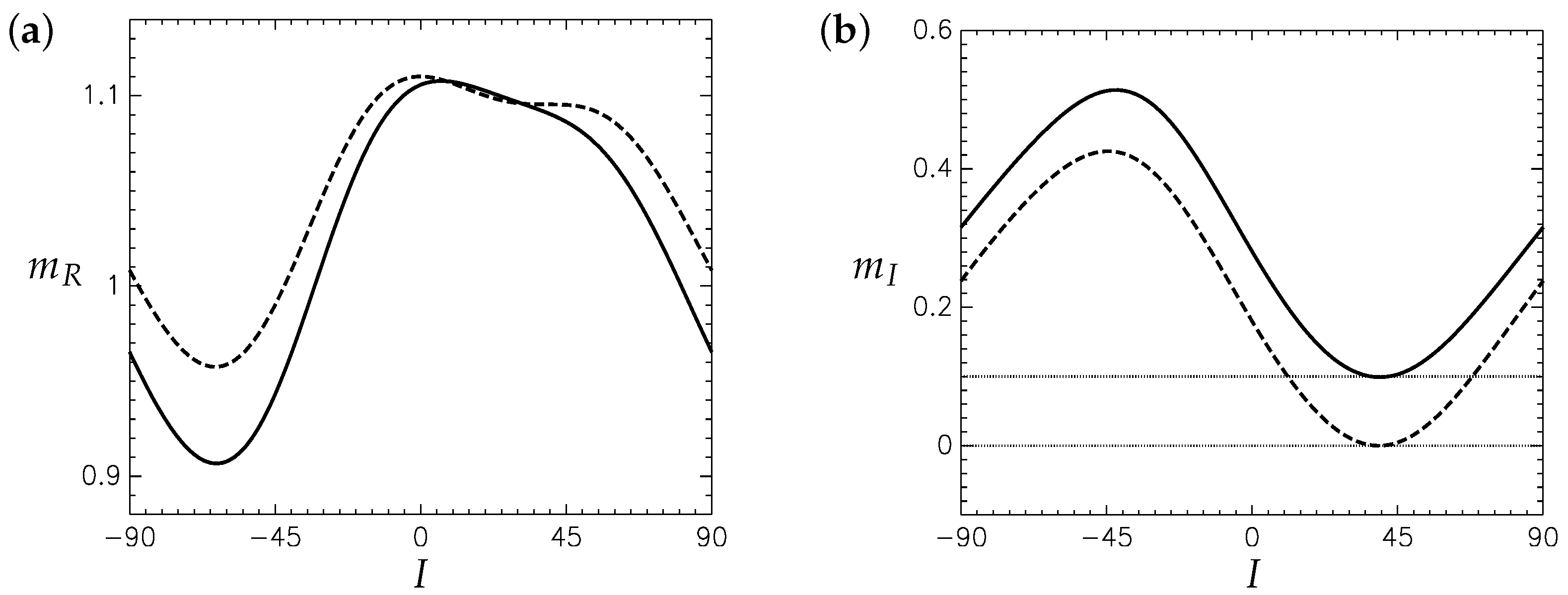Effects of Ion Drag on Ionospheric Gravity Waves in the Presence of a Strong Constant Magnetic Field

Abstract

A temporally periodic model is presented to describe the vertical profile of internal gravity waves in the F region of the Earth’s ionosphere where the waves are subject to a magnetic force due to the high concentration of ions. The configuration studied is representative of the situation where the geomagnetic field is approximately constant and is so strong that the angular gyrofrequency of the ions is very large compared with the ion-neutral collision frequency, which is in turn larger than the angular frequency of the gravity waves. We examine the situation where the gravity wave amplitude is small enough that the equations for the neutral fluid flow can be linearized. This allows for the description of wave propagation in terms of a system of coupled equations that include the effects of ion drag on waves for any orientation of the magnetic field. It is assumed that the background neutral fluid flow is nonzero and horizontal, but there is no vertical shear, and that the wave amplitude depends on altitude only, and an exact analytical solution is readily found. This dynamical model captures some essential features of ionospheric gravity waves that are consistent with observational measurements. In particular, the ion drag acts to damp the waves in the direction of vertical propagation and increase their vertical wavelength relative to the corresponding wavelength in the neutral atmosphere. The vertical damping rate and the vertical wavelength both depend on the dip angle of the magnetic field. When the magnetic field acts in the direction of the gravity lines of constant phase, there is no damping, and the vertical wavelength is the same as that of the corresponding waves in the neutral atmosphere. The dip angles that produce stronger damping also result in waves with greater wavelengths.

1. Introduction

The ionosphere is the region in the Earth’s upper atmosphere where the concentration of ions and electrons due to solar radiation is high enough to affect the propagation of radio waves (IEEE Standard [1]). The uppermost region of the ionosphere, extending from an altitude of 160 km up to 400 km, has an electron density of approximately $2\times {10}^{12}{\mathrm{m}}^{-3}$ and is known as the F region. Internal gravity waves forced in the lower and middle atmosphere propagate upwards and sometimes reach the ionosphere, where they are subject to ion drag forces and in turn excite changes in the electron and ion densities and contribute to the development of traveling ionospheric disturbances (TIDs) (see, for example, Hines [2] for an early review or the more recent review of Laštovička [3]). Gravity waves play an important role in the momentum and energy budget of the upper atmosphere and the vertical coupling of the atmosphere-ionosphere system and are responsible for a great deal of the uncertainty in predictions involving radio wave propagation [3]. Information about the structure and propagation characteristics of gravity waves in the ionosphere has been obtained from observations and measurements using satellite and sounding techniques (e.g., [4,5,6,7,8,9], and references therein). Detailed knowledge of the vertical profile of gravity wave amplitudes and their wavenumber and phase speed spectra is necessary for an accurate representation of momentum and energy transport in large-scale models of the upper atmosphere. A number of factors are believed to affect the structure of gravity waves and the associated TIDs in the F region. Analyses of ionospheric measurements of electron concentration [10,11] indicate a dependence of the wave properties on the characteristics of the meteorological sources from which the waves originate.

In addition, analyses of ionospheric vertical sounding data [12] and numerical simulations [13] show that the vertical profile of gravity wave activity increases with altitude, reaches a peak and then decreases at higher altitudes within the F region. This is in contrast to the situation in the neutral atmosphere where gravity wave amplitudes generally increase with altitude until they reach a breaking or saturation level. The theory of gravity waves in the ionosphere [14,15] would suggest that the gravity wave structure also depends on the dip angle of the geomagnetic field. GPS observations of medium-scale TIDs over Europe by Otsuka et al. [16] indicate that the frequency of occurrence of medium-scale TIDs depends strongly on latitude and suggest the possibility of gravity wave amplitude dependence on latitude and, hence, on the geomagnetic dip angle. Their analyses of these observations showed a small difference between the gravity wave amplitudes at two dip angles corresponding to two different latitudes. An earlier study of a medium-scale TID event by Hearn and Yeh [17] using the Arecibo incoherent scatter radar found variations in the the vertical wavenumber of the ionospheric gravity waves and the rate of decrease in the wave amplitude with altitude which would suggest dependence on the geomagnetic dip angle.

In the investigation presented here, we use analytical and numerical methods to study the response of gravity waves in the F region of the ionosphere to the ion drag force and the dependence of the wave amplitude on the geomagnetic dip angle, the neutral-ion collision frequency and other properties of the ionosphere. The model comprises temporally and horizontally periodic gravity waves forced with a fixed phase speed and horizontal wavenumber at the lower boundary of a rectangular domain and propagating upwards in a medium where they are subject to ion drag forces due to the geomagnetic field whose amplitude is approximately constant.

Although wave-ionosphere interactions are, in general, nonlinear, some information can be obtained from models based on linearized equations. The literature on the linear theory of gravity waves in the upper atmosphere dates back to the 1960s [2] and focuses both on the effects of ionization on the waves (e.g., [14,18,19]) and on the response of the ionosphere to the waves (e.g., [20,21,22]) and includes configurations involving other planetary atmospheres, e.g., [23]. We start here with a configuration where the wave amplitude is considered to be small enough to justify the linearization of the governing equations and depends on altitude only. The goal is to study a nonlinear configuration, where the wave amplitude is allowed to evolve with time, and the present investigation acts as a starting point.

The configuration studied is related to that examined in the classic study of Yeh and Liu [14]. It is based on the properties of the F region where, on the one hand, the plasma is in principle electrically neutral, while on the other hand, the geomagnetic field is strong, and the angular frequency is much larger than the ion-neutral collision frequency, which is in turn larger than the angular frequency of the gravity waves. To this end, the motion of the ions in the plasma is constrained toward the lines of the geomagnetic field [24]. Thus, the wave-induced ionic velocity is in the direction of the magnetic field, and its magnitude is proportional to the magnitude of the neutral velocity. Yeh and Liu [14] discussed the effect of ion drag on the wave dispersion relation for the special case where the background neutral flow velocity is zero and the electromagnetic force is parallel to the surface of the earth with a dip angle of zero. This corresponds to gravity wave propagation in the magnetic meridian plane at the magnetic equator. They linearized the governing equations and considered the waves as sinusoidal functions of time and the horizontal coordinate with an amplitude depending on altitude only. They also examined in more detail a configuration with a particular vertical profile of the neutral-ion collision frequency that allowed them to derive an exact solution.

We re-examine the Yeh and Liu model for a strong constant geomagnetic field, but we consider a more general situation with a nonzero background neutral flow velocity profile and general dip angle and investigate the effects of varying the dip angle and neutral-ion collision frequency.

In the investigation described here, we make some considerations that allow for the derivation of an exact solution. Since our investigation deals with internal gravity waves, which are of relatively small scale, the effects of the Coriolis force are considered negligible compared with the gravitational and buoyancy and ion drag forces and are therefore omitted. We consider linear equations for small-amplitude waves, and we make an anelastic approximation [25], where the neutral density is approximated by a steady altitude-dependent density function, rather than using equations for a fully compressible fluid flow. This approximation effectively filters fast acoustic waves out of the model so that we can focus on the development of the gravity waves. This investigation could be developed further to include the interplay between acoustic waves and internal gravity waves. The purpose of the investigation is to determine the effect of the ion drag on the gravity waves in the absence of other processes such as viscosity and thermal conduction, and so we omit these effects as a first approximation.

Under these approximations, the linearized equations are written in the form of a single partial differential equation, which includes the effects of the ion drag on the waves. In the absence of vertical shear in the background neutral flow, an exact solution is readily obtained. The solutions give additional insight into the propagation characteristics of the waves, which is not immediately apparent from the solution presented by [14]. In particular, we are able to obtain solutions for general dip angles, where the geomagnetic field is not necessarily parallel to the surface of the earth.

2. The Model Equations

Our model represents interactions between the neutral atmosphere and the ionosphere using the equations for conservation of momentum, mass and energy in a two-dimensional configuration given in terms of Cartesian coordinates, x and z, in the horizontal and vertical directions. The velocity of the neutral fluid flow is denoted as $\mathbf{u}=u\widehat{\mathbf{x}}+w\widehat{\mathbf{z}}$ and the plasma velocity as ${\mathbf{u}}_i=u_i\widehat{\mathbf{x}}+w_i\widehat{\mathbf{z}}$, where $\widehat{\mathbf{x}}$ and $\widehat{\mathbf{z}}$ are, respectively, the unit vectors in the horizontal and vertical directions.

In the F region of the ionosphere, the geomagnetic field is approximately constant [14,24] and very strong, of order of magnitude 30,000 nT at the equator and 60,000 nT at the poles. The angular gyrofrequency ${\omega }_{Bi}$ of the atomic oxygen ions is approximately 300 rad ${\mathrm{s}}^{-1}$ and very large compared with the ion-neutral collision frequency ${\nu }_{in}$ which is approximately 1 rad ${\mathrm{s}}^{-1}$ and is in turn much larger than the typical frequency of internal gravity waves in the atmosphere or ionosphere. This means that the ions spiral about the lines of the magnetic field and the ion velocity ${\mathbf{u}}_i$ is in the direction of the magnetic flux density vector $\mathbf{B}$ [14,26]. The effects of the background electric field are considered to be negligible, so that in the absence of a neutral wind, the plasma would be at rest. Thus, the magnitude of the ion velocity is equal to the component of the neutral velocity in the same direction, and we can write [14]

$${\mathbf{u}}_i=(\mathbf{u}·\widehat{\mathbf{B}})\widehat{\mathbf{B}}.$$

(1)

The magnetic flux density can be written as $\mathbf{B}=\left|\mathbf{B}\right|cosI\widehat{\mathbf{x}}-\left|\mathbf{B}\right|sinI\widehat{\mathbf{z}}$, where I is the magnetic dip angle measured downward from the positive horizontal x-axis in the $xz$-plane. The ion velocity can thus be written in component form as

$$\begin{array}{cc}\hfill {\mathbf{u}}_i=& \widehat{\mathbf{x}}{u}_i+\widehat{\mathbf{z}}{w}_i\hfill \\ \hfill =& \widehat{\mathbf{x}}(u{cos}^{2}I-wsinIcosI)+\widehat{\mathbf{z}}(w{sin}^{2}I-usinIcosI).\hfill \end{array}$$

(2)

The equation for the conservation of momentum for the neutral fluid flow (without viscosity and thermal conduction terms) is [15]

$$\varrho {\displaystyle \frac{D\mathbf{u}}{Dt}}=-\nabla p-g\varrho \widehat{\mathbf{z}}-{\nu }_{ni}\varrho (\mathbf{u}-{\mathbf{u}}_i),$$

(3)

where $\varrho$ and p are the density and pressure of the neutral fluid flow, ${\nu }_{ni}$ is the neutral-ion collision frequency, g is the magnitude of the acceleration due to gravity, which is approximately $9.8\mathrm{m}{\mathrm{s}}^{-2}$ near the equator, and $D/Dt$ denotes a derivative following the fluid motion.

Under the anelastic approximation, the neutral density $\varrho$ is approximated by a steady height-dependent mean density $\overline{\rho }\left(z\right)$, and the continuity equation is approximated as

$${\displaystyle \frac{\partial }{\partial x}}\left(\overline{\rho }u\right)+{\displaystyle \frac{\partial }{\partial z}}\left(\overline{\rho }w\right)=0.$$

(4)

We can then define a density-weighted streamfunction $\mathsf{\Psi }$ by

$${\displaystyle \frac{\partial \mathsf{\Psi }}{\partial z}}=-\overline{\rho }u,{\displaystyle \frac{\partial \mathsf{\Psi }}{\partial x}}=\overline{\rho }w.$$

In that case,

$$\xi (x,z,t)={\displaystyle \frac{1}{\overline{\rho }}}\left({\nabla }^2\psi -{\displaystyle \frac{1}{\overline{\rho }}}{\displaystyle \frac{d\overline{\rho }}{dz}}{\displaystyle \frac{\partial \psi }{\partial z}}\right)$$

(5)

is the component of the vorticity $\nabla \times \mathbf{u}$ in the direction perpendicular to the $xz$-plane. The conservation of energy can be expressed in terms of the neutral flow potential temperature $\vartheta$ as

$${\displaystyle \frac{\partial \vartheta }{\partial t}}+u{\displaystyle \frac{\partial \vartheta }{\partial x}}+w{\displaystyle \frac{\partial \vartheta }{\partial z}}=0.$$

(6)

We examine a formulation defined by the above equations with nondimensional variables and parameters. Denoting the corresponding dimensional variables and parameters by asterisks, the nondimensional quantities are defined as

$$x={\displaystyle \frac{x^{*}}{L}},z={\displaystyle \frac{z^{*}}{H}},t={\displaystyle \frac{U{t}^{*}}{L}},u={\displaystyle \frac{u^{*}}{U}},\overline{\rho }={\displaystyle \frac{{\overline{\rho }}^{*}}{R}},g={\displaystyle \frac{H{g}^{*}}{U^2}},{\nu }_{ni}={\displaystyle \frac{L{\nu }_{ni}^{*}}{U}},$$

(7)

where U is a typical value of the horizontal velocity component, R is a typical value of the neutral fluid density, L is a length scale of the order of magnitude of the horizontal extent of the gravity wave source and H is a length scale of the order of magnitude of the scale height of the atmosphere. Typically, $H\ll L$; thus, the vertical-to-horizontal aspect ratio of the domain $r=H/L$ can be considered as a small parameter in the analysis of the nondimensional problem. In the nondimensional formulation, the Laplacian operator is ${\nabla }^2=r^2{\displaystyle \frac{{\partial }^2}{\partial x^2}}+{\displaystyle \frac{{\partial }^2}{\partial z^2}}$.

A gravity wave perturbation is defined by considering each fluid quantity to be the sum of a horizontal mean component and a time-dependent perturbation, i.e., in the form $\overline{f}\left(z\right)+\epsilon f(x,z,t)$, where $\epsilon$ is a nondimensional parameter that represents the magnitude of the waves relative to the background flow. The background flow is a horizontal parallel flow ($\overline{w}=0$) with no vertical shear ($\overline{u}$ is constant). The absence of vertical shear in the background flow means that there is no critical level where the mean flow velocity matches the phase speed of the gravity wave perturbation; that would have introduced additional dynamics and is a situation to be examined in a subsequent investigation. We further consider exponentially decaying background density and pressures profile with scale height h:

$$\overline{\rho }\left(z\right)={\rho }_0{e}^{-z/h},\overline{p}\left(z\right)=p_0{e}^{-z/h},$$

(8)

where ${\rho }_0$ and $p_0$ are constants.

Under the anelastic approximation, the relation between the potential temperature, density and pressure gives a relation at leading order between the background flow quantities $\overline{\theta }$, $\overline{\rho }$ and $\overline{p}$:

$${\displaystyle \frac{1}{\overline{\theta }}}{\displaystyle \frac{d\overline{\theta }}{dz}}={\displaystyle \frac{1}{\gamma }}{\displaystyle \frac{1}{\overline{p}}}{\displaystyle \frac{d\overline{p}}{dz}}-{\displaystyle \frac{1}{\overline{\rho }}}{\displaystyle \frac{d\overline{\rho }}{dz}}=\left(1-{\displaystyle \frac{1}{\gamma }}\right){\displaystyle \frac{1}{h}},$$

(9)

where $\gamma =c_p/c_v$ is the ratio of the specific heat capacities of the neutral fluid at constant pressure and volume. This gives the background potential temperature as

$$\overline{\theta }={\theta }_0{e}^{-\kappa z/h},$$

(10)

where ${\theta }_0$ is a constant, $h/\kappa$ is the potential temperature scale height, $\kappa =1-1/\gamma =R/c_p$, the ratio of the ideal gas constant to the specific heat capacity at constant pressure.

Substituting the expressions $\overline{f}\left(z\right)+\epsilon f(x,z,t)$ into the equations for the total quantities (3) and (6) and dividing by $\epsilon$ gives nonlinear equations for the perturbation quantities, which are linearized by omitting the $O\left(\epsilon \right)$ terms. We then combine the linearized momentum equations by taking the difference of the x-derivative of the vertical momentum equation and the z-derivative of the horizontal momentum equation. We obtain

$$\begin{array}{cc}\hfill & \left({\displaystyle \frac{\partial }{\partial t}}+\overline{u}{\displaystyle \frac{\partial }{\partial x}}\right)\left({\nabla }^2\psi +{\displaystyle \frac{1}{h}}{\psi }_z\right)-{\displaystyle \frac{g\overline{\rho }}{\overline{\theta }}}{\theta }_x\hfill \\ \hfill & +{\nu }_{ni}({\psi }_{zz}{sin}^{2}I-r{\psi }_{xz}sin2I+r^2{\psi }_{xx}{cos}^{2}I)=0\hfill \end{array}$$

(11)

where the subscripts of x and z denote partial differentiation with respect to the respective variable, along with the linear equation for the potential temperature

$$\left({\displaystyle \frac{\partial }{\partial t}}+\overline{u}{\displaystyle \frac{\partial }{\partial x}}\right)\theta +{\displaystyle \frac{1}{\overline{\rho }}}{\displaystyle \frac{d\overline{\theta }}{dz}}{\displaystyle \frac{\partial \psi }{\partial x}}=0.$$

(12)

Combining these two equations and eliminating $\vartheta$ gives

$$\begin{array}{cc}\hfill & {\left({\displaystyle \frac{\partial }{\partial t}}+\overline{u}{\displaystyle \frac{\partial }{\partial x}}\right)}^2{\nabla }^2\psi +N^2{\psi }_{xx}+{\displaystyle \frac{1}{h}}{\left({\displaystyle \frac{\partial }{\partial t}}+\overline{u}{\displaystyle \frac{\partial }{\partial x}}\right)}^2{\psi }_z\hfill \\ \hfill & +{\nu }_{ni}\left({\displaystyle \frac{\partial }{\partial t}}+\overline{u}{\displaystyle \frac{\partial }{\partial x}}\right)({\psi }_{zz}{sin}^{2}I-r{\psi }_{xz}sin2I+r^2{\psi }_{xx}{cos}^{2}I)=0,\hfill \end{array}$$

(13)

where N is the Brunt-Väisälä frequency, which is defined in terms of the background potential temperature by

$$N^2={\displaystyle \frac{g}{\overline{\theta }}}{\displaystyle \frac{d\overline{\theta }}{dz}}.$$

(14)

Once $\psi$ is obtained by solving (13), the components of the nondimensional ion velocity vector ${\mathbf{u}}_i$ can then be expressed, according to (2), as

$$u_i(x,z,t)={\overline{u}}_i\left(z\right)+\epsilon U_i(x,z,t)\mathrm{and}{w}_i(x,z,t)={\overline{w}}_i\left(z\right)+\epsilon W_i(x,z,t),$$

(15)

where the mean components are

$${\overline{u}}_i\left(z\right)=\overline{u}{cos}^{2}I,{\overline{w}}_i\left(z\right)=-{\displaystyle \frac{1}{r}}\overline{u}sinIcosI$$

(16)

and the perturbation quantities are

$$\begin{array}{c}\hfill U_i(x,z,t)=-{\displaystyle \frac{1}{\overline{\rho }}}\left({\psi }_z{cos}^{2}I+r{\psi }_{x}sinIcosI\right),\\ \hfill W_i(x,z,t)={\displaystyle \frac{1}{\overline{\rho }}}\left({\displaystyle \frac{1}{r}}{\psi }_{z}sinIcosI+{\psi }_x{sin}^{2}I\right).\end{array}$$

(17)

We observe that in the special case considered by [14] where the magnetic field is horizontal, $sinI=0$, and so the background ionospheric flow velocity is the same as that of the neutral flow. If, on the other hand, the magnetic field is vertical, another special case, which would occur only at the magnetic pole, then $cosI=0$, and the background ionospheric flow velocity is zero.

The number of oxygen ions per unit volume ${\mathcal{N}}_i$ is given by the continuity equation

$${\displaystyle \frac{\partial {\mathcal{N}}_i}{\partial t}}+\nabla ·\left({\mathcal{N}}_i{\mathbf{u}}_i\right)=Q_i-L_i,$$

(18)

where $Q_i$ and $L_i$ are, respectively, the rates of production and loss of oxygen ions per unit volume through chemical reactions. In the F region, $Q_i\approx L_i$ [14], and so the right-hand side of (18) can be neglected. In the non-dimensional formulation, the number density can also written as the sum of a horizontal mean component and a time-dependent perturbation as

$${\mathcal{N}}_i(x,z,t)={\overline{\mathcal{N}}}_i\left(z\right)+\epsilon n_i(x,z,t)$$

(19)

and the continuity Equation (18) can thus be linearized to give

$${\displaystyle \frac{\partial n_i}{\partial t}}+{\overline{u}}_i{\displaystyle \frac{\partial n_i}{\partial x}}+{\overline{w}}_i{\displaystyle \frac{\partial n_i}{\partial z}}=-{\overline{\mathcal{N}}}_i{\displaystyle \frac{\partial U_i}{\partial x}}-{\overline{\mathcal{N}}}_i{\displaystyle \frac{\partial W_i}{\partial z}}-{\displaystyle \frac{d{\overline{\mathcal{N}}}_i}{dz}}{W}_i,$$

(20)

with $U_i$ and $W_i$ given by (17), or

$$\begin{array}{cc}\hfill & r{\displaystyle \frac{\partial n_i}{\partial t}}+r\overline{u}{cos}^{2}I{\displaystyle \frac{\partial n_i}{\partial x}}-\overline{u}sinIcosI{\displaystyle \frac{\partial n_i}{\partial z}}\hfill \\ \hfill & ={\displaystyle \frac{{\overline{\mathcal{N}}}_i}{\overline{\rho }}}[-{\psi }_{zz}sinIcosI+r{\psi }_{xz}({cos}^{2}I-{sin}^{2}I)+r^2{\psi }_{xx}sinIcosI]\hfill \\ \hfill & -{\displaystyle \frac{d}{dz}}\left({\displaystyle \frac{{\overline{\mathcal{N}}}_i}{\overline{\rho }}}\right)({\psi }_{z}sinIcosI+r{\psi }_x{sin}^{2}I).\hfill \end{array}$$

(21)

This is a first-order transport equation that describes how the ions are transported by collisions between the neutral wind and the ionospheric plasma.

3. A Temporally Periodic Solution

A special configuration is considered for which an exact temporally and horizontally periodic steady-amplitude solution for (13) can be obtained. We seek a sinusoidal solution of the form

$$\psi (x,z,t)=\varphi \left(z\right)e^{ik(x-ct)}+\mathrm{c}.\mathrm{c}.,$$

(22)

generated by imposing a boundary condition of the form $\psi ={\varphi }_{1}cos\left\{k\right(x-ct\left)\right\}$, where ${\varphi }_1$ is a real constant, at some specified value $z=z_1$ representing a gravity wave source at low altitude. The horizontal wavenumber k is taken to be positive, c is the horizontal phase speed and $\varphi \left(z\right)$ is the complex amplitude. The notation “c.c.” denotes the complex conjugate of $\varphi \left(z\right)e^{ik(x-ct)}$ added to ensure that $\psi (x,z,t)$ is real while the amplitude function $\varphi \left(z\right)$ is complex. The wave solution (22) is defined in a rectangular domain extending vertically from the source level up to infinity and extending a finite number of wavelengths in the horizontal direction with periodic boundary conditions at the ends of the horizontal domain. The equation for the wave amplitude, obtained by substituting (22) into (13), is

$$\begin{array}{cc}\hfill \left[1-{\displaystyle \frac{i{\nu }_{ni}{sin}^{2}I}{k(\overline{u}-c)}}\right]{\varphi }_{zz}& +\left[{\displaystyle \frac{1}{h}}-{\displaystyle \frac{{\nu }_{ni}rsin2I}{\overline{u}-c}}\right]{\varphi }_z\hfill \\ & \hfill +\left[{\displaystyle \frac{N^2}{{(\overline{u}-c)}^2}}-r^2{k}^2+{\displaystyle \frac{{\overline{u}}_z/h-{\overline{u}}_{zz}+i{\nu }_{ni}{r}^{2}k{cos}^{2}I}{\overline{u}-c}}\right]\varphi =0.\end{array}$$

(23)

With the mean temperature profile given in (10), $N^2=\kappa g/h$ is constant. We require that $N>r\left|k\right(\overline{u}-c\left)\right|$, as a condition for the existence of gravity waves in the neutral environment. With N and $\overline{u}$ both constant, the solution of (23) takes the form $\varphi =e^{imz}$, where

$$\begin{array}{cc}\hfill \left[1-{\displaystyle \frac{i{\nu }_{ni}{sin}^{2}I}{k(\overline{u}-c)}}\right]m^2& -i\left[{\displaystyle \frac{1}{h}}-{\displaystyle \frac{{\nu }_{ni}rsin2I}{\overline{u}-c}}\right]m\hfill \\ \hfill & -\left[{\displaystyle \frac{N^2}{{(\overline{u}-c)}^2}}-r^2{k}^2+{\displaystyle \frac{i{r}^{2}k{\nu }_{ni}{cos}^{2}I}{(\overline{u}-c)}}\right]=0.\hfill \end{array}$$

(24)

We first note that setting ${\nu }_{ni}=0$ gives the case of gravity waves in the neutral atmosphere, where

$$m=m_{neutral}={\displaystyle \frac{i}{2h}}\pm \sqrt{{\displaystyle \frac{N^2}{{(\overline{u}-c)}^2}}-r^2{k}^2-{\displaystyle \frac{1}{4h^2}}},$$

(25)

and thus the amplitude of the density-weighted wave streamfunction is proportional to $e^{-z/2h}$. This means that the wave velocity components and the potential temperature are proportional to $e^{z/2h}$.

We also note that if the first-derivative term is also neglected in (13), then the term involving $1/h$ is omitted from (25). In that limit, (23) is the Taylor-Goldstein equation [27,28], m is real and given by $m_{neutral}=\sqrt{N^2/{(\overline{u}-c)}^2-r^2{k}^2}$, and in that case the wave amplitude is independent of height. This corresponds to the Boussinesq approximation which is frequently used in gravity wave studies where the background flow is assumed to change by a very small amount over the depth of a fluid layer [29]. For waves in the ionosphere, our anelastic model gives a better representation since it describes the exponential increase in the wave amplitude with altitude that results from the density and temperature stratification, which a Boussinesq model cannot capture. The Boussinesq limit, $1/h\to 0$, is useful to consider only for mathematical comparisons. The vertical component of the group velocity in this case is

$$c_{gz}={\displaystyle \frac{Nkm}{{(r^2{k}^2+m^2)}^{3/2}}}={\displaystyle \frac{km{(\overline{u}-c)}^3}{N^2}}$$

(26)

and the standard group velocity argument of Booker and Bretherton [30] tells us that if $\overline{u}-c>0$ ($\overline{u}-c<0$), the positive (negative) sign in (25) corresponds to a wave with upward group velocity.

In the ionosphere where ${\nu }_{ni}\ne 0$, the quadratic Equation (24) has complex roots

$$\begin{array}{cc}{m}^{\pm }=\hfill & {\displaystyle \frac{i\left[\frac{1}{h}-\frac{{\nu }_{ni}rsin2I}{(\overline{u}-c)}\right]}{2\left[1-\frac{i{\nu }_{ni}{sin}^{2}I}{k(\overline{u}-c)}\right]}}\hfill \\ & \hspace{1em} \pm {\displaystyle \frac{{\left\{\left[\frac{N^2}{{(\overline{u}-c)}^2}-r^2{k}^2-\frac{1}{4h^2}+\frac{{\nu }_{ni}rsin2I}{2h(\overline{u}-c)}\right]-i\frac{{\nu }_{ni}}{k(\overline{u}-c)}\left[\frac{N^2}{{(\overline{u}-c)}^2}{sin}^{2}I-r^2{k}^2\right]\right\}}^{1/2}}{1-\frac{i{\nu }_{ni}{sin}^{2}I}{k(\overline{u}-c)}}}.\hfill \end{array}$$

(27)

In what follows, we discuss the case where $(\overline{u}-c)$ is positive, i.e., the wave phase propagation is westward relative to the direction of the background flow. In order to represent an upward-propagating wave, in that case, we must take the positive square root so that the solution is consistent with the upward-propagating neutral gravity wave solution in the limit as ${\nu }_{ni}\to 0$. If $(\overline{u}-c)$ is negative, then we must take the negative square root, and the discussion proceeds the same as described below but with some signs reversed.

We define

$$A={\displaystyle \frac{N^2}{{(\overline{u}-c)}^2}}-r^2{k}^2-{\displaystyle \frac{1}{4h^2}}+{\displaystyle \frac{{\nu }_{ni}rsin2I}{2h(\overline{u}-c)}},$$

(28)

and

$$B=-{\displaystyle \frac{{\nu }_{ni}}{k(\overline{u}-c)}}\left[{\displaystyle \frac{N^2}{{(\overline{u}-c)}^2}}{sin}^{2}I-r^2{k}^2\right]$$

(29)

and let

$$a+ib=\sqrt{A+iB}.$$

(30)

Then

$$a=+{\displaystyle \frac{1}{\sqrt{2}}}\sqrt{A+\sqrt{A^2+B^2}}\mathrm{and}b=\pm {\displaystyle \frac{1}{\sqrt{2}}}\sqrt{-A+\sqrt{A^2+B^2}}$$

(31)

Since $2ab=B$ and $a>0$, it means that the sign of b is the same as the sign of B. Thus, we take the positive sign in the expression for b in (31) if ${sin}^{2}I<r^2{k}^2{(\overline{u}-c)}^2/N^2$ ($B>0$) and the negative sign if ${sin}^{2}I>r^2{k}^2{(\overline{u}-c)}^2/N^2$ ($B<0$).

The complex expression (27) can be written in terms of a and b as

$$m={\displaystyle \frac{a+ib+i\left[\frac{1}{2h}-\frac{{\nu }_{ni}r}{(\overline{u}-c)}sinIcosI\right]}{1-\frac{i{\nu }_{ni}{sin}^{2}I}{k(\overline{u}-c)}}}.$$

(32)

The real and imaginary parts of this are

$$\begin{array}{c}\hfill m_R\left(I\right)={\displaystyle \frac{a-\left[\frac{1}{2h}-\frac{{\nu }_{ni}r}{(\overline{u}-c)}sinIcosI+b\right]\frac{{\nu }_{ni}}{k(\overline{u}-c)}{sin}^{2}I}{1+\frac{{\nu }_{ni}^2}{k^2{(\overline{u}-c)}^2}{sin}^{4}I}}\end{array}$$

(33)

and

$$\begin{array}{c}\hfill m_I\left(I\right)={\displaystyle \frac{\frac{a{\nu }_{ni}}{k(\overline{u}-c)}{sin}^{2}I+\frac{1}{2h}-\frac{{\nu }_{ni}r}{(\overline{u}-c)}sinIcosI+b}{1+\frac{{\nu }_{ni}^2}{k^2{(\overline{u}-c)}^2}{sin}^{4}I}},\end{array}$$

(34)

where $a>0$ and $sgn\left(b\right)=sgn\left(B\right)$. Considering a boundary condition $\varphi \left(z_1\right)=1$ for the wave amplitude, the solution of (13) is thus

$$\psi (x,z,t)=e^{-m_I(z-z_1)}{e}^{ik(x-ct)+i{m}_R(z-z_1)}+\mathrm{c}.\mathrm{c}.,$$

(35)

for $z_1\le z<\infty$, where $m_R$ is given by (33) and $m_I$ is given by (34).

In the Boussinesq formulation where the terms containing the factor of $1/h$ are ignored, (33) and (34) become

$$\begin{array}{c}\hfill m_R\left(I\right)={\displaystyle \frac{a+\left[\frac{{\nu }_{ni}r}{(\overline{u}-c)}sinIcosI-b\right]\frac{{\nu }_{ni}}{k(\overline{u}-c)}{sin}^{2}I}{1+\frac{{\nu }_{ni}^2}{k^2{(\overline{u}-c)}^2}{sin}^{4}I}}\end{array}$$

(36)

and

$$\begin{array}{c}\hfill m_I\left(I\right)={\displaystyle \frac{\frac{a{\nu }_{ni}}{k(\overline{u}-c)}{sin}^{2}I-\frac{{\nu }_{ni}r}{(\overline{u}-c)}sinIcosI+b}{1+\frac{{\nu }_{ni}^2}{k^2{(\overline{u}-c)}^2}{sin}^{4}I}}.\end{array}$$

(37)

In that case, the minimum value of $m_I\left(I\right)$ for $-90\le I\le 90$ is zero and it occurs at the acute angle $I=I_0={sin}^{-1}(rk(\overline{u}-c)/N)$ where $b=B=0$ and $a=\sqrt{A}$. We observe that

$$tan{I}_0={\displaystyle \frac{rk}{\sqrt{\frac{N^2}{{(\overline{u}-c)}^2}-r^2{k}^2}}}={\displaystyle \frac{k^{*}}{m_{neutral}^{*}}},$$

(38)

where $k^{*}$ and $m_{neutral}^{*}$ are the dimensional wavenumbers in the neutral atmosphere. Thus, the dip angle of $I_0$ corresponds to a situation where the magnetic field direction is in the direction of the lines of constant phase of the waves and the ion drag has no damping effect on the waves. For $I\ne I_0$, $m_I\left(I\right)$ is positive and the ion drag damps the waves; the wave amplitude is proportional to $e^{-m_I\left(I\right)z}$, according to (35). The maximum damping occurs for a dip angle I that is opposite to the direction of the wave phase lines.

In the anelastic formulation where the terms containing the factor of $1/h$ are included, the expressions for $m_R\left(I\right)$ and $m_I\left(I\right)$ include additional terms that include the factor of $1/h$. In this formulation, the dip angle that gives minimum damping is the same as in the Boussinesq case $I_0={sin}^{-1}(rk(\overline{u}-c)/N)$, but the minimum value of $m_I$ is

$$m_{min}=m_I\left(I_0\right)={\displaystyle \frac{1}{2h\left(1+\frac{{\nu }_{ni}^2{r}^4{k}^2{(\overline{u}-c)}^2}{N^4}\right)}}.$$

(39)

The graphs of $m_R\left(I\right)$ and $m_I\left(I\right)$ are shown in Figure 1 for some typical values of the gravity wave and ionospheric input parameters. The situation with minimum damping is illustrated graphically in Figure 2. These graphs are discussed in Section 4.

The case considered by [14] is that in which the waves propagate in the magnetic meridian plane at the magnetic equator; in that case, $I=0$ or $\pi$, $sinI=0$ and

$$\begin{array}{cc}{m}_R=\hfill & {\displaystyle \frac{1}{\sqrt{2}}}\{\left({\displaystyle \frac{N^2}{{(\overline{u}-c)}^2}}-r^2{k}^2-{\displaystyle \frac{1}{4h^2}}\right)\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\left[{\left({\displaystyle \frac{N^2}{{(\overline{u}-c)}^2}}-r^2{k}^2-{\displaystyle \frac{1}{4h^2}}\right)}^2+{\displaystyle \frac{{\nu }_{ni}^2{r}^4{k}^2}{{(\overline{u}-c)}^2}}\right]}^{1/2}{\}}^{1/2}\hfill \end{array}$$

(40)

and

$$\begin{array}{cc}{m}_I=\hfill & -{\displaystyle \frac{1}{2h}}+{\displaystyle \frac{1}{\sqrt{2}}}\{-\left({\displaystyle \frac{N^2}{{(\overline{u}-c)}^2}}-r^2{k}^2-{\displaystyle \frac{1}{4h^2}}\right)\hfill \\ & \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\left[{\left({\displaystyle \frac{N^2}{{(\overline{u}-c)}^2}}-r^2{k}^2-{\displaystyle \frac{1}{4h^2}}\right)}^2+{\displaystyle \frac{{\nu }_{ni}^2{r}^4{k}^2}{{(\overline{u}-c)}^2}}\right]}^{1/2}{\}}^{1/2}.\end{array}$$

(41)

In each case, the linear response of the ionosphere to the waves can be determined from the solution (35) for the wave streamfunction. The components of the ionospheric velocity perturbation $U_i$ and $W_i$ are given by the expressions (17) and the ion density perturbation $n_i$ is given by (21). The form of the function $\psi$ implies that $n_i$ must take the form

$$n_i(x,z,t)=n\left(z\right)e^{ik(x-ct)}+c.c.$$

(42)

The background number density can be represented approximately by a function of the form ${\overline{\mathcal{N}}}_i\left(z\right)={\mathcal{N}}_0{e}^{-z/h_i}$, where ${\mathcal{N}}_0$ is a constant and $h_i$, the ionospheric scale height, is approximately double that of the neutral atmosphere [26]. Using this profile in (21) gives an equation for the amplitude $n\left(z\right)$ of the perturbation,

$$-\overline{u}sinIcosI{\displaystyle \frac{dn}{dz}}+irk(\overline{u}{cos}^{2}I-c)n=\beta e^{-z/h_i}{e}^{z/h}{e}^{im(z-z_1)},$$

(43)

where

$$\begin{array}{c}\hfill \beta ={\displaystyle \frac{{\mathcal{N}}_0}{{\rho }_0}}\{(-r^2{k}^2+m^2)sinIcosI-rkm({cos}^{2}I-{sin}^{2}I)\\ \hfill +i\left({\displaystyle \frac{1}{h_i}}-{\displaystyle \frac{1}{h}}\right)(-msinIcosI+rk{sin}^{2}I)\}\end{array}$$

(44)

is a complex constant, with $m=m_R+i{m}_I$ given by (27).

The amplitude Equation (43) is solved using an integrating factor. If both $sinI\ne 0$ and $cosI\ne 0$, then ${\overline{w}}_i\ne 0$ and we obtain

$$\begin{array}{c}\hfill n_i(x,z,t)={\displaystyle \frac{\beta }{[1/h_i-1/h-im+ik\gamma )]\overline{u}sinIcosI}}{e}^{-z/h_i}{e}^{z/h}{e}^{-m_I(z-z_1)}{e}^{ik(x-ct)+i{m}_R(z-z_1)}\\ \hfill +C{e}^{ik(x-ct)+ik\gamma z}+\mathrm{c}.\mathrm{c}.,\end{array}$$

(45)

where $\gamma$ is an $O\left(r\right)$ constant given by

$$\gamma =-{\displaystyle \frac{({\overline{u}}_i-c)}{{\overline{w}}_i}}={\displaystyle \frac{r(\overline{u}{cos}^{2}I-c)}{\overline{u}sinIcosI}}$$

(46)

and C is a complex constant of integration. If the wave phase speed $c=0$, then $\gamma =rcotI$. The solution (45) comprises a sum of two oscillations. The first with the same vertical wavenumber $m_R$ as the neutral flow gravity wave represents the linear approximation for the TID signature generated in response to a small-amplitude gravity wave propagating upwards in the presence of a strong constant geomagnetic field. It has an exponentially varying amplitude with a rate of $-1/h_i+1/h-m_I$. The second term in (45) has a vertical wavenumber of $k\gamma$, which depends on the dip angle of the geomagnetic field. This term represents the transport of the ions by the background ionospheric flow, which would occur in the absence of the forced gravity waves. The constant C gives the amplitude of this component and can be determined if a boundary condition is given for the number density perturbation $n_i$ at the lower boundary of the domain $z=z_1$.

If $sinI=0$, the case considered by [14], then, ${\overline{u}}_i=\overline{u}$, ${\overline{w}}_i=0$, and there is no vertical transport of ions by the background ionospheric flow. The perturbation $n_i$ satisfies

$${\displaystyle \frac{\partial n_i}{\partial t}}+\overline{u}{\displaystyle \frac{\partial n_i}{\partial x}}={\displaystyle \frac{{\overline{\mathcal{N}}}_i}{\overline{\rho }}}{\psi }_{xz}.$$

(47)

and it comprises only the TID component, with vertical wavenumber $m_R$:

$$n_i(x,z,t)={\displaystyle \frac{i{\mathcal{N}}_{0}m}{{\rho }_0(\overline{u}-c)}}{e}^{-z/h_i}{e}^{z/h}{e}^{-m_I(z-z_1)}{e}^{ik(x-ct)+i{m}_R(z-z_1)}+\mathrm{c}.\mathrm{c}.$$

(48)

If $cosI=0$, then ${\overline{u}}_i={\overline{w}}_i=0$, i.e., there is no background ionospheric flow, and the perturbation $n_i$ satisfies

$${\displaystyle \frac{\partial n_i}{\partial t}}=-{\displaystyle \frac{{\overline{\mathcal{N}}}_i}{\overline{\rho }}}{\psi }_{xz}-{\displaystyle \frac{d}{dz}}\left({\displaystyle \frac{{\overline{\mathcal{N}}}_i}{\overline{\rho }}}\right){\psi }_x.$$

(49)

In this case,

$$n_i(x,z,t)={\displaystyle \frac{{\mathcal{N}}_0}{{\rho }_{0}c}}(-1/h_i+1/h+im)e^{-z/h_i}{e}^{z/h}{e}^{-m_I(z-z_1)}{e}^{ik(x-ct)+i{m}_R(z-z_1)}+\mathrm{c}.\mathrm{c}.$$

(50)

The components of the solutions (45) and (48) are illustrated in graphical form in Section 4, for the case where $c=0$.

In deriving the solutions in this section, we assumed that there is a lower boundary condition comprising a perturbation to the neutral flow with a single horizontal wavenumber k and a single phase speed c, and since the model is linear, this generates a gravity wave with a single horizontal wavenumber and phase speed or frequency. However, a more realistic representation would be a wave packet either localized in the horizontal direction and comprising a continuous spectrum of horizontal wavenumbers or localized in time and in the vertical direction and comprising a continuous spectrum of frequencies and vertical wavenumbers or localized in both horizontal space and time. In this linear framework, such wave packet configurations can be represented by considering $\varphi \left(z\right)$, the solution of (23), to be a function of k and c as well as z and then numerically evaluating the inverse Fourier transform

$$\psi (x,z,t)=\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{\infty }{\int }}\varphi (k,z,c)e^{ik(x-ct)}dkdc.$$

(51)

4. Graphical Illustration of the Solutions

In this section, the dependence of the solution (35) on the dip angle and other input parameters is illustrated graphically. Nondimensional variables and parameters are used; these are defined in terms of the corresponding dimensional quantities (with asterisks) according to (7), and typical values of gravity wave and ionospheric dimensional parameters are chosen. We consider gravity waves forced by a steady source and propagating upwards with phase speed $c=0\mathrm{m}{\mathrm{s}}^{-1}$ and horizontal wavelength $2\pi /k^{*}\approx 10\mathrm{km}$ in a domain approximately $35\mathrm{km}$ high with a background neutral flow horizontal speed ${\overline{u}}^{*}\approx 20\mathrm{m}{\mathrm{s}}^{-1}$ and neutral density scale height $h^{*}\approx 7\mathrm{km}$. With the acceleration due to gravity $g^{*}\approx 9.8\mathrm{m}{\mathrm{s}}^{-2}$ and with the ratio $\kappa \approx 0.286$, this means that the Brunt-Väisälä frequency is $N^{*}\approx 0.02s^{-1}$. These values correspond to a gravity wave vertical wavenumber $m_{neutral}^{*}={({N^{*}}^2/{u^{*}}^2-{k^{*}}^2-0.25/{h*}^2)}^{1/2}\approx 0.78\times {10}^{-3}{\mathrm{m}}^{-1}$ in the neutral atmosphere and a corresponding vertical wavelength $2\pi /m_{neutral}^{*}\approx 8.1\mathrm{km}$. We set the neutral-ion collision frequency to ${\nu }_{ni}^{*}\approx 1.2\times {10}^{-2}{\mathrm{s}}^{-1}$ [21] and set the ionospheric density scale height as approximately double the neutral density scale height [26].

To make the configuration nondimensional, we choose a reference vertical length scale $H\approx 1.4\mathrm{km}$, a reference horizontal length scale $L\approx 3.13\mathrm{km}$ and a reference horizontal velocity scale $U\approx 20\mathrm{m}{\mathrm{s}}^{-1}$. In the illustrative graphs, the waves are forced at $z=10$ by a boundary condition $\psi (x,10,t)=e^{ikx}+\mathrm{c}.\mathrm{c}.$ with horizontal wavenumber $k=k^{*}L=2$ in a domain given by $0\le x\le 2\pi$ and $10\le z\le 35$. The background neutral flow horizontal speed is $\overline{u}={\overline{u}}^{*}/U=1$, the density scale height is $h=h^{*}/H=5$, the potential temperature scale height is $h/\kappa =17.5$, the Brunt-Väisälä frequency is $N={(g\kappa /h)}^{1/2}=\sqrt{2}$, and the aspect ratio is $r=H/L=\sqrt{0.2}$. The vertical wavenumber in the neutral atmosphere is $m_{neutral}={(N^2/{\overline{u}}^2-r^2{k}^2-0.25/h^2)}^{1/2}\approx 1.09$. The neutral-ion collision frequency is set to ${\nu }_{ni}=1$.

According to the solutions obtained in Section 2, the waves have a vertical wavenumber $m_R\left(I\right)$ given by (33) and are damped by the ion drag with a vertical damping rate of $m_I\left(I\right)$ given by (34). As a result of the damping, the density-weighted streamfunction $\psi$ is proportional to $e^{-z/2h}{e}^{-m_{I}z}$, the neutral velocity components and potential temperature are proportional to $e^{z/2h}{e}^{-m_{I}z}$, and the ion density is proportional to $e^{-z/h_i}{e}^{z/h}{e}^{-m_{I}z}$. For comparison, we may take the limit as $1/h\to 0$ in the expressions for the solutions; this limit gives the Boussinesq approximation, but is only valid in situations where the vertical variation in the background flow is very small over the layer of fluid under consideration.

Figure 1 shows graphs of $m_R\left(I\right)$ and $m_I\left(I\right)$ for the above-listed representative values of the input parameters. The dashed curves represent the expressions (36) and (37) obtained by making the Boussinesq approximation. Under this approximation, $m_I\ge 0$ and the wave amplitude decays exponentially with altitude for all dip angles, except for the acute angle $I_0={sin}^{-1}(rk\overline{u}/N)\approx 39.23°$ where $m_I=0$ and there is no damping. At $I=I_0$ the vertical wavenumber $m_R$ is equal to its neutral value $m_{neutral}\approx 1.09$ on the dashed curve in Figure 1a. Figure 1a,b also show that the dip angles that result in stronger damping correspond to smaller vertical wavenumbers or longer vertical wavelengths and that the maximum damping rate occurs at a dip angle of $I\approx -42.1°$.

The solid curves in Figure 1a,b represent the expressions (33) and (34) obtained under the anelastic approximation, retaining all the $1/h$ terms. We note that the qualitative behaviour of $m_R$ and $m_I$ as functions of I is the same as in the dashed curves. The $m_I$ curve has a minimum at $I_0\approx 39.23°$, where $m_I=m_{min}=0.09615$, according to (39). This is indicated with a dotted line in Figure 1b. We note that this value is smaller than the neutral value of $1/\left(2h\right)=0.1$.

At $I=I_0$, the vertical wavenumber is $m_R\approx 1.09$ in Figure 1a. Over the interval of I values, the least damping occurs for angles close to $39.23°$, and the greatest damping occurs for angles close to $-42.1°$. A positive (downward) dip angle would occur in the Northern Hemisphere, and a negative (upward) dip angle would occur in the Southern Hemisphere. Again, we note that the dip angles that result in stronger damping correspond to smaller vertical wavenumbers or longer vertical wavelengths.

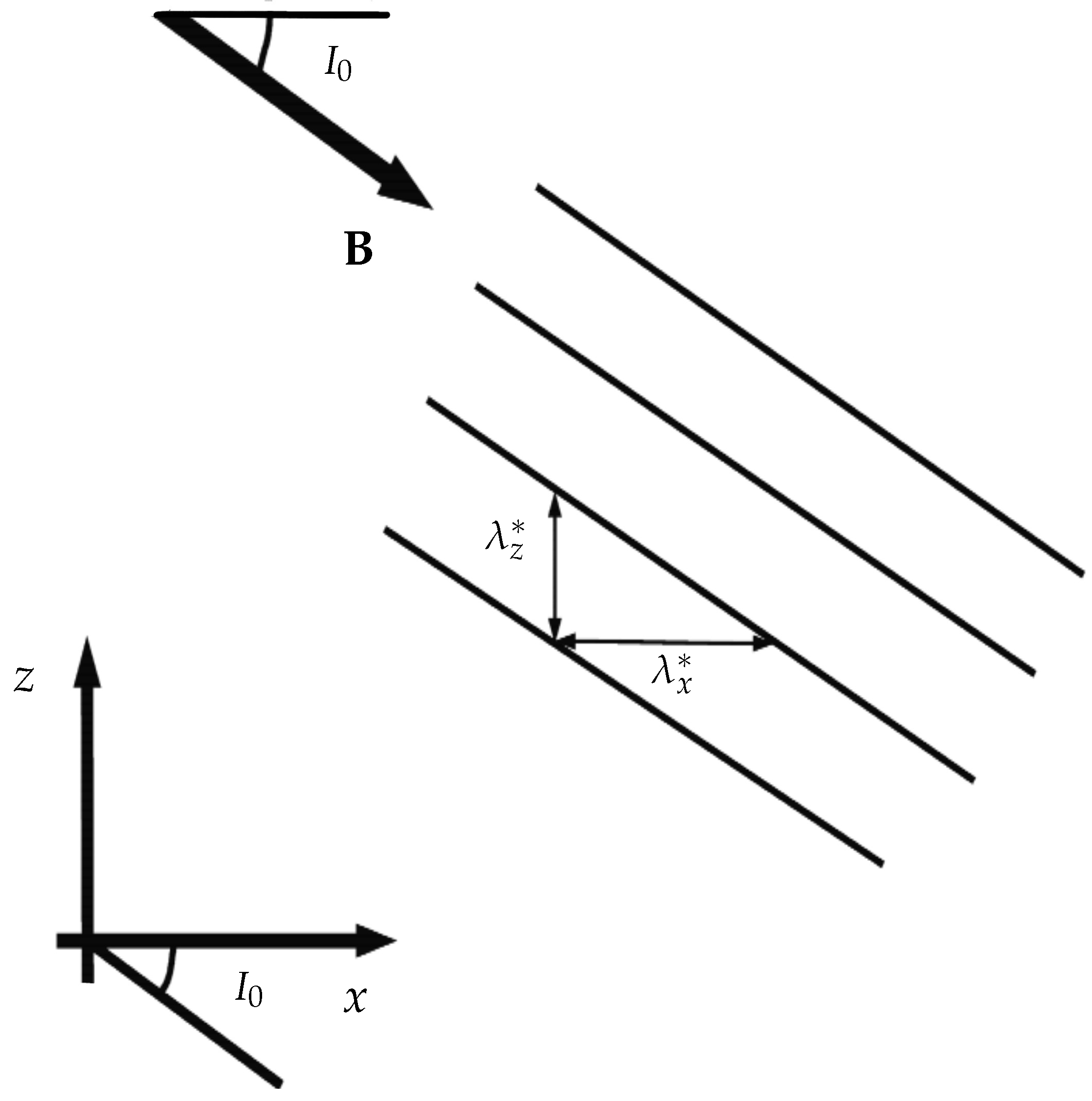
As noted in (38), the angle $I_0\approx 39.23°$ for which there is minimum wave damping corresponds to the situation where the magnetic field has the same slope as the gravity wave lines of constant phase. This is illustrated by the sketch in Figure 2.

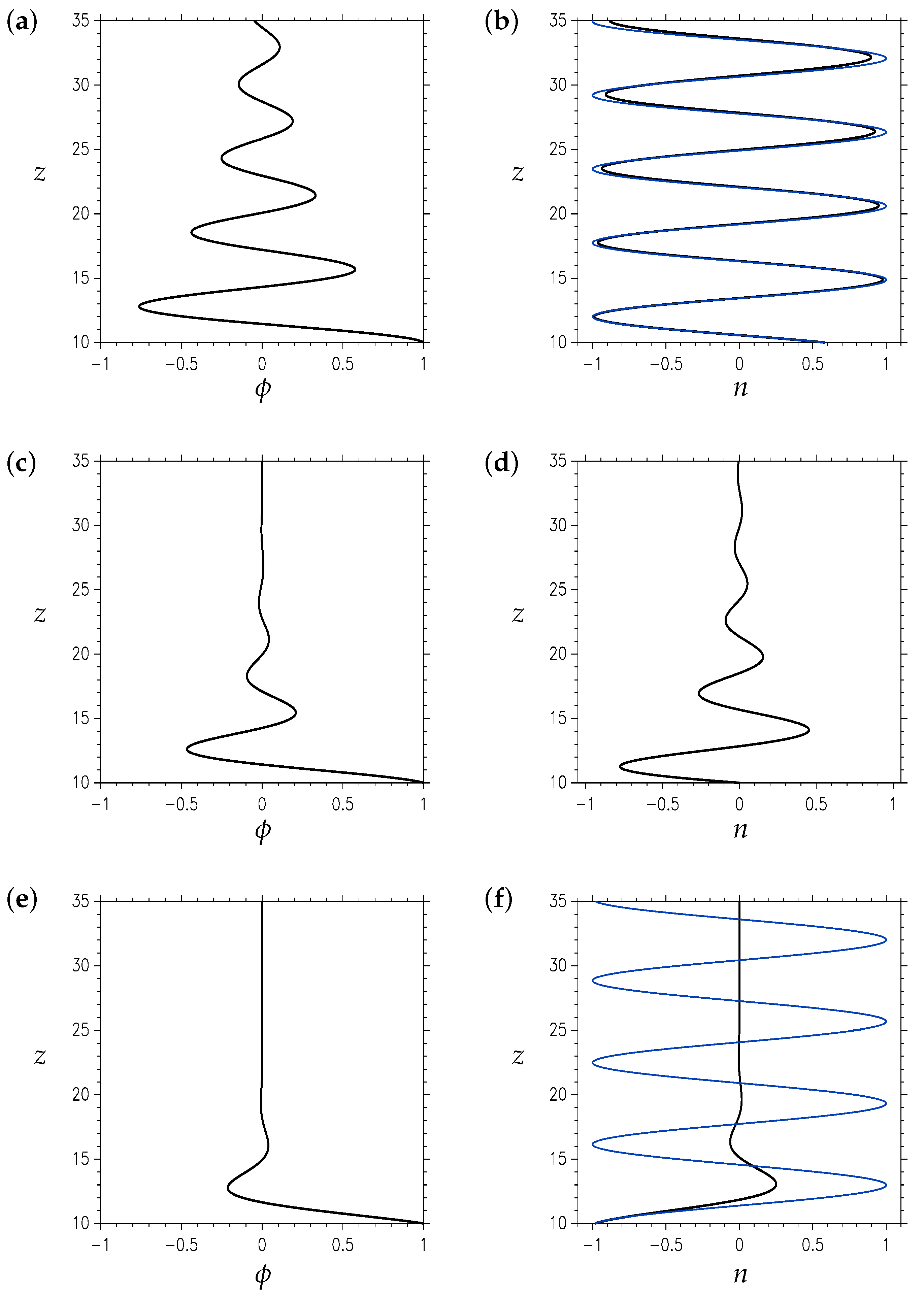
Figure 3 shows the amplitude $\varphi \left(z\right)$ of the streamfunction perturbation and the amplitude $n\left(z\right)$ of the number density perturbation as functions of altitude z for different dip angles, as given respectively by the expressions (35), (45) and (48). In Figure 3a,b, $I=39.23°\approx I_0$; thus, there is no damping of the gravity wave amplitude by the ion drag. The amplitude of the density-weighted streamfunction varies like $e^{-m_{I}z}$ with $m_I=m_{min}=0.09615$, and is shown Figure 3a. Figure 3b shows the two components of the number density perturbation solution (45); the first component, the TID with wavenumber $m_R$, is given by the black curve and the second component with wavenumber $k\gamma$ is given by the blue curve. The TID amplitude varies like $e^{-z/h_i}{e}^{z/h}{e}^{-m_{I}z}$ , while the second component has a constant amplitude. Both functions have been scaled to have an amplitude of 1 at bottom of the domain, for comparison purposes. Specifying a lower boundary condition for (45) would determine the value of the constant C and the relative magnitude of these two functions.

In Figure 3c,d, $I=0°$ and the solutions are given by (40), (41) and (48); this is the case studied by Yeh and Liu [14]. In this case, the number density solution comprises only one component in the form of a TID. This is is shown in Figure 3d, scaled to have an amplitude of 1 at bottom of the domain. In Figure 3e,f, $I=-42.1°$ which is approximately the dip angle that results in maximum damping of the gravity wave amplitude.

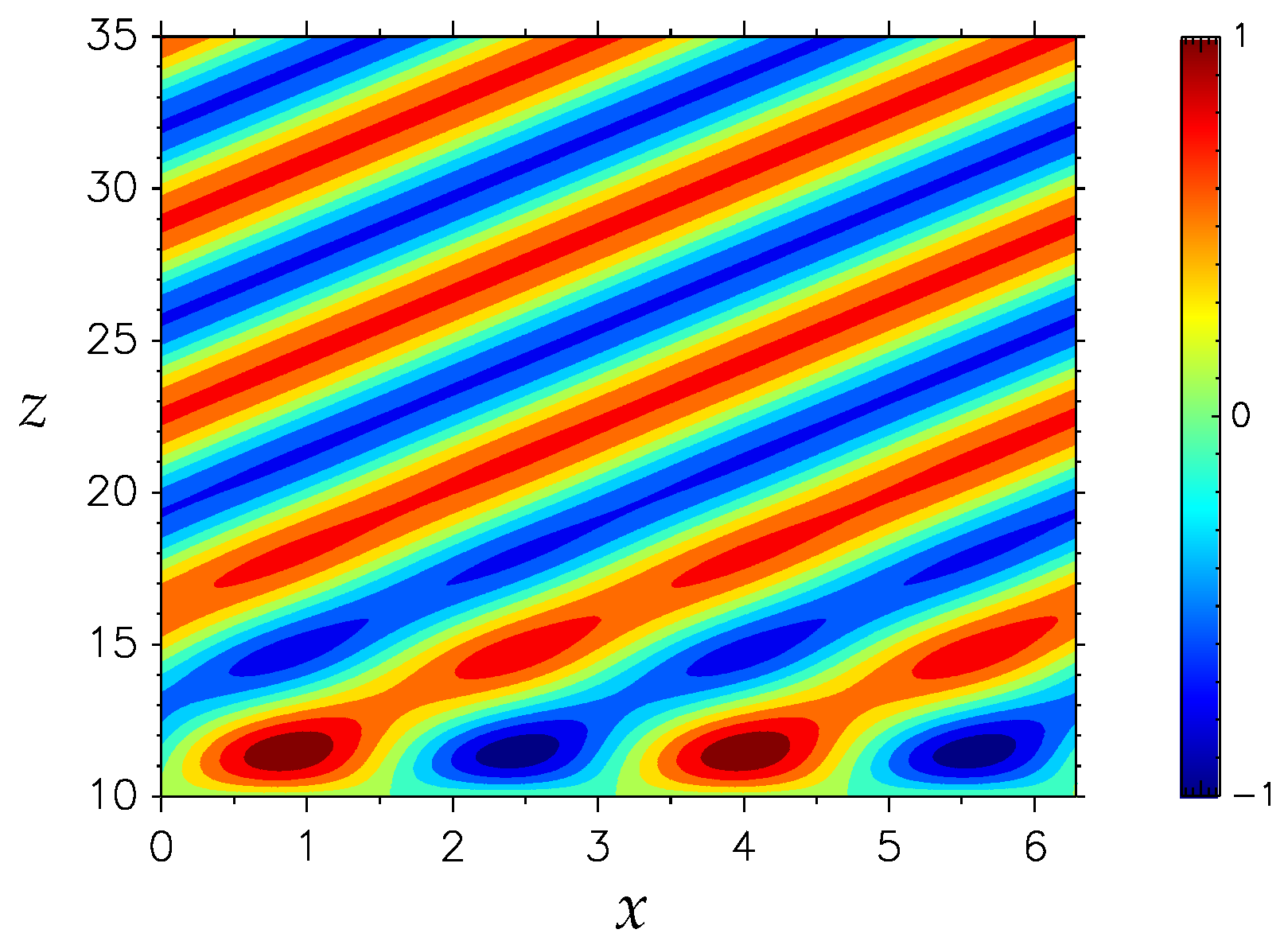
Figure 4 shows contour plots of the number density perturbation $n_i(x,z)$ given by the first term in the solution (45) or (48), corresponding to the black curves in Figure 3b,d,f. The dip angles represented are (a) $I=39°$, which gives the minimum damping of the gravity wave amplitude, (b) $I=0°$, the Yeh and Liu [14] configuration, (c) $I=-42.1°$, which gives the maximum damping of the gravity wave amplitude.

In the case with $I=39.23°$, the solution (45) is the sum of two terms proportional to $e^{i{m}_{R}z}$ (the black curve in Figure 3b and the contour plot in Figure 4a) and $e^{ik\gamma z}$ (the blue curve in Figure 3b). Both $m_R$ and $\gamma =rcot(39°)$ are positive for positive k. Thus, the solution is a superposition of two waves both of which have lines of constant phase with negative slopes, $-k/m_R$ and $-1/\gamma$. In the case with $I=0°$, the solution is given by (48) with the exponentially decreasing factor $e^{(-1/h_i+1/h-m_I)z}$. The lines of constant phase have a negative slope, $-k/m_R$. In the case with $I=-42.1°$, the solution is again given by (45), the sum of two terms proportional to $e^{i{m}_{R}z}$ (the black curve in Figure 3f and the contour plot in Figure 4c) and $e^{ik\gamma z}$ (the blue curve in Figure 3f). In this case, $m_R$ is positive, but $\gamma =rcot(-42.1°)$ is negative. Thus, the solution is a superposition of two waves, one with lines of constant phase with negative slope $-k/m_R$ and the other with lines of constant phase with positive slope $-1/\gamma$. The amplitude of the first term is damped due to the exponentially decreasing factor of $e^{(-1/h_i+1/h-m_I)z}$, while the amplitude of the latter term is constant. The structure of the solution depends on the specified lower boundary condition for the perturbation $n_i$, which determines the value of the constant C in (45). For example, specifying a zero condition $n_i(x,10,t)=0$ gives the structure shown in Figure 5, which is the superposition of waves with different phase directions.

These figures illustrate an essential feature of the solutions of our linear model, that the ion drag acts to damp the neutral waves in their direction of vertical propagation and increase their vertical wavelength relative to the corresponding wavelength in the neutral atmosphere. The vertical damping rate and the vertical wavelength both depend on the dip angle of the magnetic field. In particular, the dip angles that result in stronger damping also give waves with longer wavelengths. Thus, in a region defined by a range of latitudes and a corresponding range of dip angles, gravity waves with phase lines in the direction of the magnetic field propagate to high altitudes without attenuation, while gravity waves with relatively long vertical wavelength and phase lines in the direction opposite to the magnetic field are trapped at lower altitudes. This would result in shorter vertical wavelengths at high altitudes. These conclusions are consistent with the observations made by Hearn and Yeh [17] from their analysis of information from the Arecibo incoherent scatter radar. They concluded that, at altitudes above $350\mathrm{km}$, gravity wave vertical wavenumbers were larger than the corresponding theoretical values predicted by Clark et al. [20] and there was less damping than predicted. Our analysis suggests that such differences could result from differences in dip angle.

Otsuka et al. [16] analyzed medium-scale TID signals in total electron content (TEC) measurements obtained from over 800 GPS receivers within the European GPS receiver network and investigated perturbations caused by gravity wave activity and their possible dependence on the dip angle. They calculated the amplitude of the gravity-wave-related perturbations in the total electron content, relative to the unperturbed total electron content, at two different latitudes corresponding to dip angles of 63.5° and $74.2°$. They found a relative gravity wave amplitude of 1.09% at $63.5°$ compared with 1.04% at $74.2°$. This difference is small but consistent with the dependence on dip angle found in our solutions. For the solutions given here, the ratio of the wave amplitude at $63.5°$ to that at $74.2°$ is $exp\left\{[m_I(74.2°)-m_I(63.5°)](z-z_1)\right\}$. This ratio increases with distance above the forcing level of the waves. For the configuration where the non-Boussinesq terms are included in the solution and with the choice of input parameters chosen for the figures shown here, at an altitude where $z-z_1=1$, the ratio is approximately $1.06$, compared with the ratio of $1.09/1.04\approx 1.048$ found by [16]. Their analyses only included these two dip angles. A wider range of measured dip angles would be needed in an experimental study to confirm the extent of the dependence of the amplitude on dip angle that is indicated by our analytical solutions. This dependence will be examined fully in our future work which will involve numerical solutions guided by the present analytical results.

5. Discussion

Analytical solutions were derived to describe the propagation of internal gravity waves in the ionosphere where they are subject to electromagnetic forces from the high concentration of ions. The configuration studied is analogous to that of Yeh and Liu [14], but with the assumption that the temporal and horizontal variation in the neutral density is small enough to be neglected, except in the terms in the equations involving buoyancy forces. This allows us to obtain some additional information about the propagation characteristics of the waves, which is not immediately apparent from the solution as presented by [14]. In particular, while [14] only considered the special case of wave propagation in the magnetic meridian plane at the magnetic equator, where the magnetic force acts parallel to the surface of the earth, our investigation deals with general magnetic dip angle. Our objective was to elucidate the dependence of the gravity wave structure on the magnetic dip angle. Our solutions shows that the ion drag acts to damp the waves in their direction of propagation and shorten their vertical wavelengths and that the extent of these effects depends on the magnetic dip angle. Further, oscillations are generated in the ion density and the magnetic dip angle determines their structure, in particular their vertical profile and direction of phase propagation.

Given the relative simplicity of our model, it would be unreasonable to expect direct quantitative agreement between our solutions and measurements of gravity waves and TIDs in the upper atmosphere. However, our prediction of wave damping and its dependence on the ionization properties and on the wave parameters is consistent with the conclusions of investigations involving modelling and analyses of measurements, e.g., [3,9,12,13,16,17].

In the ionosphere, the effective neutral-ion collision frequency ${\nu }_{ni}$ varies with altitude and consequently there is the possibility of partial reflection of waves. Yeh and Liu [14] demonstrated this by examining a special height-dependent profile of $\nu$ for which it is possible to derive an analytical solution in terms of Bessel functions. We have chosen to limit our study to the case where $\nu$ is constant and there is no wave reflection, in order to be able to derive solutions for general dip angles. To extend this study to more general height-dependent profiles of $\nu$ would be beyond the scope of an analytical study, but could be accomplished by numerical simulations.

Other important effects, which were neglected in this model, include vertical shear in the background neutral flow, viscous diffusion and heat conduction, temporal variation in the wave amplitude, and nonlinearity of the perturbation equations.

If vertical shear is included in the linear configuration, then there is the possibility of the amplitude equation being singular if $\overline{u}=c$ at some level. In the absence of ion drag, the solutions of the Taylor-Goldstein equation are well-known; they can be expressed in the form of series centred at the singular critical level. The solutions are discontinuous, and each solution is modified by a phase change in $\pm \pi$ across the critical level [31]. The result of the discontinuity is that the wave amplitude is effectively zero above the critical level. This is interpreted as absorption of the waves by the background flow, and it acts as a mechanism by which gravity wave activity can be trapped below the critical level and prevented from reaching higher altitudes. Such critical-level filtering has been observed in radiosonde measurements of the stratosphere, e.g., [32]. It would be complicated to derive an analytical solution for the general situation with both ion drag and vertical shear. However, for the case [14] where the electromagnetic force is horizontal and $sinI=0$, it can be shown that the ion drag modifies the amplitude of the solution near the critical level but does not affect the phase change, so there is no qualitative effect on the behaviour of the solution near the critical level [33]. The question of whether the ion drag affects the phase change for general dip angles can be examined with numerical simulations. The investigation can also be extended to include the interplay between acoustic waves and internal gravity waves, but this would require model equations without the anelastic approximation. Such a model could be investigated numerically.

The next step of this investigation will involve using a formulation where the amplitude of the forced waves is allowed to change with time as well as with altitude. Further, the inclusion of the nonlinear terms in the model equations would lead to the development of a wave-induced mean flow. It is important to study wave-mean-flow interactions in the ionosphere since they are believed to contribute to phenomena which affect space weather, such as Equatorial Spread F (ESF) and equatorial plasma bubbles [34]. This can be studied numerically, and information may also be obtained by carrying out a weakly nonlinear analysis using the leading-order linear solutions as a starting point.