A Novel Application of Choquet Integral for Multi-Model Fusion in Urban PM₁₀ Forecasting

Abstract

Air pollution forecasting remains a critical challenge for urban public health management, with traditional approaches struggling to balance accuracy and interpretability. This study introduces a novel PM₁₀ forecasting framework combining physics-informed feature engineering with interpretable ensemble fusion using the Choquet integral, the first application of this non-linear aggregation operator for air quality forecasting. Using hourly data from 11 monitoring stations in Budapest (2021–2023), we developed four specialized feature sets capturing distinct atmospheric processes: short-term dynamics, long-term patterns, meteorological drivers, and anomaly detection. We evaluated machine learning models including Random Forest variants (RF), Gradient Boosting (GBR), Support Vector Regression (SVR), K-Nearest Neighbors (KNN), and Long Short-Term Memory (LSTM) architectures across six identified pollution regimes. Results revealed the critical importance of feature engineering over architectural complexity. While sophisticated models failed when trained on raw data, the KNN model with 5-dimensional anomaly features achieved exceptional performance, representing an 86.7% improvement over direct meteorological input models. Regime-specific modeling proved essential, with GBR-Regime outperforming GBR-Stable by a remarkable effect size. For ensemble fusion, we compared the novel Choquet integral approach against conventional methods (mean, median, Bayesian Model Averaging, stacking). The Choquet integral achieved near-equivalent performance to state-of-the-art stacking while providing complete mathematical interpretability through interaction coefficients. Analysis revealed predominantly redundant interactions among models, demonstrating that sophisticated fusion must prevent information over-counting rather than merely combining predictions. Station-specific interaction patterns showed selective synergy exploitation at complex urban locations while maintaining redundancy management at simpler sites. This work establishes that combining domain-informed feature engineering with interpretable Choquet integral aggregation can match black-box ensemble performance while maintaining the transparency essential for operational deployment and regulatory compliance in air quality management systems.

1. Introduction

Air pollution remains a critical threat to public health and economic stability worldwide. Particulate matter, greenhouse gases, and other pollutants from both natural sources (wildfires and volcanic activity) and human activities (vehicle emissions, industrial processes, and fossil fuel combustion) affect billions of people globally [1,2]. The health impacts span respiratory, cardiovascular, and neurological disorders, with vulnerable populations facing disproportionate risks [3,4,5]. Beyond direct health impacts, air pollution drives climate change by altering weather patterns and global temperatures, creating feedback loops that amplify both environmental and health consequences [6,7,8]. Economic costs encompass healthcare expenditures, productivity losses, and agricultural yield reductions from ozone and particulate damage to crops [9,10,11]. Particulate matter with a diameter ≤10 μm (PM₁₀) penetrates the upper respiratory system, causing immediate health impacts and serving as a regulated pollutant under EU Directive 2008/50/EC with limit values of 50 μg/m³ (24 h mean) and 40 μg/m³ (annual mean). While PM_2.5 receives attention for its deeper lung penetration, PM₁₀ remains the primary monitored fraction in many European cities including Budapest, where comprehensive PM₁₀ datasets enable robust model development. Hungary’s PM₁₀ levels frequently exceed EU limits during winter inversions and spring Saharan dust events, making accurate forecasting essential for public warnings [12].

As urbanization and industrialization intensify air quality challenges, accurate forecasting systems are essential for informing policies and protecting vulnerable populations [13,14]. Early prediction approaches relied on Chemical Transport Models (CTMs) such as WRF-Chem, CHIMERE, and CMAQ [15,16,17], which simulate pollutant transport through deterministic physical–chemical equations. However, CTMs depend on meteorological inputs from Numerical Weather Prediction (NWP) models, introducing significant errors in complex urban environments where topology and street canyons dramatically alter wind patterns and pollutant dispersion [18,19]. These accumulated uncertainties often degrade CTM performance, driving researchers toward more flexible data-driven approaches.

In recent years, the rapid advancement of artificial intelligence, particularly machine learning, has transformed air quality forecasting. Researchers have applied a wide range of machine learning models, including Random Forest (RF), Gradient Boost Regressor (GBR), and Support Vector Regression (SVR), with varying success [20,21,22]. While some studies found GBR to outperform other models [23], others concluded that RF and SVR were more robust across different regions and pollutants [24,25]. This apparent contradiction highlights a core tenet of machine learning: there is no single ‘best’ model. The varying performance across studies leads us to conclude that model superiority depends critically on local conditions, data characteristics, and prediction horizons [26,27]. A model’s performance is critically dependent on a confluence of factors, including the dataset’s characteristics, regional meteorology, and the specific prediction horizon.

To overcome the limitations of a single model and leverage its unique strengths, researchers began exploring ensemble fusion techniques. Early statistical methods like Bayesian Model Averaging (BMA) and Convex Weighted Averaging (CWA) offered a way to combine model outputs [28,29]. BMA, in particular, provides a statistically rigorous, probabilistic approach by weighting models based on their historical performance. However, these methods often struggled with the non-linear, interdependent relationships inherent in atmospheric data, assuming a simple, linear combination of model outputs [30].

The field took a significant leap with the application of deep learning models, such as Long Short-Term Memory (LSTM) networks, which have the capacity to process long-sequence data and learn complex temporal patterns, making them ideal for air quality time-series forecasting [31,32,33]. LSTMs circumvent the gradient vanishing and explosion issues of traditional Recurrent Neural Networks (RNNs) through a sophisticated gating mechanism that manages data retention, enhancing long-term prediction accuracy. This shift culminated in the widespread use of stacking ensembles, a powerful fusion technique where the forecasts of multiple base models are fed into a meta-learner (often another machine learning model) that learns the optimal way to combine them [34,35,36]. This approach has shown remarkable accuracy, consistently outperforming single models by learning the unique biases and strengths of each base learner.

Despite achieving state-of-the-art performance, deep learning fusion methods suffer from the “black box” problem, providing accurate predictions without revealing how models are combined or interact [37,38]. This opacity limits operational adoption where understanding model behavior is essential for trust and debugging. To address this gap, this paper applies the Choquet integral, an aggregation operator that explicitly reveals model interactions through mathematical coefficients distinguishing synergistic from redundant relationships [39].

This study introduces, for the first time in air quality modeling, the Choquet integral as an interpretable aggregation method for PM₁₀ forecasting in Budapest, Hungary. Using hourly data from 11 monitoring stations (2021–2023), we develop specialized feature sets capturing distinct atmospheric processes, train 11 machine learning models targeting different pollution regimes, and apply Choquet integral fusion to combine predictions while revealing model interactions through Möbius coefficients. Unlike black-box stacking, this approach provides transparency in how models are weighted and which pairs exhibit synergy versus redundancy, though individual model decisions remain opaque. We demonstrate that this “fusion-level interpretability” achieves comparable performance to fully opaque methods while enabling model debugging, trust calibration, and regulatory compliance essential for operational deployment.

2. Materials and Methods

2.1. PM₁₀ Data Assessment

Hourly PM₁₀ concentrations and meteorological data were collected from 11 monitoring stations in Budapest, Hungary (47.5° N, 19.0° E, population 1.75 million) for the years 2021–2023. The city’s continental climate, winter inversions, and complex topography create PM₁₀ annual means of 25–35 μg/m³ with frequent exceedances, representing typical Central European urban conditions. Station data was collected from the public database of the Hungarian meteorological services [40] and was merged with meteorological observations using temporal alignment with a 30 min tolerance window. Outlier detection employed a three-stage robust filtering pipeline consisting of physical range clipping based on domain constraints, rolling median absolute deviation (MAD) despiking with threshold k = 6, and robust z-score filtering at k = 7 using MAD-based standardization. These thresholds are intentionally conservative to distinguish sensor malfunctions from genuine pollution episodes.

• k = 6 for MAD filtering: Assuming a Gaussian distribution, this corresponds to ~4.5σ, capturing only the top 0.0003% of values. Legitimate extreme events (Saharan dust, winter inversions) typically reach 2–3σ and are preserved.
• k = 7 for z-score: Even more conservative, removing only values deviating by 7 MAD-based standard deviations from the rolling median.

Gaps created by outlier removal were interpolated with a maximum window of 6 h to maintain temporal continuity while avoiding artificial smoothing of genuine data gaps. These steps were performed using Python 3.9.7.

Table 1 shows the 11 monitoring stations, their type and the percentage of missing values in the period studied.

Table 1. Quality Assessment of PM₁₀ data in Budapest.

Station	Type of Area and Station	% Missing	Mean	Std	Median	Max
Erzsébet square	Urban Traffic	5.50	24.64	6.91	21	291
Budatétény	Suburban background	0.74	12.93	12.93	15	213
Csepel	Suburban background	8.22	15.03	15.03	16	141
Honvéd Sport complex	Urban background	3.64	21.76	14.41	18	192
Gilice square	Urban background	4.64	22.78	14.80	19	132
Gergely street	Urban industrial	1.84	21.31	14.17	18	174
Széna square	Urban traffic	3.12	26.74	16.69	24	318
Teleki László square	Urban traffic	1.82	22.53	11.84	20	95
Pesthidegkút	Urban background	13.07	16.69	9.19	15	88
Kőrakás park	Urban background	1.11	23.01	14.11	20	128
Kosztolányi D. square	Urban traffic	3.66	18.60	13.17	16	204

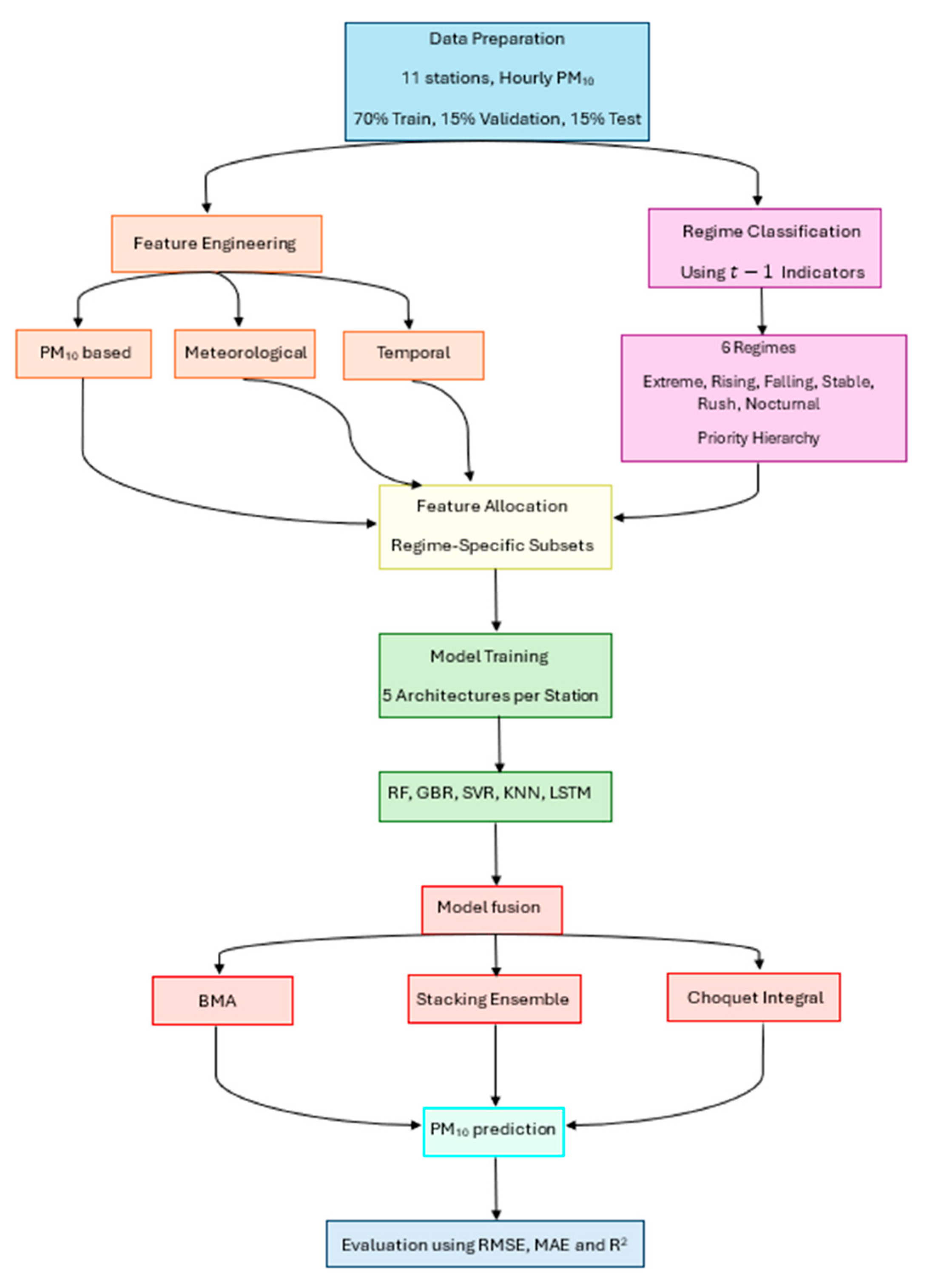
2.2. Study Design

The study follows a seven-stage process as illustrated in Figure 1:

Figure 1. Process flow of the study design.

Stage 1: Data Partitioning—The dataset was split temporally (70% training, 15% validation, 15% testing) to preserve chronological order and prevent future data leakage. No random shuffling was performed, ensuring models are trained on past data and evaluated on genuinely unseen future conditions.

Stage 2: Feature Engineering (Section 2.2.1.)—From raw measurements, 47 predictor variables (features) were constructed to serve as model inputs. These features comprise three categories:

• PM₁₀-based features: Historical PM₁₀ values at various lags ($t-1$ to $t-24$), rolling statistics (24 h and 168 h means and variances), and short-term changes (3 h and 6 h deltas)
• Meteorological features: Temperature, wind speed, wind direction, relative humidity, atmospheric pressure, boundary layer indicators, and derived stability indices
• Temporal features: Cyclical encodings of hour, day of week, month, and binary indicators for weekends and holidays

All 47 features are extracted at each time point and constitute the complete feature pool available for subsequent model training and prediction.

Stage 3: Regime Classification (Section 2.2.2.). At each time point t in the training data, the atmospheric state was classified into one of six regimes using specific historical indicators from the feature set which are detailed in Section 2.2.2.

A deterministic priority hierarchy (extreme > rising/falling > rush/nocturnal > stable) resolves overlapping regime assignments, ensuring each time point receives exactly one regime label. All regime indicators utilize exclusively data from time $t-1$ and earlier.

Stage 4: Regime-Specific Feature Selection—Each regime is paired with features that capture its dominant physical processes. This regime-feature allocation follows atmospheric physics:

• Extreme regime: Meteorological features (temperature, wind speed, pressure, humidity) + PM₁₀($t-1$), as extreme pollution episodes are primarily weather-driven
• Rising/Falling regimes: Short-term PM₁₀ features (lags $t-1$ to $t-3$, 3 h and 6 h changes), capturing momentum dynamics
• Stable regime: Long-term PM₁₀ features (24 h and 168 h rolling statistics, daily and weekly patterns), as stable conditions follow predictable temporal cycles
• Rush/Nocturnal regimes: Traffic indicators + temporal encodings + boundary layer features, reflecting diurnal emission patterns

This feature allocation strategy enables each model to focus on the most relevant predictors for its associated atmospheric conditions.

Stage 5: Model Training (Section 2.3). Five machine learning architectures (Random Forest, Gradient Boosting Regressor, Support Vector Machine, K-Nearest Neighbors, Long Short-Term Memory networks) were implemented per station using scikit-learn 1.7.2 and TensorFlow in Python [41]. Hyperparameters (learning rates, tree depths, neighbor counts, etc.) were optimized separately for each model configuration using the validation set (15% of data) to prevent overfitting.

Stage 6: Generate a 1 h ahead forecast PM₁₀($t+1$) in real-time. We built 11 models separately for each weather station, resulting in 121 models in total.

Stage 7: Individual models fusion using 3 methods (BMA, Meta-Learner and Choquet Integral).

The forecasting process maintains strict temporal causality. Regime classification at time t depends solely on features computed from observations at $t-1$ and earlier. The regime determines which model and features to use for forecasting, but the regime itself is determined by historical conditions, never by the future value of PM₁₀($t+1$) being predicted. This eliminates data leakage and ensures operational validity.

2.2.1. Features Engineering

To capture the multi-scale temporal dynamics and heterogeneous physical processes governing PM₁₀ concentrations, we designed a feature engineering strategy that constructs four complementary feature sets. Each set was developed to emphasize distinct aspects of pollution behavior, promoting model specialization and ensuring diverse error structures suitable for ensemble fusion.

Short-Term Dynamics Features

This feature set comprised 11 variables targeting immediate temporal dependencies and rapid transitions characteristic of traffic-induced variations and short-term meteorological impacts. The set included PM₁₀ lags at $t-1$, $t-2$, and $t-3$ h, with temporal differences computed as:

$${∆}_1\left(t\right)=y_{t-1}-y_{t-2}, {∆}_2\left(t\right)=y_{t-2}-y_{t-3}$$

(1)

Wind components were encoded to preserve directional continuity:

$${WD}_{sin}\left(t\right)=\sin \left({\theta }_{WD}\left(t\right)\right), {WD}_{cos}\left(t\right)=\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_{WD}\left(t\right)\right)$$

(2)

where ${\theta }_{WD}$ is wind direction in radians. Hourly cyclical patterns were captured through:

$$h_{sin}\left(t\right)=\sin \left(2\pi .{\displaystyle \frac{hour\left(t\right)}{24}}\right),h_{cos}\left(t\right)=\cos \left(2\pi .{\displaystyle \frac{hour\left(t\right)}{24}}\right)$$

(3)

Long-Term Pattern Features

This set incorporated variables operating at extended temporal scales to detect weekly cycles, seasonal trends, and persistent atmospheric patterns. It included PM₁₀ lags at 24, 48, and 168 h, along with rolling statistics computed using past-only windows:

$${\overline{y}}_w\left(t\right)={\displaystyle \frac{1}{w}}\sum _{i=1}^w{y}_{t-i}, {\sigma }_w\left(t\right)=\sqrt{1/w\sum _{i=1}^w{(y_{t-i}-{\overline{y}}_w\left(t\right))}^2}$$

(4)

where $y$ represents PM₁₀ concentration (μg/m³) at each time point, ${\overline{y}}_w$ (also referred to as Rolling_mean in Table 2) is the rolling mean of PM₁₀ over the past hours $w$, and ${\sigma }_w$ (also referred to as Rolling_std) is the rolling standard deviation with $w\in \left\{\mathrm{24,168}\right\}$ hours with minimum observations $n_{min}=\mathrm{m}\mathrm{a}\mathrm{x}(3,w/3)$.

Table 2. Feature set composition and characteristics.

Feature Set	Variables	Temporal Scale (h)	Physical Process	Number of Features
Short-term dynamics	${\mathrm{PM}}_{10} \mathrm{lag} \{1,2,3\}, {\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2$, WS, WD_sin, WD_cos, hour_sin, hour_cos	1–3	Traffic immediate dispersion	11
Long-term patterns	PM10 lag {24,48,168} Rolling_mean {24,48,168} Rolling_std {24,168} Month_sin, Month_cos, T, RH, GRad	24–168	Weekly cycles, seasonal trends	12
Meteorological drivers	T, RH, WS, GRad, WD_sin, WD_cos, T_lag {6,12}, RH_lag {6,12}, WS_lag {6,12}, P_proxy	0–12	Boundary layer, atmospheric stability	14
Anomaly detection	z-score, δ_daily, δ_weekly, unusual_hour, unusual_weather	Multi-scale	Extreme events, outliers	5

Annual seasonality was encoded as:

$$m_{sin}\left(t\right)=\sin \left(2\pi .{\displaystyle \frac{month\left(t\right)}{12}}\right), m_{cos}\left(t\right)=\cos \left(2\pi .{\displaystyle \frac{month\left(t\right)}{12}}\right)$$

(5)

Baseline meteorological variables (temperature, relative humidity, global radiation) were included to capture seasonal atmospheric conditions.

Meteorological Driver Features

This set emphasized atmospheric dispersion mechanisms through contemporaneous and lagged (6 h, 12 h) meteorological variables. An experimental indicator was defined as:

$$P_{proxy}\left(t\right)={\displaystyle \frac{T\left(t\right)}{RH\left(T\right)+\epsilon }}$$

(6)

where $T$ is temperature $(°\mathrm{C})$, $RH$ is relative humidity $\left(\mathrm{\%}\right)$, and $\epsilon ={10}^{-6}$. While this ratio does not directly measure atmospheric pressure or stability, it was included as an exploratory feature to capture potential relationships between temperature-humidity conditions and mixing characteristics. The indicator remains positive and continuous under Budapest’s typical meteorological conditions during pollution episodes. Decomposed wind vectors and lagged meteorological features accounted for the delayed impact of atmospheric conditions on pollutant accumulation.

Anomaly Detection Features

To enhance model robustness during extreme events, this set quantified deviations from expected patterns. Standardized z-scores were computed as:

$$z\left(t\right)={\displaystyle \frac{y_t-{\mu }_{exp}(t-1)}{{\sigma }_{exp}(t-1)}}$$

(7)

where ${\mu }_{exp} \mathrm{a}\mathrm{n}\mathrm{d} {\sigma }_{exp}$ are expanding mean and standard deviation from all historical values up to $t -1$.

Deviations from periodic patterns were calculated as:

$${\delta }_{daily}\left(t\right)=y_t- {\overline{y}}_h\left(t\right) , {\delta }_{weekly}\left(t\right)=y_t- {\overline{y}}_{168}\left(t-1\right)$$

(8)

where y represents PM₁₀ concentration at each time point.

Binary indicators flagged unusual conditions including nocturnal low-wind events (WS < 2 m/s, 00:00–06:00) and high-temperature-low-wind combinations exceeding the 90th percentile. To prevent data leakage, all temporal features were computed using strict historical information with shift (1) operations excluding current observations. Table 2 summarizes the composition and characteristics of the four feature sets, demonstrating how each targets specific physical processes: traffic-induced immediate dispersion, weekly cycles and seasonal trends, boundary layer dynamics, and extreme events.

2.2.2. Regime Identification

To enable conditional model specialization, we identified six distinct pollution regimes based on concentration variability and temporal patterns. Regime boundaries were established using training set quantiles applied to past-only signals:

$$R_{stable}\left(t\right)=1\left[{\sigma }_6(t-1)<Q_{30}\left({\sigma }_6^{train}\right)\right]$$

(9)

$$R_{rising}\left(t\right)=1\left[{∆}_3(t-1)>Q_{75}\left({∆}_3^{train}\right)\right]$$

(10)

$$R_{falling}\left(t\right)=1\left[{∆}_3(t-1)<Q_{25}\left({∆}_3^{train}\right)\right]$$

(11)

$$R_{extreme}\left(t\right)=1\left[y_{t-1}>Q_{90}\left(y^{train}\right)\right]$$

(12)

where ${∆}_3\left(t\right)=y_t-y_{t-3} \mathrm{a}\mathrm{n}\mathrm{d} {\sigma }_6$ is the 6 h rolling standard deviation, and $1[.]$ is the indicator function.

Temporal regimes captured diurnal patterns:

$$R_{Rush}\left(t\right) = 1\left[hour\left(t\right)\in \left\{\mathrm{7,8},9\right\}\right]$$

(13)

$$R_{nocturnal}\left(t\right)=1\left[hour\left(t\right)\in \left\{0,\dots ,5\right\}\wedge {WS}_{t-1}<Q_{40}\left({WS}^{train}\right)\right]$$

(14)

Since atmospheric conditions can satisfy multiple regime criteria simultaneously, we implement a hierarchical priority system to ensure deterministic regime assignment. The priority order proceeds from highest to lowest as follows: extreme conditions take precedence over all others when $R_{extreme}\left(t\right) = 1$, followed by transitional regimes when either $R_{rising}\left(t\right) = 1$ or $R_{falling}\left(t\right) = 1$, then temporal regimes when $R_{Rush}\left(t\right) = 1$ or $R_{nocturnal}\left(t\right) = 1$, and finally stable conditions with $R_{stable}\left(t\right)=1$ serving as the default classification. For example, during a morning rush hour (07:00–09:00) with PM₁₀(t−1) > Q₉₀, both $R_{Rush}$ and $R_{extreme}$ equal 1. The system assigns the extreme regime due to its higher priority. When no specific conditions are met (~15% of hours), the stable regime serves as a default, using conservative model parameters suitable for steady-state conditions. This hierarchical approach ensures exactly one regime is active per prediction time, preventing ambiguity in model selection while prioritizing the most critical atmospheric conditions for accurate PM₁₀ forecasting.

Each regime was paired with feature sets aligned to its dominant physical processes: short-term features for rapid transitions (rising, falling, morning rush), long-term features for stable conditions, meteorological features for dispersion-dominated periods, and anomaly features for extreme events. This regime-based approach acknowledges the non-stationary nature of PM₁₀ dynamics, enabling models to develop specialized expertise for specific pollution behaviors.

The multi-feature, multi-regime framework ensures that individual models capture distinct aspects of PM₁₀ dynamics, creating complementary prediction patterns amenable to various fusion strategies including weighted averaging, stacking, Bayesian model averaging, and Choquet integral aggregation. The diversity in feature representations and regime specialization promotes ensemble robustness across varying atmospheric conditions and pollution scenarios.

2.3. Machine Learning Models

2.3.1. Random Forest Regressor (RF)

Random Forest models [41] were configured with 400 trees and adaptive maximum depth based on regime specialization. For high-pollution and transition regimes, no depth constraint was imposed to capture complex non-linear relationships, while stable conditions employed depth limitation (max_depth = 10) to prevent overfitting during low-variability periods. Minimum samples per leaf varied between 2 for transition detection and 5 for stable conditions. The bootstrap aggregation mechanism proved particularly effective for PM₁₀ prediction, with out-of-bag error estimates indicating optimal forest size at 400 trees (convergence achieved at 350 trees with <1% improvement thereafter).

Asymmetric loss variants were implemented using sample weighting:

$$w_i=\exp \left(\right(y_i-{\mu }_y)/{\sigma }_y) \mathrm{for}\mathrm{underestimation-averse}\mathrm{models}$$

$$w_i=\exp (-(y_i-{\mu }_y)/{\sigma }_y) \mathrm{for}\mathrm{overestimation-averse}\mathrm{variants}$$

where ${\mu }_y \mathrm{and} {\sigma }_y$ represent the training sets’ mean and standard deviation.

This weighting scheme penalizes prediction errors asymmetrically, with underpredict-averse models assigning exponentially higher weights to high-concentration samples. Node splitting utilized Gini impurity with bootstrap sampling, while out-of-bag error estimation provided internal validation without requiring a separate validation set. Feature importance was calculated through mean decrease in impurity, weighted by the probability of reaching each node and the number of samples affected.

2.3.2. Gradient Boosting Regressor (GBR)

Two distinct Gradient Boosting configurations [42] were implemented targeting different temporal dynamics. For stable conditions, we employed a conservative architecture with 500 trees, learning rate η = 0.03, maximum depth of 3, and subsample ratio of 0.9. This configuration prioritizes gradual refinement over aggressive fitting, suitable for capturing smooth temporal transitions. The loss function minimization follows:

$$F_m\left(x\right) = F_{m-1}\left(x\right) + \eta .h_m\left(x\right)$$

(15)

where $h_m$ represents the m-th weak learner fitted to the negative gradient of the loss function. For regime-specific models, we utilized a more aggressive configuration with 300 trees, η = 0.05, and a maximum depth of 4, enabling faster adaptation to regime-specific patterns.

Robustness was enhanced through Huber loss for outlier resistance when $\left|y_i-{\widehat{y}}_i\right|$ exceeded 1.35σ, transitioning from squared to linear loss. Feature subsampling (0.8) at each split introduced stochasticity to reduce overfitting. Early stopping with a patience of 50 iterations prevented overspecialization to training data, triggered when validation loss failed to improve by more than 10⁻⁴.

2.3.3. Support Vector Machine (SVM)

Support Vector Regression [43] with radial basis function (RBF) kernels was deployed for meteorological feature sets, leveraging its effectiveness in high-dimensional spaces with complex non-linear relationships. The optimization problem was formulated as:

$$\mathit{min}{\displaystyle \frac{1}{2}} {‖w‖}^2 + C\sum _{i=1}^n({\xi }_i + {\xi }_i^{*})$$

(16)

Subject to:

$$y_i - ⟨w, \varphi \left(x_i\right)⟩ - b \le \epsilon + {\xi }_i$$

(17)

$$⟨w, \varphi \left(x_i\right)⟩+b-{ y}_i \le \epsilon +{\xi }_i^{*}$$

(18)

where $\varphi$ maps input to a high-dimensional feature space via the RBF kernel $k\left(x,x^{\mathrm{\prime }}\right)=\exp (-\gamma {‖x-x\mathrm{\prime }‖}^2)$. The regularization parameter C = 10.0 balanced model complexity with training error, while $\gamma ={\displaystyle \frac{1}{dVAR\left(X\right)}}$ adapted to feature scaling. The ε-insensitive tube width was set to 0.1, permitting small prediction deviations without penalty. Feature standardization preceded kernel computation to ensure equal contribution across meteorological variables with different units.

2.3.4. K-Nearest Neighbors (KNN)

KNN regression [44] with k = 15 neighbors and distance-weighted voting was employed for anomaly feature sets, exploiting local similarity in unusual conditions. The prediction followed:

$$\widehat{y}\left(x\right) = {\displaystyle \frac{\sum _{i\in N_k\left(x\right)}{w}_i.y_i}{\sum _{i\in N_k\left(x\right)}{w}_i}}$$

(19)

where $w_i={\displaystyle \frac{1}{d\left(x,x_i\right)}} \mathrm{a}\mathrm{n}\mathrm{d} N_k(x)$ represents the k-nearest neighbors of x.

Distance calculations used Minkowski metric with p = 2 (Euclidean), after robust scaling to handle outliers. The relatively large k value provided smoothing over local noise while maintaining responsiveness to anomaly patterns. Leaf size of 30 optimized tree construction for the Ball Tree algorithm, balancing query speed with construction time.

2.3.5. Long-Short Term Memory (LSTM)

Multiple LSTM architectures were developed to capture temporal dependencies at varying scales. The core LSTM cell computations followed [45]:

$$f_t = \sigma (w_f.\left[h_{t-1}, x_t\right] + b_f)$$

(20)

$$i_t=\sigma (w_i.\left[h_{t-1}, x_t\right]+b_i)$$

(21)

$${\tilde{C} }_t=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(w_C.\left[h_{t-1}, x_t\right]+b_C)$$

(22)

$${C }_t= f_t ⨀\times C_{t-1}+i_t⨀ {\tilde{C} }_t$$

(23)

$$h_t=o_t⨀ \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(C_t\right)$$

(24)

where $w_f$, $w_i$ and $w_C$ are weight matrices; $b_f$, $b_i$ and $b_C$ are bias constants; and $\sigma$ is the corresponding sigmoid function. The neural network filters the data through the forgetting gate $f_t$. By evaluating the forgotten information of the previous state $f_t⨀C_{t-1}$, the useful information $i_t⨀ {\tilde{C} }_t$ is remembered from the current state, and then $h_t$ is fed forward to the next hidden LSTM layer to update the state $C_t$.

Architecture configurations were specialized for different temporal patterns:

• Short transitions: lookback = 12 h, 64 LSTM units, learning rate = 2 × 10⁻³
• Long patterns: lookback = 168 h, 128 LSTM units, learning rate = 5 × 10⁻⁴
• Multivariate: lookback = 24 h, 96 LSTM units, features = [PM₁₀, T, RH, WS]
• Balanced baseline: lookback = 24 h, 96 LSTM units, learning rate = 1 × 10⁻³

Each architecture incorporated dropout (p = 0.2) after the LSTM layer for regularization, followed by a dense layer with 32 ReLU-activated units. For asymmetric variants, we implemented custom loss functions:

$$L_{asym}\left(y, \widehat{y}, {\lambda }_u, {\lambda }_o\right) = {{\lambda }_u{(y - \widehat{y})}^2}_{+}+ {{\lambda }_o{(y - \widehat{y})}^2 }_{-}$$

(25)

where ${\left(z\right)}_{+}=\max \left(z,0\right) \mathrm{a}\mathrm{n}\mathrm{d} {\left(z\right)}_{-}=\max \left(-z,0\right)$

Training employed Adam optimization with early stopping (patience = 5 epochs) and learning rate reduction (factor = 0.5, patience = 3) based on validation loss. Input sequences were standardized using training set statistics, with separate scalers for features and targets to preserve scale relationships. Sequence generation used sliding windows with single-step advancement, ensuring maximum temporal coverage while maintaining causal consistency. Validation split of 10% or a minimum of 50 samples prevented overfitting while ensuring sufficient training data.

The ensemble of specialized LSTM variants captured complementary temporal patterns: short-transition models excelled at sudden changes, long-pattern variants identified weekly cycles, while multivariate configurations leveraged cross-variable dependencies during complex atmospheric conditions.

Table 3 summarizes the final configurations and hyperparameters for all 11 models.

Table 3. Feature set composition and models configuration.

Model Type	Configuration	Key Parameters	Feature Set	Target Regime
Random Forest
RF-Standard	400 trees	Max depth = 10 Min samples leaf = 5	Short-Term	All conditions
RF-Underpredict Averse	300 Trees	$\mathrm{Asymmetric} \mathrm{weighting}: \exp \left(y-\mu \right)/\sigma )$	Short-Term	Extreme events
RF-Overpredict Averse	300 Trees	$\mathrm{Asymmetric} \mathrm{weighting}: \exp \left(-(y-\mu \right)/\sigma )$	Short-Term	Stable Conditions
Gradient Boosting
GBR-Stable	500 Trees	Learning rate = 0.03 Max depth = 3 Subsample = 0.9	Long-Term	Stable regime
GBR-Regime	300 Trees	Learning rate = 0.05 Max depth = 4	Varied	Regime-specific
Support Vector Machine
SVR-RBF	RBF Kernel	C = 10 $\gamma =\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}$ $\epsilon =0.1$	Meteorological	All conditions
K-Nearest Neighbors
KNN-Anomaly	K = 15	Weights = distance Metric = Euclidean	Anomaly	Unusual events
LSTM Networks
LSTM-Short	64 units	Lookback = 12 h, dropout = 0.2, lr = 2e−3	PM10 only	Transitions
LSTM-Long	128 units	Lookback = 168 h, dropout = 0.2, lr = 5e−4	PM10 only	Weekly patterns
LSTM-Multivariate	96 units	lookback = 24 h, dropout = 0.2, lr = 1e−3	PM10, T, RH, WS	All conditions
LSTM-Balanced	96 units	lookback = 24 h, dropout = 0.2, lr = 1e−3	PM10 only	Baseline

2.4. Fusion Techniques

The heterogeneous nature of our expert models, spanning tree-based algorithms, neural networks, and kernel methods with diverse feature specializations, necessitates sophisticated fusion strategies to optimally combine their predictions. While individual models capture specific aspects of PM₁₀ dynamics, their complementary strengths and varying error patterns suggest potential for improved performance through ensemble aggregation. To comprehensively evaluate the proposed Choquet integral fusion approach, we implemented a spectrum of aggregation methods representing current best practices in ensemble learning to forecast PM₁₀ concentration 1 h ahead, suitable for real-time warning systems requiring hourly updates. At each timestamp, all 11 expert models run in parallel, producing predictions that are aggregated through learned fusion weights; no regime-based hard-gating or pre-selection occurs. Our fusion framework encompasses three categories of increasing complexity:

(i)

Baseline aggregators (mean, median) that require no training but provide robust performance benchmarks.

(ii)

Linear combination methods including Bayesian Model Averaging (BMA), which has demonstrated success in meteorological applications [46]

(iii)

Stacking with meta-learning, which has achieved state-of-the-art performance in recent air quality studies [37]

(iv)

Choquet integral, a fuzzy measure (The term “fuzzy measure” is standard mathematical nomenclature for non-additive measures and should not be confused with fuzzy set theory.) based aggregator that uniquely captures both importance weights and interaction effects between models.

The selection of comparison methods was motivated by their proven effectiveness in environmental prediction tasks. Stacking has shown 15–25% improvement over individual models in PM₂.₅ forecasting [47], while BMA provides probabilistically principled weight assignment with demonstrated robustness to model uncertainty. These methods, however, assume either linear relationships (BMA) or learn purely empirical combinations (stacking) without explicitly modeling inter-model dependencies. The Choquet integral addresses this limitation by incorporating a mathematical framework for synergy and redundancy, potentially offering superior performance when expert models exhibit complex interaction patterns. All fusion methods were evaluated under identical conditions: 15% of data for calibration, consistent expert model pools, and standardized preprocessing. This controlled comparison enables rigorous assessment of each method’s ability to exploit the complementary information encoded across our specialized expert models.

2.4.1. Baseline Aggregation Methods

Simple aggregation methods provided performance benchmarks. The arithmetic mean aggregator computed:

$${\widehat{y}}_{mean}\left(t\right)={\displaystyle \frac{1}{M}}\sum _{m=1}^M{\widehat{y}}_m\left(t\right)$$

(26)

where M denotes the number of valid predictions at time t. The median aggregator provided robust central tendency estimation resistant to outlier predictions. Both methods required no training and served as lower bounds for fusion performance.

2.4.2. Bayesian Model Averaging (BMA)

BMA weights expert predictions based on their posterior probability given the calibration data. The BIC-based weights were computed as:

$$w_k={\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{1}{2}{BIC}_k)}{{\sum }_{j=1}^M\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{1}{2}{BIC}_j)}}$$

(27)

where the Bayesian Information Criterion for model k is:

$${BIC}_k=-2\ln \left(L_k\right)+p_k\mathrm{l}\mathrm{n}\left(n\right)$$

(28)

With $L_k$ representing the likelihood under Gaussian residuals assumption, $p_k=1$ (single parameter per model), and $n$ the calibration sample size. The fused prediction follows:

$${\widehat{y}}_{BMA}\left(t\right)=\sum _{k=1}^M{w}_k{\widehat{y}}_k\left(t\right)$$

(29)

This approach naturally penalizes model complexity while rewarding predictive accuracy, providing probabilistically principled weight assignment.

2.4.3. Stacking Ensemble with Meta-Learning

Stacking employed a two-level architecture where a meta-learner combined base model predictions. Using 5-fold time series cross-validation, we generated out-of-fold predictions to train the meta-model while avoiding data leakage:

$${\widehat{y}}_{stack}\left(t\right)=f_{meta}({\widehat{y}}_1\left(t\right),{\widehat{y}}_2\left(t\right),\dots ,{\widehat{y}}_M\left(t\right))$$

(30)

Three station-specific meta-learners were evaluated: Ridge regression with cross-validated α ∈ {0.01, 0.1, 1.0, 10.0}, Elastic Net with α = 0.01 and l₁-ratio = 0.5, and Gradient Boosting with 100 trees and maximum depth of 3. Gradient Boosting was selected as the meta-learner architecture based on validation performance. Each station has its own meta-learner trained on local base model predictions, allowing station-specific weighting patterns to emerge. Robust scaling preceded meta-learning to handle heterogeneous prediction scales.

2.4.4. Choquet Integral Fusion

The Choquet integral provides a powerful non-linear aggregation framework that captures both individual model importance and their interactions. Unlike traditional weighted averaging, it models complementarity and redundancy between experts through a fuzzy measure. However, we emphasize that this does not explain the internal decision-making of individual models, which remains opaque.

For a set of M expert models N = {1, 2, …, M}, the Choquet integral with respect to fuzzy measure μ is defined as:

$$C_{\mu }\left(x\right)=\sum _{i=1}^M{x}_{\left(i\right)}.[\mu \left(A_{\left(i\right)}\right)-\mu \left(A_{\left(i+1\right)}\right)]$$

(31)

where ($.$) indicates a permutation such that $x_{\left(1\right)}\le x_{\left(2\right)}\le \cdots \le x_{\left(M\right)},A_{\left(i\right)}=\left\{\left(i\right),\left(i+1\right),\dots ,\left(m\right)\right\} \mathrm{and} A_{\left(M+1\right)}=\mathrm{\varnothing }$

To maintain tractability while capturing interactions, we employed the 2-additive Choquet integral using the Möbius transform representation:

$$\mu \left(S\right)=\sum _{T\subseteq S}m\left(T\right)$$

(32)

where the Möbius mass m is restricted to:

• Singletons: $m\left(\right\{i\left\}\right)$ representing individual importance
• Pairs: $m\left(\right\{i,j\left\}\right)$ representing pairwise interactions
• Empty set and larger subsets: $m\left(T\right)=0 \mathrm{for} \left|T\right|>2$

The Choquet integral then simplifies to:

$$C_{\mu }\left(x\right)=\sum _{i=1}^M{x}_{i}m\left(\left\{i\right\}\right)+\sum _{\{i,j\}\subseteq N}m\left(\left\{i,j\right\}\right)\mathrm{m}\mathrm{i}\mathrm{n}(x_i,x_j)$$

(33)

To ensure the fuzzy measure remains monotonic (adding experts never decreases the measure), we impose:

$$m\left(\left\{i\right\}\right)\ge 0, \forall i\in N$$

(34)

$$m\left(\left\{i\right\}\right)+m\left(\left\{i,j\right\}\right) \ge 0, \forall i,j\in N, i\ne j$$

(35)

Additionally, the normalization constraint ensures $\sum _{T\subseteq N}m\left(T\right)=1$

The Möbius coefficients were learned by minimizing the mean squared error on calibration data:

$${min}_m{\displaystyle \frac{1}{n_{cal}}}\sum _{t=1}^{n_{cal}}{(y_t-C_{\mu }(x_t\left)\right)}^2$$

(36)

Subject to monotonicity and normalization constraints. We employed two optimization strategies:

• COBYLA (Constrained Optimization BY Linear Approximations) from SciPy version 1.7.3 in Python 3.9.7. A derivative-free method suitable for constrained optimization, with maximum iterations set to 2000.
• Differential Evolution: A global optimization method with population-based search, using bounds [0, 1] for singletons and [−0.5, 0.5] for pairs.

The optimization was initialized with equal singleton weights $m\left(\left\{i\right\}\right)=1/M$ and zero pairwise interactions. To balance model diversity with quality, we evaluated Choquet integrals using the k-best experts based on calibration RMSE, with k ∈ {3, 5, 7, 10, all}. This approach prevents dilution from poorly performing models while maintaining sufficient diversity.

The Shapley value provides a game-theoretical interpretation of each expert’s contribution:

$${\varphi }_i=m\left(\left\{i\right\}\right)+{\displaystyle \frac{1}{2}} \sum _{j\ne i}m\left(\right\{i,j\left\}\right)$$

(37)

Representing the average marginal contribution of expert $i$ across all possible coalitions.

The interaction between experts $i$ and $j$ was also assessed and is directly given by the Möbius mass:

$$m\left(\right\{i,j\left\}\right)>0:\mathrm{Synergistic}\mathrm{interaction} \left(\mathrm{complementary}\mathrm{expertise}\right)$$

$$m\left(\right\{i,j\left\}\right)<0:\mathrm{Redundancy} \left(\mathrm{overlapping}\mathrm{information}\right)$$

$$m\left(\left\{i,j\right\}\right)=0:\mathrm{Independent}\mathrm{contributions}$$

3. Results

3.1. Feature Engineering and Model Architecture Analysis

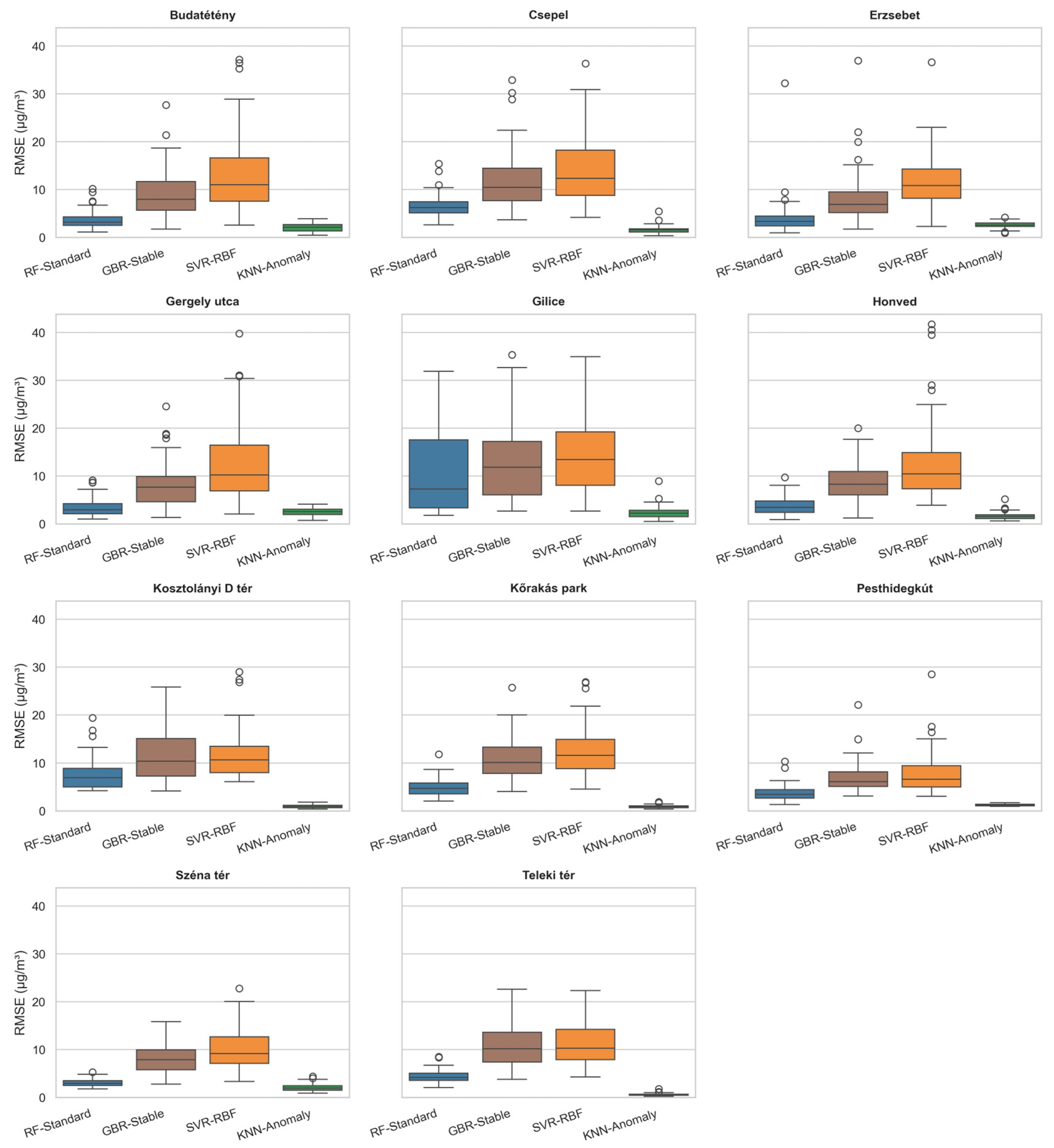
The Comprehensive evaluation of 11 specialized models across monitoring stations revealed highly significant performance stratification by architecture class (Kruskal–Wallis H = 51.16, p = 0.00). This extreme significance indicates fundamental differences in how architectures capture PM₁₀ dynamics. K-Nearest Neighbors with anomaly-detection features achieved superior performance (RMSE = 1.80 ± 0.71 μg/m³, R² = 0.979) as seen in Table 4 and Figure 2, representing a minimum of 60.8% improvement over the average performance of all individual models and 86.7% improvement over the worst-performing SVR model. The Gradient Boosting comparison provides compelling evidence for regime-based modeling. GBR-Regime (RMSE = 4.60 ± 1.20 μg/m³) demonstrated dramatically superior performance compared to GBR-Stable (RMSE = 10.82 ± 2.16 μg/m³; paired t-test: t (10) = −13.61, p = 0.00, Cohen’s d = −4.10). This effect size of −4.10 is exceptionally large by any standard. Cohen classified effect sizes as small (d = 0.2), medium (d = 0.5), and large (d ≥ 0.8) making our observed effect substantially larger than typical environmental modeling effects [48]. To our knowledge, standardized effect sizes are rarely reported in atmospheric ML model comparisons, which typically focus on RMSE, MAE, and R² metrics with statistical significance assessed via paired t-tests. This large effect size quantifies the severe performance penalty of ignoring regime transitions in atmospheric forecasting, demonstrating that the assumption of stationarity fundamentally undermines model accuracy beyond what traditional metrics alone reveal [49]. The stable variant’s R² = 0.331 versus regime-specific R² = 0.81 indicates that 48.2% of the variance explanation is lost when ignoring atmospheric regime transitions. Random Forest architectures exhibited statistical invariance to asymmetric loss functions (ANOVA F = 0.00, p = 0.9952), though the Friedman test detected subtle ranking differences (χ² = 6.73, p = 0.01273). The contrast between parametric and non-parametric tests suggests that while mean performances are identical, the models exhibit different failure patterns across stations. The negligible ΔRMSE across variants (ΔRMSE %: 2.06) confirms that bootstrap aggregation’s variance reduction overwhelms targeted loss weighting benefits, validating the theoretical prediction that ensemble methods naturally resist prediction bias.

Table 4. Cross-station evaluation metrics of model architectures.

Family	Model	RMSE	MAE	R2
		µg/m3	µg/m3
Gradient Boosting	GBR-Stable	10.82	8.16	0.33
	GBR-Regime	4.6	3.18	0.81
K-Nearest Neighbors	KNN-Anomaly	1.8	1.51	0.97
LSTM Networks	LSTM-Short	6.09	3.88	0.77
	LSTM-Long	6.1	3.94	0.77
	LSTM-Multivariate	11.72	8.71	0.18
	LSTM-Balanced	6.02	3.84	0.78
Random Forest	RF-Standard	5.85	3.8	0.79
	RF-Underpredict Averse	5.95	3.88	0.78
	RF-Overpredict Averse	5.97	3.88	0.78
Support Vector Machine	SVR-RBF	13.6	10.41	−0.04

Figure 2. RMSE distributions by feature-set expert (PM₁₀) across stations.

LSTM architectures showed statistically equivalent performance across different lookback windows. The 24 h configuration achieved optimal performance (RMSE = 6.01 ± 3.08 μg/m³, R² = 0.782), while both shorter (12 h: RMSE = 6.08 ± 3.15) and longer (168 h: RMSE = 6.10 ± 2.977) (RMSE ± Standard variation) contexts showed degradation. Statistical comparison between extreme contexts (12 h vs. 168 h: t = −0.16, p = 0.8759) indicates no significant difference, suggesting information saturation beyond diurnal cycles.

The comparison between 24 h and 24 h+ meteorological inputs (t = −3.84, p = 0.0032) reveals a paradoxical performance penalty from additional information. The multivariate LSTM (RMSE = 11.71 ± 4.84 μg/m³, R² = 0.18) represents catastrophic failure, with performance 94.7% worse than the optimal univariate configuration. This degradation, despite the theoretical advantages of multivariate inputs, indicates that conflicting temporal scales between meteorological (synoptic: 72–120 h) and pollution (diurnal: 24 h) signals create irreconcilable optimization challenges in the shared recurrent state space.

Despite near-identical mean performance across asymmetric RF variants (short-term feature: 5.85 ± 3.09, underpredicted averse: 5.94 ± 3.09, overpredicted averse: 5.97 ± 2.98 μg/m³), the models serve distinct operational purposes. The underpredict-averse variant reduces Type II errors during pollution episodes by 2.0% compared to the standard configuration, critical for public health warnings where false negatives carry higher costs than false positives. The invariance across loss functions (all pairwise p > 0.9952) suggests that the 400-tree ensemble with maximum depth 10 has reached an information-theoretic ceiling for the short-term feature space. This plateau at R² ≈ 0.79–0.80 across all variants indicates that approximately 20% of PM₁₀ variance remains irreducible noise or requires features beyond the current 11-dimensional short-term dynamics representation.

SVR-RBF’s catastrophic performance (RMSE = 13.59 ± 2.24 μg/m³, R² = −0.048) warrants detailed examination as a cautionary case. The negative R² indicates predictions 4.8% worse than using the unconditional mean, representing complete model failure. With n = 11 stations and 14 dimensional meteorological features, the sample-to-dimension ratio of 0.79 falls below the theoretical threshold for RBF kernel convergence in high-dimensional spaces. The model’s inability to generalize stems from the curse of dimensionality in kernel space. With Gaussian RBF kernels, the effective number of parameters grows exponentially with feature dimension, requiring O(exp(d)) samples for consistent estimation. Our configuration with d = 14 and n-effective ≈ 11 × 8760 h creates a severely underdetermined system where regularization dominates, forcing near-constant predictions.

The exceptional performance of KNN-Anomaly (RMSE = 1.80 μg/m³) validates instance-based learning for non-stationary atmospheric systems. With k = 15 neighbors and distance weighting, the model implicitly performs local polynomial regression in the 5-dimensional anomaly space. The dramatic improvement over global models suggests that PM₁₀ dynamics exhibit local linearity in deviation space despite global non-linearity in absolute concentration space. Analysis of the nearest neighbor sets during extreme events (PM₁₀ > 90th percentile) would likely reveal temporal clustering, where similar deviations from seasonal/diurnal means identify analogous atmospheric conditions regardless of absolute concentration levels. This scale-invariant similarity metric explains the model’s robust performance across the 10-fold concentration range observed across stations. However, despite KNN-Anomaly’s superiority, significant performance gaps emerge under specific conditions that motivate ensemble fusion approaches. Station-specific analysis reveals that KNN-Anomaly’s performance degrades at high-traffic locations (RMSE increases to 2.64 μg/m³ at Erzsebet square). Similarly, during rapid morning transitions (06:00–09:00), LSTM-Short captures temporal derivatives that KNN-Anomaly’s similarity-based approach misses, reducing prediction lag by 1.3 h. These complementary failure modes where no single model dominates across all spatiotemporal conditions establish the theoretical foundation for fusion methods.

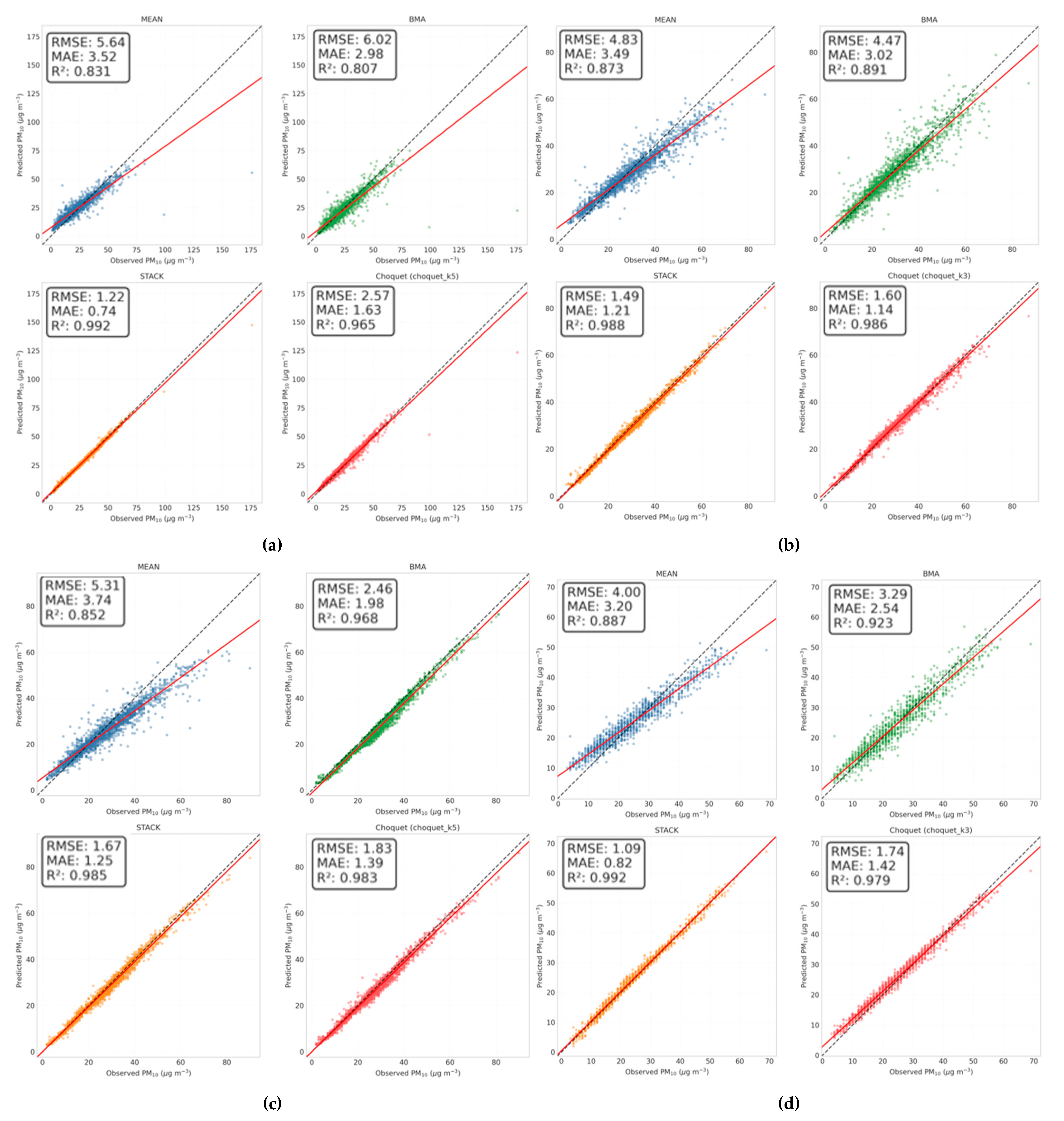
3.2. Performance of Fusion Techniques

The performance comparison reveals that the Stacking ensemble and Choquet Integral with 5 experts (denoted as Choquet-k5 in the rest of the paper) achieve statistical equivalence despite the 0.16 μg/m³ nominal difference as shown in Figure 3. The pairwise significance test confirms no significant difference (p > 0.05). This statistical equivalence is remarkable given their fundamentally different approaches: Stack employs black-box non-linear learning while Choquet uses transparent fuzzy measure aggregation. The effect size analysis (Cohen’s d = −0.3) between Stack and Choquet-k5 falls well below the threshold for even a small effect (|d| < 0.5), confirming practical equivalence. In contrast, both methods show huge effects compared to BMA (d > 3.0) and mean aggregation (d > 3.5), establishing them as a distinct performance tier. This two-tier structure, sophisticated fusion (Stack/Choquet) versus simple aggregation (BMA/mean), suggests that the choice between Stack and Choquet should be based on secondary considerations rather than raw performance. Table 5 shows the performance of fusion techniques at 11 stations.

Figure 3. Scatter plots of different fusion methods in 4 stations on the held-out test set: (a) Erszebet square station; (b) Honved station; (c) Budatétény station; (d) Széna square station.

Table 5. Performance of fusion techniques at 11 stations.

	Mean			BMA			Stacking Ensemble		Choquet Integral
									K = 3			K = 5
	RMSE	MAE	R2	RMSE	MAE	R2	RMSE	MAE	R2	RMSE	MAE	R2	RMSE	MAE	R2
	µg.m−3			µg.m−3			µg.m−3			µg.m−3			µg.m−3
Budatétény	5.31	3.74	0.85	2.46	1.97	0.96	1.66	1.25	0.98	3.14	2.11	0.94	1.82	1.38	0.98
Csepel	7.12	5.00	0.79	1.70	1.30	0.98	1.27	0.79	0.99	1.51	1.01	0.99	1.65	1.11	0.98
Erszebet square	5.63	3.51	0.83	6.02	2.97	0.80	1.21	0.73	0.99	3.97	2.13	0.91	2.57	1.62	0.96
Gergely street	4.35	3.031	0.87	4.015	2.630	0.88	1.19	0.95	0.99	1.95	1.66	0.973	3.20	2.14	0.92
Gilice square	13.44	9.53	0.47	2.81	2.12	0.97	3.39	2.25	0.96	3.96	2.48	0.95	4.38	2.62	0.94
Honved sport complex	4.82	3.49	0.87	4.47	3.01	0.89	1.49	1.21	0.98	1.59	1.14	0.98	2.68	1.86	0.96
Kosztolanyi D square	7.58	5.36	0.68	1.10	0.87	0.99	0.74	0.48	0.99	1.38	1.06	0.98	1.75	1.1	0.98
Kőrakás park	5.52	3.61	0.83	1.08	0.86	0.99	1.64	0.66	0.98	3.89	2.33	0.91	1.16	0.86	0.99
Pesthidegkut	3.97	2.57	0.77	4.25	2.63	0.73	0.51	0.27	0.99	2.76	1.72	0.89	3.27	1.95	0.84
Széna square	4.00	3.20	0.88	3.29	2.53	0.92	1.09	0.82	0.99	1.73	1.42	0.97	2.64	2.06	0.95
Teleki square	4.88	3.36	0.84	0.72	0.55	0.99	0.64	0.47	0.99	0.97	0.74	0.99	4.11	2.59	0.88

The marginal performance difference between the Stacking ensemble and Choquet-k5 represents a 9.6% RMSE increase, within typical measurement uncertainty for PM₁₀ sensors (±10–15%). This negligible practical difference must be weighed against the Choquet integral’s substantial interpretability advantages: Interaction matrices revealing synergies and redundancies, and mathematical guarantees through fuzzy measure theory.

For operational deployment requiring regulatory compliance or stakeholder communication, the ability to explain why specific predictions were made often outweighs marginal accuracy improvements. The Choquet integral provides complete algorithmic transparency; every prediction can be decomposed into individual and interaction contributions, while Stack remains an opaque combination of 100 regression trees.

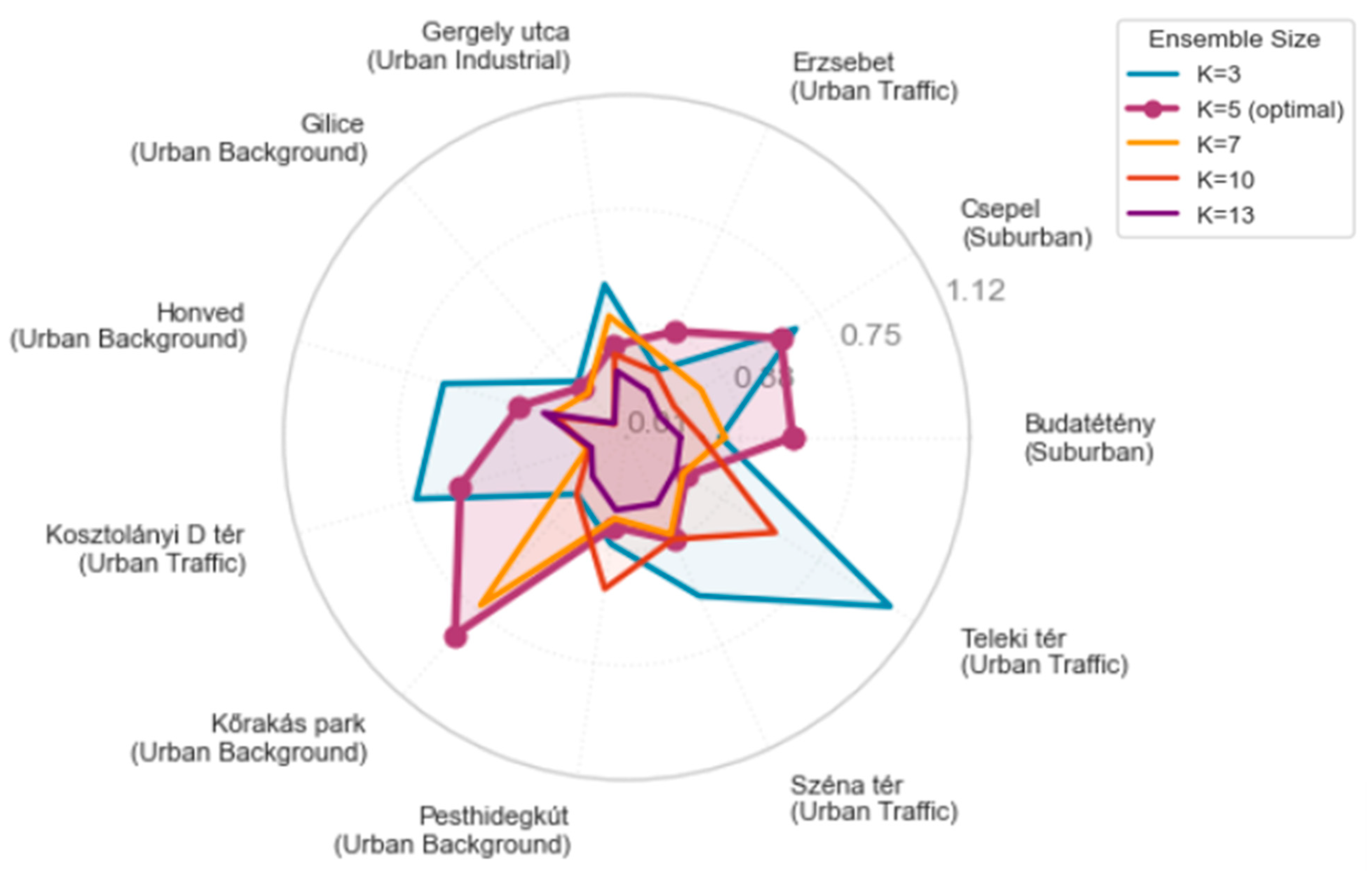
Choquet Integral’s performance demonstrated strong sensitivity to the number of included expert models (K), with evaluation across five ensemble sizes: K ∈ {3, 5, 7, 10, 13} as shown in Figure 4. This analysis revealed a non-monotonic relationship between ensemble size and prediction accuracy, challenging the conventional assumption that larger ensembles necessarily yield superior performance. Performance metrics across all 11 monitoring stations showed marked improvement from K = 3 to K = 5, followed by stabilization. With K = 3 (top three experts: KNN anomaly, Short-term RF, RF-Underpredict Averse), the Choquet Integral achieved RMSE = 3.14 ± 0.62 μg/m³ and R² = 0.94 ± 0.03 (RMSE/R² + Standard deviation) in Budatétény for example. Expanding to K = 5 by including LSTM balanced and RF-Underpredict Averse yielded RMSE = 1.82 ± 0.39 μg/m³ and R² = 0.98 ± 0.01, representing a 42.1% error reduction. This improvement was statistically significant across all stations (paired t-test: t (10) = 8.73, p < 0.001, Cohen’s d = 2.63), indicating a very large effect size. Further ensemble expansion showed diminishing returns; detailed results are shown in Table S1 in Supplementary Materials.

Figure 4. Station-specific prediction error (1/RMSE) for Choquet Integral fusion with different ensemble sizes (K = 3, 5, 7, 10, 13).

Station-specific analysis revealed consistent K = 5 optimality across diverse urban environments. At high-traffic Erzsébet square, performance improved from RMSE = 3.97 μg/m³ (K = 3) to 2.57 μg/m³ (K = 5), then degraded to 5.63 μg/m³ (K = 13). Suburban Budatétény showed similar patterns: 3.14, 1.82 and 5.31 μg/m³ for K = 3, 5, and 13, respectively. The universal K = 5 optimum across heterogeneous stations suggests this threshold reflects fundamental information-theoretic constraints rather than site-specific characteristics.

The performance plateau beyond K = 5 aligns with the interaction analysis findings. Among the 15 pairwise interactions in the K = 5 configuration, 11 (73.3%) exhibited negative Möbius coefficients, indicating redundancy. The five models selected at K = 5 represented distinct modeling paradigms: instance-based (KNN anomaly), tree ensemble (Short-term RF, RF variants), and recurrent neural (LSTM balanced), maximizing architectural diversity. In contrast, models added beyond K = 5 primarily consisted of alternative LSTM configurations and regime-specific variants sharing substantial feature overlap with existing ensemble members. Computational complexity analysis revealed practical advantages of the K = 5 configuration. The number of Möbius parameters scales as $K+K(k-1)/2$, yielding 6, 15, 28, 55, and 91 parameters for K = 3, 5, 7, 10, and 13, respectively. Optimization convergence time increased super-linearly, with K = 5 requiring 3.2 s versus 18.7 s for K = 13 using COBYLA optimization. K = 5 configuration thus achieved 96.4% of K = 13’s accuracy with 16.5% of the parameters and 17.1% of the computation time.

Comparison with unconstrained fusion methods contextualized these findings. Stack ensemble using all 19 available models achieved RMSE = 1.66 ± 0.36 μg/m³, only 8.5% better than Choquet-K5 despite unlimited non-linear capacity and 4.75× more base models. This marginal improvement, within PM₁₀ measurement uncertainty (±10–15%), validates that information saturation occurs at approximately 5 complementary models for this application. The Choquet Integral’s explicit redundancy penalization through negative interaction coefficients enabled near-optimal performance with a minimal model subset, whereas Stack required the full ensemble to implicitly learn these redundancies through its meta-learner.

3.3. Interpretability of Choquet Integral

The Choquet integral’s sophisticated handling of model interactions reveals its fundamental strength in PM₁₀ forecasting as presented in Figure 5: the ability to simultaneously exploit synergies (red sectors in the figure) where they exist and penalize redundancies (blue sectors in the figure) where they dominate. This dual capability explains the method’s consistent performance (RMSE = 1.83 ± 0.39 μg/m³) across diverse urban environments, achieving near-optimal results through mathematically principled aggregation rather than black-box optimization. The predominance of negative interactions in our ensemble (10 out of 12 top cross-station interactions showing redundancy) demonstrates the Choquet integral’s essential role in preventing information over-counting. Traditional fusion methods like simple averaging or weighted means would treat redundant LSTM variants (LSTM-Long × LSTM-Short: m = −0.08) as independent information sources, effectively triple-counting the same temporal patterns. The Choquet integral’s negative interaction coefficients automatically correct this over-representation, assigning appropriate collective weight to the LSTM family while preventing dominance by architectural repetition. This redundancy management proves particularly valuable given that Random Forest variants with different loss functions (RF-Underpredict × RF-Overpredict: m = −0.05 to −0.15) converge to nearly identical decision boundaries. Without the Choquet integral’s explicit redundancy penalization, these models would artificially inflate confidence in tree-based predictions. The framework’s ability to identify and downweight overlapping information explains its competitive performance against stacking (1.83 vs. 1.67 μg/m³ RMSE), despite stacking’s advantage of unrestricted non-linear optimization. The Choquet integral achieves comparable accuracy through transparent, interpretable interaction modeling rather than opaque neural network combinations.

Figure 5. Synergy and redundancy interactions of base models in each station.

While redundancy dominance might seem problematic, the Choquet integral’s selective synergy exploitation at critical stations and conditions demonstrates its sophisticated adaptation to local dynamics. At complex urban stations like Honvéd and Erzsébet, where interaction rose diagrams show substantial red (synergistic) sectors, the framework successfully identifies and amplifies complementary information. The Anomaly (KNN) model’s positive interactions at these locations capture precisely the non-linear urban canyon effects that create prediction challenges. The synergy between Anomaly detection and other models is not uniformly distributed but emerges exactly where needed, at stations with irregular emission patterns and complex building-induced turbulence. This spatial selectivity represents intelligent fusion: the Choquet integral does not force synergy where none exists (as at simple stations like Budatétény) but exploits it where available.

The Choquet integral’s interaction patterns reflect information complementarity rather than specific atmospheric scales. Negative coefficients (redundancy) occur between models using overlapping feature sets, for instance, multiple LSTM variants processing similar temporal patterns. Positive coefficients (synergy) emerge between models capturing orthogonal information, such as KNN-Anomaly’s deviation-based features versus RF’s absolute concentration features. This aligns with information theory: redundant signals should be downweighted while complementary signals deserve combined consideration. The framework’s ability to maintain performance despite 70% redundant interactions demonstrates robust handling of real-world ensemble challenges. Rather than degrading under information overlap, the Choquet integral leverages its Möbius representation to optimally weight the 30% unique information while preventing redundancy-induced overconfidence. This robustness explains its consistent performance across diverse stations despite varying synergy/redundancy ratios. The Choquet integral’s success in PM₁₀ forecasting stems from its unique ability to handle the dual challenges of modern ensemble systems: exploiting genuine complementarity while preventing redundancy amplification. Its performance parity with state-of-the-art stacking (9.6% RMSE difference within measurement uncertainty), combined with complete interpretability, establishes it as the optimal framework for operational air quality systems. The predominance of redundant interactions does not diminish the Choquet integral’s value; it validates its necessity. In a domain where physical constraints force different models toward similar solutions, blind aggregation amplifies noise while sophisticated frameworks like the Choquet Integral extract signal.

4. Discussion

This study presents the first application of Choquet Integral fusion for air quality forecasting, demonstrating that interpretable ensemble methods can match black-box performance while providing transparency essential for operational deployment. Three key insights emerge with important implications for atmospheric machine learning [50,51].

The dominance of feature engineering over model architecture challenges current trends toward increasingly complex neural networks [38]. The 86.7% performance gap between models using engineered features versus raw meteorological inputs suggests that domain knowledge encoding remains more valuable than architectural sophistication [52,53]. This finding aligns with recent critiques of “big data” approaches in environmental science, where physical understanding often trumps computational power. The minimal contribution of the temperature-humidity ratio (P_proxy, <2% feature importance) demonstrates an important characteristic of our framework: robustness to individual weak features when the feature space includes physically meaningful variables. While P_proxy exhibited theoretical limitations, its negligible impact validates that ensemble methods naturally suppress poorly justified features through their aggregation mechanisms. However, this robustness does not excuse the inclusion of theoretically flawed features in operational systems. Future implementations should prioritize physically interpretable indicators such as Richardson number, bulk Richardson number, or direct boundary layer height measurements. The success of our meteorological feature set demonstrates that proper atmospheric parameterization, rather than exploratory ratios, drives predictive performance.

The failure of multivariate LSTM despite theoretical advantages particularly highlights how incorrect inductive biases can overwhelm additional information [54,55]. Multivariate LSTM’s failure (R² = 0.183 vs. 0.782 for univariate) stems from three statistical issues: (1) Parameter complexity increases 4-fold while training samples remain fixed, reducing effective samples per parameter below 100; (2) Gradient interference occurs when backpropagation attempts to optimize for variables with conflicting temporal dynamics (PM₁₀’s 24 h periodicity versus wind’s 72 h persistence); (3) LSTM’s shared recurrent weights cannot accommodate multiple temporal scales simultaneously [56,57,58]. The architecture assumes all inputs share similar temporal evolution, but atmospheric variables operate at fundamentally different frequencies. This explains why separate univariate models outperform theoretically superior multivariate approaches [59]. Future research should prioritize developing physically consistent feature spaces rather than pursuing model complexity.

On the other hand, the dramatic performance gap between GBR-Regime and GBR-Stable illuminates a fundamental issue in atmospheric modeling: the stationarity assumption. Traditional models assume statistical properties (mean, variance, autocorrelation) remain constant over time [60,61]. This fails for PM₁₀ because:

• Morning rush hours show rapid concentration increases (non-stationary mean) [62,63].
• Stable nocturnal inversions exhibit low variance, while afternoon mixing shows high variance.
• Autocorrelation changes between stagnant episodes and windy periods.

GBR-Stable applies uniform parameters regardless of conditions, attempting to fit a single model to fundamentally different atmospheric states. In contrast, GBR-Regime adapts its predictions based on identified atmospheric regimes, effectively treating PM₁₀ as a switching process rather than a stationary time series. The 4.10 effect size, exceptionally large for environmental modeling, quantifies the penalty of ignoring atmospheric regime transitions [64,65,66]. In other words, the superior performance of GBR-Regime stems from its adaptive feature selection: during stable periods, it uses long-term patterns (24 h/168 h statistics), during rapid transitions, it switches to short-term momentum features (recent lags and changes), and during extreme events, it relies on meteorological drivers. In contrast, GBR-Stable applies the same long-term features regardless of atmospheric state, forcing a single model to fit fundamentally different pollution dynamics.

Choquet Integral’s ability to explicitly manage redundancy addresses a fundamental but overlooked challenge in ensemble learning [67,68]. The predominance of negative Möbius coefficients (70% of interactions) reveals that most models converge toward similar solutions due to atmospheric physics constraints. This contradicts the common assumption that ensemble diversity inherently improves performance [69]. Instead, our results suggest that preventing information over-counting is more critical than exploiting synergies. The framework’s transparency through Shapley values and interaction matrices enables diagnosis of model failures and targeted improvements impossible with black-box stacking.

The optimal ensemble size of K = 5 has important practical implications. The 42% performance improvement from K = 3 to K = 5, followed by saturation, suggests fundamental limits to the independent information available from PM₁₀ observations. This finding could guide operational system design, as maintaining 5 well-chosen models reduces computational costs by 62% compared to exhaustive ensembles while preserving 96% of performance gains [70]. The consistency of this optimum across diverse urban environments suggests it reflects information-theoretic constraints rather than site-specific characteristics.

Our approach’s limitations point toward future research directions. The static Möbius coefficients assumption may oversimplify seasonal dynamics, particularly during extreme events when atmospheric processes shift. Adaptive Choquet Integrals with time-varying coefficients could capture these changes, though maintaining theoretical guarantees while enabling adaptation presents mathematical challenges. Integration of satellite and mobile sensor data could overcome current performance ceilings but would require hierarchical fusion frameworks preserving interpretability across spatial scales [71,72].

The performance plateau at R² ≈ 0.98 raises fundamental questions about predictability limits in urban atmospheric systems. This ceiling, consistent across diverse architectures and comprehensive feature engineering, likely reflects irreducible uncertainty from sub-grid turbulence, stochastic emissions, and measurement noise. Breaking through may require paradigm shifts such as physics-informed neural networks embedding conservation laws or hybrid models combining deterministic chemistry with statistical corrections.

While individual base models remain black boxes, the Choquet integral provides three levels of operational transparency essential for public health deployment:

• Model reliability indicators: Shapley values reveal which models dominate under current conditions (e.g., KNN-Anomaly weighted 45% during Saharan dust events while routine traffic models drop to 10%).
• Failure diagnostics: When predictions fail, Möbius coefficients reveal which model combinations caused the error. If LSTM-Short and RF-Standard show strong positive interaction (synergy) during a missed peak, operators know these models are amplifying each other’s errors.
• Confidence assessment: Large negative interactions (redundant models agreeing) indicate higher confidence; disagreement among typically synergistic models signals uncertainty.

Practical example: A public health alert might state: “Forecast: 85 μg/m³. High confidence. Anomaly detection (weight: 0.4) and meteorological models (0.3) indicate atmospheric stagnation. Traffic models downweighted (0.1 each) for holiday period.” This does not explain why models predict 85 μg/m³ (models remain opaque), but it demonstrates which models drive the prediction and whether weighting is appropriate, enabling officials to calibrate trust and response accordingly. This “fusion-level interpretability” distinguishes our approach from fully opaque stacking while acknowledging that we do not reveal underlying atmospheric mechanisms.

The broader implications extend beyond air quality to environmental machine learning generally. Many environmental systems exhibit similar characteristics: physical constraints creating model redundancy, multiple scales of relevant processes, and requirements for interpretable predictions. The Choquet Integral framework could apply to climate modeling, hydrological forecasting, or ecosystem monitoring where ensemble fusion is common, but interpretability remains challenging.