Investigation and Validation of Short-Wave Scattering in the Anisotropic Ionosphere under a Geomagnetic Field
Abstract
1. Introduction
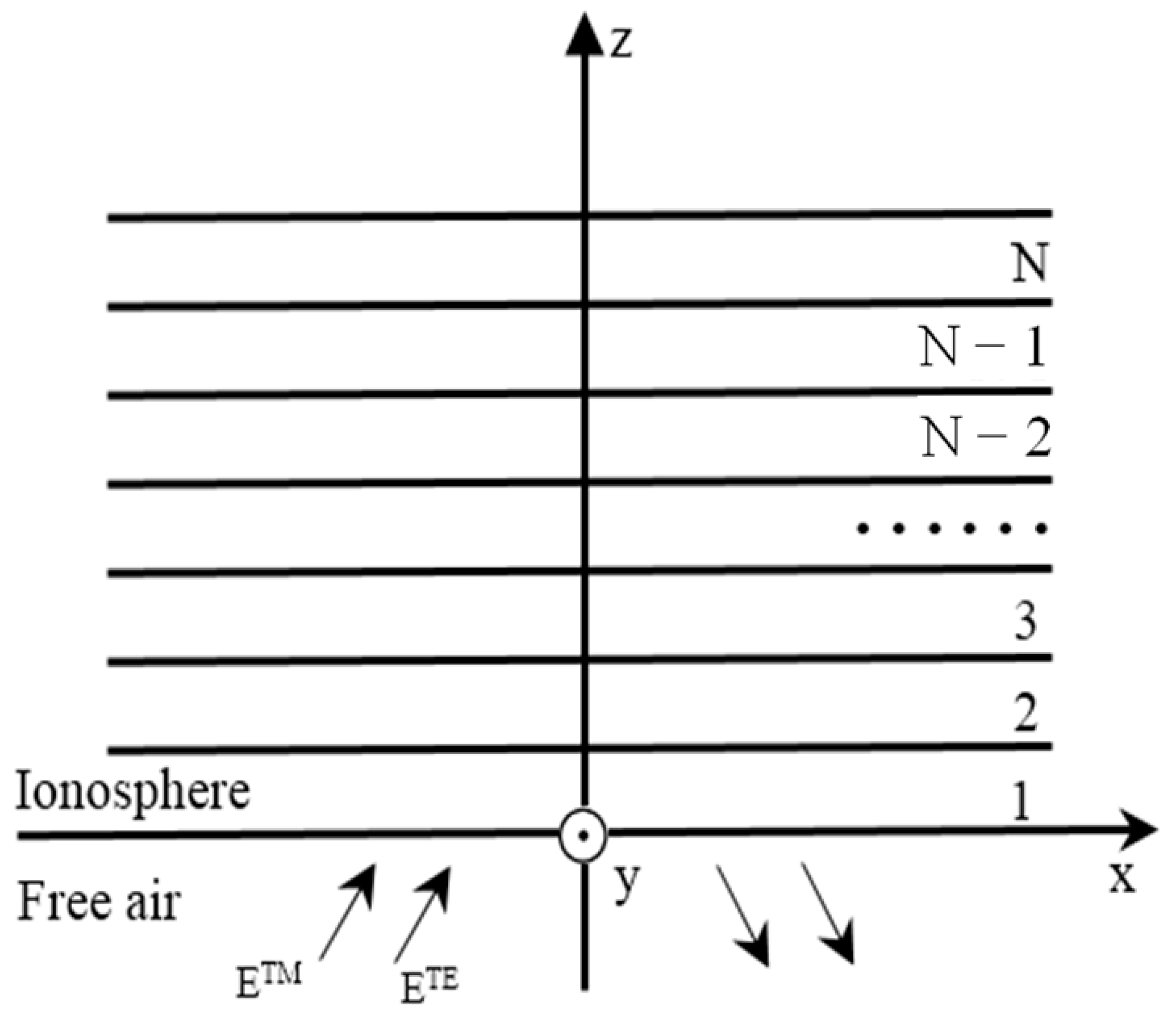
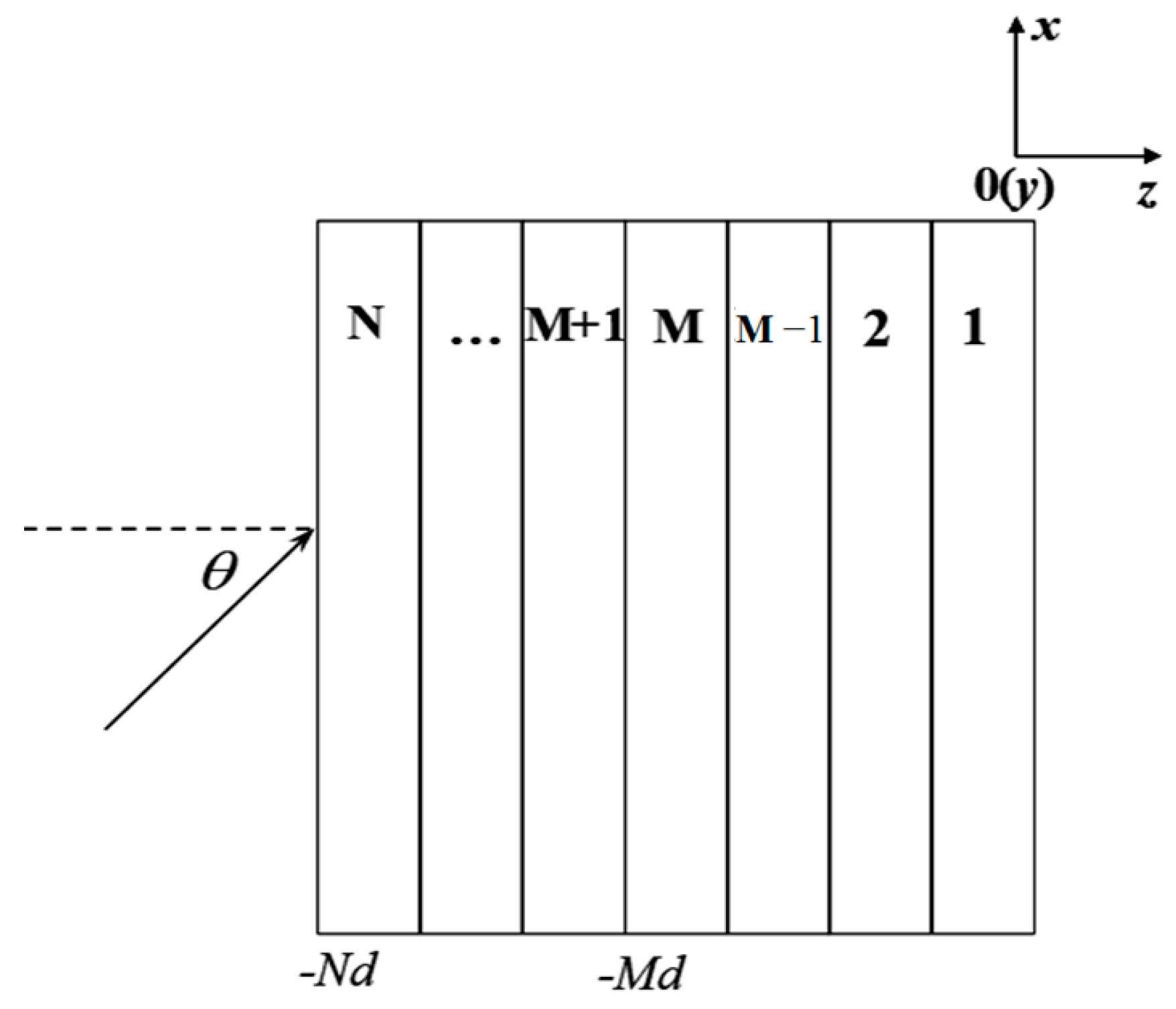
2. Multilayer Anisotropic Ionospheric Model
3. Transfer Matrix Method
Theoretical Derivation
4. Analysis and Verification of Short-Wave Electromagnetic Scattering in the Heterogeneous Anisotropic Ionosphere
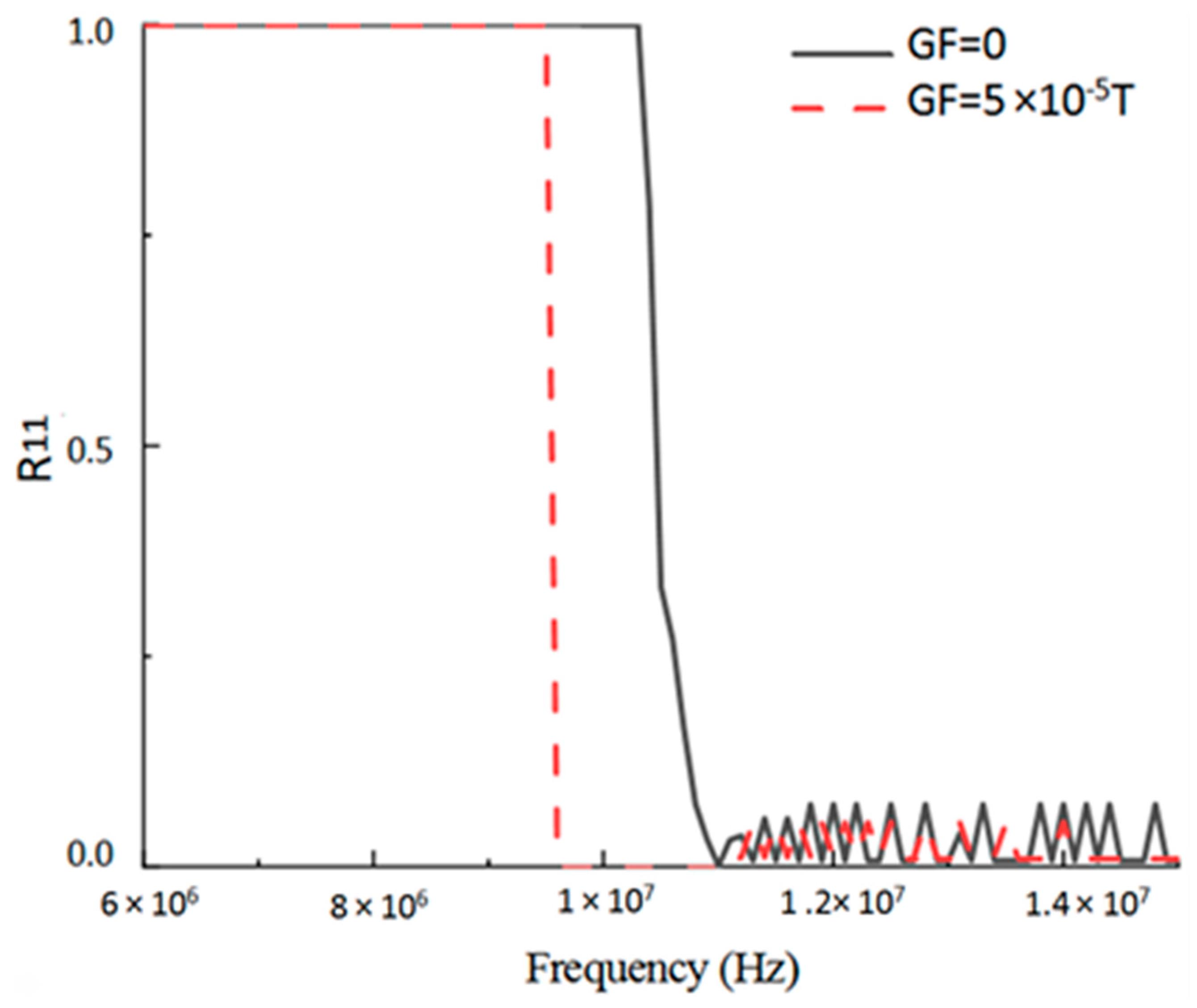
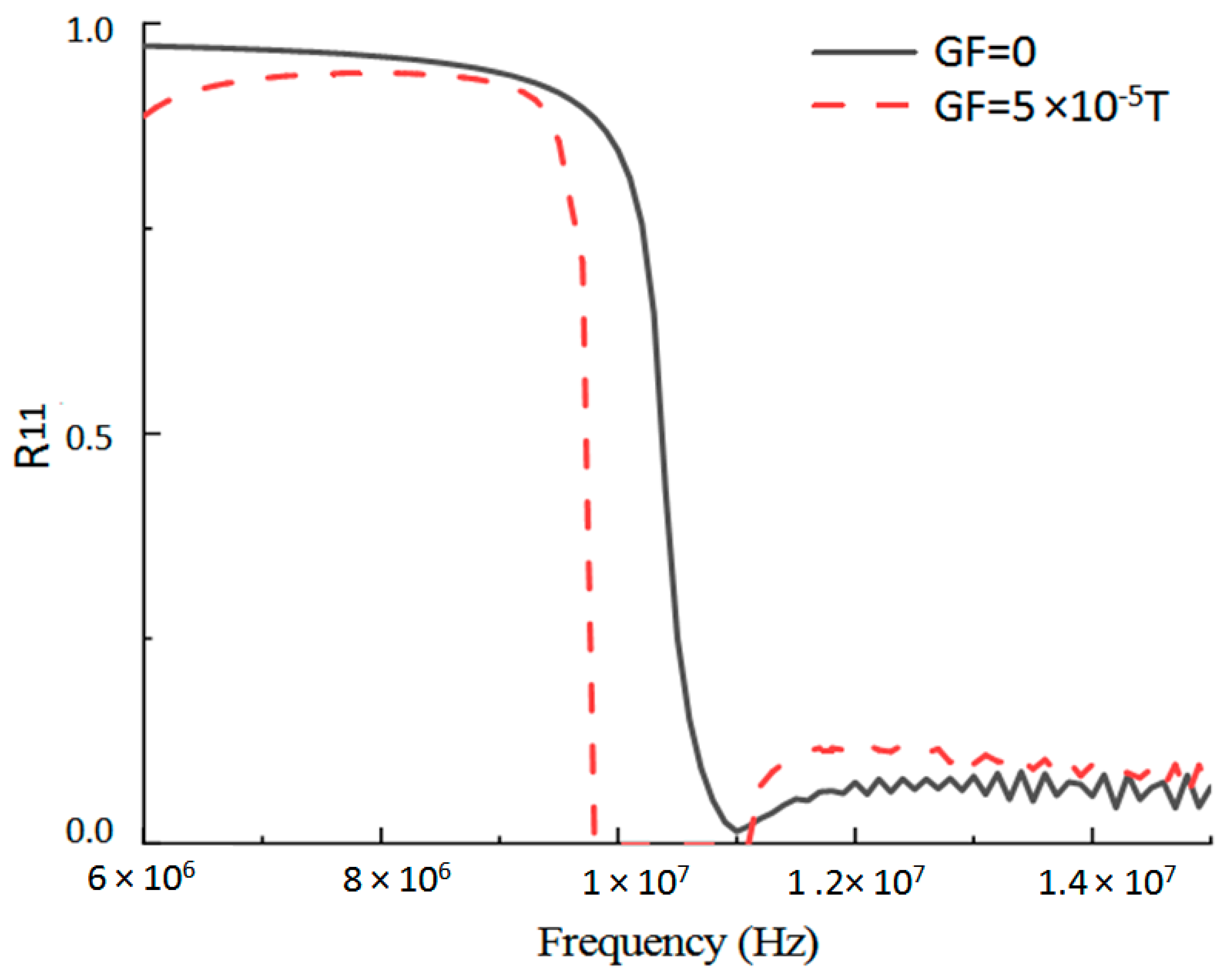
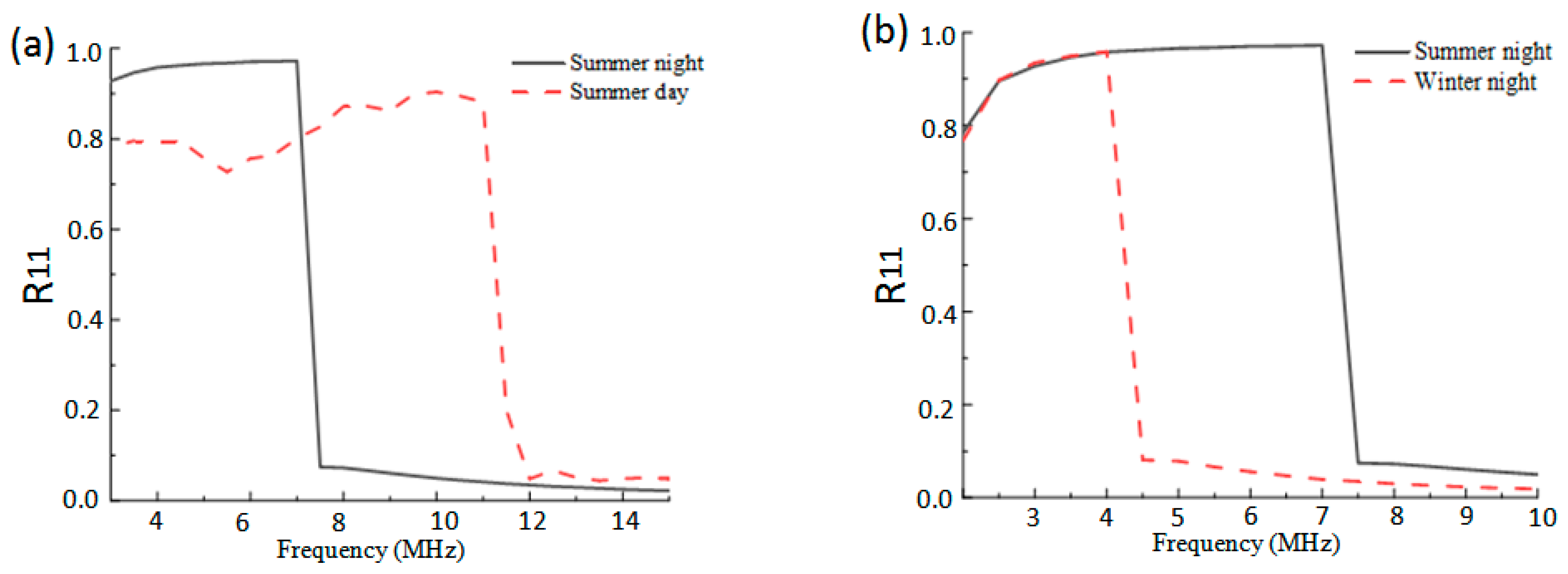
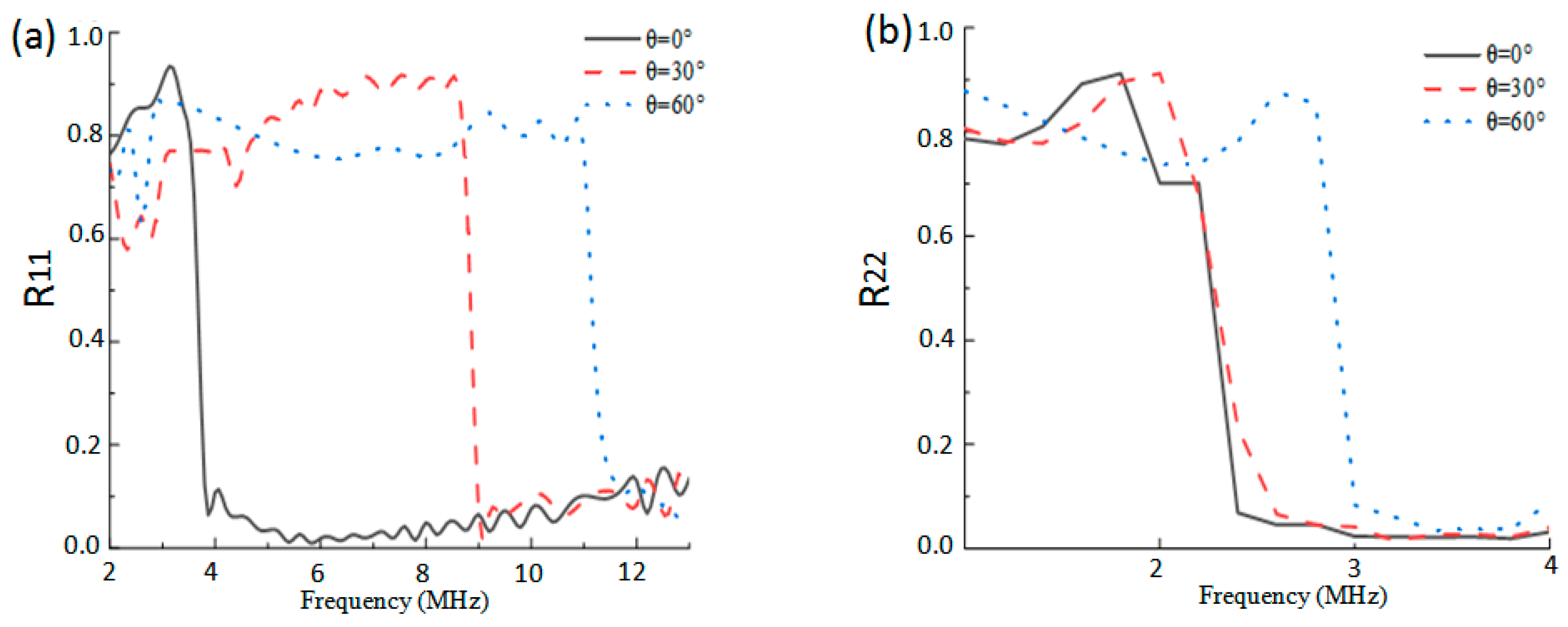
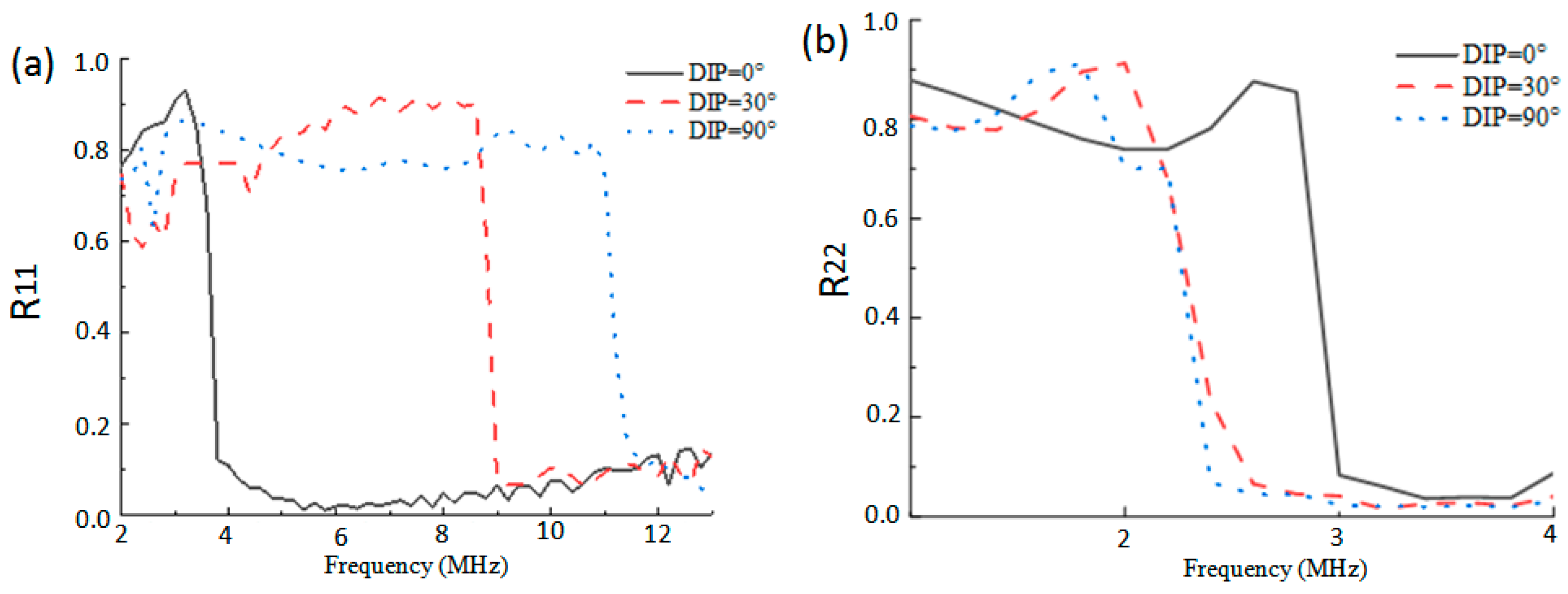
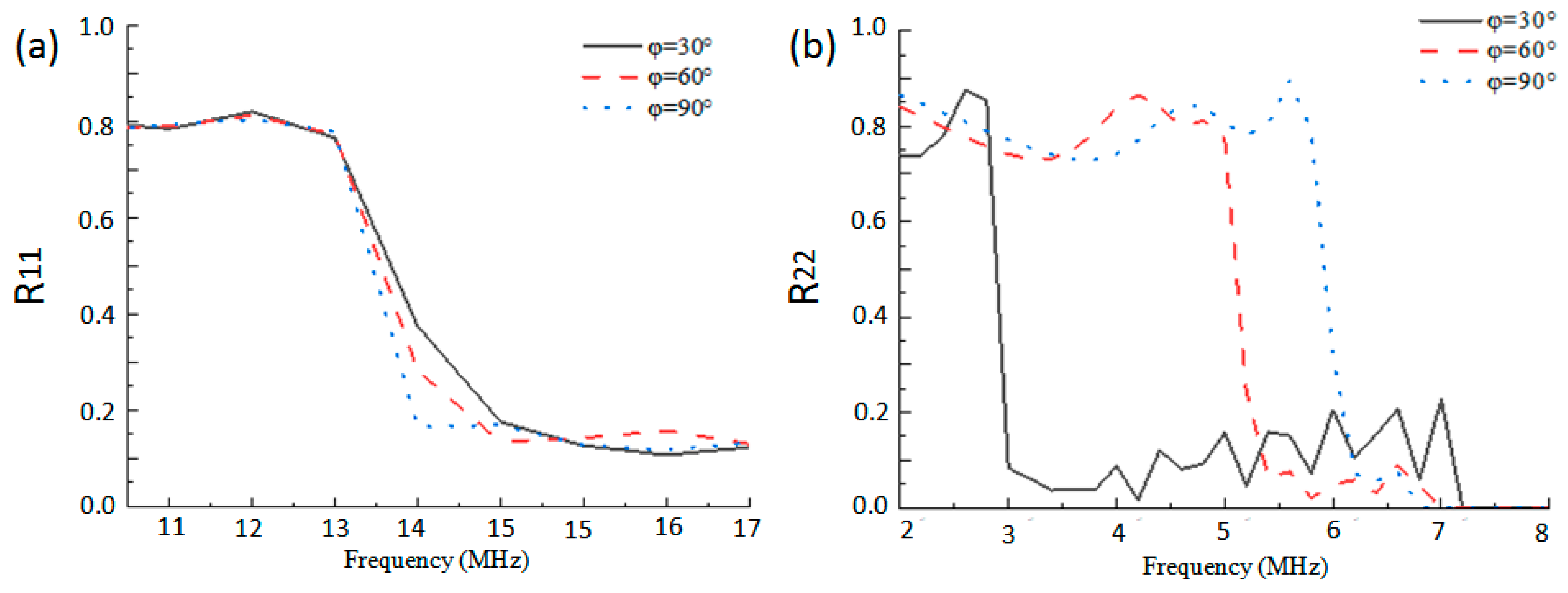
4.1. Effects of Ionospheric Anisotropy on the Highest Frequencies
4.2. Computational Comparison of Simple Ionospheric Stratification
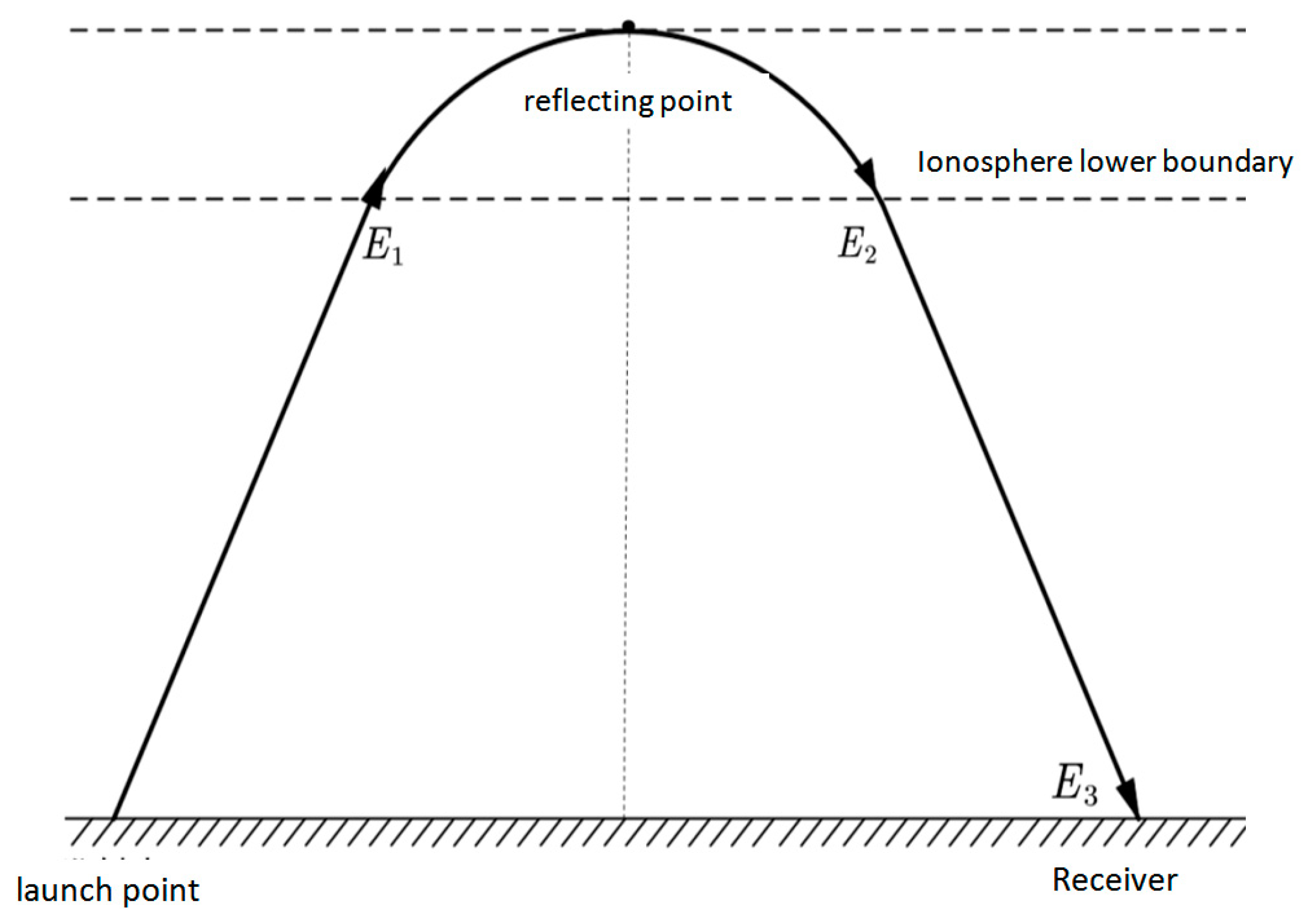
4.3. Accurate Calculation of Electromagnetic Scattering in the Complex Anisotropic Ionosphere
5. Comparison Validation
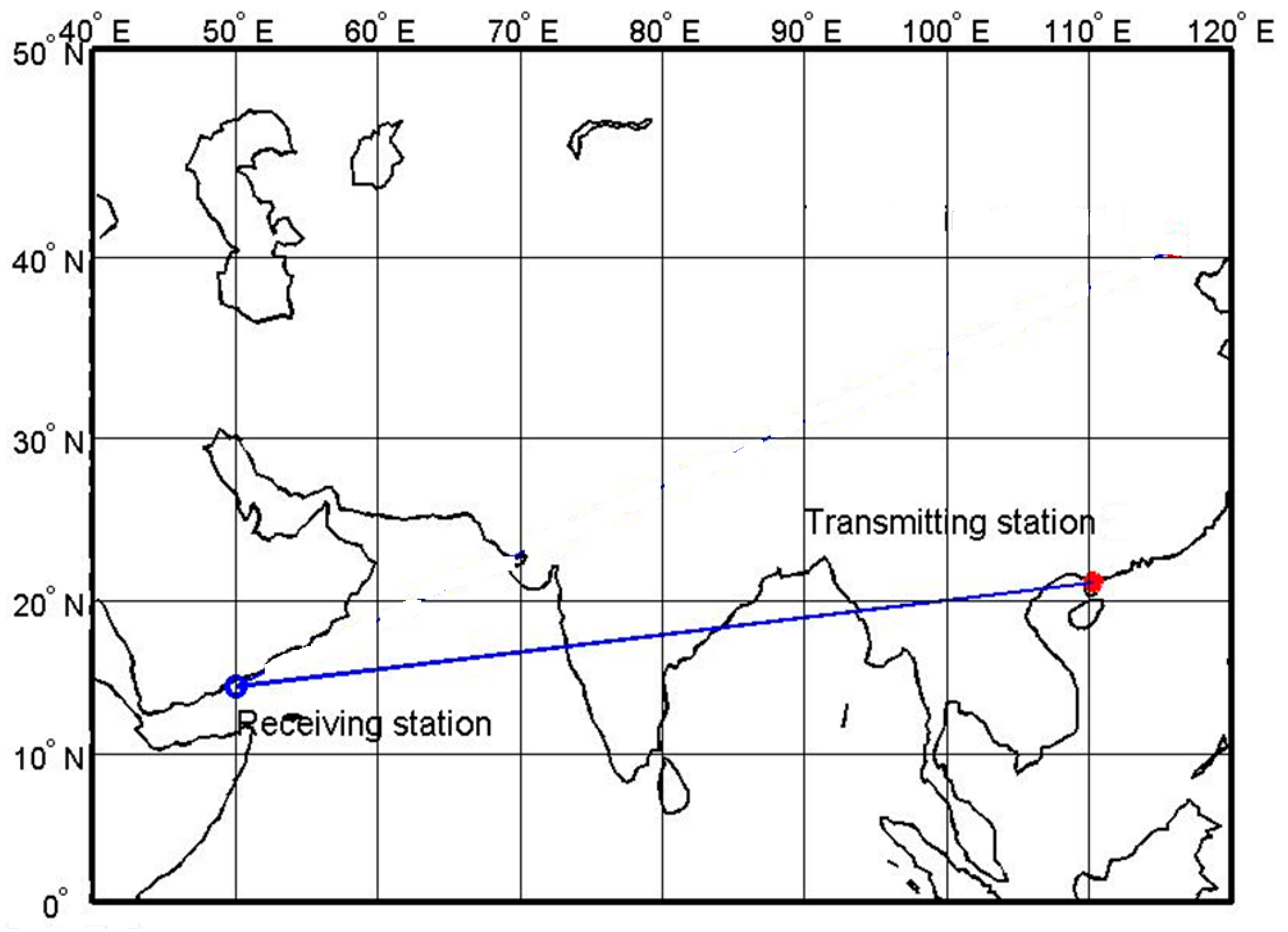
5.1. Communication Link
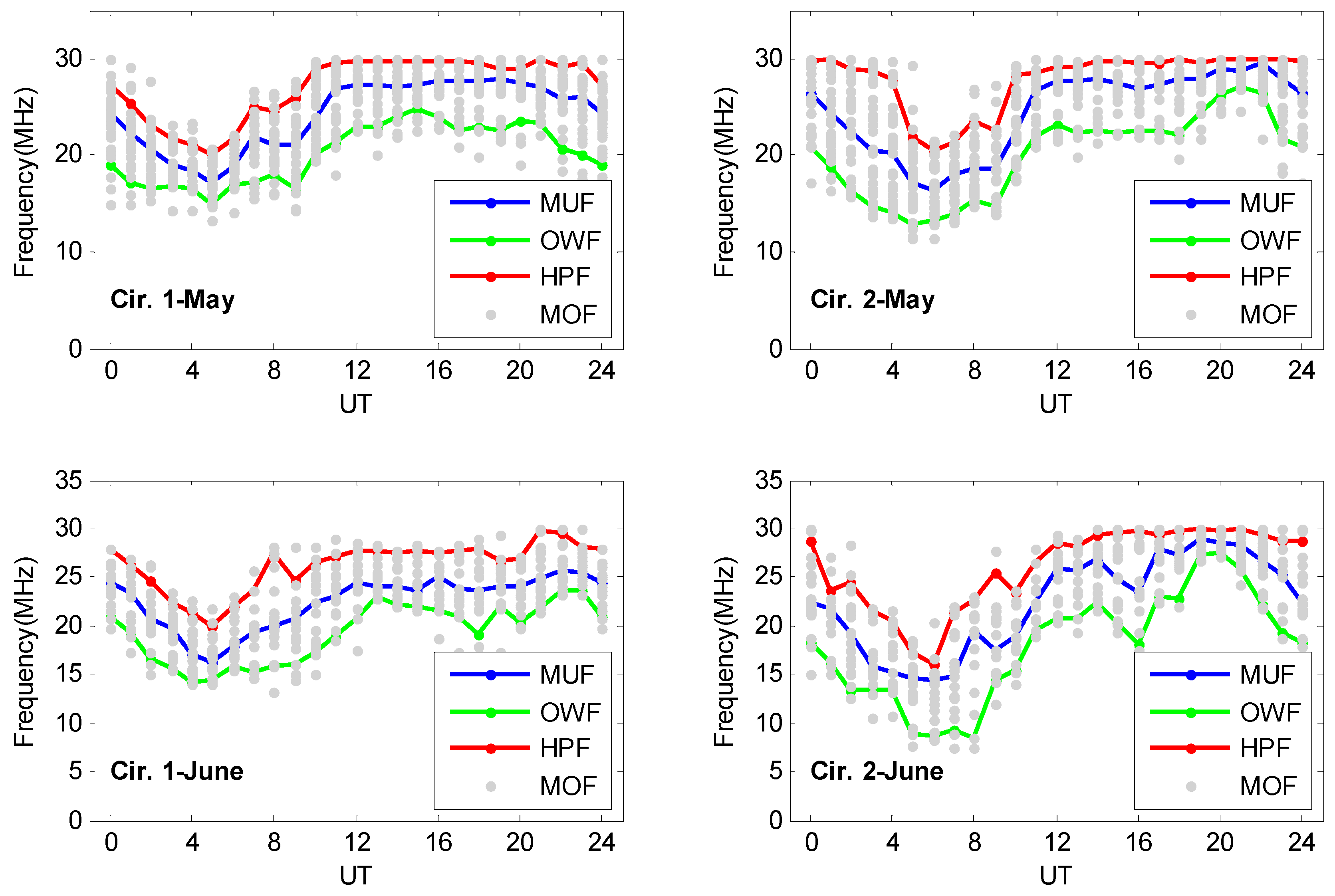
5.2. Median Field-Strength Prediction Based on the Statistical Model
5.3. Field-Strength Calculation Based on the Anisotropic Backscattering Model
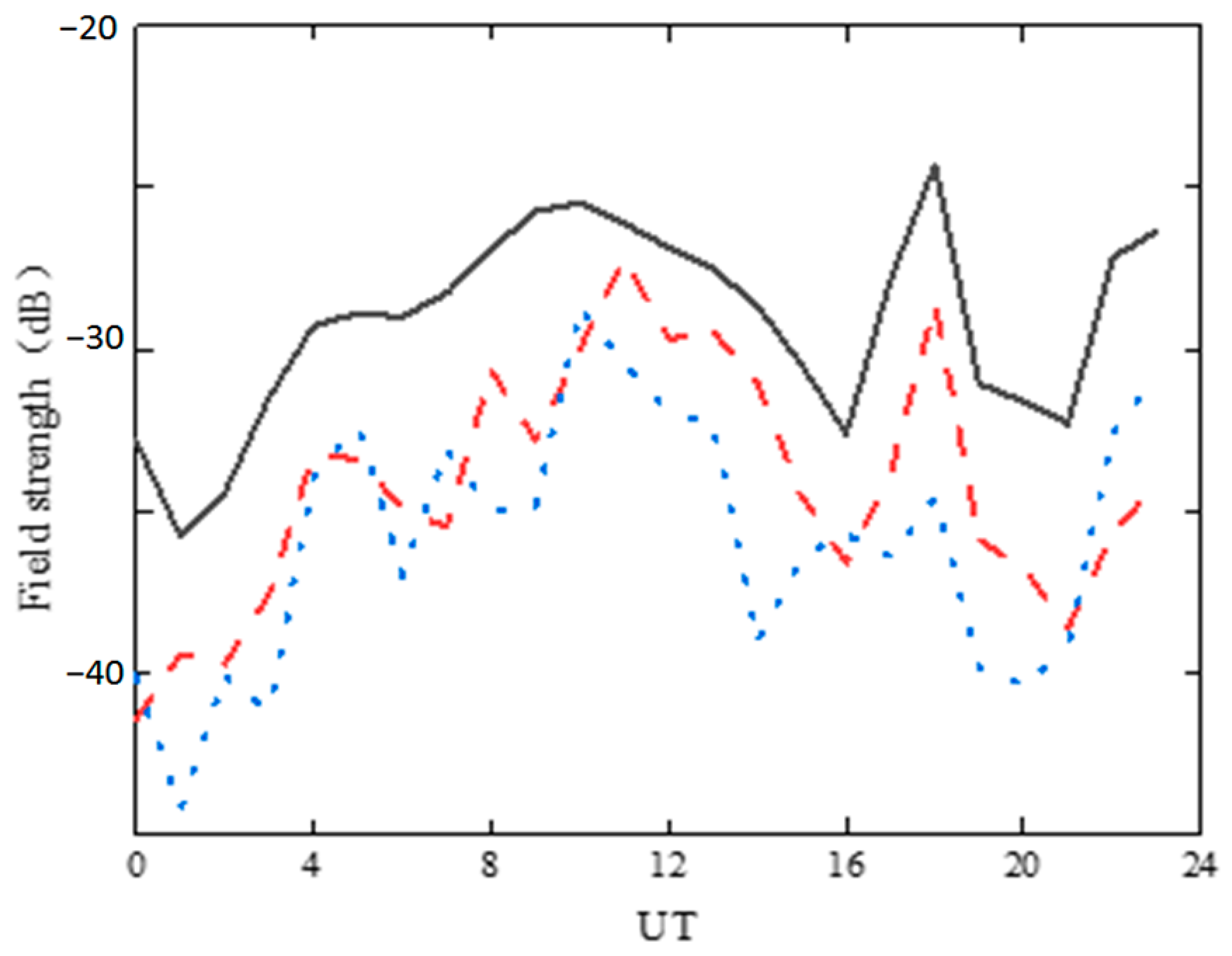
5.4. Comparative Analysis
6. Summary
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bertel, L.; Guyader, P.; Lassudrie, D.; Uchesne, P. Multiple-frequency Doppler sounding of the ionosphere: Theory and experimental comparison with incoherent scatter results. Radio Sci. 1984, 19, 879–890. [Google Scholar] [CrossRef]
- Helliwell, R.A. Whistlers and Related Ionospheric Phenomena; Stanford University Press: Stamford, CT, USA, 1965. [Google Scholar]
- Cohen, M.B.; Gross, N.C.; Higginson-Rollins, M.A.; Marshall, R.A.; Gokowski, M.; Liles, W.; Rodriguez, D.; Rockway, J. The Lower Ionospheric VLF/LF Response to the 2017 Great American Solar Eclipse Observed Across the Continent. Geophys. Res. Lett. 2018, 45, 3348–3355. [Google Scholar] [CrossRef]
- Kelso, J.M. Ray Tracing in the ionosphere. Radio Sci. 1968, 3, 1–12. [Google Scholar] [CrossRef]
- Haselgrove, J. Ray theory and a new method of raytracing. In Physics in the Ionosphere; London Press: London, UK, 1965. [Google Scholar]
- Jones, R.M. A three-dimensional ray-tracing computer program (digest of ESSA technical report, ITSA no. 17). Radio Sci. 1968, 3, 93–94. [Google Scholar] [CrossRef]
- Croft, T.A.; Hoogasian, H. Exact ray calculations in a quasi-parabolic ionosphere with no magnetic field. Radio Sci. 1968, 3, 69–74. [Google Scholar] [CrossRef]
- Dyson, P.L.; Bennett, J.A. A model of the vertical distribution of the electron concentration in the ionosphere and its application to oblique propagation studies. J. Atmos. Terr. Phys. 1988, 50, 251–262. [Google Scholar] [CrossRef]
- Norman, R.J.; Cannon, P.S. A two-dimensional analytic ray tracing technique accommodating horizontal gradients. Radio Sci. 1997, 32, 387–396. [Google Scholar] [CrossRef]
- Davies, K.; Rush, C.M. High-frequency ray paths in ionospheric layers with horizontal gradients. Radio Sci. 1985, 20, 95–110. [Google Scholar] [CrossRef]
- Coleman, C.J. On the simulation of backscatter ionograms. J. Atmos. Sol. Terr. Phys. 1997, 59, 2089–2099. [Google Scholar] [CrossRef]
- Coleman, C.J. A ray tracing formulation and its application to some problems in over-the-horizon radar. Radio Sci. 1998, 33, 1187–1197. [Google Scholar] [CrossRef]
- Xie, S.G.; Zhao, Z.Y. A new ray-tracing method-three zoning treatment. Chin. J. Radio Sci. 2001, 16, 222–226. [Google Scholar]
- Muldrew, D. An ionospheric ray-tracing technique and its application to a problem in a long-distance radio propagation. IRE Trans. Antennas Propag. 1959, 7, 393–396. [Google Scholar] [CrossRef]
- Hopkins, H.G.; Reynolds, L.G. An experimental investigation of short-distance ionospheric propagation at low and very low frequencies. Proc. IEE Part III Radio Commun. Eng. 1954, 69, 21–34. [Google Scholar]
- Song, H.; Qing, H.; Zou, X. A parallel optimization 3D numerical ray-tracing method for the fast and accurate simulation of disturbed oblique ionogram. Adv. Space Res. 2022, 70, 2894–2899. [Google Scholar] [CrossRef]
- Yaogai, H.; Zhengyu, Z.; Yuannong, Z. Ionospheric disturbances produced by chemical releases and the resultant effects on short-wave. J. Geophys. Res. 2011, 16, A07307. [Google Scholar]
- Liu, W.; Peinan, J.; Shikai, W.; Junjiang, W. A fast ray tracing algorithm in the ionosphere. Chin. J. Radio Sci. 2008, 01, 41–48. [Google Scholar]
- Jiangquan, C.; Yuhong, Y.; Xin, G.; Song, L. Simulation of shortwave 3D ray tracing with geomagnetic field. Comput. Eng. Des. 2012, 33, 300. [Google Scholar]
- Krasnov, V.M.; Kuleshov, Y.V.; Koristin, A.A.; Drobzheva, Y.V. Influence of the geomagnetic field on absorption of radiowaves. J. Atmos. Sol.-Terr. Phys. 2021, 227, 105806. [Google Scholar]
- Pan, W.Y.; Li, K. Propagation of SLF/ELF Electromagnetic Waves; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Wang, J. Observation and analysis of phase cycle slipping of VLF signals. Chin. J. Radio Sci. 2006, 21, 628–631. [Google Scholar]
- Fu, H.; Zhang, Z.; Ju, J. Calculation of shortwave propagation in anisotropic ionosphere by transfer matrix method. In Proceedings of the 2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 12–14 March 2021; IEEE: Piscataway, NJ, USA, 2021; Volume 5, pp. 1983–1986. [Google Scholar]
- Qin, Z.; Chen, M.; Zhu, B.; Du, Y.P. An improved ray theory and transfer matrix method-based model for lightning electromagnetic pulses propagating in Earth-ionosphere waveguide and its applications. J. Geophys. Res. Atmos. 2017, 122, 712–727. [Google Scholar] [CrossRef]
- Zhao, L.; Zuo, Y.; Feng, Y.J. Electromagnetic Wave Reflection of Anisotropic Layered Media with a Metallic Substrate. Chin. J. Radio Sci. 2009, 24, 5. [Google Scholar]
- Ding, Z.H.; Dai, L.D.; Yang, S.; Miao, J.S.; Wu, J. Preliminary analysis of diurnal variation characteristics of electron density in the E-F valley region of the ionosphere using incoherent scattering radar in Qujing. Chin. J. Radio Sci. 2022, 37, 357. [Google Scholar]
- Gwal, A.K.; Choudhary, S.; Chaurasia, H. Chapter 15—Space Weather Phenomenon of Polar Ionosphere Over the Arctic Region. In Understanding Present and Past Arctic Environments; Elsevier: Amsterdam, The Netherlands, 2021; pp. 325–341. [Google Scholar]
- Romero-Hernandez, E.; Denardini, C.M.; Jonah, O.F.; Essien, P.; Picanço, G.A.S.; Nogueira, P.A.B.; Rodriguez-Martinez, M.; Resende, L.C.A.; de la Luz, V.; Aguilar-Rodriguez, E.; et al. Nighttime Ionospheric TEC Study Over Latin America During Moderate and High Solar Activity. JGR Space Phys. 2020, 125, e2020JA028210. [Google Scholar] [CrossRef]
- Lopez-Urias, C.; Vazquez-Becerra, G.E.; Nayak, K.; Lopez-Montes, R. Analysis of Ionospheric Disturbances during X-Class Solar Flares (2021–2022) Using GNSS Data and Wavelet Analysis. Remote Sens. 2023, 15, 4626. [Google Scholar] [CrossRef]
- International Telecommunication Union. Method for the Prediction of the Performance of HF Circuits; ITU-RP.533; International Telecommunication Union: Geneva, Switzerland, 2007. [Google Scholar]
- Yan, Z.W.; Wang, G.; Tian, G.L.; Li, W.M.; Su, D.L.; Rahman, T. Errata to “The HF Channel EM Parameters Estimation Under a Complex Environment Using the Modified IRI and IGRF Model”. IEEE Trans. Antennas Propag. 2011, 59, 2448. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; She, J.; Fu, H.; Zhao, L.; Ji, S. Investigation and Validation of Short-Wave Scattering in the Anisotropic Ionosphere under a Geomagnetic Field. Atmosphere 2024, 15, 767. https://doi.org/10.3390/atmos15070767
Zhang Z, She J, Fu H, Zhao L, Ji S. Investigation and Validation of Short-Wave Scattering in the Anisotropic Ionosphere under a Geomagnetic Field. Atmosphere. 2024; 15(7):767. https://doi.org/10.3390/atmos15070767
Chicago/Turabian StyleZhang, Zhigang, Jingyi She, Hongwei Fu, Lin Zhao, and Shengyun Ji. 2024. "Investigation and Validation of Short-Wave Scattering in the Anisotropic Ionosphere under a Geomagnetic Field" Atmosphere 15, no. 7: 767. https://doi.org/10.3390/atmos15070767
APA StyleZhang, Z., She, J., Fu, H., Zhao, L., & Ji, S. (2024). Investigation and Validation of Short-Wave Scattering in the Anisotropic Ionosphere under a Geomagnetic Field. Atmosphere, 15(7), 767. https://doi.org/10.3390/atmos15070767




