Climatic Challenges in the Growth Cycle of Winter Wheat in the Huang-Huai-Hai Plain: New Perspectives on High-Temperature–Drought and Low-Temperature–Drought Compound Events
Abstract
1. Introduction
2. Data and Methods
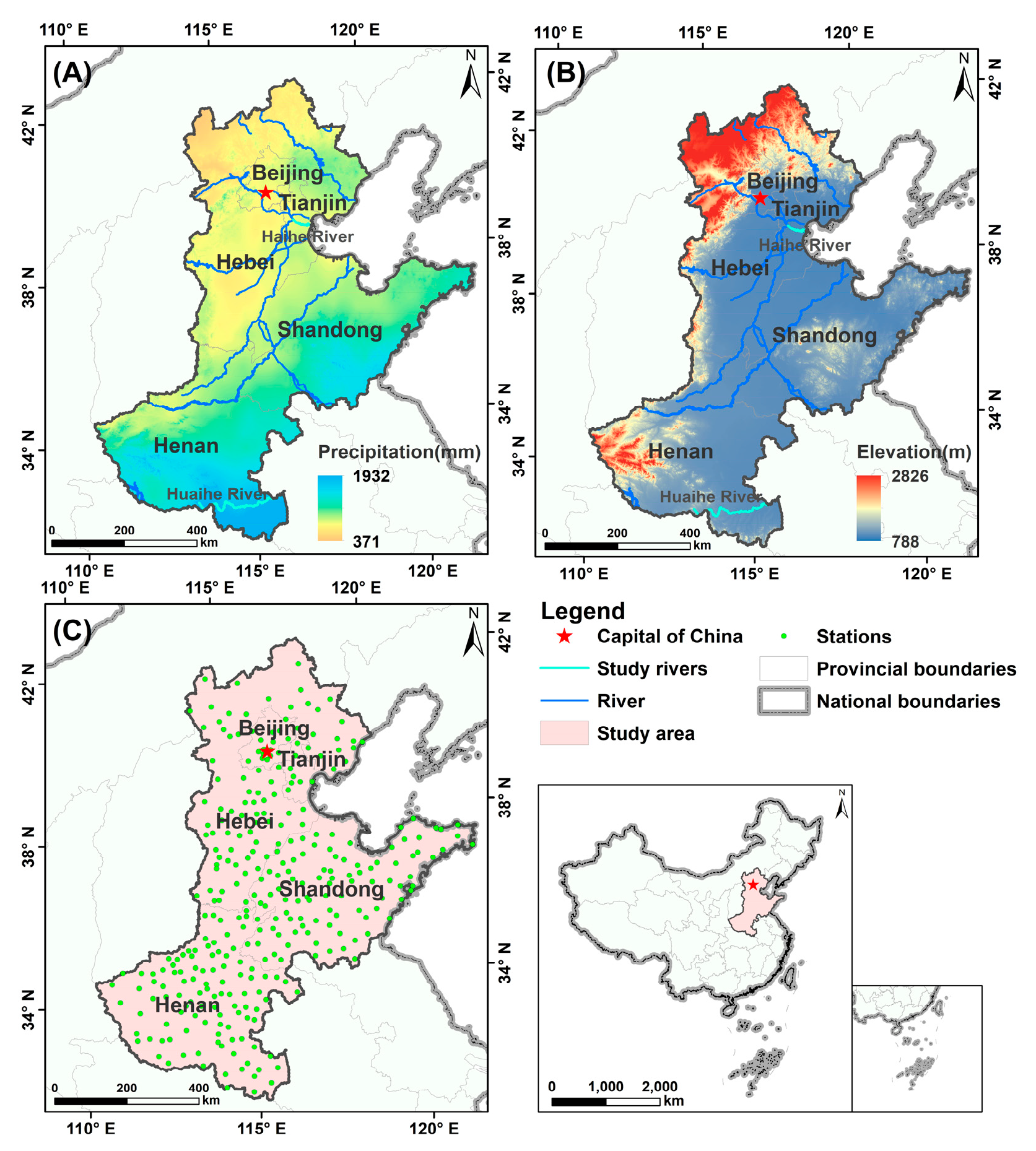
2.1. Overview of the Study Area
2.2. Data Introduction
2.2.1. Normalized Vegetation Index (NDVI)
- (1)
- MODIS Remote Sensing Data
- (2)
- GIMMS NDVI Data Processing
2.2.2. Meteorological Data
2.3. Methods
2.3.1. Standardized Precipitation Index (SPI)
- For some random independent precipitation data x, the mean precipitation and standard deviation for the time period need to be obtained first:
- 2.
- Calculate the given precipitation skewness based on the mean precipitation and standard deviation for that time period:
- 3.
- The precipitation data information is then transformed into lognormal values to calculate the gamma distribution statistic U, shape parameter β, and scale parameter α:
- 4.
- Based on the resulting shape and scale parameters, the cumulative probability of this precipitation data can be calculated and the cumulative probability is
- 5.
- Since the gamma function is not defined when x is 0, and the rainfall in the region at a given time may again be 0 mm, the cumulative probability becomeswhere q may be 0; so, the standardized precipitation index iswhere ; x is the amount of precipitation during the time period, mm; G(x) is the cumulative probability corresponding to x; and S is the positive or negative coefficient of the probability density. S = 1 when G(x) > 0.5; S = −1 when G(x) ≤ 0.5; = 2.515517, = 0.802853, = 0.010328, = 1.432788, = 0.189269, = 0.001308.
- No drought (SPI > −0.5): Winter wheat growth is unaffected and normal yields can be expected.
- Light drought (−1.0 < SPI ≤ −0.5): Winter wheat experiences minor stress, which may slow growth rates but generally does not lead to significant yield losses.
- Moderate drought (−1.5 < SPI ≤ −1.0): Winter wheat faces moderate stress, with noticeable reductions in growth and potential yield losses.
- Severe drought (−2.0 < SPI ≤ −1.5): Winter wheat undergoes severe stress, resulting in significant reductions in growth and substantial yield losses.
- Extreme drought (SPI ≤ −2.0): Winter wheat experiences extreme stress, with a high risk of crop failure due to severe water deficits.
2.3.2. Maximum-Value Composite Method
2.3.3. Copula Function
Parameter Estimation
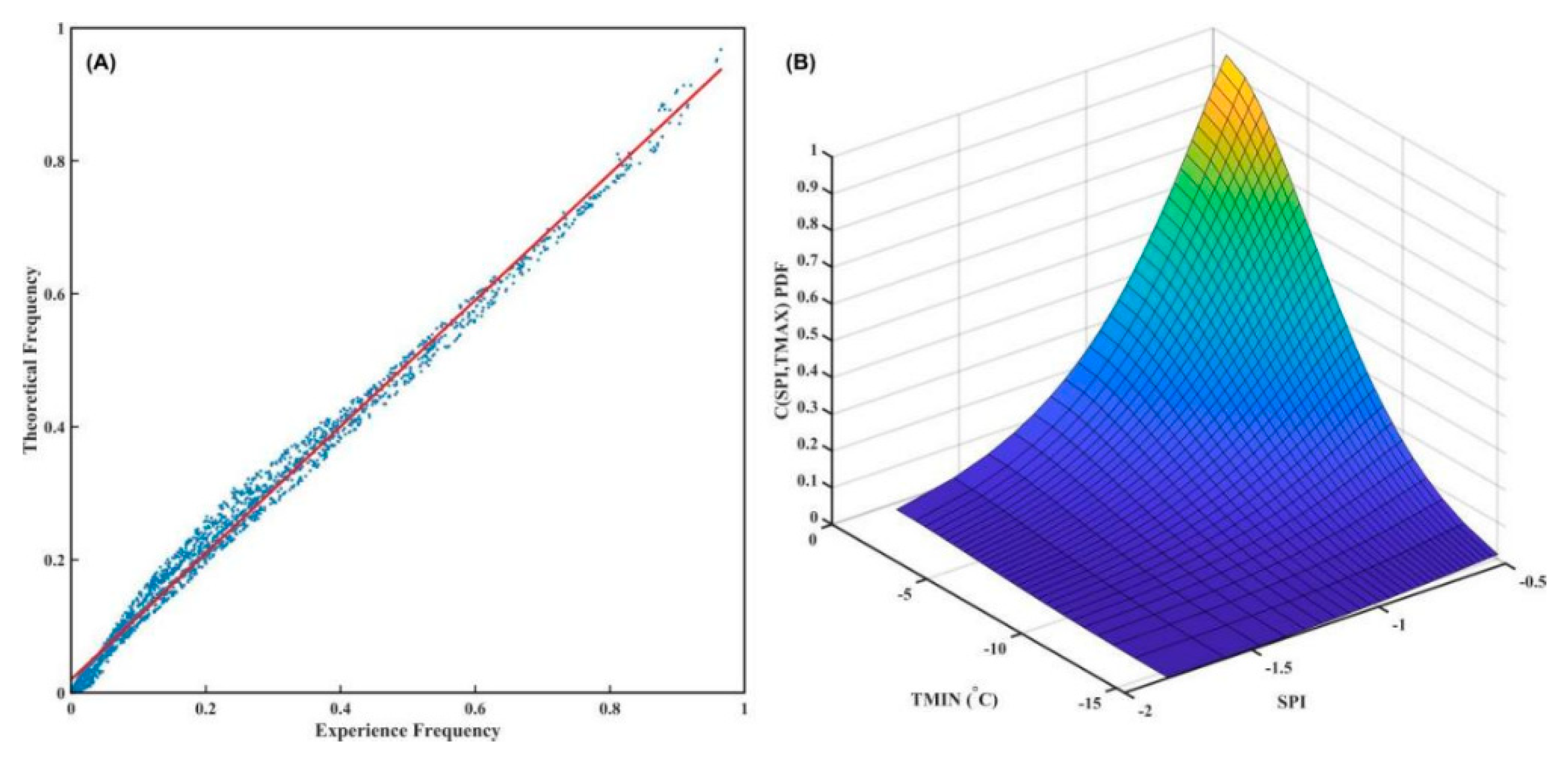
Validation and Evaluation
Correlation Analysis and Marginal Distribution Function
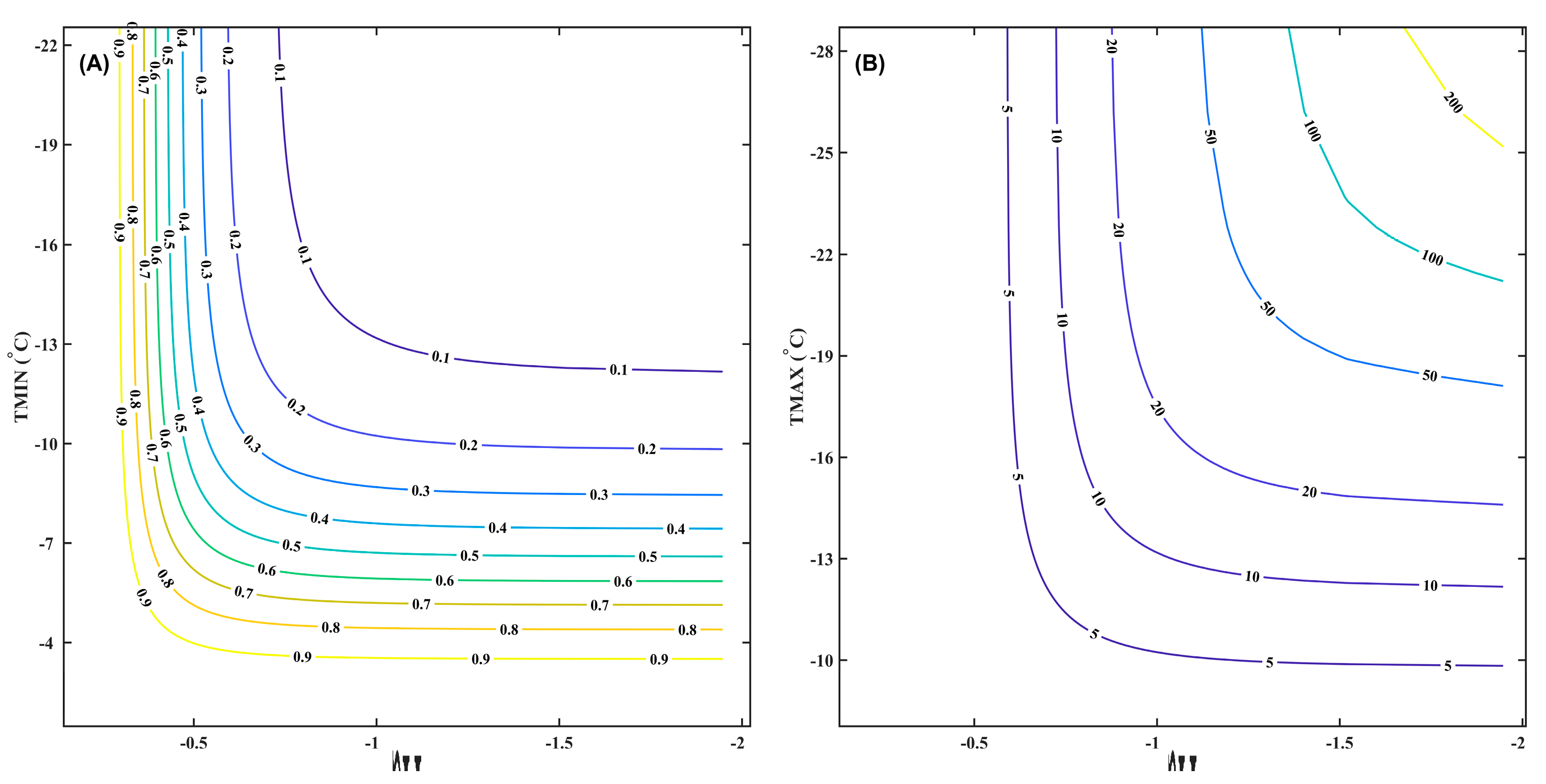
Joint Probability Distribution
Return Period Calculation
2.3.4. Random Forest
- (1)
- Using the bootstrap method with replacement, randomly select n groups of sample data from the initial training set to construct decision trees.
- (2)
- Among the multiple attribute features of the training samples, select the optimal feature for splitting each time. Each tree continues this splitting process until all training samples under that node belong to the same category.
- (3)
- To fully utilize the classification ability of each tree, allow each tree to grow to its maximum extent without any pruning.
- (4)
- Combine the generated multiple classification trees to form a random forest, and use voting to determine the final classification result.
2.3.5. Definition of Extreme Temperature–Drought Compound Events
- (1)
- Definition of High Temperature–Drought Compound Events:
- High-Temperature Event Standard: A high-temperature event is defined as when the maximum temperature is not lower than the 90th percentile threshold of historical maximum temperatures. This means that when the maximum temperature for a given month exceeds or equals the highest 10% of historical maximum temperatures for that month, a high-temperature event is considered to have occurred.
- Drought Event Standard: The drought event standard uses the Standardized Precipitation Index (SPI). A drought event is considered to have occurred when the SPI value indicates mild drought or worse. Mild drought conditions typically correspond to SPI values less than −0.5.
- High-Temperature–Drought Compound Event: When both the high-temperature event and drought event standards are met simultaneously, i.e., the maximum temperature reaches or exceeds the 90th percentile threshold and the SPI value is less than −0.5, a high-temperature–drought compound event is considered to have occurred.
- (2)
- Definition of Low-Temperature–Drought Compound Events:
- Low-Temperature Event Standard: A low-temperature event is defined as when the minimum temperature is not higher than the 10th percentile threshold of historical minimum temperatures. This means that when the minimum temperature for a given month is below or equals the lowest 10% of historical minimum temperatures for that month, a low-temperature event is considered to have occurred.
- Drought Event Standard: Similar to the high-temperature–drought compound event, the drought event standard uses the Standardized Precipitation Index (SPI). A drought event is considered to have occurred when the SPI value indicates mild drought or worse. Mild drought conditions typically correspond to SPI values less than −0.5.
- Low-Temperature–Drought Compound Event: When both the low-temperature event and drought event standards are met simultaneously, i.e., the minimum temperature reaches or falls below the 10th percentile threshold and the SPI value is less than −0.5, a low-temperature–drought compound event is considered to have occurred.
3. Results
3.1. Response of Winter Wheat to Combined High-Temperature–Drought Events
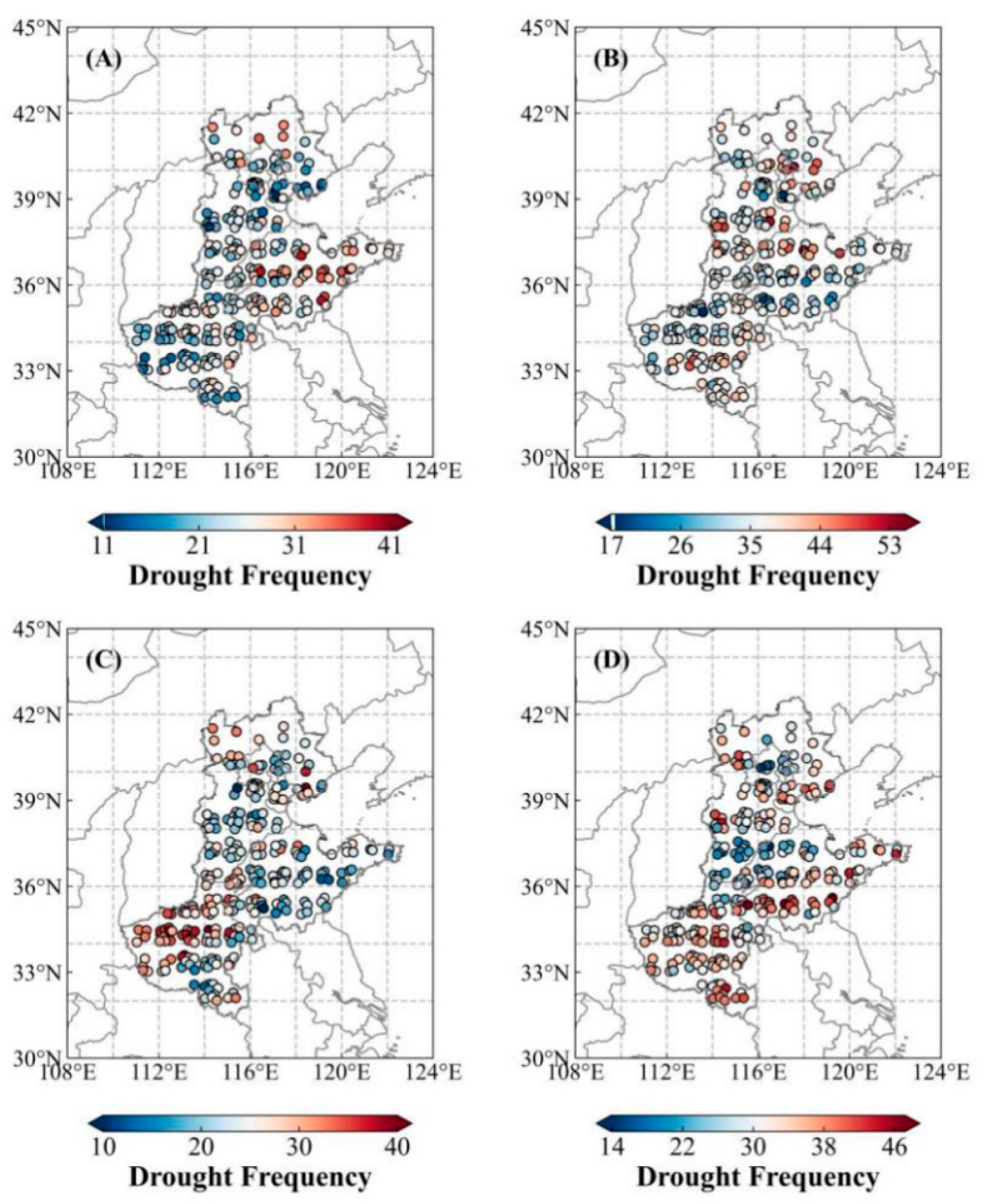
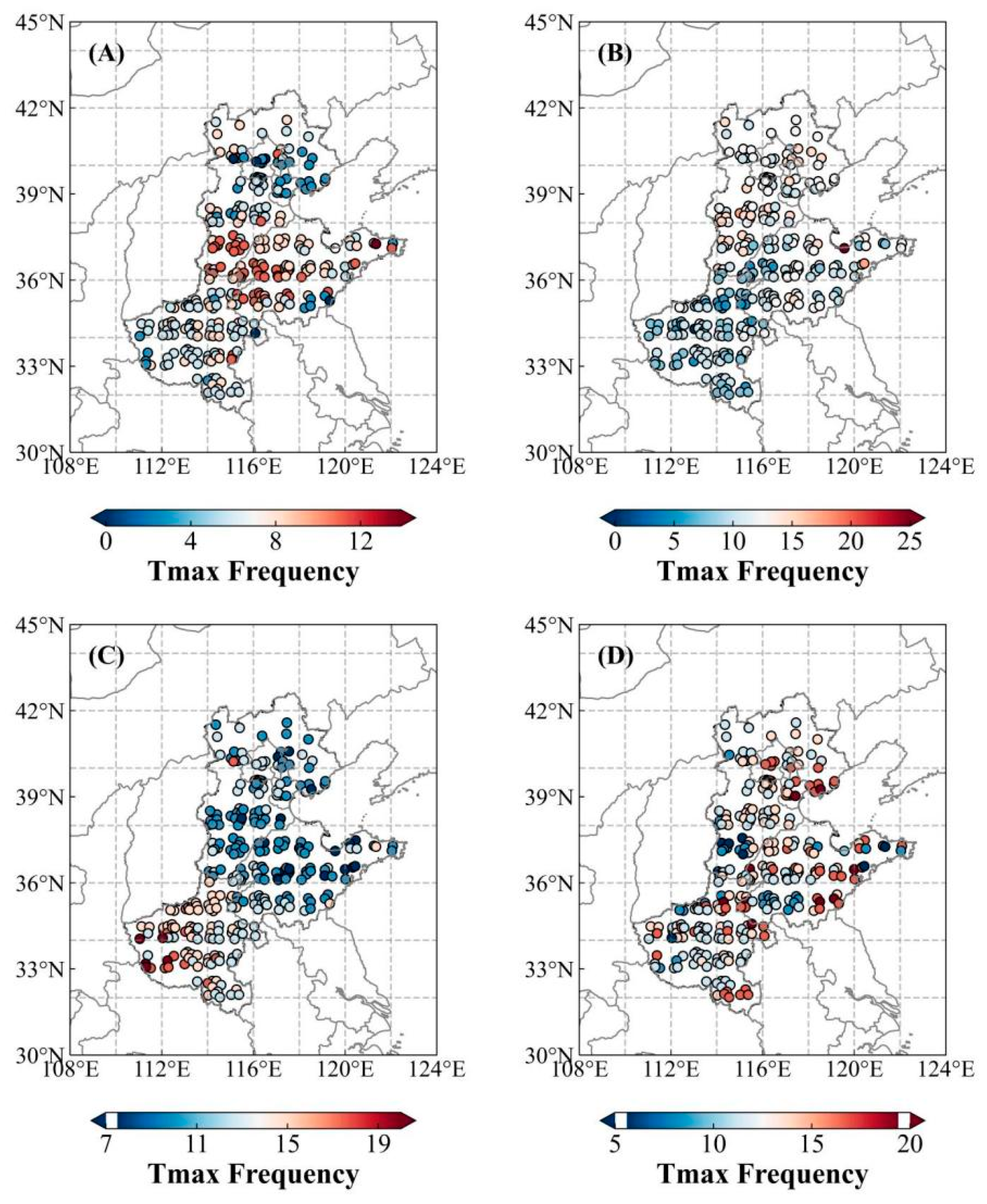
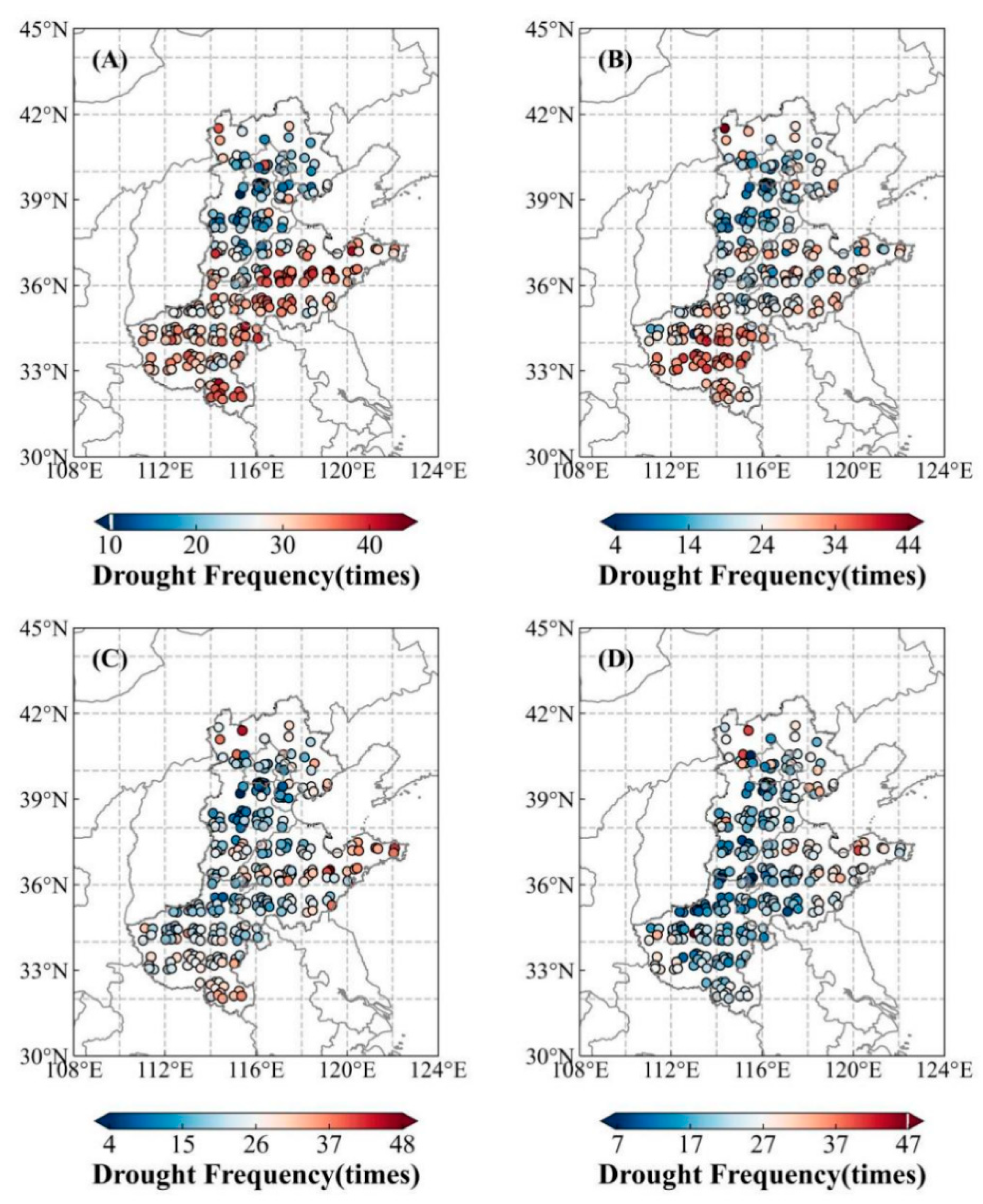
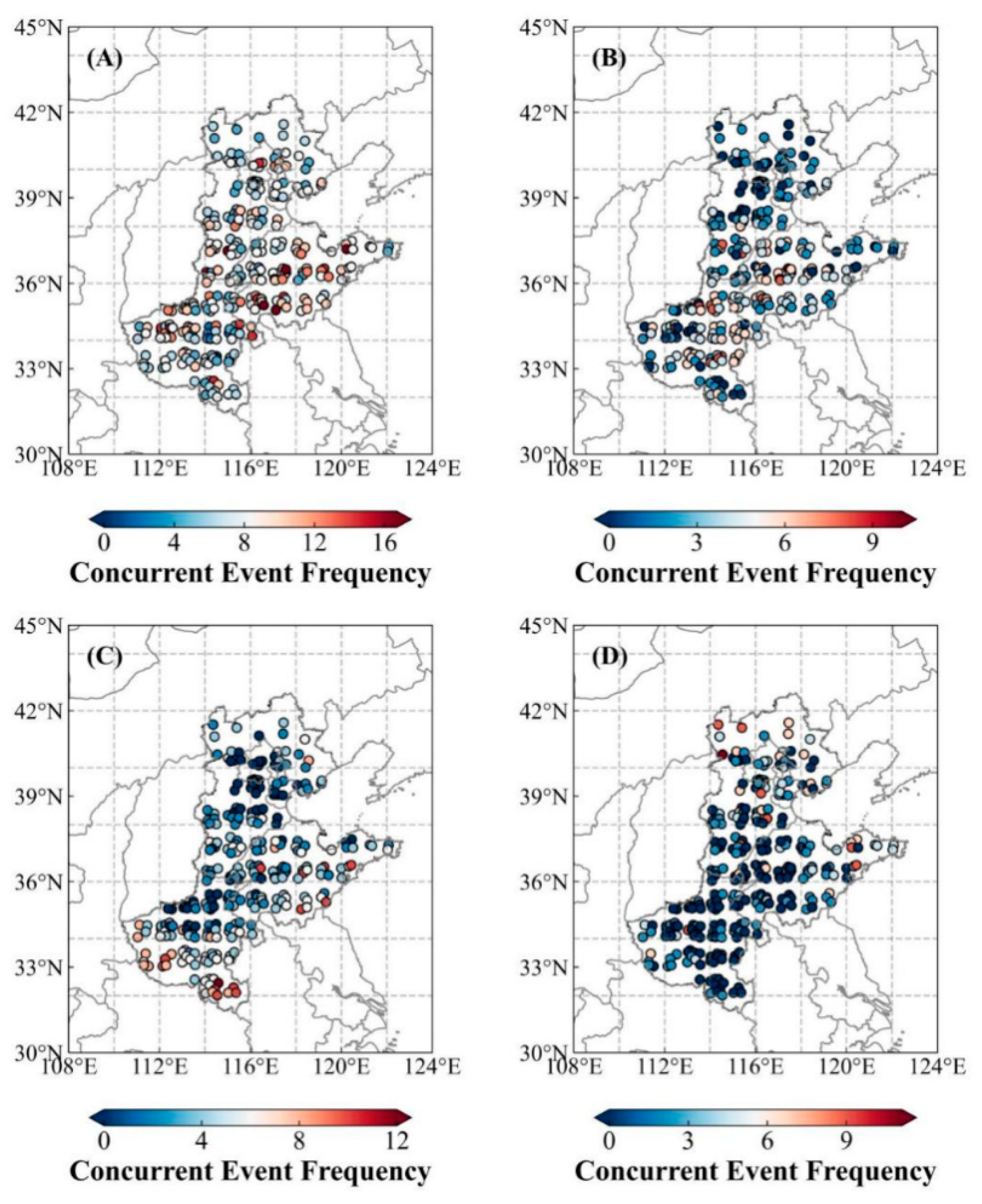
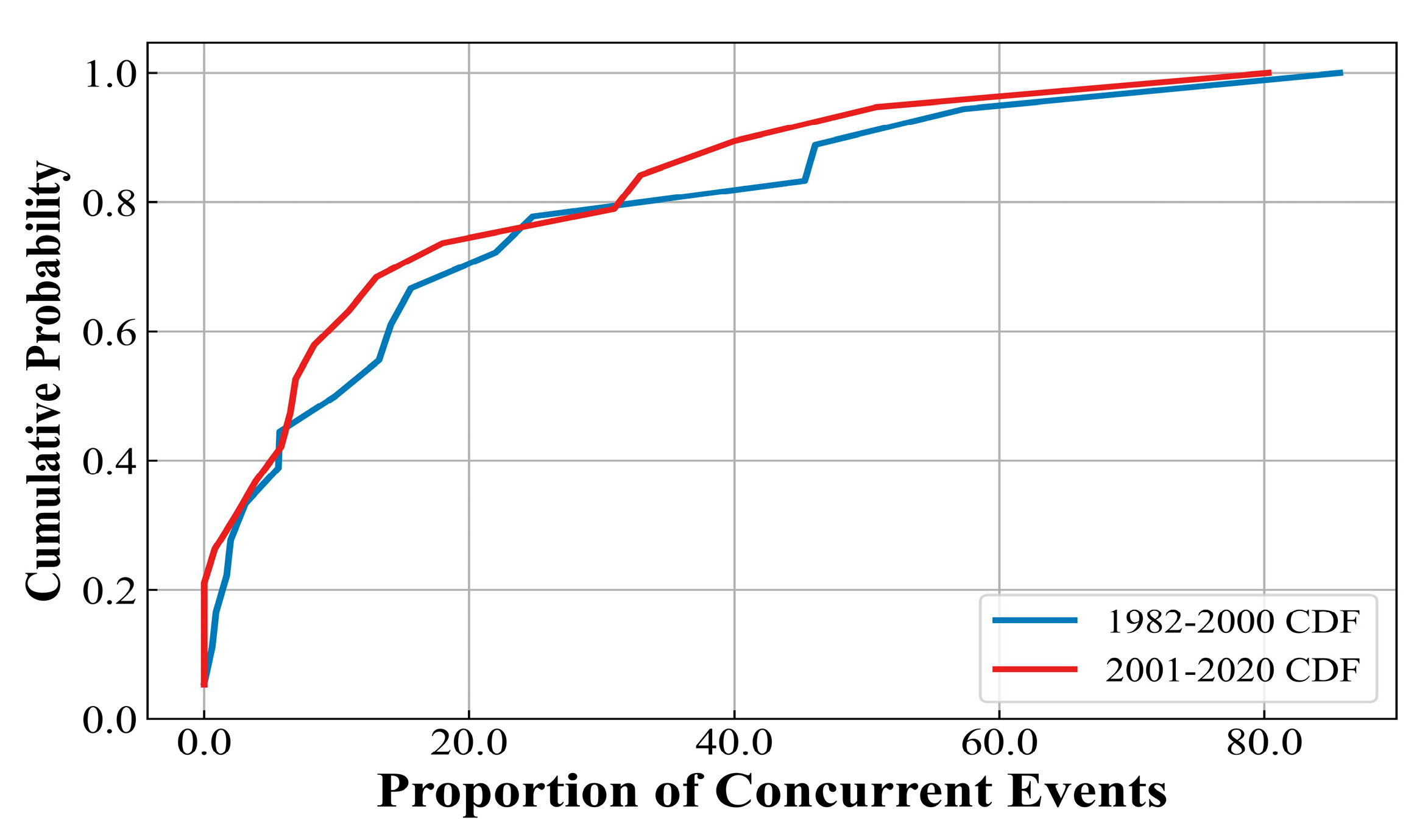
3.1.1. Spatiotemporal Distribution Characteristics of High-Temperature–Drought Compound Events
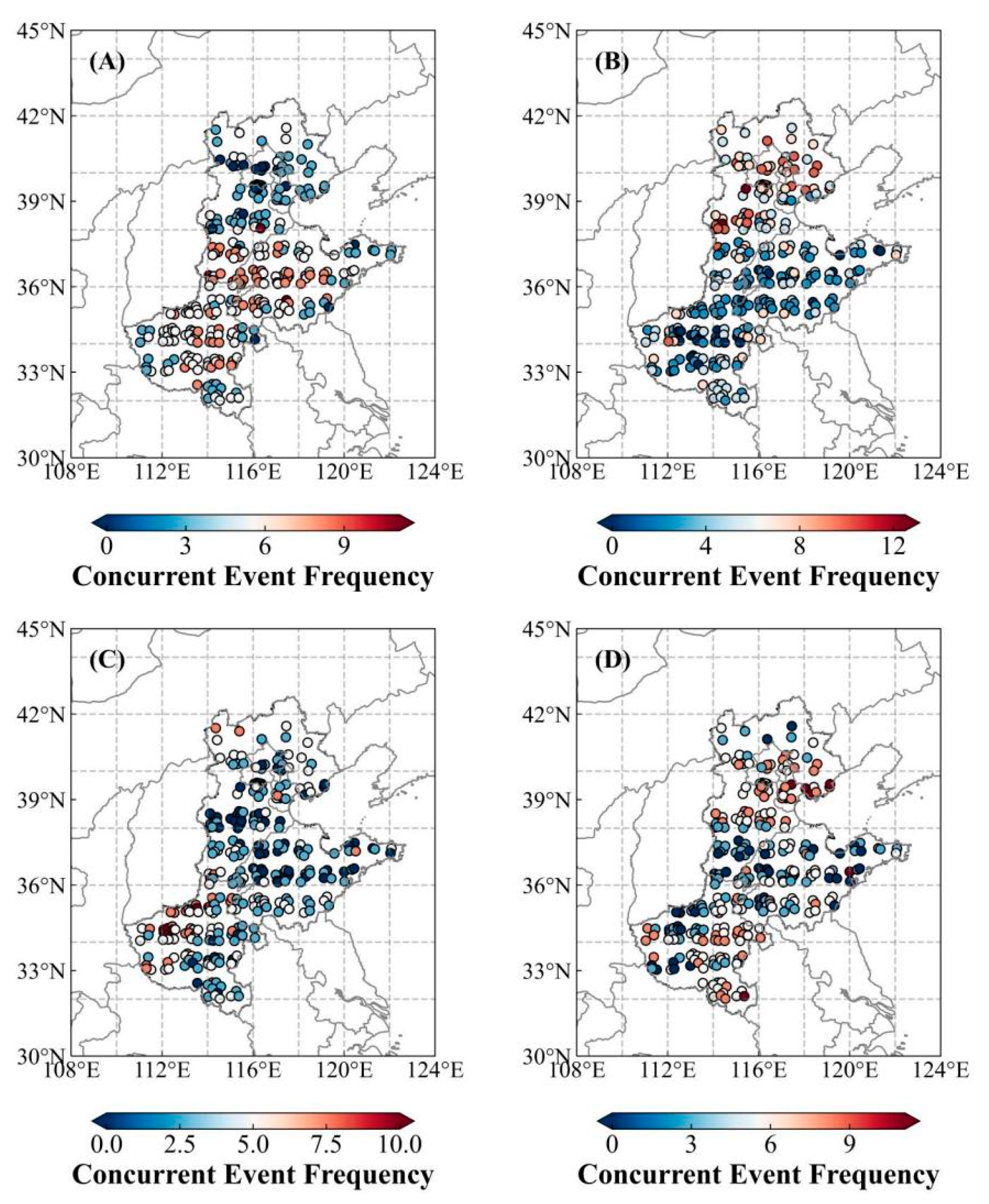
3.1.2. Sensitivity of Winter Wheat to High-Temperature–Drought Compound Events
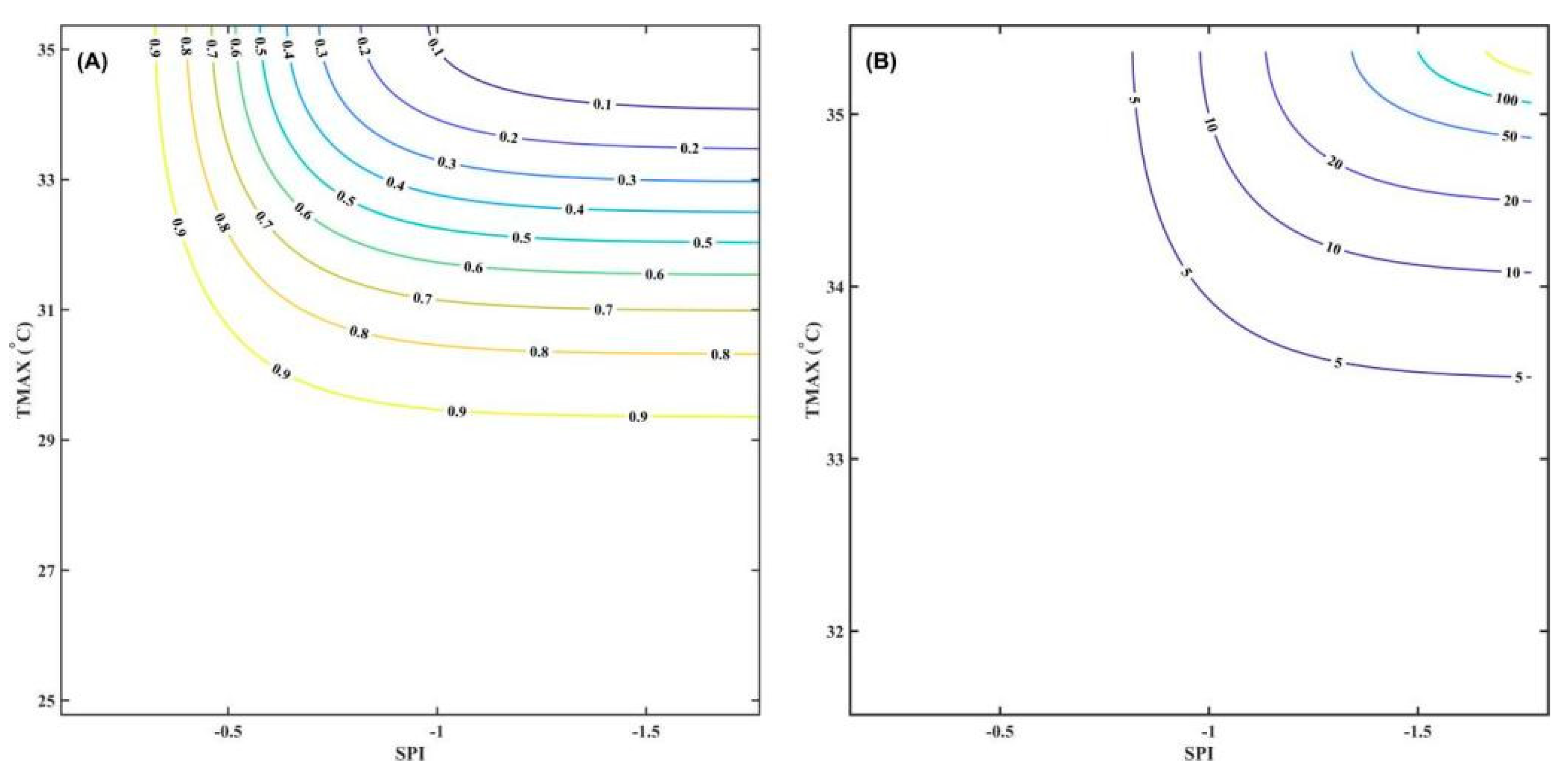
3.1.3. Copula Analysis of High-Temperature–Drought Compound Events
3.2. Response of Winter Wheat to Combined Low-Temperature–Drought Events
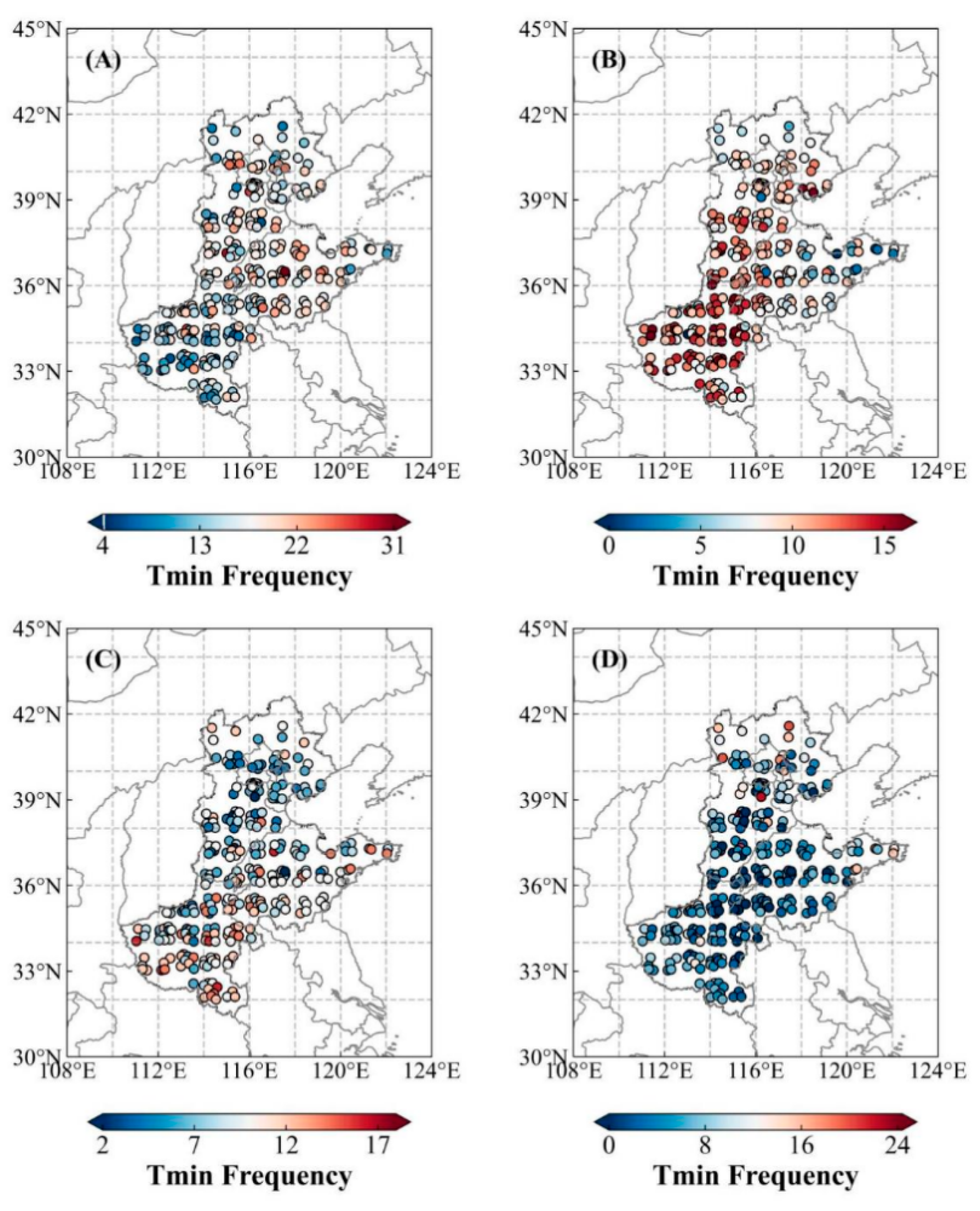
3.2.1. Spatiotemporal Distribution Characteristics of Low-Temperature–Drought Compound Events
3.2.2. Sensitivity of Winter Wheat to Low-Temperature–Drought Compound Events
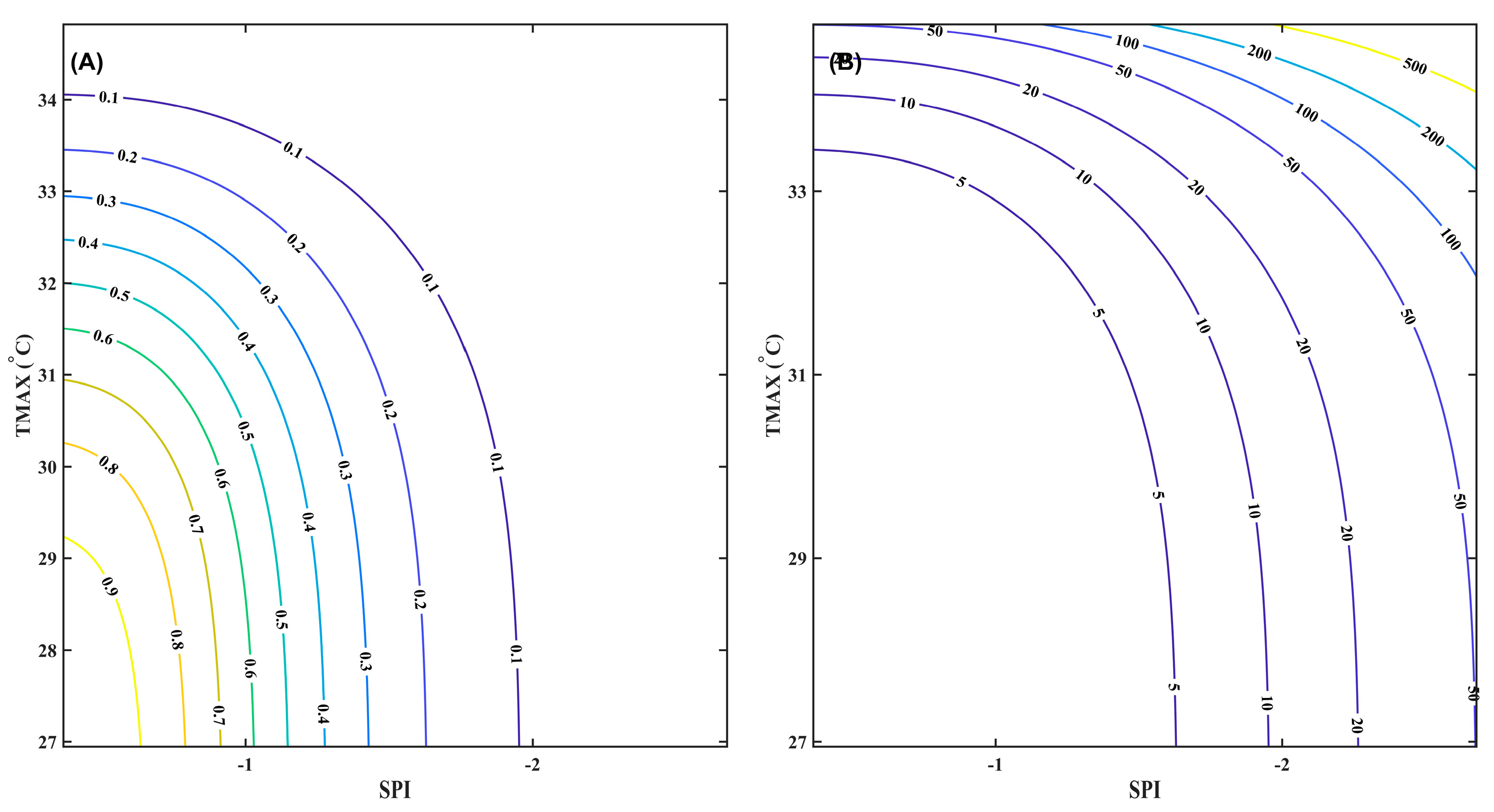
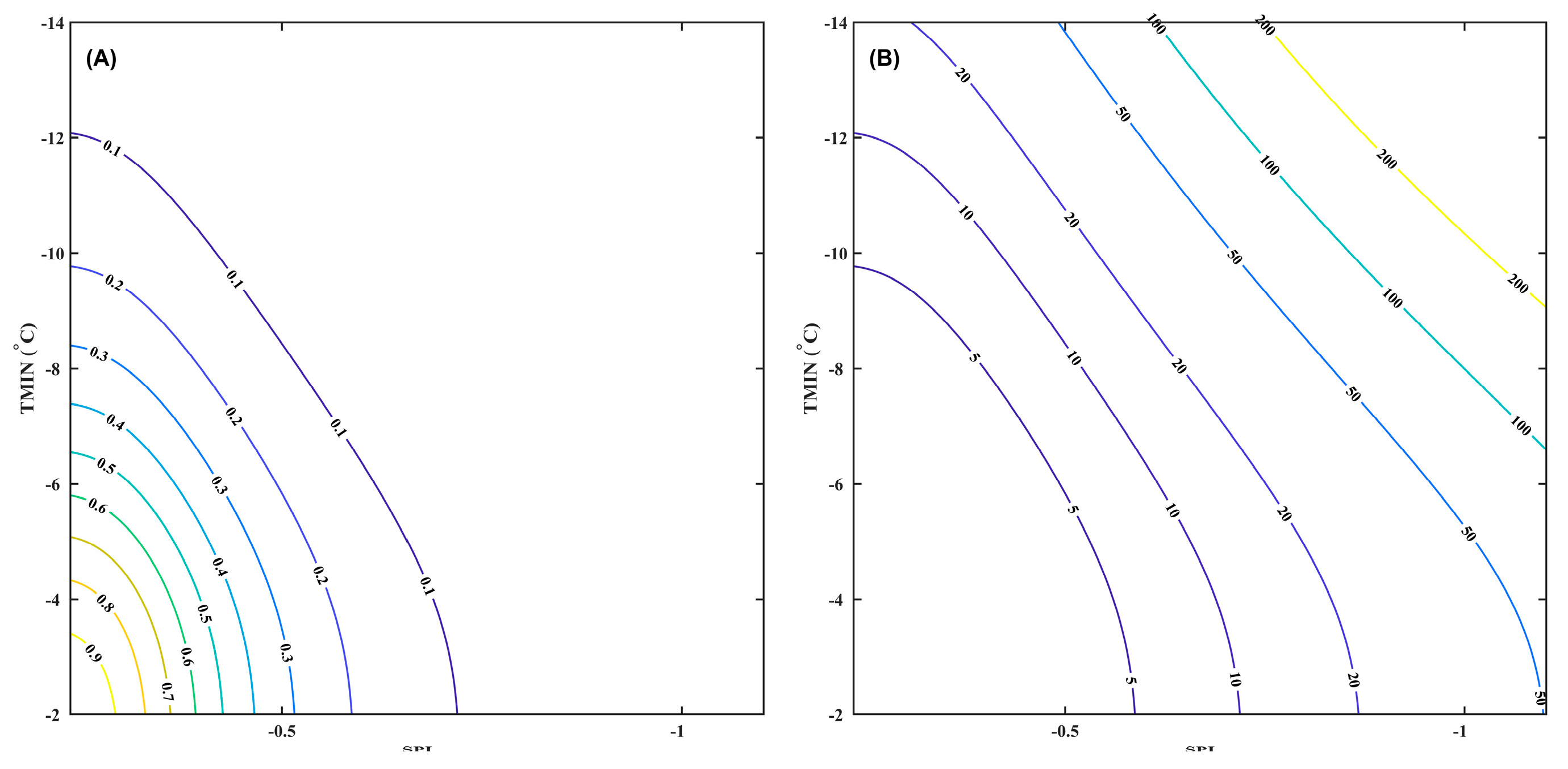
3.2.3. Copula Analysis of Low-Temperature–Drought Compound Events
4. Discussion
4.1. Impact of High-Temperature–Drought Compound Events
4.2. Impact of Low-Temperature–Drought Compound Events
4.3. Overall Impact of Climate Change on Winter Wheat Growth
4.4. Agricultural Adaptation Strategies
- (1)
- Develop water-saving projects and advanced irrigation technologies like drip and sprinkler irrigation. Promote drought-resistant crop varieties.
- (2)
- Conserve water in industrial and residential areas by optimizing processes and increasing public awareness.
- (3)
- Improve water conservancy projects, including reservoirs, irrigation channels, and rainwater collection systems. Enhance drought resistance management and scientific research.
- (4)
- Rationally allocate water resources, consider inter-basin transfers, and prioritize domestic and agricultural water use in scarce areas.
- (5)
- Maintain soil moisture by using mulch, such as straw or plastic film, to cover the soil surface and reduce evaporation. Deep tillage can also help maintain soil moisture by increasing soil porosity and enhancing the soil’s water retention capacity.
- (6)
- Plant drought-resistant crops; optimize planting schedules by adjusting planting and harvesting times based on climatic conditions to avoid crop growth during drought periods, thereby reducing water demand.
- (1)
- Improving time series analysis models: Future research will integrate deep learning models like CNN, RNN, and LSTM to better capture spatiotemporal changes in climate data and improve the accuracy of climate event analysis. Ensemble learning methods will enhance model robustness and stability, providing reliable tools for analyzing historical climate events and supporting agricultural adaptation strategies.
- (2)
- Expanding research areas and time frames: Future research will expand the study area to a national or global scope and extend the time frame to include more years of data. Integrating the latest meteorological and remote sensing data will improve the accuracy and comprehensiveness of the research, helping to identify long-term climate change trends and their impacts on agricultural production.
- (3)
- Comprehensive multi-factor analysis: Future research will include other climatic factors such as precipitation, wind speed, and humidity to assess their combined effects on winter wheat growth. Multivariate time series models will analyze the interactions among these factors, enabling more accurate predictions of winter wheat growth under varying climatic conditions.
5. Conclusions
- (1)
- Temporal and spatial distribution characteristics of high-temperature–drought compound events.
- (2)
- Sensitivity of winter wheat to high-temperature–drought compound events.
- (3)
- Recurrence period of combined heat–drought events.
- (4)
- Temporal and spatial distribution characteristics of low-temperature–drought compound events.
- (5)
- Sensitivity of winter wheat to low-temperature–drought compound events.
- (6)
- Recurrence period of low-temperature–drought compound events.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manning, C.; Widmann, M.; Bevacqua, E.; Van Loon, A.F.; Maraun, D.; Vrac, M. Increased probability of compound long-duration dry and hot events in Europe during summer (1950–2013). Environ. Res. Lett. 2019, 14, 094006. [Google Scholar] [CrossRef]
- Cook, B.I.; Mankin, J.S.; Anchukaitis, K.J. Climate Change and Drought: From Past to Future. Curr. Clim. Chang. Rep. 2018, 4, 164–179. [Google Scholar] [CrossRef]
- Bektaş, Y.; Sakarya, A. The Relationship between the Built Environment and Climate Change: The Case of Turkish Provinces. Sustainability 2023, 15, 1659. [Google Scholar] [CrossRef]
- Alonso, L.; Renard, F. A Comparative Study of the Physiological and Socio-Economic Vulnerabilities to Heat Waves of the Population of the Metropolis of Lyon (France) in a Climate Change Context. Int. J. Environ. Res. Public Health 2020, 17, 1004. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Zhai, P. More frequent and widespread persistent compound drought and heat event observed in China. Sci. Rep. 2020, 10, 14576. [Google Scholar] [CrossRef] [PubMed]
- Potopová, V.; Lhotka, O.; Možný, M.; Musiolková, M. Vulnerability of hop-yields due to compound drought and heat events over European key-hop regions. Int. J. Climatol. 2021, 41, E2136–E2158. [Google Scholar] [CrossRef]
- Han, H.; Jian, H.; Liu, M.; Lei, S.; Yao, S.; Yan, F. Impacts of drought and heat events on vegetative growth in a typical humid zone of the middle and lower reaches of the Yangtze River, China. J. Hydrol. 2023, 620, 129452. [Google Scholar] [CrossRef]
- Ye, L.; Shi, K.; Xin, Z.; Wang, C.; Zhang, C. Compound Droughts and Heat Waves in China. Sustainability 2019, 11, 3270. [Google Scholar] [CrossRef]
- Martius, O.; Pfahl, S.; Chevalier, C. A global quantification of compound precipitation and wind extremes. Geophys. Res. Lett. 2016, 43, 7709–7717. [Google Scholar] [CrossRef]
- Abdin, A.F.; Fang, Y.P.; Zio, E. A modeling and optimization framework for power systems design with operational flexibility and resilience against extreme heat waves and drought events. Renew. Sustain. Energy Rev. 2019, 112, 706–719. [Google Scholar] [CrossRef]
- Bezak, N.; Mikoš, M. Changes in the Compound Drought and Extreme Heat Occurrence in the 1961–2018 Period at the European Scale. Water 2020, 12, 3543. [Google Scholar] [CrossRef]
- Vogel, M.M.; Zscheischler, J.; Wartenburger, R.; Dee, D.; Seneviratne, S.I. Concurrent 2018 Hot Extremes Across Northern Hemisphere Due to Human-Induced Climate Change. Earth’s Future 2019, 7, 692–703. [Google Scholar] [CrossRef] [PubMed]
- Zscheischler, J.; Seneviratne, S.I. Dependence of drivers affects risks associated with compound events. Sci. Adv. 2017, 3, e1700263. [Google Scholar] [CrossRef] [PubMed]
- Bastos, A.; Ciais, P.; Friedlingstein, P.; Sitch, S.; Pongratz, J.; Fan, L.; Wigneron, J.P.; Weber, U.; Reichstein, M.; Fu, Z.; et al. Direct and seasonal legacy effects of the 2018 heat wave and drought on European ecosystem productivity. Sci. Adv. 2020, 6, eaba2724. [Google Scholar] [CrossRef] [PubMed]
- Alizadeh, M.R.; Adamowski, J.; Nikoo, M.R.; AghaKouchak, A.; Dennison, P.; Sadegh, M. A century of observations reveals increasing likelihood of continental-scale compound dry-hot extremes. Sci. Adv. 2020, 6, eaaz4571. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Zhai, P. Changes in compound drought and hot extreme events in summer over populated eastern China. Weather Clim. Extrem. 2020, 30, 100295. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Riahi, K.; Moss, R.; Edmonds, J.; Thomson, A.; Nakicenovic, N.; Kram, T.; Berkhout, F.; Swart, R.; Janetos, A.; et al. A proposal for a new scenario framework to support research and assessment in different climate research communities. Glob. Environ. Chang. 2012, 22, 21–35. [Google Scholar] [CrossRef]
- Mazdiyasni, O.; AghaKouchak, A. Substantial increase in concurrent droughts and heatwaves in the United States. Proc. Natl. Acad. Sci. USA 2015, 112, 11484–11489. [Google Scholar] [CrossRef] [PubMed]
- Russo, A.; Gouveia, C.M.; Dutra, E.; Soares, P.M.M.; Trigo, R.M. The synergy between drought and extremely hot summers in the Mediterranean. Environ. Res. Lett. 2019, 14, 014011. [Google Scholar] [CrossRef]
- Sharma, S.; Mujumdar, P. Increasing frequency and spatial extent of concurrent meteorological droughts and heatwaves in India. Sci. Rep. 2017, 7, 15582. [Google Scholar] [CrossRef]
- Lu, Y.; Hu, H.; Li, C.; Tian, F. Increasing compound events of extreme hot and dry days during growing seasons of wheat and maize in China. Sci Rep 2018, 8, 16700. [Google Scholar] [CrossRef] [PubMed]
- Dosio, A.; Mentaschi, L.; Fischer, E.; Wyser, K. Extreme heat waves under 1.5 °C and 2 °C global warming. Environ. Res. Lett. 2018, 13, 054006. [Google Scholar] [CrossRef]
- Gasparrini, A.; Guo, Y.; Sera, F.; Vicedo-Cabrera, A.M.; Huber, V.; Tong, S.; de Sousa Zanotti Stagliorio Coelho, M.; Nascimento Saldiva, P.H.; Lavigne, E.; Matus Correa, P.; et al. Projections of temperature-related excess mortality under climate change scenarios. Lancet Planet. Health 2017, 1, e360–e367. [Google Scholar] [CrossRef] [PubMed]
- Zscheischler, J.; Westra, S.; van den Hurk, B.J.J.M.; Seneviratne, S.I.; Ward, P.J.; Pitman, A.; AghaKouchak, A.; Bresch, D.N.; Leonard, M.; Wahl, T.; et al. Future climate risk from compound events. Nat. Clim. Chang. 2018, 8, 469–477. [Google Scholar] [CrossRef]
- Zscheischler, J.; Martius, O.; Westra, S.; Bevacqua, E.; Raymond, C.; Horton, R.M.; van den Hurk, B.; AghaKouchak, A.; Jézéquel, A.; Mahecha, M.D.; et al. A typology of compound weather and climate events. Nat. Rev. Earth Environ. 2020, 1, 333–347. [Google Scholar] [CrossRef]
- Bevacqua, E.; Maraun, D.; Hobæk Haff, I.; Widmann, M.; Vrac, M. Multivariate statistical modelling of compound events via pair-copula constructions: Analysis of floods in Ravenna (Italy). Hydrol. Earth Syst. Sci. 2017, 21, 2701–2723. [Google Scholar] [CrossRef]
- Leonard, M.; Westra, S.; Phatak, A.; Lambert, M.; van den Hurk, B.; McInnes, K.; Risbey, J.; Schuster, S.; Jakob, D.; Stafford-Smith, M. A compound event framework for understanding extreme impacts. WIREs Clim. Chang. 2014, 5, 113–128. [Google Scholar] [CrossRef]
- Mohammed, S.; Alsafadi, K.; Enaruvbe, G.O.; Bashir, B.; Elbeltagi, A.; Széles, A.; Alsalman, A.; Harsanyi, E. Assessing the impacts of agricultural drought (SPI/SPEI) on maize and wheat yields across Hungary. Sci. Rep. 2022, 12, 8838. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Yang, C.; Yang, Q.; Wang, J. Spatiotemporal drought analysis by the standardized precipitation index (SPI) and standardized precipitation evapotranspiration index (SPEI) in Sichuan Province, China. Sci. Rep. 2021, 11, 1280. [Google Scholar] [CrossRef]
- Wang, Q.; Zeng, J.; Qi, J.; Zhang, X.; Zeng, Y.; Shui, W.; Xu, Z.; Zhang, R.; Wu, X.; Cong, J. A multi-scale daily SPEI dataset for drought characterization at observation stations over mainland China from 1961 to 2018. Earth Syst. Sci. Data 2021, 13, 331–341. [Google Scholar] [CrossRef]
- Pei, Z.; Fang, S.; Wang, L.; Yang, W. Comparative Analysis of Drought Indicated by the SPI and SPEI at Various Timescales in Inner Mongolia, China. Water 2020, 12, 1925. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y.; Zhang, C.; Hui, G.; Hou, Y. Historical and future Palmer Drought Severity Index with improved hydrological modeling. J. Hydrol. 2022, 610, 127941. [Google Scholar] [CrossRef]
- Chen, L.; Chen, X.; Cheng, L.; Zhou, P.; Liu, Z. Compound hot droughts over China: Identification, risk patterns and variations. Atmos. Res. 2019, 227, 210–219. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.; Zhang, X. Quantifying the relationship between compound dry and hot events and El Niño–Southern Oscillation (ENSO) at the global scale. J. Hydrol. 2018, 567, 332–338. [Google Scholar] [CrossRef]
- Olmo, M.; Bettolli, M.L.; Rusticucci, M. Atmospheric circulation influence on temperature and precipitation individual and compound daily extreme events: Spatial variability and trends over southern South America. Weather Clim. Extrem. 2020, 29, 100267. [Google Scholar] [CrossRef]
- Geirinhas, J.L.; Russo, A.; Libonati, R.; Sousa, P.M.; Miralles, D.G.; Trigo, R.M. Recent increasing frequency of compound summer drought and heatwaves in Southeast Brazil. Environ. Res. Lett. 2021, 16, 034036. [Google Scholar] [CrossRef]
- Li, K.; Wang, M.; Liu, K. The Study on Compound Drought and Heatwave Events in China Using Complex Networks. Sustainability 2021, 13, 12774. [Google Scholar] [CrossRef]
- Muthuvel, D.; Mahesha, A. Spatiotemporal Analysis of Compound Agrometeorological Drought and Hot Events in India Using a Standardized Index. J. Hydrol. Eng. 2021, 26, 04021022. [Google Scholar] [CrossRef]
- Kang, Y.; Guo, E.; Wang, Y.; Bao, Y.; Bao, Y.; Mandula, N.; Runa, A.; Gu, X.; Jin, L. Characterisation of compound dry and hot events in Inner Mongolia and their relationship with large-scale circulation patterns. J. Hydrol. 2022, 612, 128296. [Google Scholar] [CrossRef]
- Wu, X.; Hao, Z.; Hao, F.; Singh, V.P.; Zhang, X. Dry-hot magnitude index: A joint indicator for compound event analysis. Environ. Res. Lett. 2019, 14, 064017. [Google Scholar] [CrossRef]
- Wu, X.; Hao, Z.; Zhang, X.; Li, C.; Hao, F. Evaluation of severity changes of compound dry and hot events in China based on a multivariate multi-index approach. J. Hydrol. 2020, 583, 124580. [Google Scholar] [CrossRef]
- Wu, X.; Hao, Z.; Hao, F.; Zhang, X. Variations of compound precipitation and temperature extremes in China during 1961–2014. Sci. Total Environ. 2019, 663, 731–737. [Google Scholar] [CrossRef] [PubMed]
- Miralles, D.G.; Gentine, P.; Seneviratne, S.I.; Teuling, A.J. Land-atmospheric feedbacks during droughts and heatwaves: State of the science and current challenges. Ann. N. Y. Acad. Sci. 2019, 1436, 19–35. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Jin, Y.; Singh, B.; Yan, X. Evolving Land–Atmosphere Interactions over North America from CMIP5 Simulations. J. Clim. 2013, 26, 7313–7327. [Google Scholar] [CrossRef]
- van den Hurk, B.; van Meijgaard, E.; de Valk, P.; van Heeringen, K.-J.; Gooijer, J. Analysis of a compounding surge and precipitation event in the Netherlands. Environ. Res. Lett. 2015, 10, 035001. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Hao, F. Compound Extremes in Hydroclimatology: A Review. Water 2018, 10, 718. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Y.; Park Williams, A.; Gentine, P. Projected increases in intensity, frequency, and terrestrial carbon costs of compound drought and aridity events. Sci. Adv. 2019, 5, eaau5740. [Google Scholar] [CrossRef] [PubMed]
- Miao, C.; Qiaohong, S.; Duan, Q.; Wang, Y. Joint analysis of changes in temperature and precipitation on the Loess Plateau during the period 1961–2011. Clim. Dyn. 2016, 47, 3221–3234. [Google Scholar] [CrossRef]
- Leng, G.; Tang, Q.; Huang, S.; Zhang, X.; Cao, J. Assessments of joint hydrological extreme risks in a warming climate in China. Int. J. Climatol. 2016, 36, 1632–1642. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections. J. Geophys. Res. Atmos. 2013, 118, 2473–2493. [Google Scholar] [CrossRef]
- Gallant, A.J.E.; Karoly, D.J.; Gleason, K.L. Consistent Trends in a Modified Climate Extremes Index in the United States, Europe, and Australia. J. Clim. 2014, 27, 1379–1394. [Google Scholar] [CrossRef]
- Ford, T.W.; Quiring, S.M. In situ soil moisture coupled with extreme temperatures: A study based on the Oklahoma Mesonet. Geophys. Res. Lett. 2014, 41, 4727–4734. [Google Scholar] [CrossRef]
- Hao, Z.; Hao, F.; Singh, V.P.; Ouyang, W.; Zhang, X.; Zhang, S. A joint extreme index for compound droughts and hot extremes. Theor. Appl. Climatol. 2020, 142, 321–328. [Google Scholar] [CrossRef]
- Ribeiro, A.F.S.; Russo, A.; Gouveia, C.M.; Pires, C.A.L. Drought-related hot summers: A joint probability analysis in the Iberian Peninsula. Weather Clim. Extrem. 2020, 30, 100279. [Google Scholar] [CrossRef]
- Feng, S.; Hao, Z.; Zhang, X.; Hao, F. Probabilistic evaluation of the impact of compound dry-hot events on global maize yields. Sci. Total Environ. 2019, 689, 1228–1234. [Google Scholar] [CrossRef] [PubMed]
- Batibeniz, F.; Ashfaq, M.; Diffenbaugh, N.S.; Key, K.; Evans, K.J.; Turuncoglu, U.U.; Önol, B. Doubling of U.S. Population Exposure to Climate Extremes by 2050. Earth’s Future 2020, 8, e2019EF001421. [Google Scholar] [CrossRef]
- Lavaysse, C.; Naumann, G.; Alfieri, L.; Salamon, P.; Vogt, J. Predictability of the European heat and cold waves. Clim. Dyn. 2019, 52, 2481–2495. [Google Scholar] [CrossRef]
- Sutanto, S.J.; Vitolo, C.; Di Napoli, C.; D’Andrea, M.; Van Lanen, H.A.J. Heatwaves, droughts, and fires: Exploring compound and cascading dry hazards at the pan-European scale. Environ. Int. 2020, 134, 105276. [Google Scholar] [CrossRef]
- Carmona, R.; Díaz, J.; Mirón, I.J.; Ortíz, C.; León, I.; Linares, C. Geographical variation in relative risks associated with cold waves in Spain: The need for a cold wave prevention plan. Environ. Int. 2016, 88, 103–111. [Google Scholar] [CrossRef]
- Smith, E.T.; Sheridan, S.C. The influence of extreme cold events on mortality in the United States. Sci. Total Environ. 2019, 647, 342–351. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Hansen, A.; Varghese, B.; Liu, Z.; Tong, M.; Qiu, H.; Tian, L.; Lau, K.K.-L.; Ng, E.; Ren, C.; et al. Cause-specific mortality attributable to cold and hot ambient temperatures in Hong Kong: A time-series study, 2006–2016. Sustain. Cities Soc. 2020, 57, 102131. [Google Scholar] [CrossRef]
- Qian, C.; Wang, J.; Dong, S.; Yin, H.; Burke, C.; Ciavarella, A.; Dong, B.; Freychet, N.; Lott, F.C.; Tett, S.F.B. Human Influence on the Record-breaking Cold Event in January of 2016 in Eastern China. Bull. Am. Meteorol. Soc. 2018, 99, S118–S122. [Google Scholar] [CrossRef]
- Sutanto, S.J.; van der Weert, M.; Wanders, N.; Blauhut, V.; Van Lanen, H.A.J. Moving from drought hazard to impact forecasts. Nat. Commun. 2019, 10, 4945. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Qiao, W.; Wang, Y.; Cao, S.; Zhang, Y. Urban drought vulnerability assessment—A framework to integrate socio-economic, physical, and policy index in a vulnerability contribution analysis. Sustain. Cities Soc. 2020, 54, 102004. [Google Scholar] [CrossRef]
- Piticar, A.; Croitoru, A.-E.; Ciupertea, F.-A.; Harpa, G.-V. Recent changes in heat waves and cold waves detected based on excess heat factor and excess cold factor in Romania. Int. J. Climatol. 2018, 38, 1777–1793. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, Z.; Zhang, S.; Rötter, R.P. Heat stress impacts on wheat growth and yield were reduced in the Huang-Huai-Hai Plain of China in the past three decades. Eur. J. Agron. 2015, 71, 44–52. [Google Scholar] [CrossRef]
- Liu, B.; Liu, L.; Tian, L.; Cao, W.; Zhu, Y.; Asseng, S. Post-heading heat stress and yield impact in winter wheat of China. Glob. Change Biol. 2014, 20, 372–381. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Liu, L.; Asseng, S.; Xia, Y.; Tang, L.; Liu, B.; Cao, W.; Zhu, Y. Estimating spring frost and its impact on yield across winter wheat in China. Agric. For. Meteorol. 2018, 260–261, 154–164. [Google Scholar] [CrossRef]
- Chen, Y.; Donohue, R.J.; McVicar, T.R.; Waldner, F.; Mata, G.; Ota, N.; Houshmandfar, A.; Dayal, K.; Lawes, R.A. Nationwide crop yield estimation based on photosynthesis and meteorological stress indices. Agric. For. Meteorol. 2020, 284, 107872. [Google Scholar] [CrossRef]
- Li, F.; Chen, J.; Zheng, J. Joint forcing of climate warming and ENSO on a dual-cropping system. Agric. For. Meteorol. 2019, 269–270, 10–18. [Google Scholar] [CrossRef]
- Ren, S.; Guo, B.; Wu, X.; Zhang, L.; Ji, M.; Wang, J. Winter wheat planted area monitoring and yield modeling using MODIS data in the Huang-Huai-Hai Plain, China. Comput. Electron. Agric. 2021, 182, 106049. [Google Scholar] [CrossRef]
- Zheng, X.; Yu, Z.; Yu, F.; Shi, Y. Grain-filling characteristics and yield formation of wheat in two different soil fertility fields in the Huang–Huai–Hai Plain. Front. Plant Sci. 2022, 13, 932821. [Google Scholar] [CrossRef] [PubMed]
- Yue, Y.; Yang, W.; Wang, L. Assessment of drought risk for winter wheat on the Huanghuaihai Plain under climate change using an EPIC model-based approach. Int. J. Digit. Earth 2022, 15, 690–711. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, G.; Ali, S.; Wang, X.; Wang, G.; Pan, Z.; Zhang, J. SPI-based drought simulation and prediction using ARMA-GARCH model. Appl. Math. Comput. 2019, 355, 96–107. [Google Scholar] [CrossRef]
- Tao, Y.; Huang, W.; Gan, W.; Shen, H. Research on Ndvi Normalization Method Based on Gf Images. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 3, 209–215. [Google Scholar] [CrossRef]
- Rüschendorf, L. Copulas, Sklar’s Theorem, and Distributional Transform. In Mathematical Risk Analysis: Dependence, Risk Bounds, Optimal Allocations and Portfolios; Rüschendorf, L., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3–34. [Google Scholar] [CrossRef]
- Li, H.; Xiong, L.; Jiang, X. Differentially Private Synthesization of Multi-Dimensional Data using Copula Functions. Adv. Database Technol. 2014, 2014, 475–486. [Google Scholar]
- Al-babtain, A.; Elbatal, I.; Yousof, H.M. A New Flexible Three-Parameter Model: Properties, Clayton Copula, and Modeling Real Data. Symmetry 2020, 12, 440. [Google Scholar] [CrossRef]
- Chen, J.; Mao, C.; Liu, Z.; Ma, C.; Sha, G.; Duan, Q.; Fan, H.; Qiu, S.; Wang, D. Stochastic planning of integrated energy system based on correlation scenario generation method via Copula function considering multiple uncertainties in renewable energy sources and demands. IET Renew. Power Gener. 2023, 17, 2978–2996. [Google Scholar] [CrossRef]
- Solea, E.; Li, B. Copula Gaussian Graphical Models for Functional Data. J. Am. Stat. Assoc. 2022, 117, 781–793. [Google Scholar] [CrossRef]
- Ota, S.; Kimura, M. Effective estimation algorithm for parameters of multivariate Farlie–Gumbel–Morgenstern copula. Jpn. J. Stat. Data Sci. 2021, 4, 1049–1078. [Google Scholar] [CrossRef]
- Zhang, W.; He, X.; Hamori, S. Volatility spillover and investment strategies among sustainability-related financial indexes: Evidence from the DCC-GARCH-based dynamic connectedness and DCC-GARCH t-copula approach. Int. Rev. Financ. Anal. 2022, 83, 102223. [Google Scholar] [CrossRef]
- Da Rocha Júnior, R.L.; dos Santos Silva, F.D.; Costa, R.L.; Gomes, H.B.; Pinto, D.D.; Herdies, D.L. Bivariate Assessment of Drought Return Periods and Frequency in Brazilian Northeast Using Joint Distribution by Copula Method. Geosciences 2020, 10, 135. [Google Scholar] [CrossRef]
- Poonia, V.; Jha, S.; Goyal, M.K. Copula based analysis of meteorological, hydrological and agricultural drought characteristics across Indian river basins. Int. J. Climatol. 2021, 41, 4637–4652. [Google Scholar] [CrossRef]
- Nabaei, S.; Sharafati, A.; Yaseen, Z.M.; Shahid, S. Copula based assessment of meteorological drought characteristics: Regional investigation of Iran. Agric. For. Meteorol. 2019, 276–277, 107611. [Google Scholar] [CrossRef]
- Shiau, J. Fitting Drought Duration and Severity with Two-Dimensional Copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Y.; Zhang, K.; Hu, M.; Weng, Q.; Zhang, H. Spatial heterogeneity modeling of water quality based on random forest regression and model interpretation. Environ. Res. 2021, 202, 111660. [Google Scholar] [CrossRef]
- Mukherjee, S.; Mishra, A.; Trenberth, K.E. Climate Change and Drought: A Perspective on Drought Indices. Curr. Clim. Chang. Rep. 2018, 4, 145–163. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, Q.; Sun, P.; Song, C. Impact of Droughts on Winter Wheat Yield in Different Growth Stages during 2001–2016 in Eastern China. Int. J. Disaster Risk Sci. 2018, 9, 376–391. [Google Scholar] [CrossRef]
- Asseng, S.; Foster, I.A.N.; Turner, N.C. The impact of temperature variability on wheat yields. Glob. Chang. Biol. 2011, 17, 997–1012. [Google Scholar] [CrossRef]
- Gu, L.; Chen, J.; Yin, J.; Xu, C.-Y.; Zhou, J. Responses of Precipitation and Runoff to Climate Warming and Implications for Future Drought Changes in China. Earth’s Future 2020, 8, e2020EF001718. [Google Scholar] [CrossRef]
- Sun, D.; Kafatos, M. Note on the NDVI-LST relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Luo, H.; Wang, L.; Fang, J.; Li, Y.; Li, H.; Dai, S. NDVI, Temperature and Precipitation Variables and Their Relationships in Hainan Island from 2001 to 2014 Based on MODIS NDVI. In Geo-Informatics in Resource Management and Sustainable Ecosystem: Proceedings of the Third International Conference, GRMSE 2015, Wuhan, China, 16–18 October 2015; Springer: Berlin/Heidelberg, Germany, 2016; pp. 336–344. [Google Scholar]
- Ichii, K.; Kawabata, A.; Yamaguchi, Y. Global correlation analysis for NDVI and climatic variables and NDVI trends: 1982–1990. Int. J. Remote Sens. 2002, 23, 3873–3878. [Google Scholar] [CrossRef]
- Humphrey, V.; Berg, A.; Ciais, P.; Gentine, P.; Jung, M.; Reichstein, M.; Seneviratne, S.I.; Frankenberg, C. Soil moisture–atmosphere feedback dominates land carbon uptake variability. Nature 2021, 592, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Keim, D.L.; Kronstad, W.E. Drought Response of Winter Wheat Cultivars Grown under Field Stress Conditions. Crop Sci. 1981, 21, 11–15. [Google Scholar] [CrossRef]
- Prasad, P.V.V.; Pisipati, S.R.; Ristic, Z.; Bukovnik, U.; Fritz, A.K. Impact of Nighttime Temperature on Physiology and Growth of Spring Wheat. Crop Sci. 2008, 48, 2372–2380. [Google Scholar] [CrossRef]
- Dore, M.H.I. Climate change and changes in global precipitation patterns: What do we know? Environ. Int. 2005, 31, 1167–1181. [Google Scholar] [CrossRef]
- Mishra, A.K. Quantifying the impact of global warming on precipitation patterns in India. Meteorol. Appl. 2019, 26, 153–160. [Google Scholar] [CrossRef]
- Lhotka, O.; Trnka, M.; Kyselý, J.; Markonis, Y.; Balek, J.; Možný, M. Atmospheric Circulation as a Factor Contributing to Increasing Drought Severity in Central Europe. J. Geophys. Res. Atmos. 2020, 125, e2019JD032269. [Google Scholar] [CrossRef]
- Manzano, A.; Clemente, M.A.; Morata, A.; Luna, M.Y.; Beguería, S.; Vicente-Serrano, S.M.; Martín, M.L. Analysis of the atmospheric circulation pattern effects over SPEI drought index in Spain. Atmos. Res. 2019, 230, 104630. [Google Scholar] [CrossRef]
- Zipper, S.C.; Keune, J.; Kollet, S.J. Land use change impacts on European heat and drought: Remote land-atmosphere feedbacks mitigated locally by shallow groundwater. Environ. Res. Lett. 2019, 14, 044012. [Google Scholar] [CrossRef]
- Hao, H.; Yang, M.; Wang, H.; Dong, N. Human activities reshape the drought regime in the Yangtze River Basin: A land surface-hydrological modelling analysis with representations of dam operation and human water use. Nat. Hazards 2023, 118, 2097–2121. [Google Scholar] [CrossRef]
- Wang, W.; Li, J.; Qu, H.; Xing, W.; Zhou, C.; Tu, Y.; He, Z. Spatial and Temporal Drought Characteristics in the Huanghuaihai Plain and Its Influence on Cropland Water Use Efficiency. Remote Sens. 2022, 14, 2381. [Google Scholar] [CrossRef]
- Wani, S.H.; Khan, H.; Riaz, A.; Joshi, D.C.; Hussain, W.; Rana, M.; Kumar, A.; Athiyannan, N.; Singh, D.; Ali, N.; et al. Chapter Six—Genetic diversity for developing climate-resilient wheats to achieve food security goals. Adv. Agron. 2022, 171, 255–303. [Google Scholar]

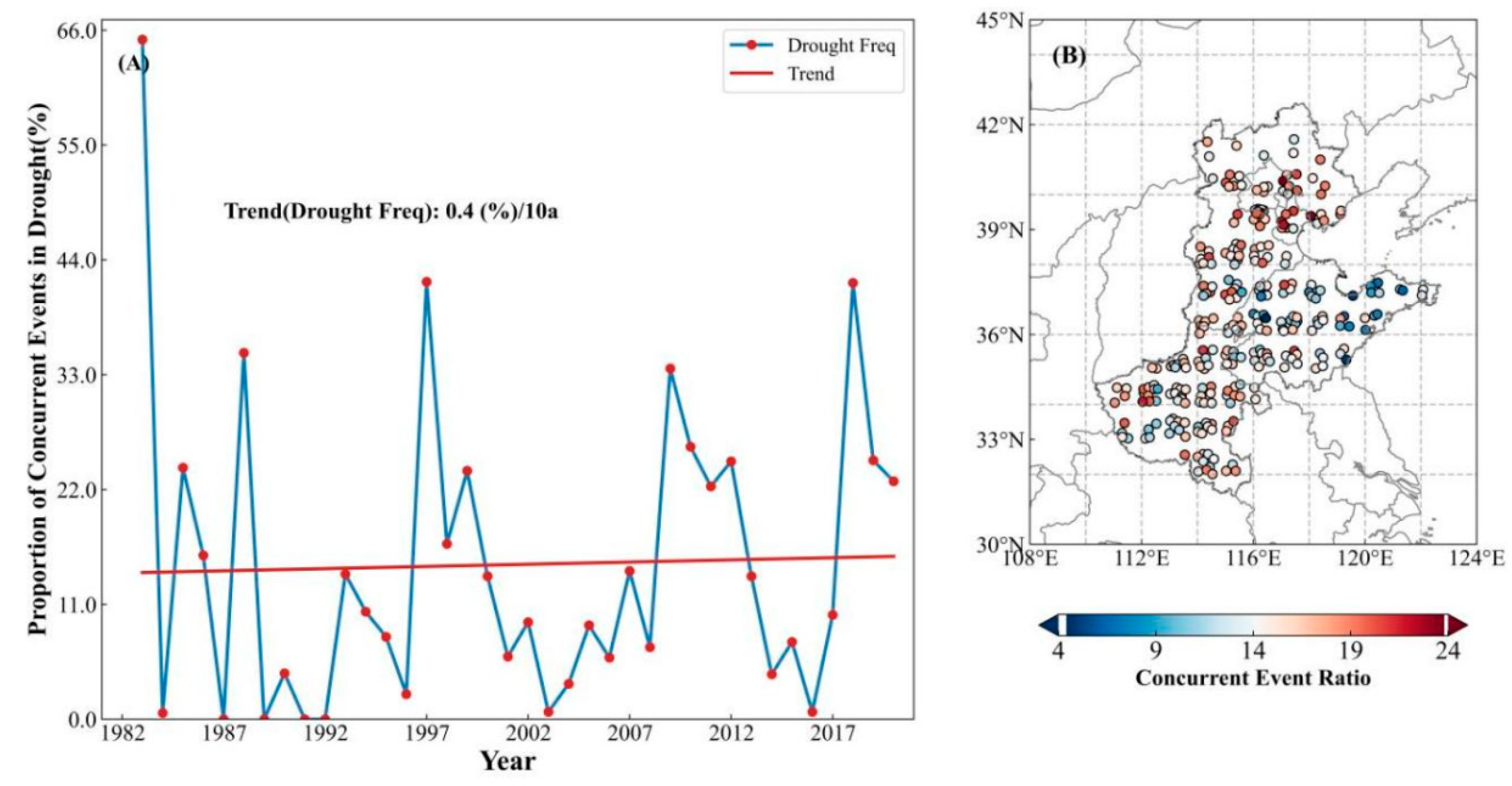
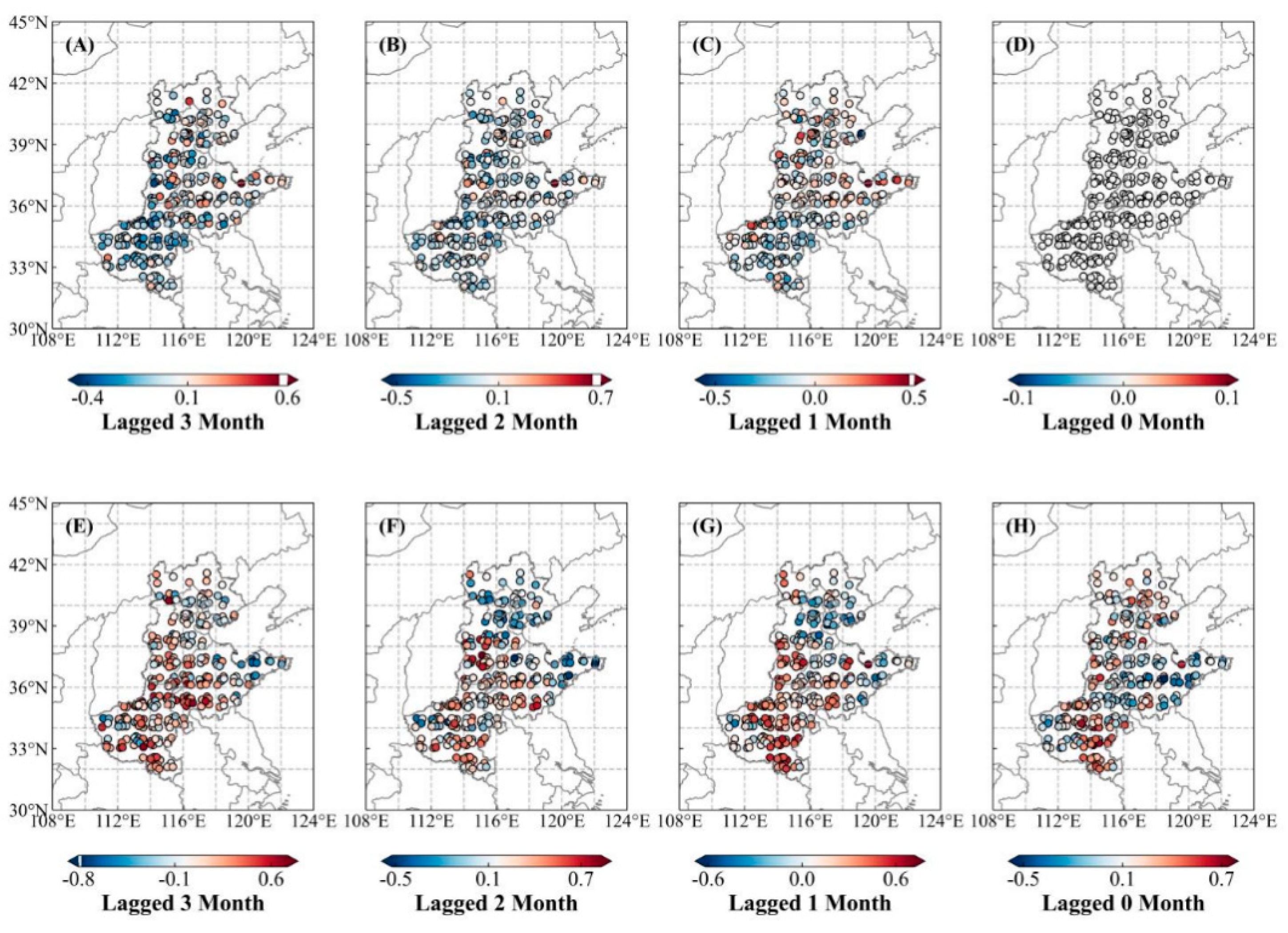
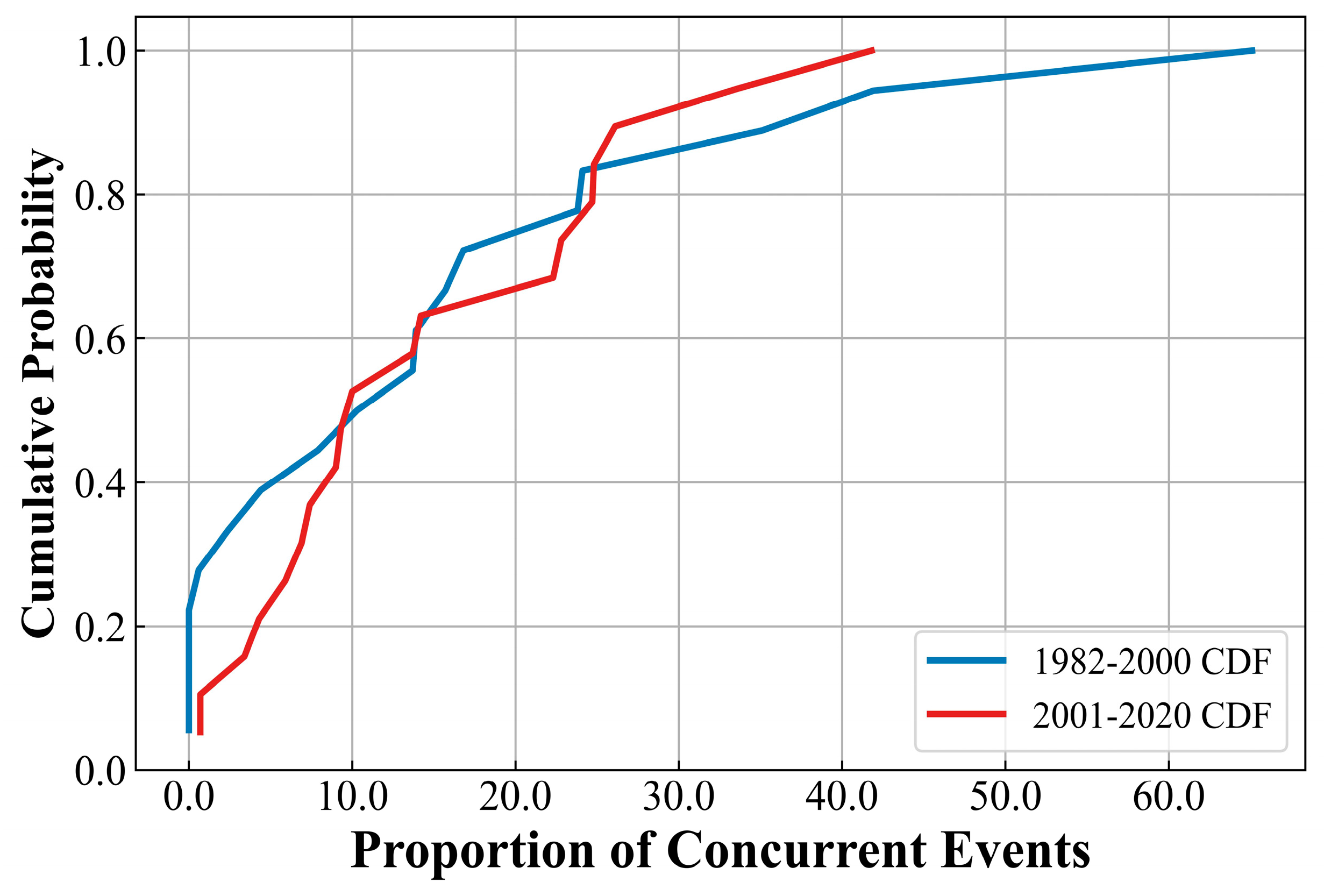
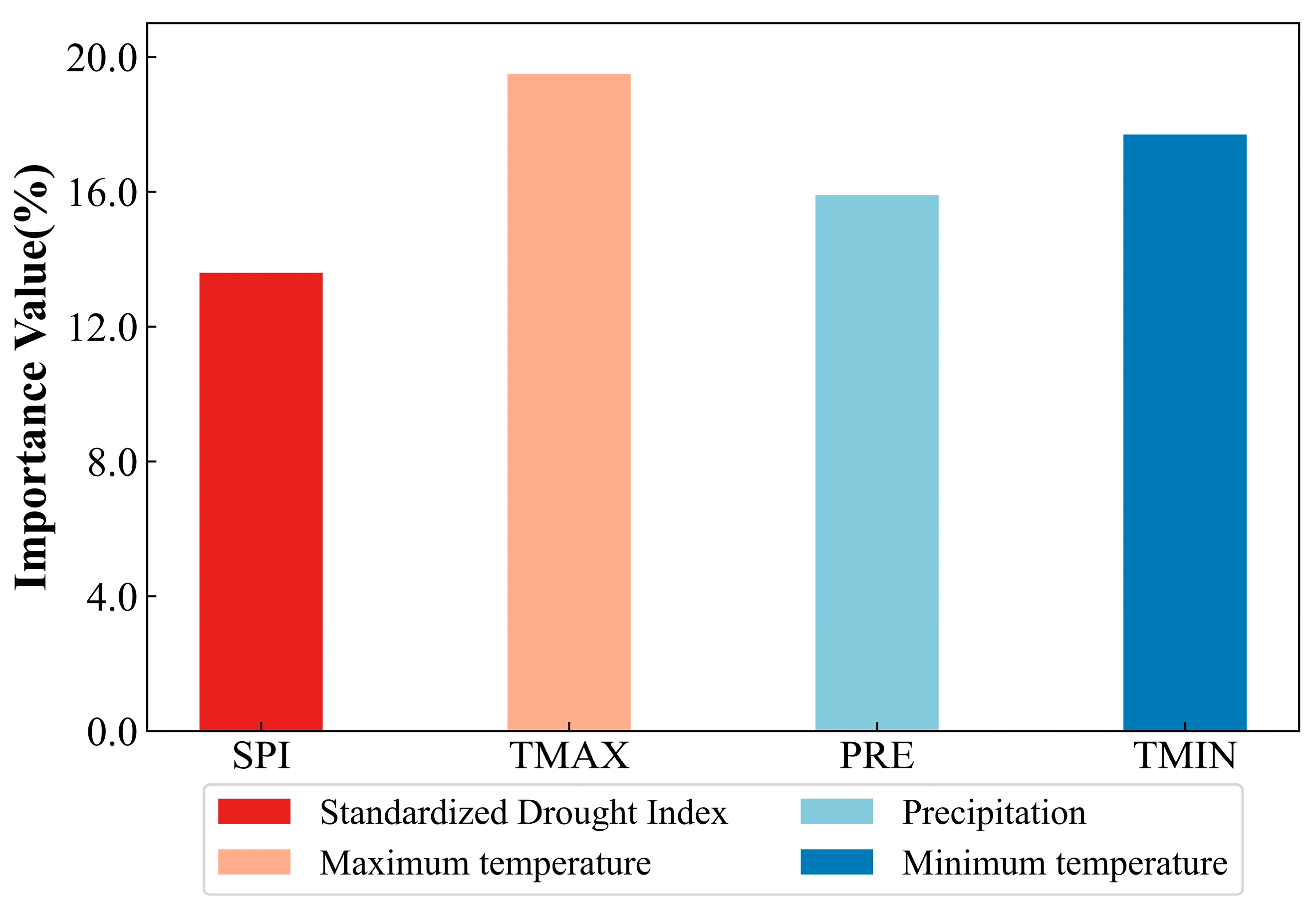




| Stage | Method | Reason for Using this Method |
|---|---|---|
| Data Processing | SPI Method | The Standardized Precipitation Index (SPI) was chosen as the indicator for drought identification and monitoring, based on the climatic characteristics of the region and data availability. Its flexible time scales allow it to accommodate various research needs, and its simple calculation makes it well suited for the 3H Plain. |
| MVC Method | The maximum-value composite (MVC) method was used to generate annual, seasonal, and monthly NDVI values, eliminating the effects of clouds and solar zenith angle, and thereby improving image quality. | |
| Copula Method | The copula function model was used to create a multidimensional joint distribution. By utilizing marginal distributions and correlation structures, commonly used copula functions were selected for correlation modeling. | |
| Random Forest Method | The random forest method was used to analyze the sensitivity changes of vegetation (NDVI) to drought and extreme temperatures across multiple time scales, providing high classification accuracy and processing efficiency. | |
| Data Analysis | Definition of Single Extreme Events | Based on research advancements both domestically and internationally, and considering the drought and climatic characteristics of the 3H Plain, single extreme events were defined. |
| Definition of Extreme Temperature–Drought Events | Composite events were identified based on the conditions of high temperature and drought or low temperature and drought, and their impacts on winter wheat growth were interpreted. |
| Drought Index | Drought Level | ||||
|---|---|---|---|---|---|
| No Drought | Light Drought | Moderate Drought | Severe Drought | Extreme Drought | |
| SPI (dimensionless) | |||||
| Copula Function Name | Mathematical Description |
|---|---|
| Clayton | |
| Frank | |
| Gaussian | |
| Gumbel | |
| t |
| Factors Name | Kendall | Spearman | Pearson | |||
|---|---|---|---|---|---|---|
| r | p Value | r | p Value | r | p Value | |
| 3H Plain_SPI_TMAX | 0.301 | 0.053 | 0.400 | 0.056 | 0.383 | 0.082 |
| Cop_Family | AIC | BIC | RMSE |
|---|---|---|---|
| Gaussian | 14.67 | 20.19 | 0.202 |
| t | 16.67 | 27.71 | 0.199 |
| Clayton | 14.63 | 20.15 | 0.180 |
| Frank | 14.67 | 20.19 | 0.198 |
| Gumbel | 14.70 | 20.22 | 0.223 |
| Factors Name | Kendall | Spearman | Pearson | |||
|---|---|---|---|---|---|---|
| r | p Value | r | p Value | r | p Value | |
| 3H Plain _SPI_TMIN | 0.148 | 0.0008 | 0.172 | 0.0007 | 0.149 | 0.0217 |
| Cop_Family | AIC | BIC | RMSE |
|---|---|---|---|
| Gaussian | 18.56 | 24.26 | 0.192 |
| t | 20.56 | 31.96 | 0.194 |
| Clayton | 17.96 | 23.66 | 0.412 |
| Frank | 18.77 | 24.46 | 0.175 |
| Gumbel | 17.96 | 23.66 | 0.412 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Li, K.; Gu, H.; Cheng, Y.; Xue, D.; Jia, H.; Du, Z.; Li, Z. Climatic Challenges in the Growth Cycle of Winter Wheat in the Huang-Huai-Hai Plain: New Perspectives on High-Temperature–Drought and Low-Temperature–Drought Compound Events. Atmosphere 2024, 15, 747. https://doi.org/10.3390/atmos15070747
Chen G, Li K, Gu H, Cheng Y, Xue D, Jia H, Du Z, Li Z. Climatic Challenges in the Growth Cycle of Winter Wheat in the Huang-Huai-Hai Plain: New Perspectives on High-Temperature–Drought and Low-Temperature–Drought Compound Events. Atmosphere. 2024; 15(7):747. https://doi.org/10.3390/atmos15070747
Chicago/Turabian StyleChen, Geng, Ke Li, Haoting Gu, Yuexuan Cheng, Dan Xue, Hong Jia, Zhengyu Du, and Zhongliang Li. 2024. "Climatic Challenges in the Growth Cycle of Winter Wheat in the Huang-Huai-Hai Plain: New Perspectives on High-Temperature–Drought and Low-Temperature–Drought Compound Events" Atmosphere 15, no. 7: 747. https://doi.org/10.3390/atmos15070747
APA StyleChen, G., Li, K., Gu, H., Cheng, Y., Xue, D., Jia, H., Du, Z., & Li, Z. (2024). Climatic Challenges in the Growth Cycle of Winter Wheat in the Huang-Huai-Hai Plain: New Perspectives on High-Temperature–Drought and Low-Temperature–Drought Compound Events. Atmosphere, 15(7), 747. https://doi.org/10.3390/atmos15070747






