Next Article in Journal
Study of the Atmospheric Transport of Sea-Spray Aerosols in a Coastal Zone Using a High-Resolution Model
Next Article in Special Issue
Dynamic Changes and Influencing Factors Analysis of Groundwater Icings in the Permafrost Region in Central Sakha (Yakutia) Republic under Modern Climatic Conditions
Previous Article in Journal
Seasonal Variations in Radon and Thoron Exhalation Rates from Solid Concrete Interior Walls Observed Using In Situ Measurements
Previous Article in Special Issue
Comparative Analysis of the Seasonal Driving Factors of the Urban Heat Environment Using Machine Learning: Evidence from the Wuhan Urban Agglomeration, China, 2020
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 15
Issue 6
10.3390/atmos15060700
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Machine Learning for Global Bioclimatic Classification: Enhancing Land Cover Prediction through Random Forests

by
Morgan Sparey
1,*,
Mark S. Williamson
1,2 and
Peter M. Cox
1,2,*
1
Faculty of Environment, Science and Economy, University of Exeter, Exeter EX4 4QF, UK
2
Global Systems Institute, Faculty of Environment, Science and Economy, University of Exeter, Exeter EX4 4QF, UK
*
Authors to whom correspondence should be addressed.
Atmosphere 2024, 15(6), 700; https://doi.org/10.3390/atmos15060700
Submission received: 25 April 2024 / Revised: 28 May 2024 / Accepted: 4 June 2024 / Published: 12 June 2024
(This article belongs to the Special Issue Impacts of Land Use and Climate Change in Urban Area: Big Data and Machine Learning)
Browse Figures
Versions Notes

Abstract

:
Traditional bioclimatic classification schemes have several inherent shortcomings; they do not represent anthropogenic impact, they contain a bias for global north representation, and they lack flexibility regarding novel climates that may arise due to climate change. Here we present an alternative approach, using a machine learning approach. We combine European Space Agency Land Cover Classification data with traditional bioclimate classification climate variables, and additional variables; latitude, elevation, and topography. We utilise a random forest algorithm to create a classification system that overcomes the limitations and biases of the traditional schemes. The algorithm produced is able to predict land cover classification globally at 0.5-degree resolution with 93% accuracy. The resulting classifications account for human impact, particularly via agriculture, are informed by the topography of a region, and avoids the biases that traditional bioclimatic schemes contain. The algorithm can provide insights into the drivers of land cover change, the spatial distribution of land cover change, the potential impacts on ecosystem services and human well-being. Furthermore, the random forest model serves as a novel approach to the prediction of future land cover, and can be used to identify regions at risk of a land cover transition. Our data-based machine learning approach produces larger land-cover changes due to climate change than a traditional bioclimatic scheme, especially in sensitive regions such as Amazonia. Overall, our new approach projects approximately 17.4 million square kilometre of land-cover change per degree celsius of global warming.

Graphical Abstract

1. Introduction

Land cover and land use changes have significant impacts on the Earth’s ecosystems, biodiversity, and climate [1,2,3,4]. Therefore, monitoring and managing land resources is essential for ensuring their sustainable use and for mitigating and adapting to the effects of climate change. Satellite data and ground-based observations are valuable tools for monitoring land cover and land use changes at a global scale. The ESA Climate Change Initiative (CCI) land cover classification system is one such tool that provides detailed information about land cover and land use changes globally.
Accurate predictions of future land cover classification are important for decision-makers to plan and implement sustainable land use practices, conservation strategies, and disaster risk reduction measures [5]. Land cover prediction models, utilising techniques such as remote sensing and machine learning algorithms, can help to forecast future land cover changes based on past and current land cover information and trends. These models can provide valuable insights into the drivers of land cover change, the spatial distribution of land cover change, and the potential impacts on ecosystem services and human well-being [6,7,8,9,10].
The Random Forest (RF) is a prominent ensemble learning algorithm renowned for its effectiveness in predictive modelling tasks across various scientific domains. First proposed by Breiman in 2001, RF operates by constructing a multitude of decision trees during training and harnessing the collective wisdom of these trees to make robust predictions. Unlike conventional decision trees prone to overfitting, RF mitigates this risk by aggregating predictions from multiple trees, thereby enhancing generalisation performance. Its ability to handle high-dimensional data, accommodate diverse data types, and provide insights into feature importance has made it a cornerstone in contemporary machine learning and data mining applications, including but not limited to bioinformatics, ecology, finance, and healthcare. Random Forests are a powerful machine learning technique for classification problems, RFs have several key advantages for this analysis, including their non-parametric nature, and the ability to determine feature importance [11,12]. The Random Forest classifier employs bagging, or bootstrap aggregating, to create an ensemble of classification and regression tree like classifiers. Additionally, it selectively explores a random subset of variables for a split at each tree node to reduce correlation among the ensemble’s classifiers [11]. This approach remains robust against noise and overfitting. Moreover, it offers computational efficiency compared to boosting methods and is moderately lighter than straightforward bagging techniques [13]. RFs have been shown to outperform statistical classification techniques in key areas including accuracy and interpretability [14].
Machine learning has already been applied to the classification of land cover and land use [15,16,17]. Random forests have already been implemented at regional scales for land cover classification prediction and have shown promising results, regions are varied and include mountainous Colorado, USA [18], Coastal and Mountainous Granada, Spain [19], and South Western Florida, USA, including rural to urban transitional regions and swamps [20]. Random forests have also been applied to determine land cover classification based on satellite imagery [21,22]. However, these previous approaches often use data that is not available for future climates. We combine climate variables often used for traditional bioclimatic schemes with current techniques used to identify land cover classification. These previous studies have also been much more narrow in scope, mapping just regions or countries. We take a global approach to create a comprehensive random forest based model for land cover classification distribution.
Bioclimate classification schemes are methods used to categorise and describe the climates of different regions based on their biological characteristics. These schemes use climatic variables such as temperature, precipitation, and other environmental factors that influence the distribution of plants and animals. The most widely used bioclimate classification scheme is the Köppen-Geiger system, which categorises climates into five main groups: tropical, dry, temperate, continental, and polar.
The Köppen-Geiger system [23] and other bioclimate classification schemes have several flaws. For example, they do not take into account the effects of anthropogenic factors such as land use changes and urbanisation, which can alter the bioclimate of a region. Furthermore, the most widely used schemes were all created by scientists of the global north and tend to display an increased sensitivity to European and North American climate variation compared to the climate of the global south. Additionally, these schemes may not be applicable in areas where there are complex topographic features. Bioclimate classification schemes typically rely on broad-scale climatic data that may not capture localised variations. This can limit their usefulness in areas with complex topography, such as mountain ranges or valleys, where climate conditions can vary significantly over short distances. Finally, bioclimate classification schemes may not fully capture the effects of climate change, as they are based on historical data and may not be applicable to future climate conditions.
We investigate the use of an XGBoost random forest classifier to predict the land cover classification based on variables used in the Whittaker bioclimatic system. The Whittaker bioclimatic system is a widely used framework for characterising and mapping terrestrial ecosystems that uses mean annual precipitation and temperature as predictors [24]. Specifically, we use the two Whittaker variables but increase temporal resolution from annual to monthly data. We also add a further three additional variables to our land cover prediction algorithm. These are topography, elevation, and latitude. These are included to account for the failings outlined in many bioclimatic classification systems like the Whittaker scheme. Furthermore, this scheme does not include human bias and arbitrary threshold values—overcoming many of the issues of traditional bioclimate schemes.
We apply our land cover scheme to model data at key warming levels and investigate the implications of these climate conditions on global land cover.
We present a random forest algorithm as an alternative to the traditional bioclimate classification schemes, and show that this approach can be used to overcome some of the key failures of the traditional system. These results have important implications for ecological monitoring, land management, and conservation efforts. First we set out our methods for the creation of our random forest algorithm and the data we assess in this study. We produce maps of the true and predicted land cover classifications for 2014 and assess model performance, investigating the potential impact that our chosen spatial resolution may have had. Following this we employ techniques to evaluate feature importance for the model as well as for a specific location. Finally we apply the RF model to climate model data and investigate the predicted global land cover at levels of warmimg from 0 to 4K above preindustrial levels.

2. Materials and Methods

2.1. Predictors for Land Classification

As previously mentioned, we use the monthly mean temperature and precipitation as predictors following many other bioclimatic classification schemes. However we also include the three additional variables topography, latitude and elevation to improve prediction accuracy.
Latitude is included in this study as a proxy for seasonality, as temperature and precipitation patterns vary with latitude and these factors play a critical role in determining the dominant vegetation types in a given region. Although seasonality is sometimes included in bioclimatic schemes, such as the Köppen-Geiger bioclimatic classification system, the Whittaker scheme and many others do not account for it.
Human impact is a key factor that influences land coverage. Human activities, such as agriculture, urbanisation, and deforestation, have a significant impact on ecosystems and can alter the composition and structure of the land [25,26,27]. High population densities often result in the conversion of natural habitats to agricultural or urban areas, which can lead to the loss of biodiversity and ecosystem services. Moreover, population growth and density can exacerbate the impact of climate change on land cover classification, such as increasing water demands for agriculture. Whilst we have not explicitly included population density in the scheme presented here, we expect that the impact of human activity and distribution is largely accounted for through other variables. Temperature and precipitation patterns largely dictate the global population distribution [28]. We enhance this information with additional variables that we expect would impact habitability—elevation and topography.
Elevation is an important factor in bioclimatic distribution due to its effects on environmental conditions such as temperature, precipitation, and atmospheric pressure, however many key issues related to orographic precipitation remain unresolved [29]. As elevation increases, temperature generally decreases due to changes in atmospheric pressure and altitude, leading to different climate zones at different elevations. Similarly, the amount and timing of precipitation often vary with elevation, leading to different soil moisture conditions, soil thawing, and water availability for plant growth [30]. These changes in temperature and precipitation can lead to different vegetation patterns at different elevations, which in turn can affect the distribution and abundance of animal species that depend on these plants for food and shelter [31]. Additionally, elevation can affect other environmental conditions such as solar radiation, wind, and atmospheric gases, which can have direct or indirect effects on biotic communities. For example, changes in solar radiation can affect the timing and success of plant photosynthesis, which can in turn affect the timing and abundance of insect populations that feed on these plants. Thus, elevation plays a critical role in bioclimatic distribution, influencing the distribution and abundance of organisms across different elevations and creating unique ecosystems at each elevation. Understanding the complex interactions involving elevation is essential for predicting how species will respond to environmental changes, including climate change, and for developing effective conservation strategies aimed at preserving biodiversity and ecosystem services. Furthermore, the elevation of a region can impact local biomes’ short to medium term reactions to weather events giving divergent responses to to dry and wet years [32].
Topography, or the physical features of the landscape, also plays an important role in determining land cover classification. Mountain ranges, for example, can create different microclimates and soil conditions, leading to the formation of different biomes on opposite sides of the same mountain [33]. Similarly, coastal regions may have different biomes depending on the direction of ocean currents, prevailing winds, and the presence of estuaries or wetlands [34,35]. The topography of a region can also have impacts on environmental conditions such as solar radiation distribution in mountainous watersheds and evapotranspiration [36].

2.2. Data

All datasets in this study were regridded and analysed at a 0.5 degree resolution. This resolution was chosen to ensure usability of results and to avoid producing predictions at a higher resolution than the lowest resolution data. Data at latitudes below 60° S was not used in this study as there is little data for the region and few land points outside of Antarctica. The original LCCS colour scheme is used despite difficulty seeing transitional regions, this was used to ensure continuity and comparability with the LCCS data output. This data is outlined in Table 1.

2.2.1. Land Cover Classification Data

Land Cover Classification data was sourced from the ESA Climate Change Initiative [37]. This data is available globally at a resolution of 300 m for the years 1992—2015. The overall accuracy of this global data is about 71.1%, however some regions and classifications are more accurate than others as they are homogeneous, unambiguous and recognisable, e.g., snow and ice cover or urban areas [40]. As this dataset is comprised of 22 discrete classes, we choose the most commonly occurring classification when regridding to the 0.5 degrees. Areas classified as water are not included. It is important to note that the classifications given by ESA are not necessarily ground truth classifications. We use these classifications as a proxy for ground truth.

2.2.2. Temperature and Precipitation Data

Historical observations of monthly mean temperature and precipitation are from the CRU TS v. 4.05 dataset [38]. For monthly analysis, mean monthly values were used.

2.2.3. Topographic Data

Topographic data from Marthews et al. [39] was made available by Dr Toby Marthews. This data for land surface water flow is included to account for bioclimates such as wetlands, flooded areas, and lichens and mosses. This dataset was originally created at 15 arcsec resolution, however a 0.5 degree dataset has also been created and was supplied when requested.

2.2.4. Elevation Data

The elevation data used is sourced from the TerrainBase, Global 5 Arc-minute Ocean Depth and Land Elevation from the US National Geophysical Data Center (NGDC) [25].

2.2.5. Climate Model Data

Data analogous to the historic observed dataset climate models originates from the ’historical’ CMIP6 experiments [41]. Models were selected from the CMIP6 multi-model ensemble based on the availability of historical experiment data and their ability to achieve a minimum warming of 4K under the ssp585 scenario. The specific models meeting these criteria are listed in Table 2.
Table 2. Details of the climate models used in this study.
Table 2. Details of the climate models used in this study.
ModelInstitutionFrequencyNominal ResolutionPublication
CanESM5CCCmamon100 km [42]
[43]
CanESM5-CanOECCCmamon100 km [44]
[45]
CESM2NCARmon100 km [46]
[47]
CESM2-WACCMNCARmon100 km [48]
[49]
IPSL-CM6A-LRIPSLmon100 km [50]
[51]
UKESM1-0-LLMet Office Hadley Centremon100 km [52]
[53]
ACCESS-CM2CSIRO-ARCCSSmon250 km [54]
[55]
AWI-CM-1-1-MRNCARmon100 km [56]
[57]
CAS-ESM2-0UCImon100 km [58]
[59]
EC-Earth3EC-Earth-Consortiummon100 km [60]
[61]
EC-Earth3-VegEC-Earth-Consortiummon100 km [62]
[63]
TaiESM1AS-RCECmon100 km[64]
[65]
The resolution of the model output data is generally coarser compared to the underlying 0.5° climatology. As a result, the anomaly corrected fields exhibit spatial variability stemming exclusively from the underlying climatology, particularly at scales not resolved by the model. Consequently, the identified changes in bioclimatic types, which rely on model anomalies, tend to appear somewhat smoother at these finer spatial scales.
We generated future land cover classification maps for projected global warming scenarios of 1.5, 2, and 4K above reference period levels using the CMIP6 ‘ssp585’ future scenario spanning 2015–2100. We chose ssp585 due to its consistency in surpassing the 4K warming threshold across all models, ensuring uniform definition of changes in land cover across varying levels of global warming. The timing for each warming level is determined based on the centred 30-year annual mean global surface air temperature above the model’s reference temperature, set as 1901–1931. Monthly mean anomalies of precipitation and surface air temperature are computed relative to this reference period. Model outputs are adjusted to align with observational data from 1901–1931 by calculating anomalies for each model and applying them to the observational climatology. Multi-model ensemble mean land cover classification maps are derived using the multi-model ensemble mean of anomalous temperature and precipitation fields at each warming level. Our focus lies predominantly on the ensemble mean, acknowledging that ensemble mean and ensemble median climates have been observed to exhibit substantial similarity in climate modelling literature [66,67,68].

2.3. Random Forest Training

An XGBoost random forest was trained using data from the years 1992–2013, initially using 100 trees, and no maximum depth. This method was selected as previous research has also shown that random forests perform well with land cover classification tasks [18,20]. The random forest approach was later edited to operate with the optimal hyperparameters.
Training data was area weighted for importance in training and a train, validation, test split was performed. Training and validation data comprises of a random 70–30 split of the years 1992–2013, whilst test data comprised the full dataset for the years 2014 and 2015. This ensures our final results and performances are relevant globally, and based on the most recent results available in the dataset. The distribution of this dataset can be seen in Figure 1. This is an unbalanced dataset, however we chose not to balance the dataset due to its inherent imbalance mirroring the natural distribution of classes. This decision was guided by our aim to prevent potential overfitting, as artificially inflating the minority class through balancing techniques can lead to an overly complex model that struggles to generalise to unseen data. Moreover, preserving the original distribution of the data allowed us to avoid information loss. This ensures that the model captures the intricate patterns present in the majority class without compromising its predictive performance.
Before training the Random Forest classifier, the dataset underwent preprocessing to ensure its suitability for modelling. This preprocessing involved steps to remove unclassified regions, and encoding categorical variables.
When analysing the decisions made by the random forest, shaply analysis was used. This analysis was carried out on 5% of the data for 2014 and 2015 [69].
When optimising the hyperparameters for the random forest a Bayesian search over the hyperparameter space was used to find optimal parameter values with available computational resources. Hyperparameters here include are set out in Table 3.
A brief description of these perameters follows:
1. 
colsample_bylevel: This parameter controls the fraction of features to consider when constructing each level of a tree within the ensemble. A setting of “None” implies the utilisation of all features at each level.
2. 
colsample_bynode: Governing the fraction of features to consider for each split decision within a tree node, this parameter regulates the diversity of feature selection at each node. A value of 0.9 signifies that 90% of the features will be randomly sampled for each split.
3. 
colsample_bytree: Dictating the fraction of features to consider when constructing each tree in the ensemble, this parameter facilitates the introduction of randomness, thereby enhancing model robustness. A value of 0.9 indicates that 90% of features will be sampled for each tree.
4. 
early_stopping_rounds: Employed for preventing overfitting and improving computational efficiency, this parameter determines the number of rounds to continue training without improvement in the evaluation metric before halting. In this instance, early stopping is not activated (“None”).
5. 
learning_rate: Central to gradient descent optimisation, this parameter governs the step size at each iteration while traversing towards the minimum of the loss function. A learning rate of 0.2 signifies a moderate step size.
6. 
max_depth: Defining the maximum depth of each tree in the ensemble, this parameter regulates the complexity of individual trees and influences the model’s capacity to capture intricate patterns within the data. A high value of 63 suggests a potentially deep tree structure.
7. 
max_leaves: This parameter specifies the maximum number of terminal nodes (leaves) in a tree, thus indirectly controlling the tree’s depth. The absence of an upper limit (“None”) implies unrestricted growth of tree nodes.
8. 
n_estimators: Determining the total number of trees in the ensemble, this parameter profoundly influences model complexity and computational efficiency. A choice of 300 trees indicates a substantial ensemble size.

3. Results

We find that using the variables monthly precipitation, monthly temperature, latitude, elevation, and topography, we can predict a region’s land cover classification well. Our model is able to correctly predict the global land coverage with an area weighted accuracy of 93.1% for land north of 60° S for 2014, and 91.7% for 2015.
Figure 2 shows maps of the true and predicted distributions of land cover classification in 2014. The majority of the globe has been correctly classified.
Figure 3 highlights regions where the random forest classifier does not correctly predict the land cover classification in 2014. These regions are generally randomly distributed across the globe. With the largest discrepancies in Eastern Europe and the Amazon. Other discrepancies are largely found at border regions between classification zones, such as south of the Sahara Desert. The sparse and well distributed nature of these misclassifications makes us confident that model performance is not impacted by climate zone. A confusion matrix of true and predicted classifications for 2015 and 2015 can be seen in Figure 4. This figure shows the classification performance for each of the classifications in the ESA scheme. This can be used to understand which classifications are being misclassified most frequently and also which classifications they are being misclassified as.
To investigate whether these misclassifications were due to downscaling of the data to the coarser resolution, we compare the distribution of misclasification with the distribution of variability of classification within each grid box.
Figure 5 shows the number of classifications within each 0.5° × 0.5° zone that was reduced for analysis. There is no significant correlation between the number of classifications in a region and the performance of the classification model. Regions such as the Sahara desert and Greenland clearly have large areas of singular classification, “Bare Areas” and “Permanent Snow and Ice” respectively. More temperate regions such as Europe and North America tend to contain more classifications.
Figure 6 shows the dominance of the most common classification for a given region. Similar to Figure 5, areas such as the Sahara and Greenland with dominant classifications. To further assess the potential reasons for misclassification, as well as to understand some of the reasoning behind the random forest, we performed shapley analysis and feature importance analysis.
Figure 7 shows the feature importance score of each variable used in analysis. Figure 7a shows the Gain metric, the Gain metric denotes the relative significance of each feature within the model, determined by aggregating the contribution of each feature across all decision trees. A higher value of this metric compared to another feature suggests its greater importance in prediction generation. We can see that this analysis indicates that latitude provides the most significant influence on model decision making. The gain metric in Figure 7a shows a much more even impact of both temperature and precipitation when compared to weight in Figure 7b. In Figure 7b F-score is a metric showing the total number of times that each feature is split on in the random forest model. This is an indication of each feature’s contribution in determining the land cover classification, however it is not a definitive measure of importance as it does not indicate the impact that the implementation of each of these variables has on prediction quality. The results here show that the precipitation over the second month of winter, followed by the third and first, are the variables that are most split upon in the random forest. These results also show that the temperature of a given month is in all but one case, the mean temperature of the second month of winter, the least split upon variable. Elevation and Topography are also shown to be split upon more than any month’s temperature.
Shapley values, derived from cooperative game theory, have emerged as a potent tool for interpreting the predictions of machine learning models. Each Shapley value represents the marginal contribution of a feature to the discrepancy between the actual prediction and the average prediction across all conceivable combinations of features. Essentially, it quantifies the importance of each feature in the model’s decision-making process. Interpreting Shapley values is straightforward: positive values indicate that the feature contributes positively to the prediction, while negative values suggest the opposite. The magnitude of the Shapley value reflects the impact of the feature on the prediction; larger values denote greater influence. Furthermore, Shapley values offer insights into feature interactions, as they consider the interplay between features when assigning importance to each individual feature. In this application of shapley analysis, the predicted variable is categorical, not a continuous value. Due to the way that the land cover classes are encoded, negative and positive SHAP values can be interpreted similarly—in terms of magnitude of impact. Figure 8 shows the SHAP values for each of the variables within the model. This analysis is for the model as a whole and we again see that latitude, elevation, and topography are ranked highly in importance. This analysis also indicates that a low temperature in spring is a very important factor in determining the land cover classification of a region. Precipitation is shown to have less extreme effects on the classification of a region.
To gain some further insight into the model, we used SHAP to investigate the explainability of individual model predictions. We have focused on an Amazon grid cell situated at 3.25° S 57.75° W.
Figure 9 shows the feature contributions towards a specific classification, in this case “Tree cover, broadleaved evergreen, closed to open (>15%)”. Classifications are represented numerically due to the way they are encoded for the RF algorithm. The arrows show each variable’s contribution to the final classification decision. This shows that latitude is the largest contributor in this instance, followed by elevation. Here the temperature of the 2nd winter month works against the final classification. This location was selected to check for insights into potential bi-stability in the Amazon.
Figure 10 shows the multi-model ensemble model mean KG classification for 1.5K, 2K and 4K of global warming above the reference period, as well as the no warming classifications. In these results you can clearly see a northward shift of boreal forests globally and a complete loss of the lichens and mosses coverage in northern Canada. The results also show a steady loss of rainforest in the Amazon, with it disappearing by 4K of warming. Interestingly the forests in the African Congo appear to expand in this period.
Figure 11 shows the percentage land area (in this study all land north of −60°) change in land cover classification from the area’s original preindustrial classification. This change appears to be approximately linear, we can see from the gradient of our linear trend line that we predict a global land area change of 10.96% per degree of warming.

4. Discussion

The land cover classification model used in this study is ably to classify global land coverage at 0.5° × 0.5° resolution to an accuracy of 93.1% for 2014, and 91.7% for 2015.
Figure 2 and Figure 3 show that the model performs well on a global scale, with misclassifications being distributed across the globe. Given the large amount of variability of landcover classification displayed throughout large temperate regions of the globe such as North America and Europe.
Many regions of the globe are no longer in their equilibrium state—their true classification has been changed by humans, for example; the classification cropland, or certain tree types. The model’s ability to identify the human-imposed classification over a region’s natural classification is impressive. One possible reason for this is that for a given latitude human have fully imposed their influence i.e., anywhere in Europe that has the climate for cropland, is already cropland. This demonstrates an area where this model may be more useful than historic bioclimate classification schemes in some applications. By identifying the real, human-influenced, nature of the landcover of a region and not the idealised classification a region may have exhibited centuries ago, this model could provide a more realistic analysis of the landcover.
One area of this study with significant potential for further investigation lies in the way that we down-scaled the landcover classification training data. As this process ignores all but the most common land cover classifications or a given grid box, it is possible that a significant amount of the miss-classification shown in our model is due to the variability within each grid box. A set of averaged climatological conditions will not be able to indicate several different classifications. Although Figure 5 gives insight into the number of classifications found within a given box, it does not account for the proportion of the box that each classification impacts. For example; a region that is 55% classification A and 45% classification B will only comprise of two classifications. Figure 6 addresses this issue, although there may be some overlap between a lack of one dominating classification for a region, and the model’s ability to predict the classification, it is not clear that this is the reason for error in prediction. For example, Alaska and Spain are two regions where there is very little dominance however the model performs well here. This provides confidence that the spatial scale of this study is appropriate, further work is needed to determine the optimal spatial scale for this work, however such research would require currently unavailable datasets. Additionally, this work does not account for any impacts of the CO2 fertilisation effect, the inclusion here was not not possible due to the short time frame of the classified data, 1992–2015 which would likely not have displayed significant changes in due to CO2 fertilisation.
Some amount of error is expected in this model, for example it has no knowledge of forest fires, this may account for some of the error seen in Australia and in the Amazon. Furthermore, the model has no knowledge of the previous year’s classification or weather, or bordering classifications. Some weather events, such as droughts or floods, could have impacts lasting longer than the year in which they occur. Such information may prove more important as the effects of future climate change become more widely felt. If applied to the prediction of future land cover classification this model may provide useful insight into future climates at various spatial resolutions. Land cover classification and land cover classification change have been shown to have an affect on the climate at relatively small scales [70] and large scales [71,72].
The results from the F-score analysis indicates that the temperature of a given month can be less specific, and therefore specificity in temperature is likely less important in classification determination, than the other variables. These results are for the entire random forest and for all classification types. A classification such as permanent snow and ice could rely more heavily on temperature than precipitation, however that would not be reflected in this piece of analysis. It is interesting that the temperature of the second month of winter is more than twice as split upon than any other variable, indicating that this may be the most sensitive variable included in this analysis in deciding the land cover classification of a region.
Latitude is more split upon than any month’s temperature. Latitude was included as a proxy measure of seasonality. The apparent sensitivity of this model to this variable lends weight to its inclusion in more traditional bioclimatic classification schemes. Elevation is the fifth most split upon variable, this is not a variable typically included in bioclimate classification schemes, although it may be represented in a combination of temperature and precipitation, these variables would not fully represent the behaviours of bioclimates at elevations. This analysis could make a compelling case for the inclusion of elevation in any future bioclimate classification scheme. The same here is true of topography.
The SHAP analysis was carried out for 5% of the data that the F-score analysis was, however it produces some very interesting results. Many of the results shown are easy to understand; for example, high latitudes have a large impact on classification as there is much less diversity in land cover at extremely high latitudes, whereas mid latitudes have much less impact on classification. Low temperatures in the middle of summer also have more of an impact than the same variable in the middle of spring or autumn. Although some of these results mirror the F-score results, both weight and gain, high rankings for elevation, latitude, and topography. The SHAP analysis places more importance on temperature in terms of impact on the model’s output, in a similar indication to the gain feature importance score. It may be that although the model is more sensitive to the specific values of precipitation—as it considers this variable more frequently, fewer splits on temperature often have more impact. For example a single split on summer month 2 temp could determine a region to be permanent snow and ice.
The individual analysis for the classification of 3.25° S 57.75° W in the Amazon rain forest reinforces the importance of both latitude and elevation. In Figure 9 precipitation in the 3rd and 2nd months of autumn are more important than temperature in the model’s decision. This demonstrates the importance of investigating individual locations and classifications in addition to the overall model performance. Our classification model could be used with historic data to explain the cause of previous land cover shifts.
To provide a more comprehensive evaluation of our proposed method, we acknowledge the importance of comparing it with alternative machine learning approaches, particularly in the context of global land cover models. While this study focuses on the development and validation of our specific method, a thorough comparison with other algorithms such as Support Vector Machines (SVM) and Neural Networks is recognised as a critical area for future research. This future work will aim to benchmark our method against these established techniques to further substantiate its efficacy and robustness.
This approach to building a land cover model provides a case for a new technique for building non-machine learning based models. We provide strong evidence here that latitude and topography are important factors for determining land cover change. As such, future, prescriptive, land cover and bioclimatic schemes should include these variables in their design. This technique for discovering feature importance could be applied to a large number of prescriptive models where traditional wisdom and inherent biases may be precluding the inclusion of helpful features.
When we apply the RF model to projected climates as shown in Figure 10 many land cover transitions are noticed. The boreal forest shifts northwards with warming. There is almost total dieback of the Amazon rainforest at 4K of warming, interestingly at the same level of warming the Congo rainforest is predicted to grow, we also see the greening of the Sahel. The northward march of the boreal forest, Amazonian dieback, and the greening of the Sahel are all trends predicted to take place under warming scenarios—our model replicating this behaviour is therefore an indicator of the validity of its results [73,74,75]. From Figure 11 we see that the predicted rate of global land cover change is 10.96% per degree of warming. This equates to approximately 17.4 million square kilometres of land cover change. This is close to a previous estimate of 13% of land cover experiencing a change in Köppen-Geiger bioclimate classification per degree of warming [76]. The inclusion of topography, elevation, and latitude accounts for the failings outlined in many bioclimatic classification systems like the Whittaker or Köppen-Geiger schemes. Furthermore, this scheme does not include human bias and arbitrary threshhold values—overcoming many of the issues of traditional bioclimate schemes.
The impact of human activity is hard encoded into the model based on human impacts during the 1992–2013 training period. As the model was trained under the influence of human impact, its resulting predictions also reflect potential human impact. One of the limitations of this model is that when used for forecasting, or hindcasting, is that it has a static perception of human impact, as such its past and future predictions will not include up to date perceptions of human impact. Additionally the model has no awareness of changes in policy decisions regarding land use. Consequentially, future predictions could be interpreted as predicted land cover at a level of warming if 1992-2013 land use practices are followed. This is more relevant for some classifications such as urban and agricultural classifications than for others such as deserts and the northward shift of the boreal forest.

5. Conclusions

In this study, we identify a new approach to classify bioclimatic zones globally. Using an XGBoost random forest algorithm and ESA land cover classification data as a proxy for land cover. The classification of these zones holds importance for ecological and environmental research, providing insights into climate patterns and their implications on biodiversity.
Our application of the XGBoost random forest algorithm proved to be successful in delineating land cover zones with a high degree of accuracy, over 90%. The robustness of the random forest model demonstrated its efficacy in handling complex spatial data and capturing patterns in global climatic variations. The results obtained not only contribute to the existing body of knowledge on bioclimatic zones but also showcase the potential of machine learning techniques, particularly random forest, in addressing environmental classification challenges.
We suggest and highlight the importance of several, previously under-considered variables, for any new potential bioclimatic scheme.
While the random forest approach works with a high degree of success, there are limitations and avenues for future research. Future studies could explore the integration of additional environmental variables, such as soil composition, to enhance the precision of classification. Furthermore, continuous monitoring and validation efforts would ensure the accuracy and reliability of the classification results over time.
In conclusion, this research contributes to the growing field of environmental science by demonstrating the applicability of machine learning techniques, specifically random forests, in the global, quantitatively informed, classification of bioclimatic zones.

Author Contributions

Conceptualization, M.S., M.S.W. and P.M.C.; Formal analysis, M.S.; Investigation, M.S.; Methodology, M.S., M.S.W. and P.M.C.; Resources, M.S.W. and P.M.C.; Supervision, M.S.W. and P.M.C.; Visualization, M.S.; Writing—original draft, M.S.; Writing—review & editing, M.S.W. and P.M.C. All authors have read and agreed to the published version of the manuscript.

Funding

M.S. was funded via a doctoral training grant awarded as part of the UKRI AI Centre for Doctoral Training in Environmental Intelligence (UKRI grant number EP/S022074/1). P.C. acknowledges funding from the Horizon Europe project OptimESM (grant number 101081193).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented were derived from resources available in the public domain, at locations listed in the paper. Processed and raw data will be made available by the authors on request. All original CMIP6 data used in this study are publicly available at https://esgf-node.llnl.gov/projects/cmip6/ (last access: 10 August 2021).

Acknowledgments

We would like to thank Toby Marthews for providing our topographic index data at the appropriate resolution for this study.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Payet, K.; Rouget, M.; Esler, K.J.; Reyers, B.; Rebelo, T.; Thompson, M.W.; Vlok, J.H.J. Effect of Land Cover and Ecosystem Mapping on Ecosystem-Risk Assessment in the Little Karoo, South Africa. Conserv. Biol. 2013, 27, 531–541. [Google Scholar] [CrossRef] [PubMed]
  2. Zimmermann, P.; Tasser, E.; Leitinger, G.; Tappeiner, U. Effects of land-use and land-cover pattern on landscape-scale biodiversity in the European Alps. Agric. Ecosyst. Environ. 2010, 139, 13–22. [Google Scholar] [CrossRef]
  3. Betts, R.A.; Falloon, P.D.; Goldewijk, K.K.; Ramankutty, N. Biogeophysical effects of land use on climate: Model simulations of radiative forcing and large-scale temperature change. Agric. For. Meteorol. 2007, 142, 216–233. [Google Scholar] [CrossRef]
  4. Bala, G.; Caldeira, K.; Wickett, M.; Phillips, T.J.; Lobell, D.B.; Delire, C.; Mirin, A. Combined climate and carbon-cycle effects of large-scale deforestation. Proc. Natl. Acad. Sci. USA 2007, 104, 6550–6555. [Google Scholar] [CrossRef] [PubMed]
  5. Feddema, J.J.; Oleson, K.W.; Bonan, G.B.; Mearns, L.O.; Buja, L.E.; Meehl, G.A.; Washington, W.M. The Importance of Land-Cover Change in Simulating Future Climates. Science 2005, 310, 1674–1678. [Google Scholar] [CrossRef] [PubMed]
  6. Veldkamp, A.; Lambin, E. Predicting land-use change. Agric. Ecosyst. Environ. 2001, 85, 1–6. [Google Scholar] [CrossRef]
  7. Welde, K.; Gebremariam, B. Effect of land use land cover dynamics on hydrological response of watershed: Case study of Tekeze Dam watershed, northern Ethiopia. Int. Soil Water Conserv. Res. 2017, 5, 1–16. [Google Scholar] [CrossRef]
  8. Yifru, B.A.; Chung, I.M.; Kim, M.G.; Chang, S.W. Assessing the Effect of Land/Use Land Cover and Climate Change on Water Yield and Groundwater Recharge in East African Rift Valley using Integrated Model. J. Hydrol. Reg. Stud. 2021, 37, 100926. [Google Scholar] [CrossRef]
  9. Estifanos, T.H.; Gebremariam, B. Modeling-impact of Land Use/Cover Change on Sediment Yield (Case Study on Omo-gibe Basin, Gilgel Gibe III Watershed, Ethiopia). Am. J. Mod. Energy 2020, 5, 84–93. [Google Scholar] [CrossRef]
  10. Li, C.; Managi, S. Land cover matters to human well-being. Sci. Rep. 2021, 11, 15957. [Google Scholar] [CrossRef]
  11. Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  12. Paul, J.; Dupont, P. Inferring statistically significant features from random forests. Neurocomputing 2015, 150, 471–480. [Google Scholar] [CrossRef]
  13. Machova, K.; Puszta, M.; Barcák, F.; Bednár, P. A comparison of the bagging and the boosting methods using the decision trees classifiers. Comput. Sci. Inf. Syst. 2006, 3, 57–72. [Google Scholar] [CrossRef]
  14. Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
  15. Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. Joint Deep Learning for land cover and land use classification. Remote Sens. Environ. 2019, 221, 173–187. [Google Scholar] [CrossRef]
  16. Abdi, A.M. Land cover and land use classification performance of machine learning algorithms in a boreal landscape using Sentinel-2 data. GISci. Remote Sens. 2020, 57, 1–20. [Google Scholar] [CrossRef]
  17. Qian, Y.; Zhou, W.; Yan, J.; Li, W.; Han, L. Comparing Machine Learning Classifiers for Object-Based Land Cover Classification Using Very High Resolution Imagery. Remote Sens. 2015, 7, 153–168. [Google Scholar] [CrossRef]
  18. Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
  19. Rodriguez-Galiano, V.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
  20. Zhang, F.; Yang, X. Improving land cover classification in an urbanized coastal area by random forests: The role of variable selection. Remote Sens. Environ. 2020, 251, 112105. [Google Scholar] [CrossRef]
  21. Sun, J.; Ongsomwang, S. Optimal parameters of random forest for land cover classification with suitable data type and dataset on Google Earth Engine. Front. Earth Sci. 2023, 11, 1188093. [Google Scholar] [CrossRef]
  22. Zhang, X.; Liu, L.; Chen, X.; Gao, Y.; Xie, S.; Mi, J. GLC_FCS30: Global land-cover product with fine classification system at 30 m using time-series Landsat imagery. Earth Syst. Sci. Data 2021, 13, 2753–2776. [Google Scholar] [CrossRef]
  23. Köppen, W. Die Wärmezonen der Erde, nach der Dauer der heissen, gem ässigten und kalten Zeit und nach der Wirkung der Wärme auf die organische Welt betrachtet. Meteorol. Z. 1884, 1, 215–226. [Google Scholar] [CrossRef]
  24. Whittaker, R. Communities and Ecosystems; MacMillan Publishing Co.: New York, NY, USA, 1975.
  25. National Geophysical Data Center; NESDIS; NOAA; U.S. Department of Commerce. TerrainBase, Global 5 Arc-Minute Ocean Depth and Land Elevation from the US National Geophysical Data Center (NGDC). 1995. Available online: https://rda.ucar.edu/datasets/ds759-2/ (accessed on 28 May 2024).
  26. Ojima, D.S.; Galvin, K.A.; Turner, B.L. The Global Impact of Land-Use Change. BioScience 1994, 44, 300–304. [Google Scholar] [CrossRef]
  27. Bucała-Hrabia, A. The impact of human activities on land use and land cover changes and environmental processes in the Gorce Mountains (Western Polish Carpathians) in the past 50 years. J. Environ. Manag. 2014, 138, 4–14. [Google Scholar] [CrossRef] [PubMed]
  28. Xu, C.; Kohler, T.A.; Lenton, T.M.; Svenning, J.C.; Scheffer, M. Future of the human climate niche. Proc. Natl. Acad. Sci. USA 2020, 117, 11350–11355. [Google Scholar] [CrossRef] [PubMed]
  29. Roe, G.H. OROGRAPHIC PRECIPITATION. Annu. Rev. Earth Planet. Sci. 2005, 33, 645–671. [Google Scholar] [CrossRef]
  30. Pellet, C.; Hauck, C. Monitoring soil moisture from middle to high elevation in Switzerland: Set-up and first results from the SOMOMOUNT network. Hydrol. Earth Syst. Sci. 2017, 21, 3199–3220. [Google Scholar] [CrossRef]
  31. Körner, C. The use of ‘altitude’ in ecological research. Trends Ecol. Evol. 2007, 22, 569–574. [Google Scholar] [CrossRef]
  32. Herrmann, S.M.; Didan, K.; Barreto-Munoz, A.; Crimmins, M.A. Divergent responses of vegetation cover in Southwestern US ecosystems to dry and wet years at different elevations. Environ. Res. Lett. 2016, 11, 124005. [Google Scholar] [CrossRef]
  33. Rita, A.; Bonanomi, G.; Allevato, E.; Borghetti, M.; Cesarano, G.; Mogavero, V.; Rossi, S.; Saulino, L.; Zotti, M.; Saracino, A. Topography modulates near-ground microclimate in the Mediterranean Fagus sylvatica treeline. Sci. Rep. 2021, 11, 8122. [Google Scholar] [CrossRef] [PubMed]
  34. Gonçalves, R.V.S.; Cardoso, J.C.F.; Oliveira, P.E.; Raymundo, D.; de Oliveira, D.C. The role of topography, climate, soil and the surrounding matrix in the distribution of Veredas wetlands in central Brazil. Wetl. Ecol. Manag. 2022, 30, 1261–1279. [Google Scholar] [CrossRef]
  35. Chytrý, K.; Willner, W.; Chytrý, M.; Divíšek, J.; Dullinger, S. Central European forest–steppe: An ecosystem shaped by climate, topography and disturbances. J. Biogeogr. 2022, 49, 1006–1020. [Google Scholar] [CrossRef]
  36. Aguilar, C.; Herrero, J.; Polo, M.J. Topographic effects on solar radiation distribution in mountainous watersheds and their influence on reference evapotranspiration estimates at watershed scale. Hydrol. Earth Syst. Sci. 2010, 14, 2479–2494. [Google Scholar] [CrossRef]
  37. ESA. Land Cover CCI Product User Guide Version 2. 2017. Available online: https://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-Ph2-PUGv2_2.0.pdf (accessed on 28 May 2024).
  38. Harris, I.; Osborn, T.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 109. [Google Scholar] [CrossRef] [PubMed]
  39. Marthews, T.R.; Dadson, S.J.; Lehner, B.; Abele, S.; Gedney, N. High-resolution global topographic index values for use in large-scale hydrological modelling. Hydrol. Earth Syst. Sci. 2015, 19, 91–104. [Google Scholar] [CrossRef]
  40. Defourny, P.; Kirches, G.; Brockmann, C.; Boettcher, M.; Peters, M.; Bontemps, S.; Lamarche, C.; Schlerf, M.; Santoro, M. Land cover CCI. Prod. User Guide Version 2012, 2, 10–1016. [Google Scholar]
  41. Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
  42. Swart, N.C.; Cole, J.N.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Jiao, Y.; et al. CCCma CanESM5 Model Output Prepared for CMIP6 CMIP Historical, 2019. [CrossRef]
  43. Swart, N.C.; Cole, J.N.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Jiao, Y.; et al. CCCma CanESM5 Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  44. Swart, N.C.; Cole, J.N.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Jiao, Y.; et al. CCCma CanESM5-CanOE Model Output Prepared for CMIP6 CMIP Historical, 2019. [CrossRef]
  45. Swart, N.C.; Cole, J.N.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Jiao, Y.; et al. CCCma CanESM5-CanOE Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  46. Danabasoglu, G. NCAR CESM2 Model Output Prepared for CMIP6 CMIP Historical, 2019. [CrossRef]
  47. Danabasoglu, G. NCAR CESM2 Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  48. Danabasoglu, G. NCAR CESM2-WACCM Model Output Prepared for CMIP6 CMIP Historical, 2019. [CrossRef]
  49. Danabasoglu, G. NCAR CESM2-WACCM Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  50. Boucher, O.; Denvil, S.; Levavasseur, G.; Cozic, A.; Caubel, A.; Foujols, M.A.; Meurdesoif, Y.; Cadule, P.; Devilliers, M.; Ghattas, J.; et al. IPSL IPSL-CM6A-LR Model Output Prepared for CMIP6 CMIP Historical, 2018. [CrossRef]
  51. Boucher, O.; Denvil, S.; Levavasseur, G.; Cozic, A.; Caubel, A.; Foujols, M.A.; Meurdesoif, Y.; Cadule, P.; Devilliers, M.; Dupont, E.; et al. IPSL IPSL-CM6A-LR Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  52. Tang, Y.; Rumbold, S.; Ellis, R.; Kelley, D.; Mulcahy, J.; Sellar, A.; Walton, J.; Jones, C. MOHC UKESM1.0-LL Model Output Prepared for CMIP6 CMIP Historical, 2019. [CrossRef]
  53. Good, P.; Sellar, A.; Tang, Y.; Rumbold, S.; Ellis, R.; Kelley, D.; Kuhlbrodt, T. MOHC UKESM1.0-LL Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  54. Dix, M.; Bi, D.; Dobrohotoff, P.; Fiedler, R.; Harman, I.; Law, R.; Mackallah, C.; Marsland, S.; O’Farrell, S.; Rashid, H.; et al. CSIRO-ARCCSS ACCESS-CM2 Model Output Prepared for CMIP6 CMIP Historical, 2019. [CrossRef]
  55. Dix, M.; Bi, D.; Dobrohotoff, P.; Fiedler, R.; Harman, I.; Law, R.; Mackallah, C.; Marsland, S.; O’Farrell, S.; Rashid, H.; et al. CSIRO-ARCCSS ACCESS-CM2 Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  56. Danek, C.; Shi, X.; Stepanek, C.; Yang, H.; Barbi, D.; Hegewald, J.; Lohmann, G. AWI AWI-ESM1.1LR Model Output Prepared for CMIP6 CMIP Historical, 2020. [CrossRef]
  57. Semmler, T.; Danilov, S.; Rackow, T.; Sidorenko, D.; Barbi, D.; Hegewald, J.; Pradhan, H.K.; Sein, D.; Wang, Q.; Jung, T. AWI AWI-CM1.1MR Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  58. Chai, Z. CAS CAS-ESM1.0 Model Output Prepared for CMIP6 CMIP Historical, 2020. [CrossRef]
  59. CAS CAS-ESM1.0 Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2018.
  60. EC-Earth-Consortium. EC-Earth-Consortium EC-Earth3 Model Output Prepared for CMIP6 CMIP historical, 2019. [CrossRef]
  61. EC-Earth-Consortium. EC-Earth-Consortium EC-Earth3 Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  62. EC-Earth-Consortium. EC-Earth-Consortium EC-Earth3-Veg Model Output Prepared for CMIP6 CMIP Historical, 2019. [CrossRef]
  63. EC-Earth-Consortium. EC-Earth-Consortium EC-Earth3-Veg Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2019. [CrossRef]
  64. Lee, W.L.; Liang, H.C. AS-RCEC TaiESM1.0 Model Output Prepared for CMIP6 CMIP Historical, 2020. [CrossRef]
  65. Lee, W.L.; Liang, H.C. AS-RCEC TaiESM1.0 Model Output Prepared for CMIP6 ScenarioMIP ssp585, 2020. [CrossRef]
  66. Sillmann, J.; Kharin, V.V.; Zhang, X.; Zwiers, F.W.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. Model evaluation in the present climate. J. Geophys. Res. Atmos. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
  67. Kim, Y.H.; Min, S.K.; Zhang, X.; Sillmann, J.; Sandstad, M. Evaluation of the CMIP6 multi-model ensemble for climate extreme indices. Weather Clim. Extrem. 2020, 29, 100269. [Google Scholar] [CrossRef]
  68. Li, J.; Miao, C.; Wei, W.; Zhang, G.; Hua, L.; Chen, Y.; Wang, X. Evaluation of CMIP6 Global Climate Models for Simulating Land Surface Energy and Water Fluxes During 1979–2014. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002515. [Google Scholar] [CrossRef]
  69. Lundberg, S.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
  70. Wichansky, P.S.; Steyaert, L.T.; Walko, R.L.; Weaver, C.P. Evaluating the effects of historical land cover change on summertime weather and climate in New Jersey: Land cover and surface energy budget changes. J. Geophys. Res. Atmos. 2008, 113, D10107. [Google Scholar] [CrossRef]
  71. Lawrence, P.J.; Chase, T.N. Investigating the climate impacts of global land cover change in the community climate system model. Int. J. Climatol. 2010, 30, 2066–2087. [Google Scholar] [CrossRef]
  72. Gibbard, S.; Caldeira, K.; Bala, G.; Phillips, T.J.; Wickett, M. Climate effects of global land cover change. Geophys. Res. Lett. 2005, 32, L23705. [Google Scholar] [CrossRef]
  73. Feng, M.; Sexton, J.; Wang, P.; Montesano, P.; Calle, L.; Carvalhais, N.; Poulter, B.; Wooten, M.; Wagner, W.; Elders, A.; et al. Northward migration of the boreal forest confirmed by satellite record. Res. Sq. 2021, preprint. [Google Scholar] [CrossRef]
  74. Boulton, C.A.; Lenton, T.M.; Boers, N. Pronounced loss of Amazon rainforest resilience since the early 2000s. Nat. Clim. Chang. 2022, 12, 271–278. [Google Scholar] [CrossRef]
  75. Pausata, F.S.; Gaetani, M.; Messori, G.; Berg, A.; Maia de Souza, D.; Sage, R.F.; deMenocal, P.B. The Greening of the Sahara: Past Changes and Future Implications. ONE Earth 2020, 2, 235–250. [Google Scholar] [CrossRef]
  76. Sparey, M.; Cox, P.; Williamson, M.S. Bioclimatic change as a function of global warming from CMIP6 climate projections. Biogeosciences 2023, 20, 451–488. [Google Scholar] [CrossRef]
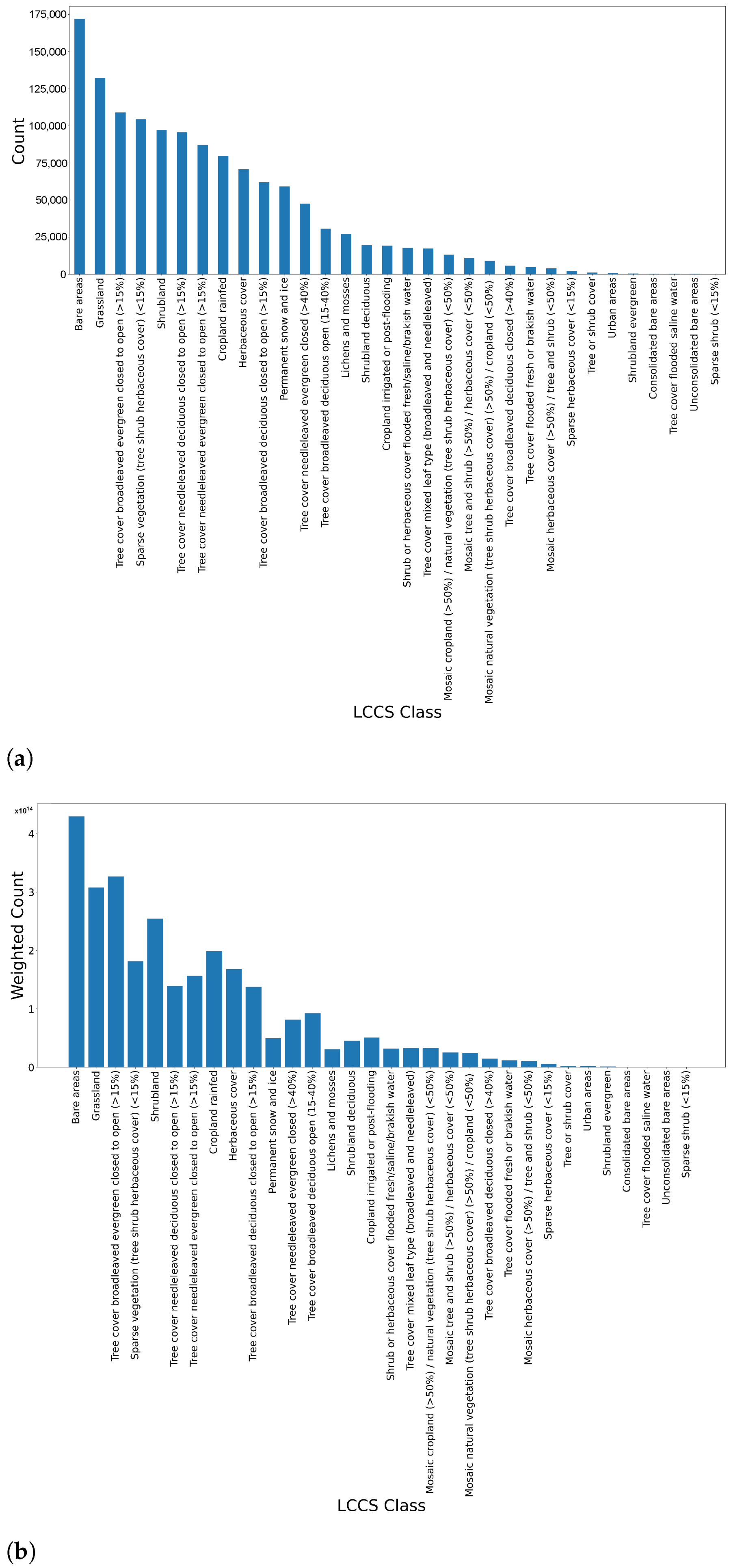
Atmosphere 15 00700 g001
Figure 1. Distribution of classes in training data 1992–2013 inclusive (a) shows the raw count of the number regions attributed to each classification (b) shows the weighted count of the number regions attributed to each classification.
Figure 1. Distribution of classes in training data 1992–2013 inclusive (a) shows the raw count of the number regions attributed to each classification (b) shows the weighted count of the number regions attributed to each classification.
Atmosphere 15 00700 g001
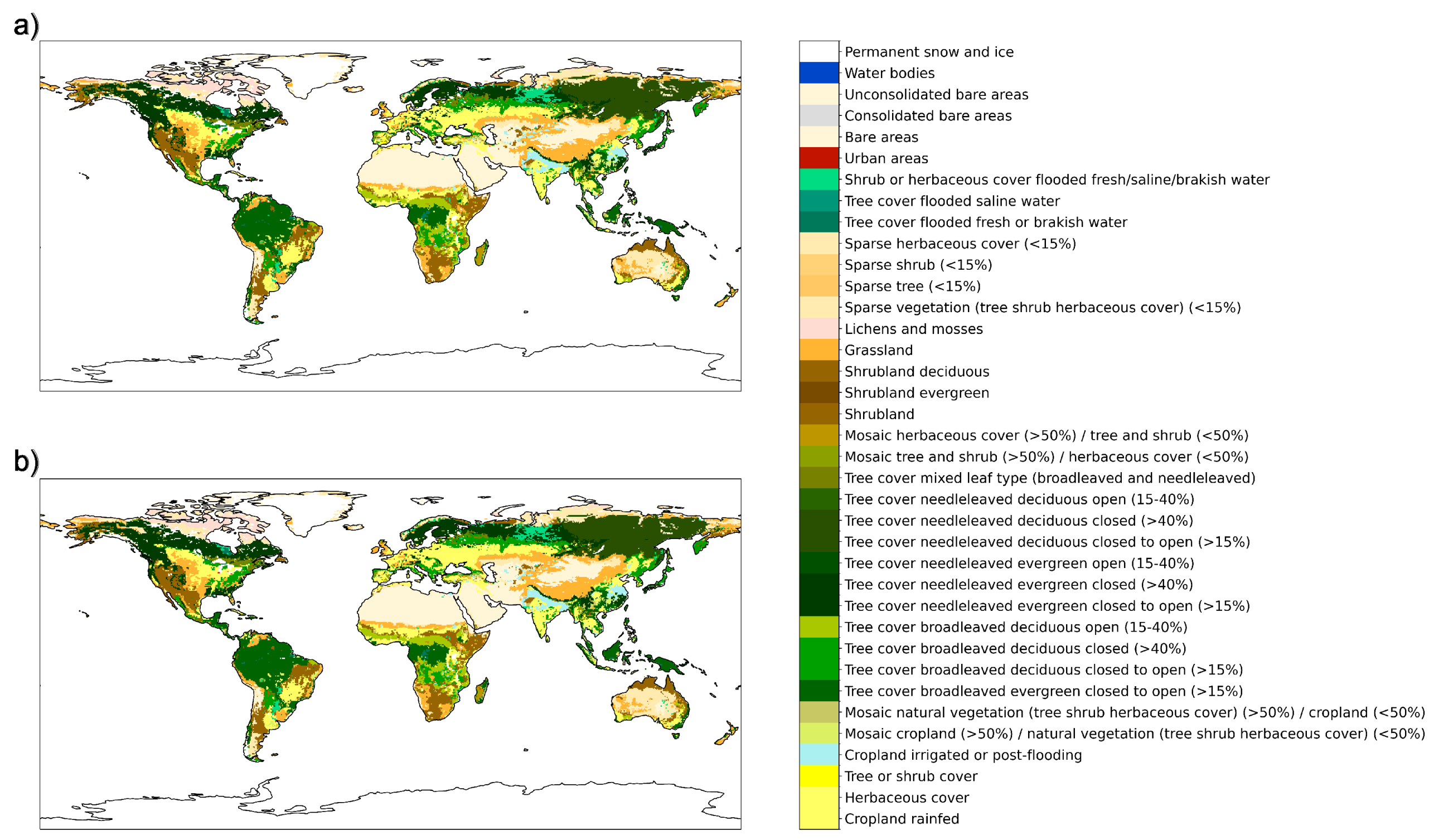
Atmosphere 15 00700 g002
Figure 2. Global land cover classification for the year 2014. (a) The top map shows the true satellite observed classification. (b) The lower map shows the predicted classifications.
Figure 2. Global land cover classification for the year 2014. (a) The top map shows the true satellite observed classification. (b) The lower map shows the predicted classifications.
Atmosphere 15 00700 g002
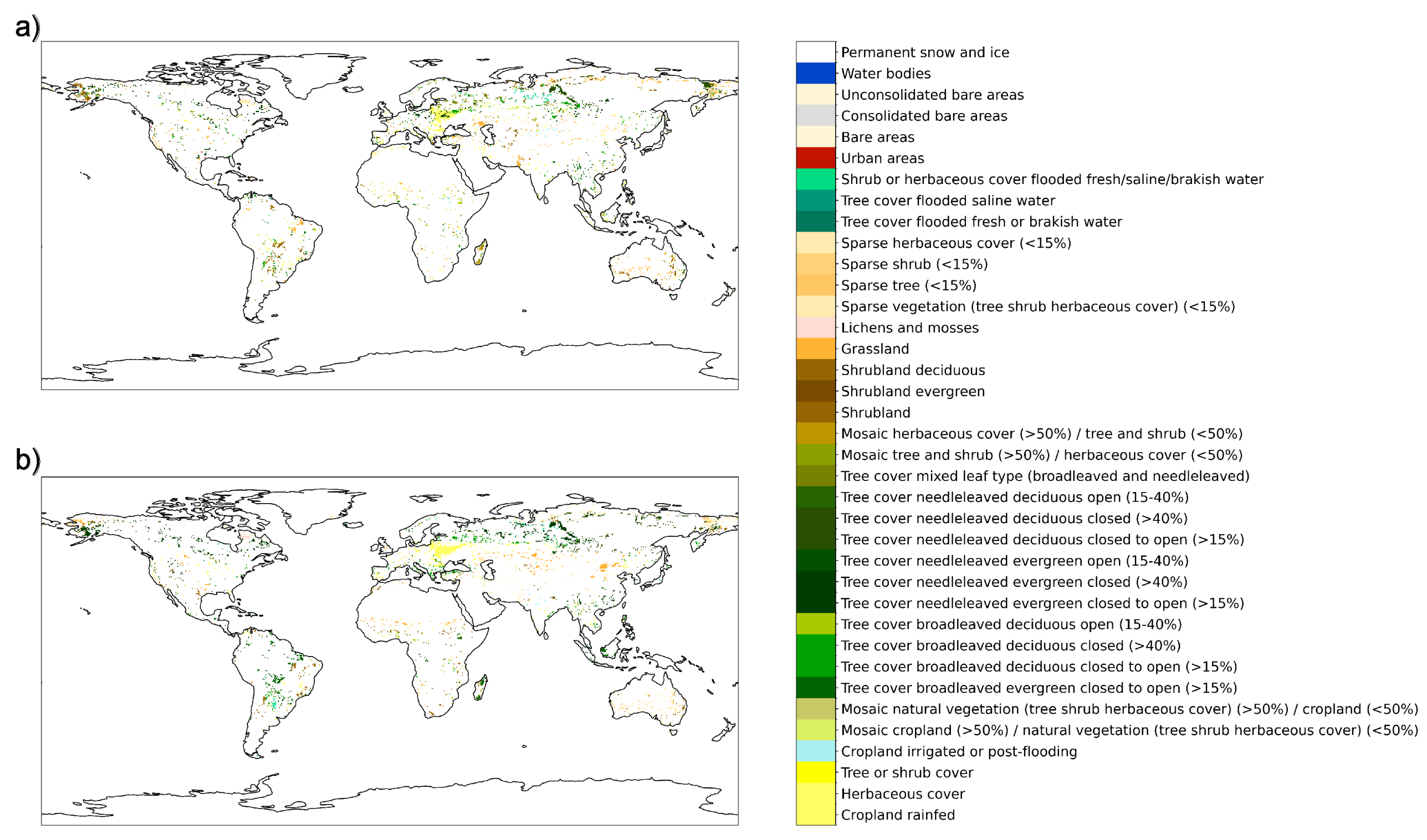
Atmosphere 15 00700 g003
Figure 3. Regions where the observed global land cover classification for the year 2014 disagree with the random forest prediction. (a) The top map shows the true satellite observed classification. (b) The lower map shows the predicted classifications.
Figure 3. Regions where the observed global land cover classification for the year 2014 disagree with the random forest prediction. (a) The top map shows the true satellite observed classification. (b) The lower map shows the predicted classifications.
Atmosphere 15 00700 g003
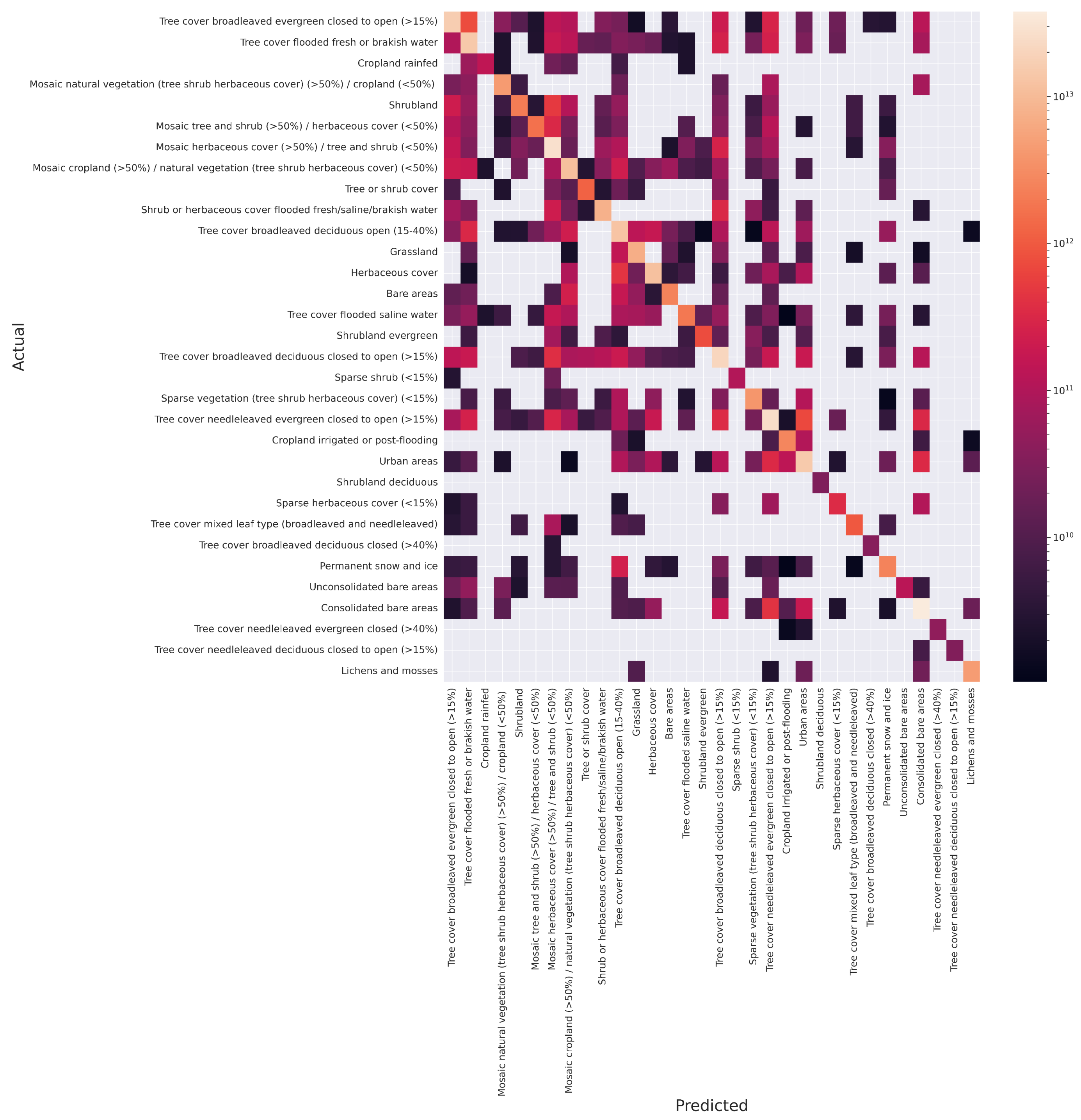
Atmosphere 15 00700 g004
Figure 4. True and predicted classifications for 2014 and 2015, note the logarithmic scale.
Figure 4. True and predicted classifications for 2014 and 2015, note the logarithmic scale.
Atmosphere 15 00700 g004
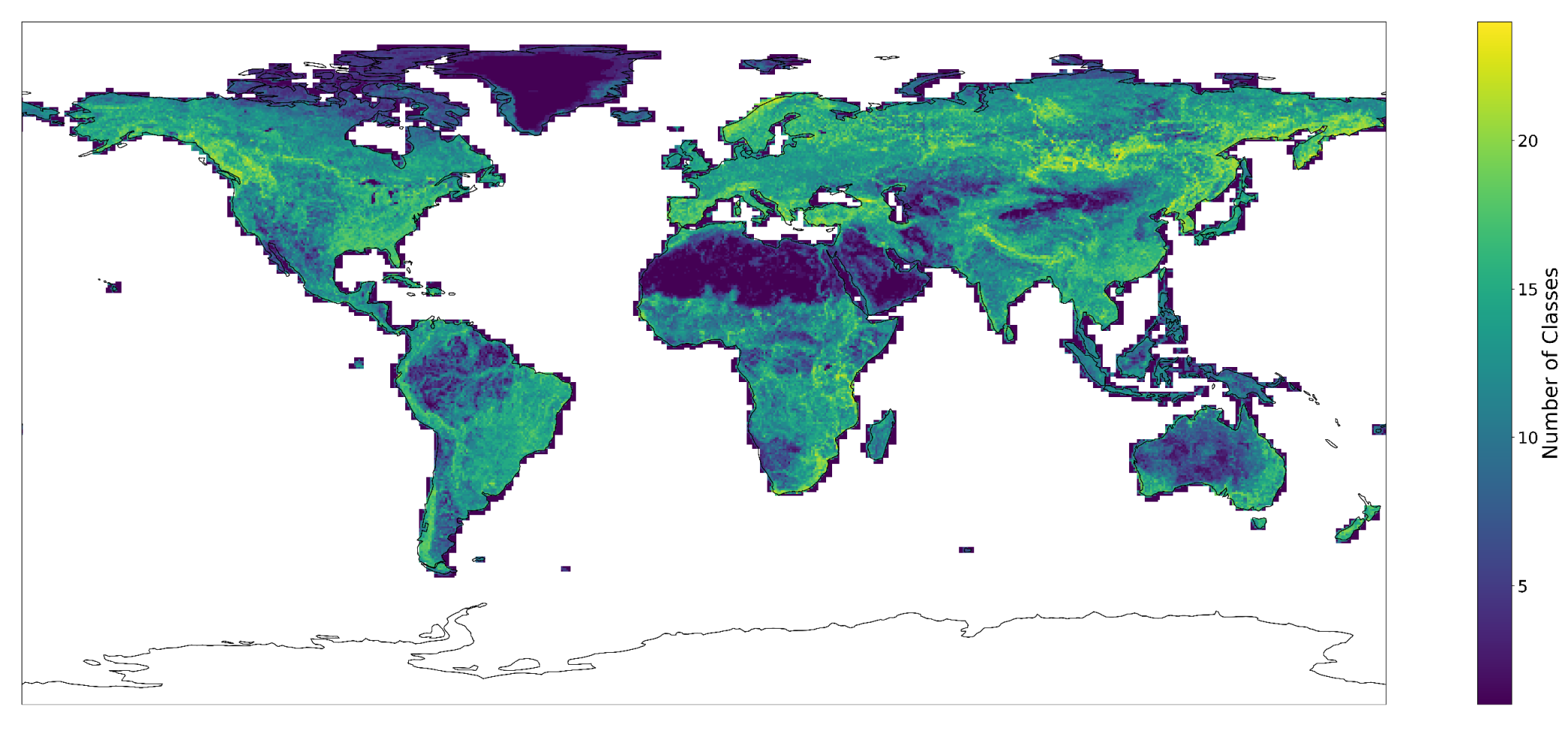
Atmosphere 15 00700 g005
Figure 5. Number of different observed land cover classifications within each 0.5° × 0.5° region that was reduced to a single, dominant classification in this analysis for the year 2014.
Figure 5. Number of different observed land cover classifications within each 0.5° × 0.5° region that was reduced to a single, dominant classification in this analysis for the year 2014.
Atmosphere 15 00700 g005
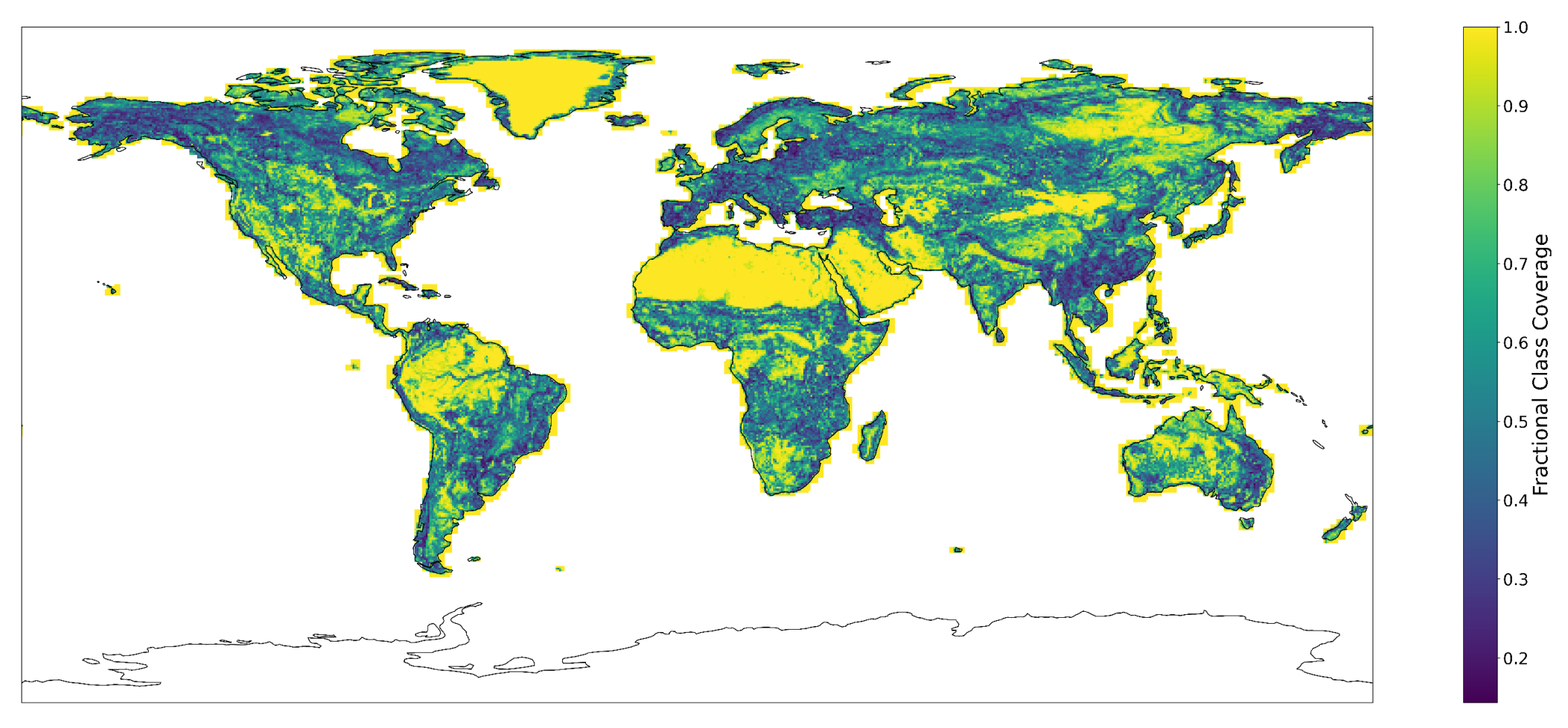
Atmosphere 15 00700 g006
Figure 6. Fraction of the most common observed global land cover classification within each 0.5° × 0.5° region for the year 2014.
Figure 6. Fraction of the most common observed global land cover classification within each 0.5° × 0.5° region for the year 2014.
Atmosphere 15 00700 g006
Atmosphere 15 00700 g007
Figure 7. Feature importance score for each variable in the model, indicating the model’s sensitivity to the feature and feature’s relative importance calculated in two ways (a) shows the feature importance based on the gain from splits which use the feature, and (b) which shows the number of times a feature is split upon in the tree.
Figure 7. Feature importance score for each variable in the model, indicating the model’s sensitivity to the feature and feature’s relative importance calculated in two ways (a) shows the feature importance based on the gain from splits which use the feature, and (b) which shows the number of times a feature is split upon in the tree.
Atmosphere 15 00700 g007
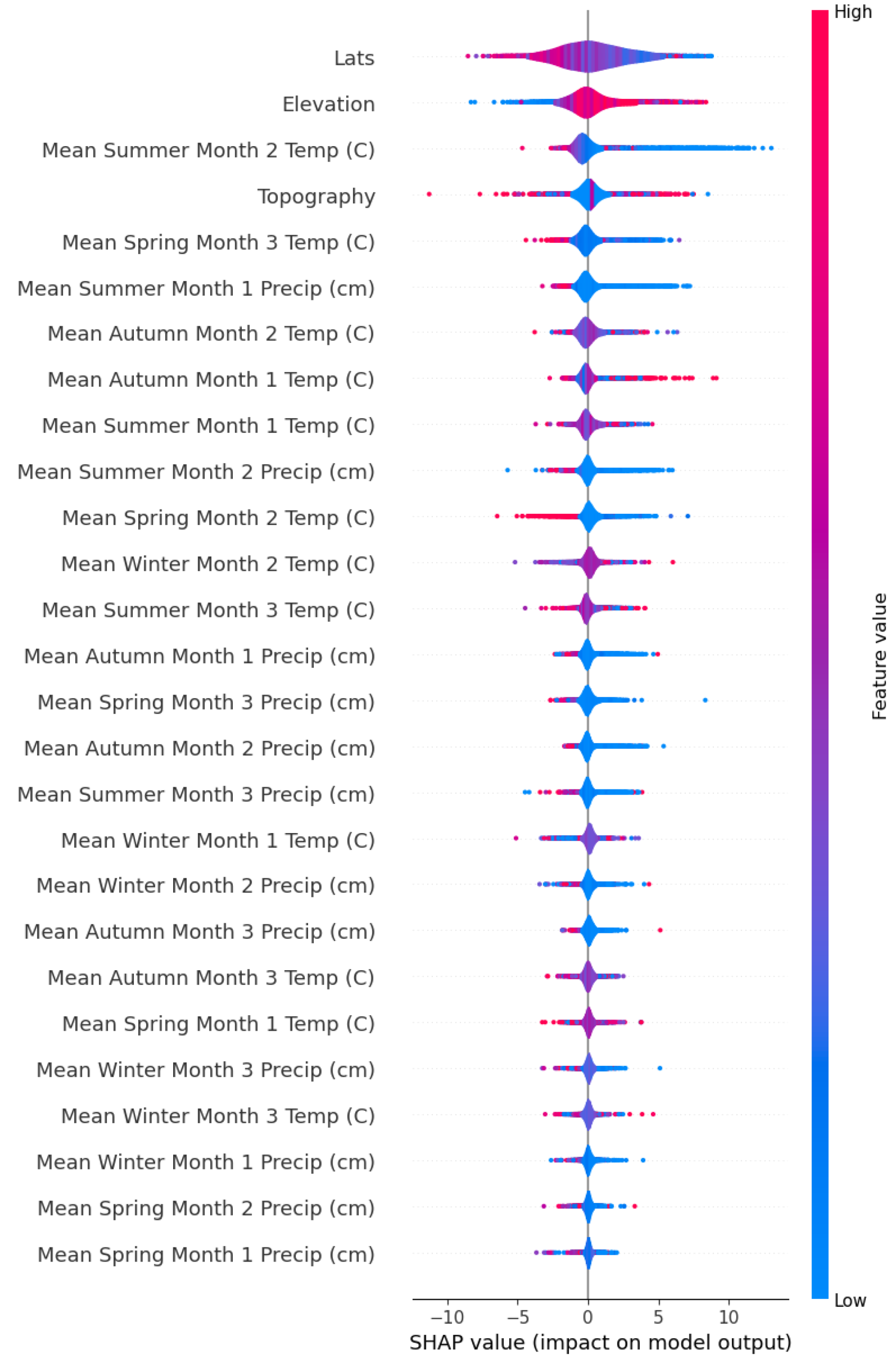
Atmosphere 15 00700 g008
Figure 8. SHAP values for each variable in the model, indicating the feature’s importance.
Figure 8. SHAP values for each variable in the model, indicating the feature’s importance.
Atmosphere 15 00700 g008
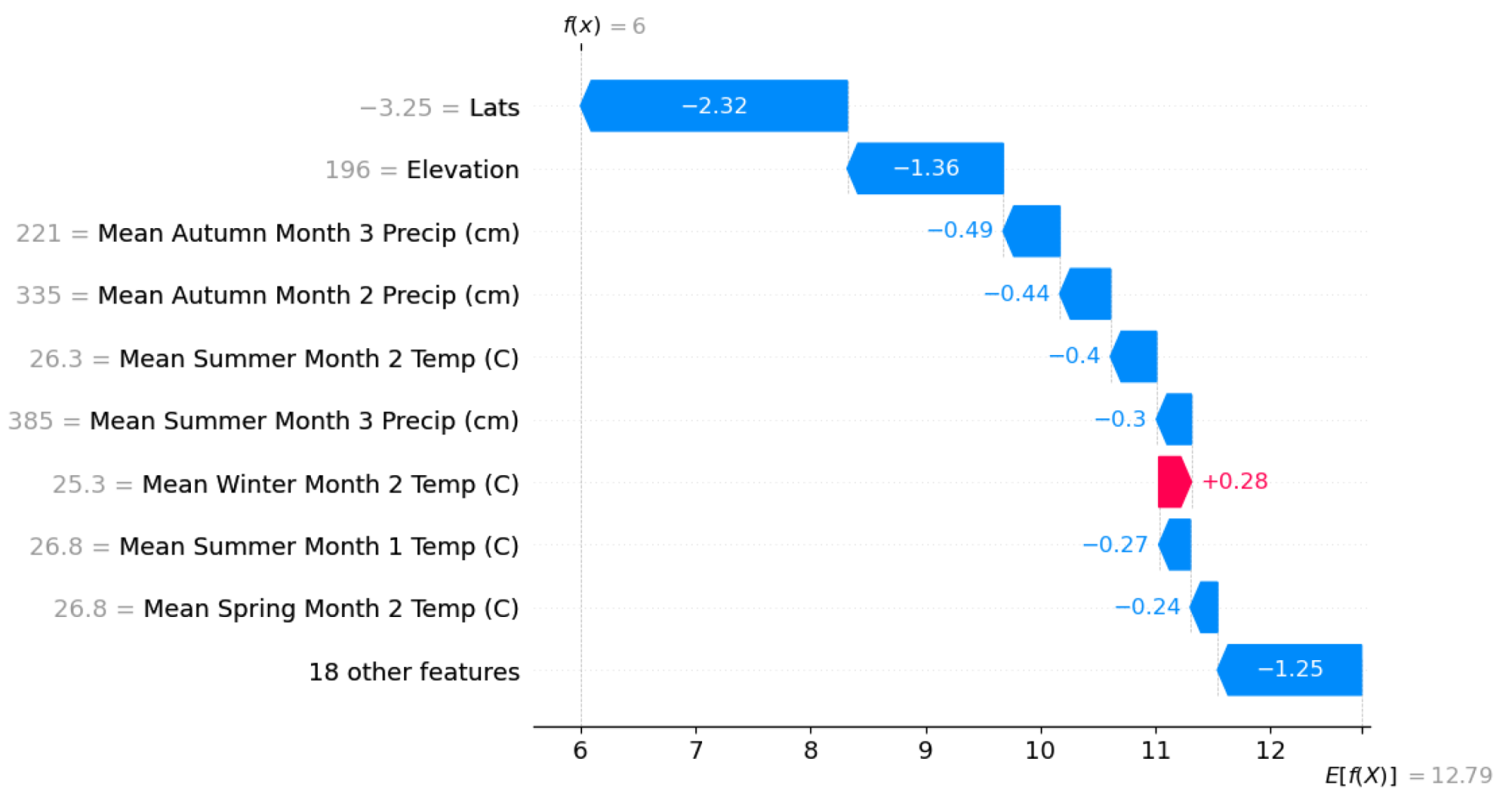
Atmosphere 15 00700 g009
Figure 9. Additive contributions of features to a model’s prediction for the specific instance 3.25° S 57.75° W.
Figure 9. Additive contributions of features to a model’s prediction for the specific instance 3.25° S 57.75° W.
Atmosphere 15 00700 g009
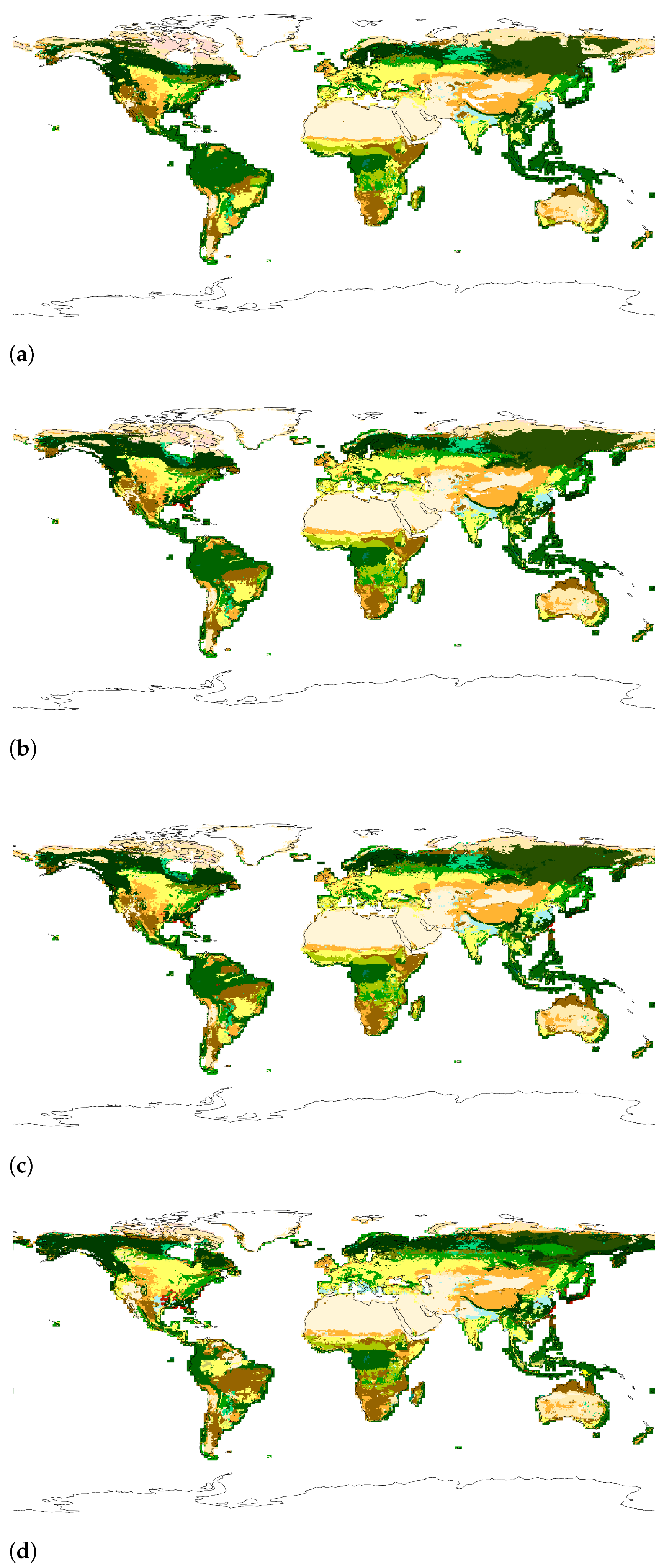
Atmosphere 15 00700 g010
Figure 10. Maps showing the predicted land cover classification at increasing levels of warming based on an ensemble of CMIP6 climate models, legend is same as in Figure 2 (a) shows the predicted land cover at preindustrial temperatures (b) shows the predicted land cover at 1.5K of warming above preindustrial (c) shows the predicted land cover at 2K of warming above preindustrial (d) shows the predicted land cover at 4K of warming above preindustrial number of times a feature is split upon in the tree.
Figure 10. Maps showing the predicted land cover classification at increasing levels of warming based on an ensemble of CMIP6 climate models, legend is same as in Figure 2 (a) shows the predicted land cover at preindustrial temperatures (b) shows the predicted land cover at 1.5K of warming above preindustrial (c) shows the predicted land cover at 2K of warming above preindustrial (d) shows the predicted land cover at 4K of warming above preindustrial number of times a feature is split upon in the tree.
Atmosphere 15 00700 g010
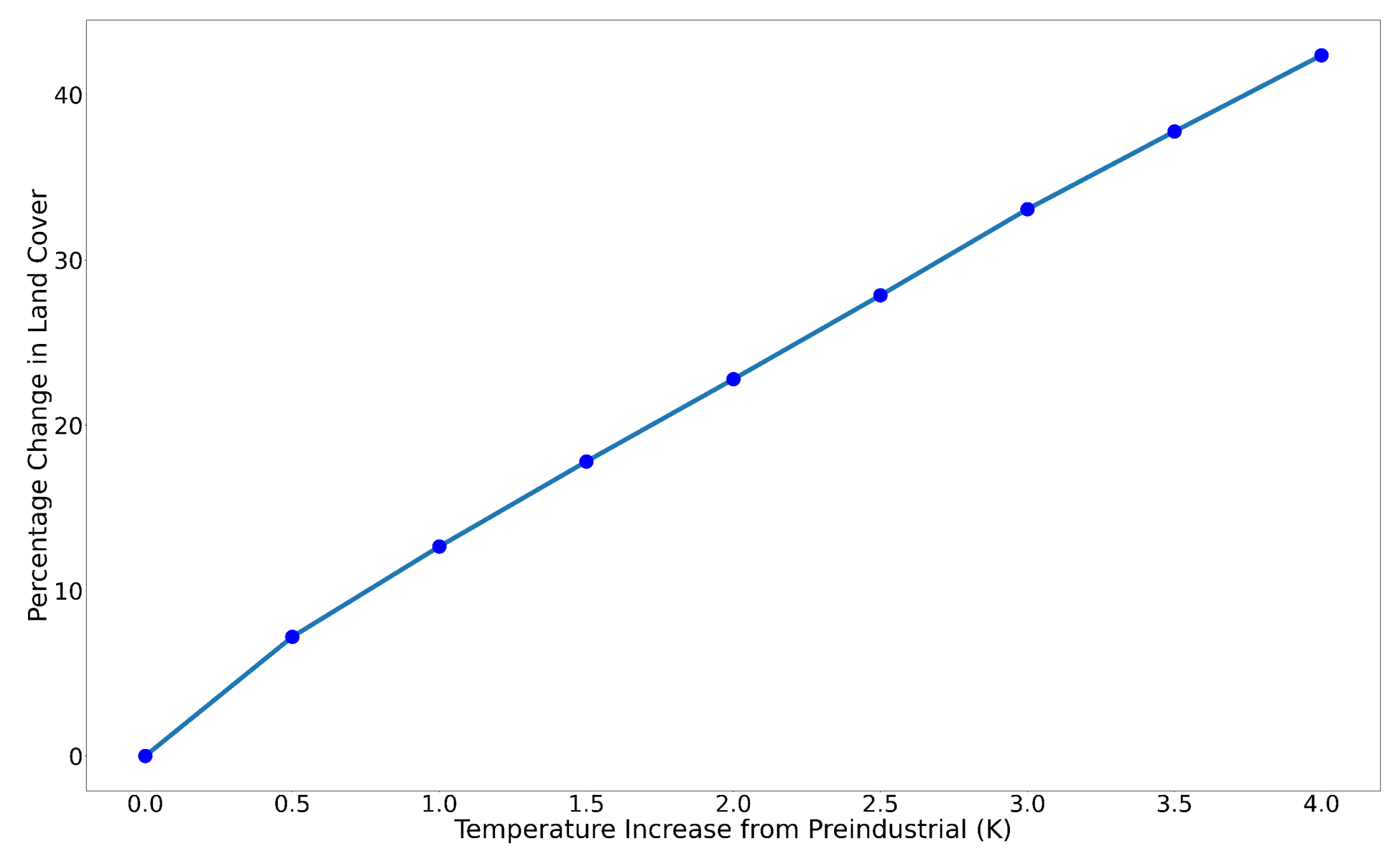
Atmosphere 15 00700 g011
Figure 11. Percentage of land cover area that has changed from its preindustrial classification at increasing levels of warming.
Figure 11. Percentage of land cover area that has changed from its preindustrial classification at increasing levels of warming.
Atmosphere 15 00700 g011
Table 1. Table highlighting the data used and it’s initial resolution and temporal availability.
Table 1. Table highlighting the data used and it’s initial resolution and temporal availability.
DataFrequencyDate RangeInitial ResolutionPublication
ESA Land Cover DataYearly1992–20150.002778° × 0.002778°[37]
TemperatureDaily1901–20190.5° × 0.5°[38]
PrecipitationDaily1901–20190.5° × 0.5°[38]
Topographic IndexSingular20140.5° × 0.5°[39]
ElevationSingular19950.0833333° × 0.0833333°[25]
Table 3. Optimal hyperperameters for model.
Table 3. Optimal hyperperameters for model.
ParameterValue
colsample_bylevelNone
colsample_bynode0.9
colsample_bytree0.9
early_stopping_roundsNone
learning_rate0.2
max_depth63
max_leavesNone
n_estimators300
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sparey, M.; Williamson, M.S.; Cox, P.M. Machine Learning for Global Bioclimatic Classification: Enhancing Land Cover Prediction through Random Forests. Atmosphere 2024, 15, 700. https://doi.org/10.3390/atmos15060700

AMA Style

Sparey M, Williamson MS, Cox PM. Machine Learning for Global Bioclimatic Classification: Enhancing Land Cover Prediction through Random Forests. Atmosphere. 2024; 15(6):700. https://doi.org/10.3390/atmos15060700

Chicago/Turabian Style

Sparey, Morgan, Mark S. Williamson, and Peter M. Cox. 2024. "Machine Learning for Global Bioclimatic Classification: Enhancing Land Cover Prediction through Random Forests" Atmosphere 15, no. 6: 700. https://doi.org/10.3390/atmos15060700

APA Style

Sparey, M., Williamson, M. S., & Cox, P. M. (2024). Machine Learning for Global Bioclimatic Classification: Enhancing Land Cover Prediction through Random Forests. Atmosphere, 15(6), 700. https://doi.org/10.3390/atmos15060700

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop