Abstract
With the ongoing advancement of globalization significantly impacting the ecological environment, the continuous rise in the Land Surface Temperature (LST) is increasingly jeopardizing human production and living conditions. This study aims to investigate the seasonal variations in the LST and its driving factors using mathematical models. Taking the Wuhan Urban Agglomeration (WHUA) as a case study, it explores the seasonal characteristics of the LST and employs Principal Component Analysis (PCA) to categorize the driving factors. Additionally, it compares traditional models with machine-learning models to select the optimal model for this investigation. The main conclusions are as follows. (1) The WHUA’s LST exhibits significant differences among seasons and demonstrates distinct spatial-clustering characteristics in different seasons. (2) Compared to traditional geographic spatial models, Extreme Gradient Boosting (XGBoost) shows better explanatory power in investigating the driving effects of the LST. (3) Human Activity (HA) dominates the influence throughout the year and shows a significant positive correlation with the LST; Physical Geography (PG) exhibits a negative correlation with the LST; Climate and Weather (CW) show a similar variation to the PG, peaking in the transition; and the Landscape Pattern (LP) shows a weak positive correlation with the LST, peaking in winter while being relatively inconspicuous in summer and the transition. Finally, through comparative analysis of multiple driving factors and models, this study constructs a framework for exploring the seasonal features and driving factors of the LST, aiming to provide references and guidance for the development of the WHUA and similar regions.
1. Introduction
With the rapid advancement of global urbanization in recent years, temperatures around the world have been gradually rising. According to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC), human-induced global warming over the past century has resulted in a current global average temperature that is 1.1 °C higher than pre-industrial levels [1,2]. Climate warming has also led to an increase in extreme weather events and natural disasters, which will have significant impacts on human life [3,4,5]. Simultaneously, numerous studies have indicated that solar radiation enhances surface thermal energy [6,7]. In urban areas, a large number of buildings and structures absorb solar radiation and generate substantial heat energy, leading to the occurrence of urban heat island (UHI) effects in local regions [8,9]. This UHI effect can significantly impact human health and living conditions [10].
In China, similar issues are present. Since the reform and opening up, Chinese cities have experienced rapid development. During the continuous expansion of urban areas, many natural ecological resources have been converted into urban construction land, severely damaging the diversity of the ecological environment, as confirmed by numerous studies [11,12]. Additionally, many studies have shown that impervious surfaces in cities easily cause local increases in the Land Surface Temperature (LST), while ecological lands such as forests, grasslands, and water bodies can mitigate temperature rises [13]. Therefore, the encroachment on ecological lands during urban development has damaged the ecological environment, impairing the natural ecosystem’s ability to regulate temperatures and causing local temperature increases. Consequently, many scholars have conducted research on the LST and UHI [14,15,16].
In light of current research, concepts such as the LST [17], UHI, and urban thermal comfort have garnered attention in the academic community [18,19,20,21]. Firstly, regarding research subjects, scholars have focused on exploring thermal environments, particularly concerning the LST, UHI, and thermal comfort [22]. Some researchers have utilized the LST to analyze and calculate the UHI, investigating its spatiotemporal characteristics. Additionally, certain scholars have calculated the Surface Urban Heat Island Intensity (SUHII) to explore its relationship with urban development [23]. Secondly, in terms of research content, emphasis has been placed on the driving factors of thermal environments and their simulation [16,19,24,25]. Currently, the investigation of the spatial driving factors of thermal environments is largely related to urban development, human activities, ecological environment changes, and natural climate characteristics. Previous studies have indicated that human activity significantly impacts the LST, primarily by increasing the local LST and thereby causing thermal differences between regions [26]. Additionally, some studies have pointed out that urban green spaces and water bodies can mitigate the increase in the LST to some extent. Regarding modeling of the driving factors, methods such as multiple linear regression [16], geographical detectors, Geographically Weighted Regression (GWR), and machine learning are commonly used [27,28,29,30]. Among these methods, multiple linear regression and geographic detector models mainly focus on investigating the influence of driving factors on the LST [27]. GWR concentrates on the spatial dimension, providing strong explanatory power at the geographic level [31]. In contrast, machine learning excels in explaining large data models [32,33,34]. Lastly, concerning the spatiotemporal scope of the research, the spatial scales mainly include the urban and natural region scales [16,19], while the temporal scales primarily encompass the diurnal variations [35], seasonal changes, and annual variations of thermal environments [36]. From the aforementioned research, it is evident that the academic community is increasingly focused on exploring urban thermal environments, which have gradually become an important environmental factor influencing human life.
We focus on the changes in the LST, aiming to investigate urban heat environment variations through the seasonal changes in the LST. The LST is a crucial indicator for measuring the urban heat environment, reflecting the changes in the thermal conditions of an area [37]. Compared to past methods that relied on meteorological stations to collect LST data, the use of remote-sensing satellite imagery in recent years has made LST calculations more accurate and temporally robust. In this study, MOD11A1 data were selected. MOD11A1 is preferred over other datasets due to its wide coverage and strong temporal continuity, making it commonly utilized in research on large-scale spatial dimensions [27,35,38].
Through summarizing and synthesizing the relevant research on the LST, it is evident that the exploration of the driving factors for the LST predominantly relies on traditional spatial regression models [39], with relatively limited application of machine-learning algorithms [40]. Compared to traditional spatial regression models, machine-learning algorithms offer advantages in terms of the fast computation speed and high accuracy when dealing with numerous nonlinear relationships. Additionally, the introduction of Shapley additive explanations (SHAP) enables more convenient and intuitive interpretation of machine-learning results [41], with existing research confirming its application in geographic contexts [32]. Currently, spatial analysis of driving factors mainly focuses on administrative boundaries [39], with limited exploration at the grid scale [42]. As mentioned earlier, research on the LST mostly centers on individual cities or broader regional levels, while studies on Urban Agglomeration (UA) and Metropolitan Area (MA) are relatively scarce [16,43].
Considering China’s urbanization development, the transition from “rapid development” to “high-quality development” has elevated the importance of UA as significant spatial development units. Compared to larger provincial or interregional urban clusters, UA exhibit characteristics of close spatial connections and strong collaborative management [44]. The Wuhan Urban Agglomeration (WHUA), centered around Wuhan City and comprising eight surrounding municipalities, holds considerable development potential. Meanwhile, this region is also one of the areas in the central part of China with relatively high summer temperatures, making it of significant research value. Some scholars have interpreted the LST of the WHUA from the perspectives of carbon emissions and urban development, revealing a certain association between carbon emissions and the LST [29]. Others have adopted a reverse-thinking approach to explore the thermal spatial pattern in this area, attempting to alleviate the urban heat island effect by identifying the heat source points [24]. Additionally, some researchers have focused on studying LST variations at the individual city level by using Wuhan City as their research scope [45,46]. However, studies on the seasonal variations and driving factors of the LST in this region are still relatively scarce. Many studies have not specifically explored the effects of driving factors on various spatial units [47], but investigating their effects on spatial units would contribute to the precise implementation of urban collaborative management policies. Therefore, it is particularly important to investigate the changes in the LST and their driving factors in this region.
In summary, this study selects the WHUA as the research area, covering different seasons as the temporal scope. Various mathematical models are employed to investigate it, exploring the driving factors’ impact on the LST across spatial units. The main research objectives include: (1) systematically studying the seasonal variations in the LST in the WHUA, (2) exploring the primary driving factors for the LST, (3) evaluating the spatial explanatory power of different models for the driving factors and selecting the optimal model for analysis, (4) investigating the spatial effects of various driving factors on the LST within the WHUA, and (5) proposing policy measures to mitigate the LST and provide references for the development of the WHUA.
2. Research Area and Data Sources
2.1. Study Area
This study selects the WHUA as the research area. The WHUA mainly includes nine cities, including Wuhan City and its surrounding areas, such as Huangshi, Huanggang, Xiaogan, Xianning, and Qianjiang. The total area of the WHUA is 57,800 km² (Figure 1) [47]. The region belongs to a subtropical monsoon climate, characterized by hot summers. At the same time, the region has experienced rapid development in recent years, with a large population and industries concentrated in this area, posing significant challenges for its future development [48].
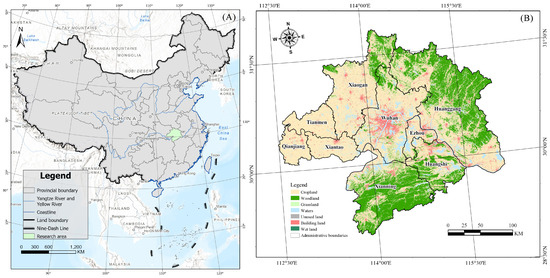
Figure 1.
Study area scope. (A) Geographic location of the study area. (B) Land use and administrative zoning in the study area in 2020.
2.2. Data Sources
This study aims to explore the seasonal variations in the LST and its driving factors. Therefore, the data sources for this study can be divided into temperature data and driving factor data.
Regarding the LST exploration, this study focuses on macro-geographical areas like the WHUA, which have relatively large research areas. Thus, MOD11A1 data were used in this study. This dataset provides LST data four times a day, making it convenient and offering high data accuracy for studying the LST at a macro-geographical scale [35,38,49].
For the investigation of the driving factors, 16 influencing factors were selected to examine their impact on the LST (see Figure 2). To eliminate differences among the data, the obtained driving factors were processed through clipping and coordinate system standardization, and their spatial resolution was unified to 1 km × 1 km to facilitate the subsequent calculations. For the specific data sources, please refer to Table A1 below.

Figure 2.
Spatial distribution of the drivers: (A) AI, (B) SHDI, (C) SLOPE, (D) WIND, (E) ROAD, (F) POP, (G) PD, (H) NPP, (I) NDVI, (J) LPI, (K) BH, (L) HUM, (M) GDP, (N) ED, (O) DEM, and (P) CA.
Through related studies, it is evident that the WHUA is located in the northern subtropics and has a distinct subtropical monsoon climate (see Figure 3) [16,27]. Therefore, the seasons in the WHUA are divided into summer, transition, and winter. Based on the precipitation and temperature data for this region, it can be observed that from June to August, the temperatures are slightly higher than in other seasons, while in May and September, the temperatures are similar and also higher than in other months. Analyzing the precipitation statistics, it is evident that the region experiences substantial rainfall from June to September. Therefore, considering the hot and rainy climate characteristics of summer, June to September is designated as the summer in this study. Similarly, based on the temperature and precipitation characteristics, November, December, January, and February are classified as winter. From March to May, the precipitation in the study area remains relatively low, and the temperatures gradually rise. In October, both the precipitation and temperature drop significantly compared to September. Considering the classification of summer and winter and aiming to maintain seasonal continuity, March, April, May, and October are designated as transition.

Figure 3.
Climate characteristics of the study area. (A) Monthly temperature data for the WHUA in 2020. (B) Monthly precipitation data for the WHUA in 2020.
3. Research Methods
3.1. LST Calculation
The LST data used for this research were sourced from the MOD11A1 dataset. Data collection for the study area was conducted using the Google Earth Engine platform. The average daytime LST for each month throughout the year was integrated for the calculation [37,50]. The pixel values of the calculated images were converted to degrees Celsius using the following formula:
where DN represents the brightness temperature in the MOD11A1 dataset.
3.2. Calculation of Relevant Indicators Based on Fragstats Software
Fragstats 4.2 is commonly used for calculating landscape pattern indices, providing good explanatory power in assessing and quantifying the spatial structure, landscape distribution, and fragment characteristics of landscapes [51,52]. In recent years, many scholars have also applied it to calculate indicators related to urban morphology, and its calculation results have been confirmed to effectively reflect urban spatial morphological characteristics [53].
Based on previous studies on landscape pattern indices and the LST, as well as research on urban morphology elements and the LST [16,27], this study selected four indicators related to landscape patterns and two indicators related to urban morphology as the driving factors for the LST. The landscape pattern indices include the Patch Density (PD), Edge Density (ED), Largest Patch Index (LPI), and Shannon’s Diversity Index (SHDI). As for the urban morphology, this study selected two indices: Class Area (CA) and Aggregation Index (AI). For the specific meanings and calculation procedures regarding these indices, please refer to the Supplementary Materials.
3.3. Spatial Feature Analysis
3.3.1. Spatial Autocorrelation
Spatial autocorrelation is commonly used in geographic research to explore the spatial distribution of features, including both global spatial autocorrelation and local spatial autocorrelation [54].
Global spatial autocorrelation describes the correlation of different spatial locations across the entire study area, often reflected by Moran’s I. Moran’s I primarily indicates the degree of spatial correlation of attribute values across all data, with values ranging from −1 to 1. A value less than 0 indicates negative correlation, equal to 0 indicates no correlation, and greater than 0 indicates positive correlation. The significance level of the Moran’s I index is tested using a standardized Z value, where a Z value greater than or less than 1.96 indicates significant spatial autocorrelation in the spatial units’ functionality [55].
Local spatial autocorrelation, on the other hand, examines the correlation between each spatial unit and its neighboring units within the study area, reflecting the clustering and differentiation of local spatial units. Based on the results of the cluster analysis, it can be categorized into five types: High–High (H-H) cluster, High–Low (H-L) cluster, Low–Low (L-L) cluster, Low–High (L-H) cluster, and No significance [27]. The specific calculation process is detailed in the Supplementary Materials.
3.3.2. Standard Deviational Ellipse (SDE)
The Standard Deviational Ellipse (SDE) is commonly used to measure the spatial distribution characteristics of features. In this study, SDE was employed to identify the seasonal spatial variation characteristics of LST. SDE constructs a spatial distribution ellipse based on basic parameters such as the standard deviation along the major and minor axes from the center, depicting the relevant spatial distribution characteristics of the research subject [56]. For specific calculation procedures, please refer to the supplementary materials.
3.4. Principal Component Analysis (PCA)
Principal Component Analysis (PCA) is a commonly used multivariate statistical method aimed at reducing the dimensionality of data while retaining information. It achieves this by linear transformation, mapping the original data into a new coordinate system where the variance of the data is maximized. This new coordinate system is composed of a set of orthogonal basis vectors called principal components, each of which is a linear combination of the various features in the original data [38]. We employed PCA to perform dimensionality reduction on the multidimensional driving factors. This enabled us to identify the primary components influencing the LST, thereby simplifying the model and facilitating a more intuitive interpretation of the driving factors. The specific calculation process is detailed in the Supplementary Materials.
3.5. Construction of Driving Factor Exploration Model
3.5.1. Model Performance Evaluation Metrics
Based on a review of the relevant literature, we selected multiple evaluation metrics, including the coefficient of determination (R2), mean absolute error (MAE), mean square error (MSE), mean absolute percentage error (MAPE), and root mean squared error (RMSE), to compare and select the optimal model for exploring the LST’s driving factors. These metrics differ in their interpretation of model accuracy. A higher R2 indicates a better model fit, while smaller MAE, MSE, MAPE, and RMSE values indicate a better model fit [57]. The specific calculation process for these metrics is detailed in the Supplementary Materials.
3.5.2. Traditional Geographic Spatial Regression Models: GWR and MGWR
Currently, geographic spatial regression models mainly include GWR and Multiscale Geographically Weighted Regression (MGWR). To assess the effectiveness of traditional geographical spatial regression models in exploring the LST’s driving factors, we selected the GWR and MGWR models for comparative analysis.
GWR, as a type of geographic spatial regression model, is widely used in geographic spatial calculations and research. It explores the spatial changes and related driving factors of the research object at a certain scale by establishing a local regression equation at each point within the spatial scope. It has good explanatory power in geographical spatial research. The MGWR model evolved from the GWR model, improving the fixed bandwidth aspect of the GWR model, thereby making the model calculations more accurate [31,58]. The specific calculation process is detailed in the Supplementary Materials.
3.5.3. Machine Learning: Extreme Gradient Boosting (XGBoost)
XGBoost is a type of Boosting algorithm initially developed by Chen et al. [59], which is widely utilized for its advantages in terms of the computational speed and accuracy. It addresses classification, regression, and prediction problems by constructing decision trees and has been extensively applied across various disciplines. In geographical spatial research, there are studies indicating that XGBoost yields superior model interpretation results compared to traditional spatial regression models [32]. Therefore, this study employs the regression function model within XGBoost. The specific calculation process is outlined below:
In this equation, k represents the total number of regression trees, denotes the prediction value of the k-th model in the i-th sample. Γ represents the space of the regression trees.
The objective function of XGBoost consists of two parts. The first part is the loss function, indicating the model’s fitting degree. The second part is the regularization term, aiming to control the complexity of the model.
In this equation, n represents the number of samples; denotes the true value of the i-th sample; represents the output value when the sample is predicted; is the loss function; and represents the regularization term, and its calculation process is as follows:
In this equation, T represents the current number of leaves, denotes the weight of the j-th leaf node, is the complexity cost introduced by additional leaves, and is a constant controlling the degree of regularization [33,60].
3.5.4. Explanation of Machine-Learning Models: Shapley Additive Explanations (SHAP)
We employ SHAP to interpret the results of the machine-learning models. This method originates from the Shapley value in game theory, initially proposed by Lundberg and Lee [41]. The Shapley value refers to the contribution of each feature to the sample [61]. It has previously been demonstrated to have a good spatial explanatory power. Therefore, we use SHAP to interpret the results of machine-learning models, where the SHAP values can be interpreted as the impact on the model output [32]. The calculation of the Shapley value for each feature X is as follows:
where represents the contribution of each feature , n is the total number of features, and and represent the model results including or excluding the i-th feature, respectively.
4. Results
4.1. Seasonal Variation Characteristics of LST in WHUA
We utilized the MOD11A1 dataset to acquire the annual LST of the WHUA, and based on data such as the wind speed and precipitation, we divided it into three seasons: summer, transition, and winter. Meanwhile, based on the administrative division of each city, the maximum, minimum, and mean values of the LST within the WHUA were extracted for comparative analysis.
As shown in Figure 4, significant temperature differences exist among different seasons. Looking at the different cities, there are significant differences in the LST among them. Overall, during summer, there are large differences between the average and maximum LST values among the various cities within the WHUA, while the differences between the minimum and maximum values are smaller during the transition and winter. In summer, Tianmen City has a higher LST than the other cities, and its LST shows relatively stable changes, while Huanggang City exhibits larger fluctuations in the LST. In the core area of the WHUA, Wuhan City, its maximum LST is second only to Huanggang City and Tianmen City. During the transition, Tianmen City has the highest maximum LST, and its LST changes show a relatively stable trend. Additionally, Wuhan City, Xianning City, and Huangshi City all show significant increases in the maximum LST during the transition. In winter, the LST fluctuations of each city are relatively small, with Xianning City having the highest maximum LST and Huanggang City having the lowest minimum LST.

Figure 4.
Seasonal variation in the LST in the WHUA: (A) summer, (B) transition, (C) winter, (D) LST values for each city in summer, (E) LST values for each city in the transition, and (F) LST values for each city in winter.
Examining the global spatial autocorrelation results (Table 1), it can be observed that the Moran’s I values are close to 1 in the different seasons, with z-scores far exceeding 1.65 and p-values close to 0. This indicates a significant clustering tendency of the LST in different seasons. Considering the local spatial autocorrelation results (Figure 5), during the summer, a distinct “H-H” clustering pattern is evident in the central urban area of Wuhan City and the northern region of Huanggang City. Additionally, prominent “H-H” clustering patterns are observed in areas where the three county-level cities of Tianmen, Qianjiang, and Xiantao intersect, as well as in the urban built-up areas of each county-level city. During the transition, notable “H-H” clustering patterns are observed in the western regions of the WHUA, specifically in the areas of Tianmen and Xiaogan. Similar clustering patterns are also observed in the urban built-up areas of various county-level cities. In winter, the clustering patterns of the LST exhibit spatial distribution differences compared to the transition and summer seasons. Significant “H-H” clustering patterns are observed in the mountainous areas in the southern and western regions of the WHUA, while the central urban area of Wuhan City and the built-up areas of other county-level cities exhibit less distinct patterns.

Table 1.
Results of the LST global autocorrelation analysis for the different seasons in the WHUA.
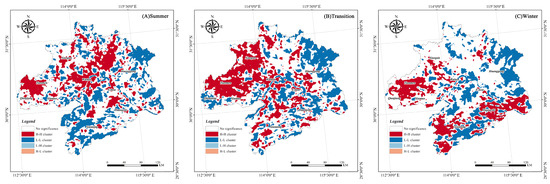
Figure 5.
Spatial clustering map of the LST for the different seasons in the WHUA: (A) summer, (B) transition, and (C) winter.
Regarding its trend, this study analyzed the spatial variation trends of the LST during different seasons using SDE analysis (Table 2). As depicted in Figure 6, the centripetal features of the LST in the WHUA are not pronounced, but a predominant “southwest-northeast” trend can still be discerned. Considering the variation trends across different seasons, it can be observed that the minor axis gradually increases starting from the summer, indicating a weakening clustering tendency of the LST. Examining the flatness, it shows a trend of initially decreasing and then increasing from summer, suggesting a gradual decrease in the directionality of the LST starting from summer, and gradually increasing by winter. Considering the change in the central point, from summer to transition, the LST center moved southwestward by 0.95 km, indicating a slight increase in the LST in the southwest of the WHUA. From transition to winter, the LST center shifted southeastward by 1.05 km, indicating a certain increase in the LST in the southeast part of the WHUA during winter.

Table 2.
SDE parameters of LST in WHUA in different seasons.
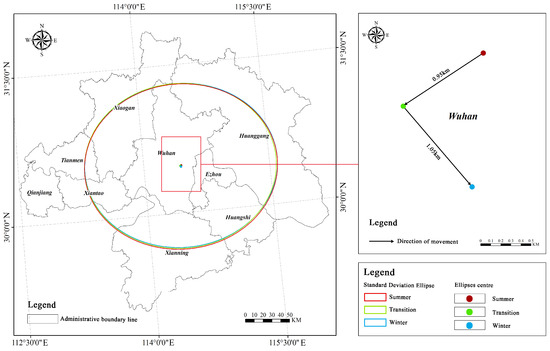
Figure 6.
SDE of the LST in the WHUA in different seasons.
4.2. Exploration of LST Drivers and Model Selection
4.2.1. Selection of LST Drivers
We selected 16 driving factors, including the DEM, SLOPE, NDVI, WIND, etc., for exploration. To eliminate multicollinearity among the driving factors, we employed Principal Component Analysis (PCA) to reduce the dimensionality of the driving factors (Table 3). We chose eigenvalues greater than one as selection criteria and selected four principal components to interpret the driving factors.

Table 3.
Total variance explained by the principal components of the LST drivers.
Meanwhile, we obtained the component matrices of each driving factor (Table 4), which included the impact of each driving factor on the different principal components. This study identified factors with higher coefficients in the principal components and organized them accordingly. Upon examination of the organized results, it was observed that the BH, NPP, GDP, CA, and POP had relatively high proportions in Principal Component 1. These factors are commonly used to represent human socioeconomic activities; thus, Principal Component 1 was designated as Human Activity (HA). Similarly, Principal Component 2 predominantly comprised the ED, LPI, PD, and SHDI, representing the Landscape Pattern (LP); Principal Component 3 was characterized by the DEM and SLOPE, representing Physical Geography (PG); and Principal Component 4 was dominated by the HUM and WIND, which are often used to represent climate and weather characteristics, hence designated as Climate and Weather (CW). In summary, this study utilized PCA to reduce the dimensionality of the factors and divided them into four principal components based on their dimensional characteristics, representing the features of HA, LP, PG, and CW, respectively, facilitating the exploration of the spatiotemporal forces of various features on the LST.

Table 4.
Component matrix for each driver.
4.2.2. Model Selection for Investigating Driving Factors
To better explore the spatial effects of the LST’s driving factors, this study compared various models, including GWR, MGWR, and XGBoost, and determined the model for investigating the driving effects based on various indicators, such as the R2, MAE, MSE, and MAPE.
By comparing different models across seasons based on various indicators, such as the R2, MAE, MSE, and MAPE (Table 5), it was observed that, within the scope and context of this study, there was little difference in the explanatory power between the GWR and MGWR models. MGWR slightly outperformed GWR in summer and winter, while GWR had a slight advantage over MGWR in the transition. XGBoost consistently outperformed both the GWR and MGWR models across different seasons. Overall, the results obtained using XGBoost were relatively good, with an R2 above 0.8 and an RMSE below 0.45, along with other favorable indicators. Regarding the model accuracy across different seasons, it was found that the driving factor fitting effect was best in summer, with an R2 of 0.84 and an RMSE of 0.4, followed by the transition, while the fitting effect was poorest in winter. Therefore, we selected XGBoost as the model for investigating the spatial driving factors.

Table 5.
Evaluation of the accuracy of exploring the results of the LST’s drivers based on different models.
4.2.3. Effects of Each Driving Factor
The introduction of local interpretability methods such as the SHAP has made the results of machine-learning computations more intuitively understandable. The SHAP values can represent the contribution of each feature in the model, providing a good solution for exploring the driving factors of the LST [32]. Previous research has shown that compared to traditional spatial statistical models, machine-learning models interpreted using the SHAP can better explore nonlinear and interaction effects in geographical space. Moreover, combining the SHAP values with geographic spatial information can better identify their spatial characteristics [33]. Therefore, this study further analyzed and explored the results obtained from the SHAP and XGBoost regression (Figure 7).
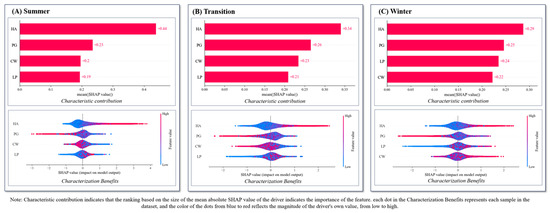
Figure 7.
An exploration of the role of the LST’s drivers in the WHUA: (A) summer, (B) transition and (C) winter.
In terms of the contribution of the driving factors, based on the mean |SHAP value|, the impact of the different driving factors on the LST can be observed. Overall, the influence of each driving factor on the LST is higher in summer than in the transition and winter, with the transition being slightly higher than winter. When considering individual driving factors, HA plays a dominant role in all the seasons, with its effect being most significant in summer and relatively weaker in the transition and winter. Following HA, PG also exhibits a noticeable advantage in influencing the LST, with its effect being most pronounced in the transition, followed by winter, and relatively weaker in summer. CW and PG show relatively consistent variations in their effects across different seasons, peaking in the transition and reaching the minimum in summer. LP reaches its maximum impact in winter and its minimum impact in summer.
Examining the specific variations in individual samples, HA demonstrates a clear positive effect on the LST, with samples having higher HA values showing a positive effect and those with lower HA values showing a negative effect. Conversely, PG exhibits a notable negative effect, with most samples with high PG values showing a significant negative effect on the LST, particularly evident in the transition and winter. For CW, its effect is more pronounced in the transition and summer, with the samples having higher CW values showing a negative effect, while those with lower CW values show a positive effect. However, in winter, there is a reversal in this effect, with most samples showing effects opposite to those in the transition and summer. As for LP, its effect is relatively inconspicuous in summer and the transition, with some samples showing a negative effect in winter for lower LP values and a positive effect for higher LP values.
In summary, the effects of various driving factors on the LST show relatively significant variations across the different seasons. This study further elucidates their spatial effects by integrating individual sample points with geographic spatial information.
4.3. Spatiotemporal Heterogeneity of LST Driving Factors
To investigate the spatial effects of the various driving factors and their differences across different seasons, this study integrates the calculated SHAP values with spatial information and performs visualization processing to obtain the spatial effects of the different driving factors on the LST across different seasons (Figure 8).

Figure 8.
Seasonal spatial role effects of the LST in the WHUA. (A) The seasonal spatial effects of HA on the LST. (B) The seasonal spatial effects of LP on the LST. (C) The seasonal spatial effects of PG on the LST. (D) The seasonal spatial effects of CW on the LST.
Considering the spatial effects, the spatial influence of HA in the WHUA mainly concentrates in the urbanized areas of each town. This influence is predominantly positive, radiating outward from the core of Wuhan City and gradually decreasing toward the periphery. Consistent with the exploration results of the driving factors mentioned earlier, this effect peaks in summer and diminishes in the transition and winter seasons, with no significant variation in the spatial influence.
Regarding PG, its positive spatial effect in the WHUA predominantly concentrates in the plains formed by Tianmen City, Qianjiang City, and Xianning City, reaching its peak in the transition. Meanwhile, it exhibits a noticeable negative effect near the mountains in the northern and southern parts of the WHUA. In summer, PG’s spatial effect resembles that of the transition but with relatively weaker intensity. However, in winter, the positive spatial effect of PG shifts, with valleys in the southern part of the WHUA becoming areas of relatively strong positive influence, while the negative effect areas remain largely unchanged.
For CW, its positive effect areas bear some resemblance to PG, primarily aggregating in the western plains of the WHUA in the summer and transition seasons and in the valleys of the southern region in winter. The negative effect areas predominantly distribute along the water systems in the southern part and the mountains in the northern part of the WHUA, with the effect peaking in the transition.
As for LP, its positive effect areas are mainly located in the southern region of the WHUA, particularly in Xianning City, and the western plains, while the negative effect areas concentrate in the central area of the WHUA, including Wuhan City and its surrounding areas. This spatial effect is relatively prominent in winter, whereas it is weaker in the summer and transition seasons.
In summary, there are certain differences in the spatial patterns of the various driving factors in the WHUA, and factors such as PG, CW, and LP exhibit spatial variations across different seasons. Further analysis should integrate their natural characteristics with urban development.
5. Discussion
5.1. Analysis of Seasonal Variations in the LST in the WHUA
The WHUA is situated with large mountain ranges to the north and south, while the central and western regions consist of plains, with the Yangtze River passing through the central part. Additionally, Wuhan City, as a crucial growth pole in Central China, serves as a pivotal support point for the Central Rise Strategy, experiencing rapid urban development and continuous growth at both the urban and population scales in recent years. Its unique natural resource conditions and socio-economic development factors have significant implications for the generation of the LST in the WHUA [48].
Combining the above research findings, it can be observed that the WHUA exhibits relatively noticeable temperature variations across different seasons, with significant differences in the LST observed among cities during the summer. The primary reason for this may be attributed to the subtropical location of Wuhan City, where temperature changes are more pronounced across different seasons [16,24,27]. Meanwhile, terrain and human activities also contribute to changes in the LST. It is not difficult to find from previous studies that with the continuous elevation of terrain, there is a significant decrease in the LST. In high-altitude areas, due to the low atmospheric pressure, there is poor insulation in the atmosphere, leading to significant heat loss [17,62]. Conversely, in urban areas, the situation is quite the opposite. The abundant building materials in urban areas have good heat absorption properties, causing an increase in the LST during daytime when the sunlight is directly incident. Additionally, research has indicated that human activity is relatively intense in summer compared to other seasons, and the significant emission of greenhouse gases from human activities is also one of the important reasons for the increase in the LST [27,39]. Therefore, the variation in the LST during summer appears to be relatively pronounced compared to other seasons.
Examining specific cities and their geographical locations, in summer, the eastern plains (primarily Tianmen City), central areas (mainly Wuhan City), and northern regions (predominantly the northern part of Huanggang City) of the WHUA exhibit relatively higher LSTs. The elevated LST in the eastern plains could be due to the flat terrain and limited natural ecological resources, hindering effective mitigation and leading to LST accumulation [63]. The central areas, characterized by densely populated urban construction, suffer from heat accumulation due to impermeable surfaces and significant greenhouse gas emissions resulting from dense human activities [64]. In the northern regions, the mountainous terrain prevents heat dissipation, causing heat accumulation near the mountains [63].
Similarly, in the transition, areas with higher LSTs resemble those in summer, mainly concentrated in the western regions of the WHUA (comprising Xiaogan City and Tianmen City), as well as in the vicinity of Wuhan City. This similarity may be attributed to the obstruction of heat dissipation caused by the northern mountain ranges, leading to heat accumulation and diffusion toward the western regions [24].
However, in winter, areas with elevated LSTs primarily shift to the southern regions (mainly Xiantao City and Huangshi City), characterized by mountainous terrain and significant built-up areas. Previous studies have indicated that human activities generate heat in winter [65,66], which, coupled with the limited dissipation of heat in valleys, leads to heat accumulation [67].
5.2. Analysis of Drivers of LST in the WHUA
Based on the principal component analysis, we categorized the 16 driving factors into four groups, HA, LP, PG, and CW, according to the proportion of each component. The aim was to reduce the differences among the driving factors, thus providing a more intuitive exploration of the factors driving LST changes. To achieve the best simulation results, traditional spatial regression models were compared with machine-learning models, with machine learning ultimately selected as the preferred model for investigating the driving factors. The entire WHUA was chosen as the study area, enabling a comprehensive temporal and spatial analysis to reflect the influence of the various driving factors across the entire spatial range.
The results of this study revealed spatial and temporal variations in the effects of the four driving factors identified through PCA on the LST. Firstly, in terms of HA, its influence on the LST was relatively high throughout the year compared to other factors, exhibiting a significant positive effect where higher HA values corresponded to higher LSTs. Spatially, its effect was concentrated in urban construction areas. Previous studies have shown that human activities and the resulting greenhouse gas emissions significantly contribute to the rising LST [29], with dense urban construction exacerbating heat accumulation and contributing to the phenomenon known as the UHI effect [68]. Moreover, considering Wuhan’s nucleation effect, HA is highly concentrated in and around Wuhan, contributing to the elevated LST in this area [69].
Secondly, PG exhibited a significant negative effect on the LST, with this effect being most pronounced in the transition, consistent with previous research findings [16]. Spatially, in summer and the transition seasons, PG’s main positive effect areas were the plains in the western part of the WHUA, while negative effects were observed in the northern and southern regions. This distribution pattern may be attributed to the significant negative correlation between PG and the LST, with lower PG in the western plains and higher PG in the northern and southern regions contributing to this spatial pattern. In winter, there was a shift in PG’s positive effect areas to the southern valleys of the WHUA, possibly due to the decreased overall LST in winter and increased human heating activities in the valleys [67].
Regarding CW, it exhibited similarities with PG in terms of timing, peaking in the transition and remaining relatively stable throughout the year. Spatially, its distribution characteristics in summer and the transition were similar, but changes were observed in winter, likely influenced by natural geographical features [70]. However, there were differences in the effect of CW compared to PG, with CW exhibiting negative effects on the LST in the transition and summer, but positive effects in winter. Previous studies have shown that climate factors such as the wind speed often have a positive effect on the LST in inland areas, and the “thermal inertia” effect of moisture in the air can lead to heating effects in local areas, contributing to the observed positive effects in winter [71].
In terms of LP, its spatial effects were relatively inconspicuous in summer and the transition but became more pronounced in winter. Significant positive effects were observed around the mountains and valleys in the southern part of the WHUA. This may be due to the formation of local heat accumulation in valleys during winter, coupled with the higher LP values in these areas [67,72]. Under suitable temperature conditions, the heat generated by plant respiration can contribute to the increased LST in winter, resulting in the observed positive effects [73,74].
In summary, this study provides insights into the spatial characteristics and underlying causes of the effects of various driving factors on the LST. Additionally, it offers theoretical support for reducing the LST.
5.3. Measures to Mitigate the LST in the WHUA
Based on the investigation of the LST’s driving factors in the WHUA, it can be observed that HA, LP, PG, and CW exhibit seasonal variations in their effects on the LST. Tailored strategies can be proposed to address the rising LST:
- (1)
- Summer Strategies: Control Urban Expansion and Optimize Land Use
Through this study, it is evident that the influence of HA on the LST is far greater than other factors. Therefore, it is necessary to consider the impact of anthropogenic factors on the LST. Controlling the urban scale, adopting a dispersed spatial layout, and organizing rational transportation networks are essential to avoid excessive urban expansion leading to population and land aggregation [69]. Particularly, in the intersecting areas of Tianmen, Xiantao, and Qianjiang in the western part of the WHUA, as well as the central city of Wuhan, efforts should be focused on strengthening control over the urban and population scales. Furthermore, it is essential to focus on the control of urban buildings and land use [75]. This can be approached from both macro and micro perspectives to regulate buildings and urban land use. By adjusting the structure of urban land use, the UHI effect can be mitigated. Reasonable planning of the urban land use layout, dispersing high-density urban clusters, and avoiding the concentration of high-density urban land use can help prevent increases in the LST [46].
- (2)
- Transition Strategies: Enhance Ecological Corridors and Green Spaces
Although HA still has a significant impact on the LST during the transition, its influence gradually diminishes compared to the summer, while the alleviating effects of factors such as PG and CW reach their maximum during this season. Therefore, attention should be paid to the influence of natural elements on the urban heat island. Utilizing natural elements to regulate the urban heat island, opening up urban ecological corridors, maintaining smooth urban wind corridors, and preventing dense urban buildings from blocking urban ventilation corridors are essential measures [45]. It is particularly important to focus on controlling the morphology and layout of the western WHUA cities. Additionally, improving the urban green space system is crucial to ensuring the integrity of green coverage both within and around the city. By combining energy-saving and environmentally friendly methods, natural elements can be utilized to alleviate the UHI effect [75]. Lastly, it is essential to strategically place urban green spaces, plazas, water bodies, and vegetation to optimize the urban green space system. This includes maintaining the continuity of ecological elements along the Yangtze River within the WHUA, constructing urban ecological corridors, and creating a multi-level network system of interconnected ecological patches. Such efforts will enhance the continuity of urban landscape spaces [76].
- (3)
- Winter Strategies: Consolidate Natural Elements and Control Human Activities
Based on this study, it can be observed that during winter, the differences in the impact of various driving factors on the LST are gradually diminishing. HA remains the primary positive force, but during this season, LP exhibits the greatest spatial impact on the LST, with a certain alleviating effect in the central area of Wuhan City. Moreover, the impact of the elevated LST on humans during winter is much lower compared to summer, and the lower temperatures in winter also affect human production and livelihoods [65]. Therefore, it is necessary to moderately control the LST fluctuations during winter. Considering the above research, attention should be paid to both human and natural factors influencing the LST. On the one hand, consolidating natural elements within the city, establishing an urban ecological corridor network, optimizing ecological nodes by assessing their ecological value, increasing vegetation coverage, optimizing urban ventilation corridors, and reasonably increasing humidity in the air to control the LST. On the other hand, controlling human activities’ impact on the city, reducing unnecessary anthropogenic heat emissions, improving building energy efficiency, and reducing energy consumption to mitigate the effects of LST fluctuations [77].
- (4)
- Establishment of Supervisory Platforms for Dynamic Control
The seasonal research strategies proposed above require an effective monitoring platform for dynamic control. Therefore, satellite remote-sensing technology combined with sensor technology, should be employed to establish a dynamic network monitoring platform for real-time and effective monitoring of the LST. Additionally, a data-sharing platform should be constructed to ensure the sharing of monitoring data and analysis results among different units and departments. Through real-time monitoring and data analysis, government departments can understand the dynamics and trends of the LST changes in a timely fashion, providing a scientific basis and decision-making support for environmental protection and governance. Furthermore, businesses and the public can understand the impact of their actions on the surrounding environment through shared monitoring data, thereby actively participating in environmental protection and sustainable development practices.
In summary, the seasonal research strategies proposed above can be implemented either sequentially or simultaneously. However, emphasizing the alignment of strategies with the corresponding time periods may provide a more precise adjustment of the LST. Dynamic monitoring strategies, on the other hand, serve as effective technological means to address future climate and environmental changes by integrating diverse information for environmental monitoring and guidance. The mitigation measures suggested based on the present research results are intended to provide references for the development and construction of the WHUA.
6. Conclusions
Since the Industrial Revolution, the continuous pursuit of productivity has accelerated urban construction and rapid population growth, while also causing significant environmental impacts. This study focuses on the urban thermal environment, using the LST as a starting point to calculate the seasonal variation characteristics of the LST in the WHUA and the spatial effects of its driving factors. Targeted measures to alleviate the LST are proposed, aiming to provide references and insights for the sustainable development of the WHUA. The specific conclusions are as follows:
- (1)
- The WHUA exhibits significant seasonal variations in the LST, with greater differences between seasons, especially notable in summer. Variations also exist among cities, with Tianmen having a relatively higher LST throughout the year, and Wuhan, Huanggang, and Xianning showing significant variations in different seasons.
- (2)
- The LST in the WHUA demonstrates obvious spatial clustering characteristics across different seasons. In summer, H-H clustering areas are mainly concentrated in the central urban area of Wuhan, the western region of WHUA, and the northern region of Huanggang. During the transition, H-H clustering areas are more evident in the western region of WHUA, with few distributions in other urban areas. In winter, spatial clustering is observed in the southern mountainous valley area of the WHUA.
- (3)
- Regarding the exploration of the driving factors, this study first reduces the multidimensional driving factors of the LST and categorizes them into four aspects: HA, LP, PG, and CW. Furthermore, a comparison between various models is conducted, with XGBoost showing better explanatory power in investigating the driving effects of the LST compared to traditional geographical spatial models.
- (4)
- Different driving factors exhibit relatively significant effects on the LST across different seasons. HA dominates in terms of the influence in all the seasons and shows a clear positive correlation with the LST. PG exhibits a significant negative correlation with the LST, reaching its peak effect during the transition. CW shows a similar pattern to PG, being negatively correlated with the LST in summer and the transition, and positively correlated in winter. LP shows its maximum effect in winter, with a weak positive correlation, while it is relatively insignificant in summer and the transition.
The LST’s spatiotemporal characteristics and the driving force exploration model constructed in this study have filled certain gaps in this research field. However, there are still areas for improvement, including the use of multi-scale grids for comparison in the exploration of driving forces, integrating day–night LST variations to investigate their spatial effects, and incorporating more factors, such as ecological environment elements, industrial development factors, and other built environment elements, to further explore the spatial effects of the LST.
Finally, this study primarily interprets the LST characteristics of the WHUA from the perspectives of geographical space and seasonality, and it explores the driving factors. Additionally, a comparative analysis of traditional geographical spatial models and machine learning in measuring the LST’s driving factors provides new insights into the study of LST dynamics. Furthermore, this research can provide new directions for the governance and improvement of urban thermal environments between regions, and the LST research framework established in this study can serve as a reference for monitoring regional thermal environments. Lastly, the measures proposed to alleviate the increase in the LST can provide references and insights for regional sustainable development.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/atmos15060671/s1, Table S1: Table describing the indicators based on Fragstats software. References [27,31,38,51,52,53,54,55,56,57,58] are cited in the supplementary materials.
Author Contributions
C.X.: writing—review and editing, validation, project administration, resources, funding acquisition. G.H.: writing—original draft, software, methodology, supervision, data curation. M.Z.: writing—review and editing, supervision, validation. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (2022YFC3800704-2).
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Ce Xu was employed by the company Guangzhou Urban Planning & Design Survey Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interes.
Appendix A

Table A1.
Sources of research data.
Table A1.
Sources of research data.
| Name of Data | Abbreviations | Data Description | Data Sources | Reference |
|---|---|---|---|---|
| Elevation | DEM | Elevation data within the study area, reflecting the height of each spatial unit | https://www.gscloud.cn/#page1/1, accessed on 20 October 2022 | [76,78] |
| Slope | SLOPE | Slope values within each spatial unit within the study area | The study utilized Arcgis 10.8 software to obtain slope data after measuring the elevation data | [76,78] |
| Normalized Difference Vegetation Index | NDVI | NDVI data for 2020 within the study area, characterizing NDVI per unit area | https://search.earthdata.nasa.gov/search, accessed on 19 February 2024 | [16,79] |
| Wind speed | WIND | 2020 wind speeds within the study area | https://www.resdc.cn/, accessed on 16 October 2023 | [28] |
| Humidity | HUM | 2020 humidity values within the study area | https://www.worldpop.org/, accessed on 21 February 2024 | [27] |
| Population density | POP | Population density per unit of space within the study area in 2020 | https://www.worldpop.org/, accessed on 21 February 2024 | [27] |
| Land use data | LU | Land use data for the study area in 2020, indicating the different types of land | https://zenodo.org/records/817694, accessed on 19 February 2024 | [80] |
| Gross domestic product | GDP | 2020 GDP data for the study area, characterizing GDP values per unit of spatial extent | https://github.com/thestarlab/ChinaGDP, accessed on 17 February 2024 | [81] |
| Night Lights | NPP | Study area 2020 night-time lighting data characterizing nighttime lighting values within each spatial unit | https://www.resdc.cn/, accessed on 3 February 2024 | [27] |
| Aggregation index | AI | The number of similar patch neighbors of each unit of space within the study area characterizes the degree of aggregation | The AI values were calculated using the built-up land data from the land use data in conjunction with the Fragstats4.2 software | [51,53] |
| Class Area | CA | Total area of patches in each spatial unit within the study area, characterizing urban growth | The CA values were calculated using the built-up land data from the land use data in conjunction with the Fragstats4.2 software | [51,53] |
| Edge Density | ED | The density of landscape patches in each spatial unit within the study area, reflecting the extent to which each landscape is segmented by boundaries | Using the ecotype land use data from the land use data, combined with Fragstats4.2 software to calculate the ED value | [51,52] |
| Patch Density | PD | Density of landscape patches in each spatial unit within the study area, characterizing the degree of landscape fragmentation | Using the ecotype land use data from the land use data, combined with Fragstats4.2 software to calculate the PD value | [51,52] |
| Largest Patch Index | LPI | The proportion of the largest landscape patches in each spatial unit within the study area characterizes the proportion of dominant patches | Using the ecotype land use data from the land use data, combined with Fragstats4.2 software to calculate the LPI value | [51,52] |
| Shannon’s Diversity Index | SHDI | The degree of landscape diversity in each spatial unit within the study area | Using the ecotype land use data from the land use data, combined with Fragstats4.2 software to calculate the SHDI value | [51,52] |
| Building heights | BH | Data on building heights within the study area, reflecting the values of building heights within each spatial unit | https://zenodo.org/record/7827315, accessed on 20 February 2024 | [82] |
| Distance from road | ROAD | The distance of each spatial unit from the road within the study area was calculated using road data from OpenStreetMap | https://www.openstreetmap.org/, accessed on 12 October 2022 | [24] |

Table A2.
Explanatory table of main abbreviations.
Table A2.
Explanatory table of main abbreviations.
| Name | Abbreviation |
|---|---|
| Land Surface Temperature | LST |
| Urban Heat Island | UHI |
| Human Activity | HA |
| Landscape Pattern | LP |
| Physical Geography | PG |
| Climate and Weather | CW |
| Wuhan Urban Agglomeration | WHUA |
| Urban Agglomeration | UA |
| Metropolitan Area | MA |
| High–High | H-H |
| High–Low | H-L |
| Low–Low | L-L |
| Low–High | L-H |
| Geographically Weighted Regression | GWR |
| Multiscale Geographically Weighted Regression | MGWR |
| Standard Deviational Ellipse | SDE |
| Principal Component Analysis | PCA |
| Patch Density | PD |
| Edge Density | ED |
| Largest Patch Index | LPI |
| Shannon’s Diversity Index | SHDI |
References
- Wang, L.; Zhang, B.-C.; Shi, Y.; Han, Z.-Y.; Lu, B. Interpretation of the IPCC AR6 on the Impacts and Risks of Climate Change. Clim. Change Res. 2022, 18, 389–394. [Google Scholar]
- Ming, A.; Rowell, I.; Lewin, S.; Rouse, R.; Aubry, T.; Boland, E. Key Messages from the IPCC AR6 Climate Science Report. Earth Environ. Sci. 2021, preprint. [Google Scholar] [CrossRef]
- Van Aalst, M.K. The Impacts of Climate Change on the Risk of Natural Disasters. Disasters 2006, 30, 5–18. [Google Scholar] [CrossRef] [PubMed]
- Hulme, M.; Barrow, E.M.; Arnell, N.W.; Harrison, P.A.; Johns, T.C.; Downing, T.E. Relative Impacts of Human-Induced Climate Change and Natural Climate Variability. Nature 1999, 397, 688–691. [Google Scholar] [CrossRef]
- Collins, M.; Chandler, R.E.; Cox, P.M.; Huthnance, J.M.; Rougier, J.; Stephenson, D.B. Quantifying Future Climate Change. Nat. Clim. Change 2012, 2, 403–409. [Google Scholar] [CrossRef]
- Ismail, A.H.; Dawi, E.A.; Almokdad, N.; Abdelkader, A.; Salem, O. Estimation and Comparison of the Clearness Index Using Mathematical Models-Case Study in the United Arab Emirates. EVERGREEN Jt. J. Nov. Carbon Resour. Sci. Green Asia Strategy 2023, 10, 863–869. [Google Scholar]
- Babatunde, O.M.; Munda, J.L.; Hamam, Y.; Monyei, C.G. A Critical Overview of the (Im) Practicability of Solar Radiation Forecasting Models. e-Prime-Adv. Electr. Eng. Electron. Energy 2023, 5, 100213. [Google Scholar] [CrossRef]
- Ismail, A.A.K.H. Prediction of Global Solar Radiation from Sunrise Duration Using Regression Functions. Kuwait J. Sci. 2022, 49, 1–8. [Google Scholar] [CrossRef]
- Serem, N.; Letting, L.K.; Munda, J. Voltage Profile and Sensitivity Analysis for a Grid Connected Solar, Wind and Small Hydro Hybrid System. Energies 2021, 14, 3555. [Google Scholar] [CrossRef]
- Buchin, O.; Hoelscher, M.-T.; Meier, F.; Nehls, T.; Ziegler, F. Evaluation of the Health-Risk Reduction Potential of Countermeasures to Urban Heat Islands. Energy Build. 2016, 114, 27–37. [Google Scholar] [CrossRef]
- Wang, B.; Hu, C.; Zhang, Y. Multi-Scenario Simulation of the Impact of Land Use Change on the Ecosystem Service Value in the Suzhou-Wuxi-Changzhou Metropolitan Area, China. Chin. Geogr. Sci. 2024, 34, 79–92. [Google Scholar] [CrossRef]
- Huang, G.; Feng, S.; Hu, C. A Study of the Spatiotemporal Evolution Patterns and Coupling Coordination between Ecosystem Service Values and Habitat Quality in Diverse Scenarios: The Case of Chengdu Metropolitan Area, China. Sustainability 2024, 16, 3741. [Google Scholar] [CrossRef]
- Ngarambe, J.; Oh, J.W.; Su, M.A.; Santamouris, M.; Yun, G.Y. Influences of Wind Speed, Sky Conditions, Land Use and Land Cover Characteristics on the Magnitude of the Urban Heat Island in Seoul: An Exploratory Analysis. Sustain. Cities Soc. 2021, 71, 102953. [Google Scholar] [CrossRef]
- Zhang, M.; Tan, S.; Liang, J.; Zhang, C.; Chen, E. Predicting the Impacts of Urban Development on Urban Thermal Environment Using Machine Learning Algorithms in Nanjing, China. J. Environ. Manag. 2024, 356, 120560. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Tan, S.; Zhang, C.; Chen, E. Machine Learning in Modelling the Urban Thermal Field Variance Index and Assessing the Impacts of Urban Land Expansion on Seasonal Thermal Environment. Sustain. Cities Soc. 2024, 106, 105345. [Google Scholar] [CrossRef]
- Hu, C.; Huang, G.; Wang, Z. Exploring the Seasonal Relationship between Spatial and Temporal Features of Land Surface Temperature and Its Potential Drivers: The Case of Chengdu Metropolitan Area, China. Front. Earth Sci. 2023, 11, 1226795. [Google Scholar] [CrossRef]
- Peng, X.; Wu, W.; Zheng, Y.; Sun, J.; Hu, T.; Wang, P. Correlation Analysis of Land Surface Temperature and Topographic Elements in Hangzhou, China. Sci. Rep. 2020, 10, 10451. [Google Scholar] [CrossRef] [PubMed]
- Al-Obaidi, I.; Rayburg, S.; Półrolniczak, M.; Neave, M. Assessing the Impact of Wind Conditions on Urban Heat Islands in Large Australian Cities. J. Ecol. Eng. 2021, 22, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Xiang, Y.; Huang, C.; Huang, X.; Zhou, Z.; Wang, X. Seasonal Variations of the Dominant Factors for Spatial Heterogeneity and Time Inconsistency of Land Surface Temperature in an Urban Agglomeration of Central China. Sustain. Cities Soc. 2021, 75, 103285. [Google Scholar] [CrossRef]
- He, J.; Hu, S. Ecological Efficiency and Its Determining Factors in an Urban Agglomeration in China: The Chengdu-Chongqing Urban Agglomeration. Urban Clim. 2022, 41, 101071. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, C.; Kafy, A.-A.; Tan, S. Simulating the Relationship between Land Use/Cover Change and Urban Thermal Environment Using Machine Learning Algorithms in Wuhan City, China. Land 2021, 11, 14. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, Y.; Hu, M.; Zhou, Y. Influence of Urban Scale and Urban Expansion on the Urban Heat Island Effect in Metropolitan Areas: Case Study of Beijing–Tianjin–Hebei Urban Agglomeration. Remote Sens. 2020, 12, 3491. [Google Scholar] [CrossRef]
- Zhao, C.; Zhu, H.; Zhang, S.; Jin, Z.; Zhang, Y.; Wang, Y.; Shi, Y.; Jiang, J.; Chen, X.; Liu, M. Long–term Trends in Surface Thermal Environment and Its Potential Drivers along the Urban Development Gradients in Rapidly Urbanizing Regions of China. Sustain. Cities Soc. 2024, 105, 105324. [Google Scholar] [CrossRef]
- Hu, C.; Li, H. Reverse Thinking: The Logical System Research Method of Urban Thermal Safety Pattern Construction, Evaluation, and Optimization. Remote Sens. 2022, 14, 6036. [Google Scholar] [CrossRef]
- Hou, H.; Su, H.; Liu, K.; Li, X.; Chen, S.; Wang, W.; Lin, J. Driving Forces of UHI Changes in China’s Major Cities from the Perspective of Land Surface Energy Balance. Sci. Total Environ. 2022, 829, 154710. [Google Scholar] [CrossRef]
- Cai, Z.; Tang, Y.; Zhan, Q. A Cooled City? Comparing Human Activity Changes on the Impact of Urban Thermal Environment before and after City-Wide Lockdown. Build. Environ. 2021, 195, 107729. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, D.; Hu, C.; Wang, Y.; Zhang, J. Seasonal Contrast and Interactive Effects of Potential Drivers on Land Surface Temperature in the Sichuan Basin, China. Remote Sens. 2022, 14, 1292. [Google Scholar] [CrossRef]
- Yang, C.; Yan, F.; Lei, X.; Ding, X.; Zheng, Y.; Liu, L.; Zhang, S. Investigating Seasonal Effects of Dominant Driving Factors on Urban Land Surface Temperature in a Snow-Climate City in China. Remote Sens. 2020, 12, 3006. [Google Scholar] [CrossRef]
- Zhang, M.; Kafy, A.-A.; Xiao, P.; Han, S.; Zou, S.; Saha, M.; Zhang, C.; Tan, S. Impact of Urban Expansion on Land Surface Temperature and Carbon Emissions Using Machine Learning Algorithms in Wuhan, China. Urban Clim. 2023, 47, 101347. [Google Scholar] [CrossRef]
- Zhang, M.; Tan, S.; Zhang, C.; Han, S.; Zou, S.; Chen, E. Assessing the Impact of Fractional Vegetation Cover on Urban Thermal Environment: A Case Study of Hangzhou, China. Sustain. Cities Soc. 2023, 96, 104663. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, F.; Zhang, H.; Dong, J. Mechanisms of Non-Stationary Influence of Urban Form on the Diurnal Thermal Environment Based on Machine Learning and MGWR Analysis. Sustain. Cities Soc. 2024, 101, 105194. [Google Scholar] [CrossRef]
- Li, Z. Extracting Spatial Effects from Machine Learning Model Using Local Interpretation Method: An Example of SHAP and XGBoost. Comput. Environ. Urban Syst. 2022, 96, 101845. [Google Scholar] [CrossRef]
- Yang, C.; Chen, M.; Yuan, Q. The Application of XGBoost and SHAP to Examining the Factors in Freight Truck-Related Crashes: An Exploratory Analysis. Accid. Anal. Prev. 2021, 158, 106153. [Google Scholar] [CrossRef] [PubMed]
- Han, D.; An, H.; Cai, H.; Wang, F.; Xu, X.; Qiao, Z.; Jia, K.; Sun, Z.; An, Y. How Do 2D/3D Urban Landscapes Impact Diurnal Land Surface Temperature: Insights from Block Scale and Machine Learning Algorithms. Sustain. Cities Soc. 2023, 99, 104933. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, W.; Zhan, Q.; Xiong, D. Spatiotemporal Patterns of Land Surface Temperature Change in the Tibetan Plateau Based on MODIS/Terra Daily Product from 2000 to 2018. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6501–6514. [Google Scholar] [CrossRef]
- He, Z.-W.; Tang, B.-H. Spatiotemporal Change Patterns and Driving Factors of Land Surface Temperature in the Yunnan-Kweichow Plateau from 2000 to 2020. Sci. Total Environ. 2023, 896, 165288. [Google Scholar] [CrossRef]
- Jumai, M.; Kasimu, A.; Liang, H.; Tang, L.; Aizizi, Y.; Zhang, X. A Study on the Spatial and Temporal Variation of Summer Surface Temperature in the Bosten Lake Basin and Its Influencing Factors. Land 2023, 12, 1185. [Google Scholar] [CrossRef]
- Gombe, K.; Asanuma, I.; Park, J. Characterization of Urban Heat Island (UHI) Changes from MODIS Times Series Using Principal Component Analysis (PCA): Case of Dar Es Salaam City Tanzania. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1554–1557. [Google Scholar]
- Sun, D.; Hu, C.; Wang, Y.; Wang, Z.; Zhang, J. Examining Spatio-Temporal Characteristics of Urban Heat Islands and Factors Driving Them in Hangzhou, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8316–8325. [Google Scholar] [CrossRef]
- Lin, J.; Qiu, S.; Tan, X.; Zhuang, Y. Measuring the Relationship between Morphological Spatial Pattern of Green Space and Urban Heat Island Using Machine Learning Methods. Build. Environ. 2023, 228, 109910. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Yu, Y.; Fang, S.; Zhuo, W. Revealing the Driving Mechanisms of Land Surface Temperature Spatial Heterogeneity and Its Sensitive Regions in China Based on GeoDetector. Remote Sens. 2023, 15, 2814. [Google Scholar] [CrossRef]
- Min, M.; Lin, C.; Duan, X.; Jin, Z.; Zhang, L. Spatial Distribution and Driving Force Analysis of Urban Heat Island Effect Based on Raster Data: A Case Study of the Nanjing Metropolitan Area, China. Sustain. Cities Soc. 2019, 50, 101637. [Google Scholar] [CrossRef]
- Fang, C. China’s Urban Agglomeration and Metropolitan Area Construction under the New Development Pattern. Econ. Geogr 2021, 41, 1–7. [Google Scholar]
- Tang, L.; Zhan, Q.; Fan, Y.; Liu, H.; Fan, Z. Exploring the Impacts of Greenspace Spatial Patterns on Land Surface Temperature across Different Urban Functional Zones: A Case Study in Wuhan Metropolitan Area, China. Ecol. Indic. 2023, 146, 109787. [Google Scholar] [CrossRef]
- Chen, H.; Deng, Q.; Zhou, Z.; Ren, Z.; Shan, X. Influence of Land Cover Change on Spatio-Temporal Distribution of Urban Heat Island—A Case in Wuhan Main Urban Area. Sustain. Cities Soc. 2022, 79, 103715. [Google Scholar] [CrossRef]
- Zhou, X.; Wu, B.; Liu, Y.; Zhou, Q.; Cheng, W. Synergistic Effects of Heat and Carbon on Sustainable Urban Development: Case Study of the Wuhan Urban Agglomeration. J. Clean. Prod. 2023, 425, 138971. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, D.; Liu, Y.; Zhang, Y.; Jing, Y.; Chen, H.; Zhang, Z.; Liu, Y. Exploring the Optimization and Management Methods of Ecological Networks Based on the Cluster Mode: A Case Study of Wuhan Metropolis, China. Land Use Policy 2024, 137, 107021. [Google Scholar] [CrossRef]
- Xing, Z.; Li, Z.L.; Duan, S.B.; Liu, X.; Zheng, X.; Leng, P.; Gao, M.; Zhang, X.; Shang, G. Estimation of Daily Mean Land Surface Temperature at Global Scale Using Pairs of Daytime and Nighttime MODIS Instantaneous Observations. ISPRS J. Photogramm. Remote Sens. 2021, 178, 51–67. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, S.; Tian, Z.; Luo, Y.; Deng, J.; Fan, J. Differences in Urban Heat Island and Its Driving Factors between Central and New Urban Areas of Wuhan, China. Environ. Sci. Pollut. Res. 2023, 30, 58362–58377. [Google Scholar] [CrossRef]
- McGarigal, K. FRAGSTATS: Spatial Pattern Analysis Program for Quantifying Landscape Structure; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Portland, OR, USA, 1995; Volume 351. [Google Scholar]
- Lamine, S.; Petropoulos, G.P.; Singh, S.K.; Szabó, S.; Bachari, N.E.I.; Srivastava, P.K.; Suman, S. Quantifying Land Use/Land Cover Spatio-Temporal Landscape Pattern Dynamics from Hyperion Using SVMs Classifier and FRAGSTATS®. Geocarto Int. 2018, 33, 862–878. [Google Scholar] [CrossRef]
- Zheng, S.; Huang, Y.; Sun, Y. Effects of Urban Form on Carbon Emissions in China: Implications for Low-Carbon Urban Planning. Land 2022, 11, 1343. [Google Scholar] [CrossRef]
- Getis, A. Reflections on Spatial Autocorrelation. Reg. Sci. Urban Econ. 2007, 37, 491–496. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H. Monitoring Spatiotemporal Characteristics of Land-Use Carbon Emissions and Their Driving Mechanisms in the Yellow River Delta: A Grid-Scale Analysis. Environ. Res. 2022, 214, 114151. [Google Scholar] [CrossRef]
- Zhao, Y.; Wu, Q.; Wei, P.; Zhao, H.; Zhang, X.; Pang, C. Explore the Mitigation Mechanism of Urban Thermal Environment by Integrating Geographic Detector and Standard Deviation Ellipse (SDE). Remote Sens. 2022, 14, 3411. [Google Scholar] [CrossRef]
- Li, W.; Zhang, E.; Long, Y. Unveiling Fine-Scale Urban Third Places for Remote Work Using Mobile Phone Big Data. Sustain. Cities Soc. 2024, 103, 105258. [Google Scholar] [CrossRef]
- Yang, L.; Yu, K.; Ai, J.; Liu, Y.; Yang, W.; Liu, J. Dominant Factors and Spatial Heterogeneity of Land Surface Temperatures in Urban Areas: A Case Study in Fuzhou, China. Remote Sens. 2022, 14, 1266. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T. Xgboost: Extreme Gradient Boosting. R Package Version 0.4-2 2015, 1, 1–4. [Google Scholar]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward Safer Highways, Application of XGBoost and SHAP for Real-Time Accident Detection and Feature Analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef]
- Shapley, L.S. A Value for N-Person Games. In Contributions to the Theory of Games (AM-28); Kuhn, H.W., Tucker, A.W., Eds.; Princeton University Press: Princeton, NJ, USA, 1953; Volume II, pp. 307–318. [Google Scholar] [CrossRef]
- He, J.; Zhao, W.; Li, A.; Wen, F.; Yu, D. The Impact of the Terrain Effect on Land Surface Temperature Variation Based on Landsat-8 Observations in Mountainous Areas. Int. J. Remote Sens. 2019, 40, 1808–1827. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, J.; Yang, G. How to Build a Heat Network to Alleviate Surface Heat Island Effect? Sustain. Cities Soc. 2021, 74, 103135. [Google Scholar] [CrossRef]
- Song, C.; Yang, J.; Wu, F.; Xiao, X.; Xia, J.; Li, X. Response Characteristics and Influencing Factors of Carbon Emissions and Land Surface Temperature in Guangdong Province, China. Urban Clim. 2022, 46, 101330. [Google Scholar] [CrossRef]
- Wu, W.; Li, L.; Li, C. Seasonal Variation in the Effects of Urban Environmental Factors on Land Surface Temperature in a Winter City. J. Clean. Prod. 2021, 299, 126897. [Google Scholar] [CrossRef]
- Yang, C.; Yan, F.; Zhang, S. Comparison of Land Surface and Air Temperatures for Quantifying Summer and Winter Urban Heat Island in a Snow Climate City. J. Environ. Manag. 2020, 265, 110563. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zhang, X.; Mirzaei, P.A.; Zhang, J.; Zhao, Z. Urban Heat Island Effect of a Typical Valley City in China: Responds to the Global Warming and Rapid Urbanization. Sustain. Cities Soc. 2018, 38, 736–745. [Google Scholar] [CrossRef]
- Lemoine-Rodríguez, R.; Inostroza, L.; Zepp, H. Does Urban Climate Follow Urban Form? Analysing Intraurban LST Trajectories versus Urban Form Trends in 3 Cities with Different Background Climates. Sci. Total Environ. 2022, 830, 154570. [Google Scholar] [CrossRef]
- Lu, Y.; Yue, W.; Liu, Y.; Huang, Y. Investigating the Spatiotemporal Non-Stationary Relationships between Urban Spatial Form and Land Surface Temperature: A Case Study of Wuhan, China. Sustain. Cities Soc. 2021, 72, 103070. [Google Scholar] [CrossRef]
- Tucker, P.; Gilliland, J. The Effect of Season and Weather on Physical Activity: A Systematic Review. Public Health 2007, 121, 909–922. [Google Scholar] [CrossRef]
- Zong, H.; Liu, Y.; Wang, Q.; Liu, M.; Chen, H. Usage Patterns and Comfort of Gardens: A Seasonal Survey of Internal Garden Microclimate in the Aged Care Homes of Chengdu City. Int. J. Biometeorol. 2019, 63, 1181–1192. [Google Scholar] [CrossRef]
- Henao, J.J.; Rendón, A.M.; Salazar, J.F. Trade-off between Urban Heat Island Mitigation and Air Quality in Urban Valleys. Urban Clim. 2020, 31, 100542. [Google Scholar] [CrossRef]
- Dobrowski, S.Z.; Abatzoglou, J.T.; Greenberg, J.A.; Schladow, S.G. How Much Influence Does Landscape-Scale Physiography Have on Air Temperature in a Mountain Environment? Agric. For. Meteorol. 2009, 149, 1751–1758. [Google Scholar] [CrossRef]
- Scafaro, A.P.; Fan, Y.; Posch, B.C.; Garcia, A.; Coast, O.; Atkin, O.K. Responses of Leaf Respiration to Heatwaves. Plant Cell Environ. 2021, 44, 2090–2101. [Google Scholar] [CrossRef]
- Zhao, Y.; Sen, S.; Susca, T.; Iaria, J.; Kubilay, A.; Gunawardena, K.; Zhou, X.; Takane, Y.; Park, Y.; Wang, X. Beating Urban Heat: Multimeasure-Centric Solution Sets and a Complementary Framework for Decision-Making. Renew. Sustain. Energy Rev. 2023, 186, 113668. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Z.; Wang, Y.; Sun, D.; Zhang, J. Combining MSPA-MCR Model to Evaluate the Ecological Network in Wuhan, China. Land 2022, 11, 213. [Google Scholar] [CrossRef]
- Peng, J.; Jia, J.; Liu, Y.; Li, H.; Wu, J. Seasonal Contrast of the Dominant Factors for Spatial Distribution of Land Surface Temperature in Urban Areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Wei, Q.; Abudureheman, M.; Halike, A.; Yao, K.; Yao, L.; Tang, H.; Tuheti, B. Temporal and Spatial Variation Analysis of Habitat Quality on the PLUS-InVEST Model for Ebinur Lake Basin, China. Ecol. Indic. 2022, 145, 109632. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Z.; Huang, G.; Ding, Y. Construction, Evaluation, and Optimization of a Regional Ecological Security Pattern Based on MSPA–Circuit Theory Approach. Int. J. Environ. Res. Public Health 2022, 19, 16184. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Huang, X. The 30 m Annual land cover dataset and its dynamics in China from 1990 to 2019. Earth Syst. Sci. Data 2021, 13, 3907–3925. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, Y.; Cao, G.; Samson, E.L.; Zhang, J. Forecasting China’s GDP at the Pixel Level Using Nighttime Lights Time Series and Population Images. GISci. Remote Sens. 2017, 54, 407–425. [Google Scholar] [CrossRef]
- Wu, W.-B.; Ma, J.; Banzhaf, E.; Meadows, M.E.; Yu, Z.-W.; Guo, F.-X.; Sengupta, D.; Cai, X.-X.; Zhao, B. A First Chinese Building Height Estimate at 10 m Resolution (CNBH-10 m) Using Multi-Source Earth Observations and Machine Learning. Remote Sens. Environ. 2023, 291, 113578. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).