Abstract
The prediction of typhoon tracks in the Northwest Pacific is key to reducing human casualties and property damage. Traditional numerical forecasting models often require substantial computational resources, are high-cost, and have significant limitations in prediction speed. This research is dedicated to using deep learning methods to address the shortcomings of traditional methods. Our method (AFR-SimVP) is based on a large-kernel convolutional spatio-temporal prediction network combined with multi-feature fusion for forecasting typhoon tracks in the Northwest Pacific. In order to more effectively suppress the effect of noise in the dataset to enhance the generalization ability of the model, we use a multi-branch structure, incorporate an atmospheric reconstruction subtask, and propose a second-order smoothing loss to further improve the prediction ability of the model. More importantly, we innovatively propose a multi-time-step typhoon prediction network (HTAFR-SimVP) that does not use the traditional recurrent neural network family of models at all. Instead, through fine-to-coarse hierarchical temporal feature extraction and dynamic self-distillation, multi-time-step prediction is achieved using only a single regression network. In addition, combined with atmospheric field reconstruction, the network achieves integrated prediction for multiple tasks, which greatly enhances the model’s range of applications. Experiments show that our proposed network achieves optimal performance in the 24 h typhoon track prediction task. Our regression network outperforms previous recurrent network-based typhoon prediction models in the multi-time-step prediction task and also performs well in multiple integration tasks.
1. Introduction
Tropical cyclones (TCs) are large-scale meteorological phenomena that originate over the surfaces of tropical or subtropical oceans. TCs are one of the major extreme meteorological disasters facing humankind, and the accurate prediction of TCs’ tracks can greatly reduce property damage and casualties. However, the formation of a TC is influenced by a variety of factors, including the meteorological environment in which the tropical cyclone is located, thermodynamic and kinetic factors, etc. In addition, numerous variables influence the trajectory of a TC, including atmospheric circulation, latitude, longitude, topography, seasonal wind fields, and ocean temperature. The interactions among these factors make tropical cyclone track prediction a great challenge. Therefore, considering the complexity of tropical cyclone prediction and its great impact on human beings, it is of great importance to study new and more efficient methods for tropical cyclone prediction.
Traditional forecasting methods are mainly categorized into statistical forecasting methods [1,2,3,4,5] and numerical forecasting methods [6,7,8,9,10,11]. Statistical forecasting methods usually look for factors of TC motion and establish relationships based on historical TC track records. For example, the climatology and persistence method (CLIPER) usually constructs the features affecting the TC track according to the variables TC latitude, longitude, wind speed, and time and establishes regression equations to realize the 72 h prediction of the TC track [12,13,14]. However, manually selected features are limited in their ability to represent the features, and this method only extracts two-dimensional features of the TC associated with the path without taking into account three-dimensional features of the TC, such as wind fields and geopotential fields at the surface of the TC, so it is difficult to produce accurate prediction results. Since the 1990s, with the improvement of computer performance, the numerical weather prediction (NWP) system [15], which simulates the partial differential equations of the atmospheric state, has gradually become the mainstream method for meteorological forecasting by various organizations. However, this method needs to deal with complex thermodynamic equations and simulate the internal structure of TCs, which requires substantial computational resources but still cannot achieve the desired prediction accuracy.
Presently, an increasing number of researchers are employing machine learning methodologies for the prediction of TC. Jinkai Tan et al. [16,17,18,19] utilized GBDT, MLP, SVM, and BP networks to capture the nonlinear relationships from input data for predicting TC trajectories. Machine learning-based methods demand minimal computational resources, resulting in a significant enhancement in inference speed when compared to conventional methodologies. However, due to the simplicity of the network structure, they are unable to efficiently capture complex relationships during TC motion. Moreover, most machine learning methods use regression to predict TCs, which loses temporal information during TC motion.
For the reasons mentioned above, traditional statistical methods and machine learning methods face difficulties in effectively predicting TC trajectories. And deep learning methods based on multilayer neural networks are more suitable for TC trajectory prediction. The current deep learning-based TC trajectory prediction methods are mainly divided into two categories based on the selection of data. One class is based on the TC trajectory sequence data and utilizes recurrent networks to capture the temporal information and nonlinear relationships from the sequence data. The other category is based on various remote sensing image data or a combination of multiple data sources to predict TC trajectories using a multimodal approach. For instance, Moradi et al. [20,21,22] employed an RNN to extract nonlinear features for 2D TCs. Leveraging the memory capabilities of RNNs, they extended the prediction horizon, yielding results over longer time spans. Additionally, they integrated variational inference, enabling the network to provide a good approximation in terms of uncertainty quantification while maintaining the prediction accuracy. However, the plain RNN suffers from the long-term dependency problem. This means that the current trajectory may be influenced by trajectories that occurred long ago. But RNNs cannot effectively learn information over large intervals. For this reason, Song Gao et al. [23,24,25] utilized long short-term memory (LSTM) networks and gated recurrent units (GRUs) to capture the long-term features of TCs. They further enhanced predictive accuracy by combining an auto-encoder (AE) and generative adversarial networks (GANs). These RNN-based methods can effectively extract the temporal features during TC motion but are not able to do anything about 3D TC features.
In order to solve the above problems, in some recent studies, researchers have preferred to use data of various forms to make predictions of TC trajectories using a multimodal fusion approach. Considering that generative adversarial networks can use past remote sensing images to automatically generate TC centers and cloud structures at future moments, Ruttgers et al. [26] used a GAN to predict TC trajectories up to 6 h ahead of time, and the predicted TC trajectory images could effectively identify the future location of TC centers, as well as the cloud structures near the TC centers. They also found that when the velocity field is used in combination with satellite images, the prediction results can be significantly improved; however, this method requires high-resolution satellite images and only takes into account the information around the TC, still not the three-dimensional structure of the TC. To comprehensively consider the three-dimensional spatial characteristics of TCs, Mudigonda et al. [27,28] proposed a spatio-temporal model based on the convolutional LSTM (ConvLSTM), which is able to capture not only the temporal dynamics but also the spatial distribution of the TC trajectory. Nonetheless, the ConvLSTM model suffers from an excessive number of parameters and can easily overfit the data, and it is difficult to extract effective 3D nonlinear features. Consequently, it is difficult to generate predicted trajectory maps that accurately reflect the exact location of TCs. Therefore, determining how to better fuse the 3D TC atmospheric state with 2D features has become a hot research topic in recent years [29,30]. Guangning Xu et al. [31,32] proposed a fusion of convolutional networks and recurrent networks, combined with segmented training, to fully integrate 2D positional features and 3D geopotential features. This approach further enhances the accuracy of trajectory prediction. Both of the above methods only consider the geopotential field features in 3D TC features, and the wind field also has an important influence on the TC trajectory. Giffard et al. [29,33] took the wind field data into account and generated predictions by fusing the geopotential field and wind field features. Pingping Wang et al. [33] designed a method combining a 3D convolutional neural network (3DCNN), gated recurrent unit (GRU), and smoothing algorithm in a hybrid optimization model. The 3DCNN is used to explore the complex relationship between wind and geopotential fields under different pressure levels, and the GRU is used to transform the TC trajectory prediction problem into a spatio-temporal sequential problem. The 24 h prediction error of this method is 112.05 km, significantly lower than that of the previous deep learning methods; however, the training time of this model is longer, and it directly stacks the wind field data with geopotential field data, which causes the interaction of noise in the multiple 3D TC features, subsequently impacting the model’s predictions.
In previous studies, TC trajectories were often predicted individually, which could lead to overfitting and a reduction in the model’s generalization capability. The main objectives of this study are to extract the 3D features of TCs more effectively, reduce the impact of anomalous mutations in TC trajectories on the prediction results, suppress the interaction among various types of noise in the dataset, and integrate TC trajectory prediction with atmospheric field reconstruction tasks to further enhance the generalization capability of the model. In addition, a spatio-temporal prediction network SimVP [34,35] is utilized to extract large-scale spatio-temporal TC features, and a novel multi-step TC prediction framework based on hierarchical temporal feature extraction and dynamic self-distillation is proposed. Finally, the medium- and long-term predictions of TC trajectories are explored.
2. Datasets
2.1. Data Sources
The dataset utilized in this study comprises two distinct components. The first is the fifth generation of reanalysis data (ERA5) for global climate and weather published by the European Center for Medium-Range Weather Forecasts (ECMWF) [36]. The reanalysis combines modeled data with observations from around the world to form a complete and consistent dataset. In contrast to the previous generation of ERA-Interim reanalysis data, ERA5 incorporates more advanced data assimilation techniques, a more comprehensive set of observational data, and enhanced model parameters. The ERA5 data can provide reanalysis data for atmospheric, oceanic, and land-related meteorological variables on an hourly basis. These data give a detailed picture of the evolution of the weather on an hourly basis. In this study, some meteorological variables from ERA5 were selected for modeling.
The second part is the TC best-trajectory dataset published by the China Meteorological Administration (CMA) [37,38]. This dataset comprises 6-hourly data on TCs developed over the NW Pacific Ocean from 1949 to the present. The CMA Best-Track dataset contains the time of occurrence of the TCs, the longitude (0.1°E), the latitude (0.1°N), the minimum pressure (hPa), and the two-minute-averaged maximum sustained winds in the vicinity of the center of the TCs. All TC data occurring in the Pacific Northwest between 1979 and 2022 were selected for this study.
2.2. Data Pre-Processing
In order to prepare the 2D TC dataset needed for this study, the CLIPER method [12] was used to transform 4 variables, namely, time, latitude, longitude, and central wind speed, in the CMA dataset into the 53 features shown in Table 1, where the subscript i denotes the value of the variable i hours ago; for instance, denotes the value of the longitude of the TC six hours ago. The 2D information of the TC is described in terms of these 53 variables, where features 1 to 15 provide the basic historical characteristics of the TC, feature 16 indicates the annual characteristics of the TC, features 17 to 28 indicate the structural change characteristics of the TC, and features 29 to 53 indicate the nonlinear characteristics of the TC. This type of feature is mainly used to describe information about the direction of movement, acceleration, and angle of movement of the TC in physical terms. Furthermore, to perform the CLIPER method, historical characteristics for the initial 24 h of tropical cyclones (TCs) are required. Consequently, in order to predict the TC trajectory beyond the initial 24 h, TCs with a duration of less than 12 time points (equivalent to 72 h) were excluded from the dataset.

Table 1.
The CLIPER features.
The 3D characterization data of TCs were obtained from the ERA5 data. There are numerous factors affecting the TC trajectory, among which the geopotential is a manifestation of the Earth’s gravity field and the effect of the Earth’s rotation, which can reflect the three-dimensional structural information of the TC. For a rotationally symmetric system such as a TC, the geopotential can help us to understand the structure of the vertical motion inside the TC, such as the distribution of updrafts and downdrafts, which are the key factors affecting the trajectory of the typhoon. And the u-wind and v-wind component scales in the wind field characteristics represent the motion components of the TC in the east–west and north–south directions, which, together, describe the three-dimensional wind field structure of the TC, which is crucial for understanding the motion characteristics of the TC and predicting its trajectory. The wind field data not only reflect the speed and direction of the TC’s movement but also reveal the airflow patterns within the TC, such as the rotating eye wall and the spiral rainbands at the periphery. Therefore, in order to fully describe the 3D spatial characteristics of TCs, we selected three meteorological variables, geopotential (Z), the u-component of wind (U), and the v-component of wind (V), in the ERA5 dataset, as shown in Figure 1. In the two-dimensional horizontal direction, the TC radius can often extend from hundreds to a thousand kilometers, so, using the center of the TC as a standard, a 15° radius range was selected with a resolution of 1° to describe the TC, where each TC at each moment can be represented by a horizontal range of 31° × 31°. In the three-dimensional vertical plane, the TC can generally be divided into three parts: the inflow layer, intermediate layer, and outflow layer; therefore, for each meteorological variable, four pressure levels of 1000, 750, 500, and 250 hPa were selected to represent the three-dimensional vertical structure of the TC.
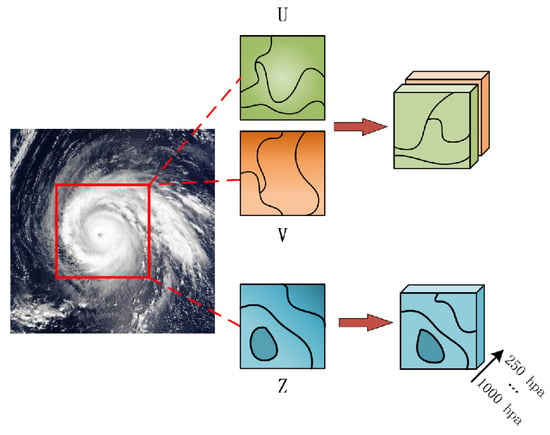
Figure 1.
Three-dimensional TC atmospheric characterization, where u, v, and z represent the wind field and geopotential features that we chose over the four isobars, and the red box is a subset of the entire TC range for which we visualize the 3D TC features.
After obtaining the 2D and 3D data of the TCs, we mapped the latitude and longitude of the center of each TC trajectory in the CMA Best-Track dataset to the ERA5 data. Then, the 3D structure of the TC was built with this center to obtain the data field of three atmospheric variables at four pressure levels. The 3D data were subsequently organized chronologically for each TC trajectory, creating a sample. Therefore, for the samples at each time step, the corresponding 3D features were obtained, and the height (H) and width (W) of the 3D features were each 31. To ensure that the geopotential data and the wind field data do not affect each other and thus produce better characterization data, these two data types were constructed separately. So, for the geopotential data, the number of channels is the same as that for the pressure level (C1), i.e., four, and for the wind field data, since there are two u-wind and v-wind variables, the value is eight (C2). For each sample at each time step, the sizes are C1 × H × W and C2 × H × W. In addition to this, the TC 2D features extracted by the CLIPER method are also used as inputs to the model for describing the 2D structure of the TC.
2.3. Segmentation of Datasets
Following data processing, the entire dataset was divided into three distinct sets based on the year: the training set, testing set, and validation set. These sets were used to train and evaluate the neural network, ensuring separate subsets for different stages of model development and assessment. Among them, 1098 TCs totaling 24,869 data points from 1979 to 2014 and 2018 to 2021 were used for training, 24 TCs totaling 451 data points from 2022 were used for validation, and, in order to make it easier to compare with other methods, we chose 82 TCs totaling 1951 data points from 2015 to 2017 for testing. The basic division of the three datasets is shown in Table 2.

Table 2.
Dataset segmentation. To facilitate comparisons with previous methods, we followed the division method used in past studies and chose the 2015–2017 TC data as the test set.
3. Methods
3.1. AFR-SimVP for Single-Step Prediction
Many recent studies have shown that large-kernel convolution has great advantages in obtaining larger effective receptive fields and more effective detailed features [39,40]. Since TC trajectory prediction can be regarded as a spatio-temporal sequence prediction problem, it is important to extract both spatial and temporal features, and a TC is also a large-scale weather event. Therefore, we believe that the SimVP network for video frame prediction based on large-kernel convolution is well suited for extracting the temporal and spatial information of the TC and reconstructing the 3D TC atmospheric field. We built the TC trajectory prediction model AFR-SimVP based on SimVP, combined with atmospheric field reconstruction and the coordinate attention mechanism, as well as second-order loss constraints, as shown in Figure 2. First, the 3D TC atmospheric features u, v, and z are extracted by the Spatial Encoder to extract the 2D spatial features on each isobaric surface through the two branches of AFR-SimVP. After extracting the TC isobaric features, the temporal features of the 3D TC variables are extracted by the Temporal Encoder, which is mainly based on large-kernel convolutional attention. Through large-kernel convolutional attention, we can more accurately capture the information interactions in the large-scale 3D atmospheric field of the TC at different time points. Finally, the 3D TC atmospheric field is reconstructed by the Decoder module. The three reconstructed atmospheric variables effectively capture the highly responsive regions of the TC trajectory through the coordinate attention mechanism. Finally, the abstract features are extracted by MLP, and the TC trajectory after 24 h is finally predicted by late fusion.
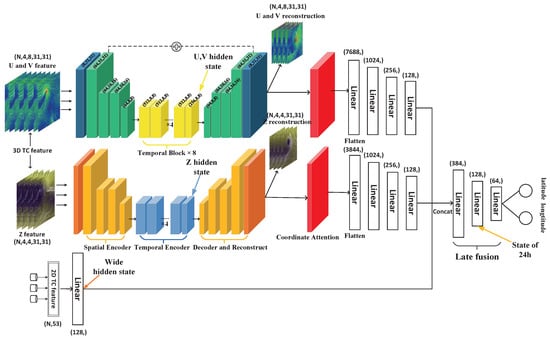
Figure 2.
The network architecture of AFR-SimVP. The Spatial Encoder is used to extract the 2D spatial features of TC variables, the Temporal Encoder is used to extract the temporal features of TCs, and the Decoder is used to reconstruct the 3D TC atmospheric field and use the reconstructed 3D atmospheric field for the soft labeling of subsequent dynamic self-distillation. The red block represents the coordinate attention mechanism, which is used to extract regions with a high response of the 3D features to the TC trajectory. The last multiple MLP layers are used to perform late fusion of the extracted features to predict the TC trajectory after 24 h. The U,V hidden state, Z hidden state, and wide hidden state together are used as the initial hidden state of AFRGRU-SimVP, and the state at 24 h is used as part of the input to AFRGRU-SimVP.
3.2. Atmospheric Field Reconstruction
Since the 3D TC reanalysis data themselves are obtained through data assimilation or post-processing, they contain a significant amount of noise, and such noise will have some impact on our predictions. And if the network is allowed to focus on the processing of a single task, overfitting can easily occur, leading to the poor generalization of the model. Therefore, we propose an atmospheric field reconstruction strategy. Previous methods often stack multiple atmospheric variables together, which allows the extraction of interactions between different atmospheric variables but also introduces more noise, leading to poorer prediction accuracy. Therefore, we propose a multi-branch structure and utilize late fusion at the end of the network to extract the relationships between the variables. To further mitigate the above effects, we perform two auxiliary reconstruction tasks on each of the two branches to reconstruct the wind field (u and v) and geopotential field (z) as atmospheric variables of the TC. It is worth mentioning that when aiming to forecast the wind speed or three-dimensional geopotential field of a TC, it is possible to utilize only the first two branches of AFR-SimVP and obtain predictions for all four time steps through a single regression (the reconstructed atmospheric variables have the same dimensions as the input data and represent predictions at four time steps). The reconstructed UV variable can be utilized to predict the TC central wind speed, while the Z variable can guide researchers in further understanding the internal state of a TC. Finally, the reconstructed atmospheric state is computed with the real future atmospheric state to calculate the loss and backpropagate it at the same time as the main task during training, and the loss is computed as shown in Equation (1):
where denotes the true values of the 3D TC variables, denotes the values predicted by the model for the u, v, and z variables, and n denotes the number of observed variables, which, in this case, are the predicted values of all isobaric meteorological variables for the z variable, that is, . Indeed, during the training process of the entire network, our objective goes beyond solely predicting the future 24 h trajectory of the tropical cyclone (TC). Simultaneously, our network is also tasked with predicting the future atmospheric state of the TC, which involves the prediction of the three-dimensional variable fields of u (longitudinal wind), v (latitudinal wind), and z (geopotential field). Moreover, these three branches are used simultaneously, and the losses of the three tasks are backpropagated simultaneously, which prevents the network from focusing on learning features that are valid for only a single task, which leads to overfitting and forces the network to learn features that are valid for all three tasks as it learns. Our experiments show that this approach enhances the generalization ability of the network and suppresses the effect of noise in the three-dimensional atmospheric variables on the main task. Additionally, integrated predictions for various TC tasks can be achieved by employing auxiliary reconstruction task branches for TC wind field and geopotential field predictions.
3.3. Second-Order Smoothing Loss
We found that when directly predicting the 24 h trajectories of TCs using regression, our model was often not able to accurately predict them where they abruptly changed, which may be due to the chaotic nature of the TCs themselves as well as the complex interactions between the different variables, which makes such abrupt changes more difficult to predict. Moreover, our predicted trajectory images tend to show different degrees of upward and downward bumps or depressions. However, after our examination of more than 1000 TC trajectory images, we found that most of the TC trajectories tend to show a smooth trend, and even though there may be some sudden abrupt changes at some points in time, the overall trajectories are smooth for most of the TCs. Given these two problems, we believe that we need to add some constraints so that the TCs predicted by the model maintain a smooth trend as much as possible and reduce the impact of abnormal mutations of TCs on our prediction results. To this end, we optimized the final trajectory prediction loss function and proposed a second-order smoothing loss function for the TC consisting of three parts, as shown in Equations (2)–(4):
where m denotes the number of samples, denotes the reference latitude and longitude of the prediction, denotes the latitude and longitude of the network prediction, and and denote the reference latitude and longitude of the prediction six hours before the prediction time point. For example, in this study, we predicted the latitude and longitude of the TC after 24 h, so here, these values represent the TC reference latitude and longitude after 18 h. Constraining the 24 h prediction result of the TC by distance loss and cosine similarity loss forces the TC to maintain a smooth curve, which improves the accuracy of the prediction, and one can also understand this method as a regularization means by adding some a priori knowledge to the model, thus making it difficult for the model to be overfitted. We tested our second-order smoothing loss on TC Nakri No. 10 in 2002, keeping the random number unchanged and training for the same number of epochs. After adding the second-order smoothing loss, the model error caused by the sudden change in the TC trajectory is effectively reduced compared with the original model, and the predicted TC curve is kept as smooth as possible, as shown in Figure 3.
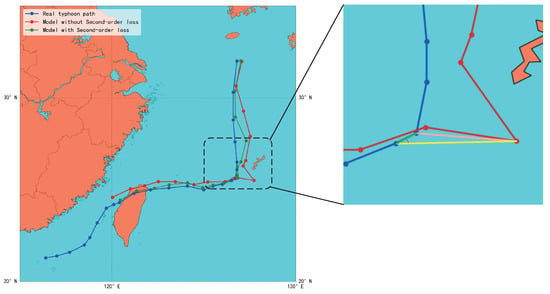
Figure 3.
The prediction results of the model after adding the second-order loss are plotted against the prediction results of the original model, where the blue curve represents the correct trajectory of Nakri, the red curve represents the prediction result curve of the original model for 24 h, and the green curve represents the prediction result curve of the model after adding the second-order loss. The pink line in the small figure represents the distance error between the predicted value and the real value, the yellow line represents the error between the predicted value and the real value at the previous moment, the green line represents the error between the real value and the real value at the previous moment, and the red angle between the green line and the yellow line represents the angle between the real position at the previous moment to the real position at this moment and the real position at the previous moment to the predicted position at this moment.
As shown in the picture above, our main optimization objective is still to limit the length of the pink line; secondly, we would like to keep the yellow line and the green line as long as possible at the same length; and lastly, we want to constrain the angle between the yellow line and the green line to be 0° as much as possible. It can be seen that by introducing the second-order smoothing loss, the model shows better prediction results with a sudden change in the TC trajectory and does not produce a huge error due to the sudden change in the TC trajectory. On the contrary, the original model without the second-order loss fails to accurately predict the sudden change in the TC trajectory, which leads to a huge prediction error. On the whole, after adding the second-order loss, the prediction curves of the model remain smoother compared with the original model, which is what we would like to see.
3.4. HTAFR-SimVP for Multi-Step Prediction
AFR-SimVP uses a regression-based approach and is able to directly predict TC trajectories after 24 h; however, short-term predictions such as 6 h and 12 h also play an important role. AFR-SimVP can only be used to perform short-term predictions by training different short-term prediction models to predict each time separately, which will undoubtedly consume a lot of resources. Therefore, we considered modifying the structure of AFR-SimVP so that it can predict each short-term time point at the same time.
If one wants to predict the trajectories of TCs at multiple time steps (6 h, 12 h, 18 h, 24 h) at the same time, a commonly used method is the recurrent network of the RNN family, where the recurrent network is utilized to extract the temporal information contained in the TC motion and thus recursively predicts the trajectories of TCs at multiple time steps [20,21,32,33]. In contrast, regression-based predictions often only predict the trajectory of the TC after one time step at a time [29,31].
We propose a novel approach that allows our regression-based AFR-SimVP network to predict TC trajectories at multiple time steps simultaneously without the use of a traditional RNN network, and the obtained prediction results outperform those of a traditional RNN-based network. We named this network the hierarchical temporal feature-based atmospheric field reconstruction TC prediction network (HTAFR-SimVP), and the specific structure is shown in Figure 4.
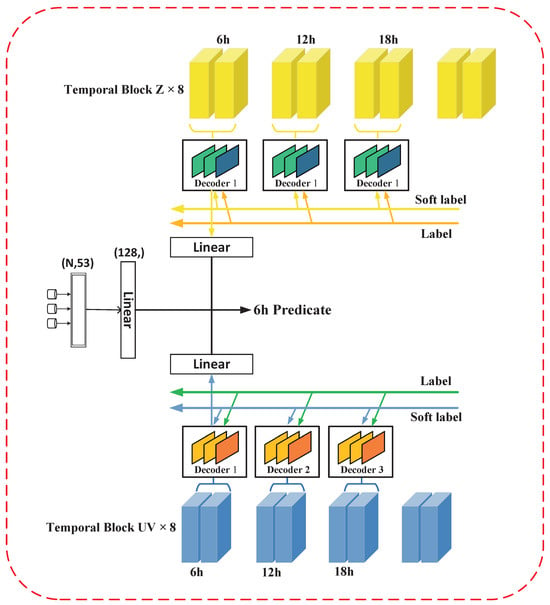
Figure 4.
The specific architecture of HTAFR-SimVP, where only the 6 h prediction process is drawn, and all other time points are similar. The Decoder is used to up-sample the feature maps of the students, and the up-sampled three-dimensional atmospheric state feature maps are utilized for auxiliary tasks, namely, TC wind field prediction and three-dimensional geopotential field prediction, where the coordinate attention block and some fully connected layers after up-sampling the network for each student are omitted. “Soft label” represents the soft label of the atmospheric state after the reconstruction of the network by the teacher, and “label” represents the real atmospheric state.
Inspired by the pyramid structure commonly used in target detection to extract multi-scale features and the self-distillation structure [41,42,43], we think that a hierarchical concept can also be used for temporal features. For a 6 h TC prediction, we think that we can achieve good prediction performance by using only fine-grained temporal features, while for longer prediction times, more coarse-grained global features are needed to guide the model’s prediction. So, we came up with the idea of a fine-to-coarse architecture that introduces the concept of multi-scale temporal features, and soft labels are obtained through dynamic self-distillation to assist the training of our model. Specifically, we use our main model, AFR-SimVP, as the teacher model and use the 24 h prediction outputs generated by the two branches of the main model as the soft-label supervised signals, and we reverse-supervise the (6 h, 12 h, 18 h) predictions, which do not require too much temporal information. We obtain eight temporal blocks by splitting the main model into four equal parts, where two blocks in each part are responsible for predicting the TC trajectory and atmospheric field at one time point, thus achieving simultaneous (6 h, 12 h, 18 h, 24 h) predictions of the TC. Among them, the first three copies serve as three students of the main model, which are supervised by the 3D TC state feature maps generated by the teacher network. And each of these four blocks is one layer more abstract than the one before it; that is, the first copy may contain only a small number of temporal features, whereas, by the fourth copy, highly abstract temporal features are generated, which is similar to a multi-scale architecture. We use the first copy to predict the TC trajectory and atmospheric field after 6 h, the second copy to predict them after 12 h, and so on. Using this architecture, we obtain 12 predictions with only one forward inference, with each student being responsible for the prediction of the 3D wind field, the 3D geopotential field, and the trajectory at that time step for 6 h, 12 h, or 18 h and the teacher being responsible for the prediction of all three tasks for 24 h.
It should be noted that, because the soft-label feature map generated by the main network teacher comes after the Decoder’s up-sampling, there may be a difference in the size of the feature maps of the three students. Therefore, here, each student is added to the bottleneck Decoder, which is used to up-sample the feature map of the student, so that the sizes of the real labels and soft labels match the calculation of the loss. In addition, the soft-label dimension generated by the main network is (4, 4, 31, 31), from which the batch dimension is omitted, where the first 4 represents the time dimension, the second 4 represents the different isobaric surfaces of the TC, and the two 31s represent the range of the TC. However, when it is used as a soft label in the three-student network, not all four time dimensions will be used; however, the corresponding time dimensions will be dynamically selected according to the different time points of the student’s prediction. For example, when a student model is making a 6 h prediction, it utilizes only the first time dimension from the teacher’s four time dimensions as a soft label. Similarly, for a 12 h prediction, the student model incorporates the first two time dimensions from the teacher’s data, and for an 18 h prediction, it utilizes the first three time dimensions from the teacher’s data.
During the experiment, we found that the teacher’s soft labels were easier to learn for the three students in the early stages of training. However, as training progressed, the predictions of the three students gradually matched those of the teacher. At this point, the hard labels were more helpful for the students’ learning. In addition, since our model has three students and the training time to reach the optimal prediction is different for each student, we found in the experiment that, compared to the other two students, the student with the 6 h prediction time point could reach the prediction accuracy matching the teacher with a faster training time, while the other two students needed a longer training time. Therefore, we used cosine weight decay to dynamically adjust the contribution of soft and hard labels and set different decay coefficients for each student, as shown in Equation (5):
where denotes the proportion of the teacher’s soft-label weight at the end of the decay; here, we set to 0.01, i denotes the decay rate for each student, and for the 6 h student, we set the decay rate to 4. This means that, when we train for 500 rounds, at 125 rounds, the weight contribution of the teacher’s soft label for the 6 h student reaches the minimum value and stops decaying. For the 12 h and 18 h students, the soft-label contribution takes longer.
3.5. AFRGRU-SimVP for Long-Term Prediction
Up to this point, our model has been able to adapt to the task of forecasting at various points in time over a 24 h period. So, is there a way to adapt our model to make longer-term predictions? We attempted to employ AFR-SimVP directly to predict the 48 h and 72 h trajectories of TCs; however, the prediction results were not satisfactory. We believe that for the prediction of a TC at 48 h and even longer, it may be difficult to achieve better prediction accuracy using a regression approach, and it is necessary to more fully extract the temporal features of the TC trajectory to achieve the desired prediction accuracy.
Therefore, to make our network applicable to the long-term prediction of TC trajectories, we added a gated recurrent network (GRU) to the network to capture the long-term temporal information of TCs. Compared to the RNN, the GRU has better long-term memory capability and does not suffer from gradient vanishing or gradient explosion problems. In order to combine both the advantages of our network in 24 h prediction and the ability of the GRU to extract long-term features, instead of simply connecting our AFR-SimVP to the GRU, we chose to first predict the 24 h trajectory of TCs using AFR-SimVP, followed by connecting the trained AFR-SimVP to the GRU, using the hidden layer state of AFR-SimVP as the initial state of the GRU and splicing the 24 h TC state and the 24 h latitude and longitude predicted by the network as the input of the first moment of the GRU. With this two-stage training approach, we retain the advantage of the network’s prediction at 24 h while fully extracting the temporal information required for long-term TC prediction. The GRU module is shown in Figure 5.
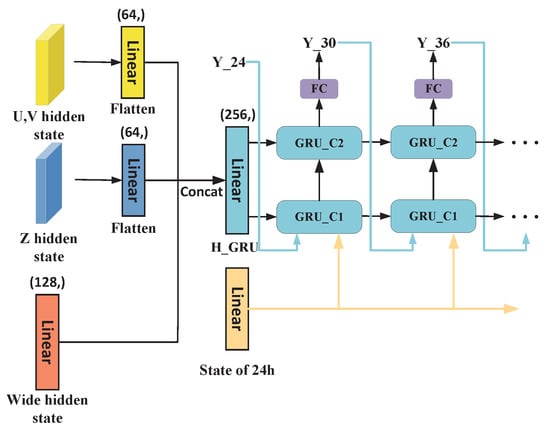
Figure 5.
The GRU structure for implementing 24 h to 72 h trajectory prediction, where initial hidden states and inputs are obtained from the AFR-SimVP network. H_GRU represents the initial hidden state of the GRU fused from the three parts of the hidden state of the AFR-SimVP network. The state at 24 h serves as part of the input for all time steps of the GRU, and the other part of the input consists of the prediction results for each time step.
According to the experiments, the AFRGRU-SimVP network can effectively extract temporal features and has a good performance in 48 h prediction while ensuring 24 h prediction accuracy, which is an improvement compared to the previous network.
3.6. Loss Function
We trained our model in an end-to-end manner. Although the model has an additional atmospheric field reconstruction task, the training time of the model does not become longer, but it is easier to train. We believe that this is because there is a complementary relationship between the three tasks, which can promote each other during the training process, leading to the faster convergence of the model. The loss function of AFR-SimVP is defined as shown in Equation (6):
where denotes the position loss, denotes the distance loss, denotes the cosine similarity loss of the angle, denotes the atmospheric state reconstruction loss of the u and v variables, denotes the atmospheric state reconstruction loss of the z variable, and the rest of the numbers are hyperparameters. For AFRGRU-SimVP, no atmospheric field reconstruction is involved, so the loss consists only of the first three components.
The teacher loss for HTAFR-SimVP is the same as above, and the loss function for the three students is shown in Equation (7):
The first three of these are consistent with the network of AFR-SimVP; and represent the loss between the student-generated atmospheric state and the true atmospheric state, and and represent the loss between the soft labels generated by the teacher’s network and the atmospheric state predicted by the student. is used to dynamically control the proportion of the loss contribution from the teacher’s soft labeling.
3.7. Training Details
We use the Pytorch framework to train our AFR-SimVP and HTAFR-SimVP in an end-to-end manner, using the Adam optimizer and setting the initial learning rate to 0.0001 and the batch size to 64. The hyperparameters and in Equation (5) are set to 1.2 and 1.2, respectively. We train the AFR-SimVP and HTAFR-SimVP on a single NVIDIA GeForce RTX 3080 GPU. The training of AFRGRU-SimVP is based on AFR-SimVP. After training AFR-SimVP, we freeze its weights, add the GRU module, and then fine-tune the network; the learning rate is still set to 0.0001, and the batch size is set to 64. This can greatly reduce the training time, and it only takes 30 min to finish AFRGRU-SimVP training.
3.8. Evaluation Metrics
The performance of the model on the test set is quantitatively evaluated through three evaluation metrics: mean absolute error (MAE), root mean square error (RMSE), and mean distance error (MDE). MAE averages the absolute error between the predicted value and the reference value. MSE is the squared mean of the difference between the predicted value and the reference value, and RMSE is the square root of MSE. Mean distance error (MDE) is a commonly used metric for measuring the mean distance error between model predictions and the ground truth. The larger the values of these metrics, the worse the model performance. These three evaluation metrics are calculated separately, as shown in Equations (8)–(10):
where m represents the number of test samples, denotes the reference position of the TC, and denotes the predicted position of the TC. R represents the radius of the Earth, and represent the predicted and true latitude values, and and represent the predicted and true longitude values, respectively.
4. Results
4.1. Effectiveness of Coordinate Attention Mechanisms
To demonstrate the effectiveness of coordinate attention, we created a graph to visualize the predicted outcome of Typhoon Bavi, the fourth typhoon in 2015. The effect of attention is visualized in Figure 6.
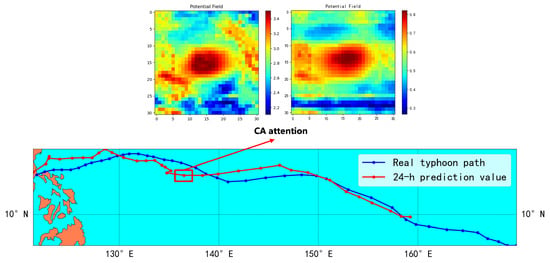
Figure 6.
The visualization of the effect of attention. The left figure represents the predicted geopotential field without adding attention, and the right figure represents the effect after adding attention.
As shown in the figure, the network fails to allocate attention to the geopotential field in the direction of the TC’s movement when no attention is added. With the addition of attention, our model effectively captures the direction in which the TC is moving. From our experiments, it is observed that the incorporation of the attention mechanism significantly enhances the prediction accuracy of tropical cyclone (TC) trajectories.
4.2. Comparison with Statistical/Deep Learning Methods in Trajectory Prediction Tasks
4.2.1. Twenty-Four-Hour Trajectory Forecast
The 24 h prediction of a TC can help people know the path of the TC in time so as to take corresponding precautions, which plays a vital role in reducing the casualties and property losses caused by a TC. We first compare our approach with traditional statistical and deep learning-based 24 h TC trajectory prediction methods, including extrapolation, the CLIPER method [13], Fusion CNN [29], AE-GRU [24], AM-convgru [31], and the more recently developed DBF-Net [32] and Smoothed-3DGRU [33]. The CLIPER method serves as a benchmark for other models and official predictions and can be used as our baseline. Fusion CNN makes use of multimodal data along similar lines to ours, but it does not take into account the interplay among various types of noise in multimodal data. The remaining several RNN-based methods can effectively capture the complex temporal features of TCs but rarely consider the role of multiple influences on TCs. Smoothed-3DGRU combines a GRU and 3DCNN and considers the temporal state while combining multiple atmospheric features; however, the model simply stacks multiple atmospheric features, which causes the noise in different features to interact, thus affecting the final prediction. To facilitate the comparison, we only change the labels during model training without changing the model structure and methodology, thus training four comparison models to predict the TC trajectories at 6 h, 12 h, 18 h, and 24 h. The comparison results of the various models are shown in Table 3.

Table 3.
Forecast errors (km) for the proposed model and traditional methods in 6 h, 12 h, 18 h, and 24 h prediction. Bold represents the minimum error.
It can be seen that our proposed AFR-SimVP outperforms previous methods for almost all prediction times. The substantial accuracy improvement achieved by our AFR-SimVP compared to the baseline proves the effectiveness of our method. Compared to Smoothed-3DGRU, our method only slightly lags behind at the 6 h prediction, but as the prediction time increases, our model gradually improves its prediction accuracy and outperforms Smoothed-3DGRU at the 12 h, 18 h, and 24 h prediction times, especially at the 24 h prediction, where it achieves a performance improvement of . This indicates that our model effectively reduces the influence of various types of noise on the prediction results and significantly improves the generalization capability.
Despite not achieving optimal prediction performance, the HTAFR-SimVP model demonstrates a notable improvement in accuracy compared to traditional multitemporal step TC prediction models based on recurrent networks, proving the effectiveness of our architecture. Compared to AFR-SimVP, HTAFR-SimVP only needs to be trained once to predict the TC trajectories at four time points simultaneously, which greatly reduces the time needed for model training.
4.2.2. Long-Term Forecasting
We attempted to apply our model to the 48 h and 72 h predictions of TCs to demonstrate the validity of our model by comparing AFR-SimVP with the RNN, GRU, and LSTM in a direct cascade with our AFRGRU-SimVP. The MAE and RMSE values between the model-predicted latitude and longitude and the true values are shown in Table 4. It can be seen that AFRGRU-SimVP obtains the best metrics at all predicted time points.

Table 4.
The long-term prediction effectiveness evaluation (MSE/RMSE) of multiple models, where RNN, LSTM, and GRU represent the direct cascading of AFR-SimVP with the recurrent network, SimVP represents our 24 h prediction model, and represents AFRGRU-SimVP. Bold highlights the best performance.
Table 5 compares the prediction results of AFRGRU-SimVP with various deep learning methods, expressed in terms of mean distance error. It is clear that the RNN-based model is significantly weaker in performance than the GRU- and LSTM-based models. This is due to the poor performance of the RNN in dealing with long-sequence problems. The GRU and LSTM, on the other hand, both introduce special gating mechanisms, which gives them an advantage in dealing with long sequences. And our AFRGRU-SimVP fully integrates the advantages of AFR-SimVP and the GRU, which also gives the model an absolute advantage in dealing with long-term TC prediction. Our two-stage training significantly improves the prediction accuracy compared to directly cascading the two parts, while the prediction error is also greater if only AFR-SimVP is used for long-term prediction. Compared to the MMSTN [25] method proposed by Huang et al., our method drastically shrinks the prediction error. Therefore, we believe that regression is more advantageous for short-term prediction, while, when it comes to long-term prediction, temporal information needs to be fully considered.

Table 5.
A comparison of the average distance error (km) of multiple deep learning models. Bold represents the best value.
As shown in Figure 7, compared to the direct-cascade recurrent network and AFR-SimVP, our strategy has a significant advantage in long-term prediction, with a significant reduction in both the maximum error and the average error in 48 and 72 h predictions.
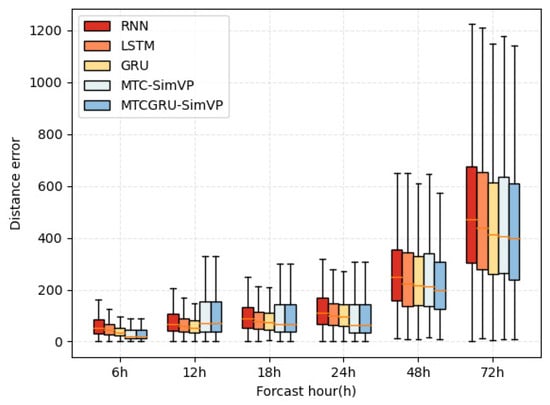
Figure 7.
Distance error box plots of 6-72 h trajectory prediction distances for three recurrent neural networks and AFR-SimVP and AFRGRU-SimVP.
Figure 8 shows a scatterplot of predicted versus true values, where we plot the predictions for 12 h, 24 h, 48 h, and 72 h. The distance between the data points and the diagonal line indicates the prediction error of the model. It can be seen that as the prediction time increases, the prediction accuracy of the model gradually decreases. On the other hand, the maximum wind speed at the center of the TC also has an effect on the prediction results of the model, and the larger the central wind speed, the higher the prediction accuracy of the model. In addition, we found that the prediction accuracy of the model decreases significantly when the TC moves northward. Based on the aforementioned comparison, we observe a strong correlation between the prediction accuracy of the TC central wind speed and the prediction accuracy of the TC trajectory. Consequently, we conducted subsequent experiments focusing on TC wind prediction.
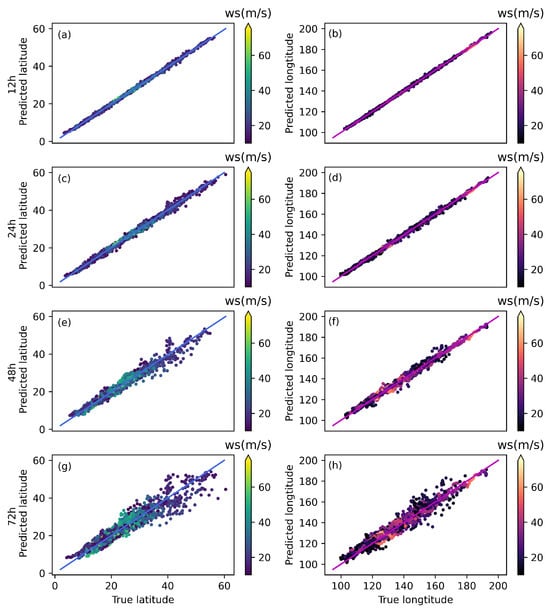
Figure 8.
The scatterplot distributions of latitude and longitude for 12 h (a,b), 24 h (c,d), 48 h (e,f), and 72 h (g,h) forecasts. Colors represent the maximum wind speed at the TC center.
4.3. Comparison with NWP Forecast Methods
We compare AFR-SimVP with numerical weather prediction models commonly used in the industry (NWP). Numerical weather prediction models are currently the mainstream models in weather forecasting operations, and we selected the global forecast models T213 and T639 released by the China Meteorological Administration (CMA) and the Shanghai Typhoon Region model (SHTP) released by the Shanghai Typhoon Research Institute of the China Meteorological Administration (CMA) in Shanghai, China [9,10,11], to compare with our method. In contrast to our method, numerical weather prediction methods often require expensive computational resources and very high-resolution data to effectively construct the partial differential equations of the atmosphere to obtain more accurate results, and this prediction method requires a long inference time, which needs to be improved for TC prediction. Our deep learning method, on the other hand, requires only a small amount of computational resources and a single inference time of only a few seconds. However, NWP can still achieve better performance than current deep learning-based methods. As shown in Table 6, our AFR-SimVP achieves a significant accuracy improvement of more than compared to T213/T639. However, compared with SHTP, our deep learning-based method still falls short.

Table 6.
A comparison of AFR-SimVP and numerical weather prediction method trajectory prediction results. The variable “#Samples” represents the number of TCs in the current year used for model testing, while “AVG” represents the average error of the model predictions for all TCs over the three-year period.
In contrast, our AFR-SimVP achieves relatively high prediction accuracies with lower-resolution (1o for all u, v, and z atmospheric field data) inputs and less computational resources, and our inference time is several orders of magnitude faster compared to NWP. In addition, we believe that by improving the resolution of the data and expanding the number of parameters in the model, our AFR-SimVP can achieve even higher prediction accuracies.
4.4. Effectiveness of Atmospheric Field Reconstruction
As an additional task in our model, atmospheric field reconstruction also significantly impacts the accuracy of trajectory prediction. As can be seen in Figure 8, there is a close relationship between the prediction accuracy of the TC central wind speed and the prediction of its track. Our model had already achieved good prediction accuracy in the trajectory prediction task. Therefore, we speculated that our model might also achieve good predictive performance in wind field reconstruction. Therefore, to demonstrate the effectiveness of our atmospheric field reconstruction strategy and integrated model, we utilized the three-dimensional atmospheric state prediction branches of AFR-SimVP and HTAFR-SimVP trained on the track prediction task to predict the central wind speed of the TC. For the purpose of facilitating comparisons, we calculated the central wind speed of the TC using the reconstructed near-surface (1000 hPa) u-wind and v-wind components from the model and approximated the intensity of the TC by using the central wind speed. We compared our prediction results with numerical forecasting methods [44,45,46,47] and deep learning approaches [48,49,50,51,52,53], and the results are shown in Table 7.

Table 7.
The proposed method is compared with previous deep learning methods and numerical forecasting methods in terms of prediction errors (m/s) for the 24 h central wind speed forecasting task. Bold represents the minimum error.
As shown in Table 7, our model also achieved comparable performance in TC central wind speed prediction, which further validates the effectiveness of the atmospheric field reconstruction tasks that we selected. In terms of average prediction errors over the past three years, our HTAFR-SimVP model achieved the best prediction accuracy. We believe this is because the students’ learning regularizes the training process of the network, allowing the teacher to benefit from the student and thereby improving the prediction accuracy. In the multi-time-step prediction task, we directly use three student models to predict the TC central wind speed at 6 h, 12 h, and 18 h. We compared these results with previous methods, and the results are shown in Table 8.

Table 8.
A comparison of the proposed method with previous deep learning approaches in terms of multi-time-step prediction errors (m/s) for the TC central wind speed. Bold represents the minimum error.
The relatively low prediction accuracy of AFR-SimVP in multi-time-step forecasting can be attributed to its direct regression of the three-dimensional wind field state on four time steps and four isobaric surfaces without fully considering the progressive relationship between different time steps. As a result, the prediction accuracy for the four time steps is not significantly different. In contrast, HTAFR-SimVP assigns each student to predict the three-dimensional wind field for a specific time step without considering other factors. By acquiring knowledge from the soft labels of the main teacher network and leveraging the hierarchical progression in the extraction of time features, HTAFR-SimVP achieves a further improvement in the prediction accuracy for multiple time steps. Compared to other deep learning models, our model not only predicts the central wind speed but also reconstructs the three-dimensional geopotential field due to the branch tasks. The three-dimensional geopotential field predicted by the model is visualized in Figure 9.
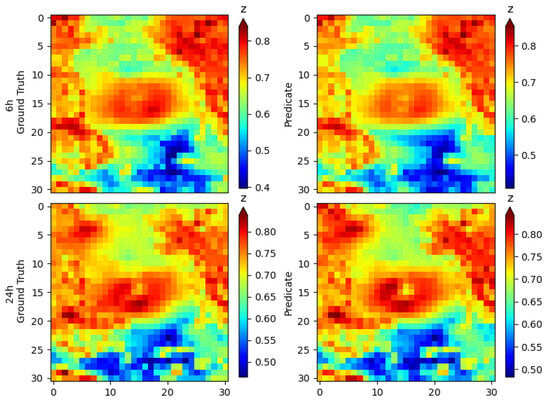
Figure 9.
The predicted results of the geopotential field at the 1000 hPa isobaric surface at a specific point along the track of Typhoon Bavi.
It can be observed that the model shows good performance in predicting the geopotential field at 6 h and 24 h intervals. This provides researchers with valuable references for further understanding the movement process of TCs and demonstrates that our model achieves good prediction results across multiple tasks.
4.5. Ablation Experiment
To further demonstrate the effectiveness of our proposed AFR-SimVP network for TC trajectory prediction, we conducted ablation experiments on the network, and by sequentially deleting modules from the network and calculating the average distance error predicted by the model, we obtained the results shown in Table 9.

Table 9.
Ablation study table. A tick indicates that the module is used, a cross indicates that it is not used.
It can be seen that each of our proposed modules and methods is effective, among which the two-stage loss, coordinate attention, and atmospheric field reconstruction drastically reduce the prediction error of the model, thus further confirming the excellent performance of AFR-SimVP in TC trajectory prediction tasks.
4.6. Visualization of Model Prediction Results
To further demonstrate the effectiveness of our proposed model in predicting TC tracks, we selected Typhoon Nangka, the 11th typhoon in 2015, and Typhoon NORU, the 6th typhoon in 2017, to visualize the 24 h paths predicted by our model. We predicted the future 24 h path based on the first 24 h historical path of the typhoon. Figure 10a,b show the 24 h prediction results for Typhoon Nangka and Typhoon NORU, respectively. The red line represents the true path of the TC, and the blue line represents the track predicted using our AFR-SimVP model.
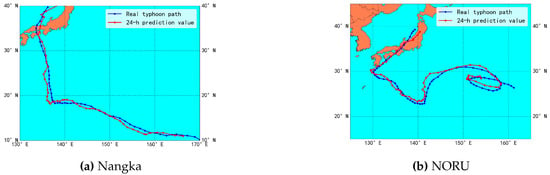
Figure 10.
Track prediction results.
As shown in the figure above, the average prediction distance of our model on the two TCs is about 80 km, which indicates that our model has fully learned the potential features of the TC trajectory motion, further proving the effectiveness of AFR-SimVP. As can be seen in the figure, both TCs contain obvious trajectory mutations during their motion, but our model is able to accurately predict such mutations in advance due to the presence of atmospheric field reconstruction tasks and second-order loss, and the overall trend of TC trajectories predicted by AFR-SimVP is smoother, which is in line with the trend of the real TC motion.
5. Conclusions and Future Work
In this paper, we propose a TC trajectory prediction network, AFR-SimVP, based on large-kernel convolutional attention and atmospheric field reconstruction, and, based on this network, combined with hierarchical temporal feature extraction and dynamic self-distillation, we propose a new architecture, HTAFR-SimVP, for the multi-step prediction of TC trajectories, which is different from the traditional RNN network. The proposed AFR-SimVP network achieves the optimal prediction accuracy for the 24 h prediction of TC trajectories, and STAFR-SimVP achieves integrated multi-task prediction at multiple time steps and achieves good performance on both the trajectory and central wind speed prediction tasks. The main contributions of this paper can be summarized as follows:
- The large-kernel convolutional attention network SimVP, combined with atmospheric field reconstruction, is used to fully extract a wide range of spatio-temporal features of TCs and reduce the impact of various types of noise in the reanalyzed data on the task of TC trajectory prediction. A second-order loss is proposed, which can further constrain the prediction results of the network, enabling the network to better predict the trajectory mutations of TCs, and the predicted TC trajectories are closer to the real trajectories of TCs.
- Introducing the hierarchical temporal feature extraction and dynamic self-distillation technique into our network, we propose a novel multi-step prediction framework. The framework uses multi-scale temporal features to segmentally predict the multi-step trajectories of TCs and uses soft labels generated by the main network to guide the learning of the shallow network, which makes the training of the network more efficient. The framework achieves multi-step prediction without using the recurrent network at all and achieves higher prediction accuracy than past TC prediction models based on recurrent networks. Meanwhile, it also provides inspiration for future research.
- Medium- and long-term predictions of TCs were explored using a two-stage training method. Combining AFR-SimVP with the GRU ensures the accuracy of short-term TC prediction so that the model has comparable performance in medium- and long-term predictions as well.
- Multiple TC prediction tasks were integrated into a single model, and good prediction results were achieved. The integrated prediction of multiple tasks can be achieved by only one inference, which greatly reduces the time needed to train multiple networks.
Since our network is based on large-kernel convolutional attention, we believe that it should have better prediction performance on higher-resolution 3D data. In addition, our hierarchical temporal feature extraction strategy is very similar to the U-Net architecture in image segmentation, so we should follow the up-sampling strategy in U-Net to progressively up-sample the highly abstract 24 h features, thereby aligning them with the 6 h features of the shallow network, and further fuse the two parts of the aligned features so as to further fuse the global temporal features with the local temporal features, letting the 24 h global temporal features guide the learning of 6 h local temporal features. This will be a direction that we will try in the future.
Author Contributions
Conceptualization, S.Y.; Data Curation, Z.Z.; Formal Analysis, W.Z.; Funding Acquisition, W.Z.; Investigation, S.Y.; Methodology, Z.Z.; Project Administration, W.Z.; Resources, S.Y.; Software, Z.Z.; Supervision, S.Y.; Validation, Z.Z.; Visualization, Z.Z.; Writing—Original Draft, Z.Z.; Writing—Review and Editing, S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
Supported by the Shenzhen Science and Technology Program (Grant No. KQTD20180411143338837).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are available from the second author on reasonable request. The data are not publicly available due to privacy.
Acknowledgments
The authors would like to thank each member of the team for their efforts.
Conflicts of Interest
Author Wei Zheng was employed by the company Shenzhen Youjia Innov Tech Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Roy, C.; Kovordányi, R. Tropical cyclone track forecasting techniques―A review. Atmos. Res. 2012, 104, 40–69. [Google Scholar] [CrossRef]
- Boussioux, L.; Zeng, C.; Guénais, T.; Bertsimas, D. Hurricane forecasting: A novel multimodal machine learning framework. Weather Forecast. 2022, 37, 817–831. [Google Scholar] [CrossRef]
- Kwon, H.J.; Lee, W.J.; Won, S.H.; Cha, E.J. Statistical ensemble prediction of the tropical cyclone activity over the western North Pacific. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Bril, G. Forecasting hurricane tracks using the Kalman filter. Environmetrics 1995, 6, 7–16. [Google Scholar] [CrossRef]
- Chen, Y.; Snyder, C. Assimilating vortex position with an ensemble Kalman filter. Mon. Weather Rev. 2007, 135, 1828–1845. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Liu, Q.; Marchok, T.; Sheinin, D.; Surgi, N.; Tuleya, R.; Yablonsky, R.; Zhang, X. Hurricane Weather Research and Forecasting (HWRF) Model Scientific Documentation. Dev. Testbed Cent. 2010, 75. Available online: https://api.semanticscholar.org/CorpusID:202704350 (accessed on 9 May 2024).
- Gopalakrishnan, S.; Liu, Q.; Marchok, T.; Sheinin, D.; Surgi, N.; Tong, M.; Tallapragada, V.; Tuleya, R.; Yablonsky, R.; Zhang, X. Hurricane Weather Research and Forecasting (HWRF) Model: 2011 Scientific Documentation; Bernardet, L., Ed.; 2011; Available online: https://api.semanticscholar.org/CorpusID:53001171 (accessed on 9 May 2024).
- Hogan, T.F.; Liu, M.; Ridout, J.A.; Peng, M.S.; Whitcomb, T.R.; Ruston, B.C.; Reynolds, C.A.; Eckermann, S.D.; Moskaitis, J.R.; Baker, N.L.; et al. The navy global environmental model. Oceanography 2014, 27, 116–125. [Google Scholar] [CrossRef]
- Bai, L.; Chen, G.; Zhang, X.; Wan, R. Verification on forecast of tropical cyclones over western north Pacific in 2015. Meteorological 2017, 43, 501–507. (In Chinese) [Google Scholar]
- Chen, G.; Zhang, X.; Bai, L.; Wan, R. Verification on Forecasts of Tropical Cyclones over Western North Pacific in 2016. Meteorological 2018, 44, 582. [Google Scholar]
- Chen, G.; Zhang, X.; Bai, L.; Wan, R. Verification on Forecasts of Tropical Cyclones over Western North Pacific and South China Sea in 2017. Meteorological 2019, 45, 577. [Google Scholar]
- Neumann, C.J. An Alternate to the HURRAN (Hurricane Analog) Tropical Cyclone Forecast System. NOAA Technical Memorandum NWS SR. 62. 1972. Available online: https://repository.library.noaa.gov/view/noaa/3605 (accessed on 9 May 2024).
- Neumann, C.J.; Lawrence, M.B. An operational experiment in the statistical-dynamical prediction of tropical cyclone motion. Mon. Weather Rev. 1975, 103, 665–673. [Google Scholar] [CrossRef]
- Neumann, C.J. A Guide to Atlantic and Eastern Pacific Models for the Prediction of Tropical Cyclone Motion. NOAA Technical Memorandum NWS NHC. 11. 1979. Available online: https://repository.library.noaa.gov/view/noaa/6557 (accessed on 9 May 2024).
- Iwasaki, T.; Nakano, H.; Sugi, M. The performance of a typhoon track prediction model with cumulus parameterization. J. Meteorol. Soc. Japan Ser. II 1987, 65, 555–570. [Google Scholar] [CrossRef][Green Version]
- Tan, J.; Chen, S.; Wang, J. Western North Pacific tropical cyclone track forecasts by a machine learning model. Stoch. Environ. Res. Risk Assess. 2021, 35, 1113–1126. [Google Scholar] [CrossRef]
- Ali, M.; Kishtawal, C.; Jain, S. Predicting cyclone tracks in the north Indian Ocean: An artificial neural network approach. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Song, H.J.; Huh, S.H.; Kim, J.H.; Ho, C.H.; Park, S.K. Typhoon track prediction by a support vector machine using data reduction methods. In Proceedings of the Computational Intelligence and Security: International Conference, CIS 2005, Xi’an, China, 15–19 December 2005; Proceedings Part I. Springer: Cham, Switzerland, 2005; pp. 503–511. [Google Scholar]
- Wang, Y.; Zhang, W.; Fu, W. Back Propogation (BP)-neural network for tropical cyclone track forecast. In Proceedings of the 2011 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; IEEE: New York, NY, USA, 2011; pp. 1–4. [Google Scholar]
- Moradi Kordmahalleh, M.; Gorji Sefidmazgi, M.; Homaifar, A. A sparse recurrent neural network for trajectory prediction of atlantic hurricanes. In Proceedings of the Genetic and Evolutionary Computation Conference 2016, Denver, CO, USA, 20–24 July 2016; pp. 957–964. [Google Scholar]
- Alemany, S.; Beltran, J.; Perez, A.; Ganzfried, S. Predicting hurricane trajectories using a recurrent neural network. In Proceedings of the AAAI Conference on Artificial Intelligence, Hawaii, HI, USA, 27 January–1 February 2019; Volume 33, pp. 468–475. [Google Scholar]
- Kapoor, A.; Negi, A.; Marshall, L.; Chandra, R. Cyclone trajectory and intensity prediction with uncertainty quantification using variational recurrent neural networks. Environ. Model. Softw. 2023, 162, 105654. [Google Scholar] [CrossRef]
- Gao, S.; Zhao, P.; Pan, B.; Li, Y.; Zhou, M.; Xu, J.; Zhong, S.; Shi, Z. A nowcasting model for the prediction of typhoon tracks based on a long short term memory neural network. Acta Oceanol. Sin. 2018, 37, 8–12. [Google Scholar] [CrossRef]
- Lian, J.; Dong, P.; Zhang, Y.; Pan, J. A novel deep learning approach for tropical cyclone track prediction based on auto-encoder and gated recurrent unit networks. Appl. Sci. 2020, 10, 3965. [Google Scholar] [CrossRef]
- Huang, C.; Bai, C.; Chan, S.; Zhang, J. MMSTN: A Multi-Modal Spatial-Temporal Network for Tropical Cyclone Short-Term Prediction. Geophys. Res. Lett. 2022, 49, e2021GL096898. [Google Scholar] [CrossRef]
- Rüttgers, M.; Lee, S.; Jeon, S.; You, D. Prediction of a typhoon track using a generative adversarial network and satellite images. Sci. Rep. 2019, 9, 6057. [Google Scholar] [CrossRef]
- Mudigonda, M.; Kim, S.; Mahesh, A.; Kahou, S.; Kashinath, K.; Williams, D.; Michalski, V.; O’Brien, T.; Prabhat, M. Segmenting and Tracking Extreme Climate Events Using Neural Networks. In Proceedings of the Deep Learning for Physical Sciences (DLPS) Workshop, Held with NIPS Conference; 2017. Available online: https://api.semanticscholar.org/CorpusID:201703393 (accessed on 9 May 2024).
- Kim, S.; Kim, H.; Lee, J.; Yoon, S.; Kahou, S.E.; Kashinath, K.; Prabhat, M. Deep-hurricane-tracker: Tracking and forecasting extreme climate events. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 7–11 January 2019; IEEE: New York, NY, USA, 2019; pp. 1761–1769. [Google Scholar]
- Giffard-Roisin, S.; Yang, M.; Charpiat, G.; Kumler Bonfanti, C.; Kégl, B.; Monteleoni, C. Tropical cyclone track forecasting using fused deep learning from aligned reanalysis data. Front. Big Data 2020, 3, 1. [Google Scholar] [CrossRef]
- Rüttgers, M.; Lee, S.; You, D. Prediction of typhoon tracks using a generative adversarial network with observational and meteorological data. arXiv 2018, arXiv:1812.01943. [Google Scholar] [CrossRef]
- Xu, G.; Xian, D.; Fournier-Viger, P.; Li, X.; Ye, Y.; Hu, X. AM-ConvGRU: A spatio-temporal model for typhoon path prediction. Neural Comput. Appl. 2022, 34, 5905–5921. [Google Scholar] [CrossRef]
- Liu, Z.; Hao, K.; Geng, X.; Zou, Z.; Shi, Z. Dual-Branched Spatio-Temporal Fusion Network for Multihorizon Tropical Cyclone Track Forecast. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3842–3852. [Google Scholar] [CrossRef]
- Wang, P.; Wang, P.; Wang, C.; Xue, B.; Wang, D. Using a 3D convolutional neural network and gated recurrent unit for tropical cyclone track forecasting. Atmos. Res. 2022, 269, 106053. [Google Scholar] [CrossRef]
- Gao, Z.; Tan, C.; Wu, L.; Li, S.Z. Simvp: Simpler yet better video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 3170–3180. [Google Scholar]
- Tan, C.; Gao, Z.; Li, S.; Li, S.Z. Simvp: Towards simple yet powerful spatiotemporal predictive learning. arXiv 2022, arXiv:2211.12509. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean. Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Lu, X.; Yu, H.; Ying, M.; Zhao, B.; Zhang, S.; Lin, L.; Bai, L.; Wan, R. Western North Pacific tropical cyclone database created by the China Meteorological Administration. Adv. Atmos. Sci. 2021, 38, 690–699. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, X.; Han, J.; Ding, G. Scaling up your kernels to 31 × 31: Revisiting large kernel design in cnns. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11963–11975. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Zhang, L.; Song, J.; Gao, A.; Chen, J.; Bao, C.; Ma, K. Be your own teacher: Improve the performance of convolutional neural networks via self distillation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3713–3722. [Google Scholar]
- Zhang, L.; Tan, Z.; Song, J.; Chen, J.; Bao, C.; Ma, K. Scan: A Scalable Neural Networks Framework towards Compact and Efficient Models. Adv. Neural Inf. Process. Syst. 2019, 32. Available online: https://proceedings.neurips.cc/paper/2019/hash/934b535800b1cba8f96a5d72f72f1611-Abstract.html (accessed on 9 May 2024).
- Morcrette, J.J.; Beljaars, A.; Benedetti, A.; Jones, L.; Boucher, O. Sea-salt and dust aerosols in the ECMWF IFS model. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Prakash, S.; Momin, I.M.; Mitra, A.K.; Bhattacharjee, P.S.; Yang, F.; Tallapragada, V. An Early Assessment of Medium Range Monsoon Precipitation Forecasts from the Latest High-Resolution NCEP-GFS (T1534) Model over South Asia. Pure Appl. Geophys. 2016, 173, 2215–2225. [Google Scholar] [CrossRef][Green Version]
- Shen, X.; Wang, J.; Li, Z.; Chen, D.; Gong, J. Research and Operational Development of Numerical Weather Prediction in China. J. Meteorol. Res. 2020, 34, 675–698. [Google Scholar] [CrossRef]
- Huang, X.; Peng, X.; Fei, J.; Cheng, X.; Ding, J.; Yu, D. Evaluation and Error Analysis of Official Tropical Cyclone Intensity Forecasts during 2005–2018 for the Western North Pacific. J. Meteorol. Soc. Japan Ser. II 2021, 99, 139–163. [Google Scholar] [CrossRef]
- Xu, X.Y.; Shao, M.; Chen, P.L.; Wang, Q.G. Tropical Cyclone Intensity Prediction Using Deep Convolutional Neural Network. Atmosphere 2022, 13, 783. [Google Scholar] [CrossRef]
- Ma, D.; Wang, L.; Fang, S.; Lin, J. Tropical cyclone intensity prediction by inter-and intra-pattern fusion based on multi-source data. Environ. Res. Lett. 2023, 18, 014020. [Google Scholar] [CrossRef]
- Xu, G.; Lin, K.; Li, X.; Ye, Y. SAF-Net: A spatio-temporal deep learning method for typhoon intensity prediction. Pattern Recognit. Lett. 2022, 155, 121–127. [Google Scholar] [CrossRef]
- Jiang, S.; Fan, H.; Wang, C. Improvement of Typhoon Intensity Forecasting by Using a Novel Spatio-Temporal Deep Learning Model. Remote Sens. 2022, 14, 5205. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, D.; Hu, G.; Wu, T.; Liu, L.; Xiao, Y.; Duan, Z. Transformer-based tropical cyclone track and intensity forecasting. J. Wind Eng. Ind. Aerodyn. 2023, 238, 105440. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, X.; Shi, L.; Wang, B.; Du, Z.; Zhang, F.; Liu, R. A neural network framework for fine-grained tropical cyclone intensity prediction. Knowl. Based Syst. 2022, 241, 108195. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).