Improved Ionospheric Total Electron Content Maps over China Using Spatial Gridding Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
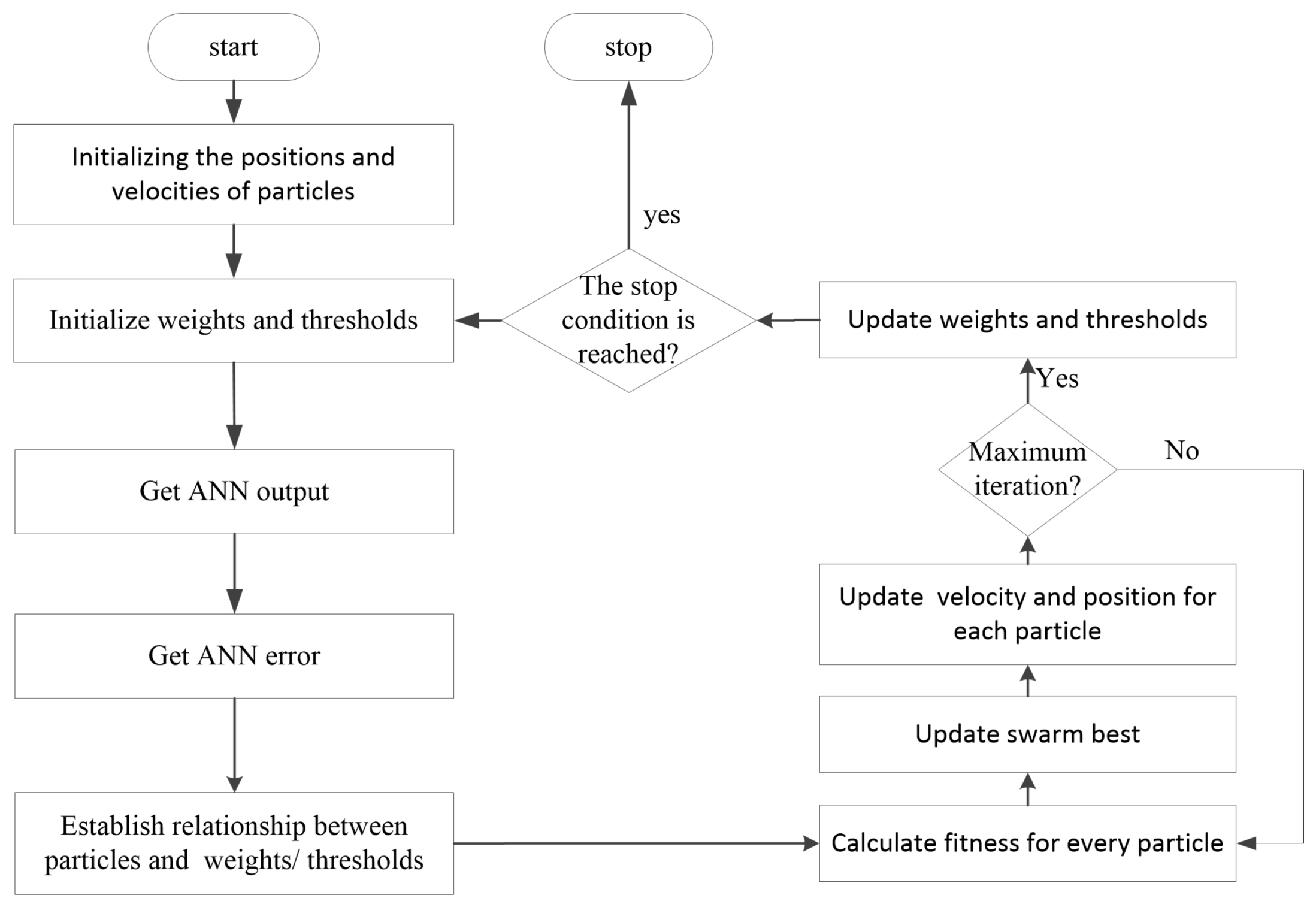
2.2. Methods
3. Results
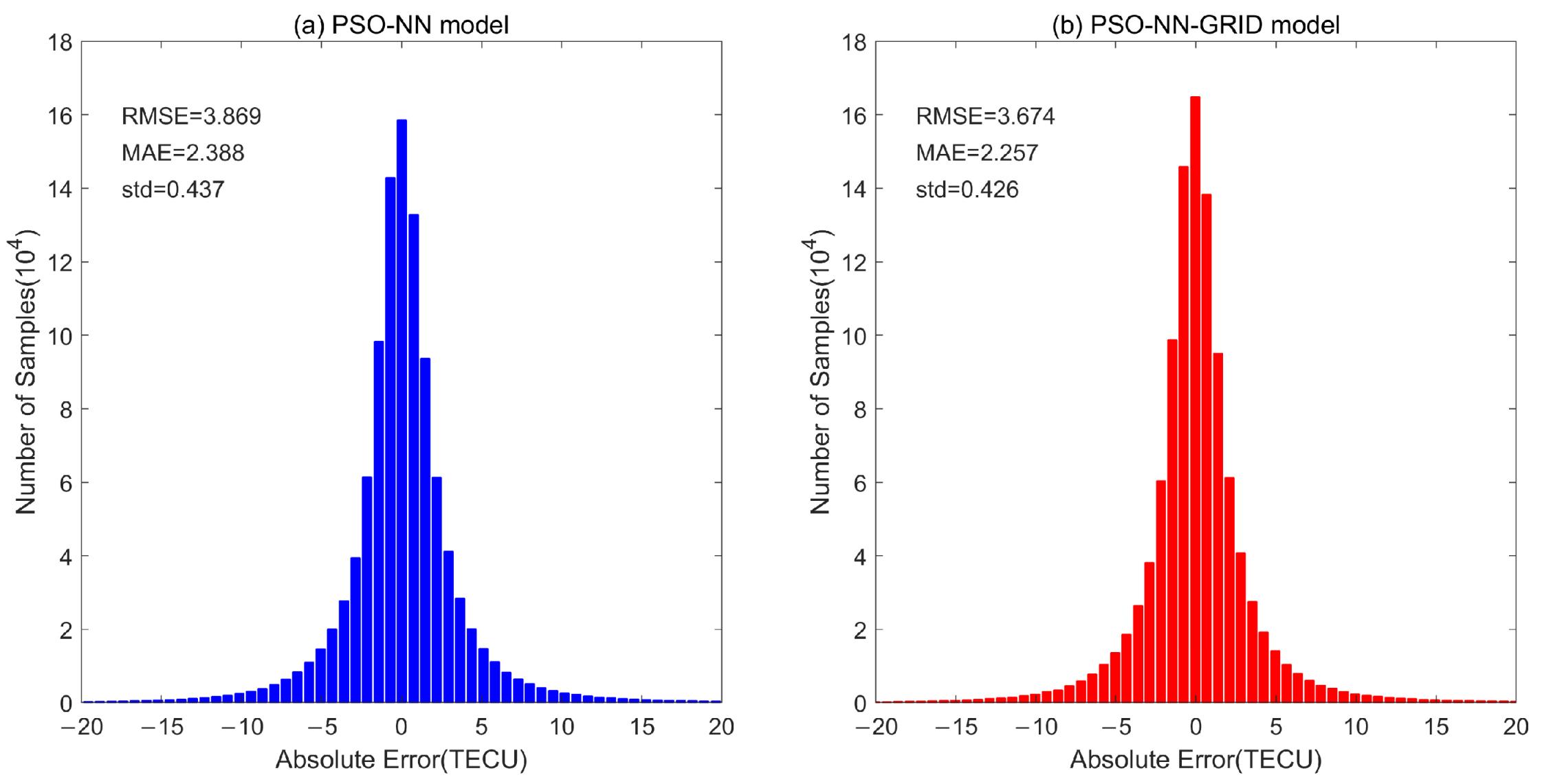
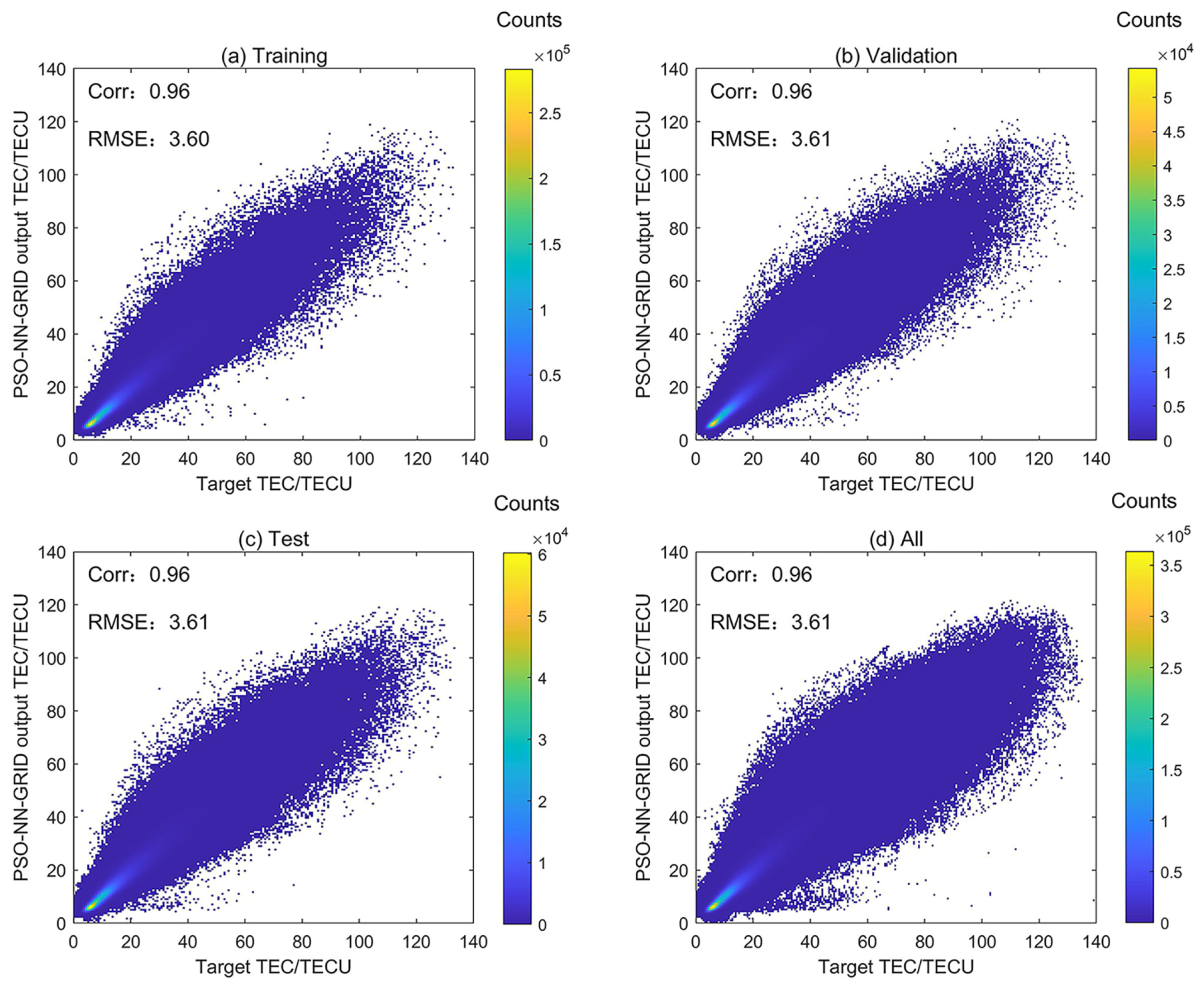
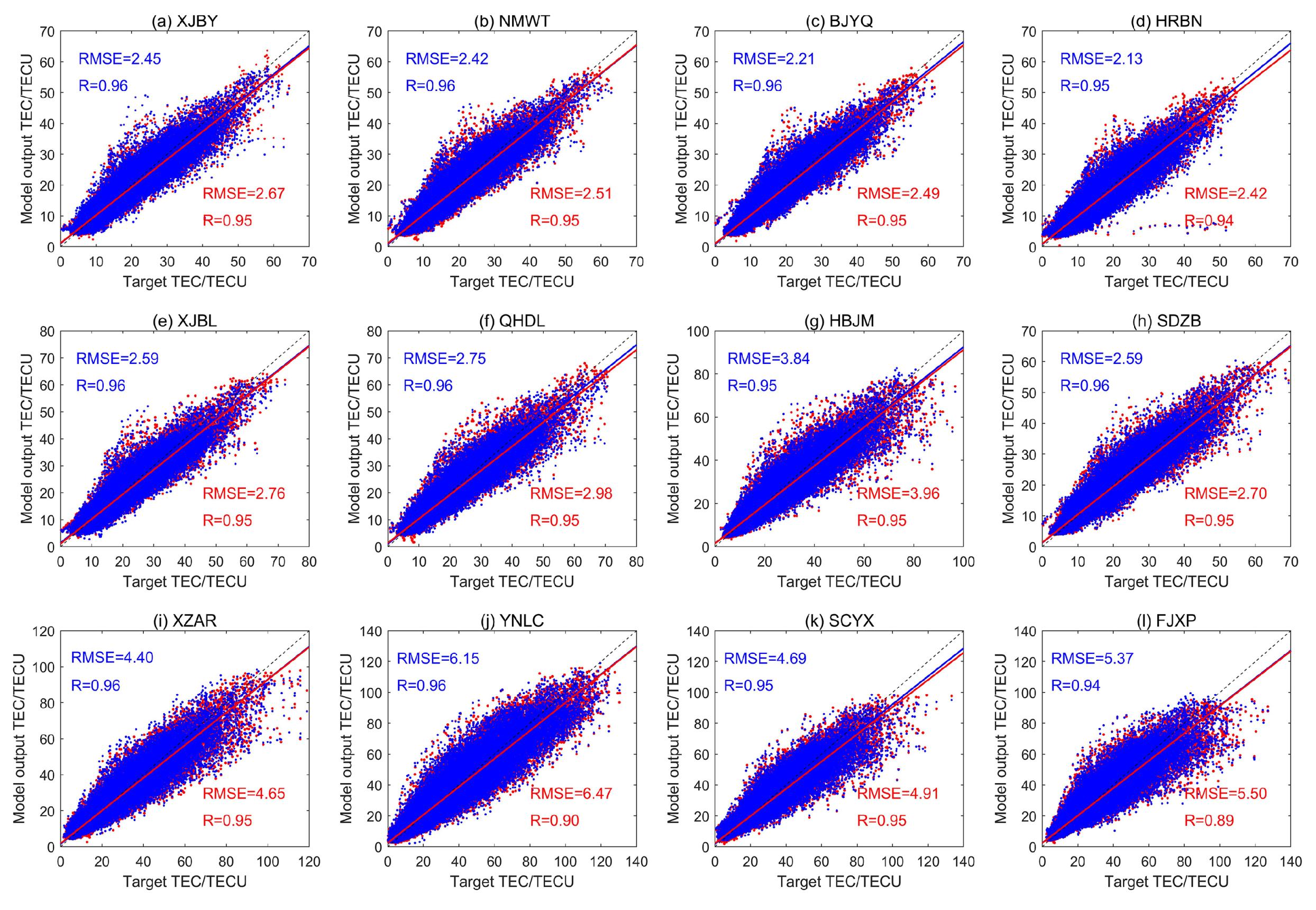
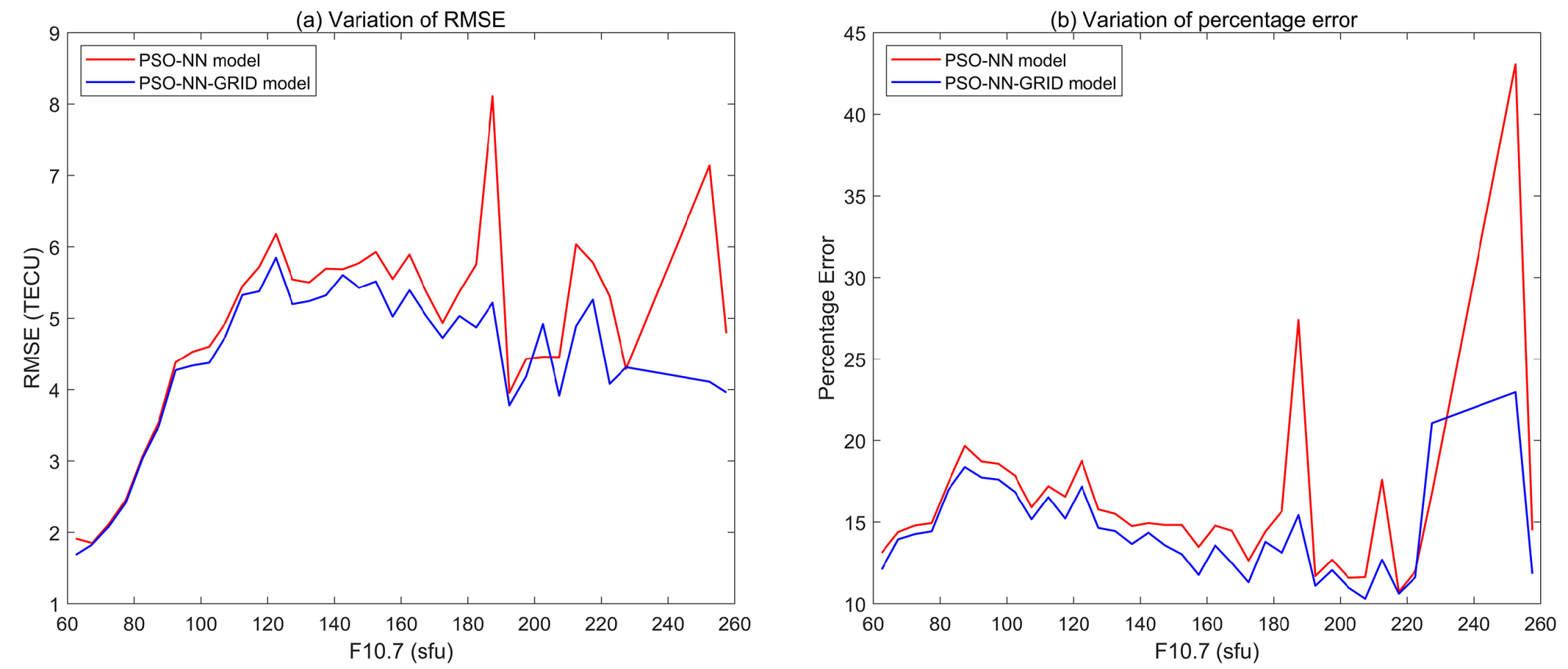
3.1. Analysis on Different Sample Data Sets
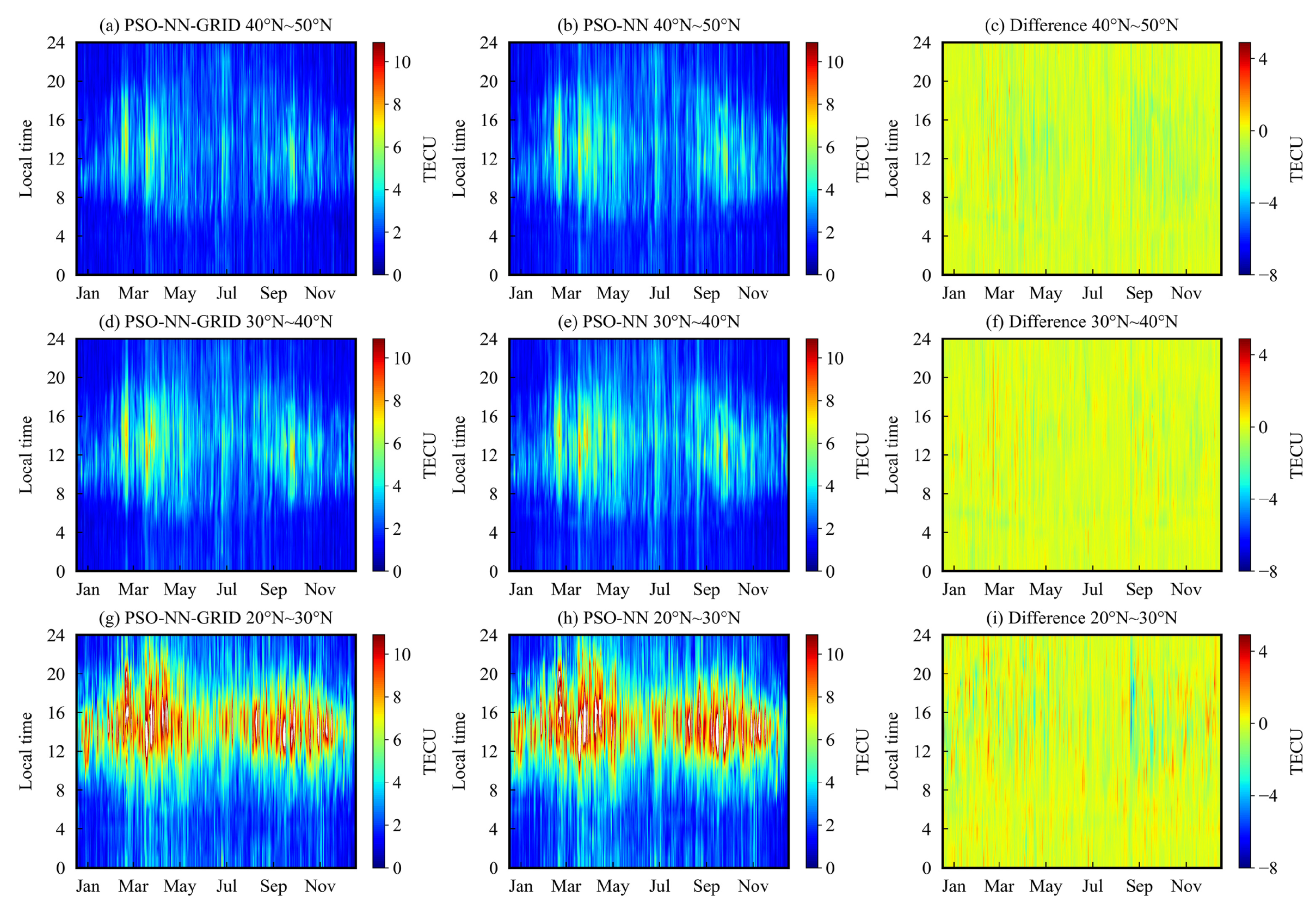
3.2. Analysis at Different Hours
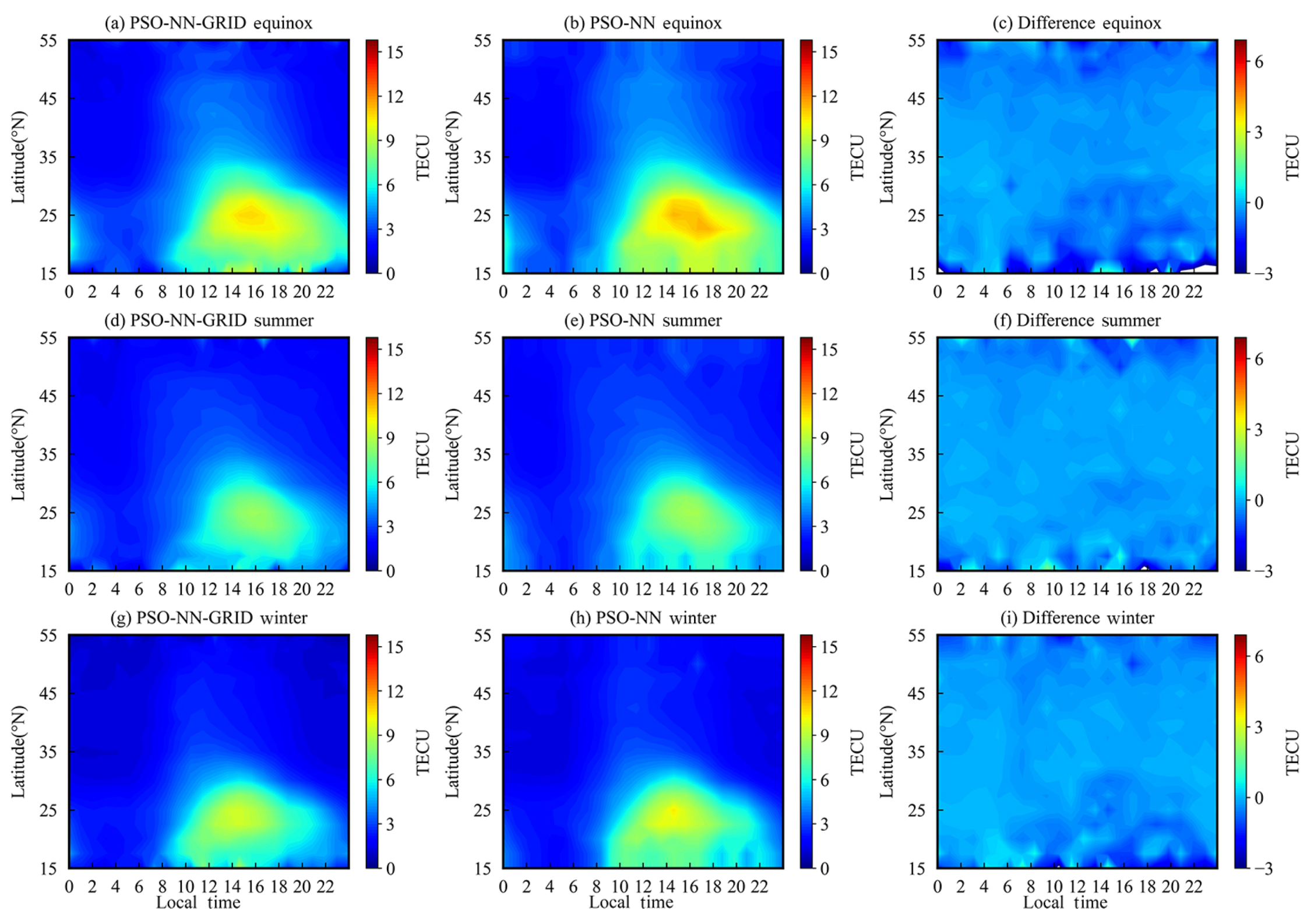
3.3. Analysis in Different Seasons
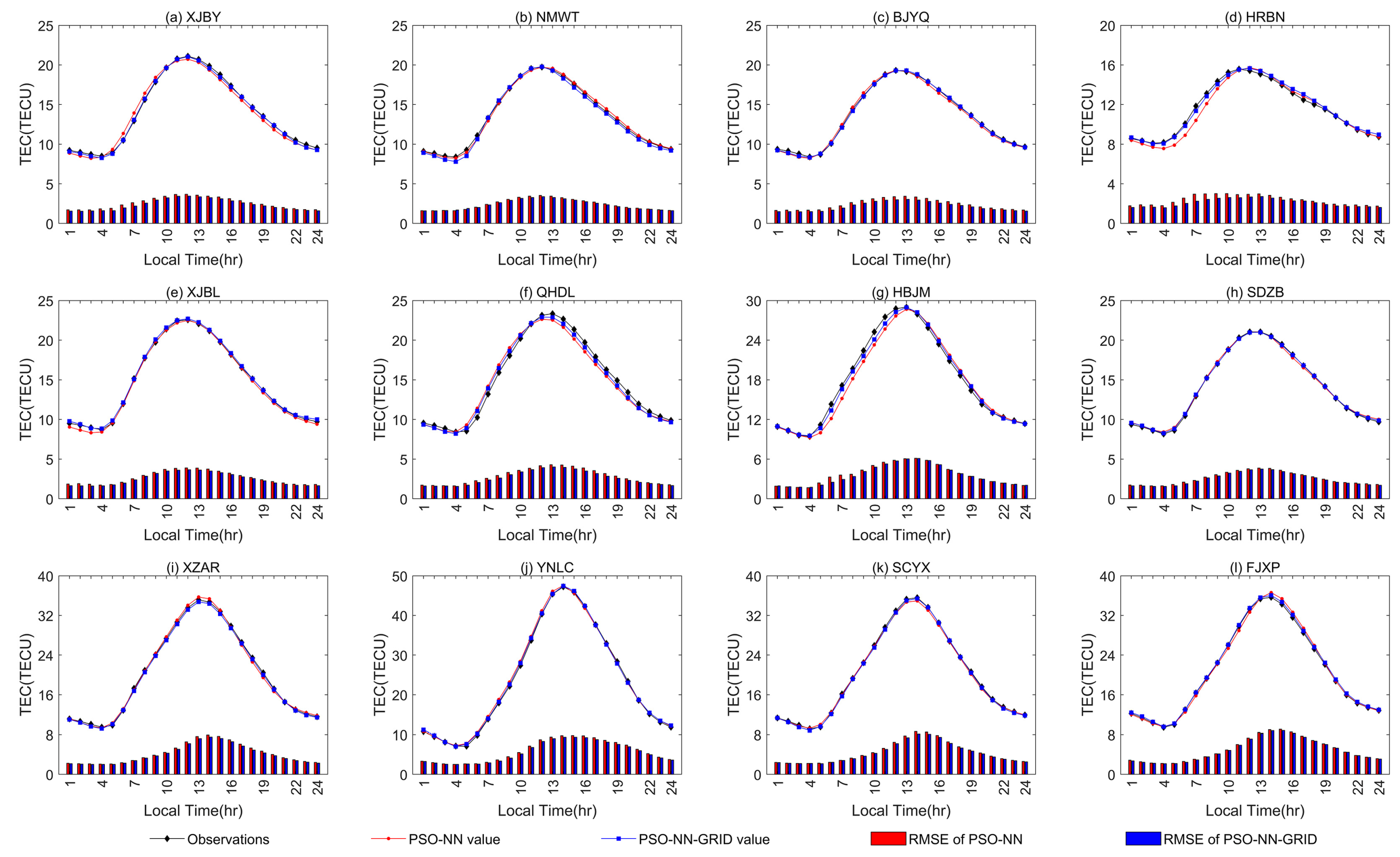
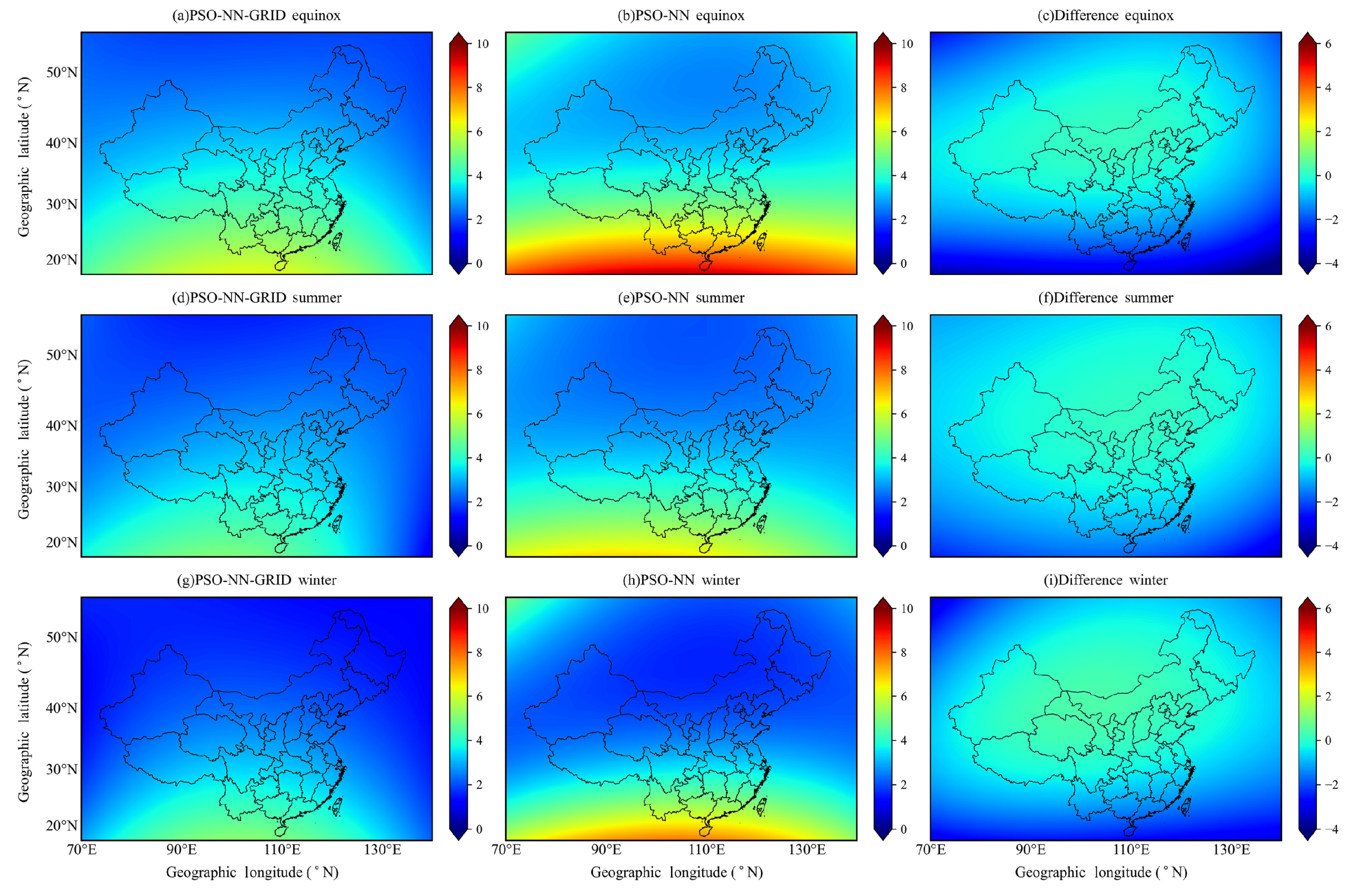
3.4. Analysis at Different Geographical Locations
3.5. Analysis under Different Solar Activity Conditions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Klobuchar, J.A. Ionospheric time-delay algorithm for single-frequency GPS users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Huo, X. Improvement of Klobuchar model for GNSS single-frequency ionospheric delay corrections. Adv. Space Res. 2016, 57, 1555–1569. [Google Scholar] [CrossRef]
- Hochegger, G.; Nava, B.; Radicella, S.; Leitinger, R. A family of ionospheric models for different uses. Phys. Chem. Earth Part C Sol. Terr. Planet. Sci. 2000, 25, 307–310. [Google Scholar] [CrossRef]
- Nava, B.; Coïsson, P.; Radicella, S.M. A new version of the NeQuick ionosphere electron density model. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1856–1862. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Bilitza, D. IRI the international standard for the ionosphere. Adv. Radio Sci. 2018, 16, 1–11. [Google Scholar] [CrossRef]
- Ridley, A.J.; Deng, Y.; Tóth, G. The global ionosphere—Thermosphere model. J. Atmos. Sol.-Terr. Phys. 2006, 68, 839–864. [Google Scholar] [CrossRef]
- Daniell, R.E.; Brown, L.D.; Anderson, D.N.; Fox, M.W.; Doherty, P.H.; Decker, D.T.; Sojka, J.J.; Schunk, R.W. Parameterized ionospheric model: A global ionospheric parameterization based on first principles models. Radio Sci. 1995, 30, 1499–1510. [Google Scholar] [CrossRef]
- Schunk, R.W.; Scherliess, L.; Sojka, J.J.; Thompson, D.C.; Anderson, D.N.; Codrescu, M.; Minter, C.; Fuller-Rowell, T.J.; Heelis, R.A.; Hairston, M.; et al. Global assimilation of ionospheric measurements (GAIM). Radio Sci. 2004, 39, RS1S02. [Google Scholar] [CrossRef]
- Bergeot, N.; Chevalier, J.-M.; Bruyninx, C.; Pottiaux, E.; Aerts, W.; Baire, Q.; Legrand, J.; Defraigne, P.; Huang, W. Near real-time ionospheric monitoring over Europe at the Royal Observatory of Belgium using GNSS data. J. Space Weather Space Clim. 2014, 4, A31. [Google Scholar] [CrossRef]
- Aa, E.; Huang, W.; Yu, S.; Liu, S.; Shi, L.; Gong, J.; Chen, Y.; Shen, H. A regional ionospheric TEC mapping technique over China and adjacent areas on the basis of data assimilation. J. Geophys. Res. Space Phys. 2015, 120, 5049–5061. [Google Scholar] [CrossRef]
- Li, M.; Yuan, Y.; Wang, N.; Li, Z.; Liu, X.; Zhang, X. Statistical comparison of various interpolation algorithms for reconstructing regional grid ionospheric maps over China. J. Atmos. Sol.-Terr. Phys. 2018, 172, 129–137. [Google Scholar] [CrossRef]
- Li, Z.; Wang, N.; Wang, L.; Liu, A.; Yuan, H.; Zhang, K. Regional ionospheric TEC modeling based on a two-layer spherical harmonic approximation for real-time single-frequency PPP. J. Geod. 2019, 93, 1659–1671. [Google Scholar] [CrossRef]
- Adolfs, M.; Hoque, M.M. A neural network-based TEC model capable of reproducing nighttime winter anomaly. Remote Sens. 2021, 13, 4559–4573. [Google Scholar] [CrossRef]
- Li, W.; Zhao, D.; He, C.; Hu, A.; Zhang, K. Advanced machine learning optimized by the genetic algorithm in ionospheric models using long-term multi-instrument observations. Remote Sens. 2020, 12, 866. [Google Scholar] [CrossRef]
- Li, X.; Zhou, C.; Tang, Q.; Zhao, J.; Zhang, F.; Xia, G.; Liu, Y. Forecasting ionospheric foF2 based on deep learning method. Remote Sens. 2021, 13, 3849. [Google Scholar] [CrossRef]
- Poole, A.W.V.; McKinnell, L.-A. On the predictability of f0F2 using neural networks. Radio Sci. 2000, 35, 225–234. [Google Scholar] [CrossRef]
- Sai Gowtam, V.; Tulasi Ram, S. An artificial neural network-based ionospheric model to predict NmF2 and hmF2 using long-term data set of FORMOSAT-3/COSMIC radio occultation observations: Preliminary results. J. Geophys. Res. Space Phys. 2017, 122, 11,743–11,755. [Google Scholar] [CrossRef]
- Song, R.; Zhang, X.; Zhou, C.; Liu, J.; He, J. Predicting TEC in China based on the neural networks optimized by genetic algorithm. Adv. Space Res. 2018, 62, 745–759. [Google Scholar] [CrossRef]
- Habarulema, J.; McKinnell, L.-A.; Cilliers, P.; Opperman, B. Application of neural networks to South African GPS TEC modelling. Adv. Space Res. 2009, 43, 1711–1720. [Google Scholar] [CrossRef]
- Habarulema, J.B.; McKinnell, L.-A.; Opperman, B.D.L. Towards a GPS-based TEC prediction model for Southern Africa with feed forward networks. Adv. Space Res. 2009, 44, 82–92. [Google Scholar] [CrossRef]
- Li, W.; Wu, X. An ionospheric total electron content model with a storm option over Japan based on a multi-layer perceptron neural network. Atmosphere 2023, 14, 634. [Google Scholar] [CrossRef]
- Okoh, D.; Habarulema, J.B.; Rabiu, B.; Seemala, G.; Wisdom, J.B.; Olwendo, J.; Obrou, O.; Matamba, T.M. Storm-time modeling of the African regional ionospheric total electron content using artificial neural networks. Space Weather 2020, 18, e2020SW002525. [Google Scholar] [CrossRef]
- Sabzehee, F.; Farzaneh, S.; Sharifi, M.A.; Akhoondzadeh, M. TEC Regional Modeling and prediction using ANN method and single frequency receiver over IRAN. Ann. Geophys. 2018, 61, GM103. [Google Scholar] [CrossRef]
- Shi, S.; Wu, S.; Zhang, K.; Li, W.; Shi, J.; Song, F. An investigation of a new artificial neural network-based TEC model using ground-based GPS and COSMIC-2 measurements over low latitudes. Adv. Space Res. 2022, 70, 2522–2540. [Google Scholar] [CrossRef]
- Tulunay, E.; Senalp, E.T.; Radicella, S.M.; Tulunay, Y. Forecasting total electron content maps by neural network technique. Radio Sci. 2006, 41, RS4016. [Google Scholar] [CrossRef]
- Maruyama, T. Regional reference total electron content model over Japan based on neural network mapping techniques. Ann. Geophys 2007, 25, 2609–2614. [Google Scholar] [CrossRef]
- Razin, M.R.G.; Voosoghi, B.; Mohammadzadeh, A. Efficiency of artificial neural networks in map of total electron content over Iran. Acta Geod. Geophys. 2015, 51, 541–555. [Google Scholar] [CrossRef]
- Okoh, D.; Seemala, G.; Rabiu, B.; Habarulema, J.B.; Jin, S.; Shiokawa, K.; Otsuka, Y.; Aggarwal, M.; Uwamahoro, J.; Mungufeni, P.; et al. A neural network-based ionospheric model over Africa from Constellation Observing System for Meteorology, Ionosphere, and Climate and ground Global Positioning System observations. J. Geophys. Res. Space Phys. 2019, 124, 10512–10532. [Google Scholar] [CrossRef]
- Shi, S.; Zhang, K.; Shi, J.; Hu, A.; Zhao, D.; Shi, Z.; Sun, P.; Wu, H.; Wu, S. Modeling TEC maps over China using particle swarm optimization neural networks and long-term ground-based GPS, COSMIC, and Fengyun data. Space Weather 2023, 21, e2022SW003357. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Li, H.; Ou, J.; Huo, X. Two-step method for the determination of the differential code biases of COMPASS satellites. J. Geod. 2012, 86, 1059–1076. [Google Scholar] [CrossRef]
- Gowtam, V.S.; Tulasi Ram, S.; Reinisch, B.; Prajapati, A. A new artificial neural network-based global three-dimensional ionospheric model (ANNIM-3D) using long-term ionospheric observations: Preliminary results. J. Geophys. Res. Space Phys. 2019, 124, 4639–4657. [Google Scholar] [CrossRef]
- Prol, F.S.; Hoque, M.M. Topside ionosphere and plasmasphere modelling using GNSS radio occultation and POD data. Remote Sens. 2021, 13, 1559. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Lin, C.-H.; Rajesh, P.K.; Lin, C.-Y.; Chang, F.-Y.; Lee, I.T.; Fang, T.-W.; Fuller-Rowell, D.; Chen, S.-P. Advances in ionospheric space weather by using FORMOSAT-7/COSMIC-2 GNSS radio occultations. Atmosphere 2022, 13, 858. [Google Scholar] [CrossRef]
- Ren, X.; Li, Y.; Mei, D.; Zhu, W.; Zhang, X. Improving topside ionospheric empirical model using FORMOSAT-7/COSMIC-2 data. J. Geod. 2023, 97, 30. [Google Scholar] [CrossRef]
- Cherniak, I.V.; Zakharenkova, I.E. Validation of FORMOSAT-3/COSMIC radio occultation electron density profiles by incoherent scatter radar data. Adv. Space Res. 2014, 53, 1304–1312. [Google Scholar] [CrossRef]
- McNamara, L.F.; Thompson, D.C. Validation of COSMIC values of foF2 and M(3000)F2 using ground-based ionosondes. Adv. Space Res. 2015, 55, 163–169. [Google Scholar] [CrossRef]
- Cherniak, I.; Zakharenkova, I.; Braun, J.; Wu, Q.; Pedatella, N.; Schreiner, W.; Weiss, J.-P.; Hunt, D. Accuracy assessment of the quiet-time ionospheric F2 peak parameters as derived from COSMIC-2 multi-GNSS radio occultation measurements. J. Space Weather Space Clim. 2021, 11, 18. [Google Scholar] [CrossRef]
- Potula, B.S.; Chu, Y.-H.; Uma, G.; Hsia, H.-P.; Wu, K.-H. A global comparative study on the ionospheric measurements between COSMIC radio occultation technique and IRI model. J. Geophys. Res. Space Phys. 2011, 116, A02310. [Google Scholar] [CrossRef]
- Lee, J.-S.; Lee, S.; Chang, S.; Ahn, B.-H. A comparison of GA and PSO for excess return evaluation in stock markets. In Proceedings of the Artificial Intelligence and Knowledge Engineering Applications: A Bioinspired Approach, Berlin/Heidelberg, Germany, 15–18 June 2005. [Google Scholar] [CrossRef]
- Mao, T.; Wan, W.; Yue, X.; Sun, L.; Zhao, B.; Guo, J. An empirical orthogonal function model of total electron content over China. Radio Sci. 2008, 43, 1–12. [Google Scholar] [CrossRef]
- Liu, J.; Chen, R.; Wang, Z.; Zhang, H. Spherical cap harmonic model for mapping and predicting regional TEC. GPS Solut. 2010, 15, 109–119. [Google Scholar] [CrossRef]

| Station Code | 2015 | 2019 | ||||
|---|---|---|---|---|---|---|
| Equinox | Summer | Winter | Equinox | Summer | Winter | |
| PSO-NN/PSO-NN-GRID | PSO-NN/PSO-NN-GRID | |||||
| HRBN | 4.25/3.48 | 3.11/2.85 | 2.68/2.32 | 1.39/1.28 | 1.37/1.33 | 1.04/1.04 |
| XJBY | 4.56/4.31 | 3.64/3.38 | 3.37/2.67 | 1.49/1.41 | 1.41/1.28 | 1.24/1.10 |
| NMWT | 4.15/3.68 | 3.47/3.28 | 2.65/2.61 | 1.44/1.31 | 1.38/1.37 | 1.06/0.97 |
| BJYQ | 4.09/3.42 | 3.43/3.04 | 2.59/2.30 | 1.34/1.18 | 1.29/1.19 | 0.99/0.92 |
| XJBL | 4.71/4.69 | 3.93/3.58 | 2.78/2.64 | 1.53/1.51 | 1.42/1.40 | 1.17/1.09 |
| SDZB | 4.41/4.21 | 3.84/3.61 | 2.73/2.68 | 1.57/1.44 | 1.34/1.32 | 1.03/0.99 |
| QHDL | 5.08/4.35 | 4.17/3.91 | 3.41/3.28 | 1.54/1.44 | 1.49/1.46 | 1.03/0.95 |
| HBJM | 7.02/6.76 | 4.97/4.86 | 4.28/4.23 | 1.87/1.86 | 1.81/1.80 | 1.15/1.15 |
| XZAR | 7.12/6.69 | 5.54/5.38 | 4.71/4.69 | 2.55/2.37 | 2.01/2.00 | 1.66/1.43 |
| SCYX | 7.88/7.64 | 5.75/5.61 | 5.72/5.41 | 2.41/2.34 | 2.19/2.18 | 1.39/1.36 |
| FJXP | 8.99/8.69 | 5.97/5.92 | 6.50/6.49 | 2.74/2.61 | 2.06/2.00 | 1.71/1.70 |
| YNLC | 9.54/9.03 | 6.62/6.61 | 8.63/8.27 | 3.71/3.64 | 3.01/3.01 | 2.67/2.53 |
| F10.7 | [0, 80) | [80, 100) | [100, 130) | [130, 160) | [160, 190) | [190, 220) | ≥220 |
|---|---|---|---|---|---|---|---|
| PSO-NN | 2.07 | 3.92 | 5.35 | 5.68 | 5.65 | 4.81 | 5.73 |
| PSO-NN-GRID | 2.05 | 3.81 | 5.10 | 5.37 | 5.08 | 4.37 | 4.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, F.; Shi, S. Improved Ionospheric Total Electron Content Maps over China Using Spatial Gridding Approach. Atmosphere 2024, 15, 351. https://doi.org/10.3390/atmos15030351
Song F, Shi S. Improved Ionospheric Total Electron Content Maps over China Using Spatial Gridding Approach. Atmosphere. 2024; 15(3):351. https://doi.org/10.3390/atmos15030351
Chicago/Turabian StyleSong, Fucheng, and Shuangshuang Shi. 2024. "Improved Ionospheric Total Electron Content Maps over China Using Spatial Gridding Approach" Atmosphere 15, no. 3: 351. https://doi.org/10.3390/atmos15030351
APA StyleSong, F., & Shi, S. (2024). Improved Ionospheric Total Electron Content Maps over China Using Spatial Gridding Approach. Atmosphere, 15(3), 351. https://doi.org/10.3390/atmos15030351







