Novel Intelligent Methods for Channel Path Classification and Model Determination Based on Blind Source Signals
Abstract
1. Introduction
2. Propagation Channel Paths and Models
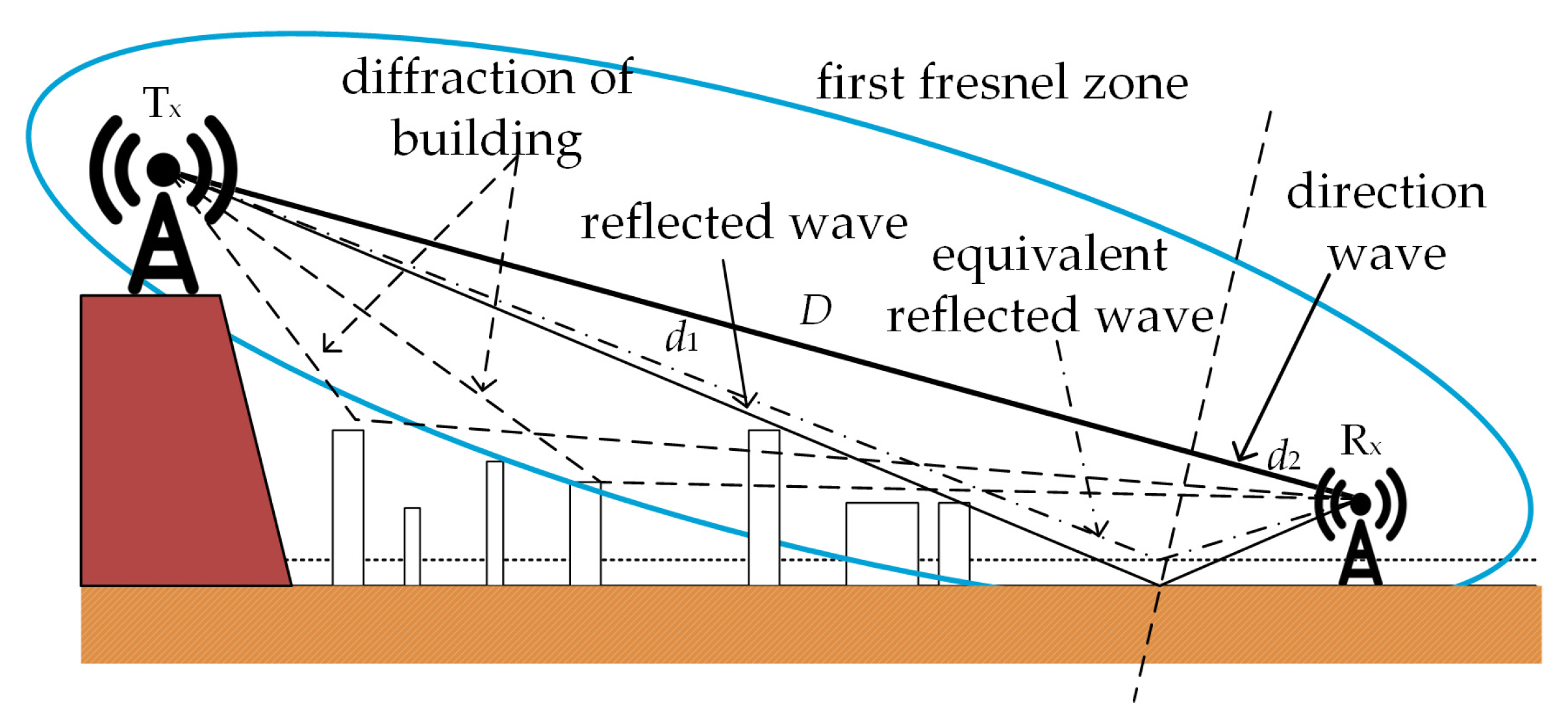
2.1. Propagation Channel Paths
2.2. Statistical Model of Wave Propagation
2.2.1. Basic Statistical Model
2.2.2. Okumura–Hata Model
2.2.3. Egli Model
2.3. Deterministic Model of Wave Propagation
3. The Intelligent Methods and Data Acquisition System
3.1. The Method of Positioning the Blind Source
3.2. Methods of Channel and Model Type Differentiation
- (1)
- Obtain all the paths, the first Fresnel zone of the receiving point, and the source transmitting point.
- (2)
- If there is a blocker, such as a building, on this path, the channel is an NLoS channel (without a direct path).
- (3)
- If there is no blocker in the first Fresnel zone, it is a LoS channel (only the direct path).
- (4)
- If there is a blocker in the first Fresnel zone, but it is not blocking the direct link between Tx and Rx, then it is a multi-LoS channel (the direct and non-direct paths).
- (1)
- Obtain a single standard parabolic equation, Egli, and Okumura–Hata model’s data.
- (2)
- The three models are used as the center to extend the domain radius outward, and the data within the radius of the connected neighborhood is a class of models.
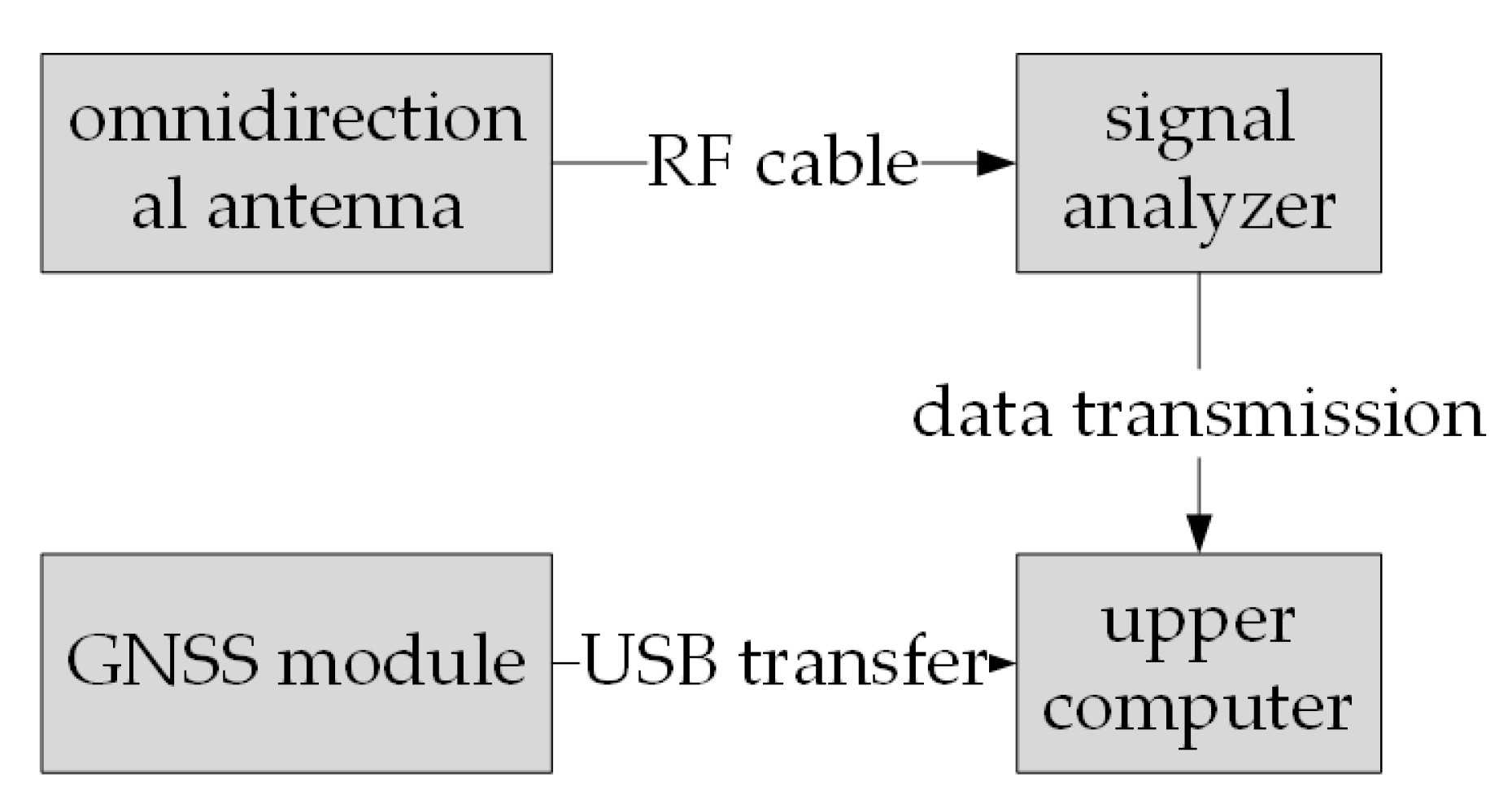
3.3. Data Acquisition System
4. Validation Results and Analysis
4.1. Measurement Data and Processing
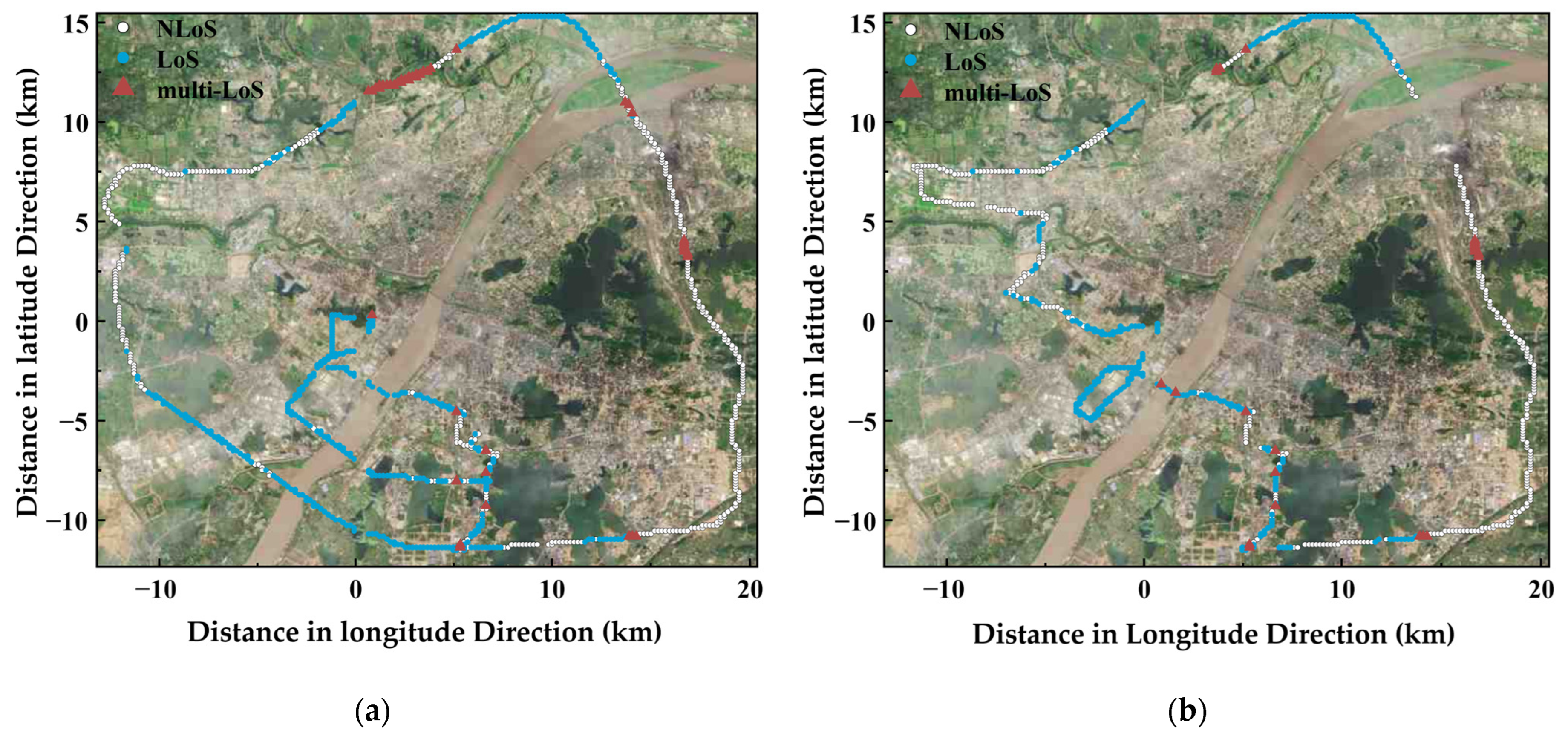
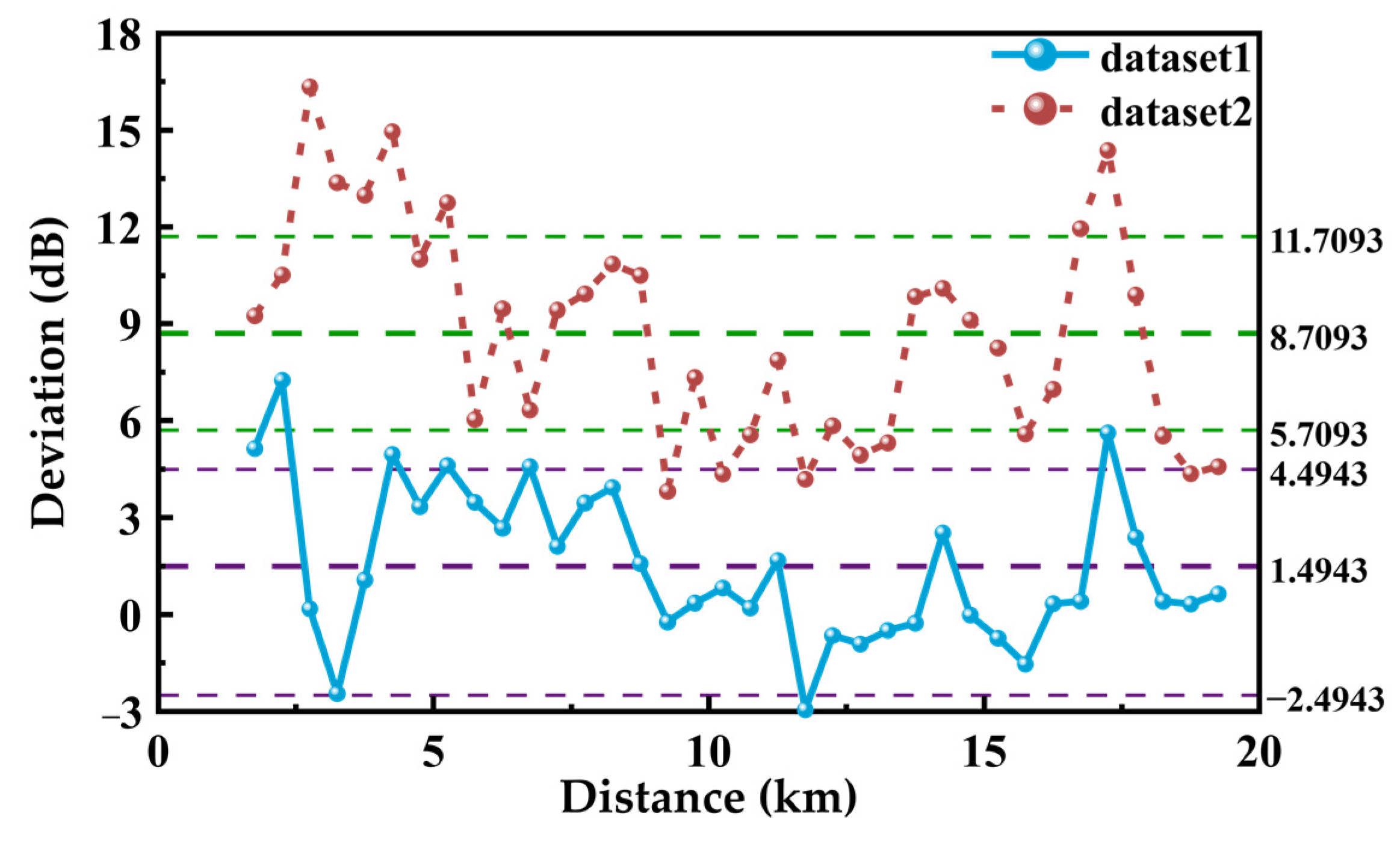
4.2. Channel Path Classification
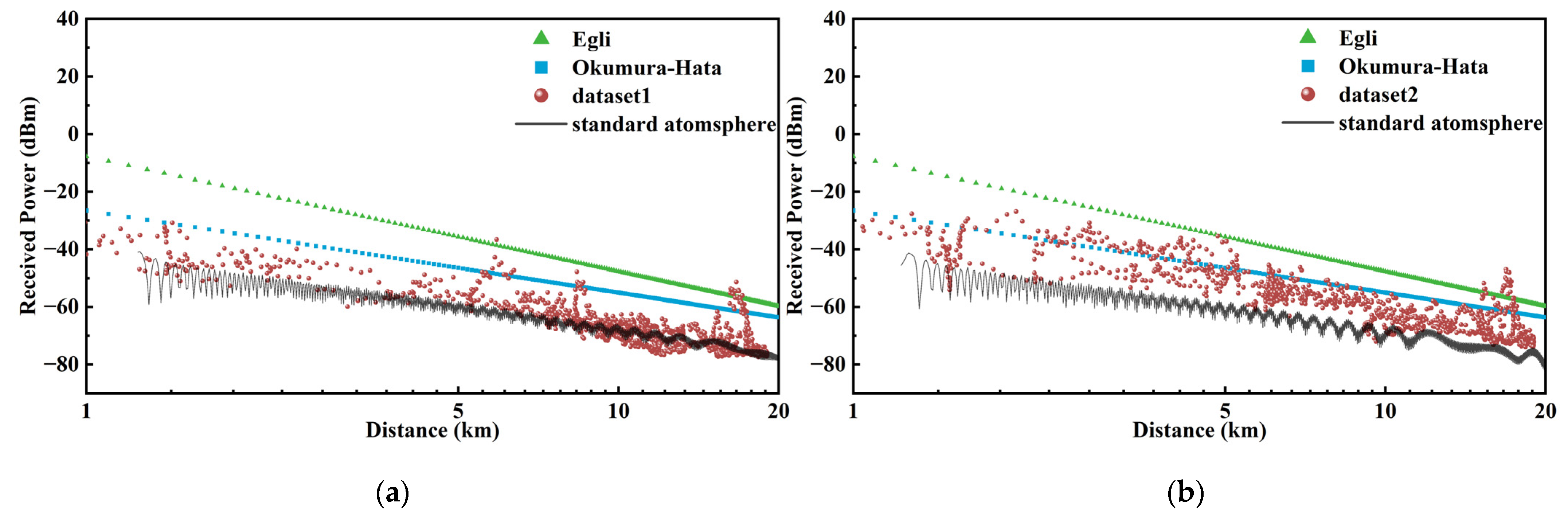
4.3. Determination of Propagation Models
4.4. Measurement Modeling
4.5. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, C.; Xiong, D.; Duan, K.; Hu, W.; Cao, L.; Huang, L.; Guo, X.; Wang, H. Field test investigation on microwave transhorizon propagation over sea surface. Chin. J. Radio Sci. 2022, 37, 214–221. (In Chinese) [Google Scholar]
- Zhao, X.; Liang, X.; Li, S.; Ai, B. Two-Cylinder and Multi-Ring GBSSM for Realizing and Modeling of Vehicle-to-Vehicle Wideband MIMO Channels. IEEE Trans. Intell. Transp. Syst. 2016, 17, 2787–2799. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; Hao, Y.; Yang, C.; Shi, Y. An SVR-Based Radio Propagation Prediction Model for Terrestrial FM Broadcasting Services in Beijing and Its Surrounding Area. IEEE Trans. Broadcast. 2023, 13, 1–12. [Google Scholar] [CrossRef]
- Zhao, X.; Du, F.; Geng, S.; Fu, Z.; Wang, Z.; Zhang, Y.; Zhou, Z.; Zhang, L.; Yang, L. Playback of 5G and Beyond Measured MIMO Channels by an ANN-Based Modeling and Simulation Framework. IEEE J. Sel. Areas Commun. 2020, 38, 1945–1954. [Google Scholar] [CrossRef]
- Zhao, X.; Abdo, A.M.A.; Xu, C.; Geng, S.; Zhang, J.; Memon, I. Dimension Reduction of Channel Correlation Matrix Using CUR-Decomposition Technique for 3-D Massive Antenna System. IEEE Access 2018, 6, 3031–3039. [Google Scholar] [CrossRef]
- Tajvidy, A. Diffraction loss model at 0.3–6 GHz for 5G cellular system in microcell urban areas. Electromagnetics 2019, 39, 168–185. [Google Scholar] [CrossRef]
- Zhang, H. mmWave Indoor Channel Measurement Campaign for 5G New Radio Indoor Broadcasting. Trans. Broadcast. 2022, 68, 331–344. [Google Scholar] [CrossRef]
- Paul, B.S.; Bhattacharjee, R. MIMO Channel Modeling: A Review. IETE Tech. Rev. 2008, 25, 315–319. [Google Scholar] [CrossRef]
- Nisirat, M.A.; Ismail, M.; Nissirat, L.; AlKhawaldeh, S.; Yuwono, T. A Hata based model utilizing terrain roughness correction formula. In Proceedings of the 2011 6th International Conference on Telecommunication Systems, Services, and Applications (TSSA), Denpasar, Indonesia,, 20–21 October 2011; pp. 284–287. [Google Scholar]
- Nisirat, M.A.; Ismail, M.; Nissirat, L.; AlKhawaldeh, S.; Tahbuob, A. Micro cell path loss estimation by means of terrain slope for the 900 and 1800 MHz. In Proceedings of the 2012 International Conference on Computer and Communication Engineering (ICCCE), Kuala Lumpur, Malaysia, 3–5 July 2012; pp. 670–674. [Google Scholar]
- Castro, B.S.L.; Gomes, I.R.; Ribeiro, F.C.J.; Cavalcante, G.P.S. COST231-Hata and SUI Models performance using a LMS tuning algorithm on 5.8GHz in Amazon Region cities. In Proceedings of the Fourth European Conference on Antennas and Propagation, Barcelona, Spain, 12–16 April 2010; pp. 1–3. [Google Scholar]
- Levy, M. Parabolic Equation Methods for Electro-Magnetic Wave Propagation; Institution of Engineering and Technology Press: London, UK, 2000; pp. 20–41. [Google Scholar]
- Son, H.W.; Myung, N.H. A deterministic ray tube method for microcellular wave propagation prediction model. IEEE Trans. Antennas Propag 1999, 47, 1344–1350. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, C.; Ji, T.F. Propagation characteristics of 3.6 GHz typical application scenarios based on parabolic equation. Chin. J. Radio Sci. 2021, 36, 604–610. (In Chinese) [Google Scholar]
- Bender, A. A Flexible System Architecture for Acquisition and Storage of Naturalistic Driving Data. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1748–1761. [Google Scholar] [CrossRef]
- Duan, K.Y.; Liu, C.G. Automatic mm Wave channel measurement and modeling technology. Comput. Eng. Des. 2022, 43, 1459–1466. (In Chinese) [Google Scholar]
- Kielgast, M.R.; Rasmussen, A.C.; Laursen, M.H.; Nielsen, J.J.; Popovski, P.; Krigslund, R. Estimation of Received Signal Strength Distribution for Smart Meters with Biased Measurement Data Set. IEEE Wirel. Commun. Lett. 2017, 6, 2–5. [Google Scholar] [CrossRef]
- Herault, J.; Jutten, C. Space or time adaptive signal processing by neural network models. AIP Conf. Proc. 1986, 151, 206. [Google Scholar]
- Wang, C.X.; Bian, J.; Sun, J.; Zhang, W.; Zhang, M. A Survey of 5G Channel Measurements and Models. IEEE Commun. Surv. Tutor. 2018, 20, 3142–3168. [Google Scholar] [CrossRef]
- Liu, P.; Jiang, T. Channel Estimation Performance Analysis of Massive MIMO IoT Systems with Ricean Fading. IEEE Internet Things J. 2021, 8, 6114–6126. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, Y.; Yin, X.; Duan, J. Measurement-based experimental statistical modeling of propagation channel in industrial IoT scenario. Radio Sci. 2020, 55, 1–14. [Google Scholar] [CrossRef]
- Wang, X.Y.; Mei, N.; Wang, X.; Fan, X.; Shi, S. Three-Dimensional Channel Modeling and Analysis of Electromagnetic Field for WiFi. In Proceedings of the 2021 13th International Symposium on Antennas, Propagation and EM Theory (ISAPE), Zhuhai, China, 1–4 December 2021; pp. 1–3. [Google Scholar]
- Wang, J.; Hao, Y.; Yang, C. A Comprehensive Prediction Model for VHF Radio Wave Propagation by Integrating Entropy Weight Theory and Machine Learning Methods. IEEE Trans. Antennas Propag. 2023, 71, 6249–6254. [Google Scholar] [CrossRef]
- Wang, J.; Hao, Y.; Yang, C. An entropy weight-based method for path loss predictions for terrestrial services in the VHF and UHF bands. Radio Sci. 2023, 58, e2023RS007769. [Google Scholar] [CrossRef]
- Kong, L.J.; Liu, Y.L.; Zhang, X.C.; Zhang, X.Y.; Zhao, H.T.; Wei, J. Channel measurement and modeling for VHF bands in typical urban scenarios. Chin. J. Radio Sci. 2020, 35, 542–550. (In Chinese) [Google Scholar]
- Yu, J.; Chen, W.; Li, F.; Li, C.; Yang, K.; Liu, Y.; Chang, F. Channel Measurement and Modeling of the Small-Scale Fading Characteristics for Urban Inland River Environment. IEEE Trans. Wirel. Commun. 2020, 19, 3376–3389. [Google Scholar] [CrossRef]
- Hata, M. Empirical formula for propagation loss in land mobile radio services. IEEE Trans. Veh. Technol. 1980, 29, 317–325. [Google Scholar] [CrossRef]
- Egli, J.J. Radio Propagation above 40 MC over Irregular Terrain. Proc. IRE 1957, 45, 1383–1391. [Google Scholar] [CrossRef]
- Hu, W.T.; Liu, C.G.; Lin, F.J. Characteristics of atmospheric ducts and its impacts on FM broadcasting in Wuhan. Chin. J. Radio Sci. 2020, 35, 856–867. (In Chinese) [Google Scholar]
- Cao, L.F.; Liu, C.G.; Cheng, R.S. An Optimized PSO Method for EM Radiation Source Positioning. In Proceedings of the National Conference of Microwave and Millimeter Wave 2023 (NCMMW2023), Qingdao, China, 14–17 May 2023. (In Chinese). [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Srinivas, M.; Patnaik, L.M. Genetic algorithms: A survey. Computer 1994, 27, 17–26. [Google Scholar] [CrossRef]
- Bansal, J.C.; Singh, P.K.; Saraswat, M.; Verma, A.; Jadon, S.S.; Abraham, A. Inertia Weight strategies in Particle Swarm Optimization. In Proceedings of the 2011 Third World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, 19–21 October 2011; pp. 633–640. [Google Scholar]
- Wu, X.; Zhong, M. Particle Swarm Optimization with Hybrid Velocity Updating Strategies. In Proceedings of the 2009 Third International Symposium on Intelligent Information Technology Application, Nanchang, China, 21–22 November 2009; pp. 336–339. [Google Scholar]
- Dziwiński, P.; Bartczuk, Ł. A New Hybrid Particle Swarm Optimization and Genetic Algorithm Method Controlled by Fuzzy Logic. IEEE Trans. Fuzzy Syst. 2020, 28, 1140–1154. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In KDD-96 Proceedings; AAAI Press: Washington, DC, USA, 1996; Volume 96, pp. 226–231. [Google Scholar]
- Dupleich, D. Multi-Band Propagation and Radio Channel Characterization in Street Canyon Scenarios for 5G and Beyond. IEEE Access 2019, 7, 160385–160396. [Google Scholar] [CrossRef]
- Cheng, R.S.; Liu, C.G.; Cao, L.F. The Influence of PE Initial Field Construction Method on Radio Wave Propagation Loss and Tropospheric Duct Inversion. Atmosphere 2024, 15, 46. [Google Scholar] [CrossRef]
- Wang, J.; Hao, Y.; Yang, C. The Current Progress and Future Prospects of Path Loss Model for Terrestrial Radio Propagation. Electronics 2023, 12, 4959. [Google Scholar] [CrossRef]
- Wang, J.; Yang, C.; Yan, N.N. Study on digital twin channel for the B5G and 6G communication. Chin. J. Radio Sci. 2021, 36, 340–348. (In Chinese) [Google Scholar]


| Parameter | Value |
|---|---|
| Maximum number of iterations | 100 |
| Population size | 80 |
| Individual learning factor | 1.4 |
| Social learning factor | 1.4 |
| Maximum inertia factor | 0.9 |
| Minimum inertia factor | 0.4 |
| Maximum exchange rate | 0.2 |
| Minimum exchange rate | 0 |
| Maximum mutation rate | 0.2 |
| Minimum mutation rate | 0 |
| Latitude/Degree | Longitude/Degree | EIRP/dBm |
|---|---|---|
| 114.27 | 30.55 | 91.27 |
| Campaign Number | Channel Type | Percentage | Number |
|---|---|---|---|
| 1 | LoS | 47.19% | 596 |
| NLoS | 44.26% | 559 | |
| Multi-LoS | 5.38% | 68 | |
| 2 | LoS | 46.28% | 548 |
| NLoS | 48.82% | 578 | |
| Multi-LoS | 2.45% | 29 |
| Model Type | Percentage | Number |
|---|---|---|
| Deterministic Model | 93.90% | 1186 |
| Egli Model | 2.05% | 26 |
| Okumura–Hata Model | 4.03% | 51 |
| M | A | |
|---|---|---|
| 25.64 (25.05, 26.23) | 57.54 (55.85, 59.24) | 1.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, L.-F.; Liu, C.-G.; Cheng, R.-S.; Tang, G.-P.; Xiao, T.; Huang, L.-F.; Wang, H.-G. Novel Intelligent Methods for Channel Path Classification and Model Determination Based on Blind Source Signals. Atmosphere 2024, 15, 280. https://doi.org/10.3390/atmos15030280
Cao L-F, Liu C-G, Cheng R-S, Tang G-P, Xiao T, Huang L-F, Wang H-G. Novel Intelligent Methods for Channel Path Classification and Model Determination Based on Blind Source Signals. Atmosphere. 2024; 15(3):280. https://doi.org/10.3390/atmos15030280
Chicago/Turabian StyleCao, Li-Feng, Cheng-Guo Liu, Run-Sheng Cheng, Guang-Pu Tang, Tong Xiao, Li-Feng Huang, and Hong-Guang Wang. 2024. "Novel Intelligent Methods for Channel Path Classification and Model Determination Based on Blind Source Signals" Atmosphere 15, no. 3: 280. https://doi.org/10.3390/atmos15030280
APA StyleCao, L.-F., Liu, C.-G., Cheng, R.-S., Tang, G.-P., Xiao, T., Huang, L.-F., & Wang, H.-G. (2024). Novel Intelligent Methods for Channel Path Classification and Model Determination Based on Blind Source Signals. Atmosphere, 15(3), 280. https://doi.org/10.3390/atmos15030280







