Understanding Rainfall Distribution Characteristics over the Vietnamese Mekong Delta: A Comparison between Coastal and Inland Localities
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Rainfall Correlation Matrix and Principal Componant Analysis
2.3. Rainfall Trend Analysis
3. Results
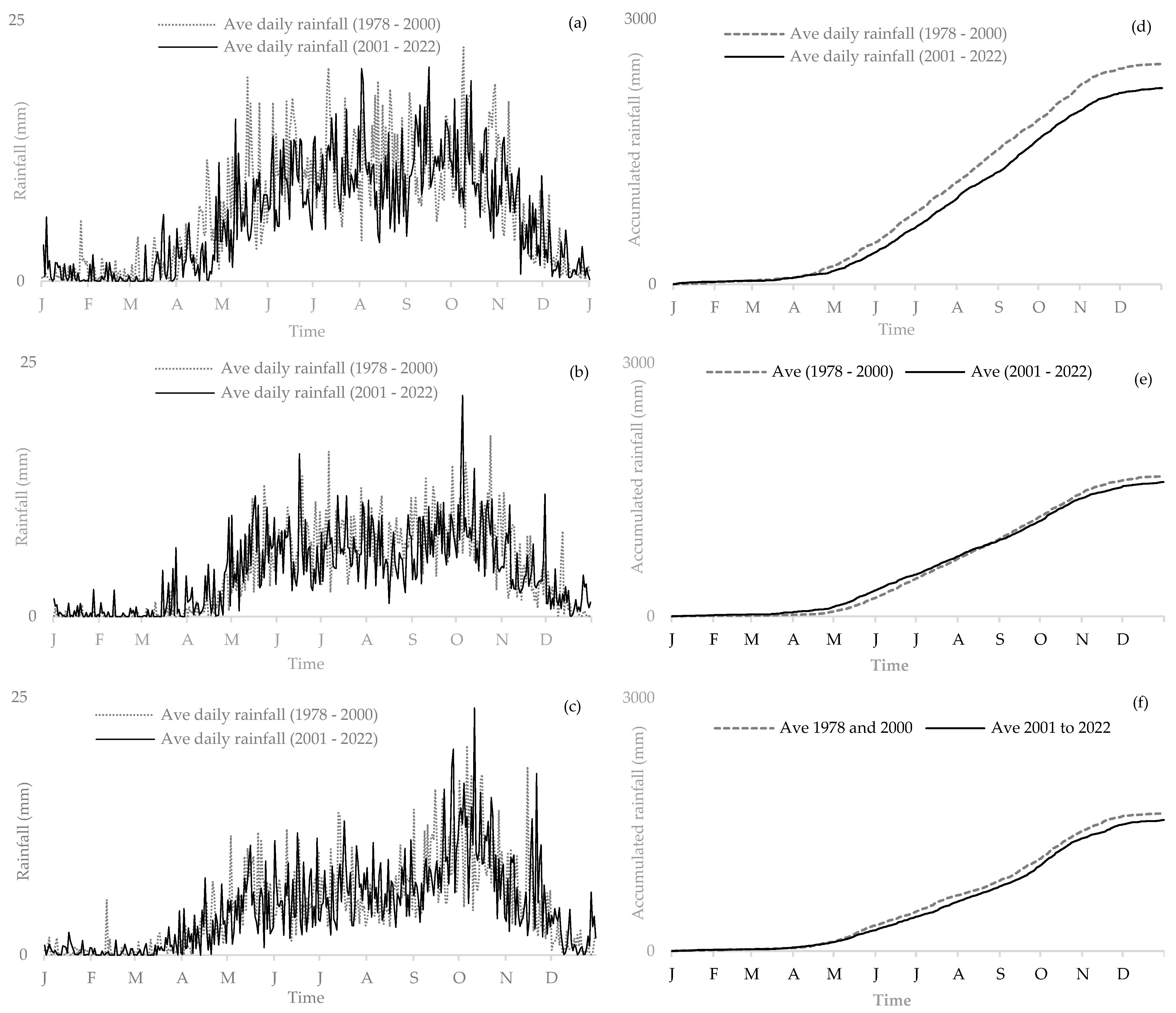
3.1. Descriptive Statistics
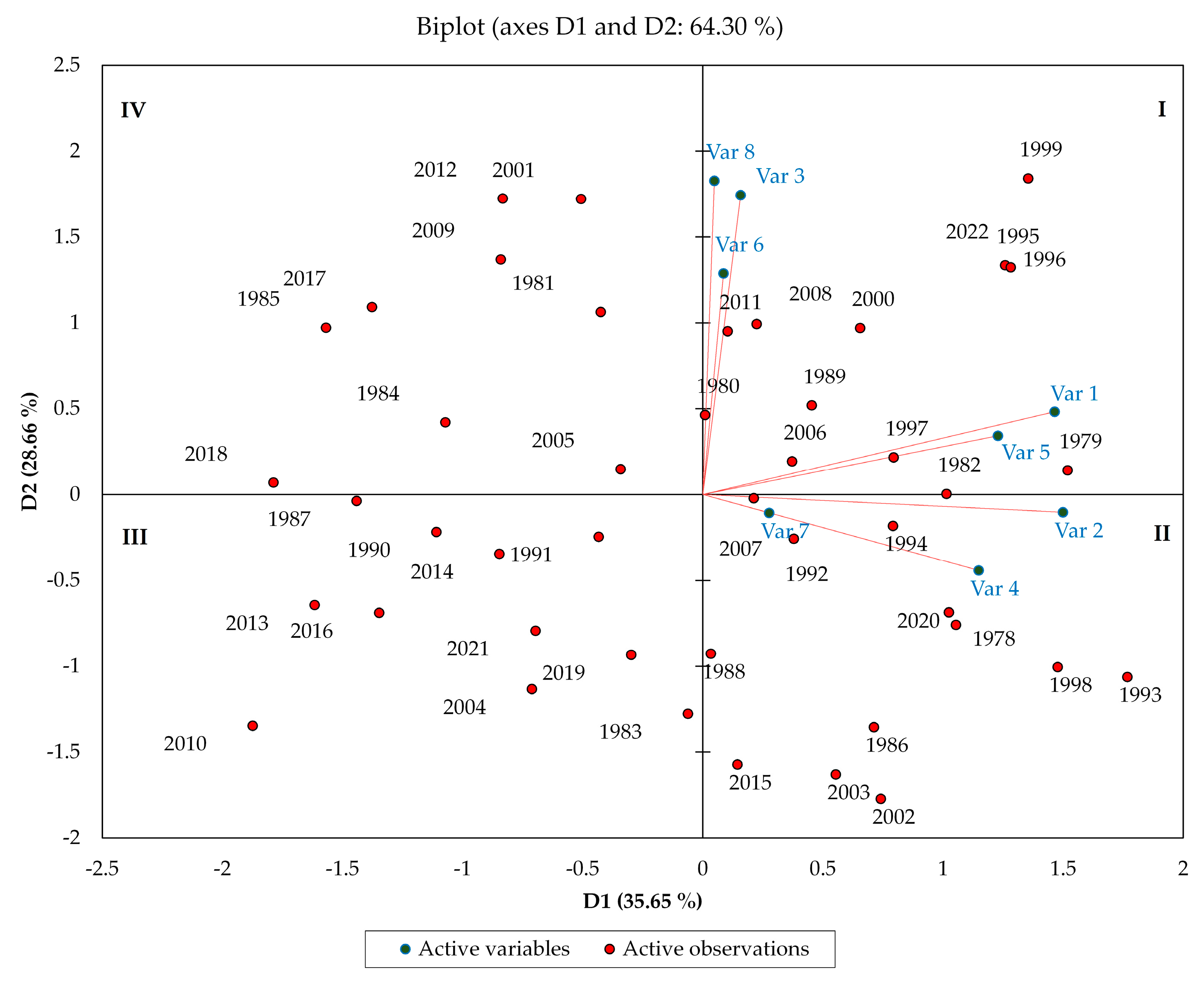
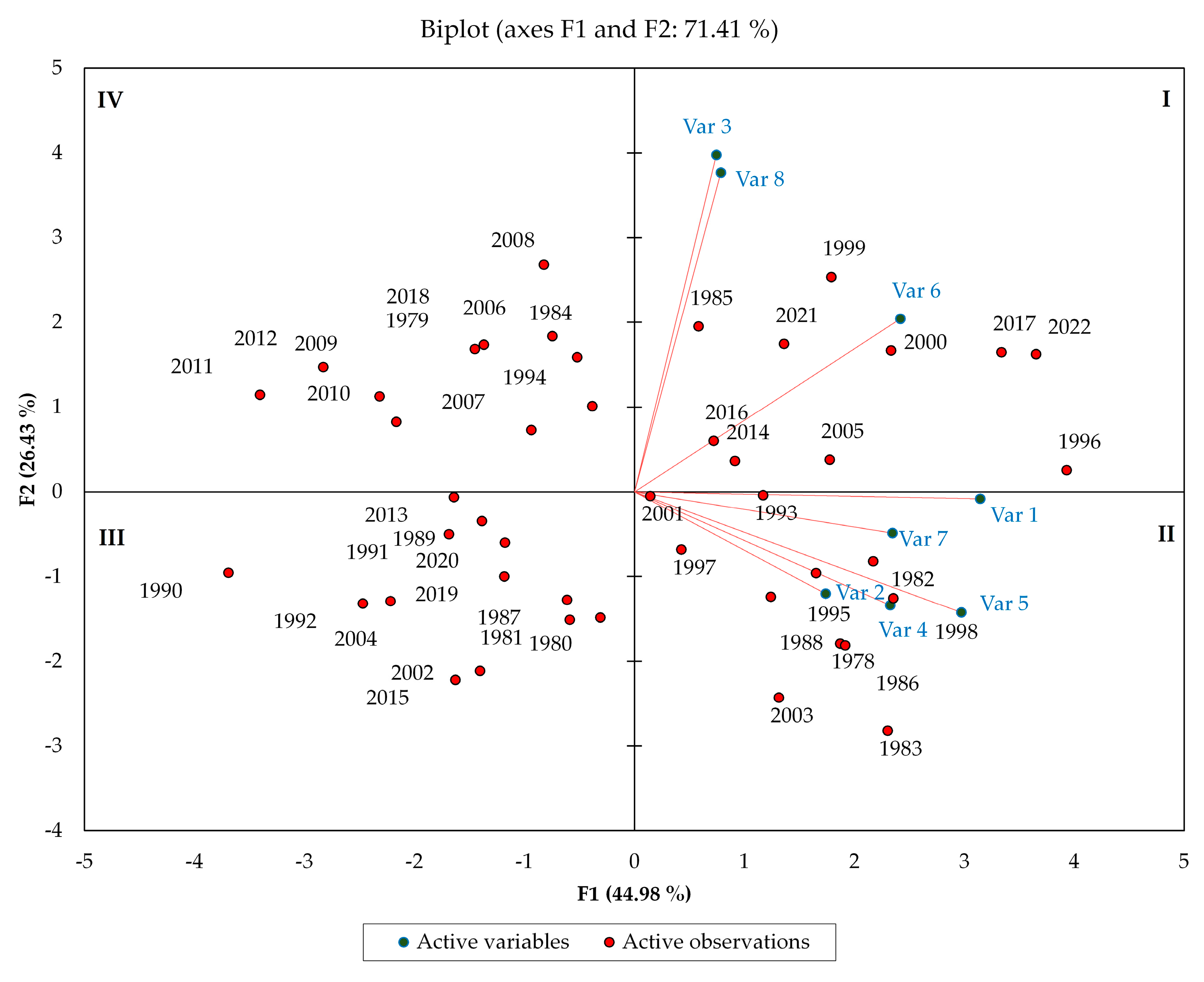
3.2. Correlation and Principal Component Analysis (PCA) for Examining Rainfall Characteristics
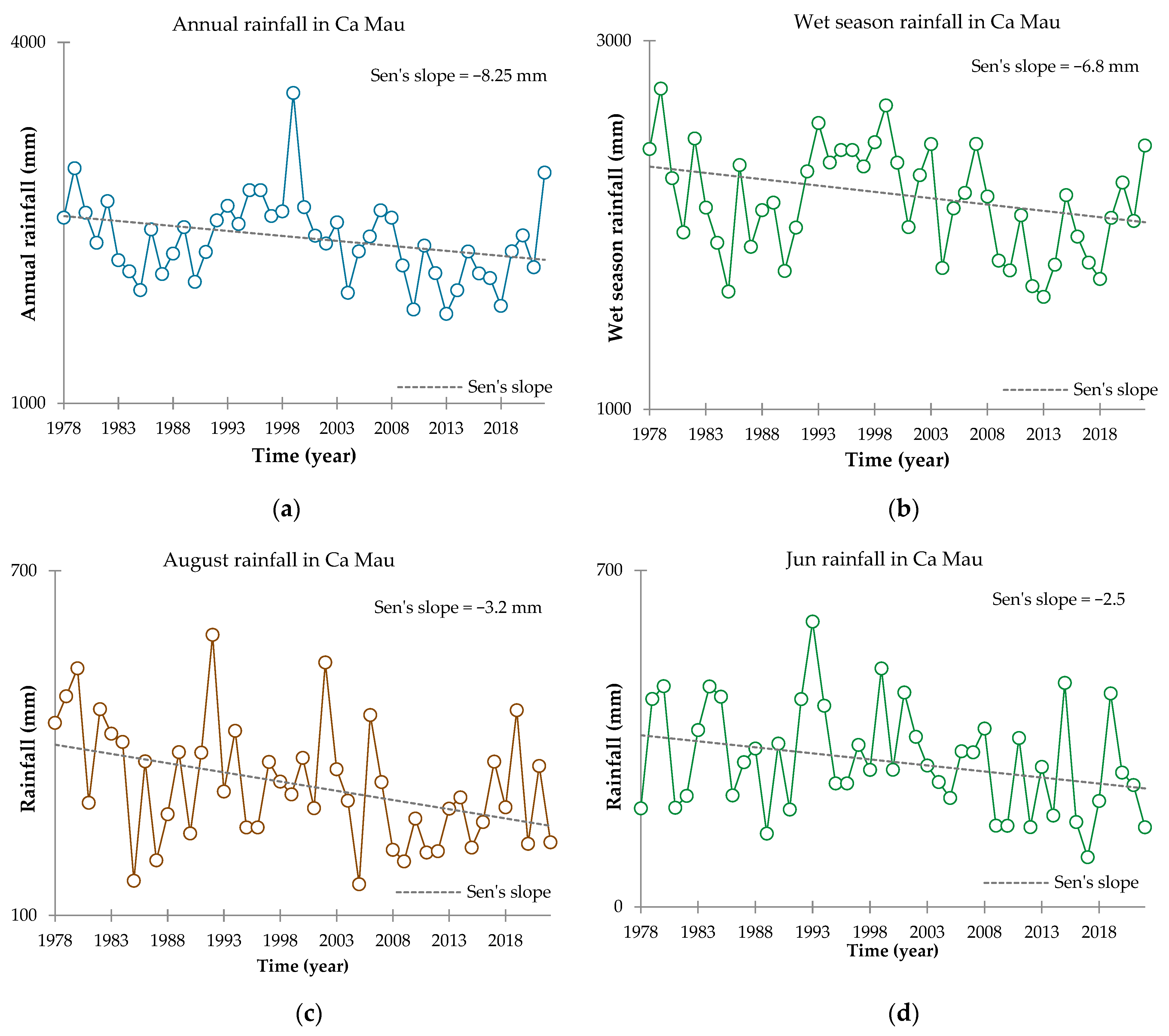
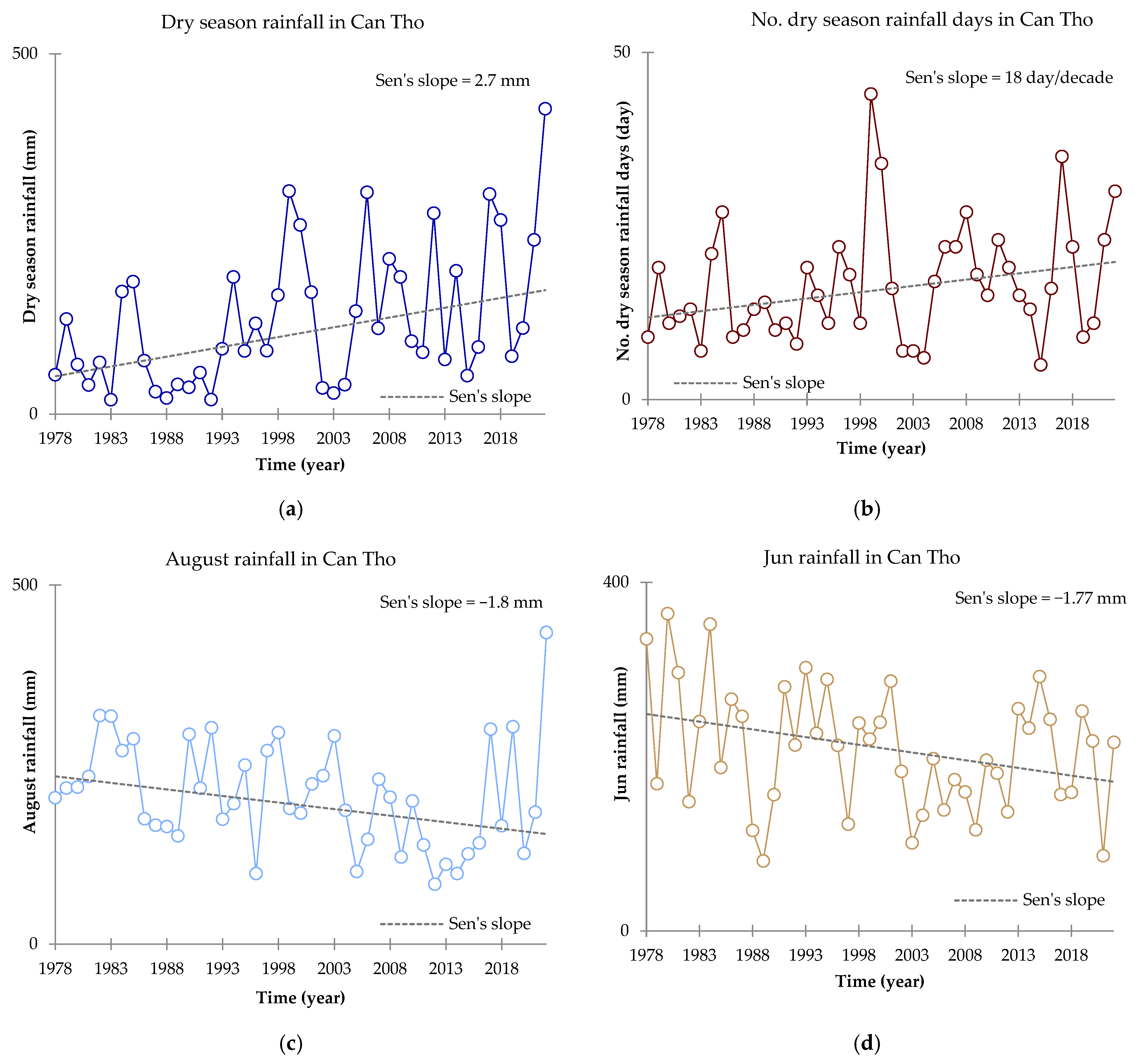
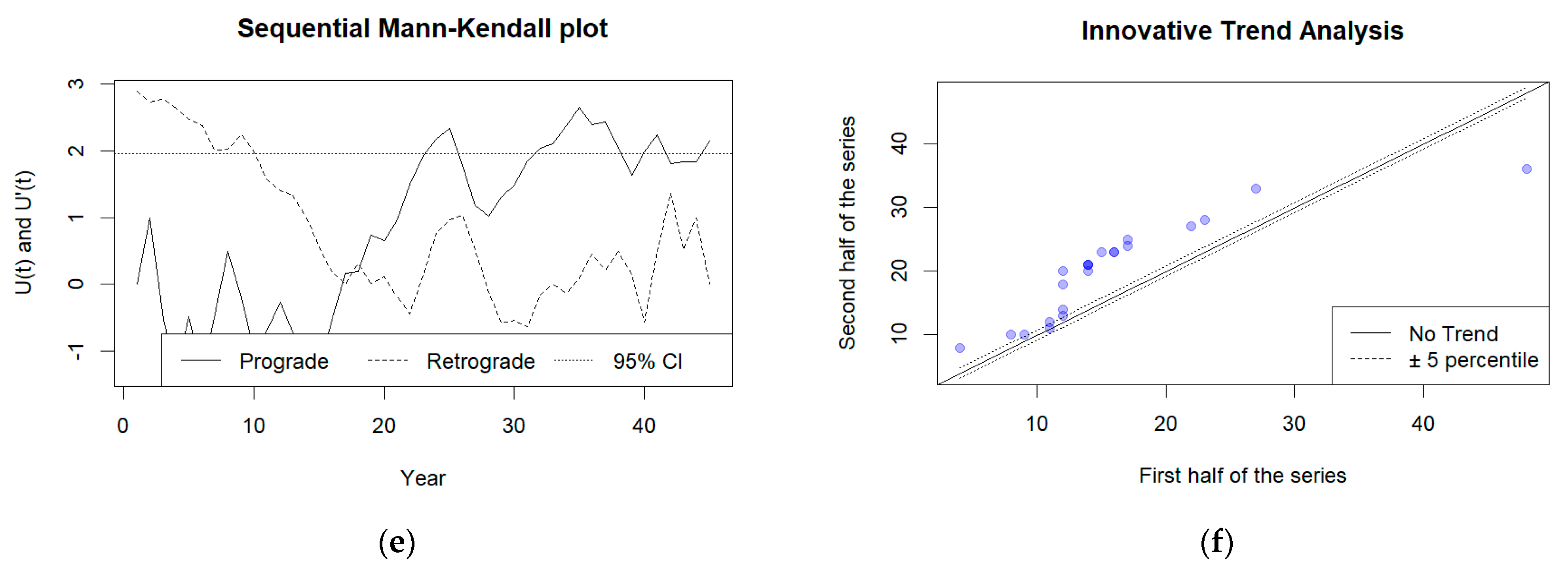
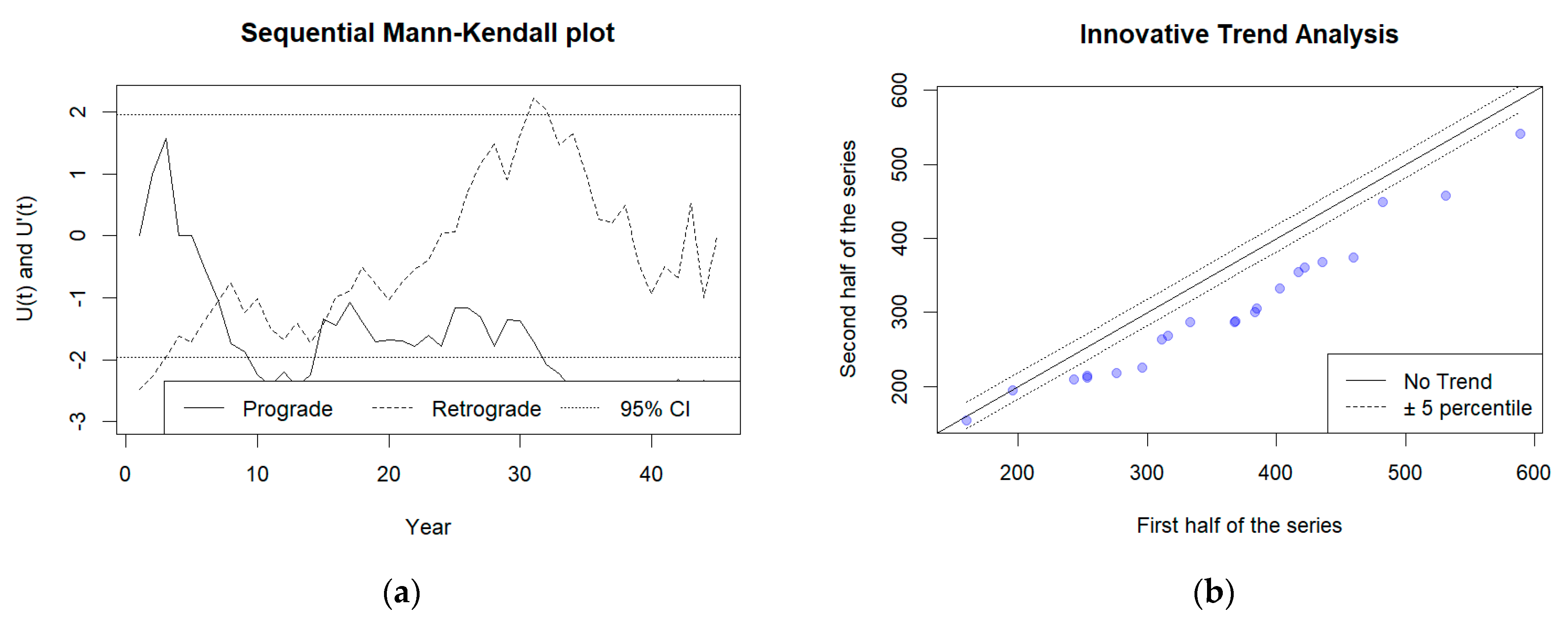
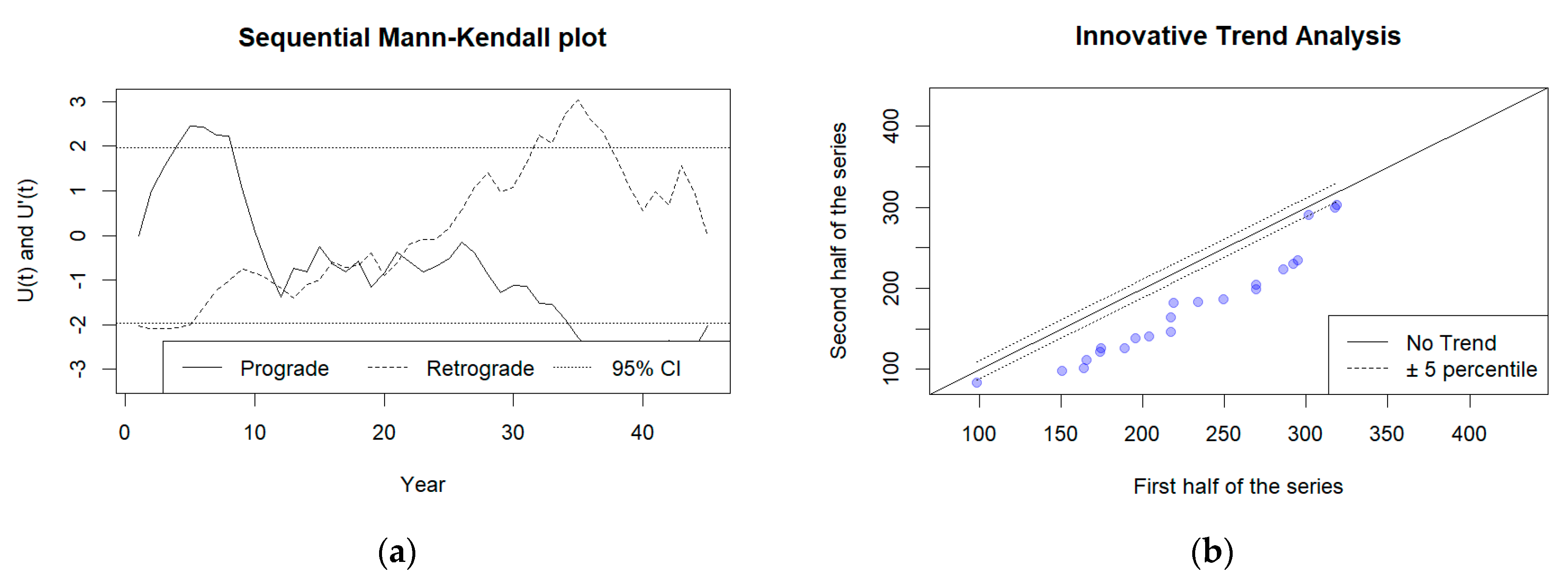
3.3. Rainfall Trend Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Juneng, L.; Tangang, F.T. Evolution of ENSO-Related Rainfall Anomalies in Southeast Asia Region and Its Relationship with Atmosphere–Ocean Variations in Indo-Pacific Sector. Clim. Dyn. 2005, 25, 337–350. [Google Scholar] [CrossRef]
- Chang, C.-P.; Wang, Z.; McBride, J.; Liu, C.-H. Annual Cycle of Southeast Asia—Maritime Continent Rainfall and the Asymmetric Monsoon Transition. J. Clim. 2005, 18, 287–301. [Google Scholar] [CrossRef]
- Li, X.-X. Heat Wave Trends in Southeast Asia during 1979–2018: The Impact of Humidity. Sci. Total Environ. 2020, 721, 137664. [Google Scholar] [CrossRef] [PubMed]
- Supari; Tangang, F.; Juneng, L.; Aldrian, E. Observed Changes in Extreme Temperature and Precipitation over Indonesia. Int. J. Climatol. 2017, 37, 1979–1997. [Google Scholar] [CrossRef]
- Yokoi, S.; Matsumoto, J. Collaborative Effects of Cold Surge and Tropical Depression–Type Disturbance on Heavy Rainfall in Central Vietnam. Mon. Weather Rev. 2008, 136, 3275–3287. [Google Scholar] [CrossRef]
- Gorin, V.A.; Scherz, M.D.; Korost, D.V.; Poyarkov, N.A. Consequences of Parallel Miniaturisation in Microhylinae (Anura, Microhylidae), with the Description of a New Genus of Diminutive South East Asian Frogs. Zoosystematics Evol. 2021, 97, 21–54. [Google Scholar] [CrossRef]
- Yang, S.; Li, Z.; Yu, J.Y.; Hu, X.; Dong, W.; He, S. El Niño–Southern Oscillation and its impact in the changing climate. Natl. Sci. Rev. 2018, 5, 840–857. [Google Scholar] [CrossRef]
- Minh, H.V.; Kumar, P.; Van Ty, T.; Duy, D.V.; Han, T.G.; Lavane, K.; Avtar, R. Understanding Dry and Wet Conditions in the Vietnamese Mekong Delta Using Multiple Drought Indices: A Case Study in Ca Mau Province. Hydrology 2022, 9, 213. [Google Scholar] [CrossRef]
- Cai, W.; McPhaden, M.J.; Grimm, A.M.; Rodrigues, R.R.; Taschetto, A.S.; Garreaud, R.D.; Dewitte, B.; Poveda, G.; Ham, Y.-G.; Santoso, A. Climate Impacts of the El Niño–Southern Oscillation on South America. Nat. Rev. Earth Environ. 2020, 1, 215–231. [Google Scholar] [CrossRef]
- Garcia, L. Overview of Early Warning Systems for Hydro-Meteorological Hazards in Selected Countries in Southeast Asia; Asian Disaster Preparedness Center: Bangkok, Thailand, 2002; p. 51. [Google Scholar]
- Nguyen-Thi, H.A.; Matsumoto, J.; Ngo-Duc, T.; Endo, N. A Climatological Study of Tropical Cyclone Rainfall in Vietnam. Sola 2012, 8, 41–44. [Google Scholar] [CrossRef]
- Anh, Q.T.; Taniguchi, K. Variations of Precipitation and Water Resources in the Northern Part of Vietnam under Climate Change. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2014, 70, I_211–I_216. [Google Scholar]
- Field, C.; Barros, V.; Dokken, D.; Mach, K.; Mastrandrea, M.; Bilir, T.; Chatterjee, M.; Ebi, K.; Estrada, Y.; Genova, R. IPCC: Climate Change 2014: Impacts, Adaptation, and Vulnerability: Summaries, Frequently Asked Questions, and Cross-Chapter Boxes: A Working Group II Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; World Meteorological Organization: Geneva, Switzerland, 2014; p. 705. [Google Scholar]
- Thao, N.D.; Takagi, H.; Esteban, M. Coastal Disasters and Climate Change in Vietnam: Engineering and Planning Perspectives; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 0-12-800479-7. [Google Scholar]
- Sivakumar, B. Global Climate Change and Its Impacts on Water Resources Planning and Management: Assessment and Challenges. Stoch. Environ. Res. Risk Assess. 2011, 25, 583–600. [Google Scholar] [CrossRef]
- DONRes, Vietnam. Updated Climate Change Scenario 2020; Ministry of Environment and Natural Resources: Ha Noi, Viet Nam, 2020; p. 254. [Google Scholar]
- Das, S.; Kamruzzaman, M.; Islam, A.R.M.T. Assessment of characteristic changes of regional estimation of extreme rainfall under climate change: A case study in a tropical monsoon region with the climate projections from CMIP6 model. J. Hydrol. 2022, 610, 128002. [Google Scholar] [CrossRef]
- Abdullah, A.Y.M.; Bhuian, M.H.; Kiselev, G.; Dewan, A.; Hassan, Q.K.; Rafiuddin, M. Extreme Temperature and Rainfall Events in Bangladesh: A Comparison between Coastal and Inland Areas. Int. J. Climatol. 2022, 42, 3253–3273. [Google Scholar] [CrossRef]
- Xuan, N.V.; Giang, N.N.L.; Ty, T.V.; Kumar, P.; Downes, N.K.; Nam, N.D.G.; Ngan, N.V.C.; Thinh, L.V.; Duy, D.V.; Avtar, R. Impacts of Dike Systems on Hydrological Regime in Vietnamese Mekong Delta. Water Supply 2022, 22, 7945–7959. [Google Scholar] [CrossRef]
- Kumar, V.; Jain, S.K.; Singh, Y. Analysis of Long-Term Rainfall Trends in India. Hydrol. Sci. J. 2010, 55, 484–496. [Google Scholar] [CrossRef]
- Guo, A.; He, L. Correlations between Summer Discharge and South Asian Summer Monsoon Subsystems in Mekong River Basin. Atmosphere 2023, 14, 958. [Google Scholar] [CrossRef]
- Tayyab, M.; Zhou, J.; Zeng, X.; Ahmed, I.; Adnan, R. Application of Statistical Nonparametric Tests in Dongting Lake, China: 1961–2012; IEEE: Piscataway, NJ, USA, 2016; pp. 197–201. [Google Scholar]
- Da Silva, R.M.; Santos, C.A.; Moreira, M.; Corte-Real, J.; Silva, V.C.; Medeiros, I.C. Rainfall and River Flow Trends Using Mann–Kendall and Sen’s Slope Estimator Statistical Tests in the Cobres River Basin. Nat. Hazards 2015, 77, 1205–1221. [Google Scholar] [CrossRef]
- Şen, Z. Innovative Trend Analysis Methodology. J. Hydrol. Eng. 2012, 17, 1042–1046. [Google Scholar] [CrossRef]
- Bora, S.L.; Bhuyan, K.; Hazarika, P.J.; Gogoi, J.; Goswami, K. Analysis of Rainfall Trend Using Non-Parametric Methods and Innovative Trend Analysis during 1901–2020 in Seven States of North East India. Curr. Sci. 2022, 122, 801–811. [Google Scholar] [CrossRef]
- Mallick, J.; Talukdar, S.; Alsubih, M.; Salam, R.; Ahmed, M.; Kahla, N.B.; Shamimuzzaman, M. Analysing the Trend of Rainfall in Asir Region of Saudi Arabia Using the Family of Mann-Kendall Tests, Innovative Trend Analysis, and Detrended Fluctuation Analysis. Theor. Appl. Climatol. 2021, 143, 823–841. [Google Scholar] [CrossRef]
- Lavane, K.; Kumar, P.; Meraj, G.; Han, T.G.; Ngan, L.H.; Lien, B.T.; Van Ty, T.; Thanh, N.T.; Downes, N.K.; Nam, N.D.; et al. Assessing the Effects of Drought on Rice Yields in the Mekong Delta. Climate 2023, 11, 13. [Google Scholar] [CrossRef]
- Minh, H.V.T.; Lavane, K.; Ty, T.V.; Downes, N.K.; Hong, T.T.K.; Kumar, P. Evaluation of the Impact of Drought and Saline Water Intrusion on Rice Yields in the Mekong Delta, Vietnam. Water 2022, 14, 3499. [Google Scholar] [CrossRef]
- Agbo, E.P.; Nkajoe, U.; Edet, C.O. Comparison of Mann–Kendall and Şen’s Innovative Trend Method for Climatic Parameters over Nigeria’s Climatic Zones. Clim. Dyn. 2023, 60, 3385–3401. [Google Scholar] [CrossRef]
- Serinaldi, F.; Chebana, F.; Kilsby, C.G. Dissecting Innovative Trend Analysis. Stoch. Environ. Res. Risk Assess. 2020, 34, 733–754. [Google Scholar] [CrossRef]
- Myhre, G.; Alterskjær, K.; Stjern, C.W.; Hodnebrog, Ø.; Marelle, L.; Samset, B.H.; Sillmann, J.; Schaller, N.; Fischer, E.; Schulz, M.; et al. Frequency of Extreme Precipitation Increases Extensively with Event Rareness under Global Warming. Sci. Rep. 2019, 9, 16063. [Google Scholar] [CrossRef]
- Minh, H.V.T.; Lavane, K.; Lanh, L.T.; Thinh, L.V.; Cong, N.P.; Ty, T.V.; Downes, N.K.; Kumar, P. Developing Intensity-Duration-Frequency (IDF) Curves Based on Rainfall Cumulative Distribution Frequency (CDF) for Can Tho City, Vietnam. Earth 2022, 3, 866–880. [Google Scholar] [CrossRef]
- Tran, D.Q.; Nguyen, N.N.; Huynh, M.V.; Bairagi, S.K.; Le, K.N.; Tran, T.V.; Durand-Morat, A. Modeling Saltwater Intrusion Risk in the Presence of Uncertainty. Sci. Total Environ. 2024, 908, 168140. [Google Scholar] [CrossRef]
- Evans, J.D. Straightforward Statistics for the Behavioral Sciences; Thomson Brooks/Cole Publishing Co.: Pacific Grove, CA, USA, 1996; ISBN 0-534-23100-4. [Google Scholar]
- Tadić, L.; Bonacci, O.; Brleković, T. An Example of Principal Component Analysis Application on Climate Change Assessment. Theor. Appl. Climatol. 2019, 138, 1049–1062. [Google Scholar] [CrossRef]
- Chan, J.C.; Shi, J. Application of Projection-pursuit Principal Component Analysis Method to Climate Studies. Int. J. Climatol. J. R. Meteorol. Soc. 1997, 17, 103–113. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, X.; Khan, A.; Zhang, Y.; Kuang, X.; Liang, X.; Taccari, M.L.; Nuttall, J. Daily Runoff Forecasting by Deep Recursive Neural Network. J. Hydrol. 2021, 596, 126067. [Google Scholar] [CrossRef]
- Maćkiewicz, A.; Ratajczak, W. Principal Components Analysis (PCA). Comput. Geosci. 1993, 19, 303–342. [Google Scholar] [CrossRef]
- Holland, S.M. Principal Components Analysis (PCA); Department of Geology, University of Georgia: Athens, GA, USA, 2008; Volume 30602, p. 2501. [Google Scholar]
- Kurita, T. Principal Component Analysis (PCA). In Computer Vision: A Reference Guide; Springer: New York, NY, USA, 2019; pp. 1–4. [Google Scholar]
- Lornezhad, E.; Ebrahimi, H.; Rabieifar, H.R. Analysis of Precipitation and Drought Trends by a Modified Mann–Kendall Method: A Case Study of Lorestan Province, Iran. Water Supply 2023, 23, 1557–1570. [Google Scholar] [CrossRef]
- Tosunoğlu, F. Trend Analysis of Daily Maximum Rainfall Series in Çoruh Basin, Turkey. J. Inst. Sci. Technol. 2017, 7, 195–205. [Google Scholar] [CrossRef]
- Hanif, M.F.; Mustafa, M.R.U.; Liaqat, M.U.; Hashim, A.M.; Yusof, K.W. Evaluation of Long-Term Trends of Rainfall in Perak, Malaysia. Climate 2022, 10, 44. [Google Scholar] [CrossRef]
- Kisi, O.; Ay, M. Comparison of Mann–Kendall and Innovative Trend Method for Water Quality Parameters of the Kizilirmak River, Turkey. J. Hydrol. 2014, 513, 362–375. [Google Scholar] [CrossRef]
- Kendall, M. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Mann, H.B. Nonparametric Tests against Trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 1987; ISBN 0-471-28878-0. [Google Scholar]
- Zeybekoğlu, U. Temperature Series Analysis of the Hirfanli Dam Basin with the Mann-Kendall and Sequential Mann-Kendall Tests. Turk. J. Eng. 2023, 7, 306–313. [Google Scholar] [CrossRef]
- Şen, Z. Trend Identification Simulation and Application. J. Hydrol. Eng. 2014, 19, 635–642. [Google Scholar] [CrossRef]
- Caloiero, T.; Coscarelli, R.; Ferrari, E. Application of the Innovative Trend Analysis Method for the Trend Analysis of Rainfall Anomalies in Southern Italy. Water Resour. Manag. 2018, 32, 4971–4983. [Google Scholar] [CrossRef]
- Alifujiang, Y.; Abuduwaili, J.; Maihemuti, B.; Emin, B.; Groll, M. Innovative Trend Analysis of Precipitation in the Lake Issyk-Kul Basin, Kyrgyzstan. Atmosphere 2020, 11, 332. [Google Scholar] [CrossRef]
- Alashan, S. An Improved Version of Innovative Trend Analyses. Arab. J. Geosci. 2018, 11, 50. [Google Scholar] [CrossRef]
- Suhaila, J.; Deni, S.M.; Wan Zin, W.Z.; Jemain, A.A. Spatial patterns and trends of daily rainfall regime in Peninsular Malaysia during the southwest and northeast monsoons: 1975–2004. Meteorol. Atmos. Phys. 2010, 110, 1–18. [Google Scholar] [CrossRef]
- Dunn, C.H. Base Development in South Vietnam, 1965–1970; Department of the Army: Monterey, CA, USA, 1973. [Google Scholar]
- Qian, W.; Ding, T.; Hu, H.; Lin, X.; Qin, A. An overview of dry-wet climate variability among monsoon-westerly regions and the monsoon northernmost marginal active zone in China. Adv. Atmos. Sci. 2009, 26, 630–641. [Google Scholar] [CrossRef]
- Chen, L.; Dong, M.; Shao, Y. The characteristics of interannual variations on the East Asian monsoon. J. Meteorol. Soc. Jpn. Ser. II 1992, 70, 397–421. [Google Scholar] [CrossRef]
- Ke, M.; Wang, Z.; Pan, W.; Luo, H.; Yang, S.; Guo, R. Extremely Strong Western Pacific Subtropical High in May 2021 Following a La Niña Event: Role of the Persistent Convective Forcing over the Indian Ocean. Asia-Pac. J. Atmos. Sci. 2023, 59, 47–58. [Google Scholar] [CrossRef]
- Freund, M.B.; Henley, B.J.; Karoly, D.J.; McGregor, H.V.; Abram, N.J.; Dommenget, D. Higher frequency of Central Pacific El Niño events in recent decades relative to past centuries. Nat. Geosci. 2019, 12, 450–455. [Google Scholar] [CrossRef]
- Soman, M.K.; Kumar, K.K. Some aspects of daily rainfall distribution over India during the south-west monsoon season. Int. J. Climatol. 1990, 10, 299–311. [Google Scholar] [CrossRef]
- Wang, B.; Li, J.; He, Q. Variable and robust East Asian monsoon rainfall response to El Niño over the past 60 years (1957–2016). Adv. Atmos. Sci. 2017, 34, 1235–1248. [Google Scholar] [CrossRef]
- Miralles, D.G.; Van Den Berg, M.J.; Gash, J.H.; Parinussa, R.M.; De Jeu, R.A.; Beck, H.E.; Holmes, T.R.; Jiménez, C.; Verhoest, N.E.; Dorigo, W.A.; et al. El Niño–La Niña cycle and recent trends in continental evaporation. Nat. Clim. Chang. 2014, 4, 122–126. [Google Scholar] [CrossRef]
- Qian, W.; Kang, H.S.; Lee, D.K. Distribution of seasonal rainfall in the East Asian monsoon region. Theor. Appl. Climatol. 2002, 73, 151–168. [Google Scholar] [CrossRef]
- Chen, G.; Lan, R.; Zeng, W.; Pan, H.; Li, W. Diurnal variations of rainfall in surface and satellite observations at the monsoon coast (South China). J. Clim. 2018, 31, 1703–1724. [Google Scholar] [CrossRef]
- Ghosh, S.; Vittal, H.; Sharma, T.; Karmakar, S.; Kasiviswanathan, K.S.; Dhanesh, Y.; Sudheer, K.P.; Gunthe, S.S. Indian summer monsoon rainfall: Implications of contrasting trends in the spatial variability of means and extremes. PLoS ONE 2016, 11, e0158670. [Google Scholar] [CrossRef]
- Paul, S.; Ghosh, S.; Mathew, M.; Devanand, A.; Karmakar, S.; Niyogi, D. Increased spatial variability and intensification of extreme monsoon rainfall due to urbanization. Sci. Rep. 2018, 8, 3918. [Google Scholar] [CrossRef]
- Gill, E.C.; Rajagopalan, B.; Molnar, P. Subseasonal variations in spatial signatures of ENSO on the Indian summer monsoon from 1901 to 2009. J. Geophys. Res. Atmos. 2015, 120, 8165–8185. [Google Scholar] [CrossRef]
- May, W. Simulation of the variability and extremes of daily rainfall during the Indian summer monsoon for present and future times in a global time-slice experiment. Clim. Dyn. 2004, 22, 183–204. [Google Scholar] [CrossRef]
- Le, P.V.; Pham, H.V.; Bui, L.K.; Tran, A.N.; Pham, C.V.; Nguyen, G.V.; Tran, P.A. Responses of groundwater to precipitation variability and ENSO in the Vietnamese Mekong Delta. Hydrol. Res. 2021, 52, 1280–1293. [Google Scholar] [CrossRef]
- Kripalani, R.H.; Kulkarni, A. Rainfall variability over South-east Asia—Connections with Indian monsoon and ENSO extremes: New perspectives. Int. J. Climatol. J. R. Meteorol. Soc. 1997, 17, 1155–1168. [Google Scholar] [CrossRef]
- Van Binh, D.; Kantoush, S.A.; Saber, M.; Mai, N.P.; Maskey, S.; Phong, D.T.; Sumi, T. Long-term alterations of flow regimes of the Mekong River and adaptation strategies for the Vietnamese Mekong Delta. J. Hydrol. Reg. Stud. 2020, 32, 100742. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, Y.; Zhang, J.; Chen, H.; Jin, J.; Liu, C.; Wang, G.; Tang, L. Spatiotemporal Projections of Precipitation in the Lancang–Mekong River Basin Based on CMIP6 Models. Remote Sens. 2023, 15, 4502. [Google Scholar] [CrossRef]
- Tri, V.P.D.; Yarina, L.; Nguyen, H.Q.; Downes, N.K. Progress toward Resilient and Sustainable Water Management in the Vietnamese Mekong Delta. Wiley Interdiscip. WIREs Water 2023, 10, e1670. [Google Scholar] [CrossRef]
- Khoi, D.N.; Nguyen, V.T.; Sam, T.T.; Ky Phung, N.; Thi Bay, N. Responses of river discharge and sediment load to climate change in the transboundary Mekong River Basin. Water Environ. J. 2020, 34, 367–380. [Google Scholar] [CrossRef]
- Rossi, C.G.; Srinivasan, R.; Jirayoot, K.; Le Duc, T.; Souvannabouth, P.; Binh, N.; Gassman, P.W. Hydrologic evaluation of the Lower Mekong River Basin with the soil and water assessment tool model. Int. Agric. Eng. J. 2009, 18, 1–13. [Google Scholar]
- Wang, C.; Leisz, S.; Li, L.; Shi, X.; Mao, J.; Zheng, Y.; Chen, A. Historical and projected future runoff over the Mekong River basin. Earth Syst. Dyn. 2024, 15, 75–90. [Google Scholar] [CrossRef]
- Räsänen, T.A.; Kummu, M. Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River Basin. J. Hydrol. 2013, 476, 154–168. [Google Scholar] [CrossRef]
- Sridhar, V.; Kang, H.; Ali, S.A. Human-induced alterations to land use and climate and their responses for hydrology and water management in the Mekong River Basin. Water 2019, 11, 1307. [Google Scholar] [CrossRef]
- Yang, J.; Yang, Y.E.; Chang, J.; Zhang, J.; Yao, J. Impact of dam development and climate change on hydroecological conditions and natural hazard risk in the Mekong River Basin. J. Hydrol. 2019, 579, 124177. [Google Scholar] [CrossRef]
- Piman, T.; Lennaerts, T.; Southalack, P. Assessment of hydrological changes in the lower Mekong Basin from Basin-Wide development scenarios. Hydrol. Process. 2013, 27, 2115–2125. [Google Scholar] [CrossRef]
- Liu, J.; Chen, D.; Mao, G.; Irannezhad, M.; Pokhrel, Y. Past and future changes in climate and water resources in the lancang–mekong River Basin: Current understanding and future research directions. Engineering 2022, 13, 144–152. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Burbano, M.; Roush, J.; Kang, H.; Sridhar, V.; Hyndman, D.W. A review of the integrated effects of changing climate, land use, and dams on Mekong river hydrology. Water 2018, 10, 266. [Google Scholar] [CrossRef]
- Li, D.; Long, D.; Zhao, J.; Lu, H.; Hong, Y. Observed changes in flow regimes in the Mekong River basin. J. Hydrol. 2017, 551, 217–232. [Google Scholar] [CrossRef]
- Thu, H.N.; Wehn, U. Data sharing in international transboundary contexts: The Vietnamese perspective on data sharing in the Lower Mekong Basin. J. Hydrol. 2016, 536, 351–364. [Google Scholar] [CrossRef]
- Heikkila, T.; Gerlak, A.K.; Bell, A.R.; Schmeier, S. Adaptation in a transboundary river basin: Linking stressors and adaptive capacity within the Mekong River Commission. Environ. Sci. Policy 2013, 25, 73–82. [Google Scholar] [CrossRef]
- Triet, N.V.K.; Dung, N.V.; Hoang, L.P.; Le Duy, N.; Tran, D.D.; Anh, T.T.; Kummu, M.; Merz, B.; Apel, H. Future projections of flood dynamics in the Vietnamese Mekong Delta. Sci. Total Environ. 2020, 742, 140596. [Google Scholar] [CrossRef] [PubMed]
- Balica, S.F.; Dinh, Q.; Popescu, I. Vulnerability and exposure in developed and developing countries: Large-scale assessments. In Hydro-Meteorological Hazards, Risks, and Disasters; Elsevier: Amsterdam, The Netherlands, 2023; pp. 103–143. [Google Scholar]
- Chinh, D.T.; Bubeck, P.; Dung, N.V.; Kreibich, H. The 2011 flood event in the Mekong Delta: Preparedness, response, damage and recovery of private households and small businesses. Disasters 2016, 40, 753–778. [Google Scholar] [CrossRef] [PubMed]
- Wassmann, R.; Hien, N.X.; Hoanh, C.T.; Tuong, T.P. Sea level rise affecting the Vietnamese Mekong Delta: Water elevation in the flood season and implications for rice production. Clim. Chang. 2004, 66, 89–107. [Google Scholar] [CrossRef]
- Triet, N.V.K.; Dung, N.V.; Merz, B.; Apel, H. Towards risk-based flood management in highly productive paddy rice cultivation–concept development and application to the Mekong Delta. Nat. Hazards Earth Syst. Sci. 2018, 18, 2859–2876. [Google Scholar] [CrossRef]
- Chinh, D.T.; Dung, N.V.; Gain, A.K.; Kreibich, H. Flood loss models and risk analysis for private households in Can Tho City, Vietnam. Water 2017, 9, 13. [Google Scholar] [CrossRef]
- Chinh, D.T.; Gain, A.K.; Dung, N.V.; Haase, D.; Kreibich, H. Multi-variate analyses of flood loss in Can Tho City, Mekong Delta. Water 2015, 8, 6. [Google Scholar] [CrossRef]
- Van Tho, N. Coastal erosion, river bank erosion and landslides in the Mekong Delta: Causes, effects and solutions. In Geotechnics for Sustainable Infrastructure Development; Springer: Singapore, 2020; pp. 957–962. [Google Scholar]
- Mekong Floods Are a Reminder of a Perennial Risk. JBA Risk Management. Mekong Delta Flood Report. Available online: https://www.jbarisk.com/products-services/event-response/mekong-delta-flood-report/ (accessed on 4 February 2024).
- MRC. Annual Mekong Flood Report 2015; Mekong River Commission: Vientiane, Laos, 2018; 106p. [Google Scholar]
- Bhattarai, R.; Mishra, B.K.; Bhattarai, D.; Khatiwada, D.; Kumar, P.; Meraj, G. Assessing Hydropower Potential in Nepal’s Sunkoshi River Basin: An Integrated GIS and SWAT Hydrological Modeling Approach. Scientifica 2024, 2024, 1007081. [Google Scholar] [CrossRef]
- Dolgorsuren, S.E.; Ishgaldan, B.; Myagmartseren, P.; Kumar, P.; Meraj, G.; Singh, S.K.; Kanga, S.; Almazroui, M. Hydrological Responses to Climate Change and Land-Use Dynamics in Central Asia’s Semi-arid Regions: An SWAT Model Analysis of the Tuul River Basin. Earth Syst. Environ. 2024. [Google Scholar] [CrossRef]
- Debnath, J.; Debbarma, J.; Debnath, A.; Meraj, G.; Chand, K.; Singh, S.K.; Kanga, S.; Kumar, P.; Sahariah, D.; Saikia, A. Flood susceptibility assessment of the Agartala Urban Watershed, India, using Machine Learning Algorithm. Environ. Monit. Assess. 2024, 196, 110. [Google Scholar] [CrossRef]
- Debnath, J.; Sahariah, D.; Nath, N.; Saikia, A.; Lahon, D.; Islam, M.N.; Hashimoto, S.; Meraj, G.; Kumar, P.; Singh, S.K.; et al. Modelling on assessment of flood risk susceptibility at the Jia Bharali River basin in Eastern Himalayas by integrating multicollinearity tests and geospatial techniques. Model. Earth Syst. Environ. 2023. [Google Scholar] [CrossRef]
- Debnath, J.; Sahariah, D.; Lahon, D.; Nath, N.; Chand, K.; Meraj, G.; Kumar, P.; Singh, S.K.; Kanga, S.; Farooq, M. Assessing the impacts of current and future changes of the planforms of river Brahmaputra on its land use-land cover. Geosci. Front. 2023, 14, 101557. [Google Scholar] [CrossRef]
- Rafiq, M.; Meraj, G.; Kesarkar, A.P.; Farooq, M.; Singh, S.K.; Kanga, S. Hazard mitigation and climate change in the Himalayas–policy and decision making. In Disaster Management in the Complex Himalayan Terrains: Natural Hazard Management, Methodologies and Policy Implications; Springer International Publishing: Cham, Switzerland, 2022; pp. 169–182. [Google Scholar]
- Tomar, P.; Singh, S.K.; Kanga, S.; Meraj, G.; Kranjčić, N.; Đurin, B.; Pattanaik, A. GIS-Based Urban Flood Risk Assessment and Management—A Case Study of Delhi National Capital Territory (NCT), India. Sustainability 2021, 13, 12850. [Google Scholar] [CrossRef]
- Dinh, Q.; Balica, S.; Popescu, I.; Jonoski, A. Climate change impact on flood hazard, vulnerability and risk of the Long Xuyen Quadrangle in the Mekong Delta. Int. J. River Basin Manag. 2012, 10, 103–120. [Google Scholar] [CrossRef]
- Nhan, N.H.; Cao, N.B. Damming the Mekong: Impacts in Vietnam and solutions. In Coasts and Estuaries; Elsevier: Amsterdam, The Netherlands, 2019; pp. 321–340. [Google Scholar]
- Hui, T.R.; Park, E.; Loc, H.H.; Tien, P.D. Long-term hydrological alterations and the agricultural landscapes in the Mekong Delta: Insights from remote sensing and national statistics. Environ. Chall. 2022, 7, 100454. [Google Scholar] [CrossRef]
- Loc, H.H.; Van Binh, D.; Park, E.; Shrestha, S.; Dung, T.D.; Son, V.H.; Truc, N.H.T.; Mai, N.P.; Seijger, C. Intensifying saline water intrusion and drought in the Mekong Delta: From physical evidence to policy outlooks. Sci. Total Environ. 2021, 757, 143919. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, W.; Suman, D.; Yu, S.; He, D. Water cooperation priorities in the Lancang-Mekong River basin based on cooperative events since the Mekong River Commission establishment. Chin. Geogr. Sci. 2019, 29, 58–69. [Google Scholar] [CrossRef]
- Schmeier, S. Regional cooperation efforts in the Mekong river basin: Mitigating river-related security threats and promoting regional development. Austrian J. Southeast Asian Stud. 2009, 2, 28–52. [Google Scholar]



| Level of Statistical Strength | Pearson Correlation Matrix (R) |
|---|---|
| Very strong | 0.80–1.00 |
| Strong | 0.60–0.79 |
| Moderate | 0.40–0.59 |
| Weak | 0.20–0.39 |
| Very weak | 0.00–0.19 |
| Variable | Observations | Minimum | Maximum | Mean | Std. Deviation | Coefficient of Variation |
|---|---|---|---|---|---|---|
| Ca Mau station | ||||||
| Annual rainfall (mm) | 45 | 1743 | 3580 | 2360 | 350 | 0.15 |
| Wet season rainfall (mm) | 45 | 1610 | 2741 | 2127 | 290 | 0.14 |
| Dry season rainfall (mm) | 45 | 26 | 930 | 233 | 152 | 0.65 |
| Daily maximum rainfall (mm) | 45 | 61 | 189 | 111 | 31 | 0.28 |
| Daily rainfall exceeding 50 mm (day) | 45 | 3 | 14 | 9 | 2 | 0.28 |
| No. rainfall days (day) | 45 | 144 | 213 | 171 | 13 | 0.08 |
| No. wet season rainfall days (day) | 45 | 131 | 163 | 145 | 8 | 0.05 |
| No. dry season rainfall days (day) | 45 | 9 | 66 | 26 | 11 | 0.43 |
| Can Tho station | ||||||
| Annual rainfall (mm) | 45 | 1160 | 2431 | 1624 | 260 | 0.16 |
| Wet season rainfall (mm) | 45 | 948 | 2009 | 1492 | 236 | 0.16 |
| Dry season rainfall (mm) | 45 | 20 | 424 | 132 | 98 | 0.74 |
| Daily maximum rainfall (mm) | 45 | 48 | 165 | 88 | 23 | 0.26 |
| Daily rainfall exceeding 50 mm (day) | 45 | 0 | 12 | 4 | 2 | 0.53 |
| No. rainfall days (day) | 45 | 119 | 185 | 154 | 13 | 0.09 |
| No. wet season rainfall days (day) | 45 | 114 | 163 | 137 | 10 | 0.07 |
| No. dry season rainfall days (day) | 45 | 5 | 44 | 17 | 8 | 0.51 |
| Moc Hoa station | ||||||
| Annual rainfall (mm) | 45 | 1047 | 2433 | 1595 | 323 | 0.20 |
| Wet season rainfall (mm) | 45 | 963 | 2142 | 1440 | 309 | 0.21 |
| Dry season rainfall (mm) | 45 | 15 | 371 | 154 | 91 | 0.59 |
| Daily maximum rainfall (mm) | 45 | 54 | 240 | 99 | 37 | 0.37 |
| Daily rainfall exceeding 50 mm (day) | 45 | 1 | 10 | 5 | 2 | 0.47 |
| No. rainfall days (day) | 45 | 113 | 177 | 144 | 14 | 0.09 |
| No. wet season rainfall days (day) | 45 | 101 | 149 | 126 | 10 | 0.08 |
| No. dry season rainfall days (day) | 45 | 4 | 48 | 18 | 9 | 0.47 |
| Variables | Var 1 | Var 2 | Var 3 | Var 4 | Var 5 | Var 6 | Var 7 | Var 8 |
|---|---|---|---|---|---|---|---|---|
| Annual rainfall (Var 1) | 1 | |||||||
| Wet season rainfall (Var 2) | 0.936 | 1 | ||||||
| Dry season rainfall (Var 3) | 0.315 | −0.009 | 1 | |||||
| Daily maximum rainfall (Var 4) | 0.533 | 0.594 | −0.076 | 1 | ||||
| Daily rainfall exceeding 50 mm (day) (Var 5) | 0.640 | 0.611 | 0.228 | 0.300 | 1 | |||
| No. rainfall days (Var 6) | 0.323 | 0.150 | 0.562 | −0.039 | 0.081 | 1 | ||
| No. wet season rainfall days (Var 7) | 0.299 | 0.313 | 0.046 | 0.141 | 0.114 | 0.628 | 1 | |
| No. dry season rainfall days (Var 8) | 0.262 | 0.012 | 0.740 | −0.122 | 0.102 | 0.677 | −0.087 | 1 |
| Variables | Var 1 | Var 2 | Var 3 | Var 4 | Var 5 | Var 6 | Var 7 | Var 8 |
|---|---|---|---|---|---|---|---|---|
| Annual rainfall (Var 1) | 1 | |||||||
| Wet season rainfall (Var 2) | 0.923 | 1 | ||||||
| Dry season rainfall (Var 3) | 0.258 | −0.068 | 1 | |||||
| Daily maximum rainfall (Var 4) | 0.448 | 0.460 | 0.060 | 1 | ||||
| Daily rainfall exceeding 50 mm (day) (Var 5) | 0.678 | 0.751 | −0.042 | 0.395 | 1 | |||
| No. of rainfall days (Var 6) | 0.590 | 0.424 | 0.422 | 0.117 | 0.210 | 1 | ||
| No. wet season rainfall days (Var 7) | 0.554 | 0.578 | −0.085 | 0.247 | 0.225 | 0.745 | 1 | |
| No. dry season rainfall days (Var 8) | 0.193 | −0.070 | 0.813 | −0.116 | −0.013 | 0.534 | −0.069 | 1 |
| Variables | Var 1 | Var 2 | Var 3 | Var 4 | Var 5 | Var 6 | Var 7 | Var 8 |
|---|---|---|---|---|---|---|---|---|
| Annual rainfall (Var 1) | 1 | |||||||
| Wet season rainfall (Var 2) | 0.938 | 1 | ||||||
| Dry season rainfall (Var 3) | 0.289 | −0.023 | 1 | |||||
| Daily maximum rainfall (Var 4) | 0.638 | 0.624 | 0.018 | 1 | ||||
| Daily rainfall exceeding 50 mm (day) (Var 5) | 0.896 | 0.826 | 0.271 | 0.632 | 1 | |||
| No. of rainfall days (Var 6) | 0.330 | 0.322 | 0.193 | 0.066 | 0.196 | 1 | ||
| No. of wet season rainfall days (Var 7) | 0.313 | 0.428 | −0.193 | 0.198 | 0.193 | 0.753 | 1 | |
| No. of dry season rainfall days (Var 8) | 0.187 | −0.006 | 0.631 | −0.131 | 0.164 | 0.603 | −0.008 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minh, H.V.T.; Lien, B.T.B.; Hong Ngoc, D.T.; Ty, T.V.; Ngan, N.V.C.; Cong, N.P.; Downes, N.K.; Meraj, G.; Kumar, P. Understanding Rainfall Distribution Characteristics over the Vietnamese Mekong Delta: A Comparison between Coastal and Inland Localities. Atmosphere 2024, 15, 217. https://doi.org/10.3390/atmos15020217
Minh HVT, Lien BTB, Hong Ngoc DT, Ty TV, Ngan NVC, Cong NP, Downes NK, Meraj G, Kumar P. Understanding Rainfall Distribution Characteristics over the Vietnamese Mekong Delta: A Comparison between Coastal and Inland Localities. Atmosphere. 2024; 15(2):217. https://doi.org/10.3390/atmos15020217
Chicago/Turabian StyleMinh, Huynh Vuong Thu, Bui Thi Bich Lien, Dang Thi Hong Ngoc, Tran Van Ty, Nguyen Vo Chau Ngan, Nguyen Phuoc Cong, Nigel K. Downes, Gowhar Meraj, and Pankaj Kumar. 2024. "Understanding Rainfall Distribution Characteristics over the Vietnamese Mekong Delta: A Comparison between Coastal and Inland Localities" Atmosphere 15, no. 2: 217. https://doi.org/10.3390/atmos15020217
APA StyleMinh, H. V. T., Lien, B. T. B., Hong Ngoc, D. T., Ty, T. V., Ngan, N. V. C., Cong, N. P., Downes, N. K., Meraj, G., & Kumar, P. (2024). Understanding Rainfall Distribution Characteristics over the Vietnamese Mekong Delta: A Comparison between Coastal and Inland Localities. Atmosphere, 15(2), 217. https://doi.org/10.3390/atmos15020217












