An Ensemble-Based Model for Specific Humidity Retrieval from Landsat-8 Satellite Data for South Korea
Abstract
1. Introduction
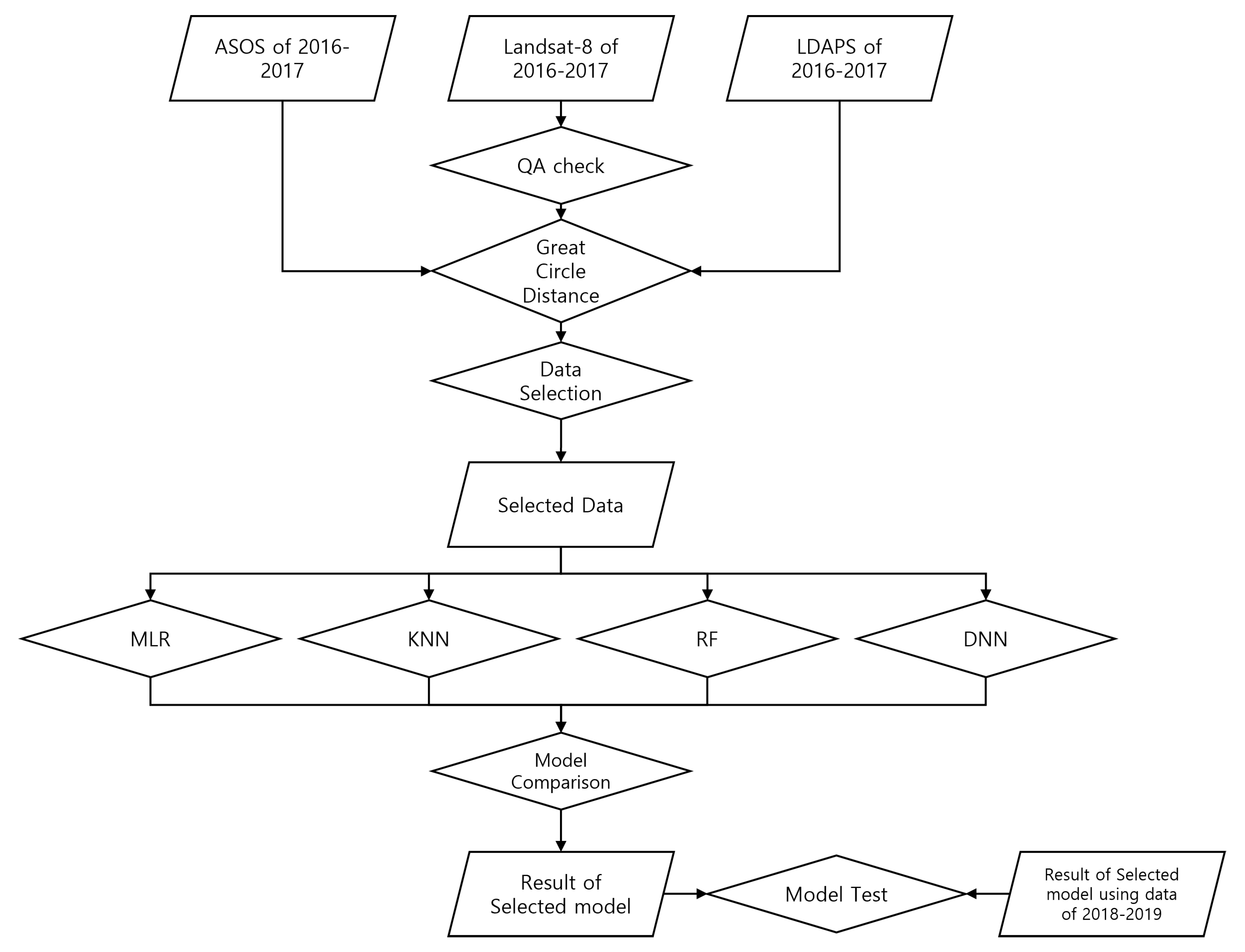
2. Materials and Methods
2.1. Study Area
2.2. Materials
2.2.1. Data from Direct Measurement
2.2.2. Data from Satellite
2.2.3. Data from Weather Prediction Model
2.3. Variables Selection
2.4. Methods
2.4.1. Multiple Linear Regression Algorithm
2.4.2. K-Nearest Neighbor Algorithm
2.4.3. Random Forest Algorithm
2.4.4. Deep Neural Network Algorithm
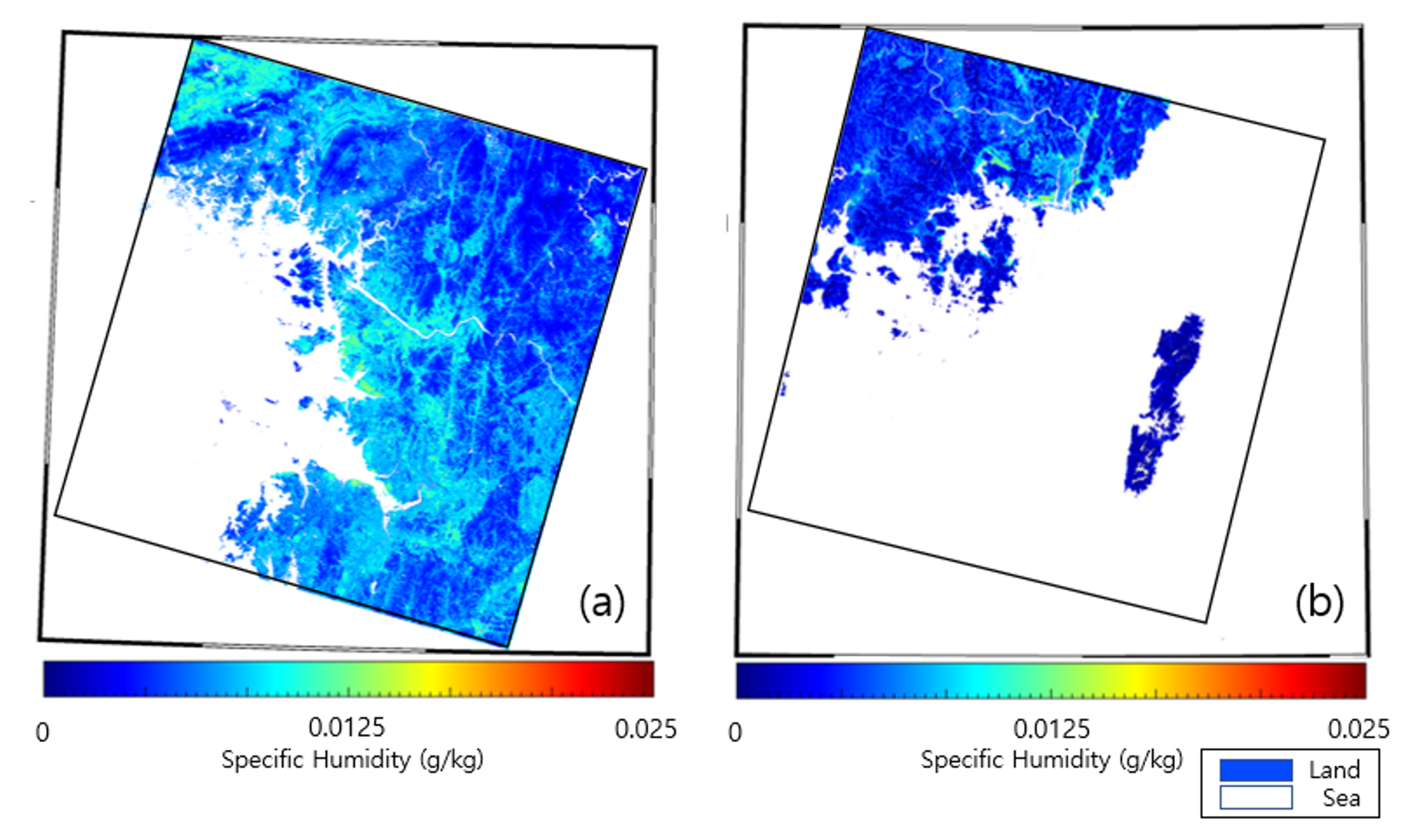
3. Results
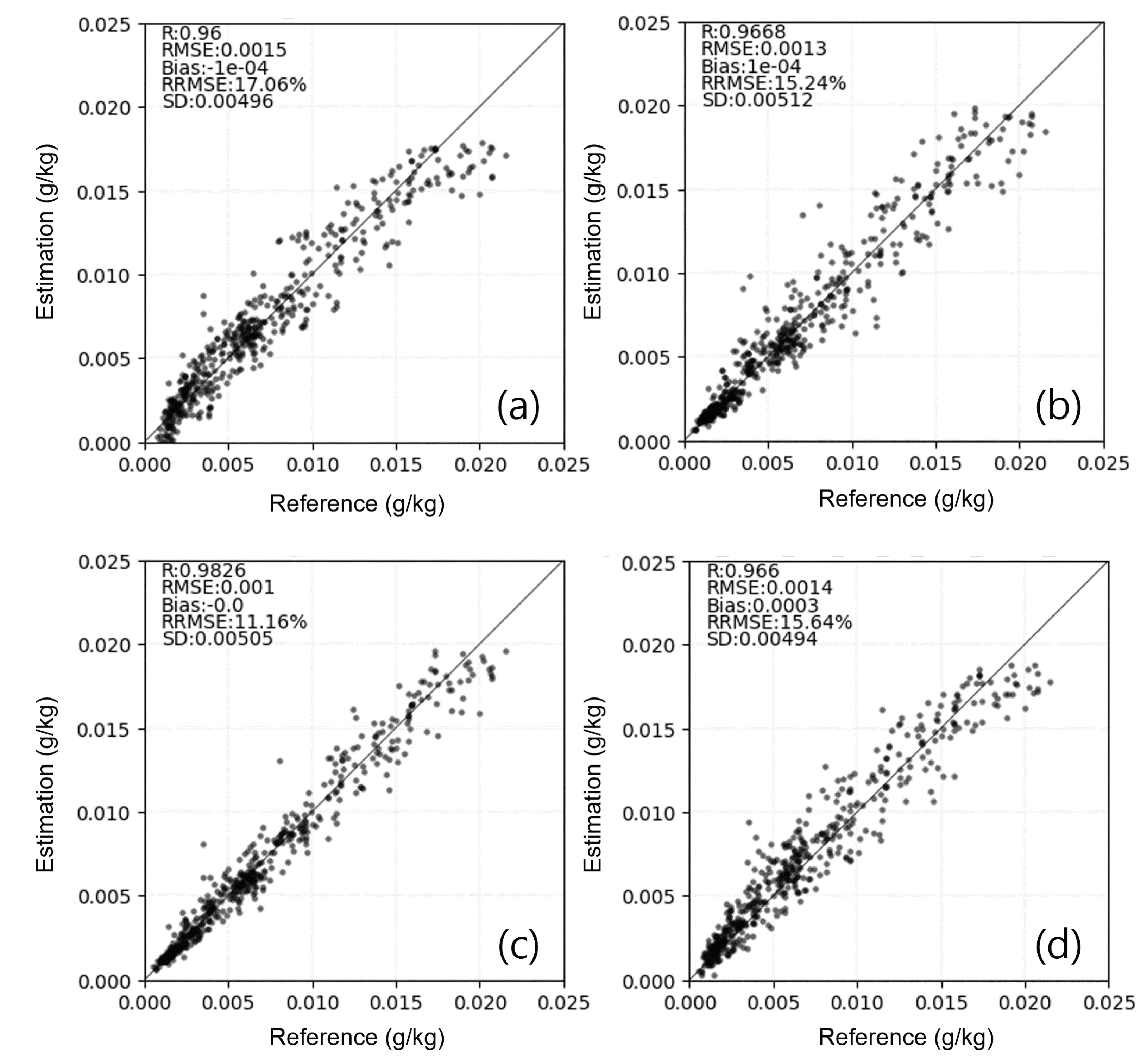
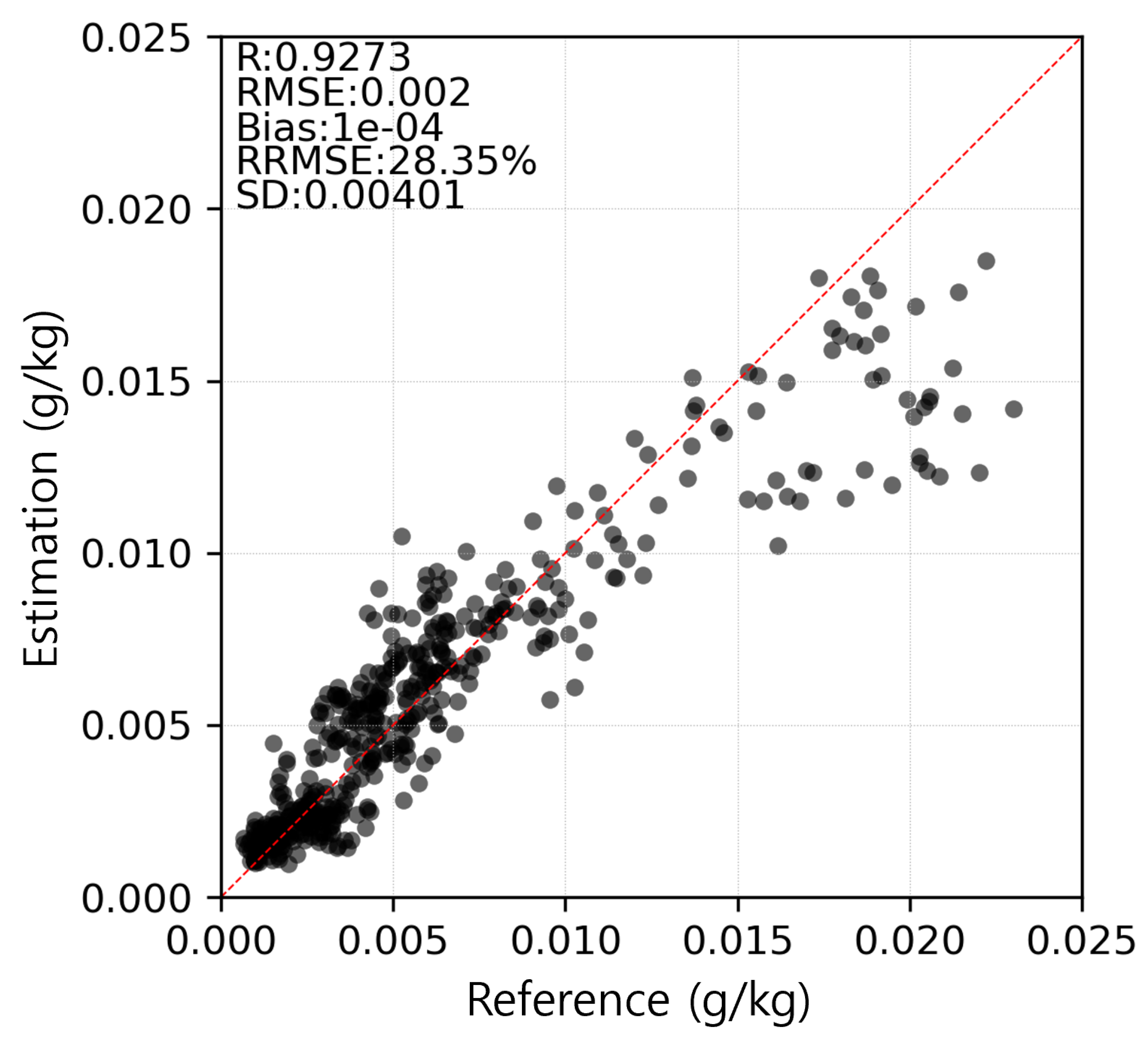
3.1. Model Comparison
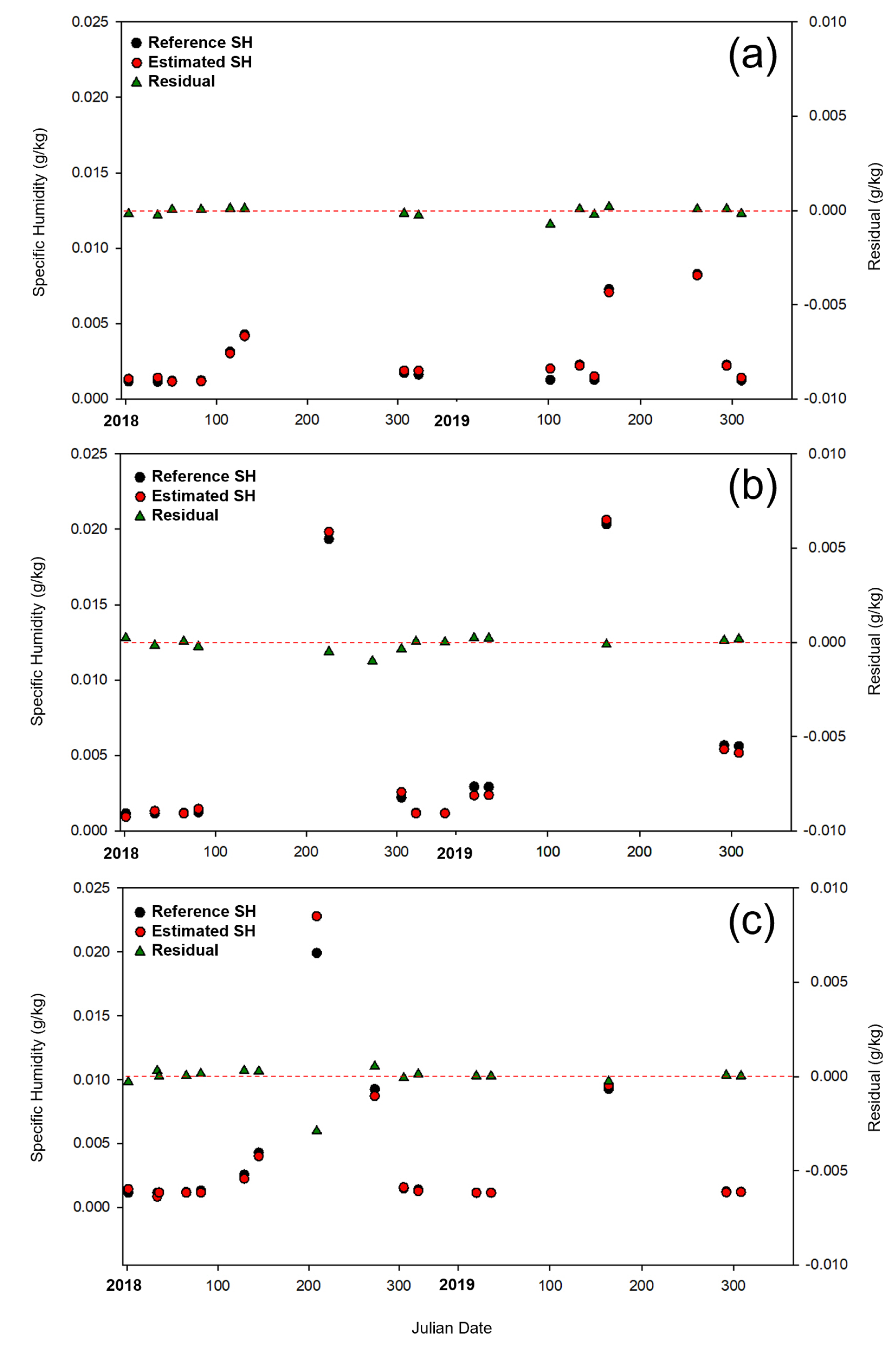
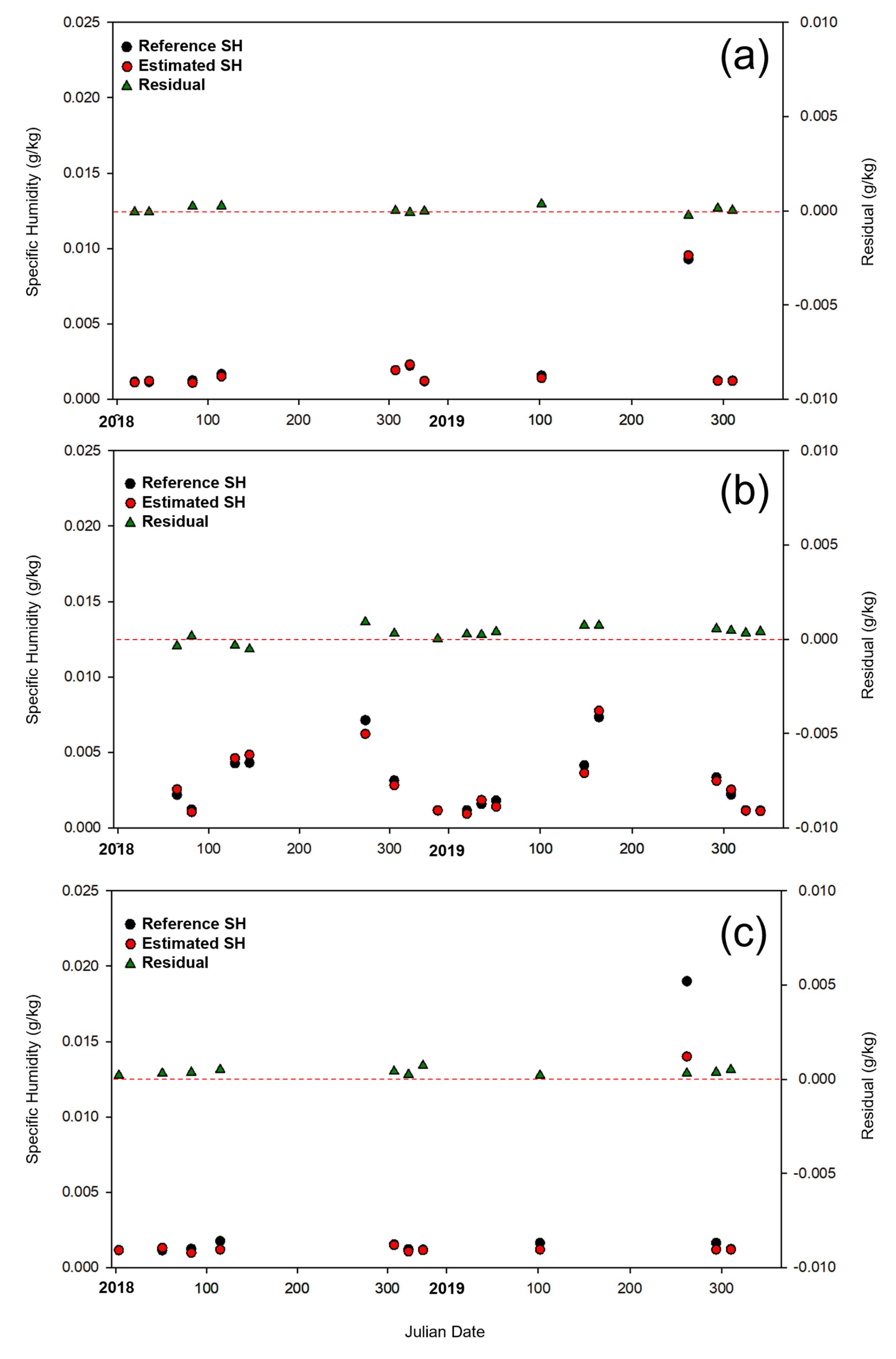
3.2. Model Test Using ASOS Point from 2018 to 2019
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jackson, D.L.; Wick, G.A.; Bates, J.J. Near-surface retrieval of air temperature and specific humidity using multisensor microwave satellite observations. J. Geophys. Res. Atmos. 2006, 111, D10306. [Google Scholar] [CrossRef]
- Ruckstuhl, C.; Philipona, R.; Morland, J.; Ohmura, A. Observed relationship between surface specific humidity, integrated water vapor, and longwave downward radiation at different altitudes. J. Geophys. Res. Atmos. 2007, 112, D03302. [Google Scholar] [CrossRef]
- Wizemann, H.D.; Ingwersen, J.; Högy, P.; Warrach-Sagi, K.; Streck, T.; Wulfmeyer, V. Three year observations of water vapor and energy fluxes over agricultural crops in two regional climates of Southwest Germany. Meteorol. Z. 2015, 24, 39–59. [Google Scholar] [CrossRef]
- Augustine, J.A.; Dutton, E.G. Variability of the surface radiation budget over the United States from 1996 through 2011 from high-quality measurements. J. Geophys. Res. Atmos. 2013, 118, 43–53. [Google Scholar] [CrossRef]
- Hartmann, D.; Ramanathan, V.; Berroir, A.; Hunt, G. Earth radiation budget data and climate research. Rev. Geophys. 1986, 24, 439–468. [Google Scholar] [CrossRef]
- Philipona, R.; Dürr, B.; Ohmura, A.; Ruckstuhl, C. Anthropogenic greenhouse forcing and strong water vapor feedback increase temperature in Europe. Geophys. Res. Lett. 2005, 32, L19809. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Water vapor feedback and global warming. Annu. Rev. Energy Environ. 2000, 25, 441–475. [Google Scholar] [CrossRef]
- Dai, A.; Wang, J.; Ware, R.H.; Van Hove, T. Diurnal variation in water vapor over North America and its implications for sampling errors in radiosonde humidity. J. Geophys. Res. Atmos. 2002, 107, ACL-11-1–ACL-11-14. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The changing character of precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1218. [Google Scholar] [CrossRef]
- Tekin, S.F.; Karaahmetoglu, O.; Ilhan, F.; Balaban, I.; Kozat, S.S. Spatio-temporal weather forecasting and attention mechanism on convolutional lstms. arXiv 2021, arXiv:2102.00696. [Google Scholar]
- Treadon, R.E.; Pan, H.L.; Wu, W.S.; Lin, Y.; Olson, W.S.; Kuligowski, R.J. Global and regional moisture analyses at NCEP. In Proceedings of the ECMWF/GEWEX Workshop on Humidity Analysis, Reading, UK, 8–11 July 2002; pp. 33–47. [Google Scholar]
- Carminati, F.; Migliorini, S.; Ingleby, B.; Bell, W.; Lawrence, H.; Newman, S.; Hocking, J.; Smith, A. Using reference radiosondes to characterise NWP model uncertainty for improved satellite calibration and validation. Atmos. Meas. Tech. 2019, 12, 83–106. [Google Scholar] [CrossRef]
- Jin, X.; Yu, L.; Jackson, D.L.; Wick, G.A. An improved near-surface specific humidity and air temperature climatology for the SSM/I satellite period. J. Atmos. Ocean. Technol. 2015, 32, 412–433. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, S.; Yang, X. Estimation of surface air specific humidity and air–sea latent heat flux using FY-3C microwave observations. Remote Sens. 2019, 11, 466. [Google Scholar] [CrossRef]
- Jackson, D.L.; Wick, G.A.; Robertson, F.R. Improved multisensor approach to satellite-retrieved near-surface specific humidity observations. J. Geophys. Res. Atmos. 2009, 114, D16303. [Google Scholar] [CrossRef]
- Liu, W.T.; Niiler, P.P. Determination of monthly mean humidity in the atmospheric surface layer over oceans from satellite data. J. Phys. Oceanogr. 1984, 14, 1451–1457. [Google Scholar] [CrossRef]
- Liu, W.T. Statistical relation between monthly mean precipitable water and surface-level humidity over global oceans. Mon. Weather Rev. 1986, 114, 1591–1602. [Google Scholar] [CrossRef]
- Schulz, J.; Schluessel, P.; Graßl, H. Water vapour in the atmospheric boundary layer over oceans from SSM/I measurements. Int. J. Remote Sens. 1993, 14, 2773–2789. [Google Scholar] [CrossRef]
- Jeong, J.H.; Ho, C.H. Changes in occurrence of cold surges over East Asia in association with Arctic Oscillation. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Woo, S.H.; Choi, J.; Jeong, J.H. Modulation of ENSO teleconnection on the relationship between arctic oscillation and wintertime temperature variation in South Korea. Atmosphere 2020, 11, 950. [Google Scholar] [CrossRef]
- Bolton, D. The computation of equivalent potential temperature. Mon. Weather Rev. 1980, 108, 1046–1053. [Google Scholar] [CrossRef]
- Choi, S.; Jin, D.; Seong, N.H.; Jung, D.; Sim, S.; Woo, J.; Jeon, U.; Byeon, Y.; Han, K.s. Near-Surface Air Temperature Retrieval Using a Deep Neural Network from Satellite Observations over South Korea. Remote Sens. 2021, 13, 4334. [Google Scholar] [CrossRef]
- Seong, N.H.; Jung, D.; Kim, J.; Han, K.S. Evaluation of NDVI estimation considering atmospheric and BRDF correction through Himawari-8/AHI. Asia-Pac. J. Atmos. Sci. 2020, 56, 265–274. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Ustin, S.L.; Roberts, D.A.; Pinzon, J.; Jacquemoud, S.; Gardner, M.; Scheer, G.; Castaneda, C.M.; Palacios-Orueta, A. Estimating canopy water content of chaparral shrubs using optical methods. Remote Sens. Environ. 1998, 65, 280–291. [Google Scholar] [CrossRef]
- Serrano, L.; Ustin, S.L.; Roberts, D.A.; Gamon, J.A.; Penuelas, J. Deriving water content of chaparral vegetation from AVIRIS data. Remote Sens. Environ. 2000, 74, 570–581. [Google Scholar] [CrossRef]
- Han, K.S.; Viau, A.; Anctil, F. An analysis of GOES and NOAA derived land surface temperatures estimated over a boreal forest. Int. J. Remote Sens. 2004, 25, 4761–4780. [Google Scholar] [CrossRef]
- Prata, A.J. Land surface temperatures derived from the advanced very high resolution radiometer and the along-track scanning radiometer: 1. Theory. J. Geophys. Res. Atmos. 1993, 98, 16689–16702. [Google Scholar] [CrossRef]
- Jebli, I.; Belouadha, F.Z.; Kabbaj, M.I.; Tilioua, A. Prediction of solar energy guided by pearson correlation using machine learning. Energy 2021, 224, 120109. [Google Scholar] [CrossRef]
- Senan, E.M.; Abunadi, I.; Jadhav, M.E.; Fati, S.M. Score and correlation coefficient-based feature selection for predicting heart failure diagnosis by using machine learning algorithms. Comput. Math. Methods Med. 2021, 2021, 8500314. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.Y.L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.W.; Chen, Y.L. Mitigating the multicollinearity problem and its machine learning approach: A review. Mathematics 2022, 10, 1283. [Google Scholar] [CrossRef]
- Sim, S.; Lee, E.; Seo, M.; Seong, N.h.; Jeong, D.; Woo, J.; Han, K.s. Deep neural network-based spatial gap-filling of MODIS ice surface temperatures over the Arctic using satellite and reanalysis data. Remote Sens. Lett. 2022, 13, 1213–1221. [Google Scholar] [CrossRef]
- Tranmer, M.; Elliot, M. Multiple linear regression. Cathie Marsh Cent. Census Surv. Res. (CCSR) 2008, 5, 1–5. [Google Scholar]
- Modaresi, F.; Araghinejad, S.; Ebrahimi, K. A comparative assessment of artificial neural network, generalized regression neural network, least-square support vector regression, and K-nearest neighbor regression for monthly streamflow forecasting in linear and nonlinear conditions. Water Resour. Manag. 2018, 32, 243–258. [Google Scholar] [CrossRef]
- Chirici, G.; Mura, M.; McInerney, D.; Py, N.; Tomppo, E.O.; Waser, L.T.; Travaglini, D.; McRoberts, R.E. A meta-analysis and review of the literature on the k-Nearest Neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 2016, 176, 282–294. [Google Scholar] [CrossRef]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modeling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- He, J.; Li, L.; Xu, J.; Zheng, C. Relu Deep Neurak Networks And Linear Finite Elememts. J. Comput. Math. 2020, 38, 502–527. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Jin, D.; Lee, K.S.; Choi, S.; Seong, N.H.; Jung, D.; Sim, S.; Woo, J.; Jeon, U.; Byeon, Y.; Han, K.S. An improvement of snow/cloud discrimination from machine learning using geostationary satellite data. Int. J. Digit. Earth 2022, 15, 2355–2375. [Google Scholar] [CrossRef]
- Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [PubMed]
- Toparlar, Y.; Blocken, B.; Maiheu, B.; Van Heijst, G. A review on the CFD analysis of urban microclimate. Renew. Sustain. Energy Rev. 2017, 80, 1613–1640. [Google Scholar] [CrossRef]

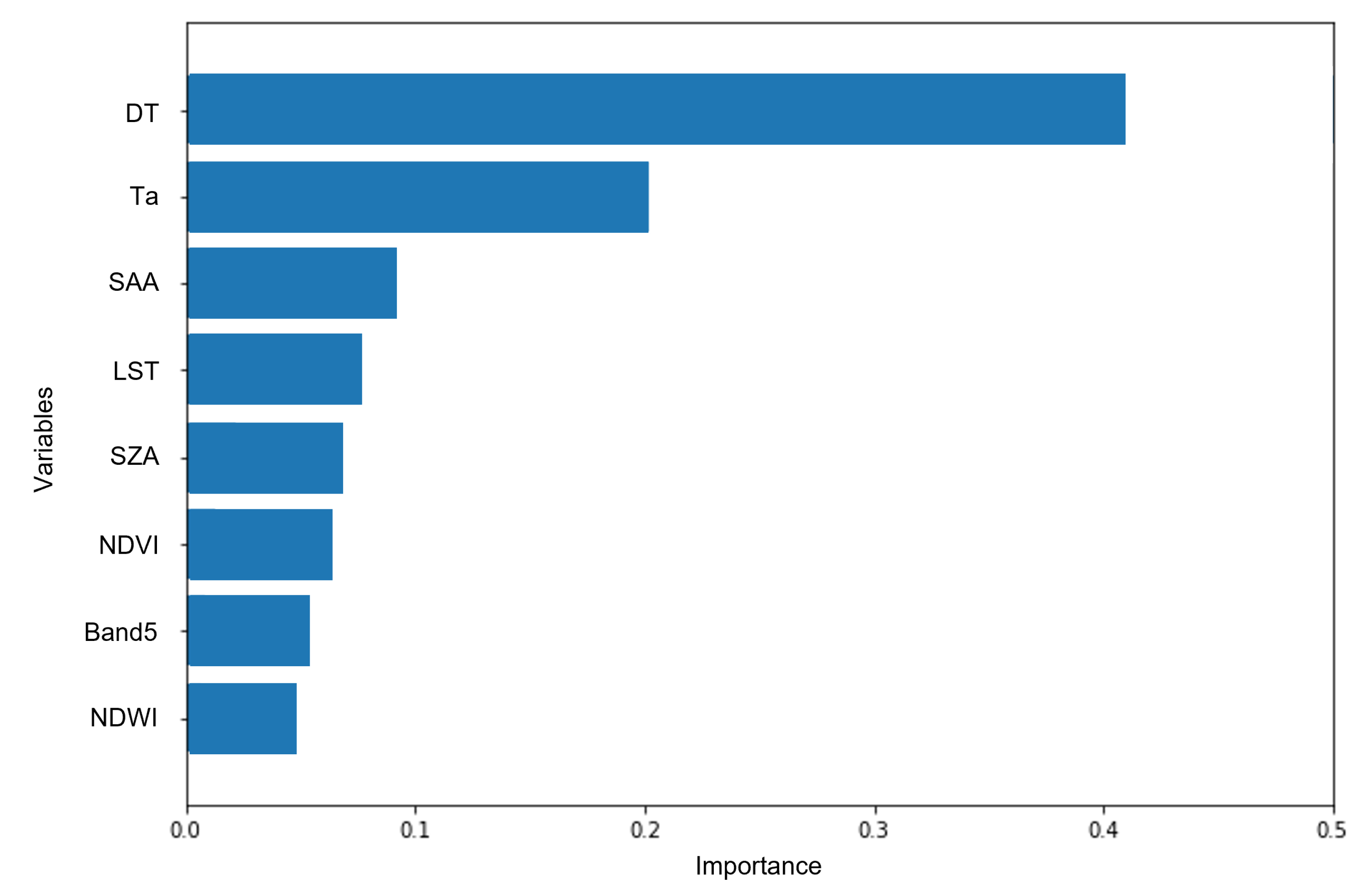
| Variables | R | Selection | Variables | R | Selection |
|---|---|---|---|---|---|
| Band 1 | −0.18 | X | NDWI | 0.613 | O |
| Band 2 | −0.233 | X | SZA | −0.644 | O |
| Band 3 | −0.061 | X | SAA | −0.768 | O |
| Band 4 | −0.39 | X | LST | 0.882 | O |
| Band 5 | 0.621 | O | Ta | 0.914 | O |
| Band 6 | 0.05 | X | DT | 0.976 | O |
| Band 7 | −0.232 | X | Soil Moisture | −0.433 | X |
| NDVI | 0.689 | O | Air Pressure | −0.433 | X |
| Mutiple Linear Regression | K-Nearest Neighbor | Random Forest | Deep Neural Network | |
|---|---|---|---|---|
| R | 0.96 | 0.9668 | 0.9826 | 0.966 |
| RMSE (g/kg) | 0.0015 | 0.0013 | 0.001 | 0.0014 |
| Bias (g/kg) | −0.0001 | 0.0001 | 0 | 0.0003 |
| RRMSE (%) | 17.06 | 15.24 | 11.16 | 15.64 |
| SD (g/kg) | 0.00496 | 0.00512 | 0.00505 | 0.00494 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, S.; Seong, N.-H.; Jung, D.; Sim, S.; Woo, J.; Kim, N.; Park, S.; Han, K.-s. An Ensemble-Based Model for Specific Humidity Retrieval from Landsat-8 Satellite Data for South Korea. Atmosphere 2024, 15, 218. https://doi.org/10.3390/atmos15020218
Choi S, Seong N-H, Jung D, Sim S, Woo J, Kim N, Park S, Han K-s. An Ensemble-Based Model for Specific Humidity Retrieval from Landsat-8 Satellite Data for South Korea. Atmosphere. 2024; 15(2):218. https://doi.org/10.3390/atmos15020218
Chicago/Turabian StyleChoi, Sungwon, Noh-Hun Seong, Daeseong Jung, Suyoung Sim, Jongho Woo, Nayeon Kim, Sungwoo Park, and Kyung-soo Han. 2024. "An Ensemble-Based Model for Specific Humidity Retrieval from Landsat-8 Satellite Data for South Korea" Atmosphere 15, no. 2: 218. https://doi.org/10.3390/atmos15020218
APA StyleChoi, S., Seong, N.-H., Jung, D., Sim, S., Woo, J., Kim, N., Park, S., & Han, K.-s. (2024). An Ensemble-Based Model for Specific Humidity Retrieval from Landsat-8 Satellite Data for South Korea. Atmosphere, 15(2), 218. https://doi.org/10.3390/atmos15020218








