Basin-Scale Daily Drought Prediction Using Convolutional Neural Networks in Fenhe River Basin, China
Abstract
1. Introduction
2. Materials and Methods
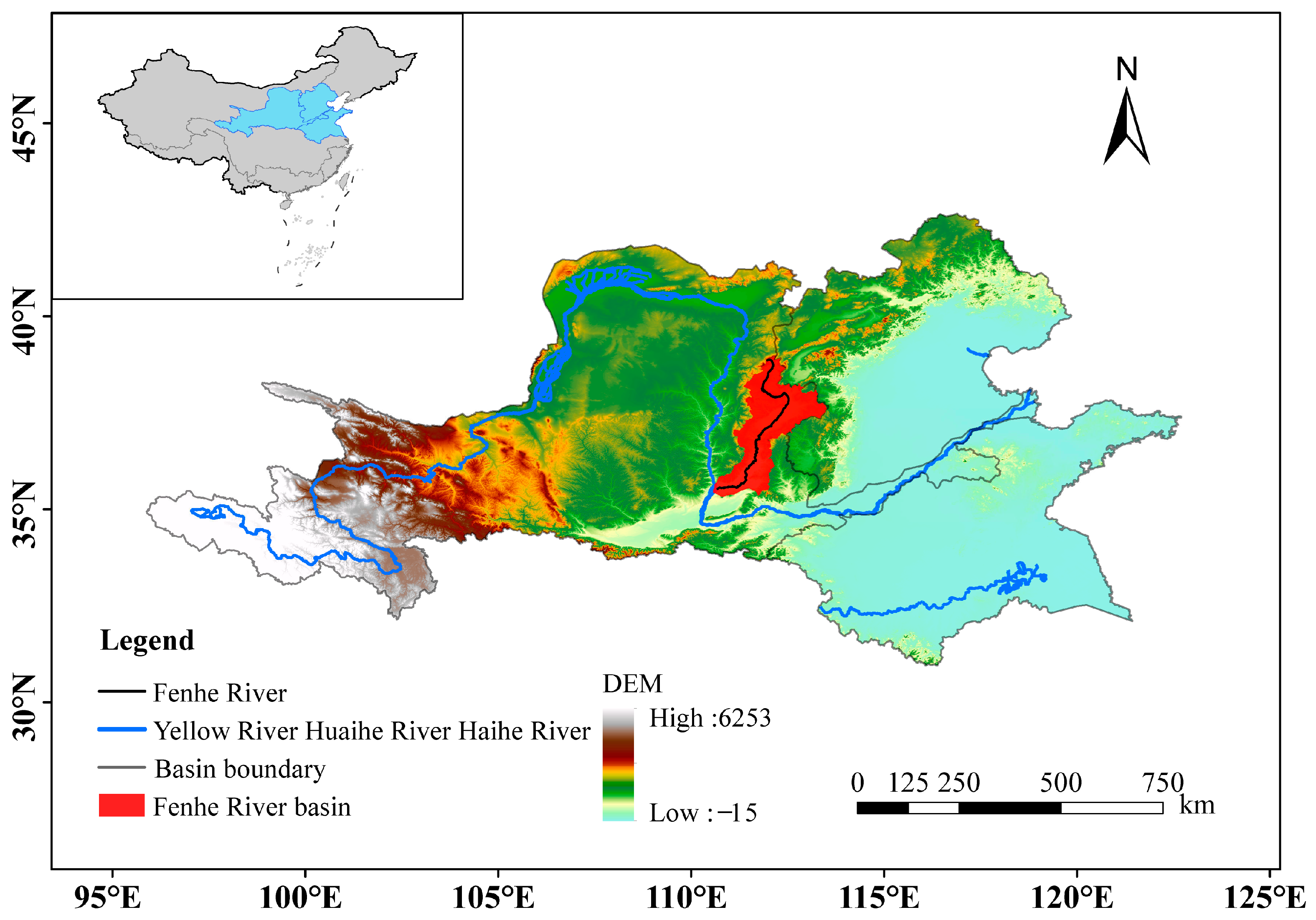
2.1. Study Area
2.2. Datasets
2.3. Methods
2.3.1. SAPEI Calculation
2.3.2. The A_CNN Model
2.3.3. Evaluation Metrics
3. Results
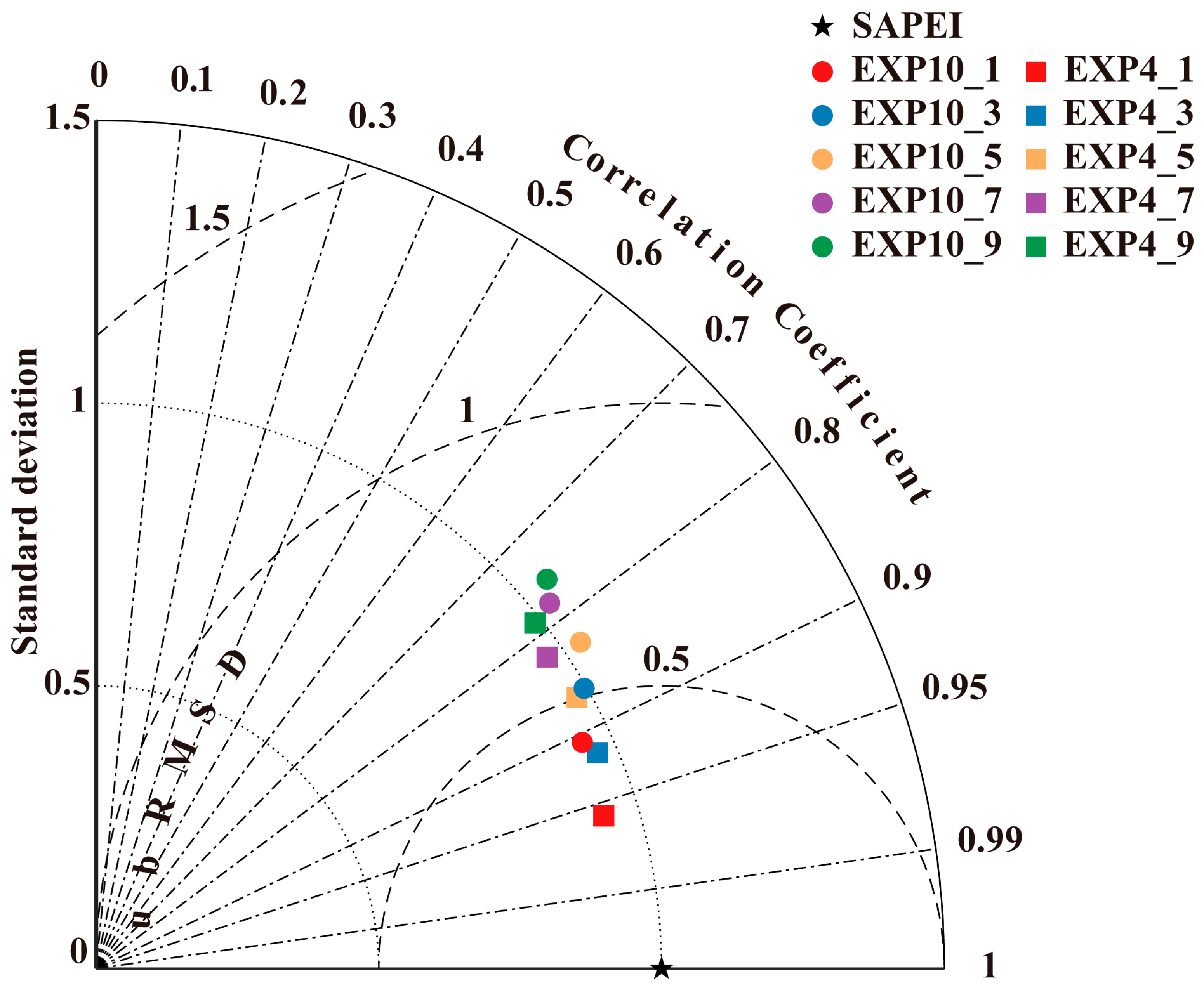
3.1. Identifying Key Variables to Enhance Prediction Accuracy
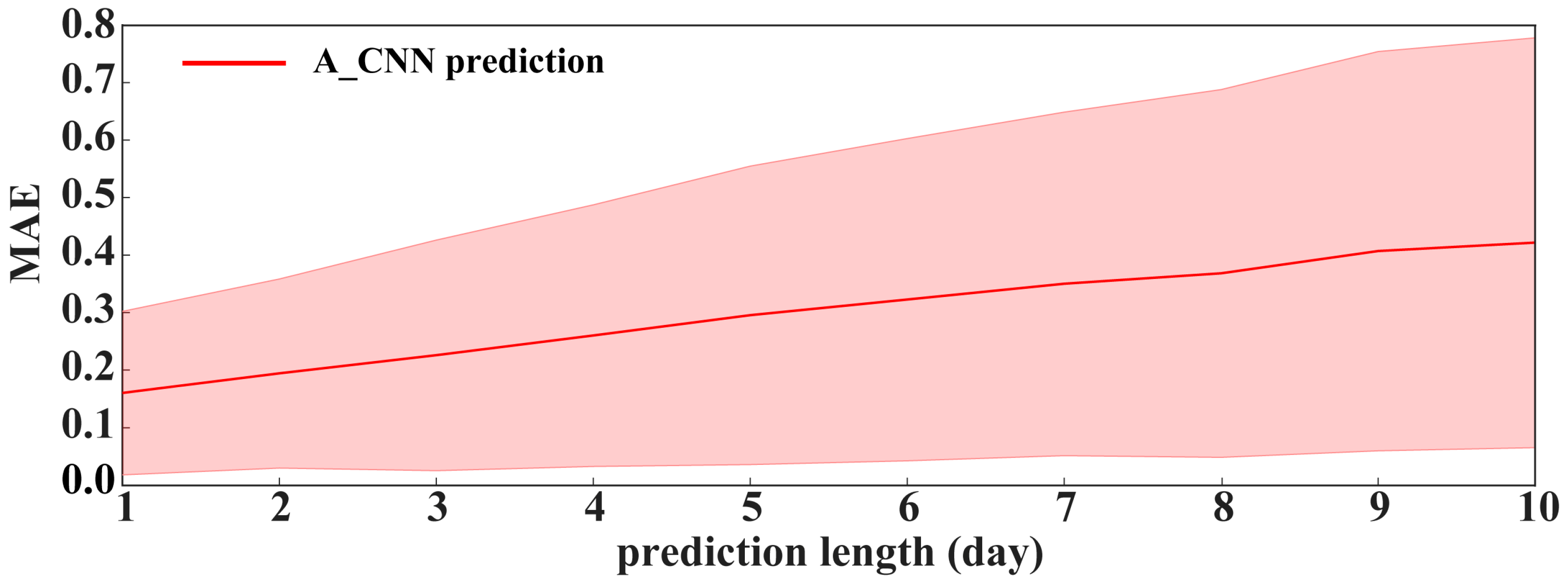
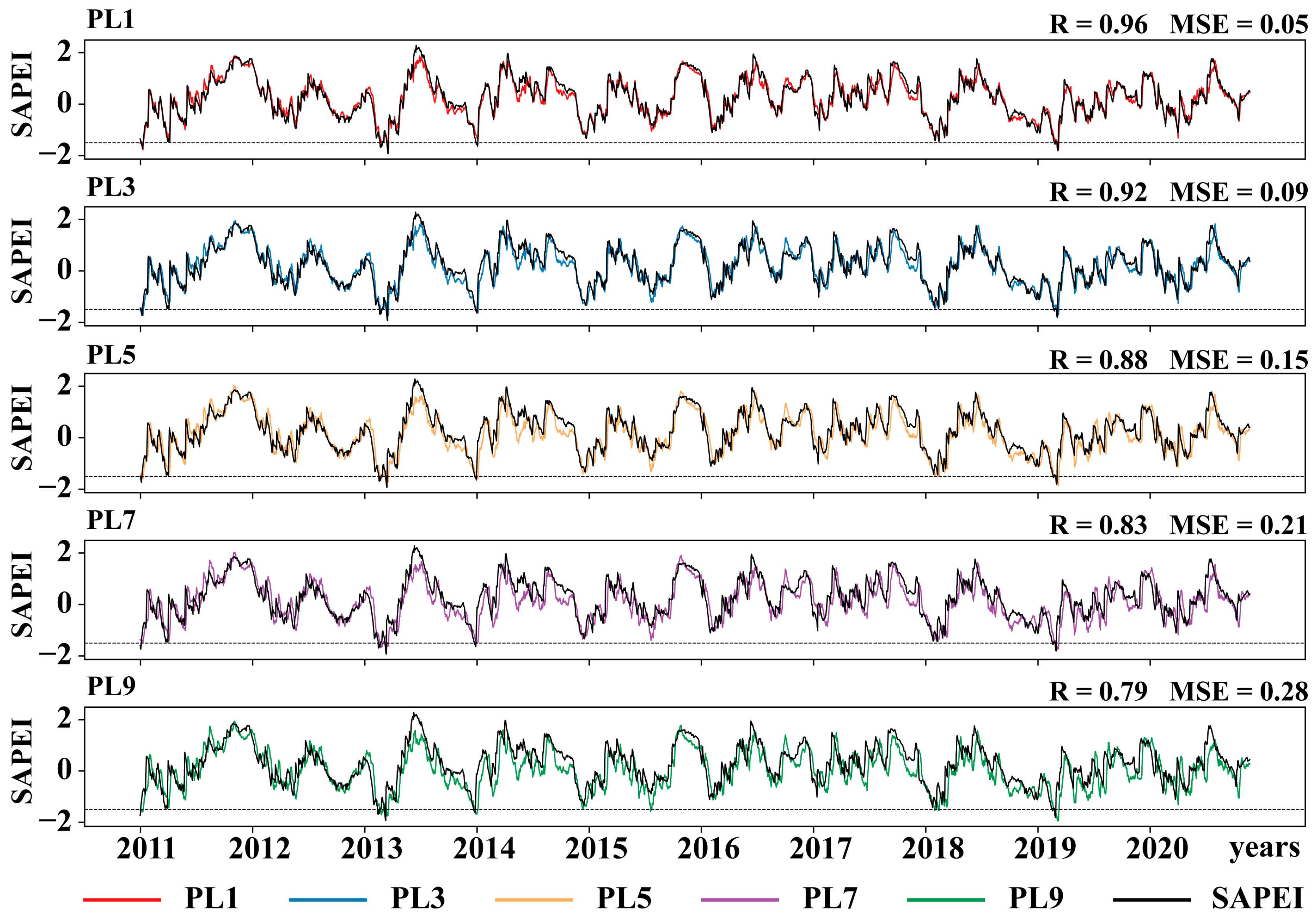
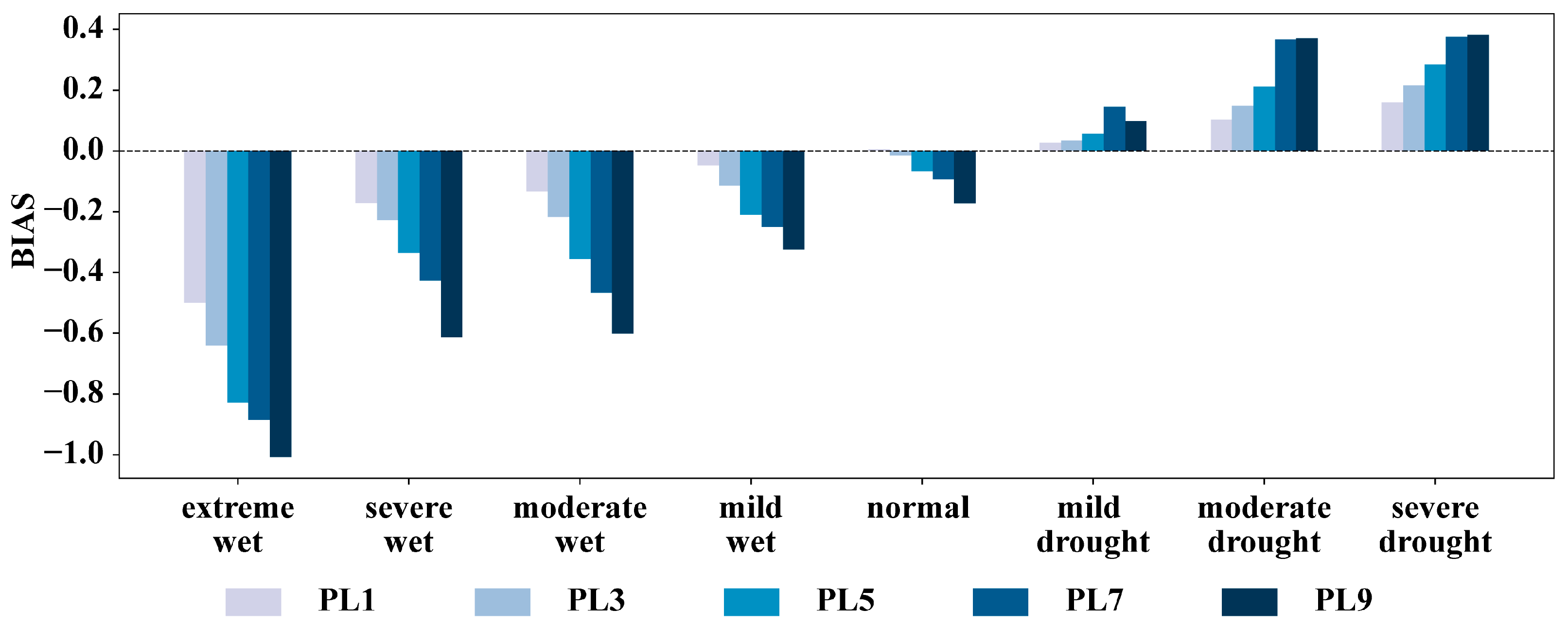
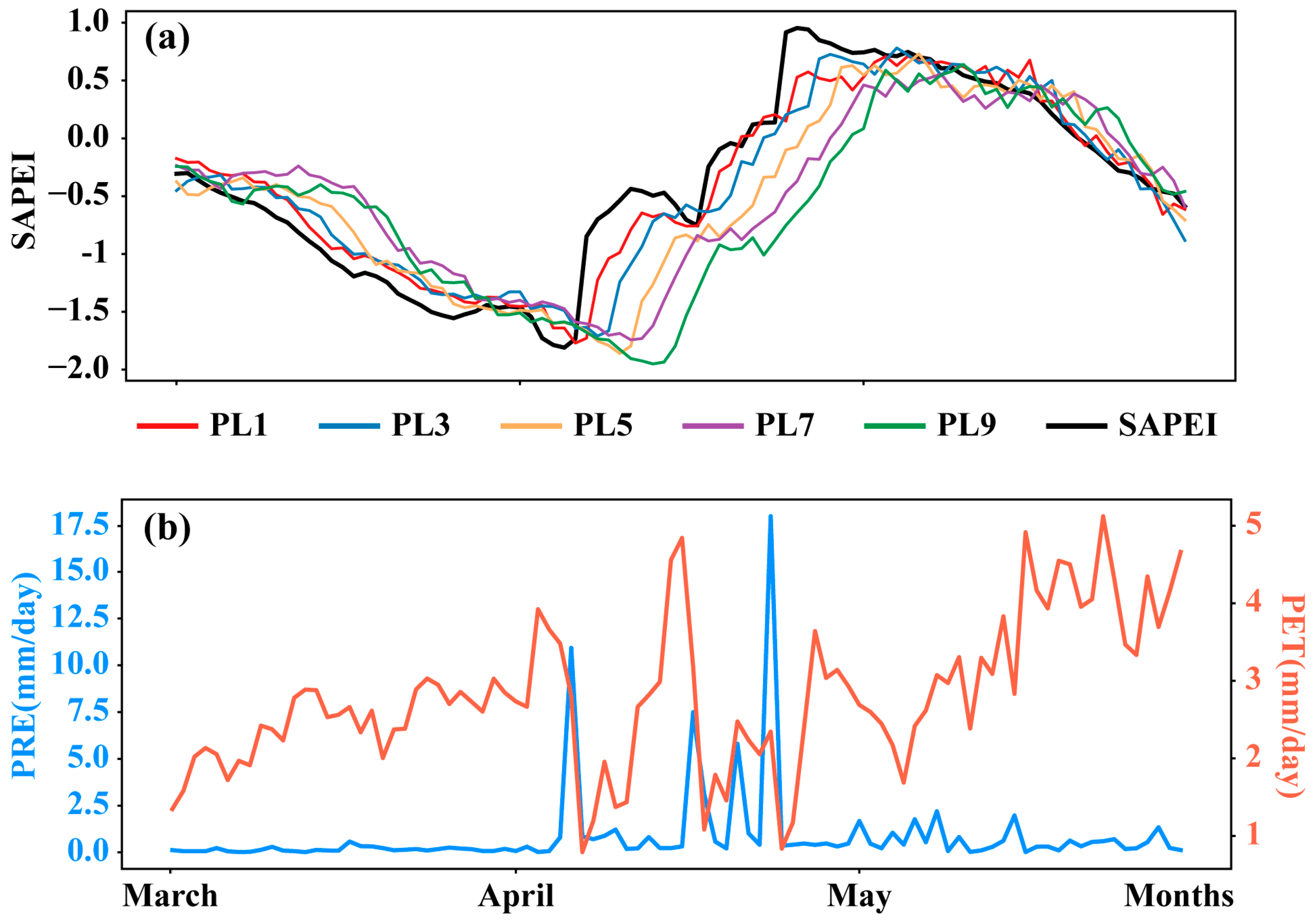
3.2. Predicting Severe Drought
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dikshit, A.; Pradhan, B.; Huete, A.; Park, H.-J. Spatial based drought assessment: Where are we heading? A review on the current status and future. Sci. Total Environ. 2022, 844, 157239. [Google Scholar] [CrossRef] [PubMed]
- Shi, H.; Zhou, Z.; Liu, L.; Liu, S. A global perspective on propagation from meteorological drought to hydrological drought during 1902–2014. Atmos. Res. 2022, 280, 106441. [Google Scholar] [CrossRef]
- Jehanzaib, M.; Yoo, J.; Kwon, H.-H.; Kim, T.-W. Reassessing the frequency and severity of meteorological drought considering non-stationarity and copula-based bivariate probability. J. Hydrol. 2021, 603, 126948. [Google Scholar] [CrossRef]
- Gavahi, K.; Abbaszadeh, P.; Moradkhani, H. How does precipitation data influence the land surface data assimilation for drought monitoring? Sci. Total Environ. 2022, 831, 154916. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chen, J.; Gu, L.; Wu, G.; Tong, S.; Xiong, L.; Xu, C.-Y. A pathway analysis method for quantifying the contributions of precipitation and potential evapotranspiration anomalies to soil moisture drought. J. Hydrol. 2023, 621, 129570. [Google Scholar] [CrossRef]
- Han, L.; Zhang, Q.; Zhang, Z.; Jia, J.; Wang, Y.; Huang, T.; Cheng, Y. Drought area, intensity and frequency changes in China under climate warming, 1961–2014. J. Arid Environ. 2021, 193, 104596. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, X.; Cheng, X.; Gun, Z.; Lin, J.; Zhao, J.; Yao, L.; Zhou, C. Drought assessment of China in 2002–2017 based on a comprehensive drought index. Agric. For. Meteorol. 2022, 319, 108922. [Google Scholar] [CrossRef]
- Su, B.; Huang, J.; Fischer, T.; Wang, Y.; Kundzewicz, Z.W.; Zhai, J.; Sun, H.; Wang, A.; Zeng, X.; Wang, G. Drought losses in China might double between the 1.5 C and 2.0 C warming. Proc. Natl. Acad. Sci. USA 2018, 115, 10600–10605. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Lai, C.; Zeng, Z.; Zhong, R.; Chen, X.; Zhou, X.; Wang, M. Does drought in China show a significant decreasing trend from 1961 to 2009? Sci. Total Environ. 2017, 579, 314–324. [Google Scholar] [CrossRef]
- Shi, X.; Ding, H.; Wu, M.; Zhang, N.; Shi, M.; Chen, F.; Li, Y. Effects of different types of drought on vegetation in Huang-Huai-Hai River Basin, China. Ecol. Indic. 2022, 144, 109428. [Google Scholar] [CrossRef]
- Zhan, C.; Liang, C.; Zhao, L.; Jiang, S.; Niu, K.; Zhang, Y. Drought-related cumulative and time-lag effects on vegetation dynamics across the Yellow River Basin, China. Ecol. Indic. 2022, 143, 109409. [Google Scholar] [CrossRef]
- Zhang, X.; Duan, Y.; Duan, J.; Chen, L.; Jian, D.; Lv, M.; Yang, Q.; Ma, Z. A daily drought index-based regional drought forecasting using the Global Forecast System model outputs over China. Atmos. Res. 2022, 273, 106166. [Google Scholar] [CrossRef]
- Balti, H.; Abbes, A.B.; Mellouli, N.; Farah, I.R.; Sang, Y.; Lamolle, M. A review of drought monitoring with big data: Issues, methods, challenges and research directions. Ecol. Inf. 2020, 60, 101136. [Google Scholar] [CrossRef]
- Durdu, Ö.F. Application of linear stochastic models for drought forecasting in the Büyük Menderes river basin, western Turkey. Stoch. Environ. Res. Risk Assess. 2010, 24, 1145–1162. [Google Scholar] [CrossRef]
- Li, H.; Sun, B.; Wang, H.; Zhou, B.; Duan, M. Mechanisms and physical-empirical prediction model of concurrent heatwaves and droughts in July–August over northeastern China. J. Hydrol. 2022, 614, 128535. [Google Scholar] [CrossRef]
- Prodhan, F.A.; Zhang, J.; Hasan, S.S.; Sharma, T.P.P.; Mohana, H.P. A review of machine learning methods for drought hazard monitoring and forecasting: Current research trends, challenges, and future research directions. Environ. Model. Softw. 2022, 149, 105327. [Google Scholar] [CrossRef]
- Feng, P.; Wang, B.; Li Liu, D.; Yu, Q. Machine learning-based integration of remotely-sensed drought factors can improve the estimation of agricultural drought in South-Eastern Australia. Agric. Syst. 2019, 173, 303–316. [Google Scholar] [CrossRef]
- Nie, H.; Yang, L.; Li, X.; Ren, L.; Xu, J.; Feng, Y. Spatial prediction of soil moisture content in winter wheat based on machine learning model. In Proceedings of the 2018 26th International Conference on Geoinformatics, Kunming, China, 28–30 June 2018; pp. 1–6. [Google Scholar]
- Dikshit, A.; Pradhan, B.; Santosh, M. Artificial neural networks in drought prediction in the 21st century–A scientometric analysis. Appl. Soft Comput. 2022, 114, 108080. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–artificial intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Coşkun, Ö.; Citakoglu, H. Prediction of the standardized precipitation index based on the long short-term memory and empirical mode decomposition-extreme learning machine models: The Case of Sakarya, Türkiye. Phys. Chem. Earth Parts A/B/C 2023, 131, 103418. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, Q.; Yu, T.; Xiang, S.; Kuang, Q.; Prinet, V.; Pan, C. Multi-modal spatio-temporal meteorological forecasting with deep neural network. ISPRS J. Photogramm. Remote Sens. 2022, 188, 380–393. [Google Scholar] [CrossRef]
- Agana, N.A.; Homaifar, A. A deep learning based approach for long-term drought prediction. In Proceedings of the SoutheastCon 2017, Concord (Charlotte), NC, USA, 30 March–2 April 2017; pp. 1–8. [Google Scholar]
- Mokhtar, A.; Jalali, M.; He, H.; Al-Ansari, N.; Elbeltagi, A.; Alsafadi, K.; Abdo, H.G.; Sammen, S.S.; Gyasi-Agyei, Y.; Rodrigo-Comino, J. Estimation of SPEI meteorological drought using machine learning algorithms. IEEE Access 2021, 9, 65503–65523. [Google Scholar] [CrossRef]
- Mei, P.; Liu, J.; Liu, C.; Liu, J. A deep learning model and its application to predict the monthly MCI drought index in the Yunnan Province of China. Atmosphere 2022, 13, 1951. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, H.; Zhang, T.; Xu, H.; Wu, D.; Gao, J. Evaluating established deep learning methods in constructing integrated remote sensing drought index: A case study in China. Agric. Water Manag. 2023, 286, 108405. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Brubaker, K.L. Characterization of the global hydrologic cycle from a back-trajectory analysis of atmospheric water vapor. J. Hydrometeorol. 2007, 8, 20–37. [Google Scholar] [CrossRef]
- Wei, J.; Dirmeyer, P.A. Sensitivity of land precipitation to surface evapotranspiration: A nonlocal perspective based on water vapor transport. Geophys. Res. Lett. 2019, 46, 12588–12597. [Google Scholar] [CrossRef]
- Ham, Y.-G.; Kim, J.-H.; Luo, J.-J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Ham, Y.-G.; Kim, J.-H.; Kim, E.-S.; On, K.-W. Unified deep learning model for El Niño/Southern Oscillation forecasts by incorporating seasonality in climate data. Sci. Bull. 2021, 66, 1358–1366. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Drought characterization from a multivariate perspective: A review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; Volume 30.
- Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating Palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W. Applicability analysis of standardized precipitation evapotranspiration index in drought monitoring in China. Plateau Meteorol. 2014, 33, 423–431. [Google Scholar]
- Yuan, X.; Wang, Y.; Ji, P.; Wu, P.; Sheffield, J.; Otkin, J.A. A global transition to flash droughts under climate change. Science 2023, 380, 187–191. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Wu, X.; Xu, C.-Y.; Guo, S.; Chen, X. Toward monitoring short-term droughts using a novel daily scale, standardized antecedent precipitation evapotranspiration index. J. Hydrometeorol. 2020, 21, 891–908. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal drought prediction: Advances, challenges, and future prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- Park, S.; Seo, E.; Kang, D.; Im, J.; Lee, M.-I. Prediction of drought on pentad scale using remote sensing data and MJO index through random forest over East Asia. Remote Sens. 2018, 10, 1811. [Google Scholar] [CrossRef]
- Wu, B.; Yang, S.; Shao, N.; Peng, R.; Guan, Y. Effects of land use change on ecosystem service value in fragile ecological area of the Loess Plateau a case study of Fenhe River Basin. Soil Water Conserv. 2019, 26, 340–345. [Google Scholar]
- Yan, D.; Wu, D.; Huang, R.; Wang, L.; Yang, G. Drought evolution characteristics and precipitation intensity changes during alternating dry–wet changes in the Huang–Huai–Hai River basin. Hydrol. Earth Syst. Sci. 2013, 17, 2859–2871. [Google Scholar] [CrossRef]
- Yuan, Y.; Yan, D.; Yuan, Z.; Yin, J.; Zhao, Z. Spatial distribution of precipitation in huang-huai-Hai River basin between 1961 to 2016, China. Int. J. Environ. Res. Public Health 2019, 16, 3404. [Google Scholar] [CrossRef]
- Hu, W.; She, D.; Xia, J.; He, B.; Hu, C. Dominant patterns of dryness/wetness variability in the Huang-Huai-Hai River Basin and its relationship with multiscale climate oscillations. Atmos. Res. 2021, 247, 105148. [Google Scholar] [CrossRef]
- Deng, Y.; Wu, D.; Wang, X.; Xie, Z. Responding time scales of vegetation production to extreme droughts over China. Ecol. Indic. 2022, 136, 108630. [Google Scholar] [CrossRef]
- Li, C.; Kattel, G.R.; Zhang, J.; Shang, Y.; Gnyawali, K.R.; Zhang, F.; Miao, L. Slightly enhanced drought in the Yellow River Basin under future warming scenarios. Atmos. Res. 2022, 280, 106423. [Google Scholar] [CrossRef]
- Wu, J.; Gao, X.-J. A gridded daily observation dataset over China region and comparison with the other datasets. Chin. J. Geophys. 2013, 56, 1102–1111. [Google Scholar]
- Yuan, W.; Zheng, Y.; Piao, S.; Ciais, P.; Lombardozzi, D.; Wang, Y.; Ryu, Y.; Chen, G.; Dong, W.; Hu, Z. Increased atmospheric vapor pressure deficit reduces global vegetation growth. Sci. Adv. 2019, 5, eaax1396. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Heggen, R.J. Normalized antecedent precipitation index. J. Hydrol. Eng. 2001, 6, 377–381. [Google Scholar] [CrossRef]
- Chen, J.; Yu, W.; Liu, R.; Yue, W.; Chen, X. Daily standardized antecedent precipitation evapotranspiration index (SAPEI) and its adaptability in Anhui Province. Chin. J. Eco-Agric. 2019, 27, 919–928. [Google Scholar]
- Miah, M.G.; Abdullah, H.M.; Jeong, C. Exploring standardized precipitation evapotranspiration index for drought assessment in Bangladesh. Environ. Monit. Assess. 2017, 189, 547. [Google Scholar] [CrossRef]
- Ma, T.; Liang, Y.; Lau, M.K.; Liu, B.; Wu, M.M.; He, H.S. Quantifying the relative importance of potential evapotranspiration and timescale selection in assessing extreme drought frequency in conterminous China. Atmos. Res. 2021, 263, 105797. [Google Scholar] [CrossRef]
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global warming and 21st century drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef]
- Oogathoo, S.; Houle, D.; Duchesne, L.; Kneeshaw, D. Vapour pressure deficit and solar radiation are the major drivers of transpiration of balsam fir and black spruce tree species in humid boreal regions, even during a short-term drought. Agric. For. Meteorol. 2020, 291, 108063. [Google Scholar] [CrossRef]
- Li, M.; Yao, J.; Guan, J.; Zheng, J. Observed changes in vapor pressure deficit suggest a systematic drying of the atmosphere in Xinjiang of China. Atmos. Res. 2021, 248, 105199. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Jayasinghe, W.L.P.; Deo, R.C.; Ghahramani, A.; Ghimire, S.; Raj, N. Development and evaluation of hybrid deep learning long short-term memory network model for pan evaporation estimation trained with satellite and ground-based data. J. Hydrol. 2022, 607, 127534. [Google Scholar] [CrossRef]
- Ayris, D.; Imtiaz, M.; Horbury, K.; Williams, B.; Blackney, M.; See, C.S.H.; Shah, S.A.A. Novel deep learning approach to model and predict the spread of COVID-19. Intell. Syst. Appl. 2022, 14, 200068. [Google Scholar] [CrossRef]
- Dai, R.; Wang, W.; Zhang, R.; Yu, L. Multimodal deep learning water level forecasting model for multiscale drought alert in Feiyun River basin. Expert Syst. Appl. 2023, 244, 122951. [Google Scholar] [CrossRef]
- Abdulla, N.; Demirci, M.; Ozdemir, S. Design and evaluation of adaptive deep learning models for weather forecasting. Eng. Appl. Artif. Intell. 2022, 116, 105440. [Google Scholar] [CrossRef]
- Ren, X.; Li, X.; Ren, K.; Song, J.; Xu, Z.; Deng, K.; Wang, X. Deep learning-based weather prediction: A survey. Big Data Res. 2021, 23, 100178. [Google Scholar] [CrossRef]
- Hu, J.; Yang, Z.; Hou, C.; Ouyang, W. Compound risk dynamics of drought by extreme precipitation and temperature events in a semi-arid watershed. Atmos. Res. 2023, 281, 106474. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B. Interpretable and explainable AI (XAI) model for spatial drought prediction. Sci. Total Environ. 2021, 801, 149797. [Google Scholar] [CrossRef]
- Otkin, J.A.; Woloszyn, M.; Wang, H.; Svoboda, M.; Skumanich, M.; Pulwarty, R.; Lisonbee, J.; Hoell, A.; Hobbins, M.; Haigh, T. Getting ahead of flash drought: From early warning to early action. Bull. Am. Meteorol. Soc. 2022, 103, E2188–E2202. [Google Scholar] [CrossRef]
- Ndiritu, S.W. Drought responses and adaptation strategies to climate change by pastoralists in the semi-arid area, Laikipia County, Kenya. Mitig. Adapt. Strategies Glob. Chang. 2021, 26, 10. [Google Scholar] [CrossRef]

| Variables | Unit |
|---|---|
| precipitation (PRE) | mm |
| relative humidity | -- |
| wind velocity | m/s |
| mean temperature | °C |
| max temperature | °C |
| min temperature | °C |
| sunshine duration | h |
| potential evapotranspiration (PET) | mm |
| vapor pressure deficit (VPD) | kPa |
| SAPEI | -- |
| Threshold Value of SAPEI | Grade Name | Cumulative Probability (%) |
|---|---|---|
| SAPEI > 2.0 | Extremely wet | 0.64 |
| 1.5 < SAPEI ≤ 2.0 | Severe wet | 5.61 |
| 1.0 < SAPEI ≤ 1.5 | Moderate wet | 11.50 |
| 0.5 < SAPEI ≤ 1.0 | Mild wet | 20.50 |
| −0.5 < SAPEI ≤ 0.5 | Normal | 45.03 |
| −1.0 < SAPEI ≤ −0.5 | Mild drought | 11.81 |
| −1.5 < SAPEI ≤ −1.0 | Moderate drought | 4.13 |
| −2.0 < SAPEI ≤ −1.5 | Severe drought | 0.78 |
| SAPEI ≤ −2.0 | Extremely drought | 0 |
| Layer | Output Shape |
|---|---|
| input layer | 56 × 28 × 120 |
| convolutional layer1 | 56 × 28 × 10 |
| max pool | 28 × 14 × 10 |
| convolutional layer2 | 28 × 14 × 10 |
| max pool | 14 × 7 × 10 |
| convolutional layer3 | 14 × 7 × 10 |
| dense1 | 50 |
| dense2 | 50 |
| output layer | 10 |
| PL1 | PL3 | PL5 | PL7 | PL9 | ||
|---|---|---|---|---|---|---|
| EXP7 | MSE | 0.413 | 0.498 | 0.503 | 0.703 | 0.648 |
| R | 0.695 | 0.693 | 0.673 | 0.631 | 0.588 | |
| EXP10 | MSE | 0.100 | 0.193 | 0.273 | 0.310 | 0.411 |
| R | 0.926 | 0.883 | 0.838 | 0.795 | 0.740 | |
| Prediction Length | NSE | KGE | MSE | R |
|---|---|---|---|---|
| PL1 | 0.922 | 0.875 | 0.046 | 0.961 |
| PL3 | 0.845 | 0.757 | 0.091 | 0.923 |
| PL5 | 0.736 | 0.522 | 0.154 | 0.877 |
| PL7 | 0.637 | 0.438 | 0.212 | 0.830 |
| PL9 | 0.508 | 0.122 | 0.286 | 0.793 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Wang, G.; Wei, X.; Liu, Y.; Duan, Z.; Hu, Y.; Jiang, H. Basin-Scale Daily Drought Prediction Using Convolutional Neural Networks in Fenhe River Basin, China. Atmosphere 2024, 15, 155. https://doi.org/10.3390/atmos15020155
Chen Z, Wang G, Wei X, Liu Y, Duan Z, Hu Y, Jiang H. Basin-Scale Daily Drought Prediction Using Convolutional Neural Networks in Fenhe River Basin, China. Atmosphere. 2024; 15(2):155. https://doi.org/10.3390/atmos15020155
Chicago/Turabian StyleChen, Zixuan, Guojie Wang, Xikun Wei, Yi Liu, Zheng Duan, Yifan Hu, and Huiyan Jiang. 2024. "Basin-Scale Daily Drought Prediction Using Convolutional Neural Networks in Fenhe River Basin, China" Atmosphere 15, no. 2: 155. https://doi.org/10.3390/atmos15020155
APA StyleChen, Z., Wang, G., Wei, X., Liu, Y., Duan, Z., Hu, Y., & Jiang, H. (2024). Basin-Scale Daily Drought Prediction Using Convolutional Neural Networks in Fenhe River Basin, China. Atmosphere, 15(2), 155. https://doi.org/10.3390/atmos15020155







