Abstract
North East Monsoon (NEM) is the major source of rainfall for the south-eastern parts of peninsular India. Short time rainfall prediction data (i.e., nowcasting) are based on the observations from Doppler weather radars which has a high spatial and temporal resolution. This study focuses on the short-term ensemble prediction system using weather radar data to predict precipitation during the NEM and is the first of its kind in the Indian region to make an assessment of the operational performance of the prediction system. Six rainfall events have been studied for the assessment of short-term prediction system where the precipitation systems are different and include a tropical storm observed over different days during the 2022 NEM season. To assess the performance of the system, Fractional Skill Scores (FSS) at a 1 km window have been computed for a lead time of 0–2 h for all the rainfall events with more than 750 samples using different optical flow methods and ensemble sizes. The best average skill score and maximum skill score obtained at a 2 h lead time is 0.65 and 0.78 for tropical storms, 0.5 and 0.78 for stratiform and 0.15 and 0.38 for convective precipitation. It has found that the performance of the model is best for precipitation systems that are widespread and have a longer life period.
1. Introduction
Water impacts human life, either by its volumetric abundance or lack of it. Water-related natural disasters are caused by extreme precipitation events, that have increased in frequency due to climate change. During these disasters, the loss of lives as well as property is significant and meteorological agencies have increased the focus on early warnings to avert the same [1,2]. Early warnings for precipitation events are a challenge due to their high spatial and temporal variability while intense precipitation at small temporal and spatial scales can lead to flash floods [3]. Hence, a high resolution forecast of precipitation is required to ensure an adequate and timely response through early warning systems [4]. Precipitation forecasts are generally based on numerical weather prediction (NWP) models where the World Meteorological Organization defines that the forecasts issued for a shorter duration of 0–3 h are called nowcasts and those for 12–72 h are called short range forecasts. Although there is continuous improvement in the reliability of these forecasts, the NWP models are computationally intensive and have a coarser resolution and the update frequency of the models is also not high enough to capture the rapidly changing precipitation parameters. As there is a time difference between initialization of the model to the final warning dissemination based on the model output to the end user, the timing and location of the rainfall are missed. In the case of extrapolation-based models that have less computational requirements and use recent observational data to perform nowcasts, the nowcasts can be generated at a higher frequency. It is observed that extrapolation-based nowcasts outperform NWP-based nowcasts for short time durations such as 0–3 h [5,6]. There are various extrapolation-based nowcasting algorithms available which can be categorized as follows: (a) cloud tracking methods that track individual rainfall cells [7,8], (b) analogue methods which predict the rainfall based on the climatological data sets of precipitation events [9,10], (c) field-based nowcast algorithms where the motion of the observed rainfall fields are advected [11,12] and (d) methods where stochastic noise is introduced to the fields to simulate the evolution of rainfall fields [13,14].
Precipitation can be observed by using various instruments such as rain gauges, disdrometers, weather radars and satellites. Thus, rainfall data can be obtained from a single instrument or from multiple instruments which are combined and quality controlled. Among the various instruments available to observe precipitation, weather radars have a high spatial coverage and temporal resolution making them the preferred source for many extrapolation-based nowcasting algorithms. Though weather radar can be used for observing hydro-meteors in the atmosphere within the range of 400–500 km, precipitation values can be accurately derived from reflectivity only up to a range of 100–120 km due to the curvature of the earth and the radar elevation angle [15,16].
The India Meteorological Department (IMD) has a wide network of weather radars with a proposal to more than double it to cover the entire country by 2025 for rainfall observation and accurate nowcasting [17]. The IMD has been using various expert systems that utilize weather radar data for nowcasting. IMD used a nowcasting application software for the Doppler weather radar network in India in 2006 named Warning Decision Support System -Integrated Information (WDSS-II) (under a USAID mission) developed by the National Severe Storms Laboratory (USA) in collaboration with the University of Oklahoma. The system was utilized for various nowcasting applications such as the estimation of storm cell rotation, tracking, hail detection, mosaic creation and for assimilation in NWP models [18]. On a similar line the IMD radar network in the year 2018 adapted the Hong Kong observatory nowcasting system SWIRLS -2 (Short-range Warning of Intense Rainstorms in Localized Systems) which has been operational in Hong Kong since 2010 [19].
The skill score of the nowcasting applications used in Indian regions have a high dependency on the characteristics of the precipitation systems. The characteristics of the precipitation system are strongly influenced by local meteorological conditions and the geographical location [20]. The factors influencing the dynamic evolution of precipitation systems is different in tropical regions as compared to mid-latitude regions [21]. Thus, the uncertainty in nowcasting arises due to difficulty in determining the advection and evolution of the precipitation fields. In addition to that, the physical models that capture the dynamic evolution of the precipitation systems cannot be resolved within the nowcast time-scales due to which different methods are used to represent them [22]. The short-term ensemble prediction system is an open-source nowcasting framework available in Python language (PySTEPS) which uses stochastic noise to resemble the evolution of the precipitation fields [13]. There have been various studies undertaken in mid-latitude regions of Europe, Australia and the USA to determine the skill score of the PySTEPS nowcasting system. It is observed that the skill scores obtained vary in each region for different precipitation types due to the effect of regional and local factors [23,24]. The present study has been undertaken to determine the effectiveness of the nowcasting system in a tropical region and is one of the first in the Indian subcontinent. The PySTEPS nowcast model was operationally utilized during the NEM season of 2022 at the Regional Meteorological Centre, Chennai, of IMD. Precipitation nowcast alerts specific to geographical areas were disseminated to the public through social media based on the nowcast output. The findings of the study may help in assessing the utility of the system for operational forecasting in tropical regions.
The details of the study are mention in the paper and the remainder of this paper is organized as follows: Section 2 describes the source, type of the data and methodology used in the study; Section 3 discusses the qualitative and quantitative results obtained in the assessment; Section 4 summarizes the findings from the study.
2. Data and Methodology
This section discusses the dataset that has been used for the study as well as the PySTEPS model used for nowcasting.
2.1. Study Domain and Datasets
The area of study is located on the east coast of India adjacent to the Bay of Bengal sea in the northern parts of the state of Tamil Nadu, India about 150 km from Chennai and is shown in Figure 1.
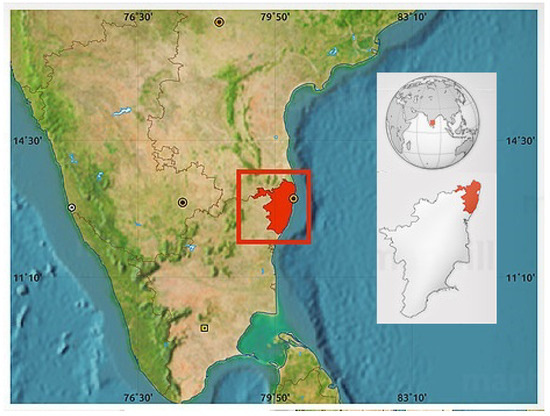
Figure 1.
Study region in the state of Tamil Nadu.
This area has a tropical climate with an annual rainfall of approximately 140.4 cm with an average of 59 rainy days. It also receives 50 percent of the annual rainfall during the North East Monsoon season from October to December. The rainfall during the monsoon season is due to synoptic scale disturbances occurring over the Bay of Bengal in the east and Arabian sea in the west. The rainfall in this area is sampled by an S-band Doppler weather radar located in Chennai and operating at a frequency of 2.87 GHz with a range resolution of 150 m and beam width of around 1.0° with scan range of 250 km. This radar is operated 24 hours a day with a short-range scan of 10 elevation angles [0.2, 1.5, 2.0, 3.0, 4.5, 6.0, 9.0, 12.0, 16.0, 21.0]. The radar generates all basic moments such as reflectivity, Doppler velocity and spectrum width. The 1.5 km Constant Altitude Plan Position Indicator (CAPPI) of reflectivity for a range of 150 km is generated every 10 min with a resolution of 500 m. A height reflectivity of 1.5 km was used to estimate rainfall to minimize the effects of clutter and beam blockage as the radar is located in the city. The rainfall rate is estimated from the reflectivity using Z-R relation with a and b taken as 267 and 1.345, respectively. The values were based on the comparison study of radar rainfall intensity with surface rain gauges from the same radar at 1.0 km height reflectivity [25]. The estimated rainfall rate is given as an input to the nowcast model.
Rainfall events that occurred during the North East Monsoon 2022 within 150 km range of the city of Chennai are used for the study. Rainfall of different intensity and types were observed throughout the day with precipitation occurring in different parts of the study domain. The classification of convective and stratiform precipitation was based on the features seen in the radar images such as bright band, horizontal reflectivity gradients and height of clouds in addition to the feedback obtained from operational meteorologists. Convective precipitation was observed on 21 October 2022, 27 October 2022 and 14 November 2022. Stratiform precipitation was observed on 21 November 2022 and mixed precipitation was observed on 5 October 2022. Measurement of precipitation during the landfall of the tropical storm “Mandous” close to the city on 9 December 2022 was also taken into consideration for the study. More than 750 samples were taken for the assessment with all days combined. A sample can be described as a single instance where nowcast was generated for the next 0–2 h based on the past rainfall. The number of samples and type of precipitation are listed in Table 1. The server configuration for running the nowcast was a quad core CPU with 20 GB RAM.

Table 1.
List of precipitation events in the study.
2.2. Overview of Nowcast Model
The PySTEPS nowcast model can be widely represented in two parts. First, the precipitation field evolution is a function of its spatial scale, hence, the field is decomposed into multiplicative cascade processing where each level of this cascade is a representation of each spatial scale. As the fields evolve temporally due to dynamic characteristics of the storm causing precipitation, it cannot be completely captured by Lagrangian persistence. Stochastic perturbations are introduced to the precipitation fields at different spatial scales. Second, to reduce the bias in the probability forecasts due to the stochastic perturbations, ensembles are used to represent the uncertainties in the extrapolation process [14].
For the multiplicative cascade processing, fast Fourier transform is applied to the precipitation field for calculating the scale decomposition and band pass filters of different frequencies based on Gaussian window. After the filtering process, the frequency bands are transformed back to spatial domain which results in cascades with each level representing a spatial scale. These cascades are used for deriving the evolution of the precipitation pattern within the forecast model. A basic flowchart representing the workflow of PySTEPS as implemented in IMD is shown in Figure 2.
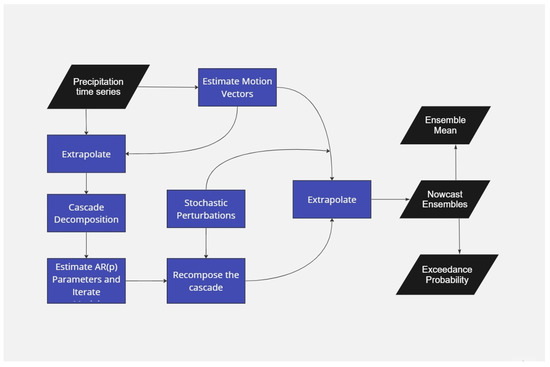
Figure 2.
Workflow of the PySTEPS nowcast module as implemented in IMD.
The predictability of the precipitation is limited by the fact that its state cannot be observed with absolute precision nor expressed without approximation of the governing laws [26]. In radar-based precipitation nowcasting, uncertainty in prediction occurs due to errors in estimation of current state of rainfall and the motion of the precipitation fields (initial conditions), and the limitations in the Lagrangian persistence method to predict the evolution of the precipitation fields and their motions. The majority of model errors in the Lagrangian approach stem from the evolution of precipitation in terms of initiation, growth, decay and dissipation processes that are against steady state assumptions.
In PySTEPS, an auto regressive (AR) process that combines the deterministic component from Lagrangian persistence with a random perturbation term is used to model the temporal evolution of the precipitation field. Separate second-order AR(2) processes are applied to each cascade level to account for the dynamic scaling of precipitation. The combination of the auto-regressive model in time and the cascade model in space allows one to control the temporal evolution and correlation structure of precipitation. For each cascade level j, the recursion formula is given by
The first term corresponds to the deterministic predictable component at cascade level j (i.e., Lagrangian persistence). The second term is a stochastic term that represents the unpredictable component at the same cascade level j, that is, mainly initiation, growth and decay of precipitation. The symbol denotes the time difference between consecutive precipitation fields that are normalized to zero mean and unit variance. The parameters in the above model are estimated from time-lagged auto-correlation coefficients for k = 1, 2 using the Yule–Walker equations [27]. The perturbation field in AR(2) is generated as a correlated Gaussian random field using FFT filtering. Each ensemble member has a different perturbation field to model the uncertainties in the forecasts [14,23,24]. The observed precipitation with motion and the forecast precipitation fields using the PySTEPS model of a sample event for t = 0, t = +30 min, t = +60 min and t = +120 min are shown in Figure 3.
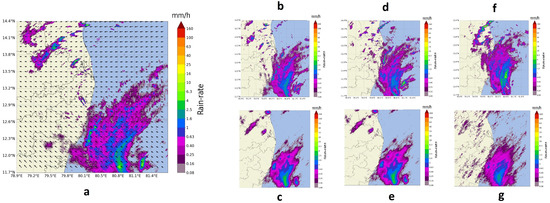
Figure 3.
(a) Observed motion at 09:20 UTC on 9 December 2022; (b) observed rain-rate + 30 min; (c) nowcast rain-rate + 30 min; (d) observed rain-rate + 60 min; (e) nowcast rain-rate + 60 min; (f) observed rain-rate + 120 min; (g) nowcast rain-rate + 120 min.
3. Results and Discussion
The assessment of the nowcasting method for different precipitation types has been performed using configurable parameters such as optical flow and the number of ensembles. Fractional skill scores (FSS) for a precipitation threshold of 0.1 mm/h have been calculated based on comparison between the nowcast output and the radar-observed precipitation for the given lead time of 0-2 h with the neighbourhood range set to 1 km [28]. A perfect forecast has an FSS of 1 and no skill has a score of 0 [29].
3.1. Optical Flow Method
In order to extrapolate the precipitation field for the forecast period, the current motion of the precipitation field needs to be estimated. Three methods are currently available in PySTEPS for the estimation of motion fields: a local Lucas-Kanade method (LK) [30], a global variational echo-tracking approach (VET) [31] and a spectral approach called dynamic and adaptive radar tracking of storms (DARTS) [32]. In the Lucas-Kanade method, the local features are tracked in a sequence of two or more radar images. The scheme includes a final interpolation step in order to produce a smooth field of motion vectors. On the other hand, the variational echo tracking algorithm is an approach essentially consisting of a global optimization routine that minimizes the cost function between the displaced and referenced image. DARTS uses a spectral approach to optical flow that is based on the discrete Fourier transform (DFT) of a temporal sequence of radar fields. The level of truncation of the DFT coefficients controls the degree of smoothness of the estimated motion field. DARTS requires a longer sequence of radar fields for estimating the motion. The motion vectors generated from all three methods for a specific event time are shown in Figure 4.
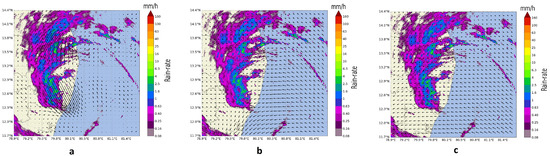
Figure 4.
Motion vectors of different optical flow methods: (a) DARTS; (b) Lucas-Kanade; (c) VET.
The selection of best optical flow method for operational scenarios is based on multiple factors. First, the requirement of data sets by different methods for generating motion vectors; second, the computing time taken for generation of motion fields; and third, the skill score of the optical flow method. DARTS require at least six instances of the observation field in sequence for estimating the motion field compared to two instances in the case of VET and LK. In an event of missed instance due to network or processing issues, the nowcast products are generated only after six observations are available in the sequence which is about 60 min for DARTS but in the case of VET and LK, the products can be generated within 20 min even if an observation is missed. In case of the computing time, LK had a processing time of just 2 s in the server for calculating the motion vectors compared to 38 s for VET and 5 s for DARTS. When comparing the skill scores, there is no significant improvement in the performance of DARTS compared to other methods though it requires six observations for computing. Among VET and LK, the FSS values do not have much difference when both their skill scores are above 0.4 which is significant for issuing nowcasting alerts. The FSS values for nowcasting using the three optical methods for a lead time of 0–120 min for sample events are shown in Figure 5 representing average performance scores in stratiform precipitation, convective precipitation and combined precipitation.
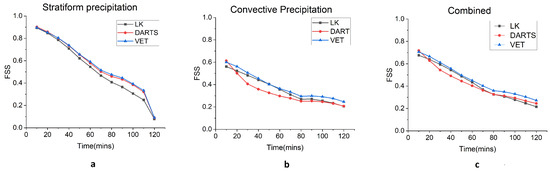
Figure 5.
FSS (1 km) for (a) stratiform precipitation; (b) convective precipitation; and (c) combined for different optical flow methods.
3.2. Number of Ensembles
The input data is of 600 × 600 pixels with the pixel resolution of 500 m. The input data ensemble size is one of the major factors in the nowcast module that determines the quality of the nowcast output because computing time increases when there is an increase in the ensemble size. Therefore, a choice has to be made to identify the optimum number of ensembles required to provide the best skill scores in a given computing environment. The impact of the ensemble size in providing high-quality nowcast data for different precipitation systems need to be assessed to determine the optimal ensemble size requirement. The FSS values for the nowcast of 0–2 h have been calculated for stratiform as well as convective precipitation types using an ensemble size of 24, 48 and 72 numbers. In addition to that, the computation time has also been calculated for generating the nowcast output for different ensemble sizes. The results are represented graphically in Figure 6. It is observed from the figure that for stratiform precipitation there is no difference in the skill score for the ensemble sizes of 24, 48 and 72. They exhibit similar skill scores throughout the lead time of 120 min. In the case of convective precipitation, the skill scores for ensemble size of 48 and 72 are better than 24 for the lead time of one hour though there is not much difference between ensemble sizes of 48 and 72. The skill scores deteriorate beyond one hour and all ensemble sizes converge to a similar skill score. However, further research needs to be undertaken to ascertain the benefits of increased ensemble size in the prediction of heavy precipitation and reducing the errors in quantitative precipitation estimates. The average computing time shows a linear relationship with the number of ensemble sizes with 95 s for ensemble size of 24, 191 s for 48 and 289 s for 72.
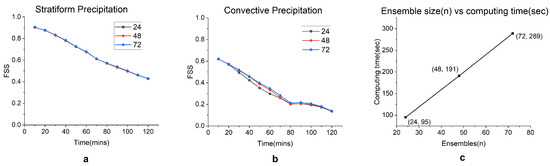
Figure 6.
FSS (1 km) for (a) stratiform precipitation; (b) convective precipitation with different ensemble sizes; and (c) computing time for ensemble sizes.
3.3. Precipitation Types
The performance analysis of the nowcast model during various kinds of precipitation events have been studied here. Box plots have been generated from the skill scores calculated for the events on different days as mentioned in Table 1 to assess the performance during different types of precipitation.
3.3.1. 5 October 2022 (Convective and Stratiform)
Two synoptic systems had influenced rainfall in the region of study on 5 October 2022. One was a cyclonic circulation in the south east Bay of Bengal (BOB) adjoining south coastal Tamil Nadu extending up to 3.1 km above mean sea level which is to the north of the domain. Another cyclonic circulation was present over the central parts of south BOB between 4.5 and 5.8 km altitude. These two synoptic systems influenced the precipitation with stratiform rainfall moving westwards from the BOB towards the coast in the morning hours. Convective activity was observed in the south-west side of the radar in the afternoon over the land which subsequently moved towards the sea as seen in Figure 7a. Eighty-eight samples were taken in the 24 h period and the FSS values of the nowcast are represented in the box plot in Figure 8a. The average skill score is 0.72 for 10 min lead time which reduces to 0.30 in 2 h lead time and the mean skill scores gradually degrade as the lead time increases. The maximum skill score is approximately 0.93 for a lead time of ten minutes and 0.62 in a lead time of 2 h, for a stratiform precipitation that had little variations in spatial scale. Most of the observed events had rainfall of a larger spatial extent (10 km or more) and moved slowly across the region. The performance degradation in some events was due to some isolated convective activity which occurred for shorter durations. It is observed that the mean skill scores of all the events have variation less than 0.15 when the lead time is 10 min while the variation increases drastically to approximately 0.5 at lead time of 120 min. It can be observed that there will be significant variation in the skill score at higher lead times when the type of precipitation events is a mix of convective as well as stratiform events.
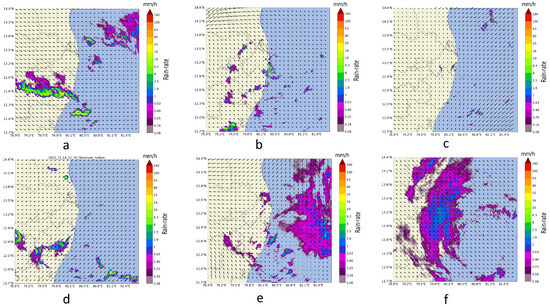
Figure 7.
Precipitation types: (a) 5 October 2022; (b) 21 October 2022; (c) 27 October 2022; (d) 14 November 2022; (e) 21 November 2022; (f) 9 December 2022.
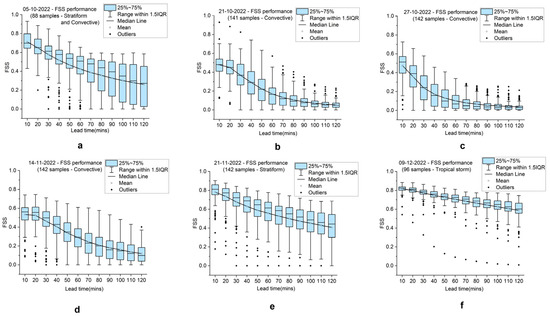
Figure 8.
FSS (1 km) box plot on: (a) 5 October 2022; (b) 21 October 2022; (c) 27 October 2022; (d) 14 November 2022; (e) 21 November 2022; (f) 9 December 2022.
3.3.2. 21 October 2022 (Convective)
A low pressure area had formed in the Andaman sea with a trough extending to Tamil Nadu through south BOB up to a height of 5.8 km. Under its influence, multiple rainfall events were observed due to convective thunderstorms with each storm lasting for 20 to 30 min and in a few cases for 60 min as seen in Figure 7b while the storms were isolated and scattered throughout the region of radar observation. The FSS performance is very poor for convective activity with mean score of 0.48 (141 samples) for a lead time of 10 min while the score becomes really low for 120 min lead time as plotted in Figure 8b. This is because the PySTEPS module can extrapolate the rainfall fields location and intensity but cannot not generate new rainfall fields based on the thermodynamic state in the atmosphere. In some cases, where the storms were slightly larger in terms of space and stayed active for a significantly longer period, skill score of 0.75 have been determined for a lead time of 60 min. However, the overall performance of the model for isolated convective activity is poor due to the isolated and short-lived nature of the storm cells.
3.3.3. 27 October 2022 (Convective)
An upper air cyclonic circulation was observed between 1.5 km and 4.5 km over south west BOB off the Tamil Nadu coast with north-easterly winds at surface level. Under the influence of cyclonic circulation, convective activity was triggered at isolated places by the convergence in the area with most of the isolated cells observed over sea area and some in the land area as seen in Figure 7c. The characteristics of the storms and performance of the nowcast model have been found similar to those observed on 27 October 2022 (Figure 8c).
3.3.4. 14 November 2022 (Convective)
A cyclonic circulation over the south east Arabian sea and associated trough extending from the cyclonic circulation to south Tamil Nadu at 0.9 km above sea level leading to convective activity over the region of observation. The convective activity was a mix of isolated cells as well as multiple cells which had a longer life time as the storms cells merged together. The mean skill score are around 0.55 for 142 samples and increasing up to 0.75 in some events for 10 min duration (Figure 8d). The mean skill score gradually reduced to 0.2 for 120 min but there were few events when the skill scores are more than 0.4. It is observed that the skill scores are better when nowcasting the convective cells which merge and form larger cells and sustain for a long period of time of more than 60 min as seen in Figure 7d.
3.3.5. 21st November 2022 (Stratiform)
In the synoptic chart, a depression was observed over south west BOB and adjoining coastal Tamil Nadu located at around 190 km east of Chennai which was causing stratiform rainfall across the region. As the system was moving westward towards the coast, the stratiform precipitation also moved along with the system towards the land area as observed in Figure 7e. The mean FSS value throughout the day for 142 samples varied from around 0.8 for a 10 min lead time to approximately 0.5 for 120 min lead time while the maximum skill score is 0.9 at 10 min to 0.78 at 120 min. The skill score performance has been very good for any lead time with a gradual decrease in mean skill score with lead time. Few individual events maintaining high skill scores throughout the 2 h can also be observed as seen in Figure 8e. Though there is some variation in skill scores across events, it is not very high—between 0 and 120 min lead time—as most of the precipitation events were of stratiform type.
3.3.6. 9th December 2022 (Tropical storm)
Cyclonic storm “Mandous” was centred in the Bay of Bengal around 130 km south-south east of Chennai and crossed the coast bringing widespread rainfall across the entire region covered in the study (Figure 7f). The nowcast model performance has been best on this day as the rainfall covered a large area and was slow-moving with steady precipitation throughout the day. The mean FSS value has been found to be 0.82 at 10 min and 0.65 at 120 min while maximum values varied from 0.88 at 10 min to 0.78 at 120 min. The average RMSE is approximately 0.5 mm/h for the nowcast period on the two days. The variation in the skill scores were also minimal throughout the lead time as seen in Figure 8f.
In addition to the fractional skill scores, the probability of detection (POD), false alarms and the critical success index (CSI) have been calculated for different precipitation types for 0–2 h. The precipitation threshold values were set as 0.1 mm/h for calculating the metrics. A grid point is considered as hit when the predicted and the observed values are greater than the threshold. If the predicted rain rate is greater while the observed rain rate is lower than the threshold then the grid point is considered as a false alarm. If the predicted rain rate is lower than the threshold but the observed rain rate is higher than the threshold then the grid point is considered as a miss. The POD is the ratio of hits to the sum of hits and misses. The CSI is the ratio of hits to the sum of hits, misses and false alarms. The CSI gives the performance skill of the nowcast module. The mean critical success index and mean probability of detection for tropical storms, convective precipitation and stratiform precipitation are shown in Figure 9.
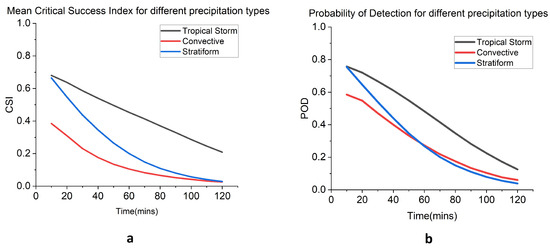
Figure 9.
(a) Mean critical success index for different precipitation types; (b) mean probability of detection for different precipitation types.
It is seen from the figure that both POD and CSI are higher for tropical storm precipitation and the values reduce gradually with an increasing lead time. This is likely due to widespread uniform precipitation persisting for a longer time duration during the tropical storm. The POD of convective and stratiform types are 0.78 and 0.6 at 10 min with the values merging to 0.3 at 60 min. The convective precipitation samples contain both isolated precipitation fields that sustain for shorter periods of 0–60 min and larger precipitation fields that sustain for more than 60 min. Hence, it is seen that for the initial 60 min, the convective POD is less than the stratiform POD but after 60 min the convective POD performs similarly to the stratiform POD. This shows that precipitation fields with a longer activity duration, even if they are of convective type, are better detected in the nowcast module. The CSI scores give a similar picture except that the stratiform type performs better than the convective type across the lead time. It can be inferred that false alarms in the convective type of precipitation increase as the lead time increases compared to stratiform which reduces the CSI score even though the POD is similar for lead times greater than 60 min.
4. Conclusions
This paper presents a comparison of the nowcast performance of different precipitation types during NEM. The Performance have been analyzed by modifying the different parameters present in the PySTEPS module, such as optical flow method and ensemble size. A comparison with computing time has also been performed to decide on an optimal configuration required to deploy the nowcast module for operational purposes. The performance of the model has been assessed using more than 750 samples of stratiform as well as convective precipitation types spread across various dates including a tropical storm. It has been observed that PySTEPS could be used in an operational scenario to generate nowcasts with a reasonably good skill score for a lead time of up to 120 min when there is widespread precipitation which persists for long periods. This kind of precipitation is prevalent in the Indian region during the South West Monsoon season, North East Monsoon season and also when the precipitation is caused by tropical storms during the summers. The challenges in predicting convective cells are largely due to their short life span and rapid change in storm dynamics. As the method used in this study is extrapolation-based nowcast, it is difficult for the model to generate new storm cells based on past precipitation data. A method which considers other atmospheric parameters such as temperature, pressure and wind along with precipitation data to model the dynamics of storms as well as atmospheric behaviour is required to predict convective cells. NWP blending in the extrapolation nowcasts and the usage of volumetric radar data may further improve the prediction of convective storms [33].
Author Contributions
B.R.: Conceptualization, Data curation, Methodology, Software, Validation, Visualization, Writing—original draft, Writing—review and editing. S.S.: Supervision, Writing—review and editing, validation. N.P.: Supervision, Writing—review and editing, validation. V.C.: Supervision, Writing—review and editing, validation. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the receipt of financial support from Indian Institute of Technology Palakkad and Colorado State University for publishing this article.
Data Availability Statement
Restrictions apply to the availability of these data. Data was obtained from India Meteorological Department and are available from the authors with the permission of India Meteorological Department.
Acknowledgments
Participation of V. Chandrasekar in this research was supported by Colorado State University. The authors wish to acknowledge and thank Shri. Arul Malar Kannan, Scientist- F, Doppler weather Radar, Chennai for providing the data sets and S. Balachandran, Deputy Director General of Meteorology, Chennai for providing support to this research. The authors also wish to thank the Director General of Meteorology, India Meteorological Department for the kind support and encouragement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Koll, R.; Ghosh, S.; Pathak, A.; Radhakrishnan, A.; Mujumdar, M.; Murtugudde, R.; Terray, P.; Rajeevan, M. A threefold rise in widespread extreme rain events over central India. Nat. Commun. 2017, 8, 708. [Google Scholar] [CrossRef]
- Alfieri, L.; Velasco, D.; Thielen-del Pozo, J. Flash flood detection through a multi-stage probabilistic warning system for heavy precipitation events. Adv. Geosci. 2011, 29, 69–75. [Google Scholar] [CrossRef]
- Chen, H.; Chandrasekar, V.; Philips, B. Principles of High-Resolution Radar Network for Hazard Mitigation and Disaster Management in an Urban Environment. J. Meteorol. Soc. Jpn. 2018, 96A, 119–139. [Google Scholar] [CrossRef]
- Jee, J.B.; Kim, S. Sensitivity Study on High-Resolution WRF Precipitation Forecast for a Heavy Rainfall Event. Atmosphere 2017, 8, 96. [Google Scholar] [CrossRef]
- Pierce, C.; Bowler, N.; Seed, A.; Jones, A.; Jones, D.; Moore, R. Use of a stochastic precipitation nowcast scheme for fluvial flood forecasting and warning. Atmos. Sci. Lett. 2005, 6, 78–83. [Google Scholar] [CrossRef]
- Lin, C.; Vasić, S.; Zawadzki, I.; Turner, B. Precipitation forecast based on numerical weather prediction models and radar nowcasts. Geophys. Res. Lett. 2004, 32. [Google Scholar] [CrossRef]
- Dixon, M.; Wiener, G. TITAN: Thunderstorm Identification, Tracking, Analysis, and Nowcasting—A Radar-based Methodology. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar] [CrossRef]
- Han, L.; Fu, S.; Zhao, L.; Zheng, Y.; Wang, H.; Lin, Y. 3D Convective Storm Identification, Tracking, and Forecasting—An Enhanced TITAN Algorithm. J. Atmos. Ocean. Technol. 2009, 26, 719–732. [Google Scholar] [CrossRef]
- Atencia, A.; Zawadzki, I. A Comparison of Two Techniques for Generating Nowcasting Ensembles. Part II: Analogs Selection and Comparison of Techniques. Mon. Weather Rev. 2015, 143, 2890–2908. [Google Scholar] [CrossRef]
- Zou, X.; Dai, Q.; Wu, K.; Yang, Q.; Zhang, S. An empirical ensemble rainfall nowcasting model using multi-scaled analogues. Nat. Hazards 2020, 103, 165–188. [Google Scholar] [CrossRef]
- Seed, A. A Dynamic and Spatial Scaling Approach to Advection Forecasting. J. Appl. Meteorol. 2003, 42, 381–388. [Google Scholar] [CrossRef]
- Bowler, N.; Pierce, C.; Seed, A. STEPS: A probabilistic precipitation forecasting scheme which merges an extrapolation nowcast with downscaled NWP. Q. J. R. Meteorol. Soc. 2007, 132, 2127–2155. [Google Scholar] [CrossRef]
- Nerini, D.; Besic, N.; Sideris, I.V.; Germann, U.; Foresti, L. A non-stationary stochastic ensemble generator for radar rainfall fields based on the Short-Space Fourier Transform. Hydrol. Earth Syst. Sci. 2017, 21, 2777–2797. [Google Scholar] [CrossRef]
- Pulkkinen, S.; Nerini, D.; Pérez Hortal, A.; Velasco-Forero, C.; Seed, A.; Germann, U.; Foresti, L. Pysteps: An open-source Python library for probabilistic precipitation nowcasting (v1.0). Geosci. Model Dev. 2019, 12, 4185–4219. [Google Scholar] [CrossRef]
- Browning, K.; Collier, C. Nowcasting of precipitating systems. Rev. Geophys. 1989, 27, 345–370. [Google Scholar] [CrossRef]
- Kumjian, M. Principles and Applications of Dual-Polarization Weather Radar. Part I: Description of the Polarimetric Radar Variables. J. Oper. Meteorol. 2013, 1, 226–242. [Google Scholar] [CrossRef]
- Roy, S.; Sharma, P.; Sen, B.; Devi, K.; Devi, S.; Gopal, N.; Mishra, K.; Katyar, S.; Singh, S.; Balakrishnan, S.; et al. A new paradigm for short-range forecasting of severe weather over the Indian region. Meteorol. Atmos. Phys. 2021, 133, 989–1008. [Google Scholar] [CrossRef]
- Bhowmik, S.; Roy, S.; Srivastava, D.K.; Mukhopadhay, B.; Thampi, S.; Reddy, Y.; Singh, H.; Venkateswarlu, S.; Adhikary, S. Processing of Indian Doppler Weather Radar data for mesoscale applications. Meteorol. Atmos. Phys. 2011, 111, 133–147. [Google Scholar] [CrossRef]
- Srivastava, D.K.; Lau, S.; Yeung, H.; Cheng, T.; Bhardwaj, P.R.; Arul Malar Kannan, B.S.; Bhowmik, S.; Singh, H. Use of SWIRLS Nowcasting System for quantitative precipitation forecast using Indian DWR data. Mausam 2012, 63, 1–16. [Google Scholar] [CrossRef]
- Sen Roy, S.; Saha, S.B.; Roy Bhowmik, S.K.; Kundu, P.K. Optimization of Nowcast Software WDSS-II for operational application over the Indian region. Meteorol. Atmos. Phys. 2014, 124, 143–166. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Middey, A. Comparison of tropical and midlatitude thunderstorm characteristics anchored in thermodynamic and dynamic aspects. Asia-Pac. J. Atmos. Sci. 2014, 50, 179–189. [Google Scholar] [CrossRef]
- Foresti, L.; Sideris, I.V.; Nerini, D.; Beusch, L.; Germann, U. Using a 10-Year Radar Archive for Nowcasting Precipitation Growth and Decay: A Probabilistic Machine Learning Approach. Weather Forecast. 2019, 34, 1547–1569. [Google Scholar] [CrossRef]
- Han, L.; Zhang, J.; Chen, H.; Zhang, W.; Yao, S. Toward the Predictability of a Radar-Based Nowcasting System for Different Precipitation Systems. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1005705. [Google Scholar] [CrossRef]
- Imhoff, R.; Brauer, C.; Overeem, A.; Weerts, A.; Uijlenhoet, R. Spatial and Temporal Evaluation of Radar Rainfall Nowcasting Techniques on 1,533 Events. Water Resour. Res. 2020, 56, e2019WR026723. [Google Scholar] [CrossRef]
- Suresh, R.; Ravichandran, P.; Gupta, J.; Thampi, S.; Kalyanasundaram, S.; Rao, P. On optimum rain rate estimation from a pulsed Doppler Weather Radar at Chennai. Mausam 2022, 56, 433–446. [Google Scholar] [CrossRef]
- Lorenz, E. Predictability: A Problem Partly Solved. Ph.D. Thesis, Shinfield Park, Reading, UK, 1995. [Google Scholar]
- Hamilton, J.D.; Susmel, R. Autoregressive conditional heteroskedasticity and changes in regime. J. Econom. 1994, 64, 307–333. [Google Scholar] [CrossRef]
- Roberts, N.; Lean, H. Scale-Selective Verification of Rainfall Accumulations from High-Resolution Forecasts of Convective Events. Mon. Weather Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
- Mittermaier, M. A “Meta” Analysis of the Fractions Skill Score: The Limiting Case and Implications for Aggregation. Mon. Weather Rev. 2018, 149, 3491–3504. [Google Scholar] [CrossRef]
- Lucas, B.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision (IJCAI). In Proceedings of the IJCAI’81: 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; Volume 81. [Google Scholar]
- Laroche, S.; Zawadzki, I. Retrievals of Horizontal Winds from Single-Doppler Clear-Air Data by Methods of Cross Correlation and Variational Analysis. J. Atmos. Ocean. Technol. 1995, 12, 721. [Google Scholar] [CrossRef]
- Ruzanski, E.; Chandrasekar, V. Weather Radar Data Interpolation Using a Kernel-Based Lagrangian Nowcasting Technique. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3073–3083. [Google Scholar] [CrossRef]
- Pulkkinen, S.; Chandrasekar, V.; von Lerber, A.; Harri, A.M. Nowcasting of Convective Rainfall Using Volumetric Radar Observations. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).