Analysis of the Response Relationship Between PWV and Meteorological Parameters Using Combined GNSS and ERA5 Data: A Case Study of Typhoon Lekima
Abstract
1. Introduction
2. Data and Methodology
2.1. Methodlogy
2.1.1. PWV Inversion
2.1.2. Wavelet Coherence (WTC)
2.2. Data
- (1)
- The dataset includes the Fifth Generation of the European Center for Medium-Range Weather Forecasts Reanalysis Data (ERA5). It comprises pressure, temperature, geopotential, and other parameters across 37 pressure levels in vertical profiles. The spatial resolution is 0.25° × 0.25°, and the temporal resolution is 1 h. (https://cds.climate.copernicus.eu/, accessed on 28 January 2024)
- (2)
- The dataset from the China Earthquake Networks Center for the year 2019 includes data from 248 GNSS stations. These data provide high-precision tropospheric zenith delays obtained through processing with GAMIT/GLOBK software (v10.7). The temporal resolution of the data is 1 h. (https://data.earthquake.cn, accessed on 21 November 2023)
- (3)
- The dataset from the University of Wyoming for the year 2019 includes data from 89 radiosonde stations in China. It consists of atmospheric parameters such as layered pressure, temperature, dew point temperature, as well as station locations and precipitable water vapor. The temporal resolution of the data is 12 h. (https://weather.uwyo.edu/upperair/sounding.html, accessed on 13 March 2024)
- (4)
- The dataset provided by the China Meteorological Administration Typhoon Network for the year 2019 includes the tracks of typhoon movements, containing information such as time, wind speed, intensity, etc. The temporal resolution of the data is 3 h. (http://typhoon.nmc.cn/web.html, accessed on 15 March 2024)
3. Calculating PWV with GNSS and ERA5 Data
3.1. Analysis of ERA5
3.2. Analysis of PWV
4. Research on the Response Relationship Between PWV and Meteorological Parameters
4.1. Typhoon Lekima
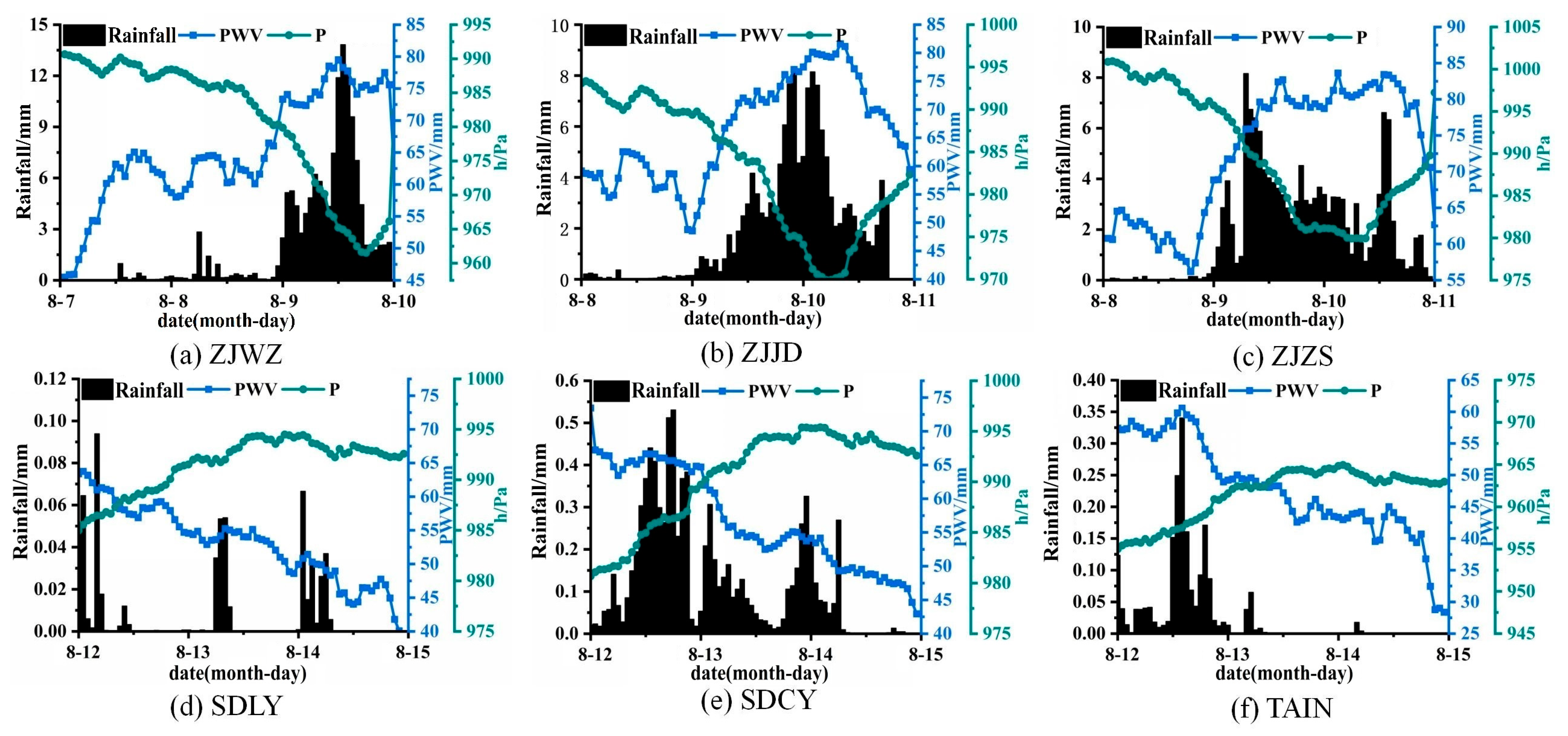
4.2. Analysis of the Response Relationship Between PWV and Pressure
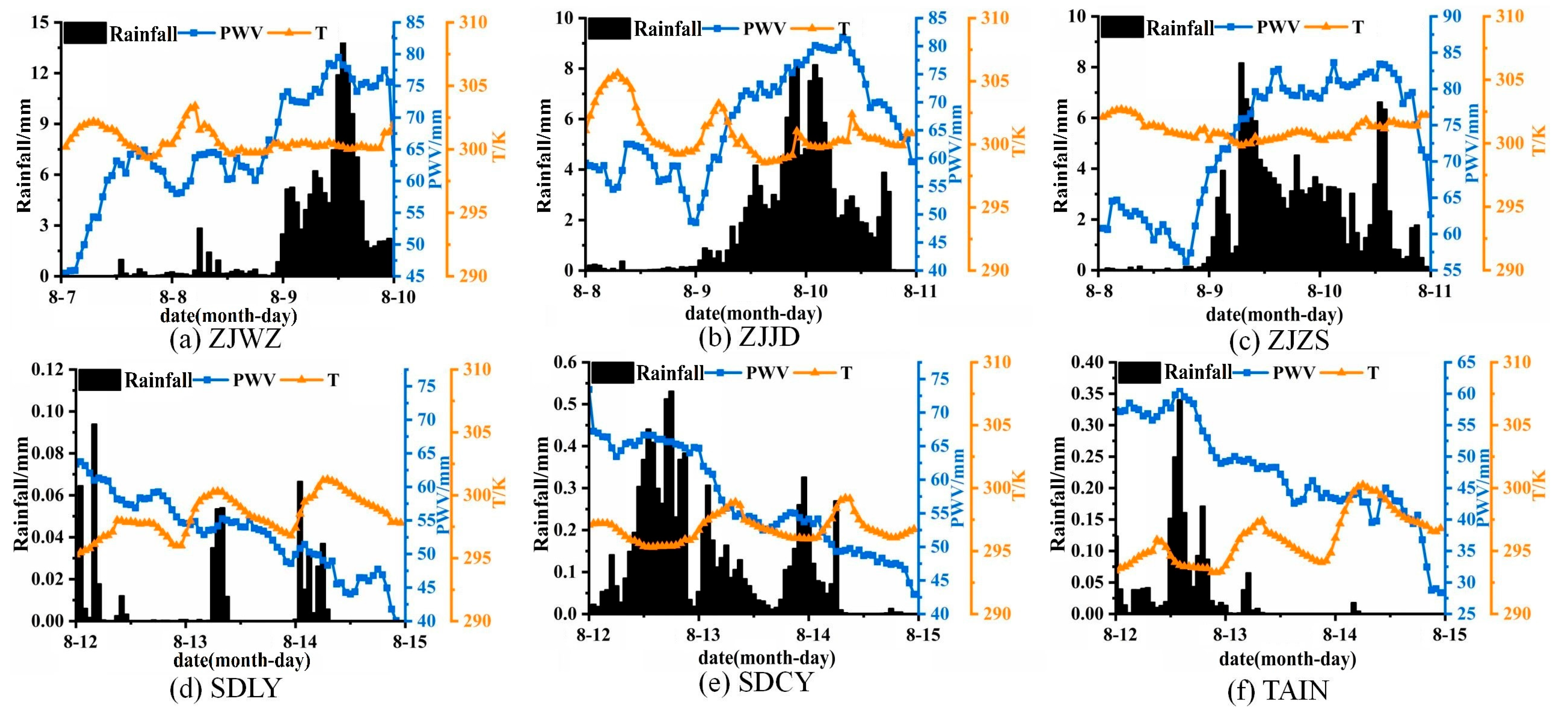
4.3. Analysis of the Response Relationship Between PWV and Temperature
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Solomon, S.; Rosenlof, K.H.; Portmann, R.W.; Daniel, J.S.; Davis, S.M.; Sanford, T.J.; Plattner, G.-K. Contributions of stratospheric water vapor to decadal changes in the rate of global warming. Science 2010, 327, 1219–1223. [Google Scholar] [CrossRef] [PubMed]
- Choy, S.; Wang, C.; Zhang, K.; Kuleshov, Y. GPS sensing of precipitable water vapour during the March 2010 Melbourne storm. Adv. Space Res. 2013, 52, 1688–1699. [Google Scholar] [CrossRef]
- Huang, L.; Mo, Z.; Xie, S.; Liu, L.; Chen, J.; Kang, C.; Wang, S. Spatiotemporal characteristics of GNSS-derived precipitable water vapor during heavy rainfall events in Guilin, China. Satell. Navig. 2021, 2, 1–17. [Google Scholar] [CrossRef]
- Hsu, P.C.; Li, T.; You, L.; Gao, J.; Ren, H.L. A spatial–temporal projection model for 10–30 day rainfall forecast in South China. Clim. Dyn. 2015, 44, 1227–1244. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the global positioning system. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Emardson, T.R.; Elgered, G.; Johansson, J.M. Three months of continuous monitoring of atmospheric water vapor with a network of Global Positioning System receivers. Geophys. Res. Atmos. 1998, 103, 1807–1820. [Google Scholar] [CrossRef]
- Vaquero-Martínez, J.; Antón, M.; de Galisteo, J.P.O.; Cachorro, V.E.; Wang, H.; Abad, G.G.; Román, R.; Costa, M.J. Validation of integrated water vapor from OMI satellite instrument against reference GPS data at the Iberian Peninsula. Sci. Total Environ. 2017, 580, 857–864. [Google Scholar] [CrossRef]
- Barman, P.; Jade, S.; Kumar, A.; Jamir, W. Inter annual, spatial, seasonal, and diurnal variability of precipitable water vapour over northeast India using GPS time series. Int. J. Remote Sens. 2016, 38, 391–411. [Google Scholar] [CrossRef]
- Ning, T.; Wang, J.; Elgered, G.; Dick, G.; Wickert, J.; Bradke, M.; Sommer, M.; Querel, R.; Smale, D. The uncertainty of the atmospheric integrated water vapour estimated from GNSS observations. Atmos. Meas. Tech. 2016, 9, 79–92. [Google Scholar] [CrossRef]
- Shoji, Y.; Sato, K.; Yabuki, M.; Tsuda, T. Comparison of shipborne GNSS-derived precipitable water vapor with radiosonde in the western North Pacific and in the seas adjacent to Japan. Earth Planets Space 2017, 69, 153. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W.; Zhang, B. A real-time precipitable water vapor monitoring system using the national GNSS network of China: Method and preliminary results. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1587–1598. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; Semmling, M.; Zus, F.; Gerland, S.; Ramatschi, M.; Ge, M.; Wickert, J.; Schuh, H. Retrieving precipitable water vapor from shipborne multi-GNSS observations. Geophys. Res. Lett. 2019, 46, 5000–5008. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W.; Zhang, S. GNSS-derived PWV and comparison with radiosonde and ECMWF ERA-Interim data over mainland China. J. Atmos. Sol.-Terr. Phys. 2018, 182, 85–92. [Google Scholar] [CrossRef]
- Champollion, C.; Masson, F.; Van Baelen, J.; Walpersdorf, A.; Chéry, J.; Doerflinger, E. GPS monitoring of the tropospheric water vapor distribution and variation during the 9 September 2002 torrential precipitation episode in the Cévennes (southern France). J. Geophys. Res. Atmos. 2004, 109, D24102. [Google Scholar] [CrossRef]
- Li, L.; Zhang, K.; Wu, S.; Li, H.; Wang, X.; Hu, A.; Shen, Z. An improved method for rainfall forecast based on GNSS-PWV. Remote Sens. 2022, 14, 4280. [Google Scholar] [CrossRef]
- Guo, M.; Zhang, H.; Xia, P. Exploration and analysis of the factors influencing GNSS PWV for nowcasting applications. Adv. Space Res. 2021, 67, 3960–3978. [Google Scholar] [CrossRef]
- Wei, P.; Xie, S.; Huang, L.; Liu, L. Ingestion of GNSS-Derived ZTD and PWV for spatial interpolation of PM2. 5 concentration in Central and Southern China. Int. J. Environ. Res. Public Health 2021, 18, 7931. [Google Scholar]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Yao, Y. A drought monitoring method based on precipitable water vapor and precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, K.; Hu, S.; Liu, J.; Shi, H.; Wei, G.; Chai, H.; Li, J.; Wang, T. Using the global navigation satellite system and precipitation data to establish the propagation characteristics of meteorological and hydrological drought in Yunnan, China. Water Resour. Res. 2023, 59, e2022WR033126. [Google Scholar] [CrossRef]
- Yeh, T.-K.; Hong, J.-S.; Wang, C.-S.; Chen, C.-H.; Chen, K.-H.; Fong, C.-T. Determining the precipitable water vapor with ground-based GPS and comparing its yearly variation to rainfall over Taiwan. Adv. Space Res. 2016, 57, 2496–2507. [Google Scholar] [CrossRef]
- Liu, J.C.; Zhong, W.; Shuang LI, U.; Lu, H.C. Allocation difference analyses of water substances during typhoon landing processes. J. Trop. Meteorol. 2018, 24, 300–313. [Google Scholar]
- Xu, H.; Zhai, G.; Li, X. Convective-stratiform rainfall separation of typhoon Fitow (2013): A 3D WRF modeling study. Terr. Atmos. Ocean. Sci. 2018, 29, 315–329. [Google Scholar] [CrossRef]
- Qi-Hua, L.L.; Han-Cheng, L.L.; Wei, Z.Z.; Wei-Chao, W.W.; Xing-Liang, G.G.; Meng, Y.Y. Meso-scale transport characteristics and budget diagnoses of water vapor in binary typhoons. Acta Phys. Sin. 2018, 67, 039201. [Google Scholar] [CrossRef]
- Zhao, Q.; Yao, Y.; Yao, W. GPS-based PWV for precipitation forecasting and its application to a typhoon event. J. Atmos. Solar-Terrestrial Phys. 2018, 167, 124–133. [Google Scholar] [CrossRef]
- He, Q.; Zhang, K.; Wu, S.; Zhao, Q.; Wang, X.; Shen, Z.; Li, L.; Wan, M.; Liu, X. Real-time GNSS-derived PWV for typhoon characterizations: A case study for super typhoon Mangkhut in Hong Kong. Remote Sens. 2019, 12, 104. [Google Scholar] [CrossRef]
- Zhu, M.; Liu, Z.; Hu, W. Observing water vapor variability during three super typhoon events in Hong Kong based on GPS water vapor tomographic modeling technique. J. Geophys. Res. Atmos. 2020, 125, e2019JD032318. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Yao, Y. A new typhoon-monitoring method using precipitation water vapor. Remote Sens. 2019, 11, 2845. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Wei, C.; Yu, J. Analysis of the Temporal and Spatial Characteristics of PWV and Rainfall with the Typhoon Movement: A Case Study of ‘Meihua’in 2022. Atmosphere 2023, 14, 1313. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Li, K.J.; Gao, P.X.; Zhan, L.S.; Shi, X.J.; Zhu, W.W. Relative phase analyses of long-term hemispheric solar flare activity. Mon. Not. R. Astron. Soc. 2009, 401, 342–346. [Google Scholar] [CrossRef]
- Tomás, R.; Li, Z.; Lopez-Sanchez, J.M.; Liu, P.; Singleton, A. Using wavelet tools to analyse seasonal variations from InSAR time-series data: A case study of the Huangtupo landslide. Landslides 2015, 13, 437–450. [Google Scholar] [CrossRef]
- Li, F.; He, L. The effects of dominant driving forces on summer precipitation during different periods in Beijing. Atmosphere 2017, 8, 44. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Rahimi, D.; Joghataei, M.; Movahedi, S. Correlation wavelet analysis for linkage between winter precipitation and three oceanic sources in Iran. Environ. Process. 2021, 8, 1027–1045. [Google Scholar] [CrossRef]
- Saastamoinen, J. Introduction to practical computation of astronomical refraction. Bull. Géod. 1972, 106, 383–397. [Google Scholar] [CrossRef]
- Li, L.; Gao, Y.; Xu, S.; Lu, H.; He, Q.; Yu, H. The New improved ZHD and weighted mean temperature models based on GNSS and radiosonde data using GPT3 and Fourier function. Atmosphere 2022, 13, 1648. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Dai, A.; Van Hove, T.; Van Baelen, J. A near-global, 2-hourly data set of atmospheric precipitable water from ground-based GPS measurements. J. Geophys. Res. 2007, 112, D11107. [Google Scholar] [CrossRef]


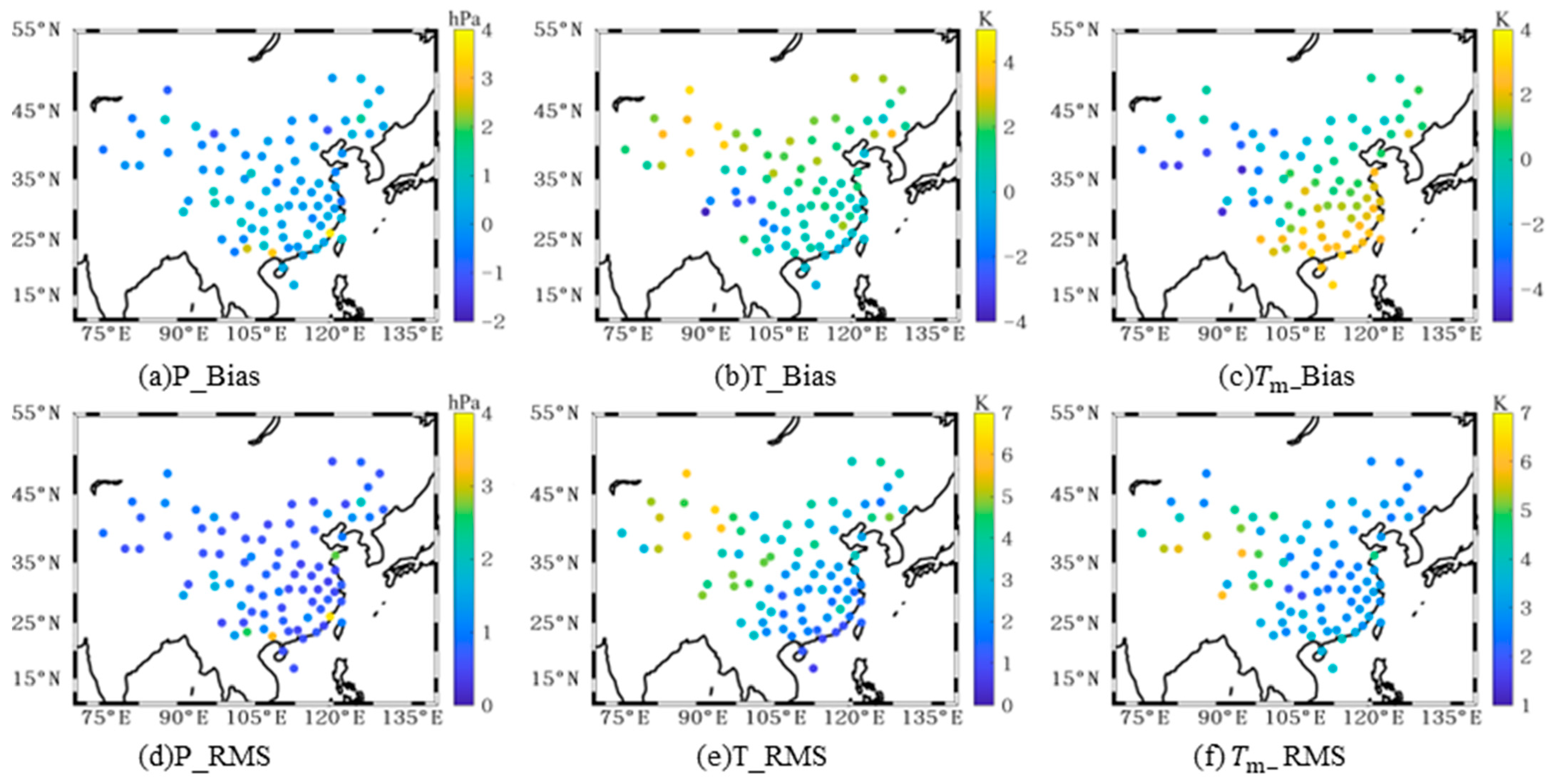





| P/hPa | T/K | /K | ||||
|---|---|---|---|---|---|---|
| Bias | RMS | Bias | RMS | Bias | RMS | |
| Max | 3.70 | 3.73 | 4.27 | 6.25 | 3.14 | 6.04 |
| Min | −1.14 | 0.45 | −3.82 | 0.71 | −4.63 | 1.83 |
| Average | 0.21 | 0.91 | 1.10 | 3.05 | 0.36 | 3.30 |
| PWVG/mm | PWVR/mm | |||
|---|---|---|---|---|
| Bias | RMS | Bias | RMS | |
| Max | 1.76 | 5.67 | 1.08 | 6.00 |
| Min | −5.04 | 1.39 | −4.62 | 1.17 |
| Average | −0.28 | 3.02 | −1.12 | 2.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Wang, X. Analysis of the Response Relationship Between PWV and Meteorological Parameters Using Combined GNSS and ERA5 Data: A Case Study of Typhoon Lekima. Atmosphere 2024, 15, 1249. https://doi.org/10.3390/atmos15101249
Gao Y, Wang X. Analysis of the Response Relationship Between PWV and Meteorological Parameters Using Combined GNSS and ERA5 Data: A Case Study of Typhoon Lekima. Atmosphere. 2024; 15(10):1249. https://doi.org/10.3390/atmos15101249
Chicago/Turabian StyleGao, Ying, and Xiaolei Wang. 2024. "Analysis of the Response Relationship Between PWV and Meteorological Parameters Using Combined GNSS and ERA5 Data: A Case Study of Typhoon Lekima" Atmosphere 15, no. 10: 1249. https://doi.org/10.3390/atmos15101249
APA StyleGao, Y., & Wang, X. (2024). Analysis of the Response Relationship Between PWV and Meteorological Parameters Using Combined GNSS and ERA5 Data: A Case Study of Typhoon Lekima. Atmosphere, 15(10), 1249. https://doi.org/10.3390/atmos15101249




