Determining the Axial Orientations of a Large Number of Flux Transfer Events Sequentially Observed by Cluster during a High-Latitude Magnetopause Crossing
Abstract
1. Introduction
2. Event Overview
2.1. Instrumentation and Data
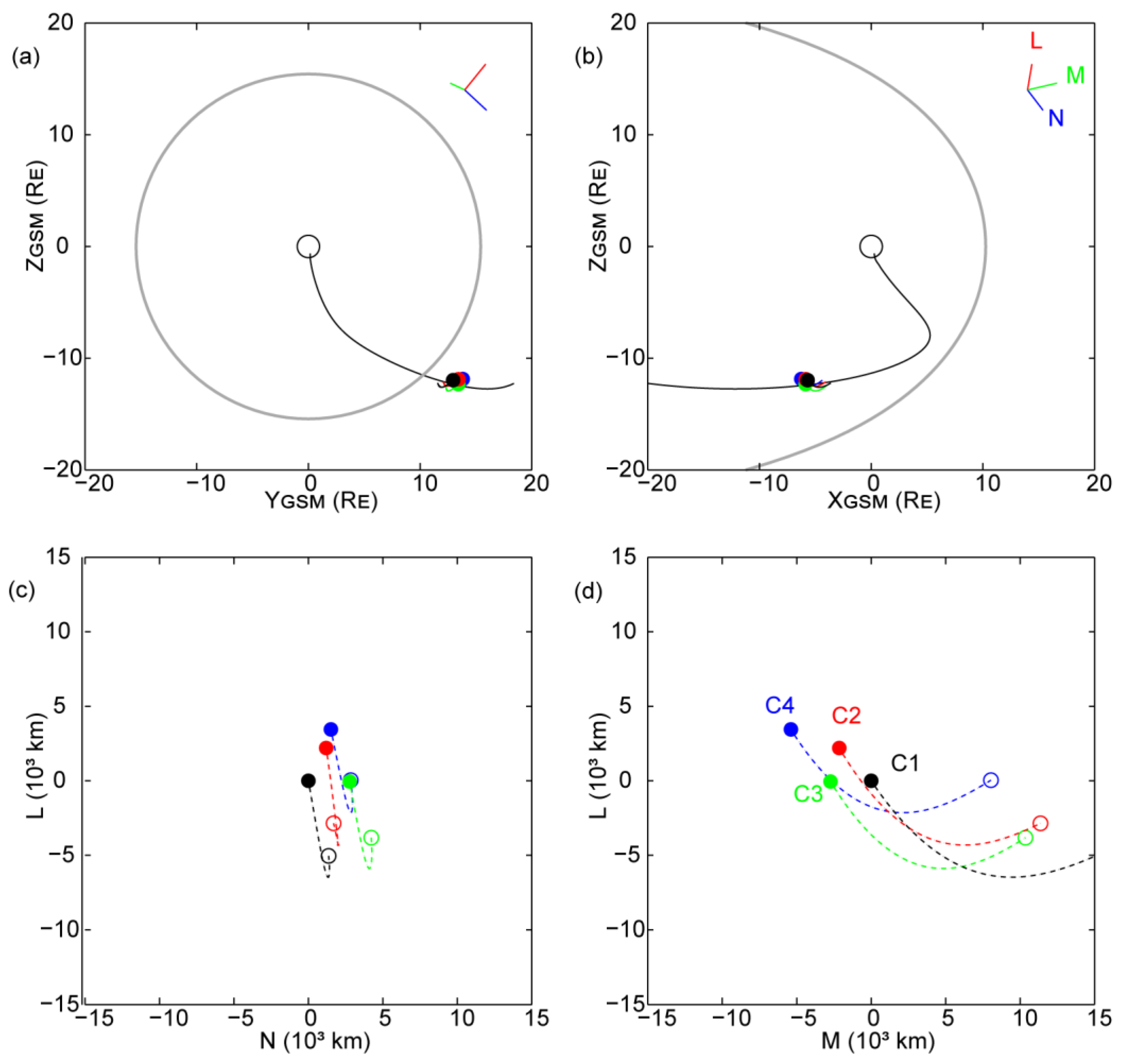
2.2. Locations and Trajectories
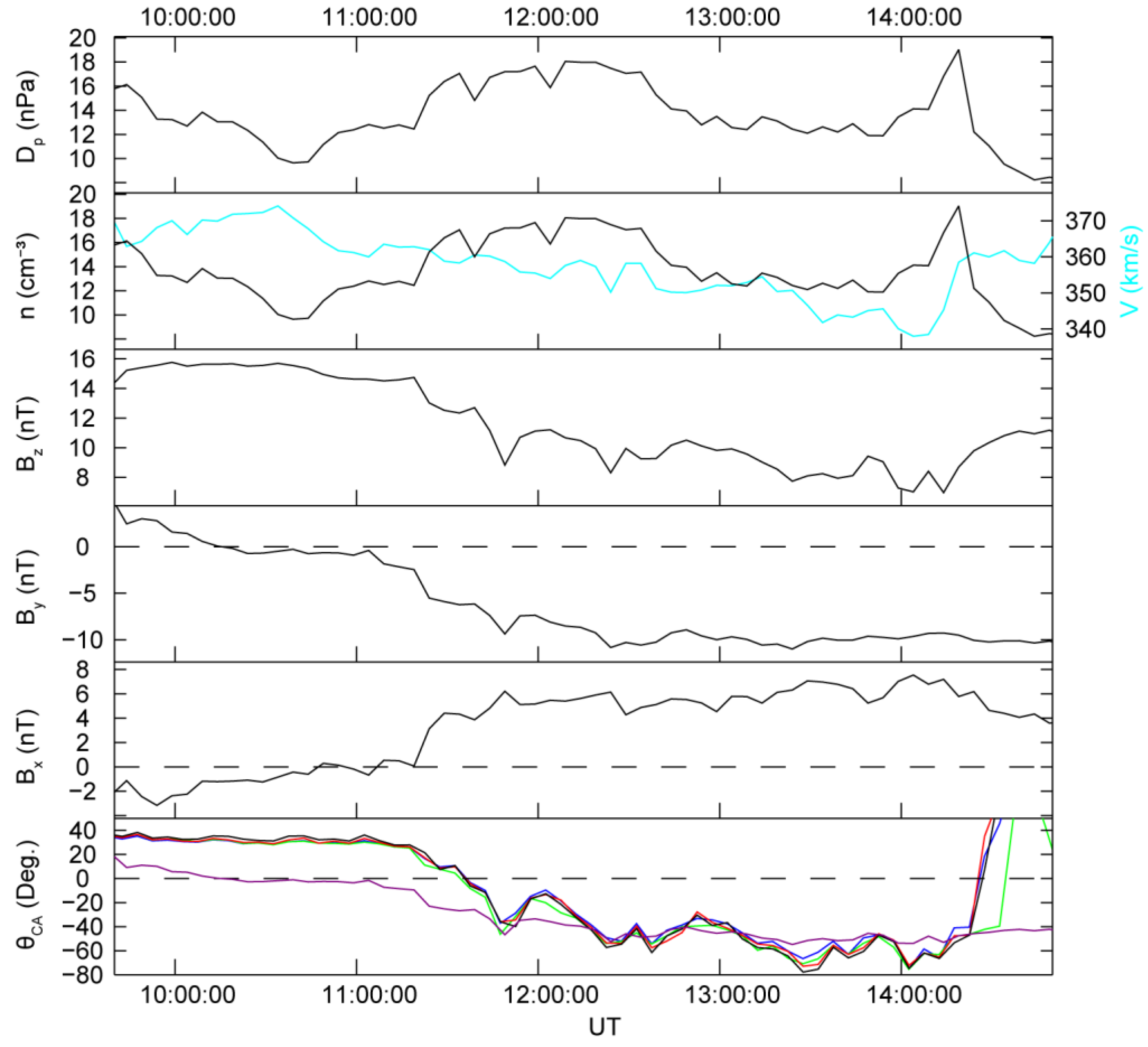
2.3. Solar Wind Condition
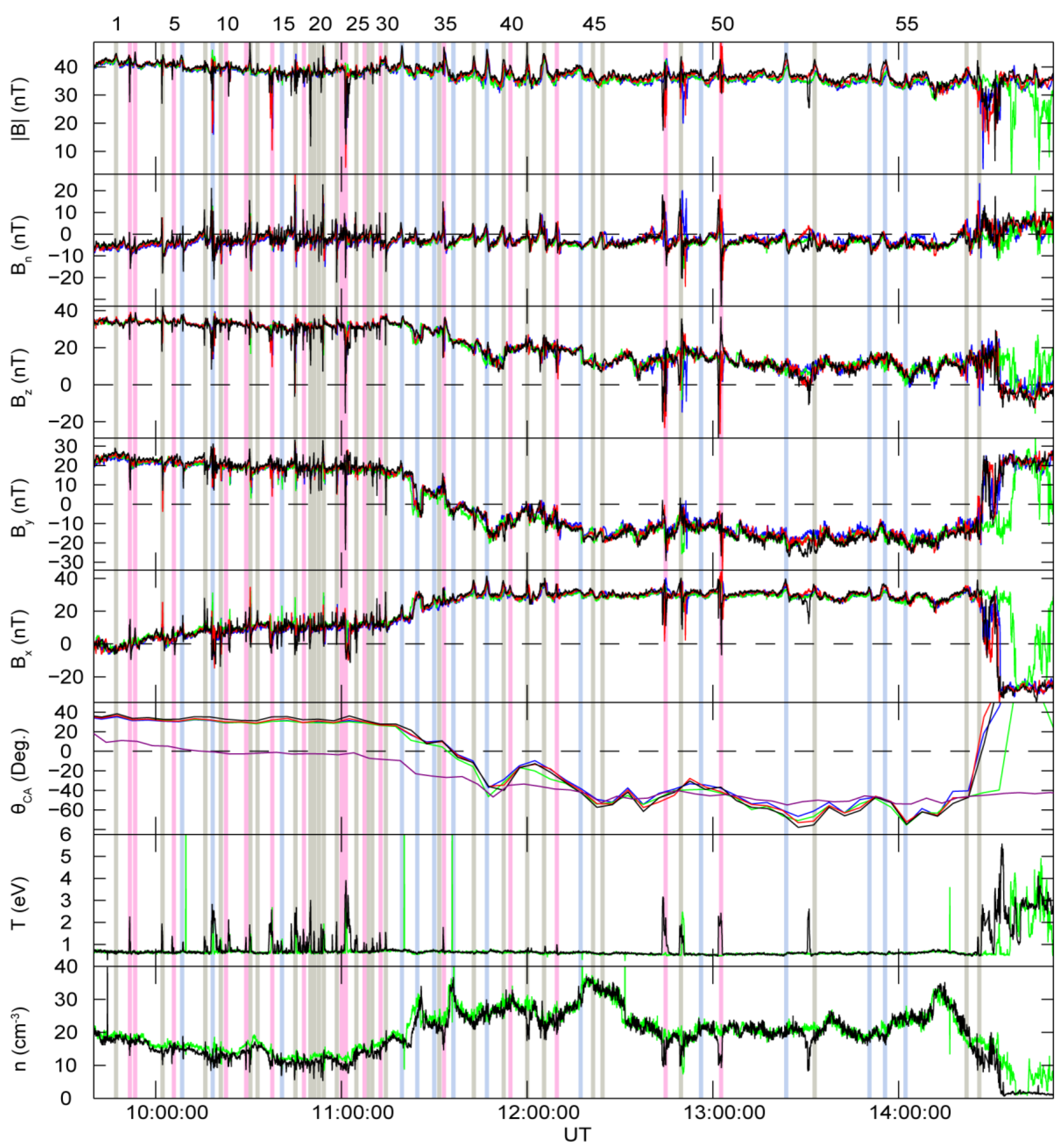
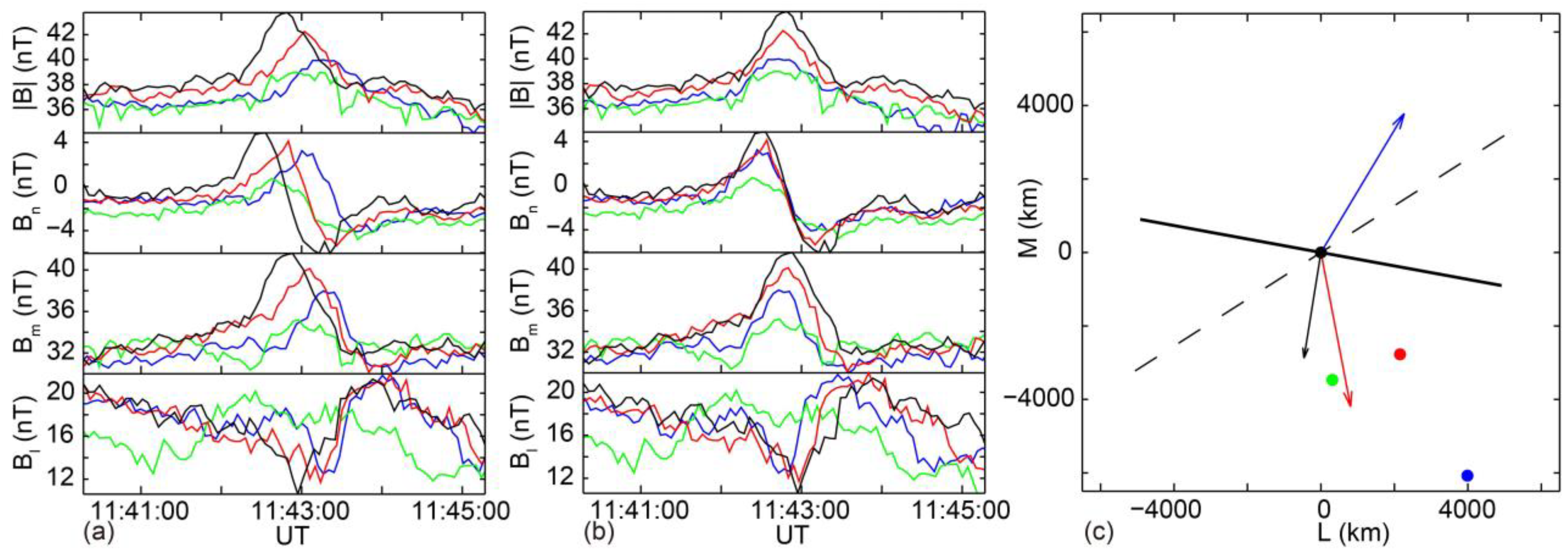
2.4. Cluster Observations
2.5. Magnetopause Normal
3. FTE Orientations from Multi-Spacecraft Timing Analysis
3.1. Multi-Spacecraft Timing Analysis
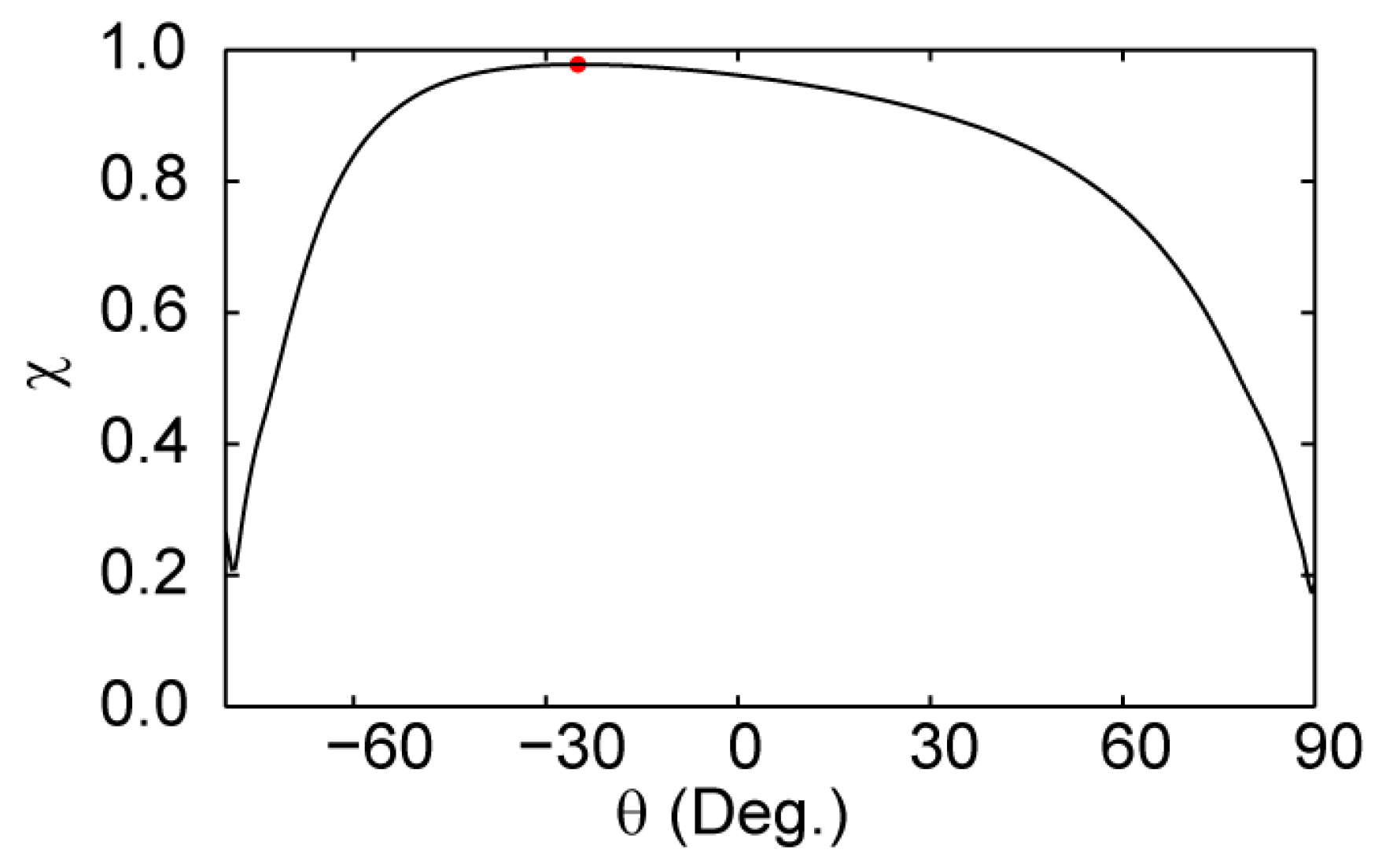
3.2. Case Event 1 (~11:19:33 UT)
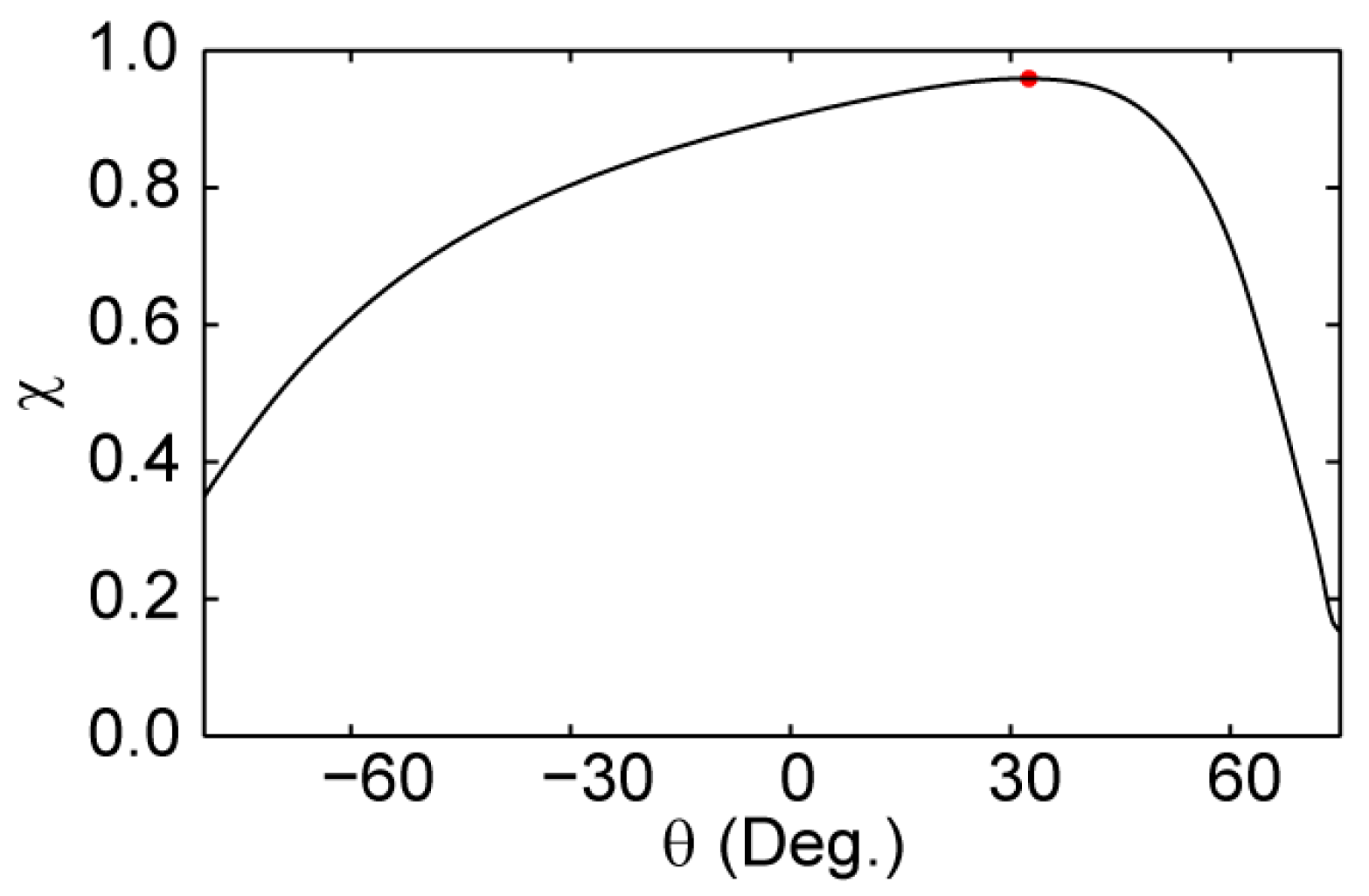
3.3. Case Event 2 (~11:42:47 UT)
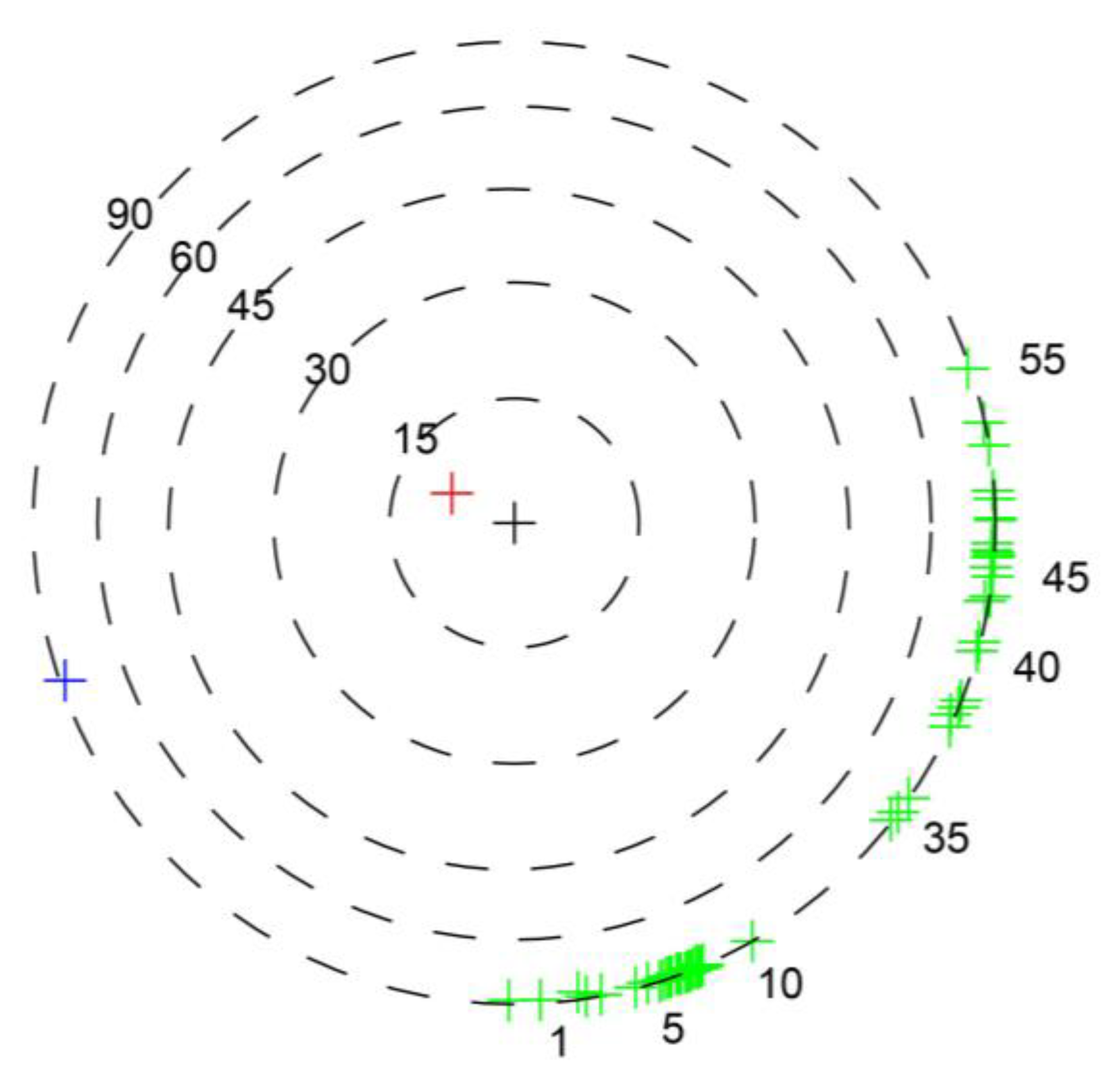
3.4. FTE Orientations of All Observed FTEs
4. Discussion
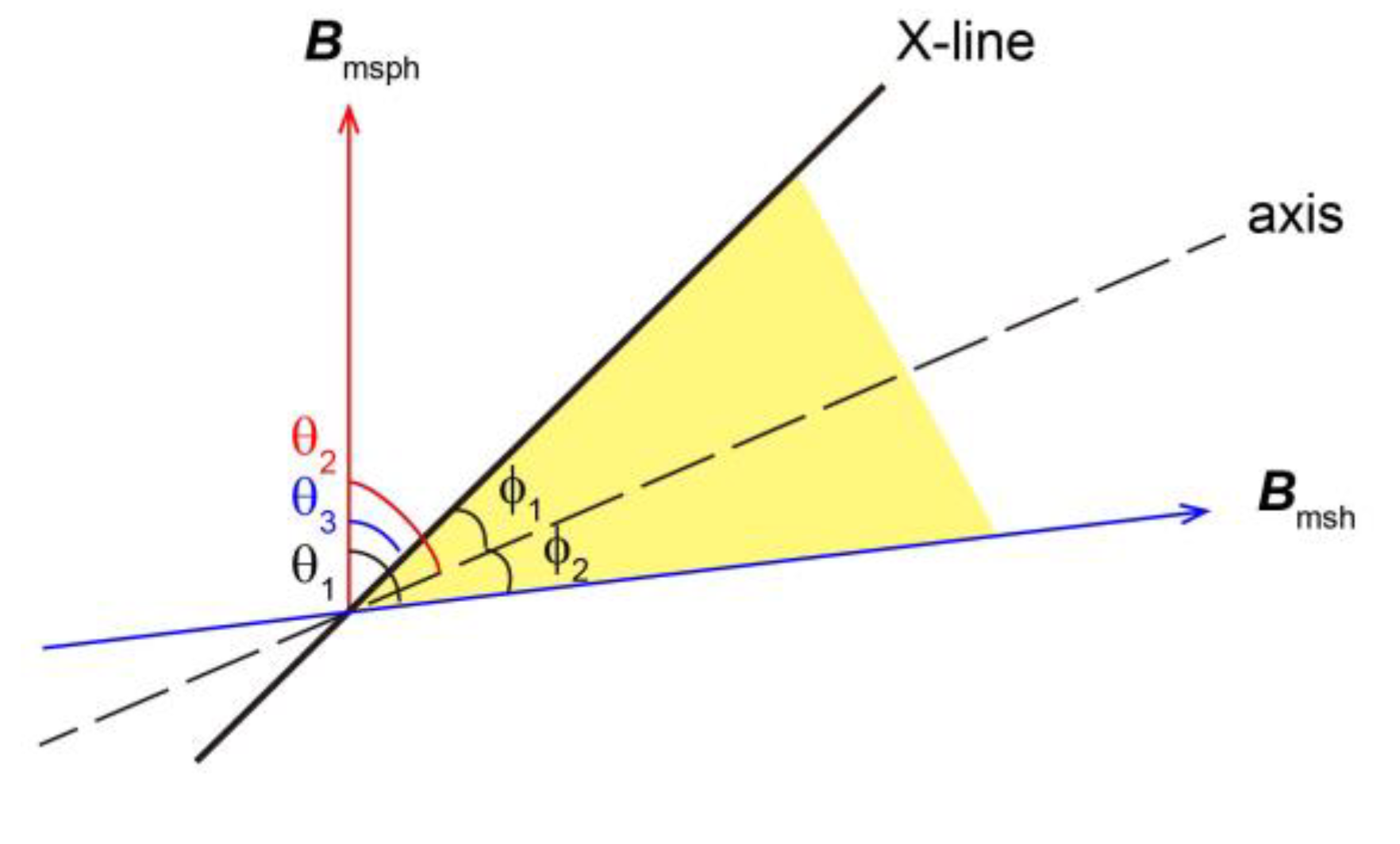
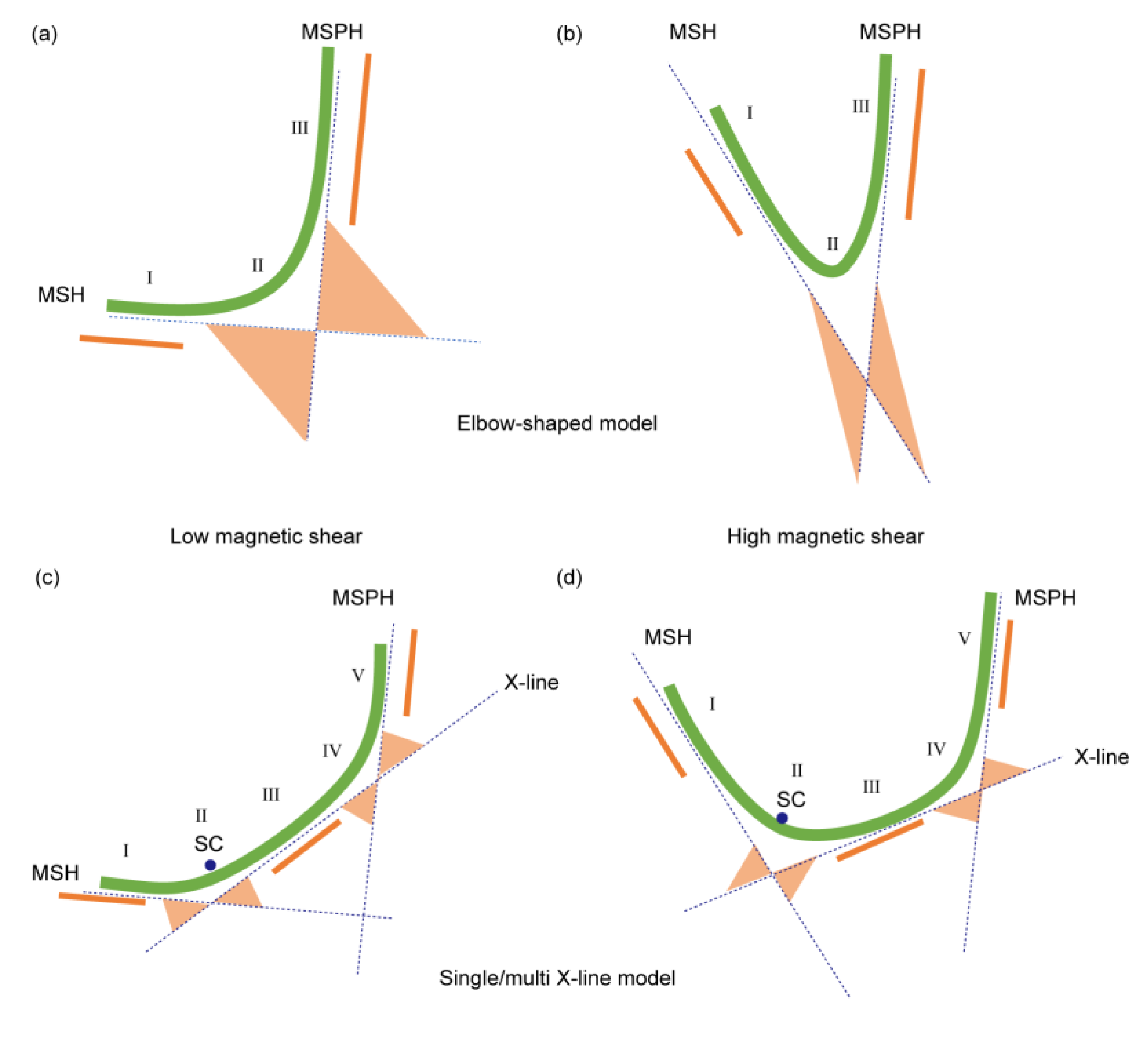
4.1. Elbow-Shaped Model
4.2. Single or Multiple X-Line Model
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dungey, J.W. Interplanetary Magnetic Field and Auroral Zones. Phys. Rev. Lett. 1961, 6, 47. [Google Scholar] [CrossRef]
- Dungey, J.W. The Structure of the Exosphere or Adventures in Velocity Space. In Geophysics, the Earth’s Environment (Proceedings of the 1962 Les Houches Summer School); De Witt, J.H.C., Le Beau, L., Eds.; Gordon and Breach: New York, NY, USA, 1963; pp. 502–552. [Google Scholar]
- Gosling, J.T.; Thomsen, M.F.; Bame, S.J.; Elphic, R.C.; Russell, C.T. Observations of Reconnection of Interplanetary and Lobe Magnetic-Field Lines at the High-Latitude Magnetopause. J. Geophys. Res. Space Phys. 1991, 96, 14097–14106. [Google Scholar] [CrossRef]
- Fuselier, S.A.; Petrinec, S.M.; Trattner, K.J.; Lavraud, B. Magnetic Field Topology for Northward IMF Reconnection: Ion Observations. J. Geophys. Res. Space Phys. 2014, 119, 9051–9071. [Google Scholar] [CrossRef]
- Russell, C.T.; Elphic, R.C. Initial ISEE Magnetometer Results—Magnetopause Observations. Space Sci. Rev. 1978, 22, 681–715. [Google Scholar] [CrossRef]
- Russell, C.T.; Elphic, R.C. ISEE Observations of Flux-Transfer Events at the Dayside Magnetopause. Geophys. Res. Lett. 1979, 6, 33–36. [Google Scholar] [CrossRef]
- Lee, L.C.; Fu, Z.F. A Theory of Magnetic-Flux Transfer at the Earth’s Magnetopause. Geophys. Res. Lett. 1985, 12, 105–108. [Google Scholar] [CrossRef]
- Scholer, M. Magnetic-Flux Transfer at the Magnetopause Based on Single X-Line Bursty Reconnection. Geophys. Res. Lett. 1988, 15, 291–294. [Google Scholar] [CrossRef]
- Paschmann, G.; Oieroset, M.; Phan, T. In-Situ Observations of Reconnection in Space. Space Sci. Rev. 2013, 178, 385–417. [Google Scholar] [CrossRef]
- Zhang, H.; Zong, Q.; Connor, H.; Delamere, P.; Facsko, G.; Han, D.; Hasegawa, H.; Kallio, E.; Kis, A.; Le, G.; et al. Dayside Transient Phenomena and Their Impact on the Magnetosphere and Ionosphere. Space Sci. Rev. 2022, 218, 40. [Google Scholar] [CrossRef]
- Fear, R.C.; Milan, S.E.; Fazakerley, A.N.; Lucek, E.A.; Cowley, S.W.H.; Dandouras, I. The Azimuthal Extent of Three Flux Transfer Events. Ann. Geophys. 2008, 26, 2353–2369. [Google Scholar] [CrossRef]
- Fear, R.C.; Milan, S.E.; Oksavik, K. Determining the Axial Direction of High-Shear Flux Transfer Events: Implications for Models of FTE Structure. J. Geophys. Res. Space Phys. 2012, 117, A09220. [Google Scholar] [CrossRef]
- Eastwood, J.P.; Phan, T.D.; Fear, R.C.; Sibeck, D.G.; Angelopoulos, V.; Oieroset, M.; Shay, M.A. Survival of Flux Transfer Event (FTE) Flux Ropes Far Along the Tail Magnetopause. J. Geophys. Res. Space Phys. 2012, 117, 9. [Google Scholar] [CrossRef]
- Trenchi, L.; Marcucci, M.F.; Reme, H.; Carr, C.M.; Cao, J.B. TC-1 Observations of a Flux Rope: Generation by Multiple X Line Reconnection. J. Geophys. Res. Space Phys. 2011, 116, A05202. [Google Scholar] [CrossRef]
- Trenchi, L.; Fear, R.C.; Trattner, K.J.; Mihaljcic, B.; Fazakerley, A.N. A Sequence of Flux Transfer Events Potentially Generated by Different Generation Mechanisms. J. Geophys. Res. Space Phys. 2016, 121, 8624–8639. [Google Scholar] [CrossRef]
- Wang, J.; Pu, Z.Y.; Zhou, X.Z.; Zhang, X.G.; Dunlop, M.W.; Fu, S.Y.; Xie, L.; Zong, Q.G.; Xiao, C.J.; Wang, X.G.; et al. Coordinated Cluster/Double Star Observations of Dayside Flux Transfer Events on 6 April 2004. Sci. China Ser. E Technol. Sci. 2008, 51, 1611–1619. [Google Scholar] [CrossRef]
- Zhong, J.; Pu, Z.Y.; Dunlop, M.W.; Bogdanova, Y.V.; Wang, X.G.; Xiao, C.J.; Guo, R.L.; Hasegawa, H.; Raeder, J.; Zhou, X.Z.; et al. Three-Dimensional Magnetic Flux Rope Structure Formed by Multiple Sequential X-Line Reconnection at the Magnetopause. J. Geophys. Res. Space Phys. 2013, 118, 1904–1911. [Google Scholar] [CrossRef]
- Li, Z.Y.; Chen, T.; Yan, G.Q. New Method for Determining Central Axial Orientation of Flux Rope Embedded within Current Sheet Using Multipoint Measurements. Sci. China Earth Sci. 2016, 59, 2037–2052. [Google Scholar] [CrossRef]
- Escoubet, C.P.; Fehringer, M.; Goldstein, M. The Cluster Mission—Introduction. Ann. Geophys. 2001, 19, 1197–1200. [Google Scholar] [CrossRef]
- Balogh, A.; Carr, C.M.; Acuna, M.H.; Dunlop, M.W.; Beek, T.J.; Brown, P.; Fornacon, K.H.; Georgescu, E.; Glassmeier, K.H.; Harris, J.; et al. The Cluster Magnetic Field Investigation: Overview of in-Flight Performance and Initial Results. Ann. Geophys. 2001, 19, 1207–1217. [Google Scholar] [CrossRef]
- Rème, H.; Aoustin, C.; Bosqued, M.; Dandouras, I.; Lavraud, B.; Sauvaud, J.A.; Barthe, A.; Bouyssou, J.; Camus, T.; Coeur-Joly, O.; et al. First Multispacecraft Ion Measurements in and near the Earth’s Magnetosphere with the Identical Cluster Ion Spectrometry (CIS) Experiment. Ann. Geophys. 2001, 19, 1303–1354. [Google Scholar] [CrossRef]
- King, J.H.; Papitashvili, N.E. Solar Wind Spatial Scales in and Comparisons of Hourly Wind and Ace Plasma and Magnetic Field Data. J. Geophys. Res. Space Phys. 2005, 110, 2004JA010649. [Google Scholar] [CrossRef]
- Sonnerup, B.U.Ö.; Scheible, M. Minimum and Maximum Variance Analysis. In Analysis Methods for Multi-Spacecraft Data; Götz Paschmann, P.W.D., Ed.; ESA Publications Division: Noordwijk, The Netherlands, 1998; pp. 185–220. [Google Scholar]
- Tsyganenko, N.A. A Model of the near Magnetosphere with a Dawn-Dusk Asymmetry—2. Parameterization and Fitting to Observations. J. Geophys. Res. Space Phys. 2002, 107, 17. [Google Scholar] [CrossRef]
- Shue, J.H.; Chao, J.K.; Fu, H.C.; Russell, C.T.; Song, P.; Khurana, K.K.; Singer, H.J. A New Functional Form to Study the Solar Wind Control of the Magnetopause Size and Shape. J. Geophys. Res. Space Phys. 1997, 102, 9497–9511. [Google Scholar] [CrossRef]
- Khrabrov, A.V.; Sonnerup, B.U.Ö. Dehoffmann-Teller Analysis. In Analysis Methods for Multi-Spacecraft Data; Götz Paschmann, P.W.D., Ed.; ESA Publications Division: Noordwijk, The Netherlands, 1998; pp. 221–248. [Google Scholar]
- Sonnerup, B.U.Ö. The Reconnecting Magnetosphere. In Magnetospheric Physics; McCormac, B.M., Ed.; D. Reidel: Dordrecht, The Netherlands, 1974; p. 23. [Google Scholar]
- Gonzalez, W.D.; Mozer, F.S. Quantitative Model for Potential Resulting from Reconnection with an Arbitrary Interplanetary Magnetic-Field. J. Geophys. Res. 1974, 79, 4186–4194. [Google Scholar] [CrossRef]


| FTE No. | Event Time | HT Velocity | FTE Axial Orientation | Magnetosheath Magnetic Field | Reconnection X-Line |
|---|---|---|---|---|---|
| 1 | 09:47:13 | (−299.3, 111.0, −63.8) | (−0.140, 0.725, 0.673) | (−2.8, 24.7, 33.0) | (−0.586, 0.734, 0.342) |
| 2 | 09:51:42 | (−294.7, 145.8, −25.3) | (−0.109, 0.717, 0.688) | (−0.3, 23.9, 33.8) | (−0.560, 0.741, 0.369) |
| 3 | 09:53:22 | (−291.2, 38.1, −165.5) | (−0.086, 0.710, 0.698) | (1.4, 20.5, 35.3) | (−0.518, 0.749, 0.411) |
| 4 | 10:02:14 | (−294.8, 209.9, 68.4) | (−0.078, 0.708, 0.701) | (4.8, 22.1, 33.5) | (−0.499, 0.752, 0.429) |
| 5 | 10:05:52 | (−290.9, 142.2, −19.9) | (−0.078, 0.708, 0.701) | (3.5, 22.6, 33.9) | (−0.516, 0.750, 0.413) |
| 6 | 10:08:33 | (−273.8, 185.5, 41.2) | (−0.347, 0.758, 0.550) | (7.8, 21.5, 33.9) | (−0.473, 0.755, 0.452) |
| 7 | 10:16:03 | (−277.9, 156.1, −2.4) | (−0.094, 0.712, 0.695) | (10.1, 21.0, 32.4) | (−0.441, 0.758, 0.479) |
| 8 | 10:18:26 | (−283.9, 211.1, 37.1) | (−0.312, 0.756, 0.575) | (9.5, 18.7, 32.2) | (−0.418, 0.759, 0.497) |
| 9 | 10:21:03 | (−272.8, 221.9, 86.5) | (−0.094, 0.712, 0.695) | (8.0, 19.7, 33.8) | (−0.451, 0.757, 0.471) |
| 10 | 10:22:42 | (−331.3, 69.4, −170.0) | (0.250, 0.557, 0.791) | (9.5, 18.8, 33.2) | (−0.427, 0.759, 0.490) |
| 11 | 10:29:15 | (−288.9, 99.4, −90.0) | (0.280, 0.539, 0.794) | (9.4, 19.1, 31.8) | (−0.421, 0.759, 0.495) |
| 12 | 10:30:36 | (−225.7, 203.4, 84.6) | (−0.124, 0.721, 0.681) | (9.8, 18.6, 32.5) | (−0.417, 0.759, 0.498) |
| 13 | 10:32:54 | (−238.8, 127.1, −2.1) | (−0.063, 0.703, 0.708) | (11.0, 17.0, 31.1) | (−0.381, 0.759, 0.526) |
| 14 | 10:37:41 | (−281.7, 168.6, −7.9) | (0.152, 0.612, 0.775) | (12.0, 19.6, 31.1) | (−0.405, 0.759, 0.508) |
| 15 | 10:40:48 | (−249.5, 217.3, 103.3) | (−0.193, 0.738, 0.646) | (9.3, 18.2, 32.0) | (−0.412, 0.759, 0.502) |
| 16 | 10:45:09 | (−260.4, 219.9, 66.6) | (0.198, 0.588, 0.784) | (12.8, 19.0, 30.7) | (−0.390, 0.759, 0.519) |
| 17 | 10:47:55 | (−294.7, 139.2, −46.0) | (0.107, 0.635, 0.764) | (9.4, 18.4, 32.7) | (−0.420, 0.759, 0.496) |
| 18 | 10:50:00 | (−306.1, 144.8, −60.0) | (0.037, 0.665, 0.745) | (12.4, 19.6, 32.2) | (−0.411, 0.759, 0.503) |
| 19 | 10:51:17 | (−319.0, 70.7, −157.0) | (0.083, 0.645, 0.758) | (9.5, 17.2, 31.7) | (−0.398, 0.759, 0.513) |
| 20 | 10:52:46 | (−275.4, 140.9, −32.9) | (−0.009, 0.684, 0.729) | (10.5, 18.1, 30.9) | (−0.395, 0.759, 0.516) |
| 21 | 10:54:19 | (−263.9, 194.5, 30.1) | (−0.147, 0.727, 0.670) | (11.2, 18.0, 31.4) | (−0.394, 0.759, 0.516) |
| 22 | 10:58:31 | (−255.9, 202.2, 47.9) | (−0.032, 0.692, 0.720) | (12.4, 17.8, 31.7) | (−0.387, 0.759, 0.522) |
| 23 | 11:00:04 | (−281.0, 158.7, −6.9) | (0.122, 0.627, 0.768) | (10.3, 18.2, 32.3) | (−0.408, 0.759, 0.505) |
| 24 | 11:01:25 | (−328.9, 159.2, −57.8) | (0.273, 0.543, 0.793) | (13.0, 19.3, 31.9) | (−0.402, 0.759, 0.510) |
| 25 | 11:04:50 | (−270.0, 140.4, −39.8) | (0.076, 0.649, 0.756) | (11.6, 16.4, 30.7) | (−0.368, 0.759, 0.536) |
| 26 | 11:07:28 | (−305.5, 96.4, −107.9) | (0.206, 0.583, 0.785) | (12.2, 17.4, 31.4) | (−0.381, 0.759, 0.526) |
| 27 | 11:08:35 | (−248.8, 182.0, 34.8) | (0.022, 0.672, 0.740) | (12.7, 18.4, 32.0) | (−0.394, 0.759, 0.516) |
| 28 | 11:09:59 | (−233.1, 178.4, 32.2) | (−0.047, 0.698, 0.714) | (12.3, 18.0, 31.1) | (−0.385, 0.759, 0.523) |
| 29 | 11:12:39 | (−325.4, 68.5, −154.6) | (0.145, 0.616, 0.773) | (11.8, 17.6, 32.1) | (−0.391, 0.759, 0.518) |
| 30 | 11:14:22 | (−306.2, 91.5, −115.2) | (−0.063, 0.703, 0.708) | (11.9, 17.8, 36.3) | (−0.423, 0.759, 0.493) |
| 31 | 11:19:33 | (−243.8, 135.1, −33.6) | (−0.253, 0.748, 0.612) | (17.1, 16.4, 31.7) | (−0.346, 0.758, 0.551) |
| 32 | 11:24:30 | (−271.1, 79.9, −111.6) | (0.190, 0.592, 0.782) | (28.5, −1.8, 22.8) | (−0.048, 0.698, 0.714) |
| 33 | 11:30:00 | (−216.7, 98.5, −41.0) | (0.145, 0.616, 0.773) | (24.1, 3.8, 27.5) | (−0.152, 0.728, 0.667) |
| 34 | 11:31:37 | (−262.9, 83.9, −98.9) | (0.429, 0.432, 0.792) | (27.1, 3.3, 26.9) | (−0.136, 0.724, 0.675) |
| 35 | 11:33:07 | (−309.2, 80.6, −153.0) | (0.488, 0.382, 0.784) | (26.7, 4.1, 28.4) | (−0.158, 0.730, 0.664) |
| 36 | 11:36:11 | (−348.7, 89.6, −189.0) | (0.190, 0.592, 0.782) | (26.6, −4.5, 23.7) | (−0.033, 0.693, 0.720) |
| 37 | 11:42:47 | (−260.1, 93.4, −91.9) | (0.581, 0.293, 0.758) | (29.5, −2.7, 21.8) | (−0.030, 0.691, 0.721) |
| 38 | 11:47:00 | (−263.9, 76.1, −100.6) | (0.352, 0.490, 0.796) | (31.9, −13.1, 11.8) | (0.149, 0.614, 0.774) |
| 39 | 11:52:26 | (−229.7, 70.8, −73.6) | (0.482, 0.388, 0.785) | (28.9, −8.9, 13.3) | (0.107, 0.634, 0.765) |
| 40 | 11:54:35 | (−274.2, 85.0, −116.2) | (0.739, 0.095, 0.666) | (29.5, −7.5, 19.1) | (0.037, 0.665, 0.745) |
| 41 | 12:00:02 | (−257.4, 83.5, −104.4) | (0.488, 0.382, 0.784) | (28.3, −3.3, 20.9) | (−0.016, 0.689, 0.726) |
| 42 | 12:05:28 | (−340.0, 112.1, −140.0) | (0.721, 0.121, 0.681) | (35.1, −9.2, 16.9) | (0.068, 0.652, 0.754) |
| 43 | 12:09:35 | (−315.5, 107.7, −128.1) | (0.779, 0.029, 0.625) | (28.3, −11.7, 15.2) | (0.112, 0.632, 0.766) |
| 44 | 12:17:16 | (−239.4, 58.3, −96.4) | (0.366, 0.480, 0.796) | (31.3, −11.9, 19.7) | (0.067, 0.653, 0.754) |
| 45 | 12:21:17 | (−261.4, 81.7, −109.1) | (0.587, 0.287, 0.756) | (30.0, −12.8, 15.4) | (0.116, 0.630, 0.767) |
| 46 | 12:24:21 | (−255.3, 73.3, −104.2) | (0.810, −0.030, 0.585) | (29.1, −13.6, 10.3) | (0.174, 0.601, 0.779) |
| 47 | 12:44:45 | (−226.4, 105.8, −73.4) | (0.739, 0.095, 0.666) | (32.1, −11.2, 13.9) | (0.115, 0.630, 0.767) |
| 48 | 12:49:41 | (−201.1, 84.6, −77.3) | (0.648, 0.218, 0.729) | (29.0, −6.9, 19.3) | (0.030, 0.668, 0.742) |
| 49 | 12:56:10 | (−143.7, 27.0, −39.5) | (−0.055, 0.700, 0.711) | (29.4, −13.2, 15.0) | (0.124, 0.626, 0.769) |
| 50 | 13:02:40 | (−291.1, 79.9, −140.1) | (0.790, 0.009, 0.612) | (31.0, −12.2, 14.5) | (0.120, 0.628, 0.768) |
| 51 | 13:23:40 | (−281.9, 76.5, −121.2) | (0.068, 0.652, 0.754) | (32.3, −17.4, 7.9) | (0.217, 0.577, 0.787) |
| 52 | 13:32:51 | (−245.7, 71.7, −100.5) | (0.756, 0.069, 0.650) | (29.4, −18.2, 6.9) | (0.240, 0.563, 0.790) |
| 53 | 13:50:34 | (−259.3, 82.4, −102.1) | (0.280, 0.539, 0.794) | (29.3, −15.2, 10.9) | (0.180, 0.598, 0.780) |
| 54 | 13:55:35 | (−243.0, 78.7, −92.4) | (0.408, 0.448, 0.794) | (31.3, −13.3, 11.9) | (0.152, 0.612, 0.775) |
| 55 | 14:02:13 | (−287.6, 116.7, −105.3) | (0.533, 0.341, 0.774) | (25.5, −19.3, 3.8) | (0.290, 0.533, 0.794) |
| 56 | 14:21:55 | (−274.4, 135.4, −82.3) | (0.760, 0.062, 0.646) | (32.6, −11.7, 10.5) | (0.151, 0.613, 0.775) |
| 57 | 14:26:02 | (−244.5, 110.9, −81.6) | (0.669, 0.193, 0.717) | (27.0, −12.2, 13.2) | (0.138, 0.619, 0.772) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Chen, T.; Li, L. Determining the Axial Orientations of a Large Number of Flux Transfer Events Sequentially Observed by Cluster during a High-Latitude Magnetopause Crossing. Atmosphere 2024, 15, 1215. https://doi.org/10.3390/atmos15101215
Li Z, Chen T, Li L. Determining the Axial Orientations of a Large Number of Flux Transfer Events Sequentially Observed by Cluster during a High-Latitude Magnetopause Crossing. Atmosphere. 2024; 15(10):1215. https://doi.org/10.3390/atmos15101215
Chicago/Turabian StyleLi, Zhaoyu, Tao Chen, and Lei Li. 2024. "Determining the Axial Orientations of a Large Number of Flux Transfer Events Sequentially Observed by Cluster during a High-Latitude Magnetopause Crossing" Atmosphere 15, no. 10: 1215. https://doi.org/10.3390/atmos15101215
APA StyleLi, Z., Chen, T., & Li, L. (2024). Determining the Axial Orientations of a Large Number of Flux Transfer Events Sequentially Observed by Cluster during a High-Latitude Magnetopause Crossing. Atmosphere, 15(10), 1215. https://doi.org/10.3390/atmos15101215






