Long-Term Study of the Synchronization Effect between Geomagnetic Field Variations and Minute-Scale Heart-Rate Oscillations in Healthy People
Abstract
1. Introduction
- (1)
- In some cases, the strong GMS or abrupt changes in cosmic-ray intensity can have not only a catastrophic but also a reversible biological effect; for example, an increase in blood pressure (without a hypertensive crisis) or other reversible changes in the general condition in groups of individuals [18,19,20,21,22];
- (2)
- Significant deterioration in patient health can be observed not only during major space-weather events, but also during moderate geomagnetic disturbances [23,24,25,26,27,28] and periods of extremely low GMA [29,30,31,32], suggesting that the system of solar–biospheric connections is non-linear and non-monotonic;
- (3)
- The observed biological effects from the GMS of different origins (caused by Corotating Interaction Regions or by the body of Coronal Mass Ejection in interplanetary space [33]) vary significantly [8,34,35]. Therefore, consideration of the origin of GMS is essential for an accurate analysis of potential bioeffects.
- (4)
- The impact of space weather on individuals can vary greatly in terms of time, magnitude, and even direction [36,37]. As a result, a new approach to studying heliobiological effects has emerged that is aimed at analyzing long-term observations of a certain individual [36,37,38,39,40,41,42]. This approach identified the specific trait features of an effect unobserved in group studies.
- (5)
2. Materials and Methods
2.1. Collection of Experimental Data
2.2. Geomagnetic Data
2.3. Analysis Procedure
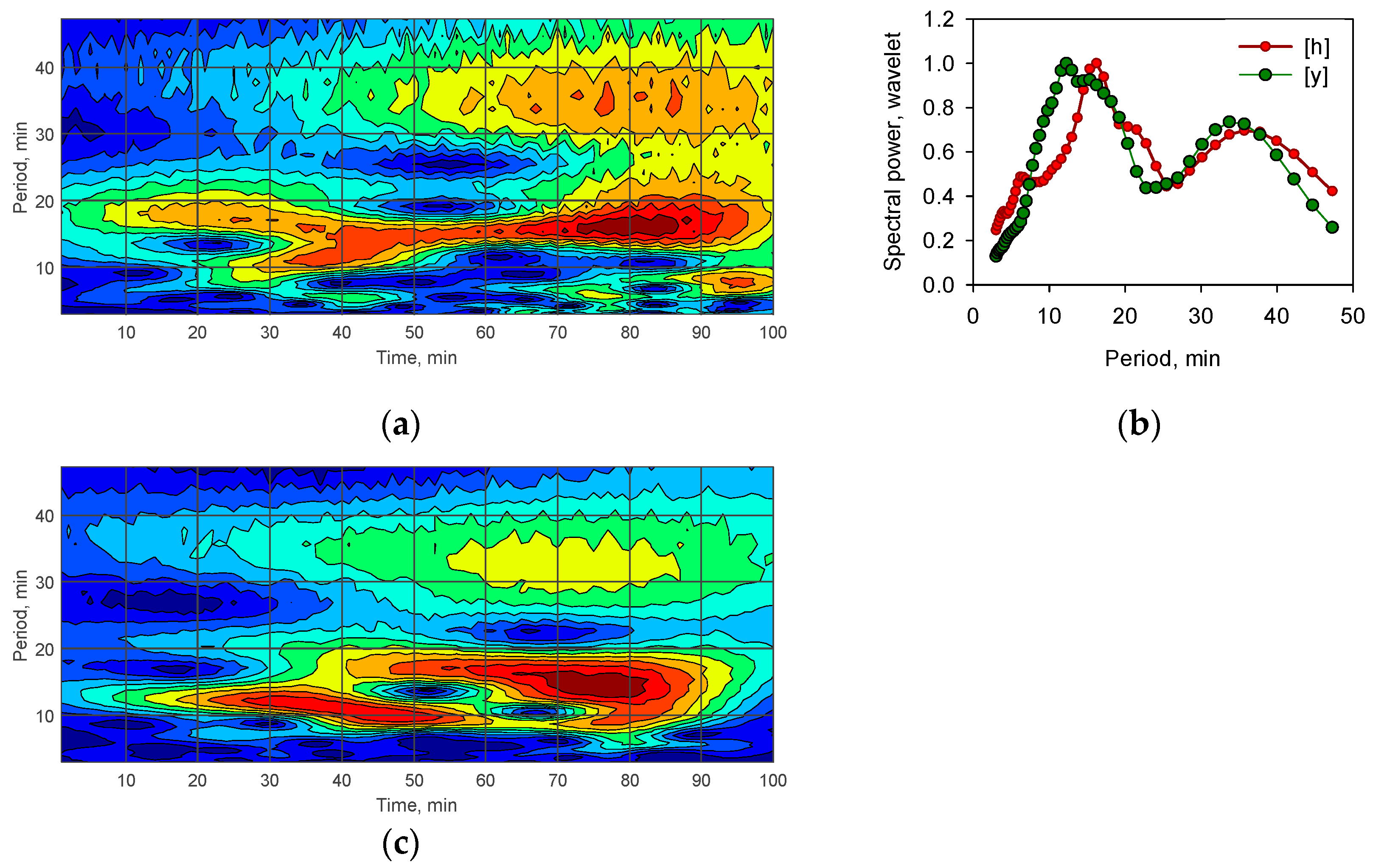
- The wavelet transformation of a 100-point segment of the HR series, within the tested periods of T = 3...50 min, produces a 2-D matrix of wavelet coefficients (W(HR)s) of size i × n, where i ranges from 1 to 50, and n denotes the point number in the data series that corresponds to the experiment’s minutes. It is worth noting that the association between i and T is monotonous but non-linear. Matrices illustrating the HR series (W(HR)) and the GMF vector Y (W(Y)) can be found in Figure 2a,c, respectively. Along the abscissa axis, the experimental time is displayed in minutes, while the T period values are displayed on the ordinate axis. The spectral density of each period is represented by red gradations.
- We calculate the arithmetic mean of the values in each row i (i = 1...50) of the wavelet matrix W(HR) and obtain the average values of the amplitudes of each period for n minutes of the experiment (vector [h], size 1 × 50). Then we normalize the vector [h] to its maximum value to facilitate comparison of their shapes. For the series of geomagnetic components X and Y of the GMF vector, we similarly compute the matrices and vectors [x] and [y]. Examples of vectors [h] and [y] are shown in Figure 2b.
- As a scalar quantity characterizing the degree of similarity/difference between the spectra of the HR and Y series, we calculate the values of Qy between a pair of vectors, [h] and [y], as the value of the scalar product of these vectors, normalized to the length of each of them, i.e., Qy = (h,y)/|h|∙|y|.
3. Results
- The Spearman correlation coefficient of the HR series against the series of each X and Y component of the GMF. Correlation cases were considered significant at p < 0.0045.
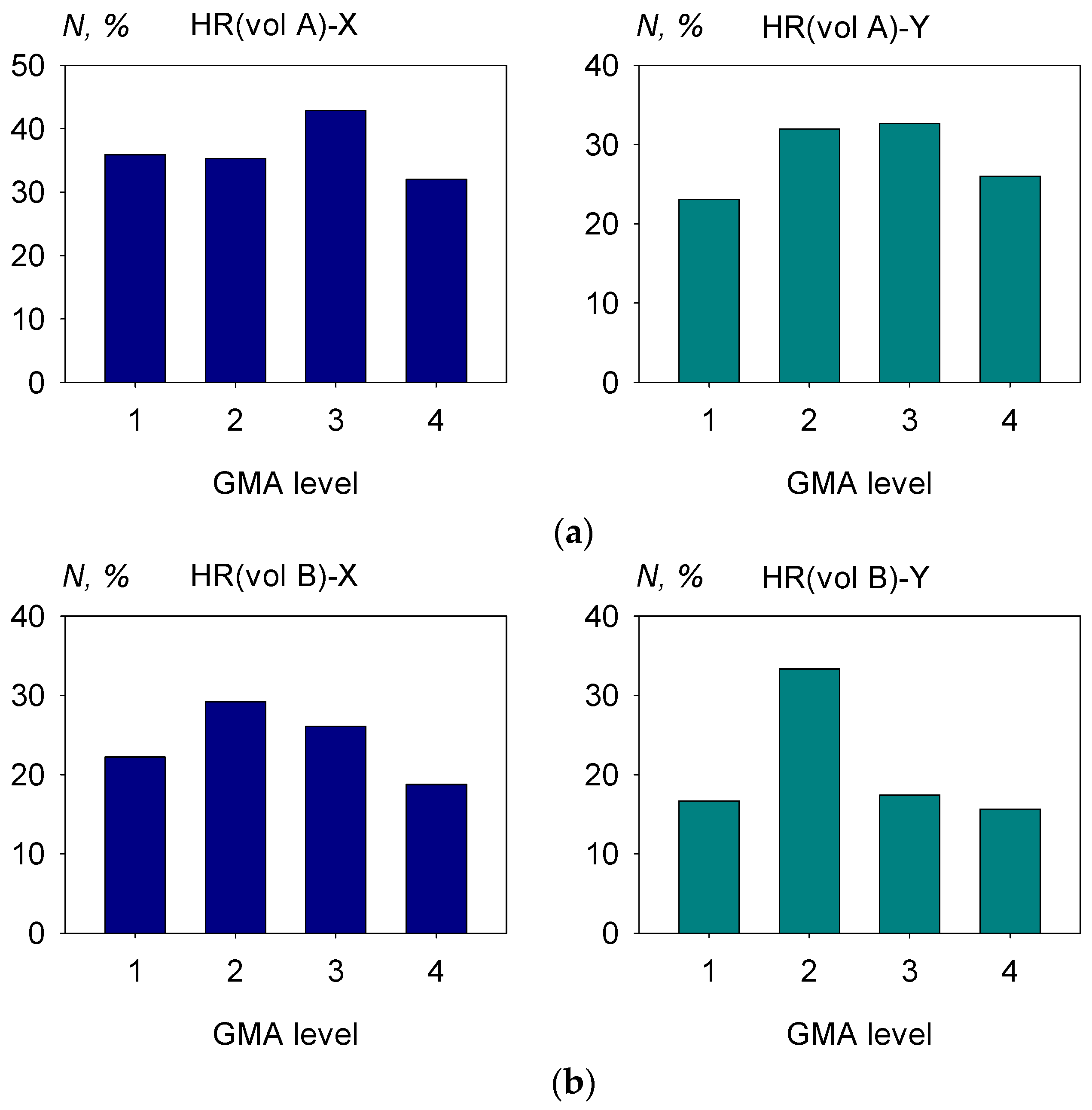
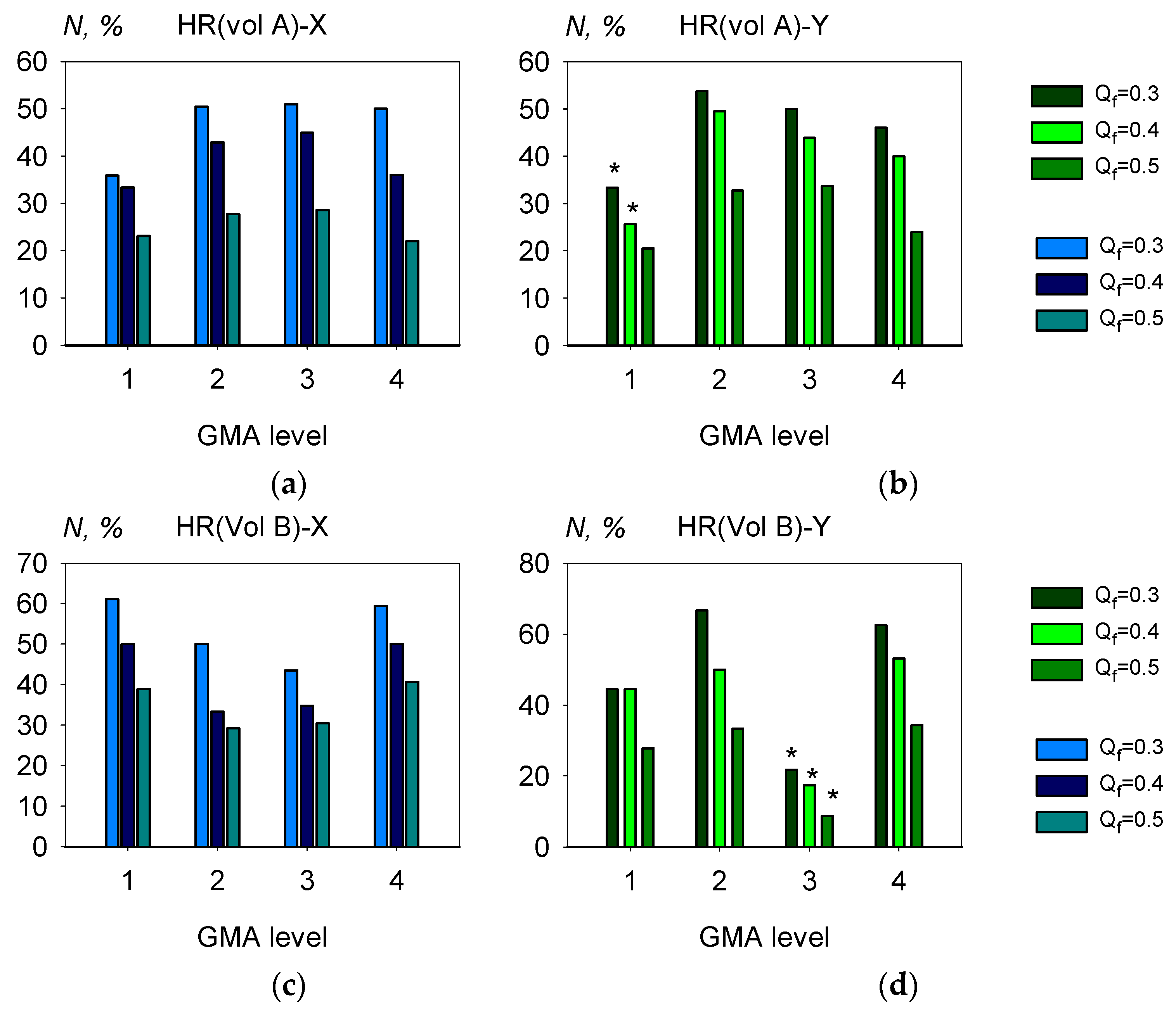
- The cosine of angles Qx and Qy between the vectors of averaged amplitudes of wavelet spectra HR [h] and the components of the GMF vectors [x] and [y] (the spectra were deemed similar when values of Qx and Qy exceeded Qf = 0.4).
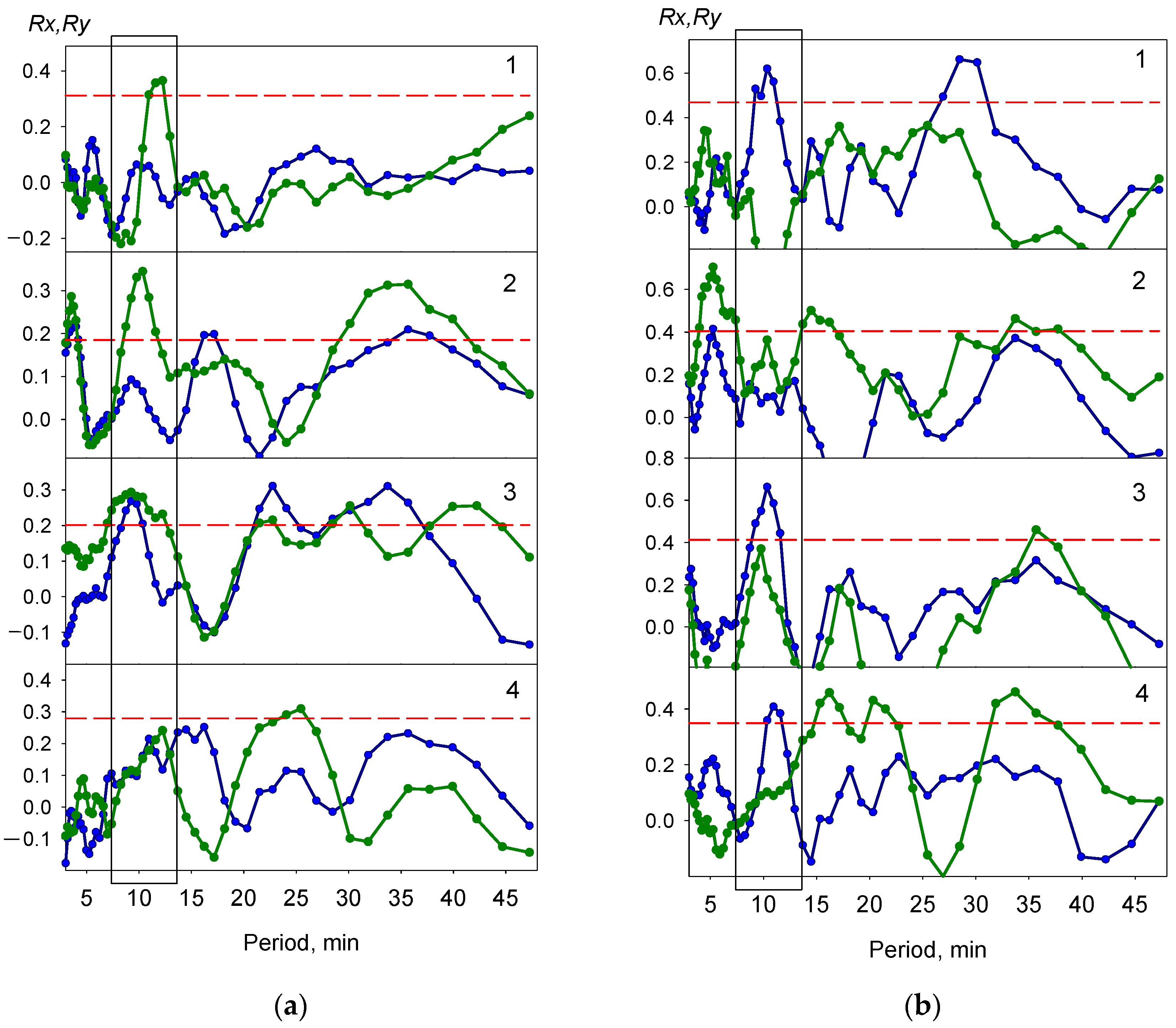
- Correlation coefficients Rx and Ry between the amplitude values of different periods ranging from 3 to 50 min (based on the full set of experiments for each of the volunteers).
3.1. Results of Cross-Correlation Analysis
3.2. The Findings of the Wavelet Spectra Similarity Analysis
3.3. Analysis of the Synchronous Occurrence of Matching Cycles in Biological and Geomagnetic Series
- (1)
- 8.3–13.0 min (maximum 10.3 min) for Volunteer A and 9.2–11.6 min (maximum 10.3 min) for Volunteer B;
- (2)
- A group of periods ranging from 25 to 40 min for Volunteer A and from 30 to 40 min for Volunteer B.There are also two groups of statistically significant periods whose boundaries are different in Figure 5a,b:
- (3)
- 15.3–18.2 min for Volunteer B; however, in Figure 5a, there is only a small peak corresponding to 20 min.
- (4)
- The oscillation period in the range of 8–13 min occurs in the HR spectra of volunteers simultaneously, with its occurrence in the spectrum of at least one of the GMF vector components. With somewhat less certainty, we can say the same about periods of 30–40 min.
- Like the case of Section 3.1 and Section 3.2, we cannot observe any difference in the extent of this effect at different GMA levels.
- The other cases of correlation, even significant ones, in some samples of the experiment should, for now, be considered noise effects that require further verification due to their unstable manifestation.
4. Discussion
4.1. Independence of the Synchronization Effect from the GMA Level
4.2. Possible Scheme of the “Rhythm Capture” Process
- Stable oscillations occur in the GMF spectrum, with a period close to 10 min (ranging from 8 to 13 min);
- These oscillations cause a “rhythm capture” of a physiological process in the human organism, which has its own oscillation period within this range and which, in turn, can influence the cardiac rhythmicity;
- Hence, the mentioned physiological process’s contribution to the establishment of cardiac rhythmicity is amplified, resulting in the manifestation of the 10 min oscillation period in the heart-rhythm spectrum.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chizhevsky, A.L. The Terrestrial Echo of Solar Storms; Mysl: Moscow, Russia, 1976; p. 366. (In Russian) [Google Scholar]
- Chijevsky, A.L. The correlation between the variation of sun-spot activity and the rise and spreading of epidemils. Rapport le 17 octobre 1930. In Proceedings of the XIII Congresso International de Hidrologia, Climatologia e Geologia Medicas, Programa des Sessoes Scientificas, 2 Sessao, Lisboa, Portugal, 1930. [Google Scholar]
- Chijevsky, A.-L. Les Epidemies et Les Perturbations Electromagnetiques Du Milieu Exterieur; Depot General Le Francois: Paris, France, 1938. [Google Scholar]
- Gnevyshev, M.N.; Novikova, K.F.; Ohl, A.I.; Tokareva, N.V. Sudden death from cardiovascular diseases and solar activity. In Influence of Solar Activity on the Atmosphere and Biosphere of the Earth; Nauka: Moscow, Russia, 1971; pp. 179–187. (In Russian) [Google Scholar]
- Villoresi, G.; Breus, T.K.; Iucci, N.; Dorman, L.I.; Rapoport, S.I. The influence of geophysical and social effects on the incidences of clinically important pathologies (Moscow, 1979–1981). Phys. Medica 1994, 10, 79–91. [Google Scholar]
- Villoresi, G.; Breus, T.K.; Dorman, L.I.; Iuchi, N. Effect of interplanetary and geomagnetic disturbances on the increase in number of clinically serious medical pathologies (myocardial infarct and stroke). Biofizika 1995, 40, 983–993. [Google Scholar]
- Baevsky, R.M.; Petrov, V.M.; Cornelissen, G.; Halberg, F.; Orth-Gomer, K.; Akerstedt, T.; Otsuka, K.; Breus, T.; Siegelova, J.; Dusek, J.; et al. Meta-analyzed heart rate variability, exposure to geomagnetic storms, and the risk of ischemic heart disease. Scr. Med. 1997, 70, 11543511. [Google Scholar]
- Villoresi, G.; Ptitsyna, N.G.; Tiasto, M.I.; Iucci, N. Myocardial infarct and geomagnetic disturbances: Analysis of data on morbidity and mortality. Biofizika 1998, 43, 623–631. [Google Scholar] [PubMed]
- Gurfinkel’, I.; Kuleshova, V.P.; Oraevskiĭ, V.N. Assessment of the effect of a geomagnetic storm on the frequency of appearance of acute cardiovascular pathology. Biofizika 1998, 43, 654–658. (In Russian) [Google Scholar] [PubMed]
- Halberg, F.; Cornelissen, G.; Otsuka, K.; Watanabe, Y.; Katinas, G.S.; Burioka, N.; Delyukov, A.; Gorgo, Y.; Zhao, Z.; Weydahl, A.; et al. Cross-spectrally coherent ~10,5- and 21-year biological and physical cycles, magnetic storms and myocardial infarctions. Neuroendocrinol. Lett. 2000, 21, 233–258. [Google Scholar] [PubMed]
- Dorman, L.I.; Iucci, N.; Ptitsyna, N.G.; Villoresi, G. Cosmic rays as indicator of space weather influence on frequency of infract myocardial, brain strokes, car and train accidents. In Proceedings of the 27th International Cosmic Ray Conference, Hamburg, Germany, 7–15 August 2001; p. 3511. [Google Scholar]
- Stoupel, E.; Domarkiene, S.; Radisauskas, R.; Abramson, E. Sudden cardiac death and geomagnetic activity: Links to age, gender and agony time. J. Basic Clin. Physiol. Pharmacol. 2002, 13, 11–22. [Google Scholar] [CrossRef]
- Cornelissen, G.; Halberg, F.; Breus, T.; Syitkina, E.; Baevsky, R.; Weydahl, A.; Watanabe, Y.; Otsuka, K.; Siegelova, J.; Fiser, B.; et al. Non-photic solar assotiations of heart rate variability and myocardial infarction. J. Atmos. Sol. Terr. Phys. 2002, 64, 707–720. [Google Scholar] [CrossRef]
- Wickramasinghe, N.C. Is the 2019 novel coronavirus related to a spike of cosmic rays? Adv. Genet. 2020, 106, 119–122. [Google Scholar] [CrossRef]
- Stoupel, E.; Kalediene, R.; Petrauskiene, J.; Starkuviene, S.; Abramson, E.; Israelevich, P.; Sulkes, J. Clinical Cosmobiology: Distribution of Deaths during 180 Months and Cosmo Physical Activity. The Lithuanian Study, 1990–2004. In The Role of Cosmic Rays. Study Report; Division of Cardiology Rabin Medical Center Tel Aviv University: Tel Aviv, Israel, 2004. [Google Scholar]
- Díaz-Sandoval, R.; Erdélyi, R.; Maheswaran, R. Could periodic patterns in human mortality be sensitive to solar activity? Ann. Geophys. 2011, 29, 1113–1120. [Google Scholar] [CrossRef]
- Feigin, V.L.; Parmar, P.G.; Barker-Collo, S.; Bennett, D.A.; Anderson, C.S.; Thrift, A.G.; Stegmayr, B.; Rothwell, P.M.; Giroud, M.; Bejot, Y.; et al. Geomagnetic Storms Can Trigger Stroke: Evidence from 6 large population-based studies in Europe and Australasia. Stroke 2014, 45, 1639–1645. [Google Scholar] [CrossRef] [PubMed]
- Ghione, S.; Mezzasalma, L.; Del Seppia, C.; Papi, F. Do geomagnetic disturbances of solar origin affect arterial blood pressure? J. Hum. Hypertens. 1998, 12, 749–754. [Google Scholar] [CrossRef] [PubMed]
- Dimitrova, S.; Stoilova, I.; Cholakov, I. Influence of local geomagnetic storms on arterial blood pressure. Bioelectromagnetics 2004, 25, 408–414. [Google Scholar] [CrossRef] [PubMed]
- Dimitrova, S.; Mustafa, F.R.; Stoilova, I.; Babayev, E.S.; Kazimov, E.A. Possible influence of solar extreme events and related geomagnetic disturbances on human cardio-vascular state: Results of collaborative Bulgarian–Azerbaijani studies. Adv. Space Res. 2009, 43, 641–648. [Google Scholar] [CrossRef]
- Azcárate, T.; Mendoza, B.; Levi, J.R. Influence of geomagnetic activity and atmospheric pressure on human arterial pressure during the solar cycle 24. Adv. Space Res. 2016, 58, 2116–2125. [Google Scholar] [CrossRef]
- Galata, E.; Ioannidou, S.; Papailiou, M.; Mavromichalaki, H.; Paravolidakis, K.; Kouremeti, M.; Trachanas, K. Impact of space weather on human heart rate during the years 2011–2013. Astrophys. Space Sci. 2017, 362, 138. [Google Scholar] [CrossRef]
- Rodriquez-Taboada, E.R.; Sierra-Figueredo, P.; Figueredo, S.S. Geomagnetic activity related to acute myocardial infarctions: Relationship in a reduced population and time interval. Geofis. Int. 2004, 43, 265–269. [Google Scholar] [CrossRef]
- Kleimenova, N.; Kozyreva, O.; Breus, T.; Rapoport, S. Pc1 geomagnetic pulsations as a potential hazard of the myocardial infarction. J. Atmos. Sol.-Terr. Phys. 2007, 69, 1759–1764. [Google Scholar] [CrossRef]
- Giannaropoulou, E.; Papailiou, M.; Mavromichalaki, H.; Gigolashvili, M.; Tvildiani, L.; Janashia, K.; Preka-Papadema, P.; Papadima, T. A study on the various types of arrhythmias in relation to the polarity reversal of the solar magnetic field. Nat. Hazards 2014, 70, 1575–1587. [Google Scholar] [CrossRef]
- Ziubryte, G.; Siauciunaite, V.; Jarusevicius, G.; McCraty, R. Local earth magnetic field and ischemic heart disease: Peculiarities of interconnection. Cardiovasc. Disord. Med. 2018, 3, 1–3. [Google Scholar] [CrossRef]
- Fdez-Arroyabe, P.; Fornieles-Callejón, J.; Santurtún, A.; Szangolies, L.; Donner, R.V. Schumann resonance and cardiovascular hospital admission in the area of Granada, Spain: An event coincidence analysis approach. Sci. Total Environ. 2020, 705, 135813. [Google Scholar] [CrossRef] [PubMed]
- Shaposhnikov, D.; Revich, B.; Gurfinkel, Y.; Naumova, E. The influence of meteorological and geomagnetic factors on acute myocardial infarction and brain stroke in Moscow, Russia. Int. J. Biometeorol. 2013, 58, 799–808. [Google Scholar] [CrossRef] [PubMed]
- Stoupel, E. Effect of geomagnetic activity on cardiovascular parameters. J. Clin. Basic Cardiol. 1999, 2, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Stoupel, E.; Babayev, E.S.; Abramson, E.; Sulkes, J. Days of “Zero” level geomagnetic activity accompanied by the high neutron activity and dynamics of some medical events—Antipodes to geomagnetic storms. Health 2013, 5, 855–861. [Google Scholar] [CrossRef]
- Stoupel, E.; Richardas, R.; Vidmantas, V.; Gailute, B.; Abdonas, T.; Evgeny, A. Data about Natural History of Some Acute Coronary Events at Days of High Cosmic Ray (CRA)-Neutron Activity and Following 48 Hours (2000–2012). Health 2016, 8, 402–408. [Google Scholar] [CrossRef][Green Version]
- Vencloviene, J.; Radisauskas, R.; Tamosiunas, A.; Luksiene, D.; Sileikiene, L.; Milinaviciene, E.; Rastenyte, D. Possible Associations between Space Weather and the Incidence of Stroke. Atmosphere 2021, 12, 334. [Google Scholar] [CrossRef]
- Borovsky, J.E.; Denton, M.H. Differences between CME-driven storms and CIR-driven storms. J. Geophys. Res. Space Phys. 2006, 111, A07S08. [Google Scholar] [CrossRef]
- Breus, T.K.; Baevskii, R.M.; Nikulina, G.A.; Chibisov, S.M.; Chernikova, A.G.; Pukhlianko, M.; Oraevskii, V.N.; Halberg, F.; Cornelissen, G.; Petrov, V.M. Effect of geomagnetic activity on the human body in extreme conditions and correlation with data from laboratory observations. Biofizika 1998, 43, 811–818. (In Russian) [Google Scholar]
- Dimitrova, S.; Stoilova, I.; Georgieva, K.; Taseva, T.; Jordanova, M.; Maslarov, D. Solar and geomagnetic activity and acute myocardial infarction morbidity and mortality. Fundam. Space Res. Supl. Compt. Rend. Acad. Bulg. Sci. 2009, 161–165. [Google Scholar]
- Shepoval’nikov, V.N.; Soroko, S.I. Human Meteo Sensitivity; Ilim: Bishkek, Kyrgyzstan, 1992; p. 247. (In Russian) [Google Scholar]
- Chernouss, S.; Vinogradov, A.; Vlassova, E. Geophysical Hazard for Human Health in the Circumpolar Auroral Belt: Evidence of a Relationship between Heart Rate Variation and Electromagnetic Disturbances. Nat. Hazards 2001, 23, 121–135. [Google Scholar] [CrossRef]
- Watanabe, Y.; Cornélissen, G.; Halberg, F.; Otsuka, K.; Ohkawa, S.I. Associations by signatures and coherences between the human circulation and helio- and geomagnetic activity. Biomed. Pharmacother. 2000, 55, 76–83. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, K.; Yamanaka, T.; Cornelissen, G.; Breus, T.; Chibisov, S.M.; Baevsky, R.; Siegelova, J.; Fiser, B.; Halberg, F. Altered chronome of heart rate variability during span of high magnetic activity. Scr. Med. 2000, 2, 113–118. [Google Scholar]
- Poskotinova, L.V.; Grigoriev, P.E. The Dependence of Typological Autonomic Features Reactions of Healthy Persons on Background Helio-Meteofactors. Hum. Ecol. 2008, 5, 3–8. (In Russian) [Google Scholar]
- Zenchenko, T.A.; Dimitrova, S.; Stoilova, I.; Breus, T.K. Individual types of blood pressure reactions of practically healthy people to the effect of geomagnetic activity. Clin. Med. 2009, 4, 18–23. (In Russian) [Google Scholar]
- Wanliss, J.; Cornélissen, G.; Halberg, F.; Brown, D.; Washington, B. Superposed epoch analysis of physiological fluctuations: Possible space weather connections. Int. J. Biometeorol. 2017, 62, 449–457. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, K.; Cornélissen, G.; Weydahl, A.; Holmeslet, B.; Hansen, T.; Shinagawa, M.; Kubo, Y.; Nishimura, Y.; Omori, K.; Yano, S.; et al. Geomagnetic disturbance associated with decrease in heart rate variability in a subarctic area. Biomed. Pharmacother. 2000, 55, 51–56. [Google Scholar] [CrossRef]
- Oinuma, S.; Kubo, Y.; Otsuka, K.; Yamanaka, T.; Murakami, S.; Matsuoka, O.; Ohkawa, S.; Cornélissen, G.; Weydahl, A.; Holmeslet, B.; et al. Graded response of heart rate variability, associated with an alteration of geomagnetic activity in a subarctic area. Biomed. Pharmacother. 2002, 56, 284–288. [Google Scholar] [CrossRef] [PubMed]
- Mitsutake, G.; Otsuka, K.; Hayakawa, M.; Sekiguchi, M.; Cornelissen, G.; Halberg, F. Does Schumann resonance affect our blood pressure? Biomed. Pharmacother. 2005, 59, S10–S14. [Google Scholar] [CrossRef]
- Papailiou, M.; Kudela, K.; Stetiarova, J.; Giannaropoulou, E.; Mavromichalaki, H.; Dimitrova, S. The effect of cosmic ray intensity variations and geomagnetic disturbances on the physiological state of aviators. Astrophys. Space Sci. Trans. 2011, 7, 373–377. [Google Scholar] [CrossRef]
- Breus, T.; Baevskii, R.; Chernikova, A. Effects of geomagnetic disturbances on humans functional state in space flight. J. Biomed. Sci. Eng. 2012, 5, 341–355. [Google Scholar] [CrossRef]
- Mavromichalaki, H.; Papailiou, M.; Dimitrova, S.; Babayev, E.S.; Loucas, P. Space weather hazards and their impact on human cardio-health state parameters on Earth. Nat. Hazards 2012, 64, 1447–1459. [Google Scholar] [CrossRef]
- Azcárate, T.; Mendoza, B.; De La Peña, S.S.; Martínez, J. Temporal variation of the arterial pressure in healthy young people and its relation to geomagnetic activity in Mexico. Adv. Space Res. 2012, 50, 1310–1315. [Google Scholar] [CrossRef]
- Dimitrova, S.; Angelov, I.; Petrova, E. Solar and geomagnetic activity effects on heart rate variability. Nat. Hazards 2013, 69, 25–37. [Google Scholar] [CrossRef]
- Ozheredov, V.A.; Chibisov, S.M.; Blagonravov, M.L.; Khodorovich, N.A.; Demurov, E.A.; Goryachev, V.A.; Kharlitskaya, E.V.; Eremina, I.S.; Meladze, Z.A. Influence of geomagnetic activity and earth weather changes on heart rate and blood pressure in young and healthy population. Int. J. Biometeorol. 2017, 61, 921–929. [Google Scholar] [CrossRef]
- Vaičiulis, V.; Radišauskas, R.; Ustinavičienė, R.; Kalinienė, G.; Tamošiūnas, A. Associations of morbidity and mortality from coronary heart disease with heliogeophysical factors. Environ. Sci. Pollut. Res. 2016, 23, 18630–18638. [Google Scholar] [CrossRef]
- Vencloviene, J.; Antanaitiene, J.; Babarskiene, R. The association between space weather conditions and emergency hospital admissions for myocardial infarction during different stages of Solar activity. J. Atmos. Sol. Terr. Phys. 2016, 149, 52–58. [Google Scholar] [CrossRef]
- Caswell, J.M.; Carniello, T.N.; Murugan, N.J. Annual incidence of mortality related to hypertensive disease in Canada and associations with heliophysical parameters. Int. J. Biometeorol. 2016, 60, 9–20. [Google Scholar] [CrossRef]
- Vencloviene, J.; Babarskiene, R.M.; Kiznys, D. A possible association between space weather conditions and the risk of acute coronary syndrome in patients with diabetes and the metabolic syndrome. Int. J. Biometeorol. 2017, 61, 159–167. [Google Scholar] [CrossRef]
- Mavromichalaki, H.; Preka-Papadema, P.; Theodoropoulou, A.; Paouris, E.; Apostolou, T. A study of the possible relation of the cardiac arrhythmias occurrence to the polarity reversal of the solar magnetic field. Adv. Space Res. 2017, 59, 366–378. [Google Scholar] [CrossRef]
- Gurfinkel, Y.I.; Vasin, A.L.; Pishchalnikov, R.Y.; Sarimov, R.M.; Sasonko, M.L.; Matveeva, T.A. Geomagnetic storm under laboratory conditions: Randomized experiment. Int. J. Biometeorol. 2018, 62, 501–512. [Google Scholar] [CrossRef]
- Gurfinkel, Y.I.; Ozheredov, V.A.; Breus, T.K.; Sasonko, M.L. The Effects of Space and Terrestrial Weather Factors on Arterial Stiffness and Endothelial Function in Humans. Biophysics 2018, 63, 299–306. [Google Scholar] [CrossRef]
- Podolská, K. The impact of ionospheric and geomagnetic changes on mortality from diseases of the circulatory system. J. Stroke Cerebrovasc. Dis. 2018, 27, 404–417. [Google Scholar] [CrossRef]
- Vencloviene, J.; Braziene, A.; Dobozinskas, P. Short-Term Changes in Weather and Space Weather Conditions and Emergency Ambulance Calls for Elevated Arterial Blood Pressure. Atmosphere 2018, 9, 114. [Google Scholar] [CrossRef]
- Vieira, C.L.Z.; Janot-Pacheco, E.; Lage, C.; Pacini, A.; Koutrakis, P.; Cury, P.R.; Shaodan, H.; Pereira, L.A.; Saldiva, P.H.N. Long-term association between the intensity of cosmic rays and mortality rates in the city of Sao Paulo. Environ. Res. Lett. 2018, 13, 24009. [Google Scholar] [CrossRef]
- Pishchalnikov, R.Y.; Gurfinkel, Y.I.; Sarimov, R.M.; Vasin, A.L.; Sasonko, M.L.; Matveeva, T.A.; Binhi, V.N.; Baranov, M.V. Cardiovascular response as a marker of environmental stress caused by variations in geomagnetic field and local weather. Biomed. Signal Process. Control 2019, 51, 401–410. [Google Scholar] [CrossRef]
- Vieira, C.L.Z.; Alvares, D.; Blomberg, A.; Schwartz, J.; Coull, B.; Huang, S.; Koutrakis, P. Geomagnetic disturbances driven by solar activity enhance total and cardiovascular mortality risk in 263 U.S. cities. Environ. Health 2019, 18, 1–10. [Google Scholar] [CrossRef]
- Sasonko, M.L.; Ozheredov, V.A.; Breus, T.K.; Ishkov, V.N.; Klochikhina, O.A.; Gurfinkel, Y.I. Combined influence of the local atmosphere conditions and space weather on three parameters of 24-h electrocardiogram monitoring. Int. J. Biometeorol. 2019, 63, 93–105. [Google Scholar] [CrossRef]
- Kiznys, D.; Vencloviene, J.; Milvidaitė, I. The associations of geomagnetic storms, fast solar wind, and stream interaction regions with cardiovascular characteristic in patients with acute coronary syndrome. Life Sci. Space Res. 2020, 25, 1–8. [Google Scholar] [CrossRef]
- Vencloviene, J.; Radisauskas, R.; Vaiciulis, V.; Kiznys, D.; Bernotiene, G.; Kranciukaite-Butylkiniene, D.; Tamosiunas, A. Associations between Quasi-biennial Oscillation phase, solar wind, geomagnetic activity, and the incidence of acute myocardial infarction. Int. J. Biometeorol. 2020, 64, 1207–1220. [Google Scholar] [CrossRef]
- Vaičiulis, V.; Venclovienė, J.; Tamošiūnas, A.; Kiznys, D.; Lukšienė, D.; Krančiukaitė-Butylkinienė, D.; Radišauskas, R. Associations between Space Weather Events and the Incidence of Acute Myocardial Infarction and Deaths from Ischemic Heart Disease. Atmosphere 2021, 12, 306. [Google Scholar] [CrossRef]
- Mavromichalaki, H.; Papailiou, M.-C.; Gerontidou, M.; Dimitrova, S.; Kudela, K. Human Physiological Parameters Related to Solar and Geomagnetic Disturbances: Data from Different Geographic Regions. Atmosphere 2021, 12, 1613. [Google Scholar] [CrossRef]
- Podolská, K. Circulatory and Nervous Diseases Mortality Patterns—Comparison of Geomagnetic Storms and Quiet Periods. Atmosphere 2022, 13, 13. [Google Scholar] [CrossRef]
- Papailiou, M.; Ioannidou, S.; Tezari, A.; Lingri, D.; Konstantaki, M.; Mavromichalaki, H.; Dimitrova, S. Space weather phenomena on heart rate: A study in the Greek region. Int. J. Biometeorol. 2023, 67, 37–45. [Google Scholar] [CrossRef] [PubMed]
- Qammar, N.W.; Petronaitis, D.; Jokimaitis, A.; Ragulskis, M.; Smalinskas, V.; Žiubrytė, G.; Jaruševičius, G.; Vainoras, A.; McCraty, R. Long Observation Window Reveals the Relationship between the Local Earth Magnetic Field and Acute Myocardial Infarction. Atmosphere 2023, 14, 1234. [Google Scholar] [CrossRef]
- Pobachenko, S.V.; Kolesnik, A.G.; Borodin, A.S.; Kalyuzhin, V.V. The contingency of parameters of human encephalograms and Schumann resonance electromagnetic fields revealed in monitoring studies. Biophysics 2006, 51, 480–483. [Google Scholar] [CrossRef]
- Zenchenko, T.A.; Medvedeva, A.A.; Khorseva, N.I.; Breus, T.K. Synchronization of human heart-rate indicators and geomagnetic field variations in the frequency range of 0.5–3.0 mHz. Izv. Atmos. Ocean. Phys. 2014, 50, 736–744. [Google Scholar] [CrossRef]
- Timofejeva, I.; McCraty, R.; Atkinson, M.; Joffe, R.; Vainoras, A.; Alabdulgader, A.; Ragulskis, M. Identification of a Group’s Physiological Synchronization with Earth’s Magnetic Field. Int. J. Environ. Res. Public Health 2017, 14, 998. [Google Scholar] [CrossRef]
- Timofejeva, I.; McCraty, R.; Atkinson, M.; Alabdulgader, A.A.; Vainoras, A.; Landauskas, M.; Šiaučiūnaitė, V.; Ragulskis, M. Global Study of Human Heart Rhythm Synchronization with the Earth’s Time Varying Magnetic Field. Appl. Sci. 2021, 11, 2935. [Google Scholar] [CrossRef]
- Alabdulgader, A.; McCraty, R.; Atkinson, M.; Dobyns, Y.; Vainoras, A.; Ragulskis, M.; Stolc, V. Long-Term Study of Heart Rate Variability Responses to Changes in the Solar and Geomagnetic Environment. Sci. Rep. 2018, 8, 2663. [Google Scholar] [CrossRef]
- Poskotinova, L.; Krivonogova, E.; Demin, D.; Zenchenko, T. Differences in the Sensitivity of the Baroreflex of Heart Rate Regulation to Local Geomagnetic Field Variations in Normotensive and Hypertensive Humans. Life 2022, 12, 1102. [Google Scholar] [CrossRef]
- Presman, A.S. Electromagnetic Field and Wildlife; Nauka: Moscow, Russia, 1968; 310p. [Google Scholar]
- Zenchenko, T.A.; Jordanova, M.; Poskotinova, L.V.; Medvedeva, A.A.; Alenikova, A.E.; Khorseva, N.I. Synchronization between human heart rate dynamics and Pc5 geomagnetic pulsations at different latitudes. Biophysics 2014, 59, 965–972. [Google Scholar] [CrossRef]
- Zenchenko, T.A.; Medvedeva, A.A.; Potolitsyna, N.N.; Parshukova, O.I.; Boiko, E.R. Correlation of the dynamics of minute-scale heart rate oscillations and biochemical parameters of the blood in healthy subjects to Pc5–6 geomagnetic pulsations. Biophysics 2015, 60, 309–316. [Google Scholar] [CrossRef]
- Zeng, W.; Liang, X.; Wan, C.; Wang, Y.; Jiang, Z.; Cheng, Z.; Cornélissen, G.; Halberg, F.; Wang, Z. Patterns of mortality from cardiac-cerebral vascular disease and influences from the cosmos. Biol. Rhythm. Res. 2014, 45, 579–589. [Google Scholar] [CrossRef]
- Zenchenko, T.A.; Breus, T.K. The Possible Effect of Space Weather Factors on Various Physiological Systems of the Human Organism. Atmosphere 2021, 12, 346. [Google Scholar] [CrossRef]
- Alabdulgade, A.; Maccraty, R.; Atkinson, M.; Vainoras, A.; Berškienė, K.; Mauricienė, V.; Navickas, Z.; Šmidtaitė, R.; Landauskas, M.; Daunoravičienė, A. Human heart rhythm sensitivity to earth local magnetic field fluctuations. J. Vibroeng. 2015, 17, 3271–3278. [Google Scholar]
- McCraty, R.; Atkinson, M.; Stolc, V.; Alabdulgader, A.A.; Vainoras, A.; Ragulskis, M. Synchronization of Human Autonomic Nervous System Rhythms with Geomagnetic Activity in Human Subjects. Int. J. Environ. Res. Public Health 2017, 14, 770. [Google Scholar] [CrossRef]
- Smolentsev, N.K. Fundamentals of wavelet theory. In Wavelets in MATLAB; DMK Press: Moscow, Russia, 2009; p. 448. [Google Scholar]
- Gmitrov, J. Baroreceptor stimulation enhanced nitric oxide vasodilator responsiveness, a new aspect of baroreflex physiology. Microvasc. Res. 2015, 98, 139–144. [Google Scholar] [CrossRef]
- Anagnostopoulos, G.; Basta, M.; Stefanakis, Z.; Vassiliadis, V.; Vgontzas, A.; Rigas, A.; Koutsomitros, S.; Baloyannis, S.; Papadopoulos, G. A study of correlation between seismicity and mental health: Crete, 2008–2010. Geomat. Nat. Hazards Risk 2013, 6, 45–75. [Google Scholar] [CrossRef]


| N | HR Med | HR, 1 Quart | HR 3 Quart | HR Min | HR Max | |
|---|---|---|---|---|---|---|
| Vol A | 306 | 69.3 | 65.2 | 73.0 | 54.0 | 84.6 |
| Vol B | 97 | 61.6 | 60.3 | 63.4 | 55.7 | 65.8 |
| N | Corr X, n | Corr X, % | Corr Y, n | Corr Y, % | Corr X or Y, n | Corr X&Y, % | |
|---|---|---|---|---|---|---|---|
| Vol A | 306 | 114 | 37 | 92 | 30 | 163 | 53 |
| Vol B | 97 | 23 | 24 | 20 | 21 | 39 | 40 |
| GMA Lev. 1 | GMA Lev. 2 | GMA Lev. 3 | GMA Lev. 4 | |
|---|---|---|---|---|
| Kp limits | 0–8 | 8.3–16 | 16.3–23.7 | 24–48.7 |
| Vol. A, number of cases | 39 | 119 | 98 | 50 |
| Vol. B, number of cases | 18 | 24 | 23 | 32 |
| N | Qx > 0.4, n | Qx > 0.4, % | Qy > 0.4, n | Qy > 0.4, % | Qx or Qy >0.4, n | Qx or Qy > 0.4, % | |
|---|---|---|---|---|---|---|---|
| Vol A | 306 | 126 | 41 | 132 | 43 | 178 | 58 |
| Vol B | 97 | 41 | 42 | 41 | 42 | 59 | 61 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zenchenko, T.A.; Khorseva, N.I.; Breus, T.K. Long-Term Study of the Synchronization Effect between Geomagnetic Field Variations and Minute-Scale Heart-Rate Oscillations in Healthy People. Atmosphere 2024, 15, 134. https://doi.org/10.3390/atmos15010134
Zenchenko TA, Khorseva NI, Breus TK. Long-Term Study of the Synchronization Effect between Geomagnetic Field Variations and Minute-Scale Heart-Rate Oscillations in Healthy People. Atmosphere. 2024; 15(1):134. https://doi.org/10.3390/atmos15010134
Chicago/Turabian StyleZenchenko, Tatiana A., Natalia I. Khorseva, and Tamara K. Breus. 2024. "Long-Term Study of the Synchronization Effect between Geomagnetic Field Variations and Minute-Scale Heart-Rate Oscillations in Healthy People" Atmosphere 15, no. 1: 134. https://doi.org/10.3390/atmos15010134
APA StyleZenchenko, T. A., Khorseva, N. I., & Breus, T. K. (2024). Long-Term Study of the Synchronization Effect between Geomagnetic Field Variations and Minute-Scale Heart-Rate Oscillations in Healthy People. Atmosphere, 15(1), 134. https://doi.org/10.3390/atmos15010134









